1 Introduction

Multibody systems are often most efficient when simulating rigid or flexible systems undergoing large rigid body motions. Collisions of bodies might interrupt the motion of the system requiring impact handling. Thereby, the timescale of impacts is much shorter (fractions of milliseconds) than the timescale of the rigid body motion before and after impact (seconds).

In general, the flexible bodies may also undergo geometric nonlinear deformations during contact, requiring the use of, e.g., finite rotations (see [1]). This is a challenging topic in research, e.g., beam-to-beam contact [2] or modeling of beams [3]. In [1], nonlinear finite elements, the absolute nodal coordinate formulation, or the floating frame of reference formulation are listed to solve such systems. Since elastic deformations of bodies typically remain small if they consist of stiff material such as steel or aluminum, this work favors the floating frame of reference formulation [4]. The large rigid body motion is represented by the motion of the floating frame, while the elastic deformation is described within this floating frame. This allows the use of linear elastic modes and linear model reduction. The floating frame of reference formulation requires global shape functions \(\mathbf {\Phi }\) which describe body flexibility. One possibility to obtain the global shape functions is from a finite element model and a subsequent model reduction. The straightforward approach involves isoparametric elements and thus the discretization of the geometry. However, a detailed impact simulation depends on an accurate representation of the geometry in the contact area. This disadvantage does not hold for the isogeometric analysis (IGA) [5]. The geometry is exactly preserved with the IGA. This is because a meshed IGA model is based on its initial geometry definition [5]. Another advantage of the IGA is that high modes are represented more accurately than with an isoparametric model [5]. This is essential for the computation of the global shape functions. The simplest way to determine a set of global shape functions is modal truncation. However, modal truncation does not capture precise local deformations in the contact area. Therefore, a modally truncated model is not appropriate for an accurate flexible multibody impact simulation and leads to inaccurate results, as shown in [6]. Alternatively, the Craig-Bampton method [7] can be used, wherein, in addition to normal modes, constraint modes are used. Thus, the model includes low- and high- frequency modes. The low frequency normal modes approximate the overall elasto dynamic behavior, and the high-frequency constraint modes give an accurate approximation of local deformations in the contact area. However, a system of equations consisting of low- and high-frequency modes is numerically stiff. Solving these equations requires small time step sizes in the numerical time integration. As an example, suppose an impact of two flexible bodies whose modes are not yet excited. The impact then excites the numerical stiff frequency band and small step sizes are required. This is computationally expensive if subsequent large rigid body motions and impacts are simulated. One solution is modally damping the high frequency modes. It increases the computational performance but computation times remain high [6, 8].

Alternatively, a quasistatic contact model can be used. It was previously used in impact simulations with isoparametric elements [9] but can also be applied to the IGA [10]. The idea of a quasistatic contact model is to neglect the dynamics of the high-frequency modes. Thereby, the numerical efficiency is increased, and the numerical stiffness is reduced. By that, it is shown in [6] that the high frequency modes only have a small influence on the dynamics. In the context of this work, this concept is applied to IGA contact models. As in [6], the quasistatic contact model is paired with a penalty method to compute the contact forces. Besides the penalty method also the Lagrange multiplier method exists [11]. It was also already used in the IGA [12,13,14]. However, to continue the previous work [6] on the quasistatic contact model, the penalty method is used.

Setting up impact simulations and solving them requires manual setup and experience by the user. In the following, three main challenges are listed below:

First, when using the penalty method, a suited penalty factor is required. It represents virtual springs between two bodies in contact preventing penetration. In [15], the penalty factor is determined optimally for the static case. However, for transient impact simulations, the penalty factor needs to be determined heuristically [16]. If the penalty factor is too small, too much penetration of the bodies occurs, and thus the deformation in the contact zone and the contact force are not resolved accurately. A too high penalty factor yields numerical instabilities.

Second, the contact model and its refinement in the contact area are usually determined heuristically. In the contact area, there must be a sufficiently high element resolution to represent the contact accurately. The refinement requires the location and the element resolution of the contact area. The effort to determine the contact location increases if large rigid body translations and especially rotations occur before the impact. The straightforward approach to refine IGA models is global refinement [5]. However, with global refinement, elements are inserted over the whole body, and the number of degrees of freedom is significantly but unnecessarily increased. Instead, hierarchical refinement [17] is used in this work to purposively refine the flexible body in the contact area. It results in a model with fewer degrees of freedom and increased computational performance [8, 12, 17].

Third, the time of the impact is relevant if large rigid body motions occur. Impact phases are highly dynamic and require significantly smaller step sizes compared to non-impact phases without acting contact forces. Therefore, the choice of the integrator and its step size have a great effect on the numerical performance.

The goal of this work is to present an adaptive algorithm that overcomes these challenges. The time of the impact, the location of the impact on the body, the appropriate element resolution in the contact area, and the penalty factor are automatically determined. As a result, multiple impacts in flexible multibody systems including large rigid body motions can be efficiently, accurately, and automatically simulated with the presented adaptive algorithm. The work is implemented in Matlab. Computationally expensive functions are compiled as C code and parallelized if possible.

This work is organized in the following way: The concepts of the floating frame of reference formulation, the IGA and the determination of the global shape functions are introduced in Sect. 2. The quasistatic contact model is detailed in Sect. 3. The adaptive algorithm for an adaptive impact simulation is described in Sect. 4. Sections 5 and 6 provide detailed discussions of two application examples. Finally, the results are summarized in Sect. 7.

2 IGA in the floating frame of reference formulation

A well-established approach when modeling flexible multibody systems is the floating frame of reference formulation [4]. A key issue in using the floating frame of reference formulation is determining the global shape functions \(\mathbf {\Phi }\). The straightforward approach to determine the global shape functions is to generate a finite element model of the flexible body and apply a model reduction technique [18]. This section briefly presents the idea of the floating frame of reference formulation, the IGA, hierarchical refinement, and the Craig-Bampton method to obtain the global shape functions \(\mathbf {\Phi }\) via model reduction. A more detailed introduction to the IGA can be found in [5].

2.1 Floating frame of reference formulation

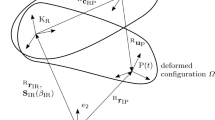
The floating frame of reference formulation describes large nonlinear rigid body motions of the body reference frame \(\textrm{K}_\textrm{R}\) within the inertial frame \(\textrm{K}_\textrm{I}\). This work uses Buckens-frames [4] as floating frames for bodies in contact and tangent-frames [4] for the remaining flexible bodies. Within these body frames \(\textrm{K}_\textrm{R}\), the elastic deformations are described. This is possible provided that the elastic deformations remain small and linear elastic. For the sake of efficiency, the elastic deformations are often approximated by \(n_\textrm{q}\) global shape functions \(\mathbf {\Phi }=\begin{bmatrix}\mathbf {\Phi }_1&...&\mathbf {\Phi }_{\textrm{n}_\textrm{q}}\end{bmatrix}\) and their corresponding elastic coordinates \({\textbf{q}}_\textrm{e}\). The equations of motion for a free flexible body are given by

$$\begin{aligned} \underbrace{\begin{bmatrix}m {\textbf{E}} &{} m\tilde{{\textbf{c}}}^\intercal &{} {\textbf{C}}_\textrm{t}^\intercal \\ m\tilde{{\textbf{c}}} &{} {\textbf{I}} &{} {\textbf{C}}_\textrm{r}^\intercal \\ {\textbf{C}}_\textrm{t} &{} {\textbf{C}}_\textrm{r} &{} \overline{{\textbf{M}}}_\textrm{e}\end{bmatrix}}_{{\textbf{M}}} \underbrace{\begin{bmatrix}{}^{\textrm{R}}\dot{{\textbf{v}}}_{\textrm{IR}} \\ {}^{\textrm{R}}\dot{\mathbf {\omega }}_{\textrm{IR}} \\ \ddot{{\textbf{q}}}_\textrm{e}\end{bmatrix}}_{\dot{{\textbf{z}}}_\textrm{II}}=\underbrace{\begin{bmatrix}{\textbf{h}}_ \textrm{dt}\\ {\textbf{h}}_\textrm{dr}\\ {\textbf{h}}_\textrm{de}\end{bmatrix}}_{{\textbf{h}}_\textrm{d}} +\underbrace{\begin{bmatrix}{\textbf{h}}_\textrm{bt}\\ {\textbf{h}}_\textrm{br}\\ {\textbf{h}}_\textrm{be}\end{bmatrix}}_{{\textbf{h}}_\textrm{b}} - \underbrace{\begin{bmatrix}{\textbf{h}}_\mathrm {\omega t}\\ {\textbf{h}}_\mathrm {\omega r}\\ {\textbf{h}}_\mathrm {\omega e}\end{bmatrix}}_{{\textbf{h}}_\mathrm {\omega }} - \underbrace{\begin{bmatrix}{\textbf{0}}\\ {\textbf{0}}\\ \overline{{\textbf{K}}}_\textrm{e}{\textbf{q}}_\textrm{e} +\overline{{\textbf{D}}}_\textrm{e}\dot{{\textbf{q}}}_\textrm{e}\end{bmatrix}}_{{\textbf{h}}_\textrm{e}}, \end{aligned}$$
(1)

where \({\textbf{E}}\) is the identity matrix, \({}^\textrm{R}{\textbf{v}}_\textrm{IR}\) is the absolute velocity of the reference frame, and \({}^\textrm{R}\mathbf {\omega }_\textrm{IR}\) is the absolute angular velocity (see [4]). The indices R and I represent the reference frame \(K_\textrm{R}\) and the inertial frame \(K_\textrm{I}\). The index at the top left indicates the coordinate frame in which the variable is defined. As an example, the velocity \({}^\textrm{R}{\textbf{v}}_\textrm{IR}\) is defined in the reference frame \(K_\textrm{R}\). In Eq. (1), the mass of the body is denoted by m, the center of mass relative to \(K_\textrm{R}\) by \({\textbf{c}}\), the translational and rotational coupling matrices by \({\textbf{C}}_\textrm{t}\) and \({\textbf{C}}_\textrm{r}\), the mass moment of inertia by \({\textbf{I}}\), and the mass, stiffness, and damping matrix of the flexible body by \(\overline{{\textbf{M}}}_\textrm{e}\), \(\overline{{\textbf{K}}}_\textrm{e}\), and \(\overline{{\textbf{D}}}_\textrm{e}\). The right-hand side of Eq. (1) is composed of the vector of discrete forces \({\textbf{h}}_\textrm{d}\), the body forces \({\textbf{h}}_\textrm{b}\), the generalized inertial forces \({\textbf{h}}_\mathrm {\omega }\), and the internal forces \({\textbf{h}}_\textrm{e}\). Occurring contact forces are part of the discrete forces \({\textbf{h}}_\textrm{d}\). If a Buckens-frame is used, the centroid \({\textbf{c}}\) becomes zero, and the translational coupling matrix \({\textbf{C}}_\textrm{t}\) vanishes [4]. The standard input data (SID) [4] provides the necessary information to evaluate the equations of motion of a free, flexible body.

2.2 Basics of the IGA

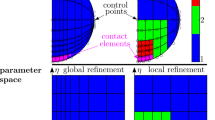
The IGA consists of three spaces: the physical space, the parameter space, and the index space. For simplicity, only the parameter space and the physical space are visualized in Fig. 1.

Fig. 1
figure 1

Example of an axisymmetric sphere that should be refined in the contact area

Full size image

A 2D model is shown to simplify the illustration. However, the following section also includes the third dimension. The parameter space consists of the local coordinates \(\xi \), \(\eta \), and \(\zeta \). The knot vectors \(\mathbf {\Xi }=\begin{bmatrix}\xi _1&\xi _2&...&\xi _\mathrm {n+p+1}\end{bmatrix}\), \(\varvec{\mathcal {H}}=\begin{bmatrix}\eta _1&\eta _2&...&\eta _\mathrm {m+q+1}\end{bmatrix}\), and \(\varvec{\mathcal {Z}}=\begin{bmatrix}\zeta _1&\zeta _2&...&\zeta _\mathrm {\ell +q+1}\end{bmatrix}\) span up the parameter space and its elements. Additionally, the n, m, and \(\ell \) local shape functions \(N_{i,\textrm{p}}\), \(M_{j,\textrm{q}}\), and \(L_{k,\textrm{r}}\) of order p, q, and r are defined in the parameter space in the respective local coordinate direction. The local shape functions are based on B-splines.

As visualized in Fig. 1, the physical space contains a set of \(n_\textrm{cp} = n * m * \ell \) control points \({\textbf{P}}_{i,j,k}\), which are arranged by the so-called control net indicated by the indices i, j, and k. The task of the control points is to span the splines to map the geometry in the physical space. In addition to the physical position, a weight \(w_{i,j,k}\) is assigned to each control point. To transform a point from the parameter space into the physical space, the non-uniform rational basis splines (NURBS) basis \(R_{i,j,k}^{\textrm{p,q,r}}(\xi ,\eta ,\zeta )\) are determined (see [5]). Using the NURBS basis \(R_{i,j,k}^{\textrm{p,q,r}}(\xi ,\eta ,\zeta )\), the NURBS solid \({\textbf{S}}\) is computed representing a point in the physical space (see [5]). The displacement field \({\textbf{d}}\) of the elastic solid can be written in matrix–vector notation as

$$\begin{aligned} {\textbf{d}} = {\textbf{N}} {\textbf{u}} = \begin{bmatrix}R_{1,1,1}^{\textrm{p,q,r}} &{} 0 &{} 0 &{} \cdots &{} 0 \\ 0 &{} R_{1,1,1}^{\textrm{p,q,r}} &{} 0 &{} \cdots &{} 0 \\ 0 &{} 0 &{} R_{1,1,1}^{\textrm{p,q,r}} &{} \cdots &{} R_\mathrm {p+1,q+1,r+1}^{\textrm{p,q,r}}\end{bmatrix}\begin{bmatrix}u_\textrm{1,1,1}^\textrm{x} \\ u_\textrm{1,1,1}^\textrm{y} \\ u_\textrm{1,1,1}^\textrm{z} \\ \vdots \\ u_\mathrm {p+1,q+1,r+1}^\textrm{z}\end{bmatrix}, \end{aligned}$$
(2)

where the NURBS of the corresponding element are summarized in the matrix \({\textbf{N}}\) and the displacements of the control points in \({\textbf{u}}\).

2.3 Refinement in the IGA

Refinement is essential for an accurate simulation. On the one hand, the entire body must be refined to represent the overall elastic deformation. On the other hand, a high element resolution in the contact area is required to accurately capture the local deformation caused by impacts.

To refine the whole body, the so-called global refinement is used in the IGA [5]. This includes order elevation and knot insertion. Order elevation increases the order of the B-splines, e.g.,  p, q or r. With knot insertion, knots are inserted in the knot vectors which results in additional elements. The global refinement in the IGA has similarities to the h- and p-refinement in the FEM [19]. The h-refinement in the FEM results in a finer mesh. Isoparametric elements are divided into smaller elements by inserting additional nodes. With p-refinement, the degree of the local shape functions is increased. Therefore, the order elevation in the IGA corresponds to the p-refinement in the FEM, and the insertion of knots corresponds to the h-refinement. When refining in FEM, manual optimization by the user is usually required [19]. This is not the case in the IGA. In addition, the geometry is not changed during refinement in the IGA. Since this work presents an adaptive impact simulation including automatic refinement, the IGA is suitable in this work. In the further course of this work, a ”coarse model” is introduced. This is a globally refined model which can represent the overall elastic deformation.

Global refinement can also be used to refine the contact area. As an example, an axisymmetric sphere represented by a semicircle is refined in the lower area (see Fig. 1). With global refinement, refining the body in the contact area creates additional elements and control points over the entire body. To avoid this, local refinement is required. One method for local refinement is hierarchical refinement, where subordinate levels are introduced. The concept of hierarchical refinement relies on the property of B-splines to be represented by a linear combination of finer B-splines defined on smaller knot intervals. For a detailed introduction to the hierarchical refinement, see [8, 17]. In the further course of this work, a ”fine model” is introduced. This is a hierarchically refined model that can represent the overall elastic deformation and the local deformations in the contact area.

2.4 Model order reduction

The global shape functions \(\mathbf {\Phi }\) are required for the incorporation of the isogeometric model into the equations of motion (1). This work assumes small elastic deformations which can be described linearly and the weak Galerkin method can be applied as for isoparametric elements [19]. From this, the equations of motion of the assembled IGA based finite element model are given by

$$\begin{aligned} {\textbf{M}}_\textrm{e}\ddot{{\textbf{u}}}_\textrm{e}+{\textbf{K}}_\textrm{e}{\textbf{u}}_\textrm{e}={\textbf{0}}, \end{aligned}$$
(3)

where \({\textbf{M}}_\textrm{e}\) is the full mass matrix, \({\textbf{K}}_\textrm{e}\) the full stiffness matrix, and \({\textbf{u}}_\textrm{e}\) the vector of the displacements of the control points. The global shape functions can be obtained by reducing the full finite element model (3). One of the simplest model reduction techniques is modal truncation. However, this approach typically generates low frequency eigenmodes which are not able to precisely describe local deformations in the contact area. This leads to inaccurate results, as shown in [6]. Alternatively, the Craig-Bampton method [7] is used which combines fixed-interface normal modes and constraint modes. The overall flexibility is represented by the normal modes and the deformations in a specific area, e.g., the contact area, by the constraint modes. Selecting predetermined control points on the exterior surface is necessary for the constrained modes. Following this procedure generates global shape functions denoted as \(\mathbf {\Phi }\), which are orthogonalized and normalized to the mass matrix. The advantage of the Craig-Bampton method is the precise representations of local deformations. However, the disadvantage is the numerical stiffness of the resulting equations of motion (1). This is due to the combination of low frequency normal modes and the high-frequency constrained modes. In previous works [8, 10, 20,21,22] on IGA impact simulations, the numerical performance is improved by modally damping the high-frequency modes. However, it is still numerically burdensome and the choice of the damping parameters critical.

3 Quasistatic contact model

Alternatively to modal damping, a quasistatic contact model can be used to improve the numerical performance of the impact simulation. In the previous work [10], the quasistatic contact model has been already applied to the IGA. The underlying contact model requires that the contact forces are computed at collocation points using a penalty method. This work uses Greville points (see [13] for more information on collocation). The procedure of the contact search is detailed in prior works [8, 10, 20,21,22]. As in the prior works, the contact force is calculated based on the penetration of the bodies, the normal gap. The normal gap is defined by the distance between the current collocation point and the closest point on the target body and is orthogonal to the exterior target surface. The contact forces are then assembled into the vector of discrete forces \({\textbf{h}}_\textrm{d}\).

In the quasistatic contact model, the equations of motion describing the elasticity are partitioned into two parts: the low frequency (lf) modes and the high-frequency (hf) modes. The partitioning can be applied to Eq. (1) resulting in

$$\begin{aligned} \begin{bmatrix}m {\textbf{E}} &{} {\textbf{0}} &{} {\textbf{0}} &{} {\textbf{0}} \\ {\textbf{0}} &{} {\textbf{I}} &{} {{\textbf{C}}_\textrm{r}^\textrm{lf}}^\intercal &{} {{\textbf{C}}_\textrm{r}^\textrm{hf}}^\intercal \\ {\textbf{0}} &{} {\textbf{C}}_\textrm{r}^\textrm{lf} &{} \overline{{\textbf{M}}}_\textrm{e}^\textrm{lf} &{} {\textbf{0}} \\ {\textbf{0}} &{} {\textbf{C}}_\textrm{r}^\textrm{hf} &{} {\textbf{0}} &{} \overline{{\textbf{M}}}_\textrm{e}^\textrm{hf}\end{bmatrix} \begin{bmatrix}{}^{\textrm{R}}\dot{{\textbf{v}}}_{\textrm{IR}} \\ {}^{\textrm{R}}\dot{\mathbf {\omega }}_{\textrm{IR}} \\ \ddot{{\textbf{q}}}_\textrm{e}^\textrm{lf} \\ \ddot{{\textbf{q}}}_\textrm{e}^\textrm{hf}\end{bmatrix}=\begin{bmatrix}{\textbf{h}}_\textrm{dt}\\ {\textbf{h}}_\textrm{dr} \\ {\textbf{h}}_\textrm{d}^\textrm{lf} \\ {\textbf{h}}_\textrm{d}^\textrm{hf}\end{bmatrix}+\begin{bmatrix}{\textbf{h}}_\textrm{bt}\\ {\textbf{h}}_\textrm{br} \\ {\textbf{h}}_\textrm{be}^\textrm{lf} \\ {\textbf{h}}_\textrm{be}^\textrm{hf}\end{bmatrix} - \begin{bmatrix}{\textbf{h}}_\mathrm {\omega t} \\ {\textbf{h}}_\mathrm {\omega r} \\ {\textbf{h}}_\mathrm {\omega e}^\textrm{lf} \\ {\textbf{h}}_\mathrm {\omega e}^\textrm{hf}\end{bmatrix} - \begin{bmatrix}{\textbf{0}} \\ {\textbf{0}} \\ \overline{{\textbf{K}}}_\textrm{e}^\textrm{lf}{\textbf{q}}_\textrm{e}^\textrm{lf} \\ \overline{{\textbf{K}}}_\textrm{e}^\textrm{hf}{\textbf{q}}_\textrm{e}^\textrm{hf}\end{bmatrix}, \end{aligned}$$
(4)

where a Buckens-frame is used and standard damping is neglected. The equations of motion (4) include \(n_\textrm{q}^\textrm{lf}\) low frequency elastic coordinates \({\textbf{q}}_\textrm{e}^\textrm{lf}\) and \(n_\textrm{q}^\textrm{hf}\) high-frequency elastic coordinates \({\textbf{q}}_\textrm{e}^\textrm{hf}\). The high frequency modes are only coupled with the rest of the system via the rigid body rotation through the matrix \({\textbf{C}}_\textrm{r}^\textrm{hf}\). In [23], it is proposed to neglect the rotational coupling \({\textbf{C}}_\textrm{r}\) for small elastic deformations, which includes the low- and high-frequency part \({\textbf{C}}_\textrm{r}^\textrm{lf}\) and \({\textbf{C}}_\textrm{r}^\textrm{hf}\). The same is proposed in [24] provided that the elastic deformations and the elastic coordinates remain small. Finally, it is shown in [9, 25] that the high-frequency coupling \({\textbf{C}}_\textrm{r}^\textrm{hf}\) is significantly smaller than the low frequency coupling \({\textbf{C}}_\textrm{r}^\textrm{lf}\). Thus, their dynamics can be neglected in Eq. (4). With these assumptions, the differential-algebraic system of equations of motion for a single body in contact follows as

$$\begin{aligned} \begin{bmatrix}m {\textbf{E}} &{} {\textbf{0}} &{} {\textbf{0}} &{} {\textbf{0}} \\ {\textbf{0}} &{} {\textbf{I}} &{} {{\textbf{C}}_\textrm{r}^\textrm{lf}}^\intercal &{} {\textbf{0}} \\ {\textbf{0}} &{} {\textbf{C}}_\textrm{r}^\textrm{lf} &{} \overline{{\textbf{M}}}_\textrm{e}^\textrm{lf} &{} {\textbf{0}} \\ {\textbf{0}} &{} {\textbf{0}} &{} {\textbf{0}} &{} {\textbf{0}} \end{bmatrix} \begin{bmatrix}{}^{\textrm{R}}\dot{{\textbf{v}}}_{\textrm{IR}} \\ {}^{\textrm{R}}\dot{\mathbf {\omega }}_{\textrm{IR}} \\ \ddot{{\textbf{q}}}_\textrm{e}^\textrm{lf} \\ {\textbf{0}} \end{bmatrix}=\begin{bmatrix}{\textbf{h}}_\textrm{dt}\\ {\textbf{h}}_\textrm{dr}\\ {\textbf{h}}_\textrm{d}^\textrm{lf} \\ {\textbf{h}}_\textrm{d}^\textrm{hf}\end{bmatrix}+\begin{bmatrix}{\textbf{h}}_\textrm{bt}\\ {\textbf{h}}_\textrm{br} \\ {\textbf{h}}_\textrm{be}^\textrm{lf} \\ {\textbf{0}} \end{bmatrix} - \begin{bmatrix}{\textbf{h}}_\mathrm {\omega t} \\ {\textbf{h}}_\mathrm {\omega r} \\ {\textbf{h}}_\mathrm {\omega e}^\textrm{lf} \\ {\textbf{0}} \end{bmatrix} - \begin{bmatrix}{\textbf{0}} \\ {\textbf{0}} \\ \overline{{\textbf{K}}}_\textrm{e}^\textrm{lf}{\textbf{q}}_\textrm{e}^\textrm{lf} \\ \overline{{\textbf{K}}}_\textrm{e}^\textrm{hf}{\textbf{q}}_\textrm{e}^\textrm{hf}\end{bmatrix}, \end{aligned}$$
(5)

where the dynamics of the high-frequency modes vanish as quasistatic behavior is assumed. However, the formulation in Eq. (5) may be inaccurate if high rotational velocities occur. The algebraic equations in the last row of Eq. (5) represent the balance of the contact forces \({\textbf{h}}_\textrm{d}^\textrm{hf}\) and the inner forces \(\overline{{\textbf{K}}}_\textrm{e}^\textrm{hf}{\textbf{q}}_\textrm{e}^\textrm{hf}\). Without these remaining equations, the elastic deformations in the contact area could not be accurately represented. The differential-algebraic system (5) can be solved directly, or the algebraic quasistatic contact equations are solved separately. However, the direct solution seems to be numerically challenging. Therefore, the algebraic equations

$$\begin{aligned} {\textbf{f}}_\textrm{qs}({\textbf{q}}_\textrm{e}^\textrm{hf}) = {\textbf{q}}_\textrm{e}^\textrm{hf} - \left( \overline{{\textbf{K}}}_\textrm{e}^\textrm{hf} \right) ^{-1} {\textbf{h}}_\textrm{d}^\textrm{hf}({\textbf{r}}_\textrm{IR}, \mathbf {\beta }_\textrm{IR}, {\textbf{q}}_\textrm{e}^\textrm{lf}, {\textbf{q}}_\textrm{e}^\textrm{hf}) = {\textbf{0}} \end{aligned}$$
(6)

are solved separately from the differential equations of motion. The quasistatic contact equations \({\textbf{f}}_\textrm{qs}\) are solved in every time step for the high-frequency elastic coordinates \({\textbf{q}}_\textrm{e}^\textrm{hf}\). The straightforward approach for the solution is Newton’s method. The required Jacobian \({\textbf{J}}_\textrm{qs}({\textbf{q}}_\textrm{e}^\textrm{hf})\) of Eq. (6) is computed numerically by first order finite differences. To counter rounding and approximation errors of the Jacobian, [26] presents a method to adjust the step sizes to control these errors. This adjustment is used in the Matlab function odenumjac to numerically approximate a Jacobian. Nevertheless, the solution of the quasistatic contact Eq. (6) can be challenging. Especially when the penalty factor is too high. This can cause rank issues in Newton’s method [6, 10]. Therefore, the penalty factor needs to be chosen with care. To save computing time, the Jacobian \({\textbf{J}}_\textrm{qs}({\textbf{q}}_\textrm{e}^\textrm{hf})\) is not numerically calculated in each Newton’s iteration. Given a large number of high-frequency elastic coordinates \({\textbf{q}}_\textrm{e}^\textrm{hf}\), this would mean many function evaluations. Updating the Jacobian with Broyden’s method [27] reduces the computational effort.

In the previous work [10], a first algorithm that solves the quasistatic contact equation (6) is already presented. The Algorithm 1 presented in this paper is an extension of it, which particularly monitors the numerical challenges.

Algorithm 1
figure a

Solution of the quasistatic contact equation (6)

Full size image

The extension is relevant to adaptively determine the penalty factor in Sect. 4.1. Algorithm 1 is explained in the following. In line 1 and 2 the Newton counter k and a flag to reset Newton’s method are initialized. Newton’s method starts with a while loop in line 3. First of all, the counter \(k_\textrm{jac}\) of the Jacobian \({\textbf{J}}_\textrm{qs}({\textbf{q}}_\textrm{e}^\textrm{hf})\) is checked. If the counter reaches its maximum value \(k_\textrm{jac}^\textrm{max}=15\), a new Jacobian is computed by finite differences. Otherwise, the previous Jacobian updated with Broyden’s method [27] is used. Then, the Jacobian is checked for singularity in line 10. A computationally efficient indicator for singularity is the reciprocal condition number (RCN) measuring the condition of a matrix [28]. If the RCN is near zero, the matrix is poorly conditioned. A value near one represents a well conditioned matrix. The RCN is determined with the Matlab function rcond. If the RCN is less, then \(\epsilon _\textrm{rcn}^\textrm{min}=10^{-10}\), the error "1" occurs. If the Jacobian is not finite, e.g., not a number (NaN) or infinite (inf), the error "2" occurs. The next but one paragraph describes how to respond to these two critical errors.

With Newton’s method, the Jacobian and the previous solution of the high-frequency elastic coordinates \({\textbf{q}}_{\textrm{e},k}^\textrm{hf}\), a new solution \({\textbf{q}}_{\textrm{e},k+1}^\textrm{hf}\) is computed in line 15. Then, Broyden’s method is applied to the Jacobian \({\textbf{J}}_\textrm{qs}({\textbf{q}}_\textrm{e}^\textrm{hf})\) in line 16. Newton’s method terminates successfully in line 17 if the solution does not change with the tolerance \(\epsilon \), here, \(\epsilon =10^{-15}\) is chosen. If the maximum number of Newton steps \(k_\textrm{max}=3 k_\textrm{jac}^\textrm{max}=45\) is reached, the non-critical error "\(-1\)" occurs.

From line 22, the occurring errors "1", "2", and "\(-1\)" are evaluated. If any error occurs the first time during the current Newton iteration, Newton’s method is reset. The reset includes the Newton counter k, the Jacobian counter \(k_\textrm{jac}\), and the high-frequency elastic coordinates \({\textbf{q}}_{\textrm{e},k}^\textrm{hf}\). The algorithm may only be reset once per Newton iteration. If an error occurs despite the reset, a distinction is made between the critical errors "1" and "2" as well as the non-critical error "\(-1\)". If the error in line 27 is critical, the quasistatic algorithm stops. If the error in line 29 is non-critical, Newton’s method terminates successfully. If no error occurs, Newton’s method continues in line 32.

After the while loop, the discrete forces \({\textbf{h}}_\textrm{d}^\textrm{lf}\) can be computed, and the Jacobian counter \(k_\textrm{jac}\) is set back to zero in line 35. Therefore, the Jacobian can be used more than the \(k_\textrm{jac}^\textrm{max}=15\) times. Testing showed that this greatly improves the computation time while the results of the contact forces are nearly identical. Without the reset of the Jacobian counter \(k_\textrm{jac}\), 3 to 4 Newton steps are required until convergence. Resetting the Jacobian counter increases the required Newton steps to 6 to 7, but reduces the number of computed Jacobians. Since computing the Jacobian is the most computationally expensive part of the quasistatic contact, the computational performance is increased even though more Newton steps are required.

4 Adaptive algorithm for impact simulations

Usually, an impact in a flexible multibody system simulation requires manual setup. The user setting up the flexible multibody system needs to determine the location of the impact point, refine the model in the respective contact area, and determine the penalty factor for which the results converge to the physical correct contact force. This work proposes the overall procedure in Fig. 2 to adaptively simulate the impact without manual setup.

Fig. 2
figure 2

Overall procedure of the adaptive impact simulation

Full size image

This includes the automation of the flexible multibody setup and the determination of the three aforementioned variables. The procedure consists of three parts: non-impact phase, adaptive processing, and impact phase. In the beginning, the user sets up the rigid and flexible bodies. The flexible bodies, which might get in contact, are represented by IGA models and have already been coarsely refined (see Sect. 2.3).

The coarse models are globally refined to represent the overall elastic deformation and are used in phases between impacts. Regarding model reduction, coarse models are modally truncated by the first \(n_\textrm{q}\) normal modes. The model refined later in the process is called the fine model (see Sect. 2.3). Fine models are hierarchically refined to represent local deformation in the contact area. The Craig-Bampton method [7] will be applied to the fine model used in the impact phase. For the Craig-Bampton method, the number of low frequency normal modes \(n_\textrm{q}^\textrm{lf}\) is identical to the number of normalmodes \(n_\textrm{q}\) of the coarse model reduced by modal truncation. Thus, the number of the equations of motion from Eq. (1) remains constant throughout the adaptive simulation. Without the quasistatic contact model, the number of equations of motion would change and the presented algorithm would not work. This is because otherwise the \(n_\textrm{q}^\textrm{hf}\) constraint modes would be part of the equations of motion.

For the solution of the equations of motion (1), different integrators and settings are chosen. The non-impact phase uses the Matlab ode23tb integrator with the maximum time step size \(\Delta t_\mathrm {non-impact}^\textrm{max}={0.1\,\mathrm{\text {m}\text {s}}}\) for the examples presented. The maximum step size \(\Delta t_\textrm{impact}^\textrm{max}=\frac{1}{2f^\textrm{max}}\) in the impact phase is determined by the Nyquist–Shannon sampling theorem [29], where \(f^\textrm{max}\) is the maximum eigenfrequency within the flexible multibody system. An explicit integrator is selected for the impact phase. An implicit integrator would chain the solution of two sets of nonlinear equations, the equations of motion (1) and the quasistatic contact Eq. (6), into each other. Instead, the explicit Matlab ode45 integrator is copied and modified. First, contact forces and high-frequency elastic coordinates are saved during the time integration. Otherwise, post-processing is as time-consuming as the simulation itself. Second, the integrator can reset the quasistatic contact model. Usually, Matlab integrators use variable step sizes. If an integration step is discarded, the initial conditions of Algorithm 1, i.e., the Jacobian \({\textbf{J}}_\textrm{qs}({\textbf{q}}_\textrm{e}^\textrm{hf})\), from the last successful step are used. In the following, the procedure of Fig. 2 is detailed:

The simulation starts with the non-impact phase shown on the lower left-hand side in Fig. 2. The goal of the non-impact phase is to simulate large rigid body motions with a large time step size and to detect contacts. In contact mechanics, one body is called the contact body (C) and the other one is the target body (T). To detect a contact during the non-impact phase, the distance and the impact location can be determined with the distance function \(f_\textrm{d}\). If the distance function

$$\begin{aligned} f_\textrm{d}(\xi _\textrm{C},\eta _\textrm{C},\zeta _\textrm{C},\xi _\textrm{T},\eta _\textrm{T}, \zeta _\textrm{T})=||{\textbf{r}}_\textrm{C}(\xi _\textrm{C},\eta _\textrm{C}, \zeta _\textrm{C})-{\textbf{r}}_\textrm{T}(\xi _\textrm{T},\eta _\textrm{T},\zeta _\textrm{T})|| \end{aligned}$$
(7)

is minimized with the Matlab optimizer fmincon and \(f_\textrm{d} \approx 0\), a contact occurs. The optimization of the distance function then yields the physical points \({\textbf{r}}_\textrm{C}\) and \({\textbf{r}}_\textrm{T}\) on the bodies where they are closest, and their corresponding local coordinates \(\xi _\textrm{C}\), \(\eta _\textrm{C}\), \(\zeta _\textrm{C}\), \(\xi _\textrm{T}\), \(\eta _\textrm{T}\) and \(\zeta _\textrm{T}\) in the parameter space. This will be the location of the impact and this information will be necessary for the generation of the adaptive model. To reduce the computational effort of minimizing Eq. (7), the minimization is not performed in every time step but with a larger time step size \(\Delta t_\textrm{search}\). As a consequence, the contact and target body may already penetrate each other in the non-impact phase. Therefore, the over-calculated time steps are discarded until no more contact occurs. Then, the impact phase is simulated. Another well known and computationally more efficient approach is the use of bounding spheres/boxes [11]. They have been already applied in the IGA [30, 31]. If the geometries of involved IGA bodies are more complex and non-convex, bounding spheres/boxes may be required in addition to minimizing Eq. (7). This is because it is challenging to find the global minimum of non-convex functions. However, since this work focuses on simple geometries typically used in research, bounding spheres/boxes are not additionally used in this work.

The next phase in Fig. 2 is the adaptive processing. The goal is to determine the penalty factor and to generate fine models for the impact phase. The fine model is based on its contact interval. The contact interval is defined in the IGA parameter space and indicates where the contact is checked on the contact and target body. Within the contact interval, there are several elements that can come into contact. The center of the interval is determined by minimizing the distance function \(f_\textrm{d}\) in Eq. (7). The width of the contact interval is determined adaptively. The procedure is explained in Sect. 4.1. An initial fine model is used in the first iteration of adaptive processing. Based on the coarse user given model, knots are inserted automatically at the center of the contact interval. The fine model is reduced with the Craig-Bampton method. Although the overall shape of the eigenmodes of the fine and the coarse model is identical, the global shape functions \(\mathbf {\Phi }\) and thus the elastic coordinates \({\textbf{q}}\) vary. Therefore, the initial conditions of the elastic coordinates \({\textbf{q}}_\textrm{e}\) are transformed from the coarse to the fine model. The procedure of this transformation is described in Sect. 4.4.

After the adaptive processing, the impact phase starts. The quasistatic contact model in Algorithm 1 is evaluated. Initially, a user given penalty factor is used. The impact simulation stops if the impact is finished, e.g., no further occurring forces, an element at the edge of the contact interval is contact, or the quasistatic contact Algorithm 1 requests a stop, e.g., due to numerical issues. If an edge element is in contact, the width of the contact interval is too small, and continuing the simulation is pointless.

Back to the adaptive processing, the utilization of the contact interval is evaluated. If the utilization is not acceptable, the width of the interval is adaptively modified and a new fine model is generated. The evaluation of utilization and the adaptive modification of the interval is detailed in Sect. 4.2. If the utilization is acceptable, the penalty factor can be adjusted according to Sect. 4.1. If the penalty factor is not yet finally determined, the penalty factor is modified, the fine model is updated and a new iteration begins. The impact phase terminates successfully, if the impact is fully simulated and the utilization and penalty factor are acceptable. In the adaptive processing, the user given coarse model is reused, it is modally truncated, and the initial conditions are transformed. The procedure now returns back to the non-impact phase. Therefore, the initial conditions of the elastic coordinates \({\textbf{q}}_\textrm{e}\) are transformed from the fine to the coarse model. The procedure is described in Sect. 4.4.

4.1 Adaptive penalty factor

In the course of the adaptive impact simulation in Fig. 2, the penalty factor is determined adaptively. When simulating multibody systems, the corresponding penalty factor \(c_\textrm{p}\) is often chosen heuristically or by hand. Thereby, the penalty factor should be chosen large enough such that the results become independent of the chosen parameter [16]. This trial-and-error approach was used to determine the penalty factor in the previous works [8, 10, 20,21,22], where the high-frequency modes were critically damped. If the penalty factor is increased beyond its converging value, the equations of motion (1) become numerically stiffer. This increases the computation time, or the numerical integration might even terminate unsuccessfully.

In this work, the penalty method is combined with the quasistatic contact model. The trial-and-error approach for the determination of the penalty factor also works here. It turns out that the value for which the penalty factor converges is identical for the modally damped contact model and quasistatic contact model. In practice, however, the penalty factor cannot be increased beyond its converging value as for a modally damped model. If the penalty factor is too high, numerical errors occur or the algorithm terminates as described in Algorithm 1. In practice, it is desired that the penalty factor is determined automatically in order to obtain an accurate result. Due to the numerical efficiency of the quasistatic contact model, it is coupled with the following method to automatically determine the penalty factor.

For a simpler parametrization, the penalty factor is composed of a multiplier \(c_\textrm{p}^\textrm{mul}\) and an exponential part \(c_\textrm{p}^\textrm{exp}\) via

$$\begin{aligned} c_\textrm{p}=c_\textrm{p}^\textrm{mul}\times 10^{c_\textrm{p}^\textrm{exp}}. \end{aligned}$$
(8)

This work proposes the procedure in Fig. 3 to determine the penalty factor.

Fig. 3
figure 3

Adaptively determine the penalty factor \(c_\textrm{p}\)

Full size image

The procedure is divided into two phases: quick increase and slow decrease of the penalty factor. In the first phase, the impact is not completely simulated, but only for \(n_\textrm{con}=30\) time steps. Testing shows that if there are no errors in the first \(n_\textrm{con}=30\) time steps of the contact, the rest of the contact will also be mostly error free. If no error occurs, the exponent \(c_\textrm{p}^\textrm{exp}\) is increased by 1 and the impact simulation restarts. If an error occurs, the second phase begins and the penalty factor is decreased slowly by reducing the multiplicator \(c_\textrm{p}^\textrm{mul}\) by 1. Then, the simulation continues at the time step, where the error occurred. During the second phase, it may occur that the penalty factor has to be reduced multiple times online.

4.2 Adaptive width of the contact interval

Besides the penalty factor, the model is refined adaptively. The model is generated in three steps: Firstly, the utilization of the contact interval in the parameter space is determined after an impact simulation. As mentioned in the previous Sect. 4 and Fig. 2, the impact simulation stops when the impact is fully simulated, an edge element is in contact, or the quasistatic algorithm requests a stop (see Fig. 3). Secondly, the width of the contact interval is modified based on the utilization. The utilization depends on how many elements within the contact interval are actually in use. Thirdly, the model is generated considering the updated contact interval. After that, the fine model is reduced with the Craig-Bampton method, and the impact simulation is performed again.

The determination of the utilization \({\mathcal {U}}_\textrm{interval}\) depends on the type of the model. It is distinguished between a 2D model (plane strain or plane stress), an axisymmetric 2D model, and a 3D model. Figure 4 shows an example for each case.

Fig. 4
figure 4

Examples of how the utilization of the contact interval is determined

Full size image

In the first two cases, the contact interval is 1D representing an exterior curve of a surface. The contact interval of a 3D solid is represented by a 2D exterior surface. Figure 4 shows three different types of elements: interval elements, edge elements, and contact elements. All elements inside the interval are interval elements. Elements at the edge of the interval are named edge elements. Contact elements are the elements, which are actually in contact. To determine the utilization \({\mathcal {U}}_\textrm{interval}\) of the contact interval, the number of contact elements \(n_\textrm{contact}\) is divided by the number of interval elements \(n_\textrm{interval}\). For a 3D model, the utilization is considered individually for both directions.

In the next step, the width of the contact interval is updated based on the utilization. The procedure is detailed in Algorithm 2.

Algorithm 2
figure b

Adaptive interval

Full size image

In line 1, if any contact element is an edge element, the contact interval is too small and the impact seems to spread over a larger area. The model is classified as unacceptable, which prevents the penalty factor from being adaptively changed as shown in Fig. 3. The width of the interval is increased by \({50\,\mathrm{\%}}\) across the board. The model is also classified as unacceptable in line 4 if the utilization is below the minimum utilization \({\mathcal {U}}_\textrm{interval}^\textrm{min}={50\,\mathrm{\%}}\). As a consequence, the width of the interval is decreased. The updated width is determined with

$$\begin{aligned} w_\textrm{interval} \Leftarrow w_\textrm{interval} \frac{{\mathcal {U}}_\textrm{interval}}{{\mathcal {U}}_\textrm{interval}^\textrm{target}}. \end{aligned}$$
(9)

The maximum rate of change is limited to \({50\,\mathrm{\%}}\). For the next two cases in line 7 and 10, the model is acceptable, and the penalty factor can be adjusted according to Fig. 3. The target value of the utilization is \({\mathcal {U}}_\textrm{interval}^\textrm{target}={70\,\mathrm{\%}}\). If the utilization is below the target value, the width of the interval is decreased. Otherwise the width \(w_\textrm{interval}\) is increased. The updated width is determined with Eq. (9).

4.3 Adaptive contact model

In the previous Sect. 4.2, the width \(w_\textrm{interval}\) of the contact interval is adaptively adjusted and the center of the contact interval is determined during the non-impact phase by minimizing the distance function \(f_\textrm{d}\) in Eq. (7). With this information, the adaptive model can be built in this section. As a reminder, the width and the center of the interval are given in the parameter space. Likewise, the model is generated in the parameter space. In the IGA, element refinement is achieved by inserting knots. The procedure is divided into two steps. Firstly, the interval is delimited by inserting knots. Secondly, knots representing the contact elements are inserted within the interval.

At the beginning of the first step, the coarse model defined by the user is given in the upper part of Fig. 5.

Fig. 5
figure 5

Iteratively build the fine model by inserting knots

Full size image

It shows the existing knots spanning up the elements and the contact interval in the parameter space. The goal is to insert knots until both boundaries of the interval are represented by knots. This procedure is illustrated by an example in Fig. 5. In this example, three knots are required to fit the lower and upper boundary of the interval. In practice, the interval does not have to be exactly represented by knots. A one percent deviation from the width of the contact interval is sufficient.

However, the goal is for the refined model to be hierarchically refined. As mentioned before in Sect. 2.3, hierarchical refinement reduces the number of elements and degrees of freedom (see Fig. 1). For the hierarchical model generation, the number of levels is limited to \(n_\textrm{lvl}^\textrm{max}=5\) and the maximum of inserted knots per level is limited to \(n_\textrm{knots}^\textrm{max}=10\). The number of levels is limited because increasing the number of levels increases the computational effort to compute the NURBS basis which is required in the evaluation of the contact forces [8, 21]. The maximum number of inserted nodes per layer is limited to avoid inserting all knots in one layer. Inserting all knots in one layer gives the same effect as the global refinement in Fig. 1. Many elements and control points would be created.

But not any number of inserted knots can be divided over a fixed number of levels. An example is given in Fig. 6, which attempts to insert three and two knots over three levels.

Fig. 6
figure 6

An example that not any number of inserted knots can be divided over a fixed number of levels during hierarchical refinement (see Fig. 1)

Full size image

As a side note, the first level represents the coarse model and the deeper levels the refinement. On the left in Fig. 6, three knots are inserted, which is equivalent to four inserted elements. Four is not a prime, it can be divided by two. As a result, two elements are inserted in the second level and the other two elements are added in the third level. Therefore, one knot is inserted in each level. However, it is not possible to distribute two knots over three levels, as shown on the right in Fig. 6. Inserting two knots is equivalent to three inserted elements. The number three is a prime number and a distribution to multiple levels is not possible.

In order to comply with the maximum number of levels \(n_\textrm{lvl}^\textrm{max}=5\) and the maximum number of inserted knots \(n_\textrm{knots}^\textrm{max}=10\) per level, the number of inserted knots cannot be gradually increased as done in Fig. 5. An allowed number of knots to approximate the contact interval is determined with Algorithm 3.

Algorithm 3
figure c

Determine an allowed number of knots to map the contact interval

Full size image

In line 2 of Algorithm 3, the number of previously inserted knots is increased by one. The new guess is now validated. The number of knots is translated to the number of inserted elements in line 3. The integer factorization in line 4 splits up the elements over the levels. Line 5 and 6 restrict the number of levels. The addition with two in line 5 represents the coarse model in the first level and the final refinement with contact elements within the interval. The number of elements is converted back to the number of knots in line 8, and it is checked in line 9 whether the maximum number of inserted knots per level is respected. With this value \(n_\textrm{knots}\), a tolerance can be used to check whether the interval can be mapped as in Fig. 5. If the search was successful, the refinement to the different levels is performed using integer factorization.

In the second step, the last hierarchy level is inserted. The user defines a number of elements \(n_\textrm{interval}^\textrm{ele}\) per coordinate direction that must be present in the interval. In this work, the parameter is defined as \(n_\textrm{interval}^\textrm{ele}=16\). Since this number cannot be maintained for every configuration, it is possible to take this into account when determining the number of inserted knots \(n_\textrm{knots}\) in Algorithm 3. If it is a 3D model where the interval is 2D, this procedure is performed for both local coordinate directions consecutively.

4.4 Transformation of initial conditions

Regarding the procedure of the adaptive simulation in Fig. 2, the elastic coordinates \({\textbf{q}}_\textrm{e}\) need to be transformed from the coarse to the fine model and vice versa. The solution of the last time step in the previous phase is required to compute the initial conditions of the next phase. The first half of this section describes the transformation from a coarse to a fine model, and the second half describes the transformation from a fine to a coarse model.

The transition from a non-impact to an impact phase requires a transformation from a coarse model to a fine model. Since the fine model is based on the coarse model, this fact can be exploited. The refinement is achieved by inserting knots. The control points \({\textbf{P}}_{i,j,k}^\textrm{fine}\) of the fine model are computed with the recursive knot insertion algorithm in [5]. The same algorithm can be used to transform the displacements \({\textbf{u}}_\textrm{e}\) of the control points. After the non-impact phase, the displacements \({\textbf{u}}^\textrm{coarse}_\textrm{e}\) of the coarse model are computed with

$$\begin{aligned} {\textbf{u}}^\textrm{coarse}_\textrm{e}=\mathbf {\Phi }^\textrm{coarse}{\textbf{q}}^\textrm{coarse}_\textrm{e}. \end{aligned}$$
(10)

Afterward, the recursive knot insertion algorithm [5] is applied to the control points \({\textbf{P}}_{i,j,k}^\textrm{coarse}\) and their displacements \({\textbf{u}}^\textrm{coarse}_\textrm{e}\). This results in the refined control points \({\textbf{P}}_{i,j,k}^\textrm{fine}\) and displacements \({\textbf{u}}^\textrm{fine}_\textrm{e}\). Finally, the elastic coordinates \({\textbf{q}}^\textrm{fine}_\textrm{e}\) must be calculated. The connection in Eq. (10) also applies to the fine model. However, the global shape functions \(\mathbf {\Phi }^\textrm{fine}\) are a non-square matrix and therefore not invertible. Therefore, the elastic coordinates \({\textbf{q}}^\textrm{fine}_\textrm{e}\) can be computed with the pseudo inverse as

$$\begin{aligned} {\textbf{q}}^\textrm{fine}_\textrm{e}=((\mathbf {\Phi }^\textrm{fine})^\intercal \mathbf {\Phi } ^\textrm{fine})^{-1}(\mathbf {\Phi }^\textrm{fine})^\intercal {\textbf{u}}^\textrm{fine}_\textrm{e} \end{aligned}$$
(11)

by solving a linear least squares problem.

After an impact phase, a non-impact phase starts and the elastic coordinates need to be transformed from a fine to a coarse model. This transition is more challenging since the fine model has more degrees of freedom than the coarse model.

After the impact phase, the fine model displacements \({\textbf{u}}^\textrm{fine}_\textrm{e}\) are computed with the global shape functions \(\mathbf {\Phi }^\textrm{fine}\) in the same way as in Eq. (10). This paper proposes to transform the initial conditions by maintaining the elastic deformation of the two models whereby

$$\begin{aligned} {\textbf{d}}^\textrm{coarse}(\xi ,\eta ,\zeta )\approx {\textbf{d}}^\textrm{fine}(\xi ,\eta ,\zeta ) \end{aligned}$$
(12)

holds at an arbitrary point \(\begin{bmatrix}\xi&\eta&\zeta \end{bmatrix}^\intercal \) in the parameter space. Remembering the computation of the elastic deformation in Eq. (2), it can be rewritten as

$$\begin{aligned} \underbrace{\underbrace{ \begin{bmatrix}d_i^\textrm{x}(\xi _i,\eta _i,\zeta _i)\\ d_i^\textrm{y}(\xi _i,\eta _i,\zeta _i)\\ d_i^\textrm{z}(\xi _i,\eta _i,\zeta _i)\end{bmatrix}}_{{\textbf{d}}_i(\xi _i,\eta _i,\zeta _i)}}_{\mathrm {fine~model}}=\underbrace{\underbrace{ \begin{bmatrix}u_{1,1,1}^\textrm{x}&{}u_{1,1,2}^\textrm{x}&{}\cdots &{}u_\mathrm {p+1,q+1,r+1}^\textrm{x}\\ u_{1,1,1}^\textrm{y}&{}u_{1,1,2}^\textrm{y}&{}\cdots &{}u_\mathrm {p+1,q+1,r+1}^\textrm{y}\\ u_{1,1,1}^\textrm{z}&{}u_{1,1,2}^\textrm{z}&{}\cdots &{}u_\mathrm {p+1,q+1,r+1}^\textrm{z}\end{bmatrix}}_{{\textbf{U}}^\textrm{coarse}_\textrm{mat}}\underbrace{\begin{bmatrix}R_{1,1,1}^\textrm{p,q,r}(\xi _i,\eta _i,\zeta _i)\\ R_{1,1,2}^\textrm{p,q,r}(\xi _i,\eta _i,\zeta _i)\\ \vdots \\ R_\mathrm {p+1,q+1,r+1}^\textrm{p,q,r}(\xi _i,\eta _i,\zeta _i)\end{bmatrix}}_{{\textbf{n}}_i(\xi _i,\eta _i,\zeta _i)}}_{\mathrm {coarse~model}}, \end{aligned}$$
(13)

where \({\textbf{d}}_i\in {\mathbb {R}}^{3\times 1}\) are the fine model deformations at a point \(\begin{bmatrix}\xi _i&\eta _i&\zeta _i\end{bmatrix}^\intercal \) in the parameter space, \({\textbf{U}}^\textrm{coarse}_\textrm{mat}\in {\mathbb {R}}^{3\times n_\textrm{cp}}\) are the displacements of the control points of an element in matrix notation, and \({\textbf{n}}_i\in {\mathbb {R}}^{n_\textrm{cp} \times 1}\) are the corresponding NURBS basis of the coarse model. Equation (13) cannot be solved directly for the displacements \({\textbf{U}}^\textrm{coarse}_\textrm{mat}\), since the NURBS basis \({\textbf{n}}_i\) is a vector and the system in Eq. (13) is underdetermined.

This paper proposes the evaluation of Eq. (13) at Gauss points of an element of the coarse model. The coarse model is globally refined. Therefore, the number of control points \(n_\textrm{cp}=(p+1)(q+1)(r+1)\) is identical to the number of Gauss points in the element of a coarse model. As an example, Fig. 7 shows an element of a coarse model with Gauss points.

Fig. 7
figure 7

Example element of a coarse model of order \(p=q=r=2\)

Full size image

By comparing the elastic deformation at all \(n_\textrm{cp}\) Gauss points at once, a square and invertible matrix \({\textbf{N}}^\textrm{coarse}_\textrm{mat}\) of the NURBS basis can be assembled to

$$\begin{aligned} {\textbf{N}}^\textrm{coarse}_\textrm{mat}&=\begin{bmatrix}{\textbf{N}}_1&{\textbf{N}}_2&\cdots&{\textbf{N}}_ {\textrm{n}_\textrm{cp}}\end{bmatrix}\in {\mathbb {R}}^{n_\textrm{cp} \times n_\textrm{cp}}. \end{aligned}$$
(14)

Thus, the elastic deformations \({\textbf{D}}^\textrm{fine}_\textrm{mat}\) of the fine model at all Gauss points must be available in

$$\begin{aligned} {\textbf{D}}^\textrm{fine}_\textrm{mat}&=\begin{bmatrix}{\textbf{d}}_1&{\textbf{d}}_2&\cdots&{\textbf{d}}_ {\textrm{n}_\textrm{cp}}\end{bmatrix}\in {\mathbb {R}}^{3\times n_\textrm{cp}}. \end{aligned}$$
(15)

Equation (13) is then extended to

$$\begin{aligned} {\textbf{D}}^\textrm{fine}_\textrm{mat}={\textbf{U}}^\textrm{coarse}_\textrm{mat}{\textbf{N}}^\textrm{coarse}_\textrm{mat} \end{aligned}$$
(16)

and solved for the displacements of the coarse model with

$$\begin{aligned} {\textbf{U}}^\textrm{coarse}_\textrm{mat}={\textbf{D}}^\textrm{fine}_\textrm{mat}({\textbf{N}}^\textrm{coarse}_\textrm{mat})^{-1}. \end{aligned}$$
(17)

This approach results in redundant results because control points are part of multiple elements. Therefore, the results are averaged over all elements and converted back to the vector format \({\textbf{u}}^\textrm{coarse}_\textrm{e}\) including the displacements of all control points in the coarse model. The elastic coordinates \({\textbf{q}}^\textrm{coarse}_\textrm{e}\) are computed with the global shape functions \(\mathbf {\Phi }^\textrm{coarse}\) and via linear least squares as in Eq. (11). The functionality of this procedure is checked in the first application example in Sect. 5. It is shown that no energy is created or lost when the simulation phase changes.

5 Application example I: wave propagation

The first application example is 2D axisymmetric and shows significant elastodynamic effects. The setup was first presented in the previous work [20] for testing non-adaptive IGA contacts. Now, the developed adaptive algorithm is applied to this setup. There are no large rigid body motions, which would make the use of the floating frame of reference formulation unnecessary. However, the goal of this setup is to validate the adaptive algorithm by preserving the wave propagation and energy of the system. Validation is necessary since the transformation of the initial conditions described in Sect. 4.4 may be a possible source of error.

The axisymmetric setup visualized in Fig. 8 consists of two spheres and a long cylindrical rod.

Fig. 8
figure 8

Wave propagation setup

Full size image

The spheres are made of steel and the rod is made of aluminum. As material parameters for steel, the Young’s modulus is chosen as \(E={210\,\textrm{GPa}}\), the density as \(\rho ={7850\,\mathrm{kg / m^3}}\), and the Poisson’s ratio as \(\nu =0.3\). The material parameters for aluminum are given by \(E={72.8\,\textrm{GPa}}\), \(\rho ={2789\,\mathrm{kg / m^3}}\), and \(\nu =0.33\). The spheres and the rod have a radius of \(r={1\,\textrm{cm}}\), and the length of the rod is \(\ell ={1\,\textrm{m}}\). The sphere on the left-hand side in Fig. 8 starts with the initial velocity \(v_0={0.1\,\mathrm{m / s}}\). It impacts the resting rod, and a wave propagates to the right side of the rod. This wave induces a second impact with the resting sphere on the right-hand side in Fig. 8. Between the rod and the right sphere, there is a small gap of length \({1\,\mathrm{\upmu \text {m}}}\). As a result, the impacts on the left and the right side of the rod occur separately in time, and the simulation can be split into different phases. Thus, the initial conditions must be transformed between the impact and non-impact phase.

The wave speed in the rod can be computed, following, e.g., [32], with

$$\begin{aligned} c_\textrm{rod}=\sqrt{E / \rho } = {5109\,\mathrm{\text {m}/ \text {s}}}. \end{aligned}$$
(18)

As suggested in [33] for a similar impact problem, the highest frequency of interest for this rod is \(f_\textrm{max}={50\,\textrm{kHz}}\). The maximum step size \(\Delta t_\textrm{max}\) for a simulation of such wave propagation problem is subsequently chosen with

$$\begin{aligned} \Delta t_\textrm{max} = \frac{1}{20f_\textrm{max}} = {1\,\mathrm{\upmu \text {s}}} \end{aligned}$$
(19)

as described in [34]. For wave propagation, the maximum length \(\ell _\textrm{max}\) of an element is then determined by

$$\begin{aligned} \ell _\textrm{max} = \frac{c_\textrm{rod}}{20 f_\textrm{max}} = {5\,\mathrm{\text {m}\text {m}}}. \end{aligned}$$
(20)

Considering the requirement in Eq. (20), the coarse model of the rod and the two spheres are generated. To represent the maximum frequency \(f_\textrm{max}={50\,\textrm{kHz}}\), the rod is modally truncated using \(n_\textrm{q}=20\) modes. The two spheres are reduced using \(n_\textrm{q}=10\) modes. The setup is then simulated for \({0.8\,\textrm{ms}}\), which is approximately the time \(4/c_\textrm{rod}={0.78\,\textrm{ms}}\) it takes for the wave to travel four times from one end to the other. The resulting model of the left sphere is displayed Fig. 9 and the left side of the rod is visualized in Fig. 10.

Fig. 9
figure 9

Adaptive model of the left sphere

Full size image
Fig. 10
figure 10

Left side of the adaptive rod model

Full size image

The final adaptively refined models are used as a reference in the simulation of the quasistatic and the damped contact models without adaptivity. The adaptive algorithm gives the penalty factors \(c_\textrm{p}^1=5 \times 10^{16}{\hbox {N / m}}\) and \(c_\textrm{p}^2=1 \times 10^{17}{\hbox {N / m}}\) for the first and the second impact. These resulting penalty factors are used in the damped and the quasistatic model.

To monitor the wave propagation, the point at the right end of the rod (see Fig. 8) is observed. The velocity in the direction of the impact of the point is displayed in Fig. 11.

Fig. 11
figure 11

Velocity of the point under observation in the top right of the rod

Full size image

Again, a very good agreement of all simulations is observed. The first impact starts at the time \(t_0\). In the beginning, both the rod and the observed point are at rest. The first impact induces a wave, which reaches the second contact area and therefore the monitored point at the time \(t_1\). As the wave has reached the end of the rod, the wave is reflected and moves back to the left side of the rod. There it is reflected again and the wave travels to the monitored point again at \(t_3\).

The contact forces of the two contacts are shown in Fig. 12.

The impact and non-impact phase of the adaptive simulation can be distinguished by the gray and light gray areas. The first impact at the time \(t_0\) on the left-hand side of the rod and the second impact on the right-hand side of the rod can be identified. Considering the velocity in Fig. 11 and the contact force in Fig. 12, all three simulations show a good agreement. The results of the wave propagation show, that the transformation of the initial conditions is functioning.

To validate the conservation of energy, the energy of the system is displayed over time in Fig. 13.

Fig. 12
figure 12

Contact force of the rod

Full size image
Fig. 13
figure 13

Energy of the system

Full size image

Since the impacts are elastic, the energy should stay constant. The initial energy E of the system is given by

$$\begin{aligned} E=\frac{1}{2}m_\textrm{sphere}v_0^2, \end{aligned}$$
(21)

where \(m_\textrm{sphere}\) is the mass of the sphere and \(v_0\) its initial velocity. It can be seen that the energy change remains well below one percent. All three simulations use the penalty method, which allows nonphysical penetration of the bodies. A minor increase of the energy is visible in the energy of the adaptive and quasistatic model. This increase is not visible in the damped model, as the damping of the high-frequency modes predominates here. The energy of the adaptive model changes abruptly at two time points during the first impact. The reasons for the jumps are the adaptive decrease of the penalty factor. When the penalty factor is decreased, the nonphysical penetration increases. However, the overall course of the energy of the adaptive model is similar to the quasistatic and the damped model. It shows that the transformation of the elastic coordinates in the adaptive simulation does not effect the energy conservation of the system. In the quasistatic model, the penalty factor is predetermined and does not have to be reduced during the simulation. Therefore, the energy of the quasistatic model remains almost constant.

Considering the computation times, the adaptive model takes \({4.5\,\mathrm{\text {min}}}\), the quasistatic model \({3.1\,\mathrm{\text {min}}}\), and the damped model takes \({12.2\,\mathrm{\text {min}}}\). The quasistatic model is the fastest, especially when compared to the damped model. The computational efficient quasistatic contact model outperforms the modally damped model. The adaptive model takes a bit longer than the quasistatic model without adaptivity since the contact model and the penalty factor are determined automatically. However, setting up the system and parameters manually is far more time-consuming.

Finally, the utilization of the contact interval can be analyzed. In the simulation of the quasistatic and the damped model, the utilization of the left and right side of the rod vary. The utilization of the first contact on the left-hand side of the rod is \(10 / 16={62.5\,\mathrm{\%}}\) and the utilization of the second contact on the right side is only \(6 / 16={37.5\,\mathrm{\%}}\). This is because the adaptive contact model of the first contact is used for both sides of the rod. Due to the nature of the IGA and its parameter space, the contact resolution at both ends of the rod cannot be different in the quasistatic model and the damped model. As shown in Fig. 12, the contact force and thus the actual contact width of the second impact is smaller than in the first impact. Therefore, the utilization of the contact interval of the second impact is smaller or even too small. This issue is not present in the adaptive model. Both impacts are simulated separately and can therefore use different contact models. The utilization of both impacts is close to the target utilization \({\mathcal {U}}_\textrm{interval}^\textrm{target}={70\,\mathrm{\%}}\). The adaptive algorithm automatically selects a suitable contact interval width, which is smaller for the second impact.

6 Application example II: flexible double pendulums

This application example demonstrates the adaptive algorithm in a flexible multibody system. The setup of two 3D flexible double pendulums is visualized in Fig. 14.

Fig. 14
figure 14

Setup of two 3D flexible double pendulums

Full size image

The lower part of a pendulum is represented by a flexible sphere, and the connection between the suspension and the sphere is modeled by a circular flexible rod. The bodies are connected by a rotational joint allowing rigid body motion in the x-z-plane. This can be efficiently handled by the floating frame of reference formulation. This setup is already presented in the previous work [8], where hierarchical refinement is investigated and the bodies are refined manually. Since the double pendulum setup is chaotic, the locations of the impacts vary. Therefore, only the first impact is simulated in [8]. Now, the goal is to validate the adaptive algorithm and simulate the system for a longer time period with multiple impacts.

The rods and the spheres are made of steel. The rods are modeled by globally refined IGA models, which are modally truncated to \(n_\textrm{q}=20\) elastic coordinates. The pendulum on the left-hand side in Fig. 14 is initially deflected by \(\alpha _0={20\,\mathrm{{}^{\circ }}}\) and \(\beta _0={21.14\,\mathrm{{}^{\circ }}}\). The two angles are chosen such that at the time of impact, it is \(\alpha =\beta ={0\,\mathrm{{}^{\circ }}}\). Both double pendulums have no initial velocity. Since gravity is under consideration with the gravitational constant \(g={9.81\,\mathrm{m / s^2}}\), the initial values of the elastic coordinates of the four flexible bodies need to be determined. A straightforward approach is to solve the equations of motion for the elastic coordinates \({\textbf{q}}_\textrm{e}\) so that the accelerations \(\ddot{q}_\textrm{e}\) vanish. The time is set to \(t={0\,\mathrm{\text {s}}}\) and the angles \(\alpha =\alpha _0\) and \(\beta =\beta _0\) remain constant.

In this application example, five different models are compared:

1. Hertz: In this approach, the rods are modeled by flexible IGA bodies, the spheres by rigid bodies, and the contact forces are computed according to the analytic solution by Hertz [35].

2. adaptive+quasistatic: The adaptive contact simulation, presented in this work, is performed. This simulation produces adaptively refined contact models that are used in the following two simulations. This model is called "adaptive model" for simplicity.

3. quasistatic: Only the quasistatic contact model without adaptivity is used in this simulation. For better comparability, the refined sphere model from the adaptive simulation is used here. This model is called "quasistatic model" for simplicity.

4. damped: This simulation uses damped contact models without adaptivity and without quasistatic contact models. The high-frequency modes resulting from the Craig-Bampton method are critically damped using modal damping. For better comparability, the refined sphere model from the adaptive simulation is used here. This model is called "damped model" for simplicity.

5. coarse+quasistatic: The coarse sphere model is used as the quasistatic contact model. This simulation shows the effect of no adaptivity, no refined contact model, and no manual adjustment of the penalty factor. This model is called "coarse contact model" for simplicity.

The simulations utilize the contact detection including Eq. (7) to switch integrator settings. The quasistatic model without adaptivity and the damped model can also be found in [10]. Since the manual impact simulations with the quasistatic and the damped model can only handle one impact, the system is only simulated for \({170\,\textrm{ms}}\). The other simulations are simulated for \({1\,\textrm{s}}\).

As mentioned before, the penalty factor in the quasistatic contact model cannot be arbitrarily increased beyond its converging value. Therefore, a penalty factor analysis is performed with the damped model in Fig. 15.

Fig. 15
figure 15

Convergence of the penalty factor

Full size image

Only minor differences are visible between the various penalty factors. In Fig. 16, the computation time of the impact is compared with the maximum occurring contact force.

Fig. 16
figure 16

Convergence of the penalty factor

Full size image

Therefore, the analysis of the penalty factor results in the converging value \(c_\textrm{p}=10^{18}{\hbox {N / m}}\) of the penalty factor with reasonable computation time and accuracy.

The simulation of the adaptive model also results in the penalty factor \(c_\textrm{p}=10^{18}{\hbox {N / m}}\). The Hertz solution, the adaptive, the quasistatic, and the damped model are all compared in Fig. 17.

Fig. 17
figure 17

Close-up view of the first impact

Full size image

Additionally, the simulation of the coarse contact model with the penalty factors \(c_\textrm{p}=10^{15}{\hbox {N / m}}\) and \(c_\textrm{p}=10^{18}{\hbox {N / m}}\) is visualized. It can be directly seen that the coarse contact model cannot represent the impact exactly. The remaining adaptive, quasistatic, and damped contact model are simulated with the penalty factor \(c_\textrm{p}=10^{18}{\hbox {N / m}}\). No significant differences are visible between them and the Hertz solution. It shows that the adaptive simulation works and that the dynamics of the high frequency modes do not significantly affect the accuracy of the results.

Now, the adaptive simulation with three impacts is monitored in Fig. 18.

Fig. 18
figure 18

Contact force of three impacts

Full size image

The three impacts nearly occur at the same time as in the Hertz reference simulation. Small time shifts are noticeable in the second and the third impact. The Hertz solution and the adaptive model drift apart over time because the adaptive model uses an IGA model and the Hertz simulation uses rigid bodies as spheres and the Hertz contact law.

In the following, the complete computation including processing is considered. If the setup is simulated with one impact for \({170\,\textrm{ms}}\), the adaptive model takes \({8.1\,\mathrm{\text {h}}}\), the quasistatic model \({1.3\,\mathrm{\text {h}}}\), the damped model \({7.0\,\mathrm{\text {h}}}\), and the coarse contact model \({7.4\,\mathrm{\text {min}}}\). Although the penalty factor and the contact model are given in the simulation of the damped model, this simulation takes much time. The reason for this is the numerical stiffness and thus the computationally expensive dynamics of the high-frequency modes. This can be observed especially in the second non-impact phase. The frequency band of the numerically stiff system is excited by the impact and small time steps are required.

The simulation of the quasistatic model is the fastest because, unlike in the adaptive simulation, the contact model and the penalty factor are already predetermined by the user’s experience. The simulation of the adaptive model is more time-consuming than the quasistatic without adaptivity. However, the setup of the quasistatic and the damped model is manual and would thus take even more time. The coarse contact model is the fastest because it is not refined. However, Fig. 17 shows that this model cannot represent the impact correctly. The detailed computation times of each part of the simulations are listed in Table 1.

Table 1 Computation times of the second application example
Full size table

The listed computation times of the phases only include the time of the actual simulation without processing. The listed complete CPU times include also the processing. There is a small difference in the first non-impact phase. This phase is computed faster with the adaptive and coarse contact model than with the quasistatic model. The reason for this is that the quasistatic contact model is already refined and the contact detection with Eq. (7) takes longer. The second non-impact phase of the damped model takes very long. The impact induced the whole frequency band and small time steps are required. A simulation until the beginning of the second impact would take too much computation time.

It is also worth noting the attempts of the adaptive algorithm. In the first three tries, the algorithm adjusts the IGA model. The initial contact interval is too large and needs to be decreased. In the fourth try, the model is acceptable and the penalty factor is increased. The first six tries of the first impact are computed relatively fast, because the impact is not fully simulated and the impact phase terminates early. According to Fig. 2, the impact phase terminates early if an edge element is in contact or on request of the quasistatic algorithm. As described in Sect. 4.1 and Fig. 3, initially only \(n_\textrm{con}=30\) contact time steps are simulated to increase the penalty factor as quickly as possible. The eighth try starts with the penalty factor \(c_\textrm{p}=10^{19}{\hbox {N / m}}\) but decreases during the simulation back to \(10^{18}{\hbox {N / m}}\). It can also be seen that only the first adaptive impact is time-consuming. The following impacts benefit from the previous findings on the penalty factor and the contact interval width. Therefore, the complete computation time of three impacts for \({1\,\textrm{s}}\) takes \({14.6\,\mathrm{\text {h}}}\). However, the simulation of the first \({170\,\textrm{ms}}\) already take \({8.1\,\mathrm{\text {h}}}\) computation time.

As can be seen in Table 1, the first six tries are required to determine values for the interval width and the penalty factor, which are close to their converging value. Providing improved initial values for these parameters would reduce the number of tries in the beginning. However, also in finite element analysis, finding appropriate contact parameters requires a trial-and-error approach. Additionally, the first tries are computed relatively fast (see Table 1), and the required pre-processing of the models only takes \({1\,\mathrm{\text {min}}}\) to \({2\,\mathrm{\text {min}}}\) for each model. As initial values, the optimal penalty factor for static simulations (see [15]), or a neural network could be used as a predictor. Using the adaptive algorithm in this work would help to automatically generate training data for the neural network. However, this is not in the scope of this work.

7 Conclusion

Overall, it can be concluded that the presented adaptive impact simulation method can be smoothly included in the floating frame of reference formulation to allow automatic impact treatment. The quasistatic contact model neglects the dynamics of the high frequency modes and thus reduces the computation time. This is especially the case in phases where large rigid body motions occur, e.g., after an impact that excites the whole frequency band. The presented algorithm in this work generates hierarchically refined contact models where the location and resolution of the impact are also adaptively determined. Additionally, the algorithm allows the adaptive determination of the penalty factor. For an efficient computation of impact and non-impact phases, a method to detect impacts is presented. To switch between impact and non-impact phases, an approach is presented in this paper to transform the elastic coordinates back and forth between the coarse and the fine model.