1 Introduction

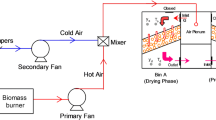
In Europe, proper drying of harvested grain crops before storage is imperative to maintain optimal moisture content and preserve quality. Inefficient drying techniques can result in substantial losses and degradation of grain quality. One widely used method in Europe for drying corn is the mixed flow dryer, where both air and grain flow through the dryer in co-current, counter-current, and crossflow directions [12]. The internal structure design of the dryer, particularly regarding material flow, significantly influences the speed at which individual particles traverse the dryer [12, 15,16,17].

The discrepancy in residence time has been identified as the root cause of under- or over-drying issues [17]. Previous research has primarily focused on improving the uniformity of material flow by adjusting the angular position and spatial distribution of the air duct blades. However, these efforts have reached a point of diminishing returns. Our novel approach, centered on modifying the entire sidewall geometry of the air duct, presents an opportunity to enhance material flow uniformity and further mitigate losses during the drying process.

In our approach, we assumed that particles should ideally require the same duration to traverse both the open space away from the dryer walls and in the vicinity of the air duct walls. This assumption is based on the premise of homogeneous airflow conditions within the dryer. However, it is important to note that our investigations did not encompass an analysis of the inhomogeneity of airflow conditions, as it falls beyond the scope of our research.

The assumption of equal duration for downward grain motion draws inspiration from a classical mechanical problem known as the brachistochrone, which has been studied for centuries. The brachistochrone problem was first posed by Johann Bernoulli in Acta Eruditorum [3]. In this problem, Bernoulli challenged the determination of the path of a point subject only to gravity, starting from point A and ending at point B (which is not on the same vertical line as A), that minimizes the travel time between the two points in a vertical plane. The mathematical formulation of the problem is the following [21]. The time to travel from A to B is:

$$t_{AB} = \mathop \int \limits_{A}^{B} \frac{{{\text{d}}s}}{v} = \mathop \int \limits_{A}^{B} \frac{{{\text{d}}s}}{{\sqrt {2gy} }}.$$

The distance between A and B is \({\text{d}}s = \sqrt {x^{\prime } \left( y \right)^{2} + 1} {\text{d}}y,\) thus

$$t_{AB} = \frac{1}{{\sqrt {2g} }}\mathop \smallint \limits_{0}^{{y_{B} }} \frac{{\sqrt {x^{\prime } \left( y \right)^{2} + 1} }}{\sqrt y }{\text{d}}y.$$

In this case we have to find the minimum of an integral. To find this function we have to apply the Euler–Lagrange equation:

$$\frac{\partial f}{{\partial x}} = \frac{d}{{{\text{d}}y}}\frac{\partial f}{{\partial x^{\prime } }}$$

where \(f\left( {x,x^{\prime } ,y} \right) = \frac{{\sqrt {x^{\prime 2} + 1} }}{\sqrt y }.\) The well-known solution found by Newton, Euler and others to this problem is a cycloidal curve:

$$x = a(\theta - \sin \theta ) {\text{and}}\;y = a(1 - \cos \theta ),$$

where a should be chosen according to the geometric boundary conditions.

Figure 1 illustrates three particles originating from the same starting point and time, initially at rest, and solely influenced by gravity. Particle 1 undergoes free fall, while particle 2 is confined to move along a frictionless inclined plane. Particle 3, on the other hand, moves along a frictionless surface in the shape of a cycloid. It is worth noting the discrepancy in vertical distances covered during the same time period by the particles. In the case of the cycloidal surface, the vertical displacement difference relative to the free-falling particle is the smallest among all other frictionless constraint surfaces. Accounting for friction introduces complexity in the calculations. Several researchers have worked to solve this problem [8, 11, 20, 23]. The resulting curve deviates only marginally from the classical frictionless solution [2]:

$$x\left( \theta \right) = \frac{C}{2}\left( {\theta - \sin \theta + \mu \left( {1 - \cos \theta } \right)} \right)\;{\text{and}}\;y\left( \theta \right) = \frac{C}{2}\left( {1 - \cos \theta + \mu \left( {\theta + \sin \theta } \right)} \right) + y_{0}$$

where C and y0 should be chosen according to the geometric boundary conditions.

Fig. 1
figure 1

Motion on a different types of curves

Full size image

2 Discrete element simulations

Acknowledging the notable distinction between a particle moving alone and the downward movement of particles within a dryer, where interactions with other particles and walls occur, we employed discrete element modelling technique (DEM) to evaluate the feasibility of implementing the proposed new geometry. The utilization of the discrete element modelling method allowed us to explore and analyse the behaviour and suitability of the modified geometry in this more realistic scenario.

The discrete element method (DEM) was originally developed by Cundall and Strack in the late 1970s [9]. This computationally intensive technique involves numerically solving the equation of motion for each component of a granular assembly, considering the interactions between particles as well as their interactions with surrounding walls. Due to the need for acceptable accuracy, the DEM procedure typically requires working with small time steps, which presents computational challenges when dealing with larger grain counts.

To model the particle dynamics within the dryer, we employed the academic version of EDEM 2.7 discrete element software. In our simulations, the evaluation of contact forces between particles was based on the “Hertz-Mindlin no-slip” contact model. The characterization of material properties and interaction parameters plays a pivotal role in determining both normal and tangential forces. The forces and moments acting between the particles in contact can be mathematically expressed by the following equations. The normal force is calculated as

$$F_{n} = \frac{4}{3}E_{0} \delta^{\frac{3}{2}} \sqrt {R_{0} } - 2\sqrt{\frac{5}{6}} \frac{{\ln C_{r} }}{{\sqrt {\ln^{2} C_{r} + \pi^{2} } }}\sqrt {2E_{0} } \sqrt[4]{{R_{0} \delta }}\sqrt {m_{0} } v_{{{\text{nrel}}}}$$

Here \(\frac{1}{{E_{0} }} = \frac{{1 - \nu_{1}^{2} }}{{E_{1} }} + \frac{{1 - \nu_{2}^{2} }}{{E_{2} }}\) is the equivalent Young modulus. A crucial parameter in determining the contact forces between particles is the δ overlap, which signifies the extent of penetration or intersection between the contacting surfaces of the particles. This overlap plays a pivotal role in the calculation of forces and moments acting between particles in the discrete element model. The normal overlap δ between two particles, labeled as i and j, can be defined as follows. Considering the positions \(x_{i}\) and \(x_{j}\), which represent the distances measured on the line connecting the centers of the two overlapping particles, along with their corresponding radii, radii \(R_{i}\) and \(R_{j}\), the normal overlap δ can be mathematically expressed as: \(\delta = R_{i} + R_{j} - \left( {x_{j} - x_{i} } \right)\). The mentioned equations introduce additional terms as follows: \(R_{0} = \frac{{R_{1} R_{2} }}{{R_{1} + R_{2} }}\), which represents the equivalent radius, combining the characteristics of both particles. It serves as a representative radius in the calculations. Likewise, \(m_{0} = \frac{{m_{1} m_{2} }}{{m_{1} + m_{2} }}\) denotes the equivalent mass, combining the properties of both particles. Lastly, \(v_{{{\text{nrel}}}}\) represents the normal component of the relative velocity between the particles. The tangential force between two particles can be calculated using:

$$F_{t} = - 8G_{0} \sqrt {R_{0} \delta } \delta_{t} - 2\sqrt{\frac{5}{6}} \frac{{\ln C_{r} }}{{\sqrt {\ln^{2} C_{r} + \pi^{2} } }}\sqrt {2G_{0} } \sqrt[4]{{R_{0} \delta }}\sqrt {m_{0} } v_{{{\text{trel}}}}$$

In the given equation, additional terms are described as follows: \(\frac{1}{{G_{0} }} = \frac{{2 - \nu_{1} }}{{G_{1} }} + \frac{{2 - \nu_{2} }}{{G_{2} }}\), which represents the reciprocal of the equivalent shear modulus between the two interacting particles. The equivalent shear modulus combines the material properties of both particles to characterize their interaction. \(\delta_{t}\) means the tangential overlap between the two particles. It quantifies the tangential displacement of the contact point until the contact ends or the particle starts to roll or slip, thus measuring the tangential deformation. Lastly, \(v_{{{\text{trel}}}}\) refers to the tangential component of the relative velocity between the particles, representing the velocity difference between the particles in the tangential direction of contact.

The tangential force between particles is bounded by the Coulomb friction limit, given as \(\mu_{{\text{s}}} F_{n}\), where \(\mu_{{\text{s}}}\) denotes the coefficient of static friction. This constraint ensures that the tangential force cannot surpass the frictional force.

Furthermore, the moment arising from rolling friction can be described as \(M_{r} = - \mu_{{\text{r}}} F_{N} R_{i} \omega_{i}\), where \(R_{i}\) denotes the distance from the contact point to the center of the i-th particle, \(\omega_{i}\) represents the unit angular velocity vector (a dimensionless quantity indicating the direction of rotation of the i-th particle), and \(\mu_{{\text{r}}}\) represents the coefficient of rolling friction. Additionally, a moment is induced on the particle due to the tangential force, given by: \(M_{t} = F_{t} R_{i}\).

During the simulations, the equation of motion for each particle is determined by applying the linear and angular momentum theorem. This leads to a system of multiple differential equations that must be solved over numerous time steps. The selection of an appropriate time step significantly impacts the numerical model’s stability. In our simulation, we opted for a time step equal to 25% of the Rayleigh-type time step:

$$\delta t = 0,25T_{R} = 0,25 \cdot \left( {0.1631\nu + 0,8766} \right)^{ - 1} \pi R\left( {\frac{{\rho_{p} }}{{G_{p} }}} \right)^{\frac{1}{2}}$$

In the context of investigating grain mass flow within a mixed flow dryer, Mellman et al. [18] explored the use of the DEM method. Their study demonstrated the applicability of the DEM approach in examining the kinematics of grain motion, even in a simplified two-dimensional model. Subsequent advancements in their methodology revealed a clear relationship between the design of the dryer’s air intake ducts and the unevenness observed in grain movement conditions [12, 22].

One of the main challenges encountered when applying the discrete element method (DEM) lies in determining the parameters that describe the mechanical behaviour of the particle assembly, a process referred to as calibration. In a detailed review by Coetzee [6], various calibration procedures were examined, and multiple methods for calibrating cohesionless particulate assemblies were presented in [7]. Keppler et al. [13] employed the standard shear testing technique to calibrate the model and assess its sensitivity to different material parameters. In certain cases, it becomes necessary to conduct measurements for calibration purposes directly at the experimental test site. Some procedures accommodate this requirement, as demonstrated in [14].

Due to time constraints associated with our experimental investigations, which were conducted within a working plant while aiming to minimize disruptions to normal operations, we opted for the simplest possible calculation method known as the angle of repose test. This approach, similar to the methods employed by Coetzee and Nel [5], Derakhshani et al. [10] and Bablena et. al [1] allowed us to carry out the measurements and calibration related calculations effectively.

The first step in the calibration process involved determining the particle shape [4]. For our experimental investigations, corn grains were used. A random sample was extracted from the grain assembly to accurately determine the shape of the individual grains. Based on our test results, the DEM model consisted of four distinct grain types as illustrated in Fig. 2.

Fig. 2
figure 2

Four types of particles used in the DEM model

Full size image

The size and distribution of the DEM particles was determined based of the average sizes listed in Table 1.

Table 1 Average sizes of grains
Full size table

Figure 3 illustrates the configuration of the angle of repose test model employed in our study. During the calibration process, we iteratively adjusted the angle of particle–particle friction within the DEM model until the simulated angle of repose matched the value obtained from our experimental investigations (namely angle of repose values α1 = 19,2°; α2 = 18,8°; α3 = 17,4°.). This iterative procedure ensured that the simulated results aligned with the measured data, allowing for accurate representation of the material properties within the model.

Fig. 3
figure 3

Angle of repose test

Full size image

The simulation results related to the different particle–particle coefficient of friction values can be seen on Fig. 4.

Fig. 4
figure 4

Simulated angle of repose values

Full size image

Based on the above results we choose the particle–particle friction value to be \(\mu_{{{\text{particle}}}} = 0.2\).

For the determination of the particle’s density, we filled a cylinder with the corn particles and measured the weight of the corn. Then we created the DEM model of the same filling procedure (using the above defined particle shapes and incidence rate) and calculated the mass of particles filling the cylinder. We modified the particle density until the same mass occurred. The particle–wall coefficient of friction was determined by using a surface of wall material having changeable inclination angle.

The Young modulus of the particle was determined based on compression test made on corn particles using Instron 5965. The analysis of the compression curves resulted 78 MPa Young modulus value, which is in acceptable agreement with the results found in the literature [19].

The calibrated material parameters can be seen in Table 2.

Table 2 Material and interaction parameters of corn particles
Full size table

In the comparison between different geometries, we examined two specific configurations. Figure 5 depicts the cycloid-shaped lamella, along with a tangent inclined at 27 degrees. This inclination angle corresponds to the original design of the drying apparatus, where the lamella’s inclination was set to 27 degrees. The geometry of the cycloid lamella is such that the lamella itself serves as the tangent at point A, while at point B, the tangent aligns with the vertical line.

Fig. 5
figure 5

Geometry used in the DEM model

Full size image

The equation governing the cycloid lamella which satisfies the above boundary conditions is as follows:

\(x = 70\left( {1 - \sqrt {1 - \frac{{y^{2} }}{4900}} } \right) + 150 \cdot \arcsin \left[ \frac{y}{70} \right].\)

To ensure optimal settling of particles in the model, a module height of 1000 mm was chosen. In gravitational settling scenarios, the granular assembly typically compresses to approximately one-third of its original height. Thus, the module height was intentionally set higher than the original size to accommodate this compression. Following the filling and settling process, the bottom of the module was opened to allow the particles to flow out of the container.

In order to assess the unevenness of the particle displacement, we implemented a method involving a thin painted strip within the particle assembly. The deformation of this initially horizontal strip was examined during the emptying process, as depicted in Fig. 6. These variations allowed us to analyse and evaluate the extent of unevenness in the particle outflow.

Fig. 6
figure 6

Outflow of particles from the drying module, the deformation of the horizontal strip in case of cycloidal and straight lamellae

Full size image

To quantify the unevenness of the particle flow, we employed the displacement ratio \(\xi\), which is numerically defined as follows:

$$\xi = \frac{{y_{\max } - y_{\min } }}{{y_{\max } }}$$

where \(y_{\max }\) represents the y-coordinate of the center of mass of the particle reaching the highest position within the designated band during a given time interval, \(y_{\min }\) represents the y-coordinate of the center of mass of the particle reaching the lowest position within the designated band during a given time interval. \(\xi { }\) is 0 for steady flow and approaches 1 as the unsteadiness increases. This number can only be used if the same time intervals are considered in all cases. By determining the coordinates of the coloured particles, it becomes straightforward to evaluate the displacement ratio. We compared the results obtained using a cycloidal lamella with those obtained using a straight lamella. This comparison allowed us to assess the impact of the lamella’s geometry on the unevenness of the particle flow.

The DEM simulations were carried out for both (straight and cycloidal) types of lamellae, considering six different values for particle–particle friction and six different values for particle–wall friction. For each combination of friction values, the simulations were repeated five times using the same settings. Consequently, a total of 120 simulations were conducted, as reflected in the figures Figs. 7 and 8.

Fig. 7
figure 7

Comparison of displacement ratios for straight and cycloidal lamellae for different particle–particle friction values

Full size image
Fig. 8
figure 8

Comparison of displacement ratios for straight and cycloidal lamellae for different particle—wall friction values

Full size image

The results obtained from the simulations clearly demonstrate that the use of a cycloidal lamella consistently yields a superior displacement ratio compared to a straight lamella. This observation holds true across a wide range of parameter combinations tested in the simulations. The improved displacement ratio achieved with the cycloidal lamella suggests its efficacy in promoting a more uniform flow of particles throughout the drying apparatus.

3 Experimental investigations

To validate our findings and further demonstrate the advantages of the cycloidal lamella design, we conducted experimental studies using a small-scale dryer model equipped with both conventional rectilinear channels and cycloidal channels. The experimental investigations allowed us to confirm the accuracy of our numerical model and provided tangible evidence of the benefits offered by the novel cycloidal lamella configuration. These experimental results serve to strengthen the reliability and practical applicability of our proposed design.

4 The model dryer

For the experimental tests, we constructed a model dryer with specific dimensions, as depicted in Fig. 9.

Fig. 9
figure 9

The model dryer

Full size image

In the model dryer, the particles descended in two distinct columns. By closely observing the movement of the coloured particles through the transparent plexiglass sidewalls, we were able to assess the unevenness of particle motion (Fig. 10). This experimental observation was then compared with the results obtained from the DEM model. The comparison allowed us to evaluate the consistency between the experimental findings and the simulated behaviour, providing further validation for the accuracy and reliability of the DEM model in capturing the real-world dynamics of particle motion in the dryer.

Fig. 10
figure 10

Coloured particle stripes in the model dryer apparatus

Full size image

The cycloidal lamella shape was approximated by multiple straight segments (for reasons of manufacturing technology capabilities) in the way shown in Fig. 11.

Fig. 11
figure 11

Approximated cycloidal shape used in the model dryer apparatus

Full size image

The measurements conducted on the model drying apparatus provided additional evidence supporting the superior displacement ratio achieved with the cycloidal lamella compared to the straight lamella. Remarkably, even when considering an approximate geometry based on manufacturing technology considerations, the cycloidal lamella consistently demonstrated significantly improved displacement ratio. These findings further emphasize the advantages offered by the cycloidal lamella design and underscore its potential for practical implementation in real-world drying systems. Figure 12 shows the results of measurements conducted by using the approximated cycloidal lamella geometry. The displacement ratios for the three separate measurements are: \(\xi_{{{\text{red}}}} = \frac{{y_{\max } - y_{\min } }}{{y_{\max } }} = \frac{4.2 - 3.5}{{4.2}} = 0.166\), \(\xi_{{{\text{blue}}}} = \frac{{y_{\max } - y_{\min } }}{{y_{\max } }} = \frac{4.6 - 3.8}{{4.6}} = 0.174\) and \(\xi_{{{\text{black}}}} = \frac{{y_{\max } - y_{\min } }}{{y_{\max } }} = \frac{4.4 - 3.9}{{4.4}} = 0.114\). The average displacement ratio evaluated using these results is 0.151. Comparing this result with the simulation data shown on Fig. 8, we can see the good performance of the cycloidal lamella construction and an acceptable correlation between the measured and simulated data.

Fig. 12
figure 12

Particle displacement in case of cycloidal lamella geometry

Full size image

5 Conclusions

To quantify the unevenness of material flow within the dryer, we used the dimensionless displacement ratio ξ. This parameter allows for the characterization of the uniformity of material movement within a designated band. The displacement ratio, ξ, is calculated as the difference between the maximum and minimum y-coordinates of the center of mass of particles within the designated band, divided by the maximum y-coordinate:

$$\xi = \frac{{y_{\max } - y_{\min } }}{{y_{\max } }}$$

This dimensionless parameter provides a suitable tool for comparing the uniformity of material movement processes within the dryer.

Using experimental investigations and numerical simulations, we have demonstrated that it is advantageous to employ cycloidal-shaped lamellae in drying devices. We found that the particle displacement ratio \(\xi\) shows linear dependence on the particle – particle and the particle – wall friction coefficients. The cycloidal lamella, under all examined friction coefficient values between particle–wall and particle–particle interactions, can result in up to a 30% improvement in the displacement ratio. Our experimental investigations also proved the correctness of our hypothesis.