Buckling optimization of additively manufactured cellular structures using numerical homogenization based on beam models

Abstract

Interest in components with detailed structures increased with the progress in advanced manufacturing techniques. Parts with lattice elements can provide improved global buckling stability compared to solid structures of the same weight. However, thin features are prone to local buckling. We present a two-scale optimization approach that simultaneously improves the local and global stability of parametrized graded lattice structures. Elastic properties and local buckling behavior are upscaled via homogenization based on geometric exact beam theory. To reduce computational effort, we construct a worst-case model for the homogenized buckling load factor, which acts as a safeguard against local buckling. We briefly discuss advantages and limitations by means of numerical examples.

1 Introduction

With the progress in additive manufacturing, there is an increased interest in both homogeneous as well as graded lattice structures. Such structures are utilized in many applications, e.g., thermal management, energy absorption, noise reduction, biomedical engineering, etc. [40]. Lattice infill can also increase the global buckling resistance of a structure [12]. However, the lattice is prone to local buckling [17].

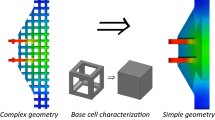
Two-scale optimization [55] may be used to design such structures without the need to resolve all the fine details of the full design in a single setting. This type of optimization assumes separation of scales, i.e., features on the smaller scale, called microscopic scale, are much smaller than features on the large or macroscopic scale, respectively. To bridge the gap between the two scales, the macroscopic response of the microstructure with respect to macroscopic stimulation has to be determined. A widely used procedure to estimate the effective mechanical response of a lattice structure is computational homogenization [19, 34]. There, the effective response of the lattice is obtained by approximating the mechanical behavior of a microstructure through the properties of a homogeneous material. The lattice may then be considered as a continuum and its mechanical properties reflect the properties of the underlying microstructure, including the material and topology of the lattice. The upscaled properties can be used in macroscopic constitutive equations. Thus, the optimization problem is solved on a rather coarse finite element mesh, where the material properties at an integration point are given by the homogenized characteristics of a periodic microstructure with infinitesimal cell size. The design variables usually describe the microstructure’s geometry or topology.

Though there is exhaustive literature on optimal design considering the buckling behavior of trusses using beam models ( [17] and references therein), few publications for continuum models exist. This might be due to several challenges when performing buckling optimization based on such a model. Those include, but are not limited to, multiple eigenvalues [42] and artificial modes in low-density regions [6, 15, 21].

Models for the buckling of periodic microstructures have been investigated for decades and, lately, stability requirements have also been employed when tailoring microstructures [2, 48]. Within the homogenization method, a representative volume element (RVE) is introduced. By convention, the RVE is defined as the smallest repeating unit cell. However, when considering structural instabilities on the micro-scale, special boundary conditions from Bloch-Floquet theory [37] or multiple repetitions within the RVE are necessary, as buckling modes usually span over multiple periods of the microstructure [19, 24, 34].

The aforementioned works only investigate the buckling behavior of a structure on a single scale, either macroscopic or microscopic. Only recently, works investigating the buckling behavior of two-scale structures on both scales have been published. Wang et al. [51] deduce local stress constraints from the slenderness ratio of the lattice rods. Christensen et al. [11] fit a Willam–Warnke failure criterion to homogenized data assuming isotropic buckling behavior and employ a two-term interpolation scheme to interpolate the buckling strength as a function of the relative lattice volume. In contrast, our approach directly uses upscaled microscopic buckling information in macroscopic simulations, and we are able to capture anisotropic buckling behavior of microstructures. We presented this approach for the first time in a two-dimensional setting [26]. In this article, we extend the work from [26] in multiple ways: First, instead of asymptotic homogenization based on the finite element method in [26], here, to upscale the lattice’s properties, we use a numerical homogenization scheme based on beam theory, which is able to capture also nonlinear effects. On the macroscopic scale however, we stick with linear theory. Second, we extend our model and method to a three-dimensional setting. This requires, among other things, the capture of the buckling responses of the base cell with respect to applied stresses from a six-dimensional space.

We want to obtain lattice structures with minimal mechanical compliance and maximal buckling resistance on both the microscopic and macroscopic scale that can be produced, e.g., by powder-bed based additive manufacturing. Buckling is treated on each scale individually, i.e., we ignore modes that span over both scales (cross-modes). In order to determine the homogenized mechanical behavior on the microscopic scale, we describe a representative lattice structure by geometrically exact rods. This has the advantage of less complexity compared to a continuum model. Also, this formulation allows for large displacements of a rod’s center line and for large rotations of each cross-section [14, 43, 44]. It is therefore used in applications to model slender structures such as nanowires, cables, and biological tissue [22, 23, 47]. The use of this theory to capture homogenized properties of lattices has already been introduced in detail in [18, 24, 28]. In this contribution, numerical homogenization is used to evaluate the homogenized stiffness of the lattice and the limit load, which is the minimal load leading to microstructural buckling. We use a nonlinear model to capture the limit load, as this approach yields more accurate results than linear buckling analysis [30, 38]. The limit load depends on the design of the microstructure as well as the acting macroscopic stress. Using the homogenized data, we build a worst-case model for the limit load: We account only for the limit load with the smallest absolute value with respect to all possible stress situations. As a consequence, our worst-case model only depends on the microstructure’s layout and the magnitude of the applied stress.

Our microstructure is parametrized by the diameter of the lattice rods. We precompute homogenized data for different stress scenarios and microstructure parameters, and calculate the worst-case for each design. Then, we apply an interpolation scheme to obtain the limit loads on the continuous parameter space. The principal idea of this method was introduced in the work of [7] and reduces computational effort during design optimization drastically. The interpolated worst-case model is then used in buckling optimization problems with the local lattice porosity or rod diameter, respectively, as design variable. To keep things simple, we employ linear models on the macroscopic scale. However, our approach can also be used in conjunction with nonlinear theory.

Our motivation for the choice of nonlinear models on the microscopic scale and linear models on the macroscopic scale is as follows. While we accept an error margin in macroscopic buckling, we want to be protected against microscopic buckling, which also motivates our worst-case approach. Hence, a lower bound on the microscopic critical stress has to be predicted accurately. Computations on the microscopic scale happen independent of the actual optimization procedure and higher computation times are acceptable, in particular because simulations for different parameter sets are independent of each other and can be run in parallel. During optimization efficiency is important, which is why we employ linear models on the macroscopic scale.

The remainder of this contribution is structured as follows: In Sect. 2, we introduce the state equations for linear elasticity and buckling analysis. Section 3 describes how beam lattices can be modeled based on geometrically exact rods. Based on this, we present the method of numerical homogenization in Sect. 4. This section also describes the design of our exemplary lattice microstructure used in numerical examples. Section 5 gives details on the homogenization with respect to buckling instabilities. In particular, we give the load scenarios that have been used to obtain the worst-case model, which is presented in Sect. 6. In Sect. 7, we formulate a two-scale sizing optimization problem. Numerical results for three different variations of this problem are presented in Sect. 8. Finally, we complete with conclusions in Sect. 9.

2 Linear elasticity and buckling analysis

In this section, we briefly recap the state equations for linear elasticity and buckling analysis on an algebraic level, as given by [48]. For continuous formulations in weak form, interested readers are referred to the work of Neves [37]. We assume a linear elasticity setting and linear bifurcation buckling condition. This means that the prebuckling displacement, stresses, and strains vary linearly with the applied load and that the load factor, which indicates stability, appears linearly in the bifurcation eigenvalue problem. We will not investigate a structural behavior beyond its critical buckling point. Linear buckling analysis of a structure under a given load consists of two steps: First, we solve the linear elasticity state equation for the structural displacement. Then, an eigenvalue problem is solved, where the eigenvalues correspond to bifurcation points, and eigenvectors are interpreted as buckling modes of deflection.

Let us consider a body $\Omega \subset {\mathbb {R}}^3$ and its discretization $\Omega _\vartriangle =\bigcup _{e=1}^\text {M} \Omega _e$ by $\text {M}$ finite elements. Then, the state equation of linear elasticity for $\Omega _\vartriangle$ is given by [56]:

$$\begin{aligned} \varvec{\textsf{K}} (\varvec{\rho })\varvec{u} = \varvec{f}, \end{aligned}$$

(1)

where $\varvec{u}$ is the sought-for vector of displacements, $\varvec{\rho }\in (0,1]^\text {M}$ is the field of the relative lattice volume, and $\varvec{f}$ is the applied load vector. In the following, we denote the solution of (1) by $\varvec{u}(\varvec{\rho })$. The relative lattice volume can be calculated from the lattice rods’ diameters. The so-called stiffness matrix is given by

$$\begin{aligned} \varvec{\textsf{K}} (\varvec{\rho }) = \mathop {\mathrm {\bigwedge }}\limits _{e=1}^\text {M} \sum _{k=1}^{\text {N}_\text {ip}} c_{e,k} \varvec{\textsf{B}} _{e,k}^\top \varvec{C}(\rho _e) \varvec{\textsf{B}} _{e,k}, \end{aligned}$$

(2)

with assembly operator denoted by $\mathop {\mathrm {\bigwedge }}\limits$ and number of integration points $\text {N}_\text {ip}$. $\varvec{C}(\rho _e)$ is the elasticity tensor, which depends on the relative lattice volume in element e. $\varvec{\textsf{B}} _{e,k}$ is the strain–displacement matrix of element e evaluated in the kth integration point and contains derivatives of the finite element’s shape functions [8]. The factor

$$\begin{aligned} c_{e,k} = \det (\varvec{J}_e) w_{e,k} \end{aligned}$$

(3)

contains the Jacobian determinant $\det (\varvec{J}_e)$ of element e and the integration weight $w_{e,k}$ associated with the kth integration point of said element.

The buckling equation is given by the eigenvalue problem

$$\begin{aligned} \left[ \varvec{\textsf{K}} (\varvec{\rho })-\Lambda \, \varvec{\textsf{G}} (\varvec{\rho },\varvec{u}(\varvec{\rho }))\right] \varvec{\phi } = \varvec{0}, \end{aligned}$$

(4)

and is solved for pairs of eigenvalues $\Lambda _\ell$ and eigenvectors $\varvec{\phi }_\ell$, $\ell \le \text {M}$. Eigenvalues of (4) are also called load factors and the minimal eigenvalue is denoted as critical load factor or buckling load factor. The critical load under which buckling occurs can be computed by multiplying the applied load $\varvec{f}$ with this buckling load factor. If the critical load factor is less than or equal to one, the structure buckles; otherwise, the structure is stable with respect to the applied load. The stress stiffness matrix (or geometric stiffness matrix) [36] in (4) is given by

$$\begin{aligned} \varvec{\textsf{G}} (\varvec{\rho },\varvec{u}(\varvec{\rho })) = \mathop {\mathrm {\bigwedge }}\limits _{e=1}^\text {M} \sum _{k=1}^{\text {N}_\text {ip}} c_{e,k} \widetilde{\varvec{\textsf{B}}}_{e,k} \varvec{\sigma } _e(\varvec{u_e}(\varvec{\rho })) \widetilde{\varvec{\textsf{B}}}_{e,k}. \end{aligned}$$

(5)

The averaged stress in element e is numerically evaluated as

$$\begin{aligned} \varvec{\sigma } _e(\varvec{u_e}(\varvec{\rho })) = \frac{1}{\text {N}_\text {ip}} \sum _{k=1}^{\text {N}_\text {ip}} \varvec{C}(\rho _e) \varvec{\textsf{B}} _{e,k} \varvec{u_e}(\varvec{\rho }), \end{aligned}$$

(6)

and $\widetilde{\varvec{\textsf{B}}}_{e,k}$ is the derivative of the matrix of the shape functions [48]. Note that both $\varvec{\textsf{B}} _{e,k}$ and $\widetilde{\varvec{\textsf{B}}}_{e,k}$ contain derivatives of the shape functions, but in distinct order. Due to (5) and (6), the stress stiffness matrix depends on the solution of (1) and thus on the load $\varvec{f}$.

3 Microstructural modelling

In this contribution, truss lattices are modeled by the theory of geometrically exact nonlinear rods [43, 44]. This formulation is able to capture large deformations of the beams center line $\textbf{r}:\left[ 0,L\right] \rightarrow {\mathbb {R}}^3$ and large rotation of the rod’s cross section and goes back to the Cosserat brothers [14]. Thereby, the rotation is parametrized by the rotation tensor $\textbf{R}:\left[ 0,L\right] \rightarrow SO (3)$, where $SO (3)$ denotes the special orthogonal group, whose elements have the properties $\textbf{R} ={\textbf{R}}^{T }$ and $det \left( \textbf{R} \right) =+1$. Further, L indicates the length of the rod. Both $\textbf{r}$ and $\textbf{R}$ define the kinematic unknowns of the presented theory. The rod’s undeformed configuration is given by

$$\begin{aligned} \textbf{X} (s,\textbf{X} _{CS })=\varvec{s}\left( s\right) +\textbf{X} _{CS }, \end{aligned}$$

(7)

where $\displaystyle {\varvec{s}\left( s\right) =\varvec{s}_0+s\,\textbf{D}_{3}}, s\in \left[ 0,L\right]$ denotes the position along the rod’s undeformed and straight arc by a starting point $\varvec{s}_0$ and the direction $\textbf{D}_{3}$. Material points lying in the rod’s cross section are denoted by $\textbf{X} _{CS }=X _{CS _{\alpha }} \textbf{D}_{\alpha }$, with $\alpha =1,\,2$, where $\textbf{D}_{i}$ build an orthonormal basis. The spatial configuration is given by

$$\begin{aligned} \textbf{x} \left( s,\textbf{X} _{CS }\right) =\textbf{r} \left( s\right) +\textbf{R} \left( s\right) \textbf{X} _{CS }. \end{aligned}$$

(8)

The derivative of the kinematic unknowns with respect to the rod’s arc length s returns the translational strains ${\textbf{v} \left( s\right) =\textbf{r} '\left( s\right) :={\frac{\partial \textbf{r}}{\partial s}\left( s\right) }}$ and the rotational strains ${\textbf{k} \left( s\right) =ax \left( \textbf{R} '\left( s\right) {\textbf{R}}^{T } \left( s\right) \right) :=ax {\left( \frac{\partial \textbf{R}}{\partial s}\left( s\right) {\textbf{R}}^{T } \left( s\right) \right) }}$, also known as curvature, where the operator $ax \left( \bullet \right)$ extracts the axial first-order tensor corresponding to the skew-symmetric tensor $\bullet$.

Ignoring distributed forces and moments, the balances of linear and angular momentum read as

$$\begin{aligned} \begin{aligned} \textbf{n} '\left( s\right)&=\varvec{0},\\ \textbf{m} '\left( s\right) +\textbf{r} '\left( s\right) \times \textbf{n} \left( s\right)&=\varvec{0},\\ \end{aligned} \end{aligned}$$

(9)

where $\textbf{n}$ describes internal forces and $\textbf{m}$ internal moments, the work conjugated quantities to the strains and curvatures, respectively. Together $\textbf{n}$ and $\textbf{m}$ are named stress resultants [25, 32]. Further, we collectively denote the translational strains $\textbf{v}$ and rotational strains $\textbf{k}$ as strain prescriptors.

In order to model rod lattices, the interaction of two intersecting rods must be properly captured. This is done by constraining the kinematic unknowns of a slave rod (denoted by subscript S) to the kinematics of a master rod (denoted by a subscript M). Assume that the slave rod with $s_S\in \left[ 0,L_S\right]$ intersects with the master rod $s_M\in \left[ 0,L_M\right]$ at $s_{S_I}$ and $s_{M_I}$ respectively. Then, the kinematic unknowns of the slave rod are constrained to the kinematic unknowns of the master rod.

$$\begin{aligned} \begin{aligned} \textbf{r} _S\left( s_{S_I}\right) =\textbf{r} _M\left( s_{M_I}\right) ,\quad \textbf{R} _S\left( s_{S_I}\right) =\textbf{R} _M\left( s_{M_I}\right) . \end{aligned} \end{aligned}$$

(10)

These constraints ensure that the intersection of the rods remains fixed throughout the deformation. Further, the angle between intersecting rods remains constant. Instead of constraining the rotations of two intersecting rods to realize semi-rigid joints, the rods are connected by a rotational spring with stiffness $\kappa$. Then, rigid joints are obtained for $\kappa \rightarrow \infty$, while pinned joints result from $\kappa \rightarrow 0$ [41]. Note, that both limits can lead to conditioning problems of the resulting stiffness matrix, which requires thoughtful treatment. In this contribution, we focus on rigid joints.

When considering intersecting rods, one may face the following issue: The theory of geometrically exact rods assumes the rods to be one-dimensional bodies. The dimension of the cross section is only considered in the constitutive behavior of the rod [4]. At the intersections, the angle between the intersecting arcs is constrained and remains constant throughout deformation. In the proximity of the intersection, however, the angle between both center lines may deviate from the fixed angle. This effect may be neglected for rods with large aspect ratio L/D, where D denotes the diameter of the rod’s cross section. In the case of small aspect ratio, the intersection must be stiffened to capture the accumulation of material as shown in Fig. 1 [16, 53]. To this end, the rod’s stiffness is increased by scaling the Young’s modulus by a factor of 10 in the proximity of the intersection. Later in this contribution, we will compare stiffened and flexible intersections.

Fig. 1

Visualization of the deformed configuration of two intersecting rods. In the first case, the angle between two intersecting center lines remains constant. In the second case, due to stiffening of the rods’ properties in the vicinity of the intersection, the angle between the rods’ contours remains nearly constant. Compared with three-dimensional continuum mechanics, the latter case yields more accurate results

4 Homogenization

Numerical homogenization represents an established method to evaluate the mechanical properties of a material with a distinct microstructure. Here, the microstructure is given by a periodic lattice and constitutes the material of a structural part on the macro-scale. Numerical homogenization methods require the separation of scales: The length-scale of the macroscopic scale (denoted by $\text {mac}$) must be larger by magnitudes than the length-scale of the substituting microscopic scale (denoted by $\text {mic}$) [19, 20]

$$\begin{aligned} l^\text {mac}\gg l^\text {mic}. \end{aligned}$$

(11)

In the context of structural parts consisting of lattice structures, this means that the structural part is significantly larger than a representative volume element (RVE) of the microstructure. The RVE may be considered as a material point of the macro-scale. To transfer mechanical properties from the micro- to the macro-scale we make use of numerical homogenization. This technique approximates the macroscopic properties of the microstructure by properties of a homogeneous material. Here, we briefly recapture the macro-to-micro and micro-to-macro transitions but restrict ourselves to the most relevant equations. For further details, we refer to Herrnböck and Steinmann [24] and other authors [18, 52].

The RVE must always fulfill the Hill–Mandel condition. This condition states that the variation of the work performed on the macro-scale equals the volume average of the variation of work on the micro-scale

$$\begin{aligned} {\textbf {P}} ^\text {mac}:\delta \textbf{F} ^\text {mac}=\frac{1}{V^\text {mic}} \int _{\text {RVE}}{\textbf {P}} ^\text {mic}:\delta \textbf{F} ^\text {mic}\,d V, \end{aligned}$$

(12)

where the Piola stress ${\textbf {P}}$ is work conjugated to the deformation gradient $\textbf{F}$ and $V^\text {mic}$ is the volume of the RVE. Further, a field of fluctuations is superimposed to the deformed configuration of the RVE such that the resulting microscopic deformation gradient ${\textbf{F} ^\text {mic}=\textbf{F} ^\text {mac}+\tilde{\textbf{F}}}$. After some straightforward computations starting from Eq. 12 and replacing continuous quantities with rod specific quantities, one obtains periodic boundary conditions for the rod’s kinematic unknowns that fulfill the Hill–Mandel condition. In particular, fluctuations of the kinematic unknowns $\textbf{r}$ and $\textbf{R}$ are equal on periodic boundaries of the RVE (denoted by $+$ and −).

$$\begin{aligned} \delta \tilde{\textbf{r}}^+=\delta \tilde{\textbf{r}}^-, \quad \delta \tilde{\textbf{R}}^+=\delta \tilde{\textbf{R}}^-. \end{aligned}$$

(13)

Here, for sake of general validity, the Hill–Mandel condition is stated for the case of finite deformations [24]. However, the resulting periodic boundary conditions on the RVE boundary are also valid for a prescribed linearized macroscopic strain field $\varvec{\varepsilon }^\text {mac}$.

Finally, we impose a macroscopic strain field on the RVE by prescribing the deformation of the RVE’s periodic edges denoted by $+$ and − with

$$\begin{aligned} \varvec{u}^+=\varvec{u}^- +\varvec{\varepsilon }^\text {mac}\,\varvec{d}^{\pm }, \end{aligned}$$

(14)

where $\varvec{d}^{\pm }$ denote a periodicity vector, relating the periodic boundaries one to the other [29]. On the boundary of the RVE, we prescribe periodic boundary conditions on the fluctuations, as displayed in Eq. 13. To compute the homogenized macroscopic stress response $\varvec{\sigma } ^\text {mac}$, we use

$$\begin{aligned} \varvec{\sigma } ^\text {mac}=\frac{1}{V^\text {mic}}\sum _{I=1}^{\text {n}_\text {r}}{\textbf{n}}_I\otimes \varvec{s}_I. \end{aligned}$$

(15)

The contact force and the material coordinate of a tip I of a rod, which is on the RVE’s node, are denoted by ${\textbf{n}}_I$ and $\varvec{s}_I$, respectively. In total, $\text {n}_\text {r}$ nodes build the RVEs edges. For more detailed insights, see Herrnböck and Steinmann [24].

Figure 2 depicts the exemplary lattice structure we focus on in our numerical examples.

Fig. 2

Visualization of the exemplary periodic rod lattice, used in our numerical examples. The unit cell has edge length l and consists of 14 rods that meet in the cells center

Each unit cell consists of 14 intersecting rods with a circular cross section. The diagonal rods are discretized into 10 elements, whereas the rods aligned with the RVE’s axes are discretized into 9 elements. In both cases, the kinematic unknowns are approximated with linear shape functions. The diameter of the cross section of each rod is given by D, the edge length of the unit cell by l. The relative volume $\rho$ can be calculated by

$$\begin{aligned} \rho (D) = \frac{V(D)}{V^\text {mic}} = \frac{V(D)}{l^3}, \end{aligned}$$

(16)

where V(D) is the volume of the lattice, which depends on the rods’ diameter D. Note that in this context, all rods have the same diameter and we do not account for individual scaling. We model the joints by increasing the stiffness of the beam elements, which are within a given radius around the intersection of lattice rods. The radius is determined by the rods’ diameter. The elastic behavior of a rod is obtained by integration of stiffness values over the rod’s cross section. The formulation was firstly derived by Arora et al [4] and further elaborated by Herrnböck et al [25, 46]. We evaluate the homogenized stiffness of the unit cell by approximating the derivative of stress with respect to strain by finite differences [33, 34]. The lattice cell presented above results in cubic symmetric material behavior, which is fully determined by three material parameters: shear modulus $\mu ^\text {mac}$, Young’s modulus $E^\text {mac}$, and Poisson’s ratio $\nu ^\text {mac}$. For instance, a unit cell with edge length $l={10\,\mathrm{\text {m}\text {m}}}$, cross sectional diameter $D={1\,\mathrm{\text {m}\text {m}}}$ and isotropic material with the parameters $\mu ^\text {mic}={80\,\mathrm{\text {G}\text {Pa}}}$ and $E^\text {mic}={207\,\mathrm{\text {G}\text {Pa}}}$ [45] returns following macroscopic properties

$$\begin{aligned} \mu ^\text {mac}={1257\,\mathrm{\text {M}\text {Pa}}},\quad E^\text {mac}={2147\,\mathrm{\text {M}\text {Pa}}},\quad \nu ^\text {mac}=0.3, \end{aligned}$$

(17)

when not stiffening the rods’ intersections and

$$\begin{aligned} \mu ^\text {mac}={1405\,\mathrm{\text {M}\text {Pa}}},\quad E^\text {mac}={2374\,\mathrm{\text {M}\text {Pa}}},\quad \nu ^\text {mac}=0.3, \end{aligned}$$

(18)

when stiffening the rods’ intersections. These values are sufficient to compute the mechanical behavior of a structural part in its linear regime. However, nonlinearities in the material behavior may appear due to buckling of single rods in the microstructure as a result of structural instabilities. To design a micro-buckling-free structure, the knowledge of limit loads is crucial. Comparing the material parameters in Eq. 17 with those in Eq. 18 shows that stiffening the rod’s intersections results in a stiffer macroscopic material behavior. The homogenization framework is validated with a primitive cubic lattice in Appendix A.

5 Limit loads

In this section, homogenized limit loads for the microstructure are determined. These are defined as loads at which the microstructure faces instabilities. Instabilities are of a structural nature for lattices. When single or multiple rods in the lattice buckle, the mechanical response shows a distinct nonlinearity [24]. In a mathematical context, structural instabilities occur when one or multiple eigenvalues $\lambda _i$ of the problem’s system matrix are no longer positive. This property is utilized to evaluate the load leading to instability ([24] and citations therein). The instability point is found by incrementally increasing the load until one eigenvalue approaches zero. Figure 3 sketches a strain–stress curve of an exemplary Eulerian buckling beam. The load $\sigma$ increases linearly with the applied axial strain $\varepsilon$. A bifurcation point may be observed ($\lambda _i=0$), where two possible paths appear. An unstable primary path ($\lambda _i<0$) and an energetically favorable secondary path ($\lambda _i>0$). The secondary path represents the buckled configuration of the rod, whereas the primary path represents the straight unbuckled, but unstable configuration of the same rod.

Fig. 3

Sketch of a load–displacement curve of a Eulerian buckling beam. After a linear increase in $\sigma$ an unstable primary path and a stable secondary path show two possible configurations of the beam

5.1 Considered load cases

The microscopic limit load $\varvec{\sigma } _l$ depends on an applied macroscopic stress $\varvec{\sigma }$ as well as the microstructure’s design. For simplicity, in the present article we will describe the design of our exemplary microstructure shown in Fig. 2 by a single value, namely its volume $\rho (D)$ given by (16). More complex parameterizations and other lattice structures can be used in our method without major changes. To evaluate $\varvec{\sigma } _l$, a macroscopic strain field is applied to the RVE. This field calculates with $\varvec{\varepsilon }(\varvec{\sigma })=\varvec{C}^{-1}\varvec{\sigma }$, where $\varvec{C}$ denotes the tangent stiffness, which is obtained from the homogenized material properties of Sect. 4.¹ A linear relation between stress and strain may be assumed in the pre-buckled configuration, and thus, the stiffness tensor of the RVE is computed using finite differences for the derivative of stress with respect to strain [44]. The stress field is incrementally increased until a structural instability is attained and the limit load $\varvec{\sigma } _l$ is computed by Eq. 15. We denote the absolute value of the limit load by

$$\begin{aligned} \lambda (\rho ,\varvec{\sigma }) = \Vert \varvec{\sigma } _l(\rho ,\varvec{\sigma })\Vert , \end{aligned}$$

(19)

which is also called microscopic buckling load factor. To precompute limit loads for all possible stress situations, we would have to examine all stresses ${\varvec{\sigma } = (\sigma _{11},\sigma _{22},\sigma _{33},\sigma _{23},\sigma _{13},\sigma _{12}) \in {\mathbb {R}}^6}$. Thankfully, this can be reduced to the investigation of a subspace of ${\mathbb {R}}^6$ as follows: Due to the linear material behavior up to the bifurcation point, the homogenized limit load and thus the microscopic buckling load factor can be assumed to depend linearly on the applied stress:

$$\begin{aligned} \lambda (\rho ,\varvec{\sigma }) = \tfrac{1}{\Vert \varvec{\sigma } \Vert } \lambda \left( \rho ,\tfrac{\varvec{\sigma }}{\Vert \varvec{\sigma } \Vert }\right) . \end{aligned}$$

(20)

It is thus sufficient to examine stresses on the unit sphere surface $S^5\in {\mathbb {R}}^6$ instead of the whole six-dimensional stress space.

For the five-dimensional stress sphere, one can choose a specific coordinate system: two coordinates correspond to the rotation of the stress with respect to the RVE (or vice versa, respectively) and three coordinates describe the type of stress. Special types of stresses include inter alia uniaxial, biaxial, and triaxial compression. To obtain limit loads for different stress scenarios, we choose the following discretization of the stress sphere: For each of the mentioned three special types of stresses we consider 250 orientations of the RVE equally distributed on 1/8 of a three-dimensional sphere, making use of the symmetry of our exemplary lattice. For this, each point $\textbf{X}$ in the material configuration of the RVE is rotated, which results in a transformed configuration $\textbf{X} ^{\star }$ by

$$\begin{aligned} \textbf{X} ^{\star }=\textbf{R} _{\textbf{E}_{1}}(\vartheta ) \,\textbf{R} _{\textbf{E}_{2}}(\varphi ) \textbf{X}. \end{aligned}$$

(21)

Here, $\textbf{R} _{\textbf{E}_{1}}(\vartheta )$ rotates around axis $\textbf{E}_{1}$ with angle $\vartheta$ and $\textbf{R} _{\textbf{E}_{1}}(\vartheta )$ around axis $\textbf{E}_{2}$ with angle $\varphi$. For different orientations of the RVE but fixed $\varvec{\sigma }$, different limit loads $\varvec{\sigma } _l$ may result. Note that a rotation of the RVE is equivalent to an inverse rotation of the stress tensor $\varvec{\sigma }$, which could be easier to implement. We only consider uniaxial, biaxial and triaxial compression for different rotations of the RVE to reduce the large amount of load cases and orientations to a manageable size. For the case of uniaxial compression, Fig. 4 displays the microscopic buckling load factor for different orientations of an exemplary RVE. Here, the RVE comprises one unit cell only and each point defines the limit load for a rotated RVE subject to uniaxial compression. For our exemplary lattice structure, the minimum limit load is obtained independent of the lattice rods’ diameter, when the RVE is aligned with the frame directions $\textbf{E}_{i}, i=1,\,2,\,3$. This is explained by considering the topology of the lattice from Fig. 2. The longest rods in the RVE are aligned with the space directions. These rods meet with the rods of adjacent RVEs in such a way, that the actual length of the rods is l, while the diagonal rods of adjacent RVEs support each other in the corners of an RVE resulting in a length of $\tfrac{\sqrt{3}}{2} l$. According to the Eulerian buckling theory, the more slender a rod is, the lower the buckling load and thus the limit load of the RVE [31].

Fig. 4

Spatial distribution of the critical load of an RVE under uniaxial compression. The magnitude of the critical load is color-coded. A minimal buckling load is present in $\textbf{E}_{i}, i=1,\,2,\,3$ direction. In the plane diagonals, a maximum is visible

With an RVE containing only one unit cell, homogenization with periodic boundary conditions can only capture buckling modes with a mode length that is smaller than the unit cell’s size. To capture buckling modes spanning over more than just one cell [19, 24], there are in general two approaches. Often Bloch-Floquet theory is used [37], which uses special complex valued boundary conditions on the RVE. Here, we choose the cell repetition approach, where multiple unit cells are included in the RVE and ordinary periodic boundary conditions are applied. In [26, Section 4.3], we have shown, that this is equivalent for a special Bloch-Floquet discretization. We perform homogenization for RVEs that contain ${\text {n}_{\text {RVE}}} ^3$ unit cells for ${\text {n}_{\text {RVE}}} \in \{1,\ldots ,5\}$. In total, this results in 3750 homogenizations for one microstructure with a given relative lattice volume or rod diameter, respectively. This framework is repeated for RVEs of different relative volume.

5.2 Limit loads as a function of lattice parameters

As discussed above, both the relative volume and the number of unit cells within the RVE influence the limit loads. Figures 5, 6 and 7 show the minimal limit load for uniaxial, biaxial, and triaxial compression. Here, we refer to the minimum as the minimal limit load for all considered orientations of the RVE. The plots show that the limit load increases with increasing relative volume. This is consistent with a stiffness gain of the RVE for increasing relative volume. Further, a dependency on ${\text {n}_{\text {RVE}}}$ is visible. For our exemplary lattice structure, we observed that for all considered cases (independent of the volume) an RVE with ${\text {n}_{\text {RVE}}} =2$ results in the smallest limit loads. In contrast, the RVE with only one repetition of the unit cell yields large limit loads. This is due to the limitation of homogenization with periodic boundary conditions being only able to capture buckling modes with a wave length shorter or equal to the RVE’s size as mentioned above. It is notable that the displayed results show the limit loads for RVEs with stiffened intersections (see Sect. 4). The limit loads for unstiffened intersections of rods show lower values. A comparison between the stiffened and unstiffened values is shown in Appendix B. In all figures, one may observe that the limit load increases drastically for high volumes of the RVE. For the sake of completeness, it should be mentioned that the limit loads for ${\text {n}_{\text {RVE}}} =2$ and ${\text {n}_{\text {RVE}}} =4$ are equal, except for marginal differences that have their origin in numerical issues. This was expected: the values for ${\text {n}_{\text {RVE}}} =4$ should be smaller or equal than the ones for ${\text {n}_{\text {RVE}}} =2$, as the buckling modes of an RVE with ${\text {n}_{\text {RVE}}} =2$ can also be seen in the analysis of an RVE with ${\text {n}_{\text {RVE}}} =4$.

Fig. 5

Lowest limit load in terms of orientation of the RVE for the case of uniaxial compression of the RVE. A dependency on ${\text {n}_{\text {RVE}}}$ is visible. The lowest limit loads are observed with ${\text {n}_{\text {RVE}}} =2$. Note, that we expect smaller or equal $\sigma _{l_{33}}$ for ${\text {n}_{\text {RVE}}} =4$ than for ${\text {n}_{\text {RVE}}} =2$. For a relative volume of 0.2 this is not seen in the data due to numerical issues

Fig. 6

Lowest limit load in terms of orientation of the RVE for the case of biaxial compression of the RVE. A dependency on ${\text {n}_{\text {RVE}}}$ is visible. The lowest limit loads are observed with ${\text {n}_{\text {RVE}}} =2$. The discrepancy between the results from ${\text {n}_{\text {RVE}}} =1$ and ${\text {n}_{\text {RVE}}} \ge 2$ is observed

Fig. 7

Lowest limit load in terms of orientation of the RVE for the case of triaxial compression of the RVE. A dependency on ${\text {n}_{\text {RVE}}}$ is visible. The lowest limit loads are observed with ${\text {n}_{\text {RVE}}} =2$. Limit loads for volumes $\ge 0.1$ and ${\text {n}_{\text {RVE}}} =3,\,4$ are missing due to numerical issues

6 Worst-case model

Next, based on the idea in [26], we combine all data in a worst-case model. Having evaluated homogenized buckling load factors for different numbers of cell repetitions ${\text {n}_{\text {RVE}}} \in {\mathbb {N}}$ and stresses on the unit stress sphere $\varvec{\sigma } \in S^5$, we select the smallest buckling load factor with respect to all unit stresses and values of ${\text {n}_{\text {RVE}}}$:

$$\begin{aligned} \lambda _\text {wc}(\rho ) = \min _{\varvec{\sigma } \in S^5, {\text {n}_{\text {RVE}}} \in {\mathbb {N}}} \lambda (\rho , \varvec{\sigma }, {\text {n}_{\text {RVE}}}) \end{aligned}$$

(22)

This worst-case model depends only on the local volume fraction. In practice, the unit sphere $S^5$ is discretized and the number of cell repetitions is bounded from above. The worst case is thus only a worst case with respect to the discretization resolution and maximal number of cell repetitions. In our case, the discretization of the unit stress sphere is done by choosing special types of stresses (uni-, bi-, and triaxial) and 250 different rotations of the RVE with respect to the applied stress (see Sect. 5.1). Note that this model can be used in arbitrary macroscopic settings. It describes the smallest buckling load factor for our chosen lattice with respect to all possible stress situations.

During optimization on the discretized macroscopic domain $\Omega _\vartriangle =\bigcup _{e=1}^\text {M} \Omega _e$, the microscopic buckling load factor has to be determined for all $\Omega _e$. We parametrize the unit cell by its relative volume $\rho$, which can be computed from the lattice rods diameters by (16). Note that in this context, inside each unit cell there are only rods with the same diameter. This parametrization allows us to precompute the worst-case buckling load factor for some volumes and then apply an interpolation scheme to obtain load factors on the continuous parameter space [7]. This greatly reduces the computational effort during structural optimization: Using the parameterization-and-interpolation approach the expensive solution of a homogenization problem for each finite element $\Omega _e$ and each design update is replaced by a cheap evaluation of the interpolation model. The microscopic buckling load factor is then given by

$$\begin{aligned} \lambda ^I(\rho ,\varvec{\sigma }) = \tfrac{1}{\Vert \varvec{\sigma } \Vert }\lambda _\text {wc}^I(\rho ), \end{aligned}$$

(23)

where $\lambda _\text {wc}^I$ is the interpolated version of (22). For the interpolation, we opt for a piecewise cubic Hermite approach [9] that results in a continuously differentiable model, which allows us to conduct gradient-based optimization later.

The worst-case approach additionally reduces computational effort during the construction of the interpolation model, as we only have to perform one-dimensional interpolation. However, it comes at the cost of possible underestimation of the actual load factor, which in turn may lead to oversized lattice rods in the optimized design. This can be overcome by replacing the worst-case approach with other interpolation models, e.g., a $C^1$-Interpolation in the six-dimensional parameter space $(\rho ,\varvec{\sigma })\in (0,1]\times S^5$. However, due to the curse of dimensionality, this requires sophisticated interpolation schemes, e.g., the differentiable sparse grid approach from [49].

7 Optimization problem formulation

We formulate different two-scale sizing problems. In contrast to topology optimization, where usually a solid/void design is of interest, we vary the diameter D of the lattice rods from ${0.5\,\mathrm{\text {m}\text {m}}}$ to ${1.8\,\mathrm{\text {m}\text {m}}}$ for a unit lattice cell with edge length of $l={10\,\mathrm{\text {m}\text {m}}}$. This corresponds to a scaling of the lattice volume fraction between $1.8\%$ and $20\%$, i.e., our admissible set for the lattice volume $\rho$ is given by

$$\begin{aligned} \mathcal {U}_{\text {ad}}= [0.01841, 0.2022]^\text {M}. \end{aligned}$$

(24)

The lower bound on the lattice rods ensures manufacturability in powder-bed-based additive manufacturing. The chosen upper bound guarantees a sufficient length-to-diameter ratio of the truss lattice, such that our beam model is valid.

We want to achieve structures with minimal mechanical compliance and good buckling stability. We treat this multi-objective problem [13] with the $\varepsilon$ constraint method [35]. For this, we choose the compliance as objective and transform the macro- and microscopic stability into inequality constraints with a lower bound v. The microscopic buckling load factor $\lambda _e^I$ for each finite element e is obtained via the worst-case model (23). The macroscopic load factors are given as solutions of the buckling state equation (4). For better numerical stability, we include not only the critical, i.e., smallest, load factor $\Lambda _1$ in the problem, but the six smallest macroscopic load factors. In summary, the optimization problem reads as follows:

$$\begin{aligned}&\min _{\varvec{\rho }\in \mathcal {U}_{\text {ad}}} \varvec{f}^\top \varvec{u}(\varvec{\rho }), \end{aligned}$$

(25)

$$\begin{aligned}&s.t.\ \Lambda _k(\varvec{\rho }) \ge v, \qquad k=1,\ldots ,6 \end{aligned}$$

(26)

$$\begin{aligned}&\lambda _e^I(\rho _e,\varvec{\sigma } _e(\varvec{\rho })) \ge v, \qquad e=1,\ldots ,\text {M} \end{aligned}$$

(27)

As the microscopic buckling load factor depends on the local stress $\varvec{\sigma } _e$, which in turn depends on the total design $\varvec{\rho }$, the derivatives of (27) are computationally expensive. For each of the constraints an adjoint problem of the same size as the state equation, (1) has to be solved [54]. To circumvent this, we globalize all local constraints by aggregating them into the following function:

$$\begin{aligned} g(\varvec{\rho }) = \frac{1}{\text {M}}\sum _{e=1}^\text {M} \max \left( v-\lambda _e^I(\rho _e,\varvec{\sigma } _e(\varvec{\rho })),0\right) ^2 \end{aligned}$$

(28)

This function is the normalized sum of the squared violations of (27), motivated by the method of least squares in regression analysis. Only load factors that are below the given threshold v contribute to the function value. The derivative of this function is computed using only a single adjoint equation in which the right-hand side is a sum of the adjoint right-hand sides of the local constraints. Thus, only one adjoint problem has to be solved, which reduces the computational effort drastically. We replace the local constraints by this globalized version, add a volume constraint, and get the final version of our optimization problem as follows:

$$\begin{aligned}&\min _{\varvec{\rho }\in \mathcal {U}_{\text {ad}}} \varvec{f}^\top \varvec{u}(\varvec{\rho }), \end{aligned}$$

(29)

$$\begin{aligned}&s.t.\ \Lambda _k(\varvec{\rho }) \ge v, \qquad k=1,\ldots ,6 \end{aligned}$$

(30)

$$\begin{aligned}&g(\varvec{\rho }) \le \epsilon , \end{aligned}$$

(31)

$$\begin{aligned}&\sum _{e=1}^\text {M} \rho _e \le V_0. \end{aligned}$$

(32)

Note, that (31) is relaxed by a small $\epsilon >0$ to increase numerical stability.

8 Numerical results

We investigate three different variations of the problem formulated in the previous section:

• (A) We minimize the compliance under a macroscopic buckling constraint, but ignore microscopic buckling. In other words, we drop Eq. 31.

• (B) We drop Eq. 30 and minimize the compliance with constraints on the microscopic buckling load factors while ignoring macroscopic buckling.

• (C) We investigate the problem as given, i.e., we minimize the compliance while constraining both macroscopic and microscopic buckling.

For the volume constraint, we choose an upper bound of $5\%$ of the design domain’s volume, i.e., $V_0 = 0.05\, |\Omega _\vartriangle |$.

We perform optimization with a column-shaped design domain with square cross section and a side-to-height ratio of 1:6 as depicted in Fig. 8. The design domain is discretized by $10\times 10\times 60$ trilinear finite elements. At the top, we apply a distributed force of ${1\,\mathrm{\text {N}}}$. Thus, the macroscopic load factor directly represents the critical load. We fix all degrees of freedom for nodes in a central region of the bottom face, while all other nodes at the bottom are only fixed in vertical direction. These boundary conditions are chosen to prevent stress peaks in the corners of the bottom face.

Fig. 8

The design domain is a cuboid with edge length ratio 1:1:6. In a central region of the bottom (red), all degrees of freedom are fixed, while at the remaining bottom face (blue) only movement in vertical direction is prevented. A distributed force acts on the entire top face

Additionally, we regularize the design through a density filter (see [10]) with a radius of 1.9 times the edge length of a finite element, which results in an average neighborhood of 22 elements.

8.1 Pure macroscopic buckling constraint

Good macroscopic buckling resistance is achieved by structures with a large second area moment perpendicular to the loading direction. Thus, we expect a design similar to a square tube if we require a large macroscopic critical load. The optimized design of a pure compliance minimization is already similar to a square tube (see Fig. 9); there is thick lattice at the design domain’s vertical edges. Due to the volume constraint, however, it is not possible for the optimization algorithm to also put thick lattice at the domain’s sides. Nevertheless, this design already exhibits a relatively large buckling resistance of ${2.53\,\mathrm{\text {N}}}$. At the top, there is intermediate design to support the entire loaded face. Between the regions of thicker lattice, the diameter of the lattice rods is at the lower bound of ${0.5\,\mathrm{\text {m}\text {m}}}$. This is an indicator that designs with better compliance could be achieved if the lattice rods were allowed to get thinner or, at the end, even vanish.

Fig. 9

Optimized design for a pure compliance minimization. Thick lattice (black) at the vertical edges supports lattice with intermediate rod diameter at the top. Inside the structure, there is nearly solely lattice with minimal rod diameter (white)

Figure 10 shows that this can be increased by $19\%$ up to a macroscopic critical load of ${3.00\,\mathrm{\text {N}}}$. At the same time, the compliance gets worse by $22\%$ from ${0.130\,\mathrm{\text {N}\text {m}}}$ to ${0.159\,\mathrm{\text {N}\text {m}}}$.

Fig. 10

Optimized function values of compliance minimization with constraints on the macroscopic buckling load factor Eq. 30 and volume Eq. 32. A gain of $20\%$ in the load factor comes at the cost of $20\%$ in the compliance. The design of the data marked by a green circle is shown in Fig. 11

The optimized design corresponding to the rightmost data point, i.e., with highest buckling load factor and worst compliance, is shown in Fig. 11. At first glance, it looks like the one from pure compliance minimization, but there are key differences. There is more lattice with thick rods at the vertical edges. The additional material required for this is made available by making the lattice in the top region thinner and thus results in a worse compliance. Again, the diameter of the lattice rods in the middle of the structure is at the lower bound.

Fig. 11

Optimized design for the marked data in Fig. 10. Compared to the design from pure compliance minimization (Fig. 9), there is a larger amount of thick lattice at the vertical edges to increase macroscopic stability. In return, the lattice at the top is thinner, which results in a larger compliance

8.2 Pure microscopic buckling constraint

As the pure compliance minimization does not account for microscopic buckling, the obtained design exhibits poor resistance against lattice buckling. According to Fig. 12, this can be greatly improved by $125\%$ from ${1.26\,\mathrm{\text {N}}}$ up to ${2.84\,\mathrm{\text {N}}}$ in terms of the microscopic load factor. The compliance is only worsened by $5\%$ from ${0.130\,\mathrm{\text {N}\text {m}}}$ to ${0.137\,\mathrm{\text {N}\text {m}}}$.

Fig. 12

Optimized function values for compliance minimization subject to microscopic buckling Eq. 31 and volume Eq. 32 constraint. A large improvement is possible with only slight loss in the compliance. The design of the data marked by a green circle is shown in Fig. 13

The optimized design for the rightmost data point is shown in Fig. 13 and is again quite similar to the compliance design. This time, however, between the thick lattice at the vertical edges, there is lattice with at least a relative volume of $3.3\%$, i.e., a rod diameter of ${0.68\,\mathrm{\text {m}\text {m}}}$. In other words, the lower bound for our design variable is not active. This is necessary to account for the present stress in the structure and achieve a good local buckling resistance.

Fig. 13

Optimized design for the marked data in Fig. 12. To increase microscopic stability, the optimized design shows lattice with increased rod diameter

8.3 Macro- and microscopic buckling constraint

Finally, we investigate the optimized designs for compliance minimization with constraints on both macro- and microscopic buckling. The obtained values can be seen in Fig. 14. From left to right, first the microscopic load factor increases. This comes with a decrease in the macroscopic buckling load factor, which is inactive anyways. For a required stability threshold of ${2.21\,\mathrm{\text {N}}}$ the two curves meet, i.e., the microscopic limit load is equal to the macroscopic critical load. Requiring higher buckling loads comes at the cost of mechanical compliance. The largest achievable critical load is ${2.51\,\mathrm{\text {N}}}$; for larger values the problem becomes infeasible.

Fig. 14

Optimized function values for compliance minimization under a volume Eq. 32 constraint and constraints on both the macroscopic Eq. 30 and microscopic Eq. 31 buckling load factor (BLF). For reference we included the curves from Fig. 10,12. The design of the data marked by a green circle is shown in Fig. 15

We look closer at the optimized design for this data with a compliance of ${0.137\,\mathrm{\text {N}\text {m}}}$ and buckling load of ${2.51\,\mathrm{\text {N}}}$ (see Fig. 15). It is similar to the design from pure compliance minimization in that there is some thick lattice at the vertical edges. In contrast to the compliance result, we do not obtain a tree shape in the upper region.

Fig. 15

Optimized design for the marked data in Fig. 14. Macroscopic stability is maintained by thick lattice at the vertical edges, while microscopic stability is achieved by a graded lattice structure. The design at the central vertical line (blue) is examined in Fig. 16

Instead, the optimized design exhibits a graded lattice structure, especially in the center of the domain, as can be seen in Fig. 16. This is due to a gradation in the stress field: As the stress increases from bottom to top, the lattice is getting thicker to achieve a nearly homogeneous buckling load factor. The minimal lattice rod diameter for the volume given in Fig. 16 is ${0.6\,\mathrm{\text {m}\text {m}}}$, while at the top it is ${0.76\,\mathrm{\text {m}\text {m}}}$. Though this might seem small, it is an increase by more than $50\%$ with respect to relative lattice volume. This clearly shows the advantage of a homogenization based model for the load factor: Choosing instead a larger lower bound for the relative lattice volume to meet stability requirements everywhere can lead to a waste of material in regions of low stress.

Fig. 16

Norm of stress, design, and microscopic buckling load factor at the central vertical line of the design shown in Fig. 15. The gradation of the stress leads to a graded lattice design to achieve a nearly homogeneous microscopic buckling load factor

9 Conclusion

We presented a method to include microstructural buckling on the macroscopic level in two-scale optimization. We used numerical homogenization as the upscaling technique. Due to the geometry of our exemplary three-dimensional lattice unit cell, we modeled the lattice struts as geometrically exact nonlinear rods. We parametrized the unit cell by its relative volume or lattice rod diameter, respectively. We obtained mechanical properties like Young’s Modulus, Poisson’s ratio, and buckling limit loads for different volumes and stress scenarios. From this data, we built a worst-case model with respect to the acting stress, which we used to obtain structures that are buckling resistant on only one or both scales.

We observed that limit loads for our exemplary truss lattice depend strongly on the direction of the applied macroscopic stress. We also showed that it is necessary to enclose multiple unit cells in an RVE. Otherwise, not all buckling modes can be captured and the smallest microscopic buckling load factor might not be detected. Especially for lattices with a relatively large diameter to rod length ratio, a stiffening of the region where rods intersect can lead to significant differences in the resulting limit load. It is expected (but still to be shown), that a stiffened intersection leads to more realistic results.

The optimized truss lattice structures showed that the gain in macroscopic buckling resistance compared to a pure compliance minimization result is not very large. However, the microscopic resistance was increased drastically with only a small loss in the mechanical compliance by increasing the relative lattice volume. The optimization with respect to both macroscopic and microscopic buckling revealed that a graded lattice structure can yield a homogeneous microscopic lattice factor due to a gradation of the stress field. This shows that a model for the microscopic buckling load factor based on homogenization is superior to just increasing the lower bound for the lattice rods’ diameter.

Further research includes dehomogenization and validation of the optimized designs.

Appendices

Appendix A: Validation of homogenization framework

We validate the multiscale homogenization framework and the evaluation of buckling loads on the case of a compressed primitive cubic lattice [5]. For this case an analytic solution in terms of Eulerian buckling beams is known. The edge length of the unit cell is $l={10\,\mathrm{\text {m}\text {m}}}$ and the rod’s radius is $r={0.25\,\mathrm{\text {m}\text {m}}}$. The homogenization results in the macroscopic properties $E^\text {M}={1617\,\mathrm{\text {M}\text {Pa}}}$, $\mu ^{M}={1.5\,\mathrm{\text {M}\text {Pa}}}\approx {0\,\mathrm{\text {M}\text {Pa}}}$ and $\nu ^\text {M}=0$. As expected, the structure shows negligible stiffness against shear but noteworthy stiffness against tension and compression. The tensile stiffness coincides with the number of rods (4 in loading direction), their circumferential area ($r^2\,\pi$), and their Young’s modulus. The macroscopic Young’s modulus $E^M$ may be calculated by

$$\begin{aligned} E^\text {M}={4\, r^2\, \pi }\frac{E^\text {m}}{ l^2}={1617\,\mathrm{\text {M}\text {Pa}}}, \end{aligned}$$

(33)

given that $E^\text {m}={206000\,\mathrm{\text {M}\text {Pa}}}$ and $l^2={100\,\mathrm{\text {m}\text {m}^2}}$, representing the area of an RVE’s face perpendicular to the loading direction. Finally, the simulation returns a buckling load of $\sigma _{I_{33}}={10.986\,\mathrm{\text {M}\text {Pa}}}$ for uniaxial compression. This is approximately four times the buckling load of a single Eulerian buckling beam with equivalent boundary conditions. For details, the reader is referred to [39]. Finally, we state that both the stiffness and the buckling load from the simulation fit the analytic solution.

Appendix B: Comparing limit loads for stiffened and unstiffened lattices

Fig. 17

Spatially lowest limit load for the case of uniaxial compression of the RVE. We compare the limit load when stiffening and not stiffening the intersections in the lattice. Stiffened intersections lead to higher values

Fig. 18

Spatially lowest limit load for the case of biaxial compression of the RVE. We compare the limit load when stiffening and not stiffening the intersections in the lattice. Stiffened intersections lead to higher values

Fig. 19

Spatially lowest limit load for the case of triaxial compression of the RVE. We compare the limit load when stiffening and not stiffening the intersections in the lattice. Stiffened intersections lead to higher values

With the beam model in Sect. 3, lattice rods are only connected in a single point and overlapping of rods cannot be captured. To model this as well, we used an artificial stiffening parameter in the region next to the intersection. We increased the stiffness of the beam elements, which are within a given radius around the intersection of lattice rods, where the radius is determined by the rods’ diameter. Figures 17, 18 and 19 show homogenized limit loads for stiffened and unstiffened intersections for uni-, bi-, and triaxial compression and ${\text {n}_{\text {RVE}}} =1,\,2,\,3$. As might be expected, lattice with stiffened intersections results in larger limit loads compared to unstiffened intersections. We believe, that a stiffened intersection can capture a more natural behavior of the lattice.