1 Introduction

The aorta is one of the essential arteries in the body. The heart pumps the blood from the left ventricle into the aorta via the aortic valve, which opens and closes with each heartbeat to allow a one-way blood flow. Aortic dissection (AD) begins when a tear occurs in the inner layer (intima) of the aortic wall. This tear allows the blood to flow between the inner and middle layers causing them to separate (dissect). This second blood-filled channel is called a false lumen, where thrombosis (blood clotting) occurs, cf. Fig. 1. Blood clotting or coagulation is the process which prevents excessive bleeding by forming a spatial structure called a thrombus. A thrombus consists of small blood cells (platelets) and fibrous protein (fibrin) that stop the bleeding at the injury site. There are two types of AD depending on the location of the dissection. In type A AD, the dissection happens in the ascending part of the aorta, where the expansion of the false lumen can push other aorta branches and reduce blood flow. In contrast, the dissection occurs in the descending part of the aorta in type B AD, which may extend into the abdomen. The formation of a thrombus involves a complex sequence of biochemical reactions [1, 2]. AD can occur due to high blood pressure leading to increased stress on the aortic wall, weakening of the wall, pre-existing aneurysm or defects in the aortic valve, to name a few factors. Approximately 75% of type B AD patients have hypertension [3, 4]. Furthermore, Virchow’s triad describes three physiological factors that can result in thrombosis. These factors are endothelial injury, hypercoagulability of blood and stasis of blood flow [5, 6].

AD is a highly fatal disease. The estimated occurrence is 5–30 cases per million people annually. Among these, the acute cases are 2-\(-\)3.5 cases per 100,000 people per year, accounting for 6000 to 10,000 cases per year in the USA alone. To understand the gravity of AD, approximately 75% of patients with a ruptured aortic aneurysm make it to the emergency department alive. However, 40% of AD patients die immediately. The mortality rate for aortic dissection is high, especially in acute cases. The mortality rate is excessive in the first seven days after type B AD due to severe complications, such as malperfusion or rupture in the aorta. In the case of such difficulties, a typical open surgery involves a 14–67% risk of irreversible damage to the spinal cord or, worse, mortality. Looking at the long-term prognosis, the survival rate of patients is 50–80% for five years and 30–60% for ten years [7,8,9,10]. The short-term and long-term diagnosis for AD remains unclear, leading to an interest in computational methods to help with the decision-making process for the treatment. We focus here on the formation and growth of a thrombus.

For modelling a thrombus, one has to consider its multiphasic structure and the associated characteristics of the constituents. A highly complicated microscopic model would prevent us from establishing a usable computational model. Therefore, we use a macroscopic continuum mechanical approach of the theory of porous media (TPM). TPM provides an excellent framework to describe the multiphasic microstructure of a thrombus [11, 12]. It allows to describe macroscopically the complicated microstructure of biological tissues which is almost impossible to determine quantitatively. TPM was developed by combining the theory of mixtures, which was developed using the framework of general thermodynamical considerations, with the concept of volume fractions [13,14,15,16,17]. It was continuously improved and developed to the current understanding of the TPM by de Boer & Ehlers [18], and Ehlers [11, 19]. De Boer has presented an excellent insight into the historical development of TPM in his book [12]. Numerous models based on TPM have been presented to describe the behaviour, growth and remodelling of the soft tissues, brain tissue, liver perfusion, intervertebral disc, bone remodelling and tumour growth [20,21,22,23,24,25,26,27,28]. The recent works using TPM for modelling biological growth motivate the use of this approach in the presented work.

Chemical, mechanical and metabolic factors drive the growth process of the thrombus. Because of the multiphasic nature of the thrombus, we present a triphasic model consisting of solid, liquid and nutrient phases. Due to the need for more detailed knowledge and parameters to quantify the influence of different factors, the model description is quite challenging. However, the effects of the blood velocity and the nutrients on the growth of thrombi are well researched [29,30,31]. Therefore, we present a velocity- and nutrient concentration-induced growth model based on the theory of porous media. We treat the highly coupled set of differential equations within the framework of the standard Galerkin procedure and implement the weak forms in the nonlinear finite element solver PANDAS.

Fig. 1
figure 1

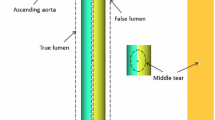
Illustrations of the true and false lumen in type B AD with entry and exit tears (left), and the initial formation of false lumen (without a thrombus) and formation of a thrombus in false lumen (right) [32]

Full size image

2 Theory of porous media

The theory of porous media provides an excellent framework to macroscopically describe the complicated microstructure of the thrombus without knowing its detailed geometry. Therefore, a representative elementary volume (REV) is locally defined, where the individual constituents are considered to be in a state of ideal disarrangement. Using the real or virtual averaging processes over the REV, the microscale information of the overall aggregate and its constituents is homogenised to macro-scale quantities. For the investigated porous body, the immiscible parts lead to a triphasic aggregate \(\varphi \) consisting of solid \(\varphi ^{S}\), which is saturated by fluid \(\varphi ^{F}\). The fluid itself consists of liquid \(\varphi ^{L}\) and nutrients \(\varphi ^{N}\), cf. Figure 2.

Fig. 2
figure 2

Illustration of the microstructure of the porous false lumen (left), macro-model obtained by volumetric homogenisation process (centre) and superimposed continua (right)

Full size image

The volume fractions \(n^{\alpha }\) of the constituents \(\varphi ^{\alpha }\), where \(\alpha \in \{{S,L,N}\}\), are defined as the local ratios of the respective partial volume elements \({\text {d}}v^\alpha \) with respect to the bulk volume element \({\text {d}}v\) of the overall aggregate \(\varphi \) as [12]

$$\begin{aligned} n^\alpha (\textbf{x},t) = \frac{{\text {d}}v^\alpha }{{\text {d}}v}, \quad \sum _{\alpha }n^\alpha (\textbf{x},t) = \sum _{\alpha }\frac{\rho ^\alpha }{\rho ^{\alpha R}} = 1, \end{aligned}$$
(1)

where \(\textbf{x}\) is the position vector in the current configuration at time t. The volume fractions \(n^\alpha \) need to permanently fulfil the saturation constraint (1)\(_2\). In the case of injury (aortic dissection), the nutrients are available in large quantities close to the injury site (false lumen). Therefore, in the presented monograph, the nutrients are described by their volume fractions \(n^\alpha \). For small concentrations of nutrients, the approach of molar concentrations should be used [11, 28]. Moreover, the partial density \(\rho ^{\alpha } = {\text {d}}m^\alpha /{\text {d}}v\) of a constituent \(\varphi ^\alpha \) can be related to its real density \(\rho ^{\alpha R} = {\text {d}}m^\alpha /{\text {d}}v^\alpha \) via its volume fraction \(n^\alpha \) (1)\(_2\). Due to the volume fraction concept, all geometric and physical quantities, such as motion, deformation and stress, are defined in the total control space. Hence, they can be interpreted as the statistical average values of the real quantities. The overall aggregate body B is defined as the connected manifold of material points \(P^\alpha \). At any time t, material points \(P^\alpha \) of all the constituents \(\varphi ^\alpha \) simultaneously occupy each spatial point \(\textbf{x}\) of the current configuration. These particles proceed from different reference positions \(\textbf{X}_\alpha \) at time \(t = t_o\), which leads to individual motion, velocity and acceleration fields for each constituent

$$\begin{aligned} \textbf{x} = \pmb {\chi }_\alpha (\textbf{X}_\alpha ,t), \quad \textbf{x}_\alpha ' = \frac{{\text {d}}\pmb {\chi }_\alpha (\textbf{X}_\alpha ,t)}{{\text {d}}t}, \quad \textbf{x}_\alpha '' = \frac{{\text {d}}^2\pmb {\chi }_\alpha (\textbf{X}_\alpha ,t)}{{\text {d}}t^2}. \end{aligned}$$
(2)

Moreover, a unique inverse motion function \(\pmb {\chi }_{\alpha }^{-1}\) needs to exist for the motion function \(\pmb {\chi }_\alpha \) to be unique. The necessary and sufficient condition for this is the existence of non-singular Jacobian \(J_\alpha \)

$$\begin{aligned} \textbf{X}_\alpha = \pmb {\chi }_{\alpha }^{-1}(\textbf{x},t), \quad \text {if} \quad J_\alpha := {\text {det}} \frac{\partial \pmb {\chi }_\alpha }{\partial \textbf{X}_\alpha } \ne 0, \end{aligned}$$
(3)

where \({\text {det}}(\cdot )\) denotes the determinant operator. Following the equations \((2)_1\) and \((3)_1\), any physical quantity can be represented as either Lagrangean (material) or Eulerian (spatial) description. Moreover, the material deformation gradient \(\textbf{F}_\alpha \) and its inverse \(\textbf{F}_{\alpha }^{-1}\) are defined as

$$\begin{aligned} \textbf{F}_\alpha = {\text {Grad}}_\alpha \, \textbf{x} =: \frac{\partial \pmb {\chi }_\alpha (\textbf{X}_\alpha ,t)}{\partial \textbf{X}_\alpha }, \quad \text {and} \quad \textbf{F}_{\alpha }^{-1} = {\text {grad}} \, \textbf{X}_\alpha =: \frac{\partial \pmb {\chi }_{\alpha }^{-1}(\textbf{x},t)}{\partial \textbf{x}}, \end{aligned}$$
(4)

During deformation, the Jacobian \(J_\alpha \) is restricted to \(J_\alpha = {\text {det}} \textbf{F}_\alpha > 0\). For scalar field functions \( \Psi \), the material time derivative is defined as

$$\begin{aligned} \Psi _{\alpha }{'}(\textbf{x},t) = \frac{\partial \Psi }{\partial t} + {\text {grad}} \Psi \cdot \textbf{x}_{\alpha }'. \end{aligned}$$
(5)

Furthermore, the balance equations for porous media are taken from the balance equations of the constituents \(\varphi ^\alpha \) in mixture theory. The local balance equations of mass for the constituents \(\varphi ^\alpha \) read as

$$\begin{aligned} (\rho ^\alpha )_\alpha ' + \rho ^\alpha \, {\text {div}} \, \textbf{x}_\alpha ' = \hat{\rho }^\alpha , \end{aligned}$$
(6)

which gives volume balance using (1) as

$$\begin{aligned} (n^\alpha )_\alpha ' + n^\alpha \, {\text {div}} \, \textbf{x}_\alpha ' = \frac{\hat{\rho }^\alpha }{\hat{\rho }^{\alpha R}}. \end{aligned}$$
(7)

The local balance of momentum is given by

$$\begin{aligned} \rho ^\alpha \textbf{x}_\alpha '' = {\text {div}} \, \textbf{T}^\alpha + \rho ^\alpha \textbf{b}^\alpha +\hat{\textbf{p}}^\alpha , \end{aligned}$$
(8)

and the local balance of moment of momentum excluding additional supply term is

$$\begin{aligned} \textbf{T}^\alpha = (\textbf{T}^\alpha )^T. \end{aligned}$$
(9)

In Eqs. (6) and (8), \({\text {div}}(\cdot )\) denotes the spatial divergence operator, \(\textbf{T}^\alpha \) is the partial Cauchy stress tensor and \(\textbf{b}\) is the external volume force per unit mass. \(\hat{\rho }^\alpha \) represents the total mass production accounting for mass exchange or phase transitions between the constituents \(\varphi ^\alpha \). Total momentum production \(\hat{\textbf{s}}^\alpha = \hat{\textbf{p}}^\alpha + \hat{\rho }^\alpha \textbf{x}_\alpha '\) contains the direct momentum exchange \(\hat{\textbf{p}}^\alpha \) resulting from the interaction force between the constituents \(\varphi ^\alpha \) as well as indirect parts resulting from the mass exchange \(\hat{\rho }^\alpha \). The total production terms are restricted by

$$\begin{aligned} \hat{\rho }^S + \hat{\rho }^L + \hat{\rho }^N = 0, \quad \hat{\textbf{s}}^S + \hat{\textbf{s}}^L + \hat{\textbf{s}}^N = \textbf{0}. \end{aligned}$$
(10)

2.1 Assumptions

The system is investigated under the condition that all the constitutes \(\varphi ^\alpha \) are materially incompressible, i.e.

$$\begin{aligned} (\rho ^{SR})_S' = 0, \quad (\rho ^{LR})_L' = 0, \quad (\rho ^{NR})_N' = 0. \end{aligned}$$
(11)

This leads to the conclusion that volumetric deformations are only a result of a change in volume fractions \(n^\alpha \). Moreover, the nutrient and the liquid phases are assumed to be in the fluid phase. For simplification, both phases are assigned the same velocity

$$\begin{aligned} \textbf{x}_N' = \textbf{x}_L' = \textbf{x}_F'. \end{aligned}$$
(12)

We assume that the liquid phase is not involved in the mass exchange. Using this assumption and Eq. (10)\(_1\), we get

$$\begin{aligned} \hat{\rho }^L = 0 \quad \longrightarrow \quad \hat{\rho }^S = -\hat{\rho }^N. \end{aligned}$$
(13)

Furthermore, only isothermal processes are considered, energy transfer due to chemical reactions is neglected, accelerations are excluded, and the internal structure of the thrombus is considered to be isotropic.

Along with the assumptions, the Clausius–Planck inequality is written as

$$\begin{aligned} \sum _{\alpha } \Bigl [ \textbf{T}^\alpha : \textbf{d}_\alpha - \rho ^\alpha (\psi ^\alpha )_\alpha ' - \hat{\textbf{p}}^\alpha \cdot \textbf{x}_\alpha ' - \hat{\rho }^\alpha \left( \psi ^\alpha + \frac{1}{2} \textbf{x}_\alpha ' \cdot \textbf{x}_\alpha '\right) \Bigr ] \ge 0, \end{aligned}$$
(14)

where \(\textbf{d}_\alpha \) is the symmetric part of spatial velocity gradient. This equation is essential for developing a thermodynamically consistent model.

3 Constitutive modelling

The dependencies of the Helmholtz free energy for the solid, liquid and nutrient phases are considered as

$$\begin{aligned} \psi ^S = \psi ^S \{n^S,\, \textbf{C}_S \}, \quad \psi ^L = \psi ^L\{n^L \}, \quad \psi ^N = \psi ^N\{n^N \}, \end{aligned}$$
(15)

where \(\textbf{C}_S = \textbf{F}_S^T\textbf{F}_S\) is the right Cauchy–Green tensor related to solid. Furthermore, the universal dissipation principle must be satisfied by the constitutive relations. Therefore, we evaluate the Clausius–Planck inequality by following the procedure of Coleman and Noll [33]. For more information regarding the evaluation of the entropy principle, the reader is referred to Bowen [34] and Ehlers [11].

At first, we evaluate \(\rho ^\alpha (\psi ^\alpha )_\alpha '\) for all the constituents \(\varphi ^\alpha \) knowing the Helmholtz free energy dependence following Eq. (15).

$$\begin{aligned} \begin{aligned}&\rho ^S (\psi ^S)_S' = 2 n^S \rho ^{SR} \textbf{F}_S \frac{\partial \psi ^S }{ \partial \textbf{C}_S } \textbf{F}_S^T: \textbf{d}_S + n^S \rho ^{SR} \frac{\partial \psi ^S}{ \partial n^S } ( n^S )_S', \\&\rho ^L (\psi ^S)_L' = n^L \rho ^{LR} \frac{\partial \psi ^L}{ \partial n^L } ( n^L )_L', \\&\rho ^N (\psi ^S)_N' = n^N \rho ^{NR} \frac{\partial \psi ^N}{ \partial n^N } ( n^N )_N'. \end{aligned} \end{aligned}$$
(16)

Initially, an additional saturation constraint (1)\(_2\) is added to the entropy inequality to ensure the fully saturated condition in the overall aggregate at any given time. This is done by introducing a Lagrangean multiplier p as a weight to the saturation condition as [12]

$$\begin{aligned} p(n^S + \underbrace{n^L + n^N}_{n^F})_S' = p({\text {grad}}n^F \cdot \textbf{w}_{FS} -(n^S)_S' -(n^L)_L' -(n^N)_N' ). \end{aligned}$$
(17)

Moreover, we multiply the volume balance of the individual constituent \(\varphi ^\alpha \) with the respective Lagrangean multipliers \(p^\alpha \) and make use of the relation \(\pmb {l}_\alpha : \textbf{I} = \textbf{d}_\alpha : \textbf{I} = {\text {div}} \textbf{x}_\alpha '\) [35]

$$\begin{aligned} p^\alpha \Bigl [ (n^\alpha )_\alpha ' + n^\alpha (\textbf{d}_\alpha : \textbf{I}) - \frac{\hat{\rho }^\alpha }{\rho ^{\alpha R}} \Bigl ] = 0. \end{aligned}$$
(18)

Now using the relations (16)–(18), (12) and the summation assumption (10)\(_{1,2}\), we can evaluate the inequality (14), following the methodology from Ricken and Bluhm [35].

$$\begin{aligned}{} & {} \textbf{d}_S: \Bigl \{ \textbf{T}^S - 2n^S \rho ^{SR} \textbf{F}_S \frac{\partial \psi ^S }{ \partial \textbf{C}_S } \textbf{F}_S^T + p^S n^S \textbf{I} \Bigr \} + \textbf{d}_L: \Bigl \{ \textbf{T}^L + p^L n^L \textbf{I} \Bigr \} \nonumber \\{} & {} \quad +\,\textbf{d}_N: \Bigl \{ \textbf{T}^N + p^N n^N \textbf{I} \Bigr \} -(n^S)_S' \Bigl \{ p - p^S + n^S \rho ^{SR} \frac{\partial \psi ^S}{\partial n^S }\Bigr \} \nonumber \\{} & {} \quad -\, (n^L)_L' \Bigl \{ p - p^L + n^L \rho ^{LR} \frac{\partial \psi ^L}{\partial n^L } \Bigr \} - (n^N)_N' \Bigl \{ p - p^N + n^N \rho ^{NR} \frac{\partial \psi ^N}{\partial n^N } \Bigr \} \nonumber \\{} & {} \quad -\, \hat{\rho }^L \Bigl \{ (\psi ^L - \frac{1}{2}\textbf{x}_L' \cdot \textbf{x}_L' + \frac{1}{\rho ^{LR}}p^L )-( \psi ^S - \frac{1}{2} \textbf{x}_S' \cdot \textbf{x}_S' + \frac{1}{\rho ^{SR}}p^S ) \Bigr \} \nonumber \\{} & {} \quad -\, \hat{\rho }^N \Bigl \{ (\psi ^N - \frac{1}{2}\textbf{x}_N' \cdot \textbf{x}_N' + \frac{1}{\rho ^{NR}}p^N )-( \psi ^S - \frac{1}{2} \textbf{x}_S' \cdot \textbf{x}_S' + \frac{1}{\rho ^{SR}}p^S ) \Bigr \} \nonumber \\{} & {} \quad -\, \textbf{w}_{FS} \cdot \Bigl \{ \hat{\textbf{p}}^F - p {\text {grad}} n^F + \hat{\rho }^S \textbf{x}_S' \Bigr \} \ge 0, \end{aligned}$$
(19)

which must hold for fixed values of the process variables and arbitrary values of freely available quantities \(\textbf{d}_\alpha , (n^\alpha )_\alpha '\) [35]. Therefore, we obtain the following structure of the entropy inequality

$$\begin{aligned}{} & {} \textbf{d}_S: \underbrace{\bigl \{...\bigr \}}_{=\textbf{0}} + \, \textbf{d}_L: \underbrace{\bigl \{...\bigr \}}_{=\textbf{0}} + \, \textbf{d}_N: \underbrace{\bigl \{...\bigr \}}_{=\textbf{0}} - (n^S)_S' \underbrace{\bigl \{...\bigr \}}_{=0} \nonumber \\{} & {} \quad -\, (n^L)_L' \underbrace{\bigl \{...\bigr \}}_{=0} - (n^N)_N' \underbrace{\bigl \{...\bigr \}}_{=0} + \underbrace{\text {Dis}}_{\ge 0} \ge 0. \end{aligned}$$
(20)

In this context, we obtain the necessary and sufficient thermodynamic restrictions. The parts concerning \((n^\alpha )_\alpha '\) give

$$\begin{aligned} p^\alpha = p + n^\alpha \rho ^{\alpha R} \frac{\partial \psi ^\alpha }{ \partial n^\alpha }. \end{aligned}$$
(21)

Furthermore, we obtain the relations for the partial Cauchy stresses using (19) and (21)

$$\begin{aligned} \textbf{T}^S= & {} -n^Sp\textbf{I} - (n^S)^2\rho ^{SR}\frac{\partial \psi ^S}{\partial n^S}\textbf{I} + \textbf{T}_E^S, \quad \textbf{T}_E^S = 2\rho ^S\textbf{F}_S\frac{\partial \psi ^S}{\partial \textbf{C}_S}\textbf{F}_S^T, \nonumber \\ \textbf{T}^L= & {} -n^Lp\textbf{I} - (n^L)^2\rho ^{LR}\frac{\partial \psi ^L}{\partial n^L}\textbf{I}, \nonumber \\ \textbf{T}^N= & {} -n^Np\textbf{I} - (n^N)^2\rho ^{NR}\frac{\partial \psi ^N}{\partial n^N}\textbf{I}. \end{aligned}$$
(22)

We can now introduce the chemical potentials \(\overline{\Psi }^\alpha \) using (19) and (21) as

$$\begin{aligned} \overline{\Psi }^\alpha = \psi ^\alpha - \frac{1}{2}\textbf{x}_\alpha ' \cdot \textbf{x}_\alpha + n^\alpha \frac{\partial \psi ^\alpha }{\partial n^\alpha } + \frac{1}{\rho ^{\alpha R}} p. \end{aligned}$$
(23)

For more information on chemical potentials, the reader is referred to Bowen [34]. Furthermore, we make use of the assumption \(\hat{\rho }^L = 0\) which gives us the dissipative part as

$$\begin{aligned} \text {Dis}= & {} - \hat{\rho }^N \underbrace{\Bigl \{ (\psi ^N - \frac{1}{2}\textbf{x}_N' \cdot \textbf{x}_N' + \frac{1}{\rho ^{NR}}p^N )-( \psi ^S - \frac{1}{2} \textbf{x}_S' \cdot \textbf{x}_S' + \frac{1}{\rho ^{SR}}p^S ) \Bigr \}}_{\overline{\Psi }^N - \overline{\Psi }^S} \nonumber \\{} & {} - \,\textbf{w}_{FS} \cdot \underbrace{\Bigl \{ \hat{\textbf{p}}^F - p {\text {grad}} n^F + \hat{\rho }^S \textbf{x}_S' \Bigr \}}_{ \hat{\textbf{p}}^F_E } \ge 0, \end{aligned}$$
(24)

where \(\hat{\textbf{p}}^F_E\) is called the extra momentum production [36]. Moreover, this gives the restrictions for the solid mass production \(\hat{\rho }^S\) and momentum production \(\hat{\textbf{p}}^F\) as postulated by Ricken and Bluhm [35]

$$\begin{aligned}{} & {} \hat{\rho }^S = \delta ^{NS}(\overline{\Psi }^N - \overline{\Psi }^S), \quad \text {where} \quad \delta ^{NS} \ge 0,\nonumber \\{} & {} \hat{\textbf{p}}^F = p {\text {grad}}n^F - \hat{\rho }^S \textbf{x}_S' - \textbf{S}_F \textbf{w}_{FS}, \end{aligned}$$
(25)

where \(\textbf{S}_F\) is the permeability tensor between the solid and fluid phases. These restrictions give us the possibility to further formulate stresses, mass production and interaction forces.

3.1 Stress

The stress relations can be introduced following the restrictions from the entropy inequality (22) and neglecting the effective or frictional fluid stress, i.e. \(\textbf{T}^F_E \approx \textbf{0}\). It is assumed that the fluid extra stress is much smaller in comparison with \(\hat{\textbf{p}}^F_E\) also known as the effective drag force. Therefore, assuming \(\partial \psi ^F/ \partial n^F = 0\) where \(\varphi ^F = \varphi ^L + \varphi ^N\) yields [11, 35]

$$\begin{aligned}{} & {} \textbf{T}^S = -n^Sp\textbf{I} - (n^S)^2\rho ^{SR}\frac{\partial \psi ^S}{\partial n^S}\textbf{I} + \textbf{T}_E^S, \quad \text {where} \quad \textbf{T}_E^S = 2\rho ^S\textbf{F}_S\frac{\partial \psi ^S}{\partial \textbf{C}_S}\textbf{F}_S^T \nonumber \\{} & {} \textbf{T}^F = \textbf{T}^L + \textbf{T}^N = -(n^L + n^N)p\textbf{I} = -n^ Fp\textbf{I}, \end{aligned}$$
(26)

where \(\textbf{I}\) is the second-order identity tensor. This also leads to \(p^N = p^L = p\) using (21). Furthermore, p is identified as the unspecified pore pressure. The total stress is defined as the sum of partial stresses and using Eq. (1)\(_2\) yields:

$$\begin{aligned} \textbf{T} = \textbf{T}^S + \textbf{T}^F = \textbf{T}_E^S - (n^S)^2\rho ^{SR}\frac{\partial \psi ^S}{\partial n^S}\textbf{I} - p\textbf{I}. \end{aligned}$$
(27)

According to the principle of material objectivity, the constitutive equations should not depend on the observer’s position. Thus, the mathematical interpretation of such an objectivity condition states that constitutive equations must be invariant under rigid body rotations of the actual configuration [37, 38]. Therefore, the free energy functions will be formulated with a dependence on the principal invariants \(I_1, I_2\) and \(I_3\) of \(\textbf{C}_S\) using [39]

$$\begin{aligned} I_1:= {\text {tr}}\textbf{C}_S, \quad I_2:= \frac{1}{2} [({\text {tr}}\textbf{C}_S)^2 - {\text {tr}}(\textbf{C}_S \cdot \textbf{C}_S)], \quad I_3:= {\text {det}}(\textbf{C}_S), \end{aligned}$$
(28)

where \({\text {tr}}(\cdot )\) denotes the trace operator. Thereon, the Helmholtz free energy function can be written as follows

$$\begin{aligned} \psi ^S = \overline{\psi }^S(n^S,I_1,I_2,I_3). \end{aligned}$$
(29)

The structure of the equation satisfies the invariance and polyconvexity conditions, which also implies quasiconvexity. That would ensure the existence of minimisers of the related variational principles in finite elasticity. For a detailed discussion on convexity conditions, the reader is referred to Dacorogna [40].

Now the Helmholtz free energy function can be constructed in the following way

$$\begin{aligned} \psi ^S = \left( \frac{n^S}{n^S_{OS}}\right) ^n\frac{1}{\rho ^S_{OS}} \underbrace{\Bigl \{\frac{\mu ^S}{2}(I_1-3) - \mu ^S {\text {ln}} J_S + \lambda ^S\frac{1}{2}( {\text {ln}} J_S)^2\Bigr \}}_{\psi ^S_{neo}}, \end{aligned}$$
(30)

where the term in the front with nutrient volume fraction \(n^S\) represents the change in solid rigidity with respect to the initial volume fraction \(n^S_{OS}\). Here \((\cdot )_{OS}\) represents the initial value of \((\cdot )\) with respect to the referential configuration of the solid. This term in the front with solid volume fraction \(n^S\) accounts for the change in solid rigidity with respect to the initial volume fraction \(n^S_{OS}\). The material parameter n helps to define the extent of dependence on change in porosity. Carter and Hayes [41] identified material parameter \(n = 3\), and it has been used in multiple porous media growth applications [24,25,26, 35]. The rest of the part \(\psi ^S_{neo}\) is the Neo–Hookean material law. \(\mu ^S\) and \(\lambda ^S\) are the macroscopic Lam\(\acute{e}\) constants.

From (30) and (26), the effective solid Cauchy stress can be obtained

$$\begin{aligned} \textbf{T}^S_E = \left( \frac{n^S}{n^S_{OS}}\right) ^{(n+1)}\Bigl \{\mu ^S(\textbf{B}_S-\textbf{I}) + \lambda ^S({\text {ln}}J_S)\textbf{I} \Bigr \}, \end{aligned}$$
(31)

where \(\textbf{B}_S\) is the left Cauchy–Green tensor \(\textbf{B}_S=\textbf{F}_S\textbf{F}_S^T\). With equations (26), (30) and (31), total solid Cauchy stress can be written as

$$\begin{aligned} \textbf{T}^S= & {} -n^Sp\textbf{I} - n\left( \frac{n^S}{n^S_{OS}}\right) ^{n+1}\Bigl \{\frac{\mu ^S}{2}(I_1-3) - \mu ^S {\text {ln}} J_S + \lambda ^S\frac{1}{2}({\text {ln}} J_S)^2\Bigr \}\textbf{I} \nonumber \\{} & {} +\,\left( \frac{n^S}{n^S_{OS}}\right) ^{(n+1)}\Bigl \{\mu ^S(\textbf{B}_S-\textbf{I}) + \lambda ^S({\text {ln}}J_S)\textbf{I} \Bigr \}. \end{aligned}$$
(32)

The effective solid Kirchhoff stress and total solid Kirchhoff stress then read as

$$\begin{aligned} \pmb {\tau }^S_E= & {} J_S\,\textbf{T}^S_E = J_S \left( \frac{n^S}{n^S_{OS}}\right) ^{(n+1)}\Bigl \{\mu ^S(\textbf{B}_S-\textbf{I}) + \lambda ^S({\text {ln}}J_S)\textbf{I} \Bigr \}, \nonumber \\ \pmb {\tau }^S= & {} -J_S\,n^Sp\textbf{I} - J_S\,n\left( \frac{n^S}{n^S_{OS}}\right) ^{n+1}\Bigl \{\frac{\mu ^S}{2}(I_1-3) - \mu ^S {\text {ln}} J_S + \lambda ^S\frac{1}{2}({\text {ln}} J_S)^2\Bigr \}\textbf{I} \nonumber \\{} & {} +\,J_S\,\left( \frac{n^S}{n^S_{OS}}\right) ^{(n+1)}\Bigl \{\mu ^S(\textbf{B}_S-\textbf{I}) + \lambda ^S({\text {ln}} J_S)\textbf{I} \Bigr \}. \end{aligned}$$
(33)

3.2 Filter Velocity

The seepage velocity \(\textbf{w}_{FS} = \textbf{x}_F' - \textbf{x}_S'\) determines the motion of the fluid in relation to the solid. The relation \(\hat{\textbf{p}}^F = \hat{\textbf{p}}^L + \hat{\textbf{p}}^N\) is considered. From the evaluation of entropy inequality (25)\(_2\), we obtain the following relation as postulated by Ricken and Bluhm [35]

$$\begin{aligned} \hat{\textbf{p}}^F = p {\text {grad}}n^F - \textbf{S}_F\textbf{w}_{FS} - \hat{\rho }^S \textbf{x}_S'. \end{aligned}$$
(34)

Using (34), (8), \(\textbf{S}_F = \alpha _{FS} \, \textbf{I}\) for an isotropic material and rearranging the equation, we get [35]

$$\begin{aligned} n^F \textbf{w}_{FS} = \frac{(n^F)^2}{\alpha _{FS}} \left( -{\text {grad}}p+\rho ^{FR}\textbf{b}-\frac{\hat{\rho }^{S}}{n^F}\textbf{x}_S' \right) . \end{aligned}$$
(35)

The material parameter \(\alpha _{FS}\) can be described either by using initial Darcy’s permeability of fluid \(k^F_{OS} \, [m/s]\) and effective fluid weight \(\gamma ^{FR} \, [N/m^3]\) or by using initial intrinsic permeability of solid \(K^S_{OS} \, [m^2]\) and dynamic fluid viscosity \(\mu ^{FR} \, [Ns/m^2]\)

$$\begin{aligned} \frac{(n^F)^2}{\alpha _{FS}} = \left( \frac{n^F}{n^F_{OS}} \right) ^m\frac{k^F_{OS}}{\gamma ^{FR}} = \left( \frac{n^F}{n^F_{OS}} \right) ^m \frac{K^S_{OS}}{\mu ^{FR}}, \end{aligned}$$
(36)

where m is a dimensionless parameter which accounts for the change of permeability [12, 26]. Here, \((n^F/n^F_{0\,S})^m K^S_{0\,S} = K^S_E\) is referred to as effective permeability, which takes into consideration the change in volume fractions. Eipper [42] proposed this porosity-dependent effective permeability where \(m\ge 0\). With Eqs. (13), (36) and (35), we finally get the following relation for seepage velocity

$$\begin{aligned} n^F\textbf{w}_{FS} = -\left( \frac{n^F}{n^F_{OS}}\right) ^m \frac{K^S_{OS}}{\mu ^{FR}}\left( {\text {grad}}p - \rho ^{FR}\textbf{b} + \frac{\hat{\rho }^S}{n^F}\textbf{x}_S' \right) . \end{aligned}$$
(37)

3.3 Mass exchange

According to (13), the mass exchange occurs between the solid and nutrient phases \(\hat{\rho }^S = -\hat{\rho }^N\). Following the evaluation of the entropy inequality (25)\(_1\), we have \(\hat{\rho }^S \ge 0\). Furthermore, making use of the postulations proposed by Ricken et al. [25, 26], and due to no expert knowledge available for the formulation of free energy functions of liquid and nutrient phases, the mass production for the solid phase is formulated. The effects of the blood velocity and the nutrients on the thrombus growth are well researched [29,30,31]. Therefore, \(\hat{\rho }^S [kg/m^3 \, s]\) is postulated as a function of \(\textbf{w}_{FS}\) and \(n^N\)

$$\begin{aligned}{} & {} \hat{\rho }^S = \hat{\rho }^S(\textbf{w}_{FS},n^N) = \mathcal {C} \, \hat{\rho }^S_{\textbf{w}_{FS}}(\textbf{w}_{FS}) \, \hat{\rho }^S_{n^N}(n^N), \nonumber \\{} & {} \hat{\rho }^S_{\textbf{w}_{FS}}(\textbf{w}_{FS}) = {\text {exp}}\bigl \{ -\Vert \textbf{w}_{FS}\Vert ^2/\beta _1 \bigr \}, \nonumber \\{} & {} \hat{\rho }^S_{n^N}(n^N) = -{\text {exp}}\bigl \{-(n^N)^2 \beta _2\bigr \} +1, \end{aligned}$$
(38)

where \(\mathcal {C}\) represents the maximum mass exchange, and \(\beta _1\) and \(\beta _2\) are the material parameters reflecting the dependence of mass exchange on the seepage velocity and nutrient volume fraction, respectively, cf. Fig. 3.

Fig. 3
figure 3

Mass productions \(\hat{\rho }^S_{\textbf{w}_{FS}}\) and \(\hat{\rho }^S_{n^N}\) dependence on the seepage velocity \(\textbf{w}_{FS}\) and nutrient volume fraction \(n^N\), respectively

Full size image

4 Numerical treatment

Considering the assumptions, balance equations and constitutive relations from the preceding sections, we have a set of six independent variables

$$\begin{aligned} \mathcal {U} = \mathcal {U}(\textbf{x},t) = \bigl \{ \textbf{u}_S, \textbf{w}_{FS}, n^S,n^N,n^L,p \bigr \}, \end{aligned}$$
(39)

where \(\textbf{u}_S\) is the displacement of the solid phase. Using Darcy’s formulation for the seepage velocity \(\textbf{w}_{FS}\) (35), the set of unknowns could be decreased to five. Furthermore, the saturation condition (1)\(_2\) (\(n^L = 1 - n^S - n^N\)) reduces the set of unknowns to four

$$\begin{aligned} \mathcal {U} = \mathcal {U}(\textbf{x},t) = \bigl \{ \textbf{u}_S, n^S,n^N,p \bigr \}. \end{aligned}$$
(40)

Once this is concluded, the weak formulation for the governing equations is formulated in the framework of the standard Galerkin procedure (Bubnov–Galerkin). This is achieved by multiplying the momentum balance of the mixture, volume balance of the mixture, solid and nutrients with the test functions \(\delta \textbf{u}_S\), \(\delta p\), \(\delta n^S\) and \(\delta n^N\), respectively. As a result, the weak formulation of the triphasic model reads

  • Momentum balance of mixture:

    $$\begin{aligned} \mathcal {G}_{\textbf{u}_S}= & {} \int _{\Omega }(\textbf{T}): {\text {grad}} \delta \textbf{u}_S {\text {d}}v - \int _{\Omega }(\rho ^S + \rho ^F)\textbf{b} \cdot \delta \textbf{u}_S {\text {d}}v \nonumber \\{} & {} -\,\int _{\Omega }\hat{\rho }^S\textbf{w}_{FS} \cdot \delta \textbf{u}_S {\text {d}}v - \int _{\Gamma _{\textbf{t}}} \bar{\textbf{t}}\cdot \delta \textbf{u}_S {\text {d}}a = 0, \end{aligned}$$
    (41)

  • Volume balance of mixture:

    $$\begin{aligned} \mathcal {G}_p= & {} \int _{\Omega } {\text {div}}\textbf{x}_S'\,\delta p {\text {d}}v - \int _{\Omega } n^F\textbf{w}_{FS}\cdot {\text {grad}} \delta p {\text {d}}v\nonumber \\{} & {} +\,\int _{\Omega } \hat{\rho }^S(\frac{1}{\rho ^{NR}} - \frac{1}{\rho ^{SR}})\,\delta p {\text {d}}v + \int _{\Gamma _q} \underbrace{n^F \textbf{w}_{FS} \cdot \textbf{n}}_{:= q} \,\delta p {\text {d}}a = 0, \end{aligned}$$
    (42)

  • Volume balance of solid:

    $$\begin{aligned} \mathcal {G}_{n^S} = \int _{\Omega } (n^S)_S' \, \delta {n^S}{\text {d}}v + \int _{\Omega } n^S{\text {div}}\textbf{x}_S'\,\delta {n^S} {\text {d}}v - \int _{\Omega } \frac{\hat{\rho }^S}{\rho ^{SR}}\,\delta {n^S}{\text {d}}v = 0, \end{aligned}$$
    (43)

  • Volume balance of nutrients:

    $$\begin{aligned} \mathcal {G}_{n^N}= & {} \int _{\Omega }\left( ({n^N})_S' + n^N{\text {div}}\textbf{x}_S' - \frac{\hat{\rho }^N}{\rho ^{NR}}\right) \,\delta {n^N}{\text {d}}v + \underbrace{\int _{\Omega } {\text {grad}} n^N \cdot {\text {grad}} \delta n^N {\text {d}}v}_{:=r} \nonumber \\{} & {} -\,\int _{\Omega }n^N\textbf{w}_{FS} \cdot {\text {grad}} \delta n^N {\text {d}}v + \int _{\Gamma _{\upsilon }} n^N \textbf{w}_{FS} \cdot \textbf{n} \, \delta {n^N} {\text {d}}a = 0. \end{aligned}$$
    (44)

    In the weak formulation, from (41) to (44), \(\bar{\textbf{t}}\) is the external load vector acting on the Neumann boundary \(\Gamma _{\textbf{t}}\), \(n^F \textbf{w}_{FS} \cdot \textbf{n}\) is the fluid mass efflux on the Neumann boundary \(\Gamma _{q}\) and \(n^N \textbf{w}_{FS} \, \cdot \, \textbf{n}\) is the nutrient mass efflux on the Neumann boundary \(\Gamma _{\upsilon }\), where \(\textbf{n}\) is the outward oriented unit surface normal. Also, the transport equation for nutrients consists of the general structure of an advection equation. It is known that using the given approach for formulating weak forms, equation (44) generates large oscillations if not properly stabilised or if the mesh size is not excessively small. Therefore, an artificial diffusion term (r) is added only to the volume balance of nutrients (44) to stabilise the transport equation. For more information on the mass transport equation and the stabilisation schemes, the reader is referred to Santos et al. [43] and the references therein.

5 Numerical example

In this section, we present a numerical example of the formation and growth of a thrombus in type B aortic dissection using a realistic two-dimensional geometry of false lumen. The constitutive equations for the solid stress \(\textbf{T}^S\), the mass production term \(\hat{\rho }^S\) and the seepage velocity \(\textbf{w}_{FS}\) provide the thrombus-specific material laws. In addition, the coupled set of governing equations presents the capabilities of the model. We implement the weak forms of balance equations in the FE package PANDAS, where time and space adaptive methods are widely applied. However, modelling the growth of living tissues has its challenges. In the case of thrombosis, it is not straightforward to obtain the data and perform experiments on living tissues. Therefore, the parameters are chosen that give reasonable results for specific cases.

Fig. 4
figure 4

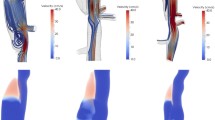
3-d model of the aorta with a true and false lumen (left) [44]. Cutting plane and the resulting 2-d cross section of the lumens (right)

Full size image
Fig. 5
figure 5

Discretisation and boundary conditions of the false lumen geometry

Full size image

In the numerical example, we want to use a 2-d cross section of a realistic geometry of the false lumen to model thrombosis. To obtain the cross section, we use a 3-d model of an aorta consisting of a true and false lumen [44], cf. Fig. 4 (left). We cut this model in the \(x-y\) plane represented as the cutting plane in Fig. 4 (top right). This gives us the 2-d geometry in the \(x-y\) plane, cf. Fig. 4 (bottom right). However, because we are modelling thrombosis in the false lumen, the geometry of the false lumen is of interest to us. Therefore, we create and discretise the false lumen’s geometry using CUBIT, consisting of 1063 elements, cf. Fig. 5. The geometry consists of a solid matrix saturated with fluid, consisting of liquid and nutrient phases. Furthermore, we arbitrarily choose the entry and exit tears position. The boundary conditions at the entry tear include \(n^S = 0.4\) and \(q = 0.1\) m/s. The bottom exit tear (dotted line) is the drained surface with \(p=0.0\) N/m\(^2\). The rest of the boundaries are undrained surfaces, cf. Fig. 5. Also, the right side of the false lumen is fixed in both the x and y directions. We use the Taylor Hood elements for spatial discretisation, where quadratic approximation is used for the solid displacements \(\textbf{u}_S\) and linear approximation for the pressure p, solid volume fraction \(n^S\) and nutrient volume fraction \(n^N\). The simulation is performed using the parameters given in Table 1 and with a time step size of 100 s. Here, we assume zero Poisson’s ration (\(\lambda ^S = 0\)) for the solid skeleton. This is done for simplicity and lack of material data [35, 45,46,47].

Table 1 Parameters for thrombi growth
Full size table

We can now discuss the results while drawing an analogy with the process of thrombosis. At time \(t = 0\) hours, the initial solid volume fraction \(n^S\) is 0.2 because of the presence of subendothelial collagen, wall cells and activated platelets on the formation of the false lumen. As the fluid enters via the entry tear, it creates high- and low-velocity regions, cf. Fig. 6. Because of different velocity profiles and the availability of nutrients, the process of thrombosis begins, and the solid volume fractions start increasing, cf. Fig. 7. This can be compared to primary haemostasis, where the platelets accumulate at the injury site and form a platelet plug. The solid volume fraction \(n^S\) increases further due to the mass exchange rate (38)\(_3\) dependence on seepage velocity \(\textbf{w}_{FS}\) and nutrient volume fraction \(n^N\), which can be compared to secondary haemostasis. During secondary haemostasis, the clotting factors interact in a complicated series of chemical reactions leading to the formation of fibrin fibre. The platelets and the fibrin fibre form a mesh leading to the development of a stable plug. This process continues further to form a permanent solid plug called a thrombus. Furthermore, Fig. 8 shows that the permeability in the false lumen decreases with an increase in the solid volume fraction. This means that as the thrombus grows and there is more solid, the ability of the fluid to move through porous media decreases. Moreover, we observe a singularity at the exit tear due to the sharp edges, which is a numerical artefact [48, 49].

Fig. 6
figure 6

Norm of the seepage velocity \(\Vert \textbf{w}_{FS} \Vert \) at different stages in time

Full size image
Fig. 7
figure 7

Change in solid volume fractions \(n^S\) at different stages in time

Full size image
Fig. 8
figure 8

Effective permeability \(K^S_E\) at different stages in time

Full size image

Further, we can explore the features of the model. We can vary the material parameters and the boundary conditions to adapt the model for specific cases.

5.1 Influence of material parameters in mass exchange

The material parameters, \(\beta _1\) and \(\beta _2\), in Eq. (38) can be varied to change the dependence of mass exchange rate on the seepage velocity and nutrient volume fraction. In the above example, the default values of 0.05 and 5.0 are used for \(\beta _1\) and \(\beta _2\), respectively. To begin with, we vary the material parameter \(\beta _1\) leading to a change in seepage velocity influence. From this, we can see that as we increase the value of \(\beta _1\), forming a thrombus is easier due to growth happening for the wider range of seepage velocities, cf. Fig. 9.

Fig. 9
figure 9

Change in solid volume fractions \(n^S\) for different values of \(\beta _1\) at \(t = 83\) hr

Full size image

Furthermore, we vary the values of the material parameter \(\beta _2\) and change the influence of nutrient volume fraction on growth. As the value of \(\beta _2\) increases, we allow the thrombus growth for a more extensive range of nutrient volume fraction \(n^N\), leading to higher growth because of the increased availability of nutrients, cf. Fig. 10.

Fig. 10
figure 10

Change in solid volume fractions \(n^S\) for different values of \(\beta _2\) at \(t = 83\) hr

Full size image

5.2 Change in Neumann boundary condition

Moreover, we can see the effects due to variation in the fluid mass influx q on the Neumann boundary \(\Gamma _{q}\). An increase in the fluid mass influx q at the entry tear results in higher seepage velocity. Because of the mass exchange dependence on the seepage velocity, forming a thrombus in the false lumen, especially in the middle section, is difficult, cf. Fig. 11. This also fits well with the physiological understanding of thrombosis and the Virchow triad, where it is difficult to form blood clots when the blood velocity is high [5].

Fig. 11
figure 11

Change in solid volume fractions \(n^S\) for different values of q at \(t=83\) hr

Full size image

The above analysis shows that the triphasic model accommodates the well-known Virchow triad, which describes three physiological factors that can result in thrombosis. The first one, endothelial injury, is included in the form of the presence of a false lumen. On the formation of a false lumen, the endothelium is damaged, which lines the inner layer of the blood vessels. The endothelial injury stimulates the platelets and coagulation process. The second factor is hypercoagulability, which is an increased tendency of coagulation in the body due to inherited or acquired disorders. The material parameter \(\beta _2\) and \(\mathcal {C}\) can be used to adapt the model for such a scenario. Also, the material parameter \(\beta _2\) can be used to include this increased tendency of coagulation. The third factor, the stasis of blood, is present in the form of mass exchange dependency on the seepage velocity [5, 50]. Here, the material parameter \(\beta _1\) can be used to adapt the model for the specific case. Finally, the fluid mass efflux q boundary condition can be used to incorporate the factor of high blood pressure, which is known to be the major cause of aortic dissection.

6 Conclusions

A triphasic model has been developed for the thrombus’s growth, capable of describing its growth and nonlinear behaviour. The theory of porous media (TPM) provides an excellent framework to consider the multiphasic nature of a thrombus. Therefore, we used TPM to develop a thermodynamically consistent model using a smeared model of solid and nutrient-rich liquid phases. The constitutive relations are proposed based on the restrictions obtained by evaluating the entropy inequality. The mass exchange between the solid and nutrient phases is formulated, which depends on the nutrient concentration and the seepage velocity. The simulations show the growth of the thrombus in low-blood-velocity regions. Here, we see that the material parameters play an important role in incorporating the physiological factors that can result in thrombosis, according to the Virchow triad. We have an additional parameter to incorporate the factor of inherited or acquired disorders leading to hypercoagulability. The stasis of blood and endothelial injury, along with hypertension, are also incorporated into the model. Moreover, the triphasic model gives the advantage of including the mass exchange between the nutrient and solid phases without altering the amount of liquid which fits well with the physiological understanding of thrombosis. The model also proves its usefulness in actual cases.

However, biological modelling is challenging. There is a need to quantify the different factors responsible for thrombi growth and determine the material parameters from additional experiments. This would also give us more accurate boundary conditions and possibilities to guide the growth process in a much more accurate way. This would also lead to the potential splitting of the mass production formulation into two approaches: primary and secondary haemostasis. These two processes consist of the major part of the thrombus formation. Moreover, the non-Newtonian behaviour of blood should be considered in the model. Also, there is a lack of availability of enough medical data. With enough medical data (CT/MRI scans) taken at different stages of thrombosis, it would be possible to validate the model with further improvements.

Moreover, the model can be extended to different cases of AD, such as type A AD or false lumen with multiple tears. A larger set of medical and experimental data can aid in developing, validating and training such models and performing patient-focused simulations. Additionally, because the short-term and long-term diagnosis of AD, especially type B AD, is unclear, all the models for different AD cases can be combined to develop a numerical laboratory and help in decision-making. Furthermore, the model of thrombosis could be extended to conditions where the formation of the blood clot is critical, such as deep venous thrombosis, hypercoagulability disorders and disseminated intravascular coagulation (DIC). Understanding the mechanics of growth in such chronic conditions can open new directions in medical device design, personalised medicine, prognosis and controlling disease progression [51].