Skip to main content
SpringerLink
Log in

Vibration characteristics analysis of anisotropic metal rubber medium-thick cylindrical shells

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

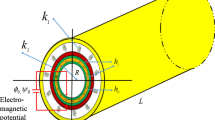
This paper is to analyze the vibration characteristics of a metal rubber medium-thick cylindrical shell (MR-MTCS) influenced by material anisotropy. The parameters of the metal rubber (MR) are determined by the inclined helix-pyramid model (IHPM). The control equations for MR-MTCS are determined by first-order shear deformation theory (FSDT) and Rayleigh–Ritz method. The results show that the anisotropy of MR has a significant effect on the vibration characteristics of MR-MTCS. Among them, the anisotropy of Young's modulus has the most significant effect on the vibration characteristics. In addition, the effect of MR anisotropy on the vibration characteristics of MR-MTCS increases with the increase of axial half-wave number m and decreases with the increase of axial wave number n.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Data availability

All data generated during this study are included in this published paper.

Abbreviations

h :

Cylindrical shell thickness (m)

R :

The radius of the middle surface of the cylindrical shell (m)

L :

Cylindrical shell length (m)

u, v, w :

Displacement of the shell along x, θ, z direction (m)

ψ x, ψ θ :

Rotation angles normal to the direction of x- and θ-axis (rad)

a x , a θ :

Lame coefficient in the x, θ direction in the middle surface (−)

R x, R θ :

The radius of curvature in the x, θ direction in the middle surface (m)

A x, A θ :

Lamé coefficient along x, θ direction in cylindrical shell (−)

n m :

Number of screws of equivalent spring unit (−)

E i :

Young's modulus of MR (MPa)

ε x, ε θ :

Normal strain of shell along x, θ direction (−)

γ xθ, γ θz, γxz :

Shear strain of the shell normal to the z-axis, x-axis and θ-axis (−)

k u ,k v ,k w :

Stiffness coefficient along x, θ, z direction

κ x, κ θ :

Slope of strain εx, εθ along the z-direction (−)

E, E m :

Young's modulus of cylindrical shell and metal wire (GPa)

μ :

Poisson's ratio of MR (−)

μ m :

Poisson's ratio of metal wire

ρ :

Density of the shell (kg/m3)

N, Q s :

Membrane stresses (Pa)

M :

Membrane moments (Pa.m)

K s :

Transverse shear correction factor (−)

U,U spr :

Strain energy of the shell and elastic support (N.m)

T :

Shell kinetic energy (N.m)

δ :

Variable score symbols (−)

t,T 0,T 1 :

Times, starting moment, ending moment (s)

ω :

Round frequency(rad)

n :

Circumferential wave number (−)

m :

Axial half wave number (−)

δ kl :

Kronecker constant (−)

f :

Natural frequency of MR-MTCS (Hz)

η :

Modal loss factor of MR-MTCS

β :

Half cone angle of equivalent spring unit (rad)

\({\upeta }_{{\text{ m,n}}}^{{\text{ N}}}\) :

Modal loss factor at N (%)

\({\text{f}} _{{\text{m,n}}}^{{\text{ N}}}\) :

Natural frequency at N (Hz)

W L ,W U :

Mechanical work during loading and unloading (N.m)

ρm, \({\overline{\rho }} \) :

Relative density of MR samples and blanks (%)

\(\mu_{c} { }\) :

Friction coefficient of 304 stainless steel (%)

a, b :

Load correction factor (−)

α :

Guidance angle (rad)

d, D :

Wire diameter and helix diameter (mm)

N :

Polynomial truncation number (−)

C :

Spring index of the helix unit (−)

φ , \({\overline{{\varphi }}}\) :

Inclination angle of the helix unit and its mean value (rad)

r :

Molding ratio of MR(−)

K T :

Axial stiffness of the helix unit (N/m)

K V :

Tangential stiffness of the helix unit (N/m)

References

  1. .Chegodaev DE, Mylukin OP, Koltygin EV,: Design of metal rubber components. National Defense Industry Press, Beijing (2000)

    Google Scholar 

  2. Chandrasekhar, K., Rongong, J., Cross, E.: Mechanical behaviour of tangled metal wire devices. Mech. Syst. Signal Process. 118, 13–29 (2019). https://doi.org/10.1016/j.ymssp.2018.08.021

    Article  Google Scholar 

  3. Yang, P., Bai, H., Xue, X., Xiao, K., Zhao, X.: Vibration reliability characterization and damping capability of annular periodic metal rubber in the non-molding direction. Mech. Syst. Signal Process 132, 622–639 (2019). https://doi.org/10.1016/j.ymssp.2019.07.020

    Article  Google Scholar 

  4. Xue, X., Yang, P., Shao, Y., Bai, H.: Manufacture technology and anisotropic behaviour of elastic-porous metal rubber. Int. J. Lightweight Mater. Manuf. 3(2), 88–99 (2020). https://doi.org/10.1016/j.ijlmm.2019.08.005

    Article  Google Scholar 

  5. Ma, Y., Zhang, Q., Dobah, Y., Scarpa, F., Fraternali, F., Skelton, R.E., Zhang, D., Hong, J.: Meta-tensegrity: Design of a tensegrity prism with metal rubber. Compos. Struct. 206, 644–657 (2018). https://doi.org/10.1016/j.compstruct.2018.08.067

    Article  Google Scholar 

  6. Xia, X., Wu, S., Sun, S., Du, Q., Long, F.: Lateral hysteretic behavior of a novel metal rubber bridge bearing. Eng. Struct. 256, 114051 (2022). https://doi.org/10.1016/j.engstruct.2022.114051

    Article  Google Scholar 

  7. Zhang, C., Ao, H., Jiang, H.: Macro-microstatic stiffness prediction model of metal rubber. Adv. Theory Simul. (2021). https://doi.org/10.1002/adts.202100008

    Article  Google Scholar 

  8. Wang, Y., Zhang, Z., Xue, X., Zhang, L.: Experimental investigation on enhanced mechanical and damping performance of corrugated structure with metal rubber. Thin-Walled Struct. 154, 106816 (2020). https://doi.org/10.1016/j.tws.2020.106816

    Article  Google Scholar 

  9. Wang, Y., Ma, Y., Hu, W., Hong, J.: Research on the variable mechanical properties and application in vibration control of soft magnetic entangled metallic wire material. Smart Mater. Struct. 30(4), 45026–45029 (2021)

    Article  Google Scholar 

  10. Chegodaev DE (2000) Design of metal rubber components.

  11. Yuyan, L., Xieqing, H., Wenxiong, M.: A theoretical model and experimental investigation of a nonlinear constitutive equation for elastic porous metal rubbers. Mech. Compos. Mater. 41(4), 303–312 (2005). https://doi.org/10.1007/s11029-005-0056-2

    Article  Google Scholar 

  12. Xue, X., Ruan, S., Bai, H., Chen, X., Shao, Y., Lu, C.: An enhanced constitutive model for the nonlinear mechanical behavior of the elastic-porous metal rubber. Mech. Mater. 148, 103447 (2020). https://doi.org/10.1016/j.mechmat.2020.103447

    Article  Google Scholar 

  13. Peng, W., Bai, H., Zheng, J.: A micromechanics constitutive model of the metal rubber materials based on the radial and axial combined deformation of the microsprings. J. Exp. Mech. (2005)

  14. Ma, Y., Zhang, Q., Zhang, D., Scarpa, F., Liu, B., Hong, J.: The mechanics of shape memory alloy metal rubber. Acta Mater. 96, 89–100 (2015). https://doi.org/10.1016/j.actamat.2015.05.031

    Article  Google Scholar 

  15. Wang, Y.Q., Ye, C., Zu, J.W.: Nonlinear vibration of metal foam cylindrical shells reinforced with graphene platelets. Aerosp. Sci. Technol. 85, 359–370 (2019). https://doi.org/10.1016/j.ast.2018.12.022

    Article  Google Scholar 

  16. .Reddy, J.N.: Mechanics of laminated composite plates and shells : theory and analysis. Mechanics of laminated composite plates and shells: theory and analysis (2004)

  17. Sofiyev, A.H., Hui, D., Haciyev, V.C., Erdem, H., Yuan, G.Q., Schnack, E., Guldal, V.: The nonlinear vibration of orthotropic functionally graded cylindrical shells surrounded by an elastic foundation within first order shear deformation theory. Compos. B Eng. 116, 170–185 (2017). https://doi.org/10.1016/j.compositesb.2017.02.006

    Article  Google Scholar 

  18. Sofiyev, A.H., Kuruoglu, N.: Combined effects of transverse shear stresses and nonlinear elastic foundations on the nonlinear dynamic response of heterogeneous orthotropic cylindrical shells. Compos. Struct. 166, 153–162 (2017). https://doi.org/10.1016/j.compstruct.2017.01.058

    Article  Google Scholar 

  19. Shen, H.: Boundary layer theory for the nonlinear vibration of anisotropic laminated cylindrical shells. Compos. Struct. 97, 338–352 (2013). https://doi.org/10.1016/j.compstruct.2012.10.027

    Article  Google Scholar 

  20. Toorani, M.H., Lakis, A.A.: Large amplitude vibrations of anisotropic cylindrical shells. Comput. Struct. 82(23), 2015–2025 (2004). https://doi.org/10.1016/j.compstruc.2003.07.007

    Article  Google Scholar 

  21. Wang, Y., Wu, D.: Free vibration of functionally graded porous cylindrical shell using a sinusoidal shear deformation theory. Aerosp. Sci. Technol. 66, 83–91 (2017). https://doi.org/10.1016/j.ast.2017.03.003

    Article  Google Scholar 

  22. Song, X., Cao, T., Gao, P., Han, Q.: Vibration and damping analysis of cylindrical shell treated with viscoelastic damping materials under elastic boundary conditions via a unified Rayleigh-Ritz method. Int. J. Mech. Sci. 165, 105158 (2020). https://doi.org/10.1016/j.ijmecsci.2019.105158

    Article  Google Scholar 

  23. Guo, Chenchen, Liu, T., Wang, Q., Qin, Bin, Shao, W., Wang, A.: Spectral-Tchebychev technique for the free vibration analysis of composite laminated stepped and stiffened cylindrical shells with arbitrary boundary conditions. Compos. Struct. 272, 114193 (2021). https://doi.org/10.1016/j.compstruct.2021.114193

    Article  Google Scholar 

  24. Miao, X., Li, C., Pan, Y.: Research on the dynamic characteristics of rotating metal–ceramic matrix DFG-CNTRC thin laminated shell with arbitrary boundary conditions. Thin-Walled Struct. 179, 109475 (2022). https://doi.org/10.1016/j.tws.2022.109475

    Article  Google Scholar 

  25. Wang, Y.Q., Ye, C., Zu, J.W.: Vibration analysis of circular cylindrical shells made of metal foams under various boundary conditions. Int. J. Mech. Mater. Des. 15(2), 333–344 (2019). https://doi.org/10.1007/s10999-018-9415-8

    Article  Google Scholar 

  26. Soldatos, K.P., Messina, A.: Vibration studies of cross-ply laminated shear deformable circular cylinders on the basis of orthogonal polynomials. J. Sound. Vib. 218(2), 219–243 (1998). https://doi.org/10.1006/jsvi.1998.1769

    Article  MATH  Google Scholar 

  27. Miao, X., Li, C., Jiang, Y., Zhang, Z.: Free vibration analysis of three-layer thin cylindrical shell with variable thickness two-dimensional FGM middle layer under arbitrary boundary conditions. J. Sandw. Struct. Mater. 24(2), 973–1003 (2021). https://doi.org/10.1177/10996362211020429

    Article  Google Scholar 

  28. Qin, Z., Chu, F., Zu, J.: Free vibrations of cylindrical shells with arbitrary boundary conditions: A comparison study. Int. J. Mech. Sci. 133, 91–99 (2017). https://doi.org/10.1016/j.ijmecsci.2017.08.012

    Article  Google Scholar 

  29. Mason, J.C., Handscomb, D.C.: Chebyshev polynomials. Chapman and Hall/CRC, Boca Raton (2002)

    Book  MATH  Google Scholar 

  30. Ilanko, S., Monterrubio, L., Mochida, Y.: The Rayleigh-Ritz method for structural analysis. Wiley, New York (2014)

    Book  MATH  Google Scholar 

  31. Ye, T., Jin, G., Shi, S., Ma, X.: Three-dimensional free vibration analysis of thick cylindrical shells with general end conditions and resting on elastic foundations. Int. J. Mech. Sci. 84, 120–137 (2014). https://doi.org/10.1016/j.ijmecsci.2014.04.017

    Article  Google Scholar 

  32. Messina, A., Soldatos, K.P.: Ritz-type dynamic analysis of cross-ply laminated circular cylinders subjected to different boundary conditions. J. Sound. Vib. 227(4), 749–768 (1999)

    Article  MATH  Google Scholar 

  33. Suchao, L.I., Guo, A., Wang, W., Mao, C., Hui, L.I.: Study on constitutive model of shape memory alloy pseudo-rubber based on layer decomposition. J. Build. Struct. (2016)

  34. Chenyu, W., Wenhao, P., Suchao, L., Qinghe, F.: Study on constitutive model of metal pseudo-rubber isolator based on the statistical contact properties. Industrial Construction (Chinese) (2021)

Download references

Acknowledgements

The authors thank Haiyang Liu for helpful discussion.

Author information

Authors and Affiliations

  1. School of Mechanical Engineering and Automation, Northeastern University, Shenyang, 110819, China

    Yan Bai & He Li

Authors
  1. Yan Bai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. He Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

YB contributed to conceptualization, methodology, software, and writing—original draft. HL contributed to supervision, project administration, funding acquisition, and writing—review and editing.

Corresponding author

Correspondence to He Li.

Ethics declarations

Conflict of interest

No conflict of interest exists in the submission of this manuscript, and the manuscript is approved by all authors for publication.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author (s) or other rights holder (s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

Equation (19) for M, K and Kspr has the following expressions:

$$ {\varvec{M}} = \left[ {\begin{array}{*{20}c} {{\varvec{M}}_{11}^{sub} } & {\mathbf{0}} & {\mathbf{0}} & {{\varvec{M}}_{14}^{sub} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\varvec{M}}_{22}^{sub} } & {\mathbf{0}} & {\mathbf{0}} & {{\varvec{M}}_{25}^{sub} } \\ {\mathbf{0}} & {\mathbf{0}} & {{\varvec{M}}_{33}^{sub} } & {\mathbf{0}} & {\mathbf{0}} \\ {{\varvec{M}}_{41}^{sub} } & {\mathbf{0}} & {\mathbf{0}} & {{\varvec{M}}_{44}^{sub} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\varvec{M}}_{52}^{sub} } & {\mathbf{0}} & {\mathbf{0}} & {{\varvec{M}}_{55}^{sub} } \\ \end{array} } \right] $$
(A1)
$$ {\varvec{M}}_{11}^{sub} = {\varvec{M}}_{22}^{sub} = {\varvec{M}}_{33}^{sub} = \frac{1}{2}hL\pi R^{2} \rho \omega^{2} \int_{0}^{1} {{\varvec{P}}_{u} {\varvec{P}}_{u} dx} $$
(A2)
$$ {\varvec{M}}_{41}^{sub} = {\varvec{M}}_{14}^{sub} = {\varvec{M}}_{52}^{sub} = {\varvec{M}}_{25}^{sub} = \frac{1}{24}h^{3} L\pi R\rho \omega^{2} \int_{0}^{1} {{\varvec{P}}_{u} {\varvec{P}}_{u} dx} $$
(A3)
$$ {\varvec{M}}_{44}^{sub} = {\varvec{M}}_{55}^{sub} = \frac{1}{24}h^{3} L\pi R^{2} \rho \omega^{2} \int_{0}^{1} {{\varvec{P}}_{u} {\varvec{P}}_{u} dx} $$
(A4)
$$ {\varvec{K}} = {\varvec{K}}^{(1)} + {\varvec{K}}^{(2)} + {\varvec{K}}^{(3)} $$
(A5)
$$ {\varvec{K}}_{spr} \user2{ = K}_{spr}^{\left( 0 \right)} + {\varvec{K}}_{spr}^{\left( 1 \right)} $$
(A6)
$$ {\varvec{K}}^{(1)} = \left[ {\begin{array}{*{20}c} {{\varvec{K}}_{11}^{\left( 1 \right)} } & {\mathbf{0}} & {\mathbf{0}} & {{\varvec{K}}_{14}^{\left( 1 \right)} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\varvec{K}}_{22}^{\left( 1 \right)} } & {{\varvec{K}}_{23}^{\left( 1 \right)} } & {\mathbf{0}} & {{\varvec{K}}_{25}^{\left( 1 \right)} } \\ {\mathbf{0}} & {{\varvec{K}}_{32}^{\left( 1 \right)} } & {{\varvec{K}}_{33}^{\left( 1 \right)} } & {\mathbf{0}} & {{\varvec{K}}_{35}^{\left( 1 \right)} } \\ {{\varvec{K}}_{41}^{\left( 1 \right)} } & {\mathbf{0}} & {\mathbf{0}} & {{\varvec{K}}_{44}^{\left( 1 \right)} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\varvec{K}}_{52}^{\left( 1 \right)} } & {{\varvec{K}}_{53}^{\left( 1 \right)} } & {\mathbf{0}} & {{\varvec{K}}_{55}^{\left( 1 \right)} } \\ \end{array} } \right] $$
(A7)
$$ {\varvec{K}}^{(2)} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {{\varvec{K}}_{12}^{\left( 2 \right)} } & {{\varvec{K}}_{13}^{\left( 2 \right)} } & {\mathbf{0}} & {{\varvec{K}}_{15}^{\left( 2 \right)} } \\ {{\varvec{K}}_{21}^{\left( 2 \right)} } & {\mathbf{0}} & {\mathbf{0}} & {{\varvec{K}}_{24}^{\left( 2 \right)} } & {\mathbf{0}} \\ {{\varvec{K}}_{31}^{\left( 2 \right)} } & {\mathbf{0}} & {\mathbf{0}} & {{\varvec{K}}_{24}^{\left( 2 \right)} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\varvec{K}}_{42}^{\left( 2 \right)} } & {{\varvec{K}}_{43}^{\left( 2 \right)} } & {\mathbf{0}} & {{\varvec{K}}_{45}^{\left( 2 \right)} } \\ {{\varvec{K}}_{51}^{\left( 2 \right)} } & {\mathbf{0}} & {\mathbf{0}} & {{\varvec{K}}_{54}^{\left( 2 \right)} } & {\mathbf{0}} \\ \end{array} } \right] $$
(A8)
$$ {\varvec{K}}^{(3)} = \left[ {\begin{array}{*{20}c} {{\varvec{K}}_{11}^{\left( 3 \right)} } & {\mathbf{0}} & {\mathbf{0}} & {{\varvec{K}}_{14}^{\left( 3 \right)} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\varvec{K}}_{22}^{\left( 3 \right)} } & {\mathbf{0}} & {\mathbf{0}} & {{\varvec{K}}_{25}^{\left( 3 \right)} } \\ {\mathbf{0}} & {\mathbf{0}} & {{\varvec{K}}_{33}^{\left( 3 \right)} } & {\mathbf{0}} & {\mathbf{0}} \\ {{\varvec{K}}_{41}^{\left( 2 \right)} } & {\mathbf{0}} & {\mathbf{0}} & {{\varvec{K}}_{44}^{\left( 2 \right)} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\varvec{K}}_{52}^{\left( 2 \right)} } & {\mathbf{0}} & {\mathbf{0}} & {{\varvec{K}}_{53}^{\left( 2 \right)} } \\ \end{array} } \right] $$
(A9)
$$ {\varvec{K}}_{11}^{(1)} = \frac{{G_{12} Ln^{2} \pi R}}{{2\left( { - 1 + \nu_{12} \nu_{21} } \right)}}\left[ \begin{gathered} - L_{9} + L_{5} \nu_{12} \nu_{21} + L_{6} \left( { - 1 + \nu_{12} \nu_{21} } \right) + \hfill \\ L_{7} \left( { - 1 + \nu_{12} \nu_{21} } \right) \hfill \\ \end{gathered} \right]\int_{0}^{1} {{\varvec{P}}_{u} {\varvec{P}}_{u} dx} $$
(A10)
$$ {\varvec{K}}_{14}^{(1)} = \frac{L\pi R}{{648\left( { - 1 + \nu_{12} \nu_{21} } \right)}}\left( \begin{gathered} - 324G_{12} hn^{2} + 648G_{12} L_{2} n^{2} R - \hfill \\ 648G_{12} L_{3} n^{2} R + 648G_{12} L_{4} n^{2} R + \hfill \\ 324G_{12} hn^{2} \nu_{12} \nu_{21} - 648G_{12} L_{2} n^{2} R\nu_{12} \nu_{21} + \hfill \\ 648G_{12} L_{3} n^{2} R\nu_{12} \nu_{21} - 648G_{12} L_{4} n^{2} R\nu_{12} \nu_{21} \hfill \\ \end{gathered} \right)\int_{0}^{1} {{\varvec{P}}_{u} {\varvec{P}}_{{\varphi_{x} }} dx} $$
(A11)
$$ {\varvec{K}}_{22}^{(1)} = \frac{L\pi R}{{2\left( { - 1 + \nu_{12} \nu_{21} } \right)}}\left\{ \begin{gathered} L_{14} \left[ { - E_{1} n^{2} + G_{13} K_{s} \left( { - 1 + \nu_{12} \nu_{21} } \right)} \right] + \hfill \\ L_{12} \left[ { - E_{2} n^{2} + G_{23} K_{s} \left( { - 1 + \nu_{12} \nu_{21} } \right)} \right] + \hfill \\ L_{13} \left[ { - E_{2} n^{2} + G_{23} K_{s} \left( { - 1 + \nu_{12} \nu_{21} } \right)} \right] \hfill \\ \end{gathered} \right\}\int_{0}^{1} {{\varvec{P}}_{v} {\varvec{P}}_{v} dx} $$
(A12)
$$ K_{23}^{(1)} = \frac{L\pi R}{{648\left( { - 1 + \nu_{12} \nu_{21} } \right)}}\left( \begin{gathered} 324E_{2} L_{5} n + 324G_{23} K_{s} L_{5} n + 324E_{2} L_{6} n + \hfill \\ 324G_{23} K_{s} L_{6} n + 324E_{1} L_{7} n + 324G_{13} K_{s} L_{7} n - \hfill \\ 324G_{23} K_{s} L_{5} n\nu_{12} \nu_{21} - 324G_{23} K_{s} L_{6} n\nu_{12} \nu_{21} - \hfill \\ 324G_{13} K_{s} L_{7} n\nu_{12} \nu_{21} \hfill \\ \end{gathered} \right)\int_{0}^{1} {{\varvec{P}}_{v} {\varvec{P}}_{w} d} x $$
(A13)
$$ {\varvec{K}}_{25}^{(1)} = \frac{L\pi R}{{648\left( { - 1 + \nu_{12} \nu_{21} } \right)}}\left( \begin{gathered} - 108E_{1} hn^{2} - 216E_{2} hn^{2} + \hfill \\ 324G_{23} K_{s} L_{5} R + 324G_{23} K_{s} L_{6} R + \hfill \\ 324G_{13} K_{s} L_{7} R + 648E_{1} L_{2} n^{2} R - \hfill \\ 648E_{2} L_{3} n^{2} R + 648E_{2} L_{4} n^{2} R - \hfill \\ 324G_{23} K_{s} L_{5} R\nu_{12} \nu_{21} - 324G_{23} K_{s} L_{6} R\nu_{12} \nu_{21} - \hfill \\ 324G_{13} K_{s} L_{7} R\nu_{12} \nu_{21} \hfill \\ \end{gathered} \right)\int_{0}^{1} {{\varvec{P}}_{v} {\varvec{P}}_{{\varphi_{\theta } }} dx} $$
(A14)
$$ {\varvec{K}}_{32}^{(1)} = \frac{Ln\pi R}{{2\left( { - 1 + \nu_{12} \nu_{21} } \right)}}\left\{ \begin{gathered} L_{14} \left[ {E_{1} + G_{13} K_{s} \left( {1 - \nu_{12} \nu_{21} } \right)} \right] + \hfill \\ L_{12} \left[ {E_{2} + G_{23} K_{s} \left( {1 - \nu_{12} \nu_{21} } \right)} \right] + \hfill \\ L_{13} \left[ {E_{2} + G_{23} K_{s} \left( {1 - \nu_{12} \nu_{21} } \right)} \right] \hfill \\ \end{gathered} \right\}\int_{0}^{1} {{\varvec{P}}_{w} {\varvec{P}}_{v} dx} $$
(A15)
$$ {\varvec{K}}_{33}^{(1)} = \frac{L\pi R}{{648\left( { - 1 + \nu_{12} \nu_{21} } \right)}}\left( \begin{gathered} - 324E_{2} L_{5} - 324E_{2} L_{6} - 324E_{1} L_{7} - \hfill \\ 324G_{23} K_{s} L_{6} n^{2} - 324G_{13} K_{s} L_{7} n^{2} - \hfill \\ 324G_{23} K_{s} L_{9} n^{2} + 324G_{23} K_{s} L_{5} n^{2} \nu_{12} \nu_{21} + \hfill \\ 324G_{23} K_{s} L_{6} n^{2} \nu_{12} \nu_{21} + 324G_{13} K_{s} L_{7} n^{2} \nu_{12} \nu_{21} \hfill \\ \end{gathered} \right)\int_{0}^{1} {{\varvec{P}}_{w} {\varvec{P}}_{w} dx} $$
(A16)
$$ {\varvec{K}}_{35}^{(1)} = \frac{L\pi R}{{648\left( { - 1 + \nu_{12} \nu_{21} } \right)}}\left( \begin{gathered} 108E_{1} hn + 216E_{2} hn - 648E_{1} L_{2} nR + \hfill \\ 648E_{2} L_{3} nR - 648E_{2} L_{4} nR - \hfill \\ 324G_{23} K_{s} L5nR - 324G_{23} K_{s} L_{6} nR - \hfill \\ 324G_{13} K_{s} L_{7} nR + 324G_{23} K_{s} L_{5} nR\nu_{12} \nu_{21} + \hfill \\ 324G_{23} K_{s} L_{6} nR\nu_{12} \nu_{21} + 324G_{13} K_{s} L_{7} nR\nu_{12} \nu_{21} \hfill \\ \end{gathered} \right)\int_{0}^{1} {{\varvec{P}}_{w} {\varvec{P}}_{{\varphi_{\theta } }} dx} $$
(A17)
$$ {\varvec{K}}_{41}^{(1)} = \frac{1}{2}G_{12} Ln^{2} \pi R\left( {h - 2L_{2} R + 2L_{3} R - 2L_{4} R} \right)\int_{0}^{1} {{\varvec{P}}_{{\varphi_{x} }} {\varvec{P}}_{u} dx} $$
(A18)
$$ {\varvec{K}}_{44}^{(1)} = \frac{{L\pi R^{2} }}{{ - 6 + 6\nu_{12} \nu_{21} }}\left\{ \begin{gathered} \left( { - 1 + \nu_{12} \nu_{21} } \right)\left[ {G_{23} K_{s} h + 3G_{23} K_{s} \left( { - 2L_{2} + L_{7} } \right)R - } \right. \hfill \\ \left. {3G_{12} n^{2} h - 3G_{12} n^{2} \left( {2L_{2} - 2L_{8} + L_{9} } \right)R} \right] + \hfill \\ G_{13} K_{s} \left[ {2h\left( { - 1 + \nu_{12} \nu_{21} } \right) - 3R\left( { - 4L_{4} + L_{5} + } \right.} \right. \hfill \\ L_{6} - 2L_{8} + L_{9} + 4L_{4} \nu_{12} \nu_{21} - L_{6} \nu_{12} \nu_{21} + \hfill \\ \left. {\left. {2L_{8} \nu_{12} \nu_{21} - 2L_{9} \nu_{12} \nu_{21} + 4L_{3} - 4L_{3} \nu_{12} \nu_{21} } \right)} \right] \hfill \\ \end{gathered} \right\}\int_{0}^{1} {{\varvec{P}}_{{\varphi_{x} }} {\varvec{P}}_{{\varphi_{x} }} } dx $$
(A19)
$$ {\varvec{K}}_{52}^{(1)} = \frac{L\pi R}{{ - 6 + 6\nu_{12} \nu_{21} }}\left\{ \begin{gathered} - E_{1} n^{2} \left( {h - 6L_{2} R} \right) - 2E_{2} n^{2} \left[ {h + 3\left( {L_{3} - L_{4} } \right)R} \right] - \hfill \\ 3K_{s} R\left[ {G_{23} \left( {L_{12} + L_{13} } \right) + G_{13} L_{14} } \right]\left( { - 1 + \nu_{12} \nu_{21} } \right) \hfill \\ \end{gathered} \right\}\int_{0}^{1} {{\varvec{P}}_{{\varphi_{\theta } }} {\varvec{P}}_{v} dx} $$
(A20)
$$ K_{53}^{(1)} = \frac{Ln\pi R}{{ - 6 + 6\nu_{12} \nu_{21} }}\left\{ \begin{gathered} E_{1} \left( {h - 6L_{2} R} \right) + 2E_{2} \left[ {h + 3\left( {L_{3} - L_{4} } \right)R} \right] + \hfill \\ 3K_{s} R\left[ {G_{23} \left( {L_{5} + L_{6} } \right) + G_{13} L_{7} } \right]\left( { - 1 + \nu_{12} \nu_{21} } \right) \hfill \\ \end{gathered} \right\}\int_{0}^{1} {{\varvec{P}}_{{\varphi_{\theta } }} {\varvec{P}}_{w} dx} $$
(A21)
$$ K_{55}^{(1)} = \frac{{L\pi R^{2} }}{{ - 6 + 6\nu_{12} \nu_{21} }}\left\{ \begin{gathered} E_{1} n^{2} \left( {h - 6L_{2} R} \right) + E_{2} n^{2} \left( {2h + 6L_{8} R - 3L_{9} R} \right) + \hfill \\ 3K_{s} \left( {G_{23} \left( {L_{5} + L_{6} } \right) + G_{13} L_{7} } \right)R\left( { - 1 + \nu_{12} \nu_{21} } \right) \hfill \\ \end{gathered} \right\}\int_{0}^{1} {{\varvec{P}}_{{\varphi_{\theta } }} {\varvec{P}}_{{\varphi_{\theta } }} dx} $$
(A22)
$$ {\varvec{K}}_{11}^{(2)} = \frac{{Ln\pi R\left[ { - E_{1} \nu_{12} + G_{12} \left( { - 1 + \nu_{12} \nu_{21} } \right)} \right]}}{{ - 2 + 2\nu_{12} \nu_{21} }}\left[ \begin{gathered} h - 2L_{2} R + 2L_{3} R - \hfill \\ 2L_{4} R + L_{5} R + L_{6} R + L_{7} R \hfill \\ \end{gathered} \right]\int_{0}^{1} {{\varvec{P}}_{u} \user2{P^{\prime}}_{u} dx} $$
(A23)
$$ {\varvec{K}}_{13}^{(2)} = \frac{{E_{1} L\pi R\nu_{12} }}{{ - 2 + 2\nu_{12} \nu_{21} }}\left[ \begin{gathered} h - 2L_{2} R + 2L_{3} R - \hfill \\ 2L_{4} R + L_{6} R + L_{7} R + \hfill \\ L_{9} R \hfill \\ \end{gathered} \right]\int_{0}^{1} {{\varvec{P}}_{u} \user2{P^{\prime}}_{w} dx} $$
(A24)
$$ {\varvec{K}}_{15}^{(2)} = \frac{{L\left( {2L_{3} - 2L_{4} - 2L_{8} + L_{9} } \right)n\pi R^{3} \left( {G_{12} + E_{1} \nu_{12} - G_{12} \nu_{12} \nu_{21} } \right)}}{{2 - 2\nu_{12} \nu_{21} }}\int_{0}^{1} {{\varvec{P}}_{u} {\varvec{P}}_{{\varphi_{\theta } }} dx} $$
(A25)
$$ {\varvec{K}}_{21}^{(2)} = - \frac{{Ln\pi R\left( { - E_{1} \nu_{12} + G_{12} \left( { - 1 + \nu_{12} \nu_{21} } \right)} \right)}}{{ - 2 + 2\nu_{12} \nu_{21} }}\left[ \begin{gathered} h - 2L_{2} R + 2L_{3} R - \hfill \\ 2L_{4} R + L_{5} R + L_{6} R + \hfill \\ L_{7} R \hfill \\ \end{gathered} \right]\int_{0}^{1} {{\varvec{P}}_{v} {\varvec{P}}_{u} dx} $$
(A26)
$$ {\varvec{K}}_{24}^{(2)} = \frac{{Ln\pi R^{3} \left( {2L_{3} - 2L_{4} - 2L_{8} + L_{9} } \right)\left( {G_{12} + E_{1} \nu_{12} - G_{12} \nu_{12} \nu_{21} } \right)}}{{ - 2 + 2\nu_{12} \nu_{21} }}\int_{0}^{1} {{\varvec{P}}_{v} {\varvec{P}}_{{\varphi_{x} }} dx} $$
(A16)
$$ {\varvec{K}}_{31}^{(2)} = - \frac{{E_{1} L\pi R\nu_{12} }}{{ - 2 + 2\nu_{12} \nu_{21} }}\left( \begin{gathered} h - 2L_{2} R + \hfill \\ 2L_{3} R - 2L_{4} R + \hfill \\ L_{5} R + L_{6} R + L_{7} R \hfill \\ \end{gathered} \right)\int_{0}^{1} {{\varvec{P}}_{w} {\varvec{P}}_{u} dx} $$
(A27)
$$ {\varvec{K}}_{34}^{(2)} = - \frac{L\pi R}{{ - 6 + 6\nu_{12} \nu_{21} }}\left\{ \begin{gathered} 3E_{1} R\nu_{12} \left( {2L_{3} - 2L_{4} - 2L_{8} + L_{9} } \right) + \hfill \\ G_{23} K_{s} \left( {h - 6L_{2} R + 3L_{7} R} \right)\left( { - 1 + \nu_{12} \nu_{21} } \right) + \hfill \\ G_{13} K_{s} \left[ {2h\left( { - 1 + \nu_{12} \nu_{21} } \right) + 3R\left( { - 4L_{3} + 4L_{4} - } \right.} \right. \hfill \\ L_{6} + 2L_{8} - 2L_{9} + 4L_{3} \nu_{12} \nu 21 - 4L_{4} \nu_{12} \nu_{21} + \hfill \\ \left. {\left. {L_{5} \nu_{12} \nu_{21} + L_{6} \nu_{12} \nu_{21} - 2L_{8} \nu_{12} \nu_{21} + L_{9} \nu_{12} \nu_{21} } \right)} \right] \hfill \\ \end{gathered} \right\}\int_{0}^{1} {{\varvec{P}}_{w} {\varvec{P}}_{{\varphi_{x} }} dx} $$
(A28)
$$ {\varvec{K}}_{42}^{(2)} = \frac{{Ln\pi R^{3} \left( {2L_{3} - 2L_{4} - 2L_{8} + L_{9} } \right)\left( {G_{12} + E_{1} \nu_{12} - G_{12} \nu_{12} \nu_{21} } \right)}}{{2 - 2\nu_{12} \nu_{21} }}\int_{0}^{1} {{\varvec{P}}_{{\varphi_{x} }} {\varvec{P}}_{v} dx} $$
(A29)
$$ {\varvec{K}}_{43}^{(2)} = \frac{{L\pi R^{2} }}{{ - 6 + 6\nu_{12} \nu_{21} }}\left\{ \begin{gathered} 3E_{1} \left( {2L_{3} - 2L_{4} - 2L_{8} + L_{9} } \right)R\nu_{12} + \hfill \\ G_{23} K_{s} \left( {h - 6L_{2} R + 3L7R} \right)\left( { - 1 + \nu_{12} \nu_{21} } \right) + \hfill \\ G_{13} K_{s} \left[ {2h\left( { - 1 + \nu_{12} \nu_{21} } \right) - 3R\left( { - 4L_{4} + L_{5} + } \right.} \right. \hfill \\ L_{6} - 2L_{8} + L_{9} + 4L_{4} \nu_{12} \nu_{21} - L_{6} \nu_{12} \nu_{21} + \hfill \\ 2L_{8} \nu_{12} \nu_{21} - 2L_{9} \nu_{12} \nu_{21} + L_{3} \left( {4 - 4\nu_{12} \nu_{21} } \right) \hfill \\ \end{gathered} \right\}\int_{0}^{1} {{\varvec{P}}_{{\varphi_{x} }} {\varvec{P}}_{w} dx} $$
(A30)
$$ {\varvec{K}}_{45}^{(2)} = \frac{{Ln\pi R\left[ {h^{3} + 12\left( {L_{10} + 2L_{3} - 2L_{8} + L_{9} } \right)R^{3} } \right]\left[ { - E_{1} \nu_{12} + G_{12} \left( { - 1 + \nu_{12} \nu_{21} } \right)} \right]}}{{24\left( { - 1 + \nu_{12} \nu_{21} } \right)}}\int_{0}^{1} {{\varvec{P}}_{{\varphi_{x} }} {\varvec{P}}_{w} dx} $$
(A31)
$$ {\varvec{K}}_{51}^{(2)} = \frac{{Ln\pi R^{3} \left( {2L_{3} - 2L_{4} - 2L_{8} + L_{9} } \right)\left( {G_{12} + E_{1} \nu_{12} - G_{12} \nu_{12} \nu_{21} } \right)}}{{ - 2 + 2\nu_{12} \nu_{21} }}\int_{0}^{1} {{\varvec{P}}_{{\varphi_{\theta } }} {\varvec{P}}_{u} dx} $$
(A32)
$$ {\varvec{K}}_{54}^{(2)} = - \frac{{Ln\pi R\left[ {G_{12} \left( { - 1 + \nu_{12} \nu_{21} } \right) - E_{1} \nu_{12} } \right]}}{{24\left( { - 1 + \nu_{12} \nu_{21} } \right)}}\left( \begin{gathered} 12R^{3} L_{10} + 24R^{3} L_{3} - \hfill \\ 24R^{3} L_{8} + 12R^{3} L_{9} \hfill \\ \end{gathered} \right)\int_{0}^{1} {{\varvec{P}}_{{\varphi_{\theta } }} {\varvec{P}}_{{\varphi_{x} }} dx} $$
(A33)
$$ {\varvec{K}}_{11}^{\left( 3 \right)} = \frac{{L\pi R^{2} }}{{ - 6 + 6\nu_{12} \nu_{21} }}\left[ \begin{gathered} 2E_{1} h + E_{2} h + 3E_{2} \left( { - 2L_{2} + L_{7} } \right)R + \hfill \\ 3E_{1} \left( {4L_{3} - 4L_{4} + L_{6} - 2L_{8} + 2L_{9} } \right)R \hfill \\ \end{gathered} \right]\int_{0}^{1} {{\varvec{P}}_{u} {\varvec{P}}_{u} dx} $$
(A34)
$$ {\varvec{K}}_{14}^{\left( 3 \right)} = \frac{L\pi R}{{648\left( { - 1 + \nu 12\nu 21} \right)}}\left[ \begin{gathered} 26E1h^{3} + E2h^{3} + \hfill \\ 324E1\left( {L10R^{3} + } \right. \hfill \\ 4L3R^{3} - 2L4R^{3} - \hfill \\ \left. {4L8R^{3} + 2L9R^{3} } \right) \hfill \\ \end{gathered} \right]\int_{0}^{1} {{\varvec{P}}_{u} {\varvec{P}}_{{\varphi_{x} }} dx} $$
(A35)
$$ {\varvec{K}}_{22}^{\left( 3 \right)} = - \frac{1}{2}G_{12} L\pi R^{2} \left( \begin{gathered} h - 2L_{2} R + 4L_{3} R - \hfill \\ 4L_{4} R + L_{5} R + L_{6} R + \hfill \\ L_{7} R - 2L_{8} R + L_{9} R \hfill \\ \end{gathered} \right)\int_{0}^{1} {{\varvec{P}}_{v} {\varvec{P}}_{v} dx} $$
(A36)
$$ {\varvec{K}}_{25}^{\left( 3 \right)} = - \frac{1}{24}G_{12} L\pi R\left( \begin{gathered} h^{3} + 12L_{10} R^{3} + 48L_{3} R^{3} - \hfill \\ 24L_{4} R^{3} - 48L_{8} R^{3} + 24L_{9} R^{3} \hfill \\ \end{gathered} \right)\int_{0}^{1} {{\varvec{P}}_{v} {\varvec{P}}_{{\varphi_{\theta } }} dx} $$
(A37)
$$ {\varvec{K}}_{33}^{\left( 3 \right)} = - \frac{{K_{s} L\pi R^{2} }}{{ - 6 + 6\nu_{12} \nu_{21} }}\left\{ \begin{gathered} G_{23} \left( {h + 3\left( { - 2L_{2} + L_{7} } \right)R} \right)\left( { - 1 + \nu_{12} \nu_{21} } \right) + \hfill \\ G_{13} \left[ {2h\left( { - 1 + \nu_{12} \nu_{21} } \right) + 3R\left( { - 4L_{3} + 4L_{4} - } \right.} \right. \hfill \\ L_{6} + 2L_{8} - 2L_{9} + 4L3\nu_{12} \nu_{21} - 4L_{4} \nu_{12} \nu_{21} + \hfill \\ L_{5} \nu_{12} \nu_{21} + L_{6} \nu_{12} \nu_{21} - 2L_{8} \nu_{12} \nu_{21} + L_{9} \nu_{12} \nu_{21} \hfill \\ \end{gathered} \right\}\int_{0}^{1} {{\varvec{P}}_{v} {\varvec{P}}_{{\varphi_{\theta } }} dx} $$
(A38)
$$ {\varvec{K}}_{41}^{\left( 3 \right)} = - \frac{L\pi R}{{648\left( { - 1 + \nu_{12} \nu_{21} } \right)}}\left[ \begin{gathered} 26E_{1} h^{3} + E_{2} h^{3} + \hfill \\ 324E_{1} R^{3} \left( {L_{10} + } \right. \hfill \\ \left. {4L_{3} - 2L_{4} - 4L_{8} + 2L_{9} } \right) \hfill \\ \end{gathered} \right]\int_{0}^{1} {{\varvec{P}}_{{\varphi_{x} }} {\varvec{P}}_{u} dx} $$
(A39)
$$ {\varvec{K}}_{44}^{\left( 3 \right)} = \frac{{L\pi R^{2} }}{{648\left( { - 1 + \nu_{12} \nu_{21} } \right)}}\left[ \begin{gathered} 26E_{1} h^{3} + E_{2} h^{3} + \hfill \\ 648E_{1} R^{3} \left( {L_{10} + } \right. \hfill \\ \left. {2L_{3} - 2L_{8} + L_{9} } \right) \hfill \\ \end{gathered} \right]\int_{0}^{1} {{\varvec{P}}_{{\varphi_{x} }} {\varvec{P}}_{{\varphi_{x} }} dx} $$
(A40)
$$ {\varvec{K}}_{52}^{\left( 3 \right)} = - \frac{1}{24}G_{12} L\pi R\left[ {h^{3} + 12\left( {L_{10} + 4L_{3} - 2L_{4} - 4L_{8} + 2L_{9} } \right)R^{3} } \right]\int_{0}^{1} {{\varvec{P}}_{{\varphi_{\theta } }} {\varvec{P}}_{{\varphi_{x} }} dx} $$
(A41)
$$ {\varvec{K}}_{55}^{\left( 3 \right)} = - \frac{1}{24}G_{12} L\pi R^{2} \left[ {h^{3} + 24\left( {L_{10} + 2L_{3} - 2L_{8} + L_{9} } \right)R^{3} } \right]\int_{0}^{1} {{\varvec{P}}_{{\varphi_{\theta } }} {\varvec{P}}_{{\varphi_{\theta } }} dx} $$
(A42)
$$ {\varvec{K}}_{spr}^{\left( 0 \right)} = \frac{1}{2}\pi R^{2} \left[ {\begin{array}{*{20}c} {K_{{u_{0} }} {\varvec{P}}_{u} {\varvec{P}}_{u} } & 0 & 0 & 0 & 0 \\ 0 & {K_{{v_{0} }} {\varvec{P}}_{v} {\varvec{P}}_{v} } & 0 & 0 & 0 \\ 0 & 0 & {K_{{w_{0} }} {\varvec{P}}_{w} {\varvec{P}}_{w} } & 0 & 0 \\ 0 & 0 & 0 & {K_{{\varphi_{x0} }} {\varvec{P}}_{{\varphi_{x} }} {\varvec{P}}_{{\varphi_{x} }} } & 0 \\ 0 & 0 & 0 & 0 & {K_{{\varphi_{\theta 0} }} {\varvec{P}}_{{\varphi_{\theta } }} {\varvec{P}}_{{\varphi_{\theta } }} } \\ \end{array} } \right]_{x = 0} $$
(A43)
$$ {\varvec{K}}_{spr}^{\left( 1 \right)} = \frac{1}{2}\pi R^{2} \left[ {\begin{array}{*{20}c} {K_{{u_{1} }} {\varvec{P}}_{u} {\varvec{P}}_{u} } & 0 & 0 & 0 & 0 \\ 0 & {K_{{v_{1} }} {\varvec{P}}_{v} {\varvec{P}}_{v} } & 0 & 0 & 0 \\ 0 & 0 & {K_{{w_{1} }} {\varvec{P}}_{w} {\varvec{P}}_{w} } & 0 & 0 \\ 0 & 0 & 0 & {K_{{\varphi_{x1} }} {\varvec{P}}_{{\varphi_{x} }} {\varvec{P}}_{{\varphi_{x} }} } & 0 \\ 0 & 0 & 0 & 0 & {K_{{\varphi_{\theta 1} }} {\varvec{P}}_{{\varphi_{\theta } }} {\varvec{P}}_{{\varphi_{\theta } }} } \\ \end{array} } \right]_{x = 1} $$
(A44)

Appendix B

Expressions exist in Appendix A as shown below:

$$ L_{1} = \ln \left( { - \frac{h + 2R}{{h - 2R}}} \right) $$
(B1)
$$ L_{2} = {\varvec{arccoth}}\left( \frac{6R}{h} \right) $$
(B2)
$$ L_{3} = {\varvec{arccoth}}\left( {\frac{h}{2h - 6R}} \right) $$
(B3)
$$ L_{4} = {\varvec{arccoth}}\left( {\frac{h}{2h + 6R}} \right) $$
(B4)
$$ L_{5} = \ln \left[ {\frac{{3\left( {h + 2R} \right)}}{h + 6R}} \right] $$
(B5)
$$ L_{6} = \ln \left( {\frac{h - 6R}{{3h - 6R}}} \right) $$
(B6)
$$ L_{7} = \ln \left( {1 - \frac{2h}{{h - 6R}}} \right) $$
(B7)
$$ L_{8} = {\varvec{arccoth}}\left( {2 - \frac{6R}{h}} \right) $$
(B8)
$$ L_{9} = \ln \left( {1 + \frac{2h}{{h + 6R}}} \right) $$
(B9)
$$ L_{10} = \ln \left( {\frac{h + 6R}{{3h + 6R}}} \right) $$
(B10)
$$ L_{11} = \ln \left[ {\frac{{\left( {h - 6R} \right)\left( {h + 2R} \right)}}{{\left( {h - 2R} \right)\left( {h + 6R} \right)}}} \right] $$
(B11)
$$ L_{12} = \ln \left( {\frac{h - 6R}{{h - 2R}}} \right) $$
(B12)
$$ L_{13} = \ln \left( {\frac{h + 2R}{{h + 6R}}} \right) $$
(B13)
$$ L_{14} = \ln \left( { - \frac{h + 6R}{{h - 6R}}} \right) $$
(B14)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bai, Y., Li, H. Vibration characteristics analysis of anisotropic metal rubber medium-thick cylindrical shells. Arch Appl Mech 93, 3553–3579 (2023). https://doi.org/10.1007/s00419-023-02453-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-023-02453-w

Keywords

Search

Navigation