Lévy-type solutions for the buckling analysis of unsymmetrically laminated plates with rotational restraints for various plate theories

Abstract

The stability behaviour of unsymmetrical laminated structures made of fibre-reinforced plastics is significantly influenced by bending–extension coupling and the comparatively low transverse shear stiffnesses. The aim of this work is to improve the analytical stability analysis of unsymmetrically laminated structures. With the discrete plate theory, the stability of laminated structures can be reduced to single laminated plates. The structure is divided into individual segments, and the surrounding structure is modelled by rotational elastic restraints. The governing equations for single plates under specific boundary conditions can be solved exactly with Lévy-type solutions. In this study, Lévy-type solutions for the mentioned boundary conditions under biaxial compressive load is described for the classical laminated plate theory, the first-order shear deformation theory and the third-order shear deformation theory (TSDT). In addition to transverse shear, bending–extension couplings of unsymmetrical cross-ply and antisymmetrical angle-ply laminates are considered. For the implementation of boundary conditions for the rotational restraints in the context of TSDT, a new set of conditions is formulated. The investigation shows very good agreement of the buckling load with comparative finite element analyses for different layups.

1 Introduction

Several theories are available to describe the mechanical behaviour of composite laminates. These laminated plate theories reflect the anisotropy of laminated plates and consider the transverse shear deformations in different ways. The classical laminated plate theory (CLPT) neglects the transverse shear deformations, i.e. the cross section remains flat and perpendicular to the mid-plane, see [1]. The neglect of shear compliance is appropriate in a good approximation for thin laminates. A constant shear deflection is assumed by the first-order shear deformation theory (FSDT) and gives more realistic results even for thicker laminates, see [2,3,4]. From a physical point of view, the shear stresses at the top and bottom surface of the plate have to disappear, but this is not reflected in the FSDT due to the resultant constant shear strains. In order to keep this error as small as possible on average, the shear correction factor K is introduced, which is in the present investigation assumed with the ‘classical’ value 5/6. The third-order shear deformation theory (TSDT) describes a cubic cross-sectional deformation, which represents a clearly more realistic representation and thus does not require the introduction of the shear correction factor, see [5, 6]. Therefore, the TSDT is also suitable for very thick laminates or laminates with pronounced shear compliance.

In addition to the very well-known approximation methods for determining the stability behaviour of fibre-reinforced plastic composites, such as mesh-based methods (finite element method (FEM), finite strip method (FSM), boundary element method), semi-analytical methods (most prominently Ritz and Galerkin method) and closed-form analytical methods (explicit solution for the critical load by means of energetic methods), there are also exact solutions for stability problems of laminates. For this purpose, the Navier and Lévy-type solutions are available, which allow an exact solution for certain boundary conditions.

The Navier solution provides an exact solution in the context of the buckling problem for an all-sided simply supported laminate that is subjected to a simple or biaxial constant compressive load. This solution is generated using trigonometric shape functions that satisfy all boundary conditions and differential equations at the same time. This provides an explicit equation of the critical load. The Navier solution is in principle accessible for all orthotropic laminates and includes not only symmetric cross-ply but also unsymmetric cross-ply and antisymmetric angle-ply laminates. In the framework of the CLPT, the Navier solutions that consider bending–extension couplings can be found in [7,8,9,10]. In the context of FSDT, these solutions are published in [3, 11], which refer to the frequency analysis of unsymmetric laminates. The slightly modified procedure for buckling analysis is described in [12]. For the TSDT the publications [12,13,14] are to be mentioned. The main disadvantage of the Navier solution is the limitation to simply supported boundary conditions.

The Lévy-type solutions can be derived for a much wider range of boundary conditions. Two opposite edges are arbitrary in their supports, the remaining two are simply supported. Load case and laminate properties are taken from the Navier solution (constant biaxial compressive load, orthotropic laminates). The Lévy-type solution makes the same approach as the Navier solution in one coordinate direction. This approach satisfies the boundary conditions of the simple support and thus simultaneously reduces the partial differential equations into ordinary differential equations. This solution method is used in many studies for different boundary conditions, laminate types and laminated plate theories. If symmetrical laminates are considered, all bending–extension couplings disappear, and the in-plane displacements do not have to be considered in the scope of the buckling analysis. In the context of the CLPT, the problem reduces to one differential equation and will be addressed in the following. For the investigation of flange buckling of composite I-beams, a Lévy-type solution for SFSR laminates is presented in [15]. The abbreviations mean: simple support (S), free edge (F), rotational restraint (R). The rotational restraint is determined by the material properties of the web. A detailed consideration of the restraint stiffness of SFSR laminates can be found in [16]. Flange buckling of composite I- and box-beams is studied in [17] using Lévy-type solutions. Herein, SFSR and SRSR plates are considered. The Lévy-type solution used here for the SRSR plate is applied to an omega-stringer-stiffened panel in [18]. A detailed consideration of the Lévy-type solution in relation to SFSR and SRSR laminates can be found in [19]. A solution for the SRSR plate under biaxial compression is published in [20]. For various combinations of free, simply supported and clamped unloaded edges, the solutions for a constant compressive load are described in [21]. In order to solve the so-called Windenburg problem of orthotropic composite plates with one free reinforced unloaded edge, a beam is coupled with a plate edge in [22] and solved exactly using a Lévy-type solution. For the description of the local buckling of composite beams under non-constant compressive load or bending, a Lévy-type solution is presented in [23], which allows to assemble the beam of several individual plates. For each plate, a Lévy-type approach is made, and the corresponding boundary and continuity conditions are formulated. The result is a transcendental equation for the critical load of the entire beam. In [24] a Lévy-type solution is presented that describes the critical compressive load of an omega-stringer-stiffened panel. All the individual segments, including the omega-stringer, are also modelled here. This detailed description of the system leads to a very precise prediction of the local buckling behaviour.

In the framework of the FSDT and TSDT, three coupled differential equations are available for the buckling problem of symmetrical laminates, which are discussed in the following publications. In [25] a Lévy-type solution for the boundary conditions of simply supported, clamped and free edges is described in the framework of TSDT. The differential equation system is converted into a first-order system and then solved as part of the space state approach. This solution assumes linear strains and is also studied in [26]. In [27], however, a nonlinear correlation of the strains is given for the external potential. In addition to the previously described space state approach, solutions are also proposed in [28, 29] which do not carry out a reduction in the order but give special solutions and their different cases. Solutions for CLPT, FSDT and TSDT are considered here. The comparison of the theories shows a good agreement with the TSDT for the FSDT with the shear correction factor 5/6. The CLPT, on the other hand, clearly overestimates the critical buckling load for small relative widths. For transversely isotropic materials, a Lévy-type solution is presented in [30]. In this, the differential equations are again decoupled and a connection between the cross-sectional rotations is established. In [31], besides Navier solutions, Lévy-type solutions for orthotropic symmetric laminates are developed in the framework of TSDT. The in-plane displacements are considered, but the bending–extension couplings of unsymmetric laminates are neglected. The method is modular with respect to the strain measures and can reproduce von Kármán and Green–Lagrange strain measures. The Lévy-type solution is applied to different plate assemblies, such as stiffened plates.

In the linear buckling analysis of unsymmetric laminates, the pre-buckling state is neglected. This applies to methods that take into account bending–extension couplings in a direct way as well as in a indirect way, such as the reduced bending stiffness method, which can be found, for example, in [32, 33]. However, unsymmetric laminates can exhibit lateral deflections as a result of in-plane loading. Therefore, Leissa [34] developed conditions for the unsymmetrical plates to remain flat under in-plane loading. These are investigated in [35] with respect to different boundary conditions. In [36] similar conditions are formulated by extending the concept of bifurcation. The author concludes that the eigenvalue analysis provides a useful limit value for the buckling load as long as the bending deformations in the pre-buckling state are small. This is confirmed in [37] by means of nonlinear post-buckling analyses. In contrast to the previously shown studies, Diaconu and Weaver [38] investigates long rectangular plates and shows that the deformations in the pre-buckling region are small in the centre of the plate and occur significantly near the loaded edges. Furthermore, it is found there is a particularly good agreement between nonlinear and linear analysis for small pre-buckling deformations. These observations again agree with the statement from [36], where it is stated that in bifurcational buckling the deformations in the pre-buckling state are small, and the bending shape is different from the buckling shape. Thus, linear buckling analysis can give useful results. However, for a more detailed simulation, nonlinear buckling analysis should be used.

The bending–extension coupling of unsymmetric laminates effects a coupling of the in-plane and out-of-plane differential equations. In the context of Lévy-type solutions, all differential equations as well as boundary conditions have to be considered. The considered laminates can be unsymmetric, but still need to have orthotropic properties. For the CLPT, FSDT and TSDT this procedure is presented for antisymmetric cross-ply laminates in [39] for the boundary conditions simply supported, clamped and free edges. In [40] antisymmetric cross-ply and angle-ply laminates are treated in the context of CLPT. The three coupled differential equations are transformed into a single differential equation of eighth degree. Within the FSDT, the Lévy-type solution for antisymmetric angle-ply laminates is given in [41]. Biaxial pressure is treated for the boundary conditions simply supported, clamped and free edges. To the best of the authors’ knowledge, the solution for antisymmetric angle-ply laminates in the context of TSDT cannot be found in the literature.

The stability of fibre-reinforced composite structures can be described with the discrete plate theory. For this purpose, the structure is divided into individual segments and the supporting effect of the surrounding structure is modelled by means of elastic restraints and suitable boundary conditions. This is shown schematically for a stiffened panel and an I-beam in Fig. 1. The literature review shows that in the context of Lévy-type solutions for unsymmetric laminates, no investigations concerning elastic restraints were conducted. Particularly, the Lévy-type solution in the context of antisymmetric angle-ply laminates is not found for TSDT with respect to buckling analysis.

The aim of this work is to close the last mentioned lack in the literature and to develop the remaining Lévy-type solution for antisymmetric angle-ply laminates in the context of TSDT for the stability problems. Another focus is on the insufficient description of rotational restraints in the context of TSDT, for which a better description is required. Since there is no comprehensive investigation of the rotational restraint of unsymmetric laminates in the literature, this work also wants to address this field. Here, Lévy-type solutions for unsymmetric cross-ply and antisymmetric angle laminates in the framework of CLPT, FSDT and TSDT are presented in a consistent and compact notation. Based on these solutions, the rotational elastic restraint for the mentioned laminated plate theories is investigated.

In [43] a closed-form approximate solution for the mentioned problem, which is outlined in Fig. 1, is presented for CLPT, FSDT and TSDT. Herein, it is shown that good agreements are obtained for unsymmetric cross-ply laminates, but large deviations can occur for antisymmetric angle-ply laminates. The present method also addresses this area and wants to demonstrate that analytical solutions with remarkably high accuracy can also be achieved for this problem. The present solution considers the same plate types and boundary conditions as in [43] and additionally presents an exact description of the problem.

Fig. 1

Stiffened composite panel (left), composite beam (right). Schematic sketch of the discrete plate analysis of the plate types SRSR (left) and SFSR (right). The individual plates are loaded with a compressive load $N_{xx}^{0}$ and supported with the rotational restraints $(k_0, k_b)$

2 Laminated plate theories

In this section, the basic quantities are defined, and a consistent definition is introduced. This is the basis for the formulations in the following sections. For this purpose, the laminate theories considered, CLPT, FSDT, and TSDT, are given in condensed notation. These can be found in detailed form in relevant textbooks and in [1, 3, 5].

Fig. 2

Kinematics and cross-sectional deformation for the classical laminated plate theory (CLPT, cross sections flat and normal to the mid-plane, cf. Equation (1)), the first-order shear deformation theory (FSDT, constant transverse shear deformation, cf. Equation (2)), the third-order shear deformation theory (TSDT, cubic cross-sectional deformation, cf. Equation (3)

The theories differ essentially in the deformation of the cross section, as shown in Fig. 2. The quantities u, v, and w indicate the displacements in the direction of the x, y, and z coordinates, respectively. The angles $\psi _{{x}}$ and $\psi _{{y}}$ define the cross-sectional rotation around the x- and y-axis, respectively. The mentioned quantities are described in relation to the x-coordinate direction in Fig. 2. The displacement field of CLPT (1) is based on the assumptions of the classical Kirchhoff plate theory, which means that the cross sections remain flat and normal to the mid-plane in the deformed state.

$$\begin{aligned} u(x,y,z)&=u_0(x,y)-z\frac{\partial w_0(x,y)}{\partial x}, \nonumber \\ v(x,y,z)&=v_0(x,y)-z\frac{\partial w_0(x,y)}{\partial y}, \nonumber \\ w(x,y,z)&=w_0(x,y). \end{aligned}$$

(1)

In the framework of FSDT, the cross sections also remain flat. However, rotations of the cross sections are enabled as described in Eq. (2). This leads to constant shear deformations and shear stresses. From a physical point of view, however, the shear stresses should disappear at the top and bottom surfaces of the laminate; thus, the so-called shear correction factor K is introduced to keep this error low on average.

$$\begin{aligned} u\left( {x,y,z} \right)&= u_0 \left( {x,y} \right) + z\,\psi _x \left( {x,y} \right) , \nonumber \\ v\left( {x,y,z} \right)&= v_0 \left( {x,y} \right) + z\,\psi _y \left( {x,y} \right) , \nonumber \\ w\left( {x,y} \right)&= w_0 \left( {x,y} \right) . \end{aligned}$$

(2)

The displacement field of TSDT (3) eliminates both hypotheses mentioned and describes cross-sectional rotations as well as shear deformations. All three theories have in common that the laminate thickness t does not change in the deformed state.

$$\begin{aligned} u(x,y,z)&= u_0 (x,y) + z\psi _x (x,y) - \frac{{4z^3 }}{{3t^{2} }}\left( {\psi _x (x,y) + \frac{{\partial w_0 (x,y)}}{{\partial x}}} \right) , \nonumber \\ v(x,y,z)&= v_0 (x,y) + z\psi _y (x,y) - \frac{{4z^3 }}{{3t^{2} }}\left( {\psi _y (x,y) + \frac{{\partial w_0 (x,y)}}{{\partial y}}} \right) , \nonumber \\ w(x,y)&= w_0 (x,y). \end{aligned}$$

(3)

The constitutive law of the laminated plate theories can be represented in general terms as:

$$\begin{aligned} \underline{\overline{N}}=\underline{\underline{S}}\,\underline{\varepsilon }. \end{aligned}$$

(4)

The resulting forces and moments are summarised in the vector $\underline{\overline{N}}$ and the corresponding strains in the vector $\underline{\varepsilon }$. The laminate stiffness matrix is denoted by $\underline{\underline{S}}$. The quantities mentioned differ in the various theories. For the CLPT, the constitutive law results in Eq. (5). The FSDT additionally considers the shear forces $\underline{Q}$, whereas transverse shear stiffnesses $\underline{\underline{A}} ^S$ are reduced by the shear correction factor K, as shown in Eq. (6). Due to the cross-sectional warping in the TSDT, further terms are added in Eq. (7).

$$\begin{aligned} \text {CLPT:}&\left[ \begin{array}{*{20}c} \underline{N}\\ \underline{M} \end{array}\right] = \left[ {\begin{array}{*{20}c} {\underline{\underline{A}} } &{} {\underline{\underline{B}} } \\ {\underline{\underline{B}} } &{} {\underline{\underline{D}} } \\ \end{array}} \right] \left[ \begin{array}{*{20}c} \underline{\varepsilon }^{(1)} \\ \underline{\kappa } \end{array}\right] \end{aligned}$$

(5)

$$\begin{aligned} \text {FSDT:}&\left[ \begin{array}{*{20}c} \underline{N}\\ \underline{M} \\ \underline{Q} \end{array}\right] = \left[ {\begin{array}{*{20}c} {\underline{\underline{A}} } &{} {\underline{\underline{B}} } &{} {\underline{\underline{0}} } \\ {\underline{\underline{B}} } &{} {\underline{\underline{D}} } &{} {\underline{\underline{0}} } \\ {\underline{\underline{0}} } &{} {\underline{\underline{0}} } &{} {K\underline{\underline{A}} ^\textrm{S}} \\ \end{array}} \right] \left[ \begin{array}{*{20}c} \underline{\varepsilon }^{(1)} \\ \underline{\varepsilon }^{(2)} \\ \underline{\gamma }^{(1)} \end{array}\right] \end{aligned}$$

(6)

$$\begin{aligned} \text {TSDT:}&\left[ \begin{array}{*{20}c} \underline{N}\\ \underline{M} \\ \underline{P} \\ \underline{Q} \\ \underline{R} \\ \end{array}\right] = \left[ {\begin{array}{*{20}c} {\underline{\underline{A}} } &{} {\underline{\underline{B}} } &{} {\underline{\underline{E}} } &{} {\underline{\underline{0}} } &{} {\underline{\underline{0}} } \\ {\underline{\underline{B}} } &{} {\underline{\underline{D}} } &{} {\underline{\underline{F}} } &{} {\underline{\underline{0}} } &{} {\underline{\underline{0}} } \\ {\underline{\underline{E}} } &{} {\underline{\underline{F}} } &{} {\underline{\underline{H}} } &{} {\underline{\underline{0}} } &{} {\underline{\underline{0}} } \\ {\underline{\underline{0}} } &{} {\underline{\underline{0}} } &{} {\underline{\underline{0}} } &{} {\underline{\underline{A}} ^\textrm{S}} &{} {\underline{\underline{D}} ^\textrm{S}} \\ {\underline{\underline{0}} } &{} {\underline{\underline{0}} } &{} {\underline{\underline{0}} } &{} {\underline{\underline{D}} ^\textrm{S}} &{} {\underline{\underline{F}} ^\textrm{S}} \\ \end{array}} \right] \left[ \begin{array}{*{20}c} \underline{\varepsilon }^{(1)} \\ \underline{\varepsilon }^{(2)} \\ \underline{\varepsilon }^{(3)} \\ \underline{\gamma }^{(1)} \\ \underline{\gamma }^{(2)} \end{array}\right] \end{aligned}$$

(7)

The individual quantities from the constitutive laws are composed of the following terms:

$$\begin{aligned} \underline{\varepsilon }^{(1)}= & {} \left[ \begin{array}{*{20}c} \frac{\partial u_0 }{\partial x} \\ \frac{\partial v_0}{\partial y} \\ \frac{\partial u_0}{\partial y}+\frac{\partial v_0 }{\partial x} \end{array}\right] , \quad \underline{\varepsilon }^{(2)} =\left[ \begin{array}{*{20}c} {\frac{\partial \psi _x }{\partial x}} \\ {\frac{\partial \psi _y }{\partial y}} \\ {\frac{\partial \psi _x }{\partial y} + \frac{\partial \psi _y }{\partial x}} \end{array}\right] ,\nonumber \\ \underline{\varepsilon }^{(3)}= & {} \left[ \begin{array}{*{20}c} { - {\frac{4}{3t^{2} }}\left( {\frac{\partial \psi _x }{\partial x}} + {\frac{\partial ^2 w_0 }{\partial x^2 }} \right) } \\ { - {\frac{4}{3t^{2} }}\left( {\frac{\partial \psi _y }{\partial y}} + {\frac{\partial ^2 w_0 }{\partial y^2 }} \right) } \\ { - {\frac{4}{3t^{2} }}\left( {\frac{\partial \psi _x }{\partial y}} + {\frac{\partial \psi _y }{\partial x}} + 2{\frac{\partial ^2 w_0 }{\partial x \partial y}} \right) } \end{array}\right] , \quad \underline{\kappa }= \left[ \begin{array}{*{20}c} -\frac{\partial ^2 w_{0}}{\partial x^2} \\ -\frac{\partial ^2 w_{0}}{\partial y^2} \\ -2\frac{\partial ^2 w_{0}}{\partial x \partial y} \end{array}\right] , \nonumber \\ \underline{\gamma }^{(1)}= & {} \left[ \begin{array}{*{20}c} {\psi _y + \frac{\partial w_0 }{\partial y} } \\ {\psi _x + \frac{\partial w_0 }{\partial x} } \end{array}\right] , \quad \underline{\gamma }^{(2)}= \left[ \begin{array}{*{20}c} { - {\frac{ 4}{ t^{2} }}\left( {\psi _y + {{\frac{ \partial w_0 }{ \partial y}}}} \right) }\\ { - {\frac{ 4}{ t^{2} }}\left( {\psi _x + {{\frac{ \partial w_0 }{ \partial x}}}} \right) } \end{array}\right] ,\nonumber \\ \underline{N}= & {} \left[ \begin{array}{*{20}c} N_{xx}^0 \\ N_{yy}^0 \\ N_{xy}^0 \end{array}\right] , \quad \underline{M}=\left[ \begin{array}{*{20}c} M_{xx}^0 \\ M_{yy}^0 \\ M_{xy}^0 \end{array}\right] , \quad \underline{Q}=\left[ \begin{array}{*{20}c} Q_{y} \\ Q_{x} \end{array}\right] ,\nonumber \\ \underline{P}= & {} \left[ \begin{array}{*{20}c} P_{xx} \\ P_{yy} \\ P_{xy} \end{array}\right] , \quad \underline{R}=\left[ \begin{array}{*{20}c} R_{y} \\ R_{x} \end{array}\right] . \end{aligned}$$

(8)

The stiffness matrix $\underline{\underline{S}}$ is composed of different single layer parameters as described in the following. The reduced stiffness matrix of the single layer is symmetric (${Q_{ij}=Q_{ji}}$ for $i,j=1,2,6$) and composed of the following engineering constants of the single layer:

$$\begin{aligned} \begin{array}{lll} Q_{11}=\frac{E_{11}}{1-\nu _{12}\nu _{21}},&{} Q_{22}=\frac{E_{22}}{1-\nu _{12}\nu _{21}},&{} Q_{12}=\frac{\nu _{12}E_{22}}{1-\nu _{12}\nu _{21}}, \\ Q_{16}=0, &{}Q_{26}=0, &{}Q_{66}=G_{12}. \end{array} \end{aligned}$$

(9)

The transformed reduced stiffnesses ${\bar{Q}}_{ij}$ can be determined with the following transformations, where $\varphi$ indicates the angle between the on-axis and the off-axis coordinate system of the individual layers:

$$\begin{aligned} \underline{\underline{\bar{Q}}}=\underline{\underline{T}} \,\!_Q\,\underline{\underline{{Q}}}\,\underline{\underline{T}}^\textrm{T}\!\!\!_Q \quad&\text {with}\quad \underline{\underline{T}}\,\!_Q=\left[ \begin{array}{ccc} {c}^{2}&{}\quad {s}^{2}&{}\quad -2\,cs\\ {s}^{2}&{}\quad {c}^{2}&{}\quad 2\,cs\\ cs&{}\quad -cs&{}\quad {c}^{2}-{s}^{2}\end{array} \right] \nonumber \\&\text {and} \quad s=\sin (\varphi ), \quad c=\cos (\varphi ). \end{aligned}$$

(10)

The submatrices of $\underline{\underline{S}}$ are defined in Eq. (11) and due to the symmetry of $Q_{ij}$ they are symmetric as well.

$$\begin{aligned} A_{ij}&=\int \nolimits _{-\frac{t}{2}}^{\frac{t}{2}}{\bar{Q}}_{ij}\textrm{d}z,&B_{ij}&=\int \nolimits _{-\frac{t}{2}}^{\frac{t}{2}}{\bar{Q}}_{ij}z\textrm{d}z,&D_{ij}&=\int \nolimits _{-\frac{t}{2}}^{\frac{t}{2}}{\bar{Q}}_{ij}z^2\textrm{d}z,&\nonumber \\ E_{ij}&=\int \nolimits _{-\frac{t}{2}}^{\frac{t}{2}}{\bar{Q}}_{ij}z^3\textrm{d}z,&F_{ij}&=\int \nolimits _{-\frac{t}{2}}^{\frac{t}{2}}{\bar{Q}}_{ij}z^4\textrm{d}z,&H_{ij}&=\int \nolimits _{-\frac{t}{2}}^{\frac{t}{2}}{\bar{Q}}_{ij}z^6\textrm{d}z,&\nonumber \\ \text {for }&(i,j = 1,2,6).{} & {} \end{aligned}$$

(11)

The single layer transverse shear stiffnesses $C_{44}=G_{23}$ and $C_{55}=G_{13}$ can be transformed from the local into the global coordinate system as follows:

$$\begin{aligned} \underline{\underline{\bar{C}}}=\underline{\underline{T}}\,\!_C \left[ \begin{array}{cc} G_{23}&{}\quad 0\\ 0&{}\quad G_{13}\end{array} \right] \underline{\underline{T}}^\textrm{T}\!\!\!_C \quad&\text {with}\quad \underline{\underline{T}}\,\!_C= \left[ \begin{array}{cc} c&{}\quad s\\ -s&{}\quad c\end{array} \right] \\\nonumber&\text {and} \quad s=\sin (\varphi ), \quad c=\cos (\varphi ). \end{aligned}$$

(12)

The stiffness quantities relating to the transverse shear stiffnesses are denoted by the superscript S and can be calculated as follows:

$$\begin{aligned} A_{ij}^{\textrm{S}}=\int _{-\frac{t}{2}}^{\frac{t}{2}}{\bar{C}}_{ij}\textrm{d}z,&D_{ij}^{\textrm{S}}=\int _{-\frac{t}{2}}^{\frac{t}{2}}{\bar{C}}_{ij}z^2\textrm{d}z,&F_{ij}^{\textrm{S}}=\int _{-\frac{t}{2}}^{\frac{t}{2}}{\bar{C}}_{ij}z^4\textrm{d}z,\nonumber \\&\text {for } (i,j = 4,5) \end{aligned}$$

(13)

In this publication, orthotropic laminates are considered. Consequently, the following entries of the stiffness matrices disappear:

$$\begin{aligned} A_{16}&=A_{26}=D_{16}=D_{26}=F_{16}=F_{26}=H_{16}=H_{26} \nonumber \\&=A_{45}=D_{45}=F_{45}=0. \end{aligned}$$

(14)

In the context of unsymmetrical laminates, this results in two laminate types. On the one hand, the unsymmetric cross-ply laminate, which has the following zero entries in addition to Eq. (14):

$$\begin{aligned} B_{16}=B_{26}=E_{16}=E_{26}=0. \end{aligned}$$

(15)

On the other hand, the antisymmetric angle-ply laminate, which, besides the zero entries of Eq. (14), shows the following:

$$\begin{aligned} B_{11}=B_{12}=B_{22}=B_{66}=E_{11}=E_{12}=E_{22}=E_{66}=0. \end{aligned}$$

(16)

3 Basic equations of the stability problem

This section contains the basic equations that are required to describe the stability problem from Fig. 3. With the formulation of the potential energy and its variation, the boundary conditions, the equilibrium conditions as well as the resulting partial differential equations can be formulated, which are the basis for the Lévy-type solution that follows in the next section. The potential energy of the individual plates from Fig. 3 is composed on the one hand of the internal energy $\Pi _\text {i}$ and the external energy $\Pi _\textrm{e}$, which can be expressed as follows:

$$\begin{aligned} \Pi _\textrm{i}&= \frac{1}{2} \int _{0}^{b} \int _{0}^{a} {\underline{\varepsilon }} ^\textrm{T} \underline{\overline{N}} \,\textrm{d}x \,\textrm{d}y, \end{aligned}$$

(17)

$$\begin{aligned} \Pi _\textrm{e}&= - \frac{N_\text {cr}}{2}\int _0^b {\int _0^a \left\{ \xi _x\left( {\frac{{\partial w_0 }}{{\partial x}}} \right) ^2 + \xi _y \left( {\frac{{\partial w_0 }}{{\partial y}}} \right) ^2\right\} \textrm{d}x \, \textrm{d}y}. \end{aligned}$$

(18)

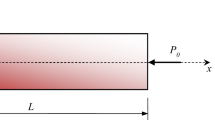
In Eq. (18), the load factors $\xi _x$ and $\xi _y$ represent, respectively, the proportional values of the critical load $N_\text {cr}$ to the two compressive loads, it holds: $N_{xx}^0=\xi _xN_\text {cr}$ and $N_{yy}^0=\xi _y N_\text {cr}$. On the other hand, the stored energy of the rotational restraints $\Pi _\text {s}$ needs to be considered. The rotation angle of the cross section can be expressed by:

$$\begin{aligned} \overline{\varphi }=\frac{\partial v(x,y,z)}{\partial z}. \end{aligned}$$

(19)

The evaluation of Eq. (19) for the three laminated plate theories shows no dependence with respect to thickness direction for CLPT and FSDT, see Eqs. (20) and (21). The TSDT, on the other hand, shows a dependence with respect to z, as shown in Eq. (22).

$$\begin{aligned} \text {CLPT:}\quad&\overline{\varphi }={\frac{{\partial w_0 }}{{\partial y}}} \end{aligned}$$

(20)

$$\begin{aligned} \text {FSDT:}\quad&\overline{\varphi }=\psi _y \end{aligned}$$

(21)

$$\begin{aligned} \text {TSDT:}\quad&\overline{\varphi }=\psi _y (x,y) - \frac{{4z^2 }}{{t^{2} }}\left( {\psi _y (x,y) + \frac{{\partial w_0 (x,y)}}{{\partial y}}} \right) \end{aligned}$$

(22)

The rotational restraints are distributed over the entire cross section, which have a constant stiffness per thickness t. The following relationship applies to the potential:

$$\begin{aligned} \Pi _\text {s}=\frac{1}{2}\int \limits _{0}^{a} \int \limits _{-t/2}^{t/2} \left\{ \frac{k_0}{t} \left[ \overline{\varphi }^2\right] _{y=0} + \frac{k_b}{t} \left[ \overline{\varphi }^2\right] _{y=b}\right\} \textrm{d}z \, \textrm{d}x. \end{aligned}$$

(23)

Evaluating Eq. (23) leads to the following expressions:

$$\begin{aligned} \mathrm {CLPT:}\quad&\Pi _\textrm{s} = \frac{1}{2}\int _0^a \!{\left\{ {k_{0}\left[ { {\frac{{\partial w_0 }}{{\partial y}}} \bigg \vert _{y = 0}} \right] ^2 \! + k_{b}\left[ { {\frac{{\partial w_0 }}{{\partial y}}} \bigg \vert _{y = b} } \right] ^2 } \right\} \textrm{d}x} \end{aligned}$$

(24)

$$\begin{aligned} \mathrm {FSDT:}\quad&\Pi _\textrm{s} = \frac{1}{2}\int _0^a {\left\{ {k_{0}\left[ {\psi _y \left( {x, 0} \right) } \right] ^2 + k_{b}\left[ {\psi _y \left( {x, b} \right) } \right] ^2 } \right\} } \textrm{d}x \end{aligned}$$

(25)

$$\begin{aligned} \mathrm {TSDT:}\quad&\Pi _\textrm{s}=\frac{1}{2}\int _{0}^{a} \left\{ k_0 \left[ \frac{8}{15}\, \psi _{y} ^{2}-\frac{4}{15}\,\psi _{y} {\frac{\partial w_0}{ \partial y}} +\frac{1}{5}\, \left( {\frac{\partial w_0 }{\partial y}} \right) ^{2}\right] _{y=0} \right. \nonumber \\&\quad \left. +\, k_b \left[ \frac{8}{15}\, \psi _{y} ^{2}-\frac{4}{15}\,\psi _{y} {\frac{\partial w_0}{ \partial y}} +\frac{1}{5}\, \left( {\frac{\partial w_0 }{\partial y}} \right) ^{2}\right] _{y=b}\right\} \textrm{d}x \end{aligned}$$

(26)

The potential from Eq. (26) has the possibility to describe the energy of a cross-sectional rotation and warping at the same time. This consideration is new and reflects the potential energy of the rotational elastic restraint in a meaningful way. The total potential energy $\Pi$ results in:

$$\begin{aligned} \Pi = \Pi _\textrm{i} + \Pi _\textrm{e} + \Pi _\textrm{s}. \end{aligned}$$

(27)

Fig. 3

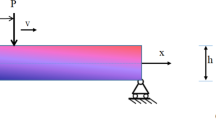
Boundary conditions and geometrical properties of the considered plates SRSR and SFSR with length a, width b and rotational elastic restraints $k_0,k_b$. The constant compressive loads $N_{xx}^{0}$ and $N_{yy}^{0}$ depend on $N_{\text {cr}}$. The respective load portions are controlled by $\xi _x$ and $\xi _y$ and take values from ${0 \text { to } 1}$

The variation of the potential from Eq. (28) enables to determine the equilibrium conditions as well as the boundary conditions. For that purpose, the corresponding constitutive law (5), (6) or (7) is inserted into the potential (27). Subsequently, this equation is varied, and the constitutive law is resubstituted.

$$\begin{aligned} \delta \Pi = \delta \Pi _\text {i} +\delta \Pi _\textrm{e} +\delta \Pi _\text {s} =0. \end{aligned}$$

(28)

For reasons of brevity, this is only shown for the TSDT. Particular attention is drawn here to the new potential formulation (26) and the resulting boundary conditions from the variation in Eq. (30).

$$\begin{aligned} \delta \Pi _\textrm{i}\!+\!\delta \Pi _\textrm{a}=\,&-\!\!\int _{0}^{b}\!\!\int _{0}^{a}\!\left\{ \left( {\frac{\partial N_{{xx}}^0}{\partial x}} \! + \!{\frac{\partial N_{{xy}}^0}{\partial y}} \right) \delta u_{0}\right. +\left( {\frac{\partial N_{{xy}}^0}{\partial x}} +{\frac{\partial N_{{yy}}^0}{\partial y}} \right) \delta v_{0}\nonumber \\&+ \left( -\xi _xN_\textrm{cr} {\frac{\partial w_{0}^{2}}{\partial {x}^{2}}} -\xi _yN_\textrm{cr} {\frac{\partial w_{0}^{2}}{\partial {y}^{2}}} - {\frac{4}{{t}^{2}}}\left[ {\frac{\partial R_{x}}{\partial x}} +{\frac{\partial R_{y}}{\partial y}} \right] \right. \nonumber \\&\left. +\, {\frac{4 }{3{t}^{2}}}\left[ {\frac{\partial ^{2} P_{{xx}}}{\partial {x}^{2}}}\! +\!{\frac{\partial ^{2} P_{{yy}} }{\partial {y}^{2}}} \!+\!2{\frac{\partial ^{2} P_{{xy}}}{\partial {x}\partial {y}}}\right] \!+\!{\frac{\partial Q_{x}}{\partial x}}\!+\!{\frac{\partial Q_{y} }{\partial y}} \right) \delta w_{0}\nonumber \\&+\left( {\frac{\partial M_{{xx}}}{\partial x}}+{\frac{\partial M_{{xy}}}{\partial y}} -{\frac{4}{3{t}^{2}}}\left[ {\frac{\partial P_{{xx}}}{\partial x}} +{\frac{\partial P_{{xy}}}{\partial y}} \right] -Q_{x}\right. \nonumber \\&\left. +\,{\frac{4 }{{t}^{2}}}R_{x} \right) \delta \psi _{x}+ \left( {\frac{\partial M_{{xy}}}{\partial x}}\! +\!{\frac{\partial M_{{yy}}}{\partial y}}-{\frac{4}{3{t}^{2}}}\left[ {\frac{\partial P_{{xy}}}{\partial x}}\! +\!{\frac{\partial P_{{yy}}}{\partial y}}\right] \right. \nonumber \\&\left. \left. -Q_{y} + \,{\frac{4}{{t}^{2}}}R_{y} \right) \delta \psi _{y} \right\} \textrm{d}x\,\textrm{d}y+\int _{0}^{a}\bigg \lbrace \bigg [ N_{{xy}}^0 \delta u+N_{{yy}}^0 \delta v \nonumber \\&+ \left( -\xi _yN_\textrm{cr} { \frac{\partial w_{0}}{\partial y}}+{\frac{4}{3{t}^{2}}} \left[ {\frac{\partial P_{{yy}}}{\partial y}}+2{\frac{\partial P_{{xy}}}{\partial x}} \right] + Q_{y}\right. \nonumber \\&\left. -\,{\frac{4}{{t}^{2}}} R_{y} \right) \delta \,w_{0}+\left( M_{{xy}} -{\frac{ 4 }{3{t}^{2}}}P_{{xy}} \right) \delta \psi _{x} \nonumber \\&\left. + \left( M_{{yy}}-{\frac{ 4}{3{t}^{2}}}P_{{yy}}\right) \delta \psi _{y} -{\frac{4}{3{t}^{2}}}P_{{yy}} \delta \left( {\frac{\partial w_{0}}{\partial y}}\right) \right] \bigg \vert _{0}^{b} \bigg \rbrace \textrm{d}x \nonumber \\&+\int _{0}^{b} \left\{ N_{{xx}}^0 \delta u+N_{{xy}}^0 \delta v +\left( -\xi _xN_\textrm{cr} { \frac{\partial w_{0}}{\partial x}} \right. \right. \nonumber \\&\left. +\,{\frac{ 4 }{3{t}^{2}}}\left[ {\frac{\partial P_{{xx}}}{\partial x}}+2 {\frac{\partial P_{{xy}}}{\partial y}} \right] + Q_{x} -\,{\frac{4 }{{t}^{2}}} R_{x} \right) \delta \,w_{0} \nonumber \\&+ \left( M_{{xx}} -{\frac{ 4 }{3{t}^{2}}}P_{{xx}} \right) \delta \psi _{x}+ \left( M_{{xy}} -{\frac{ 4}{3{t}^{2}}}P_{{xy}} \right) \delta \psi _{y}\nonumber \\&\left. -{\frac{4}{3{t}^{2}}}P_{{xx}} \delta \left( {\frac{\partial w_{0}}{\partial x}}\right) \, \right\} \bigg \vert _{0}^{a}\textrm{d}y - \left( {\frac{8}{3{t}^{2}}}P_{{xy}} \delta \,w_{0}\right) \bigg \vert _{0}^{a}\bigg \vert _{0}^{b} \end{aligned}$$

(29)

$$\begin{aligned} \delta \Pi _\textrm{s} =\,&\int _{0}^{a}\bigg \lbrace k_{0} \left[ \left( \frac{8}{15}\psi _{y} -\frac{2}{15} \frac{\partial w_{0}}{\partial y} \right) \delta \psi _{y}\right] _{y=0} \nonumber \\&+k_{b} \left[ \left( \frac{8}{15}\psi _{y}-\frac{2}{15} \frac{\partial w_{0}}{\partial y} \right) \delta \psi _{y}\right] _{y=b}\nonumber \\&+k_0 \left[ \left( -\frac{2}{15}\psi _{y}+\frac{1}{5} \frac{\partial w_{0}}{\partial y} \right) \delta \left( \frac{\partial w_{0}}{\partial y}\right) \right] _{y=0}\nonumber \\&+k_b \left[ \left( -\frac{2}{15}\psi _{y}+\frac{1}{5} \frac{\partial w_{0}}{\partial y} \right) \delta \left( \frac{\partial w_{0}}{\partial y}\right) \right] _{y=b} \bigg \rbrace \textrm{d}x \end{aligned}$$

(30)

In order that Eq. (28) can be satisfied, the terms from Eqs. (29) and (30) must vanish individually. Consequently, the first five bracketed terms in (29) provide the equilibrium conditions and the remaining terms from (29) and (30) the boundary conditions of the system. Each boundary term can be satisfied in two ways. Either the variable to be varied $\delta ()$ disappears or the corresponding bracket term becomes zero. This results in the boundary conditions of the SRSR and SFSR plate described below, which are outlined in Fig. 3. At the edge $x=0,a$ the following applies for the simple support (S):

$$\begin{aligned} \left. \begin{array}{l} \text {cross-ply:} \\ N_{xx}^0=v_0=0, \\ \text {angle-ply:}\\ N_{xy}^0=u_0=0, \\ \end{array}\right\} \left\{ \begin{array}{l} \text {CLPT:} \\ w_0=M_{xx}^0=0.\\ \text {FSDT:} \\ w_0=M_{xx}^0=\psi _y=0.\\ \text {TSDT:} \\ w_0=M_{xx}^0=\psi _y=P_{xx}=0.\\ \end{array}\right. \end{aligned}$$

(31)

At the edges $y=0,b$ the following applies for the simple support with the rotational restraint (R):

$$\begin{aligned} \left. \begin{array}{l} \text {cross-ply:} \\ N_{yy}^0=u_0=0, \\ \text {angle-ply:} \\ N_{xy}^0=v_0=0,\\ \end{array}\!\!\right\} \left\{ \!\! \begin{array}{l} \text {CLPT:} \\ w_0= \left\{ \!\! \begin{array}{l} \left[ -M_{yy}^0 - k_{0}{\frac{{\partial w_0 }}{{\partial y}}}\right] _{y = 0} = 0.\\ \left[ M_{yy}^0 - k_{b}{\frac{{\partial w_0 }}{{\partial y}}}\right] _{y = b} = 0. \end{array} \right. \\ \text {FSDT:} \\ w_0=\psi _x= \left\{ \!\! \begin{array}{l} \left[ -M_{yy}^0 + k_{0}\psi _{y}\right] _{y = 0} = 0.\\ \left[ M_{yy}^0 + k_{b}\psi _{y}\right] _{y = b} = 0. \end{array} \right. \\ \text {TSDT:} \\ \begin{array}{l} w_0=\psi _x\\ =\left[ \frac{4}{3t^{2}} P_{yy} + k_{0}\left( -\frac{2}{15}\psi _y+\frac{1}{5}\frac{\partial w_{0}}{\partial y}\right) \right] _{y = 0}\\ =\left[ - \frac{4}{3t^{2}} P_{yy} + k_{b}\left( -\frac{2}{15}\psi _y+\frac{1}{5}\frac{\partial w_{0}}{\partial y}\right) \right] _{y = b} \\ =\left[ -M_{yy}^0 + \frac{4}{3t^{2}} P_{yy} + k_{0}\left( \frac{8}{15}\psi _y-\frac{2}{15}\frac{\partial w_{0}}{\partial y}\right) \right] _{y = 0}\\ =\left[ M_{yy}^0 - \frac{4}{3t^{2}} P_{yy} + k_{b}\left( \frac{8}{15}\psi _y-\frac{2}{15}\frac{\partial w_{0}}{\partial y}\right) \right] _{y = b} \\ = 0. \end{array} \end{array}\right. \end{aligned}$$

(32)

From the new energy consideration of the potential energy of the rotational elastic restraint in the framework of the TSDT, see Eq. (26), new boundary conditions result by variation of the total potential, as described in Eq. (32). This boundary condition contains for the limiting case $k_0=k_b=0$ the simply supported edge ($w_0=\psi _x=P_{yy}=M_{yy}^{0}=0$). In the case of $k_0=k_b=\infty$ the values $\partial w_0 / \partial y$ and $\psi _y$ converge to zero so that they are in sum with the finite values $P_{yy}$ and $M_{yy}^{0}.$ This corresponds directly to the fully clamped edge where the following applies: $\partial w_0 / \partial y = \psi _y = 0$. Consequently, the new boundary conditions can represent both limiting cases. At the edge $y=b$ the following applies to the free edge (F):

$$\begin{aligned} \begin{array}{cc} \text {cross-ply,} \\ \text {angle-ply:} \\ N_{yy}^0=N_{xy}^0=0, \end{array} \left\{ \begin{array}{l} \text {CLPT:} \\ M_{yy}^0=\frac{\partial M_{yy}^0}{\partial y } + 2\frac{\partial M_{xy}^0}{\partial x }= 0.\\ \text {FSDT:} \\ M_{yy}^0=M_{xy}^0= Q_y= 0.\\ \text {TSDT:} \\ \left\{ \begin{array}{c} M_{yy}^0 - \frac{4}{3t^{2}} P_{yy}=P _{yy}=M_{xy}^0 - \frac{4}{3t^{2}} P_{xy}\\ =\frac{4}{3t^{2}} \left( \frac{\partial P_{yy}}{\partial y} +2 \frac{\partial P_{xy}}{\partial x} \right) + Q_{y} - \frac{4}{t^{2}} R_{y}=0. \end{array}\right. \end{array}\right. \end{aligned}$$

(33)

Due to the different coupling terms of unsymmetrical cross-ply and antisymmetrical angle-ply laminates, it is advisable to adapt the boundary conditions with the selected approaches. This leads to different in-plane boundary conditions as shown in Eqs. (31)–(33).

The differential equations are obtained by substituting the constitutive law into the equilibrium conditions. For TSDT, the equilibrium conditions are represented in the first five terms of Eq. (29) and the constitutive law can be found in Eq. (7). The differential equations can be formulated for CLPT, FSDT and TSDT in compact matrix notation as follows:

$$\begin{aligned} L_{ij} \Phi _i=0, \left\{ \begin{array}{ll} i,j= 1,2,3 &{}\text {for CLPT} \\ i,j= 1,..,5 &{}\text {for FSDT} \\ &{}\text {and TSDT} \end{array} \right. \text {with } \Phi _i= \left[ \begin{array}{c} u_{0} \left( x ,y \right) \\ v_{0} \left( x ,y \right) \\ w_{0} \left( x ,y \right) \\ \psi _{{x}} \left( x ,y \right) \\ \psi _{{y}} \left( x ,y \right) \end{array}\right] . \end{aligned}$$

(34)

It is important to note that $L_{ij}$ is symmetrical and consequently ${L_{ij}=L_{ji}}$ is valid. The derivatives are specified in the following with the derivative operator $d_{i,...}$. The operator $d_{i,...}$ indicates with $i=x$ a derivative to x $\left( {\partial }/{\partial x}\right)$ and with $i=y$ a derivative to y $\left( {\partial }/{\partial y}\right)$. A repeated index denotes multiple derivation. The different theories have the following entries, in which the TSDT contains the abbreviation ${\tau }={4}/\left( {3\,{t}^{2}}\right)$:

$$\begin{aligned} \text {CLPT:}&\nonumber \\ L_{11}=\,&A_{11}\,d_{{x,x}}+A_{66}\,d_{{y,y}} ,\quad L_{12}=\left( A_{12}+A_{66} \right) \, d_{{x,y}} ,\nonumber \\ L_{13}=\,&\left( -B_{12}-2\,B_{66} \right) d_{{x,y,y}}-B_{11}\,d_{{x,x,x}}-3\,B _{16}\,d_{{x,x,y}}-B_{26}\,d_{{y,y,y}} ,\nonumber \\ L_{22}=\,&A_{22}\,d_{{y,y}}+A_{66}\,d_{{x,x}} ,\nonumber \\ L_{23}=\,&\left( -B_{12}-2\,B_{66} \right) d_{{x,x,y}}-B_{16}\,d_{{x,x,x}}-3\,B _{26}\,d_{{x,y,y}}-B_{22}\,d_{{y,y,y}} ,\nonumber \\ L_{33}=\,&\left( 2\,D_{12}+4\,D_{66} \right) d_{{x,x,y,y}}+\xi _xN_\text {cr}\,d_{{x,x}}\nonumber \\&+\xi _yN_\text {cr}\,d_{{y,y}}+D_{11}\,d_{{x,x,x,x}}+D_{22}\,d_{{y,y,y,y} }, \end{aligned}$$

(35)

$$\begin{aligned} \text {FSDT:}&\nonumber \\ L_{11}=\,&A_{11}\,d_{{x,x}}+A_{66}\,d_{{y,y}} ,\quad L_{12}=d_{{x,y}} \left( A_{12}+A_{66} \right) ,\quad L_{13}=0 ,\nonumber \\ L_{14}=\,&B_{11}\,d_{{x,x}}+2\,B_{16}\,d_{{x,y}}+B_{66}\,d_{{y,y}} ,\nonumber \\ L_{15}=\,&\left( B_{12}+B_{66} \right) d_{{x,y}}+B_{16}\,d_{{x,x}}+B_{26}\,d_{{ y,y}} ,\nonumber \\ L_{22}=\,&A_{22}\,d_{{y,y}}+A_{66}\,d_{{x,x}} ,\quad L_{23}=0 ,\nonumber \\ L_{24}=\,&\left( B_{12}+B_{66} \right) d_{{x,y}}+B_{16}\,d_{{x,x}}+B_{26}\,d_{{y,y}} ,\nonumber \\ L_{25}=\,&B_{22}\,d_{{y,y}}+2\,B_{26}\,d_{{x,y}}+B_{66}\,d_{{x,x}} ,\nonumber \\ L_{33}=\,&\left( -KA_{55}+\xi _xN_\text {cr} \right) d_{{x,x}}- \left( KA_{ 44}-\xi _yN_\text {cr} \right) \, d_{{y,y}} ,\nonumber \\ L_{34}=\,&-KA_{55}\,d_{{x}} ,\quad L_{35}=-KA_{44}\,d_{{y}} ,\nonumber \\ L_{44}=\,&-KA_{55}\,+D_{11}\,d_{{x,x}}+D_{66}\,d_{{y,y}} ,\nonumber \\ L_{45}=\,&\left( D_{12}+D_{66} \right) \,d_{{x,y}} ,\nonumber \\ L_{55}=\,&-KA_{44}\,+D_{22}\,d_{{y,y}}+D_{66}\,d_{{x,x}} , \end{aligned}$$

(36)

$$\begin{aligned} \text {TSDT:}&\nonumber \\ L_{11}=\,&A_{11}\,d_{{x,x}}+A_{66}\,d_{{y,y}} ,\quad L_{12}= \left( A_{12}+A_{66} \right) \, d_{{x,y}} ,\nonumber \\ L_{13}=\,&-\tau \, \left[ \left( E_{12}+2\,E_{66} \right) d_{{x,y,y}}+E_{11}\,d_{{x,x,x}} \right. \nonumber \\&\left. +\,3\,E_{16}\,d_{{x,x,y}}+E_{26}\,d_{{y,y,y}} \right] ,\nonumber \\ L_{14}=\,&\left( -\tau \,E_{11}+B_{11} \right) d_{{x,x}}- \left( 2\,\tau \, E_{16}-2\,B_{16} \right) d_{{x,y}} \nonumber \\&- \left( \tau \,E_{66}-B_{66} \right) \,d_{{y,y}} ,\nonumber \\ L_{15}=\,&\left[ \tau \left( -E_{66}-E_{12} \right) +B_{12}+B_{66} \right] d_{{ x,y}}- \left( \tau \,E_{16}-B_{16} \right) d_{{x,x}} \nonumber \\&- \left( E_{26}\,\tau -B_{26} \right) \, d_{{y,y}} ,\quad L_{22}=A_{22}\,d_{{y,y}}+A_{66}\,d_{{x,x}} ,\nonumber \\ L_{23}=\,&-\tau \, \left[ \left( E_{12}+2\,E_{66} \right) d_{{x,x,y}}+E_{16}\,d_{{x,x,x}}\right. \nonumber \\&\left. +\,3\,E_{26}\,d_{{x,y,y}}+E_{22}\,d_{{y,y,y}} \right] ,\nonumber \\ L_{24}=\,&\left[ \tau \left( -E_{66}-E_{12} \right) +B_{12}+B_{66} \right] d_{{ x,y}}+ \left( -\tau \,E_{16}+B_{16} \right) d_{{x,x}} \nonumber \\&- \left( \tau \,E_{26}-B_{26} \right) \, d_{{y,y}} ,\nonumber \\ L_{25}=\,&\left( -\tau \,E_{66}+B_{66} \right) d_{{x,x}}+ \left( -2\tau \,E_{26} +2\,B_{26} \right) d_{{x,y}} \nonumber \\&- \left( \tau \,E_{22}-B_{22} \right) \, d_{{y,y}} ,\nonumber \\ L_{33}=\,&2\,{\tau }^{2} \left( H_{12}+2\,H_{66} \right) d_{{x,x,y,y}}+{\tau }^{2}H_{11}\,d_ {{x,x,x,x}}+{\tau }^{2}H_{22}\,d_{{y,y,y,y}} \nonumber \\&+\left( -9\,{\tau }^{2}F_{55}+6\,\tau \,D_{55}-A_{55}+\xi _xN_\text {cr} \right) d_{{x,x}} \nonumber \\&+ \left( -9\,{\tau }^{2}F_{44}+6\,\tau \,D_{44}-A_{44}+\xi _yN_\text {cr} \right) \, d_{{y,y}} ,\nonumber \\ L_{34}=\,&\tau \, \left[ \tau \left( H_{12}+2\,H_{66} \right) -F_{12}-2\,F_{66} \right] d_{{x,y,y}} \nonumber \\&+\tau \, \left( \tau \,H_{11}-F_{11} \right) d_{{x,x,x}}- \left( 9\, {\tau }^{2}F_{55}-6\,\tau \,D_{55}+{A_{55}} \right) \, d_{{x}} ,\nonumber \\ L_{35}=\,&\tau \, \left[ \tau \left( H_{12}+2\,H_{66} \right) -F_{12}-2\,F_{66} \right] d_{{x,x,y}} \nonumber \\&+\tau \, \left( \tau \, H_{22}-F_{22} \right) d_{{y,y ,y}}- \left( 9\,{\tau }^{2} F_{44}-6\,\tau \, D_{44}+A_{44} \right) d_{{y}} ,\nonumber \\ L_{44}=\,&\left( {\tau }^{2} H_{11}-2\,\tau \,F_{11}+D_{11} \right) d_{{x,x}}\nonumber \\&+ \left( {\tau }^{2} H_{66}-2\,\tau \,F_{66}+D_{66} \right) d_{{y,y}}\nonumber \\&- \left( 9\, {\tau }^{2}F_{55}-6\,\tau \,D_{55}+A_{55} \right) ,\nonumber \\ L_{45}=\,&\left[ {\tau }^{2}\left( H_{12}+H_{66} \right) - 2\,\tau \left( F_{12}+F_{66} \right) +D_{12}+D_{66} \right] \,d_{{x,y}},\nonumber \\ L_{55}=\,&\left( {\tau }^{2}H_{66}-2\,\tau \,F_{66}+D_{66} \right) d_{{x,x}}\nonumber \\&+ \left( {\tau }^{2} H_{22}-2\,\tau \,F_{22}+D_{22} \right) d_{{y,y}}\nonumber \\&- \left( 9\,{\tau }^{2} F_{44}-6\,\tau \,D_{44}+A_{44} \right) . \end{aligned}$$

(37)

4 Lévy-type solution

Based on the orthotropic laminate behaviour considered, the general form of the ansatz functions provides a separation of variables with respect to the x- and y-directions. Due to the different coupling effects and boundary conditions, a distinction must be made between cross- and angle-plies. The respective laminate types are described in Eqs. (14), (15), and (16), respectively. The ansatz function $\Phi _i^\textrm{CP}$ from Eq. (38) apply to the unsymmetrical cross-ply laminate.

$$\begin{aligned} \Phi _i^\textrm{CP}= \left[ \begin{array}{c} \cos \left( \beta \,x \right) U \left( y \right) \\ \sin \left( \beta \,x \right) V \left( y \right) \\ \sin \left( \beta \,x \right) W \left( y \right) \\ \cos \left( \beta \,x \right) X \left( y \right) \\ \sin \left( \beta \,x \right) Y \left( y \right) \end{array}\right] , \quad \Phi _i^\textrm{AP}= \left[ \begin{array}{c} \sin \left( \beta \,x \right) U \left( y \right) \\ \cos \left( \beta \,x \right) V \left( y \right) \\ \sin \left( \beta \,x \right) W \left( y \right) \\ \cos \left( \beta \,x \right) X \left( y \right) \\ \sin \left( \beta \,x \right) Y \left( y \right) \end{array}\right] \end{aligned}$$

(38)

For the antisymmetric angle-ply laminate the ansatz functions $\Phi _i^\textrm{AP}$ result from Eq. (38). Both sets of ansatz functions fulfil the boundary conditions (31) at the edges $x=0,a$ identically and contain the abbreviation $\beta ={{m\,\pi }/{a}}$. The approaches also satisfy the differential equations with respect to the x-coordinate. Inserting the approaches into the partial differential equations reduces them to ordinary differential equations in which only derivatives with respect to y appear (${(')=(\partial /\partial y)}$). Since the approaches and coupling terms of the cross- and angle-ply laminate differ, different ordinary differential equations arise here, which are presented in the following for CLPT, FSDT and TSDT. The Lévy-type solutions presented in the next section solve the ordinary differential equations from this section. They can also be found in a similar form in the publications [39] for cross-ply laminates and in [41] for antisymmetric angle-ply laminates in the framework of the FSDT. In order to make the results of the present investigation comprehensible and to enable the reader to use all relevant methods in one consistent notation, they are all presented in the following.

4.1 CLPT cross-ply laminate

In the framework of CLPT, Eq. (34) is considered with the components from (35). The approach $\Phi _{i}^\textrm{CP}$ of the cross-ply laminate (38) is inserted here and the partial differential equation system reduces to an ordinary one. The order of the resulting system can be reduced by some transformations to the following system:

$$\begin{aligned} {U}^{''}=\,&c_{1}\,U+c_{2}\,{V}^{'}+c_{3}\,W+c_{4}\,{W}^{''} ,\nonumber \\ {V}^{''} =\,&c_{5}\,{U}^{'}+c_{6}\,V+c_{7}\,{W}^{'}+c_{8}\,{W}^{'''} ,\nonumber \\ {W}^{''''} =\,&c_{9}\,U+c_{10}\,{V}^{'}+c_{11}\,W+c_{12}\,{W}^{''} . \end{aligned}$$

(39)

The abbreviations in Eq. (39) are defined in Appendix A.1. In the context of the state space concept, Eq. (39) is transformed into a first-order system with the following transformation:

$$\begin{aligned} U=\,&Z_1,\quad U^{'}=Z_2, \quad V=Z_3,\quad V^{'}=Z_4, \nonumber \\ W=\,&Z_5,\quad W^{'}=Z_6, \quad W^{''}=Z_7, \quad W^{'''}=Z_8. \end{aligned}$$

(40)

This leads to the following first-order differential equation system:

$$\begin{aligned} \underline{Z}^{'}\left( y\right) = \underline{\underline{C}} \,\underline{Z} \end{aligned}$$

(41)

and can be written as:

$$\begin{aligned} \begin{bmatrix} {Z_{{1}}}^{'}\\ {Z_{{2}}}^ {'}\\ {Z_{{3}}}^{'}\\ {Z_{{4}}}^{' }\\ {Z_{{5}}}^{'}\\ {Z_{{6}}}^{'} \\ {Z_{{7}}}^{'}\\ {Z_{{8}}}^{'} \end{bmatrix} = \underbrace{ \begin{bmatrix} 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ c_{1}&{}\quad 0&{}\quad 0&{}\quad c_{2}&{}\quad c_{3}&{}\quad 0&{}\quad c_{4}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 &{}\quad 0\\ 0&{}\quad c_{5}&{}\quad c_{6}&{}\quad 0&{}\quad 0&{}\quad c_{7}&{}\quad 0&{}\quad c_{8} \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1\\ c_{9}&{}\quad 0 &{}\quad 0&{}\quad c_{10}&{}\quad c_{11}&{}\quad 0&{}\quad c_{12}&{}\quad 0 \end{bmatrix} }_{\underline{\underline{C}}} \begin{bmatrix} Z_{{1}}\\ Z_{{2}} \\ Z_{{3}}\\ Z_{{4}} \\ Z_{{5}}\\ Z_{{6}} \\ Z_{{7}}\\ Z_{{8}} \end{bmatrix} . \end{aligned}$$

(42)

4.2 CLPT angle-ply laminate

Substituting the approach $\Phi _i^\textrm{AP}$ of the antisymmetric angle-ply laminate (38) into the differential equation of the CLPT (34) with (35) leads after some transformations to:

$$\begin{aligned} {U}^{''} =\,&c_{1}\,U+c_{2}\,{V}^{'}+c_{3}\,{W}^{'}+c_{4}\,{W}^{'''} ,\nonumber \\ {V}^{''} =\,&c_{5}\,{U}^{'}+c_{6}\,V+c_{7}\,W+c_{8}\,{W}^{''} ,\nonumber \\ {W}^{''''} =\,&c_{9}\,{U}^{'}+c_{10}\,V+c_{11}\,W+c_{12}\,{W}^{''} . \end{aligned}$$

(43)

The abbreviations in Eq. (43) can be found in Appendix A.2. Equation (43) can be transformed into the following first-order differential equation system using (40):

$$\begin{aligned} \begin{bmatrix} {Z_{{1}}}^{'}\\ {Z_{{2}}}^ {'}\\ {Z_{{3}}}^{'}\\ {Z_{{4}}}^{' }\\ {Z_{{5}}}^{'}\\ {Z_{{6}}}^{'} \\ {Z_{{7}}}^{'}\\ {Z_{{8}}}^{'} \end{bmatrix} =\underbrace{ \begin{bmatrix} 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ c_{1}&{}\quad 0&{}\quad 0&{}\quad c_{2}&{}\quad 0&{}\quad c_{3}&{}\quad 0&{}\quad c_{4}\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 &{}\quad 0\\ 0&{}\quad c_{5}&{}\quad c_{6}&{}\quad 0&{}\quad c_{7}&{}\quad 0&{}\quad c_{8}&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1\\ 0&{}\quad c_{9} &{}\quad c_{10}&{}\quad 0&{}\quad c_{11}&{}\quad 0&{}\quad c_{12}&{}\quad 0 \end{bmatrix} }_{\underline{\underline{C}}} \begin{bmatrix} Z_{{1}}\\ Z_{{2}} \\ Z_{{3}}\\ Z_{{4}} \\ Z_{{5}}\\ Z_{{6}} \\ Z_{{7}}\\ Z_{{8}} \end{bmatrix}. \end{aligned}$$

(44)

4.3 FSDT cross-ply laminate

In the context of FSDT, Eq. (34) is used with (36). If the approach $\Phi _i^\textrm{CP}$ of the cross-ply laminate (38) is inserted into this equation, the following ordinary differential equation system is obtained after a few transformations:

$$\begin{aligned} {U}^{''} =\,&c_{1}\,U+c_{2}\,{V}^{'}+c_{3}\,W+c_{4}\,X+c_{5}\,{Y}^{'} ,\nonumber \\ {V}^{''}=\,&c_{6}\,{U}^{'}+c_{7}\,V+c_{8}\,{W}^{'}+c_{9}\,{X}^{'}+c_{10}\,Y ,\nonumber \\ {W}^{''}=\,&c_{11}\,W+c_{12}\,X+c_{13}\,{Y}^{'} ,\nonumber \\ {X}^{''}=\,&c_{14}\,U+c_{15}\,{V}^{'}+c_{16}\,W+c_{17}\,X+c_{18}\,{Y}^{'} ,\nonumber \\ {Y}^{''}=\,&c_{19}\,{U}^{'}+c_{20}\,V+c_{21}\,{W}^{'}+c_{22}\,{X}^{'}+c_{23}\,Y. \end{aligned}$$

(45)

The abbreviations in Eq. (45) can be found in Appendix A.3. With the following transformation, the differential equation system of the FSDT from Eq. (45) is transformed into a first-order system:

$$\begin{aligned} U=\,&Z_1,\quad U^{'}=Z_2, \quad V=Z_3,\quad V^{'}=Z_4, \nonumber \\ W=\,&Z_5,\quad W^{'}=Z_6, \quad X=Z_7,\quad X^{'}=Z_8, \nonumber \\ Y=\,&Z_9,\quad Y^{'}=Z_{10}. \end{aligned}$$

(46)

The first-order ordinary differential equation system resulting from the transformation has the form:

$$\begin{aligned} \begin{bmatrix} {Z_{{1}}}^{'}\\ {Z_{{2}}}^ {'}\\ {Z_{{3}}}^{'}\\ {Z_{{4}}}^{' }\\ {Z_{{5}}}^{'}\\ {Z_{{6}}}^{'} \\ {Z_{{7}}}^{'}\\ {Z_{{8}}}^{'} \\ {Z_{{9}}}^{'}\\ {Z_{{10}}}^{'} \end{bmatrix} =\underbrace{ \left[ \begin{array}{cccccccccc} 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ c_{1}&{}\quad 0&{}\quad 0&{}\quad c_{2}&{}\quad c_{3}&{}\quad 0&{}\quad c_{4}&{}\quad 0&{}\quad 0&{}\quad c_{5}\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad c_{6}&{}\quad c_{7}&{}\quad 0&{}\quad 0&{}\quad c_{8}&{}\quad 0&{}\quad c_{9}&{}\quad c_{10}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad c_{11}&{}\quad 0&{}\quad c_{12}&{}\quad 0&{}\quad 0&{}\quad c_{13}\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ c_{14}&{}\quad 0&{}\quad 0&{}\quad c_{15}&{}\quad c_{16}&{}\quad 0&{}\quad c_{17}&{}\quad 0&{}\quad 0&{}\quad c_{18}\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1\\ 0&{}\quad c_{19}&{}\quad c_{20}&{}\quad 0&{}\quad 0&{}\quad c_{21}&{}\quad 0&{}\quad c_{22}&{}\quad c_{23}&{}\quad 0 \end{array}\right] }_{\underline{\underline{C}}} \begin{bmatrix} Z_{{1}}\\ Z_{{2}} \\ Z_{{3}}\\ Z_{{4}} \\ Z_{{5}}\\ Z_{{6}} \\ Z_{{7}}\\ Z_{{8}} \\ Z_{{9}}\\ Z_{{10}} \end{bmatrix}. \end{aligned}$$

(47)

4.4 FSDT angle-ply laminate

For antisymmetric angle-ply laminates, the approach $\Phi _i^\textrm{AP}$ from Eq. (38) is substituted into the differential equation of FSDT (34) with (36). After some transformations, this leads to the following ordinary differential equation system:

$$\begin{aligned} {U}^{''}=\,&c_{1}\,U+c_{2}\,{V}^{'}+c_{3}\,{W}^{'}+c_{4}\,{X}^{'}+c_{5}\,Y ,\nonumber \\ {V}^{''}=\,&c_{6}\,{U}^{'}+c_{7}\,V+c_{8}\,W+c_{9}\,X+c_{10}\,{Y}^{'} ,\nonumber \\ {W}^{''}=\,&c_{11}\,W+c_{12}\,X+c_{13}\,{Y}^{'} ,\nonumber \\ {X}^{''}=\,&c_{14}\,{U}^{'}+c_{15}\,V+c_{16}\,W+c_{17}\,X+c_{18}\,{Y}^{'} ,\nonumber \\ {Y}^{''}=\,&c_{19}\,U+c_{20}\,{V}^{'}+c_{21}\,{W}^{'}+c_{22}\,{X}^{'}+c_{23}\,Y. \end{aligned}$$

(48)

The abbreviations in Eq. (48) can be found in Appendix A.4. Using the transformation from Eq. (46), the differential equation system (43) can be transformed to the following first-order system:

$$\begin{aligned} \begin{bmatrix} {Z_{{1}}}^{'}\\ {Z_{{2}}}^ {'}\\ {Z_{{3}}}^{'}\\ {Z_{{4}}}^{' }\\ {Z_{{5}}}^{'}\\ {Z_{{6}}}^{'} \\ {Z_{{7}}}^{'}\\ {Z_{{8}}}^{'} \\ {Z_{{9}}}^{'}\\ {Z_{{10}}}^{'} \end{bmatrix} = \underbrace{ \left[ \begin{array}{cccccccccc} 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ c_{1}&{}\quad 0&{}\quad 0&{}\quad c_{2}&{}\quad 0&{}\quad c_{3}&{}\quad 0&{}\quad c_{4}&{}\quad c_{5}&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad c_{6} &{}\quad c_{7}&{}\quad 0&{}\quad c_{8}&{}\quad 0&{}\quad c_{9}&{}\quad 0&{}\quad 0&{}\quad c_{10}\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 &{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad c_{11}&{}\quad 0&{}\quad c_{12}&{}\quad 0&{}\quad 0&{}\quad c_{13} \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad c_{14 }&{}\quad c_{15}&{}\quad 0&{}\quad c_{16}&{}\quad 0&{}\quad c_{17}&{}\quad 0&{}\quad 0&{}\quad c_{18}\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 &{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1\\ c_{19}&{}\quad 0&{}\quad 0&{}\quad c_{20}&{}\quad 0&{}\quad c_{21}&{}\quad 0&{}\quad c_{22 }&{}\quad c_{23}&{}\quad 0 \end{array}\right] }_{\underline{\underline{C}}} \begin{bmatrix} Z_{{1}}\\ Z_{{2}} \\ Z_{{3}}\\ Z_{{4}} \\ Z_{{5}}\\ Z_{{6}} \\ Z_{{7}}\\ Z_{{8}} \\ Z_{{9}}\\ Z_{{10}} \end{bmatrix} . \end{aligned}$$

(49)

4.5 TSDT cross-ply laminate

For the cross-ply laminate in the context of TSDT, substituting the approach $\Phi _i^\textrm{CP}$ from Eq. (38) into the differential equation system (34) with (37) leads after some transformations to:

$$\begin{aligned} {U}^{''}=\,&c_{1}\,U+c_{2}\,{V}^{'}+c_{3}\,W+c_{4}\,{W}^{''}+c_{5}\,X+c_{6}\,{Y}^{'} ,\nonumber \\ {V}^{''}=\,&c_{7}\,{U}^{'}+c_{8}\,V+c_{9}\,{W}^{'}+c_{10}\,{W}^{'''}+c_{11}\,{X}^{'}+c_{12}\,Y ,\nonumber \\ {W}^{''''}=\,&c_{13}\,U+c_{14}\,{V}^{'}+c_{15}\,W+c_{16}\,{W}^{''}+c_{17}\,X+c_{18}\,{Y}^{'} ,\nonumber \\ {X}^{''}=\,&c_{19}\,U+c_{20}\,{V}^{'}+c_{21}\,W+c_{22}\,{W}^{''}+c_{23}\,X+c_{24}\,{Y}^{'} ,\nonumber \\ {Y}^{''}=\,&c_{25}\,{U}^{'}+c_{26}\,V+c_{27}\,{W}^{'}+c_{28}\,{W}^{'''}+c_{29}\,{X}^{'}+c_{30}\,Y. \end{aligned}$$

(50)

The abbreviations in Eq. (50) can be found in Appendix A.5. With the transformation (51), Eq. (50) can be transformed into the first-order system (52).

$$\begin{aligned} U=\,&Z_1,\quad U^{'}=Z_2, \quad V=Z_3,\quad V^{'}=Z_4, \nonumber \\ W=\,&Z_5,\quad W^{'}=Z_6, \quad W^{''}=Z_7, \quad W^{'''}=Z_8, \nonumber \\ X=\,&Z_9,\quad X^{'}=Z_{10}, \quad Y=Z_{11},\quad Y^{'}=Z_{12}. \end{aligned}$$

(51)

$$\begin{aligned} \begin{bmatrix} {Z_{{1}}}^{'}\\ {Z_{{2}}}^ {'}\\ {Z_{{3}}}^{'}\\ {Z_{{4}}}^{' }\\ {Z_{{5}}}^{'}\\ {Z_{{6}}}^{'} \\ {Z_{{7}}}^{'}\\ {Z_{{8}}}^{'} \\ {Z_{{9}}}^{'}\\ {Z_{{10}}}^{'} \\ {Z_{{11}}}^{'}\\ {Z_{{12}}}^{'} \end{bmatrix} = \underbrace{ \left[ \begin{array}{cccccccccccc} 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ c_{1}&{}\quad 0&{}\quad 0&{}\quad c_{2}&{}\quad c_{3}&{}\quad 0&{}\quad c_{4}&{}\quad 0&{}\quad c_{5}&{}\quad 0&{}\quad 0&{}\quad c_{6}\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad c_{7}&{}\quad c_{8}&{}\quad 0&{}\quad 0&{}\quad c_{9}&{}\quad 0&{}\quad c_{10}&{}\quad 0&{}\quad c_{11}&{}\quad c_{12}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ c_{13}&{}\quad 0&{}\quad 0&{}\quad c_{14}&{}\quad c_{15}&{}\quad 0&{}\quad c_{16}&{}\quad 0&{}\quad c_{17}&{}\quad 0&{}\quad 0&{}\quad c_{18}\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ c_{19}&{}\quad 0&{}\quad 0&{}\quad c_{20}&{}\quad c_{21}&{}\quad 0&{}\quad c_{22}&{}\quad 0&{}\quad c_{23}&{}\quad 0&{}\quad 0&{}\quad c_{24}\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1\\ 0&{}\quad c_{25}&{}\quad c_{26}&{}\quad 0&{}\quad 0&{}\quad c_{27}&{}\quad 0&{}\quad c_{28}&{}\quad 0&{}\quad c_{29}&{}\quad c_{30}&{}\quad 0 \end{array}\right] }_{\underline{\underline{C}}} \begin{bmatrix} Z_{{1}}\\ Z_{{2}} \\ Z_{{3}}\\ Z_{{4}} \\ Z_{{5}}\\ Z_{{6}} \\ Z_{{7}}\\ Z_{{8}} \\ Z_{{9}}\\ Z_{{10}} \\ Z_{{11}}\\ Z_{{12}} \end{bmatrix} \end{aligned}$$

(52)

4.6 TSDT angle-ply laminate

The antisymmetric angle-ply laminate has the approach $\Phi _i^\textrm{AP}$ from Eq. (38). This is used in Eq. (34) with (37) in the framework of TSDT. This results in an ordinary differential equation system, the order of the system can be reduced by suitable reshaping and can be written as:

$$\begin{aligned} {U}^{''}=\,&c_{1}\,U+c_{2}\,{V}^{'}+c_{3}\,{W}^{'}+c_{4}\,{W}^{'''}+c_{5}\,{X}^{'}+c_{6}\,Y,\nonumber \\ {V}^{''}=\,&c_{7}\,{U}^{'}+c_{8}\,V+c_{9}\,W+c_{10}\,{W}^{''}+c_{11}\,X+{Y}^{'}c_{12},\nonumber \\ {W}^{''''}=\,&c_{13}\,{U}^{'}+c_{14}\,V+c_{15}\,W+c_{16}\,{W}^{''}+c_{17}\,X+c_{18}\,{Y}^{'},\nonumber \\ {X}^{''}=\,&c_{19}\,{U}^{'}+c_{20}\,V+c_{21}\,W+c_{22}\,{W}^{''}+c_{23}\,X+c_{24}\,{Y}^{'},\nonumber \\ {Y}^{''}=\,&c_{25}\,U+{V}^{'}c_{26}+c_{27}\,{W}^{'}+c_{28}\,{W}^{'''}+c_{29}\,{X}^{'}+c_{30}\,Y. \end{aligned}$$

(53)

The abbreviations in Eq. (53) can be found in Appendix A.6. With the transformation (51), the differential equation system (53) can be transformed into the following first-order system:

$$\begin{aligned} \begin{bmatrix} {Z_{{1}}}^{'}\\ {Z_{{2}}}^ {'}\\ {Z_{{3}}}^{'}\\ {Z_{{4}}}^{' }\\ {Z_{{5}}}^{'}\\ {Z_{{6}}}^{'} \\ {Z_{{7}}}^{'}\\ {Z_{{8}}}^{'} \\ {Z_{{9}}}^{'}\\ {Z_{{10}}}^{'} \\ {Z_{{11}}}^{'}\\ {Z_{{12}}}^{'} \end{bmatrix} = \underbrace{ \left[ \begin{array}{cccccccccccc} 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ c_{1}&{}\quad 0&{}\quad 0&{}\quad c_{2}&{}\quad 0&{}\quad c_{3}&{}\quad 0&{}\quad c_{4}&{}\quad 0&{}\quad c_{5}&{}\quad c_{6}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad c_{7}&{}\quad c_{8}&{}\quad 0&{}\quad c_{9}&{}\quad 0&{}\quad c_{10}&{}\quad 0&{}\quad c_{11}&{}\quad 0&{}\quad 0&{}\quad c_{12}\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad c_{13}&{}\quad c_{14}&{}\quad 0&{}\quad c_{15}&{}\quad 0&{}\quad c_{16}&{}\quad 0&{}\quad c_{17}&{}\quad 0&{}\quad 0&{}\quad c_{18}\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad c_{19}&{}\quad c_{20}&{}\quad 0&{}\quad c_{21}&{}\quad 0&{}\quad c_{22}&{}\quad 0&{}\quad c_{23}&{}\quad 0&{}\quad 0&{}\quad c_{24}\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1\\ c_{25}&{}\quad 0&{}\quad 0&{}\quad c_{26}&{}\quad 0&{}\quad c_{27}&{}\quad 0&{}\quad c_{28}&{}\quad 0&{}\quad c_{29}&{}\quad c_{30}&{}\quad 0 \end{array}\right] }_{\underline{\underline{C}}} \begin{bmatrix} Z_{{1}}\\ Z_{{2}} \\ Z_{{3}}\\ Z_{{4}} \\ Z_{{5}}\\ Z_{{6}} \\ Z_{{7}}\\ Z_{{8}} \\ Z_{{9}}\\ Z_{{10}} \\ Z_{{11}}\\ Z_{{12}} \end{bmatrix} . \end{aligned}$$

(54)

For the differential equation systems shown, a solution method is presented in the next section.

4.7 The transcendental equation

The first-order differential equation systems shown previously are solved in the following with the space state approach, which can be found, for example, in [25, 42]. A general solution of the ordinary differential equation system is given by:

$$\begin{aligned} \underline{Z}^{}(y)=\textrm{e}^{{\,\underline{\underline{C}}\,y}}\,\underline{K}. \end{aligned}$$

(55)

The vector $\underline{K}$ contains constant coefficients and can be described by the boundary conditions. In the case that $\underline{\underline{C}}$ is diagonalisable, the matrix $\textrm{e}^{{\,\underline{\underline{C}}\,y}}$ can be defined as follows:

$$\begin{aligned} \textrm{e}^{{\,\underline{\underline{C}}\,y}} = \underline{\underline{L}} \begin{bmatrix} \textrm{e}^{\lambda _{1}y} &{}\quad &{}\quad 0 \\ &{}\quad \ddots &{}\quad \\ 0 &{}\quad &{}\quad \textrm{e}^{\lambda _{k}y} \end{bmatrix} \underline{\underline{L}}^{-1}. \end{aligned}$$

(56)

The matrix $\underline{\underline{L}}$ contains the eigenvectors of $\underline{\underline{C}}$, and $\lambda _{1..\,k}$ represent the respective eigenvalues. The dimension of the matrix $\underline{\underline{C}}$ depends on the different laminated plate theories; therefore, the number of eigenvalues is different, resulting in: $k=8$ for CLPT, $k=10$ for FSDT and $k=12$ for TSDT. Equation (56) is only valid as a solution if no multiple eigenvalues occur, i.e. the matrix $\underline{\underline{C}}$ is diagonalisable. This is true for all cases investigated. Substitution of Eq. (55) into the corresponding boundary conditions leads to a homogeneous system of equations of the type:

$$\begin{aligned} \underline{\underline{M}}\,\underline{K}=0. \end{aligned}$$

(57)

The coefficient matrix $\underline{\underline{M}}$ with dimension ${k \times k}$ depends on the underlying theory, as described before. A non-trivial solution of (57) requires a vanishing determinant of the coefficient matrix:

$$\begin{aligned} \det \left( \underline{\underline{M}}\right) =0. \end{aligned}$$

(58)

This leads to a transcendental equation for the buckling load $N_{\textrm{cr}}$ which is exact with respect to the underlying theoretical framework. However, the method described can cause numerical problems. First, zero entries on the main diagonal of $\underline{\underline{C}}$ are problematic for eigenvalue analysis. Second, the problem $\det (\underline{\underline{M}})=0$ is generally ill-conditioned. For both problems there are solution strategies described in Appendix B. Supplemental solution strategies are described below. In order to solve the transcendental equation, it is useful to have a suitable starting value for the buckling load and half wave number $m_{\textrm{int}}$. This starting point is determined with the closed-form solution from [43]. The present Lévy-type solution is determined for $m_{\textrm{int}}-1$, $m_{\textrm{int}}$, and $m_{\textrm{int}}+1$. The lowest buckling loads of the three solutions are of interest and define the half wave number of the Lévy-type solution. This procedure makes Lévy-type solutions much more efficient and robustly. For the solution algorithm, moreover, the very large gradients of $\det (\underline{\underline{M}})$ might cause difficulties as well. Therefore, the objective function is scaled with $\det (\underline{\underline{M}})^{-1}$ from the starting value.

The solutions presented here can also be applied directly to symmetrical orthotropic laminates without any modifications.

5 Results and discussion

5.1 Comparison with literature values

The present Lévy-type solution is compared with literature values for different $E_{11}/E_{22}$ ratios for verification. The material parameters of the single layer are: ${G_{12}=G_{13}=0.6\, E_{22}}$, ${G_{23}=0.5\, E_{22}}$, ${\nu _{12}=0.25}$. In Table 1 the non-dimensional buckling loads of an SSSS plate under axial compression from [39] are compared with the present solution. The two solutions present in both cases a Lévy-type solution and address the same laminated plate theories. The deviation of the two solutions is 0.00%. This indicates the viability of the present solution and their correct implementation.

Table 1 Investigation of the degree of orthotropy of a ${\left[ (0^{\circ }/90^{\circ })_n\right] }$ laminate for an SSSS plate with respect to the non-dimensional buckling load: $\overline{N}_{\textrm{cr}} ={N_\textrm{cr}\, b^{2}}/\left( { E_{22}\,t^3}\right)$, $a/b=1$, $b/t=10$, $\xi _x=1$, $\xi _y=0$

5.2 Finite element model

Comparative finite element analyses (FEA) have been carried out using the commercial software Abaqus. The model used employs quadratic shell elements (S8R) which exhibit Reissner–Mindlin kinematics. This corresponds to the kinematics of the FSDT used in this work. The laminate stiffness values $\underline{\underline{A}}$, $\underline{\underline{B}}$, $\underline{\underline{D}}$, $K\underline{\underline{A_s}}$ are directly assigned at the element level and therefore the same as in the analytical modelling. The boundary conditions of the analytical model used in the FSDT (Eqs. (31–33)) were adopted in the FE model. In detail, the boundary conditions of the model shown in Fig. 4 are as follows: Edge ($x=0,\,a$): Cross-ply: U3 = UR1 = 0, U2 = 0$^*$; Angle-ply: U3 = UR1 = 0, U1 = 0$^*$; Edge with rotational restraints ($y=0,\,b$): Cross-ply: U3 = UR2 = 0, U2 = 0$^*$; Angle-ply: U3 = UR2 = 0, U1 = 0$^*$; free edge ($y=b$): no displacement boundary conditions; Vertices ($x=0,\, y=0$): U1 = U2 = 0; Vertices ($x=a,\, y=0$): U2 = 0. The values marked with $^*$ apply exclusively to the eigenvalue analysis. At the edges ${(y=0,\,b)}$ the rotational restraint stiffnesses $k_0$, $k_b$, which are given per length in the analytical model, are converted to the respective nodes of the FE model: $k_0^{FE}={k_0 \,a}/{n_{\text {edge}}}$ and $k_b^{FE}={k_b\, a}/{n_{\text {edge}}}$. The quantity $n_{\text {edge}}$ represents the number of nodes of the respective edge. The external load $N_{\textrm{cr}}$ is implemented as a line load as in the analytical model. The minimum element edge length is 1/16 of the smallest edge, it provides a relative deviation of less than 0.1 %.

Fig. 4

The FE model with coordinate system (x, y, z), the displacements (U1, U2, U3) and the rotations (UR1, UR2, UR3). The plate is loaded with a line load $N_{\text {cr}}$ and has the length a and the width b

Fig. 5

Cross-ply laminate ${\left[ (0^{\circ }/90^{\circ })_2\right] }$: The non-dimensional buckling load $\overline{N}_{\textrm{cr}}$ is given as a function of the non-dimensional rotational restraints $\overline{k}_i$ for axial compression ($\xi _x=1, \xi _y=0$), different relative widths b/t (5, 10, 100) and the boundary conditions SRSR and SFSR with the aspect ratio of $a/b=10$

5.3 Investigation of the rotational restraint stiffness

In this section, the present Lévy-type solution is compared with the FEA (see previous section) and the closed-form (CF) solutions from [43]. The CF solution is an approximate solution for SRSR and SFSR laminates for the laminate theories as well as laminate types considered here. This solution provides an explicit expression for the buckling load and is therefore extremely computationally efficient. The present Lévy-type solution, on the other hand, is an exact solution of the differential equation, which has an extremely high accuracy. The comparison to FEA is to demonstrate that plausible results are produced with the present method. The CF solution serves as an additional comparison to literature values and is also used as a starting value for the present Lévy-type solution. The material parameters of the single layer are given below for this analysis: ${E_{{11}}= 16.2\,E_{{22}}}$, ${{G_{12}}=G_{{13}}= 0.52\,E_{{22}}}$, ${G_{{23}}= 0.445\,E_{{22}}}$, ${\nu _{{12}}= 0.3}$. In the framework of FSDT, a shear correction factor of 5/6 is used.

Fig. 6

Angle-ply laminate ${\left[ (45^{\circ }/-45^{\circ })_2\right] }$: The non-dimensional buckling load $\overline{N}_{\textrm{cr}}$ is given as a function of the non-dimensional rotational restraints $\overline{k}_i$ for axial compression ($\xi _x=1, \xi _y=0$), different relative widths b/t (5, 10, 100) and the boundary conditions SRSR and SFSR with the aspect ratio of $a/b=10$

Fig. 7

Cross-ply laminate ${\left[ (0^{\circ }/90^{\circ })_n\right] }$: The non-dimensional buckling load $\overline{N}_{\textrm{cr}}$ is given in terms of the aspect ratio a/b for axial compression ($\xi _x=1, \xi _y=0$) and the relative width of $b/t=10$.The ply repetitions $n=1, 2, \infty$ for the boundary conditions SRSR and SFSR with the rotational elastic restraints ${k_0=k_b=10^5}$ N and ${k_0=10^4}$ N, respectively, are considered

Fig. 8

Angle-ply laminate ${\left[ (\theta /-\theta )_n\right] }$: The non-dimensional buckling load $\overline{N}_{\textrm{cr}}$ is given in terms of the ply angle $\theta$ for axial compression ($\xi _x=1, \xi _y=0$) and the relative width of $b/t=10$. The ply repetitions $n=1, 2, \infty$ for the boundary conditions SRSR and SFSR with the rotational elastic restraints ${k_0=k_b=10^5}$ N and ${k_0=10^4}$ N, respectively, are considered

For the cross-ply laminate, a very good agreement between the solutions is observed. In Fig. 5, all three analysis methods show comparable results over the whole range of the restraint stiffness. The FEA is based on the kinematics of the FSDT, so a comparison is appropriate in this framework. The maximum deviations between the Lévy-type solution and the FEA with respect to the FSDT are 0.90% (SRSR) and 3.52% (SFSR), which occur at $b/t=100$. The CF solutions show small deviations of 3.93% (SRSR) and 7.67% (SFSR) with respect to the Lévy-type solution. In the context of FSDT, the buckling behaviour of the studied cross-ply laminate is very well replicated, as shown in Fig. 5. The comparison of the Lévy-type solution for FSDT with the solution for TSDT gives maximum deviations of $-$ 1.81%; thus, both solutions reflect the buckling behaviour well for all shown b/t ratios. This is in contrast to the CLPT solutions. The different b/t ratios do not affect the CLPT solution in the non-dimensional diagram in Fig. 5. As indicated in the upper magnification of Fig. 5, the CLPT lines are exactly on top of each other. This leads to a significant overestimation of the critical load for decreasing b/t ratios. For $b/t=5$ the deviations of the CLPT with respect to FSDT are 228.13% (SRSR) and 32.64% (SFSR). In comparison, the CLPT solutions for thin-walled laminates ($b/t=100$) show very good results; the maximum deviation is 0.62%.

Results for an angle-ply laminate are shown in Fig. 6. The comparison between the FEA and the Lévy-type solution within the framework of FSDT shows deviations of $-$ 0.67% (SRSR) and $-$ 0.15% (SFSR). The CF solution shows significantly larger deviations of 9.22% (SRSR) and 40.46% (SFSR). Considering that the CF solutions are mainly used for preliminary design and optimisation, they offer appropriate results for the SRSR plates. In the case of SFSR angle-ply laminates, it may be necessary to use other analysis methods such as the Lévy-type solution. The comparison between the FSDT and TSDT Lévy-type solution is in good agreement as well; the deviations are between $-$ 1.12% and 1.57%. The CLPT, as previously noted, significantly overestimates the buckling load for thick-walled laminates ($b/t=5$) by 314.93% (SRSR) and 81.23% (SFSR).

Based on the results from Figs. 5 and 6 the CF approximate solution shows deviations from the Lévy-type solution and especially for the angle-ply laminates are partly very large. With high demands on the quality of the results, the Lévy-type solutions offer an excellent solution in the field of analytical methods.

5.4 Investigation of the layer repetitions and the ply angle

The material properties of the investigated single layer can be taken from the previous section. Due to the newly derived boundary conditions regarding the rotational elastic restraint in the framework of TSDT, this section focuses on the TSDT solution. The FSDT Lévy-type solution shows comparable results to the TSDT Lévy-type solution anyway and the CLPT clearly overestimates the buckling load for the relative widths considered.

To investigate the ply repetitions n, a ${\left[ (0^{\circ }/90^{\circ })_n\right] }$ laminate is studied in Fig. 7. Considering first the stiffness matrix $S_{ij}$, see Eq. (7), only the coupling stiffnesses $B_{ij}$ and $E_{ij}$ depend on n. These decrease with increasing n. For the case ${n=\infty }$ these are set to zero. In Fig. 7, a good agreement of the non-dimensional buckling load from the FEA and Lévy-TSDT solution is observed with respect to the aspect ratio a/b. For the case ${n=1}$ the largest deviations of $-$ 3.71% (SRSR) and $-$ 3.02% (SFSR) are observed. These decrease with increasing n to $-$ 0.84% and $-$ 0.34%, respectively.

The angle-ply laminate ${\left[ (\theta /-\theta )_n\right] }$ is investigated with respect to the ply repetitions n and the fibre angle $\theta$ under an axial compressive load. For all angles, a good agreement of the non-dimensional buckling load between FEA and Lévy-TSDT solutions in Fig. 8 is observed. As already noted for the cross-ply laminate from Fig. 7, the largest deviations for the angle-ply laminate are also found in the case of ${n=1}$ and take the values $-$ 3.82% (SRSR, $\theta =50^{\circ }$) and $-$ 2.21% (SFSR, $\theta =15^{\circ }$). These decrease with increasing n to $-$ 1.18% and $-$ 0.20%, respectively.

In Figs. 5, 6, 7 and 8, a very good agreement of the FEA and Lévy-FSDT as well as Lévy-TSDT can be shown. Particularly, the good agreement of the Lévy-TSDT solution shows that the newly presented boundary condition for the rotational elastic restraint can be applied in the whole stiffness range. It is important to emphasise that with the selected boundary conditions within the framework of the TSDT, the simple support and the fixed clamping can be controlled by means of the stiffness values $k_0$ and $k_b$, respectively.

6 Conclusion

In this paper, it is shown that the Lévy-type solution adequately describes the buckling behaviour of unsymmetric laminates with rotational restraints. The present study presents the outstanding Lévy-type solutions for stability analysis. In addition, the further Lévy-type solutions for unsymmetric laminates are presented in a consistent and compact notation, which facilitates their application.

The result shows a very good agreement of the buckling load between FEA and Lévy-FSDT as well as Lévy-TSDT. The Lévy-CLPT solution significantly overestimates the critical load for small relative widths, as expected. Concerning the layer repetitions, there is also a good agreement between the Lévy-type solution and the FEA for the cross-ply and angle-ply laminate, which decreases with an increasing number of layers. The angle-ply laminate also shows very good agreement with respect to the ply angle. The comparison between Lévy-type and FE solutions shows that the Lévy-type solution produces plausible results. However, the Lévy solution provides the exact solution to the problem and, for the cases mentioned, a higher-quality result than the FEA. Furthermore, the boundary conditions of the rotational elastic restraint are discussed and those of the TSDT are new formulated. Particularly, the good agreement of the Lévy-TSDT solution shows that the presented boundary condition for the rotational restraint can be applied in the whole stiffness range and provides reliable results. It is important to emphasise that with the selected boundary conditions, a simple support and a fixed clamping can be represented by means of the restraint stiffness values.

For the presented Lévy-type solutions, a solution strategy is developed, which makes it possible to design the methods robustly and computationally efficient and highly accurate at the same time.

The comparison with the closed-analytical method, which is the starting point for the Lévy-type solution, shows very good agreement for cross-ply laminates. In the case of angle-ply laminates, greater deviations of the CF solution can be observed in some cases. Here, the Lévy-type solutions provide a useful supplement. The Lévy solution is to be preferred for high accuracy requirements.

Appendices

Appendix A: Coefficients of ordinary differential equations

1.1 A.1: CLPT cross-ply laminate

To represent the ordinary differential equation of a cross-ply laminate, the following abbreviations are used within the CLPT (as in Eq. (39)), which further include abbreviations from Eq. (A7):

$$\begin{aligned} c_{1}=\,&-{\frac{k_{1}}{k_{2}}},\quad c_{2}=-{\frac{k_{3}}{k_{2}}},\quad c_{3}=-{\frac{k_{4}}{k_{2}}},\quad c_{4}=-{\frac{k_{5}}{k_{2}}},\nonumber \\ c_{5}=\,&{\frac{k_{3}}{k_{7}}},\quad c_{6}=-{\frac{k_{6}}{k_{7}}},\quad c_{7}=-{\frac{k_{8}}{k_{7}}},\quad c_{8}=-{\frac{k_{9}}{k_{7}}},\nonumber \\ c_{9}=\,&{\frac{k_{1}\,k_{3}\,k_{9}-k_{1}\,k_{5}\,k_{7}+k_{4}\,k_{7}\,k_{2}}{ \left( k_{7}\,k_{12}-{k_{9}}^{2} \right) k_{2}}} ,\nonumber \\ c_{10}=\,&{\frac{k_{2}\,k_{6}\,k_{9}-k_{2}\,k_{7}\,k_{8}+{k_{3}}^{2}k_{9}-k_{3} \,k_{5}\,k_{7}}{ \left( k_{7}\,k_{12}-{k_{9}}^{2} \right) k_{2}}},\nonumber \\ c_{11}=\,&{\frac{-k_{10}\,k_{7}\,k_{2}+k_{3}\,k_{4}\,k_{9}-k_{4}\,k_{5}\,k_{7} }{ \left( k_{7}\,k_{12}-{k_{9}}^{2} \right) k_{2}}} ,\nonumber \\ c_{12}=\,&{\frac{-k_{11}\,k_{2}\,k_{7}+k_{2}\,k_{8}\,k_{9}+k_{3}\,k_{5}\,k_{9}- {k_{5}}^{2}k_{7}}{ \left( k_{7}\,k_{12}-{k_{9}}^{2} \right) k_{2}}}. \end{aligned}$$

(A1)

1.2 A.2: CLPT angle-ply laminate

The representation of the ordinary differential equation of an angle-ply laminate in the context of CLPT (as in Eq. (43)) contains the following abbreviations, which again include the abbreviations from Eq. (A7):

$$\begin{aligned} c_{1}=\,&-{\frac{k_{1}}{k_{2}}},\quad c_{2}={\frac{k_{3}}{k_{2}}},\quad c_{3}=-{\frac{k_{13}}{k_{2}}},\quad c_{4}=-{\frac{k_{14}}{k_{2}}},\nonumber \\ c_{5}=\,&-{\frac{k_{3}}{k_{7}}},\quad c_{6}=-{\frac{k_{6}}{k_{7}}},\quad c_{7}=-{\frac{k_{15}}{k_{7}}},\quad c_{8}=-{\frac{k_{16}}{k_{7}}},\nonumber \\ c_{9}=\,&{\frac{k_{1}\,k_{14}\,k_{7}-k_{13}\,k_{2}\,k_{7}+k_{14}\,{k_{3}}^{2}- k_{16}\,k_{2}\,k_{3}}{ \left( k_{2}\,k_{12}-{k_{14}}^{2} \right) k_{7}}},\nonumber \\ c_{10}=\,&{\frac{k_{14}\,k_{3}\,k_{6}+k_{15}\,k_{2}\,k_{7}-k_{16}\,k_{2}\,k_{6}}{ \left( k_{2}\,k_{12}-{k_{14}}^{2} \right) k_{7}}},\nonumber \\ c_{11}=\,&{\frac{-k_{10}\,k_{2}\,k_{7}+k_{14}\,k_{15}\,k_{3}-k_{15}\,k_{16}\,k_ {2}}{ \left( k_{2}\,k_{12}-{k_{14}}^{2} \right) k_{7}}},\nonumber \\ c_{12}=\,&{\frac{-k_{11}\,k_{2}\,k_{7}+k_{13}\,k_{14}\,k_{7}+k_{14}\,k_{16}\,k_ {3}-{k_{16}}^{2}k_{2}}{ \left( k_{2}\,k_{12}-{k_{14}}^{2} \right) k_{7}}}. \end{aligned}$$

(A2)

1.3 A.3: FSDT cross-ply laminate

The representation of the ordinary differential equation of a cross-ply laminate in the framework of FSDT (as in Eq. (45)) contains the following abbreviations, which again include the abbreviations from Eq. (A7):

$$\begin{aligned} c_{1}=\,&{\frac{k_{1}\,k_{26}-k_{17}\,k_{18}}{{k_{18}}^{2}-k_{2}\,k_{26}}},\quad c_{2}={\frac{-k_{18}\,k_{19}+k_{26}\,k_{3}}{{k_{18}}^{2}-k_{2}\,k_{26}}},\nonumber \\ c_{3}=\,&{\frac{k_{23}\,k_{18}}{{k_{18}}^{2}-k_{2}\,k_{26}}},\quad c_{4}={\frac{k_{17}\,k_{26}-k_{18}\,k_{25}}{{k_{18}}^{2}-k_{2}\,k_{26}}},\nonumber \\ c_{5}=\,&{\frac{-k_{18}\,k_{27}+k_{19}\,k_{26}}{{k_{18}}^{2}-k_{2}\,k_{26}}},\quad c_{6}={\frac{k_{12}\,k_{3}+k_{19}\,k_{9}}{k_{7}\,k_{12}-{k_{9}}^{2}}},\nonumber \\ c_{7}=\,&{\frac{-k_{12}\,k_{6}-k_{20}\,k_{9}}{k_{7}\,k_{12}-{k_{9}}^{2}}},\quad c_{8}=-{\frac{k_{24}\,k_{9}}{k_{7}\,k_{12}-{k_{9}}^{2}}},\nonumber \\ c_{9}=\,&{\frac{k_{12}\,k_{19}+k_{27}\,k_{9}}{k_{7}\,k_{12}-{k_{9}}^{2}}},\quad c_{10}={\frac{-k_{12}\,k_{20}-k_{28}\,k_{9}}{k_{7}\,k_{12}-{k_{9}}^{2}}},\nonumber \\ c_{11}=\,&-{\frac{k_{21}}{k_{22}}},\quad c_{12}=-{\frac{k_{23}}{k_{22}}},\quad c_{13}=-{\frac{k_{24}}{k_{22}}},\nonumber \\ c_{14}=\,&{\frac{-k_{1}\,k_{18}+k_{17}\,k_{2}}{{k_{18}}^{2}-k_{2}\,k_{26}}},\quad c_{15}={\frac{-k_{18}\,k_{3}+k_{19}\,k_{2}}{{k_{18}}^{2}-k_{2}\,k_{26}}},\nonumber \\ c_{16}=\,&{\frac{k_{2}\,k_{23}}{-{k_{18}}^{2}+k_{2}\,k_{26}}},\quad c_{17}={\frac{-k_{17}\,k_{18}+k_{2}\,k_{25}}{{k_{18}}^{2}-k_{2}\,k_{26}}},\nonumber \\ c_{18}=\,&{\frac{-k_{18}\,k_{19}+k_{2}\,k_{27}}{{k_{18}}^{2}-k_{2}\,k_{26}}},\quad c_{19}={\frac{k_{19}\,k_{7}+k_{3}\,k_{9}}{k_{7}\,k_{12}-{k_{9}}^{2}}},\nonumber \\ c_{20}=\,&{\frac{-k_{20}\,k_{7}-k_{6}\,k_{9}}{k_{7}\,k_{12}-{k_{9}}^{2}}},\quad c_{21}=-{\frac{k_{24}\,k_{7}}{k_{7}\,k_{12}-{k_{9}}^{2}}},\nonumber \\ c_{22}=\,&{\frac{k_{19}\,k_{9}+k_{27}\,k_{7}}{k_{7}\,k_{12}-{k_{9}}^{2}}},\quad c_{23}={\frac{-k_{20}\,k_{9}-k_{28}\,k_{7}}{k_{7}\,k_{12}-{k_{9}}^{2}}}. \end{aligned}$$

(A3)

1.4 A.4: FSDT angle-ply laminate

The representation of the ordinary differential equation of an angle-ply laminate in the framework of FSDT (as in Eq. (48)) contains the following abbreviations, which again include the abbreviations from Eq. (A7):

$$\begin{aligned} c_{1}=\,&{\frac{-k_{1}\,k_{12}-k_{14}\,k_{30}}{k_{2}\,k_{12}-{k_{14}}^{2}}},\quad c_{2}={\frac{k_{12}\,k_{3}+k_{14}\,k_{31}}{k_{2}\,k_{12}-{k_{14}}^{2}}},\nonumber \\ c_{3}=\,&-{\frac{k_{24}\,k_{14}}{k_{2}\,k_{12}-{k_{14}}^{2}}},\quad c_{4}={\frac{-k_{12}\,k_{29}+k_{14}\,k_{27}}{k_{2}\,k_{12}-{k_{14}}^{2}}},\nonumber \\ c_{5}=\,&{\frac{-k_{12}\,k_{30}-k_{14}\,k_{28}}{k_{2}\,k_{12}-{k_{14}}^{2}}},\quad c_{6}={\frac{-k_{14}\,k_{29}+k_{26}\,k_{3}}{{k_{14}}^{2}-k_{7}\,k_{26}}},\nonumber \\ c_{7}=\,&{\frac{k_{14}\,k_{30}+k_{26}\,k_{6}}{{k_{14}}^{2}-k_{7}\,k_{26}}},\quad c_{8}={\frac{k_{23}\,k_{14}}{-{k_{14}}^{2}+k_{7}\,k_{26}}},\nonumber \\ c_{9}=\,&{\frac{k_{14}\,k_{25}+k_{26}\,k_{30}}{{k_{14}}^{2}-k_{7}\,k_{26}}},\quad c_{10}={\frac{k_{14}\,k_{27}+k_{26}\,k_{31}}{{k_{14}}^{2}-k_{7}\,k_{26}}},\nonumber \\ c_{11}=\,&-{\frac{k_{21}}{k_{22}}},\quad c_{12}=-{\frac{k_{23}}{k_{22}}},\quad c_{13}=-{\frac{k_{24}}{k_{22}}},\nonumber \\ c_{14}=\,&{\frac{k_{14}\,k_{3}-k_{29}\,k_{7}}{{k_{14}}^{2}-k_{7}\,k_{26}}},\quad c_{15}={\frac{k_{14}\,k_{6}+k_{30}\,k_{7}}{{k_{14}}^{2}-k_{7}\,k_{26}}},\nonumber \\ c_{16}=\,&{\frac{k_{23}\,k_{7}}{-{k_{14}}^{2}+k_{7}\,k_{26}}},\quad c_{17}={\frac{k_{14}\,k_{30}+k_{25}\,k_{7}}{{k_{14}}^{2}-k_{7}\,k_{26}}},\nonumber \\ c_{18}=\,&{\frac{k_{14}\,k_{31}+k_{27}\,k_{7}}{{k_{14}}^{2}-k_{7}\,k_{26}}},\quad c_{19}={\frac{-k_{1}\,k_{14}-k_{2}\,k_{30}}{k_{2}\,k_{12}-{k_{14}}^{2}}},\nonumber \\ c_{20}=\,&{\frac{k_{14}\,k_{3}+k_{2}\,k_{31}}{k_{2}\,k_{12}-{k_{14}}^{2}}},\quad c_{21}=-{\frac{k_{2}\,k_{24}}{k_{2}\,k_{12}-{k_{14}}^{2}}},\nonumber \\ c_{22}=\,&{\frac{-k_{14}\,k_{29}+k_{2}\,k_{27}}{k_{2}\,k_{12}-{k_{14}}^{2}}},\quad c_{23}={\frac{-k_{14}\,k_{30}-k_{2}\,k_{28}}{k_{2}\,k_{12}-{k_{14}}^{2}}}. \end{aligned}$$

(A4)

1.5 A.5: TSDT cross-ply laminate

The representation of the ordinary differential equation of an angle-ply laminate in the framework of FSDT (as in Eq. (50)) contains the following abbreviations, which again include the abbreviations from Eq. (A7):

$$\begin{aligned} c_{1}=\,&{\frac{-k_{1}\,k_{49}+k_{34}\,k_{35}}{k_{2}\,k_{49}-{k_{35}}^{2}}},\quad c_{2}={\frac{-k_{3}\,k_{49}+k_{35}\,k_{36}}{k_{2}\,k_{49}-{k_{35}}^{2}}},\nonumber \\ c_{3}=\,&{\frac{-k_{32}\,k_{49}-k_{35}\,k_{44}}{k_{2}\,k_{49}-{k_{35}}^{2}}},\quad c_{4}={\frac{-k_{33}\,k_{49}-k_{35}\,k_{45}}{k_{2}\,k_{49}-{k_{35}}^{2}}},\nonumber \\ c_{5}=\,&{\frac{-k_{34}\,k_{49}+k_{35}\,k_{48}}{k_{2}\,k_{49}-{k_{35}}^{2}}},\quad c_{6}={\frac{k_{35}\,k_{50}-k_{36}\,k_{49}}{k_{2}\,k_{49}-{k_{35}}^{2}}},\nonumber \\ c_{7}=\,&{\frac{-k_{3}\,k_{52}+k_{36}\,k_{40}}{{k_{40}}^{2}-k_{7}\,k_{52}}},\quad c_{8}={\frac{-k_{39}\,k_{40}+k_{52}\,k_{6}}{{k_{40}}^{2}-k_{7}\,k_{52}}},\nonumber \\ c_{9}=\,&{\frac{k_{37}\,k_{52}-k_{40}\,k_{46}}{{k_{40}}^{2}-k_{7}\,k_{52}}},\quad c_{10}={\frac{k_{38}\,k_{52}-k_{40}\,k_{47}}{{k_{40}}^{2}-k_{7}\,k_{52}}},\nonumber \\ c_{11}=\,&{\frac{-k_{36}\,k_{52}+k_{40}\,k_{50}}{{k_{40}}^{2}-k_{7}\,k_{52}}},\quad c_{12}={\frac{k_{39}\,k_{52}-k_{40}\,k_{51}}{{k_{40}}^{2}-k_{7}\,k_{52}}},\nonumber \\ c_{13}=\,&{\frac{ \left( -c_{11}\,k_{38}-c_{29}\,k_{47}-k_{45} \right) c_{19} -c_{1}\,c_{7}\,k_{38}}{c_{10}\,k_{38}+c_{28}\,k_{47}+k_{43}}}\nonumber \\&+{\frac{ -c_{1}\,c_{25}\,k_{47}+c_{1}\,k_{33}+k_{32}}{c_{10} \,k_{38}+c_{28}\,k_{47}+k_{43}}},\nonumber \\ c_{14}=\,&{\frac{ \left( -c_{11}\,c_{20}-c_{2}\,c_{7}-c_{8} \right) k_{38}+ \left( -c_{2}\,c_{25}-c_{20}\,c_{29}-c_{26} \right) k_{47}}{c_{10}\,k_{38}+c_{28}\,k_{47}+k_{43}}} \nonumber \\&{\frac{ +c_{2}\,k_{33}-c_{20}\,k_{45}-k_{37}}{c_{10}\,k_{38}+c_{28}\,k_{47}+k_{43}}},\nonumber \\ c_{15}=\,&{\frac{ \left( -c_{11}\,k_{38}-c_{29}\,k_{47}-k_{45} \right) c_{21} -c_{3}\,c_{7}\,k_{38}}{c_{10}\,k_{38}+c_{28}\,k_{47}+k_{43}}}\nonumber \\&+{\frac{ -c_{25}\,c_{3}\,k_{47}+c_{3}\,k_{33}-k_{41}}{c_{10} \,k_{38}+c_{28}\,k_{47}+k_{43}}},\nonumber \\ c_{16}=\,&{\frac{ \left( -c_{11}\,c_{22}-c_{4}\,c_{7}-c_{9} \right) k_{38}+ \left( -c_{22}\,c_{29}-c_{25}\,c_{4}-c_{27} \right) k_{47}}{c_{10}\,k_{38}+c_{28}\,k_{47}+k_{43}}}\nonumber \\&+{\frac{ +k_{33}\,c_{4}-k_{45}\,c_{22}-k_{42} }{c_{10}\,k_{38}+c_{28}\,k_{47}+k_{43}}},\nonumber \\ c_{17}=\,&{\frac{ \left( -c_{11}\,k_{38}-c_{29}\,k_{47}-k_{45} \right) c_{23}-c _{5}\,c_{7}\,k_{38}}{c_{10}\,k_{38}+c_{28}\,k_{47}+k_{43}}}\nonumber \\&+{\frac{ -c_{25}\,c_{5}\,k_{47}+c_{5}\,k_{33}-k_{44}}{c_{10}\,k_{38}+c_{28}\,k_{47}+k_{43}}} ,\nonumber \\ c_{18}=\,&{\frac{ \left( -c_{11}\,c_{24}-c_{6}\,c_{7}-c_{12} \right) k_{38}+ \left( -c_{24}\,c_{29}-c_{25}\,c_{6}-c_{30} \right) k_{47}}{c_{10}\,k_{38}+c_{28}\,k_{47}+k_{43}}} \nonumber \\&+{\frac{ +c_{6}\,k_{33}-c_{24}\,k_{45}-k_{46}}{c_{10}\,k_{38}+c_{28}\,k_{47}+k_{43}}},\nonumber \\ c_{19}=\,&{\frac{k_{1}\,k_{35}-k_{2}\,k_{34}}{k_{2}\,k_{49}-{k_{35}}^{2}}},\quad c_{20}={\frac{-k_{2}\,k_{36}+k_{3}\,k_{35}}{k_{2}\,k_{49}-{k_{35}}^{2}}},\nonumber \\ c_{21}=\,&{\frac{k_{2}\,k_{44}+k_{32}\,k_{35}}{k_{2}\,k_{49}-{k_{35}}^{2}}},\quad c_{22}={\frac{k_{2}\,k_{45}+k_{33}\,k_{35}}{k_{2}\,k_{49}-{k_{35}}^{2}}},\nonumber \\ c_{23}=\,&{\frac{-k_{2}\,k_{48}+k_{34}\,k_{35}}{k_{2}\,k_{49}-{k_{35}}^{2}}},\quad c_{24}={\frac{-k_{2}\,k_{50}+k_{35}\,k_{36}}{k_{2}\,k_{49}-{k_{35}}^{2}}},\nonumber \\ c_{25}=\,&{\frac{k_{3}\,k_{40}-k_{36}\,k_{7}}{{k_{40}}^{2}-k_{7}\,k_{52}}},\quad c_{26}={\frac{k_{39}\,k_{7}-k_{40}\,k_{6}}{{k_{40}}^{2}-k_{7}\,k_{52}}},\nonumber \\ c_{27}=\,&{\frac{-k_{37}\,k_{40}+k_{46}\,k_{7}}{{k_{40}}^{2}-k_{7}\,k_{52}}},\quad c_{28}={\frac{-k_{38}\,k_{40}+k_{47}\,k_{7}}{{k_{40}}^{2}-k_{7}\,k_{52}}},\nonumber \\ c_{29}=\,&{\frac{k_{36}\,k_{40}-k_{50}\,k_{7}}{{k_{40}}^{2}-k_{7}\,k_{52}}},\quad c_{30}={\frac{-k_{39}\,k_{40}+k_{51}\,k_{7}}{{k_{40}}^{2}-k_{7}\,k_{52}}}. \end{aligned}$$

(A5)

1.6 A.6: TSDT angle-ply laminate

The representation of the ordinary differential equation of an angle-ply laminate in the context of FSDT (as in Eq. (53)) contains the following abbreviations, which again include the abbreviations from Eq. (A7):

$$\begin{aligned} c_{1}=\,&{\frac{-k_{1}\,k_{52}+k_{56}\,k_{57}}{k_{2}\,k_{52}-{k_{57}}^{2}}},\quad c_{2}={\frac{k_{3}\,k_{52}-k_{57}\,k_{60}}{k_{2}\,k_{52}-{k_{57}}^{2}}},\nonumber \\ c_{3}=\,&{\frac{k_{46}\,k_{57}-k_{52}\,k_{53}}{k_{2}\,k_{52}-{k_{57}}^{2}}},\quad c_{4}={\frac{k_{47}\,k_{57}-k_{52}\,k_{54}}{k_{2}\,k_{52}-{k_{57}}^{2}}},\nonumber \\ c_{5}=\,&{\frac{-k_{50}\,k_{57}-k_{52}\,k_{55}}{k_{2}\,k_{52}-{k_{57}}^{2}}},\quad c_{6}={\frac{k_{51}\,k_{57}-k_{52}\,k_{56}}{k_{2}\,k_{52}-{k_{57}}^{2}}},\nonumber \\ c_{7}=\,&{\frac{-k_{3}\,k_{49}-k_{55}\,k_{57}}{k_{7}\,k_{49}-{k_{57}}^{2}}},\quad c_{8}={\frac{-k_{49}\,k_{6}+k_{56}\,k_{57}}{k_{7}\,k_{49}-{k_{57}}^{2}}},\nonumber \\ c_{9}=\,&{\frac{-k_{44}\,k_{57}-k_{49}\,k_{58}}{k_{7}\,k_{49}-{k_{57}}^{2}}},\quad c_{10}={\frac{-k_{45}\,k_{57}-k_{49}\,k_{59}}{k_{7}\,k_{49}-{k_{57}}^{2}}},\nonumber \\ c_{11}=\,&{\frac{k_{48}\,k_{57}-k_{49}\,k_{56}}{k_{7}\,k_{49}-{k_{57}}^{2}}},\quad c_{12}={\frac{-k_{49}\,k_{60}+k_{50}\,k_{57}}{k_{7}\,k_{49}-{k_{57}}^{2}}},\nonumber \\ c_{13}=\,&{\frac{ \left( -c_{19}\,c_{29}-c_{26}\,c_{7}-c_{25} \right) k_{47}+ \left( -c_{19}\,c_{5}-c_{2}\,c_{7}-c_{1} \right) k_{54}}{c_{28}\,k_{47}+c_{4}\,k_{54}+k_{43}}}\nonumber \\&+{\frac{ -c_{19}\,k_{45}+c_{7}\,k_{59}-k_{53}}{c_{28}\,k_{47}+c_{4}\,k_{54}+k_{43}}} ,\nonumber \\ c_{14}=\,&{\frac{ \left( -c_{29}\,k_{47}-c_{5}\,k_{54}-k_{45} \right) c_{20}-c_{2}\,c_{8}\,k_{54}}{c_{28} \,k_{47}+c_{4}\,k_{54}+k_{43}}}\nonumber \\&+{\frac{ -c_{26}\,c_{8}\,k_{47}+c_{8}\,k_{59}+k_{58}}{c_{28}\,k_{47}+c_{4}\,k_{54}+k_{43}}},\nonumber \\ c_{15}=\,&{\frac{ \left( -c_{29}\,k_{47}-c_{5}\,k_{54}-k_{45} \right) c_{21}-c_ {2}\,c_{9}\,k_{54}}{c_{28}\,k_{47}+c_{4}\,k_{54}+k_{43}}}\nonumber \\&+{\frac{-c_{26}\,c_{9}\,k_{47}+c_{9}\,k_{59}-k_{41}}{c_{28}\,k_{47}+c_{4}\,k_{54}+k_{43}}},\nonumber \\ c_{16}=\,&{\frac{ \left( -c_{10}\,c_{26}-c_{22}\,c_{29}-c_{27} \right) k_{47}+ \left( -c_{10}\,c_{2}-c_{22}\,c_{5}-c_{3} \right) k_{54}}{c_{28}\,k_{47}+c_{4}\,k_{54}+k_{43}}}\nonumber \\&+{\frac{-c_{22}\,k_{45}+c_{10}\,k_{59}-k_{42}}{c_{28}\,k_{47}+c_{4}\,k_{54}+k_{43}}},\nonumber \\ c_{17}=\,&{\frac{ \left( -c_{2}\,k_{54}-c_{26}\,k_{47}+k_{59} \right) c_{11}}{c_{28}\,k_{47}+c_{4}\,k_{54}+k_{43}}}\nonumber \\&+{\frac{ +\left( -c_{29}\,k_{47}-c_{5}\,k_{54}-k_{45} \right) c_{23}-k_{44}}{c_{28}\,k_{47}+c_{4}\,k_{54}+k_{43}}},\nonumber \\ c_{18}=\,&{\frac{ \left( -c_{12}\,c_{26}-c_{24}\,c_{29}-c_{30} \right) k_{47}+ \left( -c_{12}\,c_{2}-c_{24}\,c_{5}-c_{6} \right) k_{54}}{c_{28}\,k_{47}+c_{4}\,k_{54}+k_{43}}}\nonumber \\&+{\frac{ -c_{24}\,k_{45}+c_{12}\,k_{59}-k_{46}}{c_{28}\,k_{47}+c_{4}\,k_{54}+k_{43}}},\nonumber \\ c_{19}=\,&{\frac{k_{3}\,k_{57}+k_{55}\,k_{7}}{k_{7}\,k_{49}-{k_{57}}^{2}}},\quad c_{20}={\frac{-k_{56}\,k_{7}+k_{57}\,k_{6}}{k_{7}\,k_{49}-{k_{57}}^{2}}},\nonumber \\ c_{21}=\,&{\frac{k_{44}\,k_{7}+k_{57}\,k_{58}}{k_{7}\,k_{49}-{k_{57}}^{2}}},\quad c_{22}={\frac{k_{45}\,k_{7}+k_{57}\,k_{59}}{k_{7}\,k_{49}-{k_{57}}^{2}}},\nonumber \\ c_{23}=\,&{\frac{-k_{48}\,k_{7}+k_{56}\,k_{57}}{k_{7}\,k_{49}-{k_{57}}^{2}}},\quad c_{24}={\frac{-k_{50}\,k_{7}+k_{57}\,k_{60}}{k_{7}\,k_{49}-{k_{57}}^{2}}},\nonumber \\ c_{25}=\,&{\frac{k_{1}\,k_{57}-k_{2}\,k_{56}}{k_{2}\,k_{52}-{k_{57}}^{2}}},\quad c_{26}={\frac{k_{2}\,k_{60}-k_{3}\,k_{57}}{k_{2}\,k_{52}-{k_{57}}^{2}}},\nonumber \\ c_{27}=\,&{\frac{-k_{2}\,k_{46}+k_{53}\,k_{57}}{k_{2}\,k_{52}-{k_{57}}^{2}}},\quad c_{28}={\frac{-k_{2}\,k_{47}+k_{54}\,k_{57}}{k_{2}\,k_{52}-{k_{57}}^{2}}},\nonumber \\ c_{29}=\,&{\frac{k_{2}\,k_{50}+k_{55}\,k_{57}}{k_{2}\,k_{52}-{k_{57}}^{2}}},\quad c_{30}={\frac{-k_{2}\,k_{51}+k_{56}\,k_{57}}{k_{2}\,k_{52}-{k_{57}}^{2}}}. \end{aligned}$$

(A6)

1.7 A.7: Additional abbreviations

Equations (A1–A6) contain the following abbreviations, wherein ${\beta ={ {m\,\pi }/{a}}}$ and ${{\tau }={4}/{\left( 3\,{t}^{2}\right) }}$:

$$\begin{aligned} k_{1}=\,&-A_{11}\,{\beta }^{2},\quad k_{2}=A_{66},\quad k_{3}= \left( A_{12}+A_{66} \right) \beta ,\nonumber \\ k_{4}=\,&B_{11}\,{\beta }^{3},\quad k_{5}= -\left( B_{12}+2\,B_{66} \right) \beta ,\quad k_{6}=-A_{66}\,{\beta }^{2},\nonumber \\ k_{7}=\,&A_{22},\quad k_{8}= \left( B_{12}+2\,B_{66} \right) {\beta }^{2},\quad k_{9}=-B_{22},\nonumber \\ k_{10}=\,&D_{11}\,{\beta }^{4}-\xi _xN_\text {cr}\,{\beta }^{2},\quad k_{11}=- \left( 2\,D_{12}+4\,D_{66} \right) {\beta }^{2}+\xi _yN_\text {cr},\nonumber \\ k_{12}=\,&D_{22},\quad k_{13}=3\,B_{16}\,{\beta }^{2},\quad k_{14}=-B_{26},\quad k_{15}=B_{16}\,{\beta }^{3},\nonumber \\ k_{16}=\,&-3\,B_{26}\,\beta ,\quad k_{17}=-B_{11}\,{\beta }^{2},\quad k_{18}=B_{66},\nonumber \\ k_{19}=\,&\left( B_{12}+B_{66} \right) \beta ,\quad k_{20}=-B_{66}\,{\beta }^{2},\nonumber \\ k_{21}=\,&\left( KA_{55}-\xi _xN_\text {cr} \right) {\beta }^{2},\quad k_{22}=-KA_{44}+\xi _yN_\text {cr},\nonumber \\ k_{23}=\,&A_{55}\,K\beta ,\quad k_{24}=-KA_{44},\quad k_{25}=-D_{11}\,{\beta }^{2}-KA_{55},\nonumber \\ k_{26}=\,&D_{66},\quad k_{27}= \left( D_{12}+D_{66} \right) \beta ,\quad k_{28}=-D_{66}\,{\beta }^{2}-KA_{44},\nonumber \\ k_{29}=\,&-2\,B_{16}\,\beta ,\quad k_{30}=-B_{16}\,{\beta }^{2},\quad k_{31}=2\,B_{26}\,\beta ,\nonumber \\ k_{32}=\,&E_{11}\,{\beta }^{3}\tau ,\quad k_{33}=- \left( E_{12}+2\,E_{66} \right) \beta \,\tau ,\nonumber \\ k_{34}=\,&\left( E_{11}\,\tau -B_{11} \right) {\beta }^{2},\quad k_{35}=-E_{66}\,\tau +B_{66},\nonumber \\ k_{36}=\,&\left( - \left( E_{66}+E_{12} \right) \tau +B_{12}+B_{66} \right) \beta ,\nonumber \\ k_{37}=\,&\left( E_{12}+2\,E_{66} \right) {\beta }^{2}\tau ,\quad k_{38}=-\tau \,E_{22},\nonumber \\ k_{39}=\,&\left( E_{66}\,\tau -B_{66} \right) {\beta }^{2},\quad k_{40}=-\tau \,E_{22}+B_{22},\nonumber \\ k_{41}=\,&H_{11}\,{\tau }^{2}{\beta }^{4}+ \left( 9\,F_{55}\,{\tau }^{2}-6\,D_{55} \,\tau +A_{55}-\xi _xN_\text {cr} \right) {\beta }^{2},\nonumber \\ k_{42}=\,&-2\,{\tau }^{2} \left( H_{12}+2\,H_{66} \right) {\beta }^{2}-9\,F_{44}\, {\tau }^{2}+6\,D_{44}\,\tau -A_{44}+\xi _yN_\text {cr},\nonumber \\ k_{43}=\,&H_{22}\,{\tau }^{2},\nonumber \\ k_{44}=\,&\tau \, \left( H_{11}\,\tau -F_{11} \right) {\beta }^{3}+ \left( 9\, F_{55}\,{\tau }^{2}-6\,D_{55}\,\tau +A_{55} \right) \beta ,\nonumber \\ k_{45}=\,&- \left( \left( H_{12}+2\,H_{66} \right) \tau -F_{12}-2\,F_{66}\right) \tau \,\beta ,\nonumber \\ k_{46}=\,&- \left( \left( H_{12}+2\,H_{66} \right) \tau -F_{12}-2\,F_{66} \right) \tau \,{\beta }^{2}-9\,F_{44}\,{\tau }^{2}\nonumber \\&+6\,D_{44}\,\tau -A_{44},\quad k_{47}=\tau \, \left( H_{22}\,\tau -F_{22} \right) ,\nonumber \\ k_{48}=\,&- \left( H_{11}\,{\tau }^{2}-2\,F_{11}\,\tau +D_{11} \right) {\beta }^{2} -9\,F_{55}\,{\tau }^{2}+6\,D_{55}\,\tau -A_{55},\nonumber \\ k_{49}=\,&H_{66}\,{\tau }^{2}-2\,F_{66}\,\tau +D_{66},\nonumber \\ k_{50}=\,&\left( \left( H_{12}+H_{66} \right) {\tau }^{2} - \left( 2\,F_ {12}+2\,F_{66} \right) \tau +D_{12}+D_{66} \right) \beta ,\nonumber \\ k_{51}=\,&- \left( H_{66}\,{\tau }^{2}-2\,F_{66}\,\tau +D_{66} \right) {\beta }^{2} -9\,F_{44}\,{\tau }^{2}+6\,D_{44}\,\tau -A_{44},\nonumber \\ k_{52}=\,&H_{22}\,{\tau }^{2}-2\,F_{22}\,\tau +D_{22},\quad k_{53}=3\,E_{16}\,{\beta }^{2}\tau ,\nonumber \\ k_{54}=\,&-E_{26}\,\tau ,\quad k_{55}= \left( 2\,E_{16}\,\tau -2\,B_{16} \right) \beta ,\nonumber \\ k_{56}=\,&\left( E_{16}\,\tau -B_{16} \right) {\beta }^{2},\quad k_{57}=-E_{26}\,\tau +B_{26},\nonumber \\ k_{58}=\,&E_{16}\,{\beta }^{3}\tau ,\quad k_{59}=-3\,E_{26}\,\beta \,\tau ,\nonumber \\ k_{60}=\,&\left( -2\,E_{26}\,\tau +2\,B_{26} \right) \beta . \end{aligned}$$

(A7)

Appendix B Solution strategies

The following solution strategies are extracted from [42]. The eigenvalue analysis of the matrix $\underline{\underline{C}}$ is difficult from a numerical point of view. The following procedure provides a workaround to avoid the difficult zero entries on the principal diagonal. A constant value c is added to the principal diagonal elements of $\underline{\underline{C}}$:

$$\begin{aligned} \overline{\underline{\underline{C}}} =\underline{\underline{C}}+\begin{bmatrix} c &{}\quad &{}\quad 0 \\ &{}\quad \ddots &{}\quad \\ 0 &{}\quad &{}\quad c \end{bmatrix}. \end{aligned}$$

(B8)

The relation between the eigenvalues is as follows:

$$\begin{aligned} \lambda _{i}=\overline{\lambda }_{i}-c,\quad \text {for}\,\, i=1,..,k. \end{aligned}$$

(B9)

The eigenvectors of $\overline{\underline{\underline{C}}}$ and $\underline{\underline{C}}$ are equal.

Furthermore, $\det (\underline{\underline{M}})$ is often ill-conditioned. Therefore, a procedure is presented which avoids the calculation of $\det (\underline{\underline{M}})$, extracted from [42]. The solution (56) can be expressed with the following substitution: $\overline{\underline{K}}=\underline{\underline{L}}^{-1}\,\underline{K}$ as:

$$\begin{aligned} \underline{Z}^{}(y)=\underline{\underline{L}} \begin{bmatrix} \textrm{e}^{\lambda _{1}y} &{}\quad &{}\quad 0 \\ &{}\quad \ddots &{}\quad \\ 0 &{}\quad &{}\quad \textrm{e}^{\lambda _{k}y} \end{bmatrix} \overline{\underline{K}}. \end{aligned}$$

(B10)

The substitution of this solution into the boundary conditions leads to:

$$\begin{aligned} \overline{\underline{\underline{M}}}\,\overline{\underline{K}}=0. \end{aligned}$$

(B11)

The resubstitution of $\overline{\underline{\underline{M}}}$ into the system of equations (B11) yields:

$$\begin{aligned} \overline{\underline{\underline{M}}}\,\underline{\underline{L}}^{-1}\,\underline{K}\,=0. \end{aligned}$$

(B12)

The non-trivial solution of (B12) is given by:

$$\begin{aligned} \det (\overline{\underline{\underline{M}}}\,\underline{\underline{L}}^{-1})=0, \end{aligned}$$

(B13)

which can be split into:

$$\begin{aligned} \frac{\det (\overline{\underline{\underline{M}}})}{\det (\underline{\underline{L}})}=0. \end{aligned}$$

(B14)

Equation (B14) is the buckling condition for the critical load $N_{\textrm{cr}}$ and produces the same results as condition (58). The shown procedure avoids the calculation of $\underline{\underline{L}}^{-1}$ and calculates the determinant of $\overline{\underline{\underline{M}}}$ and $\underline{\underline{L}}$ which are better conditioned than $\underline{\underline{M}}$.