Reflection of plane waves from the stress-free boundary of a nonlocal elastic solid half-space containing double porosity

Abstract

Reflection phenomena of a set of coupled longitudinal waves/shear wave striking obliquely against the mechanically stress-free boundary surface of a uniform nonlocal elastic solid half-space with double porosity structure have been investigated. Employing the appropriate nonlocal stress-free boundary conditions at the surface, the formulae for reflection coefficients and their corresponding energy ratios have been derived for the dissipative and non-dissipative models. Their variations have been computed against the angle of incidence for a specific model. It is found that all the reflection coefficients depend upon the presence of the nonlocality, porosities of both types, frequency and angle of incidence. Their impact on various coefficients is also studied numerically and depicted graphically.

1 Introduction

The problems of propagation of elastic waves and their reflection/transmission phenomena from the discontinuous boundary surfaces in elastic materials have been of continued interest since long. Elastic waves traveling through the Earth’s medium are called seismic waves, and the subject dealing with the study of these waves is called seismology. Knowing the fact that the Earth is multilayered media made up of different materials possessing different characteristics, seismic waves suffer from reflection and transmission phenomena at the discontinuities between the different layers. These reflected and transmitted waves carry a lot of information about the medium through which they travel. They are also very helpful in the exploration of Earth’s interior and valuable deposits beneath the earth surface like minerals, oils and hydrocarbons, etc. The reflection/transmission phenomena of elastic waves find applications in the field of geophysics, earthquake engineering, seismology, etc. The literature pertaining to the reflection and transmission phenomena of elastic waves from the boundary surfaces in classical elastic media is available in abundance, for example, see Ewing et al. [1], Achenbach [2], Aki and Richards [3], among several others. Around 1980s, the classical elastic theory was extended to the theory of elastic materials with voids by Cowin and his co-worker [4, 5]. An elastic material with voids is a porous material, whose skeletal or matrix material is elastic and the voids are vacuous pores containing nothing of mechanical or energetic significance, but occupy certain surface area and volume. The bulk density of the material is written as a product of the density of the matrix material and the void volume fractional field. In this theory, the deformation involves the strain field related to matrix material along with the change in void volume fractional field associated with the voids of the medium. The change in void volume fraction is introduced as an independent additional kinematic variable along with an associated force termed as “equilibrated stress.” Incorporating void volume fraction and the associated force, the constitutive relations and field equations for homogeneous isotropic elastic material with voids were developed. Using this theory, Puri and Cowin [6] explored the possibility of plane wave propagation in an infinite elastic material with voids and found that there may exist three plane waves propagating with distinct speeds. Two of them are coupled dilatational waves influenced by the presence of voids, while the remaining one is an independent transverse wave, which is no different from the classical shear wave. Ciarletta and Sumbatyan [7] investigated the reflection phenomena of incident coupled longitudinal waves/shear wave from the stress-free boundary of an elastic half-space with voids. Ieşan [8] extended the theory of elastic material with voids to thermoelastic material with voids by incorporating the theory of coupled thermoelasticity. Later, Ieşan and Quintanilla [9] developed the nonlinear and linear theories of thermoelastic materials possessing double porosity structure and presented the field equations for homogeneous isotropic material. Using their theory, Svanadze [10, 11] studied the plane harmonic waves and uniqueness theorems in the theory of rigid/elastic bodies with double porosity structure. He presented the connection between the plane waves, uniqueness of solutions and existence of eigenfrequencies. Singh et al. [12] explored the propagation of plane harmonic waves in an infinite thermoelastic medium with double porosity structure and also studied the reflection of coupled longitudinal waves from the insulated and stress-free boundary surface. Some recent research articles dealing with the theory of elastic solid with single/double voids are attempted by Biswas and Abo-Dahab [13], Long and Fan [14], Kumar and Tomar [15] and De Cicco [16]. The detailed literature about double/multi-porosity continua and its mathematical aspects have been nicely presented in a book by Straughan [17].

In the nonlocal theory of elasticity, introduced by Eringen and his co-worker (see Eringen and Edelen [18] and Eringen [19, 20]), the stresses at a point in the region of a continuum body depend not only on the strains at that point but also on the strains at all its surrounding points by considering the remote action forces between the atoms unlike classical elasticity. It is emphasized that the nonlocal effect becomes more prominent when the external characteristic length (e.g., wavelength, size of the sample) and the internal characteristic length (e.g., the lattice parameter, size of the grain) are comparable while dealing with the problems of waves and vibrations. In nano-materials such as carbon nanotubes, the length scales are sufficiently small and it is found that Eringen’s nonlocal model is most suitable for dealing with such models. Some notable researches based on Eringen’s nonlocal theory of elasticity are contained in Altan [21, 22], Chirita [23], Shaat et al. [24], among several others. Using Eringen’s model of nonlocality, Singh et al. [25] developed the theory of nonlocal elastic materials with voids and derived the field equations. They have also investigated the propagation of plane waves and their reflection from the stress-free boundary surface by using local boundary conditions. They found that all the reflection coefficients are influenced by the presence of nonlocality and presence of voids in the medium. They observed that the reflection coefficients corresponding to the coupled longitudinal waves increase, while the reflection coefficients corresponding to the transverse wave decrease with an increase in the nonlocality parameter of the medium when a set of coupled longitudinal waves is made incident. Several authors [26]–[31] have attempted reflection/transmission of plane waves in nonlocal media to study the effect of nonlocality on reflection/transmission coefficients by using appropriate local boundary conditions. Recently, Kumar et al. [32] developed the theory of nonlocal elastic material with double porosity structure by incorporating additional voids in the theory of nonlocal elastic solid with voids [25]. They have explored the propagation of plane harmonic waves in an infinite nonlocal elastic materials with double porosity structure.

In the present work, we investigated the reflection phenomenon of plane waves from the stress-free boundary surface of a nonlocal elastic half-space having double porosity structure using nonlocal boundary conditions. The reflection coefficients and the corresponding energy ratios are derived when a set of plane coupled longitudinal waves/transverse wave is made incident obliquely at the stress-free surface of the half-space. All the reflection coefficients and corresponding energy ratios are found to be the functions of nonlocality, porosity, elastic properties, frequency and angle of incidence. For a particular numerical model, the effect of various parameters corresponding to voids and nonlocality is studied numerically on the reflection coefficients and depicted graphically. Some reduced cases have been analyzed from the present formulation.

2 Relations and equations

Following Kumar et al. [32], the constitutive relations for nonlocal elastic solid containing double porosity within the context of Eringen’s nonlocal model of elasticity are given by

$$\begin{aligned} \left( 1-\epsilon ^2 \nabla ^2\right) t_{ij}&=t^L_{ij}=2\mu e_{ij}(\textbf{x})+(\lambda e_{kk}(\textbf{x})+b\phi (\textbf{x})+d\psi (\textbf{x}))\delta _{ij}, \end{aligned}$$

(1)

$$\begin{aligned} \left( 1-\epsilon ^2 \nabla ^2\right) \xi&=\xi ^L=-\tau _\phi {\dot{\phi }}(\textbf{x})-\alpha _1 \phi (\textbf{x})-be_{ii}(\textbf{x})-\alpha _3\psi (\textbf{x}), \end{aligned}$$

(2)

$$\begin{aligned} \left( 1-\epsilon ^2 \nabla ^2\right) \sigma ^{(1)}_i&=(\sigma ^{(1)}_i)^L= \alpha \phi _{,i}(\textbf{x})+b_1\psi _{,i}(\textbf{x}), \end{aligned}$$

(3)

$$\begin{aligned} \left( 1-\epsilon ^2 \nabla ^2\right) \zeta&=\zeta ^L=- \tau _\psi {\dot{\psi }}(\textbf{x})-\alpha _3 \phi (\textbf{x})-de_{ii}(\textbf{x})-\alpha _2\psi (\textbf{x}), \end{aligned}$$

(4)

$$\begin{aligned} \left( 1-\epsilon ^2 \nabla ^2\right) \sigma ^{(2)}_i&=(\sigma ^{(2)}_i)^L=b_1\phi _{,i}(\textbf{x})+\gamma \psi _{,i}(\textbf{x}), \end{aligned}$$

(5)

where $i,j = 1,2,3;$ $\nabla ^2$ is the Laplacian operator; $\epsilon$ is the nonlocality parameter defined by $\epsilon = e_0a$, $e_0$ is the material constant and a is the internal characteristic length depending upon the material properties. The local constitutive parameters $\lambda$ and $\mu$ are Lamé constants. $t_{ij}$ is the nonlocal stress tensor, $\tau _\phi$ and $\tau _\psi$ are the dissipation parameters; $\sigma ^{(1)}_i$ and $\sigma ^{(2)}_i$ are the nonlocal equilibrated stress vectors; $\xi$ and $\zeta$ are the nonlocal intrinsic equilibrated body forces; $\phi$ and $\psi$ are the change in void volume fractions corresponding to the first and second kind of voids, respectively; $e_{ij}$ is the Lagrangian strain tensor in the context of linear theory; $\delta _{ij}$ is the Kronecker delta. The constitutive coefficients b, d, $\alpha _1$, $\alpha _2$, $\alpha _3$, $\alpha$, $\gamma$ and $b_1$ are the void parameters corresponding to the first and second type of voids. A superposed dot represents the partial time derivative. The superscript “L” represents the local effects and $\textbf{x}$ is the local point in the considered material. An index followed by a comma indicates partial differentiation with respect to spatial variable.

The equations of motion for the linear isotropic nonlocal elastic materials with double porosity structure in the absence of body forces and after applying the Helmholtz decomposition on displacement vector $\textbf{u}$ by introducing scalar and vector potential p and $\textbf{U}$, respectively, are given by (see Kumar et al. [32])

$$\begin{aligned}{} & {} (\lambda +2\mu )\nabla ^2 p+b\phi +d\psi = \rho (1-\epsilon ^2\nabla ^2)\ddot{p}, \end{aligned}$$

(6)

$$\begin{aligned}{} & {} \nabla ^2(\alpha \phi +b_1\psi -b p)-(\alpha _1\phi +\alpha _3\psi +\tau _\phi {\dot{\phi }}) = (1-\epsilon ^2\nabla ^2)\chi _1\ddot{\phi }, \end{aligned}$$

(7)

$$\begin{aligned}{} & {} \nabla ^2(b_1\phi +\gamma \psi -d p)-(\alpha _3\phi +\alpha _2\psi +\tau _\psi {\dot{\psi }}) = (1-\epsilon ^2\nabla ^2)\chi _2\ddot{\psi }, \end{aligned}$$

(8)

$$\begin{aligned}{} & {} \mu \nabla ^2\textbf{U}=\rho (1-\epsilon ^2\nabla ^2)\ddot{\textbf{U}}. \end{aligned}$$

(9)

Here, $\rho$ is the mass density; $\chi _1$ and $\chi _2$, respectively, represent the equilibrated inertia per unit mass per unit volume corresponding to the first and second kind of voids. Note that the equations (6)-(8) are coupled in scalar potentials $p,~\phi$ and $\psi$, while equation (9) is independent in vector potential $\textbf{U}$.

3 Wave propagation

Kumar et al. [32] have explored the possibility of propagation of plane harmonic waves in an infinite nonlocal elastic material possessing double porosity. They found that there may propagate three sets of coupled longitudinal waves and a lone shear wave traveling at distinct speeds. Each set of coupled longitudinal waves is influenced by the presence of nonlocality and voids in the medium, while the lone shear wave is affected by the presence of nonlocality only. Borrowing the notations of Kumar et al. [32], the speeds of traveling waves and coupling parameters are given as follows.

(a) The speeds of three coupled longitudinal waves are given by the roots of the following bicubic equation:

$$\begin{aligned} Pc^6+Qc^4+Rc^2+S=0, \end{aligned}$$

(10)

where the expression of coefficients P,  Q,  R and S is given as

$$\begin{aligned} P=\;&\rho [\eta _0+\omega (\iota \chi _0-\tau _\phi \tau _\psi \omega )],\\ Q=\;&-(\mu _0\eta _0+\varsigma _1)+\omega ^2(\tau _\phi \tau _\psi \mu _0-\rho \varsigma _0)-\iota \omega (b^2\tau _\psi +d^2\tau _\phi +\mu _0 \chi _0)\\&-\iota \rho \omega ^3\left[ \Upsilon _1-\epsilon ^2(2\omega ^2\Upsilon _3 -\alpha _1\tau _\psi -\alpha _2\tau _\phi )\right] \\&+\rho \epsilon ^2\omega ^2[\beta _0+3\chi _1\chi _2\omega ^4-2\omega ^2\Upsilon _2-\tau _\phi \tau _\psi \epsilon ^2],\\ R=\;&\omega ^2\left[ \mu _0\varsigma _0+\beta _1+\rho \alpha _0\omega ^2-\epsilon ^2(\chi _2b^2+\chi _1d^2) \right. \\&+\iota \omega (\mu _0-\rho \epsilon ^2 \omega ^2)[\Upsilon _1- \epsilon ^2 \omega (\iota \Upsilon _2+\omega \Upsilon _3)] \\&-2\rho \epsilon ^2\omega ^4(\chi _2\alpha _1+\chi _1\gamma )+\rho \epsilon ^2\omega ^2(\alpha \alpha _2+\gamma \alpha _1-2\alpha _3b_1) \\&\left. -\chi _1\chi _2\epsilon ^2\omega ^4(2\mu _0-3\rho \epsilon ^2\omega ^2)\right] ,\\ S=\;&\omega ^4\left[ \chi _1\chi _2\epsilon ^4\omega ^4-(\chi _2\alpha +\chi _1\gamma )\epsilon ^2\omega ^2+\alpha _0 \right] (\rho \epsilon ^2\omega ^2-\mu _0), \\ \eta _1 =\;&\chi _1\omega ^2-\alpha _1, \,\, \eta _2= \chi _2\omega ^2-\alpha _2, \,\, \mu _0= \lambda +2\mu , \,\, \alpha _0= \alpha \gamma -b_1^2, \\ \varsigma _0 =\;&\alpha \eta _2+\gamma \eta _1+2b_1\alpha _3, \;\; \varsigma _1= d^2\eta _1+b^2\eta _2+2bd\alpha _3, \;\; \beta _0 =\; \alpha _1\alpha _2-\alpha _3^2, \\ \chi _0=\;&\eta _1\tau _\psi +\eta _2\tau _\phi , \;\; \eta _0=\eta _1\eta _2-\alpha _3^2, \beta _1 = \alpha d^2+\gamma b^2-2bdb_1, \\ \Upsilon _1 =\;&\alpha \tau _\psi +\gamma \tau _\phi , \;\; \Upsilon _2 =\; \chi _1\alpha _2+\chi _2\alpha _1,\;\; \Upsilon _3 = \chi _1 \tau _\psi +\chi _2 \tau _\phi . \end{aligned}$$

Here, $\omega$ denotes the angular frequency, which is related to the speed c and wavenumber k through relation $\omega =kc$. Since the coefficients of bicubic equation (10) are complex-valued, there exist six complex-valued roots. Among these six roots, three will have positive real part representing the speeds of three sets of coupled longitudinal waves advancing in positive direction. We shall denote these roots by $c_1$, $c_2$ and $c_3$ representing the speeds of three sets of coupled longitudinal waves.

(b) The speed of lone shear wave is given by $c_4=\sqrt{c^2_t-\epsilon ^2 \omega ^2};$ $c_t$ being the speed of the shear wave in classical elastic medium.

The phase speeds $V_i,~(i=1,2,3,4)$ and their corresponding attenuation coefficients $Q_i,~(i=1,2,3,4)$ of these waves propagating in the medium can be obtained from the formulae given by Borcherdt [33], which are as follows:

$$\begin{aligned} V_i=\frac{[\Re (c_i)]^2+[\Im (c_i)]^2}{\Re (c_i)}, \quad Q_i=-\frac{\omega \Im (c_i)}{[\Re (c_i)]^2+[\Im (c_i)]^2}. \end{aligned}$$

Here, $\Re (\cdot )$ and $\Im (\cdot )$ represent, respectively, the real and imaginary parts of $(\cdot ).$

The expressions of coupling parameters $\Omega _{2c}$ and $\Omega _{3c}$ between the displacement and change in void volume fraction of the first and second type of voids, respectively, are given by

$$\begin{aligned} \Omega _{2c}= & {} \frac{\rho \omega ^2(c^2_\ell -\epsilon ^2\omega ^2-c^2)+d\Omega _{3c}c^2}{bc^2}, \\ \Omega _{3c}= & {} \frac{(d+Ab)\omega ^2}{\omega ^2(Ab_1-\epsilon ^2\omega ^2\chi _2+\gamma )+c^2(A\alpha _3-\iota \omega \tau _\psi -\eta _2)}, \end{aligned}$$

and

$$\begin{aligned} A =\frac{b_1\omega ^2+\alpha _3c^2}{\omega ^2(\epsilon ^2\omega ^2\chi _1-\alpha )+c^2(\eta _1+\iota \omega \tau _\phi )},~~c^2_\ell = \frac{\lambda +2\mu }{\rho }. \end{aligned}$$

The detailed discussion about these coupling parameters can be seen in Kumar et al. [32].

4 Reflection phenomenon

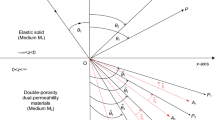
We considered an isotropic and homogeneous nonlocal elastic solid half-space possessing double porosity structure. With reference to a rectangular Cartesian coordinate system Oxyz,  the considered half-space can be defined as

$$\begin{aligned} M=\left\{ (x,y,z);~-\infty<x,y<\infty ,0\le z<\infty \right\} , \end{aligned}$$

whose boundary surface is given by $z = 0$ and $z-$axis is pointing vertically downward into the half-space. For a two-dimensional problem in $x-z$ plane, the displacement components and change in void volume fractions can be taken as

$$\begin{aligned} \mathbf{{u}}(x,z,t) = (u(x,z,t),0,w(x,z,t)), \;\; \phi = \phi (x,z,t), \;\; \psi = \psi (x,z,t), \end{aligned}$$

along with ${\partial (\cdot )}/{\partial y} =0$. As explained earlier in Sect. 2, the relevant components of displacement vector $\textbf{u}$ are given by

$$\begin{aligned} u = p_{,x}-U_{,z},\qquad w= p_{,z}+U_{,x}, \end{aligned}$$

(11)

where U is the $y-$component of vector $\textbf{U}$.

We consider a set of coupled longitudinal waves/shear wave traveling through half-space M with phase speed $V_n,~(n = 1,2,3,4)$, having amplitude $A_{0n}$ and striking obliquely at the boundary $z = 0$ of the half-space M making an angle $\theta _n$ with the normal to the boundary surface. We shall assume that the boundary surface $z=0$ of the half-space M is mechanically stress-free. In order to satisfy the boundary conditions at the free surface, we postulate the existence of following reflected waves as:

• 1. Three sets of coupled longitudinal waves with amplitudes $A_i{,} ~(i=1,2,3)$, traveling with phase speeds $V_i$ and making angles $\theta _i$, respectively, with the normal.

• 2. An independent shear wave with amplitude $A_4$ traveling with phase speed $V_4$ and making an angle $\theta _4$ with the normal.

The total wave field in the considered half-space M can be written as

(i) For the incidence of a set of time harmonic plane coupled longitudinal waves propagating with phase speed $V_n,~ (n=1,2,3)$, we have

$$\begin{aligned} \{p, \phi , \psi \}=&A_{0n}\{1, \Omega _{2c_n}, \Omega _{3c_n}\}\exp \{\iota k_n(x\sin \theta _n-z\cos \theta _n)-\iota { \omega } t \}\nonumber \\&+\sum _{i=1}^{3}A_i \{1, \Omega _{2c_i}, \Omega _{3c_i}\}\exp \{\iota k_i(x\sin \theta _i+z\cos \theta _i)-\iota { \omega } t\}, \end{aligned}$$

(12)

$$\begin{aligned} U=&A_4\exp \{\iota k_4(x\sin \theta _4+z\cos \theta _4)-\iota { \omega }t\}. \end{aligned}$$

(13)

(ii) For the incidence of a plane shear wave propagating with phase speed $V_4$, we have

$$\begin{aligned} \{p, \phi , \psi \} =&\sum _{i=1}^{3}A_i \{1, \Omega _{2c_i}, \Omega _{3c_i}\}\exp \{\iota k_i(x\sin \theta _i+z\cos \theta _i)-\iota { \omega }t\}, \end{aligned}$$

(14)

$$\begin{aligned} U =\;&A_{04}\exp \{\iota k_4(x\sin \theta _4-z\cos \theta _4)-\iota { \omega }t\}\nonumber \\&+A_4\exp \{\iota k_4(x\sin \theta _4+z\cos \theta _4)-\iota { \omega }t\}, \end{aligned}$$

(15)

where ${ \omega }$ is the common angular frequency, $k_i$ is the wavenumber, which is related to the phase speed $V_i$ through the relation ${ k_i = \omega /V_i}, ~ (i = 1,2,3,4)$. The expressions of coupling parameters $\Omega _{2c_i}$, $\Omega _{3c_i},$ $(i=1,2,3)$ can be obtained from the expression of $\Omega _{2c}$, $\Omega _{3c}$ by replacing c with $c_i$. The stress-free boundary conditions must be satisfied for any x and t on the boundary surface $z=0$, and all exponentials in (12)–(15) must be common. Therefore, we have the Snell’s law given by

$$\begin{aligned} \frac{\sin \theta _n}{V_n}=\frac{\sin \theta _i}{V_i}= {k_0/\omega },~~i = 1,2,3,4. \end{aligned}$$

(16)

Here, $k_0$ is an apparent wavenumber.

4.1 Nonlocal boundary conditions and reflection coefficients

The boundary surface of the half-space M is assumed to be mechanically stress-free; therefore, all nonlocal stresses must vanish at the surface, i.e., $t_{zz}=t_{zx}= \sigma ^{(1)}_{z}=\sigma ^{(2)}_{z}=0$ at $z=0$. The nonlocal stresses can be obtained in terms of local stresses by operating $(1-\epsilon ^2\nabla ^2)^{-1}$ to both sides of (1)-(5) (See Eringen [34]). We shall assume that the nonlocal parameter $\epsilon$ is so small that its third and higher powers are negligible. Thus, by using (11) the nonlocal boundary conditions can now be written in terms of the potentials p, $\phi$, $\psi$ and U as

$$\begin{aligned}{} & {} (1+\epsilon ^2\nabla ^2)\left[ (\lambda +2\mu )\nabla ^2p+2\mu (U_{,zx}-p_{,xx})+(b\phi +d\psi )\right] =0, \end{aligned}$$

(17)

$$\begin{aligned}{} & {} (1+\epsilon ^2\nabla ^2)\left( 2p_{,xz}-U_{,zz}+U_{,xx}\right) =0, \end{aligned}$$

(18)

$$\begin{aligned}{} & {} (1+\epsilon ^2\nabla ^2)\left( \alpha \phi _{,z}+b_1\psi _{,z}\right) =0, \end{aligned}$$

(19)

$$\begin{aligned}{} & {} (1+\epsilon ^2\nabla ^2)\left( b_1\phi _{,z}+\gamma \psi _{,z}\right) =0. \end{aligned}$$

(20)

Here, the approximation $(1-\epsilon ^2\nabla ^2)^{-1}\approx (1+\epsilon ^2\nabla ^2)$ has been used as the higher-order terms are negligible. Inserting the expressions of potentials given in (12)-(15) into the boundary conditions (17)-(20), we obtain a system of four non-homogeneous linear equations in four unknowns. This system of equations can be written in matrix form as

$$\begin{aligned}{}[a_{ij}][X_j] = [b_{i}], \end{aligned}$$

(21)

where $[a_{ij}]$ is a $4\times 4$ square matrix, $[X_j]$ and $[b_i]$ are $4\times 1$ column vectors. The nonzero entries of matrix $[a_{ij}]$ are given by

$$\begin{aligned} \begin{aligned} a_{1j}&= R_jK_j,~a_{14} = 2\mu K_4\cot \theta _4,~~a_{2j} = 2K_j\cot \theta _j,~~a_{24} = K_4(1-\cot ^2\theta _4),\\ a_{3j}&= G_jK_j\cot \theta _j,~ a_{4j} = H_jK_j\cot \theta _j, \\ G_j&= \alpha \Omega _{2c_j}+b_1\Omega _{3c_j},~ H_j = b_1\Omega _{2c_j}+\gamma \Omega _{3c_j}, \\ R_j&= \left[ \lambda +(\lambda +2\mu )\cot ^2\theta _j-\frac{b}{k_0^2}\Omega _{2c_j}-\frac{d}{k_0^2}\Omega _{3c_j}\right] ,~~ j = 1,2,3,\\ K_m&= {1-\epsilon ^2k_0^2(1+\cot ^2\theta _m)},~~m = 1,2,3,4. \end{aligned} \end{aligned}$$

(22)

The entries of column vector $[b_i]$ are given by

(i) For the incidence of coupled longitudinal waves having phase speed $V_n,~(n=1,2,3)$, we have

$$\begin{aligned} b_1 = -R_nK_n,~~b_2 = 2K_n\cot \theta _n,~b_3 = G_nK_n\cot \theta _n,~~b_4 = H_nK_n\cot \theta _n. \end{aligned}$$

(23)

(ii) For the incidence of shear wave having phase speed $V_4$, we have

$$\begin{aligned} b_1&= 2\mu K_4\cot \theta _4, ~b_2 = K_4(\cot ^2\theta _4-1),~b_3 = b_4 = 0. \end{aligned}$$

(24)

The entries $X_i~(=\dfrac{A_i}{A_{0n}}), i=1,2,3,4$ represent the reflection coefficients corresponding to the four reflected waves.

On solving the matrix equation (21), the expressions of various reflection coefficients are obtained in closed form as

(i) For the incidence of coupled longitudinal waves having phase speed $V_n,~(n=1,2,3)$, we obtain

$$\begin{aligned} X_1 =&\frac{K_n\left\{ 4\mu \cot \theta _2\cot \theta _3\cot \theta _4\cot \theta _n{\tilde{M}}_n-(\cot ^2\theta _4-1){\tilde{\Gamma }}_n\right\} }{K_1\left\{ 4\mu \cot \theta _1\cot \theta _2\cot \theta _3\cot \theta _4M_1+(\cot ^2\theta _4-1)\Gamma _1\right\} },\\ X_2 =&\frac{L_{n3}K_n\cot \theta _n-L_{13}K_1\cot \theta _1X_1}{L_{23}K_2\cot \theta _2},\\ X_3 =&\frac{(H_nL_{23}-H_2L_{n3})K_n\cot \theta _n-(H_1L_{23}-H_2L_{13})K_1\cot \theta _1X_1}{H_3K_3L^2_{23}\cot \theta _3},\\ X_4 =&-\frac{K_n{\tilde{\Gamma }}_n+K_1\Gamma _1X_1}{2\mu \cot \theta _2\cot \theta _3\cot \theta _4K_4H_3L_{23}} \end{aligned}$$

(ii) For the incidence of shear wave having phase speed $V_4$, we obtain

$$\begin{aligned} X_1 =&\frac{4\mu \cot \theta _2\cot \theta _3\cot \theta _4(\cot ^2\theta _4-1)K_4G_3L_{32}}{K_1\left\{ (G_3F_1\cot \theta _3-G_1F_3\cot \theta _1)L_{32}\cot \theta _2+(G_3F_2\cot \theta _3-G_2F_3\cot \theta _2)L_{13}\cot \theta _1\right\} },\\ X_2 =&\frac{K_1L_{13}\cot \theta _1X_1}{K_2L_{32}\cot \theta _2}, \;\; X_3 = \frac{K_1(G_1L_{23}+G_2L_{31})\cot \theta _1X_1}{K_3G_3L_{32}\cot \theta _3},\\ X_4 =&-1+ \frac{2K_1\cot \theta _1X_1}{K_4(\cot ^2\theta _4-1)}\left[ 1+\frac{L_{13}}{L_{32}}+\frac{G_1L_{23}+G_2L_{31}}{G_3L_{32}}\right] . \end{aligned}$$

The expressions of various symbols used above are as follows:

$$\begin{aligned} L_i&= H_3-H_i,\;\; {\tilde{L}}_n = H_3-H_n, \;\; L_{ij}= G_iH_j-G_jH_i,~~i,j=1,2,3\\ M_1&=L_1L_{23}-L_2L_{13}, \;\; {\tilde{M}}_n ={\tilde{L}}_nL_{23}-L_2L_{n3}, \;\; N_i = H_3R_i\cot \theta _3-H_iR_3\cot \theta _i,\\ \Gamma _1&= N_1L_{23}\cot \theta _2-N_2L_{13}\cot \theta _1,\;\; {\tilde{N}}_n= H_3R_n\cot \theta _3+H_nR_3\cot \theta _n, \\ {\tilde{\Gamma }}_n&= {\tilde{N}}_nL_{23}\cot \theta _2+N_2L_{n3}\cot \theta _n,\;\; F_n = R_n(\cot ^2\theta _4-1)+4\mu \cot \theta _4\cot \theta _n. \end{aligned}$$

We note that the reflection coefficients under both the cases (i) and (ii) depend upon nonlocality parameter, voids parameters, angle of incidence, frequency and the material properties. All the reflection coefficients are found to be complex-valued due to the presence of dissipation parameters $\tau _{\phi }$ and $\tau _{\psi }$ in their expressions. For non-dissipative model, the reflection coefficients can be easily obtained by setting $\tau _{\phi }=\tau _{\psi }=0$ in the above expressions.

5 Special cases

5.1 Nonlocal elastic solid with single porosity

In the absence of one kind of voids from the medium, we shall be left with the nonlocal elastic solid with single type of voids. For definiteness, setting the parameters corresponding to the second type of voids to zero, i.e., $d=\gamma =b_1=\alpha _2=\alpha _3=\chi _2=0$, we see that $V_2=\Omega _{3c}=A_2=0$ and equation (20) is satisfied identically. Then, the matrix equation (21) reduces to a system of three non-homogeneous equations given by

$$\begin{aligned}{}[a'_{ij}][X'_j] = [b'_i],~~i,j=1,3,4. \end{aligned}$$

The nonzero entries of matrix $[a'_{ij}]$ are given as

$$\begin{aligned} a'_{1j}&= R'_jK_j, \;\; a'_{14} = 2\mu K_4\cot \theta _4, \;\; a'_{2j} = 2K_j\cot \theta _j,\\ a'_{24}&= K_4(1-\cot ^2\theta _4), \;\; a'_{3j} = \Omega '_{2c_j}K_j\cot \theta _j, \end{aligned}$$

where

$$\begin{aligned} R'_j= \lambda +(\lambda +2\mu )\cot ^2\theta _j-\frac{b}{k_0^2}\Omega '_{2c_j}, \;\; \Omega '_{2c_j} = \frac{\rho \omega ^2}{bc_j^2}\left[ c^2_\ell -(c_j^2+\epsilon ^2\omega ^2)\right] ,~~ j = 1,3. \end{aligned}$$

The entries of column vector $[b'_i]$ are given by

(i) For the incidence of coupled longitudinal waves having phase speed $V_n,~(n=1,~3)$, we have

$$\begin{aligned} b'_1&= -R'_nK_n,~~b'_3 = 2K_n\cot \theta _n,~~b'_4 = K_n\cot \theta _n,~~n= 1,3. \end{aligned}$$

(ii) For the incidence of shear wave having phase speed $V_4$, we have

$$\begin{aligned} b'_1&= 2\mu K_4\cot \theta _4, ~b'_3 = K_4(\cot ^2\theta _4-1),~b'_4 = 0. \end{aligned}$$

The reflection coefficients for case (i) are obtained as

$$\begin{aligned} X'_1&= \frac{K_n\left\{ 4\mu B_n\cot \theta _3\cot \theta _4\cot \theta _n-{\tilde{N}}_n(\cot ^2\theta _4-1)\right\} }{K_1\left\{ 4\mu B_1\cot \theta _1\cot \theta _3\cot \theta _4+N'_1(\cot ^2\theta _4-1)\right\} },\\ X'_3&=\frac{\Omega '_{2c_n}K_n\cot \theta _n-\Omega '_{2c_1}K_1\cot \theta _1X_1'}{\Omega '_{2c_3}K_3\cot \theta _3},\,\, X'_4 =2\frac{\cot \theta _1K_1B_1X'_1-\cot \theta _nB_nK_n}{\Omega '_{2c_3}K_4(\cot ^2\theta _4-1)}. \end{aligned}$$

The reflection coefficients for case (ii) are obtained as

$$\begin{aligned} X'_1&= \frac{4\mu K_4\Omega '_{2c_3}\cot \theta _3\cot \theta _4(\cot ^2\theta _4-1)}{K_1\left\{ N_1'(\cot ^2\theta _4-1)+4\mu B_1\cot \theta _1\cot \theta _3\cot \theta _4\right\} },\\ X'_3&= -\frac{\Omega '_{2c_1}K_1\cot \theta _1X_1'}{\Omega '_{2c_3}K_3\cot \theta _3}, \;\; X'_4 =\frac{2B_1K_1\cot \theta _1X_1'-\Omega '_{2c_3}K_4(\cot ^2\theta _4-1)}{\Omega '_{2c_3}K_4(\cot ^2\theta _4-1)}. \end{aligned}$$

The expressions of various symbols used in these coefficients are given as

$$\begin{aligned} {\tilde{N}}_n&= R'_n\Omega '_{2c_3}\cot \theta _3+R'_3\Omega '_{2c_n}\cot \theta _n,~B_n = \Omega '_{2c_3}-\Omega '_{2c_n}, \\ N_1'&= R'_1\Omega '_{2c_3}\cot \theta _3-R'_3\Omega '_{2c_1}\cot \theta _1. \end{aligned}$$

We see that all these reflection coefficients depend upon nonlocality, void parameters and angle of incidence.

5.2 Local elastic solid with double porosity

To neglect the effect of nonlocality from the half-space, we shall set $\epsilon = 0$. Then, we shall be left with the local elastic solid with double porosity structure. In this case, each value of $K_m,~(m= 1,2,3,4)$ becomes unity and rest the expressions of reflection coefficients remain the same as given in Subsection 5.1. The phase speeds of all the waves become independent of nonlocal parameter. Also, the coupling parameters reduce to

$$\begin{aligned} \begin{aligned} \Omega _{2c}&= \frac{\rho \omega ^2c^2_\ell -c^2(\rho \omega ^2+d\Omega _{3c})}{bc^2}, \;\; \Omega _{3c} = \frac{(d+Ab)\omega ^2}{\omega ^2(Ab_1+\gamma )+c^2(A\alpha _3-\iota \omega \tau _\psi -\eta _2)}, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} A =\frac{b_1\omega ^2+\alpha _3c^2}{c^2(\eta _1+\iota \omega \tau _\phi )-\omega ^2\alpha }. \end{aligned}$$

We see that all the reflection coefficients become independent of nonlocality parameter.

5.3 Local elastic solid with single porosity

On setting the nonlocality parameter to zero, i.e., $\epsilon = 0$ in the model under Subsection 5.1, we shall be left with local elastic solid with voids. In this case too, each value of $K_m,~(m = 1,3,4)$ becomes unity. The expressions of all the reflection coefficients remain the same as in the Subsection 5.1 for the incidence of coupled waves or shear wave. But the phase speeds of propagating waves become independent of nonlocality and the coupling parameter reduces to

$$\begin{aligned} \Omega '_{2c}= \frac{\rho \omega ^2(c^2_\ell -c^2)}{bc^2}. \end{aligned}$$

The expressions of all the reflection coefficients obtained under this case match with those of Ciarletta and Sumbatyan [7] for the corresponding problem apart from notations.

5.4 Nonlocal elastic solid

In the absence of void parameters from the model under Subsection 5.1, we shall be left with the nonlocal elastic solid. Setting the void parameters, i.e., $\alpha ,~b,~\alpha _1$ and $\tau _\phi$ to zero, we found that the phase speed of one of the coupled longitudinal waves and the corresponding amplitude and the coupling parameter vanish, i.e., $V_1= A_1 =0$(say) and $\Omega '_{2c} = 0$. The expressions of reflection coefficients are obtained as

(i) For the incidence of longitudinal wave having phase speed $V_3$, we obtain

$$\begin{aligned} \begin{aligned} X^{''}_3&= \frac{-2\mu K_4\cot \theta _4X^{''}_4}{K_3\left[ \lambda +(\lambda +2\mu )\cot ^2\theta _3\right] }-1,\\ X^{''}_4&= \frac{4\cot \theta _3K_3\left[ \lambda +(\lambda +2\mu )\cot ^2\theta _3\right] }{K_4\left\{ (1-\cot ^2\theta _4)\left[ \lambda +(\lambda +2\mu )\cot ^2\theta _3\right] -4\mu \cot \theta _3\cot \theta _4\right\} } \end{aligned} \end{aligned}$$

(ii) For the incidence of shear wave having phase speed $V_4$, we obtain

$$\begin{aligned} X^{''}_3&= \frac{2\mu K_4\cot \theta _4(1-\cot ^2\theta _4)}{K_3\left\{ (1-\cot ^2 \theta _4)\left[ \lambda +(\lambda +2\mu )\cot ^2\theta _4\right] -4\mu \cot \theta _4\right\} },\\ X^{''}_4&= \frac{-2K_3\cot \theta _3 X^{''}_3}{K_4(1-\cot ^2\theta _4)}-1. \end{aligned}$$

Here, the quantities $V_3$ and $V_4$ are the phase speed of longitudinal and shear waves, respectively, in nonlocal elastic medium.

5.5 Classical elastic solid

Further, neglecting the nonlocality from the model under Subsection 5.4, we shall be left with Cauchy elastic solid. The expressions of reflection coefficients shall remain the same as given in Subsection 5.4, and the speeds of longitudinal and shear waves will match with those of in the classical elasticity.

6 Energy partitioning

Here, we wish to find the amount of energy carried along different reflected waves out of the amount of energy carried along the incident wave. For a particular model, we shall verify that the sum of energy ratios corresponding to the various reflected waves at the boundary surface is close to unity at each angle of incidence. Following Achenbach [2], the energy flux $P^*$ across a surface element of the boundary surface, the rate at which the energy is communicated per unit area of the surface of nonlocal elastic solid with double voids, is given by

$$\begin{aligned} P^*=t_{zz}{\dot{w}}+t_{zx}{\dot{u}}+\sigma ^{(1)}_z{\dot{\phi }}+\sigma ^{(2)}_z{\dot{\psi }}. \end{aligned}$$

(25)

The time averaging of $P^*$ over a complete period is denoted by $\langle P^*\rangle$, which gives the average energy transmission per unit surface area per unit time. Let $\langle P_{0n}^*\rangle$ be the time average energy carried along incident wave with phase speed $V_n,~(n = 1,2,3,4)$ and $\langle P_i^*\rangle , ~ (i=1,2,3,4)$ be the time average energy carried along the reflected waves propagating with phase speeds $V_i$. We define the energy ratio $E_i, ~(i=1,2,3,4)$ corresponding to the energy carried along $i^{th}$ reflected wave at $z=0$ to the energy carried along the incident wave as

$$\begin{aligned} E_i=\frac{\langle P_i^*\rangle }{\langle P_{0n}^*\rangle }. \end{aligned}$$

(26)

The expressions of energy ratios for various reflected waves are written in closed form as

$$\begin{aligned} \begin{aligned} E_i&=-X_i^2\left[ (\lambda +2\mu )k_i^2-\Omega _{2c_i}(b+\alpha \Omega _{2c_i}+b_1\Omega _{3c_i})-\Omega _{3c_i}(d+\gamma \Omega _{3c_i} +b_1\Omega _{2c_i})\right] \\ {}&~~~~\times K_ik_i\cos \theta _i E_0^{-1},\\ E_4&= - X_4^2 \mu k_4^3K_4\cos \theta _4 E_0^{-1},~~ i = 1,2,3, \end{aligned} \end{aligned}$$

(27)

where $E_0$ is the expression of energy carried along the incident wave.

The expression of $E_0$ is given by

$\mathbf (i)$ For the incidence of coupled longitudinal waves having speed $V_n,~(n=1,2,3)$, we have

$$\begin{aligned} E_0 =&\left[ (\lambda +2\mu )k_n^2-\Omega _{2c_n}(b+\alpha \Omega _{2c_n}+b_1\Omega _{3c_n}) \right. \\&\left. -\Omega _{3c_n}(d+\gamma \Omega _{3c_n} +b_1\Omega _{2c_n})\right] K_n k_n\cos \theta _n. \end{aligned}$$

(ii) For the incidence of shear wave having phase speed $V_4$, we have

$$\begin{aligned} E_0= \mu K_4k_4^3\cos \theta _4. \end{aligned}$$

7 Surface Response

Using equations (11)–(15), the response of the solid particles at the surface $z=0$ of the half-space M due to the incidence of coupled longitudinal waves/shear wave propagating with phase speed $V_n~(n = 1,2,3,4)$ can be expressed in terms of reflection coefficients. The displacement components u,  w, and change in void volume fractions $\phi ,~ \psi$ corresponding to the void of the first and second type, respectively, at $z=0$ are given as follows

(i) For the incidence of coupled longitudinal waves having phase speed $V_n~(n = 1,2,3)$, we have

$$\begin{aligned} u =\;&\iota A_{0n} \left[ k_n\sin \theta _n+\sum _{i=1}^{3}k_i\sin \theta _i\left( \frac{A_i}{A_{0n}}\right) -k_4\cos \theta _4\left( \frac{A_4}{A_{0n}}\right) \right] \\&\times \exp \{\iota k_nx\sin \theta _n-\iota \omega t\},\\ w =\;&\iota A_{0n} \left[ -k_n\cos \theta _n+\sum _{i=1}^{3}k_i\cos \theta _i\left( \frac{A_i}{A_{0n}}\right) -k_4\sin \theta _4 \left( \frac{A_4}{A_{0n}}\right) \right] \\&\times \exp \{\iota k_nx\sin \theta _n-\iota \omega t\}, \\ \phi =\;&A_{0n}\left[ \Omega _{2c_n}+\sum _{i=1}^{3}\Omega _{2c_i}\left( \frac{A_i}{A_{0n}}\right) \right] \exp \{\iota k_nx\sin \theta _n-\iota \omega t\}, \\ \psi =\;&A_{0n} \left[ \Omega _{3c_n}+\sum _{i=1}^{3}\Omega _{3c_i}\left( \frac{A_i}{A_{0n}}\right) \right] \exp \{\iota k_nx\sin \theta _n-\iota \omega t\}. \end{aligned}$$

(ii) For the incidence of shear wave having phase speed $V_4$, we have

$$\begin{aligned} \begin{aligned} u&= \iota A_{04} \left[ \sum _{i=1}^{3}k_i\sin \theta _i\left( \frac{A_i}{A_{04}}\right) +\left( 1-\frac{A_4}{A_{04}}\right) k_4\cos \theta _4\right] \exp \{\iota k_4x\sin \theta _4-\iota \omega t\},\\ w&= \iota A_{04} \left[ \sum _{i=1}^{3}k_i\cos \theta _i\left( \frac{A_i}{A_{04}}\right) +\left( 1+\frac{A_4}{A_{04}}\right) k_4\sin \theta _4\right] \exp \{\iota k_4x\sin \theta _4-\iota \omega t\},\\ \phi&= A_{04}\left[ \sum _{i=1}^{3}\Omega _{2c_i}\left( \frac{A_i}{A_{04}}\right) \right] \exp \{\iota k_4x\sin \theta _4-\iota \omega t\},\\ \psi&= A_{04} \left[ \sum _{i=1}^{3}\Omega _{3c_i}\left( \frac{A_i}{A_{04 }}\right) \right] \exp \{\iota k_4x\sin \theta _4-\iota \omega t\}. \end{aligned} \end{aligned}$$

It is clear that the surface response is functions of coordinate x, frequency $\omega$ angle of incidence $\theta _n$ as well as reflection coefficients for each type of incident wave.

8 Numerical results and discussion

To study the behavior of reflection coefficients and corresponding energy ratios due to the incidence of coupled longitudinal waves/shear wave striking at the stress-free boundary of the half-space containing double voids, a hypothetical numerical model is considered. The numerical values of relevant material parameters have been borrowed from Puri and Cowin [6] and Eringen [35]. The parameters corresponding to the second type of voids are considered close to that of the first type of voids keeping in view that they must satisfy the required thermodynamical constraints. These values are listed in Table 1.

Table 1 Numerical values of material parameters

Figure 1 depicts the variation of reflection coefficients $|X_i |,~(i = 1,2,3,4)$ with angle of incidence $\theta _3$ in the range $0^\circ \le \theta _3\le 90^\circ$ for the incidence of a set of coupled longitudinal waves having phase speed $V_3$ at $f =50~$kHz for Voigt $(\tau _{\phi }\ne 0,~\tau _{\psi }\ne 0)$ and non-Voigt $(\tau _{\phi }=\tau _{\psi }=0)$ models. The coefficients $|X_1 |$ and $|X_2 |$ are depicted after magnifying by a factor of 15. The reflection coefficients $|X_1 |$ and $|X_2 |$ attain values 0.0239 and 0.0132, respectively, at normal incidence, and they remain almost constant up to $\theta _3 = 45^\circ$. Beyond $\theta _3 =45^\circ$, there is a sudden increase in both the reflection coefficients and they attain their maximum value at $\theta _3 = 50.72^\circ$ and $\theta _3= 50.95^\circ$, respectively. The sharp rise in the reflection coefficients is due to the appearance of critical angles in the considered numerical model. These critical angles arose due to the fact that the phase speed $V_3$ of incidence set of coupled longitudinal waves is found to be less than that of reflected sets of coupled waves with phase speeds $V_1$ and $V_2$ at the chosen frequency of 50 kHz. After their respective critical angles, these reflection coefficients decrease sharply and tend to zero as $\theta _3 \rightarrow 90^\circ$. The reflection coefficient $|X_3 |$ starts with a maximum value of 1 at $\theta _3 = 0^\circ$ and decreases till the angle $64.63^\circ$ to a value of 0.3827. Beyond $\theta _3 = 64.63^\circ$, the reflection coefficient $|X_3 |$ starts increasing and tends to the value 1 at grazing incidence. Moreover, the reflection coefficient $|X_4 |$ starts with zero value at normal incidence and increases with an increase in the angle of incidence $\theta _3$ till $\theta _3= 47.89^\circ$. After this, the value of $|X_4 |$ starts decreasing and tends to zero at grazing incidence. It is clear from Fig. 1 that there is no comparable difference in the values of reflection coefficients for both Voigt and non-Voigt models.

Fig. 1

Variation of reflection coefficients $|X_i |$ against the angle of incidence ($\theta _3$) of coupled longitudinal waves having phase speed $V_3$ for Voigt ($\tau _\phi \not = 0$, $\tau _\phi \not =0$) and non-Voigt ($\tau _\phi = \tau _\phi =0$) models

Fig. 2

Variation of energy ratios $|E_i |$ against the angle of incidence ($\theta _3$) of coupled longitudinal waves having phase speed $V_3$ for Voigt ($\tau _\phi \not = 0$, $\tau _\phi \not =0$) and non-Voigt ($\tau _\phi = \tau _\phi =0$) models

Figure 2 depicts the variation of energy ratios $|E_i |,~(i = 1,2,3,4)$ of reflected waves with respect to the angle of incidence $\theta _3$ for both Voigt and non-Voigt models. The variations of $|E_i |$ are analogous to the corresponding reflection coefficients as was expected. It is shown numerically that the sum of all the absolute energy ratios remains unity in the considered range of the angle of incidence. This shows that there is no loss of energy at the boundary surface at each angle of incidence.

Figures 3, 4, 5 and 6 represent the variation of phase change $Z_i,~(i=1,2,3,4),$ associated with reflection coefficients, of reflected waves having phase speeds $V_i, ~(i=1,2,3,4)$ with angle of incidence of coupled longitudinal waves having phase speed $V_3$ for the case of Voigt and non-Voigt models, respectively. It is observed from these figures that there is change in phase at the critical angles of reflected waves. It is also observed that in case of non-Voigt model, the change in phase of reflected waves is zero below the respective critical angles of reflected wave as these reflection coefficients are real-valued below their respective critical angles.

Fig. 3

Variation of phase change of reflected coupled longitudinal waves having phase speed $V_1$ with respect to angle of incidence ($\theta _3$) for incident coupled longitudinal waves having phase speed $V_3$

Fig. 4

Variation of phase change of reflected coupled longitudinal waves having phase speed $V_2$ with respect to angle of incidence ($\theta _3$) for incident coupled longitudinal waves having phase speed $V_3$

Fig. 5

Variation of phase change of reflected coupled longitudinal waves having phase speed $V_3$ with respect to angle of incidence ($\theta _3$) for incident coupled longitudinal waves having phase speed $V_3$

Fig. 6

Variation of phase change of reflected shear waves having phase speed $V_4$ with respect to angle of incidence ($\theta _3$) for incident coupled longitudinal waves having phase speed $V_3$

Figure 7 depicts the variation of reflection coefficients $|X_i |,~(i = 1,2,3,4)$ with respect to the angle of incidence $\theta _4$ due to incident transverse wave having phase speed $V_4$ at $f=50$ kHz for both Voigt and non-Voigt models. The reflection coefficients $|X_1 |$ and $|X_2 |$ have been depicted after magnifying by a factor of $10^2$. In both models, the reflection coefficients $|X_1 |$ and $|X_2 |$ begin with the zero value at normal incidence and they increase slowly with angle of incidence and show a sharp rise in their values at $22.78^\circ$ and $22.82^\circ$, respectively, due to the appearance of critical angles. Beyond their respective critical angles, $|X_1 |$ and $|X_2 |$ start decreasing and become close to zero at the angle $\theta _4 = 30.1^\circ$. Beyond $\theta _4 =30.1^\circ$, their values start increasing slowly and increase up to $\theta _4=33.82^\circ$ and then decrease to almost zero at $\theta _4 = 45^\circ$, then again their values start increasing slowly and increases up to $\theta _4=67.28^\circ$. Beyond $\theta _4= 67.28^\circ$ their values start decreasing and tend to zero at grazing incidence. The reflection coefficient $|X_3 |$ shows a linearly increasing behavior in the range $0^\circ \le \theta _4\le 27^\circ$ from a value 0 to a value of 1.903. Beyond $\theta _4 = 27^\circ$, its value increases rapidly to 3.465 at $\theta _4= 30^\circ$. After this, $|X_3 |$ starts decreasing and it decreases to zero at $\theta = 45^\circ$. After $\theta _4= 45^\circ$, the value of reflection coefficient $|X_3 |$ increases to 0.8828 at $\theta _4= 68^\circ$ and then decreases to the zero value at $\theta _4=90^\circ$. The value of reflection coefficient $|X_4 |$ starts from 1 at normal incidence and then decreases to 0.3828 at $\theta _4=26.99^\circ$. After $\theta {_4}=26.99^\circ$, its value starts increasing and increases to 1 at $\theta _4=30.01^\circ$. Beyond $\theta _4= 30.01^\circ$, the value of reflection coefficient $|X_4 |$ remains constant and have value equal to unity. Here, we note that there is no significant change in the values of reflection coefficients for Voigt and non-Voigt models.

Fig. 7

Variation of reflection coefficients $|X_i |$ against the angle of incidence ($\theta _4$) of shear wave having phase speed $V_4$ for Voigt ($\tau _\phi \not = 0$, $\tau _\phi \not =0$) and non-Voigt ($\tau _\phi = \tau _\phi =0$) models

Figure 8 depicts the behavior of energy ratios of reflected waves with the angle of incidence $\theta _4$ of shear wave. We see that the behavior of absolute values of energy ratios is similar to the corresponding absolute values of reflection coefficients. From Fig. 9, it is shown that the sum of absolute values of all the energy ratios is unity. In another way, we can see that the sum of real parts of all the energy ratios is equal to unity and sum of the imaginary parts is zero which also verifies the conservation of energy method used by Ainslie and Burns [36], Singh and Tomar [37] and recently by Kumar and Tomar [31].

Fig. 8

Variation of energy ratios $|E_i |$ against the angle of incidence ($\theta _4$) of shear wave having phase speed $V_4$ for Voigt ($\tau _\phi \not = 0$, $\tau _\phi \not =0$) and non-Voigt ($\tau _\phi = \tau _\phi =0$) models

Fig. 9

Variation of sum of real, imaginary parts and absolute values of energy ratios $E_i$ versus angle of incidence ($\theta _4$) of shear wave having phase speed $V_4$ for Voigt ($\tau _\phi \not = 0$, $\tau _\phi \not =0$) and non-Voigt ($\tau _\phi = \tau _\phi =0$) models

Figures 10, 11, 12 and 13 illustrate the behavior of phase change, associated with reflection coefficients, of reflected waves having phase $Z_i,~(i=1,2,3,4)$ of reflected waves having phase speed $V_i,~(i=1,2,3,4)$, respectively, with the angle of incidence of shear wave having phase speed $V_4$ for both Voigt and non-Voigt models. It is observed from these figures that there is change in phase of reflected waves at the critical angles. It is also observed that the phase change of all the reflected waves is zero below their respective critical angles in case of non-Voigt model.

Fig. 10

Variation of phase change of reflected coupled longitudinal waves having phase speed $V_1$ with respect to angle of incidence ($\theta _4$) for incident shear wave having phase speed $V_4$

Fig. 11

Variation of phase change of reflected coupled longitudinal waves having phase speed $V_2$ with respect to angle of incidence ($\theta _4$) for incident shear wave having phase speed $V_4$

Fig. 12

Variation of phase change of reflected coupled longitudinal waves having phase speed $V_3$ with respect to angle of incidence ($\theta _4$) for incident shear wave having phase speed $V_4$

Fig. 13

Variation of phase change of reflected shear wave having phase speed $V_4$ with respect to angle of incidence ($\theta _4$) for incident shear wave having phase speed $V_4$

Figures 14 and 15, respectively, represent the variation of reflection coefficients $|X_i |,~(i=1,2,3,4)$ and energy ratios $|E_i |,~(i=1,2,3,4)$ of all the reflected waves due to the incidence of coupled longitudinal waves having phase speed $V_3$ against the non-dimensional nonlocality parameter ${\bar{\epsilon }}=\epsilon k_{\ell }$, where $k_{\ell } = \dfrac{\omega }{c_{\ell }}$, at an angle of $\theta _3= 10^\circ$ at $f= 50$ kHz having a range between $1.5\times 10^{-3}<{\bar{\epsilon }}<3\times 10^{-1}$. The reflection coefficients $|X_1 |$, $|X_2 |$ and $|X_3 |$ are poorly influenced by the parameter ${{\bar{\epsilon }}}$, while the values of coefficient $|X_4 |$ is strongly affected by the nonlocal parameter. The value of reflection coefficient $|X_3 |$ is found to be equal to 0.9675 at ${\bar{\epsilon }} = 1.5\times 10^{-3}$ and then increases slightly to the value 0.9725 at ${\bar{\epsilon }} = 3\times 10^{-1}$. The value of reflection coefficient $|X_4 |$ starts from 0.171 at ${\bar{\epsilon }} = 1.5\times 10^{-3}$ and its value remains almost constant up to the value ${\bar{\epsilon }} = 1\times 10^{-1}$. Thereafter, its value starts increasing and increases to the value 0.2472 at $3\times 10^{-1}$. We also note that the reflection coefficients $|X_1 |$, $|X_2 |$ show a decreasing behavior, while the reflection coefficients $|X_3 |$ and $|X_4 |$ show an increasing behavior with nonlocal parameter ${{\bar{\epsilon }}}$. It is clear from Fig. 15 that the behavior of energy ratios is almost similar to the corresponding reflection coefficients. During the variation of nonlocal parameter, the sum of all energy ratios is found to be equal to unit satisfying law of conservation of energy at the boundary surface.

Fig. 14

Variation of reflection coefficients $|X_i |$ against nonlocality parameter (${\bar{\epsilon }}$) for incident coupled longitudinal waves having phase speed $V_3$ at $\theta _3=10^\circ$

Fig. 15

Variation of energy ratios $|E_i |$ against nonlocality parameter (${\bar{\epsilon }}$) for incident coupled longitudinal waves having phase speed $V_3$ at $\theta _3=10^\circ$

Figures 16 and 17 depict the variation of reflection coefficients and corresponding energy ratios versus $\bar{\epsilon }$ for the case of incidence of shear wave having speed $V_4$ at an angle $\theta _4 = 5^\circ$ at $f =50$ kHz. In the above considered range of non-dimensional nonlocality parameter, all the reflection coefficients show decreasing behavior. The value of $|X_1 |$ decreases from $2.8\times 10^{-4}$ to $1.799\times 10^{-4}$, while the value of $|X_2 |$ decreases from $1.5\times 10^{-4}$ to $1.0\times 10^{-4}$ in the considered range of nonlocality. Similarly, the reflection coefficient $|X_3 |$ decreases from 0.3469 to 0.2415, while the reflection coefficient $|X_4 |$ is slightly influenced by the nonlocality in considered range. In this range, its value decreases slightly from to 0.969 to 0.964. From Fig. 17, we can see that the behavior of all energy ratios $|E_1 |$, $|E_2 |$, $|E_3 |$ and $|E_4 |$ is similar to their respective reflection coefficients. One can note from Figs. 15 and 17 that the sum of energies of all the reflected waves is not unity for high values of non-dimensional nonlocality parameter. This is due to the fact that the approximation $(1-\epsilon ^2\nabla ^2)^{-1} \approx (1+\epsilon ^2\nabla ^2)$ has been used in the study.

Fig. 16

Variation of reflection coefficients $|X_i |$ against nonlocality parameter (${\bar{\epsilon }}$) for incident shear wave having phase speed $V_4$ at $\theta _4=5^\circ$

Fig. 17

Variation of energy ratios $|E_i |$ against nonlocality parameter (${\bar{\epsilon }}$) for incident shear wave having phase speed $V_4$ at $\theta _4=5^\circ$

Figures 18, 19, 20, 21 and 22 depict the variation of $|X_i |,~(i=1,2,3,4)$ with respect to the void parameters $b, ~ b_1, ~\alpha _3, ~\gamma$ and $\alpha$ ranging between $1\times 10^9~\text{ Pa }\le b\le 1.4\times 10^{10}~\text{ Pa }$, $5\times 10^4~\text{ Pa } \text{ m}^2\le b_1\le 8\times 10^{7}~\text{ Pa } \text{ m}^2$, $5\times 10^4~\text{ Pa }\le \alpha _3\le 1.5\times 10^{10}~\text{ Pa }$, $8\times 10^{9}~\text{ Pa } \text{ m}^2\le \gamma \le 4\times 10^{10}~\text{ Pa } \text{ m}^2$ and $8\times 10^{9}~\text{ Pa } \text{ m}^2\le \alpha \le 4\times 10^{10}~\text{ Pa } \text{ m}^2$, respectively, for the case of incidence of coupled longitudinal waves having phase speed $V_3$ at $f = 50$ kHz and $\theta _3 = 20^\circ$. We note that the values of reflection coefficients $|X_1 |$ and $|X_2 |$ are very small, while the values of reflection coefficients $|X_3 |$ and $|X_4 |$ are almost constant with respect to all the considered void parameters. Hence, the reflection coefficients are not much influenced by these void parameters.

Fig. 18

Variation of reflection coefficients $|X_i |$ against void parameter (b) for incident coupled longitudinal waves having phase speed $V_3$ at $\theta _3=20^\circ$

Fig. 19

Variation of reflection coefficients $|X_i |$ against void parameter ($b_1$) for incident coupled longitudinal waves having phase speed $V_3$ at $\theta _3=20^\circ$

Fig. 20

Variation of reflection coefficients $|X_i |$ against void parameter ($\alpha _3$) for incident coupled longitudinal waves having phase speed $V_3$ at $\theta _3=20^\circ$

Fig. 21

Variation of reflection coefficients $|X_i |$ against void parameter ($\gamma$) for incident coupled longitudinal waves having phase speed $V_3$ at $\theta _3=20^\circ$

Fig. 22

Variation of reflection coefficients $|X_i |$ against void parameter ($\alpha$) for incident coupled longitudinal waves having phase speed $V_3$ at $\theta _3=20^\circ$

Figure 23 depicts the variation of reflection coefficients $|X_i |,~(i=1,2,3,4)$ at an angle of $\theta _3=20^\circ$ with respect to the frequency parameter f on logarithmic scale ranging between $2\times 10^3~\text{ Hz }\le f\le 10^6~\text{ Hz }$ for the case of incidence of coupled longitudinal waves having phase speed $V_3$. We see that the value of reflection coefficient $|X_1 |$ decreases with an increase in linear frequency. It starts with a value 0.5663 at $f = 2\times 10^3$ Hz and then decreases to the zero value at $f=8\times 10^4$ Hz, and it remains zero afterward. The value of coefficient $|X_2 |$ is found to be very small in magnitude, and therefore it has been depicted after multiplying by a factor of $10^2$. The coefficient $|X_2 |$ has a value of $5.728\times 10^{-3}$ at $f= 2\times 10^3$ Hz; thereafter, it starts decreasing and attains the value $1.161\times 10^{-3}$ at $f= 8160$ Hz. After this, it starts increasing and reaches to $2.079\times 10^{-3}$ at $f = 2.1\times 10^4$ Hz. Beyond $f = 2.1\times 10^4$ Hz, it starts decreasing and tends to zero for further increase in value of frequency. The value of reflection coefficient $|X_3 |$ is found to be equal to 0.32 at $f = 2\times 10^3$ Hz and it increases to 0.8824 at $f = 5\times 10^4$ Hz. Beyond $f = 5\times 10^4$ Hz, $|X_3 |$ remains almost constant. The reflection coefficient $|X_4 |$ starts with a value of 0.2869 at $f = 2\times 10^3$ Hz and increases to 0.3201 at $f = 3.630\times 10^3$ Hz. Beyond this, it remains almost constant like $|X_3 |$.

Fig. 23

Variation of reflection coefficients $|X_i |$ against frequency (f) on logarithmic scale for incident coupled longitudinal waves having phase speed $V_3$ at $\theta _3=20^\circ$

Figures 24 and 25 depict the variation of absolute values of normalized surface displacements u, w and change in void fractional fields $\phi$, $\psi$, respectively, with respect to the angle of incidence for coupled dilatational waves having phase speed $V_3$. Here, the absolute values of u,  w have been normalized by the absolute value of w at normal incidence. It is found that the normalized value of vertical displacement w starts decreasing from unity with an increase in the angle of incidence and it tends to zero for grazing incidence. While the value of horizontal displacement u starts increasing from zero and tends to maximum value to 0.6993 at $\theta _3 = 58.81^\circ ,$ thereafter it tends to zero at grazing incidence. It is also observed from Fig. 24 that there is a slight decrease in the values of displacements at angles $50.72^\circ$ and $50.95^\circ$. This is due to the critical angles faced by the reflected waves corresponding to phase speed $V_1$ and $V_2$, respectively. In Fig. 25, the values of $\phi , ~\psi$ have been normalized with the absolute value of $\phi$ at normal incidence. It is observed that the normalized value of $\phi$ starts from unity and remains almost constant up to $44^\circ$, then there is sharp rise and goes to the maximum value 36.05 at critical angle $50.72^\circ$. Thereafter, it tends to value 0.5583 at grazing incidence. A similar behavior is also observed for $\psi$, it starts from value of 1.18, then increases to the maximum value 42.47 near the critical angle $50.95^\circ$, and then ultimately tends to the value 0.32 as $\theta _3\rightarrow 90^\circ$.

Fig. 24

Variation of absolute value of normalized surface displacements $|u |$, $|w |$ with respect to angle of incidence ($\theta _3$) for incident coupled longitudinal waves having phase speed $V_3$

Fig. 25

Variation of absolute value of normalized surface void fractional fields $|\phi |$, $|\psi |$ with respect to angle of incidence ($\theta _3$) for incident coupled longitudinal waves having phase speed $V_3$

Figures 26 and 27 depict the variation of absolute values of normalized surface displacements u, w, and void fractional fields $\phi$, $\psi$, respectively, with respect to the angle of incidence of shear wave having phase speed $V_4$. Here, the values of u,  w have been normalized by the absolute value of u at normal incidence and the values of $\phi , ~\psi$ have been normalized with the absolute value of $\phi$ at normal incidence. It is observed that the horizontal displacement u starts from unity and then slightly decreases to 0.9635 at $20.01^\circ$; thereafter, its value increases to 1.732 as angle of incidence tends to $30.02^\circ$. Thereafter, it tends to zero value at $45^\circ$ and then starts increasing to the value 0.2408 at $65.95^\circ$. Beyond $65.95^\circ$, it decreases to zero at grazing incidence. The value of vertical displacement w starts increasing from zero to the value 0.3495 at an angle $25.47^\circ$ and then decreases to 0.025 at $30.01^\circ$. Beyond $30.01^\circ$, it increases sharply to the value 0.8199 at $36.09^\circ$ and then decreases to zero at grazing incidence. From Fig. 27, it is observed that the normalized value of $\phi$ starts from unity and increases slowly up to $20^\circ$, then shows a sharp rise to the maximum value 80.35 at the angle $22.78^\circ$. Beyond $22.78^\circ$, it decreases to value 1.697 at $29.86^\circ$, and then increases to the value 2.351 at $32.22^\circ$. Thereafter, its value tends to unity at grazing incidence. Similarly, the value of $\psi$ starts from 1.182 and then shows a maximum value 60.31 at $22.85^\circ$. Beyond this, the value decreases to 1.004 at $29.89^\circ$, then it increases to the value 2.786 at $32.28^\circ$, thereafter its value decreases to 1.182 at grazing incidence.

Fig. 26

Variation of absolute value of normalized surface displacements $|u |$, $|w |$ with respect to angle of incidence ($\theta _4$) for incident shear wave having phase speed $V_4$

Fig. 27

Variation of absolute value of normalized surface void fractional fields $|\phi |$, $|\psi |$ with respect to angle of incidence ($\theta _4$) for incident shear wave having phase speed $V_4$

9 Conclusions

In the present paper, we have studied the reflection phenomena of plane waves from the stress-free boundary surface of a linear nonlocal homogeneous and isotropic elastic solid half-space having double porosity structure. Employing nonlocal stress-free boundary conditions, the reflection coefficients for the incidence of coupled longitudinal waves having phase speed $V_n,~(n= 1,2,3)$ and shear wave having phase speed $V_4$ are obtained. The following conclusions can be inferred from this study.

• 1. All the reflection coefficients depend on nonlocality of the medium, void parameters, angle of incidence, frequency of the incident wave and material moduli.

• 2. The maximum amount of the incident energy goes along that reflected wave, which travels with the same speed as that of the incident wave for initial range of angles, irrespective of whether the incident wave is coupled longitudinal waves or shear wave.

• 3. The reflected waves, which is predominantly corresponding to the change in void volume fraction of the first and second kind of voids, face critical angles in both the cases of incidence.

• 4. The reflection coefficient corresponding to the incident wave remains almost the same in the considered range of ${{\bar{\epsilon }}}$ in both the cases.

• 5. In case of incident coupled longitudinal waves with phase velocity $V_3$, the reflection coefficient $|X_4 |$ shows an increasing behavior with nonlocal parameter ${{\bar{\epsilon }}}$, while the coefficients $|X_1 |$ and $|X_2 |$ remain almost constant.

• 6. In case of incident shear wave, the reflection coefficients $|X_1 |$, $|X_2 |$ and $|X_3 |$ decrease with nonlocal parameter ${{\bar{\epsilon }}}$.

• 7. All the reflection coefficients are found to be influenced poorly by void parameters $b, b_1, \alpha _3, \gamma$ and $\alpha$ in case of incidence of coupled longitudinal waves propagating with phase velocity $V_3$.

• 8. The sum of energy ratios corresponding to various reflected waves is found to be unity in all the cases of incidence. This shows that there is no dissipation of energy at boundary surface for each angle of incidence.

• 9. It is found that there is a phase shift in the reflected waves, who face critical angles. Also, in case of non-dissipative (dissipative) model, the phase change is zero (nonzero) below the respective critical angles for reflected coupled longitudinal waves.

The double porosity continua have applications in manmade materials, geophysics, mathematical biology, seismology, nuclear waste treatment, nuclear material behavior, study of lava from Mount Etna and many other engineering branches (see Straughan [17]).