1 Introduction

The process of reflection/refraction is of great importance (practically as well as theoretically) in various scientific fields, such as hydrogeology, engineering geology, seismology and petroleum geophysics. The process of reflection/refraction occurs due to the discontinuity encountered at the interface of two media. In exploration geophysics and seismology, seismic (reflection/refraction phenomenon) methods are used to analyze the fluid content in subsurface reservoirs. The feedback from reservoir rocks is carried out on the basis of reflected/refracted wave signals. The wave aspect (reflection/refraction) through interfaces provides accurate information of earthquake processes, prospecting techniques, and also it is used in the detection of nuclear explosions. In recent years, the problems of reflection/refraction at the interface between two different media have been investigated extensively by Tomar and Arora (2006), Dai et al. (2006a, b), Dai and Kuang (2008), Yeh et al. (2010), Kumar and Sharma (2013), Kumar and Saini (2012, 2016), Bhagwan and Tomar (2015), Goyal and Tomar (2015) and Shekhar and Parvez (2015, 2016), etc.

Generally, most subsurface sedimentary rocks are heterogeneous in nature. It is generally observed that realistic heterogeneous reservoirs have a dual-porosity network: One is matrix porosity, and another is fracture porosity. The matrix (storage) porosity occupies most of the volume of the reservoir, while fracture (crack) porosity occupies very little volume. These two porosities are distinguished on the basis of permeability as the fracture (crack) permeability is greater than the matrix permeability. Double-porosity dual-permeability materials theory plays an important role for the characterization of highly fractured reservoirs. Therefore, it is indispensable to recognize the reflection/refraction signatures in realistic heterogeneous porous rocks. It is well known that in heterogeneous rocks, the viscous loss is mainly due to the equilibration that occurs when fluid flows from high-pressure regions to relatively low-pressure regions (Batzle et al. 2006). The extension of Biot’s poroelasticity to double-porosity porous solid was carried out by Berryman and Wang (1995, 2000). They derived the phenomenological equations for double-porosity/dual-permeability media. They found that three longitudinal waves and one shear wave exist in a double-porosity medium. Later, Pride and Berryman (2003a, b) modified the governing equations developed by Berryman and Wang (1995, 2000) for mesoscopic fluid flow in double-porosity dual-permeability materials by using the volume averaging technique. In recent years, the main credit goes to Sharma (2013, 2014, 2015a, b, 2016, 2017a, b) for comprehensive discussion on wave propagation in double-porosity solids. Sharma (2017a) studied the effects of wave frequency, wave inhomogeneity, pore-fluid viscosity and skeletal permeability on the propagation and attenuation of waves in double-porosity dual-permeability (DP2) materials. Sharma (2017b) studied the propagation and attenuation of inhomogeneous waves in double-porosity dual-permeability materials. He graphically analyzed the effects of pore-fluid viscosity, wave inhomogeneity and composition of double porosity on inhomogeneous propagation of waves. He also studied the variations in the fluid-flow profile for different values of pore-fluid viscosity, skeleton permeability, wave frequency and wave inhomogeneity. Based on the Berryman and Wang theory, the reflection/transmission process at the boundary of double-porosity media was investigated by Dai et al. (2006a, b) and Dai and Kuang (2008), but the concept of wave-induced fluid-flow and double-porosity structure was completely ignored in these articles. Ba et al. (2011) developed the Biot–Rayleigh theory of wave propagation in double-porosity media. Bai et al. (2015) investigated ultrasound wave transmission through a multilayered structure consisting of DP2 media saturated with water in a rectangular box immersed in water. Two particular examples of double-porosity dual-permeability materials are considered for numerical computations. One of them is ROBU® (the individual grains are compacted microscopic beads of borosilicate glass 3.3), and another is Tobermorite 11Å (the individual porous cement grains have irregular shapes). These two materials obey the Berryman’s extension of Biot’s theory (Berryman and Wang 1995, 2000). Later, Bai et al. (2016) studied the acoustic plane wave transmission through double-porosity media saturated with water. They minimized the gap existing between theoretical and experimental data by modifying the two theoretically estimated parameters (i.e., frame bulk and shear moduli). To analyze the compressional-wave dissipation process in a double-porosity/dual-fluid medium, a triple-layer patchy (TLP) model has been developed by Sun et al. (2016). The phenomenological equations of the TLP model are proposed on the basis of Biot’s theory. Zheng et al. (2017) investigated the wave attenuation and phase velocity dispersion induced by wave-induced mesoscopic fluid flow on the basis of double-porosity, dual-permeability theory.

In the present problem, the reflection/refraction phenomena at the interface of an elastic solid and double-porosity dual-permeability medium are illustrated. The mathematical model developed by Berryman and Wang (1995, 2000), Pride and Berryman (2003a, b) and Pride et al. (2004) is employed to study the wave propagation in DP2 media. The double-porosity dual-permeability medium represents a realistic heterogeneous porous structure. The elastic solid behaves non-dissipatively, while double-porosity dual-permeability materials behave dissipatively to wave propagation due to the presence of viscosity in the pore fluid. All the waves (i.e., incident and reflected) in an elastic medium are considered as homogeneous (i.e., with the same directions of propagation and attenuation), while all the refracted waves in double-porosity dual-permeability materials are inhomogeneous (i.e., with different directions of propagation and attenuation). The coefficients of reflection and refraction for a given incident wave are obtained as a non-singular system of linear equations. The energy shares of reflected and refracted waves are obtained in the form of an energy matrix. A numerical example is considered to calculate the partition of incident energy among various reflected and refracted waves. The effect of incident direction on the partition of the incident energy is analyzed with a change in wave frequency, wave-induced fluid-flow, pore-fluid viscosity and double-porosity structure. It has been confirmed from the numerical interpretation that during reflection/refraction processes, conservation of incident energy is obtained at each angle of incidence.

2 Basic equations

The equations of motion for double-porosity dual-permeability materials in the absence of body force are defined as (Pride and Berryman 2003a; Sharma 2017a)

$$\begin{aligned} & \sigma_{ij,j} = \rho \ddot{u}_{i} + \rho_{\text{f}} \ddot{v}_{i} + \rho_{\text{f}} \ddot{w}_{i} , \\ & ( - p_{\text{f1}} ),_{i} = \rho_{\text{f}} \ddot{u}_{i} + \rho_{2} \ddot{v}_{i} + \rho_{3} \ddot{w}_{i} , \\ & ( - p_{\text{f2}} ),_{i} = \rho_{\text{f}} \ddot{u}_{i} + \rho_{3} \ddot{v}_{i} + \rho_{4} \ddot{w}_{i} , \\ \end{aligned}$$
(1)

where \(u_{i}\) and \(v_{i} (w_{i} )\) define the average displacement components of solid and average displacement components of pore-fluid particles relative to the solid in the first (second) porous phase, respectively. A dot over a variable represents the time derivative. \(\sigma_{ij}\) is the stress tensor, and \((p_{\text{f1}} , p_{\text{f2}} )\) are pore fluid pressures in two porous phases. \(\rho ( = (1 - \phi^{*} )\rho_{\text{s}} + \phi^{*} \rho_{\text{f}} )\) is the density of the double-porosity dual-permeability solid. \(\rho_{\text{s}}\) and \(\rho_{\text{f}}\) define the density of solid and fluid constituents, respectively. The total porosity \((\phi^{*} )\) is given by \(\phi^{*} = \nu_{1} \phi_{1}^{*} + \nu_{2} \phi_{2}^{*} ,\) where \(\nu_{1}\) and \(\nu_{2} ( = 1 - \nu_{1} )\) denote the volume fractions of the two phases in the double-porosity dual-permeability composite. \(\phi_{1}^{*}\) and \(\phi_{2}^{*}\) denote the intrinsic porosities of the two phases. The dynamical constants in (1) are defined as follows

$$\rho_{2} = \iota \frac{\eta }{\omega }\chi_{11} ,\rho_{3} = \iota \frac{\eta }{\omega }\chi_{12} ,\rho_{4} = \iota \frac{\eta }{\omega }\chi_{22} ,$$

where \((\chi_{11} ,\chi_{12} ,\chi_{13} ) = (\kappa_{22} , - \kappa_{12} ,\kappa_{11} ) /(\kappa_{11} \kappa_{22} - \kappa_{12}^{2} )\). \(\eta\) represents the viscosity of water. \(\omega\) is the angular wave frequency. These coefficients are defined as the inverse of the second-order symmetric permeability tensor \(\left\{ {\kappa_{lm} } \right\}\) (Sharma 2017a).

The linear constitutive relations for double-porosity dual-permeability materials are defined as (Pride and Berryman 2003a; Sharma 2017a)

$$\begin{aligned} & \sigma_{ij} = \left\{ {\left( {b_{11} - \frac{2}{3}G} \right)\nabla \cdot {\mathbf{u}} + b_{12} \nabla \cdot {\mathbf{v}} + b_{13} \nabla \cdot {\mathbf{w}}} \right\}{\mathbf{I}} + G(u_{i,j} + u_{j,i} ), \\ & - p_{\text{f1}} = \left\{ {b_{12} \nabla \cdot {\mathbf{u}} + b_{22} \nabla \cdot {\mathbf{v}} + b_{23} \nabla \cdot {\mathbf{w}}} \right\}{\mathbf{I}}, \\ & - p_{\text{f2}} = \left\{ {b_{13} \nabla \cdot {\mathbf{u}} + b_{23} \nabla \cdot {\mathbf{v}} + b_{33} \nabla \cdot {\mathbf{w}}} \right\}{\mathbf{I}}, \\ \end{aligned}$$
(2)

where \({\mathbf{u}}\) and \({\mathbf{v}}({\mathbf{w}})\) define the average displacement of the solid and average displacement of pore-fluid particles relative to the solid in the first (second) porous phase, respectively. G is the rigidity modulus of the porous frame.

and

$${\mathbf{I}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right].$$

In the presence of wave-induced fluid flow (WIFF), the anelastic coefficients \(b_{ij}\) are defined as (Sharma 2017a)

$$\begin{aligned} & b_{ij} = c_{ij} - \frac{{(c_{i2} - c_{i3} )(c_{j2} - c_{j3} )}}{{c_{22} + c_{33} - 2c_{23} - \iota \omega /\gamma (\omega )}};\quad \gamma (\omega ) = \gamma_{0} \sqrt {1 - \iota \frac{\omega }{{\omega_{c} }}} , \\ & \gamma_{0} = \frac{{\nu_{1} \kappa_{11} }}{{\eta L_{1}^{2} }},\quad \omega_{c} = \frac{{\eta B_{1} K_{1} }}{{\kappa_{11} \alpha_{1} }}\left( {\frac{V}{S}\gamma_{0} } \right)^{2} ,\quad \frac{V}{S} = \frac{{R^{3} }}{{3r^{2} }}, \\ \end{aligned}$$

where V/S measures the volume-to-surface ratio of phase 2 as embedded in phase 1. r is the radius of sphere (phase 2) which is included at the center of a sphere (phase 1) of radius R. L1 denotes the average distance over which a fluid-pressure gradient exists in phase 1, in the final stages of equilibration (Pride and Berryman 2003b). In the absence of wave-induced fluid flow (WIFF), the anelastic coefficients bij = cij. The elastic coefficients cij are defined as the inverse of the symmetric compliance tensor aij. The symmetric compliance tensor aij, i, j = 1, 2, 3, is related to the various measurable quantities of the porous aggregate as in Sharma (2017a).

After substituting Eq. (2) in (1), we get

$$\nabla \left[ {\left( {b_{11} + \frac{1}{3}G} \right)\nabla \cdot {\mathbf{u}} + b_{12} \nabla \cdot {\mathbf{v}} + b_{13} \nabla \cdot {\mathbf{w}}} \right]{\mathbf{I}} + G\nabla^{2} {\mathbf{u}} = \rho \ddot{u}_{i} + \rho_{\text{f}}\ddot v_{i} + \rho_{\text{f}} \ddot w_{i} ,$$
(3)
$$\nabla \left[ {b_{12} \nabla \cdot {\mathbf{u}} + b_{22} \nabla \cdot {\mathbf{v}} + b_{23} \nabla \cdot {\mathbf{w}}} \right]{\mathbf{I}} = \rho_{f} \ddot{u}_{i} + \rho_{ 2} \ddot{v}_{i} + \rho_{ 3} \ddot{w}_{i} ,$$
(4)
$$\nabla \left[ {b_{13} \nabla \cdot {\mathbf{u}} + b_{23} \nabla \cdot {\mathbf{v}} + b_{33} \nabla \cdot {\mathbf{w}}} \right]{\mathbf{I}} = \rho_{f} \ddot{u}_{i} + \rho_{ 3} \ddot{v}_{i} + \rho_{ 4} \ddot{w}_{i} .$$
(5)

3 Plane harmonic wave

Through the usual Helmholtz resolution of a vector, the three displacement vectors are written as

$${\mathbf{u}} = \nabla \phi_{0} + \nabla \times \psi_{0} ,\quad \nabla \cdot \psi_{0} = 0,$$
(6)
$${\mathbf{v}} = \nabla \phi_{1} + \nabla \times \psi_{1} ,\quad \nabla \cdot \psi_{1} = 0,$$
(7)
$${\mathbf{w}} = \nabla \phi_{2} + \nabla \times \psi_{2} ,\quad \nabla \cdot \psi_{2} = 0.$$
(8)

In terms of these displacement potentials \((\phi_{0} ,\phi_{1} ,\phi_{2} ,\psi_{0} ,\psi_{1} ,\psi_{2} ),\) Eqs. (3)–(5) are expressed as follows:

$$b_{11}^{*} \nabla^{2} \phi_{0} + b_{12} \nabla^{2} \phi_{1} + b_{13} \nabla^{2} \phi_{2} = \rho \ddot{\phi }_{0} + \rho_{\text{f}} \ddot{\phi }_{1} + \rho_{\text{f}} \ddot{\phi }_{2} ,$$
(9)
$$b_{12} \nabla^{2} \phi_{0} + b_{22} \nabla^{2} \phi_{1} + b_{23} \nabla^{2} \phi_{2} = \rho_{\text{f}} \ddot{\phi }_{0} + \rho_{2} \ddot{\phi }_{1} + \rho_{3} \ddot{\phi }_{2} ,$$
(10)
$$b_{13} \nabla^{2} \phi_{0} + b_{23} \nabla^{2} \phi_{1} + b_{33} \nabla^{2} \phi_{2} = \rho_{\text{f}} \ddot{\phi }_{0} + \rho_{3} \ddot{\phi }_{1} + \rho_{4} \ddot{\phi }_{2} ,$$
(11)
$$G\nabla^{2} \psi_{0} = \rho \ddot{\psi }_{0} + \rho_{\text{f}} \ddot{\psi }_{1} + \rho_{\text{f}} \ddot{\psi }_{2} ,$$
(12)
$$0 = \rho_{\text{f}} \ddot{\psi }_{0} + \rho_{2} \ddot{\psi }_{1} + \rho_{3} \ddot{\psi }_{2} ,$$
(13)
$$0 = \rho_{\text{f}} \ddot{\psi }_{0} + \rho_{3} \ddot{\psi }_{1} + \rho_{4} \ddot{\psi }_{2} ,$$
(14)

where \(b_{11}^{*} = b_{11} + \frac{4}{3}G.\)

For time harmonic \(( \sim e^{ - \iota \omega t} )\) potentials \((\phi_{0} ,\phi_{1} ,\phi_{2} )\) represent the propagation of harmonic waves with angular frequency \(\omega\) in the two-dimensional x–z plane, relations (9)–(11) transform to

$$(b_{11}^{*} \nabla^{2} + \omega^{2} \rho )\phi_{0} + (b_{12} \nabla^{2} + \omega^{2} \rho_{\text{f}} )\phi_{1} + (b_{13} \nabla^{2} + \omega^{2} \rho_{\text{f}} )\phi_{2} = 0,$$
(15)
$$(b_{12} \nabla^{2} + \omega^{2} \rho_{\text{f}} )\phi_{0} + (b_{22} \nabla^{2} + \omega^{2} \rho_{2} )\phi_{1} + (b_{23} \nabla^{2} + \omega^{2} \rho_{3} )\phi_{2} = 0,$$
(16)
$$(b_{13} \nabla^{2} + \omega^{2} \rho_{\text{f}} )\phi_{0} + (b_{23} \nabla^{2} + \omega^{2} \rho_{3} )\phi_{1} + (b_{33} \nabla^{2} + \omega^{2} \rho_{4} )\phi_{2} = 0.$$
(17)

Equations (16) and (17) of this system are solved into two relations, given by

$$\left( {a_{2} \nabla^{4} + a_{1} \omega^{2} \nabla^{2} + a_{0} \omega^{4} } \right)\phi_{1} = \left( {b_{2} \nabla^{4} + b_{1} \omega^{2} \nabla^{2} + b_{0} \omega^{4} } \right)\phi_{0} ,$$
(18)
$$\left( {a_{2} \nabla^{4} + a_{1} \omega^{2} \nabla^{2} + a_{0} \omega^{4} } \right)\phi_{2} = \left( {c_{2} \nabla^{4} + c_{1} \omega^{2} \nabla^{2} + c_{0} \omega^{4} } \right)\phi_{0} ,$$
(19)

where

$$\begin {aligned} & b_{2} = b_{13} b_{23} - b_{12} b_{33} ,\\ & b_{1} = \rho_{3} b_{13} + \rho_{\text{f}} b_{23} - \rho_{4} b_{12} - \rho_{\text{f}} b_{33} , \\ & b_{0} = \rho_{\text{f}} (\rho_{3} - \rho_{4} ), \end{aligned}$$
$$\begin {aligned} & a_{2} = b_{22} b_{33} - b_{23}^{2} ,\\ & a_{1} = \rho_{4} b_{22} + \rho_{2} b_{33} - 2\rho_{3} b_{23}, \\ & a_{0} = \rho_{2} \rho_{4} - \rho_{3}^{2} , \end{aligned}$$
$$\begin {aligned} & c_{2} = b_{12} b_{23} - b_{13} b_{22} ,\\ & c_{1} = \rho_{3} b_{12} + \rho_{\text{f}} b_{23} - \rho_{2} b_{13} - \rho_{\text{f}} b_{22} ,\\ & c_{0} = \rho_{\text{f}} (\rho_{3} - \rho_{2} ). \end{aligned}$$

On using above relations into Eq. (15), we get

$$\left[ {C_{3} \nabla^{6} + \omega^{2} C_{2} \nabla^{4} + \omega^{4} C_{1} \nabla^{2} + \omega^{6} C_{0} } \right]\phi_{0} = 0,$$
(20)

where

$$\left( {\begin{array}{*{20}c} {C_{3} } \\ {C_{2} } \\ {C_{1} } \\ {C_{0} } \\ \end{array} } \right) = \left[ {\begin{array}{*{20}c} {a_{2} } & {b_{2} } & {c_{2} } \\ {a_{1} } & {b_{1} } & {c_{1} } \\ {a_{0} } & {b_{0} } & {c_{0} } \\ 0 & 0 & 0 \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {b_{11}^{*} } \\ {b_{12} } \\ {b_{13} } \\ \end{array} } \right) + \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ {a_{2} } & {b_{2} } & {c_{2} } \\ {a_{1} } & {b_{1} } & {c_{1} } \\ {a_{0} } & {b_{0} } & {c_{0} } \\ \end{array} } \right]\left( {\begin{array}{*{20}c} \rho \\ {\rho_{f} } \\ {\rho_{f} } \\ \end{array} } \right).$$

Differential Eq. (20) is decomposed into three Helmholtz equations, given by

$$\prod\limits_{i = 1}^{3} {\left( {\nabla^{2} + \frac{{\omega^{2} }}{{\alpha_{i}^{2} }}} \right)} \phi_{0} = 0,$$
(21)

which implies the existence of three dilatational waves propagating with phase velocities \(\alpha_{i} (i = 1,2,3)\). These velocities are derived from the roots of a cubic equation in α2, given by

$$C_{0} \alpha^{6} - C_{1} \alpha^{4} + C_{2} \alpha^{2} - C_{3} = 0.$$
(22)

In the descending order of real parts, the velocities α1, α2, α3 correspond to the dilatational waves, which are identified as P1, P2, P3 waves, respectively. In the considered double-porosity dual-permeability materials, the potential function for aggregate dilation is expressed as follows:

$$\phi_{0} = \Psi_{1} + \Psi_{2} + \Psi_{3} ;\quad \left( {\nabla^{2} + \frac{{\omega^{2} }}{{\alpha_{i}^{2} }}} \right)\Psi_{j} = 0,$$
(23)

which, on using in relations (18)–(19), yields

$$\phi_{1} = \mu_{1} \Psi_{1} + \mu_{2} \Psi_{2} + \mu_{3} \Psi_{3} ,$$
(24)
$$\phi_{2} = \lambda_{1} \Psi_{1} + \lambda_{2} \Psi_{2} + \lambda_{3} \Psi_{3} ,$$
(25)

where

$$\mu_{j} = \frac{{b_{2} - b_{1} \alpha_{j}^{2} + b_{0} \alpha_{j}^{4} }}{{a_{2} - a_{1} \alpha_{j}^{2} + a_{0} \alpha_{j}^{4} }},\quad \lambda_{j} = \frac{{c_{2} - c_{1} \alpha_{j}^{2} + c_{0} \alpha_{j}^{4} }}{{a_{2} - a_{1} \alpha_{j}^{2} + a_{0} \alpha_{j}^{4} }},\quad j = 1,\,2,\,3.$$

Analogous to scalar potentials, for time harmonic \(( \sim e^{ - \iota \omega t} )\) vector potentials \(\left( {\psi_{0} ,\,\psi_{1} ,\,\psi_{2} } \right)\), Eqs. (12)–(14) are solved into

$$(G\nabla^{2} + \omega^{2} \rho )\psi_{0} + \omega^{2} \rho_{\text{f}} \psi_{1} + \omega^{2} \rho_{\text{f}} \psi_{2} = 0,$$
(26)
$$\{ \psi_{1} ,\psi_{2} \} = \{ \mu_{4} ,\lambda_{4} \} \psi_{0} ;\quad \mu_{4} = \frac{{(\rho_{3} - \rho_{4} )\rho_{\text{f}} }}{{\rho_{2} \rho_{4} - \rho_{3}^{2} }},\quad \lambda_{4} = \frac{{(\rho_{3} - \rho_{2} )\rho_{\text{f}} }}{{\rho_{2} \rho_{4} - \rho_{3}^{2} }}.$$
(27)

Solving the above relations, we get a Helmholtz equation, given by

$$\left( {\nabla^{2} + \frac{{\omega^{2} }}{{\beta^{2} }}} \right)\psi_{0} = 0,\quad \beta = \sqrt {\frac{G}{{\rho + \rho_{\text{f}} \left( {\mu_{4} + \lambda_{4} } \right)}}} ,$$
(28)

which defines the existence of a shear wave propagating with velocity \(\beta .\)

4 Displacements

For two-dimensional motion in x–z plane, the displacement components of solid and fluid phases are given by

$$u_{x} = \sum\limits_{j = 1}^{3} {\frac{{\partial \Psi_{j} }}{\partial x} - \frac{{\partial \Psi_{4} }}{\partial z},\quad u_{z} = \sum\limits_{j = 1}^{3} {\frac{{\partial \Psi_{j} }}{\partial z} + \frac{{\partial \Psi_{4} }}{\partial x},} }$$
(29)
$$v_{x} = \sum\limits_{j = 1}^{3} {\mu_{j} \frac{{\partial \Psi_{j} }}{\partial x} - \mu_{4} \frac{{\partial \Psi_{4} }}{\partial z},\quad v_{z} = \sum\limits_{j = 1}^{3} {\mu_{j} \frac{{\partial \Psi_{j} }}{\partial z} + \mu_{4} \frac{{\partial \Psi_{4} }}{\partial x},} }$$
(30)
$$w_{x} = \sum\limits_{j = 1}^{3} {\lambda_{j} \frac{{\partial \Psi_{j} }}{\partial x} - \lambda_{4} \frac{{\partial \Psi_{4} }}{\partial z},\quad w_{z} = \sum\limits_{j = 1}^{3} {\lambda_{j} \frac{{\partial \Psi_{j} }}{\partial z} + \lambda_{4} \frac{{\partial \Psi_{4} }}{\partial x},} }$$
(31)

where \(\Psi_{4} = (\psi_{0} )_{y} .\)

5 Elastic solid

The isotropic stress–strain relation of an elastic solid is given by

$$\tau_{ij} = \lambda_{e} \nabla \cdot {\mathbf{u}}^{e} {\mathbf{I}} + \mu_{e} (u_{i,j}^{e} + u_{j,i}^{e} ),$$
(32)

where \(\lambda_{e}\) and \(\mu_{e}\) are Lame’s constants. \({\mathbf{u}}^{e}\) is the displacement vector. The corresponding expressions for a displacement vector \({\mathbf{u}}^{e}\) are written as

$$u_{x}^{e} = \frac{{\partial \phi_{e} }}{\partial x} - \frac{{\partial \psi_{e} }}{\partial z},\quad u_{z}^{e} = \frac{{\partial \phi_{e} }}{\partial z} + \frac{{\partial \psi_{e} }}{\partial x}.$$
(33)

The displacement potentials \(\phi_{e}\) (for the P wave) and \(\psi_{e}\) (for the SV wave) satisfy the wave equations, given by

$$\nabla^{2} \phi_{e} = \frac{1}{{\alpha_{e}^{2} }}\frac{{\partial^{2} \phi_{e} }}{{\partial t^{2} }},\quad \nabla^{2} \psi_{e} = \frac{1}{{\beta_{e}^{2} }}\frac{{\partial^{2} \psi_{e} }}{{\partial t^{2} }},$$
(34)

where \(\alpha_{e} = \sqrt {\frac{{\lambda_{e} + 2\mu_{e} }}{{\rho_{e} }}}\) and \(\beta_{e} = \sqrt {\frac{{\mu_{e} }}{{\rho_{e} }}}\) are the velocities of longitudinal and transverse waves, respectively.

6 Formulation of the problem

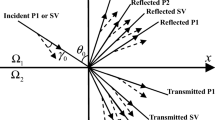
A rectangular Cartesian coordinate system (x, y, z) is considered to represent the present problem. Our aim is to study the problem of reflection and refraction in the x–z plane, resulting from the oblique incidence of a plane wave at the interface z = 0. We consider a uniform elastic solid (occupies the region − ∞ < z < 0) is in welded contact with a double-porosity dual-permeability material (occupies the region 0 < z < ∞) at the interface z = 0. A plane harmonic wave propagates with velocity \(v_{0}\) and angular frequency ω through the upper half-space (i.e., the elastic solid) incident at the boundary z = 0 with an angle of incidence θ0. Consequently, two waves (i.e., P and SV) are reflected back in the upper half-space (i.e., elastic solid) and four refracted waves (i.e., P1, P2, P3, SV) are generated in lower half-space (i.e., double-porosity dual-permeability materials) as shown in Fig. 1.

Fig. 1
figure 1

Geometry of the problem

Full size image

7 Boundary conditions

The boundary conditions to determine the reflection/refraction coefficients of plane waves at the welded contact of the two media are described on the basis of various articles including Deresiewicz and Skalak (1963), Tomar and Arora (2006), Sharma (2009), Kumar and Saini (2012) and Goyal and Tomar (2015). The appropriate boundary conditions for the welded contact of two media are the continuity of stress components and displacement components. The boundary conditions at plane interface z = 0 are expressed as follows:

$$\begin{aligned} & \tau_{zz} = \sigma_{zz} + ( - p_{f1} ) + ( - p_{f2} ),\quad \tau_{zx} = \sigma_{zx} , \\ & \dot{u}_{x}^{e} = \dot{u}_{x} ,\quad \dot{u}_{z}^{e} = \dot{u}_{z} ,\quad \dot{u}_{z} = \dot{v}_{z} ,\quad \dot{u}_{z} = \dot{w}_{z} . \\ \end{aligned}$$
(35)

8 Reflection and refraction

In the present work, our aim is to study the reflection and refraction of plane harmonic waves at the interface z = 0 between an elastic solid and DP2 materials. As the elastic solid is non-dissipative, therefore all the waves (i.e., incident and reflected) in the elastic solid are homogeneous (i.e., having the same directions of propagation and attenuation) in nature. Therefore, the displacement potentials that identify the particle motions associated with the incident and reflected waves in an elastic solid are expressed as

$$\begin {aligned} \phi_{e} =&F_{e0} \exp [\iota \omega \{ xs + zq_{0} - t\} ] \\ & + F_{e1} \exp [\iota \omega \{ xs - zq_{{\alpha_{e} }} - t\} ], \end{aligned}$$
(36)
$$\begin {aligned} \psi_{e} = & G_{e0} \exp [\iota \omega \{ xs + zq_{0} - t\} ] \\& + G_{e1} \exp [\iota \omega \{ xs - zq_{{\beta_{e} }} - t\} ]. \end{aligned}$$
(37)

where arbitrary coefficients \(F_{e0} (G_{e0} )\) and \(F_{e1} (G_{e1} )\) represent the amplitudes of the incident P(SV) and reflected P(SV) waves, respectively. According to Snell’s law, the horizontal slowness s( = sin θ0/v0) will remain the same for all the reflected and refracted waves. Then, q0( = cos θ0/v0) is the vertical slowness of the incident wave. \(q_{{\alpha_{e} }} = \frac{{\cos \theta_{1} }}{{\alpha_{e} }}\left( {q_{{\beta_{e} }} = \frac{{\cos \theta_{1} }}{{\beta_{e} }}} \right)\) is the vertical slowness of the reflected P(SV) wave and

$$v_{0} = \left\{ {\begin{array}{*{20}l} {\alpha_{e} ,\quad {\text{for}}\;{\text{incident}}\;{\text{P - wave}},} \hfill \\ {\beta_{e} ,\quad {\text{for}}\;{\text{incident}}\;{\text{SV - wave}}.} \hfill \\ \end{array} } \right.$$

A DP2 material is considered dissipative due to the presence of viscosity in pore fluid. Therefore, all the refracted waves are inhomogeneous (i.e., with different directions of propagation and attenuation) in nature due to the dissipative nature of the medium. Following Borcherdt (2009), the displacement potentials identify the particle motions associated with four refracted waves in DP2 materials expressed as

$$\Psi_{j} = F_{j} \exp ({\mathbf{A}}_{j} \cdot r) \cdot \exp \{ \iota ({\mathbf{P}}_{j} \cdot r - \omega t)\} ,\quad (j = 1,2,3,4),$$
(38)

The arbitrary coefficients \(F_{j} ,(j = 1,2,3,4),\) represent the amplitudes of the refracted P1, P2, P3 and SV waves, respectively. The propagation vectors \(({\mathbf{P}}_{j} )\) and attenuation vectors \(({\mathbf{A}}_{j} )\) of four refracted waves are defined by

$${\mathbf{P}}_{j} = k_{R} \hat{x} + q_{jR} \hat{z},\quad {\mathbf{A}}_{j} = - k_{I} \hat{x} - q_{jI} \hat{z},$$
(39)

where the subscripts R and \(I\) denote the real and imaginary parts of the corresponding complex quantities. In terms of angle between the propagation vector and attenuation vector \((\tilde {\gamma }_{j} )\) and angle of refraction \((\tilde{\theta }_{j} )\) in DP2 materials, \(k\) is written as

$$k = \left| {{\mathbf{P}}_{j} } \right|\sin \tilde{\theta }_{j} - \iota \left| {{\mathbf{A}}_{j} } \right|\sin (\tilde{\theta }_{j} - \tilde{\gamma }_{j} ).$$
(40)

According to Snell’s law, all the reflected and refracted waves must have same horizontal slowness.

$$k_{R} = s\omega .$$
(41)

kR ≥ 0 ensures propagation in the positive x-direction. The real wave number k (i.e., \(k_{I} = 0\)) in dissipative double-porosity dual-permeability materials implies that \(\tilde{\gamma }_{j} = \tilde{\theta }_{j} ,(j = 1,\,2,\,3,\,4),\) i.e., attenuation vectors for the four refracted waves are directed in the z-direction. Hence, all the refracted waves are inhomogeneous waves with fixed attenuation direction, which is normal to the plane boundary z = 0.

The vertical slowness of all the refracted waves is defined as follows.

$$q_{j} = p \cdot v\left[ {\left( {\frac{\omega }{{\alpha_{j} }}} \right)^{2} - k^{2} } \right]^{{\frac{1}{2}}} ,\quad (j = 1,2,3,4).$$
(42)

p·v denotes the principal value of the complex quantity derived from the square root.

8.1 Amplitudes and phase shifts

For stresses and displacements calculated from the potentials in (36)–(38), boundary conditions (35) are satisfied through a system of six simultaneous inhomogeneous equations, given by

$$\sum\limits_{j = 1}^{6} {d_{ij} Y_{j} = f_{i} ,\quad (i = 1,2,3,4,5,6).}$$
(43)

The system of Eq. (43) is solved numerically for complex unknowns Yj by using the Gauss elimination method. The magnitudes of complex unknowns \(Y_{j} ,\,(j = 1,\,2,\,3,\,4,\,5,\,6)\), define the ratios of the amplitudes of corresponding reflected/refracted waves relative to the amplitude of the incident wave and p·v of arg(\(Y_{j}\)) defines the phase shift of these reflected/refracted waves. The coefficients dij are as follows.

$$\begin{aligned} & d_{11} = 2\mu_{e} s^{2} - \rho_{e} ,\quad d_{12} = 2\mu_{e} s\frac{{d_{{\beta_{e} }} }}{\omega },\quad d_{16} = 2sG\frac{{d_{4} }}{\omega },\quad d_{21} = 2\mu_{e} s\frac{{d_{{\alpha_{e} }} }}{\omega }, \\ & d_{22} = \mu_{e} \left\{ {\left( {\frac{{d_{{\beta_{e} }} }}{\omega }} \right)^{2} - (s)^{2} } \right\},\quad d_{26} = G\left\{ {s^{2} - \left( {\frac{{d_{4} }}{\omega }} \right)^{2} } \right\},\quad d_{31} = s,\quad d_{32} = \frac{{d_{{\beta_{e} }} }}{\omega }, \\ & d_{36} = \frac{{d_{4} }}{\omega },\quad d_{41} = - \frac{{d_{{\alpha_{e} }} }}{\omega },\quad d_{42} = s,\quad d_{46} = - s,\quad d_{5} = 0,\quad d_{52} = 0, \\ & d_{56} = (1 - \mu_{4}) s,\quad d_{61} = 0,\quad d_{62} = 0,\quad d_{66} = (1 - \lambda_{4} )s, \\ & d_{1j} = \eta_{j - 2} (s)^{2} + \xi_{j - 2} \left( {\frac{{d_{j - 2} }}{\omega }} \right)^{2} ,\quad d_{2j} = 2sG\frac{{d_{j - 2} }}{\omega },\quad d_{3j} = - s, \\ & d_{4j} = - \frac{{d_{j - 2} }}{\omega },\quad d_{5j} = (1 - \mu_{j - 2} )\frac{{d_{j - 2} }}{\omega },\quad d_{6j} = (1 - \lambda_{j - 2} )\frac{{d_{j - 2} }}{\omega },\quad (j = 3,4,5), \\ \end{aligned}$$

where

$$\eta_{j} = h_{1} + h_{2} \mu_{j} + h_{3} \lambda_{j} ,\;\xi_{j} = h_{1} + h_{2} \mu_{j} + h_{3} \lambda_{j} + 2G,\quad (j = 1,2,3),$$
$$\begin {aligned} h_{1} = b_{11} + b_{12} + & b_{13} - \frac{2}{3}G,\quad h_{2} = b_{12} + b_{22} + b_{23} ,\\ &h_{3} = b_{13} + b_{23} + b_{33} . \end{aligned}$$

From Eqs. (41) and (42), we can write

$$\frac{{d_{{\alpha_{e} }} }}{\omega } = \left( {\frac{1}{{\alpha_{e}^{2} }} - s^{2} } \right)^{{\frac{1}{2}}} ,\quad \frac{{d_{{\beta_{e} }} }}{\omega } = \left( {\frac{1}{{\beta_{e}^{2} }} - s^{2} } \right)^{{\frac{1}{2}}}\quad {\text{and}} \quad \frac{{d_{j} }}{\omega } = p \cdot v \cdot \left( {\frac{1}{{\alpha_{j}^{2} }} - s^{2} } \right)^{{\frac{1}{2}}} ,\quad (j = 1,2,3,4).$$

p·v is evaluated with restriction \(d_{jI} \ge 0\) to satisfy decay condition in DP2 materials. Residues \(f_{i} (i = 1,\,2,\,3,\,4,\,5,\,6)\) in system (43) are written as follows.

  1. i.

    For the incident P wave

    $$\begin {aligned} f_{1} = - d_{11} ,\;f_{2} = & d_{21} ,\;f_{3} = - d_{31} ,\;f_{4} = d_{41} ,\\ & f_{5} = 0,\;f_{6} = 0. \end{aligned}$$
  2. ii.

    For the incident SV wave

    $$\begin {aligned} f_{1} = d_{12} ,\;f_{2} =& - d_{22} ,\;f_{3} = d_{32} ,\;f_{4} = - d_{42} ,\\ & f_{5} = 0,\;f_{6} = 0.\end{aligned}$$

8.2 Energy shares

In this article, our aim is to study the distribution of incident energy among distinct reflected and refracted waves at a surface element of unit area across the interface z = 0 between two media. According to Achenbach (1973), the rate at which energy is communicated per unit area of the surface (i.e., energy flux across the surface element) is the scalar product of surface traction and particle velocity, denoted by Q. For an isotropic elastic solid, the average rate of energy transmission at z = 0 is given by

$$\left\langle {Q_{e}^{*} } \right\rangle = \frac{1}{2}\Re \left[ {\tau {}_{xz}\bar{\dot{u}}_{x}^{e} + \tau {}_{zz}\bar{\dot{u}}_{z}^{e} } \right].$$
(44)

where bar over a quantity defines its complex conjugate. The energy matrix \(E_{i} \,(i = 1,\,2),\) is a column matrix of order two, defined by

$$E_{i} = \frac{{\left\langle {Q_{ei}^{*} } \right\rangle }}{{\left\langle {Q_{e0}^{*} } \right\rangle }},\quad (i = 1,2),$$
(45)

where \(\left\langle {Q_{e0}^{*} } \right\rangle = \rho_{e} \omega^{4} \Re \left( {q_{0} } \right),\;\left\langle {Q_{e1}^{*} } \right\rangle = \rho_{e} \omega^{4} \left| {Z_{1} } \right|^{2} \Re \left( {\frac{{d_{{\alpha_{e} }} }}{\omega }} \right),\;\left\langle {Q_{e2}^{*} } \right\rangle = \rho_{e} \omega^{4} \left| {Z_{2} } \right|^{2} \Re \left( {\frac{{d_{{\beta_{e} }} }}{\omega }} \right).\)

Here, E1 and E2 represent the energy share of reflected P and SV waves, respectively.

For DP2 materials, the average rate of energy transmission at z = 0 is given by

$$\left\langle {Q_{ij}^{*} } \right\rangle = \Re \left( {\sigma_{zx}^{(i)} } \right)\Re (\dot{u}_{x}^{(j)} ) + \Re \left( {\sigma_{zz}^{(i)} } \right)\Re (\dot{u}_{z}^{(j)} ) + \Re \left( { - p_{f1}^{(i)} } \right)\Re (\dot{v}_{z}^{(j)} ) + \Re \left( { - p_{f2}^{(i)} } \right)\Re (\dot{w}_{z}^{(j)} ),$$
(46)

and evaluated as

$$\begin{aligned} & \left\langle {Q_{ij}^{*} } \right\rangle = - \omega^{4} \Re \left[ {\left\{ {2G\frac{{d_{i} }}{\omega }s\bar{s} + \left( {\chi_{i} \gamma_{i} + 2G\left( {\frac{{d_{i} }}{\omega }} \right)^{2} } \right)\frac{{\bar{d}_{j} }}{\omega } + \delta_{i} \gamma_{i} \bar{\mu }_{j} \frac{{\bar{d}_{j} }}{\omega } + \varepsilon_{i} \gamma_{i} \bar{\lambda }_{j} \frac{{\bar{d}_{j} }}{\omega }} \right\}Z_{i + 2} \bar{Z}_{j + 2} } \right], \\ & \left\langle {Q_{i4}^{*} } \right\rangle = - \omega^{4} \Re \left[ {\left\{ {2sG\frac{{d_{i} }}{\omega }\frac{{\bar{d}_{4} }}{\omega } + \left( {\chi_{i} \gamma_{i} + 2G\left( {\frac{{d_{i} }}{\omega }} \right)^{2} } \right)\bar{s} + \delta_{i} \gamma_{i} \bar{\mu }_{4} \bar{s} + \varepsilon_{i} \gamma_{i} \bar{\lambda }_{4} \bar{s}} \right\}Z_{i + 2} \bar{Z}_{6} } \right], \\ & \left\langle {Q_{4j}^{*} } \right\rangle = - \omega^{4} \Re \left[ {\left\{ {G\gamma_{0} \bar{s} + 2sG\frac{{d_{4} }}{\omega }\frac{{\bar{d}_{j} }}{\omega }} \right\}Z_{6} \bar{Z}_{j + 2} } \right], \\ & \left\langle {Q_{44}^{*} } \right\rangle = - \omega^{4} \Re \left[ {\left\{ { - G\gamma_{0} \frac{{\bar{d}_{4} }}{\omega } + 2G\frac{{d_{4} }}{\omega }s\bar{s}} \right\}Z_{6} \bar{Z}_{6} } \right], \\ \end{aligned}$$

where

$$\begin{aligned} & \gamma_{0} = s^{2} - \left( {\frac{{d_{4} }}{\omega }} \right)^{2} ,\;{\text{and}}\; \, \gamma_{j} = s^{2} + \left( {\frac{{d_{j} }}{\omega }} \right)^{2} ,\;\chi_{j} = b_{11} + \mu_{j} b_{12} + \lambda_{j} b_{13} - \frac{2}{3}G, \\ & \delta_{j} = b_{12} + \mu_{j} b_{22} + \lambda_{j} b_{23} ,\;\varepsilon_{j} = b_{13} + \mu_{j} b_{23} + \lambda_{j} b_{33} ,\quad (j = 1,2,3). \\ \end{aligned}$$

The concept of interaction energy (Borcherdt 2009; Krebes 1983) or the interference energy (Ainslie and Burns 1995) between two dissimilar waves is also involved due to the dissipative nature of double-porosity dual-permeability materials. Thus, when a plane wave impinges at the plane interface z = 0, then in addition to the energy transmitted to refracted waves, a finite amount of energy is carried toward (negative value of interaction energy) and away (positive value of interaction energy) from the interface due to the interaction of reflected waves themselves. In the present geometry, the medium supports the propagation of four refracted waves. Hence, to describe the distribution of incident energy at the surface z = 0, an energy matrix is defined as

$$E_{ij} = - \frac{{\left\langle {Q_{ij}^{*} } \right\rangle }}{{\left\langle {Q_{e0}^{*} } \right\rangle }},\quad (i,j = 1,2,3,4).$$
(47)

The energy matrix \({\mathbf{E}}\) represents the energy share of the four refracted waves and interference energy between two dissimilar waves in the DP2 materials. Terms E11, E22, E33 and  E44 define the energy shares of refracted P1, P2, P3 and SV waves, respectively. A relation \(E_{\text{RR}} = \sum\nolimits_{i = 1}^{4} {\left( {\sum\nolimits_{j = 1}^{4} {E_{ij} - E_{ii} } } \right)}\) calculates the share of interaction energy among all the refracted waves. During the process of reflection/refraction across the interface z = 0, the conservation of incident energy at each angle of incidence is given by the relation E1 + E2 + E11 + E22 + E33 + E44 + ERR = 1.

9 Numerical results and discussion

9.1 Numerical example

We consider the distribution of incident energy among reflected and refracted waves across z = 0 between an elastic solid and double-porosity dual-permeability materials. DP2 materials consist of two distinct porous phases, both saturated with the same viscous fluid. It is assumed that each sphere of DP2 composite of radius R contains at its center a small sphere of radius r of phase 2. In this example, a parameter ɛ = r/R is used to define ν2 = ɛ3, ν1 = 1 − ɛ3 and \(V /S = R^{3} /(3r^{2} ) = r /(3\varepsilon^{3} )\). Then, from Pride and Berryman (2003a) \(L_{1}^{2} = \left( {\frac{r}{\varepsilon }} \right)^{2} \left( {\frac{9}{14} - \frac{3}{4}\varepsilon } \right).\) The value chosen for κ12 = κ21 is \(10^{ - 20} {\text{m}}^{ 2} .\) The bulk moduli (K1, K2) for two porous phases used to determine the elastic coefficients are (Pride et al. 2004)

$$K_{m} = (1 - \phi_{m}^{*} )K_{s} /(1 + \tilde{c}_{m} \phi_{m}^{*} ),\quad (m = 1,2).$$

In this model, elastic behavior of the composite is employed through bulk modulus \(K = (1 - \phi^{*} )K_{s} /(1 + \tilde{c}_{0} \phi^{*} )\) and frequency-independent rigidity modulus \(G = (1 - \phi^{*} )G_{s} /(1 + 1.5\tilde{c}_{0} \phi^{*} ),\) for consolidation parameter \(\tilde{c}_{0} = \nu_{1} \tilde{c}_{1} + \nu_{2} \tilde{c}_{2} ,\) taken from Pride et al. (2004).

In addition, Skempton’s coefficients (B1, B2) for two porous phases are (Pride et al. 2004)

$$B_{m} = (K_{s} - K_{m} )/[K_{s} - K_{m} + \phi_{m}^{*} K_{m} (K_{s} /K_{f} - 1)],\quad (m = 1,2).$$

Numerical values of material parameters for the matrix and two distinct porous phases are given in Table 1.

Table 1  Material parameters for the matrix and two distinct porous phases
Full size table

Following Bullen (1962), \(\rho_{e} = 2650\;{\text{Kg/m}}^{ 3} ,\,\alpha_{e} = 5270\;{\text{m/s,}}\,\beta_{\text{e}} = 3170\;{\text{m/s}}\) are the values chosen for the density and wave velocities in granite.

9.2 Numerical discussion

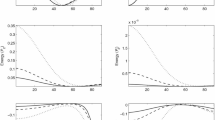
The aim of the above numerical example is to confine the role of various physical properties (like incident direction, wave frequency, pore characteristics, wave-induced fluid-flow, pore-fluid viscosity and double-porosity structure) on the partition of incident energy among various reflected and refracted waves across the interface z = 0 between two media. The distribution of incident energy with incident direction θ0 ∈ (0, 90°) across the interface z = 0 is shown in Figs. 2, 3, 4, 5 and 6 (for the incident P wave) and in Figs. 7, 8, 9, 10 and 11 (for the incident SV wave). The detailed discussion on figures is as follows.

Fig. 2
figure 2

Energy shares of reflected (P, SV), refracted (P1, P2, P3, SV) waves and interaction energy (ERR) with incident direction (θ0) for three different values of embedded porous fraction \((\varepsilon = r /R);\) \(\omega = 2\pi \times 1\;{\text{kHz,}}\,\eta = 1\;{\text{mPa}}\,{\text{s,}}\,r = 0.01\;{\text{m;}}\) incident P wave

Full size image
Fig. 3
figure 3

Energy shares of reflected (P, SV), refracted (P1, P2, P3, SV) waves and interaction energy (ERR) with incident direction (θ0) for three different values of wave frequency ω; \(\eta = 1\;{\text{mPa}}\,{\text{s,}}\;\varepsilon = 1 / 5 ,\;r = 0.001\;{\text{m;}}\) incident P wave

Full size image
Fig. 4
figure 4

Energy shares of reflected (P, SV), refracted (P1, P2, P3, SV) waves and interaction energy (ERR) with incident direction (θ0) for three different values of embedded sphere size r; \(\omega = 2\pi \times 1\;{\text{kHz,}}\;\eta = 1\;{\text{mPa}}\,{\text{s,}}\;\varepsilon = 1 / 4 ;\) incident P wave

Full size image
Fig. 5
figure 5

Energy shares of reflected (P, SV), refracted (P1, P2, P3, SV) waves and interaction energy (ERR) with incident direction (θ0) for three different values of pore-fluid viscosity (η); \(\omega = 2\pi \times 1\;{\text{kHz,}}\;\varepsilon = 1 /5 ,\;r = 0.01\;{\text{m;}}\) incident P wave

Full size image
Fig. 6
figure 6

Effect of WIFF on the energy shares of reflected (P, SV), refracted (P1, P2, P3, SV) waves and interaction energy (ERR) with incident direction (θ0); \(\omega = 2\pi \times 1\;{\text{kHz,}}\;\eta = 1\;{\text{mPa}}\,{\text{s,}}\;\varepsilon = 1 /5,\;r = 0.001\;{\text{m;}}\) incident P wave

Full size image
Fig. 7
figure 7

Same as Fig. 2 but for the incident SV wave

Full size image
Fig. 8
figure 8

Same as Fig. 3 but for the incident SV wave

Full size image
Fig. 9
figure 9

Same as Fig. 4 but for the incident SV wave

Full size image
Fig. 10
figure 10

Same as Fig. 5 but for the incident SV wave

Full size image
Fig. 11
figure 11

Same as Fig. 6 but for the incident SV wave

Full size image

9.2.1 Incident P wave

Figure 2 displays the effect of the embedded porous fraction (ɛ = r/R) on the variation of energy shares of reflected and refracted waves with incident direction θ0. It is clear that all the reflected and refracted waves are significantly affected by ɛ except the reflected P wave on which the effect of ɛ is almost insignificant. Near normal and grazing incidence, most of the incident energy is reflected back in the form of the P wave. The refracted P1 wave is strengthened with the decrease in ɛ. The refracted SV wave is strengthened with an increase in ɛ for θ0 ∈ (40°, 85°). For θ0 ∈ (0, 30°), the refracted P2 and P3 waves are getting stronger with an increase in ɛ, while beyond 65° an inverse effect of ɛ is noticed on these waves. A significant effect of ɛ is noticed on the interaction energy beyond 40°. The effect of frequency on the reflected and refracted waves with incident direction θ0 is exhibited in Fig. 3. The energy shares of reflected and refracted SV waves increase with the increase in frequency for θ0 ∈ (50°, 82°). However, the reflected P wave does not show a noticeable change with frequency. The variational patterns of refracted (P1, P2) waves are almost alike, that is, it increases with the increase in frequency beyond 40°. The refracted P3 wave is strengthened with the increase in frequency for θ0 ∈ (0, 62°). The major effect of frequency is observed on the interaction energy beyond 40°. The impact of size (r) of embedded sphere on the variation of energy shares with incident direction θ0 is shown in Fig. 4. It is clearly visible from the figure that the effect of r on the reflected waves is negligible. However, a significant effect of r is observed on the interaction energy and refracted waves except the refracted SV wave. The refracted (P1, P2) waves are strengthened, and the P3 wave weakens with a decrease in r beyond 40°. The effect of pore-fluid viscosity η on the energy shares is shown in Fig. 5. The impact of η is almost insignificant on the reflected P wave. Further, it is observed that the variational pattern of reflected and refracted SV waves is almost alike with respect to η. No impact of η is observed on the reflected and refracted SV waves below 50° and beyond 85°. A significant impact of η is found on all the refracted longitudinal waves and interaction energy. The refracted P2 wave is strengthened with a decrease in η. At grazing incidence, a negligible impact of η is found on all the reflected and refracted waves. The variation of energy shares with incident direction \(\theta_{0}\) in the presence and absence of WIFF is shown in Fig. 6. In the presence of WIFF, the refracted P1, P2 waves strengthen in comparison with the absence of WIFF for \(\theta_{0} \in (20^{ \circ } ,\,89^{ \circ } )\). A small impact of the presence of WIFF is observed on the reflected P wave in the range \(\theta_{0} \in (50^{ \circ } ,\,85^{ \circ } )\). The reflected and refracted SV waves strengthen a lot in the absence of WIFF in comparison with the presence of WIFF for \(\theta_{0} \in (40^{ \circ } ,\,85^{ \circ } )\). A small interaction between two dissimilar waves in DP2 materials is observed in the absence of WIFF.

9.2.2 Incident SV wave

Figure 7 displays the effect of embedded porous fraction \((\varepsilon = r /R)\) on the variation of energy shares of reflected and refracted waves with incident direction \(\theta_{0}\). A critical angle is observed around 40° for the non-attenuated reflected P wave. It is clear that all the reflected and refracted waves are significantly affected by ɛ except the post-critical incidence of the reflected P wave. Near normal (grazing) incidence, most of the incident energy is refracted (reflected) in the form of the SV wave. The behavior of the reflected SV wave is almost opposite to that of the refracted SV wave with respect to ɛ. Similar to the incident P wave, a significant effect of ɛ is noticed on the interaction energy. The interaction between two dissimilar waves in DP2 materials is almost negligible, particularly for \(\varepsilon = 1 /2\). Peaks are noticed in all energy shares near critical incidence of the reflected P wave. The effect of frequency on the reflected and refracted waves with incident direction θ0 is shown in Fig. 8. A small impact of wave frequency is noticed near the critical incidence of the P wave on reflected (P, SV) waves and the refracted SV wave. Similar to the incident P wave, the variational pattern of refracted (P1, P2) waves are almost alike, that is, it increases with an increase in frequency. A maximum increase is noted in energy shares of refracted (P1, P2) waves around 44°, particularly for \(\omega = 2\pi \times 1\;{\text{kHz}}\). Near critical incidence, a sharp peak is noticed in the energy share of the refracted P3 wave at low frequency. The interaction between two dissimilar waves is almost negligible, particularly for \(\omega = 2\pi \times 0.1\;{\text{kHz}}\). The impact of size (r) of the embedded sphere on the variation of energy shares with incident direction θ0 is shown in Fig. 9. It is clear from the figure that the effect of r on the reflected P wave is negligible. However, a small impact of r is observed on the reflected and refracted SV waves beyond post-critical incidence of the reflected P wave. The refracted (P1, P2) waves are strengthened, and the P3 wave weakens with a decrease in r. No interaction is observed between two dissimilar waves for precritical incidence, particularly for \(r = 0.1\;{\text{m}}\). However, significant interaction is observed between two dissimilar waves beyond critical incidence for any value of r. The effect of pore-fluid viscosity (η) on the energy shares is shown in Fig. 10. A very small impact of η is noticed on the reflected and refracted SV waves beyond post-critical incidence. The impact of η is quite significant on the reflected P wave for θ0 ∈ (27°, 38°). A significant impact of η is found on all the refracted longitudinal waves and interaction energy. The refracted P1, P2 waves are strengthened with a decrease in η. At both normal and grazing incidences, a negligible impact of η is found on all the reflected and refracted waves. The variation of energy shares with incident direction θ0 in the presence and absence of WIFF is shown in Fig. 11. In the presence of WIFF, the refracted P1, P waves strengthen in comparison with the absence of WIFF. A small impact of the presence of WIFF is observed on the reflected P wave for θ0 ∈ (25°, 40°). The reflected (refracted) SV wave strengthens (weakens) a lot in the presence of WIFF beyond critical incidence, that is, their behavior is quite opposite to each other. A small interaction between two dissimilar waves is observed in the absence of WIFF.

10 Conclusions

In the present article, the theoretical procedure to calculate the reflection/refraction coefficients at the interface of an elastic solid and double-porosity dual-permeability medium as a function of incident direction, wave frequency and various materials properties of the DP2 medium is presented. The mathematical model developed by Berryman and Wang (1995, 2000), Pride and Berryman (2003a, b) and Pride et al. (2004) is employed to study the wave propagation in DP2 media. The four (three longitudinal and one shear) waves are exist in the DP2 media. The propagation of these waves is represented with the potential functions. The elastic solid behaves non-dissipatively, while double-porosity dual-permeability materials behave in a dissipative manner to wave propagation due to the presence of pore-fluid viscosity. All the waves (i.e., incident and reflected) in an elastic medium are considered as homogeneous (i.e., with the same directions of propagation and attenuation), while all the refracted waves in double-porosity dual-permeability materials are inhomogeneous (i.e., with different directions of propagation and attenuation). A numerical example is considered to calculate the partition of incident energy among various reflected and refracted waves. The effect of incident direction on the partition of the incident energy is analyzed with a change in wave frequency, wave-induced fluid-flow, pore-fluid viscosity and double-porosity structure. The following conclusions may be drawn on the basis of discussion of numerical results in the previous section.

  1. 1.

    A significant impact of embedded porous fraction (ɛ) is observed on the reflected SV wave, refracted P1, P2, P3, SV waves and interaction energy for both incidences (i.e., P and SV). However, only a small impact of ɛ is observed on the reflected P wave. For both incidences, the interaction between two dissimilar waves in DP2 materials is almost negligible, particularly for ε = 1/2.

  2. 2.

    For the incident P wave, the energy share of the refracted P3 wave is quite significant, while it is negligible for the incident SV wave.

  3. 3.

    Near normal and grazing incidence of the P wave, most of the incident energy is reflected back in the form of the reflected P wave, while near normal (grazing) incidence of the SV wave, most of the incident energy is refracted (reflected) in the form of the SV wave.

  4. 4.

    The refracted P1, P2 waves are strengthened a lot with the increase in frequency (ω) for both incidences.

  5. 5.

    For both incidences, the refracted P1, P2 waves are strengthened and the refracted P3 wave weakens with the decrease in embedded sphere size (r).

  6. 6.

    For both incidences, a significant impact of pore-fluid viscosity η is found on all the refracted longitudinal waves and interaction energy. The refracted P1, P2 waves are strengthened with a decrease in η.

  7. 7.

    For both incidences, in the presence of WIFF, the refracted P1, P2 waves are strengthened. Moreover, a small interaction between two dissimilar waves in DP2 materials is observed in the absence of WIFF.

  8. 8.

    A critical angle is observed around 40° for the non-attenuated reflected P wave for the incident SV wave.

  9. 9.

    Finally, it has been confirmed from the numerical interpretation that during reflection/refraction process, the conservation of incident energy is obtained at each angle of incidence.

The process of reflection/refraction is used to measure the waves which create earthquakes and to detect hydrocarbons (like, oil and gas) and water present inside the earth’s surface as well as their exploration. The geophysical structure of the earth and its material properties is determined on the basis of reflected/refracted wave signals. In recent years, seismic methods (reflection/refraction phenomena) are used in life science for medical diagnosis and therapy in the treatment of human beings.