A modified Green’s function approach to particle image velocimetry pressure estimates with an application to microenergy harvesters

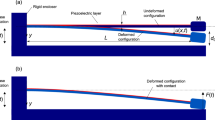
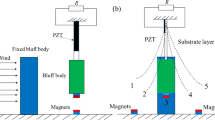
Abstract

Performance of simple, fluidic harvesters consisting of a piezoelectric cantilever strongly relies on a time-dependent fluid forcing they experience. To quantify this forcing, an analytical solution of  a pressure Poisson equation (PPE) is presented that uses particle image velocimetry (PIV) data to calculate pressure around the harvester. This analytical solution is based on a modified Green’s function approach and provides a favorable method of calculating the pressure field from PIV data. It eliminates a need to compute higher-order derivatives of velocity that are present in the viscous terms and it eliminates the need to integrate Navier–Stokes equations to find the pressure along the boundaries of interest. An experiment was carried out to validate this solution. Pressure distribution along the piezoelectric cantilever was calculated by solving PPE analytically as a single vortex passed over it. This distribution was then integrated to calculate the net force acting on the beam. Euler–Bernoulli theory was then used to predict the beam’s dynamic response based on the calculated pressure. Using dielectric properties of the piezoelectric harvester, the voltage and total power output were computed from the motion of the beam. These values were compared to the voltage and power directly measured during the experiment.

Appendices

Appendix 1

This appendix presents the solution if the boundary value problem shown as Eqs. (19)–(21) to obtain Hilbert’s function $H(x, y; \xi , \eta )$

$$\frac{{\partial }^{2}H}{\partial {\xi }^{2}}+\frac{{\partial }^{2}H}{\partial {\eta }^{2}}=\delta \left(\xi -x\right)\delta \left(\eta -y\right)-\beta \left(\xi ,\eta \right)$$

(19)

with

$$\int_{0}^{H} {\int }_{0}^{L}\beta \left(\xi , \eta \right)\mathrm{d}\xi \mathrm{d}\eta =1$$

(20)

and boundary conditions:

$$\frac{\partial H}{\partial \xi }\left(0, \eta \right)=\frac{\partial H}{\partial \xi }\left(L, \eta \right)=\frac{\partial H}{\partial \eta }\left(\xi ,0\right)=\frac{\partial H}{\partial \eta }\left(\xi , W\right)=0$$

(21)

Using a finite cosine transform in $\xi$

$$\widehat{{H}_{n}}= {\int }_{o}^{L}H\mathrm{cos}\frac{n\pi \xi }{L} \mathrm{d}\xi$$

(22)

Equation (20) becomes:

$$- \frac{{n}^{2}{\pi }^{2}}{{L}^{2}} \widehat{{H}_{n}}+\frac{{\partial }^{2} \widehat{{H}_{n}} }{\partial {\eta }^{2}}=\delta \left(\eta -y\right) \mathrm{cos}\frac{n\pi x}{L}-{\int }_{o}^{L}\beta (\xi , \eta )\mathrm{cos}\frac{n\pi \xi }{L} \mathrm{d}\xi$$

(23)

Similarly, applying a finite cosine transform in $\eta$ Eq. (23) becomes:

$$-\frac{{n}^{2}{\pi }^{2}}{{L}^{2}}\widehat{\widehat{{H}_{nm}}}-\frac{{m}^{2}{\pi }^{2}}{{W}^{2}}\widehat{\widehat{{H}_{nm}}}=\mathrm{cos}\frac{n\pi x}{L}\mathrm{cos}\frac{m\pi y}{W}-\widehat{\widehat{{\beta }_{nm}}}$$

(24)

Solving for $\widehat{\widehat{{H}_{nm}}}$

$$\widehat{{\widehat{{H_{nm} }}}} = - \frac{{\cos \frac{n\pi x}{L}\cos \frac{m\pi y}{W} - \widehat{{\widehat{{\beta_{nm} }}}}}}{{\frac{{n^{2} \pi^{2} }}{{L^{2} }} + \frac{{m^{2} \pi^{2} }}{{W^{2} }}}}$$

(25)

The simplest choice of the function $\beta \left(\xi , \eta \right)$, which satisfies condition (20), is

$$\beta \left(\xi , \eta \right)=\frac{1}{LW}$$

(26)

Finite cosine transform of this function in $\xi$ and $\eta$ gives

$$\widehat{\widehat{\beta }}= \left\{\begin{array}{c}1\quad n=m=0\\ 0\quad \text{otherwise}\end{array}\right.$$

(27)

Thus, the inversion of (25) yields:

$$\begin{aligned} H\left( {x,y; \xi , \eta } \right) & = H_{0} - \frac{2}{{\pi^{2} }}\frac{L}{W}\mathop \sum \limits_{n = 1}^{\infty } \frac{1}{{n^{2} }}\cos \frac{n\pi \xi }{L}\cos \frac{n\pi x}{L} \\ & \quad - \frac{2}{{\pi^{2} }}\frac{W}{L}\mathop \sum \limits_{m = 1}^{\infty } \frac{1}{{m^{2} }}\cos \frac{m\pi \eta }{W}\cos \frac{m\pi y}{W} \\ & \quad - \frac{4LW}{{\pi^{2} }}\mathop \sum \limits_{n = 1}^{\infty } \mathop \sum \limits_{m = 1}^{\infty } \frac{{\cos \frac{n\pi \xi }{L}\cos \frac{m\pi \eta }{W}\cos \frac{n\pi x}{L}\cos \frac{m\pi y}{W}}}{{n^{2} W^{2} + m^{2} L^{2} }} \\ \end{aligned}$$

(28)

where ${H}_{o}$ is an indeterminate constant whose value maybe arbitrary set. The Hilbert’s function has the symmetry property $H\left(x, y; \xi , \eta \right)=H(\xi , \eta ;x, y)$. A sample plot of Hilbert’s function for $x=y=0.5$ on the domain $0\le \xi \le 1$ and $0\le \eta \le 1$ is shown in Fig. 

Fig. 23

Sample plot of a Hilbert’s function for $x=y=0.5$ on a domain $0\le \xi \le 1$ and $0\le \eta \le 1$

23.

Appendix 2

The force estimated by the PPE can be used to predict the transverse motion of the cantilever beam by solving the Euler–Bernoulli equation

$$EI\frac{{\partial }^{4}{y}_{b}(x, t)}{\partial {x}^{4}}+\rho A\frac{{\partial }^{2}{y}_{b}(x, t)}{\partial {t}^{2}}+c \frac{\partial {y}_{b}\left(x, t\right)}{\partial t }=g(x, t)$$

(29)

Equation (29) is solved assuming a solution of the form

$${y}_{b}\left(x, t\right)= \sum_{n=1 }^{\infty }{W}_{n}\left(x\right){\eta }_{n}(t)$$

(30)

The modal shape function ${W}_{n}\left(x\right)$ is obtained using fixed-end and free-end boundary conditions for a cantilever beam of length $L$, resulting in the classical expression

$${W}_{n}\left(x\right)= {A}_{n}{w}_{n}\left(x\right)={A}_{n}\left\{\left(\mathrm{cos}\left({\xi }_{n}x\right)-\mathrm{cosh}\left({\xi }_{n}x\right)\right)- \frac{\mathrm{cos}\left({\xi }_{n}L\right)+\mathrm{cosh}\left({\xi }_{n}L\right)}{\mathrm{sin}\left({\xi }_{n}L\right)+\mathrm{sinh}\left({\xi }_{n}L\right)}\left(\mathrm{sin}\left({\xi }_{n}x\right)-\mathrm{sinh}\left({\xi }_{n}x\right)\right)\right\}$$

(31)

with the eigenvalues ${\xi }_{n}$ given by the real roots of the transcendental equation

$$1+\mathrm{cos}\left({\xi }_{n}L\right)\mathrm{cosh}\left({\xi }_{n}L\right)=0$$

(32)

The coefficient ${A}_{n}$ is arbitrary and for convenience may be defined so as to satisfy the condition

$$\int_{0}{L}\rho A{W}_{n}^{2}\left(x\right)\mathrm{d}x=\rho A {A}_{n}^{2}\int_{0}^{L}{w}_{n}^{2}\left(x\right)\mathrm{d}x=1$$

(33)

The function ${\eta }_{n}\left(t\right)$ in Eq. (30) satisfies the modal equation

$$\frac{{\mathrm{d}}^{2}{\eta }_{n}}{\mathrm{d}{t}^{2}}+2 {\zeta }_{n} {\omega }_{n}\frac{\mathrm{d}{\eta }_{n}}{\mathrm{d}t}+{\omega }_{n }^{2}{\eta }_{n}=p(t)$$

(34)

where ${\omega }_{n}=\sqrt{\frac{EI}{\rho A} }{{\xi }_{n}}^{2}$ is the natural frequency, ${\zeta }_{n}=\frac{c}{2\rho A{\omega }_{n}}$ is the damping coefficient, and $p\left(t\right)$ is the normalized forcing function:

$$p\left(t\right)= \int_{0}^{L}{W}_{n}\left(x\right)g\left(x, t\right)\mathrm{d}x$$

(35)

The solution to Eq. (34) is

$$\eta_{n} \left( t \right) = \frac{1}{{\omega_{d} }}\mathop \int \limits_{0}^{t} p\left( \tau \right)e^{{ - \zeta_{n} \omega_{n} \left( {t - \tau } \right)}} \sin \left( {\omega_{d} \left( {t - \tau } \right)} \right){\text{d}}\tau \;{\text{for}}\;0 \le {\text{t}} \le t_{0}$$

(36)

$$\eta_{n} \left( t \right) = \left[ {\eta_{n} \left( {t_{0} } \right)\cos \left( {\omega_{d} \left( {t - t_{0} } \right)} \right) + \frac{1}{{\omega_{d} }}\left( {\frac{{{\text{d}}\eta_{n} }}{{{\text{d}}t}}\left( {t_{0} } \right) + \zeta_{n} \omega_{n} \eta_{n} \left( {t_{0} } \right)} \right){\text{sin }}\left( {\omega_{d} \left( {t - t_{0} } \right)} \right)} \right]e^{{ - \zeta_{n} \omega_{n} \left( {t - t_{0} } \right)}} \;{\text{for}}\,t \ge t_{0}$$

where ${\omega }_{d}={\omega }_{n}\sqrt{{1-\zeta }_{n}^{2}}$. The solution consists of two segments: one for times $0\le \mathrm{t}\le {t}_{0}$ associated with the motion due to the distributed force on the cantilever; the second associated with the free vibration after time ${t}_{0}$, once the vortex exerts no force on the cantilever.