1 Introduction

The structure of a linked rolling cylinder with springs may be one of the important applications of the principle vibration's sources, such as in electric engines, vibrating structures, rockets, and train motors. Therefore, it is vital to completely comprehend its vibrational motion to offer a better design solution for reducing the vibration utilizing a decent plan. In this way, different sorts of frequencies and mode states of this structure are huge in the planning stage. To avoid structural familiarity, it is critical to understand where the resonance occurs.

The dynamical motions of such vibrating systems are found in many works, for example [1,2,3,4,5,6,7,8,9,10]. The spring pendulum's chaotic motion is explored in [1,2,3] for a fixed suspension point as in [1, 2] or a moving one in a circular path [3]. The controlling non-autonomous systems of equations of motion (EOM) are reduced to approximate autonomous systems using the technique of multiple scales (TMS) [11]. Hopf bifurcation and a series of period-doubling bifurcations [12] are demonstrated according to the existence of these systems, which lead to chaotic motions.

Many works, for example [4,5,6,7,8,9], investigate the behavior of several pendulums’ types as a simple and intuitive model of a nonlinear system. The damped motion of a spring is investigated in [4] when the pivot point follows an elliptic path, in which some special cases have been analyzed from the obtained approximate solutions, while the rigid body pendulum’s motion in space is investigated numerically in [5] and [6]. The time series of the results and the corresponding diagrams of phase planes are discussed. The planar motion of an externally activated pendulum connected with a dynamic absorber that can move transversely and longitudinally is examined in [7]. The nonlinear dynamical vertical movement of a 2DOF vibrating system including nonlinear spring with nonlinear damping is studied in [8]. The analytic outcomes demonstrate that the reducing amplitude’s goal and oscillation can be achieved in view of modifying the parameters of the system besides the stimulating frequency’s value, whereas the motion of excited forced cart pendulum is investigated in [9]. It is noted that for dissipation with small amplitude, the hovering movements are shown to be asymptotically stable. Recently, the same problem is investigated in the framework of its approximate solution in [10], in which the authors classified and examined the arising resonances in light of the obtained modulation equations. In [13], the authors have given novel research that makes use of analytical methods to look into the nonlinear properties exhibited by diverse nonlinear events. The asymptotic method and the TMS are proven to be a practical and clear strategy for approaching mechanics and are relevant to a wide range of engineering and science domains.

The dynamics of a forced spring pendulum with viscous damping are studied in [14] and [15] under the influence of applied nonstationary restrictions that act on the point of suspension to travels in a specified path. The authors restricted the angular velocity of this point to be constant and to move along a circular trajectory [14] and a Lissajous curve [15]. A damped spring with linear and nonlinear stiffness is used to explore the motion of a linked rigid body pendulum in [16, 17] and [18, 19] to generalize the works in [4] and [15], respectively. The uniformly approximate solutions are obtained utilizing the TMS, in which three different time scales are used. The external and parametric resonance cases have been examined simultaneously.

The vibration of a sliding pendulum with clearances without considering its horizontal motion is investigated in [20]. Two models that would simulate the system's clearances with 2DOF and 3DOF are developed using nonlinear springs and dampers. Based on the obtained solutions, internal and primary resonances are studied. A controlled electromagnetic seismic damper was used to investigate the ability to dampen vibrations in a nonlinear gravitational vibratory system in [21], while the free motion of a coupled slip absorber to the motion of carrying body over a hinged roller is explored in [22].

The behavior of a nonlinear mechanical system of 3DOF double pendulum is examined in [23], in which the authors focused their study on the vibrations in the neighborhood of simultaneous internal and exterior resonances. Using the TMS, the implicit form of the resonance response functions, as well as the equations governing the modulation of amplitudes and phases, was established. Recently in [24] and [25], the authors investigated the rotatory plane motion of auto-parametric systems with 3DOF to create new vibrating dynamical motions. They comprise a primary system with a damped Duffing oscillator and a secondary one which is a damped spring pendulum. The domains of stability and instability are studied using the Routh–Hurwitz criterion [12], in which the system’s behavior is found to be stable across a wide range of system’s parameters.

The parametric resonances of a double pendulum exposed to vertical kinematic excitation are examined experimentally and theoretically in [26]. Theoretically, the TMS was used to generate differential equations for the slow temporal development of phases and amplitudes in the presence of parametric resonances conditions. The authors used a nonclassical strategy that included the insertion of three temporal variables proportional to the first, second, and fourth powers of a small parameter. They performed three phases of the perturbation technique corresponding to the odd powers of this parameter. The trigonometric functions are expanded around the position of stable equilibrium.

The planar motion of a nonlinear damped spring with immovable point is examined in [27]. A polynomial approximate approach is proposed in, to formulate the approximate regulating governing system of the EOM with trigonometric nonlinearities. This approach ensures that the sine and cosine functions are accurately approximated not only around a specific location, but also throughout a preset interval. The interval’s size is determined in accordance with the research goals and the predicted range of the fluctuation of angle coordinate. As a result, the proposed approach could be the solution that provides improved resonance responses with geometric nonlinearities for mechanical systems. The fundamental resonance's resonant vibrations are analyzed, as well as the steady-state resonant responses. The approximate analytic solutions of a vibrating motion of a cylinder in a vertical direction are investigated in [28] using the TMS up to the second order of approximation. The stability of the fixed points at the case of steady state is examined and analyzed using the Routh–Hurwitz nonlinear stability.

In this work, the motion of a 2DOF auto-parametric dynamical system consisting of a coupled rolling cylinder with a damped spring, in which the other spring’s end is connected to a wall, is examined. The fundamental system of motion is derived, in the existence of an acted excited external force using Lagrange's equations of second type. This system has been solved analytically utilizing the TMS up to the third order of approximation, in which the emergent secular terms are eliminated. The solvability constraints and the equations of modulation are obtained according to the examined resonance cases. The amplitudes, adjusted phases, and acquired solutions are depicted in time histories in certain plots to show the system's motion at any instant. The emerged fixed points are examined in the steady-state case. Routh–Hurwitz's nonlinear stability strategy is utilized to investigate the system's stability, and the various areas of stabilities and instabilities are portrayed and analyzed. The nonlinear amplitudes’ properties of the equations of modulation, as well as their stabilities, are explored and presented. Based on the application of used methodology on the investigated dynamical system, then we can regard the acquired results as novel and original.

2 The dynamical model

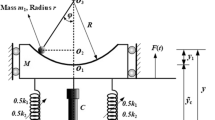
Consider the rolling motion of a cylinder with mass \(m_{1}\) and radius \(r\) without slipping, on a circular surface of mass \(M\) and radius \(R\) with friction damping coefficient \(C_{2}\) between the circular surface and the cylinder [29]. The system of these masses is attached with a damped linear elastic spring, of stiffness \(k\) and a damping coefficient \(C_{1}\), in which the spring’s other end is connected to a fixed point \(O_{1}\) as seen in Fig. 1.

Fig. 1
figure 1

The dynamical system

Full size image

Let \(g\) denote the earth’s gravitational acceleration, \(x\) and \(\theta\) be the displacement on the \(x\) direction and the rotation angle at the center \(O\) of the circular surface. The motion is forced by an external excitation harmonic force \(F(t) = F_{1} \,\cos (\Omega_{1} \,t)\) along \(x\) horizontal direction, in which \(\Omega_{1}\) and \(F_{1}\) are the frequency and amplitude of the force \(F\), respectively. The motion is considered for a rolling cylinder without slip, in which the fraction between the sliding block and the ground is neglected.

Based on the preceding explanation of the dynamical system, the kinetic and potential energies \(T\) and \(V\) can be formulated as follows

$$\begin{aligned} T & = \frac{1}{2}m_{1} v^{2} + \frac{1}{2}M\,\dot{x}^{2} + \frac{1}{4}m_{1} (R - r)^{2} \dot{\theta }^{2} , \\ V & = \frac{1}{2}k\,x^{2} + m_{1} g(R - r)(1 - cos\theta ), \\ \end{aligned}$$
(1)

where the derivatives are considered concerning \(t\).

The regulating EOM can be obtained utilizing the next Lagrange’s equations

$$\begin{aligned} \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial \dot{x}}}} \right) - \left( {\frac{\partial L}{{\partial x}}} \right) & = F_{1} \,\cos (\Omega_{1} \,t) - C_{1} \dot{x}, \\ \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial \dot{\theta }}}} \right) - \left( {\frac{\partial L}{{\partial \theta }}} \right) & = - C_{2} \dot{\theta }, \\ \end{aligned}$$
(2)

where \(L = T - V\) is known by the Lagrangian. It must be noted that, for the viscous effects of damping and rotation, it is assumed that the friction forces have the terms \(- C_{1} \dot{x}\) and \(- C_{2} \dot{\theta }\), respectively.

Take a look at the below list of dimensionless parameters.

$$\begin{aligned} J & = (M + m_{1} ),\,\,\,\,I = (R - r),\,\,\,\,\,\,u = \frac{x}{I},\,\,\,\omega_{1}^{2} = \frac{k}{J},\,\,\,\,\tilde{d} = \frac{{m_{1} \,I}}{J},\,\,\,\,\,\,\omega_{2}^{2} = \frac{2g}{{3I}}\,\,, \\ s & = \frac{1}{2}m_{1} I,\,\,\,\,\,\,\,m = \frac{{m_{1} }}{J}\,,\,\,\,\,\,\,\,\tilde{f}_{1} = \frac{{F_{1} \,}}{I\,J},\,\,\,\tilde{h} = \frac{2s}{{3I}},\,\,\,\,\tilde{c}_{1} = \frac{{C_{1} }}{I\,J},\,\,\,\,\tilde{c}_{2} = \frac{{2C_{2} }}{{3m_{1} I^{2} }}. \\ \end{aligned}$$
(3)

Therefore, the dimensionless forms of the EOM can be obtained by the substitution of (1) and (3) into (2) as follows

$$\begin{gathered} \ddot{u} + \omega_{1}^{2} u + \tilde{d}\,\ddot{\theta }\cos \theta - s\,\dot{\theta }^{2} \sin \theta \,\, = \tilde{f}_{1} \,\cos (\Omega_{1} \,t) - \tilde{c}_{1} \dot{u} \hfill \\ \ddot{\theta } + \omega_{2}^{2} \,\sin \theta + \tilde{h}\,\ddot{u}\cos \theta = - \tilde{c}_{2} \dot{\theta }. \hfill \\ \end{gathered}$$
(4)

The previous system of Eqs. (4) composing two second-order nonlinear differential equations.

3 The used methodology

The major aim of this section is to derive the analytic approximate solutions of the governing system (4) utilizing the TMS up to the third order of approximation with a high degree of accuracy, and to investigate the various resonance circumstances [30]. To achieve this aim, we employ Taylor expansion to represent the functions \(\sin \theta\) and \(\cos \theta\) in expansion forms till the third order, which are valid in the nearness of static equilibrium's positions. As a result, Eqs. (4) can be expressed as

$$\begin{gathered} \ddot{u} + \omega_{1}^{2} u - \frac{1}{2}\tilde{d}(\theta^{2} - 2)\ddot{\theta } + \frac{1}{6}s\,\theta \dot{\theta }^{2} (\theta^{2} - 6) = \tilde{f}_{1} \,\cos (\Omega_{1} \,t) - \tilde{c}_{1} \dot{u}, \hfill \\ \ddot{\theta } + \omega_{2}^{2} \theta - \frac{{\tilde{h}}}{2}(\theta^{2} - 2)\ddot{u} - \omega_{2}^{2} \frac{{\theta^{3} }}{6} = - \tilde{c}_{2} \dot{\theta }. \hfill \\ \end{gathered}$$
(5)

Now, using the new variables \(\xi\) and \(\phi\) to express the generalized coordinates \(u\) and \(\theta\) as follows

$$u(\tau ) = \varepsilon \,\xi (\tau ;\varepsilon ),\quad \theta (\tau ) = \varepsilon \,\phi (\tau ;\varepsilon ),$$
(6)

where \(0 < \varepsilon < < 1\) is a small parameter. Based on the TMS, one can look to the approximate solutions of the variables \(\xi\) and \(\phi\) as follows

$$\begin{aligned} \xi & = \sum\limits_{k = 1}^{3} {\varepsilon^{k} \xi_{k} (\tau_{0} ,\,\tau_{1} ,\,\tau_{2} )} + O(\varepsilon^{4} ), \\ \phi & = \sum\limits_{k = 1}^{3} {\varepsilon^{k} \phi_{k} (\tau_{0} ,\,\tau_{1} ,\,\tau_{2} )} + O(\varepsilon^{4} ). \\ \end{aligned}$$
(7)

Here \(\tau_{n} = \varepsilon^{n} t\,\,(n = 0,\,1\,,\,2)\) represent the various time scales, where \(\tau_{0}\) is the fast one, while \(\tau_{1}\) and \(\tau_{2}\) are the slow scales.

To deal with these scales, the following operators are used to modify the derivatives relative to \(t\) into other ones relative to these scales

$$\begin{aligned} \frac{{\text{d}}}{{{\text{d}}t}} & = \frac{\partial }{{\partial \tau_{0} }} + \varepsilon \frac{\partial }{{\partial \tau_{1} }} + \varepsilon^{2} \frac{\partial }{{\partial \tau_{2} }}, \\ \frac{{{\text{d}}^{2} }}{{{\text{d}}t^{2} }} & = \frac{{\partial^{2} }}{{\partial \tau_{0}^{2} }} + 2\varepsilon \frac{{\partial^{2} }}{{\partial \tau_{0} \partial \tau_{1} }} + \varepsilon^{2} \left( {\frac{{\partial^{2} }}{{\partial \tau_{1}^{2} }} + 2\frac{{\partial^{2} }}{{\partial \tau_{0} \partial \tau_{2} }}} \right) + O(\varepsilon^{3} ). \\ \end{aligned}$$
(8)

Terms of \(O(\varepsilon^{3} )\) and higher are discarded due to the smallness of \(\varepsilon\). The generalized forces, coefficients of damping, and the related mass parameters are considered to be small. Then, we will be able to write

$$\tilde{f}_{1} = \varepsilon^{3} \,f_{1} ,\,\,\,\,\tilde{c}_{1} = \varepsilon^{2} \,c_{1} ,\,\,\,\,\,\,\tilde{c}_{2} = \varepsilon^{2} \,c_{2} ,\,\,\,\,\,\tilde{d} = \varepsilon d,\,\,\,\,\tilde{h} = \varepsilon h.$$
(9)

Substituting (6)–(9) in (5) and then equalling the coefficients of similar powers of \(\varepsilon\), then one can obtain easily the below groups of partial differential equations (PDE).

Coefficient of \((\varepsilon )\)

$$\frac{{\partial^{2} \xi_{1} }}{{\partial \tau_{0}^{2} }} + \omega_{1}^{2} \xi_{1} = 0.$$
(10)
$$\frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0}^{2} }} + \omega_{2}^{2} \phi_{1} = 0.$$
(11)

Coefficient of \((\varepsilon^{2} )\)

$$\frac{{\partial^{2} \xi_{2} }}{{\partial \tau_{0}^{2} }} + \omega_{1}^{2} \xi_{2} = - 2\frac{{\partial^{2} \xi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - \,\,d\,\frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0}^{2} }},\,$$
(12)
$$\frac{{\partial^{2} \phi_{2} }}{{\partial \tau_{0}^{2} }} + \omega_{2}^{2} \phi_{2} = - 2\frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0} \tau_{1} }} + h\,\,\frac{{\partial^{2} \xi_{1} }}{{\partial \tau_{0}^{2} }}.$$
(13)

Coefficient of \((\varepsilon^{3} )\)

$$\begin{aligned} \frac{{\partial^{2} \xi_{3} }}{{\partial \tau_{0}^{2} }} + \omega_{1}^{2} \xi_{3} & = f_{1} \cos \,\Omega_{1} \,\tau_{0} - \frac{{\partial^{2} \xi_{1} }}{{\partial \tau_{1}^{2} }} + \phi_{1} \left( {\frac{{\partial \phi_{1} }}{{\partial \tau_{0} }}} \right)^{2} - c_{1} \frac{{\partial \xi_{1} }}{{\partial \tau_{0} }} - 2\frac{{\partial^{2} \xi_{1} }}{{\partial \tau_{0} \partial \tau_{2} }} \\ & \quad + 2d\frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - 2\frac{{\partial^{2} \xi_{2} }}{{\partial \tau_{0} \partial \tau_{2} }}\, + d\frac{{\partial^{2} \phi_{2} }}{{\partial \tau_{0}^{2} }}\,, \\ \end{aligned}$$
(14)
$$\begin{aligned} \frac{{\partial^{2} \phi_{3} }}{{\partial \tau_{0}^{2} }} + \omega_{2}^{2} \phi_{3} & = \frac{1}{6}\omega_{2}^{2} \,\phi_{1}^{3} - \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{1}^{2} }} - 2\left( {\frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0} \partial \tau_{2} }} + \frac{{\partial^{2} \phi_{2} }}{{\partial \tau_{0} \partial \tau_{1} }}} \right) \\ & \quad + 2h\,\frac{{\partial^{2} \xi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - c_{2} \frac{{\partial \phi_{1} }}{{\partial \tau_{0} }} + h\,\frac{{\partial^{2} \xi_{2} }}{{\partial \tau_{0}^{2} }}. \\ \end{aligned}$$
(15)

It is interesting to note that the equations of the previous systems (10)–(15) can be solved one by one. To accomplish this, we will proceed with the general solutions of (10) and (11) as follows

$$\xi_{1} \, = {\rm A}_{1} e^{{i\omega_{1} \tau_{0} }} + \overline{\rm A}_{1} e^{{ - i\omega_{1} \tau_{0} }} .\,$$
(16)
$$\phi_{1} = {\rm A}_{2} e^{{i\omega_{2} \tau_{0} }} + \overline{\rm A}_{2} e^{{ - i\omega_{2} \tau_{0} }} ,$$
(17)

where \({\rm A}_{j} \,(j = 1,\,2)\) denote the undetermined complex functions of \(\tau_{j}\), while \(\overline{\rm A}_{j}\) representing their complex conjugate.

The substitution of the solutions (16) and (17) in Eqs. (12) and (13) produces secular terms. The required conditions for removing these terms have the forms

$$\frac{{\partial {\rm A}_{1} }}{{\partial \tau_{1} }} = 0,\,\,\,\,\,\frac{{\partial {\rm A}_{2} }}{{\partial \tau_{1} }} = 0,$$
(18)

which means that \({\rm A}_{j}\) are functions of \(\tau_{2}\) only.

As a result, the second-order solutions become

$$\xi_{2} = - \frac{{\omega_{2}^{2} \,d\,{\rm A}_{2} }}{{\omega_{1}^{2} - \,\omega_{2}^{2} }}e^{{i\omega_{2} \tau_{0} }} + CC,\,$$
(19)
$$\phi_{2} = - \frac{{\omega_{1} h\,{\rm A}_{1} }}{{\omega_{2}^{2} - \omega_{1}^{2} }}e^{{i\omega_{1} \tau_{0} }} + CC,$$
(20)

where \(CC\) denote the complex conjugates of the previous terms.

According to the above procedure, the third approximation necessitates the elimination of terms that produce secular ones. Therefore, the following conditions are obtained

$$\frac{{h\,\omega_{1}^{4} {\rm A}_{1} }}{{(\omega_{2}^{2} - \,\omega_{1}^{2} )}} - 2\,i\,\omega_{1} (c_{1} {\rm A}_{1} + \frac{{\partial {\rm A}_{1} }}{{\partial \tau_{2} }}) = 0,$$
(21)
$$2{\rm A}_{2}^{2} \overline{\rm A}_{2} \omega_{2}^{2} - 2i\omega_{2} (\frac{{\partial {\rm A}_{2} }}{{\partial \tau_{2} }} + c_{2} {\rm A}_{2} ) + \frac{{h\,d\omega_{2}^{2} {\rm A}_{2} \,}}{{(\omega_{1}^{2} - \omega_{2}^{2} )}} = 0.$$
(22)

Henceforth, the third-order solutions of Eqs. (14) and (15) have the forms

$$\xi_{3} = \frac{{f_{1} e^{{i\Omega_{1} \tau_{0} }} }}{{2(\omega_{1}^{2} - \Omega_{1}^{2} )}} + \frac{{\,2\,\,\omega_{2}^{2} \overline{\rm A}_{2} \,{\rm A}_{2}^{2} \,e^{{i\omega_{2} \tau_{0} }} }}{{\omega_{1}^{2} - \omega_{2}^{2} }}\, - \frac{{\,\omega_{2}^{2} {\rm A}_{2}^{3} e^{{3i\,\omega_{2} \tau_{0} }} }}{{\omega_{1}^{2} - 9\omega_{2}^{2} }} + CC,$$
(23)
$$\phi_{3} = - \frac{{\,\,{\rm A}_{2}^{3} }}{48}e^{{3\,i\,\omega_{2} \tau_{0} }} + CC.$$
(24)

The functions \({\rm A}_{j} \,(j = 1,\,2)\) may be determined by using the criterion of deleting secular terms (18), (21), and (22).

Based on the above approximate solutions, one can obtain and categorize the emerging cases of resonance when the dominators of these solutions tend to zero [31] as follows:

The system comes to external (primary) resonance when \(\Omega_{1} \approx \omega_{1}\) is satisfied, while we can discover the internal resonance occurs at \(\omega_{1} \approx \omega_{2}\). It should be emphasized that when any of these resonances is realized, the dynamical behavior of the system can be challenging. On the other hand, the achieved solutions are valid when the vibrations deviate from resonances.

4 Conditions of solvability

This section presents the stability of the investigated dynamical system when the resonance cases of external and internal are satisfied simultaneously in accordance with the system’s solvability criteria and the equations of modulation. Based on the previous analysis of the end part of the above section, the external resonance and the internal one occurs when \(\Omega_{1} \approx \omega_{1}\) and \(\omega_{1} \approx \omega_{2}\), respectively. This means that \(\Omega_{1}\) and \(\omega_{1}\) are very near to \(\omega_{1}\) and \(\omega_{2}\), respectively. Therefore, the detuning parameters \(\sigma_{j} \,\,(j = 1,\,2)\) can be introduced according to

$$\begin{gathered} \Omega_{1} = \omega_{1} + \sigma_{1} , \hfill \\ \omega_{1} = \omega_{2} + \sigma_{2} . \hfill \\ \end{gathered}$$
(25)

These parameters may be regarded as a measure of the vibrations from the strict resonance [32]. Consequently, we can express them in terms of \(\varepsilon\) as follows

$$\sigma_{j} = \varepsilon \,\tilde{\sigma }_{j} \,\,\,\,\,(j = 1,\,2).$$
(26)

Substitute (25) and (26) in Eqs. (12)–(15) and pay attention to the secular terms, then eliminating these terms to gain the criteria of solvability for the second and third orders of approximation.

  • For the 2nd order of approximation

    $$\frac{{\partial A_{1} }}{{\partial \tau_{1} }} = 0,\,\,\,\,\,\,\,\,\frac{{\partial A_{2} }}{{\partial \tau_{1} }} = 0.$$
    (27)

  • For the 3rd approximation

    $$\begin{gathered} \frac{1}{2}f_{1} \,e^{{i\tau_{1} \tilde{\sigma }_{1} }} - 2\,i\,\omega_{1} \,(c_{1} {\rm A}_{1} + \frac{{\partial {\rm A}_{1} }}{{\partial \tau_{2} }}) - \frac{{h\omega_{1}^{4} {\rm A}_{1} }}{{\omega_{2}^{2} - \,\omega_{1}^{2} }} = 0, \hfill \\ 2\,\omega_{2}^{2} \,{\rm A}_{{_{2} }}^{2} \overline{\rm A}_{2} - 2i\omega_{2} (\frac{{\partial {\rm A}_{2} }}{{\partial \tau_{2} }} + \,c_{2} {\rm A}_{2} ) + 2\,i\frac{{h\,\,\omega_{1} \,{\rm A}_{1} \,}}{{\omega_{2}^{2} - \,\omega_{1}^{2} }} - \frac{{h\,d\,\omega_{2}^{4} \,{\rm A}_{2} \,}}{{\omega_{1}^{2} - \,\omega_{2}^{2} }} = 0.\, \hfill \\ \end{gathered}$$
    (28)

Based on the above illustration, we can see that the conditions of solvability have four nonlinear PDE with respect to the unknown functions \(A_{j}\). It is worthy to mention that these functions are only affected by the scale \(\tau_{2}\), as indicated from conditions (27). In the form of polar notation, we can express these functions as follows

$$A_{j} = \frac{{\tilde{a}_{j} (\tau_{2} )}}{2}e^{{i\tilde{\psi }_{j} \tau_{2} }} ,\,\,\,\,\,\,\,a_{j} = \varepsilon \tilde{a}_{j} \,\,\,\,\,\,\,(\,j = 1,\,2),$$
(29)

where \(\tilde{\psi }_{j}\) and \(\tilde{a}_{j}\) are real functions of the phases and amplitudes, respectively, of the solutions \(\xi\) and \(\phi\).

Referring to dependency of \(A_{j}\) on \(\tau_{2}\), we can write

$$\frac{{\partial A_{j} }}{\partial \tau } = \varepsilon^{2} \frac{{\partial A_{j} }}{{\partial \tau_{2} }}\,\,\,\,(j = 1,\,2).\,\,\,\,\,$$
(30)

Based on these conditions, Eqs. (28) may be converted into ordinary differential equations (ODE) using the modified phases listed below [33]

$$\begin{gathered} \gamma_{1} (\tau_{1} ,\tau_{2} ) = \tau_{1} \,\tilde{\sigma }_{1} - \psi_{1} (\tau_{2} ), \hfill \\ \gamma_{2} (\tau_{1} ,\tau_{2} ) = \tau_{1} \,\tilde{\sigma }_{2} - \psi_{2} (\tau_{2} ). \hfill \\ \end{gathered}$$
(31)

Substitute (29)–(31) into (28) and then distinguishing the real and imaginary portions to obtain directly the following autonomous system of four first-order ODE

$$\begin{gathered} a_{1} \frac{{d\gamma_{1} }}{d\tau } = \frac{{f_{1} }}{{2\omega_{1} }}\cos \gamma_{1} + a_{1} \sigma_{1} - \frac{{h\,a_{1} \omega_{1}^{4} }}{{2\omega_{1} (\omega_{2}^{2} - \,\omega_{1}^{2} )\,}}, \hfill \\ \frac{{da_{1} }}{d\tau } = \frac{{f_{1} }}{{2\omega_{1} }}\sin \gamma_{1} - \,\frac{{a_{1} c_{1} }}{2}, \hfill \\ a_{2} \frac{{d\gamma_{2} }}{d\tau } = a_{2} \sigma_{2} - \frac{{\omega_{2} a_{2}^{3} }}{4} - \frac{{h\,d\,\omega_{2}^{3} \,a_{2} }}{{\omega_{1}^{2} - \,\omega_{2}^{2} }} - \frac{{h\,a_{1} \,\cos \gamma_{2} }}{{\omega_{2} }}, \hfill \\ \frac{{da_{2} }}{d\tau } = - \frac{{h\,a_{1} \,sin\gamma_{2} }}{{\omega_{2} }} - \,\frac{{a_{2} c_{2} }}{2}. \hfill \\ \end{gathered}$$
(32)

The solutions of this system \(a_{j}\) and \(\gamma_{j}\) describe the modulation of the amplitudes and phases regarding to the dimensionless time \(\tau\) when the examined resonances under study occur simultaneously. These solutions are depicted graphically in Figs. 2, 3, 4 and 5 taking into considerations the values \(f = 10^{ - 3} ,\,c_{1} = 0.05\,,\)\(c_{2} = 0.03\,,\,\sigma_{1} = 0.005,\) and \(\sigma_{2} = 0.01\).

Fig. 2
figure 2

The time dependency of \(a_{1} (\tau );\,\,\,\tau \in [0,500]\): a when \(c_{1} = (0.5,0.05,0.005),\) b at \(c_{2} = (0.3,0.03,0.003)\), c when \(\omega_{2} = (0.467,0.572,0.808)\)

Full size image
Fig. 3
figure 3

The time dependency of \(a_{1} (\tau );\,\,\,\tau \in [0,30]\): a when \(c_{1} = (0.5,0.05,0.005),\) b at \(c_{2} = (0.3,0.03,0.003)\), c when \(\omega_{2} = (0.467,0.572,0.808)\)

Full size image
Fig. 4
figure 4

The time dependency of \(a_{2} (\tau );\,\,\,\tau \in [0,500]\): a when \(c_{1} = (0.5,0.05,0.005),\) b at \(c_{2} = (0.3,0.03,0.003)\), c when \(\omega_{2} = (0.467,0.572,0.808)\)

Full size image
Fig. 5
figure 5

The time dependency of \(a_{2} (\tau );\,\,\,\tau \in [0,30]\): a when \(c_{1} = (0.5,0.05,0.005),\) b at \(c_{2} = (0.3,0.03,0.003)\), c when \(\omega_{2} = (0.467,0.572,0.808)\)

Full size image

It would be interesting to further investigation of the curves included in parts of Fig. 2. These parts represent the change in \(a_{1} (\tau )\) at \(\tau \in [0,500]\) when \(c_{1} ( = 0.5,0.05,0.005),\) \(c_{2} = (0.3,0.03,0.003)\), and \(\omega_{2} = (0.467,0.572,0.808)\) as seen in portions (a), (b), and (c), respectively. These graphs have decay behaviors with the change of time till the time interval is completed. Curves of Fig. 3 show the same variation of the amplitude \(a_{1}\) with time but with a small range of the time interval, i.e., at \(\tau \in [0,30]\). The reason is to go back to see the nature of the curves’ oscillations as in Fig. 3 and to give an induction about these oscillations for a large time scale as graphed in Fig. 2.

The temporal histories of the amplitude \(a_{2}\) and the phases \(\gamma_{1}\) and \(\gamma_{2}\) are drawn in parts of Figs. 4, 6, and 7 when \(\tau \in [0,500]\). Figure 5 shows the same variation of the amplitude \(a_{2}\) with time but with a small range of the time interval, i.e., at \(\tau \in [0,30]\). The previously concluded remarks are satisfied for the plotted curves in parts of Fig. 4. Alternatively, the time variation of \(\gamma_{1}\) and \(\gamma_{2}\) increases and decreases with time as seen in curves of Figs. 6 and 7, respectively.

Fig. 6
figure 6

The time dependency of \(\gamma_{1} (\tau );\,\,\,\tau \in [0,500]\): a when \(c_{1} = (0.5,0.05,0.005)\), b at \(c_{2} = (0.3,0.03,0.003)\), c when \(\omega_{2} = (0.467,0.572,0.808)\)

Full size image
Fig. 7
figure 7

The time dependency of \(\gamma_{2} (\tau );\,\,\,\tau \in [0,500]\): a when \(c_{1} = (0.5,0.05,0.005),\) b at \(c_{2} = (0.3,0.03,0.003)\), c when \(\omega_{2} = (0.467,0.572,0.808)\)

Full size image

These notes are consistent with the equations of system (32), in which the good effect for the variation of the damping parameters and frequencies on the amplitudes and their corresponding phases is evident from drawn curves in these figures.

A closer inspection of the curves of Figs. 8, 9, 10 and 11 reveals the variation of the obtained approximate solutions of the springe’s elongation \(u\) and the rotating angle \(\theta\) with time when \(\tau \in [0,500]\) as drawn in Figs. 8 and 10, and \(\tau \in [0,30]\) as graphed in Figs. 9 and 11. These figures have been calculated in acoordance with the used parameter previously when \(c_{1} ,c_{2} ,\) and \(\omega_{2}\) have different values. The behavior of the presented solutions has decay procedures with the variation of the mentioned parameters previously. Therefore, the dynamical motion is stable during the time frame under consideration. Moreover, the amplitudes of the waves increase with the increase in \(c_{1}\) and \(c_{2}\) values as depicted in portions (a) and (b) of these figures, while this variation decreases when \(\omega_{2}\) increases as graphed in parts (c) of Figs. 10 and 11.

Fig. 8
figure 8

The time behavior of the solution \(u\) at \(\tau \in [0,500]\): a when \(c_{1} = (0.5,0.05,0.005),\) b at \(c_{2} = (0.3,0.03,0.003),\) and c when \(\omega_{2} = (0.467,0.572,0.808)\)

Full size image
Fig. 9
figure 9

The time behavior of the solution \(u\) at \(\tau \in [0,30]\): a when \(c_{1} = (0.5,0.05,0.005),\) b at \(c_{2} = (0.3,0.03,0.003),\) and c when \(\omega_{2} = (0.467,0.572,0.808)\)

Full size image
Fig. 10
figure 10

The time behavior of the solution \(\theta\) at \(\tau \in [0,500]\): a when \(c_{1} = (0.5,0.05,0.005),\) b at \(c_{2} = (0.3,0.03,0.003),\) and c when \(\omega_{2} = (0.467,0.572,0.808)\)

Full size image
Fig. 11
figure 11

The time behavior of the solution \(u\) at \(\tau \in [0,30]\): a when \(c_{1} = (0.5,0.05,0.005),\) b at \(c_{2} = (0.3,0.03,0.003),\) and c when \(\omega_{2} = (0.467,0.572,0.808)\)

Full size image

To confirm the employed perturbation approach is accurate, the numerical solutions (NS) regarding the original system are gained utilizing the Runge–Kutta method from the fourth order and compared with the approximate solutions (AS). This comparison is graphed in parts of Fig. 12 to demonstrate their high consistency, revealing the high reliability of the derived analytic approximate solutions. The phase diagrams when \(\tau \in [0,500]\) for \(a_{1} (\gamma_{1} )\) and \(a_{2} (\gamma_{2} )\) are plotted in Figs. 13 and 15, respectively.

Fig. 12
figure 12

The deviation between the AS and the NS at \(\omega_{2} = 0.808\): a regarding the solution \(u\), b regarding the solution \(\theta\)

Full size image
Fig. 13
figure 13

The variation of the amplitude \(a_{1}\) via its corresponding phase \(\gamma_{1}\): a when \(c_{1} = (0.5,0.05,0.005),\) b at \(c_{2} = (0.3,0.03,0.003),\) c when \(\omega_{2} = (0.467,0.572,0.808)\) at \(\tau \in [0,500]\)

Full size image
Fig. 14
figure 14

The variation of the amplitude \(a_{1}\) via its corresponding phase \(\gamma_{1}\): a when \(c_{1} = (0.5,0.05,0.005),\) b at \(c_{2} = (0.3,0.03,0.003),\) c when \(\omega_{2} = (0.467,0.572,0.808)\) at \(\tau \in [0,30]\)

Full size image
Fig. 15
figure 15

The variation of amplitude \(a_{2}\) via its corresponding phase \(\gamma_{2}\): a when \(c_{1} = (0.5,0.05,0.005),\) b at \(c_{2} = (0.3,0.03,0.003),\) c when \(\omega_{2} = (0.467,0.572,0.808)\) at \(\tau \in [0,500]\)

Full size image

5 Steady-state solutions

This section's main purpose is to look at the model's steady-state vibrations, in which the vibrations of the transient process vanish due to the system’s damping. In such instances, the zero derivatives of the adjusted phases \(\gamma_{j} \,\,(j = 1,2)\) and the amplitudes \(a_{j}\) are used to determine the steady-state conditions [34]. Therefore, the system of Eqs. (32) is quite useful in characterizing them. Then, we consider \(\frac{{d\gamma_{j} }}{dt} = \frac{{da_{j} }}{dt} = 0\) to getting the following algebraic equations

$$\begin{gathered} \frac{{f_{1} }}{{2\omega_{1} }}\cos \gamma_{1} + a_{1} \sigma_{1} - \frac{{h\,a_{1} \omega_{1}^{4} }}{{2\omega_{1} (\omega_{2}^{2} - \,\omega_{1}^{2} )\,}} = 0, \hfill \\ \frac{{f_{1} }}{{2\omega_{1} }}\sin \gamma_{1} - \,\frac{{a_{1} c_{1} }}{2} = 0, \hfill \\ a_{2} \sigma_{2} - \frac{{\omega_{2} a_{2}^{3} }}{4} - \frac{{h\,d\,\omega_{2}^{3} \,a_{2} }}{{\omega_{1}^{2} - \,\omega_{2}^{2} }} - \frac{{h\,a_{1} \,\cos \gamma_{2} }}{{\omega_{2} }} = 0, \hfill \\ \frac{{h\,a_{1} \,sin\gamma_{2} }}{{\omega_{2} }} + \frac{{a_{2} c_{2} }}{2} = 0. \hfill \\ \end{gathered}$$
(33)

If we can get rid of \(\gamma_{j}\), the below equations in terms of \(a_{j}\) and \(\sigma_{j}\) can be obtained

$$\begin{gathered} \frac{1}{{2\omega_{1}^{2} }}f_{1}^{2} = (a_{1} \sigma_{1} - \frac{{h\,a_{1} \,\omega_{1}^{4} }}{{2\omega_{1} (\omega_{2}^{2} - \,\omega_{1}^{2} )\,}})^{2} + \frac{1}{4}\,c_{1}^{2} a_{1}^{2} , \hfill \\ \frac{{h^{2} \,a_{1}^{2} \,}}{{(\omega_{2}^{2} - \omega_{1}^{2} )^{2} }} = (a_{2} \sigma_{2} - \frac{{\omega_{2} a_{2}^{3} }}{4} - \frac{{h\,d\,\omega_{2} a_{2}^{3} }}{{\omega_{1}^{2} - \,\omega_{2}^{2} }})^{2} + \frac{1}{4}\,c_{2}^{2} a_{2}^{2} .\, \hfill \\ \end{gathered}$$
(34)

It is worthy to note that the assessment of the stability analysis of the studied system includes steady-state vibrations. Therefore, we examine the system's behavior in a region relatively near to the location of the fixed points. Then we consider the substitutions [35]

$$\begin{gathered} a_{1} = a_{10} + a_{11} ,\,\,\,\,\,\,\,\,a_{2} = a_{20} + a_{21} , \hfill \\ \gamma_{1} = \gamma_{10} + \gamma_{11} ,\,\,\,\,\,\,\,\,\gamma_{2} = \gamma_{20} + \gamma_{21} . \hfill \\ \end{gathered}$$
(35)

Here \(a_{j0} \,\,(j = 1,2)\) and \(\gamma_{j0}\) represent the unperturbed steady-state solution, whereas \(a_{j1}\) and \(\gamma_{j1}\) are the corresponding small perturbations. Making use of (35) into (32) to obtain the below linearized system, we get

$$\begin{gathered} a_{10} \frac{{d\gamma_{11} }}{d\tau } = \frac{{f_{1} }}{{2\omega_{1} }}\sin \gamma_{10} \gamma_{11} + a_{11} \sigma_{1} - \frac{{h\,a_{11} \omega_{1}^{4} }}{{2\omega_{1} (\omega_{2}^{2} - \,\omega_{1}^{2} )\,}}, \hfill \\ \frac{{da_{11} }}{d\tau } = \frac{{f_{1} }}{{2\omega_{1} }}\cos \gamma_{10} \gamma_{11} - \,\frac{{a_{11} c_{1} }}{2}, \hfill \\ a_{20} \frac{{d\gamma_{21} }}{d\tau } = a_{21} \sigma_{2} - \frac{{3\omega_{2} a_{20}^{3} a_{21} }}{4} - \frac{{h\,d\,\omega_{2}^{3} \,a_{21} }}{{\omega_{1}^{2} - \,\omega_{2}^{2} }} - \frac{h\,}{{\omega_{2} }}(a_{10} \,\sin \gamma_{20} \gamma_{21} + a_{11} \,\cos \gamma_{20} ), \hfill \\ \frac{{da_{21} }}{d\tau } = - \frac{h\,}{{\omega_{2} }}(a_{10} \,\cos \gamma_{20} \gamma_{21} + a_{11} \,sin\gamma_{20} ) - \,\frac{{a_{21} c_{2} }}{2}. \hfill \\ \end{gathered}$$
(36)

Based on the definitions of the small perturbation \(a_{j1}\) and \(\gamma_{j1}\), one can formulate their solutions as a linear combination of \(k_{s} \,e^{\lambda \tau } \,\,(s = 1,2,3,4)\) in which \(k_{s}\) are constants and \(\lambda\) is the eigenvalue of these perturbations. The roots’ real parts of the below characteristic equation ought to be negative if the solutions \(a_{j0}\) and \(\gamma_{j0}\) are stable asymptotically [36]

$$\lambda^{4} + \Gamma_{1} \lambda^{3} + \Gamma_{2} \lambda^{2} + \Gamma_{3} \lambda + \Gamma_{4} = 0,$$
(37)

where \(\Gamma_{s} \,\,(s = 1,2,3,4)\) have the forms

$$\begin{aligned} \Gamma_{1} & = \frac{1}{2}(c_{1} + c_{2} ) - \frac{{f_{1} \,}}{{2\,a_{10} \omega_{1} }}\sin \gamma_{10} + \frac{{h\,a_{10} }}{{\,a_{20} \omega_{2} }}\sin \gamma_{20} , \\ \Gamma_{2} & = \frac{{c_{1} c_{2} }}{4} - \left( {\frac{3}{4}ha_{20} + \frac{{d\,h^{2} \omega_{2}^{2} }}{{\,2a_{20} \,}}} \right)a_{10} \cos \gamma_{20} \\ & \quad - \frac{{\,(c_{1} + c_{2} )}}{{4\,a_{10} \omega_{1} }}f_{1} \sin \gamma_{10} + \frac{1}{2}\left[ {\frac{{ha_{10} c_{2} }}{{a_{20} \omega_{2} }} - \frac{{f_{1} }}{{\,\omega_{1} }}\left( {c_{1} + \frac{{h\,sin\gamma_{10} }}{{a_{10} \,\omega_{2} }}} \right)} \right]sin\gamma_{20} \\ & \quad + \left[ {\frac{{h\,a_{10} \sigma_{2} }}{{\,a_{20} \omega_{1} }} - \frac{{f_{1} }}{{a_{10} }}\left( {\frac{{\,h\,\omega_{1}^{2} }}{4\,\,} + \frac{{\sigma_{1} }}{{4\,\,\omega_{1} }}} \right)} \right]\cos \gamma_{10} , \\ \Gamma_{3} & = \left[ {\left( {3\,h\,a_{20} - \frac{{4\,h\sigma_{2} }}{{\,a_{20} \omega_{2} }}} \right)\,\cos \gamma_{20} + \frac{{\,c_{1} c_{2} }}{{a_{10} \omega_{1} }}} \right]\frac{{f_{1} }}{{8\,\omega_{1} }}sin\gamma_{10} + \left( {\frac{{c_{1} \sigma_{2} }}{{2\,a_{20} \omega_{2} }} - \frac{{d\omega_{2}^{2} c_{1} }}{{4\,a_{20} \,}} - \frac{3}{8}\,a_{20} c_{1} } \right) \\ & \quad \times ha_{10} \cos \gamma_{20} + \left( {\frac{{2c_{1} \sigma_{1} }}{{\,\,\omega_{1} }} - h\,\omega_{1}^{2} c_{2} } \right)\frac{{f_{1} }}{{8a_{10} }}\cos \gamma_{10} + \left( {\frac{{\,a_{10} c_{1} }}{{4\,a_{20} \,}} - \frac{{f_{1} sin\gamma_{10} }}{{4\,a_{10} \omega_{1} }}} \right)\frac{{h\,c_{2} }}{{\omega_{2} }}sin\gamma_{20} \\ & \quad + \frac{{df_{1} h^{2} \omega_{2}^{2} }}{{4\,a_{20} \omega_{1} }}\cos \gamma_{20} sin\gamma_{10} + \left( {\frac{{\,2\sigma_{2} }}{{\,a_{10} \omega_{1} }} - \frac{{h\,\omega_{1}^{2} }}{{\,a_{20} \,}}} \right)\frac{{f_{1} h}}{{4\omega_{2} }}\cos \gamma_{10} sin\gamma_{20} , \\ \Gamma_{4} & = \left( {\frac{3\,}{4}a_{20} - \frac{{\sigma_{2} \,}}{{\,a_{20} \omega_{2} }}} \right)\frac{{f_{1} hc_{1} }}{{4\omega_{1} }}\cos \gamma_{20} sin\gamma_{10} - \left( {\frac{{3\,\sigma_{1} a_{20} }}{{8\,\omega_{1} }} - \frac{{h\,c_{2} \omega_{1}^{2} }}{{4\,a_{20} \omega_{2} }}} \right)f_{1} h\cos \gamma_{10} sin\gamma_{20} \\ & \quad + \left( {\frac{{\sigma_{1} }}{{\omega_{1} }}\cos \gamma_{10} - c_{1} sin\gamma_{10} } \right)\frac{{f_{1} h\,c_{2} }}{{4\,a_{20} \omega_{2} }}sin\gamma_{20} + \frac{{f_{1} d\,h^{2} \,}}{{8\,a_{20} \omega_{1} }}c_{1} \omega_{2}^{2} \cos \gamma_{20} sin\gamma_{10} + (\frac{{h\sigma_{2} \,}}{{2\omega_{2} }} \\ & \quad - \frac{1}{4}dh^{2} \omega_{2}^{2} )\frac{{\sigma_{1} f_{1} }}{{\omega_{1} a_{20} }}\cos \gamma_{10} sin\gamma_{10} + \left( {dh\omega_{2}^{2} + \frac{{3a_{10} }}{{2a_{20} }} - \frac{{2\sigma_{2} }}{{4\omega_{2} }}} \right)\frac{{h^{2} f_{1} \omega_{1}^{2} }}{{8a_{20} }}\cos \gamma_{10} \cos \gamma_{20} . \\ \end{aligned}$$
(38)

Now, we may formulate the basic conditions of the stability for specific steady-state solutions in the forms that agree with the criteria of Routh–Hurwitz [12] as follows

$$\begin{gathered} \Gamma_{1} > 0, \hfill \\ \Gamma_{1} \Gamma_{2} - \Gamma_{3} > 0, \hfill \\ \Gamma_{3} (\Gamma_{1} \Gamma_{2} - \Gamma_{3} ) - \Gamma_{4} \Gamma_{1}^{2} > 0, \hfill \\ \Gamma_{4} > 0. \hfill \\ \end{gathered}$$
(39)

The stability analysis of the fixed points is tested in the framework of the solutions at the steady state taking into account the requirements of Routh–Hurwitz through various graphs of Eq. (34). The results are displayed in Figs. 16, 17, 18 and 19 to show the variation of \(a_{2}\) versus \(a_{1}\) for different values of \(c_{1} ,c_{2} ,\) and \(\omega_{2}\), in which these figures are plotted based on the following data

$$\begin{gathered} c_{1} ( = 0.5,0.05,0.005),\,c_{2} ( = 0.3,0.03,0.003),\,\,\varepsilon = 0.005, \hfill \\ f_{1} = 0.001,\,\omega_{2} ( = 0.808,0.572,0.467),\,\sigma_{1} = 0.02,\,\,\sigma_{2} = 0.02. \hfill \\ \end{gathered}$$
Fig. 16
figure 16

Four intersection fixed points of the amplitudes \(a_{1}\) and \(a_{2}\) at \(c_{1} = 0.5,\) \(\omega_{2} = 0.467,\) and \(c_{2} = 0.3\)

Full size image
Fig. 17
figure 17

Two intersection fixed points of the amplitudes \(a_{1}\) and \(a_{2}\) at \(c_{1} = 0.05,\) \(\omega_{2} = 0.467,\) and \(c_{2} = 0.3\)

Full size image
Fig. 18
figure 18

Two intersection fixed points of the amplitudes \(a_{1}\) and \(a_{2}\) at \(c_{2} = 0.03,\)\(c_{1} = 0.5,\) and \(\omega_{2} = 0.467\)

Full size image
Fig. 19
figure 19

Four intersection fixed points of the amplitudes \(a_{1}\) and \(a_{2}\) at \(\omega_{2} = 0.572,\)\(c_{1} = 0.5,\) and \(c_{2} = 0.3\)

Full size image

The intersections of the curves of these graphs give rise to so-called fixed points, as before, which define the solutions of the equations of the system (34). These points firmly determine the axial amplitudes and the adjusted steady-state vibration. Furthermore, vibrations in the steady state might be either stable or not. Small pink circles indicate the stable fixed points, in which conditions (39) are satisfied, while the gray circles express the unstable ones. An inspection of these figures shows that four fixed points are obtained when \(c_{1} = 0.5\), \(\omega_{2} = 0.467\) and \(c_{2} = 0.3\) as seen in Fig. 16; three of them are unstable; and the latter point is stable. On the other hand, Fig. 17 is calculated according to the same previous data ​​at \(c_{1} = 0.05\), \(\omega_{2} = 0.467\), and \(c_{2} = 0.3\) to yield two fixed points, and one of them is stable. To get a better overview of these points, let's examine the plotted curves in Figs. 18 and 19 which are drawn at (\(c_{2} = 0.03\),\(c_{1} = 0.5\) and \(\omega_{2} = 0.467\)) and (\(\omega_{2} = 0.572\),\(c_{1} = 0.5\) and \(c_{2} = 0.3\)), respectively. Two fixed points were achieved, one stable and the other is unstable.

Now, we are going to examine the stability of the investigated dynamical system applying the Routh–Hurwitz nonlinear stability criteria. Some parameters like the coefficients of damping \(c_{1} ,c_{2} ,\) the frequency \(\omega_{1} ,\) and the parameters of detuning \(\sigma_{1} ,\sigma_{2}\) play principal roles in the process of stabilization of this system. Specific operations with various parameters of the system are performed to gain the stability diagram of the system (32). The phase plane paths are used to depict the attributes of the adjusted amplitudes \(a_{1}\) and \(a_{2}\), which are created over time in distinct parameter domains.

Variations of feasible fixed points on different detuning parameters \(\sigma_{1}\) are shown in Figs. 20, 21, 22, 23, 24, 25 and 26. Parts \((a)\) and \((b)\) of these figures show the response curves for the variation of the amplitudes \(a_{1}\) and \(a_{2}\) via detuning parameter \(\sigma_{1}\), respectively. They are drawn according to the following data

$$\begin{gathered} c_{1} ( = 0.5,0.05,0.005),\,c_{2} ( = 0.2,0.02,0.002),\,\,\varepsilon = 0.005, \hfill \\ f_{1} = 0.001,\,\omega_{2} ( = 0.808,0.572,0.467),\,\sigma_{2} = 0.01. \hfill \\ \end{gathered}$$
Fig. 20
figure 20

The frequency response when \(c_{1} = 0.5\)

Full size image
Fig. 21
figure 21

The frequency response when \(c_{1} = 0.05\)

Full size image
Fig. 22
figure 22

The frequency response when \(c_{1} = 0.005\)

Full size image
Fig. 23
figure 23

The frequency response when \(c_{2} = 0.03\)

Full size image
Fig. 24
figure 24

Frequency response when \(c_{2} = 0.003\)

Full size image
Fig. 25
figure 25

Frequency response when \(\omega_{2} = 0.467\)

Full size image
Fig. 26
figure 26

Frequency response when \(\omega_{2} = 0.572\)

Full size image

The inspection of the parts of Fig. 21 reveals that they are graphed at \(c_{1} = 0.5\) and \(\omega_{2} = 0.808\), in which the system was discovered to contain only one fixed point independent on the value of \(\sigma_{2}\) over the whole domain. In this region \(- 1 \le \sigma_{1} \le 0.05\), the fixed point is stable, whereas in \(0.05 < \sigma_{1} \le 1\) it is unstable. Moreover, the stable fixed points for the response curves at \(c_{1} = 0.05\) and \(c_{1} = 0.005\) are found in Figs. 21 and 22 at the domains of \(- 1 \le \sigma_{1} \le 0.01\) and \(- 1 \le \sigma_{1} \le 0\), respectively, when \(\omega_{2} = 0.808\), whereas the unstable ones exist in the zones \(0.01 < \sigma_{1} \le 1\) and \(0 < \sigma_{1} \le 1\).

The good impact of various values of \(c_{2} \,\) and \(\omega_{2}\) on the curves of frequency response is observed in Figs. 23, 24 and 25, 26, respectively. Also, the influence of the detuning parameter \(\sigma_{2}\) on the curve of frequency response is shown in Fig. 27, in which the solid curves express the region of stable fixed point and the dashed ones represent the unstable fixed region. These numbers show that the system still has a fixed point, which suggests a transcritical bifurcation of the system. This implies that when the parameters change, the system mode does not have any qualitative behavior.

Fig. 27
figure 27

The frequency response when \(\sigma_{2} = 0.11\)

Full size image

Finally, Figs. 28, 29 and 30 show the projection of the modulation equations trajectories on the planes \(uu^{\prime}\) and \(\theta \theta^{\prime}\), in which they are drawn when \(c_{1} = (0.5,0.05,0.005),\)\(c_{2} = (0.3,0.03,0.003),\) and \(\omega_{2} = (0.467,0.572,0.808)\), respectively. For these values of the parameters, different closed curves are obtained which means that the considered system's motion is steady and chaotic-free.

Fig. 28
figure 28

The modulation equations projection at \(c_{1} = (0.5,0.05,0.005)\): a regarding the plane \(u\,u^{\prime}\), b regarding the plane \(\theta \,\theta^{\prime}\)

Full size image
Fig. 29
figure 29

The modulation equations projection at \(c_{2} = (0.3,0.03,0.003)\): a and b regarding the planes \(u\,u^{\prime}\) and \(\theta \,\theta^{\prime}\), respectively

Full size image
Fig. 30
figure 30

The modulation equations projection at \(\omega_{2} = (0.467,0.572,0.808)\): a and b regarding the planes \(u\,u^{\prime}\) and \(\theta \,\theta^{\prime}\), respectively

Full size image

To show the characteristics of the nonlinear amplitude of Eq. (32) and to analyze their stability, we will start with the next transformation [37]

$$A_{1} = (p_{1} + \,i\,q_{1} )e^{{i\,\sigma_{1} \tau_{2} \,}} ,\,\,\,\,\,\,\,\,A_{2} = (p_{2} + \,i\,q_{2} )e^{{i\,\sigma_{2} \tau_{2} \,}} .$$
(40)

Making use of (40) into (32), then separate the real and imaginary components to get

$$\begin{aligned} 2\omega_{1} q^{\prime}_{1} & = \frac{{h\,\omega_{1}^{4} }}{{\omega_{2}^{2} - \omega_{1}^{2} }}p_{1} - 2\omega_{1} p_{1} \sigma_{1} - 2c_{1} \omega_{1} q_{1} - \frac{{f_{1} }}{2}, \\ 2\omega_{1} p^{\prime}_{1} & = 2\omega_{1} q_{1} \sigma_{1} - \frac{{h\,\omega_{1}^{4} }}{{\omega_{2}^{2} - \omega_{1}^{2} }}q_{1} - 2c_{1} \omega_{1} p_{1} , \\ 2\omega_{2} q^{\prime}_{2} & = \frac{{h\,d\omega_{2}^{4} }}{{\omega_{1}^{2} - \omega_{2}^{2} }}p_{2} - 2c_{2} \omega_{2} q_{2} + \frac{{2h\,\omega_{1} }}{{\omega_{2}^{2} - \omega_{1}^{2} }}q_{2} - 2\omega_{2} p_{2} \sigma_{2} - 2\omega_{2}^{2} (p_{2}^{3} + q_{2}^{2} p_{2} ), \\ 2\omega_{2} p^{\prime}_{2} & = 2\omega_{2} q_{2} \sigma_{2} - \frac{{h\,d\omega_{2}^{4} }}{{\omega_{1}^{2} - \omega_{2}^{2} }}q_{2} - 2c_{2} \omega_{2} p_{2} + \frac{{2h\,\omega_{1} }}{{\omega_{2}^{2} - \omega_{1}^{2} }}p_{2} + 2\omega_{2}^{2} (q_{2}^{3} + p_{2}^{2} q_{2} ). \\ \end{aligned}$$
(41)

The adjusted amplitudes are then tweaked in various parameter areas throughout time, and the attributes of the amplitudes are displayed in phase diagram curves, as drawn in Figs. 31, 32 and 33 taking into account the next chosen data

$$\begin{gathered} f_{1} = 0.0001,\,\,\,\,\,\,\sigma_{2} = 0.05,\,\,\,\,\,\,\varepsilon = 0.005,\,\,\,\,\,\,c_{1} ( = 0.5,0.05,0.005), \hfill \\ c_{2} ( = 0.3,0.03,0.003),\,\,\,\,\,\,\,\omega_{1} ( = 0.467,0.572,0.808)\,. \hfill \\ \end{gathered}$$
Fig. 31
figure 31

a and b describe the variation \(p_{1}\) and \(q_{1}\) versus \(\tau\) at \(c_{1} ( = 0.5,0.05,0.005)\), (c) explores the trajectories’ projection of the modulation equations on \(p_{1} q_{1}\) at the same values of \(c_{1}\)

Full size image
Fig. 32
figure 32

a and b describe the variation \(p_{1}\) and \(q_{1}\) versus \(\tau\) at \(c_{2} ( = 0.003,0.03,0.3)\), (c) explores the trajectories’ projection of the modulation equations on \(p_{1} q_{1}\) at the same values of \(c_{2}\)

Full size image
Fig. 33
figure 33

a and b describe the variation \(p_{1}\) and \(q_{1}\) versus \(\tau\) at \(\omega_{2} ( = 0.467,0.572,0.808)\), c explores the trajectories’ projection of the modulation equations on \(p_{1} q_{1}\) at the same values of \(\omega_{2}\)

Full size image

Figure 31 depicts the modified phases’ variation \(p_{1}\) and \(q_{1}\) overtime \(\tau\) and the projection of the modulation equation's route on the phase plane \(p_{1} q_{1}\) at various values of \(c_{1}\). Parts (a) and (b) have decay curves, while spiral curves are drawn on part (c). Then, one can conclude that the dynamical behavior of the above system of Eq. (41) has a stable manner, in which the transformations (40) are used. The influence of different values of \(c_{2}\) on the system’s behavior has a slight effect, as seen in Fig. 32, which is due to the formulations of Eqs. (41). On the other hand, the good impact of the frequency values is evident from the plotted curves in Fig. 33. The changed amplitudes decrease with time, eventually approaching zero, as can be seen in Figs. 31, 32 and 33. The spiral's path, among several other things, is a significant indicator of the stationary behavior of the dynamical systems.

6 Conclusion

The motion of a 2DOF auto-parametric dynamical system consisting of a linked rolling cylinder with a damped spring has been studied. This motion has been considered under the influence of an excitation force. The guiding system of motion has been constructed using Lagrange's equations and has been solved using the TMS up to third order of approximation. The equations of modulation have been constructed in the framework of the conditions of solvability. The primary external and internal resonances have been examined simultaneously. Routh–Hurwitz criteria have been utilized to examine the arising fixed points of the system at the steady state, and the stability analysis, in view of the stability and instability zones, has been investigated. The temporal variations of the amplitudes, modified phases, and obtained solutions have been drawn in a few specific plots to indicate the influence of the system's parameters on the motion. Moreover, the properties of nonlinear amplitudes of the equations of modulation have been examined and reported, as well as their stabilities. The obtained results are considered novel and original since the applied methodology is employed on a specific dynamical system. This work is significant because it has immediate applications in the disciplines of engineering machines like reducing the harmful vibrations in machines, tall buildings, chimneys, bridges, television towers, and antennas.