1 Introduction

The open circular hole is a frequently used design feature, for instance, in bolted joint connections commonly idealised as superposition of the pin-load and open hole in the context of bearing-bypass load interaction [8]. This connection technique is widely used in aeronautics. Corresponding efficient and accurate assessment means are crucial to ensure both safe and light-weight optimal designs and, hence, are of great interest for industrial purposes. The overall structural analysis starts with a mechanical idealisation. In many cases, the structure’s thickness is much smaller than the longitudinal and lateral dimensions and a plate model is applicable. The material can be a composite laminate and if its layup is symmetric and the external loading lies within the plate’s plane, then a plane stress model is applicable. Its stress field is then determined, and a failure analysis is conducted subsequently. This can be performed by analytical methods, which provide advantages in terms of low computational effort and can be documented in technical handbooks. Due to these benefits, the present paper shall focus on analytical means.

The stress analysis of open holes has been the scope of many scientists with different degree of complexity such as material anisotropy, shape of the hole, finite width and loading along the outer boundaries. An extensive review is provided by Sevenois and Koussios [56]. Further, Koord et al. [29] summarise frequently used analytical methods and validate them against both 2D and 3D Finite Element analyses as well as against strains from the experiment. The stress field of an isotropic, infinite plate with central circular opening under uniform tension was determined by Kirsch [27] using the Airy stress function [54, 70]. The elliptical hole in an infinite, isotropic plate was addressed by Savin [55] considering many load cases using complex potentials of Muskhelishvili [38]. Problems with anisotropic plate material were treated by Lekhnitskii’s complex potential formalism [33]. The elliptical hole without bending extension coupling in an infinite anisotropic plate under uniform tension, biaxial loading and shearing was analysed by Lekhnitskii [33] himself. The corresponding problem including bending extension coupling is investigated by Becker [6] as well as Ukadgaonker and Rao [73] regarding arbitrary hole shape as well as arbitrarily oriented homogeneous loading and with arbitrarily oriented loading functions [74].

For finite-width problems, existing solutions can be distinguished in heuristic approaches and analysis methods aiming to fulfil the finite setting’s boundary conditions. Concerning the former, Tan [61, 63] uses correction factors scaling the infinite solution for an ellipse under uniform tension by Lekhnitskii [33] such that the integrated stresses along the actual width of the finite problem equilibrate the external load. The approach is further enhanced by adapting the stresses to Heywood formula [22] based on photoelasticity. This yields good correlation for the stress concentrations and their decay in the hole vicinity [64]. However, the Tan concept of heuristically scaling the stresses is based on the assumption that the finite domain problem’s stress decay has the same shape as that of the infinite domain setting. The good agreement for open holes is therefore rather a coincidence than physically motivated. Hence, applicability to other problems cannot be concluded. For instance, it has been revealed that this heuristic approach leads to erroneous results for both isotropic bolted joints [45, 47] and open holes with finite dimensions [44] when assessing the stresses along the entire net section plane.

Works capturing finite width by fulfilling the boundary conditions of the finite-domain problem may be categorised into approaches employing auxiliary functions and concepts based on boundary collocation technique. To name some examples of the former, the following authors treat an isotropic plate using Airy stress functions: Howland [23] deals with the finite open-hole problem and Sjöström [58] additionally covers hole eccentricity. A general methodology how to render finite-domain problems using series or double series of appropriate biharmonic functions is provided by Teodorescu [69]. These rather old contributions are tailored to a specific problem setting and adaption to others may not be feasible. More recent concepts capturing finite dimensions by fulfilling the corresponding stress-free edges are mostly based on the boundary collocation technique. Therein, the goal is to satisfy the prescribed boundary conditions at selected points. For instance, Ogonowski [49] shows agreement with the stress concentration factors of Pilkey and Pilkey [51] for a quasi-isotropic laminate within the width-to-diameter ratio range \(2\le w/d\le 12\) and regarding the circumferential stresses for a \([0^\circ /\pm 45^\circ /90^\circ ]_\mathrm {s}(50\%/40\%/10\%)\) laminate with a rather high value of \(w/d=8\) with Finite Element (FE) values. Lin and Ko [35] calculate failure loads based on analytical stresses and the Theory of Critical Distances for both open holes under uniform and biaxial tension for up to \(w/d\ge 7.25\) yielding good correlation with experiments. Note that assessing if finite-width effects on the stress field are modelled adequately by comparing failure loads may be unsuitable since their deviations also may be due to inaccuracies in the failure prediction model being just an idealisation of the real physical mechanisms. Further, the ratio of \(w/d\ge 7.25\) involves rather slight finite-width effects. Hufenbach and Kroll [26] implement finite dimensions including mechanical and hygrothermal loads revealing good results in comparison to FE for \(w/d=6\) in the unbalanced laminates of \([30^\circ ]\) and \([60^\circ ]\). In Hufenbach et al. [24], good results are obtained compared to experimentally determined strains for \(w/d= \{2;5\}\). Moreover, Hufenbach et al. [25] additionally consider nonconstant tractions along the straight boundaries with an arbitrarily oriented elliptical hole drilled in the plate. For the uniform tension case, accurate results of an elliptical hole with the geometrical ratios \(w/(2a)=1.67, b/a=3\) are shown, where a represents the major semi-axis and b the minor semi-axis. To name a few works dealing with the finite pin-loaded-hole problem related to the open hole, Knight [28] models infinite height and finite width. Note that this problem setting might be also referred to as pinned hole or filled hole and is commonly taken as 2D idealisation for bolted joints. Further, de Jong [12] captures finite plate dimensions using heuristic correction factors. Aiming to reduce the computational effort, Echavarría et al. [14] adapt this method by taking the first terms of the series for stress field modelling only. Kratochvil and Becker [30] approximate the finite rectangular plate as an elliptical domain. Grüber et al. [18] cover bending extension coupling within the rather large width-to-diameter ratios \(w/d=\{15,45\}\) with slight or even vanishing finite-width effects. More recent studies that employ an approach to continuously fulfil stress-free boundary conditions of finite domains without the necessity of optimisation routines are the following. The open hole is treated by Nguyen-Hoang and Becker [44] for isotropic plates, which is extended for bolted joints with isotropic [47] and orthotropic plate material [48]. The corresponding stress results show good agreement to FE data. Furthermore, the approach is based on a general methodology that can be easily modified to other symmetric problem settings. Due to these benefits, the present paper shall extend and generalise the existing methodology to orthotropic composite laminate structures by using complex potentials for the stress state representation. Once validated against FE analyses, the effects of finite width and material orthotropy on the characteristic stresses are studied. The overall complex stress calculus has been suggested in LTH Design criteria [46], a technical handbook used in the European aviation and space industry. Hence, the method can be seen as suitable for practical contexts as well.

Based on the present calculus’ stress results, a failure analysis to predict brittle crack initiation is conducted. Generally, the corresponding means for prediction can be classified into local and nonlocal concepts. The former was applied to many problems [39,40,41, 50] and involve the evaluation of the stress concentration directly at the hole edge. However, the drawback in terms of light-weight optimal design is the fact that local criteria are not capable of modelling the size effect and hence underestimate the sustainable load for finite-sized holes. Contrary, nonlocal criteria as the commonly used Theory of Critical Distances (TCD) and the recent state of the art concept of Finite Fracture Mechanics (FFM) are capable of capturing the size effect and therefore shall be employed in the present study. For more details regarding the phenomenon size effect, please refer to [3,4,5, 13, 17, 77]. The TCD has been applied to many problems including open holes [7, 59, 62, 76] and pin-loaded holes [45, 78]. Note that for finite-width open holes, the corresponding net section stresses have been derived using the heuristic approach by Tan [61, 63]. In the context of the TCD [65,66,67,68, 76], failure is postulated if the net section stresses at or averaged along the characteristic distance equals the material’s plain strength. This length is generally identified by experiments and is assumed to be invariant to the defect size’s absolute value contradicting Camanho and Lambert [8], where it has been identified as a structural and not as a material parameter since a dependency on geometric properties, such as finite boundaries, is shown. Therefore, the characteristic distance is generally not applicable to other configurations, but possibly to a certain extent. This matter shall be further analysed in the present paper. In doing so, the recent state of the art concerning the brittle-failure-prediction concept of Finite Fracture Mechanics serves as reference. This approach addressed by Leguillon [31] postulates failure, in particular the initiation of a finite-sized crack, if both the stress and the energy-release rate reach a corresponding critical value [11]. FFM has been applied and experimentally confirmed to many problems. Regarding an uniaxially loaded open hole, Li and Zhang [34] treat infinite geometry and isotropic material. Hebel and Becker [21] consider composite laminates with anisotropic behaviour using a numerical approach contrary to Camanho et al. [7] using the enhanced Tan solution to determine the stresses of the open-hole problem with a finite-width geometry of \(w/d=\{5,6\}\) and a quasi-isotropic laminate. Martin et al. [36] extend the investigation to finite-width and orthotropic laminates. Felger et al. [16] analyse both symmetric and asymmetric crack patterns in anisotropic finite-width open holes under uniform tension using an asymptotic approach combining means of complex potentials and matched asymptotics, which also is applied to elliptical holes [15]. Further, the open hole under combined tension and in-plane bending is numerically analysed by Rosendahl et al. [53]. Related to the open hole, tensile failure of bolted joints likely occurring for \(w/d\le 4\) [20] is focussed in Catalanotti and Camanho [9] based on FE analyses of the idealisation as filled-hole problem. Nguyen-Hoang and Becker [45] further use FFM to analyse the size effect for \(w/d=\{2;3\}\) and to investigate to which extend the TCD may be applied in bolted-joints assessment. This is based on a preliminary stress calculus based on analytical means, which is enhanced yielding good agreement for isotropic bolted joints [47] and excellent correlation for open holes [44]. This accurate stress calculation methodology shall be extended to the orthotropic case and then be used to conduct a failure analysis by means of TCD and FFM subsequently. This allows to study the impact of finite laminate dimensions on the effective failure load reduction in the context of the size effect and to compare the two failure prediction concepts of different modelling complexity. All in all, the present paper provides an efficient and comprehensive framework for the structural assessment of open holes in composite laminates with finite dimensions.

2 Determination of the stress field

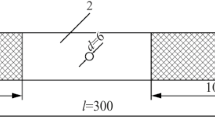
The stress field for the open-hole problem with finite width w and hole diameter d as shown in Fig. 1 is determined. Herein, the quantity \(\sigma _0\) denotes the tensile load applied at infinity. The stresses of this boundary value problem are determined by means of complex potentials.

Fig. 1
figure 1

Finite-width open-hole plate under remote tension

Full size image

2.1 Fundamentals of complex potentials

The complex potentials method is summarised based on Savin [55], Lekhnitskii [33] and Sadd [54]. Let us assume a two-dimensional plane stress or plane strain state with linear elastic and anisotropic material behaviour. Hooke’s law for the plate then reads

$$\begin{aligned} \begin{bmatrix} \varepsilon _x\\ \varepsilon _y\\ \gamma _{xy} \end{bmatrix} = \begin{bmatrix} S_{11}&{}S_{12} &{}S_{16} \\ S_{21}&{}S_{22} &{}S_{26} \\ S_{16}&{}S_{26} &{}S_{66} \end{bmatrix} \cdot \begin{bmatrix} \sigma _x\\ \sigma _y\\ \tau _{xy} \end{bmatrix}, \end{aligned}$$
(1)

where \(\varepsilon _x,\varepsilon _y,\gamma _{xy}\) denote the in-plane strains and \(S_{ij}\) the compliances. As the material is chosen to be a composite laminate corresponding effective compliances shall be inserted, which can be calculated according to Halpin [19] and Tsai [71]. The stresses then are related to a smeared idealisation whose plane strains equal those of the laminate. The stresses of each single ply may be calculated using classical laminate theory. Further, the compatibility condition is

$$\begin{aligned} \frac{\partial ^2\varepsilon _x}{\partial y^2}+\frac{\partial ^2\varepsilon _y}{\partial x^2}=\frac{\partial ^2 \gamma _{xy}}{\partial x\partial y}. \end{aligned}$$
(2)

With vanishing body forces, the stress components can be expressed using the Airy stress function F automatically satisfying the equilibrium. In particular

$$\begin{aligned} \sigma _x&=\frac{\partial ^2 F}{\partial y^2},&\sigma _y&=\frac{\partial ^2 F}{\partial x^2},&\tau _{xy}&=-\frac{\partial ^2 F}{\partial x \partial y}, \end{aligned}$$
(3)
$$\begin{aligned} \sigma _r&=\frac{1}{r}\frac{\partial F}{\partial r}+\frac{1}{r^2} \frac{\partial ^2F}{\partial \varphi ^2},&\sigma _\varphi&=\frac{\partial ^2 F}{\partial r^2},&\tau _{r\varphi }&=-\frac{\partial }{\partial r}\left( \frac{1}{r}\frac{\partial F}{\partial \varphi }\right) . \end{aligned}$$
(4)

Deriving the strains in Eq. (1), inserting in Eq. (2) and expressing the Cartesian stress components using Eq. (3) yields the governing equation

$$\begin{aligned} S_{22}\frac{\partial ^4 F}{\partial x^4}-2S_{26}\frac{\partial ^4 F}{\partial x^3\partial y}+\big (2S_{12}+S_{66}\big )\frac{\partial ^4 F}{\partial x^2 \partial y^2}-2S_{16}\frac{\partial ^4}{\partial x \partial y^3}+S_{11}\frac{\partial ^4 F}{\partial y^4}=0. \end{aligned}$$
(5)

Let us search for solutions of the form \(F=F(x+\mu y)\). Herein, \(\mu \) represents a constant, which can be regarded as value characterising the degree of anisotropy. Inserting this ansatz into Eq. (5) eventually leads to the characteristic equation

$$\begin{aligned} S_{11}\,\mu ^4-2S_{16}\,\mu ^3+\big (2S_{12}+S_{66}\big )\,\mu ^2-2S_{26}\,\mu +S_{22}\mathrel {=}0. \end{aligned}$$
(6)

Based on finite nonzero elastic moduli, its roots are complex [33] and so is the constant \(\mu \) appearing in the conjugate pairs \(\mu _3={\overline{\mu }}_1,\mu _4={\overline{\mu }}_2\) with \(\mu _i=\alpha _i+\mathrm {i}\,\beta _i,\; \{\alpha _i,\beta _i\}\in {\mathbb {R}} \). The solution has then the general form

$$\begin{aligned} F=2\,\mathrm {Re}\,\big [F_1(z_1)+F_2(z_2)\big ]\quad \text {with}\quad z_j=x+\mu _jy. \end{aligned}$$
(7)

For reasons of convenience, let us introduce the complex potentials

$$\begin{aligned} \varPhi _1(z_1)=\frac{\mathrm {d}F_1}{\mathrm {d}\,z_1}=F_1^\prime ,\quad \varPhi _2(z_2)=\frac{\mathrm {d}F_2}{\mathrm {d}\,z_2}=F_2', \end{aligned}$$
(8)

by which the corresponding stress components can be expressed as follows:

$$\begin{aligned} \sigma _x&= 2\,\mathrm {Re}\big [\mu _1^2\,\varPhi '_1(z_1)+\mu _2^2\,\varPhi '_2(z_2)\big ],\nonumber \\ \sigma _y&= 2\,\mathrm {Re}\big [\varPhi '_1(z_1)+\varPhi '_2(z_2)\big ],\nonumber \\ \tau _{xy}&=-2\,\mathrm {Re}\big [\mu _1\,\varPhi '_1(z_1)+\mu _2\,\varPhi '_2(z_2)\big ], \end{aligned}$$
(9)
$$\begin{aligned} \sigma _r&=2\mathrm {Re}\big [(\sin \varphi -\mu _1\cos \varphi )^2\,\varPhi '_1(z_1)\nonumber \\&\qquad +(\sin \varphi -\mu _2\cos \varphi )^2\varPhi '_2(z_2)\big ],\nonumber \\ \sigma _\varphi&=2\mathrm {Re}\big [(\cos \varphi +\mu _1\sin \varphi )^2\,\varPhi '_1(z_1)\nonumber \\&\qquad +(\cos \varphi +\mu _2\sin \varphi )^2\,\varPhi '_2(z_2)\big ],\nonumber \\ \tau _{r\varphi }&=2\,\mathrm {Re}\big [(\sin \varphi -\mu _1\cos \varphi )\,(\cos \varphi +\mu _1\sin \varphi )\,\varPhi '_1(z_1)\nonumber \\&\qquad +(\sin \varphi -\mu _2\cos \varphi )\,(\cos \varphi +\mu _2\sin \varphi )\,\varPhi '_2(z_2)\big ]. \end{aligned}$$
(10)

The complex potentials are now to be chosen in such a way that the corresponding stresses satisfy the given stress boundary conditions (BCs). With the hole radius \(R=d/2\), these then read

$$\begin{aligned} \lim _{y\rightarrow \pm \infty }\sigma _y (x,y)&=\sigma _0,\quad \sigma _r(R,\varphi )=\tau _{r\varphi }(R,\varphi )=0, \end{aligned}$$
(11)
$$\begin{aligned} \sigma _x(\pm w/2,y)&=\tau _{xy}(\pm w/2,y)=0. \end{aligned}$$
(12)

This is achieved by taking the infinite open hole solution [33, 54, 55] satisfying the BCs in Eq. (11) and supplementing it by three types of auxiliary potentials and functions enabling to fulfil those in Eq. (12) additionally. The first type cancels the nonzero shear tractions \(\tau _{xy}(\pm w/2,y)\) and the second is dedicated to eliminate the normal tractions \(\sigma _{x}(\pm w/2,y)\). The third type eventually mitigates deviations in the hole BCs, which may arise due to the other two.

2.2 Complex potentials modelling the infinite dimensions problem

The determination of the complex potentials \(\varPhi _{j=1,2}^\mathrm {inf}\) modelling the open hole in an infinite plate under uniform tension in y-direction is briefly summarised according to Lekhnitskii [33] and Sadd [54]. In this context, fundamentals how to render hole tractions are introduced. The solution is provided by \(\varPhi _j^\mathrm {inf}=\varPhi _j^\mathrm {inf,1}+\varPhi _j^\mathrm {inf,2}\), where the former first potential describes the plain plate under uniform tension yielding nonzero tractions along the hole boundary whereas the second enables their cancellation. The potentials \(\varPhi _j^\mathrm {inf,1}\) have the general form

$$\begin{aligned} \varPhi _j^\mathrm {inf,1}(z_j)=A_j\,z_j \end{aligned}$$
(13)

and corresponding stresses can be derived using Eqs. (9), (10). Their complex coefficients \(A_j=a_j+\mathrm {i}\,b_j\) are calculated by the requirements

$$\begin{aligned} \lim _{y\rightarrow \pm \infty }\sigma _x^\mathrm {inf,1} (x,y)=\lim _{y\rightarrow \pm \infty }\tau _{xy}^\mathrm {inf,1} (x,y)=0,\quad \lim _{y\rightarrow \pm \infty }\sigma _y^\mathrm {inf,1} (x,y)=\sigma _0. \end{aligned}$$
(14)

Since the system of equations is underdetermined, \(b_1=0\) is arbitrarily set and we obtain

$$\begin{aligned} \begin{aligned} a_1&=\frac{1}{2}\, \frac{\alpha _2^2+\beta _2^2}{(\alpha _1-\alpha _2)^2-\beta _1^2+\beta _2^2}\,\sigma _0,\quad a_2=\frac{1}{2}\,\frac{\alpha _1^2-2\alpha _1\alpha _2-\beta _1^2}{(\alpha _1-\alpha _2)^2-\beta _1^2+\beta _2^2}\,\sigma _0,\\ b_1&=0,\quad b_2=\frac{1}{2\,\beta _2}\frac{\alpha _2\big [\alpha _1(\alpha _1-\alpha _2)-\beta _1^2\big ]+\alpha _1\,\beta _2^2}{(\alpha _1-\alpha _2) ^2-\beta _1^2+\beta _2^2}\,\sigma _0. \end{aligned} \end{aligned}$$
(15)

The corresponding tractions along the hole edge can be determined using Eq. (10) and read

$$\begin{aligned} \sigma _{r}^\mathrm {inf,1}(R,\varphi )=\sigma _0\sin ^2\varphi ,\quad \tau _{r\varphi }^\mathrm {inf,1}(R,\varphi )=\sigma _0\sin \varphi \cos \varphi . \end{aligned}$$
(16)

The potentials \(\varPhi _j^\mathrm {inf,2}\) compensating these nonzero stress BCs while keeping the uniaxial stress state at infinity unchanged shall now be found. In doing so, use is made of the mapping functions

$$\begin{aligned} \zeta _j=\frac{z_j\pm \sqrt{z_j^2-R^2\big (1+\mu _j^2\big )}}{R\,\big (1-\mathrm {i}\,\mu _j\big )}, \end{aligned}$$
(17)

which project the infinite open-hole domain onto the circular unit domain and tractions are applied on its single external boundary. The sign in the mapping functions is chosen such that the stresses of complex potentials expressed using \(\zeta _j\) are continuously differentiable along any path and yield physical values. For instance, the circumferential stresses for the open-hole problem under uniaxial tension shall be positive throughout the net section plane \(y=0\). In particular, we shall select

$$\begin{aligned} \zeta _j= {\left\{ \begin{array}{ll} \zeta _j^+\quad \text {for}\quad 0 \le \varphi \le \pi /2\quad \vee \quad 3/2\pi<\varphi \le 2\pi \\ \zeta _j^-\quad \text {for}\quad \pi /2<\varphi \le 3/2\pi . \end{array}\right. } \end{aligned}$$
(18)

Furthermore, when obtaining field quantities along the straight edges \(x=\pm w/2\) a change of sign needs to be considered if the coefficient \(\alpha _j\) of the laminate’s complex parameter \(\mu _j\) is nonzero. E.g. this occurs for a \([\pm 45^\circ ]_\mathrm {s}\)-laminate. The location of sign change \(y_{j}^*\) is then determined by solving

$$\begin{aligned} \sqrt{(x+\mu _jy_{j}^*)^2-R(1+\mu _j^2)}\,\Big |_{x=\pm w/2}=0. \end{aligned}$$
(19)
Fig. 2
figure 2

Schematic of conformal mapping. The mapping functions \(f(z_k),f^{-1}(\zeta _k)\) depend on the original domain’s shape

Full size image

The different potentials \(\varPhi _1,\varPhi _2\) may yield other values of \(y_{j}^*\), which must be taken into account before adding them when calculating the stresses using Eqs. (9), (10). The complex potentials modelling any arbitrary traction with vanishing force resultants along a closed contour are of the form

$$\begin{aligned} \begin{aligned} \varPhi _1^\mathrm {HBC}(z_1)&=\sum _{n=1}^{N}{\tilde{B}}_{1n}\zeta _1^{-n},\\ \varPhi _2^\mathrm {HBC}(z_2)&=-\sum _{n=1}^{N}{\tilde{B}}_{2n}\zeta _2^{-n}, \end{aligned} \end{aligned}$$
(20)

where the complex coefficients \({\tilde{B}}_{jn}\) depend on the tractions’ shape. Note that for doubly symmetrical problems [37] as the current open-hole setting, tractions integrated over a closed contour result in vanishing force resultants. To determine the coefficients \({\tilde{B}}_{jn}\), let \(p_x(s),p_y(s)\) be the loading functions along any contour with the arc parameter s and \({\tilde{\sigma }}_x,{\tilde{\sigma }}_y,{\tilde{\tau }}_{xy}\) the prescribed stress BCs. Refer to Fig. 3 for illustration. For the general case of multiply connected regions bounded by a single external and one or more internal boundaries, the relationship between these quantities reads

$$\begin{aligned} \begin{aligned} p_x(s)&=\pm \int _{0}^{{\tilde{s}}}X_n\,\mathrm {ds},&X_n&={\tilde{\sigma }}_x\cos (n,x)+{\tilde{\tau }}_{xy}\cos (n,y),\\ p_y(s)&=\mp \int _{0}^{{\tilde{s}}}Y_n\,\mathrm {ds},&Y_n&={\tilde{\tau }}_{xy}\cos (n,x)+{\tilde{\sigma }}_y\cos (n,y). \end{aligned} \end{aligned}$$
(21)
Fig. 3
figure 3

External forces \(X_n,Y_n\) along external contour, which are equilibrated by the stress compontents \(\sigma _r,\tau _{r\varphi }\)

Full size image

Herein, the quantities \(X_n, Y_n\) denote the components of the external force along the contour’s arc length parameter s equilibrated by the stress components. The upper/lower sign in the formulae is chosen if the contour is located along an external/internal boundary. For the case of the circular unit domain with an external edge only, on which the tractions are applied, the upper sign is hence selected. With

$$\begin{aligned} \cos (n,x) =\pm \frac{\mathrm {d}y}{\mathrm {d}s},\quad \cos (n,y) =\mp \frac{\mathrm {d}x}{\mathrm {d}s} \end{aligned}$$
(22)

one obtains

$$\begin{aligned} \begin{aligned} \int _{0}^{{\tilde{s}}}X_n\,\mathrm {d}s&=\int _{0}^{{\tilde{s}}}{\tilde{\sigma }}_x, \mathrm {d}y-{\tilde{\tau }}_{xy}\,\mathrm {d}x,\\ \int _{0}^{{\tilde{s}}}Y_n\,\mathrm {d}s&=\int _{0}^{{\tilde{s}}}\tau _{xy}\, \mathrm {d}y-{\tilde{\sigma }}_{y}\,\mathrm {d}x. \end{aligned} \end{aligned}$$
(23)

For the circular hole along \(r=R\) with

$$\begin{aligned} \begin{aligned} x&=R\cos \varphi ,&y&=R\sin \varphi \\ \rightarrow \mathrm {d}x&=-R\sin \varphi \,\mathrm {d}\varphi ,&\mathrm {d}y&=R\cos \varphi \,\mathrm {d}\varphi , \end{aligned} \end{aligned}$$
(24)

Eq. (23) further specialises to

$$\begin{aligned} \begin{aligned} \int _{0}^{{\tilde{s}}}X_n\,\mathrm {d}s&=R\int _{0}^{{\tilde{\varphi }}}{{\tilde{\sigma }}}_r(R,\varphi ) \cos \varphi -{{\tilde{\tau }}}_{r\varphi }(R,\varphi )\sin \varphi \,\mathrm {d}\varphi ,\\ \int _{0}^{{\tilde{s}}}Y_n\,\mathrm {d}s&=R\int _{0}^{{\tilde{\varphi }}}{{\tilde{\tau }}}_{r\varphi }(R,\varphi )\cos \varphi +{{\tilde{\sigma }}}_{r}(R,\varphi )\sin \varphi \,\mathrm {d}\varphi . \end{aligned} \end{aligned}$$
(25)

Inserting in Eq. (21) eventually yields the loading functions. In general, the stress boundary conditions along the hole edge can be any functions expandable in a Fourier series. Then, for the present open-hole problem, the corresponding loading functions along the boundary of the circular unit domain with \(R=1\) can be expressed by

$$\begin{aligned} \begin{aligned} p_x^\mathrm {F}(s)&=\sum _{n=1}^{N}\left\{ C_{n}\,\mathrm {e}^{\mathrm {i}n\varphi }+{\overline{C}}_{n}\,\mathrm {e}^{\mathrm {-i}n\varphi }\right\} ,\\ p_y^\mathrm {F}(s)&=\sum _{n=1}^{N}\left\{ B_{n}\,\mathrm {e}^{\mathrm {i}n\varphi }+{\overline{B}}_{n}\,\mathrm {e}^{\mathrm {-i}n\varphi }\right\} . \end{aligned} \end{aligned}$$
(26)

Therein, the complex Fourier coefficients are

$$\begin{aligned} \begin{aligned} C_n&=\frac{1}{2\pi }\int _{0}^{2\pi }p_x(s)\,\mathrm {e}^{-\mathrm {i}\,n\varphi }\,\mathrm {d}\varphi ,\\ B_n&=\frac{1}{2\pi }\int _{0}^{2\pi }p_y(s)\,\mathrm {e}^{-\mathrm {i}\,n\varphi }\,\mathrm {d}\varphi . \end{aligned} \end{aligned}$$
(27)

The complex potentials enabling to model loading functions with vanishing force resultants then read

$$\begin{aligned} \begin{aligned} \varPhi _1^\mathrm {HBC}(z_1)&=\sum _{n=1}^{N}\underbrace{\frac{{\overline{C}}_n-\mu _2\,{\overline{B}}_n}{\mu _1-\mu _2}}_{={\tilde{B}}_{1n}}\zeta _1^{-n},\\ \varPhi _2^\mathrm {HBC}(z_2)&=-\sum _{n=1}^{N}\underbrace{\frac{{\overline{C}}_n-\mu _1\,{\overline{B}}_n}{\mu _1-\mu _2}}_{={\tilde{B}}_{2n}}\zeta _2^{-n}. \end{aligned} \end{aligned}$$
(28)

Note that the complex coefficients \({\tilde{B}}_j\) are determined by calculating the tractions of \(\varPhi _j^\mathrm {HBC}\) using

$$\begin{aligned} \begin{aligned} p^\mathrm {HBC}_x(s)&=2\,\mathrm {Re}\,\big [\mu _1\varPhi _1^\mathrm {HBC}(z_1)+\mu _2\varPhi _2^\mathrm {HBC}(z_2)\big ],\\ p^\mathrm {HBC}_y(s)&=2\,\mathrm {Re}\,\big [\varPhi _1^\mathrm {HBC}(z_1)+\varPhi _2^\mathrm {HBC}(z_2)\big ] \end{aligned} \end{aligned}$$
(29)

and equating them with Eq. (26). With that any undesirable violation of the hole boundary conditions may be cured by potentials of the type of \(\varPhi _j^\mathrm {HBC}\). Regarding the infinite open hole, the potentials \(\varPhi ^\mathrm {inf,2}_j\) aiming to model the nonzero tractions \(\sigma _r^\mathrm {inf,1}(R,\varphi ),\tau _{r\varphi }^\mathrm {inf,1}(R,\varphi )\) of \(\varPhi ^\mathrm {inf,1}_j\) eventually read

$$\begin{aligned} \begin{aligned} \varPhi _1^\mathrm {inf,2}(z_1)&=\frac{{\overline{C}}^\mathrm {inf,2}_1-\mu _2\,{\overline{B}}^\mathrm {inf,2}_1}{\mu _1-\mu _2}\zeta _1^{-1},\\ \varPhi _2^\mathrm {inf,2}(z_2)&=-\frac{{\overline{C}}^\mathrm {inf,2}_1-\mu _1\,{\overline{B}}^\mathrm {inf,2}_1}{\mu _1-\mu _2}\zeta _2^{-1},\\ \text {with}\quad {\overline{B}}^\mathrm {inf,2}_1&=-R\,\sigma _0/2,\quad {\overline{C}}^\mathrm {inf,2}_1\mathop =\;0. \end{aligned} \end{aligned}$$
(30)

Both partial potentials superimposed fulfil the hole BCs and the solution for the infinite open-hole problem is determined. When quasi-isotropic laminates involving \(\mu _j=\mathrm {i}\) shall be investigated, complex potentials may be still used. The arising singularity in the denominator of the mapping functions in Eq. (17) can be circumvented by introducing a small artificial anisotropy [10, 72]. However, the authors consider to use Airy stress functions for stress state representation as more feasible. The corresponding infinite-domain solution addressed by Kirsch [27] reads [54, 70]

$$\begin{aligned} \begin{aligned} F^\mathrm {inf}&= F^\mathrm {inf,1^*}+F^\mathrm {inf,2^*},\quad \text {with}\\ F^\mathrm {inf,1^*}&=\frac{\sigma _0}{4}\bigg [(1+\cos 2\varphi )\,r^2\bigg ],\\ F^\mathrm {inf,2^*}&=\frac{\sigma _0}{4}\left[ \left( \frac{R^4}{r^2}-2R^2\right) \cos 2\varphi -2R^2\ln \frac{r}{R}\right] , \end{aligned} \end{aligned}$$
(31)
Fig. 4
figure 4

Free body diagram of the finite-width open hole. Only stresses relevant for equilibrium in loading direction are shown

Full size image
Fig. 5
figure 5

Schematic of periodic arrangement technique. For a better understanding, the whole infinite open hole problem is shown although in fact only its non-uniform tension part \(\varPhi _{j}^\mathrm {inf,2}\) producing nonzero shear stresses along the straight edges \(x=\pm w/2\) is periodically arranged

Full size image

Along the straight edges \(x=\pm w/2\) of the actual finite-domain problem, the tractions of the infinite-domain solution are nonzero, however. Auxiliary potentials shall now be determined and superimposed such that these tractions vanish.

2.3 Elimination of shear tractions at straight edges

In the following, auxiliary potentials of the first type aiming to cancel nonzero tractions \(\tau ^\mathrm {inf}_{xy}(\pm w/2,y)\) occurring in the infinite open-hole solution modelled by \(\varPhi ^\mathrm {inf}_j\) are developed. These are effective in load direction and their cancellation is essential to equilibrate the external load by the net section stresses alone (Fig.  4). A robust cancellation is provided by the following periodic arrangement shown in Fig. 5. Therein, the auxiliary plates are shifted copies of the infinite open-hole problem. Along the edges \(x=\pm w/2\), these have shear tractions with same magnitude but reversed sign and thus enable cancellation. For the present open-hole problem, the shear stresses \(\tau _{xy}\) are caused by the part \(\varPhi _{j}^\mathrm {inf,2}\). The potentials \(\varPhi _{j}^\mathrm {inf,1}\) represent the plain plate under uniform tension. Therefore, only \(\varPhi _{j}^\mathrm {inf,2}\) needs to be taken into account. Then, the arrangement for \(\varPhi _{j}^\mathrm {inf}\) is calculated by

$$\begin{aligned} \varPhi ^{\mathrm {inf}}_{ij}(x+\mu _j\,y)&= {\left\{ \begin{array}{ll} \varPhi ^{\mathrm {inf}}_{j}(x+\mu _j\,y) &{}\quad \text {for~}i=1,\\ \varPhi ^{\mathrm {inf,2}}_{ij}(x_i+\mu _j\,y)&{}\quad \text {for~}i> 1, \end{array}\right. } \end{aligned}$$
(32)
$$\begin{aligned} \text {with }\quad [x_i]&= \begin{bmatrix} x_1 &{} x_2&{} x_3&{} x_4&{} ... \\ \end{bmatrix}\nonumber \\&= \begin{bmatrix} x&x-w&x+w&x-2w&... \end{bmatrix}. \end{aligned}$$
(33)

Be reminded that the index i refers to the position how the auxiliary plate is arranged (Fig. 5) and \(j=1,2\) denotes the two parts of complex potentials. The superimposed periodic arrangement is eventually obtained by

$$\begin{aligned} \mathrm {PA}\big (\varPhi ^{\mathrm {inf}}_{j}\big )=\sum _{i=1}^{\,n_x}\varPhi ^{\mathrm {inf}}_{ij}. \end{aligned}$$
(34)

Herein, the quantity \(\mathrm {PA}(\cdot )\) represents the operator executing this arrangement for any stress field and \(n_x\) represents the total number of plates in use. To assess the method’s capabilities, the authors consider a small error \(\le \,1\%\) in the load transfer due to remaining shear stresses as tolerable. For further details refer to [44].

2.4 Elimination of normal tractions at straight edges

Nonzero tractions \(\sigma _x(\pm w/2)\) perpendicular to the load direction of the superimposed mirrored auxiliary field \(\mathrm {PA}(\varPhi _{j}^\mathrm {inf})\) shall be cancelled. Let \(\sigma _{x,k}^\mathrm {SE\bot }(\pm w/2,y)\) be the tractions of an arbitrary symmetric stress field k to be mitigated. Let us further assume it to be expandable in the Fourier series

$$\begin{aligned} \sigma _{x,k}^\mathrm {SE\bot }(\pm w/2,y)/\sigma _0=&\frac{f^{\,\sigma _x}_{k,0}}{2}+\sum _{n_k=1}^{N_k}f^{\,\sigma _x}_{k,n}\cos \alpha _n\,y\quad \text {with } \end{aligned}$$
(35)
$$\begin{aligned} \alpha _n=\frac{2n\pi }{l},\quad f^{\,\sigma _x}_{k,n}=&\frac{2}{l}\int _{0}^{l}\sigma _{x,k}^\mathrm {dev}(\pm w/2,y)\cos \alpha _n\,y\,\mathrm {d}y. \end{aligned}$$
(36)

Herein, the wave length l should be chosen sufficiently large, e.g. \(l=40d\). This allows that an undisturbed uniform stress-state establishes sufficiently far away from the hole in load-/y-direction. Further, the correction function shall not cause additional shear stresses along \(x=\pm w/2\),

$$\begin{aligned} \tau _{xy,k}^\mathrm {SE\bot }(\pm w/2,y)=0. \end{aligned}$$
(37)

The tractions in Eqs. (35), (37) can be modelled by the stress function of the form [32, 33]

$$\begin{aligned} F_k^{\mathrm {SE\bot }}/\sigma _0=a_k\,y^2+\sum _{n=1}^{N_k}\phi _{k,n}(x)\,A_{k,n}\cos \alpha _n\,y, \end{aligned}$$
(38)

where the entities \(\phi _{k,n}(x)\) denote unknown functions with respect to x. For orthotropic plates, the governing equations then can be expressed using the laminate’s in-plane engineering constants \(E_x,E_y,G_{xy}, \nu _{xy}\) as

$$\begin{aligned} \frac{\mathrm {d^4}\phi _{k,n}}{\mathrm {d}x^4}-\left( \frac{E_y}{G_{xy}}-2\nu _{xy}\,\frac{E_y}{E_x}\right) \frac{\mathrm {d^2}\phi _{k,n}}{\mathrm {d}x^2}+\frac{E_y}{E_x}\,\phi _{k,n}=0. \end{aligned}$$
(39)

The corresponding characteristic equation is

$$\begin{aligned} s^4-E_x\left( \frac{1}{G_{xy}}-2\,\frac{\nu _{xy}}{E_x}\right) s^2+\frac{E_y}{E_x}=0 \end{aligned}$$
(40)

and for finite and nonzero values of \(E_x, E_y, G_{xy}\), three different cases need to be considered:

  • case I: The roots are equal and real, which occurs for quasi-isotropic laminates with \(s=s_1=s_2=1\).

  • case II: The roots are real but not equal. For the laminates treated, this occurs for \([0^\circ ]\), \([0^\circ /90^\circ ]_\mathrm {s}\) and \( [ 0^\circ /\pm 45^\circ /90^\circ ]_\mathrm {s}(50\%/40\%/10\%).\)

  • case III: The roots are complex with the form \(s_1=h\pm t\,\mathrm {i},s_2=-h\pm t\,\mathrm {i}, \{h,t\}\in {\mathbb {R}} \). This occurs for angle-ply laminates as \([\pm 45^\circ ]_\mathrm {s}\).

The general solution for the corresponding ansatz of \(\phi _{k,n}\) then is

$$\begin{aligned} \begin{aligned} \phi _{k,n}^\mathrm {I}&=C^{\phi _{k,n}}_1\cosh \alpha _n\,x+C^{\phi _{k,n}}_2\sinh \alpha _n\,x+ C^{\phi _{k,n}}_3x\cosh \alpha _n\,x+C^{\phi _{k,n}}_4x\sinh \alpha _n\,x,\\ \phi _{k,n}^\mathrm {II}&=C^{\phi _{k,n}}_1\cosh s_1\alpha _n\,x+C^{\phi _{k,n}}_2\sinh s_2\alpha _n\,x+ C^{\phi _{k,n}}_3\cosh s_2\alpha _n\,x+C^{\phi _{k,n}}_4\sinh s_2\alpha _n\,x,\\ \phi _{k,n}^\mathrm {III}&=\left( C^{\phi _{k,n}}_1\cosh s\alpha _n\,x+C^{\phi _{k,n}}_2\sinh s\alpha _n\,x\right) \cos t\alpha _nx+ \left( C^{\phi _{k,n}}_3\cosh s\alpha _n\,x+C^{\phi _{k,n}}_4\sinh s\alpha _n\,x\right) \sin t\alpha _nx. \end{aligned} \end{aligned}$$
(41)

The derivatives of \(\phi _{k,n}\) are

$$\begin{aligned} \frac{\mathrm {d}\,\phi _{k,n}^\mathrm {I}}{\mathrm {d}x}&= \alpha _n\left( C^{\,\phi _{k,n}}_1\sinh \alpha _n\,x+C^{\,\phi _{k,n}}_2\cosh \alpha _n\,x\right) \nonumber \\&\qquad + C^{\,\phi _{k,n}}_3\Big (\alpha _n\,x\sinh \alpha _n\,x+\cosh \alpha _n\,x\Big )+ C^{\,\phi _{k,n}}_4\Big (\alpha _n\,x\cosh \alpha _n\,x+\sinh \alpha _n\,x\Big ), \end{aligned}$$
(42)
$$\begin{aligned} \frac{\mathrm {d^2}\phi _{k,n}^\mathrm {I}}{\mathrm {d}x^2}&= \alpha _n^2\left( C^{\,\phi _{k,n}}_1\cosh \alpha _n\,x+C^{\,\phi _{k,n}}_2\sinh \alpha _n\,x\right) \nonumber \\&\qquad + C^{\,\phi _{k,n}}_3\left( \alpha _n^2\,x\cosh \alpha _n\,x+2\alpha _n\sinh \alpha _n\,x\right) + C^{\,\phi _{k,n}}_4\left( \alpha _n^2\,x\sinh \alpha _n\,x+2\alpha _n\cosh \alpha _n\,x\right) , \end{aligned}$$
(43)
$$\begin{aligned} \frac{\mathrm {d}\,\phi _{k,n}^\mathrm {II}}{\mathrm {d}x}&=\alpha _n\,\Big (s_1\,C^{\,\phi _{k,n}}_1\sinh s_1 \alpha _n \,x+s_1\,C^{\,\phi _{k,n}}_2\cosh s_1 \alpha _n \,x\nonumber \\&\qquad +s_2\,C^{\,\phi _{k,n}}_3\sinh s_2 \alpha _n \,x+s_2\,C^{\,\phi _{k,n}}_4\cosh s_2 \alpha _n \,x\Big ), \end{aligned}$$
(44)
$$\begin{aligned} \frac{\mathrm {d^2}\,\phi _{k,n}^\mathrm {II}}{\mathrm {d}x^2}&=\alpha _n^2\,\Big (s_1^2\,C^{\,\phi _{k,n}}_1\cosh s_1 \alpha _n \,x+s_1^2\,C^{\,\phi _{k,n}}_2\sinh s_1 \alpha _n \,x\nonumber \\&\qquad +s_2^2\,C^{\,\phi _{k,n}}_3\cosh s_2 \alpha _n \,x+s_2^2\,C^{\,\phi _{k,n}}_4\sinh s_2 \alpha _n \,x\Big ), \end{aligned}$$
(45)
$$\begin{aligned} \frac{\mathrm {d}\,\phi _{k,n}^\mathrm {III}}{\mathrm {d}x}&= \alpha _n\,\bigg \{\cosh s\alpha _n\,x\,\Big [\big (C^{\,\phi _{k,n}}_2s+C^{\,\phi _{k,n}}_3t\big )\cos t\alpha _n\,x+\big (C^{\,\phi _{k,n}}_4s-C^{\,\phi _{k,n}}_1t\big )\sin t\alpha _n\,x \Big ]\nonumber \\&\qquad +\sinh s\alpha _n\,x\,\Big [\big (C^{\,\phi _{k,n}}_1s+C^{\,\phi _{k,n}}_4t\big )\cos t\alpha _n\,x+\big (C^{\,\phi _{k,n}}_3s-C^{\,\phi _{k,n}}_2t\big )\sin t\alpha _n\,x \Big ]\bigg \}, \end{aligned}$$
(46)
$$\begin{aligned} \frac{\mathrm {d^2}\,\phi _{k,n}^\mathrm {III}}{\mathrm {d}x^2}&= \alpha _n^2\,\bigg \{\cosh s\alpha _n\,x\,\Big [\big (2C^{\,\phi _{k,n}}_4s\,t+C^{\,\phi _{k,n}}_1(s+t)\,(s-t)\big )\cos t\alpha _n\,x\nonumber \\&\qquad +\big (C^{\,\phi _{k,n}}_3(s+t)\,(s-t)-2C^{\,\phi _{k,n}}_2st\big )\sin t\alpha _n\,x \Big ]\nonumber \\&\qquad +\sinh s\alpha _n\,x\,\Big [\big (C^{\,\phi _{k,n}}_2(s+t)\,(s-t)+2C^{\,\phi _{k,n}}_3st\big )\cos t\alpha _n\,x\nonumber \\&\qquad +\big (C^{\,\phi _{k,n}}_4(s+t)\,(s-t)-2C^{\,\phi _{k,n}}_1st\big )\sin t\alpha _n\,x \Big ]\bigg \}. \end{aligned}$$
(47)

To determine the free coefficients \(A_{l,n}^\mathrm {VE\bot }, C^{\phi _{n}}_1\)-\(C^{\phi _{n}}_4\), the stress components of \(F_k^{\mathrm {SE\bot }}\) are derived using Eq. (3) yielding

$$\begin{aligned} \sigma _{x,k}^{\mathrm {SE\bot }}/\sigma _0&=2a_k-\sum _{n=1}^{N_k}\alpha _n^2\,\phi _{k,n}(x)\,A_{k,n}\cos \alpha _n\,y, \end{aligned}$$
(48)
$$\begin{aligned} \sigma _{y,k}^{\mathrm {SE\bot }}/\sigma _0&=\sum _{n=1}^{N_k}\frac{\mathrm {d^2}\phi _{k,n}}{\mathrm {d}x^2}\,A_{k,n}\cos \alpha _n\,y, \end{aligned}$$
(49)
$$\begin{aligned} \tau _{xy,k}^{\mathrm {SE\bot }}/\sigma _0&=\sum _{n=1}^{N_k}\alpha _n\frac{\mathrm {d}\phi _{k,n}}{\mathrm {d}x}\,A_{k,n}\sin \alpha _n\,y. \end{aligned}$$
(50)

Equating the deviations expanded by the Fourier series in Eq. (35) with Eq. (48) and taking into account vanishing shear tractions in Eq. (37) yields \(A_{l,n}^\mathrm {VE\bot }, C^{\phi _{n}}_1\)-\(C^{\phi _{n}}_4\). In particular, the coefficients \(C^{\,\phi _{k,n}}_i\) are calculated using

$$\begin{aligned} \phi _{k,n}(\pm w/2)&=1\quad \text {for mathematical convenience}, \end{aligned}$$
(51)
$$\begin{aligned} \tau _{xy,k}^\mathrm {SE\bot }(\pm w/2,y)&=0\quad \Rightarrow \left. \quad \frac{\mathrm {d}\,\phi _{k,n}}{\mathrm {d}x}\right| _{x=\pm w/2}=0. \end{aligned}$$
(52)

This yields for case I

$$\begin{aligned} C^{\,\phi _{k,n}}_1=\frac{2\sinh w/2\,\alpha _n+\alpha _nw\cosh w/2\,\alpha _n}{\sinh w\,\alpha _n+w\,\alpha _n},\quad C^{\,\phi _{k,n}}_2=C^{\,\phi _{k,n}}_3=0,\quad C^{\,\phi _{k,n}}_4=-\frac{2\,\alpha _n\sinh w/2\,\alpha _n}{\sinh w\,\alpha _n+w\,\alpha _n}, \end{aligned}$$
(53)

for case II

$$\begin{aligned} \begin{aligned} C^{\,\phi _{k,n}}_1&=\frac{s_2}{s_2\cosh s_1\,w/2\,\alpha _n-s_1\coth s_2\,w/2\,\alpha _n\sinh s_1\,w/2\,\alpha _n},&C^{\,\phi _{k,n}}_2&=0\\ C^{\,\phi _{k,n}}_3&=\frac{s_1}{s_2\coth s_1\,w/2\,\alpha _n\sinh s_2\,w/2\,\alpha _n-s_1\cosh s_2\,w/2\,\alpha _n},&C^{\,\phi _{k,n}}_4&=0 \end{aligned} \end{aligned}$$
(54)

and for case III

$$\begin{aligned} \begin{aligned} C^{\,\phi _{k,n}}_1&=\frac{4s\cosh s\,w/2\,\alpha _n\sin t\,w/2\,\alpha _n+2t\cos t\,w/2\,\alpha _n\sinh s\,w/2\,\alpha _n}{s\sin t\,w/2\,\alpha _n+t\cosh s\,w/2\,\alpha _n},\quad \\ C^{\,\phi _{k,n}}_2&=C^{\,\phi _{k,n}}_3=0,\\ C^{\,\phi _{k,n}}_4&= \frac{2t\cosh s\,w/2\,\alpha _n\sin t\,w/2\,\alpha _n-2s\cos t\,w/2\,\alpha _n\sinh s\,w/2\,\alpha _n}{s\sin t\,w/2\,\alpha _n+t\sinh s\,w/2\,\alpha _n}. \end{aligned} \end{aligned}$$
(55)

Regarding \(A_{k,n}\), equating the coefficients in Eqs. (35), (48) and taking into account Eq. (51) yields

$$\begin{aligned} a_k=\dfrac{f_{k,0}^{\,\sigma _x}}{4},\quad A_{k,n}= -\dfrac{f_{k,n}^{\,\sigma _x}}{\alpha _n^2}. \end{aligned}$$
(56)

Refer to Nguyen-Hoang and Becker [47] for detailed documentation. With this the stress function \(F_k^\mathrm {SE\bot }\) is fully determined. The introduced correction functions and potentials address a certain set of BCs only and may interfere with other, e.g. the stress-free hole condition. This can be cured by using complex potentials \(\varPhi _{k}^\mathrm {HBC}\) again. For the quasi-isotropic case, the corresponding Airy stress functions to cure nonzero hole tractions read [44]

$$\begin{aligned} F_k^\mathrm {\,HBC}= R^2\bigg [b_{k}^{\sigma _{r}}\ln \frac{r}{R}+\sum _{n=1}^{N_k}\bigg \{B_{k,n}\left( \frac{R}{r}\right) ^{2n}+C_{k,n}\left( \frac{R}{r}\right) ^{2n-2}\bigg \}\cos 2n\varphi \bigg ]\,\sigma _0. \end{aligned}$$
(57)

Its coefficients are determined by equating the stress deviations expanded in the Fourier series

$$\begin{aligned} \begin{aligned} \sigma _{r,{k}}(R,\varphi )/\sigma _0&=\frac{f_{k,0}^{\,\sigma _r}}{2}+\sum _{n=1}^{\;\;N_k^*} f_{k,n}^{\,\sigma _r}\cos n\varphi ,\\ \tau _{r\varphi ,{k}}(R,\varphi )/\sigma _0&=\sum _{n=1}^{\;\;N_k^*} g_{k,n}^{\tau _{r\varphi }}\sin n\varphi \quad \text {with}\\ f_{k,n}^{\,\sigma _r}&=\frac{1}{\pi }\frac{1}{\sigma _0}\int _0^{2\pi }\sigma _{r,k}^\mathrm {dev}(R,\varphi )\cos n\varphi \,\mathrm {d}\varphi ,\\ \quad g_{k,n}^{\tau _{r\varphi }}&=\frac{1}{\pi }\frac{1}{\sigma _0}\int _0^{2\pi }\tau _{r\varphi , k}^\mathrm {dev}(R,\varphi )\sin n\varphi \,\mathrm {d}\varphi \end{aligned} \end{aligned}$$
(58)

with those modelled by \(F_k^\mathrm {HBC}\). This results in

$$\begin{aligned} b_{k}^{\sigma _r}=\frac{1}{2}\,f_{k,0}^{\,\sigma _r},\quad B_{k,n}=-\frac{1}{n(2n+1)}\left[ \frac{1}{2}\,g_{k,2n}^{\tau _{r\varphi }}+n(2n-1)\,C_{k,n}\right] ,\quad C_{k,n}=\frac{1}{2}\frac{g_{k,2n}^{\tau _{r\varphi }}-f_{k,2n}^{\,\sigma _r}}{2n-1}. \end{aligned}$$
(59)

To satisfy all BCs simultaneously, the correction functions and potentials are employed iteratively until arising deviations are negligibly small [44, 47].

Fig. 6
figure 6

Excerpt of the Finite Element model for \(w/d=3\)

Full size image
Table 1 Elastic ply properties of Hexcel IM7-8552 [7]. Fibres oriented parallel to y-axis
Full size table

3 Discussion of the stress results

Different layups of the Hexcel IM7-8552 material are investigated. The elastic ply properties are taken from Camanho et al. [7] and summarised in Table 1. The stress results for configurations involving a width-to-diameter ratio in the range \(w/d=\{3,10\}\) are presented and verified using a Finite Element model implemented in Abaqus. The large geometry property \(w/d=10\) is chosen such that finite-width effects have decayed and the corresponding problem may be treated as within an infinite domain. Continuum plane stress elements with 8 nodes (CPS8) are used. Uniform tension of \(\sigma _0=1~\mathrm {MPa}\) is applied in a hole distance of \(y=20\,d.\) Figure 6 shows details of the FE model and introduces the dimensionless coordinate

$$\begin{aligned} \xi = \frac{x-R}{w/2-R}, \end{aligned}$$
(60)

with \(\xi =0\) at the hole boundary and \(\xi =1\) reaching the free straight edge. To qualitatively analyse the impact of the virtual auxiliary potentials on the load transfer, let us exemplarily plot the force flux using the stress vector

$$\begin{aligned} \mathbf {t}_y=\begin{bmatrix} \sigma _x &{} \tau _{xy} \\ \tau _{xy} &{} \sigma _y \end{bmatrix} \cdot \begin{bmatrix} 0\\ 1 \end{bmatrix} = \begin{bmatrix} \tau _{xy}\\ \sigma _y \end{bmatrix}, \end{aligned}$$
(61)
Fig. 7
figure 7

Flux of stress vectors \(\mathbf {t}_y\) for an quasi-isotropic laminate with \(w/d=3\)

Full size image
Fig. 8
figure 8figure 8

Circumferential and net section stresses of the laminates’ idealisation as an orthotropic plate with smeared stiffnesses. For \(w/d=10\), finite-width effects have decayed and the infinite domain solution [33] is used. Note that the fibre orientation \(\vartheta \) is counted anticlockwise with \(\vartheta =0^\circ \) being parallel to the y-axis/direction of external load

Full size image

for a laminate with quasi-isotropic elastic properties and \(w/d=3\) shown in Fig. 7. The force flux of the present calculus is tangent to the straight edges and to the hole boundary as in the FE solution. This confirms qualitatively that the stress boundary conditions are satisfied. For quantitative assessment, let us investigate the circumferential and the net section stresses for different layups and a geometry ratio of \(w/d=\{3,10\}\) in Fig. 8. The present calculation yields excellent agreement with a maximum error magnitude of 1.4% occurring in the \([\pm 45^\circ ]_\mathrm {s}\)-laminate’s net section stresses. Note that its peak \(\sigma _{\varphi ,\mathrm {max}}\) does not lie in the net section area \(\varphi =\{0,\pi \}\) but is slightly shifted along the hole boundary in the circumferential direction. The present solution’s performance shall be also compared to the net section stress approximations by Tan [61, 63, 64]. Be reminded that these are based on two concepts: Firstly, the Tan approach in which the net section stresses of the infinite open-hole problem are heuristically scaled such that their integration along the width of the actual finite domain problem equilibrates the external load and secondly, the enhanced Tan-Heywood approach (Tan-HW) where the stresses are adapted to the Heywood formula [22] based on photoelasticity. The finite-width correction factor \(K_\mathrm {T}^\mathrm {Tan}/K_\mathrm {T}^\mathrm {inf}\) of the Tan approach is derived by

$$\begin{aligned} \begin{aligned}&\sigma _y^\mathrm {Tan}(x,0)=\frac{K_\mathrm {T}^\mathrm {Tan}}{K_\mathrm {T}^\mathrm {inf}}\,\sigma _y^\mathrm {inf}(x,0),\\&{2}\frac{K_\mathrm {T}^\mathrm {Tan}}{K_\mathrm {T}^\mathrm {inf}}\int _{R}^{w/2}\sigma _y^\mathrm {inf}(x,0)\,\mathrm dx=\sigma _0\cdot w. \end{aligned} \end{aligned}$$
(62)

Regarding the enhanced Tan-Heywood approach, the correction factor \(K_\mathrm {T}^\mathrm {Tan-HW}/K_\mathrm {T}^\mathrm {inf}\) is determined by

$$\begin{aligned} K_\mathrm {T}^\mathrm {Tan-HW}/K_\mathrm {T}^\mathrm {inf}=\ \Bigg [\frac{3\,(1-d/w)}{2+(1-d/w)^3}+\frac{1}{2}\bigg (\frac{d}{w}\, M\bigg )^6(K_\mathrm {T}^\mathrm {inf}-3)\bigg \{1-\left( \frac{d}{w}\,M\right) ^2\bigg \}\Bigg ]^{-1}, \end{aligned}$$
(63)

with

$$\begin{aligned} \begin{aligned} M^2&=\left\{ \sqrt{1-8\left[ \frac{3(1-d/w)}{2+(1-d/w)^3}-1\right] }-1\right\} \cdot \frac{1}{2\,(d/w)^2},\\ K_\mathrm {T}^\mathrm {inf}&=1+\sqrt{\frac{2}{A_{11}}\left( \sqrt{A_{11}A_{22}}-A_{12}+\frac{A_{11}A_{22}-A_{12}^2}{2\,A_{66}}\right) }\\&=\sigma _y^\mathrm {inf}(R,0)/\sigma _0. \end{aligned} \end{aligned}$$
(64)

Therein, the quantities \(A_{ij}\) denote the laminate’s in-plane stiffnesses in the frame of classical laminate theory [19, 71]. Note that the formula for \(K_\mathrm {T}^\mathrm {inf}\) is adapted to the nomenclature of the present work with a fibre orientation \(\vartheta =0^\circ \) parallel to the y-axis. For the quasi-isotropic case, the correction factors specialise to

$$\begin{aligned} \begin{aligned} K_\mathrm {T}^\mathrm {Tan}/K_\mathrm {T}^\mathrm {inf}&=\frac{2}{2-(d/w)^2-(d/4)^4},\\ K_\mathrm {T}^\mathrm {Tan-HW}/K_\mathrm {T}^\mathrm {inf}&=\frac{2+(1-d/w)^3}{3\,(1-d/w)}. \end{aligned} \end{aligned}$$
(65)

Let us assess the net section stresses derived by the Tan formulae. When comparing the entire net section plane \( 0\le \xi \le 1\) and assessing the highest error magnitude, deviations for all approaches are quite high as summarised in Table 2. However, literature [7, 66, 67, 76] as well as Sec. 4 of the present work reveal that nonlocal failure criteria require the stress evaluation in the hole edge’s vicinity when assessing a technically relevant hole diameter not smaller than a few millimetres. Hence, the range of interest is limited which shall be roughly assumed to lie within \(0\le \xi \le 0.2\). Therein, both the Tan and Tan-Heywood approaches perform better than along the range \(\xi >0.2\). Their solution quality depends on how pronounced the finite-width effect of a laminate is. In particular, it is slight for \([0^\circ ], [0^\circ /90^\circ ]_\mathrm {s}\) as well as \([0^\circ /\pm 45^\circ /90^\circ ]_\mathrm {s}(50\%/40\%/10\%)\)-laminates and their stress concentration is mainly due to the material anisotropy only slightly increasing with decreasing w/d (Fig. 8). For these laminates, the approaches by Tan and Tan-Heywood yield a good approximation within \(0\le \xi \le 0.2\) and are not further shown in Fig. 8 for reasons of limited space.

Contrary, \([\pm 45^\circ ]_\mathrm {s}\) and quasi-isotropic laminates (QI) show pronounced finite-width effects and the heuristic approaches’ errors are larger within \(0\le \xi \le 0.2\), except for the Tan-Heywood concept yielding excellent results for QI laminates. However, for the remaining cases, the stresses derived by solving the actual boundary value problem shall be taken, especially when each percent accuracy matters in light-weight optimal design. Concerning \([\pm 45^\circ ]_\mathrm {s}\) calculated by both the Tan and Tan-Heywood approach as well as regarding the QI-laminate with Tan’s approach, their net section stresses in the critical range \(\xi \le 0.2\) underestimate the FE solution and can be therefore regarded as nonconservative approximation. Further, the net section stresses by Tan-Heywood violate the equilibrium. In particular, their integral along the width of the finite problem unphysically yields an excessive load transfer value of up to \(\chi _{\sigma _y}=1.08\) although a value of 1 should be obtained. With this, the present method is validated and based on its stresses, a failure analysis concerning brittle crack initiation shall be conducted.

Table 2 Maximum error magnitudes of heuristically determined stresses
Full size table

4 Failure analysis

First, the fundamentals of the nonlocal brittle failure prediction concepts Theory of Critical Distances (TCD) and Finite Fracture Mechanics (FFM) are introduced. These are capable of capturing the hole size effect contrary to local criteria [39,40,41, 50]. Based on the present stress solution, failure loads for the configuration with \(w/d=6\) are calculated and validated against experimental data published by Camanho et al. [7]. Then, the finite-width influence on the the failure load reduction in the context of the size effect is analysed. The failure analysis of the present work shall be dedicated to quasi-isotropic laminates due to the limited experimental data available to the authors. However, the methodology for orthotropic laminates is the same.

4.1 Theory of Critical Distances

In the frame of the Theory of Critical Distances using line method, the average net section stresses

$$\begin{aligned} {\overline{\sigma }}_y(\tilde{r_c})=\frac{1}{\tilde{r_c}}\int _{0}^{\tilde{r_c}}\sigma _y(x^*,0)\,\mathrm {d}x^* \quad \text {with~} x^*=x-R \end{aligned}$$
(66)

are investigated, where \(\tilde{r_c}\) denotes an arbitrary hole distance. Failure is assumed if the average net section stress within the characteristic hole distance \(\tilde{r_c}=r_c\) equals the longitudinal tensile strength \(X_\mathrm {T}^\mathrm {L}\) of the plain material,

$$\begin{aligned} {\overline{\sigma }}_y({r_c})=X_\mathrm {T}^\mathrm {L}. \end{aligned}$$
(67)

The characteristic distance can be calculated based on the Theory of Critical Distances by Taylor [65,66,67,68] with

$$\begin{aligned} r_{c,\mathrm {T}}=\frac{2}{\pi }\left( \frac{K_c}{X_\mathrm {T}^\mathrm {L}}\right) ^2=1.632~\mathrm {mm}, \end{aligned}$$
(68)

where the fracture toughness is \(K_{c}=42.8~\mathrm {MPa}\sqrt{\mathrm {m}}\) and the plane strength is \(X_\mathrm {T}^\mathrm {L}=845.1~\mathrm {MPa}\) for the Hexcel IM7-8552 material investigated [7, 9].

Another way to determine the characteristic distance is by calibration to the experimental failure load [76]. In doing so, the failure load is applied in the present calculus and the calibrated characteristic distance may be determined using the failure condition in Eq. (67). In all TCD approaches, the failure load for configurations with any diameter d can be calculated using the normalised characteristic distance

$$\begin{aligned} \xi _{r_c}=\frac{2r_c}{(w/d-1)\,d}, \end{aligned}$$
(69)

and then

$$\begin{aligned} \sigma _{\mathrm {F,TCD}}=\frac{X_\mathrm {T}^\mathrm {L}}{\displaystyle \frac{1}{\xi _{r_c}}\int _{0}^{\xi _{r_c}}\sigma _y(\xi ,0)\,\big |_{\sigma _0=1}\,\mathrm {d}\xi }. \end{aligned}$$
(70)

Herein, the net section stresses caused by the unit load shall be taken. The TCD assumes the characteristic distance to be invariant with respect to the defect size. However, this quantity has been identified as structural and not as material parameter [1, 8, 52, 59, 62] being dependant on geometrical properties as w/d but also on the absolute value of d itself. Therefore, the calibrated characteristic distance is generally not applicable to other configurations, but possibly to a certain extent. This matter shall be further analysed which is of interest, especially if conducting more experiments for calibration is not affordable. In doing so, the failure prediction concept of Finite Fracture Mechanics serves as reference since there is no additional experimental data available to the authors. Moreover, FFM is the more sophisticated failure prediction model purely based on physical input parameters.

4.2 Finite Fracture Mechanics

In the context of Finite Fracture Mechanics [75], the instantaneous initiation of a finite-sized crack is assumed if both stress and energy criteria are satisfied. This condition is called coupled criterion introduced by Leguillon [31] and generally yields an optimisation problem to calculate the minimal load and the corresponding crack length extension \(\varDelta a\) leading to its initiation. The open-hole problem is characterised by a monotonic decrease in the stresses and a monotonic increase in the energy release rate with respect to \(\varDelta a\). Let \(a=R+\varDelta a\) be the overall defect size (ref. pictogram in Fig. 10), then the coupled criterion specialises to the conditions

$$\begin{aligned} \dfrac{1}{\varDelta a}\int _{R}^{R+\varDelta a}\sigma _y(x,0)\,\mathrm {d}x=X_\mathrm {T}^\mathrm {L}\quad \wedge \quad \frac{1}{\varDelta a}\int _{R}^{R+\varDelta a}K_\mathrm {I}^2(a)\,\mathrm {d}a=K_\mathrm {Ic}^2, \end{aligned}$$
(71)

where \(K_\mathrm {I}\) denotes the mode I stress intensity factor of a hypothetically initiated crack with the finite size a. For the net section stresses, the values of the present calculus are taken, whereas regarding the stress intensity factor, closed-form approximations from literature are chosen. Since experimental data available to the authors treat quasi-isotropic laminates, the failure analysis will focus on these and the corresponding stress intensity factor [43] can be calculated by

$$\begin{aligned} \begin{aligned} K_I&=\sigma _0 F_h\,F_w\sqrt{\pi a}, \\ F_h&=\sqrt{1-\frac{R}{a}}\,f_n,\\ f_n&=1+0.358\lambda +1.425\lambda ^2-1.578\lambda ^3+2.156\lambda ^4,\quad \text {with}\quad \lambda =R/a,\\ F_w&=\sqrt{\sec \frac{\pi R}{w}\sec \frac{\pi a}{w}}. \end{aligned} \end{aligned}$$
(72)

These formulae are adapted to the nomenclature of the present paper and were derived by fitting to the results of Newman [42] as well as Shivakumar and Forman [57], where the former work treats finite and the latter infinite dimensions both using complex potential formulation by Muskhelishvili [38]. The formulae for the stress intensity factor are also documented in the handbook by Tada et al. [60] Note that the stress intensity is affected by the material orthotropy [2], which must be taken into account when extending the method. The coupled criterion shall be now evaluated for the quasi-isotropic case. Let \({\tilde{\sigma }}_y(x,0)\) and \({{\tilde{K}}}_\mathrm {I}(a)\) be the corresponding field quantities caused by the unit load \(\sigma _0=1\). Then, scaling these with the unknown failure load \(\sigma _{\mathrm {F,FFM}}\) and eliminating the latter in the coupled criterion Eq. (71) yields

$$\begin{aligned} \frac{\dfrac{1}{\varDelta a}\left[ \displaystyle \int _{R}^{R+\varDelta a} {{\tilde{\sigma }}}_y(x,0)\,\mathrm {d}x\right] ^2}{\displaystyle \int _{R}^{R+\varDelta a}{{\tilde{K}}}_\mathrm {I}^2(a)\,\mathrm {d}a}=\left( \frac{X_\mathrm {T}^\mathrm {L}}{K_\mathrm {Ic}}\right) ^2 \end{aligned}$$
(73)
Fig. 9
figure 9

Crack length \(\varDelta a\) at failure. The marker x denotes the calibrated characteristic distances derived using configurations with different hole diameter d

Full size image
Table 3 Failure stresses for \([90/0/\pm 45]_\mathrm {4s}\)-laminate with \(w/d=6\)
Full size table

enabling to determine \(\varDelta a\). Back substitution in the stress or energy criterion Eq. (71) leads to \(\sigma _{\mathrm {F,FFM}}\). The predicted failure loads based on the different approaches are discussed and validated against experimental data in the next section.

4.3 Discussion of the failure analysis: validation to the experiment

At first, failure stress predictions by TCD and FFM are discussed for the quasi-isotropic laminate \([90/0/\pm 45]_\mathrm {4s}\) with \(w/d=6\) and validated against experimental data. Then, the finite-width effect is analysed by treating configurations with \(w/d=\{3,6,10\}\). In the frame of FFM, the coupled criterion reveals the crack length \(\varDelta a\) being dependent on the hole’s diameter (Fig. 9). Herein, with increasing defect size d, the crack length reaches a plateau, in which it can be approximated by a constant value. If the TCD approaches are based on a characteristic distance lying nearby this plateau, the concept should yield similar results as FFM. This is true for the TCD approach by Taylor (TCD-T). Regarding the TCD using calibrated characteristic distances (TCD-CLB), the value of \(r_{c,\mathrm {clb}}\) depends on the particular test set chosen for calibration (Table 3). In general, larger hole diameters shall be selected since the higher d, the closer the plateau area. However, different values of calibrated characteristic distances \(r_{c,\mathrm {clb}}\) with respect to the corresponding test configuration’s diameter d are shown in Fig. 9 and convergence to a constant value is not observable. Nevertheless, the test set with the largest diameter shall be chosen for calibration leading to \(r_{c,\mathrm {clb}}=1.849\) mm. Note that the selection of the particular calibration test set is for the current open-hole problem rather insignificant since \(\varDelta a\) rapidly reaches a plateau value. Further, failure stresses have been derived by the TCD-CLB method using all available test sets for calibration yielding a maximum error magnitude of \(\le 5\%\) beyond \(d\ge 2\) mm compared to FFM (Fig. 13) and of 8% compared to the experiment. Note that only the deviations regarding the TCD-CLB with the chosen calibration distance of \(d_\mathrm {clb}=10\) mm are listed in Table 3 to limit the amount of data. Therein, all approaches yield failure loads with acceptable error magnitude and thus can be considered as reliable assessment means. The proximity of the plateau value of \(\varDelta a\) to \(r_{c,\mathrm {clb}}\) may be also interpreted as follows. The calibrated characteristic distance can be regarded as experimentally determined crack length. Since the corresponding quantity predicted by the FFM concept lies close to it, this crack initiation model can be seen as further confirmed. Note that FFM results are actually the same as those by Camanho et al. [7] based on stresses of the enhanced heuristic Tan-Heywood approach [63]. This is due to the fact that for \(w/d=6\) rather slight finite-width effects occur and the stresses along the net section plane of the actual boundary value problem are almost the same as those of the heuristic approach. However, for small w/d the authors recommend to use the stress solution of the actual finite boundary value problem especially for quasi-isotropic and \([\pm 45^\circ ]_\mathrm {s}\)-laminates involving pronounced finite-width effects.

Fig. 10
figure 10

Normalised failure loads by FFM with \(X_\mathrm {T}^\mathrm {L}=845.1\) MPa

Full size image

4.4 Discussion of the failure analysis: finite-width effect

Let us investigate how finite width influences the failure load. The FFM shall serve as data source since further experiments are not available for the authors. The crack length with respect to d is shown in Fig. 9 for \(w/d=\{3,6,10\}\). Herein, the corresponding plateau values are quite similar and lie near both characteristic distances \(r_{c,\mathrm {clb}},r_{c,\mathrm {T}}\). Hence, it can be expected that these quantities can be also used for the TCD approaches for defect sizes in the plateau. However, below \(d<10\) mm the crack length extension \(\varDelta a\) shows a different behaviour for the geometry ratios treated. To assess if the TCD approaches are nevertheless applicable, their normalised deviations to FFM shall be analysed. But first, let us investigate the FFM failure stresses normalised to the plain material strength \(X_\mathrm {T}^\mathrm {L}\) in Fig. 10. In here, a significant decrease of the failure load is observable due to the size effect. To investigate the interaction in between finite width and defect size on the failure stresses, let us analyse the reduction factors

$$\begin{aligned} \begin{aligned} \eta _{w/d}&=\frac{\sigma _{\mathrm {F,FFM}}(w/d=\{3,6\},d)}{\sigma _{\mathrm {F,FFM}}(w/d=10,d)},\\ \eta _{d}&=\frac{\sigma _{\mathrm {F,FFM}}(w/d,d)}{\sigma _{\mathrm {F,FFM}}(w/d,d=1~\mathrm {mm})}. \end{aligned} \end{aligned}$$
(74)
Fig. 11
figure 11

Reduction factor describing finite-width effect on the failure load

Full size image
Fig. 12
figure 12

Reduction factor describing size effect on the failure load

Full size image

Regarding \(\eta _{w/d}\), failure stresses of \(w/d=10\) are selected as reference since for this configuration finite-width effects have decayed and thus can be treated as infinite domain problem. In Fig. 11, the quantity \(\eta _{w/d}\) reveals a converging behaviour similar to the FFM derived crack length \(\varDelta a\). The finite-width influence on the failure stress mitigation is higher, the smaller the defect size. Moreover, the family of curves of \(\eta _{d}\) in Fig. 12 shows that the hole size effect is affected by the degree of finite width. In particular, the wider w/d and the larger d, the more significant is the failure stress reduction.

Concerning the TCD approaches, the corresponding deviations of the failure stress prediction are within a tolerable limit (Fig. 14). For \(w/d=10\), both TCD-CLB and TCD-T concepts yield error magnitudes \(<\,3\)% and regarding \(w/d=3\), the former approach leads to inaccuracies \(<\,5\)% for \(d\ge 6\) mm and the latter concept for \(d\ge 3\) mm. The following can be hence concluded for the present open-hole problem with quasi-isotropic laminate. The use of a single characteristic distance is sufficient to adequately capture the hole size effect without the necessity to model the crack length dependency for both small and large finite geometry values w/d within a wide defect size range. This even applies for the characteristic distance by Taylor although the length parameter \(r_{c,\mathrm {T}}\) is not related to the open-hole problem but to \(r_{p}\), the effective crack length of the mode I through crack in an infinite isotropic plate [60] with \(r_{p}=r_{c,\mathrm {T}}/4\). What this problem and the open hole have in common is the external loading uniformly introduced at infinity. Since \(r_{c,\mathrm {T}}\) can be used as an approximation to model \(\varDelta a\) of the open hole, it may be concluded that the considered shape of the defect (crack vs. hole) as well as finite-width effects have a less significant impact on the crack length \(\varDelta a(d)\). However, for the filled hole/pin-loaded hole within a finite domain [45], the TCD-T approach is applicable in a diameter range much smaller than that of the present open-hole problem. It might be concluded from these observations that the way how the external load is introduced (uniform tension at infinity vs. sinusoidal radial stresses along the hole boundary) and the stress decay’s leading order (1/r for filled holes [45, 47] and \(1/r^2\) for open holes [27, 44, 54, 70]) have a more significant impact on the crack length \(\varDelta a\) and the overall fracture behaviour.

The employed nonlocal failure criteria emphasize that capturing the hole size effect is essential for a light-weight optimal design. The extreme cases of defect sizes are \(d\rightarrow 0\) for which the failure stress specialises to the plain material strength and \(d\rightarrow \infty \) where it coincides with local criteria. The failure stress of a finite hole diameter is in between and for a sufficient material exploitation, nonlocal criteria requiring accurate net section stresses and not only stress concentrations are vital. For further validation, more experiments should be conducted, especially regarding fracture in orthotropic laminates, since the used failure concepts are just models of crack propagation mechanisms occurring in real structures with brittle material.

Fig. 13
figure 13

Normalised deviations to FFM failure load for \(w/d=6\): TCD-CLB approach with respect to the calibration diameter \(d_\mathrm {clb}\) and TCD-T concept

Full size image
Fig. 14
figure 14

Normalised deviations to FFM failure load. For the calibrated characteristic distance, the configuration with \(d=10\) mm and \(w/d=6\) is chosen

Full size image

5 Conclusion

In the present paper, the stress field for the orthotropic finite domain open-hole composite laminate problem under uniform tension is derived using complex potentials. This is achieved by taking the solution of the corresponding infinite-domain problem and supplementing it with auxiliary functions and potentials to fulfil vanishing tractions along the straight edges of the actual finite-width problem. The auxiliary functions include Fourier series expansions to continuously model the deviations enabling their cancellation and novel periodic arrangements of the infinite open-hole problem, which are advantageous in terms of computational effort. The results are in excellent agreement with FE net section stresses for different layups containing errors in the order of only \(1\%\). Based on the calculated stresses, a failure analysis to predict brittle crack initiation is conducted using the nonlocal concepts Theory of Critical Distances (TCD) and Finite Fracture Mechanics (FFM). The results are validated against the experiment showing good agreement. FFM is used to model the failure load’s decrease due to the size effect, which is revealed to be more significant the wider the width-to-diameter ratio w/d. Further, its relative decrease due to finite width is more pronounced the smaller the defect size d. The concept TCD being calibrated to a specific configuration proves to be applicable within a wide value range of w/d and d when using the recent state-of-the-art failure concept FFM as reference.