Interaction of crack and hole: effects on crack trajectory, crack driving force and fracture toughness

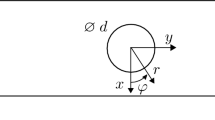
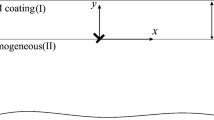
Abstract

The paper investigates the effectiveness of a circular hole as a crack arrester. A hole represents an elastic inhomogeneity, which is able to attract neighboring cracks, to deflect and stop them from propagating. The interaction between a crack and a neighboring hole is studied, as well as its effects on failure stress and fracture toughness. For this purpose, a numerical model using the configurational force concept and a damage-based approach, the ductile damage plasticity modeling, are combined. In the first part of the paper, an efficient approach is presented to approximate the crack trajectory and the crack driving force in the proximity of a circular hole. The main purpose is to determine the maximum distance at which cracks can be trapped. This is performed for uni- and biaxial loading conditions, and for surface and interior cracks. The second part investigates the improvement in failure stress and fracture toughness, if cracks are trapped by a hole. Hereby perfect and imperfect holes, which contain a defect at the hole boundary, are considered. It is found that the crack trapping distance is affected by the boundary and loading conditions. The increases in failure stress and fracture toughness due to the trapping of a crack depend primarily on the hole size and the defect size at the boundary. The procedures presented in this paper can be applied to composites with arrays of holes or second phase particles of arbitrary shapes.

Appendices

Appendix A: Effect of crack extension increment on crack trajectory interpolation

Besides the initial crack tip location, the only variable parameter for the interpolation procedure is the crack extension increment Δa. The magnitude of Δa can have a significant influence on the crack trajectory, if it is not appropriately chosen, see the example shown in Fig. 

Fig. 15

Influence of the magnitude of the crack extension increment Δa on a the crack trajectory and b the relative trapping zone size λ_tr, evaluated for a surface crack under uniaxial loading

15. Crack trajectories are indicated in Fig. 15a for three different Δa/r-values. All cracks have started at the beginning of the interpolation zone, l_x/r =  − 8. It is seen that the magnitude of the trapping zone λ_tr decreases with increasing Δa. The crack extension increment Δa was varied over a wide range (Fig. 15b). It is seen that the trapping zone λ_tr remains almost unchanged for Δa/r < 0.1.

If not specified otherwise, a normalized crack extension increment of Δa/r = 0.01 is taken for the crack trajectory interpolation procedure in the current work. Decreasing the crack extension increment below this value does not improve the accuracy of the predicted trajectory; only the computation time increases. It should be remarked that this crack extension increment would not be applicable, if the specimen configuration or the loading conditions were significantly changed. It might be interesting in this respect that Lei et al. (2012) have used locally varying crack extension increments, depending on the crack propagation velocity.

Appendix B: Effect of crack kinking on crack trejectory interpolation

The CTI method does not take into account the actual kinking of a crack near the hole, Sect. 3. After a crack has kinked, the new crack faces are no longer perpendicular to the external load and a mixed-mode loading condition is induced to the crack tip, see e.g. Suresh and Shih (1986). Therefore, it is important to investigate whether crack kinking would lead to other crack trajectories and to other magnitudes of the crack driving force.

Comparisons are made between the results of the interpolation procedure and the conventional iterative crack propagation procedure that allows consecutive kinking. We assume initially straight cracks of length a₀ = 20 mm lying on the mid-plane of the specimen. The hole center is located at a position given by x_f = 30 mm, y_f = ${{l}}_{\text{y}}^{\text{tr}}$, where ${{l}}_{\text{y}}^{\text{tr}}$ denotes the trapping distance for the considered boundary and loading conditions. A crack extension increment, Δa = r/5, is used to save computation time, as the iterative procedure is extremely time-consuming. Computations are performed for surface cracks subjected to uniaxial and biaxial loading conditions. To calculate S_tip for the iterative procedure, the magnitude of the crack driving force in the kinked configuration with a hole is related to the crack driving force of a straight crack in the homogeneous material where the crack length is the projected length of the kinked crack trajectory. Note that, for good comparison, the results of the iterative procedure are re-calculated with the increment, Δa = r/5 and the crack trajectory interpolation starts in horizontal direction at l_x/r =  − 5, which leads to somewhat different λ_tr − values than those reported in the sections above with the much finer increments.

The results are summarized in Fig. 

Fig. 16

Comparison between the CTI method (interpolation) of Sect. 3 and the iterative method where crack kinking is taken into account. Compared are the crack trajectory and the normalized crack driving force S_tip for a surface crack subjected to a uniaxial loading, b biaxial loading (β = 1), and c biaxial loading (β =  − 1)

16. For the surface crack under uniaxial loading (Fig. 16a) both the crack trajectory and the normalized crack driving force along the trajectory S_tip are in good agreement with the interpolated results. For biaxial loading with β = 1, the crack experiences a slightly stronger attraction to the hole when kinking is considered (Fig. 16b). The opposite effect occurs for β =  − 1; the crack feels a weaker attraction when kinking is considered (Fig. 16c). Since the crack driving force is strongly influenced by the distance between crack tip and hole, the variations of S_tip along the crack trajectory show quite significant differences, especially, if in one case the crack enters the hole and in the other case not (Fig. 16c). A good matching between the interpolated and the iterative trajectory exists outside the trapping zone.

It should be noted that only the magnitudes of the relative trapping distances λ_tr are important for the current study, and these values are practically equal in both procedures. It is clear that the results of the current paper could not have been achieved by application of the iterative procedure, since it would be much too time consuming. Also for future investigations, as described in Sect. 6, the iterative procedure would be computationally inefficient.

Appendix C: Parameter study for the ductile damage plasticity model

It is investigated in this appendix, how the FE mesh size e_d, the magnitude of the equivalent plastic strain for damage initiation $\bar{\varepsilon}_{0}^{\text{pl}}$, and the magnitude of the specific fracture energy G_f influence the results of the ductile damage plasticity model. We consider a specimen with a surface crack subjected to uniaxial tension. The material is homogeneous, i.e. without a hole, denominated as the reference configuration in Fig. 12c. The FE mesh around the tip is rectangular with a constant mesh size e_d. The material response is described by Fig. 12d with the parameters as given in Sect. 5.1, if not specified otherwise.

The computations are performed using an implicit dynamic formulation with an adaptive time incrementation method. The specimen is loaded by prescribing the applied stress σ_∞ at the upper and lower boundary, which is gradually increased. Damage is initiated at the first element directly ahead of the tip, causing a stiffness degradation. The first element at the tip is deleted when the damage variable reaches D = 1. Subsequently, the crack starts to propagate in an unstable manner until the specimen is completely fractured. Therefore, the failure stress ${\sigma}_{\text{f}}^{\text{ref}}$ is determined by the initiation and evolution of damage in the first element directly in front of the initial crack. For an accurate determination of the failure stress, both the adaptive time increment and the increase in loading are significantly reduced, if the applied stress σ_∞ comes close to the failure stress ${\sigma}_{\text{f}}^{\text{ref}}$.

Figure 17a shows the influence of the element size e_d on the failure stress ${\sigma}_{\text{f}}^{\text{ref}}$ for given parameters, $\overline{\varepsilon }_{o}^{{{\text{pl}}}}$ and G_f. The specific fracture energy G_f is calculated according to Eq. (11). An increase of the element size leads to an increase of the notch tip size. Therefore, the stress concentration near the crack tip decreases according to Eq. (12), which causes decelerated damage evolution and a higher failure stress ${\sigma}_{\text{f}}^{\text{ref}}$. It is seen that ductile damage plasticity modelling usually requires a fitting to experimental data and an adaption of the parameters depending on the mesh size. This is especially important, if high stress concentrations are present in the material, such as near the tip of a crack. Note that the specimen with a perfect hole exhibits the same failure stresses σ_f for different mesh sizes. Therefore, it would be even more problematic if the crack of Fig. 12c, which has been modeled as a rectangular notch with a distance e_d between the crack faces, were replaced by an infinitely sharp crack.

Figure 17b shows that the equivalent plastic strain for damage initiation $\bar{\varepsilon}_{0}^{\text{pl}}$ does not influence the failure stress ${\sigma}_{\text{f}}^{\text{ref}}$ within the region $\bar{\varepsilon}_{0}^{\text{pl}}\leq {10}^{-4}$. For higher values, plastic yielding becomes more important, and the failure stress increases.

Figure 17c shows that the magnitude of the specific fracture energy G_f does not influence the failure stress ${\sigma}_{\text{f}}^{\text{ref}}$. This is so at least for G_f ≤ 6 J/m². The reason might be that ${\sigma}_{\text{f}}^{\text{ref}}$ is determined by the failure of the first element in front of the tip so that the subsequent damage evolution in the ligament of the specimen does not play a role. It should be noted that, for a given small mesh size e_d, an increase of G_f can excessively increase the computation time.

Fig. 17

Uniaxially loaded specimen with surface crack. Influence of a FE mesh size e_d, b the equivalent plastic strain for damage initiation $\overline{\varepsilon }_{0}^{{{\text{pl}}}}$, c the specific fracture energy G_f on the failure stress $\sigma_{{\text{f}}}^{{{\text{ref}}}}$