Skip to main content
SpringerLink
Log in

Numerical and experimental investigations into feedback control of continuous beam structures under moving loads

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

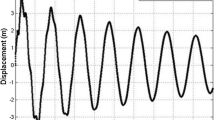
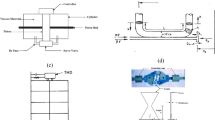
This paper presents and validates a novel approach to designing an active controller for a small-scale experimental structure subjected to the action of multiple moving loads. Many of the numerically validated active control methods presented in the literature assume that the synthesised control solution can be applied directly to the structure. When a real structure is investigated, the closed-loop stability and performance of the system are affected by the actuators’ dynamics and by the signal-to-noise ratio. In some cases when the structure is complex, the model used for the structure can have controllability and observability problems. In this study, an active control solution is designed using a simplified model, and then, it is experimentally validated. The control voltage dependent on the measured displacement signals is fed back to the structure via electrodynamic actuators. The objective of the control is to reduce the structure’s deflection under the action of the loads at sensors’ locations. Numerical and experimental results prove that using linear or cubic displacement feedback control the vibration amplitudes can be significantly reduced. The controller can tolerate speed variations, but it always needs to include compensation in order to increase the stability margins of the controlled system. The linear displacement feedback has a better performance at low values of the deflection, whereas the cubic displacement feedback shows a better robustness performance at high values of moving masses and speed variations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

References

  1. Raja, S., Pashilkar, A.A., Sreedeep, R., Kamesh, J.V.: Flutter control of a composite plate with piezoelectric multilayered actuators. Aerosp. Sci. Technol. 10, 435–441 (2006)

    Article  Google Scholar 

  2. Vesali, F., Rezvani, M.A., Molatefi, H.: Simulation of the dynamic interaction of rail vehicle pantograph and catenary through a modal approach. Arch. Appl. Mech. 90, 1475–1496 (2020)

    Article  Google Scholar 

  3. Hue, W.: Vertical dynamics of a single-span beam subjected to moving mass-suspended payload system with variable speeds. J. Sound Vib. 418, 36–54 (2018)

    Article  Google Scholar 

  4. Ariaei, A., Ziaei-Rad, S., Malekzadeh, M.: Dynamic response of a multi-span Timoshenko beam with internal and external flexible constraints subject to a moving mass. Arch. Appl. Mech. 83, 1257–1272 (2013)

    Article  Google Scholar 

  5. Stancioiu, D., Ouyang, H., Mottershead, J.E., James, S.: Experimental investigations of a multi-span flexible structure subjected to moving masses. J. Sound Vib. 330, 2004–2016 (2011)

    Article  Google Scholar 

  6. Yang, Y., Ouyang, H., Stancioiu, D.: Numerical studies of vibration of four-span continuous plate with rails excited by moving car with experimental validation. Int. J. Struct. Stab. Dyn. 17, 1750119 (2017)

    Article  Google Scholar 

  7. Chen, X., Ma, W., Luo, S.: A vehicle-track beam matching index in EMS maglev transportation system. Arch. Appl. Mech. 90, 773–787 (2020)

    Article  Google Scholar 

  8. Daniel, Y., Lavan, O., Levy, R.: Multiple-tuned mass dampers for multimodal control of pedestrian bridges. J. Struct. Eng. 138, 1173–1178 (2012)

    Article  Google Scholar 

  9. Shi, X., Cai, C.S.: Suppression of vehicle-induced bridge vibration using tuned mass damper. J. Vib. Control 14, 1037–1054 (2008)

    Article  Google Scholar 

  10. Martinez-Rodrigo, M.D., Museros, P.: Optimal design of passive viscous dampers for controlling the resonant response of orthotropic plates under high-speed moving loads. J. Sound Vib. 330, 1328–1351 (2011)

    Article  Google Scholar 

  11. Samani, F.S., Pellicano, F.: Vibration reduction on beams subjected to moving loads using linear and nonlinear dynamic absorbers. J. Sound Vib. 325, 742–754 (2009)

    Article  Google Scholar 

  12. Sloss, J.M., Adali, S., Sadek, I.S., Bruch, J.C.: Displacement feedback control of beams under moving loads. J. Sound Vib. 122, 457–464 (1988)

    Article  Google Scholar 

  13. Nikkhoo, A., Rofooei, F.R., Shadnam, M.R.: Dynamic behavior and modal control of beams under moving mass. J. Sound Vib. 306, 712–724 (2007)

    Article  MathSciNet  Google Scholar 

  14. Liu, X., Wang, Y., Ren, X.: Optimal vibration control of moving-mass beam systems with uncertainty. J. Low Freq. Noise Vib. Act. Control 39, 803–817 (2019)

    Article  Google Scholar 

  15. Lin, Y.H., Trethewey, M.W.: Active vibration suppression of beam structures subjected to moving loads: a feasibility study using finite elements. J. Sound Vib. 166, 383–395 (1993)

    Article  Google Scholar 

  16. Kong, E., Song, J.S., Kang, B.B., Na, S.: Dynamic response and robust control of coupled maglev vehicle and guide way system. J. Sound Vib. 330, 6237–6253 (2011)

    Article  Google Scholar 

  17. Zarfam, R., Khaloo, A.R.: Vibration control of beams on elastic foundation under a moving vehicle and random lateral excitations. J. Sound Vib. 331, 1217–1232 (2012)

    Article  Google Scholar 

  18. Stancioiu, D., Ouyang, H.: Optimal vibration control of beams subjected to moving mass at constant speed. J. Vib. Control 22, 3202–3217 (2016)

    Article  MathSciNet  Google Scholar 

  19. Pi, Y., Ouyang, H.: Vibration control of beams subjected to a moving mass using a successively combined control method. Appl. Math. Model. 40, 4002–4015 (2016)

    Article  MathSciNet  Google Scholar 

  20. Qiana, C.Z., Tang, J.S.: A time delay control for a nonlinear dynamic beam under moving load. J. Sound Vib. 309, 1–8 (2008)

    Article  Google Scholar 

  21. Bani-Hani, K.A., Alawneh, M.R.: Prestressed active post-tensioned tendons control for bridges under moving loads. Struct. Control Health Monit. 14, 357–383 (2007)

    Article  Google Scholar 

  22. Wasilewski, M., Pisarski, D.: Adaptive semi-active control of a beam structure subjected to a moving load traversing with time-varying velocity. J. Sound Vib. 481, 115404 (2020)

    Article  Google Scholar 

  23. Kong, E., Song, J.S., Kang, B.B., Na, S.: Dynamic response and robust control of coupled maglev vehicle and guideway system. J. Sound Vib. 330, 6237–6253 (2011)

    Article  Google Scholar 

  24. Auperin, M., Dumolin, C., Magonette, G.E., Marazzi, F., Forsterling, H., Bonefeld, R., Hooper, A., Jenner, A.G.: Active control in civil engineering: from conception to full scale applications. J. Struct. Control 8, 123–178 (2001)

    Article  Google Scholar 

  25. Shelley, S.J., Lee, K.L., Aksel, T., Aktan, A.E.: Active-control and forced-vibration studies on highway bridge. J. Struct. Eng. 121, 1306–1312 (1995)

    Article  Google Scholar 

  26. Casado, C.M., Diaz, I.M., de Sebastian, J., Poncela, V.A., Lorenzana, A.: Implementation of passive and active vibration control on an in-service footbridge. Struct. Control Health Monit. 20, 70–87 (2013)

    Article  Google Scholar 

  27. Moutinho, C., Cunha, A., Caetano, E.: Analysis and control of vibrations in a stress-ribbon footbridge. Struct. Control Health Monit. 18, 619–634 (2011)

    Article  Google Scholar 

  28. Patten, W.N., Sack, R.L., He, Q.: Controlled semi-active hydraulic vibration absorber for bridges. J. Struct. Eng. 122, 187–192 (1996)

    Article  Google Scholar 

  29. Dyniewicz, B., Konowrocki, R., Bajer, C.I.: Intelligent adaptive control of the vehicle span\track system. Mech. Syst. Signal Process. 58, 1–14 (2015)

    Article  Google Scholar 

  30. Pisarski, D.: Optimal control of structures subjected to traveling load. J. Vib. Control 24, 1283–1299 (2018)

    Article  MathSciNet  Google Scholar 

  31. Ashasi-Sorkhabi, A., Goorts, K., Mercan, O., Narasimhan, S.: Mitigating pedestrian bridge motions using a deployable autonomous control system. J. Bridge Eng. 24(1), 04018101 (2019)

    Article  Google Scholar 

  32. Pereira, E., Diaz, I.M., Hudson, H.J., Reynolds, P.: Optimal control-based methodology for active vibration control of pedestrian structures. Eng. Struct. 80, 153–162 (2014)

    Article  Google Scholar 

  33. Liu, J., Qu, W.L., Pi, Y.L.: Active/robust control of longitudinal vibration response of floating-type cable-stayed bridge induced by train braking and vertical moving loads. J. Vib. Control 16(6), 801–825 (2010)

    Article  MathSciNet  Google Scholar 

  34. Sievert, L., Stancioiu, D., Matthews, C., Rothwell, G., Jenkinson, I.: Numerical and experimental investigation of time-varying vibration control for beams subjected to moving masses. Int. Conf. Struct. Eng. Dyn. ICEDyn, Viana do Castelo, Portugal (2019)

  35. Stancioiu, D., Ouyang, H.: Model-based active control of a continuous structure subjected to moving loads. J. Phys Conf. Ser. 744, 012001 (2016)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Engineering, Technology and Maritime Operations, Liverpool John Moores University, Byrom Street, Liverpool, L3 3AF, UK

    D. Stancioiu

  2. School of Engineering, Liverpool University, Brownlow Hill, Liverpool, L63 3GF, UK

    H. Ouyang & J. Yang

  3. School of Civil Engineering, Central South University, Shao-Shan-Nan Road, Changsha, 410075, China

    J. Yang

  4. Joint International Research Laboratory of Key Technology for Rail Traffic Safety, Shao-Shan-Nan Road, Changsha, 410075, China

    J. Yang

Authors
  1. D. Stancioiu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. H. Ouyang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to D. Stancioiu.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Stancioiu, D., Ouyang, H. & Yang, J. Numerical and experimental investigations into feedback control of continuous beam structures under moving loads. Arch Appl Mech 91, 2641–2659 (2021). https://doi.org/10.1007/s00419-021-01910-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-021-01910-8

Keywords

Search

Navigation