Skip to main content
SpringerLink
Log in

Dynamic response of a multi-span Timoshenko beam with internal and external flexible constraints subject to a moving mass

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

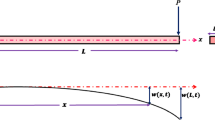
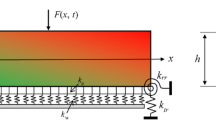
An analytical transfer matrix method is presented to determine the effect of intermediate flexible constraints on the dynamic behavior of a multi-span beam subject to a moving mass. By using the Timoshenko beam theory on separate beams and applying the compatibility requirements on each constraint point, the relationships between every two adjacent spans can be obtained. By using a transfer matrix method, eigensolutions of the entire system can be determined. The forced responses can then be calculated by the modal expansion theory using the determined eigenfunctions. Some numerical results are presented to show the effects of intermediate constraints and locations on the dynamic response of the multi-span beams. It will be seen that the general formulation developed here can cover a large array of problems such as cracked or intermediately constrained beams.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Chen Y.: Distribution of vehicular loads on bridge girders by the FEA using ADINA: modeling, simulation, and comparison. Comput. Struct. 72, 127–139 (1999)

    Article  Google Scholar 

  2. Wu T.X., Thompson D.J.: The effects of local preloads on the foundation stiffness and vertical vibration of railway track. J. Sound Vib. 219, 881–904 (1999)

    Article  Google Scholar 

  3. Todd M.D., Vohra S.T.: Shear deformation correction to transverse shape reconstruction from distributed strain measurements. J. Sound Vib. 219, 881–904 (1999)

    Article  Google Scholar 

  4. Ziaei-Rad S., Ariaei A., Imregun M.: Vibration analysis of Timoshenko beams under uniform partially distributed moving masses. J. Multi-body Dyn. 221, 551–566 (2007)

    Google Scholar 

  5. Lee H.P.: Dynamic response of a beam with intermediate point constraints subject to a moving load. J. Sound Vib. 171, 361–368 (1994)

    Article  MATH  Google Scholar 

  6. Wang R.T.: Vibration of multi-span Timoshenko beams to a moving force. J. Sound Vib. 207, 731–742 (1997)

    Article  MATH  Google Scholar 

  7. Yang Y.B., Liao S.S., Lin B.H.: Impact formulas for vehicle moving over simple and continuous beams. J. Struct. Eng. 121, 1644–1650 (1995)

    Article  Google Scholar 

  8. Chatterjee P.K., Datta T.K., Surana C.S.: Vibration of continuous bridges under moving vehicle. J. Sound Vib. 169, 619–632 (1994)

    Article  MATH  Google Scholar 

  9. Ichikawa M., Miyakawa Y., Matsuda A.: Vibration analysis of the continuous beam subjected to a moving mass. J. Sound Vib. 230, 493–506 (2000)

    Article  Google Scholar 

  10. Shames I.J., Dym C.L.: Energy and Finite Element Methods in Structural Mechanics. McGraw-Hill, New York (1985)

    MATH  Google Scholar 

  11. Lin H.P., Chang S.C.: Free vibration analysis of multi-span beams with intermediate flexible constraints. J. Sound Vib. 281, 155–169 (2005)

    Article  Google Scholar 

  12. Salawu OS.: Detection of structural damage through changes in frequency: a review. Eng. Struct. 19, 718–723 (1997)

    Article  Google Scholar 

  13. Lin H.P.: Direct and inverse methods on free vibration analysis of simply supported beams with a crack. Eng. Struct. 26, 427–436 (2004)

    Article  Google Scholar 

  14. Loya J.A., Rubio L., Fernández-Sáez J.: Natural frequencies for bending vibrations of Timoshenko cracked beams. J. Sound Vib. 290, 640–653 (2006)

    Article  Google Scholar 

  15. Mahmoud M.A., Zaid M.A.: Dynamic response of a beam with a crack subject to a moving mass. J. Sound Vib. 256, 591–603 (2002)

    Article  Google Scholar 

  16. Lin H.P., Chang S.C.: Forced responses of cracked cantilever beams subjected to a concentrated moving load. Int. J. Mech. Sci. 48, 1456–1463 (2006)

    Article  MATH  Google Scholar 

  17. Bilello C., Bergman L.A.: Vibration of damaged beams under a moving mass: theory and experimental validation. J. Sound Vib. 274, 567–582 (2004)

    Article  Google Scholar 

  18. Ariaei A., Ziaei-Rad S., Ghayour M.: Vibration analysis of beams with open and breathing cracks subjected to moving masses. J. Sound Vib. 326, 709–724 (2009)

    Article  Google Scholar 

  19. Ariaei A., Ziaei-Rad S., Ghayour M.: Transverse vibration of a multiple-Timoshenko beam system with intermediate elastic connections due to a moving load. Arch. Appl. Mech. 81, 263–281 (2011)

    Article  Google Scholar 

  20. Dadfarnia M., Jalili N., Esmailzadeh E.: A comparative study of the Galerkin approximation utilized in the Timoshenko beam theory. J. Sound Vib. 280, 1132–1142 (2005)

    Article  Google Scholar 

  21. Ariaei, A., Ziaei-Rad, S., Ghayour, M.: Critical velocities for beams subjected to moving constant loads. In: 37th International of Congress and Exposition on Noise Control Engineering, Inter-Noise 2008, 26–28 October, Shanghai, China

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Faculty of Engineering, University of Isfahan, Hezar Jerib Ave., Isfahan, Iran

    A. Ariaei & M. Malekzadeh

  2. Department of Mechanical Engineering, Isfahan University of Technology, 84156-83111, Isfahan, Iran

    S. Ziaei-Rad

Authors
  1. A. Ariaei
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Ziaei-Rad
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Malekzadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Ariaei.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ariaei, A., Ziaei-Rad, S. & Malekzadeh, M. Dynamic response of a multi-span Timoshenko beam with internal and external flexible constraints subject to a moving mass. Arch Appl Mech 83, 1257–1272 (2013). https://doi.org/10.1007/s00419-013-0745-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-013-0745-6

Keywords

Search

Navigation