An uncoupled theory of FG nanobeams with the small size effects and its exact solutions

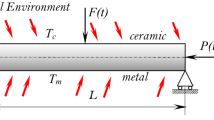
Abstract

Due to unphysical coupling induced by the material inhomogeneity, FG (functionally graded) nanobeam problems were formulated in a very complex way so that they cannot be analytically solved. In this paper, an uncoupled theory is proposed for FG nanobeams considering their small size effects. First, with the aid of the neutral axis, the axial displacement is expressed in terms of generalized displacements for FG nanobeams. Based on the nonlocal strain gradient theory, the generalized stresses and strains are accordingly defined and uncoupled constitutive relations are derived. Based on the principle of virtual work, an uncoupled theory is eventually established, including governing equations and boundary conditions. Within the present framework, analytical solutions to FG nanobeams are obtained for the first time for general boundary conditions. These solutions not only re-evaluate the previous results but shed light on the small size effects of FG nanobeams.

Appendices

Appendix A: Values of the three dimensionless rigidity parameters

In this section, values of the three rigidity parameters (i.e., $K_{P}$, $\eta$ and $\xi$) for different deformation modes (i.e., $g(z)$) are evaluated with different material properties varying with z. To this end, the typical FG materials (FG1 and FG3) and other four ones in Pei et al. [39], shown in Fig. 7, are examined, in which Poisson’s ratio $\nu$ is assumed to be invariant and hence $G(z) = E(z)/\left[ {2(1 + \nu )} \right]$ holds.

Fig. 7

Variation of Young’s modulus $E(z)$ for different materials

• H: The homogeneous material with constant Young’s modulus as

  $$E(z) = E_{0} \quad \left( { - \frac{h}{2} \le z \le \frac{h}{2}} \right)$$

  (A-1)

• FG1: The FG material with Young’s modulus linearly varying as

  $$E^{*} (z) = (E_{2} - E_{1} )\left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} + E_{1} \quad \left( { - \frac{h}{2} \le z \le \frac{h}{2}} \right)$$

  (A-2)

  where $E_{1} = 1000\;\text{GPa}$, $E_{2} = 250\;\text{GPa}$ and $k = 3$. For the purpose to show FG1 in Fig. 7, it is necessary to take $E(z) = E^{*} (z) - E_{1}$ and $E_{0} = E_{2} - E_{1}$.

• FG2: The FG material with Young’s modulus exponentially varying as

  $$E\text{(}z\text{)} = E_{0} \frac{{e^{{{z \mathord{\left/ {\vphantom {z h}} \right. \kern-0pt} h}}} - e^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0pt} 2}}} }}{{e^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} - e^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0pt} 2}}} }}\quad \left( { - \frac{h}{2} \le z \le \frac{h}{2}} \right)$$

  (A-3)

• FG3: The FG material with Young’s modulus exponentially varying as

  $$E^{*} (z) = E_{2} \left( {\frac{{E_{1} }}{{E_{2} }}} \right)^{{\left( {\frac{z}{h} + \frac{1}{2}} \right)}}$$

  (A-4)

  where $E_{1} = 380\;\text{GPa}$ and $E_{2} = 70\;\text{GPa}$. For the purpose to show FG3 in Fig. 7, it is necessary to take $E(z) = E^{*} (z) - E_{2}$ and $E_{0} = E_{1} - E_{2}$.

• FG4: The FG material with Young’s modulus exponentially varying as

  $$E\text{(}z\text{)} = E_{0} \left( {\frac{z}{h} + \frac{1}{2}} \right)\quad \left( { - \frac{h}{2} \le z \le \frac{h}{2}} \right)$$

  (A-5)

• FG5: The FG material with Young’s modulus sinusoidally varying as

  $$E\text{(}z\text{)} = E_{0} \sin\left[ {\frac{\pi }{2}\left( {\frac{z}{h} + \frac{1}{2}} \right)} \right]\quad \left( { - \frac{h}{2} \le z \le \frac{h}{2}} \right)$$

  (A-6)

Next, we evaluate the three rigidity parameters of above six materials, respectively, for the four deformation modes listed in Table 1.

1.1 Case 1: for the third-order deformation mode

In this case, we have $g(z) = z^{3}$ from Table 1 and the values of three rigidity parameters are obtained as tabulated in Table 3.

1.2 Case 2: for the sine deformation mode

In this case, we can take $g(z) = z - \frac{h}{\pi }\sin \left( {\frac{\pi z}{h}} \right)$ from Table 1 and the values of three rigidity parameters are obtained as tabulated in Table 4.

1.3 Case 3: for the hyperbolic sine deformation mode

In this case, we can take $g(z) = z - h{\text{sinh}} \left( {\frac{z}{h}} \right)$ from Table 1 and the values of three rigidity parameters are obtained as tabulated in Table 5.

1.4 Case 4: for the exponential deformation mode

In this case, we can take $g(z) = z \cdot \left[ {1 - e^{{ - 2 \cdot \left( {z/h} \right)^{2} }} } \right]$ and the values of three rigidity parameters are obtained as tabulated in Table 6.

To sum up, from Tables 3, 4, 5 and 6, it is seen that for the six different materials and the four different deformation modes, the absolute value of $\eta$ is not greater than 3.10%, and that of $\xi$ is not greater than 3.18%. Though not being theoretically proved yet, it is considerably reasonable for us to believe that $\eta$ and $\xi$ are two relatively small quantities (i.e. $\eta < < 1\;\text{and}\;\xi < < K_{P}$).

Table 3 The three rigidity parameters for the third-order deformation mode

Table 4 The three rigidity parameters for the sine deformation mode

Table 5 The three rigidity parameters for the hyperbolic sine deformation mode

Table 6 The three rigidity parameters for the exponential deformation mode

Appendix B: Derivation of higher-order generalized stresses

Higher-order generalized stresses are of great importance in prescribing non-classical boundary conditions. In this appendix, they are further investigated.

Taking M₁ as example, from the second of Eq. (23), we have

$$M_{1} - l^{2} M^{\prime}_{0} = 0$$

(B-1)

Making use of the first of Eq. (22), Eq. (B-1) yields

$$M_{1} - l^{2} M_{1}^{\prime \prime } = l^{2} M^{\prime}$$

(B-2)

Together with the second of Eq. (25), Eq. (B-2) is further cast as

$$\left( {l_{c}^{2} - l^{2} } \right)M_{1} = l^{2} \left( {l_{c}^{2} M^{\prime} - l^{2} B_{2} \kappa^{\prime}} \right)$$

(B-3)

If $l_{c}^{2} - l^{2} \ne 0$, we can immediately obtain

$$M_{1} = l^{2} B_{2} \kappa^{\prime} + l^{2} l_{c}^{2} \left( {M^{\prime} - B_{2} \kappa^{\prime}} \right)/\left( {l_{c}^{2} - l^{2} } \right)$$

(B-4)

For the case of $l_{c}^{2} - l^{2} = 0$, we have from Eq. (B-2) and the second of Eq. (25)

$$M^{\prime} = B_{2} \kappa^{\prime}$$

(B-5)

Thus, under this circumstance, Eq. (B-4) can be understood from the limiting viewpoint by approaching $l_{c}$ to $l$.