Analyzing size effects in a cracked orthotropic layer under antiplane shear loading

Abstract

Scale-dependent stress intensity factors in an anti-plane cracked orthotropic material layer are evaluated using strain gradient theory. Both volumetric and surface strain gradient material characteristic lengths represented as l and $l^{'}$, respectively, are employed to obtain semi-analytical solutions. The surface strain gradient effect is considered for both positive and negative $l^{'}$ values. The layer edges are assumed stress-free and oriented parallel to the crack plane. The presence of orthotropy can either increase or decrease the stress intensity factors depending on if it is greater or smaller than unity. The volumetric strain gradient effect reduces the stress intensity factor and it is more pronounced for smaller layer thickness. It was found that the negative surface gradient leads to a more complaint crack, while the positive surface gradient increases crack stiffness. Overall, the surface gradient effect is less significant in comparison with the volumetric gradient effect.

Appendices

Appendix

Classical case

The conditions at the crack line ($y =$ 0) are given as

$$\begin{aligned}&\tau _{yz} (x,0)=-\tau _{1} \left| x \right| <a, \end{aligned}$$

(A.1)

$$\begin{aligned}&w_{z} (x,0)=0 \left| x \right| \ge a, \end{aligned}$$

(A.2)

The application of integral transform technique on the displacement solution that satisfies the non-trivial equilibrium equation in z-direction $\left( {\partial ^{2}w_{z} /\partial x^{2}+\partial ^{2}w_{z} /\partial y^{2}=0} \right)$for the orthotropic material is written as [48]

$$\begin{aligned} w_{z} (x,y)=\frac{2}{\pi }\int \limits _0^\infty {\left[ {A\left( s \right) e^{-(sy/\sqrt{\beta })}+B(s)e^{(sy/\sqrt{\beta })}} \right] } \cos (sx)\text{ d }s, \quad y\ge 0 \end{aligned}$$

(A.3)

with the aid of (A.3), $\tau _{yz} =G\left( {\partial w_{z} /\partial y} \right)$may be expanded as

$$\begin{aligned} \tau _{yz} (x,y)=-\frac{2}{\pi }c_{44} \int \limits _0^\infty {s\left[ {A\left( s \right) e^{-(sy/\sqrt{\beta })}-B\left( s \right) e^{(sy/\sqrt{\beta })}} \right] } \cos \left( {sx} \right) \text{ d }s, \quad y\ge 0 \end{aligned}$$

(A.4)

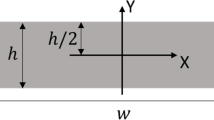
Here, $c_{44}$ is the shear modulus of the material, A(s) and B(s) are constants to be determined from the boundary conditions. For stress-free boundaries, the shear stresses at the upper and lower edge (i.e., $y =\pm h)$ of the layer for all values of x would be zero. Mathematically, it may be written as

$$\begin{aligned} \tau _{yz} (x,\pm h)=0, \quad \left| x \right| <\infty \end{aligned}$$

(A.5)

Due to geometrical symmetry, the only upper half of the layer is considered. From (A.4) and (A.5), it may be shown that $B(s)=e^{-(2sh/\sqrt{\beta })}A(s)$, so if $A(s)=E(s)/(1+e^{-(2sh/\sqrt{\beta })})$ then $B(s)=e^{-(2sh/\sqrt{\beta })}E(s)/(1+e^{-(2sh/\sqrt{\beta })})$, where E(s) is an unknown function to be determined. The conditions (A.1) and (A.2) are satisfied if E(s) is the solution of dual integral equations given as

$$\begin{aligned}&\int \limits _0^\infty {E(s)\cos (sx)\mathrm{d}s=0,} \quad x\ge a \end{aligned}$$

(A.6a)

$$\begin{aligned}&\int \limits _0^\infty {sF_{sc} (s)} E(s)\cos (sx)\mathrm{d}s=\frac{\pi \tau _{1} \sqrt{\beta }}{2G}, \quad x<a \end{aligned}$$

(A.6b)

With $F_{sc} (s)=(1-e^{-(2sh/\sqrt{\beta })})/(1+e^{-(2sh/\sqrt{\beta })})$, here “sc” in subscript represents the “stress-free boundaries & classical” case.