1 Introduction

Natural fibers are of particular interest in view of sustainability developments, see [6]. Man-made cellulose fiber reinforced injection molded components are an interesting alternative to glass fiber reinforced plastics for certain applications due to their high mechanical properties (elongation at break: 13%) and lower density (1.5 g\(\,\hbox {cm}^{-3}\)). They also have a lower bending stiffness than glass fibers. Man-made cellulose fibers are bent during the injection molding process which leads to faster fiber entanglement and a lower fiber preferred orientation, see [9]. In other words, the lower bending stiffness does also not imply alignment as a straight fiber resulting in an anisotropy of the component properties. Furthermore, it is known, see, for example [14], that a fiber reinforced specimen has different material properties over its thickness, which is caused—apart from the melt flow behavior of the thermoplastic—by the spatial distribution of the fiber orientation. Applications from glass fiber reinforced plastic, where the short fibers are straight lines, are discussed in a number of publications, see, for example [7, 8, 13, 18]. In these publications, the fiber orientation of glass fiber reinforced samples has already been extensively investigated. There, the fiber orientation and the fiber length are mainly evaluated. However, a curved fiber has no unique orientation. Furthermore, it can reach various geometrical forms. Thus, measures, principally describing the specific form, are of particular interest.

Since \(\mu \)-CTs can provide coordinates of each fiber, these can be drawn on to apply interpolation concepts so that a continuous function is assigned to each fiber. These functions can be evaluated, i.e. geometrical measures can be provided. There are two possibilities: first, the simplest approach is to draw on polygon approximations using the coordinates describing the fiber, which is easy to be implemented. Second, continuous formulations can be applied implying further measures such as curvature, and torsion. The latter terms will be explained in detail in Sect. 2. We draw on a spline concept to interpolate the coordinates so that each fiber obtains a continuous representation, and, accordingly, the possibility to apply concepts in differential geometry.

The article is structured as follows: since we are interested to introduce measures of curvilinear fibers, a summary of the description of the local behavior of curves is provided. In a second step, global mean values are proposed. These mean values are the orientation, curvature, torsion, and a mean deviation from a straight line. Afterwards, one special interpolation method, which is based on classical, natural splines, is drawn on to evaluate the proposed measures. Afterwards, a discretized, simplified version is offered. Both schemes are compared using real \(\mu \)-CT data of a man-made cellulose fiber reinforced polypropylene specimen. In this article, the distributions of the measures are discussed.

2 Measures of curvilinear curves

First, we recap some basics in the description of curves, and, subsequently, some measures of curvilinear fibers are proposed characterizing their orientation, curvature and torsion.

2.1 Properties of curves

A curve in the three-dimensional case is described by the position vector \(\mathbf {r} (\xi )\), \(\mathbf {r} \in \mathbb {E}^3\), which depends on a parameter \(\xi \), \(\xi \in [\xi _1,\xi _2]\). The tangent vector is given by

$$\begin{aligned} \mathbf {g} _\xi (\xi ) = \frac{\displaystyle \mathrm {d}\mathbf {r} }{\displaystyle \mathrm {d}\xi } = \mathbf {r} ,_\xi , \quad \mathbf {g} _\xi \in \mathbb {E}^3, \end{aligned}$$
(1)

see, for example, [3, 11]. The arc length

$$\begin{aligned} s(\xi ) = \int _{\xi _1}^{\xi } \Vert \mathbf {g} _\xi (\hat{\xi })\Vert \; \mathrm {d}\hat{\xi }, \quad s \in [0,L] \end{aligned}$$
(2)

represents the length of the covered path from point \(\xi _1\) until point \(\xi \) on the curve, whereas

$$\begin{aligned} L = \int _{\xi _1}^{\xi _2} \Vert \mathbf {g} _\xi (\xi )\Vert \; \mathrm {d}\xi , \end{aligned}$$
(3)

denotes the length of the curve between two points \(\xi _1\) and \(\xi _2\) (\(\xi _2 > \xi _1\)), see Fig. 1a.

Fig. 1
figure 1

Geometrical description of curves

Full size image
$$\begin{aligned} s,_\xi = \Vert \mathbf {g} _\xi \Vert = \sqrt{\mathbf {g} _\xi \cdot \mathbf {g} _\xi } \ne 0 \end{aligned}$$
(4)

defines the rate of the arc length representing the norm of the tangent vector or the square root of the metric coefficient concerned. Since \(s,_\xi \ne 0\) holds, there exists a function \(\hat{\xi }(s)\) having the derivative

$$\begin{aligned} \hat{\xi },_s = \frac{\displaystyle \mathrm {d}\hat{\xi }}{\displaystyle \mathrm {d}s} = \frac{\displaystyle 1}{\displaystyle \Vert \mathbf {g} _\xi \Vert }. \end{aligned}$$
(5)

In this sense, we will need the mapping between the parameter \(\xi \) and the arc length s. In this case, the curve can also be related to the arc length

$$\begin{aligned} \hat{\mathbf { r}} (s(\xi )) = \mathbf {r} (\xi ), \end{aligned}$$
(6)

so that the tangent vector (1) reads

$$\begin{aligned} \mathbf {g} _\xi = \mathbf {r} ,_\xi = \hat{\mathbf { r}} ,_s s,_\xi = \hat{\mathbf { r}} ,_s \Vert \mathbf {g} _\xi \Vert \end{aligned}$$
(7)

leading to the obvious property

$$\begin{aligned} \mathbf {e} _t(s) := \frac{\mathbf {g} _\xi }{\Vert \mathbf {g} _\xi \Vert } = \frac{\mathbf {r} ,_\xi }{\Vert \mathbf {r} ,_\xi \Vert } = \hat{\mathbf { r}} ,_s, \quad \text {i.e.} \; \Vert \mathbf {e} _t(s)\Vert = 1. \end{aligned}$$
(8)

\(\mathbf {e} _t\) is called the unit tangent vector. Using the property

$$\begin{aligned} \frac{\displaystyle \mathrm {d}}{\displaystyle \mathrm {d}s} \left( \mathbf {e} _t \cdot \mathbf {e} _t \right) = 2 \mathbf {e} _t \cdot {\mathbf {e} _t},_s = 0, \end{aligned}$$
(9)

we can see that the vector \({\mathbf {e} _t},_s = \hat{\mathbf { r}} ,_{ss}\) is orthogonal to \(\mathbf {e} _t\), see Eq. (8). This property is chosen to define the unit normal vector

$$\begin{aligned} \mathbf {e} _n := \frac{{\mathbf {e} _t},_s}{\Vert {\mathbf {e} _t},_s\Vert } = \frac{\hat{\mathbf { r}} ,_{ss}}{\Vert \hat{\mathbf { r}} ,_{ss}\Vert }. \end{aligned}$$
(10)

The norm of \(\hat{\mathbf { r}} ,_{ss}\) represents the curvature of the curve

$$\begin{aligned} \kappa (s) := \Vert \hat{\mathbf { r}} ,_{ss}\Vert = \Vert {\mathbf {e} _t},_s\Vert . \end{aligned}$$
(11)

The two vectors \(\mathbf {e} _t\) and \(\mathbf {e} _n\) are chosen to define the binormal unit vector

$$\begin{aligned} \mathbf {e} _b(s) := \mathbf {e} _t(s) \times \mathbf {e} _n(s), \end{aligned}$$
(12)

see Fig. 1a, i.e. the natural basis or trihedron of the curve. Using the Frenet equations, see [11],

$$\begin{aligned} {\mathbf {e} _t},_s = \kappa \mathbf {e} _n, \qquad {\mathbf {e} _n},_s = -\kappa \mathbf {e} _n + \tau \mathbf {e} _b, \qquad {\mathbf {e} _b},_s = -\tau \mathbf {e} _n \end{aligned}$$
(13)

motivates an additional local measure—apart the curvature— namely the torsion \(\tau \). Eq. (13)\(_1\) is already provided by Eq. (10) using definition (11), i.e. \(\kappa \) represents the (local) deviation of the curve from a straight line. \(\tau \) is a measure for the (local) deviation of a curve from a flat course, which can be seen at Eq. (13)\(_{2,3}\), where the curve remains in the \((\mathbf {e} _t,\mathbf {e} _n)\)-plane. The torsion itself can be calculated by

$$\begin{aligned} \tau = {\mathbf {e} _n},_s \cdot \mathbf {e} _b = - {\mathbf {e} _b},_s \cdot \mathbf {e} _n, \end{aligned}$$
(14)

see Eq. (13)\(_{2,3}\). Its sign represents the rotation (right- or left handed).

All these expressions look quite simple if an arc length representation is given. However, later on only the parametric representation \(\mathbf {r} (\xi )\) is provided, which requires a different representation. Here, we follow the presentation in [2]. For the subsequent calculations,

$$\begin{aligned} \frac{\displaystyle \mathrm {d}}{\displaystyle \mathrm {d}\xi } \Vert \mathbf {r} ,_\xi \Vert ^n = n \Vert \mathbf {r} ,_\xi \Vert ^{n-2} (\mathbf {r} ,_\xi \cdot \mathbf {r} ,_{\xi \xi }) \end{aligned}$$
(15)

is required. Then, the product and chain rule leads to

$$\begin{aligned} {\mathbf {e} _t},_s = \hat{\mathbf { r}} ,_{ss} = \frac{\displaystyle \mathrm {d}}{\displaystyle \mathrm {d}s} \big ( \mathbf {r} ,_\xi \Vert \mathbf {r} ,_\xi \Vert ^{-1} \big ) = \frac{\displaystyle 1}{\displaystyle \Vert \mathbf {r} ,_\xi \Vert ^4} \big ( \Vert \mathbf {r} ,_\xi \Vert ^2 \mathbf {r} ,_{\xi \xi } - (\mathbf {r} ,_\xi \cdot \mathbf {r} ,_{\xi \xi }) \mathbf {r} ,_\xi \big ), \end{aligned}$$
(16)

see Eqs. (5) and (7). This expression is necessary to determine the curvature in Eq. (13)\(_1\) by calculating the cross product with \(\mathbf {e} _t\)

$$\begin{aligned} {\mathbf {e} _t},_s \times \mathbf {e} _t = \kappa \mathbf {e} _n \times \mathbf {e} _t = -\kappa \mathbf {e} _b, \end{aligned}$$
(17)

i.e. using the norm of both sides, we obtain after some calculations

$$\begin{aligned} \kappa = \Vert {\mathbf {e} _t},_s \times \mathbf {e} _t\Vert = \frac{\displaystyle 1}{\displaystyle \Vert \mathbf {r} ,_\xi \Vert ^3} \Vert \mathbf {r} ,_\xi \times \mathbf {r} ,_{\xi \xi }\Vert . \end{aligned}$$
(18)

Now, using again Eq. (13)\(_{1}\) with (16) and (18), we arrive at the representation for the unit normal vector

$$\begin{aligned} \mathbf {e} _n = \frac{\Vert \mathbf {r} ,_\xi \Vert ^2 \mathbf {r} ,_{\xi \xi } - (\mathbf {r} ,_\xi \cdot \mathbf {r} ,_{\xi \xi }) \mathbf {r} ,_\xi }{\Vert \mathbf {r} ,_\xi \Vert \Vert \mathbf {r} ,_\xi \times \mathbf {r} ,_{\xi \xi }\Vert }. \end{aligned}$$
(19)

With the help of Eqs. (8) and (19), the biaxial unit vector (12) reads

$$\begin{aligned} \mathbf {e} _b = \frac{\mathbf {r} ,_\xi \times \mathbf {r} ,_{\xi \xi }}{\Vert \mathbf {r} ,_\xi \times \mathbf {r} ,_{\xi \xi }\Vert }. \end{aligned}$$
(20)

Finally, we would like to express the torsion \(\tau \) by the parameter representation. For this purpose, Eq. (13)\(_{3}\) is chosen and the binormal unit vector (12) is inserted

$$\begin{aligned} \tau \mathbf {e} _n = -{\mathbf {e} _b},_s = -\frac{\displaystyle \mathrm {d}}{\displaystyle \mathrm {d}s} (\mathbf {e} _t \times \mathbf {e} _n) = \frac{\kappa ,_s}{\kappa ^2} \mathbf {e} _t \times {\mathbf {e} _t},_s - \frac{\displaystyle 1}{\displaystyle \kappa } \mathbf {e} _t \times {\mathbf {e} _t},_{ss}. \end{aligned}$$
(21)

This is multiplied with \(\mathbf {e} _n = (1/\kappa ) {\mathbf {e} _t},_s\) leading to

$$\begin{aligned} \tau = \frac{\displaystyle 1}{\displaystyle \kappa ^2} (\mathbf {e} _t \times {\mathbf {e} _t},_s) \cdot {\mathbf {e} _t},_{ss}, \end{aligned}$$
(22)

i.e. with Eq. (16) and the chain-rule we arrive at an expression of the form

$$\begin{aligned} {\mathbf {e} _t},_{ss} = \frac{\displaystyle \mathrm {d}}{\displaystyle \mathrm {d}s} {\mathbf {e} _t},_s = \frac{\displaystyle \mathrm {d}}{\displaystyle \mathrm {d}\xi } {\mathbf {e} _t},_s \xi ,_s = \alpha \mathbf {r} ,_\xi + \beta \mathbf {r} ,_{\xi \xi } + \gamma \mathbf {r} ,_{\xi \xi \xi }. \end{aligned}$$
(23)

(Here, we need only the term \(\gamma = \Vert \mathbf {r} ,_\xi \Vert ^{-3}\), whereas \(\alpha \) and \(\beta \) will vanish in the subsequent calculations.) We insert Eqs. (16) and (23) into Eq. (22) yielding

$$\begin{aligned} \tau = \frac{\displaystyle 1}{\displaystyle \kappa ^2} \frac{\displaystyle 1}{\displaystyle \Vert \mathbf {r} ,_\xi \Vert ^6} (\mathbf {r} ,_\xi \times \mathbf {r} ,_{\xi \xi }) \cdot \mathbf {r} ,_{\xi \xi \xi } = \frac{(\mathbf {r} ,_\xi \times \mathbf {r} ,_{\xi \xi }) \cdot \mathbf {r} ,_{\xi \xi \xi }}{\Vert \mathbf {r} ,_\xi \times \mathbf {r} ,_{\xi \xi }\Vert ^2} \end{aligned}$$
(24)

with \(\kappa \) from Eq. (18). Thus, all required quantities are provided in dependence of the parameter \(\xi \).

2.2 Measures defining a straight line (fiber)

Short glass or carbon fibers can be modeled as straight lines. For a straight line, \(\hat{\mathbf { r}} (s) = \mathbf {r} _1 + s \mathbf {e} _t\), we have \(\kappa = 0\), and \(\tau \) is defined to be zero (\(\mathbf {e} _n\) is in this case arbitrary, but orthonormal to \(\mathbf {e} _t\)), i.e. only the length L and the orientation \(\mathbf {e} _t\) are chosen for characterizing purposes. The orientation is given by Eq. (8), \(\hat{\mathbf { r}} ,_s = \mathbf {e} _t\), see Fig. 2. Thus, we need the starting and the end point of a fiber, \(\mathbf {r} _1\) and \(\mathbf {r} _2\), respectively,

$$\begin{aligned} \mathbf {e} _t = \frac{\mathbf {r} _2 - \mathbf {r} _1}{\Vert \mathbf {r} _2 - \mathbf {r} _1\Vert }, \qquad L = \Vert \mathbf {r} _2 - \mathbf {r} _1\Vert . \end{aligned}$$
(25)

The orientation vector \(\mathbf {e} _t\) can be expressed in a spherical coordinate system by the two angles \(\varphi \) and \(\vartheta \),

$$\begin{aligned} \mathbf {e} _t = \sin \vartheta \cos \varphi \; \mathbf {e} _1 + \sin \vartheta \sin \varphi \; \mathbf {e} _2 + \cos \vartheta \; \mathbf {e} _3, \end{aligned}$$
(26)

see, for example, [12]. Frequently, the two angles

$$\begin{aligned} \vartheta = \arccos |\mathbf {e} _t \cdot \mathbf {e} _3|, \qquad \varphi = \arccos \frac{|\mathbf {e} _t \cdot \mathbf {e} _1|}{\sin \vartheta } \end{aligned}$$
(27)

are chosen for characterizing the orientation of fibers in composites, see, for example, [1, 17]. Thus, straight fibers are simple to be evaluated.

2.3 Measures defining a curve

Since we are interested in scalar measures representing some “mean-value” of measures characterizing curvilinear fibers, we introduce two approaches. First, given data points representing a spatial curve are interpolated to obtain a continuous representation (piece-wise \(\mathcal {C}^\infty \), but globally \(\mathcal {C}^2\) continuous). Based on these approximations, the measures (mean curvature, torsion, direction, and deviation from straight line) are calculated. Afterwards, these measures are provided without the interpolation concept, i.e. only the data points are evaluated directly.

2.3.1 Mean values using continuous interpolation

Before defining the mean values of interest, a fiber—given by \({n_{\text {d}}}\) data points \(\mathbf {d} _k\), \(k=1,\ldots ,{n_{\text {d}}}\)—should be represented by an interpolating function,

$$\begin{aligned} \mathbf {r} (\xi ) = \hat{x}_k(\xi ) \mathbf {e} _k = \hat{x}_1(\xi ) \mathbf {e} _1 + \hat{x}_2(\xi ) \mathbf {e} _2 + \hat{x}_3(\xi ) \mathbf {e} _3. \end{aligned}$$
(28)

As a first approach, piece-wise polynomials of the third order are chosen,

$$\begin{aligned} \hat{x}_{ki}(\xi ) = a_{ki} + b_{ki} (\xi - \xi _i) + c_{ki} (\xi - \xi _i)^2 + \hat{d}_{ki} (\xi - \xi _i)^3, \quad \text {for} \quad \xi _i \le \xi < \xi _{i+1}, \quad i=1,\ldots ,{n_{\text {d}}}-1, \end{aligned}$$
(29)

where the sampling points \(\xi _i\) are estimated using the Chord-approach

$$\begin{aligned} \xi _i = \sum _{j=1}^{i-1} \Vert \mathbf {d} _{j+1} - \mathbf {d} _j\Vert , \quad i=2,\ldots ,{n_{\text {d}}}, \end{aligned}$$
(30)

with \(\xi _1 = 0\). The index i defines the interval, \(i=1,\ldots ,{n_{\text {d}}}-1\), and \(k=1,2,3\) the coordinate direction. In other words, we have \(\hat{x}_k(\xi ) = \hat{x}_{ki}(\xi )\) in interval i, \(\xi _i \le \xi < \xi _{i+1}\). Obviously, we obtain for \(\xi = \xi _i\) the parameters

$$\begin{aligned} a_{ki} = \mathbf {d} _i \cdot \mathbf {e} _k = d_{ik}, \quad i=1,\ldots ,{n_{\text {d}}}-1 \end{aligned}$$
(31)
Fig. 2
figure 2

Straight line and spherical coordinate representation

Full size image

of each coordinate, \(k=1,2,3\) (starting point implies \(\mathbf {r} (\xi _1) = \mathbf {d} _1\)). Using this approach, the first three derivatives can be determined

$$\begin{aligned} \begin{aligned} \hat{x}'_{ki}(\xi )&= b_{ki} + 2 c_{ki} (\xi - \xi _i) + 3 d_{ki} (\xi - \xi _i)^2, \\ \hat{x}''_{ki}(\xi )&= 2 c_{ki} + 6 d_{ki} (\xi - \xi _i), \\ \hat{x}'''_{ki}(\xi )&= 6 d_{ik}. \end{aligned} \end{aligned}$$
(32)

In each interval i, four unknowns are given, i.e. we have \(4 \times ({n_{\text {d}}}-1)\) unknowns. Thus, we need the same number of equations. With Eq. (31) and the end point \(\mathbf {r} (\xi _{n_{\text {d}}}) = \mathbf {d} _{n_{\text {d}}}\), there are \({n_{\text {d}}}\) equations. Furthermore, we require that the following conditions are fulfilled at the point \(\xi _{i+1}\)

$$\begin{aligned} \hat{x}_{ki}(\xi _{i+1}) = \hat{x}_{ki+1}(\xi _{i+1}), \quad \hat{x}'_{ki}(\xi _{i+1}) = \hat{x}'_{ki+1}(\xi _{i+1}), \quad \hat{x}''_{ki}(\xi _{i+1}) = \hat{x}''_{ki+1}(\xi _{i+1}), \end{aligned}$$
(33)

\(i=1,\ldots ,{n_{\text {d}}}-2\), leading to \(3\times ({n_{\text {d}}}-2)\) equations. Thus, two additional equations are required. Here, we draw on natural splines, i.e. we assume curvature free starting and ending points

$$\begin{aligned} \hat{x}''_{k1}(\xi _1) = 0, \quad \hat{x}''_{k{n_{\text {d}}}-1}(\xi _{n_{\text {d}}}) = 0. \end{aligned}$$
(34)

The index \(ki+1\) in Eq. (33) defines the kth component (or its derivatives), see Eq. (28), in interval \(i+1\). To avoid a comma separation, which is chosen for derivatives, a comma-free notation is chosen. This holds for \(k{n_{\text {d}}}-1\) in Eq. (34) as well, i.e. the evaluation of the kth function defined in interval \({n_{\text {d}}}-1\). The numerical implementation to solve the linear system of equations is provided in [5], see [4] as well. In other words, the given data points are exactly fulfilled. The curves are continuous of second order. In conclusion, the parameters \(a_{ki}\), \(b_{ki}\), \(c_{ki}\), \(\hat{d}_{ki}\), \(i=1,{n_{\text {d}}}-1\), \(k=1,2,3\), are assumed to be known in the following. This implies that in each interval the position vector and its derivatives

$$\begin{aligned} \mathbf {r} _i(\xi ) = \hat{x}_{ki}(\xi ) \mathbf {e} _k, \quad \mathbf {r} _i,_\xi (\xi ) = \hat{x}'_{ki}(\xi ) \mathbf {e} _k, \quad \mathbf {r} _i,_{\xi \xi }(\xi ) = \hat{x}''_{ki}(\xi ) \mathbf {e} _k, \quad \mathbf {r} _i,_{\xi \xi \xi }(\xi ) = \hat{x}'''_{ki}(\xi ) \mathbf {e} _k \end{aligned}$$
(35)

are known in each interval i, \(\xi _i \le \xi < \xi _{i+1}\), \(i=1,\ldots ,{n_{\text {d}}}-1\).

In the following, we define the measures determining fibers. First, the length of a fiber has to be computed using definition (3)

$$\begin{aligned} L = \int _0^{\xi _{n_{\text {d}}}} \Vert \mathbf {r} ,_\xi (\xi )\Vert \; \mathrm {d}\xi = \sum _{i=1}^{{n_{\text {d}}}-1} \int _{\xi _i}^{\xi _{i+1}} \Vert \mathbf {r} _i,_\xi (\xi )\Vert \; \mathrm {d}\xi . \end{aligned}$$
(36)

The integrals can, for example, be evaluated using Simpson’s rule, see, for instance, [16], with \(\varDelta \xi = (\xi _{i+1}-\xi _i)/n_S\), \(n_S\) is the number of subintervals between two data points. Then, we have to calculated at the integration points \(\xi ^{(l)} = \xi _i + (l-1) \varDelta \xi \),

$$\begin{aligned} \int _{\xi _i}^{\xi _{i+1}} f(\xi ) \; \mathrm {d}\xi \approx \frac{\varDelta \xi }{6} \sum _{l=1}^{n_S} \left( f(\xi ^{(l)}) + 4 f(\xi ^{(l)} + \varDelta \xi /2) + f(\xi ^{(l)}+\varDelta \xi ) \right) . \end{aligned}$$
(37)

In the following, all integrals are evaluated using this integration scheme. (Of course, other schemes or adaptive quadrature rules are possible.)

Next, the mean curvature

$$\begin{aligned} \kappa _M := \frac{\int _0^{\xi _{n_{\text {d}}}} \kappa (\xi ) \Vert \mathbf {r} ,_\xi (\xi )\Vert \; \mathrm {d}\xi }{\int _0^{\xi _{n_{\text {d}}}} \Vert \mathbf {r} ,_\xi (\xi )\Vert \; \mathrm {d}\xi } = \frac{\displaystyle 1}{\displaystyle L} \int _0^{\xi _{n_{\text {d}}}} \frac{\Vert \mathbf {r} ,_\xi \times \mathbf {r} ,_{\xi \xi }\Vert }{\Vert \mathbf {r} ,_\xi \Vert ^2} \; \mathrm {d}\xi , \end{aligned}$$
(38)

the mean torsion

$$\begin{aligned} \tau _M := \frac{\displaystyle 1}{\displaystyle L} \int _0^{\xi _{n_{\text {d}}}} \frac{(\mathbf {r} ,_\xi \times \mathbf {r} ,_{\xi \xi }) \cdot \mathbf {r} ,_{\xi \xi \xi }}{\Vert \mathbf {r} ,_\xi \times \mathbf {r} ,_{\xi \xi }\Vert ^2} \Vert \mathbf {r} ,_\xi (\xi )\Vert \; \mathrm {d}\xi , \end{aligned}$$
(39)

and the mean orientation (direction)

$$\begin{aligned} \mathbf {r} _M,_\xi := \frac{\displaystyle 1}{\displaystyle L} \int _0^{\xi _{n_{\text {d}}}} \mathbf {r} ,_\xi \Vert \mathbf {r} ,_\xi (\xi )\Vert \; \mathrm {d}\xi \end{aligned}$$
(40)

are defined, see Eqs. (18) and (24). In this sense, the two angles (27) can be chosen for a mean orientation,

$$\begin{aligned} \vartheta _M = \arccos \left| \frac{\mathbf {r} _M,_\xi }{\Vert \mathbf {r} _M,_\xi \Vert } \cdot \mathbf {e} _3\right| , \qquad \varphi _M = \arccos \frac{\left| \frac{\mathbf {r} _M,_\xi }{\Vert \mathbf {r} _M,_\xi \Vert }\cdot \mathbf {e} _1\right| }{\sin \vartheta _M}. \end{aligned}$$
(41)

An additional quantity is the deviation of the curved line to a straight line. The straight line is defined by

$$\begin{aligned} \mathbf {r} _L(\lambda ) = \mathbf {r} _C + \lambda \mathbf {r} _M,_\xi , \end{aligned}$$
(42)

where

$$\begin{aligned} \mathbf {r} _C := \frac{\displaystyle 1}{\displaystyle L} \int _0^{\xi _{n_{\text {d}}}} \mathbf {r} (\xi ) \Vert \mathbf {r} ,_\xi (\xi )\Vert \; \mathrm {d}\xi \end{aligned}$$
(43)

defines the center of the line (fiber), see Fig. 3. The distance of a point of the line \(\mathbf {r} (\xi )\) to the straight line (42) is given by

$$\begin{aligned} {d}(\xi ) = \left\| (\mathbf {r} _C - \mathbf {r} (\xi )) \times \frac{\mathbf {r} _M,_\xi }{\Vert \mathbf {r} _M,_\xi \Vert } \right\| , \end{aligned}$$
(44)

see, for instance, [10], so that the mean value is defined by

$$\begin{aligned} d_M := \frac{\displaystyle 1}{\displaystyle L} \int _0^{\xi _{n_{\text {d}}}} {d}(\xi ) \Vert \mathbf {r} ,_\xi (\xi )\Vert \; \mathrm {d}\xi = \frac{\displaystyle 1}{\displaystyle L} \int _0^{\xi _{n_{\text {d}}}} \left\| (\mathbf {r} _C - \mathbf {r} (\xi )) \times \frac{\mathbf {r} _M,_\xi }{\Vert \mathbf {r} _M,_\xi \Vert } \right\| \Vert \mathbf {r} ,_\xi (\xi )\Vert \; \mathrm {d}\xi . \end{aligned}$$
(45)

In conclusion, we have several measures defining a curve (length L (36), mean curvature \(\kappa _M\) (38), mean torsion \(\tau _M\) (39), mean orientations \((\vartheta _M,\varphi _M)\) (41), and the mean deviation \(d_M\) (45) from the mean orientation line (42)).

Fig. 3
figure 3

Center point of a line and the straight line approximation of a curve

Full size image

Particularly, the length might be of interest to estimate—together with a mean diameter—the volume of the fiber, or the orientation vector \(\mathbf {n} = \mathbf {r} _M,_\xi /\Vert \mathbf {r} _M,_\xi \Vert \) in Eq. (40) is drawn on to determine an orientation tensor \(\mathrm {\mathbf {N}} = \mathbf {n} \otimes \mathbf {n} \), see [15]. However, new measures such as mean curvature or mean deviation to a straight line give insight into the flow behavior and the weakness of natural fibers relative to the matrix material.

2.3.2 Mean values using simplified approach

Apart from the more precise definitions using interpolated points in Sect. 2.3.1, an alternative, simplified access drawing on rough approximations of the derivatives by numerical differentiation and the integrals applying a trapezoidal rule can be provided.

Again the chord method (30) is applied using

$$\begin{aligned} \varDelta \xi _i := \Vert \mathbf {d} _{i+1} - \mathbf {d} _i\Vert , \quad i=1,\ldots ,{n_{\text {d}}}-1. \end{aligned}$$
(46)

In a first step, we compute at all data points \(i=1,\ldots ,{n_{\text {d}}}\) the first three derivatives using the approximations in “Appendix A”. The tangent vector reads, according to Eq. (65),

$$\begin{aligned} \mathbf {r} ,_\xi (\xi _i) \approx \mathbf {r} _i,_\xi := \frac{\varDelta \xi _{i-1}^2}{D_i} \varDelta \mathbf {d} _{i} + \frac{\varDelta \xi _{i}^2}{D_i} \varDelta \mathbf {d} _{i-1}, \quad i=2,\ldots ,{n_{\text {d}}}-1 \end{aligned}$$
(47)

with

$$\begin{aligned} \varDelta \mathbf {d} _{i} = \mathbf {d} _{i+1} - \mathbf {d} _i, \qquad D_i = \varDelta \xi _{i-1} \varDelta \xi _i (\varDelta \xi _{i-1} + \varDelta \xi _i), \qquad \varDelta \xi _i = \xi _{i+1}-\xi _i. \end{aligned}$$
(48)

The tangent vectors at the first and the last point can be estimated using Eq. (67),

$$\begin{aligned} \mathbf {r} _1,_\xi = \frac{\varDelta \mathbf {d} _1}{\varDelta \xi _{1}}, \qquad \mathbf {r} _{n_{\text {d}}},_\xi = \frac{\varDelta \mathbf {d} _{{n_{\text {d}}}-1}}{\varDelta \xi _{{n_{\text {d}}}-1}} \end{aligned}$$
(49)

The second derivative reads according to Eq. (70)

$$\begin{aligned} \mathbf {r} _i,_{\xi \xi } = A_i (\varDelta \mathbf {d} _i - \varDelta \mathbf {d} _{i-1}) + B_i \mathbf {r} _i,_\xi , \quad i=2,\ldots ,{n_{\text {d}}}-1, \end{aligned}$$
(50)

with the abbreviations

$$\begin{aligned} A_i = \frac{2}{\varDelta \xi _{i-1}^2 + \varDelta \xi _{i}^2}, \qquad B_i = \varDelta \xi _{i-1} - \varDelta \xi _i. \end{aligned}$$
(51)

Here, too, we must estimate the derivatives at the first and last point, see Eq. (71),

$$\begin{aligned} \mathbf {r} _1,_{\xi \xi } = \frac{\mathbf {r} _2,_\xi - \mathbf {r} _1,_\xi }{\varDelta \xi _1}, \qquad \mathbf {r} _{n_{\text {d}}},_{\xi \xi } = \frac{\mathbf {r} _{n_{\text {d}}},_\xi - \mathbf {r} _{{n_{\text {d}}}-1},_\xi }{\varDelta \xi _{{n_{\text {d}}}-1}}. \end{aligned}$$
(52)

Finally, the third derivative of the spatial curve is estimated using Eq. (72)

$$\begin{aligned} \mathbf {r} _i,_{\xi \xi \xi } = \frac{\varDelta \xi _{i-1}^2}{D_i} (\mathbf {r} _{i+1},_{\xi \xi } - \mathbf {r} _{i},_{\xi \xi }) + \frac{\varDelta \xi _{i}^2}{D_i} (\mathbf {r} _{i},_{\xi \xi } - \mathbf {r} _{i-1},_{\xi \xi }), \quad i=2,\ldots ,{n_{\text {d}}}-1, \end{aligned}$$
(53)

where the third derivatives at both the first as well as last point have to be estimated, see Eq. (73),

$$\begin{aligned} \mathbf {r} _1,_{\xi \xi \xi } := \frac{\mathbf {r} _2,_{\xi \xi } - \mathbf {r} _1,_{\xi \xi }}{\varDelta \xi _1}, \quad \mathbf {r} _{n_{\text {d}}},_{\xi \xi \xi } := \frac{\mathbf {r} _{n_{\text {d}}},_{\xi \xi } - \mathbf {r} _{{n_{\text {d}}}-1},_{\xi \xi }}{\varDelta \xi _{{n_{\text {d}}}-1}}. \end{aligned}$$
(54)

Obviously, numerical differentiation makes higher-order derivatives more and more inaccurate.

Since all derivatives are known at the data points, the measures of Sect. 2.3.1 can be calculated. For this purpose, a simple numerical integration scheme has to be applied. Since the trapezoidal rule

$$\begin{aligned} \int _{\xi _1=0}^{\xi _{n_{\text {d}}}} f(\xi ) \; \mathrm {d}\xi \approx \sum _{i=1}^{{n_{\text {d}}}-1} \frac{f(\xi _i) + f(\xi _{i+1})}{2} \varDelta \xi _i = \frac{\displaystyle 1}{\displaystyle 2} (f(\xi _1) \varDelta \xi _1 + f(\xi _{n_{\text {d}}}) \varDelta \xi _{{n_{\text {d}}}-1}) + \sum _{i=2}^{{n_{\text {d}}}-1} f(\xi _i) \varDelta \xi _i, \end{aligned}$$
(55)

is more accurate—for nearly the same computational work—than the left rectangular integration scheme

$$\begin{aligned} \int _{\xi _1=0}^{\xi _{n_{\text {d}}}} f(\xi ) \; \mathrm {d}\xi \approx \sum _{i=1}^{{n_{\text {d}}}-1} f(\xi _i) \varDelta \xi _i, \end{aligned}$$
(56)

use is made of the trapezoidal rule to compute the integrals.

The mean measures using the trapezoidal rule are assembled in Table 1.

Table 1 Approximated measures characterizing a curvilinear fiber with the differential formulas (47), (49), (50), and (52)–(54)
Full size table

3 Example

In the following, we apply the two concepts to real \(\mu \)-CT data of a man-made cellulose fiber reinforced polypropylene specimen. The data are generated using a 3D X-ray microscope Xradia 520 Versa from Zeiss. The fibers were detected with the program Avizo (version 9.4.0 of the company FEI). The considered volume element of the sample has a size of approximately \(208.5\,\upmu \hbox {m}\times 629.6\,\upmu \hbox {m}\times 629.6\,\upmu \hbox {m}\). This produces the fibers shown in Fig. 4. Here, we are not interested in discussing whether it makes sense considering fibers which are cut at the edge surfaces of the cube-like region or not. We are interested in how the applied schemes work with some data.

Fig. 4
figure 4

\(\mu \)-CT data of man-made cellulose fibers (coordinates in \(\upmu \hbox {m}\))

Full size image

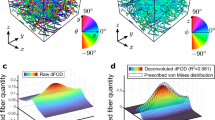
To obtain more insight in the fiber distribution, we draw on the concepts of Sects. 2.3.1 and 2.3.2. Figures 5 and 6 compile the results. The length computation shows very similar results of both methods, the interpolation concept, and the simplified scheme, see Fig. 5a and b.

Fig. 5
figure 5

Distribution of fiber length, mean curvature, and torsion

Full size image
Fig. 6
figure 6

Distribution of mean orientation angles and mean distance to straight line

Full size image

The mean curvature in Fig. 5c and d, however, shows slightly different results, since the simplified method draws on the second derivative, and derivatives using differential formulas roughen the results. This is the essential drawback in the mean torsion computation shown in Fig. 5e–f, where the third derivative of the curve vector is evaluated. Since there are some fibers with “kinks”, totally unrealistic values are computed using the simplified version to determine the torsion of a fiber. The estimation of the mean fiber orientation, represented by the angles \(\vartheta _M\) and \(\varphi _M\), is appropriate for both schemes, see Fig. 6a–d, which holds for the mean distance of the fibers relative to the center line (42) in Fig. 6e–f.

4 Conclusions

In this paper, the quantitative properties of man-made cellulose fibers are proposed. Since these fibers represent curvilinear functions in the matrix material, some characteristic measures are of particular interest. We propose several measures describing curvilinear lines: length, mean curvature, mean torsion, mean direction, and a mean distance to a straight line. To describe the curvilinear fibers, the discrete data points are interpolated by a first concept. This interpolation is based on splines to obtain a continuous representation. In a second scheme, only the discrete data points are evaluated. There, the required first three derivatives are based on differential derivative formulas leading to a much simpler evaluation process. However, it turns out that the third derivative leads to very inadequate results in some situations so that the measure of mean torsion, i.e. a measure of the deviation of a curve from a plane, is not suitable. All other measures lead—for the distribution of a real \(\mu \)-CT scan data—to similar results. Thus, both methods are a promising tool for evaluating the fiber measures, except for torsion, where only the more sophisticated evaluation procedure is necessary.