1 Introduction

Self-adaptive systems are designed to adjust their dynamical characteristics depending on certain operating conditions. In comparison with active systems, passive systems have the advantage that neither a control unit nor an external energy source is needed, which makes them interesting, e.g., for energy harvesting [2, 3] and vibration suppression applications [13, 17].

In various experiments, carried out independently by different research groups [2, 3, 11, 12, 16, 19], a clamped–clamped beam under harmonic base excitation with attached slider has shown self-adaptive behavior. After initially small vibrations, the slider moved to a certain position and the vibration level increased substantially. Hereby a signature move was observed [2, 11, 12], which is shown in Fig. 1, and described in the following. A video of this intriguing behavior is available online [1]. While the system vibrates initially at small level, the slider moves toward the clamping. At a certain point, the vibrations jump to a higher level and the slider turns back toward the beam’s center. This movement goes along with a further increase of the vibration level. At a certain position, which can be different from the beam’s center, the slider stops and large vibrations are maintained at steady state. This behavior was observed for a broad range of excitation frequencies. There is no conclusive theory explaining this complex self-adaptive behavior.

Fig. 1
figure 1

Example for self-adaptive signature move. Black: Beam’s deformation at center. Red: Normalized position of slider. A video of this behavior is available here: [1]. (Color figure online)

Full size image

Miller et al. [11, 12] proposed a first model of the system. They described the beam in terms of linear Euler–Bernoulli theory. The slider was modeled as a rigid body and assumed to be vertically constrained to the beam, which corresponds to a tight fit with no clearance. This leads to the conclusion that the slider moves to an antinode of the vibrational deflection shape. In all experimental observations, the beam’s vibrational deflection shape had only one antinode at the beam’s center. Consequently, this model always predicts that the slider moves toward the beam’s center and stays there.

Krack et al. [7] refined the model of Miller et al. by taking into account a small clearance between slider and beam, which gives rise to unilateral and frictional contact interactions. It was shown that these contact interactions are responsible for the movement of the slider away from the beam’s center. Without friction, the slider never reaches a fixed horizontal location along the beam, but keeps cycling around the beam’s center. For a too tight fit (too small clearance between slider and beam), the slider never moves away from the center, in contrast to the experimental observations. The self-adaption was shown to work for a broad, yet limited, range of excitation frequencies around the system’s first natural frequency. However, the model failed to predict the jump to high vibration levels and that the slider turns around to further move toward the beam’s center.

Under axial constraints, the transverse deformation of a beam is associated with a midplane stretching. This is known to cause a strong geometric stiffening effect, which leads to strongly nonlinear behavior in case of sufficiently large transverse deformations of the beam [15, 18]. Despite the fact that the measured deformations exceeded the beam’s thickness, this effect was neglected in the aforementioned models.

While preparing the current paper, the group of Yu et al. [19] independently worked on the beam-slider system. To the authors’ knowledge, they are the first to publish results on the effect of the beam’s geometric nonlinearity on the system’s self-adaptive behavior. Just as Miller et al. [11], they assume that the slider is transversely constrained to the beam (tight fit without clearance), thus neglecting unilateral contact interactions. Using this model, they demonstrated theoretically that the system with bonded slider has (at most two) coexisting limit states. If the slider is placed sufficiently close to the clamping, it moves monotonously toward the beam’s center and stops there, while the vibration level increases continuously to high level. These theoretical results are in good agreement with the experimental investigations [19]. As the unilateral contact interactions were neglected, however, the signature move, involving a slider movement away from the beam’s center and a jump of the vibration level [2, 11, 12], could not be explained with their model. Yu et al. [19] also showed that if the slider is initially placed sufficiently close to the beam’s center and the system starts with low vibration levels, the system never reaches high vibration levels. This implies that the system can only adapt once. As soon as the vibrations decay to low level (e.g. if the excitation level is temporarily decreased or the excitation frequency is temporarily far from resonance), the slider remains at the beam’s center, and the system looses its ability to adapt itself in order to reach high vibration levels. To overcome this, Yu et al. [20] proposed to introduce an inclination with respect to the gravity field. If the vibrations decay, gravity pulls the slider toward the clamping, which may recover the system’s self-adaptability.

With this work, we intend to provide, for the first time, a conclusive theoretical explanation of the above described signature move. To this end, we extend the model developed in our previous study [7] by the geometric stiffening nonlinearity in Sect. 2. We then validate the model by reproducing experimental results available in the literature in Sect. 3. Besides the signature move, we consider also cases of unsuccessful adaption processes, in order to gain further confidence that the model captures all essential characteristics. In Sect. 4, the self-adaptive behavior is analyzed and comprehensively explained. The paper ends with conclusions in Sect. 5.

2 Extension of model by the beam’s geometric nonlinearity

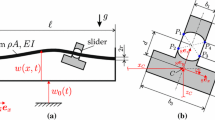
In this section, the model of [7] is extended to consider the beam’s geometric nonlinearity due to bending-stretching coupling. A schematic of the model is shown in Fig. 2. In Sect. 2.1, the beam’s nonlinear equation of motion is given. In Sect. 2.2, a closed-form expression is derived for the approximation of the system’s first natural frequency, as function of the slider position and the beam’s vibration level. The validity of this approximation is analyzed using a nonlinear modal analysis. The contact model and the numerical simulation is described in Sect. 2.3.

Fig. 2
figure 2

a Two-dimensional model of self-adaptive system. b Detail of slider

Full size image

2.1 Geometric nonlinearity due to bending-stretching coupling

Within this work, the beam’s transverse elastic deformations w(x, t) are described in terms of the N lowest-frequency bending modes. Here x is the spatial coordinate in the direction of the beam’s length and t the time. The clamping and the support frame are assumed to be perfectly rigid. We assume the beam to be homogeneous, with constant cross section area A and density \(\rho \), and to behave linear elastically, with the Young’s modulus E. As in the experiments, the beam’s length is assumed to be much larger than the thickness, such that Euler–Bernoulli theory is justified and, accordingly, we neglect shear, Poisson effect, rotational and longitudinal inertia. The vibrational amplitude is assumed to be small in comparison with the beam’s length; however, we consider nonlinear terms due to stretching enforced by the clamped–clamped boundary conditions. As shown e.g. in [4, 15, 18], this leads to the following equation system (for the clamped–clamped beam without slider):

$$\begin{aligned}&w(x,t) \approx \sum _{n=1}^N \varphi _n\left( x\right) q_n(t), \end{aligned}$$
(1)
$$\begin{aligned}&\ddot{q}_n + 2D_n \omega _n^\mathrm {lin} \dot{q}_n + \left( \omega _n^\mathrm {lin} \right) ^2 q_n + \sum _{j=1}^N \sum _{k=1}^N \sum _{l=1}^N b_{j,k,l}^{(n)} q_j q_k q_l = \gamma _n \ddot{w}_0(t) \quad \quad \mathrm {with} \quad n=1,2,\ldots ,N , \end{aligned}$$
(2)
$$\begin{aligned}&b_{j,k,l}^{(n)} = - \frac{EA}{2L} \int _0^L \varphi '_j \varphi '_k \mathrm {d}x \int _0^L \varphi ''_l\varphi _n \mathrm {d}x . \end{aligned}$$
(3)

Differentiation with respect to t and x is denoted \(\dot{()}\) and \(()'\). Equation 1 represents the ansatz, which assumes that the beam’s deformation can be well approximated by a linear combination of the N lowest-frequency mode shapes, \(\varphi _n(x)\) (mass-normalized), of the underlying linear system (linear Euler-Bernoulli theory). \(\omega _n^\mathrm {lin}\) are the associated natural frequencies, \(D_n\) the modal damping ratios and \(q_n\) the modal coordinates. Furthermore, \(\gamma _n =-\,\rho A \int _{0}^{L} \varphi _n \mathrm {d}x\) and \(\ddot{w}_0\) is the imposed base acceleration. Equation 2 is the equation of motion, condensed to the transverse direction. Equation 3 defines the coefficients of the cubic nonlinear polynomial that describes the beam’s geometric stiffness nonlinearity.

For this work, we evaluate the integrals in Eq. 3 numerically using Matlab. An alternative is to apply the stiffness evaluation procedure or implicit condensation [9, 10, 14] using a standard finite element tool.

To underline the significance of the geometric nonlinearity, the lowest natural frequency is plotted in Fig. 3 as a function of vibrational amplitude at the beam’s center. The beam’s properties are set as specified in Sect. 3.1. The natural frequency is determined by nonlinear modal analysis (NMA) and compared to a single-mode single-term Harmonic Balance (HB) approximation. For the NMA, the extended periodic motion concept [6] is used, which is also applicable to damped systems. To this end, a HB approach with modal truncation after \(N=7\) modes is considered, using the free Matlab tool NLvib [8]. The harmonic truncation order is set to \(H=10\), such that the condition \(\mathrm {max}(\omega _1){\cdot } H>\omega _N^\mathrm {lin}\) holds in the considered amplitude range. Increasing N and H does not change the picture in the considered amplitude range, but yields additional loops for higher amplitude levels which are not relevant for this work.

The single-term, single-mode HB approach of the undamped system, see e.g. [15], yields the natural frequency

$$\begin{aligned} \omega ^\mathrm {SHB}_1=\sqrt{\left( \omega _1^\mathrm {lin} \right) ^2+\frac{3}{4}b_{1,1,1}^{(1)}{\hat{q}}_1^2}. \end{aligned}$$
(4)
Fig. 3
figure 3

Lowest natural frequency of the copper beam (System 1) without slider as a function of vibrational amplitude. Black: Nonlinear modal analysis. Green: Single-mode single-term HB approximation. (Color figure online)

Full size image

Herein \({\hat{q}}_1\) denotes the amplitude of the first modal coordinate which is linked to the physical amplitude at the beam’s center via \({{\hat{w}}_{L/2}=\varphi _1(L/2) {\cdot } {\hat{q}}_1}\). Both approaches match very well up to \({\hat{w}}_{L/2}/h \approx 2.6\), where h is the beam’s thickness. The deviations for larger amplitudes, including a loop in the NMA at \({\hat{w}}_{L/2}/h \approx 4\), can be explained by modal interactions, see e.g. [5], which cannot be captured with the single mode approximation in Eq. 4. However, the largest vibration levels encountered in the present study remain sufficiently small, \({\hat{w}}_{L/2}/h\le 2.5\). It can thus be stated that the approximation in Eq. 4 is valid in the range of vibration levels relevant in the present study.

2.2 Approximation of the system’s fundamental natural frequency

An approximation of the beam-slider system’s first natural frequency, as function of the slider position, was provided in [7]. Hereby the influence of the slider’s mass and inertia on the beam’s linear natural frequency was approximated using the Rayleigh quotient. Here, we extend this approximation to consider also the beam’s geometric stiffening effect. To this end, we replace the linear natural frequency by the single-mode single-term HB approximation of Eq. 4, giving

$$\begin{aligned} {\tilde{\omega }}_1^2\left( {{\hat{q}}}_1,x_C\right) :=\frac{\left( \omega _1^\mathrm {lin} \right) ^2 + \frac{3}{4}b_{1,1,1}^{(1)} {\hat{q}}_1 ^2}{1+m \left( \varphi _1(x_C)\right) ^2+J_{yy}^{(C)} \left( \varphi '_1(x_C)\right) ^2}. \end{aligned}$$
(5)

The approximated natural frequency \({\tilde{\omega }}_1\) is now a function of the amplitude \({\hat{q}}_1\) and slider position \(x_C\). The result of this function and different projections are shown in Fig. 4. One can see that both vibrational amplitude (geometric nonlinearity) and slider position (additional mass/inertia) have a crucial influence on the system’s natural frequency in this range. For the given mass ratio, changing the slider position from the clamping to the center alone decreases the natural frequency by 64%. Increasing the beam’s amplitude, e.g., from zero to \({\hat{w}}_{L/2}/h=2.5\) doubles the natural frequency.

Fig. 4
figure 4

Approximation for the first natural frequency as a function of slider position and vibrational amplitude according to Eq. 5 for System 1: a 3D-plot. b–d Different projections

Full size image

2.3 Slider model, contact model and numerical simulation

The slider is assumed to be a rigid body with three degrees of freedom (horizontal and vertical translation plus rotation). We consider gravity acting on the slider as indicated in Fig. 2. This is in accordance with the orientation of the experiments [3, 11] and the model from [7]. The slider’s inner geometry is such that contact may occur only at the four points indicated in Fig. 2. Unilateral and dry frictional contact interactions between beam and slider are modeled by the Signorini and Coulomb laws combined with Newton’s impact law. These are set-valued contact laws, which are associated with velocity jumps, and thus, standard time integration algorithms for continuous ordinary differential equation systems cannot be applied. Instead, the equation of motion is transformed to a measure differential inclusion, which is solved numerically by Moreau’s time stepping scheme. The dynamic contact problem is resolved using an augmented Lagrangian approach. In accordance with preliminary convergence studies, modal truncation after \(N=7\) modes and a fixed time step of \(\Delta t =2 \pi / (5 \omega _N)\) is applied for all simulations. The contact model and simulation procedure are adopted from [7].

3 Validations against measurements reported in literature

In this section, the extended model is validated by means of experimental results. It should be emphasized that the dynamics of the self-adaptive system have been experimentally well-established. Results are available from experiments carried out independently by at least three different research groups, including authors of this and our previous study [2]. Therefore, the objective of this work is not to report further experimental data, but to provide the first conclusive theoretical explanation of the well-supported experimental observations. Consequently, we validate our model based on measurements available from literature. First, the different configurations are specified in Sect. 3.1. The signature move yielding successful adaption is analyzed in Sect. 3.2. Different kinds of unsuccessful adaption are analyzed in Sect. 3.3.

3.1 Nominal parameters

The simulations are compared to measurements from two different, representative references, [3] (System 1, beryllium-copper beam) and [11] (System 2, aluminum beam). The beam’s material properties and geometric dimensions, the slider’s mass and rotational inertia are given for System 2 directly in [11], c.f. Table 1. For System 1, these are specified in [12].

Table 1 Nominal parameters
Full size table

3.2 Successful adaption and signature move

Experimental results from [11] are shown in Fig. 5a. The beam’s deformation was measured in terms of the voltage of a strain gauge on the beam’s top. The slider’s horizontal position is normalized with respect to the beam’s length so that a value of 0.5 corresponds to the beam’s center. The system successfully adapted itself to reach high vibration levels, and it showed the aforementioned signature move: Starting from its initial location \(x_C/L \approx 0.8\), the slider moved slowly toward clamping. During this process, the beam’s amplitude was comparatively small. At a certain point, the slider turned and moved toward the beam’s center, while the vibration level grew significantly. In the depicted case, the slider moved all the way to the center. In other experiments, the slider stopped before reaching the center [2, 12, 19]. In all these cases, the system reached and maintained high vibration levels.

Figure 5b shows the simulation results corresponding to Fig. 5a. Apparently, the model explains the self-adaption process, including the signature move qualitatively. It should be emphasized that our model is the first one to correctly predict this intricate behavior. Models that neglect the geometric nonlinearity cannot reproduce this signature move [7, 11], as will be explained in Sect. 4. Models that assume a tight fit (slider vertically constrained to beam), and thus do not account for unilateral contact interactions, cannot reproduce the movement of the slider away from the beam’s center [11, 19]. This is further supported by the rattling noise evident in the video [1]. This proves that both the beam’s geometric nonlinearity and unilateral contact interactions are crucial to explain the intricate dynamics presented in Fig. 5a. Furthermore, friction in the beam-slider attachment is crucial, as shown in Sect. 4.1.

The adaption process is quicker in the simulation. In [7], it was shown that the speed of the adaption depends, among others, on the friction coefficient and the clearance. These parameters were not reported in the reference [11] and thus had to be estimated (estimated values see Table 1).

Fig. 5
figure 5

Self-adaptive process of System 2 at \(f_\mathrm {ex}=55\,\mathrm {Hz}\), \(\hat{\ddot{w}}_0=15.7\,\mathrm {m}/\mathrm {s}^2\). a Experimental results, reprinted with author’s permission from [11]. Black: Voltage of a strain gauge as measure for the beam’s deformation. Purple: Normalized position of slider. b Simulation results. Black: Beam’s deformation at center. Red: Normalized position of slider. (Color figure online)

Full size image

3.3 Unsuccessful adaption

In addition to successful cases of the self-adaptive process, Gregg et al. [3] reported different experiments with unsuccessful adaption, i.e., where the system failed to maintain large vibrations. Those observations are useful to further validate the model proposed in the present work. Two examples are analyzed in the following, an unstable adaption and a quasi-stable adaption.

Measurements of an unstable adaption are shown in Fig. 6a (reprint from [3]). Here, the beam’s transverse deformation at the center is visualized. Like in successful adaptions, the beam’s vibrational amplitude was initially small, while the slider moved toward clamping. After a jump to higher vibrational amplitude at \(t \approx 22\mathrm {s}\), the slider did not turn but moved further toward clamping which resulted in a continuous decrease of amplitude. Gregg et al. [3] attributed this to a too large clearance between slider and beam. To reproduce this behavior with our model, System 1 is considered; however, with increased clearance, \(R/h=1.2\). The result is in good accordance with the experiment, see Fig. 6b.

Fig. 6
figure 6

Unstable process. a Experimental results, reprinted with author’s permission from [3]. Blue: Beam’s deformation at center. b Simulation results, System 1 with parameters \(f_\mathrm {ex}=130\,\mathrm {Hz}\), \(\hat{\ddot{w}}_0=20\,\mathrm {m}/\mathrm {s}^2\), \(R/h=1.2\). Black: Beam’s deformation at center. Red: Position of slider. (Color figure online)

Full size image

Measurements of a quasi-stable adaption are shown in Fig. 7a (reprint from [3]). Again, the initial vibrational amplitude was small in this experiment. After \(t \approx 70 \mathrm s\), the amplitude jumped to a much higher level, which was retained only for a few seconds. After that, the amplitude jumped between high and low level recurrently. The slider was described to ‘oscillate in and out of resonance’ [3]. Unfortunately, the according system parameters were not available from the experimental study. To reproduce this behavior in the simulation, the system parameters are set as specified in Table 1; however, the clearance is slightly enlarged by 5%, and the slider’s mass and inertia are doubled. The result is in good qualitative agreement with the experiment, see Fig. 7b. It should be remarked that the mean value of the beam’s transverse displacement, measured here from the non-deformed configuration, is not zero due to gravity. Compared to the other simulation results shown in this work, this effect is more pronounced here due to the increased slider mass and the relatively small vibration level.

Fig. 7
figure 7

Quasi-stable process. a Experimental results, reprinted with author’s permission from [3]. Blue: Beam’s deformation at center. b Simulation results, System 1 with parameters \(f_\mathrm {ex}=150\,\mathrm {Hz}\), \(\hat{\ddot{w}}_0=10\,\mathrm {m}/\mathrm {s}^2\), \(R/h=1.1\), \(m/m_\mathrm {ref}=J_{yy}^{(C)}/J_{yy,\mathrm {ref}}^{(C)}=2\). Black: Beam’s deformation at center. Red: Position of slider. (Color figure online)

Full size image

To conclude, the proposed model correctly reproduces, for the first time, the signature move of the self-adaptive system, and reported cases of unsuccessful adaption. It also confirms the sensitivity with respect to the clearance between slider and beam, and the slider’s mass, as reported from experimental investigations [3].

4 Analysis of the self-adaptive behavior

The aim of this section is to establish a comprehensive explanation of the self-adaption process. In Sect. 4.1, we demonstrate that the geometric nonlinearity and dry friction are essential ingredients for explaining the system dynamics. In Sect. 4.2, we prove that the timescales of vibration and slider movement along the beam are indeed well separated, such that the adaptive system closely follows the periodic vibration response obtained for axially fixed slider. With this, we explain why the slider needs to initially move away from the beam’s center to reach high vibration level and that this is only possible if the slider is not fitted too tightly to the beam. Moreover, we attribute the jump phenomenon with a turning point bifurcation of the periodic response with respect to the slider position. In Sect. 4.3, we analyze why the slider stops before reaching the vibration antinode at the center.

4.1 Are geometrical and frictional nonlinearity needed to explain the self-adaptive behavior?

In Fig. 8a, the signature move is again illustrated, yet for System 1 instead of System 2 and for a slightly different initial slider location, c.f. Fig. 5b. For the simulation results in Fig. 8b, the beam’s geometric nonlinearity is turned off, while the contact interactions are still considered. The slider now moves to a certain position away from the beam’s center and stays there. The vibration level increases continuously. In the first 9 seconds, the reference and the simulation without geometric nonlinearity agree reasonably. Thus, the geometric nonlinearity is not needed to explain that the slider moves away from center. However, the vibrations are smaller and do not jump to a high level. Also, the slider does not turn around to approach the beam’s center. Finally, a closer look into the beam’s vibration shows that its response is highly irregular, as opposed to the reference in Fig. 8a. Apparently, these deficiencies can be explained by the fact that linear beam theory is not appropriate: The vibration level reached after 13 seconds is so large that they would cause a nonlinear geometric hardening effect which would shift the system’s natural frequency by 24%.

For the simulation results in Fig. 8c, the beam’s geometric nonlinearity is turned on again, but the dry friction between beam and slider is switched off, \(\mu =0\). Now the slider oscillates axially along the beam around the beam’s center, while the beam’s vibration level strongly modulates. The modulation frequency is twice the frequency of the slider’s horizontal oscillation. The period of this oscillation is much longer than the excitation period; i.e., the re-arrangement of the slider takes place on a much longer timescale than the vibrations (as also in the signature move). Apparently, dry friction in the beam-slider attachment, however small, is needed to stabilize the slider’s positioning.

Fig. 8
figure 8

Simulation of System 1 at \(f_\mathrm {ex}=130\,\mathrm {Hz}\), \(\hat{\ddot{w}}_0=30\,\mathrm {m}/\mathrm {s}^2\). Black: Beam’s deformation at center. Red: Position of slider. a Reference. b Without geometric nonlineraities. c Without friction between beam and slider. (Color figure online)

Full size image

In conclusion, this means that both the beam’s geometric nonlinearity and the dry stick-slip friction in the beam-slider attachment are needed to explain the signature move of the self-adaptive system. Finally, the clearance between slider and beam, which gives rise to unilateral contact interactions, is crucial, which is further analyzed in Sect. 4.2.

4.2 Why does the slider have to move toward the clamping and the vibration level jump to reach high vibration level?

The results so far suggest that the slider re-arrangement and the vibration take place on well-spaced timescales. It seems therefore justified to separate the complicated problem by imposing a certain slider position and studying just the nonlinear vibration response. A schematic of this modified system is depicted in Fig. 9, and the results are shown in Fig. 10b. Essentially, this is a bifurcation diagram which depicts how the steady-state vibration level of the beam’s center depends on the horizontal slider position \(x_C\) (control parameter). The orange curve is generated by initially placing the slider near the beam’s center, and stepwise increasing the horizontal slider location toward the clamping. The green curve is generated by initially placing the slider near the clamping and stepwise decreasing the horizontal slider location toward the beam’s center. In each step, the initial conditions are adopted from the previous step, and the simulation runs until a steady state is reached. This corresponds to a sequential path continuation procedure. It should be noted that only the slider’s horizontal translation is constrained. Vertical translation and rotation are left as degrees of freedom, and the dynamic contact interactions between slider and beam are taken into account.

Fig. 9
figure 9

System with prescribed horizontal slider position: a Schematic of model. b Definition of horizontal reaction force \(F_x\)

Full size image

The form of the diagram in Fig. 10b is similar to that of the frequency response of a Duffing oscillator with softening characteristic. In that case, however, the control parameter is the excitation frequency, while it is here the horizontal slider position. Still, one can clearly see that two branches of steady-state vibrations coexist for slider positions around the center, more specifically in the range \(x_C/L < 0.78\) (and \(x_C/L > 0.22\) owing to the system’s symmetry). It seems likely that the low-level branch has a turning point at \(x_C/L \approx 0.78\), and there is an unstable overhanging branch. The stable low-level branch and the overhanging branch would form a closed loop, with mirror symmetry with respect to the beam’s center. Unfortunately, the branch of unstable periodic vibration states cannot be found with time integration of the transient. A further analysis of the unstable branch is hence considered beyond the scope of the present study.

As the timescales of the axial slider movement and the vibrations are well separated, the stable vibration states determined for fixed slider form the subspace on which the self-adaptive system can operate. Simulation results of the self-adaptive system (with horizontally free slider) are also depicted in Fig. 10b. Here, the slider is initially placed near the beam’s center and the system starts with no vibration energy. The low-level branch (orange) is reached first. The transient dynamics of the self-adaptive system closely follows the steady vibration states determined for horizontally fixed slider. Here, the transient amplitude is defined as peak-to-peak/2 value, determined and plotted for each excitation period. Assuming that the system has the tendency to maximize its vibrations, the results in Fig. 10b explain why the slider first has to move away from the beam’s center, the vibration level then jumps, and the slider turns around.

The results depicted in Fig. 11 were obtained for a very small clearance between slider and beam, i.e., for a slider tightly fitted to the beam. In this case, the slider moves directly toward the vibration antinode at the beam’s center. This proves that a sufficiently large clearance is needed to enable the unilateral contact interactions required for the signature move. Only with sufficiently large clearance, the slider can move away from the beam’s center to reach high-level vibrations.

Fig. 10
figure 10

Simulation of System 1 at \(f_\mathrm {ex}=145\,\mathrm {Hz}\), \(\hat{\ddot{w}}_0=20\,\mathrm {m}/\mathrm {s}^2\): a time-history of self-adaptive process. Black: Beam’s deformation at center. Red: Position of slider. b Vibrational amplitude versus slider position. Orange/Green: Increasing/decreasing prescribed slider position with step length \(\Delta x_C/L=0.003\). Black: Self-adaptive process, arrows indicate direction of time. Dashed gray: Relation between amplitude and slider position for resonance according to Eq. 5. (Color figure online)

Full size image
Fig. 11
figure 11

Simulation of System 1 with insufficient clearance (\(R/h=1.01\)) at \(f_\mathrm {ex}=145\,\mathrm {Hz}\), \(\hat{\ddot{w}}_0=20\,\mathrm {m}/\mathrm {s}^2\): a time-history of self-adaptive process. Black: Beam’s deformation at center. Red: Position of slider. b Vibrational amplitude versus slider position. Orange/Green: Increasing/decreasing prescribed slider position with step length \(\Delta x_C/L=0.003\). Black: Self-adaptive process, arrow indicates direction of time. Dashed gray: Relation between amplitude and slider position for resonance according to Eq. 5. (Color figure online)

Full size image

Figure 10b shows also the resonance curve, defined by the coincidence of the excitation frequency (here fixed) and the natural frequency (dependent on slider position \(x_C\) and vibration amplitude \({{\hat{w}}}_{L/2}\)). To determine this curve, the natural frequency is approximated as in Eq. 5, i.e., the points on the resonance curve are defined by \({{\hat{w}}}_{L/2}(x_C) = \lbrace {{\hat{w}}}_{L/2}\vert {{\tilde{\omega }}_1({{\hat{w}}}_{L/2},x_C) = 2\pi f_\mathrm {ex}}\rbrace \). During its adaption process, the self-adaptive system has the tendency to approach the resonance curve.

Finally, besides the signature move, a second, less complex adaption process is possible as shown in Fig. 12: If the slider is initially placed sufficiently close to clamping, \(x_C/L > 0.78\), only one stable vibration state exists, and the self-adaptive system only follows the (green) high-level branch. In this case, the slider does not turn around but moves monotonously toward the beam’s center, and the vibration level does not jump. This behavior does also occur for a tightly fitted slider, see Fig. 13. Consequently, for tightly fitted slider, high level vibrations can only be reached if the slider is initially placed sufficiently close to the beam’s clamping. This implies that a tightly fitted slider (no clearance) permits only a one-time adaption: As soon as the excitation level drops or the excitation frequency exceeds the system’s operating range, the system with tightly fitted slider will forever remain on the low-level branch, and never reach large vibrations again (without external help), and thus looses its ability to adapt itself. Of course, such a one-time adaption is of rather limited practical value. This is the only scenario discussed in [19].

Fig. 12
figure 12

Simulation of System 1 at \(f_\mathrm {ex}=145\,\mathrm {Hz}\), \(\hat{\ddot{w}}_0=20\,\mathrm {m}/\mathrm {s}^2\): a time-history of self-adaptive process. Black: Beam’s deformation at center. Red: Position of slider. b Vibrational amplitude versus slider position. Orange/Green: Increasing/decreasing prescribed slider position. Black: Self-adaptive process, arrow indicates direction of time. Dashed gray: Relation between amplitude and slider position for resonance according to Eq. 5. (Color figure online)

Full size image
Fig. 13
figure 13

Simulation of System 1 with decreased clearance (\(R/h=1.01\)) at \(f_\mathrm {ex}=145\,\mathrm {Hz}\), \(\hat{\ddot{w}}_0=20\,\mathrm {m}/\mathrm {s}^2\): a time-history of self-adaptive process. Black: Beam’s deformation at center. Red: Position of slider. b Vibrational amplitude versus slider position. Orange/Green: Increasing/decreasing prescribed slider position. Black: Self-adaptive process, arrow indicates direction of time. Dashed gray: Relation between amplitude and slider position for resonance according to Eq. 5. (Color figure online)

Full size image

4.3 Why does the slider not go all the way to the beam’s center?

We now address the question why the slider stops at \(x_C^\mathrm {ss}/L \approx 0.57\) rather than going all the way to the beam’s center (\(x_C^\mathrm {ss}/L=0.5\)). To explain this behavior, the modified system with horizontally fixed slider is again simulated. The horizontal component, \({\bar{F}}_x^\mathrm {ss}(x_C)\), of the time-averaged steady-state contact force is determined, c.f. Fig. 9. This is the force needed to keep the slider at its current position \(x_C\). Owing to the system’s symmetry, we discuss only the slider’s behavior in the right half of the beam, \(x_C/L>0.5\). A positive \({\bar{F}}_x^\mathrm {ss}>0\) would drive the free slider toward clamping, a negative \({\bar{F}}_x^\mathrm {ss}<0\) toward the beam’s center, and \({\bar{F}}_x^\mathrm {ss}=0\) corresponds to a stationary position of the free slider. The results are depicted in Fig. 14 . Consider first the results obtained for stepping the slider from the clamping toward the beam’s center (Fig. 14a, b). The vertical black line indicates the steady state slider position of the self-adaptive process. One can see several zero crossings of \({\bar{F}}_x^\mathrm {ss}\) close to this position. Indeed, \({\bar{F}}_x^\mathrm {ss}\) barely reaches positive values in this range. Still, this is sufficient to stop the slider from further advancing toward the beam’s center. Crossings with \(\partial {\bar{F}}_x^\mathrm {ss}/\partial x<0\) indicate stable and \(\partial {\bar{F}}_x^\mathrm {ss}/\partial x>0\) unstable equilibria. To the right of these zero crossings, there is a range up to \(x_C^\mathrm {ss}/L \approx 0.85\), where \({\bar{F}}_x^\mathrm {ss}\) is negative, which means that the force acts toward center. This is consistent with the self-adaptive simulations shown in Figs. 10 and 12. Interestingly there is an unstable equilibrium at the beam’s center, but several stable equilibria away from center. This is consistent with different experimental observations, where the slider’s steady-state position was away from the beam’s center [2, 11, 12, 19]. This phenomenon does not occur if a tight fit of the slider is assumed (no clearance, no unilateral contacts) [11, 19]. Consequently, the unilateral contact interactions are needed to explain that the slider stops before reaching the beam’s center.

Consider now the results obtained for stepping the slider from the beam’s center toward clamping (Fig. 14c, d). Left of the jumping point, one can see a range with positive \({\bar{F}}_x^\mathrm {ss}\); thus, the force points toward jumping point here. Right of the jumping point, there is a range where the force is negative, thus pointing to the beam’s center. The results are here in agreement with those in Fig. 14a, b. In conclusion, the evaluation of \({\bar{F}}_x^\mathrm {ss}(x_C)\) can be used to predict the slider movement, and in particular, the range of initial slider positions that gives rise to high vibration levels (successful adaption).

Fig. 14
figure 14

a, b Results from simulations with decreasing prescribed slider position of System 1 at \(f_\mathrm {ex}=145\,\mathrm {Hz}\), \(\hat{\ddot{w}}_0=20 \mathrm {m}/\mathrm {s}^2\). a Steady-state amplitude. b Average horizontal force acting on slider in steady state during one excitation period. c, d Same for simulations with increasing prescribed slider position

Full size image

5 Conclusions

The model proposed in the present work explains, for the first time, the experimentally observed complex self-adaptive process. A focus was placed on the system’s signature move, which involves the slider movement toward the clamping, followed by a jump to high vibrations, and subsequent turning of the slider toward the beam’s center. Besides this, cases of unstable or quasi-stable adaption were qualitatively reproduced by simulation. It was demonstrated that without dry friction, the slider keeps cycling around the beam’s center and never reaches a fixed position. Without the beam’s geometric stiffening nonlinearity (due to bending-stretching coupling), the vibrations do not jump to high levels. Without unilateral contact interactions, the slider never moves toward the clamping but always toward the beam’s center. These interactions are also responsible for the occurrence of several stable equilibrium slider positions away from the beam’s center and thus explain that the slider stops before reaching the center. Finally, it was found that the clearance between slider and beam, which gives rise to the unilateral contact interactions, is actually needed to achieve recurrent self-adaptive behavior. In contrast, if the slider is fitted tightly to the beam (no clearance), the system looses its ability to adapt itself as soon as the vibration level falls below a certain threshold (e.g. if the excitation is temporarily switched off). Future work could focus on a thorough quantitative comparison of simulation and measurements in a broad parameter range and analyzing the system’s suitability as broadband energy harvester or vibration absorber.