Skip to main content
SpringerLink
Log in

Analysis of Hooke-like isotropic hypoelasticity models in view of applications in FE formulations

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

This paper presents an analysis of the constitutive relations of Hooke-like isotropic hypoelastic material models in Lagrangian and Eulerian forms generated using corotational stress rates with associated spin tensors from the family of material spin tensors. Explicit expressions were obtained for the Lagrangian and Eulerian tangent stiffness tensors for the hypoelastic materials considered. The main result of this study is a proof that these fourth-order tensors have full symmetry only for material models generated using two corotational stress rates: the Zaremba–Jaumann and the logarithmic ones. In the latter case, the Hooke-like isotropic hypoelastic material is simultaneously the Hencky isotropic hyperelastic material. For the material models considered, basis-free expressions for the material and spatial tangent stiffness tensors are obtained that can be implemented in FE codes. In particular, new basis-free expressions are derived for the tangent stiffness (elasticity) tensors for the Hencky isotropic hyperelastic material model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Notes

  1. The history of the derivation of this type of constitutive relations is described in [81, 83]. In these papers, the role of Zaremba (1903) and Jaumann (1911) as pioneers in this area of continuum mechanics is highlighted.

  2. Nevertheless, it is possible to construct scenarios of thermomechanical processes that give the current stress distribution in the Earth’s crust, as was done, e.g., in a simulation study [2, 50] of geophysical processes using the commercial MSC.Marc code.

  3. Hill [40] defines elasto-plastic materials as materials for which some objective rate of the Cauchy stress tensor \(\varvec{\sigma }^\nabla \) is linked to the stretching tensor \({\mathbf {d}}\) by a first-order homogeneous relation, but the coefficients of this relation also implicitly depend on the tensor \({\mathbf {d}}\).

  4. In some papers (cf., [76]), the Gurtin–Spear corotational rate is referred to as the Sowerby–Chu corotational rate [75] one.

  5. Hereinafter, tensors having both major and twice minor symmetries will be called supersymmetric (cf., [44]) or fully symmetric (cf., [26]) tensors.

  6. The number m (\(1\le m\le 3\)) will be called the eigenindex.

  7. Hereinafter, the notation \(\sum _{i\ne j=1}^{m}\) denotes the summation over \(i,j=1,\ldots , m\) and \(i\ne j\) and this summation is assumed to vanish when \(m=1\).

  8. Hereinafter, the subset \({\mathcal {T}}^{2\,+}_\text {orth}\subset {\mathcal {T}}^2\) denotes the set of all proper orthogonal second-order tensors (i.e., the tensors \(\varvec{\varPsi }\) such that \(\varvec{\varPsi }\cdot \varvec{\varPsi }^T={\mathbf {I}}\) and \(\det \varvec{\varPsi }=1\)).

  9. Hereinafter, we assume that all the tensors \({\mathbf {H}}\in {\mathcal {T}}^2\) are sufficiently smooth functions of a monotonically increasing parameter t (time), and we define the material time derivative (material rate) of the tensor \({\mathbf {H}}\): \(\dot{{\mathbf {H}}}\equiv \partial {\mathbf {H}}/\partial t\).

  10. The tensors \(\varvec{\varOmega }^L,\,\varvec{\omega }^E\in {\mathcal {T}}^2_{\text {skew}}\) are the twirl tensors of the Lagrangian and Eulerian triads, respectively.

  11. Hereinafter, the tensor \({\mathbb {O}}\) is the zero fourth-order tensor.

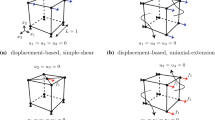
  12. In most of the studies cited, hypoelasticity relations are written in Eulerian form using the Cauchy stress tensor \(\varvec{\sigma }\), rather than the Kirchhoff stress tensor \(\varvec{\tau }\), to determine corotational stress rates. However, in the simple shear problem, \(J=1\), whence \(\varvec{\sigma }=\varvec{\tau }\), so that for all hypoelasticity models in the simple shear problem, the constitutive relations of Hooke-like isotropic hypoelastic material models based on corotational rates have form (30).

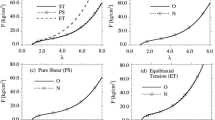
  13. The oscillating behavior of the Cauchy stress tensor components for this material model was first noted by Prager [69].

  14. The Green–Naghdi corotational rate of the Eulerian tensor \({\mathbf {h}}\in {\mathcal {T}}^2\) is defined as \({\mathbf {h}}^{GN} \equiv \dot{{\mathbf {h}}} - \varvec{\omega }^R \cdot {\mathbf {h}} + {\mathbf {h}} \cdot \varvec{\omega }^R\).

  15. The more general statement holds: For the isotropic Cauchy elastic material, tensors in pairs \((\bar{\varvec{\tau }},{\mathbf {U}})\) and \((\varvec{\tau },{\mathbf {V}})\) are coaxial (cf., [63]).

  16. In particular, hypoelastic materials do not depend on natural time (cf., [40]).

  17. The last statement can be generalized: The Cauchy stress tensor \(\varvec{\sigma }\) and any Eulerian strain tensor \({\mathbf {e}}\) from the Hill family are work-conjugate not in the classical sense due to the equality \({\mathbf {e}}^{\varDelta }={\mathbf {d}}\), where \({\mathbf {e}}^{\varDelta }\) is some convective rate of this tensor which is a corotational rate only if \({\mathbf {e}}={\mathbf {e}}^{(0)}\) and this corotational rate is logarithmic (cf., [16]).

  18. Sometimes, the Hill stress rate is called the Biezeno–Hencky stress rate (cf., [45]).

  19. More precisely, the tensors used in (30)\(_2\) have Eulerian objectivity, which is only considered in [83]. Starting from the book by Ogden [63], objective tensors include Lagrangian tensors, along with Eulerian ones.

  20. This statement contradicts the statement (see [60]) of the equivalence of hypoelasticity formulations based on any corotational rate, including the Gurtin–Spear one.

References

  1. Atluri, S.N.: On constitutive relations at finite strain: hypo-elasticity and elasto-plasticity with isotropic or kinematic hardening. Comput. Methods Appl. Mech. Eng. 43, 137–171 (1984)

    MATH  Google Scholar 

  2. Babichev, A.V., Korobeynikov, S.N., Polyansky, O.P., Reverdatto, V.V.: Computer modeling of folding in rocks. Doklady Earth Sci. 455(1), 327–330 (2014)

    Google Scholar 

  3. Bathe, K.J.: Finite Element Procedures. Prentice-Hall, Upper Saddle River (1996)

    MATH  Google Scholar 

  4. Batra, R.C.: Comparison of results from four linear constitutive relations in isotropic finite elasticity. Int. J. Non-Linear Mech. 36, 421–432 (2001)

    MATH  Google Scholar 

  5. Batra, R.C.: Elements of Continuum Mechanics. AIAA, Reston (2006)

    MATH  Google Scholar 

  6. Bažant, Z.P.: A correlation study of formulations of incremental deformation and stability of continuous bodies. J. Appl. Mech. 38, 919–928 (1971)

    MATH  Google Scholar 

  7. Bažant, Z.P.: Finite strain generalization of small-strain constitutive relations for any finite strain tensor and additive volumetric-deviatoric split. Int. J. Solids Struct. 33(20–22), 2887–2897 (1996)

    MATH  Google Scholar 

  8. Bažant, Z.P., Vorel, J.: Energy-conservation error due to use of Green-Naghdi objective stress rate in finite-element codes and its compensation. J. Appl. Mech. 81, 021008 (2014)

    Google Scholar 

  9. Beatty, M.F.: Topics in finite elasticity: hyperelasticity of rubber, elastomers, and biological tissues—with examples. Appl. Mech. Rev. 40(12), 1699–1734 (1987)

    Google Scholar 

  10. Belytschko, T., Liu, W.K., Moran, B.: Nonlinear Finite Elements for Continua and Structures. Wiley, Chichester (2000)

    MATH  Google Scholar 

  11. Bertram, A.: Elasticity and Plasticity of Large Deformations: An Introduction, 3rd edn. Springer, Heidelberg (2012)

    MATH  Google Scholar 

  12. Bigoni, D.: Nonlinear Solid Mechanics: Bifurcation Theory and Material Instability. Cambridge University Press, Cambridge (2012)

    MATH  Google Scholar 

  13. Biot, M.A.: Mechanics of Incremental Deformations: Theory of Elasticity and Viscoelasticity of Initially Stressed Solids and Fluids, Including Thermodynamic Foundations and Applications to Finite Strain. Wiley, New York (1965)

    Google Scholar 

  14. Bonet, J., Wood, R.D.: Nonlinear Continuum Mechanics for Finite Element Analysis, 2nd edn. Cambridge University Press, Cambridge (2008)

    MATH  Google Scholar 

  15. Bruhns, O.T., Xiao, H., Meyers, A.: Self-consistent Eulerian rate type elasto-plasticity models based upon the logarithmic stress rate. Int. J. Plast. 15, 479–520 (1999)

    MATH  Google Scholar 

  16. Bruhns, O.T., Meyers, A., Xiao, H.: On non-corotational rates of Oldroyd’s type and relevant issues in rate constitutive formulations. Proc. R. Soc. Lond. A 460, 909–928 (2004)

    MathSciNet  MATH  Google Scholar 

  17. Bruhns, O.T.: The Prandtl–Reuss equations revisited. Z. Angew. Math. Mech. 94(3), 187–202 (2014)

    MathSciNet  MATH  Google Scholar 

  18. Chaves, E.W.V.: Notes on Continuum Mechanics. Springer, Barcelona (2013)

    MATH  Google Scholar 

  19. Crisfield, M.A.: Non-linear Finite Element Analysis of Solids and Structures: Vol. 2. Advanced Topics. Wiley, Chichester (1997)

    MATH  Google Scholar 

  20. Curnier, A., Rakotomanana, L.: Generalized strain and stress measures: critical survey and new results. Eng. Trans. 39(3–4), 461–538 (1991)

    MathSciNet  Google Scholar 

  21. Curnier, A.: Computational Methods in Solid Mechanics. Kluwer, Dordrecht (1994)

    MATH  Google Scholar 

  22. de Borst, R., Crisfield, M.A., Remmers, J.J.C., Verhoosel, C.V.: Non-linear Finite Element Analysis of Solids and Structures, 2nd edn. Wiley, Chichester (2012)

    MATH  Google Scholar 

  23. de Souza Neto, E.A., Peric, D., Owen, D.J.R.: Computational Methods for Plasticity: Theory and Applications. Wiley, Chichester (2008)

    Google Scholar 

  24. Dienes, J.K.: On the analysis of rotation and stress rate in deforming bodies. Acta Mech. 32, 217–232 (1979)

    MathSciNet  MATH  Google Scholar 

  25. Dienes, J.K.: A discussion of material rotation and stress rate. Acta Mech. 65, 1–11 (1986)

    MATH  Google Scholar 

  26. Federico, S.: Covariant formulation of the tensor algebra of non-linear elasticity. Int. J. Non-Linear Mech. 47, 273–284 (2012)

    Google Scholar 

  27. Flanagan, D.P., Taylor, L.M.: An accurate numerical algorithm for stress integration with finite rotations. Comput. Methods Appl. Mech. Eng. 62, 305–320 (1987)

    MATH  Google Scholar 

  28. Freed, A.D.: Soft Solids: A Primer to the Theoretical Mechanics of Materials. Birkhäuser, Cham (2014)

    MATH  Google Scholar 

  29. Fung, Y.C.: Foundations of Solid Mechanics. Prentice-Hall, Englewood Cliffs (1965)

    Google Scholar 

  30. Fung, Y.C., Tong, P.: Classical and Computational Solid Mechanics. World Scientific, Singapur (2001)

    MATH  Google Scholar 

  31. Gambirasio, L., Chiantoni, G., Rizzi, E.: On the consequences of the adoption of the Zaremba–Jaumann objective stress rate in FEM codes. Arch. Comput. Methods Eng. 23, 39–67 (2016)

    MathSciNet  MATH  Google Scholar 

  32. Green, A.E., McInnis, B.C.: Generalized hypo-elasticity. Proc. R. Soc. Edinburgh. Secti. A Math. 67(3), 220–230 (1967)

    MathSciNet  MATH  Google Scholar 

  33. Gurtin, M.E., Spear, K.: On the relationship between the logarithmic strain rate and the stretching tensor. Int. J. Solids Struct. 19(5), 437–444 (1983)

    MathSciNet  MATH  Google Scholar 

  34. Hackett, R.M.: Hyperelasticity Primer. Springer, Heidelberg (2016)

    Google Scholar 

  35. Halleux, J.P., Donea, J.: A discussion of Cauchy stress formulations for large strain analysis. In: Bergan, P.G., Bathe, K.J., Wunderlich, W. (eds.) Finite Element Methods for Nonlinear Problems: Europe-US Symposium, pp. 61–74. Springer, Berlin (1986)

    Google Scholar 

  36. Hashiguchi, K.: Elastoplasticity Theory. Springer, Berlin (2009)

    MATH  Google Scholar 

  37. Hashiguchi, K., Yamakawa, Y.: Introduction to Finite Strain Theory for Continuum Elasto-Plasticity. Wiley, Hoboken (2013)

    Google Scholar 

  38. Healy, B.E., Dodds Jr., R.H.: A large strain plasticity model for implicit finite element analyses. Comput. Mech. 9, 95–112 (1992)

    MATH  Google Scholar 

  39. Hill, R.: A general theory of uniqueness and stability in elastic–plastic solids. J. Mech. Phys. Solids 6(3), 236–249 (1958)

    MATH  Google Scholar 

  40. Hill, R.: Some basic principles in the mechanics of solids without a natural time. J. Mech. Phys. Solids 7(3), 209–225 (1959)

    MathSciNet  MATH  Google Scholar 

  41. Hill, R.: On constitutive inequalities for simple materials – I. J. Mech. Phys. Solids 16(4), 229–242 (1968)

    MATH  Google Scholar 

  42. Hill, R.: Aspects of invariance in solid mechanics. In: Yih, C.-S. (ed.) Advances in Applied Mechanics, vol. 18, pp. 1–75. Academic Press, New York (1978)

    Google Scholar 

  43. Holzapfel, G.A.: Nonlinear Solid Mechanics: A Continuum Approach for Egineering. Wiley, Chichester (2000)

    MATH  Google Scholar 

  44. Itskov, M.: Tensor Algebra and Tensor Analysis for Engineers (with Applications to Continuum Mechanics), 4th edn. Springer, Heidelberg (2015)

    MATH  Google Scholar 

  45. Ji, W., Waas, A.M., Bažant, Z.P.: On the importance of work-conjugacy and objective stress rates in finite deformation incremental finite element analysis. J. Appl. Mech. 80, 041024 (2013)

    Google Scholar 

  46. Johnson, G.C., Bammann, D.J.: A discussion of stress rates in finite deformation problems. Int. J. Solids Struct. 20(8), 725–737 (1984)

    MATH  Google Scholar 

  47. Korobeynikov, S.N.: Nonlinear strain analysis of solids. Sib. Div. Russ. Acad. Sci, Novosibirsk (2000). (in Russian)

  48. Korobeynikov, S.N.: Objective tensor rates and applications in formulation of hyperelastic relations. J. Elast. 93, 105–140 (2008)

    MathSciNet  MATH  Google Scholar 

  49. Korobeynikov, S.N.: Families of continuous spin tensors and applications in continuum mechanics. Acta Mech. 216(1–4), 301–332 (2011)

    MATH  Google Scholar 

  50. Korobeinikov, S.N., Reverdatto, V.V., Polyanskii, O.P., Sverdlova, V.G., Babichev, A.V.: Surface topography formation in a region of plate collision: mathematical modeling. J. Appl. Mech. Tech. Phys. 53(4), 577–588 (2012)

    MATH  Google Scholar 

  51. Korobeynikov, S.N., Oleinikov, A.A., Babichev, A.V., Larichkin, A.Y., Alyokhin, V.V.: Computer implementation of Lagrangian formulation of Hencky’s isotropic hyperelastic material constitutive relations. Far East. Math. J. 13(2), 229–249 (2013). (in Russian)

    Google Scholar 

  52. Korobeynikov, S.N.: Basis-free expressions for families of objective strain tensors, their rates, and conjugate stress tensors. Acta Mech. 229, 1061–1098 (2018)

    MathSciNet  MATH  Google Scholar 

  53. Korobeynikov, S.N.: Objective symmetrically physical strain tensors, conjugate stress tensors, and Hill’s linear isotropic hyperelastic material models. J. Elast. 136, 159–187 (2019)

    MathSciNet  MATH  Google Scholar 

  54. Lehmann, T., Guo, Z.H., Liang, H.: The conjugacy between Cauchy stress and logarithm of the left stretch tensor. Eur. J. Mech. A Solids 10(4), 395–404 (1991)

    MathSciNet  MATH  Google Scholar 

  55. Lin, R.C., Schomburg, U., Kletschkowski, T.: Analytical stress solutions of a closed deformation path with stretching and shearing using the hypoelastic formulations. Eur. J. Mech. A Solids 22, 443–461 (2003)

    MATH  Google Scholar 

  56. Lin, R.C.: Hypoelasticity-based analytical stress solutions in the simple shearing process. Z. Angew. Math. Mech. 83(3), 163–171 (2003)

    MathSciNet  MATH  Google Scholar 

  57. Liu, C.S., Hong, H.K.: Non-oscillation criteria for hypoelastic models under simple shear deformation. J. Elast. 57, 201–241 (1999)

    MathSciNet  MATH  Google Scholar 

  58. Luehr, C.P., Rubin, M.B.: The significance of projection operators in the spectral representatin of symmetric second order tensors. Comput. Methods Appl. Mech. Eng. 84, 243–246 (1990)

    MATH  Google Scholar 

  59. MARC Users Guide: Vol. A. Theory and Users Information. MSC.Software Corporation, Santa Ana (2015)

  60. Metzger, D.R., Dubey, R.N.: Objective tensor rates and frame indifferent constitutive models. Mech. Res. Commun. 13(2), 91–96 (1986)

    MathSciNet  MATH  Google Scholar 

  61. Neff, P., Ghiba, I.D., Lankeit, J.: The exponentiated Hencky-logarithmic strain energy. Part I: constitutive issues and rank-one convexity. J. Elast. 121, 143–234 (2015)

    MathSciNet  MATH  Google Scholar 

  62. Nguyen, N., Waas, A.M.: Nonlinear, finite deformation, finite element analysis. Z. Angew. Math. Phys. 67, 35 (2016)

    MathSciNet  MATH  Google Scholar 

  63. Ogden, R.W.: Non-linear Elastic Deformations. Ellis Horwood, Chichester (1984)

    MATH  Google Scholar 

  64. Perić, D.: On consistent stress rates in solid mechanics: computational implications. Int. J. Numer. Methods Eng. 33, 799–817 (1992)

    MATH  Google Scholar 

  65. Peyraut, F., Feng, Z.Q., He, Q.C., Labed, N.: Robust numerical analysis of homogeneous and non-homogeneous deformations. Appl. Numer. Math. 59, 1499–1514 (2009)

    MathSciNet  MATH  Google Scholar 

  66. Pinsky, P.M., Ortiz, M., Pister, K.S.: Numerical integration of rate constitutive equations in finite deformation analysis. Comput. Methods Appl. Mech. Eng. 40, 137–158 (1983)

    MATH  Google Scholar 

  67. Plešek, J., Kruisova, A.: Formulation, validation and numerical procedures for Hencky’s elasticity model. Compos. Struct. 84, 1141–1150 (2006)

    Google Scholar 

  68. Prager, W.: An elementary discussion of definitions of stress rates. Q. Appl. Math. 18, 403–407 (1960)

    MathSciNet  MATH  Google Scholar 

  69. Prager, W.: Einführung in die Kontinuumsmechanik. Birkhäuser, Basel, Stuttgart (1961) [Prager, W.: Introduction to Mechanics of Continua. Dover Publications, Mineola, N.Y. (2004)]

  70. Reinhardt, W.D., Dubey, R.N.: Eulerian strain-rate as a rate of logarithmic strain. Mech. Res. Commun. 22(2), 165–170 (1995)

    MATH  Google Scholar 

  71. Reinhardt, W.D., Dubey, R.N.: Coordinate-independent representation of spins in continuum mechanics. J. Elast. 42, 133–144 (1996)

    MathSciNet  MATH  Google Scholar 

  72. Reinhardt, W.D., Dubey, R.N.: Application of objective rates in mechanical modeling of solids. J. Appl. Mech. 63(3), 692–698 (1996)

    MathSciNet  MATH  Google Scholar 

  73. Simo, J.C., Hughes, T.J.R.: Computational Inelasticity. Springer, N.Y., Berlin, Heidelberg (1998)

    MATH  Google Scholar 

  74. Simo, J.C., Pister, K.S.: Remarks on rate constitutive equations for finite deformation problems: computational implications. Comput. Methods Appl. Mech. Eng. 46, 201–215 (1984)

    MATH  Google Scholar 

  75. Sowerby, R., Chu, E.: Rotations, stress rates and strain measures in homogeneous deformation processes. Int. J. Solids Struct. 20, 1037–1048 (1984)

    MATH  Google Scholar 

  76. Szabó, L., Balla, M.: Comparison of some stress rates. Int. J. Solids Struct. 25(3), 279–297 (1989)

    MathSciNet  Google Scholar 

  77. Thomas, T.Y.: On the structure of the stress–strain relations. PNAS Eng. 41, 716–720 (1955)

    MathSciNet  MATH  Google Scholar 

  78. Truesdell, C.: The simplest rate theory of pure elasticity. Commun. Pure Appl. Math. 8, 123–132 (1955)

    MathSciNet  MATH  Google Scholar 

  79. Truesdell, C.: Hypo-elasticity. J. Ration. Mech. Anal. 4, 83–133 (1955)

    MathSciNet  MATH  Google Scholar 

  80. Truesdell, C.: Hypo-elastic shear. J. Appl. Phys. 27, 441–447 (1956)

    MathSciNet  Google Scholar 

  81. Truesdell, C.: Remarks on hypo-elasticity. J. Res. Natl. Bur. Stand. B Math. Math. Phys. 67B, 141–143 (1963)

    MathSciNet  MATH  Google Scholar 

  82. Truesdell, C., Toupin, R.A.: The classical field theories. In: Flügge, S. (ed.) Encyclopedia of Physics, III(1), pp. 226–793. Springer, Berlin (1960)

    Google Scholar 

  83. Truesdell, C., Noll, W.: The non-linear field theories of mechanics. In: Flügge, S. (ed.) Encyclopedia of Physics, vol. III/3. Springer, Berlin (1965)

    Google Scholar 

  84. Trusov, P.V., Shveykin, A.I.: On motion decomposition and constitutive relations in geometrically nonlinear elastoviscoplasticity of crystallites. Physical Mesomechanics 20(4), 377–391 (2017)

    Google Scholar 

  85. Vorel, J., Bažant, Z.P., Gattu, M.: Elastic soft-core sandwich plates: critical loads and energy errors in commercial codes due to choice of objective stress rate. J. Appl. Mech. 80, 041034 (2013)

    Google Scholar 

  86. Vorel, J., Bažant, Z.P.: Review of energy conservation errors in finite element softwares caused by using energy-inconsistent objective stress rates. Adv. Eng. Softw. 72, 3–7 (2014)

    Google Scholar 

  87. Wriggers, P.: Nonlinear Finite Element Methods. Springer, Berlin (2008)

    MATH  Google Scholar 

  88. Xiao, H., Bruhns, O.T., Meyers, A.: Logarithmic strain, logarithmic spin and logarithmic rate. Acta Mech. 124, 89–105 (1997)

    MathSciNet  MATH  Google Scholar 

  89. Xiao, H., Bruhns, O.T., Meyers, A.: Hypo-elasticity model based upon the logarithmic stress rate. J. Elast. 47, 51–68 (1997)

    MathSciNet  MATH  Google Scholar 

  90. Xiao, H., Bruhns, O.T., Meyers, A.: On objective corotational rates and their defining spin tensors. Int. J. Solids Struct. 35(30), 4001–4014 (1998)

    MathSciNet  MATH  Google Scholar 

  91. Xiao, H., Bruhns, O.T., Meyers, A.: Strain rates and material spins. J. Elast. 52, 1–41 (1998)

    MathSciNet  MATH  Google Scholar 

  92. Xiao, H., Bruhns, O.T., Meyers, A.: Direct relationship between the Lagrangean logarithmic strain and the Lagrangean stretching and the Lagrangean Kirchhoff stress. Mech. Res. Commun. 25(1), 59–67 (1998)

    MathSciNet  MATH  Google Scholar 

  93. Xiao, H., Bruhns, O.T., Meyers, A.: Objective corotational rates and unified work-conjugacy relation between Eulerian and Lagrangean strain and stress measures. Arch. Mech. 50(6), 1015–1045 (1998)

    MathSciNet  MATH  Google Scholar 

  94. Xiao, H., Bruhns, O.T., Meyers, A.: A natural generalization of hypoelasticity and Eulerian rate type formulation of hyperelasticity. J. Elast. 56, 59–93 (1999)

    MathSciNet  MATH  Google Scholar 

  95. Xiao, H., Bruhns, O.T., Meyers, A.: Existence and uniqueness of the integrable-exactly hypoelastic equation \(\overset{\circ }{\varvec {\tau }}{}^{\ast }=\lambda (\text{ tr }\,\mathbf{D})\mathbf{I}+2\mu \mathbf{D}\) and its significance to finite inelasticity. Acta Mech. 138, 31–50 (1999)

    Google Scholar 

  96. Xiao, H., Bruhns, O.T., Meyers, A.: The choice of objective rates in finite elastoplasticity: general results on the uniqueness of the logarithmic rate. Proc. R. Soc. Lond. A 456, 1865–1882 (2000)

    MathSciNet  MATH  Google Scholar 

  97. Xiao, H., Chen, L.S.: Hencky’s elasticity model and linear stress-strain relations in isotropic finite hyperelasticity. Acta Mech. 157, 51–60 (2002)

    MATH  Google Scholar 

  98. Xiao, H., Bruhns, O.T., Meyers, A.: Objective stress rates, path-dependence properties and non-integrability problems. Acta Mech. 176, 135–151 (2005)

    MATH  Google Scholar 

  99. Xiao, H., Bruhns, O.T., Meyers, A.: Objective stress rates, cyclic deformation paths, and residual stress accumulation. ZAMM (Z. Angew. Math. Mech.) 86(11), 843–855 (2006)

    MathSciNet  MATH  Google Scholar 

  100. Xiao, H., Bruhns, O.T., Meyers, A.: Elastoplasticity beyond small deformations. Acta Mech. 182, 31–111 (2006)

    MATH  Google Scholar 

  101. Xiao, H., Bruhns, O.T., Meyers, A.: The integrability criterion in finite elastoplasticity and its constitutive implications. Acta Mech. 188, 227–244 (2007)

    MATH  Google Scholar 

  102. Zhu, Y., Kang, G., Kan, Q., Bruhns, O.T.: Logarithmic stress rate based constitutive model for cyclic loading in finite plasticity. Int. J. Plast. 54, 34–55 (2014)

    Google Scholar 

Download references

Acknowledgements

The supports from the Russian Foundation for Basic Research (Grant No. 18-08-00358) and Grant from Russian Federation Government No. P220-14.W03.31.0002 are gratefully acknowledged. The author thanks the anonymous reviewers whose comments and suggestions helped in revising the manuscript.

Author information

Authors and Affiliations

  1. Lavrentyev Institute of Hydrodynamics, Novosibirsk, Russia, 630090

    S. N. Korobeynikov

Authors
  1. S. N. Korobeynikov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. N. Korobeynikov.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Korobeynikov, S.N. Analysis of Hooke-like isotropic hypoelasticity models in view of applications in FE formulations. Arch Appl Mech 90, 313–338 (2020). https://doi.org/10.1007/s00419-019-01611-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-019-01611-3

Keywords

Mathematics Subject Classification

Search

Navigation