Elastic stress–strain analysis of an infinite cylindrical inclusion with eigenstrain

Abstract

The ensemble of interstitial atoms as C attracted to a dislocation is well established as “Cottrell cloud” phenomenon. The deposition of the interstitial atoms in octahedral or tetrahedral positions in a bcc lattice may yield a remarkable internal stress state according to their anisotropic misfit eigenstrains. The stress fields of the atoms may then lead to a significant change in the stress field, e.g., around a dislocation. In such a case, the interstitial atoms are situated near the dislocation core in cylindrical volume elements along the dislocation line. As the occupancy of the sites in each cylinder by interstitial atoms can be considered as constant, also the eigenstrain state tensor is constant in the cylinder. A complete set of analytical expressions for the eigenstress state inside and outside of the cylinder is presented. The resultant stress field is then given by superposition, which allows also the determination of the interaction energy between the Cottrell cloud and the dislocation.

1 Introduction

The problem of interaction between dislocations and interstitial atoms as carbon or hydrogen is of increasing interest with respect to a detailed understanding of Cottrell clouds [1], and their kinetics [2]. To calculate the main physical quantity, i.e., the interaction energy between the stress field of a distinct dislocation and of the interstitial atoms, one can use the superposition of the elastic fields generated by the dislocation and by eigenstrains due to deposition of the atoms in interstitial positions. Here the pioneering work by Cochardt et al. [3] can be mentioned, who explained in detail the interaction of a dislocation with a single interstitial atom in the bcc lattice; see also the later Krempasky et al. [4]. There exist three types of anisotropic octahedral positions for interstitial atoms being shorter in one of the three main crystallographic $\langle 100 \rangle$ directions in the bcc lattice. Thus, deposition of an atom in one of the octahedral position leads to a remarkably anisotropic eigenstrain in the region of the deposited atom, which can be considered as a spherical inclusion of the volume $\omega$ of a substitutional atom with a given eigenstrain tensor ${\varvec{\upvarepsilon }}_i^\omega$ depending on the type i, $i=1,2,3$, of the octahedral position. This problem of interaction was dealt with also by Friedel [5], Sect. 15.4., in recent papers by Cahn [6, 7], Mishin and Cahn [8] and Cai et al. [9]. In most studies, the anisotropic eigenstrain is replaced by a volume misfit, which is approved for interstitial atoms in fcc lattice or for substitutional atoms in any cubic lattice. In such a case, a rather simple analytical solution for the stress field inside and outside of the inclusion exists. Experimental work, see Wilde et al. [10], and atomistic simulations, Veiga et al. [11], Waseda et al. [12], has shown that an arrangement of interstitial atoms may exist leading to a significant overall stress field stemming from eigenstrains of atoms deposited in the three types of octahedral interstitial positions in the bcc lattice. Since the interaction energy of atoms with the stress field of a distinct dislocation depends significantly on the type of the octahedral interstitial positions, also the local site fraction of atoms in various types of octahedral interstitial positions is significantly different in thermodynamic equilibrium. As a result, the eigenstrains by deposition of interstitial atoms can significantly change the deformation field generated by the dislocation.

The treatment of the interaction with a cloud of interstitial atoms can be, e.g., performed for an edge dislocation, embedded in an infinite elastic lattice, with the dislocation line coinciding with the z-axis. Then the cloud of interstitial atoms around the dislocation is independent of z coordinate. The distribution of the interstitial atoms can then be described by a set of cylinders of infinite length along the z-axis having small cross sections and possessing in their whole volume constant site fractions of atoms in all three types of interstitial positions. Then the eigenstrain in each cylinder can be calculated and considered as given.

The goal of this paper is to check existing analytical relations for the stress state due to anisotropic eigenstrain state in an infinite cylinder embedded in infinite lattice and to provide a fully analytical solution for the stress field inside and outside of the cylinder. These results will provide the base for a thermodynamic kinetic model treating interaction of interstitial atoms with a moving dislocation.

2 Problem description

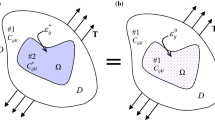
According to the recent atomistic simulations [11, 12], we assume a cylindrical inclusion as a representative volume element with the radius R in the x–y-plane normal to the z-axis, which may coincide with the dislocation line. We consider a homogeneous eigenstrain state with the in-plane components ${\varepsilon _x^{\text {eig}}}$, ${\varepsilon _y^{\text {eig}}}$, ${\varepsilon _{\textit{xy}}^{\text {eig}}}$ and the component ${\varepsilon _z^{\text {eig}}}$ in the z-direction acting in the inclusion and no eigenstrain in the surrounding matrix. For the sake of completeness, it should be mentioned that the role of eigenstrains, ${\varepsilon _{\textit{xz}}^{\text {eig}}}$, ${\varepsilon _{\textit{yz}}^{\text {eig}}}$ can be dealt with extra by a simple use of Hooke’s law. All the eigenstrain components may have different values.

The cylindrical inclusion is restricted with respect to its expansion in z-direction by the surrounding material. Therefore, we assume, as simplest representation of the constraint in z-direction, a plane strain state with zero total strain in z-direction $({\varepsilon _z \equiv 0})$. A recent atomistic study [8] has shown that the assumption of isotropic material is acceptable for cubic crystals. The isotropic material constants as Young’s modulus E and Poisson’s ratio $\nu$ are assumed to be spatially constant in both the inclusion and the surrounding matrix; see Fig. 1.

Fig. 1

Sketch of setting

From pioneering works by Eshelby [13, 14], it follows that a homogeneous eigenstrain in an ellipsoidal inclusion induces a homogeneous stress field in the inclusion. If one approximates the cylinder by a needle-like spheroid with R for axes a and b and an infinite length of axis c, one may utilize the solutions with normal and shear eigenstrains in Mura’s book [15], Chpt. 2 there, or the results worked out in Fischer and Böhm [16]. However, it must be kept in mind that the interstitials interact due to their exterior stress field with the adjacent interstitials and the dislocations. Therefore, the exterior stress field is of immediate relevance. The according mathematical framework in context with the Eshelby concept is rather extensive and somewhat demanding; see also Chpt. 2 in Mura [15] and the treatment by Li et al. [17, 18] for inclusions embedded in a finite domain. Our intention to provide easy-to-handle relations for the stress field of a cloud forced us to look for a straightforward solution of our particular problem. Since we have also to consider a shear eigenstrain in the cylinder, the analytical concept by Markenscoff and Dundurs [19], dealing also with a shear eigenstrain in an annulus and the corresponding comment by Shodja and Korshidi [20] concerning the disappearance of the singularities of stresses, motivated us to follow an exact analytical solution.

Since we assume an infinite domain, we expect rather easy-to-handle equations for the stress and deformation state utilizing the Airy function in polar coordinates. Here we refer to the pioneering work by Michell [21] who provided a set of solutions of the biharmonic equation in polar coordinates already in 1899; see also the book by Mal and Singh [22], Sect. 7.5, the book by Barber [23], Sect. 8.4, and the book by Bower [24], Sect. 5.2.3. Such an approach is in accordance with that applied in classical works on circular holes in disks (plates), e.g., by Kirsch [25], more than a century ago, by Bickley [26] and Sen [27].

3 Theory and solution concept

We introduce cylindrical coordinates $r,\vartheta ,z$ and the according displacements u, v, w. The kinematic relations between the total strain components $\varepsilon _r ,\varepsilon _\vartheta , \varepsilon _z$ and the shear angles $\gamma _{r\vartheta }, \gamma _{rz}, \gamma _{\vartheta z}$ in terms of u, v, w and the equilibrium equations can be taken from any continuum mechanics textbook. Hooke’s law links the stress components $\sigma _r, \sigma _\vartheta , \sigma _z, \sigma _{r\vartheta }, \sigma _{rz}, \sigma _{\vartheta z}$ to the elastic strain contributions. Furthermore, we use the following abbreviations

$$\begin{aligned} \cos \vartheta =c, \quad \sin \vartheta =s, \quad \cos 2\vartheta =c_2 , \quad \sin 2\vartheta =s_2 . \end{aligned}$$

(1)

3.1 Solution for the area eigenstrain ${\varepsilon ^{\text {eig}}}$

Although the solution for this problem is known, for the sake of completeness we start the stress calculation with an in-plane (area) eigenstrain ${\varepsilon ^{\text {eig}}}$ together with an eigenstrain ${\varepsilon _z^{\text {eig}}}$ in z-direction keeping in mind that $\varepsilon _z \equiv 0$, which yields

$$\begin{aligned} \sigma _z =-E{\varepsilon _z^{\text {eig}}} +\nu ({\sigma _r +\sigma _\vartheta }). \end{aligned}$$

(2)

Expressing the equilibrium equation only in u(r), since $v=0$ and $w=0$, one finds after some analysis

$$\begin{aligned} u=Ar+B/r. \end{aligned}$$

(3)

The integration constants A, B can be calculated from the two contact conditions

$$\begin{aligned} r=R: u |_\mathrm{i} = u |_\mathrm{o},\quad r=R: \sigma _r|_\mathrm{i} = \sigma _r |_\mathrm{o}. \end{aligned}$$

(4)

The subscripts “i” and “o” stand for inside and outside of the inclusion, resp. Finally, we have the following solution for the nonzero stress components as

$$\begin{aligned} 0\le & {} r\le R \qquad \sigma _r=\sigma _\vartheta =-\frac{E \left( {{\varepsilon ^{\text {eig}}}+\nu \varepsilon _z^{\text {eig}}}\right) }{2({1-\nu ^{2}})},\quad \sigma _z=-\frac{E\left( {\nu \varepsilon ^{\text {eig}}+\varepsilon _z^{\text {eig}}}\right) }{({1-\nu ^{2}})}, \end{aligned}$$

(5.1)

$$\begin{aligned} r> & {} R \qquad \qquad \sigma _r=\frac{-E \left( {\varepsilon ^{\text {eig}}+\nu \varepsilon _z^{\text {eig}}}\right) }{2({1-\nu ^{2}})}\frac{R^{2}}{r^{2}}, \quad \sigma _\vartheta =-\sigma _r,\quad \sigma _z=-E\varepsilon _z^{\text {eig}} . \end{aligned}$$

(5.2)

Note that only a deviatoric in-plane stress state exists for $r\ge R$ and $\varepsilon _z^{\text {eig}} =0$. This fact is denoted as “Bitter–Crum” theorem; for details, see Fratzl and Penrose [28].

3.2 Solution concept for ${\varepsilon _x^{\text {eig}}} \ne 0$ and $\varepsilon _y^{\text {eig}} \ne 0$

First we calculate the stress state for $\varepsilon _x^{\text {eig}} \ne 0$ only and transform the according eigenstrain tensor in polar coordinates as

$$\begin{aligned} {\varvec{\upvarepsilon }}_x^{\text {eig}} =\frac{\varepsilon _x^{\text {eig}}}{2} ({\mathbf{I}+\mathbf{P}}), \quad \mathbf{P}=\left[ {\begin{array}{cc} c_2 &{} -s_2 \\ -s_2 &{} -c_2 \\ \end{array}} \right] , \end{aligned}$$

(6)

with I as unit tensor and the abbreviations by Eq. (1). The first part with I of the r.h.s. of Eq. (6) represents a homogeneous eigenstrain with the solutions of Sect. 3.1 for $\varepsilon ^{\text {eig}}={\varepsilon _x^{\text {eig}}}/2$ and $\varepsilon _z^{\text {eig}} =0$. The second part with $\mathbf{P}$ represents a tensor varying with the angle $2\vartheta$. Here we select a proper biharmonic Airy stress function $\phi (r,\vartheta )$, inspired by the solution of the “inclusion problem,” by Mal and Singh [22], Example 7.5–8, as

$$\begin{aligned} {\phi }= ({Ar^{2}+Cr^{4}}) c_2 \quad \hbox {for} \quad 0\le r\le R, \quad {\phi }= ({B/r^{2}+D})c_2 \quad \hbox {for} \quad r\ge R. \end{aligned}$$

(7)

We find the nonzero stress components by the following operation, see [21], Sect. 5.2.3 there,

$$\begin{aligned} \sigma _r= & {} 1/r {\partial \phi }/{\partial r}+1/{r^{2}}{\partial ^{2}\phi }/{\partial \vartheta ^{2}}, \nonumber \\ \sigma _\vartheta= & {} {\partial ^{2}\phi }/{\partial r^{2}},\quad \sigma _{r\vartheta } ={-\partial }/{\partial r} ({1/r\;{\partial \phi }/{\partial \vartheta }}), \end{aligned}$$

(8)

yielding

$$\begin{aligned} 0\le r\le R \qquad \sigma _r= & {} -2Ac_2 ,\quad \sigma _\vartheta = \left( {2A+12Cr^{2}}\right) c_2 , \nonumber \\ \sigma _{r\vartheta }= & {} \left( {2A+6Cr^{2}}\right) s_2; \end{aligned}$$

(9.1)

$$\begin{aligned} r\ge R \qquad \qquad \sigma _r= & {} \left( {-{6B}/{r^{4}}-{4D}/{r^{2}}}\right) c_2, \quad \sigma _\vartheta = \left( {{6B}/{r^{4}}}\right) c_2,\nonumber \\ \sigma _{r\vartheta }= & {} \left( {{-6B}/{r^{4}}-{2D}/{r^{2}}}\right) s_2 . \end{aligned}$$

(9.2)

The integration constants A, B, C, D can be calculated from four contact conditions as

$$\begin{aligned} r=R: \qquad u |_\mathrm{i} = u |_\mathrm{o} ,\; \vartheta |_\mathrm{i} = \vartheta |_\mathrm{o} ,\quad \; {\sigma _r} |_\mathrm{i} = {\sigma _r } |_\mathrm{o} ,\quad \; {\sigma _{r\vartheta }} |_\mathrm{i} = {\sigma _{r\vartheta }} |_\mathrm{o} . \end{aligned}$$

(10)

According to Eshelby [13], the stress state must be homogeneous in the inclusion with the consequence that C must become zero. Furthermore, the contact conditions enforce the calculation of $u (r, \vartheta )$ and $v (r,\vartheta )$ via the integration of the kinematic equations for $\varepsilon _r$ and $\varepsilon _\vartheta$, combined with Hooke’s law (including $\varepsilon _z =0$ yielding $\sigma _z =\nu ({\sigma _r +\sigma _\vartheta }))$, as

$$\begin{aligned} E\varepsilon _r= & {} {E\partial u}/{\partial r}=\sigma _r -\nu \sigma _\vartheta -\nu ^{2} ({\sigma _r +\sigma _\vartheta }) +E\varepsilon _x^{\text {eig}} {c_2 }/2, \end{aligned}$$

(11.1)

$$\begin{aligned} E\varepsilon _\vartheta= & {} E{ ({{\partial v}/{\partial \vartheta }+u})}/r = ( {-\nu \sigma _r +\sigma _\vartheta -\nu ^{2} ({\sigma _r +\sigma _\vartheta })}) - E\varepsilon _x^{\text {eig}} {c_2 }/2. \end{aligned}$$

(11.2)

The integration of Eqs. (11) involves two functions, namely $f_u (\vartheta )$ in $u ({r,\vartheta })$ and $g_v (r)$ in $v ({r,\vartheta })$. These two functions can be found by employing $E\varepsilon _{r\vartheta }$ with Eu and Ev from above as

$$\begin{aligned} E\varepsilon _{r\vartheta } = E{\left( {\frac{1}{r}\frac{\partial u}{\partial \vartheta }+\frac{\partial v}{\partial r}-\frac{v}{r}}\right) }\Big /2 = ({1+\nu })\sigma _{r\vartheta } -E\varepsilon _x^{\text {eig}} {s_2 }/2. \end{aligned}$$

(12)

Inserting now u together with $f_u (\vartheta )$ and v together with $g_v (r)$ in Eq. (12) shows that both $f_u (\vartheta )$ and $g_r (r)$ can be interpreted as “rigid” body motions and, therefore, can be skipped.

To summarize, the calculation of the coefficients $A,\, B,\, C,\, D$ and, consequently, the stresses makes a lot of algebraic operations necessary, which were left to mathematica (https://www.wolfram.com/mathematica/) but result indeed in $C=0$, see above, and rather simple equations for the stresses. Using the abbreviation $\tilde{E}={E\varepsilon _x^{\text {eig}}}/ {({8 ({1-\nu ^{2}})})}$ and denoting the stress terms corresponding to P in Eq. (6) with a subscript “P” yield

$$\begin{aligned} 0\le r\le R: \qquad \sigma _r^{\mathbf{P}}= & {} -\tilde{E}c_2 ,\quad \sigma _\vartheta ^{\mathbf{P}} =\tilde{E}c_2 ,\nonumber \\ \sigma _{r\vartheta }^{\mathbf{P}}= & {} \tilde{E}s_2 ,\quad \sigma _z^{\mathbf{P}} =0; \end{aligned}$$

(13.1)

$$\begin{aligned} r\ge R:\qquad \qquad \sigma _r^{\mathbf{P}}= & {} -\tilde{E}\left( {{4R^{2}}/{r^{2}}-{3R^{4}}/{r^{4}}} \right) c_2 , \quad \sigma _\vartheta ^{\mathbf{P}} =-\tilde{E}\left( {{3R^{4}}/{r^{4}}} \right) c_2 ,\nonumber \\ \sigma _{r\vartheta }^{\mathbf{P}}= & {} \tilde{E}\left( {{3R^{4}}/{r^{4}}-{2R^{2}}/{r^{2}}} \right) s_2 , \quad \sigma _z^{\mathbf{P}} =-4\nu \tilde{E}{R^{2}}/{r^{2}}. \end{aligned}$$

(13.2)

Let us check now the stress state inside the inclusion with respect to the x–y system. This means that stresses $\sigma _r^{\mathbf{P}}, \sigma _\vartheta ^{\mathbf{P}}, \sigma _{r\vartheta }^{\mathbf{P}}$ must be transformed into the x–y system. The components $\sigma _x^{\mathbf{P}}, \sigma _y^{\mathbf{P}}, \sigma _{\textit{xy}}^{\mathbf{P}}$ follow after some algebra

$$\begin{aligned} 0\le r\le R:\sigma _x^{\mathbf{P}} =- \tilde{E},\quad \sigma _y^{\mathbf{P}} = \tilde{E}, \quad \sigma _{\textit{xy}}^{\mathbf{P}} =0. \end{aligned}$$

(13.3)

This result is in accordance with the Eshelby [13] theorem, stating that the stress state must be homogeneous in the inclusion for a homogeneous eigenstrain.

The problem of calculating the stress state to an eigenstrain field $\varepsilon _y^{\text {eig}}$ only is easily solved by rotation of the total configuration by $\pi /2$ in relation to the eigenstrain field $\varepsilon _x^{\text {eig}}$, yielding, in analogy to Eq. (6),

$$\begin{aligned} {\varvec{\upvarepsilon }}_y^{\text {eig}} = \frac{\varepsilon _y^{\text {eig}} }{2} ({\mathbf{I}-\mathbf{P}}). \end{aligned}$$

(14)

The superposition of ${\varvec{\upvarepsilon }}_x^{\text {eig}}$ and ${\varvec{\upvarepsilon }}_y^{\text {eig}}$ yields for the homogeneous eigenstrain $\varepsilon ^{\text {eig}}={({\varepsilon _x^{\text {eig}} + \varepsilon _y^{\text {eig}}})}/2$ and for the contribution due to P the eigenstrain difference $\Delta \varepsilon ^{\text {eig}}=\varepsilon _x^{\text {eig}} -\varepsilon _y^{\text {eig}}$ and with the abbreviations $\tilde{E}^{I}={E ( {\varepsilon ^{\text {eig}}+\nu \varepsilon _z^{\text {eig}}})}/{8 ({1-\nu ^{2}} )} \quad \tilde{E}_\varepsilon ^{\mathbf{P}} ={E\Delta \varepsilon ^{\text {eig}}}/{8 ({1-\nu ^{2}})}$,

$$\begin{aligned} 0\le r\le R:\quad \sigma _r= & {} -4\tilde{E}^{\mathbf{I}}- \tilde{E}_\varepsilon ^{\mathbf{P}} c_2 ,\quad \sigma _\vartheta =-4\tilde{E}^{\mathbf{I}}+\tilde{E}_\varepsilon ^{\mathbf{P}} c_2,\nonumber \\ \sigma _{r\vartheta }= & {} \tilde{E}_\varepsilon ^{\mathbf{P}} s_2 ,\quad \sigma _z =-E\frac{\left( {\nu \varepsilon ^{\text {eig}}+\varepsilon _z^{\text {eig}} } \right) }{\left( {1-\nu ^{2}} \right) }; \end{aligned}$$

(15.1)

$$\begin{aligned} r\ge R:\quad \sigma _r= & {} -4\tilde{E}^{\mathbf{I}}{R^{2}}/{r^{2}}-\tilde{E}_\varepsilon ^{\mathbf{P}} \left( {{4R^{2}}/{r^{2}}-{3R^{4}}/{r^{4}}} \right) c_2 , \quad \sigma _\vartheta =4\tilde{E}^{\mathbf{I}}{R^{2}}/{r^{2}}-3\tilde{E}_\varepsilon ^{\mathbf{P}} \left( {{R^{4}}/{r^{4}}} \right) c_2 ,\nonumber \\ \sigma _{r\vartheta }= & {} \tilde{E}_\varepsilon ^{\mathbf{P}} \left( {{3R^{4}}/{r^{4}}-{2R^{2}}/{r^{2}}} \right) s_2 , \quad \sigma _z =-4\nu \tilde{E}_\varepsilon ^{\mathbf{P}} \left( {{R^{2}}/{r^{2}}} \right) c_2. \end{aligned}$$

(15.2)

Fig. 2

Eigenstrain $\varepsilon _x^{\text {eig}}, E\varepsilon _x^{\text {eig}} = 8 ({1-\nu ^{2}})$; (a) stress state $\sigma _x, \sigma _y$ along x-axis, (b) shear stress $\sigma _{r\vartheta }$ along r at $\vartheta =45^{\circ }$

3.3 Solution concept for $\varepsilon _{\textit{xy}}^{\text {eig}}$

We complete the results by calculating the stress state according to the shear eigenstrain $\varepsilon _{\textit{xy}}^{\text {eig}}$ (or the shear angle $\gamma _{\textit{xy}}^{\text {eig}} =2\varepsilon _{\textit{xy}}^{\text {eig}}$) only and consider a coordinate system $x'{-}y'{-}z$ rotated by an angle of $\pi {/}4$ in relation to the master x–y–z coordinate system with the eigenstrains $\varepsilon _{{x}'}^{\text {eig}} =\varepsilon _{\textit{xy}}^{\text {eig}}$ and $\varepsilon _{{y}'}^{\text {eig}} =-\varepsilon _{\textit{xy}}^{\text {eig}}$. Then we can apply the solution concept for $\varepsilon _x^{\text {eig}}$ and $\varepsilon _y^{\text {eig}}$, however, in the $x'{-}y'{-}z$ coordinate system with $\varepsilon ^{\text {eig}}=0$, $\Delta \varepsilon ^{\text {eig}} = \gamma _{\textit{xy}}^{\text {eig}}$ and $\varepsilon _z^{\text {eig}} =0$. Using the abbreviation $\tilde{E}_\gamma ^{\mathbf{P}} ={E\varepsilon _{\textit{xy}}^{\text {eig}}}/ {4 ({1-\nu ^{2}})}$ and noting that ${\vartheta }' = \vartheta -\pi /4$, the relations in the master coordinate system read as

$$\begin{aligned} 0\le r\le R \qquad \sigma _r= & {} -\tilde{E}_\gamma ^{\mathbf{P}} s_2 ,\quad \sigma _\vartheta =\tilde{E}_\gamma ^{\mathbf{P}} s_2 ,\nonumber \\ \sigma _{r\vartheta }= & {} -\tilde{E}_\gamma ^{\mathbf{P}} c_2 ,\quad \sigma _z =0; \end{aligned}$$

(15.1)

$$\begin{aligned} R<r \quad \qquad \sigma _r= & {} -\tilde{E}_\gamma ^{\mathbf{P}} \left( {{4R^{2}}/{r^{2}}-{3R^{4}}/{r^{4}}}\right) s_2 ,\quad \sigma _\vartheta =-3\tilde{E}_\gamma ^{\mathbf{P}} \left( {{R^{4}}/{r^{4}}}\right) s_2 ,\nonumber \\ \sigma _{r\vartheta }= & {} -\tilde{E}_\gamma ^{\mathbf{P}} \left( {{3R^{4}}/{r^{4}}-{2R^{2}}/{r^{2}}}\right) c_2 ,\quad \sigma _z =-4v\tilde{E}_\gamma ^{\mathbf{P}} \left( R^{2}/r^{2}\right) s_2 . \end{aligned}$$

(15.2)

4 Representative examples and discussion

We demonstrate two examples in a dimension-free form. Assuming $E \varepsilon _x^{\text {eig}} =8 ({1-\nu ^{2}})$, we demonstrate $\sigma _x$ and $\sigma _y$ along the x-axis in Fig. 2a and $\sigma _{r\vartheta }$ along the radius r for $\vartheta =45^{\circ }$ in Fig. 2b. Assuming $E\varepsilon _{\textit{xy}}^{\text {eig}} =4 ({1-\nu ^{2}})$ we demonstrate $\sigma _r$ and $\sigma _\vartheta$ along the radius r for $\vartheta =45^{\circ }$ in Fig. 3a and $\sigma _{\textit{xy}}$ along the x-axis in Fig. 3b. All curves are checked by a finite element study with ABAQUS (http://www.3ds.com/de/produkte-und-services/simulia/produkte/abaqus/).

Fig. 3

Eigenstrain $\varepsilon _{\textit{xy}}^{\text {eig}}, E\varepsilon _{\textit{xy}}^{\text {eig}} = 4 ({1-\nu ^{2}})$; (a) normal stresses $\sigma _r, \sigma _\vartheta$ along r at $\vartheta =45^{\circ }$, (b) shear stress $\sigma _{\textit{xy}}$ along x-axis

It is interesting to note that the stresses outside of the inclusion, dominated by a $({R/r})^{2}$ term, decay to nearly zero over a remarkably long distance of approximately 10R.

For practical application of the results, we present for each kind of eigenstrain (i.e., $\varepsilon _x^{\text {eig}}, \varepsilon _y^{\text {eig}}, \varepsilon _{\textit{xy}}^{\text {eig}}, \varepsilon _z^{\text {eig}}$) the stress fields in a Cartesian coordinate system in “Appendix.”

Appendix: Eigenstress fields in a Cartesian coordinate system

With the abbreviations in Eq. (1), we have

$$\begin{aligned} \sigma _x= & {} c^{2}\sigma _r +s^{2}\sigma _\vartheta -s_2 \sigma _{r\vartheta } , \quad \sigma _y =s^{2}\sigma _r +c^{2}\sigma _\vartheta -s_2 \sigma _{r\vartheta }\nonumber \\ \end{aligned}$$

(A.1)

$$\begin{aligned} \sigma _{\textit{xy}}= & {} sc ({\sigma _r -\sigma _\vartheta }) +c_2 \sigma _{r\vartheta } , \quad \sigma _z =-E\varepsilon _z^{\text {eig}} +\nu ({\sigma _r +\sigma _\vartheta }), \end{aligned}$$

(A.2)

with $c=x/r$, $s=y/r$ and $r^{2}=x^{2}+y^{2}$ and $\bar{{x}}=x/R$, $\bar{{y}}=y/R$ and $\bar{{r}}=r/R$.

Expressing the relations for the individual cases of eigenstrain yields:

$$\begin{aligned} \varepsilon _x^{\text {eig}} \ne 0 \end{aligned}$$

Inside

$$\begin{aligned} \sigma _x =-\frac{3E\varepsilon _x^{\text {eig}} }{8\left( {1-\nu ^{2}}\right) }, \quad \sigma _y =-\frac{E\varepsilon _x^{\text {eig}} }{8\left( {1-\nu ^{2}}\right) }, \quad \sigma _z =-\frac{Ev\varepsilon _x^{\text {eig}} }{2\left( {1-\nu ^{2}}\right) }. \end{aligned}$$

Outside

$$\begin{aligned} \sigma _x= & {} -\frac{E\varepsilon _x^{\text {eig}} \left[ {2\bar{{r}}^{4}\left( {\bar{{x}}^{2}-\bar{{y}}^{2}}\right) + 4\bar{{r}}^{2}\bar{{x}}^{2}\left( {\bar{{x}}^{2}-3\bar{{y}}^{2}}\right) -3 \left( {\bar{{x}}^{4}-6\bar{{x}}^{2}\bar{{y}}^{2} +\bar{{y}}^{4}}\right) }\right] }{8\left( {1-\nu ^{2}}\right) \bar{{r}}^{8}},\\ \sigma _y= & {} \frac{E\varepsilon _x^{\text {eig}} \left[ {2\bar{{r}}^{4} \left( {\bar{{x}}^{2}-\bar{{y}}^{2}}\right) -4\bar{{r}}^{2}\bar{{y}}^{2} \left( {3\bar{{x}}^{2}-\bar{{y}}^{2}}\right) -3 \left( {\bar{{x}}^{4}- 6\bar{{x}}^{2}\bar{{y}}^{2}+\bar{{y}}^{4}}\right) }\right] }{8\left( {1-\nu ^{2}}\right) \bar{{r}}^{8}},\\ \sigma _{\textit{xy}}= & {} -\frac{E\varepsilon _x^{\text {eig}} \bar{{x}}\bar{{y}} \left[ {\bar{{r}}^{4}+\left( {2\bar{{r}}^{2}-3}\right) \left( {\bar{{x}}^{2}-\bar{{y}}^{2}}\right) }\right] }{2\left( {1-\nu ^{2}}\right) \bar{{r}}^{8}}, \quad \sigma _z =-\frac{Ev\varepsilon _x^{\text {eig}} \left( {\bar{{x}}^{2}-\bar{{y}}^{2}}\right) }{2\left( {1-\nu ^{2}}\right) \bar{{r}}^{4}}. \end{aligned}$$

$$\begin{aligned} \varepsilon _y^{\text {eig}}\ne & {} 0 \end{aligned}$$

Inside

$$\begin{aligned} \sigma _x =-\frac{E\varepsilon _y^{\text {eig}} }{8\left( {1-\nu ^{2}}\right) }, \quad \sigma _y =-\frac{3E\varepsilon _y^{\text {eig}} }{8\left( {1-\nu ^{2}}\right) }, \quad \sigma _z =-\frac{Ev\varepsilon _y^{\text {eig}} }{2\left( {1-\nu ^{2}}\right) }. \end{aligned}$$

Outside

$$\begin{aligned} \sigma _x= & {} -\frac{E\varepsilon _y^{\text {eig}} \left[ {2\bar{{r}}^{4}\left( {\bar{{x}}^{2}-\bar{{y}}^{2}}\right) - 4\bar{{r}}^{2}\bar{{x}}^{2} \left( {\bar{{x}}^{2}-3\bar{{y}}^{2}}\right) + 3 \left( {\bar{{x}}^{4}-6\bar{{x}}^{2}\bar{{y}}^{2}+\bar{{y}}^{4}}\right) } \right] }{8\left( {1-\nu ^{2}}\right) \bar{{r}}^{8}},\\ \sigma _y= & {} \frac{E\varepsilon _y^{\text {eig}} \left[ {2\bar{{r}}^{4}\left( {\bar{{x}}^{2}-\bar{{y}}^{2}}\right) + 4\bar{{r}}^{2}\bar{{y}}^{2}\left( {3\bar{{x}}^{2}-\bar{{y}}^{2}}\right) +3 \left( {\bar{{x}}^{4}-6\bar{{x}}^{2}\bar{{y}}^{2}+\bar{{y}}^{4}}\right) } \right] }{8\left( {1-\nu ^{2}}\right) \bar{{r}}^{8}},\\ \sigma _{\textit{xy}}= & {} -\frac{E\varepsilon _y^{\text {eig}} \bar{{x}}\bar{{y}} \left[ {\bar{{r}}^{4}-\left( {2\bar{{r}}^{2}-3}\right) \left( {\bar{{x}}^{2}- \bar{{y}}^{2}}\right) }\right] }{2\left( {1-\nu ^{2}}\right) \bar{{r}}^{8}}, \quad \sigma _z =-\frac{Ev\varepsilon _y^{\text {eig}} \left( {\bar{{x}}^{2}-\bar{{y}}^{2}}\right) }{2\left( {1-\nu ^{2}}\right) \bar{{r}}^{4}}. \end{aligned}$$

$$\begin{aligned} \varepsilon _{\textit{xy}}^{\text {eig}}\ne & {} 0 \end{aligned}$$

Inside

$$\begin{aligned} \sigma _x =\sigma _y =0,\quad \sigma _{\textit{xy}} =-\frac{E\varepsilon _{\textit{xy}}^{\text {eig}} }{4\left( {1-\nu ^{2}}\right) }, \end{aligned}$$

Outside

$$\begin{aligned} \sigma _x= & {} -\frac{E\varepsilon _{\textit{xy}}^{\text {eig}} \bar{{x}}\bar{{y}} \left[ {\bar{{r}}^{2} \left( {3\bar{{x}}^{2}-\bar{{y}}^{2}}\right) - 3\left( {\bar{{x}}^{2}-\bar{{y}}^{2}}\right) }\right] }{\left( {1-\nu ^{2}}\right) \bar{{r}}^{8}}, \quad \sigma _y =\frac{E\varepsilon _{\textit{xy}}^{\text {eig}} \bar{{x}}\bar{{y}} \left[ {\bar{{r}}^{2} \left( {\bar{{x}}^{2}-3\bar{{y}}^{2}}\right) -3\left( {\bar{{x}}^{2}-\bar{{y}}^{2}}\right) }\right] }{\left( {1-\nu ^{2}}\right) \bar{{r}}^{8}},\\ \sigma _{\textit{xy}}= & {} \frac{E\varepsilon _{\textit{xy}}^{\text {eig}} \left( {2\bar{{r}}^{2}-3}\right) \left( {\bar{{x}}^{4}-6\bar{{x}}^{2}\bar{{y}}^{2}+\bar{{y}}^{4}}\right) }{4\left( {1-\nu ^{2}}\right) \bar{{r}}^{8}}, \quad \sigma _z =-\frac{2Ev\varepsilon _{\textit{xy}}^{\text {eig}} \left( {\bar{{x}}\bar{{y}}}\right) }{\left( {1-\nu ^{2}}\right) \bar{{r}}^{4}}. \end{aligned}$$

$$\begin{aligned} \varepsilon _z^{\text {eig}}\ne & {} 0 \end{aligned}$$

Inside

$$\begin{aligned} \sigma _x =-\frac{E\nu \varepsilon _z^{\text {eig}} }{2\left( {1-\nu ^{2}}\right) }, \quad \sigma _y =-\frac{E\nu \varepsilon _z^{\text {eig}} }{2\left( {1-\nu ^{2}}\right) }, \quad \sigma _z =-\frac{E\varepsilon _z^{\text {eig}} }{\left( {1-\nu ^{2}}\right) }. \end{aligned}$$

Outside

$$\begin{aligned} \sigma _x= & {} -\frac{E\nu \varepsilon _z^{\text {eig}} \left( {\bar{{x}}^{2}-\bar{{y}}^{2}}\right) }{2\left( {1-\nu ^{2}}\right) \bar{{r}}^{4}}, \quad \sigma _y =\frac{E\nu \varepsilon _z^{\text {eig}} \left( {\bar{{x}}^{2}-\bar{{y}}^{2}}\right) }{2\left( {1-\nu ^{2}}\right) \bar{{r}}^{4}},\\ \sigma _{\textit{xy}}= & {} -\frac{E\nu \varepsilon _z^{\text {eig}} \bar{{x}}\bar{{y}}}{\left( {1-\nu ^{2}}\right) \bar{{r}}^{4}},\quad \sigma _z =0. \end{aligned}$$