Skip to main content
SpringerLink
Log in

Prediction of fatigue crack growth retardation using a cyclic cohesive zone model

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

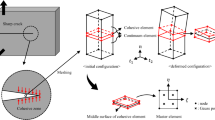
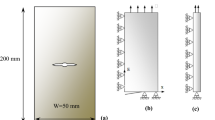
Abstract

Cohesive zone modeling of fatigue crack growth retardation in aerospace titanium alloy Ti–6Al–4V subjected to a single overload during constant amplitude is presented in this work. The cyclic softening behavior of the bulk material is simulated according to the Ohno–Wang’s cyclic plasticity theory. The fracture process zone is represented by an irreversible cohesive law which governs the material separation of fatigue crack. The material degradation mechanism is described by the gradual reduction of the unloading cohesive stiffness after each loading cycle. The fatigue crack growth behaviors are examined using the proposed cohesive model under both constant and variable amplitude loadings. The computational results are verified according to the experimental data, which confirm that the present model can be applied to predict the transient retardation in fatigue crack growth rate of the Ti–6Al–4V alloy accurately.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Paris, P.C., Gomez, M.P., Anderson, W.P.: A rational analytic theory of fatigue. Trend Eng. 13, 9–14 (1961)

    Google Scholar 

  2. Kondo, Y.: Fatigue under variable amplitude loading. In: Milne, I., Ritchie, R.O., Karihaloo, B. (eds.) Comprehensive Structural Integrity, pp. 263–279. Pergamon, Oxford (2003)

    Google Scholar 

  3. Newman, J.C.: Modeling of fatigue crack growth: numerical models. In: Milne, I., Ritchie, R.O., Karihaloo, B. (eds.) Comprehensive Structural Integrity, pp. 209–220. Pergamon, Oxford (2003)

    Chapter  Google Scholar 

  4. Dugdale, D.S.: Yielding of steel sheets containing slits. J. Mech. Phys. Solids 8, 100–104 (1960)

    Article  Google Scholar 

  5. Tvergaard, V., Hutchinson, J.W.: The relation between crack growth resistance and fracture process parameters in elastic–plastic solids. J. Mech. Phys. Solids 40, 1377–1397 (1992)

    Article  MATH  Google Scholar 

  6. Yuan, H., Lin, G., Cornec, A.: Verification of a cohesive zone model for ductile fracture. J. Eng. Mater. Technol. 118, 192–200 (1996)

    Article  Google Scholar 

  7. Roy, Y.A., Dodds Jr., R.H.: Simulation of ductile crack growth in thin aluminum panels using 3-D surface cohesive elements. Int. J. Fract. 110, 21–45 (2001)

    Article  Google Scholar 

  8. Scheider, I., Brocks, W.: Simulation of cup-cone fracture using the cohesive model. Eng. Fract. Mech. 70, 1943–1961 (2003)

    Article  Google Scholar 

  9. Wang, G., Li, S.F.: A penny-shaped cohesive crack model for material damage. Theor. Appl. Fract. Mech. 42, 303–316 (2004)

    Article  Google Scholar 

  10. Xu, Y., Yuan, H.: Applications of normal stress dominated cohesive zone models for mixed-mode crack simulation based on extended finite element methods. Eng. Fract. Mech. 78, 544–558 (2011)

    Article  Google Scholar 

  11. Rashid, F.Md, Banerjee, A.: Implementation and validation of a triaxiality dependent cohesive model: experiments and simulations. Int. J. Fract. 181, 227–239 (2013)

    Article  Google Scholar 

  12. Schwalbe, K.-H., Scheider, I., Cornec, A.: Guidelines for Applying Cohesive Models to the Damage Behaviour of Engineering Materials and Structures. Springer, Berlin (2012)

    Google Scholar 

  13. Park, K., Paulino, G.H.: Cohesive zone models: a critical review of traction–separation relationships across fracture surfaces. Appl. Mech. Rev. 64, 060802 (2013)

    Article  Google Scholar 

  14. Kuna, M., Roth, S.: General remarks on cyclic cohesive zone models. Int. J. Fract. 196, 147–167 (2015)

    Article  Google Scholar 

  15. de Andres, A., Perez, J.L., Ortiz, M.: Elastoplastic finite element analysis of three-dimensional fatigue crack growth in aluminum shafts subjected to axial loading. Int. J. Solids Struct. 36, 2231–2258 (1999)

    Article  MATH  Google Scholar 

  16. Serebrinsky, S., Ortiz, M.: A hysteretic cohesive-law model of fatigue-crack nucleation. Scr. Mater. 53, 1193–1196 (2005)

    Article  Google Scholar 

  17. Roth, S., Hütter, G., Kuna, M.: Simulation of fatigue crack growth with a cyclic cohesive zone model. Int. J. Fract. 188, 23–45 (2014)

    Article  Google Scholar 

  18. Ural, A., Krishnan, V.R., Papoulia, K.D.: A cohesive zone model for fatigue crack growth allowing for crack retardation. Int. J. Solids Struct. 46, 2453–2462 (2009)

    Article  MATH  Google Scholar 

  19. Beaurepaire, P., Schuëller, G.I.: Modeling of the variability of fatigue crack growth using cohesive zone elements. Eng. Fract. Mech. 78, 2399–2413 (2011)

    Article  Google Scholar 

  20. Nguyen, O., Repetto, E.A., Ortiz, M., Radovitzky, R.A.: A cohesive model of fatigue crack growth. Int. J. Fract. 110, 351–369 (2001)

    Article  Google Scholar 

  21. Eliaš, J., Le, J.-L.: Modeling of mode-I fatigue crack growth in quasi-brittle structures under cyclic compression. Eng. Fract. Mech. 96, 26–36 (2012)

    Article  Google Scholar 

  22. Roe, K.L., Siegmund, T.: An irreversible cohesive zone model for interface fatigue crack growth simulation. Eng. Fract. Mech. 70, 209–232 (2003)

    Article  Google Scholar 

  23. Maiti, S., Geubelle, P.H.: Cohesive modeling of fatigue crack retardation in polymers: crack closure effect. Eng. Fract. Mech. 73, 22–41 (2006)

    Article  Google Scholar 

  24. Jiang, H., Gao, X., Srivatsan, T.S.: Predicting the influence of overload and loading mode on fatigue crackgrowth: A numerical approach using irreversible cohesive elements. Finite Elem. Anal. Des. 45, 675–685 (2009)

    Article  Google Scholar 

  25. Zhang, M., Zhang, J., McDowell, D.L.: Microstructure-based crystal plasticity modeling of cyclic deformation of Ti–6Al–4V. Int. J. Plast. 23, 1328–1348 (2007)

    Article  MATH  Google Scholar 

  26. Ohno, N., Wang, J.: On modelling of kinematic hardening for ratcheting behaviour. Nucl. Eng. Des. 153, 205–212 (1995)

    Article  Google Scholar 

  27. Dunne, F., Petrinic, N.: Introduction to Computational Plasticity. Oxford University Press, Oxford (2005)

    MATH  Google Scholar 

  28. Kang, G., Dong, Y., Liu, Y., Jiang, H.: Macroscopic and microscopic investigations on uniaxial ratchetting of two-phase Ti–6Al–4V alloy. Mater. Charact. 92, 26–35 (2014)

    Article  Google Scholar 

  29. Paggi, M., Wriggers, P.: A nonlocal cohesive zone model for finite thickness interfaces-Part I: mathematical formulation and validation with molecular dynamics. Comput. Mater. Sci. 50, 1625–1633 (2011)

    Article  Google Scholar 

  30. Krull, H., Yuan, H.: Suggestions to the cohesive traction–separation law from atomistic simulations. Eng. Fract. Mech. 78, 525–533 (2011)

    Article  Google Scholar 

  31. Brocks, W.: Cohesive strength and separation energy as characteristic parameters of fracture toughness and their relation to micromechanics. SID 1, 233–243 (2005)

    Google Scholar 

  32. Brocks, W., Scheider, I., Schödel, M.: Simulation of crack extension in shell structures and prediction of residual strength. Arch. Appl. Mech. 76, 655–665 (2006)

    Article  MATH  Google Scholar 

  33. Hutchinson, J.W.: Closing in on the crack tip. In: Willis, J.R. (ed.) IUTAM Symposium on Nonlinear Analysis of Fracture, pp. 81–91. Kluwer Academic Publishers, Dordrecht (1997)

    Chapter  Google Scholar 

  34. Allahverdizadeh, N., Gilioli, A., Manes, A., Giglio, M.: An experimental and numerical study for the damage characterization of a Ti–6Al–4V titanium alloy. Int. J. Mech. Sci. 93, 32–47 (2015)

    Article  Google Scholar 

  35. Li, H., Yuan, H., Li, X.: Assessment of low cycle fatigue crack growth under mixed-mode loading conditions by using acohesive zone model. Int. J. Fatigue 75, 39–50 (2015)

    Article  Google Scholar 

  36. Li, H., Chandra, N.: Analysis of crack growth and crack-tip plasticity in ductile materials using cohesive zone models. Int. J. Plast. 19, 849–882 (2003)

    Article  MATH  Google Scholar 

  37. ABAQUS Version 6.11. User Subroutines Reference Manual. Dassault Systemes Simulia Corp., Providence (2011)

  38. Korsunsky, A.M., et al.: Crack tip deformation fields and fatigue crack growth rates in Ti–6Al–4V. Int. J. Fatigue 31, 1771–1779 (2009)

    Article  Google Scholar 

  39. ASTM E 647-00: Standard Test Method for Measurement of Fatigue Crack Growth Rates (2000)

  40. Liu, J., Xiang, C., Yuan, H.: Prediction of 3D small fatigue crack propagation in shot-peend specimens. Comput. Mater. Sci. 46, 566–571 (2009)

    Article  Google Scholar 

  41. Xu, Y., Yuan, H.: On the damage accumulation in the cyclic cohesive zone model for XFEM analysis of mixed-mode fatigue crack growth. Comput. Mater. Sci. 46, 579–585 (2009)

    Article  Google Scholar 

  42. Li, H., Yuan, H.: Cohesive zone modeling of low cycle fatigue cracks in cracked and notched specimens. Fatigue Fract. Eng. Mater. Struct. 36, 1246–1257 (2013)

    Article  Google Scholar 

Download references

Acknowledgements

Financial support provided by the National Natural Science Foundation of China (No. 11502204) and research start-up fund of Northwestern Polytechnical University (No. G2015KY0303) are acknowledged.

Author information

Authors and Affiliations

  1. School of Mechanics, Civil Engineering and Architecture, Northwestern Polytechnical University, Xi’an, 710129, China

    Huan Li & Chun Li

  2. School of Aerospace Engineering, Tsinghua University, Beijing, 100084, China

    Huang Yuan

Authors
  1. Huan Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chun Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Huang Yuan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Huan Li.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, H., Li, C. & Yuan, H. Prediction of fatigue crack growth retardation using a cyclic cohesive zone model. Arch Appl Mech 87, 1061–1075 (2017). https://doi.org/10.1007/s00419-017-1232-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-017-1232-2

Keywords

Search

Navigation