Apatite evidence for a fluid-saturated, crystal-rich magma reservoir forming the Quellaveco porphyry copper deposit (Southern Peru)

Abstract

Large volume, intermediate-felsic magma reservoirs are the source of melt and mineralising fluids which generate porphyry copper deposits. Cooling and crystallisation of hydrous magmas drives the exsolution and expulsion of a magmatic volatile phase—a process which remains challenging to constrain in porphyry Cu systems where the record of magma volatile compositions is rarely preserved. Here, we use the halogen compositions of apatite inclusions shielded as inclusions within zircon to constrain volatile evolution in magma reservoirs which pre-date and are synchronous with porphyry Cu mineralisation at Quellaveco, Southern Peru. Geochemical and textural data confirm that the zircon-included apatites escaped re-equilibration with hydrothermal fluids, unlike apatites found in the groundmass of the same rocks. We, therefore, recommend that future studies attempting to reconcile magmatic volatile budgets using apatite in porphyry Cu systems should focus on apatite inclusions in zircon. By combining the apatite inclusion data with numerical modelling, we find evidence that the magma reservoir sourcing porphyry Cu mineralisation remained fluid-saturated for the entire period recorded by apatite crystallisation. By contrast, the pre-mineralisation batholith shows more variable, potentially fluid-undersaturated behaviour. Our modelling suggests that in order to attain the porphyry melt volatile compositions inferred from apatite, the magma reservoir must have exsolved a large proportion of its volatile budget, consistent with having been held at high crystallinity (40–60% crystals). This crystallisation interval coincides with peak chlorine and copper extraction from intermediate-felsic magmas, and would have permitted efficient fluid migration and accumulation at the roof of the system. We suggest that the storage of large-volume, long-lived, crystal-rich magma reservoirs in magmatic arcs may be a critical step in generating world-class porphyry copper deposits.

Introduction

Volatiles dissolved in arc magmas are responsible for a number of phenomena on Earth, including mineral deposit formation, explosive volcanic eruptions and transfer of aerosols to the atmosphere. The high volatile content of arc magmas is thought to originate from the mantle source hydrated by the down-going slab and is further enriched during fractional crystallisation (Wallace 2005; Plank et al. 2013). As these magmas ascend through the crust, decompression (“first boiling”) and crystallisation (“second boiling”) cause these volatiles to exsolve into a fluid phase which ultimately fuels volcanic eruptions and ore deposit formation (Edmonds and Woods 2018; Tattitch et al. 2021). During fluid saturation, certain metals (e.g. Cu, Au and Mo) are preferentially partitioned into the fluid phase relative to the melt and the metalliferous fluids are released into surrounding rock and may form a porphyry Cu deposit (Candela and Holland 1984; Cline and Bodnar 1991). The timing of fluid saturation (relative to decompression and crystallisation) in a magma reservoir is expected to play an important role in controlling the location, size and grade of porphyry deposits.

Porphyry Cu deposits are closely associated with large-volume batholiths which are emplaced at 5–15 km in the crust (Sillitoe 2010). Once exsolved, the magmatic volatile phase is thought to migrate through the batholith towards the apex of the magma reservoir, where pressure release triggers expulsion of melt and fluid into overlying rock leading to Cu mineralisation (Sillitoe 2010; Lamy-Chappuis et al. 2020). Field observations of cross-cutting relationships have provided evidence that multiple stages of porphyry magma emplacement and hydrothermal veining are archetypal features of porphyry Cu deposits (Gustafson and Hunt 1975) forming over timespans between 10⁵ and 10⁶ years (Chelle-Michou et al. 2014; Buret et al. 2016; Tapster et al. 2016; Large et al. 2021), although individual pulses of hydrothermal activity occur over shorter durations of <10,000 years (Mercer et al. 2015). Therefore, repeated sequences of recharge, cooling, crystallisation and fluid-melt extraction are thought to occur in the magma reservoir during the lifespan of a porphyry system. Some models invoke porphyry deposit formation from batholiths which are emplaced incrementally and may be kept at high melt fractions (Schöpa et al. 2017; Korges et al. 2020). Other models have argued for the rapid emplacement of large-volume intrusions which cool monotonously over the measured timescales, causing progressive exsolution of fluid (Large et al. 2021). Some authors have also suggested the importance of a high crystallinity magma reservoir (Buret et al. 2016; Tapster et al. 2016), since numerical modelling has demonstrated enhanced fluid migration and focussing in crystal-rich magmas (Parmigiani et al. 2016). The dynamics of the parental magmatic system and the behaviour of volatile components during its lifetime are thus critical to understanding the genesis of porphyry Cu systems.

Constraining the behaviour of volatiles during the evolution of magmatic systems is challenging, because during ascent and crystallisation of magmas, volatiles will saturate and escape the petrological record (Edmonds and Woods 2018). In addition, many studies rely on the study of glassy melt inclusions, which may experience post-entrapment modification, or be rarely preserved, as is the case for the strongly hydrothermally altered igneous rocks that host porphyry Cu systems. One increasingly popular method to constrain magma volatile evolution is using the composition of igneous apatite which is unique in that it incorporates three of the important ore-forming components: water, chlorine and sulphur (Piccoli and Candela 2002). However, using apatite to quantify magmatic volatile concentrations is difficult, because these elements exhibit non-ideal partitioning behaviour (Webster et al. 2009; Riker et al. 2018). Fortunately, recent advances have developed a framework to reconstruct melt volatile evolution using apatite in spite of these challenges (Li and Hermann 2017; Li and Costa 2020). Consequently, several studies have used apatite volatile compositions to constrain the timing and style of volatile saturation in magmatic systems (Stock et al. 2016; Humphreys et al. 2021; Kendall-Langley et al. 2021), including in porphyry environments (Chelle-Michou and Chiaradia 2017; Cao et al. 2021; Xing et al. 2021; Huang et al. 2023). However, studies have shown that halogens in apatite are highly susceptible to re-equilibration with hydrothermal fluids (Bouzari et al. 2016). Therefore, the reliability of these data in porphyry systems may be contentious and some authors have proposed future research should focus on apatites included in robust phases such as zircon, which may be shielded from such modification (Brugge 2020; Li et al. 2021; Kendall-Langley et al. 2021).

Here, we report major element compositions of apatites from a suite of igneous rocks from the Quellaveco District, Southern Peru, which both pre-date and formed synchronously with the generation of a giant porphyry Cu-Mo deposit. We focus on apatite inclusions within zircon crystals, which we show to retain a robust record of magmatic volatile concentrations. We develop a numerical modelling framework to reconstruct fluid saturation in magmas associated with porphyry Cu deposits, and provide evidence that such systems are underlain by fluid-saturated, crystal-rich magma reservoirs.

Fig. 1

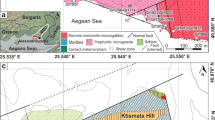
A Simplified geological map of the Yarabamba Batholith from Nathwani et al. (2021) modified after Bellido (1979). Annotated symbols indicate the positions of Yarabamba samples collected in the field. Dashed lines indicate the pit locations of the three giant porphyry Cu–Mo deposits in the district. Inset map shows the location of the district in Peru. B Geological map of the Quellaveco porphyry Cu–Mo deposit modified from Nathwani et al. (2021) after Simmons (2013). The locations of drill-holes which were sampled are marked

Regional geology

Quellaveco is a giant porphyry Cu–Mo deposit in Southern Peru, which commenced production in 2022, and hosts ore reserves of 1.67 billion tonnes at 0.53% Cu (Anglo American, Annual Report 2021). Quellaveco is one of three giant Palaeocene-Eocene porphyry Cu deposits located in the district, which were emplaced at ca. 55 Ma: Quellaveco, Toquepala and Cuajone (Simmons et al. 2013; Nathwani et al. 2021). All three deposits are hosted by the precursor Yarabamba Batholith (Fig. 1A), which was incrementally assembled between 67–58 Ma. Previous zircon U–Pb LA-ICP-MS geochronology (Simmons et al. 2013; Nathwani et al. 2021) has defined at least three discrete phases of plutonic activity: the Yarabamba Monzonite (ca. 67 Ma), the Toquepala Granodiorite (ca. 61 Ma) and the Quellaveco Granodiorite (ca. 59 Ma). The latter intrusion is the principal host rock to the porphyry system at Quellaveco and exhibits whole-rock and zircon compositions more akin to the porphyry Cu intrusions (e.g. high whole-rock Sr/Y and zircon Eu/Eu*), suggesting a transition in the locus of magmatism to deeper crustal levels at ca. 60 Ma (Nathwani et al. 2021). The Quellaveco porphyry Cu deposit is composed of at least six intrusive phases (Simmons 2013; Sillitoe and Mortensen 2010) which form stock and dyke complexes (Fig. 1). The porphyry intrusions are dominated by plagioclase, K-feldspar, quartz and biotite phenocrysts (mostly 40–60 % phenocrysts) hosted in a fine-grained groundmass. The emplacement of each intrusive phase was accompanied by intense hydrothermal alteration (potassic, phyllic and propylitic) and Cu mineralisation which generally declines in intensity through the lifetime of the system (Simmons 2013).

Analytical methods

Sample selection

Representative samples of Yarabamba and Quellaveco intrusive rocks were selected for apatite compositional analysis. “Groundmass” apatites, a term used herein to describe apatites not included within zircon, were analysed in situ from 15 polished thin sections. Apatite inclusions in zircon were analysed from zircon grains from 12 different samples which were mounted in epoxy. One set of zircon mounts is that used for zircon U–Pb geochronology and trace element chemistry by Nathwani et al. (2021); mineral separation procedures can be found therein. Due to the low yield of apatite inclusions in zircon, a further set of zircons was separated at Zirchron LLC in Arizona, USA. Samples were crushed by jaw crushing and disc pulverisation, followed by heavy liquid and magnetic separation. Zircons were picked from the separates, mounted in epoxy and polished to expose mineral inclusions.

Electron probe microanalysis

Major element electron probe microanalyses (EPMA) of both groundmass and inclusion apatites were conducted using a Cameca SX100 in the Imaging and Analysis Centre (IAC), Natural History Museum, London. Two separate analytical protocols were used (Table S1). The first used a higher energy (HE) approach suited to the analysis of a larger number of elements. This involved a spot size of 10 $\mu {\textrm{m}}$, a 20 kV accelerating voltage and a 20 nA current. Elements measured were P, Na, Si, Al, K, S, Mn, Fe, Sr, La, Ce, Pr, Nd, Ca, Cl, Mg, Ba, Y, As and F. This approach was only used on groundmass apatites. The second approach was optimised for reliable halogen data acquisition from apatite inclusions in zircon, and used a lower energy (LE) to reduce anisotropic diffusion of halogens under the electron beam (Stormer et al. 1993; Goldoff et al. 2012; Stock et al. 2015). The LE approach used a 5 $\mu {\textrm{m}}$ spot size, with a 10 kV accelerating voltage and a 10 nA current. Elements measured were P, Na, Si, Mg, Al, Cl, S, Mn, Fe, Ca, K and F.

During each analytical session, a Durango apatite standard was analysed to monitor accuracy and any analytical drift. The Durango apatite crystal was mounted in an epoxy block and orientated so the c-axis of the crystal was perpendicular to the electron beam to mitigate halogen diffusion (Stormer et al. 1993). The HE approach produced mean Durango apatite F concentrations of 4.68% (n = 9, $\sigma = 0.24$; Table S2) which far exceeds the documented F concentration in Durango apatite of 3.53% (Young et al. 1969) and the theoretical stoichiometric limit of 3.76 wt% (Åmli 1975). A subset of groundmass apatites were analysed by both the HE and LE approaches to allow a comparison between the two techniques (Fig. S1). Surprisingly, there was no clear bias of the HE approach towards higher F concentrations. This may be related to a lower degree of F diffusion due to the lower concentrations of F in the natural samples. Notwithstanding this, the halogen concentrations derived from the HE approach were only used for qualitative comparisons. Durango apatite F concentrations determined by the LE approach produced more acceptable results, with a mean concentration of 3.54% (n = 106, $\sigma = 0.24$; Table S2). Apatite stoichiometry was calculated following the approach of Ketcham (2015) which corrects for mixing of halogens and hydroxyl in the anion site. Propagation of analytical uncertainties indicates that the $2\sigma$ uncertainty on X_OH values is 0.24.

Analyses were filtered to include only those with totals between 96 and 103 wt% because those significantly above indicate strong electron beam induced halogen migration whereas those significantly below indicate incomplete analyses. For apatite inclusions in zircon, analyses were further filtered to exclude analyses with > 4 wt% SiO₂ and < 49 wt% CaO since they indicate a significant contribution from the zircon host. More minor contamination of an apatite analysis by the zircon host reduces the concentrations of halogens in apatite but is not expected to modify the ratios of Cl, F and OH which are used in this study. Further information on EPMA analytical procedures and Durango apatite can be found in the Supplementary Tables.

Secondary ion mass spectrometry

Secondary ion mass spectrometry (SIMS) was performed at the NERC Edinburgh Ion Microprobe Facility (EIMF), based at the University of Edinburgh. These analyses were carried out on gold-coated grain mounts which had not been previously analysed by any microanalytical technique in order to eliminate damage to the epoxy by SEM rastering which could compromise SIMS analysis. Two analytical approaches were used: the first was conducted using a Cameca IMS 7f ion microprobe using an approximate spot size of 10 $\mu {\textrm{m}}$, low ¹⁶O^- primary beam current of 1.0 nA, an energy of 13.0 keV and an energy window of ± 20 eV. Because this approach yielded a small number of successful analyses due to high detection limits, a second approach was used to reduce the spot size. This involved use of the Cameca IMS 1270 at the EIMF using a Cs⁺ beam with a current of 1.9 nA and an energy slit of ± 20 eV. In-house apatite standards (BAH2, DUR3, HOL, ILM, Will and YAT) mounted in indium were regularly analysed and calibration curves were produced, normalised to Ca assuming a 39.36 wt% concentration in apatite. Further details on the SIMS methodology are given in the Supplementary Material.

Apatite LA-ICP-MS trace element mapping

Textural analysis of the groundmass apatites was performed by scanning electron microscope-cathodoluminescence (SEM-CL) using a Zeiss EVO SEM. The instrument was operated using a 3.0 nA beam current and 10 kV accelerating voltage. LA-ICP-MS mapping of apatite crystals was carried out using a 193 nm Iridia laser ablation system and Agilent 8900 ICP-QQQ-MS. All imaging experiments were carried out using a 3 µm square beam, a fluence of 3.5 J cm^{– 2}, a repetition rate of 192 Hz and a scan speed of 48 $\mu {\textrm{ms}}^{-1}$, corresponding to 12 laser pulses per 3 µm pixel (dosage). A gas blank (20 s) was gathered between each sample. NIST SRM 612 (Jochum et al. 2011) was measured as a raster every four unknowns for calibration and drift correction. Trace element concentrations in apatite were calculated on a pixel-by-pixel basis using the sum normalisation tool in HDIP employing the stoichiometric Ca concentration (39.36 wt %) as an internal standard. Further details on LA-ICP-MS mapping can be found in the Supplementary Material.

Modelling approach

Reconstructing melt volatile ratios using apatite compositions

It has been documented by many experiments that the partitioning behaviour of halogens in apatite is non-Nernstian, hence the apatite/melt partition coefficients (K_D) of Cl, F and OH vary over two orders of magnitude at a given temperature and pressure (Mathez and Webster 2005; Webster et al. 2009; Doherty et al. 2014; McCubbin et al. 2015; Li and Hermann 2017). This partitioning behaviour precludes the simple use of apatite compositions to re-calculate melt halogen contents. Consequently, K_D values have instead been considered as exchange coefficients, which express the partitioning relationship between two volatile elements. This can be formulated by the consideration of mole fractions of two anions (e.g. A and B) into apatite ($X_{A}^{{{\text{ap}}}}$, $X_{B}^{{{\text{ap}}}}$) and in the melt ($X_{A}^{{{\text{melt}}}}$, $X_{B}^{{{\text{melt}}}}$):

$$\begin{aligned} K{_{D}}{_{A-B}^{ap-melt}} = \frac{X_{A}^{ap}\cdot {}X_{B}^{melt}}{X_{A}^{melt}\cdot {}X_{B}^{ap}} \end{aligned}$$

(1)

These distribution coefficients show less variation at a given temperature and pressure (Li and Costa 2020) but can, particularly at low temperatures, still show variation over an order of magnitude (McCubbin et al. 2015). Recently, attempts have been made to use thermodynamic approaches to constrain the partitioning behaviour further, explicitly considering the non-ideal mixing of Cl–F–OH in apatite solution (Li and Hermann 2017; Li and Costa 2020). Li and Costa (2020) used thermodynamic principles and multivariate regression on experimental datasets to derive a best-fit equation for apatite-melt OH–Cl–F exchange coefficients as a function of apatite composition ($X_{OH}^{ap}$, $X_{Cl}^{ap}$, $X_{F}^{ap}$ and temperature (T)):

$$\begin{aligned} ln\left( {K_{{OH - F}}^{{ap}} } \right)\, = & - \frac{1}{{RT}}{\mkern 1mu} \,((94600 \pm 5600) - 40 \pm 0.1 \cdot T \\ & \, - 1000 \cdot (7 \pm 4{\mkern 1mu} \,(X_{F}^{{ap}} - X_{{OH}}^{{ap}} ) - 11 \pm 7 \cdot X_{{Cl}}^{{ap}} )) \\ \end{aligned}$$

(2)

$$\begin{aligned} ln(K_{{OH - Cl}}^{{ap}} ) = & - \frac{1}{{RT}}\,((72900 \pm 2900) - 34 \pm 0.3 \cdot T \\ & - 1000 \cdot (5 \pm 2\,(X_{{Cl}}^{{ap}} - X_{{OH}}^{{ap}} ) - 10 \pm 8 \cdot X_{F}^{{ap}} )) \\ \end{aligned}$$

(3)

Therefore, for a given apatite composition and temperature, the exchange coefficient can be calculated and thus the ratio of volatile components in the melt. Attempts to use these to calculate absolute values of Cl, F or OH in the melt either require: (i) knowledge of one or two of these concentrations from independent methods e.g. melt inclusions (Li and Costa 2020); or (ii) the use of experimental data to calibrate absolute concentrations as a function of volatile ratios, e.g. regressing experimental data to calculate melt Cl from melt F/Cl (Li and Hermann 2017; Kendall-Langley et al. 2021). The former scenario is challenging for porphyry Cu rocks where melt inclusions are rarely preserved. Experimental calibrations are unlikely to be realistic for porphyry systems where initial melt volatile composition is unconstrained and separation and loss of a magmatic volatile phase is likely. An alternative approach to interpreting apatite volatile compositions is to model magma volatile evolution and forward model apatite compositions that would be in equilibrium with the modelled melts (Stock et al. 2016, 2018; Humphreys et al. 2021). Humphreys et al. (2021) randomly varied exchange coefficients (plus other parameters) in their model and filtered the best-fit parameters to constrain the most likely magmatic conditions during apatite crystallisation. However, in this study, we back-calculate melt volatile ratios using apatite, and then compare the calculated melt volatile ratios with numerical models of magma volatile evolution. This approach is favoured because it avoids estimating apatite-melt exchange coefficients, which can instead be quantified for each apatite. The Li and Costa (2020) method is used to calculate exchange coefficients for each apatite composition, for a given temperature, where temperature is calculated from average Ti-in-zircon temperatures for each sample (Watson et al. 2006; Nathwani et al. 2021). Average temperatures for a single sample were deemed sufficient because no relationship was found between apatite inclusion composition and the host zircon Ti content (Fig. S2), either because of the low spatial resolution of the LA-ICP-MS measurement of the zircon host, the zircon and apatite not being in equilibrium or due to a weak temperature dependency of apatite-melt OH–Cl–F partitioning. Ti-in-zircon temperatures were calculated using the approach of Loucks et al. (2020), which applies a pressure correction (Ferriss et al. 2008) to the experimentally calibrated Ti-in-zircon thermometer Ferry and Watson (2007) so that it can be applied to pressures below 1 GPa for which it is calculated. Parameters used in these calculations were: an SiO₂ activity of 1.0 (due to the presence of quartz), a TiO₂ activity of 0.7 (an average value for arc-related dacites calculated from coexisting oxide chemistry; Ghiorso and Gualda (2013)) and a pressure of 200 MPa. For each apatite composition, it is then possible to calculate the melt volatile ratios (F/Cl, Cl/OH and F/OH).

Modelling melt volatile evolution under fluid-saturated and fluid-undersaturated conditions

The melt volatile ratios (melt ${\text{X}}_{{{\text{Cl}}}} {\text{/X}}_{{{\text{OH}}}}$, ${\text{X}}_{{\text{F}}} {\text{/X}}_{{{\text{OH}}}}$ and ${\text{X}}_{{\text{F}}} {\text{/X}}_{{{\text{Cl}}}}$) calculated from apatite using the methodology described above can be compared to numerical models of volatile evolution in differentiating magmas. Therefore, we developed a modelling framework, appropriate for intermediate-felsic magmas to produce hypothetical melt volatile ratios to allow us to identify conditions within both the pre- and syn-mineralisation intrusions. The focus here is on melt volatile evolution during crystallisation (“second boiling”) rather than related to decompression (“first boiling”) because apatite and zircon are thought to more likely record the former process (i.e. they crystallise relatively late and down to the solidus; Miles et al. (2013); Nathwani et al. (2020)).

Following the approach of Stock et al. (2018), fluid-saturated, and fluid-undersaturated models are developed. The models implement a Monte Carlo approach where, in each model simulation, parameters are randomly selected from pre-defined, realistic ranges (Table S6). This allows the model to account for the large uncertainty in starting conditions. For a given, randomly drawn pressure (200–400 MPa), the water solubility (H₂O_sat) is calculated using the relationship derived from the MagmaSat model of Ghiorso and Gualda (2015). The Python implementation of MagmaSat, VESIcal (Iacovino et al. 2021) was used, which, following linear regression, yields the following relationship for H₂O_sat as a function of pressure (P) (Fig. S3):

$${\text{H}}_{{\text{2}}} {\text{O}}_{{{\text{sat}}}} {\text{ = 0}}{\text{.01719P}}\,{\text{(MPa) + 2}}{\text{.3555}}$$

(4)

This calibration is appropriate for dacite–rhyolite bulk compositions (as appropriate for Quellaveco rocks) and was calibrated using the range of experimental glass compositions of Caricchi and Blundy (2015). These experiments were selected as they are for calc-alkaline magmatic systems in the upper crust, which is appropriate because the starting composition of these experiments (65 wt% SiO₂) broadly coincides with the bulk composition of the Quellaveco porphyry intrusions (64–70 wt% SiO₂). At fluid saturation, the Cl (Cl_sat) and F (F_sat) concentrations in the melt are randomly selected from within ranges typical for arc andesites (Cl = 0.2$-$0.6 wt% and F = 0.01$-$0.2 wt%; Aiuppa et al. (2009)). Each simulation in the model initiates at 100% melt and then progressively cools and crystallises the magma at 1% crystallisation increments along a liquid line of descent. For the fluid-saturated model, a liquid line of descent was modelled using the experiments of Caricchi and Blundy (2015). Melt SiO₂ and temperature are varied with crystallisation using second and first order polynomial regressions on these experiments, where F is the percentage melt in the system (Fig. S4):

$$\begin{aligned}{} & {} T (^{\circ }C) = -0.029831 \cdot F^{2} + 6.59111 \cdot F + 569.22220 \end{aligned}$$

(5)

$${\text{SiO}}_{{\text{2}}} ({\text{wt\% }}) = - 0.17031 \cdot F + 82.05777$$

(6)

In the fluid-undersaturated model, melt SiO₂ and temperature are not input parameters, hence a separate regression was not necessary. In all models, the initial SiO₂ was varied across the range observed for the Quellaveco porphyry intrusions. During crystallisation, a putative concentration of water in the melt (H₂O^*), assuming no water exsolution, is calculated for a given crystallisation increment (1-F):

$${\text{H}}_{{\text{2}}} {\text{O}}^{*} = \frac{{{\text{H}}_{{\text{2}}} {\text{O}}_{{{\text{sat}}}} }}{{{\text{K}}_{{{\text{D(H}}_{{\text{2}}} {\text{O)}}}}^{{{\text{min/melt}}}} + F\left( {1 - K_{{{\text{D(H}}_{{\text{2}}} {\text{O)}}}}^{{{\text{min/melt}}}} } \right)}}$$

(7)

The bulk crystal-melt partition coefficient (${\text{K}}_{{{\text{D(H}}_{{\text{2}}} {\text{O)}}}}^{{{\text{min/melt}}}}$) is varied between 0.01 and 0.1 to account for incorporation of water into hydrous phases (e.g. amphibole and biotite). The approach of Popa et al. (2021) is then followed, using mass balance to calculate the mass fraction of water exsolved at each increment (m_melt):

$$_{{{\text{exsolved}}}}^{{{\text{H}}_{{\text{2}}} {\text{O}}}} = \frac{{{\text{H}}_{{\text{2}}} {\text{O}}^{{\text{*}}} - {\text{H}}_{{\text{2}}} {\text{O}}_{{{\text{sat}}}} }}{{100}}$$

(8)

According to the ideal gas law, the density of the magmatic volatile phase can be calculated for a given molecular mass (M_r), pressure (P) and temperature (T):

$$\rho _{{{\text{vapour}}}} = \frac{{{\text{M}}_{{\text{r}}} {\text{P}}}}{{{\text{TR}}}}$$

(9)

The molecular mass is assumed to be that of water vapour (0.018). According to mass balance, at each increment the mass percentage of water remaining in the system can be calculated:

$$_{{{\text{melt}}}}^{{{\text{H}}_{{\text{2}}} {\text{O}}}} = 1 - \,\left( {{\text{m}}_{{{\text{exsolved}}}}^{{{\text{H}}_{{\text{2}}} {\text{O}}}} + \left( {1 - F} \right)} \right)$$

(10)

If the fluid-melt partition coefficients of Cl and F are known, this then allows the behaviour of these species to be calculated. For Cl, the $D_{{{\text{Cl(i)}}}}^{{{\text{fluid}} - {\text{melt}}}}$ can be calculated using the experimental calibration of Tattitch et al. (2021) at each crystallisation increment i, as a function of melt Cl (Cl_melt), melt SiO₂ and pressure (P):

$$D_{{{\text{Cl(i)}}}}^{{{\text{fluid}} - {\text{melt}}}} = D_{0} \frac{{e^{{a \cdot {\text{Cl}}_{{{\text{melt(i}} - {\text{1)}}}} \, + \,b \cdot {\text{SiO}}_{{{\text{2(i}} - {\text{1)}}}} }} }}{{1 + e^{{\frac{{P_{0} - P}}{c}}} }}$$

(11)

where the constants and standard deviation error of the weighted regression are: a = 0.4078 ± 0.4815, b = 0.1456 ± 0.01821, c = 34.47 ± 3.823, P₀ = 175.8 ± 11.61, D₀ = 0.0005862 ± 0.0008231. The salinity of the instantaneous fluid can then be calculated as

$${\text{NaCl}}_{{{\text{fluid}}}} = D_{{{\text{Cl(i)}}}}^{{{\text{fluid}} - {\text{melt}}}} \cdot {\text{Cl}}_{{{\text{melt(i)}}}} \cdot m$$

(12)

where m is the molecular mass ratio of NaCl and Cl (1.65). The bulk partition coefficient of Cl ($D_{Cl(i)}$) during differentiation must account for the mineral-melt and fluid-melt partition coefficients of Cl which can be formulated as (Tattitch et al. 2021)

$$\begin{aligned} D_{{{\text{Cl(i)}}}} \, = & \,D_{{{\text{Cl}}}}^{{{\text{min}} - {\text{melt}}}} \cdot \,\left( {1 - \frac{{{\text{H}}_{{\text{2}}} {\text{O}}_{{{\text{sat}}}} }}{{{\text{100}}}} \cdot \frac{{100}}{{100 - {\text{NaCl}}_{{{\text{fluid}}}} }}} \right) \\ & + D_{{{\text{Cl}}}}^{{{\text{fluid}} - {\text{melt}}}} \cdot \frac{{H_{2} O_{{sat}} }}{{100}} \cdot \frac{{{\text{100}}}}{{{\text{100}} - {\text{NaCl}}_{{{\text{fluid}}}} }} \\ \end{aligned}$$

(13)

$D_{Cl}^{min-melt}$ is varied between 0.01 and 0.1 to account for incorporation into hydrous phases (e.g. amphibole, biotite, apatite). The Cl concentration in the melt at a given crystallisation increment i is given by (Tattitch et al. 2021)

$${\text{Cl}}_{{{\text{melt(i)}}}} = \frac{{{\text{Cl}}_{{{\text{melt(i)}}}} }}{{D_{{{\text{Cl(i)}}}} + \frac{{F_{i} }}{{F_{{i - 1}} }}\,\left( {1 - D_{{{\text{Cl(i)}}}} } \right)}}$$

(14)

The behaviour of F during fluid saturation ($D_{{{\text{F(i)}}}}^{{{\text{fluid}} - {\text{melt}}}}$) is less well constrained. Experiments have generally shown that F is preferentially retained in the melt during fluid saturation at compositions relevant to this study. At 200–500 MPa, $D_{{{\text{F(i)}}}}^{{{\text{fluid}} - {\text{melt}}}}$ has been shown to be <0.1 (Webster and Holloway 1990), and more recent experiments show that $D_{{{\text{F(i)}}}}^{{{\text{fluid}} - {\text{melt}}}}$ is generally <1 in felsic magma systems (Cassidy et al. 2021). $D_{{{\text{F(i)}}}}^{{{\text{fluid}} - {\text{melt}}}}$ is, therefore, varied between 0.01 and 0.1 to account for variably fluid-incompatible behaviour of F. In order to allow comparison between the volatile ratios derived from apatite compositions and those of the numerical model, the concentrations from the numerical model are converted to mole fractions in the melt (Li and Hermann 2017) and the molar OH_melt can be calculated using the water speciation model of Zhang (1999).

Fig. 2

Examples of SEM-BSE (A–E) and SEM-CL (F–J) images of apatite crystals showing varying degrees of alteration. A and F Yarabamba Monzonite (QVC075); B and G Toquepala Granodiorite (QVC082); C and H Granodiorite Porphyry (QVC091); D and I Early Porphyry (QVC034); E and J Late Porphyry (QVC061). Dark circles are EPMA spots and white inclusions are monazite (mnz) crystals

Fig. 3

LA-ICP-MS trace element maps of three groundmass apatite crystals (Ce and Th are shown) from three different samples showing the increasing degree of alteration that occurs in samples with a proximity/association to mineralisation at Quellaveco. The Yarabamba monzonite shows typical igneous zoning. The Quellaveco Granodiorite apatites show no evidence of igneous zoning and exhibit patchy zonation, potentially due to alteration. The early porphyry apatites typically show strong alteration, manifested as exsolutions of monazite grains and cracks annealed by Ce-rich domains

Results

Groundmass apatites

Textural observations

Groundmass apatites exhibit a range of textures, with large differences between the Yarabamba Batholith apatites and the Quellaveco porphyry apatites (Figs. 2 and 3). Apatites from the Yarabamba Monzonite (ca. 67 Ma) are the only ones that demonstrate clear igneous zoning and do not show unequivocal signs of alteration (Figs. 2A, F and 3). The later pre-mineralisation Toquepala Granodiorite (ca. 61 Ma), contains apatite that shows varying degrees of alteration, often with patchy zones which have a brighter CL response (Fig. 2B and G). The precursor Yarabamba host of the Quellaveco porphyry deposit, the Quellaveco Granodiorite (ca. 58 Ma), contains apatite with weak-moderate signs of alteration. By contrast, Quellaveco porphyry rocks (ca. 57–54 Ma) show evidence for intense hydrothermal alteration, particularly in the earliest porphyry phases, such as the Quellaveco Granodiorite Porphyry and Early Porphyry (Fig. 2C, D, H and I). These apatites frequently contain inclusions of monazite at the cores of crystals which coincide with crystal domains with a weak CL response. Other secondary phases include sericite, quartz, biotite and sulphides. These apatite crystals have complex CL textures, often with three domains of varying CL brightness which coincide with a mottled appearance under BSE. Laser mapping (Fig. 3) reveals that these strongly altered apatites contain ubiquitous exsolutions of REE, Th and U-rich domains, which coincide with darker CL zones, indicating incomplete exsolution of monazite. These apatites have complementary REE, Th and U-depleted domains which have a brighter CL response. The intermineral, late and post-mineralisation porphyry intrusions exhibit weak alteration styles such as thin veinlets within apatite that exhibit a brighter CL response (Fig. 2E and J).

Apatite compositions

Groundmass apatites, except for those from the Yarabamba Monzonite, generally display high F concentrations (2.5–3.6 wt%) and low Cl (0.1–1.0 wt%). These apatites (additionally excluding the Toquepala Granodiorite) also have high MnO (> 0.25 wt%). The Cl concentrations in groundmass apatites correlate positively with MnO and MgO (Fig. S5). Two divergent trends in MnO and MgO versus Cl are apparent, with the Yarabamba Monzonite and Toquepala Granodiorite apatites showing strongly decreasing Cl with decreasing MnO whereas, in the other apatites, Cl decreases gradually with decreasing MnO (Fig. S5). The Yarabamba Monzonite groundmass apatites exhibit markedly lower F concentrations (1.0$-$2.3 wt%) and higher Cl (1.1$-$3.0 wt%). All groundmass apatites generally have low SO₃, with many concentrations less than 0.10 wt% or below the detection limit (< 0.04 wt%).

Fig. 4

Ternary plots of molar proportions of Cl, F and OH anions in the hydroxyl site of apatite for: a groundmass apatites and; b apatite inclusions in zircon. OH values are calculated by difference following the approach of Ketcham (2015)

Fig. 5

SEM-cathodoluminesence images of apatite inclusions in zircon from the Yarabamba Batholith (a–d) and the Quellaveco porphyry Cu intrusions (e–l). Images are ordered from the oldest to youngest intrusive units in the district. The position of identified apatite inclusions is marked (ap) and other inclusions are predominantly melt inclusions (mi). Abbreviated unit names are: Yarabamba monzonite (a), Toquepala granodiorite (b and c), Quellaveco granodiorite (d) and Granodiorite porphyry (e–f). Scale bars for all sub-figures are 100 $\mu {\textrm{m}}$

Apatite inclusions in zircon

Textural observations

Zircons from the Yarabamba Batholith range from anhedral-subhedral in the least evolved Yarabamba Monzonite to euhedral and prismatic crystals in the more evolved Toquepala Granodiorite and Quellaveco Granodiorite (Nathwani et al. 2023). Quellaveco porphyry zircons are generally prismatic and euhedral in shape. All zircons are considered igneous in origin due to these shapes, ubiquitous oscillatory and sector zoning and the absence of cracks and inclusions of hydrothermal minerals (Fig. 5.) Apatite inclusions in these zircons were found throughout their hosts from core to rim with no tendency to be hosted within specific zones. The average size was 5–10 $\mu {\textrm{m}}$ with the largest crystals being 20 $\mu {\textrm{m}}$ in length and the smallest being nano-inclusions which were not analysable.

Fig. 6

Volatile ratio plots of A X_Cl/X_OH vs. X_F/X_OH and B X_Cl/X_OH vs. X_F/X_Cl for apatite inclusions in zircon illustrating the trends between and within samples. Both EPMA (black outline) and SIMS (red outline) data are shown. The $2\sigma$ error bars are propagated analytical uncertainties from EPMA data

Apatite compositions

Clear differences in major element compositions are observed between groundmass apatites and apatite inclusions in zircon (Figs. 4 and 6 and Table S3). First, the apatite inclusions in zircon show more diverse compositions within and between samples, particularly within the Yarabamba Batholith units. Yarabamba Monzonite (ca. 67 Ma) apatite inclusions in zircon do not show systematic variation but are typified by generally higher F and lower Cl concentrations compared to other samples. Toquepala Granodiorite (ca. 61 Ma) apatite inclusions yield X_Cl/X_OH ratios that vary greatly with X_F/X_OH (Fig. 6). In the Toquepala Granodiorite, apatite inclusion Cl also seems to positively correlate with MgO (Fig. S5). The latest member of the Yarabamba Batholith, the Quellaveco Granodiorite (ca. 59 Ma), has apatite inclusion compositions more similar to the Quellaveco porphyry intrusions than to the batholith samples, except for noticeably higher Cl. In general, Yarabamba Batholith apatite inclusions have low SO₃ contents, with median values < 0.01 wt% (Fig. 7). The lowest SO₃ concentrations are in the earliest phase (Yarabamba Monzonite), with many SO₃ values close to/at detection limit.

Apatite inclusions from the Quellaveco porphyries (ca. 57–54 Ma) show homogeneous compositions, characterised by both lower F (< 2 wt%) and Cl (< 1 wt%) than those from the Yarabamba Batholith. They also exhibit higher and more variable SO₃ concentrations, up to 0.95 wt%. In general, higher SO₃ contents are found in the later units e.g. Dacite Dykes have 0.3$-$0.5 wt% median SO₃ (Fig. 7). Where apatite inclusions were analysed that were not completely enclosed in the host zircon, the compositions were more similar to the groundmass apatites rather than the completely enclosed inclusions, characterised by lower Cl and higher MnO.

Unfortunately, cross-correlation of data from the EPMA and SIMS analytical techniques on single crystals was not possible due to the semi-destructive nature of SIMS analysis and the small crystal size. Instead, only a comparison of ranges of data for a given sample were possible (see Figs. S6 and S7). In general, overall differences between samples (e.g. higher F in Yarabamba Monzonite and Toquepala Granodiorite) are present in data obtained by both EPMA and SIMS. Estimated X_OH values from EPMA are consistent with those measured directly by SIMS. Those estimated from SIMS, where positive secondary ions were counted, show a bias towards lower X_OH values due to higher X_Cl and X_F, likely a result of high and variable background concentrations during SIMS analysis from outgassing of the epoxy.

Fig. 7

Measured EPMA SO₃ contents of apatite inclusions in zircon per sample, plotted in relative age order based on cross-cutting relationships from oldest (left) to youngest (right). Individual SO₃ concentrations are given (translucent) and medians (opaque). Quoted ages are based on the zircon U–Pb weighted means given in Nathwani et al. (2021) and uncertainties can be found therein. Samples without zircon U–Pb weighted mean ages are those which were not dated by Nathwani et al. (2021) and are only temporally constrained by their unit and cross-cutting relationships

Discussion

Apatite inclusions in zircon as a recorder of primary melt composition

The clear differences in composition between apatite inclusions in zircon and groundmass apatites suggest they record different stages of magma evolution, and/or that the groundmass apatites have re-equilibrated with later melts or hydrothermal fluids. The presence of igneous zoning and a paucity of hydrothermal alteration textures in the Yarabamba Monzonite apatites (the oldest rock and most distal to a hydrothermal centre), allows us to assess the former (Fig. 3). The groundmass apatites for this unit contrast with those of other lithologies, showing higher Cl, lower F and higher OH and preserve igneous zoning features, suggesting they may have escaped re-equilibration with hydrothermal fluids (Fig. 4a) as fluid alteration is known to decrease apatite Cl content (Bouzari et al. 2016). Furthermore, these groundmass apatites exhibit much higher Cl and lower F than the inclusions, suggesting, in the absence of hydrothermal alteration, that they crystallised at a different stage of magma evolution to the apatite inclusions. The generally lower MgO contents of these groundmass apatites (< 0.02 wt%), compared to the inclusions in zircon, suggest that the groundmass apatites crystallised from more evolved melts (Prowatke and Klemme 2006; Nathwani et al. 2020). This late crystallisation is supported by the predominant occurrence of groundmass apatite as isolated microphenocrysts in the porphyritic matrix, rather than as inclusions in other minerals.

In the other batholith and porphyry samples, the presence of alteration assemblages and patchy CL alteration in groundmass apatites (Figs. 2 and 3), and their trace element heterogeneity (Fig. 3), suggests they underwent re-equilibration with hydrothermal fluids. The chemical homogeneity of these groundmass apatites, with high F and low Cl, is consistent with this (Bouzari et al. 2016; Brugge 2020). This is also supported by the observation that apatites only partially enclosed by their zircon host have compositions more akin to the groundmass apatites suggesting they also experienced fluid-equilibration. Lower Cl is consistent with hydrothermal alteration because Cl is far more compatible in fluids than in apatite (D_Cl^{fluid/apatite} 9-43; Webster et al. (2009)) and Cl also has very high diffusivity in apatite (Li et al. 2020). This is also in agreement with the documentation of decreasing Cl in apatite with progressive hydrothermal alteration in other porphyry Cu systems (Bouzari et al. 2016; Cao et al. 2021). Further evidence for re-equilibration is also suggested by the higher Mn contents of the groundmass apatites (Fig. S5) which has previously been shown to be a common feature of apatites affected by hydrothermal alteration in porphyry Cu deposits (Mao et al. 2016; Loader 2017; Brugge 2020).

Several studies have proposed that apatite inclusions in zircon are useful recorders of magma evolution (Bruand et al. 2016; Jennings et al. 2011; Li et al. 2021; Kendall-Langley et al. 2021; Meng et al. 2021) and can provide a record free of hydrothermal re-equilibration in porphyry systems. Since the primary aim of this paper is to better constrain magmatic processes prior to and during porphyry Cu formation, we focus herein on the data from apatite inclusions in zircon.

The evolution of magmatic volatiles at Quellaveco

Evaluation of the evolution of melt volatile species using apatite inclusions in zircon first requires consideration of the timing of apatite and zircon crystallisation relative to other mineral phases and fluid exsolution. Ti-in-zircon thermometry of these zircons yields temperatures of 650–800 °C for porphyry rocks and 750 to 890 °C for batholith rocks (Nathwani et al. 2021), suggesting protracted crystallisation up to the solidus for these hydrous, intermediate-felsic magmas. This conclusion is consistent with trace element systematics of Quellaveco zircons which suggest significant prior and co-crystallisation of plagioclase and apatite (Nathwani et al. 2021). A comparison of Ti-in-zircon temperatures of zircons containing apatite inclusions versus all zircons in the Quellaveco porphyries shows no discernible difference (Fig. S8), which suggests apatite crystallised for the duration of zircon crystallisation. Marxer and Ulmer (2019) showed that calc-alkaline intermediate batholiths will typically achieve zircon saturation at 800–850 °C and $\sim$50% crystallinity, and this relatively late crystallisation is supported by the prior plagioclase crystallisation inferred from zircon compositions.. We emphasise that the apatite inclusion in zircon record may, therefore, not capture volatile evolution close to the liquidus. Furthermore, high precision geochronology of zircons from other porphyry systems indicates that they can record over 100 kyr of magma cooling, crystallisation and replenishment (e.g. Large et al. (2018); Buret et al. (2016)). Apatite inclusion in zircon data at Quellaveco should thus be interpreted in the context of a potentially protracted evolution of the magmatic system during cooling, crystallisation and rejuvenation by magmas from a deeper reservoir.

Melt sulphur content

One of the most anomalous elements in porphyry Cu systems, relative to unmineralised granitoids, is sulphur. Therefore, constraining the budget and behaviour of sulphur in magmas sourcing porphyry Cu deposits using apatite has attracted interest (Streck and Dilles 1998; Chelle-Michou and Chiaradia 2017). The more variable and higher apatite S concentrations in the Quellaveco porphyry rocks relative to the Yarabamba rocks (Fig. 7), may be the result of a number of processes within the magmatic system. One interpretation is that the Quellaveco magmas had higher bulk S concentrations, relative to the Yarabamba magmas. This would be in line with many other studies which have suggested that magmas sourcing porphyry Cu deposits may be S-rich based on the occurrence of S-rich apatite (Chelle-Michou et al. 2017; Meng et al. 2021) and saturation of igneous anhydrite (Stern et al. 2007; Chambefort et al. 2008; Hutchinson and Dilles 2019). However, a key control on S partitioning into apatite is melt fO₂, because the dominant valence state of S shifts from S^2- dominated ($\textrm{S}^{6+}/\Sigma \textrm{S} = 0$) to S⁶⁺ dominated (($\textrm{S}^{6+}/\Sigma \textrm{S} = 1$) over a narrow range in fO₂ (Jugo et al. 2010). The far greater compatibility of S⁶⁺ in apatite, over S^2- and S⁴⁺, leads to an increase of $D_{S}^{{{\text{apatite/melt}}}}$ from 0.02 to 3.20 between FMQ-1 and FMQ+3 (Konecke et al. 2019). As a result, the lower concentrations of apatite S in the Yarabamba rocks may reflect less oxidised conditions relative to the porphyry magmas, which would be in line with their less evolved compositions and emplacement under a weakly compressional tectonic regime where they underwent shallower/less protracted magmatic differentiation and thus less depletion in Fe²⁺ (Ulmer et al. 2018; Nathwani et al. 2021). We also note that additional factors may influence the increase in apatite S observed in this study, such as interactions of apatite with S-rich fluids prior to complete enclosure in their zircon host (Van Hoose et al. 2013), interactions of apatite with S-rich residual melts (Parat et al. 2002) or the relative timing of apatite saturation relative to fluid and/or sulphide saturation. Given the sensitivity of apatite S to fO₂ and the uncertainties associated with constraining fO₂, we prefer not to calculate melt S concentrations here (Parat et al. 2011). However, we emphasise the observation that high S zircon-hosted or unaltered matrix apatites appear to be a potential characteristic of mineralised porphyry systems (Chelle-Michou and Chiaradia 2017; Parra-Avila et al. 2022).

Melt chlorine content

The halogen compositions of apatite inclusions from the Quellaveco porphyries record the behaviour of these species during the extraction of melt and fluid from a magma reservoir to generate a giant magmatic-hydrothermal system. Because volatile components such as Cl and water are thought to be critical in forming porphyry Cu deposits (Candela and Holland 1986; Cline and Bodnar 1991; Tattitch et al. 2021), these data may provide useful insights into the controls on Cu mineralisation. The characteristically low Cl/OH and low F/OH ratios of apatite inclusions in the Quellaveco porphyries, relative to apatite inclusions in the Yarabamba Batholith, may indicate crystallisation from a magma that was low in Cl and F and/or high in OH. This could be caused by the magmatic system being fluid saturated at the time of apatite and zircon crystallisation (Stock et al. 2018, 2016; Humphreys et al. 2021) which would result in preferential removal of Cl over F and OH from the melt.

Fig. 8

Numerical model of melt compositions A X_Cl/X_OH vs. X_F/X_OH and B X_Cl/X_OH vs. X_F/X_Cl for a fluid-saturated magma evolving as a function of melt crystallisation. Each line of dots indicates a single model simulation and only 100 model simulations are shown for simplicity. Refer to text for details of the modelling. Symbols indicate the melt compositions inferred for Quellaveco intrusions from apatite inclusions in zircon using the Li and Costa (2020) model (refer to Fig. 4 for the legend)

Fig. 9

Numerical model of melt compositions A X_Cl/X_OH vs. X_F/X_OH and B X_Cl/X_OH vs. X_F/X_Cl for a fluid-undersaturated magma evolving as a function of melt crystallisation. Each line of dots indicates a single model simulation and only 100 model simulations are shown for simplicity. Refer to text for details of the modelling. Symbols indicate the melt compositions inferred for Quellaveco intrusions from apatite inclusions in zircon using the Li and Costa (2020) model (refer to Fig. 4 for the legend)

Resolving fluid-saturated and fluid-undersaturated magma evolution

In order to evaluate the key controls on apatite volatile compositions, we implement our modelling strategy (see “Modelling approach” section for full details). This permits back-calculation of melt volatile ratios from apatite compositions, and we use numerical modelling to compare these melt volatile ratios to predict they key controls on the apatite/melt compositions in the Yarabamba and Quellaveco magmatic systems. Monte Carlo simulations of the fluid-saturated numerical model were run, showing melt volatile evolution as a function of degree of crystallinity (F) and a comparison with melt compositions inferred from individual apatite inclusion compositions from the Yarabamba and Quellaveco rocks. A total of 10,000 simulations were run, with a subset of 100 shown for ease of comparison with the melt compositions inferred from apatite (Fig. 8). An additional end-member scenario that was also considered was apatite crystallisation under fluid-undersaturated conditions. For a felsic melt containing 4 wt% H₂O, water saturation would occur at approximately 100 MPa, which is at the lower end of the pressure range under which magma bodies sourcing porphyry Cu deposits are thought to accumulate (200 ± 100 MPa Sillitoe (2010)), and where batholith-building magmas would likely stall and crystallise. In this model, as crystallisation proceeds, the evolution of volatile species is predominantly driven by their bulk partition coefficients during crystallisation (D^min-melt). 100 Monte Carlo simulations of this fluid-undersaturated model were performed (Fig. 9). Ultimately, the magma in this model would volatile saturate due to “second boiling”, however, we prefer having two end-member models to compare with our data as this requires fewer assumptions (e.g. the timing of transition between fluid-undersaturated and saturated behaviour).

The melt volatile ratios back-calculated from apatite using the Li and Costa (2020) approach, can be compared with the two numerical models to evaluate the behaviour of volatile species in the magmatic system sourcing the Quellaveco porphyries. During crystallisation under fluid-saturated conditions (Fig. 8), the modelled melt exhibits increasing F/Cl, decreasing Cl/OH and increasing F/OH, which is consistent with Cl and F being generally fluid compatible and incompatible, respectively, during fluid saturation of intermediate-felsic magmas (Tattitch et al. 2021; Cassidy et al. 2021). These trends, albeit modelled under different conditions, are consistent with other models of fluid-saturated melt evolution derived from apatite data (Stock et al. 2018; Popa et al. 2021). The modelled trends under fluid-saturated conditions are broadly compatible with the trend observed in the Quellaveco porphyry melts (as inferred from apatite compositions) and, therefore, the Quellaveco porphyry apatites are considered to have crystallised under fluid-saturated conditions. By contrast, a proportion of the Yarabamba Batholith melt volatile ratios cannot be explained entirely by fluid-saturated evolution. A number of the Yarabamba Monzonite and Toquepala Granodiorite compositions lie outside the simulated compositions for fluid-saturated behaviour and/or the directions of their trends are not entirely consistent with the models (most apparent in Fig. 8A). As such, the Yarabamba Batholith apatite data are largely inconsistent with crystallisation under fluid-saturated melt evolution.

The fluid-undersaturated model shows less consistent trends in melt volatile evolution, which are strongly dependent on the crystal-melt partition coefficient selected for the given simulation. Generally, Cl/OH increases and F/Cl decreases with fluid-undersaturated crystallisation, whereas melt F/OH shows little change with crystallisation at lower F/Cl but increases significantly with crystallisation at elevated F/Cl. Nonetheless, these modelled trends appear to better account for the full range and dispersion of inferred batholith melt compositions (Fig. 9), but are unable to reproduce those for the Quellaveco porphyries. We, therefore, suggest that the Quellaveco porphyries and the Yarabamba Batholith were fluid saturated and fluid undersaturated, respectively, at the time of apatite crystallisation. The existence of fluid-undersaturated conditions in the Yarabamba Batholith is also consistent with the inferred lower H₂O ($\le$4%) contents of these magmas, as shown by their less evolved compositions, lower Eu/Eu* and lower Sr/Y ratios (Nathwani et al. 2021).

One important control on the variable trends in the Yarabamba Batholith samples could be cooling because, with decreasing temperature, apatite increasingly prefers F over Cl and especially OH (Riker et al. 2018). Temperature differences between samples are accounted for as far as possible using average Ti-in-zircon temperatures for a given sample; however, this will not account for temperature-related trends within a given sample. Therefore, part of the scatter in the volatile ratio estimates for the batholith could be attributed to cooling, but this remains challenging to isolate from other controls and analytical uncertainties. An alternative explanation for the model results is that the apatites from the batholith crystallised earlier in the magmatic evolution, prior to fluid saturation. We consider this unlikely, however, given that in less evolved magmas (e.g. the Yarabamba), zircon would be expected to crystallise later and apatite inclusions would, therefore, be more likely to record fluid-saturated behaviour (Watson and Harrison 1983). The Yarabamba zircons also exhibit less euhedral, weakly zoned crystal textures, in accordance with potentially later crystallisation.

Evidence for a fluid-saturated crystal-rich magma reservoir beneath porphyry Cu deposits

The inherently low Cl/OH and F/OH of the Quellaveco porphyry melts, as inferred from apatite inclusions in zircon, suggests that the magmatic system sourcing the Quellaveco porphyry deposit remained fluid saturated for the duration of Cu mineralisation. This does not exclude the possibility that the system may have undergone transient fluid undersaturation (e.g. by magma recharge) during magma evolution, when apatite was not a crystallising phase. By contrast, precursor non-mineralising magmas may not have reached fluid saturation until later in their evolution, after the formation of apatite inclusions in zircon. Later, fluid saturation in the Yarabamba magmas relative to the Quellaveco magmas is unlikely to be related to deeper storage of the Yarabamba magmas (allowing higher water solubility) due to the emplacement of Yarabamba magmas at shallow levels prior to substantial compression and crustal thickening in the region (Pardo-Casas and Molnar 1987; Nathwani et al. 2021). Instead, we suggest it is more likely that the parental Yarabamba magmas contained lower initial water contents compared to the Quellaveco porphyry magmas (perhaps due to shallower/less protracted fractional crystallisation) which would lead to later fluid saturation.

Fig. 10

Histograms which compare model conditions of “successful” and all simulations from the fluid-saturated model for A melt Cl at fluid saturation; B melt F at fluid saturation, C melt H₂O at fluid saturation; D pressure; E degree of magma crystallisation and; F melt SiO₂. “Successful” simulations are those which intersect Quellaveco porphyry melt compositions inferred from apatite (Li and Costa 2020). For degree of crystallisation (E) and melt SiO₂ (F), these are calculated based on the crystallinity and melt SiO₂ when the models overlap with the porphyry melt compositions. These histograms are based on 10,000 Monte Carlo simulations of the fluid-saturated model

An additional observation from the apatite inclusion data is that the Quellaveco Granodiorite, which pre-dates the bulk of Cu mineralisation at Quellaveco (by ca. 2 Myr), exhibits similar Cl–F–OH chemistry to the porphyries, albeit with slightly higher Cl (Fig. 4). This may hint at apatite crystallisation from a magma that had undergone slightly less fluid loss. Irrespective, these data suggest that the latest member of the Yarabamba Batholith was fluid saturated at zircon-apatite saturation. Nathwani et al. (2021) showed that this unit displays zircon trace element chemistry similar to the Quellaveco porphyries and postulated that the paucity of mineralisation associated with the unit could be related to an insufficient volume of magma to source the required volume of fluids.

The Quellaveco porphyry melt volatile compositions inferred from apatite inclusions in zircon lie within the melt compositions modelled under fluid-saturated magmatic evolution (Fig. 8). A proportion of the fluid-saturated model simulations are able to reproduce the Quellaveco melt composition, whilst the remainder do not. The specific simulations which are able to reproduce the Quellaveco melt compositions may represent the most likely magmatic conditions under which the Quellaveco apatites crystallised and thus under which the porphyry magmas evolved. We term these simulations as “successful simulations” and they are identified as any fluid-saturated simulation which overlaps with a porphyry melt composition calculated from apatite. We made a comparison of the conditions (e.g. pressure and initial H₂O, Cl and F contents) of these “successful” simulations compared to all fluid-saturated simulations, including the crystallinity and melt SiO₂ within each simulation which reproduces Quellaveco melt compositions (Fig. 10).

Notably, there is little difference in many parameters between the “successful” and all fluid-saturated simulations (Fig. 10), such as the H₂O and Cl content of the initial magma. The model predicts that the magmas are on the lower end (0.07 wt%) of expected F concentrations for arc-related dacites (0.01$-$0.15 wt%; Aiuppa et al. (2009)). The most significant characteristic of “successful” simulations is that they equate to higher crystallinities of the magma (40–60%; Fig. 10E) and higher melt SiO₂ (70–75 %; Fig. 10F). We also performed a sensitivity analysis to test the effect of using different aTiO₂ to estimate the temperatures required to calculate the apatite-melt exchange coefficients, and found that a similar result is returned for aTiO₂ between 0.5 and 1.0, with the interpreted crystallinity and silica contents becoming less clear at aTiO₂ = 0.5. Therefore, our modelling suggests that the Quellaveco magmatic system was at high crystallinity (40–60%) and high melt SiO₂ (70–75 wt%) at the time of zircon and apatite crystallisation.

Fig. 11

Modelled instantaneous fluid Cl and Cu exsolved from magmas in the numerical model as a function of the crystallinity of the magma (F). Graphs show 1000 simulations each, where colours indicate the density of trajectories ranging from low (blue) to high (yellow). Violin plot on x-axis shows the crystallinity of “successful” model simulations which are able to reproduce the melt volatile ratios of the Quellaveco porphyries (as derived from apatite inclusion chemistry). Violin plots along y-axis show a literature compilation of Cl and Cu contents of intermediate density-fluid inclusions (ID-FI) for igneous intrusions from Kouzmanov and Pokrovski (2012) (horizontal lines indicate the position of each data point). These fluids are not brine saturated at the temperatures and pressures of the models (Driesner and Heinrich 2007)

Enhanced copper extraction and fluid migration in crystal-rich magmas

The presence of a crystal-rich, felsic magma reservoir would have several implications for both the composition and accumulation of fluids expelled from the Quellaveco magmatic system. First, the model implies that the residual melt in the system would have been driven to evolved compositions, consistent with experimental data which show that 50% crystallisation of a bulk andesitic composition produces rhyolitic residual melt (Marxer and Ulmer 2019). Felsic melt inclusions have been documented in several porphyry Cu deposits including Rio Blanco-Los Bronces (Davidson and Kamenetsky 2001), Bajo de la Alumbrera (Halter et al. 2005) and Bingham Canyon (Zhang and Audétat 2017). This residual felsic melt would have a strong influence on exsolved fluid chemistry: more evolved melt compositions favour the separation of more saline fluids because $D_{Cl(i)}^{fluid-melt}$ (> 10) is highest in felsic magmas (Tattitch et al. 2021). Chlorine is thought to be the key transporting agent for Cu in magmatic-hydrothermal systems (Candela and Holland 1984; Zajacz et al. 2012), so that elevated Cl would lead to higher concentrations of Cu in exsolved fluids.

Following the approach of Tattitch et al. (2021), Cu concentrations of instantaneous fluids exsolved from a melt can be calculated in order to quantify the effect of crystallisation on fluid composition. Using the experimental calibration of Tattitch and Blundy (2017), the fluid-melt partition coefficient for Cu ($D_{{{\text{Cu}}}}^{{{\text{fluid}} - {\text{melt}}}}$) can be calculated as a function of fluid NaCl ($X_{{{\text{NaCl}}}}^{{{\text{fluid}}}}$), H₂O ($X_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{{{\text{fluid}}}}$) and H₂S ($X_{{{\text{H}}_{{\text{2}}} {\text{S}}}}^{{{\text{fluid}}}}$):

$$\begin{aligned}{} & {} D_{fluid/melt}^{Cu} = 8 \cdot 10^{4}\cdot [(X^{fluid}_{NaCl})^{2} \cdot (X^{fluid}_{H_{2}}O)^{14} \cdot \nonumber \\{} & {} \quad (1+180 \cdot X^{fluid}_{H_{2}S})] + 380 \cdot X^{fluid}_{NaCl} + 0.8 \end{aligned}$$

(15)

The fluid NaCl is used from the previous model steps and the fluid H₂S is assumed to be zero for simplicity. Fluid NaCl can then be used to calculate the Cu concentration of fluids extracted from the magma during volatile evolution. $D_{{{\text{Cu}}}}^{{{\text{fluid/melt}}}}$ is integrated with the Cu concentration of the melt, which is calculated in each simulation by a randomly selected $D_{{{\text{Cu}}}}^{{{\text{min}} - {\text{melt}}}}$ (between 0 and 0.1) and initial Cu concentration of the melt (between 10 and 150 ppm; Chiaradia (2014)). With progressive crystallisation of the magma, the Cl and Cu concentrations of exsolved fluids increase from 2.5$-$5.0 wt% Cl and 0–1500 ppm Cu at 0% crystallisation, to 1–13 wt% Cl and 0–4000 ppm Cu at 50% crystallisation (Fig. 11). This increase is principally related to the increasing silica content of the residual melt, which leads to enhanced fluid-melt Cl partitioning (Tattitch et al. 2021). Past this crystallinity, the ranges in instantaneous Cl and Cu concentrations progressively decrease as the melt becomes depleted in these components due to prior fluid extraction. “Successful” model simulations (i.e. those which reproduce the porphyry melt volatile ratios) are plotted as a violin plot alongside these simulations. This analysis suggests that the Quellaveco apatite inclusions record a crystallinity interval (40–60% of an initial andesitic starting composition) which coincides with highest overall instantaneous concentrations of Cl and Cu. Therefore, we speculate that if the magmatic system was held at this crystallinity (i.e. mush-type) for an extended period, this may have been a key factor in generating the giant porphyry Cu deposit at Quellaveco. We additionally note that the extraction efficiency of Cu would also be further promoted if the modelled processes occurred in the mid-crust (200–400 MPa) rather than at shallower depths, due to the pressure dependency of $D_{{{\text{fluid/melt}}}}^{{{\text{Cu}}}}$ (Tattitch et al. 2021).

A second key implication of a high crystallinity magma beneath the Quellaveco porphyry Cu system is its influence on the accumulation and migration of exsolving fluids. Several studies have identified crystal-rich magmas as efficient reservoirs from which focussed fluids can be efficiently extracted (Huber et al. 2011; Oppenheimer et al. 2015; Parmigiani et al. 2016). Lamy-Chappuis et al. (2020) used numerical modelling to show that, above a critical volatile content, highly permeable capillary tubes can develop in mush regions as bubbles coalesce (at 50–70% crystallinity), promoting rapid, intrusion-scale fluid extraction. They also showed that, dependent on intrusion geometry, fluids may coalesce to a single area of fluid release, thereby allowing the large-scale fluid focussing required to form a porphyry Cu deposit. It is envisaged that fluids would accumulate beneath an impermeable carapace at the roof of the magmatic system, followed by episodic injection of melts and fluids upwards, as is observed in several porphyry systems (Dilles 1987; Proffett 2003; Sillitoe 2010). By contrast, under initially fluid-undersaturated conditions, a magma will be unable to develop these channel-flow mush domains as they fluid saturate after the optimal crystallinity window for bubble coalescence (Parmigiani et al. 2016; Lamy-Chappuis et al. 2020), resulting in unmineralised plutons such as the pre-ore Yarabamba Batholith. Notably, the proposed crystallinity remains close to the rheological lock-up of magmatic systems (ca. 50 vol.% crystals; Huber et al. (2011)). We do, however, consider this crystallinity realistic given that the volume % of phenocrysts in the Quellaveco porphyry rocks (and for many porphyry Cu rocks) can typically exceed 50 vol% crystals. Therefore, the hypothesis that porphyry Cu systems may be sourced from crystal-rich magmas is in agreement with the diagnostically porphyritic texture of their igneous rocks. Eventually, remobilisation of the magma would be required to emplace porphyry stocks and dykes, which could be facilitated by reheating and volatile fluxing through the system (Huber et al. 2010), perhaps triggered by mafic magma injections or underplating of the mush zone (Hattori and Keith 2001; Large et al. 2018). Another crucial property of a crystal-rich, fluid-saturated magma reservoir, is that its rheology would reduce the likelihood of eruption (Chelle-Michou and Rottier 2021), a process widely thought to be detrimental to the ore-forming potential of a magmatic system (Pasteris 1996; Buret et al. 2017). We hypothesise that such large, crystal-rich magma reservoirs, which are ultimately locally remobilised to generate small volume, shallow crustal porphyry stocks, are key to the generation of giant porphyry Cu deposits.

Conclusions

This paper has documented the evolution of volatile species in a magmatic system that produced a giant porphyry Cu deposit. The clear contrast between compositions of groundmass apatites and those included in zircons highlights the importance of analysing apatite inclusions in zircon in hydrothermally altered igneous rocks in order to provide robust constraints on magmatic volatile evolution. Integration of apatite inclusion in zircon major element data with thermodynamic modelling of apatite-melt F–Cl–OH partitioning and numerical modelling has provided insights into magma volatile evolution during porphyry system development. This reveals that the underlying magma reservoir at Quellaveco was fluid saturated during the Myr duration in which porphyry intrusions were emplaced and mineralisation developed, and was likely a crystal-rich system. By contrast, the pre-mineralisation Yarabamba Batholith appears not to have undergone significant fluid loss prior to apatite crystallisation. The presence of a high crystallinity magma reservoir at Quellaveco would have promoted efficient extraction of Cu from the magma from highly evolved, rhyolitic melt, and would have hindered eruptive destruction of the ore-forming magmatic-hydrothermal system. Thus, it is concluded that the construction of crystal-rich hydrous magma reservoirs in arc crust may be a critical step in forming world-class porphyry Cu systems.