Water speciation and hydrogen isotopes in hydrous stishovite: implications for the deep Earth water cycle

Abstract

Stishovite is a key mineral for understanding the deep Earth water cycle because of its potential as a main carrier for water into the transition zone and lower mantle. During subduction-related metamorphism of basaltic oceanic crust, stishovite stabilizes at 8–9 GPa and comprises 10–25 vol% of the bulk mineralogy, with some experimental studies indicating that stishovite can accommodate 3.5 wt% H₂O or more in the transition zone and upper lower mantle. This large water solubility has been explained by a hydrogarnet substitution mechanism (1Si⁴⁺ ↔ 4H⁺) and/or the incorporation of interstitial molecular water. To investigate water speciation and hydrogen isotope behavior, we synthesized partially deuterated hydrous stishovite at 9 GPa and 450 °C in a multi-anvil press (MA). The hydrous stishovite contains on average 1.69 ± 0.05 wt% water, which is consistent with earlier MA studies but is significantly lower than the 3.5 wt% reported from in situ diamond anvil cell (DAC) studies made at higher pressures and temperatures. ¹H MAS NMR spinning sideband characteristics suggest a high abundance of interstitial molecular water in hydrous stishovite, while the presence of a hydrogarnet defect cannot be ruled out. Unit-cell volumes and deuterium enrichment in the quenched hydrous stishovite indicate that ~ 45% of the water is lost from the stishovite upon quenching and decompression of the experiment, consistent with a higher solubility. This implies that the pristine water contents of a P–T–fO₂ equilibrated hydrous stishovite cannot be quenched to 1 atm and room temperature from classical MA experiments. We further present a capillary-based recovery method for fluid from experimental capsules, allowing direct determination of the D/H ratio of the experimental fluid and indirect determination of the hydrous stishovite. Using Rayleigh modeling to account for the quench-related water loss, we find that, at 450 °C and 9 GPa, deuterium is 3.5–4.5 times enriched in hydrous stishovite relative to coexisting aqueous fluid. This is opposite of what is commonly observed for mineral–fluid pairs above 300 °C, rendering hydrous stishovite a potential sink for deuterium and decreasing the D/H ratio of coexisting aqueous fluids. Partial decomposition (30–60%) of hydrous stishovite during mantle upwelling and production of primary basaltic melts could be accompanied by high-temperature D/H fractionation, decreasing the hydrogen isotope composition of such melts towards “mantle-like” δD values between −75 and −220‰.

Introduction

The high-pressure SiO₂ polymorph stishovite is a major constituent (~ 10–25 vol%) of deeply subducted oceanic crust at pressures > 9 GPa (Irifune et al. 1994; Litasov and Ohtani 2005; Ono 1998), and might be an important host for water (i.e., H, OH, or H₂O) in the transition zone and lower mantle (Lin et al. 2020, 2022; Nisr et al. 2020; Walter 2021). Al-rich stishovite (< 4 wt% Al₂O₃) has been shown to incorporate up to  ~0.3 wt% H₂O via a Si⁴⁺ ↔ Al³⁺  + H¹⁺ substitution mechanism based on samples quenched to 1 atm and 300 K from high pressure–temperature conditions in a multi-anvil (MA) apparatus (Litasov et al. 2007). Water solubility remains high for CaCl₂-structured Al-rich post-stishovite (β-stishovite), where MA experiments constrain H₂O concentrations to ~ 1.1 wt% and indicate even larger solubilities for higher P–T conditions due to an increasing solubility of Al³⁺ (Ishii et al. 2022). Much larger H₂O contents, up to 3.2 wt%, have been reported for Al-free stishovite synthesized under low-temperature hydrothermal conditions (350–550 °C 9–10 GPa) in a MA (Nisr et al. 2017; Spektor et al. 2016; Spektor et al. 2011). Further, Lin et al. (2020, 2022) report values in excess of 3 wt% H₂O in stishovite and β-stishovite synthesized in the diamond anvil cell (DAC) at pressures > 30 GPa, where unit cell volume expansions of up to 6% relative to anhydrous stishovite were observed.

To explain such large water contents, both a hydrogarnet substitution mechanism has been proposed where Si⁴⁺ is substituted by 4H⁺ (i.e., SiO₄⁴⁻↔ H₄O₄⁴⁻; Nisr et al. 2020; Spektor et al. 2011, 2016), as well as an interstitial molecular water incorporation mechanism (Lin et al. 2022). Notably, Lin et al. (2020, 2022) performed room-temperature DAC decompression experiments showing that as much as 90% of the water may be lost from the structure along a retrograde pressure path. Lin et al. (2022) demonstrated that the observed in situ unit cell volume change (∆V/V = (V_hydrous − V_anhydrous)/V_anhydrous) of DAC-synthesized stishovite matches theoretically calculated ∆V/V for stishovite with interstitial molecular H₂O (Fig. 1). In contrast, the ∆V/V of MA-synthesized stishovite is suggested to follow the theoretical ∆V/V for stishovite containing hydrogarnet defects. These findings imply that water can be stored as Si–O–H and molecular H₂O in stishovite, but there is a lack of direct evidence for molecular H₂O in its structure.

Fig. 1

Experimental and theoretical calculations of the stishovite unit cell volume expansion (∆V/V) versus H₂O content. Solid black lines represent density functional theory calculations of the volume expansion when water is stored as either a hydrogarnet defect (Si⁺ = 4 H⁺) (average of GGA and LDA results from Nisr et al. 2020, which are consistent with calculations in Lin et al. 2022), or incorporated as molecular H₂O in interstitial lattice positions (Lin et al. 2022). Data from Spektor et al. (2011), Nisr et al. (2017) and this study are from P–T-quenched samples synthesized in the multi-anvil press at ~ 10 GPa, 350–550 °C. H₂O contents in Spektor et al. (2011) are determined with TGA. H₂O contents in Nisr et al. (2017) are determined from the calibration of Spektor et al. (2011). H₂O contents of individual experiments in this study are determined from mass balance and the average of the experimental run products determined by LOI. Data from Lin et al. (2022) are from T-quenched stishovite taken at their synthesis pressures (~ 44–56 GPa, quenched to 300 K from ~ 1850 K) with water contents determined from the starting compositions. Dashed gray line is the y = 0 baseline

Along with the potential for hydrous stishovite to be a major host of water to the lower mantle, questions arise about the extent to which a pristine hydrogen reservoir in the mantle has been altered by recycled water after more than 3 Ga of subduction of hydrous surface material. For example, recent studies used mixing models of recycled oceanic crust and primordial mantle to explain characteristic hydrogen isotope systematics observed in MORBs and OIBs (Dixon et al. 2017; Loewen et al. 2019). However, our current understanding of high-temperature hydrogen isotope effects, which can impact the interpretation of measured D/H ratios, remains limited. The direction of deuterium partitioning between hydrous fluids, melts, and other water-bearing ultra-high-pressure (UHP) phases relevant to the mantle is largely unknown. The study of heavily deuterated stishovite is an experimental avenue to investigate the general direction of deuterium partitioning between UHP mineral phases and fluids, and offers insight into an environment where access to natural samples is limited.

In this study, we investigate water speciation in Al-free stishovite and the accompanying hydrogen isotope exchange with coexisting hydrous fluid. We synthesized anhydrous, protonated, and partially deuterated hydrous stishovite at 450 °C and 9 GPa and used hydrogen nuclear magnetic resonance (¹H NMR) and vibrational spectroscopy to reveal H speciation in the stishovite and deduce the hydrogen isotope composition of the system components. We report evidence for the presence of molecular H₂O in hydrous stishovite, discuss a potentially large D/H isotope partitioning between stishovite and the coexisting aqueous fluid, and outline implications for the interpretation of mantle D/H ratios observed from submarine basalts and melt inclusions.

Experimental and analytical methods

Glass and stishovite synthesis

The synthesis of hydrous stishovite involved two experimental steps. First, SiO₂ glass starting material with 8 wt% water was produced from General Electric (GE) semiconductor-quality fused silica glass (less than 10 ppm impurities) using a piston-cylinder press. Two batches were prepared, one with D₂O + H₂O and the other with H₂O only. The hydrous SiO₂ glass was then utilized for the synthesis of (i) partly deuterated and (ii) pure H₂O-bearing stishovite in a multi-anvil press. Nominally anhydrous stishovite was directly produced from GE fused silica glass. Details of the synthesis steps are outlined in the following and are summarized in Table 1. All experiments and sample analyses were conducted at the Earth and Planets Laboratory (EPL) of the Carnegie Institution for Science unless stated otherwise.

Table 1 Multi anvil experiments—starting material, water contents, unit cell volumes, and hydrogen isotopes

Hydrous SiO₂ glass synthesis

The GE glass was finely ground under ethanol, dried, and sieved to < 150 µm mesh before firing at 950 °C for 2 h to remove organic and volatile impurities. The GE glass was loaded together with D₂O (99.9%, Cambridge Isotope Laboratories) or H₂O (Milli-Q) in a platinum capsule (5 mm outer diameter and 14 mm length) in a proportion that resulted in a final hydrous SiO₂ glass containing 8 wt% water. The Pt capsule was carefully crimped under a microscope and welded shut under a stream of Argon using a PUK pulsed arc welder. The bottom of the capsule was carefully cooled with a moist tissue to prevent evaporation of water. The hydrous glass synthesis was performed in a piston-cylinder press using a ¾-inch MgO–Pyrex-talc assembly with a tapered graphite furnace. Run conditions were 1500 °C and 1.5 GPa for 2 h, and rapid quench (ca. 60 °C/s) proceeded under near-isobaric conditions. The temperature was controlled with a Pt-Pt₉₀Rh₁₀ (Type S) thermocouple connected to a Watlow F4T thermocontroller. Weight control with a Sartorius CP2P microbalance during the capsule preparation process, as well as before and after the experiment, assured no loss or gain of volatiles during the synthesis run. Hydrous glass products appear transparent and vesicle-free and yield no signs of a free volatile phase (e.g., no observed water loss during capsule opening under a microscope, no glass meniscus), suggesting that all water is dissolved in the SiO₂ glass. Loss on ignition (LOI) analysis performed at 1200 °C for one hour confirms 8.1 ± 0.05 wt% H₂O (Mettler Toledo XPR 2 microbalance, ETH Zurich). The hydrous character of the SiO₂ glass was also confirmed by Raman spectroscopy, showing OH and OD stretch bands at c. 3600 and 2500 cm⁻¹, respectively (Fig. 3, discussed below). The strong O–H band reveals significant H₂O contamination in the nominally ¹H-free D₂O–SiO₂ glass, suggesting hydrogen diffusion through the platinum capsule from the pressure medium (cf. Kueter et al. 2022). Platinum is permeable to hydrogen, particularly at high temperatures. The reaction of H₂O released from the talc pressure medium of the piston-cylinder assembly during the experiment likely reacted with the graphite furnace. Thermodynamic calculations predict 5 mol% H₂ for the COH fluid expected for the employed pressure and temperature conditions (Connolly 2005). We suspect that hydrogen diffusion from the capsule exterior into the charge is accompanied by a mass-conserving isotope exchange reaction in the form of H₂ + D₂O ↔ HD + HDO, lowering the D₂O concentration in the experimental charge. This process produced a deuterated SiO₂ glass with 36 mol% H₂O and 64 mol% D₂O (D/H ratio 1.79), determined from the area integration of the Raman signal of the glass (supplementary information). For the purpose of our study, this creates an advantage, as an H₂O/D₂O system allows for the investigation of possible isotope effects and improves the resolution of the ¹H NMR spectra (Eckman 1982). For future studies aimed at investigating a pure D₂O–SiO₂ system, we recommend synthesizing a glass precursor either in a gas pressure vessel or in a piston-cylinder press using an anhydrous pressure medium (e.g., BaCO₃, NaCl). The glass starting materials were dry crushed, sieved to < 150 µm, and stored in a desiccator.

Stishovite synthesis

Synthesis experiments were performed in 2.4 mm outer diameter, 4 mm length gold capsules filled with the hydrous SiO₂ glass. Empty capsules were first heated at 1000 °C overnight, then filled with the starting material and welded shut with the PUK arc welder. All capsules were leak tested by immersing them in acetone overnight and monitoring weight changes with a microbalance. The stishovite syntheses were performed in a 1500-ton Presnall-type 6/8 multi-anvil press, using 32-mm tungsten carbide cubes, with 8-mm truncation edge length, a 14-mm edge length MgO octahedral pressure medium, and a rhenium-foil heater. Temperature was monitored with a Type C thermocouple (Tungsten Rhenium alloy, W5%Re/W26%Re). All experiments were pressurized at a rate of 0.4 GPa/h to 9 GPa and then manually heated at ca. 40 °C/min to 450 °C and held for 48 h. Quenching was achieved by turning off the power supply; room temperature was reached in a few seconds. Experiments were decompressed at 0.4 GPa/h. Water extruding from the capsule after piercing with a needle provides evidence for stishovite syntheses under water-saturated conditions. For Runs 2, 4, 5, and 6, free water in the capsule was recovered using the fused silica capillary technique described in the supplementary information (Fig. 2, Fig. S1). Dry stishovite was synthesized from GE glass at 9 GPa and 1000 °C and in a run held for 48 h. Pierced capsules were exposed to vacuum (10^–3 mbar) for 12–24 h to remove all volatiles. Information on starting material, water contents, unit cell volumes, and hydrogen isotopes are summarized in Table 1.

Fig. 2

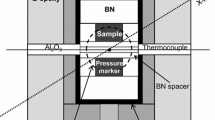
Sampling of experimental aqueous fluid using a preconditioned fused silica capillary. A A cleaned Au capsule is fixed in a vice grip and pierced. The extruding water is soaked up by capillary forces. B The experimental fluid is then transferred to the center part of the capillary by applying a low pressure on the opposing capillary orifice. C The capillary ends are fused with a blow torch. Detailed description and video are available in the supplementary materials

Scanning electron microscopy (SEM)

Small aliquots of glass and stishovite powder were spread on carbon tape glued on aluminum stubs and coated with an ~ 1 nm thick layer of iridium. Samples were introduced into a Zeiss Auriga field emission SEM and typically imaged at 8–9 mm working distance applying a 15 kV acceleration voltage and a probe current of ~ 1 nA.

Powder X-ray diffraction analysis

Powder X-ray diffraction (PXRD) measurements were performed on recovered samples using a Bruker D8 Discover diffractometer equipped with a CuK_α microfocus source and high-resolution LYNXEYE XE silicon strip detector with Soller silts. A small amount of recovered powder (< 1 mg) was pressed as a flat pellet onto a zero-background silicon wafer and aligned at the diffractometer center. Coupled θ/2θ scans were collected in reflection mode with a 500 mm beam from 2θ ≈ 25–100° with a 0.025° step size and 2-s dwell time. Instrumental calibration was verified in the same geometry using NIST powder standards SRM 1976b and 660c. Lattice parameter determination was performed through full-profile Le Bail refinement of diffraction patterns using JADE (Materials Data, Inc.) analysis software, including background, peak profile, and sample displacement parameters.

Vibrational spectroscopy

Raman spectra were acquired with a Jasco IRS-3100 confocal micro-Raman spectrometer equipped with a 532 nm laser operating at about 31 mW at the sample. Spectra were acquired unpolarized with 600 grooves/mm (1300–4200 cm⁻¹ covering the O–H and O–D stretch region) gratings, 0.1 × 6 mm slit, and 60-s acquisition time using two iterations. The spectral resolutions are < 25 and < 8.5 cm⁻¹, respectively. Wavelength calibration was performed using the first-order diamond Raman signal at 1332 cm⁻¹. Background correction and peak fitting were performed with the Multipeak Fit program in IGOR Pro v.2 software from Wavemetrics.

Fourier-transform infrared (FTIR) spectra were obtained using a Bruker Vertex spectrometer with a Hyperion microscope equipped with a mercury cadmium telluride (MCT) detector. The total spectral range spanned 500–8300 cm⁻¹ with a resolution of 4 cm⁻¹. FTIR analyses were made using a 0.56 mm thick pellet containing a 26:1 (by mass) mixture of KBr and the combined products of Runs 1, 2, 4, and 5. The pellet was made by grinding the respective precursors together and compressing the resulting mixture with a Specac 13 mm pellet die and a Carver 3850 Mini C manual benchtop press. This sample was dried overnight in a Fisher Scientific Isotemp 282A vacuum oven at 120 °C to remove adsorbed water. Transmitted light was collimated to a window size of 500 µm², and spectra were collected using 512 scans and referenced to a pure KBr pellet.

NMR spectroscopy

Hydrogen NMR was performed with a Varian-Chemagnetics Infinity 300 solid-state NMR spectrometer at the W. M. Keck facility at Carnegie EPL, employing a static magnetic field of 7.05 T. Dried stishovite samples were gently crushed and loaded in ZrO₂ rotors (2.5 and 5.0 mm O.D. for ¹H and ²H, respectively). Protium (¹H) NMR spectra acquisition was performed at a magic angle spinning (MAS) probe-frequency (ω_r/2π) of 22 kHz (drift is less than ± 20 Hz). RF coil ¹H background suppression followed a DEPTH four-pulse sequence. The acquisition was performed with a ¹H 90° pulse length of 2.5 µs followed by a 10-s recycle delay to account for a ¹H spin–lattice relaxation time of about 2 s. Spectral width was set to 200 kHz, and the spectra referenced with respect to tetramethylsilane defined as 0 ppm. A total of 8000 spectra were acquired per sample.

²H NMR spectroscopy was performed at an RF frequency of 46.08 MHz and magic angle spinning frequencies of 8000 ± 1 Hz. The magnitude of the quadrupolar coupling interaction in deuterated materials can be as large as 204 kHz (Cody et al. 2020), resulting in a signal spanning 400 kHz. As the MAS frequency is much less than the quadrupolar interaction, the ²H NMR spectrum from powdered solids consists of multiple spinning sidebands, whose intensities map out the shape of the ²H quadrupolar powder pattern (Cody et al. 2020; Wang et al. 2015). For O–D groups, this powder pattern is a characteristic “Pake” powder pattern arising from a high degree of radial symmetry of the electric field gradient surrounding the deuterium nucleus. In the case of D₂O molecules, rapid 180° flips average the symmetry of the electric field gradient to one with a very high degree of biaxiality (Cody et al. 2020; Eckert et al. 1988; Schmidt-Rohr and Spiess 2012; Wang et al. 2015). Thus, in theory, the symmetry of the ²H NMR spectrum can be used to distinguish OD from D₂O in deuterated stishovite. However, the gyromagnetic ratio of ²H is six times smaller than that of ¹H, and the ²H signal is spread over ~ 32 peaks spanning 400 kHz, whereas the ¹H exhibits a close cluster of peaks spanning 3.3 kHz. Consequently, spectra are much more difficult to acquire for ²H NMR than for ¹H NMR.

Unfortunately, our attempts to acquire ²H MAS NMR spectra were unsuccessful. The total water contents of the recovered hydrous stishovite samples are small, containing ~ 1.7 wt% (cf. “Hydrous stishovite characterization” section) and the total weight of sample recovered is low at ~ 60 mg. FTIR and Raman indicate that ~ 50% of the water in four of the runs is deuterated. Multiple attempts revealed only very weak peaks that, while indicating the presence of deuterium, were too weak to ascertain the symmetry of the quadrupolar interaction. Aside from the low absolute deuterium abundance, we speculate that deuterons in the stishovite lattice have very unfavorable T₁ characteristics, necessitating long recycle delays that do not allow sufficient acquisition numbers to achieve acceptable signal-to-noise D NMR spectra. Thus, ²H MAS NMR spectra will not be discussed further.

Results and discussion

Hydrous stishovite characterization

Piercing of Runs 1, 2, 4, 5 and 6 liberated water from the capsule interior (Fig. 2, S1), indicating that the hydrous silica glass precursor released an excess fluid phase during stishovite synthesis. SEM imaging reveals a network of tetragonal crystals ~ 0.5–2 µm in size, organized in a texture with open porosity (Fig. 3A, B). Because rare remains of strongly corroded glass fragments were recognized in Run 1 (Fig. 3A) before further experiments, the glass material was ground again and sieved through a finer mesh (< 150 µm), with the result that no residual glass fragments were recognized in subsequent runs (2–6). The run products appear as white to light-gray, fine-grained material. PXRD and Raman spectroscopy identified the SiO₂ phase as stishovite (Fig. 4). Additionally, coesite was observed as a dominant phase in Run 3, but piercing did not deliver a fluid phase. The experiment failed after 15 min, possibly due to a capsule rupture, where extruding water oxidized the rhenium heater. Post-quenching water could be collected for Runs 2, 4, 5, and 6 using a capillary recovery technique described in detail in the supplement (Fig. 2, Fig. S1). Differential weighing of the capsules before and after piercing indicated that ~ 1/3 of the capsule fluid could be recovered using this method. Vacuum drying at 70 °C for 24 h and subsequent weighing indicated that 75–83% of the total water in the capsule was present as fluid. 17–25% of the water remained in the capsule after the vacuum drying, which is assigned as structurally bound within the stishovite. This assumption is based on the observed open porosity of sintered stishovite imaged by SEM. Based on weight, our hydrous stishovite contains between 1.5 and 2.1 wt% water (average 1.9 ± 0.3 wt%). LOI analysis of the combined Runs 1, 2, 4, and 5 yields 1.69 ± 0.05 wt% water. This is slightly higher than the 1.4 wt% water reported for stishovite synthesized under the same conditions reported by Spektor et al. (2011, 2016), possibly due to the use of deuterated water.

Fig. 3

A Corroded glass fragment embedded in a porous network of µm-sized tetragonal stishovite crystals (Run 1). B Close up of the stishovite material, showing intergrown crystallites (Run 1). C Raman spectra for the wave number region of the O–H and O–D stretching resonance. Shown are non-background corrected spectra. Red: Hydrous SiO₂ glass used for the stishovite synthesis. A pronounced O–H resonance near 3500 cm⁻¹ evidences the presence of protonated water in the starting material, introduced by diffusive H₂–D₂ exchange during the glass synthesis (cf. “Hydrous SiO₂ glass synthesis” section ). Black: Experimental water recovered from experiments using a capillary sampling technique (Fig. 2; supplementary information)

Fig. 4

PXRD patterns of anhydrous (red) and hydrous stishovite (black: D₂O/H₂O, blue: H₂O only). The left panel shows an overview, and the right panel zooms in on the 220 reflection at ca. 63° (2Θ) to show the Bragg peak shift of the hydrous sample. Dashed gray lines denote the Bragg angles of the anhydrous stishovite reflections. Note that only the hk0 reflexes (e.g., 220) are moving, hkl are not affected (e.g., 111), indicating expansion along the a lattice parameter of the stishovite unit cell. Asterisk: Au from the capsule. Non-annotated reflexes in Run 3 are from coesite

The presence of structural water is also indicated from powder X-ray diffraction analysis. Figure 4 compares the PXRD patterns of anhydrous stishovite (Run 7, red) with the hydrous stishovite. Indices following hk0 (i.e., 110, 120, 220, 310) are shifted to lower Bragg angles in the hydrated samples, indicating that the unit cell expanded along the a lattice parameter when hydrated (See right panel in Fig. 4). No shift is observed for the hkl associated with the c lattice parameter. This is consistent with previous studies showing volume expansion along the a lattice parameter (~ 4.178 Å for anhydrous, 4.18–4.3 Å for hydrous stishovite), while the c lattice parameter shows no systematic variation (~ 2.665 Å) (Spektor et al. 2016).

The splitting of Bragg reflections (e.g., the 220), as observed by Spektor et al. (2016) for hydrous stishovite synthesized at < 400 °C or deuterated stishovite synthesized at 450 °C, was not observed in our samples. The corresponding unit cell volumes determined for our hydrous stishovite are 46.8 ± 0.2 ų (46.75 ± 0.05 ų excluding Run 3) and are expanded by ~ 0.4% relative to our anhydrous stishovite (46.57 ± 0.04 ų). The unit cell volumes are compared with literature data for hydrous stishovite (Figs. 5, 10). The strongly expanded unit cell volumes observed for “phase-separated” stishovite (46.9–47.6 ų) described by Spektor et al. (2016) were reproduced in our 15 min Run 3 (47.12 ± 0.02 ų, Fig. 5). Peak broadening in the PXRD suggests that most stishovite crystallites in Run 3 are < 100 nm compared to the µm-sized crystals in the other runs. It is possible that water incorporation has a greater effect on the stishovite lattice expansion for small, early crystallites and becomes less pronounced once the crystals grow. Comparing the XRD patterns and Bragg reflections of our protonated and deuterated stishovite does not reveal any measurable isotope effect on the lattice parameters. Prolonged storage under room conditions had no altering effect on the stishovite; lattice parameters remained unchanged between the first PXRD acquisition right after synthesis and 6 months later, suggesting that hydrous stishovite retained at least some portion of its original structural water once quenched to room temperature. This is consistent with prior FTIR observations of water-rich (post-) stishovite performed over a 4-month time interval described by Ishii et al. (2022).

Fig. 5

Measured unit cell volumes of stishovite synthesized in this study. 1σ uncertainties mostly within symbol size. Run 7 is anhydrous

Figure 6 shows the FTIR spectrum of the combined Runs 1, 2, 4, and 5 in the range of 1200–400 cm⁻¹, where water-related resonances can be expected. The blended sample was used for FTIR analysis instead of recording individual spectra to minimize material loss to the KBr pellet. Our attempt to perform ²H NMR spectroscopy necessitated the blending of replicates. The double peaks of the O–D and O–H stretching bands at 2029 and 2145 cm⁻¹, as well as 2646 and 2880 cm⁻¹, are resolved. The observed vibrations are similar to the FTIR spectra reported by Spektor et al. (2011, 2016) and suggest X–O stretching oscillations (X=D, H). Although Spektor and coworkers attribute these vibrations to the hydrogarnet defect, they acknowledge that this defect is typically represented by a single O–X stretching band (Rossman and Aines 1991). To explain the band doublet, the authors propose the presence of two O–X oscillators with slightly different O–X⋯O configurations. Notably, the band at ~ 2650 cm⁻¹ was previously observed in water-poor Al-rich stishovite (Frigo et al. 2019; Litasov et al. 2007) and both the bands near 2650 and 2900 cm⁻¹ were detected in hydrous post-stishovite (i.e., β-stishovite with CaCl₂ structure; (Ishii et al. 2022). In both studies, these bands appear highly pleochroic, indicating that water is structurally oriented within the crystal lattice.

Fig. 6

Unpolarized FTIR spectrum of hydrous stishovite (combined samples Run 1, 2, 4, and 5). The FTIR analysis was performed after combining the four replicate runs required for ²H NMR spectroscopy. Therefore, the presented FTIR spectrum represents a combination spectrum for partly deuterated stishovite. Clearly visible are the stretching bands for O–D near 2029 and 2145 cm⁻¹ and O–H near 2646 and 2880 cm⁻¹. The inlay shows unpolarized FTIR spectra for hydrous Al-rich Stishovite synthesized by Litasov et al. (2007). The Al-free, low-T stishovite from our study lacks the prominent band near 3120 cm⁻¹, but all spectra show a signal near 2650 cm⁻¹. Sample K-342 also yields minor bands near 2890 cm⁻¹, coinciding with those observed in our spectrum

A weak signal observed at 3390 cm⁻¹ was previously assigned to intergranular molecular H₂O (Spektor et al. 2016). In our deuterated system, a corresponding signal for molecular D₂O should be expected near 2530 cm⁻¹ due to an isotopic high-frequency shift, but could be overlapped by the low-frequency shoulder of the prominent 2646 cm⁻¹ O–H stretching band. However, the 3390 cm⁻¹ O–H stretching band is closely related to the 1634 cm⁻¹ H–O–H bending mode observed in our spectra (Seki et al. 2020). Deuteration would create D–O–H and D–O–D bending modes near 1450 and 1205 cm⁻¹, respectively. Those modes are not observed, but would be expected if experimental fluid is trapped in intergranular pockets. This suggests that the 3390 and 1634 cm⁻¹ bands are due to atmospheric water adsorbed after opening the experiments. We further observe two bands at 1348 and 1418 cm⁻¹. Similar bands were previously described separately from D₂O-stishovite and H₂O stishovite (Frigo et al. 2019; Spektor et al. 2016). Spektor et al. (2016) attributed the bands to the hydrogarnet defect, while Frigo et al. (2019) assign the bands to lattice overtones.

Characterization of water in stishovite from ¹H NMR

The ¹H MAS NMR spectra of five different runs of hydrous stishovite are presented in Fig. 7. All ¹H NMR spectra exhibit an intense peak at 11.5 ppm. Runs 2–6 show a discrete, slightly weaker peak at 5.8 ppm, and in each run, a weaker peak at 1.5 ppm is also evident. Close inspection of the 11.5 ppm signal shows the existence of a shoulder near 9 ppm in all the Runs (Fig. 7, arrow). The ¹H NMR spectra are broadly comparable with the ¹H NMR spectra of Spektor et al. (2011). However, in the present spectra, the highest frequency and middle frequency peaks (at 11.5 and 5.8 ppm) are at slightly higher frequencies than those previously reported (10.5–11 ppm, and 4.7 ppm) for reasons that are not currently known. Spektor et al. (2016) reported ¹H NMR spectra with a split peak at 11.4 and 10.8 ppm (at room temperature) that narrowed to a single peak at 11.1 ppm (at 100 °C). In our dataset there is no indication of peak splitting at room temperature and all the samples present the same main features in the ¹H NMR spectra (Fig. 7). However, differences in proton peak intensities are evident from run to run: spectral shapes of the deuterated Runs 1 and 4, and Runs 2 and 5 are similar but differ between the pairs in the relative intensity of the lower-frequency signals (i.e., Runs 2 and 5 yield higher low-frequency intensities). The 11.5 ppm signal of deuterated Runs 1–5 exhibits stronger intensities and significantly smaller signal width relative to the protonated Run 6, resulting from isotope dilution (Eckman 1982).

Fig. 7

Left: ¹H NMR center bands show three main contributions: near 1.5 ppm (low frequency, LF), 5.8 ppm (mid-frequency, MF), and 11.5 ppm (high frequency, HF). Similarities in signal shapes are seen between the partially deuterated Runs 1 and 4 and Runs 2 and 5, but general variability in the NMR spectra is apparent. The purely protonated Run 6 shows a wider HF band relative to the partially deuterated stishovite. The arrow indicates a shoulder near 9 ppm. Right: Low-frequency spinning side band (SSB). Dashed lines correspond to the centerband peak positions, and their corresponding positions in the SSB spectra

The chemical shift of the ¹H NMR signal is indicative of the bond lengths in an O–H⋯O configuration, where the ¹H frequency increases with increasing O–H bond distance (Berglund and Vaughan 1980; Eckert et al. 1988; Xue and Kanzaki 2004). A shift to higher frequencies suggests stronger hydrogen bonds. Low-frequency signals in the range of ~ 1–7 ppm are commonly observed in SiO₂–H₂O systems and indicate numerous proton environments and hydrogen bonding configurations. In this study, such environments account for 20–44% of the total proton environment. Previous studies assigned resonances between 3.2 and 4.7 ppm to dissolved H₂O and silanol groups (Si–OH) in hydrous SiO₂ glasses (Kohn et al. 1989). However, in our study, remains of the glass starting material were only found in Run 1 (Fig. 3A), which also yields the lowest intensity of low-frequency signals, suggesting that undetected glassy remains are unlikely to explain the low-frequency signals. Instead, we propose that chemically and physically absorbed water (i.e., silanol-terminations and adsorbed molecular water) on silicate surfaces may better explain the observed resonances, as suggested by Kinney et al. (1993). Several lines of evidence support this explanation. The 5.8 ppm feature shows similar peak width characteristics in Runs 2, 5, and 6, indicating no isotope dilution effect on the peak width, which would be expected if the hydrogen were trapped inside the stishovite. In fact, surficial hydrogen bonding could explain the observed variability of the low-frequency signals, because chemically and physically absorbed deuterated water would quickly exchange with protons from the ambient humidity. For this to be the case, Runs 1 and 4 must have had shorter exposure times to lab air, while Runs 2 and 5 were exposed longer. However, we did not track the sample exposure time to verify this. Spektor et al. (2016) assigned a 5 ppm signal to intergranular molecular water, but in our samples, the lack of isotope dilution effect and FTIR evidence (missing H–O–D and D–O–D bending modes) do not support this hypothesis. The 1.5 ppm feature is likely due to surface hydroxyl groups (Kinney et al. 1993) and a minor contribution from organic contamination cannot be ruled out (Yesinowski et al. 1988). Since the 5.8 and 1.5 ppm features are attributed to surface water and not relevant for hydrogen dissolved in the stishovite, they will not be discussed with regard to the water speciation in the stishovite.

The 11.5 ppm resonance and its shoulder near 9 ppm indicate at least two hydrogen environments with relatively strong hydrogen bonds (i.e., long covalent O–H bonds), which is expected for hydrogen in solids. Further, the isotope dilution effect on the signal width and the consistent signal intensity suggests that the hydrogen is bound in the stishovite. However, ¹H NMR frequencies cannot distinguish OH groups from H₂O groups, and each peak may be due to either OH or H₂O groups or a mixture of the two.

Whereas peak frequencies cannot discriminate between different water species, the intensity of spinning sidebands (SSB) observed during moderate to rapid MAS can be used to resolve isolated OH groups from H₂O groups. At MAS frequencies > 8 kHz, SSB intensities report residual dipolar coupling interactions between ¹H’s. Dipolar interactions between ¹H’s scale strongly non-linearly with ¹H–¹H distance, r, and the dipolar coupling decays in strength proportional to 1/r³; (Levitt 2013). For immobilized H₂O molecules in solids, the ¹H–¹H distances are short and dipolar coupling strength will be relatively strong, thus creating more intense SSB. For isolated OH groups, ¹H–¹H distances are inherently more distant and resulting SSB are small to non-existent, particularly with the 22 kHz MAS frequency employed here. In the right panel of Fig. 7, ¹H NMR spectra are expanded to show the SSB intensities for Runs 1–6. In Run 6 with 100% H₂O, the relatively strong SSB intensity indicates that a significant proportion of ¹H exists in the form of H₂O. The SSB intensity is distinctly weaker in the mixed D₂O–H₂O Runs 1–5, which is consistent with isotopic dilution. In water with a D:H of 50:50, one predicts ~ 50% HDO, ~ 25% H₂O, and 25% D₂O. ¹H NMR only detects protium, so the signals observed in Fig. 7 are derived only from HDO and H₂O (assuming only water molecules are present), but only H₂O will contribute to SSBs as H–D dipolar coupling is too weak and will be averaged to nearly zero at 22 kHz MAS. Therefore, the sideband intensity for the mixed D₂O–H₂O Runs 1–5 are expected to be ~ 50% that of Run 6 (100% H), which can indeed be observed visually from Fig. 7 and is displayed by the center band to spinning sideband ratio (∑SSB/CB) in Fig. S3. In the previous ¹H NMR studies of hydrous stishovite (Spektor et al. 2016, 2011), only the center band was shown, so the intensity of SSBs in their ¹H NMR is not available for comparison with those in the present study.

∑SSB/CB can, in theory, be used to ascertain the proportion of H₂O and Si–OH (e.g., Cody et al. 2020). However, as neither the ¹H–¹H distances of H₂O in the stishovite structure nor the molecular motion of H₂O in the various H environments detected was known, only a qualitative assessment of the water speciation in the stishovite structure was possible. In Fig. 8, we present theoretical calculations performed with the SIMPSON solid-state NMR simulation program (Bak et al. 2000). We calculated ∑SSB/CB for interproton distances between 1.4 and 2.9 Å (cross symbols) and fitted the points by an exponential expression, i.e., $\frac{\mathrm{\Sigma SSB}}{\mathrm{CB}}=0.006+48.492{\mathrm{e}}^{-3.234\cdot d}$, where d is the interproton distance. Substances with short interproton distances such as molecular water will plot on the curve with larger ∑SSB/CB, while the ratio decreases towards greater interproton distance. Isolated protons such as in silanol speciation (Si–OH), or protons in H–D configuration will not create SBBs and the ∑SSB/CB converges to zero. As a test, we matched the measured ∑SSB/CB ratio of gypsum (CaSO₄⋅2H₂O; 0.333; from Cody et al. 2020) to the curve, which yields an interproton distance of 1.55 Å, indistinguishable from ¹H–¹H distances obtained from earlier ¹H NMR, neutron, and X-ray diffraction studies (Cole and Lancucki 1974; Mcknett et al. 1975). The observed variation in SSB intensity for the deuterated stishovite reflects the variability of stishovite D/H ratio (cf. “Isotope effect” section). ∑SSB/CB decreases with increasing deuterium content, as indicated by the increasing D/H ratio of the stishovite (Fig. 8). As visible in Fig. 8, this isotope dilution effect on ∑SSB/CB is also observed for variously deuterated sodium tetrasilicate (NS4) glasses containing 8 wt% water (Kueter et al. 2022). Note also that the 100% H₂O NS4 glass plots close to the gypsum data point. Its slightly lower ∑SSB/CB can be attributed to a slightly higher mobility of the H₂O molecules in the glass compared to the rigid binding in the gypsum mineral lattice (Cody et al. 2020).

Fig. 8

Correlation of the spinning side band to center band intensity ratio (∑SSB/CB) and the intramolecular ¹H–¹H distance. Data are fitted to a theoretical ∑SSB/CB curve calculated for interproton distances between 1.4 and 2.9 Å (cross symbols). The ∑SSB/CB ratio of gypsum (gray circle) corresponds to an interproton distance of 1.55 Å, within 0.01 Å of accepted literature values. Projection of ∑SSB/CM ratios measured from our hydrous stishovite samples indicates interproton distances between 1.8 and 2.1 Å (red circles). The 100% H₂O Run 6 has the highest ∑SSB/CB because isotope dilution decreases the SSB intensity. To illustrate the isotope dilution effect, a series of variously deuterated hydrous sodium tetrasilicate glasses are plotted (orange triangles, from Kueter et al. 2022). Interproton distances reported by Spektor et al. (2011; abbreviated S’11, light blue circles) give very low ∑SSB/CB ratios. The 4H configuration in a hydrogarnet defect increases the ∑SSB/CB ratios slightly (dark blue circle). Inset: ¹H NMR spectra of gypsum (Cody et al. 2020) and stishovite (Run 6). Asterisks denote spinning sidebands. Bracketed values are the D/H ratios of the stishovite, cf. “Isotope effect” section

We simulated the solid-state ¹H NMR spectrum of a 4-H hydrogarnet cluster at 22 kHz MAS to determine whether this could produce significant SSB intensity (Fig. S4; Bak et al. 2000). The hydrogarnet defect suggested by previous studies is a 1Si⁴⁺ by 4H⁺ substitution that forms a distorted tetrahedron of Si–OH terminations (Nisr et al. 2017; Spektor et al. 2016, 2011). Based on two-dimensional double quantum/single quantum correlation NMR spectroscopy, Spektor et al. (2011) obtained interproton distances of 2.6 and 2.9 Å (with dipolar coupling strengths of 7.0 and 4.8 kHz, respectively). This is a sufficient distance such that at 22 kHz MAS frequency, minimal spinning sideband intensity should be detected (Cody et al. 2020) and the corresponding ∑SSB/CB would be low (0.017 and 0.01, Fig. 8, light blue circles). However, in these hydrogarnet clusters, each H interacts magnetically with three other H’s, potentially enhancing the amount of dipolar coupling over that of a spin pair. Indeed, even though the H’s in the 4-H cluster are 2.6 and 2.9 Å apart, larger SSB are predicted at 22 kHz MAS frequency, resulting in ∑SSB/CB = 0.034 (Fig. 8, dark blue circle). However, this 4-H cluster SSB intensity is far weaker than what is observed in our stishovite ¹H NMR spectra (∑SSB/CB 0.06–0.14, avg = 0.09); Fig. 8, red circles). This indicates that even if there are some 4-H clusters in the current hydrous stishovite experiments, they would be very subordinate, with the majority of H being in the form of H₂O.

The ∑SSB/CB of hydrous stishovite is reduced by ~ 1/2 relative to that of gypsum; this reduced dipolar coupling could be due to a more stretched H–O–H configuration of the interstitial H₂O molecules. Although the reduced dipolar coupling may also be a result of mobile H₂O molecules in interstitial lattice spaces (which is indirectly indicated by quench-induced water loss from the stishovite which implies rather fast diffusion of water in the mineral; cf. “Isotope effect” section), we suggest that because the magnitude of dipolar coupling scales by inverse cube, a small increase of the interproton distance near the gypsum endmember would decrease the SSB intensity dramatically (Cody et al. 2020). This hypothesis is further corroborated by the chemical shift of the center band, that is at 4 ppm for gypsum and 11.5 ppm for stishovite (cf. inlay in Fig. 8). For oxygen-bound hydrogen, a high-frequency chemical shift is indicative of an increased length of the covalent bond, commonly induced by the strong attraction of a hydrogen acceptor oxygen in a hydrogen bond configuration (Si–O–H⋯O–Si) (Berglund and Vaughan 1980; Eckert et al. 1988). This suggests that the covalent O–H bond length for H₂O in hydrous stishovite is greater than for gypsum, and could indicate a distortion and widening of the H–H distance of the interstitial H₂O molecule.

Isotope effect

The partially deuterated experimental system allows for the investigation of the direction of hydrogen isotope fractionation during stishovite synthesis. We estimated the D/H ratio of the hydrous SiO₂ glass and of the recovered experimental fluid based on the signal areas of the O–H and O–D Raman resonances near 3500 and 2550 cm⁻¹, respectively. A cubic baseline correction was applied to all spectra, and the signals were then fitted with Gaussian peaks to obtain the signal areas (supplementary information). Zarei et al. (2018) noted variations in the Raman cross sections of O–X species (X = D, H) at varying D₂O concentrations, requiring correction of any D/H ratio obtained from water by Raman spectroscopy. We analyzed gravimetric mixtures of H₂O and D₂O (25–100% D₂O) in fused silica capillaries but found no significant deviation of the D₂O concentration obtained by Raman spectroscopy from the nominal D₂O concentration (Fig. S2). Hence, no correction was applied. Variations in the Raman scattering cross sections of glass-bound Si–OX groups cannot be ruled out. The O–X vibrations for the hydrous stishovite could not be resolved due to poor signal-to-noise ratio. Even if successful, Raman-based determination of the D/H ratio would have been questionable due to 20–45% adsorbed H on the stishovite surface, as indicated by ¹H NMR. Therefore, the D/H ratio of stishovite was estimated through mass balance calculations based on the D/H ratio of the recovered fluid.

The hydrous SiO₂ glass contains 8.1 wt% water with a hydrogen isotope ratio ${\left(D/H\right)}^{\mathrm{SM}}$= 1.79. It can be expected that all water is released from the decomposing glass during the 48 h experiment and is either present in the stishovite or as a free fluid. The total water content in an experiment (${m}_{\mathrm{Aq}}^{\mathrm{SM}}$) is defined by the amount of hydrous SiO₂ glass loaded into the capsule (${m}^{\mathrm{SM}}$). The weight of the post-experimental free fluid (${m}_{\mathrm{Aq}}^{\mathrm{fl}}$) next to the hydrous stishovite was obtained from the weight difference between an unopened and a pierced, vacuum-dried capsule using a microbalance. From this, one obtains the mass of the hydrous stishovite (${m}^{\mathrm{Stv}}$) and the mass of the water in the hydrous stishovite (${m}_{\mathrm{Aq}}^{\mathrm{Stv}}$):

$${m}^{\mathrm{Stv}}= {m}^{\mathrm{SM}}- {m}_{\mathrm{Aq}}^{\mathrm{fl}},$$

(1)

$${m}_{\mathrm{Aq}}^{\mathrm{Stv}}= {m}_{\mathrm{Aq}}^{\mathrm{SM}}- {m}_{\mathrm{Aq}}^{\mathrm{fl}}.$$

(2)

The D/H ratio of the hydrous stishovite can now be calculated as follows:

$${\left(D/H\right)}^{\mathrm{Stv}}=\frac{{{\left(D/H\right)}^{\mathrm{SM}}-X}_{\mathrm{Aq}}^{\mathrm{fl}}\cdot {\left(D/H\right)}^{\mathrm{fl}}}{{X}_{\mathrm{Aq}}^{\mathrm{Stv}}},$$

(3)

where

$${X}_{\mathrm{Aq}}^{\mathrm{fl}}= \frac{{m}_{\mathrm{Aq}}^{\mathrm{fl}}}{{m}_{\mathrm{Aq}}^{\mathrm{SM}}}$$

(4)

and

$${X}_{\mathrm{Aq}}^{\mathrm{Stv}}= \frac{{m}_{\mathrm{Aq}}^{\mathrm{Stv}}}{{m}_{\mathrm{Aq}}^{\mathrm{SM}}}=1-{X}_{\mathrm{Aq}}^{\mathrm{fl}}.$$

(5)

The ${\left(D/H\right)}^{\mathrm{SM}}$ and ${\left(D/H\right)}^{\mathrm{fl}}$ was determined from Raman spectroscopy and is the area ratio of the O–D and O–H resonances (Fig. 3C); ${\left(D/H\right)}^{x}={A}_{{\mathrm{D}}_{2}\mathrm{O}}^{x}/{A}_{{\mathrm{H}}_{2}\mathrm{O}}^{x}$, where x is either SM or the fluid recovered from the experiment. The average ${\left(D/H\right)}^{\mathrm{fl}}$ and ${\left(D/H\right)}^{\mathrm{stv}}$ are 0.98 ± 0.1 and 4.6 ± 2.0, respectively. Individual values are given in Table 1, additional information on the calculations can be found in the supplementary information. The reported 1σ uncertainties arise from weighing precisions and the reproducibility of the Raman acquisition. The equation

$${\alpha }_{\mathrm{Stv}/\mathrm{fluid}}^{\mathrm{app}}=\frac{{\left(D/H\right)}^{\mathrm{Stv}}}{{\left(D/H\right)}^{\mathrm{fl}}}$$

(6)

gives an apparent hydrogen isotope fractionation factor for the stishovite–aqueous fluid pair. We obtain ${\alpha }_{\mathrm{Stv}/\mathrm{fluid}}^{\mathrm{app}}$ = 5.0 ± 1.1, 4.9 ± 1.5 and 4.2 ± 0.8 (avg. ~ 4.7 ± 0.7), all of which indicates strong enrichment of deuterium in the hydrous stishovite relative to the coexisting fluid. However, the apparent fractionation factor is not representative of equilibrium D/H fractionation during experiments at 450 °C and 9 GPa, as will be discussed below.

Two issues related to the experimental setup need to be considered first when interpreting the results. First, the low-frequency ¹H NMR data indicates the presence of protons attached to the surface of stishovite, which may impact the mass balance calculations by lowering the estimated mass of water present in the stishovite (i.e., lower ${m}_{\mathrm{Aq}}^{\mathrm{stv}}$). However, it is difficult to determine the precise effect of surface protons on the mass balance, as they could be chemisorbed to surface oxygens of the stishovite lattice or physisorbed as layers of molecular water. Nevertheless, a lower ${m}_{\mathrm{Aq}}^{\mathrm{stv}}$ would increase ${\alpha }_{\mathrm{Stv}/\mathrm{fluid}}^{\mathrm{app}}$, without changing the overall conclusion that deuterium is preferably partitioning in the stishovite. We also note that ∑SSB/CB correlates with the stishovite D/H (Fig. 8). Second, it is important to consider diffusive hydrogen exchange between the multi-anvil assembly and the experimental charge in the gold capsule. Unlike the piston-cylinder assembly that contains a talc pressure medium that can decompose during the experiment and release a hydrous fluid phase, the multi-anvil assembly parts are all nominally anhydrous but will contain a nominal level of absorbed water. Assuming, however, a flux of water from the assembly, dynamic equilibrium with the Re foil heater would impose an fH₂ of around 0.036 bar (the fH₂ of the experiment is neglectable) until the Re heater is oxidized to ReO₂ (and consequently fails, which was not observed except for Run 3). Calculating the hydrogen permeability of the Au capsule using Eq. 9 of Chou (1986) suggests accumulated H₂ contamination in the nanomole range over the course of 48 h. This contamination is in the order of permil relative to the total amount of hydrogen already present in the capsules and, thus, cannot significantly change the bulk D/H ratio of the experiment.

The ${\alpha }_{\mathrm{Stv}/\mathrm{fluid}}^{\mathrm{app}}$ value likely does not reflect the D/H fractionation during experimental run conditions, but is instead skewed by the water loss from the stishovite lattice during decompression. The diffusive loss of water inevitably affects the D/H ratio of the residual hydrogen in the stishovite as consequence of a kinetic separation of the water isotopologues. The magnitude of the kinetic isotope fractionation can be approximated with Graham's law, where

$${\varepsilon }_{\mathrm{Stv}/\mathrm{fl}}=\frac{{D}_{i}}{{D}_{j}}=\sqrt{\frac{{m}_{j}}{{m}_{i}}},$$

(7)

and D and m are the diffusivities and masses of species i and j. Due to the higher mass difference, the kinetic enrichment for hydrogen diffusion is larger than for the diffusion of molecular water species (${\varepsilon }_{\mathrm{stv}/\mathrm{fl}}$ = 1.41 vs. ${\varepsilon }_{\mathrm{stv}/\mathrm{fl}}$ 1.05). The kinetic isotope fractionation by unidirectional water loss from stishovite can then be described with a closed system Rayleigh distillation process, i.e.,

$${\left(\frac{D}{H}\right)}_{t}^{\mathrm{Stv}}={\left(\frac{D}{H}\right)}_{{t}_{0}}^{\mathrm{Stv}}+{\varepsilon }_{\mathrm{stv}/\mathrm{fl}}\cdot \mathrm{ln}\left({f}_{\mathrm{Aq}}^{\mathrm{Stv}}\right),$$

(8)

where f denotes the fraction of water or hydrogen present in the stishovite at a given timestep t (Hayes 2004; Mariotti et al. 1981). Figure 9 shows the Rayleigh modeling for water diffusion (blue curves) and hydrogen diffusion (red curves) and the D/H composition and residual water fraction (${f}_{\mathrm{Aq}}^{\mathrm{Stv}}$) of stishovite from runs 2, 4 and 5 (red symbols). The ${f}_{\mathrm{Aq}}^{\mathrm{Stv}}$ value was calculated assuming that the hydrous stishovite was saturated with 4.1 wt % water during the run conditions of 9 GPa and 450 °C (Eq. 3 of Lin et al. 2022). The blue curve with ${\left(\frac{D}{H}\right)}_{{t}_{0}}^{\mathrm{Stv}}$= 1.79 depicts the D/H evolution of hydrous stishovite in the case of no initial hydrogen isotope fractionation between mineral and water during the experiment (D/H = 1.79 is the bulk isotope composition of the system). This model fails to explain the observed D/H ratio of the hydrous stishovite. Instead, ${\left(\frac{D}{H}\right)}_{{t}_{0}}^{\mathrm{stv}}$ must be ~ 3.5–4.5 to fit with the observed data. In other words, during run conditions, the hydrous stishovite was 3.5–4.5 times enriched in deuterium relative to the coexisting aqueous fluid. This indicates a strong partitioning of deuterium into hydrous stishovite at the experimental conditions of 450 °C and 9 GPa. This is a notable finding because at > 300 °C, deuterium partitions into the volatile phase for most hydrous mineral–aqueous fluid pairs (e.g., Saccocia et al. 2009; Vennemann and ONeil 1996). This means that if the isotope effect persists at higher temperatures, hydrous stishovite could act as a sink for deuterium, decreasing the D/H ratio of a coexisting aqueous fluid. This is, to our knowledge, the first experimental constraint on the direction of hydrogen isotope fractionation between a hydrous UHP phase and a coexisting aqueous fluid.

Fig. 9

Closed system Rayleigh modeling of the stishovite D/H evolution. Symbols: D/H composition and residual water fraction (${f}_{\mathrm{Aq}}^{\mathrm{Stv}}$) of stishovite from runs 2, 4 and 5. Red and blue lines: Rayleigh trends for hydrogen (H, D) and molecular water (H₂O, D₂O) diffusion from the stishovite, respectively. (D/H)^Stv values at x = 1.0 are theoretically the initial D/H compositions of equilibrated stishovite during and experimental run and prior decompression, ${\left(\frac{D}{H}\right)}_{{t}_{0}}^{\mathrm{Stv}}$. Diffusive hydrogen loss increases the D/H ratio of the residual water remaining in the stishovite. Assuming 3.5 wt% water saturation at run conditions, quenched stishovite has lost on average about 45% of its initial water content. The Rayleigh modeling predicts an initial ${\left(\frac{D}{H}\right)}_{{t}_{0}}^{\mathrm{Stv}}$ between 3.5 and 4.5, indicating a strong partitioning of deuterium into the hydrous stishovite during experiment. Shaded area is 1σ uncertainty and applies to all curves

Comparison of Al-free hydrous stishovite in DAC and MA experiments

Lin et al. (2020, 2022) and Nisr et al. (2020) report that stishovite and post-stishovite (CaCl₂ structure, hereafter referred to as β-stishovite) synthesized in the laser-heated DAC have highly inflated unit cell volumes at high pressures and temperatures relative to anhydrous stishovite (ΔV/V). Relative unit cell volumes exceeding + 5% implied the incorporation of weight percent levels of H₂O, even at very high temperatures (e.g., > 2000 K). The studies of Spektor et al. (2011, 2016) and Nisr et al. (2017, 2020) suggested that water solution in stishovite occurs via the hydrogarnet substitution and a calibration was formulated based on unit cell volume changes predicted from first principles density functional theory (DFT) calculations. Lin et al. (2020) applied the Nisr et al. (2017) formulation to calculate H₂O contents in their high-pressure samples resulting in  exceptionally high H₂O concentrations exceeding 10 wt% in many instances.

Lin et al. (2022) used variations in bulk system water content to constrain solubility directly in the system SiO₂–H₂O at ~ 50 GPa and ~ 1800 K and found saturation at ~ 3.5 wt% H₂O (Fig. 1). They also developed an empirical function, based on experimental data, to estimate the maximum water solubility of stishovite as a function of pressure and temperature (Eq. 3 in Lin et al. 2022). Using this function, the maximum H₂O solubility of the stishovite synthesized in this study was calculated to be 4.1 wt%. Lin et al. (2022) also presented first principles DFT molecular dynamics calculations simulating multiple possible substitution mechanisms in stishovite and β-stishovite over a range of high pressures and temperatures. They found that the observed rate of volume change in stishovite (ΔV/V) as a function of bulk H₂O content (pre-saturation) matched that expected for interstitial substitution of molecular H₂O (Fig. 1) but was far greater than what predicted for the hydrogarnet substitution. Lin et al. (2022) formulated a calibration of the interstitial substitution based on their DFT results, and application to the experiments show that stishovite contains ~ 3 wt% H₂O at 40 GPa and temperatures of ~ 1500–2000 K, reducing to ~ 2 wt% by 70 GPa just below the phase transition to β-stishovite. β-stishovite is predicted to contain a similar amount at the phase transition (~ 75 GPa in Lin et al. 2022), but water solubility apparently reduces with pressure to ~ 0.5 wt% H₂O by ~ 130 GPa. For comparison, water solubility seemingly increases for Al-rich stishovite and β-stishovite (4 wt% Al₂O₃) from ~ 0.2 to ~ 0.7 wt% near the transition at 24–28 GPa, ~ 2000–2200 K based on P–T-quenched samples synthesized in the multi-anvil apparatus (Ishii et al. 2022).

Lin et al. (2022) noted that estimating H₂O contents using unit cell volumes from samples synthesized in either the MA or DAC at HPHT and quenched to 1 atm and 300 K is highly uncertain. Figure 10a demonstrates the large variability in measured unit cell volumes for samples synthesized in the MA at ~ 9–10 GPa and 350–550 °C (including data from this study). Similarly, P–T-quenched samples of hydrous stishovite synthesized in the DAC exhibit an even larger range in unit cell volumes. Even samples synthesized under approximately similar P–T conditions in the DAC yield highly variable unit cell volumes once quenched to 1 atm, 300 K.

Fig. 10

a Observed unit cell volumes at 1 atm, ~ 300 K, for anhydrous (Andrault et al. 2003; Baur and Khan 1971; Hill et al. 1983; Kirfel et al. 2001; Ross et al. 1990; Yamanaka et al. 2000) and hydrous (Spektor et al. 2011, 2016; Nisr et al. 2017) stishovite (SiO₂) synthesized in multi-anvil presses and diamond anvil cells (Lin et al. 2020, 2022; Nisr et al. 2020). b Observed unit cell volumes of hydrous stishovite synthesized at high pressures and temperatures in the diamond anvil cell (e.g., > 4 GPa, < 1500 K) from the studies of Lin et al. (2020, 2022). Data were taken upon decompression at 300 K from high-pressure synthesis conditions. Shown as solid lines are model volume compression curves for SiO₂ as a function of H₂O content based on the DFT-based calibration of Lin et al. (2022) for interstitial incorporation of H₂O. The experimental data follow these curves at high pressures but show a conspicuous decrease in unit cell volume at pressures less than about 10 GPa. Also shown are all the data from panel (a) taken at 1 atm, 300 K

To assess the effect of decompression, Lin et al. (2020, 2022) measured unit cell volumes along 300 K decompression paths from high pressure in three samples (Fig. 10b), and observed that the volume differences relative to anhydrous stishovite observed at high pressure are not preserved to 1 atm. They observed that all samples follow decompression paths at high pressures that parallel those for isothermal equations of state for interstitial molecular H₂O in stishovite. However, they observed a marked increase in the rate of change in unit cell volume relative to 300 K isothermal decompression curves (Fig. 10b) at pressures below about 10 GPa, with samples approaching the anhydrous decompression curve. Lin et al. (2022) not only interpreted this behavior as water loss during decompression but also noted the inconsistency among samples (Fig. 10). This interpretation is consistent with the deuterium enrichment in the quenched stishovite discussed in the previous section, although the isotope systematics cannot reveal whether molecular hydrogen or water is diffusing from the stishovite lattice.

Our NMR observations suggest that a large proportion of the H in our P–T-quenched hydrous stishovite samples is in the form of molecular H₂O. This is consistent with the observations of Lin et al. (2022) based on observed volume changes as a function of H₂O content (Fig. 1). We note that the hydrogarnet substitution cannot be excluded from our NMR results. However, because the volume expansion with H₂O content is much less for the interstitial substitution, it is difficult to quantify its relative importance in stishovite at high pressure and temperature conditions. It is our hypothesis that the variability in unit cell volume observed in P–T-quenched samples, and the clear kinks along the decompression path to smaller relative volumes (Fig. 10b), occurs because molecular H₂O is not entirely preserved within samples upon P–T quench but is dominant at high pressures and temperatures (e.g., the volume expansion is well explained at high P–T by this mechanism; Fig. 1). However, if the hydrogarnet substitution is also occurring simultaneously, it will account for some amount of water substitution in stishovite at high pressures and temperatures.

Water in Al-free and Al-bearing stishovite

Previous MA studies synthesized Al-free (or Al-poor at the ppm-level) stishovite under water-saturated conditions at temperatures ranging from 1200 to 1800 °C, using either chemically simple systems (Bolfan-Casanova et al. 2000; Bromiley et al. 2006; Litasov et al. 2007; Pawley et al. 1993), or more natural MORB and granitic compositions (Chung and Kagi 2002; Frigo et al. 2019). The P–T-quenched stishovite produced in these studies is nearly anhydrous and commonly contains less than 100 ppm wt H₂O, which is significantly different from in situ DAC studies that report up to 3.5 wt% H₂O (Lin et al. 2022) and the results of synthesis experiments in MA at ~ 9 GPa at < 550 °C (this study, Spektor et al. 2011, 2016). The reason for the difference is unclear and there are various possible explanations. One possible cause is the increased diffusion of hydrogen in the capsule material, which some authors think it may lead to water loss (Litasov et al. 2007). However, many studies report evidence of coexisting fluid phases after experiments and textural evidence suggesting the presence of a likely hydrous silicate melt (e.g., Bromiley et al. 2006; Chung and Kagi 2002; Frigo et al. 2019). Additionally, H diffusion as a cause of water loss would require a redox partner for accommodating the oxygen produced by the dissociation of the water molecule. Another explanation is that hydrous stishovite is a metastable phase formed as an intermediate during the phase transition from coesite to stishovite under water-saturated conditions, as suggested by Spektor et al. (2016). However, this interpretation is not supported by DAC experiments where hydrous stishovite is directly synthesized from amorphous SiO₂ at > 970 °C (Lin et al. 2020, 2022). Finally, Al (and other) impurities in the stishovite lattice affect the capacity to accommodate interstitial molecular water, leading to two potential, contrasting scenarios: (i) limiting the lattice’s ability to incorporate molecular water, or (ii) enabling rapid diffusive water loss during quenching. Previous studies have shown a positive correlation between H and Al, with up to 3000 ppm H being incorporated into Al-saturated stishovite (Litasov et al. 2007). Al incorporation increases the nominally anhydrous stishovite unit cell volume drastically by 0.17 ų per + 1 wt% Al₂O₃ (based on Litasov’s data; cf. supplementary information to our study), due to the larger ionic radius of Al versus Si. With respect to scenario (i), the additional Al may reduce the ability to incorporate molecular water due to steric effects. In scenario (ii), however, an inflated Al–stishovite crystal lattice could significantly increase the diffusivity of molecular water, making it more prone to loss during the quenching process. The experiments of Litasov et al. (2007) may indeed show remains of this interstitial water. The authors describe an intense FTIR band at 2656–2667 cm⁻¹ and a weak band at ~ 2900 cm⁻¹ like the ~ 2650 and 2880 cm⁻¹ bands observed in low-T hydrous stishovite (Fig. 6). The ~ 2660 cm⁻¹ band was observed for both Al-free and Al-bearing stishovite, indicating that it is unrelated to Al impurities and possibly related to molecular water based on our ¹H NMR results. Notably, the intensity of the 2665 cm⁻¹ band correlates positively with the Al content and is also significantly increased for Al-free stishovite containing 0.1 wt% FeO (Sample A-810 in Litasov et al. (2007)). This suggests that an inflated stishovite lattice, resulting from an increased concentration of large-radii contaminants, may have incorporated large amounts of interstitial water, which was mostly but not entirely lost during quenching. In summary, the role of Al and other impurities for the formation and stability of hydrous stishovite remains poorly understood. The discussion above highlights the need for further experimental and theoretical studies to elucidate the complex interplay between impurities, water incorporation, and quenching effects in hydrous stishovite.

Implications for the deep Earth water cycle

The potential role of hydrous, high-pressure SiO₂ phases in hosting and transporting water into the deep Earth has been extensively discussed (Ishii et al. 2022; Lin et al. 2022; Litasov et al. 2007; Walter 2021). Here, we build on previous work with a focus on how hydrous stishovite may affect mantle hydrogen isotopes.

Hydrous phases in altered oceanic crust progressively dehydrate during subduction, with nearly complete dehydration by ~ 300 km depth (Maruyama and Okamoto 2007; van Keken et al. 2011). Along a cold crustal slab geotherm, stishovite appears at approximately 250 km depth at ~ 700 °C (Poli and Schmidt 2002) comprising some 10–25 vol% of the mineral assemblage, possibly just overlapping with the last phase of crustal dehydration (Lin et al. 2022; Walter 2021). Conversely, hydrous minerals in the serpentinized peridotite section of the slab (i.e., antigorite, Phase A, Phase E, 10 Å-Phase) can transport and release water in the deeper upper mantle, transition zone and shallow lower mantle (Komabayashi and Omori 2006; Litasov and Ohtani 2007; Schmidt and Poli 2013; Shirey et al. 2021; van Keken et al. 2011; Walter 2021). If there is an effective mechanism to hydrate stishovite in the crustal portion of the slab, hydrous stishovite may host all the water estimated to be present in the down-going slab at these depths (Ishii et al. 2022; Lin et al. 2020, 2022; van Keken et al. 2011; Walter 2021). In this case, stishovite may incorporate and prevent the release of water from the slab into the surrounding mantle and transport water into the deep lower mantle and possibly even to the core–mantle boundary (Ishii et al. 2022; Lin et al. 2022).

Beyond its implications for net water transport to the deep lower mantle, stishovite hydration in subducting slab crust by dehydration of serpentinized peridotite has implications for the deep Earth hydrogen isotope inventory as it may convey the slab's D/H signature to the deeper portions of the mantle (Fig. 11). The δD-values¹ of serpentinites average around −55 ± 9‰ [−32 to −69‰, Histogram in Fig. 11] (Alt et al. 2012; Alt and Shanks 2006; Barnes et al. 2009; Früh-Green et al. 1996; Sakai et al. 1990; Wenner and Taylor 1973). In a cold slab, serpentinized peridotite retains most of its water content and may not undergo significant D/H fractionation during limited dehydration reactions. Consequently, the D/H signature of the serpentinite could potentially be transferred to hydrous stishovite upon the ultimate breakdown of hydrous peridotite phases. Subsequently, multiple processes come into play that can either modify or preserve the D/H signature of the slab. Here, we consider two scenarios in which hydrous stishovite may play a role in the deep mantle D/H signature.

Fig. 11

Deep Earth water cycling. The subduction of water-rich lithosphere carries mostly mineral-bound water into the mantle. Crustal lithologies are mostly dehydrated before stishovite (stv) becomes stable at ~ 250 km depth. However, hydrous silicates in the serpentinized peridotite section of the slab carries water to deeper levels. Their breakdown coincides with the stability of stishovite, which volumetrically is able to incorporate all water released by the dehydrating slab mantle. Limited devolatilization of serpentinized peridotite in cold slabs will preserve the serpentinite D/H signature (−55 ± 9‰, histogram). The slab D/H signature is then either preserved in the hydrous stishovite (and post-stishovite phases) throughout the rest of the cycle, or could exchange with a primitive hydrogen reservoir in the deep mantle. Entrainment of recycled crust in the upwelling mantle could pass on the inherited serpentinite D/H signature to primary melts, consistent with δD estimates ~ 50‰ for mantle source region of low ³He/⁴He submarine basaltic glasses. Partial decomposition of hydrous stishovite may introduce D/H fractionation, creating lighter δD-signatures (Loewen et al. 2019). For example, > 80% decomposition of hydrous stishovite might produce “mantle-like” signatures of −70 to −220‰, consistent with a −75‰ δD endmember for high ³He/⁴He submarine basaltic glasses (Dixon et al. 2017; Hallis et al. 2015).

• (i) Crustal slab sections stalling at the transition zone may impose its D/H signature or exchange hydrogen isotopes with coexisting hydrous mantle phases, such as wadsleyite or ringwoodite. Shaw et al. (2008) calculated that the δD signature of a 10 km thick slab with 0.5% water would, at 1600 °C, retain its D/H signature for about 200 Myr. Consequently, longer residence times could change the slab D/H signature towards a possibly lighter mantle value. Similarly, crustal slab sections that get entrained in lower mantle may diffusively exchange isotopes with a primitive hydrogen source. The δD values of the deep mantle are largely unconstrained, with estimates ranging from less than −220‰ (“solar nebular” component”) (Hallis et al. 2015) to −75‰ (“chondritic” component) (Loewen et al. 2019).

• (ii) Crustal slab sections entrained in the upwelling mantle may impose its D/H ratio to incipient melts. A complete breakdown of hydrous stishovite, either by partial melting or via phase transition to coesite (which is a poor water carrier) would transfer the D/H signature to basaltic melt or released hydrous fluid (−55 ± 9‰). Submarine basalts with low ³He/⁴He ratios (RA < 10), indicating a significant crustal slab component, exhibit a mantle endmember with a δD value near −50‰ (Loewen et al. 2019), consistent with nearly complete devolatilization of hydrous stishovite in or below the source region of associated primary basaltic melts. In contrast, ocean island basalt (OIB) glasses characterized by high ³He/⁴He ratios (RA > 22.5) tend towards a mantle endmember with a δD value near −75‰ or even lighter (e.g., Dixon et al. 2017; Hallis et al. 2015). It has been suggested that the involvement of primordial water contributes to these isotopic compositions (Hallis et al. 2015; Loewen et al. 2019). Alternatively, the heating and decompression of stishovite-bearing recycled crust could lead to the fractional loss of water, resulting in a deuterium-depleted fluid or melt. For example, the observed δD range of −75 to −220‰ for OIB glasses and melt inclusions (Dixon et al. 2017; Hallis et al. 2015; Loewen et al. 2019) could be explained by a > 54% fractional water loss from hydrous stishovite, which initially had a “slab signature” of −55‰ and was heated to 1400 °C (cf. supplementary materials). Notably, for hydrous MORB compositions at lower transition zone pressures (20–25 GPa), experiments suggest that the modal stishovite content decreases by ca. 50% (from 25 to 12 vol%) when heated from ca. 1000 to 1600 °C (Litasov and Ohtani 2005).

Although above scenarios are speculative, it is important to emphasize that high-temperature deuterium fractionation processes could result in an isotopically heterogeneous mantle. Fractionation processes involving hydrous stishovite may have the potential to produce low D/H signatures similar to expected primordial D/H values. While this introduces complexity in interpreting water signatures in MORBs and OIBs, it also presents an opportunity to gain a better understanding of melting processes in recycled oceanic crust and the overall deep Earth water cycle. Advancing our knowledge in this field requires detailed studies on the D/H fractionation mechanisms of stishovite, its polymorphs, other hydrogen-rich ultrahigh-pressure mineral phases, fluids, and melts.

Conclusions

We studied the hydrogen speciation and hydrogen isotope behavior of partially deuterated hydrous stishovite synthesized at 9 GPa and 450 °C in a multi-anvil press (MA). Our three main findings are summarized as follows:

• (i) Water in hydrous stishovite is mostly in the molecular form. The characteristics of ¹H MAS NMR spinning sidebands in hydrous stishovite suggest that a significant portion of hydrogen is stored as molecular H₂O. The presence of a hydrogarnet defect (1Si⁴⁺ ↔ 4H⁺) suggested by earlier studies is also possible and may contribute additional water in the structure.

• (ii) Molecular water in hydrous stishovite is easily lost upon decompression. Our quenched hydrous stishovite contains on average 1.7 wt% H₂O, consistent with previous MA stishovite syntheses at similar conditions. However, the H₂O concentrations in MA-synthesized stishovite are much lower compared to DAC-synthesized stishovite, which exhibits solubilities of ~ 3.5 wt% water at 50 GPa and 1580 °C. Consistent with this observation, our Rayleigh modeling of hydrogen isotopes suggests that diffusive water loss occurs during quenching and decompression. This is indicated by the elevated deuterium concentration in our hydrous stishovite and can be attributed to a faster escape of mineral-bound H₂O relative to HDO and D₂O. This interpretation is consistent with previous in situ DAC diffraction experiments that demonstrated sharp non-linear drops in stishovite unit cell volumes upon decompression, attributed to the diffusive loss of hydrogen (Lin et al. 2020, 2022).

• (iii) Hydrous stishovite is a deuterium sink. We introduced a capillary-based recovery method for fluid extraction from experimental capsules. Using this technique, we determined the D/H ratio of the experimental fluid and indirectly that of the hydrous stishovite. The data indicate strong partitioning of deuterium into the hydrous stishovite, leaving behind a deuterium-depleted aqueous fluid. This is opposite of what is commonly observed for mineral–fluid pairs above 300 °C, where the fluid phase is usually enriched in deuterium.

The capacity of stishovite to accommodate slab fluids released at > 10 GPa from serpentine-derived hydrous minerals is a potential mechanism to preserve the D/H slab signature throughout mantle recycling. During upwelling of hot mantle, complete stishovite breakdown can release water and transfer the D/H slab signature to primary melts, consistent with the D/H ratio of low ³He/⁴He submarine basaltic glasses. Fractional water loss from incomplete stishovite breakdown could mimic low “mantle-like” D/H ratios as observed from low δD basaltic glasses and melt inclusions within hot-spot regions.

Our study highlights the importance of hydrous stishovite for the deep Earth water cycle, and warrants further experimental and theoretical investigation. Preserving the pristine water content of P–T-equilibrated hydrous stishovite appears challenging, emphasizing the need for in situ experiments or suitable data correction methods. Complementary molecular dynamics simulations would be beneficial. Future experimental studies could address H₂O (and D₂O) solubility and speciation of Al-bearing stishovite (pure or in mineral assemblage), its thermal conductivity, the geometric properties of interstitial molecular H₂O, and hydrogen isotope partitioning at varying synthesis conditions.