Abstract
Subsurface magmatic–hydrothermal systems are often associated with elevated electrical conductivities in the Earthʼs crust. To facilitate the interpretation of these data and to allow distinguishing between the effects of silicate melts and fluids, the electrical conductivity of aqueous fluids in the system H2O–HCl was measured in an externally heated diamond anvil cell. Data were collected to 700 °C and 1 GPa, for HCl concentrations equivalent to 0.01, 0.1, and 1 mol/l at ambient conditions. The data, therefore, more than double the pressure range of previous measurements and extend them to geologically realistic HCl concentrations. The conductivities \(\sigma\) (in S/m) are well reproduced by a numerical model log \(\sigma\) = −2.032 + 205.8 T−1 + 0.895 log c + 3.888 log \(\rho\) + log\(\Lambda_{0}\)(T,\(\rho\)), where T is the temperature in K, c is the HCl concentration in wt. %, and \(\rho\) is the density of pure water at the corresponding pressure and temperature conditions. \(\Lambda_{0}\)(T,\(\rho\)) is the limiting molar conductivity (in S cm2 mol−1) at infinite dilution, \(\Lambda_{0}\)(T,\(\rho\)) = 2550.14 − 505.10\(\rho\) − 429,437 T−1. A regression fit of more than 800 data points to this model yielded R2 = 0.95. Conductivities increase with pressure and fluid densities due to an enhanced dissociation of HCl. However, at constant pressures, conductivities decrease with temperature because of reduced dissociation. This effect is particularly strong at shallow crustal pressures of 100–200 MPa and can reduce conductivities by two orders of magnitude. We, therefore, suggest that the low conductivities sometimes observed at shallow depths below the volcanic centers in magmatic–hydrothermal systems may simply reflect elevated temperatures. The strong negative temperature effect on fluid conductivities may offer a possibility for the remote sensing of temperature variations in such systems and may allow distinguishing the effects of magma intrusions from changes in hydrothermal circulation. The generally very high conductivities of HCl–NaCl–H2O fluids at deep crustal pressures (500 MPa–1 GPa) imply that electrical conductors in the deep crust, as in the Altiplano magmatic province and elsewhere, may at least partially be due to hydrothermal activity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Hydrothermal systems develop around many magmatic intrusions in the continental crust (e.g., Barnes 1979). They are powered by the heat released from the magma body and may contain volatiles exsolved from the magma itself or water from meteoric sources. Such magmatic–hydrothermal systems are responsible for the formation of ore deposits that are the main economic source of Cu, Mo, W, Sn, and other metals (e.g., Hedenquist and Lowenstern 1994). On the other hand, hydrothermal activity is often associated with active volcanism. Various phenomena, such as ground motions, seismicity, variations in heat flux or surface temperature, may be due to changes in the magmatic system itself (e.g., the intrusion of a new batch of magma) or of the associated hydrothermal system (e.g., Hurwitz and Lowenstern 2014). Disentangling these effects can be essential for forecasting future eruptions.
Measurements of electrical conductivity either by magnetotelluric methods (e.g., Kelbert et al. 2012) or (at shallow depth) by electrodes directly inserted into the ground (e.g., Gresse et al. 2018) may be able to detect both magmatic and hydrothermal activity, as both silicate melts and aqueous fluids are usually by orders of magnitude more conductive than the surrounding rocks (e.g., Gaillard 2004, Sinmyo and Keppler 2014). Indeed, zones of elevated electrical conductivity have been detected below numerous volcanoes, including Vesuvius (Manzella et al. 2004), the Campi Flegrei (Gresse et al. 2018; Troiano et al. 2014), Mt. St. Helens (Wynn et al. 2016), Yellowstone (Kelbert et al. 2012), the Altiplano Puna volcanic complex (Comeau et al. 2015), Merapi (Müller and Haak 2004; Commer et al. 2006), Mt. Unzen (Srigutomo et al. 2008), Mt. Fuji (Aizawa et al. 2005) and many others (e.g., Hoffmann-Rothe et al. 2001; Yamaya et al. 2009; Aizawa et al. 2011; Díaz et al. 2015; Kanda et al. 2019). Conductive fluids may also allow the visualization of regional fault systems from magnetotelluric data (Pavez et al. 2020). However, the quantitative interpretation of these measurements for a long time was hampered by the lack of electrical conductivity data for fluids at the relevant pressures and temperatures. Traditionally, such data were measured with externally heated autoclaves, which limited pressures to a maximum of 400 MPa (e.g., Franck 1956; Frantz and Marshall 1984; Ho et al. 2001; Balashov et al. 2017). Moreover, most of the measurements were carried out in physical chemistry with solutions of very low concentrations to constrain dissociation constants and ionic mobilities. There are also some limited shock wave data for the conductivity of dilute (0.1 m) HCl and KCl at higher pressures (Hamann and Linton 1969). Conductivity data for NaCl-bearing aqueous fluids with geologically realistic concentrations were first provided by Sinmyo and Keppler (2017) and later expanded to 5 GPa by Guo and Keppler (2019). Additional recent experimental studies include conductivity measurements in polyphase systems, such as quartzite–H2O–NaCl at 1 GPa (Shimojuku et al 2014) as well as measurements of the conductivity of complex solutions from geothermal fluids at relatively low pressures (up to 32 MPa) by Kummerov et al. (2020). However, particularly in hydrothermal systems around active volcanoes, HCl may be a significant component of the fluid, as it is often a prominent constituent of volcanic gases (Symonds et al. 1990). From previous measurements (Frantz and Marshall 1984), it is known that the conductivity of aqueous HCl can be significantly larger than that of NaCl solutions. Indeed, Kanda et al. (2019) attributed the elevated conductivity below Aso volcano in Japan to the presence of a highly acidic fluid.
To allow a better interpretation of the magnetotelluric data for magmatic–hydrothermal systems, we provide here new measurements of the electrical conductivity of H2O–HCl fluids to 1 GPa and 700 ºC. In addition to their direct application for remote sensing, the data also yield important insights into the dissociation of HCl in the fluid and, therefore, into general fluid properties.
Methods
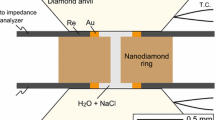
Electrical conductivities were measured in a Bassett-type externally heated diamond anvil cell using a method similar to that described by Ni et al. (2014). The basic experimental setup is shown in Fig. 1. A disc made of nanocrystalline diamond (Irifune et al. 2003) with 1.5 mm outer diameter, a thickness of 0.5 mm and a central drillhole of 0.1 mm is sandwiched between two rhenium gaskets (250 \({\mu m}\) thick). Because of the very corrosive nature of the HCl-bearing fluid, the gasket is lined by gold on the inside; a thin gold layer in contact with the diamond disc was used to improve sealing. In a few experiments, gaskets made of iridium or iridium gaskets lined with gold were also used. The entire package of the two gaskets with the diamond disc in between was sandwiched between two (type I) diamonds with 1 mm culet size. The sample chamber was filled with 0.01, 0.1 or 1 M HCl solutions prepared by diluting a certified standard solution. 1 M stands for a concentration of 1 mol/l at standard conditions. The bulk density of the fluid inside the sample chamber was controlled by adjusting the size of a vapor bubble in the loaded solution. The cell was heated by molybdenum coils around the tungsten carbide seats below the diamonds. Pads of mica and zirconia fibers around the gaskets and the diamonds helped to reduce heat loss. During heating, the cell was flushed by an argon–H2 (2%) mixture to prevent oxidation of the heaters or the diamonds. Upon heating, the cell usually behaves as a nearly isochoric system, although some deformation may occur at high temperature. Temperature was measured by two type-K thermocouples attached to the diamonds. In some experiments, the bulk density of the fluid inside the sample chamber was determined from the homogenization temperature (disappearance of the vapor bubble) upon heating and cooling. If the temperatures measured upon heating and cooling were close to each other (typically within 10 ºC or less), the bulk density of the fluid and the pressure at a given temperature were calculated from the equation of state of pure water (Wagner and Pruß 2002). Given that the HCl concentrations studied are rather low, this should be a rather good approximation. In most experiments, however, a clear natural zircon crystal was used as a pressure sensor inside the sample chamber and the pressures were directly measured from the Raman shift of the strongest zircon band at 1008 cm−1 (Schmidt et al. 2013). These measurements were carried out with a Horiba Labram 800 HR UV confocal Raman spectrometer using the 514 nm line of an argon laser at 200 mW output power for excitation.
The two rhenium gaskets served as electrodes for the electrical conductivity measurements. They were connected by four platinum wires to a Solartron 1260 impedance analyzer. Full impedance spectra were measured from 30 to 10 MHz. The measured ohmic resistances R can be converted into conductivities σ through the relationship.
where the cell constant Kcell was calibrated using the known conductivities of the solutions measured at standard conditions. Since the cell constant is largely determined by the geometry of the borehole in the diamond (Fig. 1), which remains essentially unchanged under all conditions, it is relatively insensitive to deformation in the remaining part of the sample chamber. However, strong deformation of the gaskets during a run could affect the cell constant and this is likely the main source of error in these experiments. The accuracy in resistance measurements with the instrument used is specified by the manufacturer as 0.1% for the range of 10 \(\Omega\)–100 k\(\Omega\) at 10 kHz. However, changes in the cell constant may in some experiments introduce errors in the order of 10% relative. The accessible pressure and temperature range for this type of experiment are mostly limited by the mechanical stability of the diamond platelet. Fracturing of the platelet at elevated P and T causes immediate fluid loss and an increase in resistivity by many orders of magnitude. However, the quality of the impedance spectra measured with an intact cell assembly is essentially independent of pressure and temperature.
Results
All experimental data and all relevant details of the measurements are compiled in Supplementary Online Table 1. Figure 2 shows the complex impedance spectra of a 0.1 M HCl measured in the externally heated diamond cell to 400 ºC. The data show a well-developed impedance arc, which is attributed to the combined ohmic and capacitive resistance of the sample. The data for 0.01 M HCl fluids usually yielded similar spectra. Measurements were usually evaluated by fitting the data to a model of an ohmic and capacitive resistor in parallel, plus an additional ohmic resistor representing the resistance of the electrodes. In cases where clear minima were visible on both sides of the impedance arc, the position of these minima was sometimes used to directly calculate the ohmic resistance. For 1 M HCl solutions, the impedance arc was usually not well resolved anymore, as shown in Fig. 3. For these experiments, the ohmic resistance was obtained from the intercept with the x axis or by a procedure similar to that described by Sinmyo and Keppler (2017), i.e., by plotting the resistance for 0.1–1 MHz against \(\omega^{{ - 1/2}}\) and linearly extrapolating to infinite frequency \(\omega\).
Examples for complex impedance spectra of aqueous 0.1 M HCl fluids to 400 ºC, as measured in an externally heated diamond anvil cell. 0.1 M refers to a concentration of 0.1 mol HCl/l solution at ambient conditions. The maximum pressure is 545 MPa at 400 ºC. Model fit curves for the measured data are also shown. For further details, see Supplementary Table 1, run Nr. 09.01.17
Examples for complex impedance spectra of aqueous 1 M HCl fluids to 450 ºC, as measured in an externally heated diamond anvil cell. 1 M refers to a concentration of 1 mol HCl/l solution at ambient conditions. The maximum pressure is 1043 MPa at 450 ºC. b is an enlarged view of a, showing the intercept with the horizontal axis, which yields the ohmic resistance. Note the decrease of resistance with increasing temperature. For further details, see Supplementary Table 1, run Nr. 28.02.18
All experimental results are compiled in Fig. 4. The left panels in this figure show the measure conductivity as a function of temperature, while the right panels show the pressure as a function of temperature. The symbols for every experimental series in the left and the right panel are the same, such that the relationship between temperature, pressure, and conductivity can be recognized. Since the experiments usually followed a more or less isochoric path (with possible deviations due to gasket deformation, particularly at high temperature), the pressures generally increase with temperature. Increasing pressure at constant temperature increases conductivity, but the effect is rather small at low temperatures, where the fluid has a liquid-like density and the compressibility is low. In an isochoric measurement cycle, conductivity usually increased to 400–500 ºC and then decreased again at higher temperatures. This is due to the combined effect of pressure and temperature on both ion mobilities and on dissociation, as will be discussed below. Detailed inspection of Fig. 4 shows that in a few cases, the relative sequence of measured electrical conductivities is not exactly the same as one would expect from the sequence of the P, T paths in the diagrams in the right panel. These effects are likely due to a deformation of the cell assembly and an associated error in the cell constant, which affected the measurements. However, overall, the data in Fig. 4 appear quite regular and no attempt was made to remove individual measurements from the entire data set.
Summary of measured electrical conductivities for 1 M HCl (a), 0.1; HCl (c) and 0.01 M HCl (e). The pressure temperature paths of the corresponding experiments are given in the diagrams on the right (b, d, f). The symbols in the left and the right panels are the same for the same series of experiments. 1 M refers to a concentration of 1 mol HCl/l solution at ambient conditions
Discussion
The electrical conductivity of an aqueous fluid depends on the mobility of the individual ions and on the degree of dissociation of the solute, which controls the concentration of the ions available for charge transport. Frantz and Marshall (1984) have determined the limiting molar conductivities of HCl at infinite dilution (\(\Lambda_{0}\), in cm2 S mol−1) for temperatures between 100 and 400 ºC and fluid densities from 0.75 to 1 g/cm3. These data are well reproduced by an equation
where T is temperature in K and ρ is the density of pure water in g/cm3 at given pressure and temperature. A regression fit yielded \(\lambda_{1}\) = 2550.14 ± 99.57, \(\lambda_{2}\) = −505.10 ± 117.76, \(\lambda_{3}\) = −429,437 ± 22,442 (R2 = 0.97). Figure 5 compares measured and predicted values, including also some data from Ho et al. (2001) and Balashov et al. (2017) measured at relatively low pressures up to about 30 MPa. Note that in contrast to the regression equation used by Sinmyo and Keppler (2017) for the limiting molar conductivity of NaCl, Eq. (2) does not contain a T−2 term. Tests showed that for HCl, the inclusion of such a term does not improve the quality of the fit. Alternative numerical models for predicting limiting molar conductivities were proposed by Marshall (1987); they are, however, much more complicated than the regression equation used here.
Comparison between predicted and measured values for the limiting molar conductivity of HCl at infinite dilution. Red dots are data from Frantz and Marshall (1984). They were fitted to a model \(\Lambda_{{0}} \, = \,\lambda_{{1}} + \lambda_{{2}} \rho + \lambda_{{3}}/T\) with \(\lambda_{1}\) = 2,550.14 ± 99.57, \(\lambda_{2}\) = −505.10 ± 117.76, \(\lambda_{3}\) = −429,437 ± 22,442; R2 = 0.97. For comparison, data from Ho et al. (2001; blue circles) and Balashov et al. (2017; green circles) are also shown for fluid densities >0.5 g/cm3. For lower fluid densities, the uncertainties in the measured values become very large
The conductivity data acquired in this study as well as those of Frantz and Marshall (1984) were fitted to a regression model
where \(\sigma\) is the conductivity in S/m, c is the concentration of HCl in wt. % and the other parameters are defined as above. For a theoretical justification of this equation, see Sinmyo and Keppler (2017). In brief, the fluid conductivity depends on the ionic conductivities—which are themselves functions of fluid density, temperature, and concentration—and on the degree of dissociation of the solute, which is again a function of fluid density, temperature, and concentration. Capturing all these effects together in one single equation would lead to an extremely complicated expression. Therefore, the procedure introduced by Sinmyo and Keppler (2017) uses some simplifications, notably (i) the concentration dependence of ionic conductivities is ignored (which is a minor simplification), and (ii) more importantly, it is assumed that the solute does not approach total dissociation. The latter assumption holds very well for relatively concentrated (wt. % level HCl content) fluids, which are geologically most important. However, it will necessarily lead to some systematic errors for very dilute fluids.
The best fit for Eq. (3) was obtained with A = − 2.032 ± 0.029, B = 205.8 ± 13.6, C = 0.895 ± 0.011, D = 3.888 ± 0.089 (R2 = 0.95). Figure 6 compares the measured and predicted conductivities and Fig. 7 shows the residuals of the fit as a function of concentration and of reciprocal temperature. In general, the equation correctly predicts conductivities to within 0.5 log units or better. Significant deviations occur at very low concentrations, which are, however, not particularly relevant for geological applications. These deviations are expected since Eq. (3) assumes only partial dissociation of HCl into H+ (or H3O+) and Cl−, while at very low concentrations, total dissociation will occur. Note that the regression coefficient C in front of the concentration term is below unity, which means that the conductivity is not directly proportional to HCl concentration, but increases more slowly. This is due to the reduced degree of dissociation of HCl at high concentrations.
Comparison between predicted and measured conductivities (in S/m) of H2O–HCl fluids to 1 GPa and 700. The data for 1 M and 0.1 M HCl are from this study, the data for 0.01 M HCl and below include both measurements from this study and those by Frantz and Marshall (1984). All data were fitted to a model log \(\sigma\) = A + B/T + C log c + D log ρ + log \(\Lambda_{0}\)(T,\(\rho\)) with A = −2.032 ± 0.029, B = 205.8 ± 13.6, C = 0.895 ± 0.011, D = 3.888 ± 0.089, R2 = 0.95
Differences between the measured electrical conductivities and those predicted by the numerical regression model \(({\text{log}}\sigma_{{{\text{observed}}}} \, - \,{\text{log}}\sigma_{{{\text{predicted}}}} )\), as a function of (a) concentration and (b) reciprocal temperature. The few outliers on the left side of b correspond to data points for very low concentrations (0.01 M or below)
Figure 8 shows the electrical conductivities of an aqueous fluid containing 5 wt. % HCl as a function of temperature to 800 °C and for pressures between 100 MPa and 1 GPa, as predicted from Eq. (3). Conductivities of a fluid containing 5 wt. % NaCl according to the model of Sinmyo and Keppler (2017) are shown for comparison. Under all conditions, the conductivities of the HCl-bearing fluid are about 0.5 log units higher than those of the NaCl fluid. Partially, this is due to the smaller molar weight of HCl as compared to NaCl, such that a 5 wt. % HCl solution contains more potential charge carriers than a 5 wt. % NaCl solution. This effect, however, accounts only for a difference by 0.2 log units, while the remaining part of the difference is due to the “extra mobilityˮ of the proton, which may be attributed to the Grotthuss mechanism of proton jumping between adjacent water molecules or larger molecule clusters (Agmon 1995; Lapid et al. 2005). In general, the conductivities of HCl-bearing aqueous fluids increase with pressure, but decrease with temperature. These effects are entirely due to changes in HCl dissociation. With increasing pressure, fluid density and, therefore, the dielectric constant of the solvent increase, which favors dissociation; while increasing temperature reduces the dielectric constant—not only by reducing fluid density, but also by increasing the statistical disorder of water molecules—such that the dissociation of HCl decreases. The temperature effect is particularly strong at low pressures, where the fluid density changes greatly as a function of temperature. In particular, at 100 MPa, i.e., at conditions relevant for shallow magmatic systems, the conductivity decreases by about two orders of magnitude for a temperature increase from 400 to 800 °C. It should be obvious that a quantitative assessment of such effects is essential for a correct interpretation of conductivity measurements in magmatic–hydrothermal systems.
Predicted electrical conductivities of aqueous fluids with 5 wt. % HCl based on this study and conductivities of aqueous fluids with 5 wt. % NaCl after Sinmyo and Keppler (2017)
For a precise evaluation of the degree of dissociation \(\alpha\) of HCl in the fluid at high pressures and temperatures, additional conductivity measurements at very low concentrations would be required to precisely constrain the limiting molar conductivity of HCl at infinite dilution and the dependence of ionic conductivities on concentration. While such measurements are beyond the scope of this study, a very approximate estimate of α may be obtained from the relationship \(\alpha\) ≈ \(\sigma\)\(\Lambda_{0}\)−1c−1, where \(\sigma\) is the measured conductivity, \(\Lambda_{0}\) is the limiting molar conductivity at infinite dilution under the same P, T conditions, and c is the concentration of HCl in moles/l under the given P, T conditions (note that due to different fluid density, c at P, T will be different from c under ambient conditions). Such a calculation would suggest that in a fluid containing 5 wt. % HCl, the solute is nearly half dissociated at 1 GPa and 800 ºC, while the dissociation decreases to about 5% at the same temperature and 200 MPa. This is, however, only a very rough order-of-magnitude estimate.
Remote sensing of magmatic–hydrothermal systems
The effect of a small fraction of aqueous fluid in the pore space of a rock on the bulk electrical conductivity of the system depends strongly on the connectivity of the fluid, which is determined by the dihedral wetting angle (e.g., Watson and Brenan 1987). Only for dihedral angles <60°, the fluid may form an interconnected network, which may greatly enhance bulk rock conductivity. On the other hand, for dihedral angles >60°, the fluid will be located in isolated pores and its effect on bulk conductivity will be small or negligible. Watson and Brenan (1987) studied the dihedral angle of aqueous fluids in dunite, quartz, and some other minerals. They found that for a pure H2O fluid, in dunite the dihedral angle is always >60°, indicating that the fluid will segregate into isolated pores. However, they noted that for the quartz–fluid system, the dihedral angle is drastically reduced upon addition of NaCl, to values as low as 40°. In a more recent study, Huang et al. (2019) also observed a reduction of the dihedral angles in the olivine–fluid system to values <60° upon addition of NaCl. In the light of these data, one may plausibly assume that in most crustal lithologies, a HCl and/or NaCl-bearing fluid will likely form an interconnected network and, therefore, strongly enhance bulk conductivity. We, therefore, estimate the bulk conductivity \(\sigma_{{\text{b}}}\) of a rock containing some small fraction of a H2O–HCl–NaCl fluid using the Hashin and Shtrikman (1962) upper bound model.
where \(\phi\) is the fluid fraction (by volume) and \(\sigma_{{\text{f}}}\) and \(\sigma_{{\text{s}}}\) are the conductivities of the fluid and the solid, respectively.
Figure 9 shows calculated bulk conductivities for rocks containing variable fractions of an interconnected fluid containing 5 wt. % HCl and/or NaCl. The concentration of 5 wt. % (HCl+NaCl) is geologically plausible for a hydrothermal system in the continental crust, if it contains a large contribution of primary magmatic fluid. Data on the Cl and H2O contents of melt inclusions from primitive arc basalts translate into NaCl/H2O ratios of 5–10 wt. % (Métrich and Wallace 2008). Data for more fractionated magmas in continental settings are more variable, but cover a similar range. Primary magmatic fluids may be diluted by meteoric water or by seawater in a hydrothermal system, depending on the geologic setting. The salinity of seawater is equivalent to 3.5 wt. % NaCl and, therefore, not far away from the assumed concentration. The fluid conductivities used in Fig. 9 were calculated from Eq. (3) with the data from this study for HCl and the regression fit of Sinmyo and Keppler (2017) for NaCl. The conductivities of the solid phase were assumed to be 2.5 × 10–5 S/m at 500 ºC and 5 × 10–4 S/m at 800 ºC, similar to the data for feldspars reported by Maury (1968). The data may be compared to the conductivities of some deep conductive zones below active volcanoes worldwide. The data indicate that the elevated conductivities do not necessarily imply the presence of magma, but they may be equally well explained by a small fraction of magmatic–hydrothermal fluid being present in the rock. Laumonier et al. (2017) suggested that the elevated conductivities near 1 S/m in the deep crust of the Altiplano Puna volcanic complex (Comeau et al. 2015) and other locations require the presence of andesitic magma with very high water contents (up to 10 wt.%). Our calculations offer an alternative explanation. Depending on fluid composition, pressure, and temperature, as little as 1–10% by volume of saline fluid could account for the observed conductivity of 1 S/m as well (Fig. 9). Due to the low density of aqueous fluids (1.01 g/cm3 at 1 GPa and 500 ºC and 0.69 g/cm3 at 500 MPa and 800 ºC for pure water), these numbers translate into weight fraction of aqueous fluid as low as 0.25–3 wt. %. Obviously, the two alternatives do not exclude each other; a crystallizing, volatile-rich magma body may well be surrounded by a deep hydrothermal system and this possibility was already considered by Comeau et al. (2015). Moreover, Laumonier et al. (2017) assume that the magma below the Altiplano Puna magmatic complex had reached water saturation, such that the development of some kind of hydrothermal activity around the intrusion would be expected. Andesitic magmas are typically rich in dissolved HCl (e.g., Symonds et al. 1990) and therefore, they should release a highly conductive fluid upon solidification. However, from the point of view of forecasting possible eruptions and assessing volcanic risk, it would obviously desirable to be able to distinguish between elevated conductivities produced by magmas and conductivity anomalies related to hydrothermal systems. The conductivity data alone are likely inconclusive. However, the combination with seismic tomography may allow a distinction between magmas and hydrothermal fluids, since to account for the same bulk conductivity, the volume fraction of magma required is much larger than the volume fraction of fluid. This may imply a stronger visibility of magma bodies in seismic tomography. Notably, the zone of elevated electrical conductivity (0.1–1 S/m) in the crust below Mount Rainier (Cascades, USA) does not appear to clearly correlate with low seismic velocities (McGary et al. 2014), which may suggest the involvement of some small fraction of saline fluid. Saline fluids likely also contribute to many zones of elevated conductivity in the upper crust, which are often interpreted as shallow magma chambers and/or hydrothermal systems. For example, the resistivity of about 3 \(\Omega {\text{m}}\) below Uturuncu volcano in Bolivia at a depth around 5 km below the surface (Comeau et al. 2015) could be accounted for by about 8–16 volume % of a fluid with 5 wt. % NaCl and/or HCl at a temperature of 600 ºC. Due to the low density of the fluid, this would translate to just 1.4–2.7 wt. % of the bulk rock. This estimate is, however, very sensitive to the assumed temperature, which has a strong effect on fluid conductivity at pressures relevant for the upper crust (Fig. 8).
Electrical conductivity of deep crust containing variable fractions of HCl- or NaCl-bearing aqueous fluid, according to a Hashin–Shtrikman upper bound model. Shown are two extreme cases, 5 wt. % HCl at 500 and 1 GPa and 5 wt. % NaCl at 800 °C and 500 MPa. The conductivities of NaCl–HCl mixed fluids in the temperature range between 500 and 800 °C and at pressures between 500 MPa and 1 GPa will all fall between these two extremes. The approximate conductivity of the Altiplano Puna conductor in the mid crust (Comeau et al. 2015) is shown for comparison
Conductivity anomalies at shallow depth, where geothermal gradients make the presence of magmas unlikely, have often been attributed to hydrothermal systems, e.g., the Campi Flegrei (Gresse et al. 2018) or the Turi basin in Northern Chile (Mancini et al. 2019). Curiously, however, the elevated conductivities in such systems are often attributed to the presence of hydrothermal alteration products such as smectites and illite (e.g., Kristinsdottir et al. 2010; Mancini et al. 2019), despite the fact that the highly conductive fluid itself is a much more obvious possibility. Very likely, this is because until recently, experimental calibrations of fluid conductivities and predictive numerical models were largely missing.
The strong temperature dependence of fluid conductivities at shallow crustal pressures (Fig. 8) may lead to some unexpected effects. For example Díaz et al. (2015) observed a highly conductive layer in a depth of about 1 km surrounding Lasterria volcano Chile, which they attributed to a hydrothermal system. Curiously, this anomaly appears to diminish or disappear below the volcano itself. Díaz et al. (2015) attributed this resistive zone to a crystallized magma chamber. While this interpretation is possible, the conductivity data in Fig. 8 suggest an alternative interpretation: At low pressures of 100 MPa and below, the increase in temperature expected upon approaching an active volcanic center by itself could cause a drop in conductivity by orders of magnitude. This strong temperature effect on conductivity could potentially be useful in monitoring active volcanoes with an extensive hydrothermal system, such as the Campi Flegrei (Troiano et al. 2014) or the Yellowstone area (Kelbert et al. 2012). Large temperature increases, e.g., upon intrusion of a new batch of magma at depth should cause a marked reduction of the electrical conductivity of any hydrothermal system located above the heat source.
References
Agmon N (1995) The Grotthus mechanism. Chem Phys Lett 244:456–462
Aizawa K, Yoshimura R, Oshiman N, Yamazaki K, Uto T, Ogawa Y, Tank SB, Kanda W, Sakanaka S, Furukawa Y, Hashimoto T, Uyeshima M, Ogawa T, Shiozaki I, Hurst AW (2005) Hydrothermal system beneath Mt. Fuji volcano inferred from magnetotellurics and electric self-potential. Earth Planet Sci Lett 235:343–355
Aizawa K, Kanda W, Ogawa Y, Iguchi M, Yokoo A, Yakiwara H, Sugano T (2011) Temporal changes in electrical resistivity at Sakurajima volcano from continuous magnetotelluric observations. J Volcanol Geothermal Res 199:165–175
Balashov VN, HnedkovskyL WRH (2017) Electrical conductances of aqueous electrolytes at high temperatures: limiting mobilities of several ions including the proton and HCl dissociation constant. J Mol Liquids 239:31–44
Barnes HL (1979) Geochemistry of hydrothermal ore deposits. Wiley, New York
Comeau MJ, Unsworth MJ, Ticona F, Sunagua M (2015) Magnetotelluric images of magma distribution beneath Volcán Uturuncu, Bolivia: implications for magma dynamics. Geology 43:243–246
Commer M, Helwig SL, Hördt A, Scholl C, Tezkan B (2006) New results on the resistivity structure of Merapi Volcano (Indonesia), derived from three-dimensional restricted inversion of long-offset transient electromagnetic data. Geophys J Int 167:1172–1187
Díaz D, Heise W, Zamudio F (2015) Three-dimensional resistivity image of the magmatic system beneath Lastarria volcano and evidence for magmatic intrusion in the back arc (northern Chile). Geophys Res Lett 42:5212–5218
Franck EU (1956) Hochverdichteter Wasserdampf III. Ionendisoziation von HCl, KOH, und H2O in überkritischem Wasser. Zeitschrift für Physikalische Chemie 8:192–206
Frantz JD, Marshall WL (1984) Electrical conductances and ionization constants of salts, acids, and bases in supercritical aqueous fluids: I. Hydrochloric acid from 100 to 700 °C and at pressures to 4000 bars. Am J Sci 284:651–667
Gaillard F (2004) Laboratory measurements of electrical conductivity of hydrous and dry silicic melts under pressure. Earth Planet Sci Lett 218:215–228
Gresse M, Vandemeulebrouck J, ByrdinaS CG, Roux P, Rinaldi AP, Wathelet M, Ricci T, Letort J, Petrillo Z, Tuccimei P, Lucchetti C, Sciarra A (2018) Anatomy of a fumarolic system inferred from a multiphysics approach. Sci Rep 8:7580
Guo H, Keppler H (2019) Electrical conductivity of NaCl-bearing aqueous fluids to 900 °C and 5 GPa. J Geophys Res 124:1397–1411
Hamann SD, Linton M (1969) Electrical conductivities of aqueous solutions of KCl, KOH and HCl, and the ionization of water at high shock pressures. Trans Faraday Soc 65:2186–2196
Hashin Z, Shtrikman S (1962) A variational approach to the theory of the effective magnetic permeability of multiphase materials. J Appl Phys 33:3125–3131
Hedenquist JW, Lowenstern JB (1994) The role of magmas in the formation of hydrothermal ore-deposits. Nature 370:519–527
Ho PC, Palmer DA, Gruszkiewicz MS (2001) Conductivity measurements of dilute aqueous HCl solutions to high temperatures and pressures using a flow-through cell. J Phys Chem B 105:1260–1266
Hoffmann-Rothe A, Ritter O, Haak V (2001) Magnetotelluric and geomagnetic modelling reveals zones of very high electrical conductivity in the upper crust of central Java. Phys Earth Planet Int 124:131–151
Huang YS, Nakatani T, Nakamura M, McCammon C (2019) Saline aqueous fluid circulation in mantle wedge inferred from olivine wetting properties. Nat Commun 10:5557
Hurwitz S, Lowenstern JB (2014) Dynamics of the Yellowstone hydrothermal system. Rev Geophys 51:375–411
Irifune T, Kurio A, Sakamoto S, Inoue T, Sumiya H (2003) Materials—ultrahard polycrystalline diamond from graphite. Nature 421:599–600
Kanda W, Utsugi M, Takakura S, Inoue H (2019) Hydrothermal system of the active crater of Aso volcano (Japan) inferred from a three-dimensional resistivity structure model. Earth, Planets and Space 71:37
Kelbert A, Egbert GD, deGroot-Hedlin C (2012) Crust and upper mantle electrical conductivity beneath the Yellowstone Hotspot Track. Geology 40:447–450
Kristinsdottir LH, Flovenz OG, Anarson K, Bruhn D, Milsch H, Spangenberg E, Kulenkampf J (2010) Electrical conductivity and P-wave velocity in rock samples from high-temperature Icelandic geothermal fields. Geothermics 39:94–105
Kummerow J, Raab S, Schuessler JA, Meyer R (2020) Non-reactive and reactive experiments to determine the electrical conductivities of aqueous geothermal solutions up to supercritical conditions. J Volcanol Geotherm Res 391:106388
Lapid H, Agmon N, Petersen MK, Voth GA (2005) A bond-order analysis of the mechanism for hydrated proton mobility in liquid water. J Chem Phys 122:014506
Laumonier M, Gaillard F, Muire D, Blundy J, Unsworth M (2017) Giant magmatic water reservoirs at mid-crustal depth inferred from electrical conductivity and the growth of the continental crust. Earth Planet Sci Lett 457:173–180
Mancini R, Díaz D, Brasse H, Godoy B, Hernández MJ (2019) Conductivity distribution beneath the San Pedro-Linzor volcanic chain, North Chile, using 3D magnetotelluric modeling. J Geophys Res 124:4386–4398
Manzella A, Volpi G, Zaja A, Meju M (2004) Combined TEM-MT investigation of shallow-depth resistivity structure of Mt Somma-Vesuvius. J Volcanol Geothermal Res 131:19–32
Marshall WL (1987) Reduced state relationship for limiting electrical conductances of aqueous ions over wide ranges of temperature and pressure. J Chem Phys 87:3639–3643
Maury R (1968) Conductibilité électrique des tectosilicates. I. Méthode et résultats expérimentaux. Bulletin de la Société française de Minéralogie et de Cristallographie 91:267–278
McGary RS, Evans RL, Wannamaker PE, Jimmy Elsenbeck J, Rondenay S (2014) Pathway from subducting slab to surface for melt and fluids beneath Mount Rainier. Nature 511:338–340
Métrich N, Wallace PJ (2008) Volatile abundances in basaltic magmas and their degassing paths tracked by melt inclusions. Rev Mineral 9:363–402
Müller A, Haak V (2004) 3-D modeling of the deep electrical conductivity of Merapi volcano (Central Java): integrating magnetotellurics, induction vectors and the effects of steep topography. J Volcanol Geothermal Res 138:205–222
Ni H, Chen Q, Keppler H (2014) Electrical conductivity measurements of aqueous fluids under pressure with a hydrothermal diamond anvil cell. Rev Sci Instruments 85:115107
Pavez M, Schill E, Held S, Diaz D, Kohl T (2020) Visualizing preferential magmatic and geothermal fluid pathways via electric conductivity at Villarrica Volcano, S-Chile. J Volcanol Geothermal Res 400:106913
Schmidt C, Steele-MacInnis M, Watenphul A, Wilke M (2013) Calibration of zircon as a Raman spectroscopic pressure sensor to high temperatures and application to water-silicate melt systems. Am Mineral 98:643–650
Shimojuku A, Yoshino T, Yamazaki D (2014) Electrical conductivity of brine-bearing quartzite at 1 GPa: implications for fluid content and salinity of the crust. Earth Planets Space 66:2
Sinmyo R, Keppler H (2017) Electrical conductivity of NaCl-bearing aqueous fluids to 600 ℃ and 1 GPa. Contrib Mineral Petrol 172:4
Srigutomo W, Kagiyama T, Kanda W, Munekane H, Hashimoto T, Tanaka Y, Utada H, Utsugi M (2008) Resistivity structure of Unzen Volcano derived from time domain electromagnetic (TDEM) survey. J Volcanol Geothermal Res 175:231–240
Symonds RB, Rose WI, Gerlach TM, Briggs PH, Harmon RS (1990) Evaluation of gases, condensates, and SO2 emissions from Augustine volcano, Alaska. Bull Volcanol 52:355–374
Troiano A, Di Giuseppe MG, Patella D, Troise C, De Natale G (2014) Electromagnetic outline of the Solfatara–Pisciarelli hydrothermal system, Campi Flegrei (Southern Italy). J Volcanol Geothermal Res 277:9–21
Wagner W, Pruß A (2002) The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use. J Phys Chem Ref Data 31:387–535
Watson EB, Brenan JM (1987) Fluids in the lithosphere, 1. Experimentally-determined wetting characteristics of CO2–H2O fluids and their implications for fluid transport, host-rock physical properties and fluid inclusion formation. Earth Planet Sci Lett 85:497–515
Wynn J, Mosbrucker J, Pierce H, Spicer K (2016) Where is the hot rock and where is the ground water—using CSAMT to map beneath and around Mount St. Helens. J Environ Eng Geophys 21:79–87
Yamaya Y, Mogi T, Hashimoto T, Ichihara H (2009) Hydrothermal system beneath the crater of Tarumai volcano, Japan: 3-D resistivity structure revealed using audio-magnetotellurics and induction vector. J Volcanol Geothermal Res 187:193–202
Acknowledgments
We thank Tetsuo Irifune and the PRIUS program of Ehime University in Japan for providing the platelets of nanocrystalline diamond used for the conductivity measurements. Constructive reviews by Fabrice Gaillard and Dionysis Foustoukos helped to improve the manuscript. This study was supported by Deutsche Forschungsgemeinschaft (DFG; Ke 501/11).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Othmar Muntener.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Klumbach, S., Keppler, H. Electrical conductivity of HCl-bearing aqueous fluids to 700 ºC and 1 GPa. Contrib Mineral Petrol 175, 114 (2020). https://doi.org/10.1007/s00410-020-01754-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00410-020-01754-5