Amphibole and apatite insights into the evolution and mass balance of Cl and S in magmas associated with porphyry copper deposits

Abstract

Chlorine and sulfur are of paramount importance for supporting the transport and deposition of ore metals at magmatic–hydrothermal systems such as the Coroccohuayco Fe–Cu–Au porphyry–skarn deposit, Peru. Here, we used recent partitioning models to determine the Cl and S concentration of the melts from the Coroccohuayco magmatic suite using apatite and amphibole chemical analyses. The pre-mineralization gabbrodiorite complex hosts S-poor apatite, while the syn- and post-ore dacitic porphyries host S-rich apatite. Our apatite data on the Coroccohuayco magmatic suite are consistent with an increasing oxygen fugacity (from the gabbrodiorite complex to the porphyries) causing the dominant sulfur species to shift from S²⁻ to S⁶⁺ at upper crustal pressure where the magmas were emplaced. We suggest that this change in sulfur speciation could have favored S degassing, rather than its sequestration in magmatic sulfides. Using available partitioning models for apatite from the porphyries, pre-degassing S melt concentration was 20–200 ppm. Estimates of absolute magmatic Cl concentrations using amphibole and apatite gave highly contrasting results. Cl melt concentrations obtained from apatite (0.60 wt% for the gabbrodiorite complex; 0.2–0.3 wt% for the porphyries) seems much more reasonable than those obtained from amphibole which are very low (0.37 wt% for the gabbrodiorite complex; 0.10 wt% for the porphyries). In turn, relative variations of the Cl melt concentrations obtained from amphibole during magma cooling are compatible with previous petrological constraints on the Coroccohuayco magmatic suite. This confirms that the gabbrodioritic magma was initially fluid undersaturated upon emplacement, and that magmatic fluid exsolution of the gabbrodiorite and the pluton rooting the porphyry stocks and dikes were emplaced and degassed at 100–200 MPa. Finally, mass balance constraints on S, Cu and Cl were used to estimate the minimum volume of magma required to form the Coroccohuayco deposit. These three estimates are remarkably consistent among each other (ca. 100 km³) and suggest that the Cl melt concentration is at least as critical as that of Cu and S to form an economic mineralization.

Introduction

The formation of porphyry copper systems critically depends on the availability of volatiles (e.g., H₂O, Cl, S) and metals (e.g., Cu, Au) in the silicate melt at the time of fluid saturation and exsolution. These elements are usually sourced from andesitic to dacitic magmas that undergo outgassing upon cooling and crystallization at upper crustal depth, and subsequently transported to higher crustal levels where extensive sulfide precipitation might occur if appropriate conditions are met (Hedenquist and Lowenstern 1994; Dreher et al. 2005; Sillitoe 2010; Pettke et al. 2010; Simon and Ripley 2011; Chelle-Michou et al. 2017). Importantly, chlorine and sulfur are critical elements of ore-forming fluids due to their capacity to form ligands with ore metals (e.g., Cu, Au, Pb, Zn, Fe, Mo) as well as with other cations (e.g., H⁺, K⁺, Na⁺, Ca⁺) which permit their transport to the site of ore deposition and cause hydrothermal alteration (Candela and Holland 1984; Williams et al. 1995, 1997; Frank et al. 2003; Simon et al. 2004, 2006; Williams-Jones and Heinrich 2005; Zajacz and Halter 2009; Zajacz et al. 2010, 2012; Kouzmanov and Pokrovski 2012; Pokrovski et al. 2015; Tattitch and Blundy 2017).

The study of volatiles in crystalline magmatic rocks such as those associated with porphyry systems is hindered by the fact that these rocks have lost the majority of their volatile budget during degassing and that the resulting mineral assemblage and mineral chemistry in the crystalline rock would be only minimally influenced by these elements. In addition, melt inclusions that might have preserved the volatile content at magmatic conditions are not always available (or large enough) within the crystal cargo of magmatic rocks. Nevertheless, common hydrous minerals such as biotite, amphibole and apatite may keep record of the evolution of various volatiles in the magma from which they crystallized (e.g., Coulson et al. 2001; Parat et al. 2011a; Zhang et al. 2012, 2017; Rasmussen and Mortensen 2013; Chambefort et al. 2013; Van Hoose et al. 2013; Teiber et al. 2015; Scott et al. 2015; Bao et al. 2016).

Here, we aim at decoding the Cl and S record of amphibole and apatite from the magmatic suite associated with the Eocene Coroccohuayco porphyry–skarn Cu (–Au–Fe) deposit, Peru. This system evolved from gabbroic to rhyodacitic composition through 5 Ma (Chelle-Michou et al. 2015a) and represents an opportunity to understand the evolution of volatiles in a long-lived magmatic system and try to identify the tipping point leading to the formation of an economic mineralization. These results can further be used to obtain mass balance constraints on the volume of magma required to form such a deposit.

Geological background

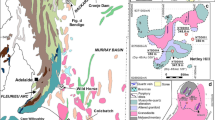
The Coroccohuayco Fe–Cu–Au porphyry–skarn deposit is located at the southern tip of the Andahuaylas-Yauri batholith of southern Peru, in the Tintaya mining district (which includes Tintaya, Antapaccay, Quechua, Ccatun Pucara; Fig. 1). This calc-alkaline batholith represents the plutonic root of the subduction-related Eocene magmatic arc and is emerging as an important Cu–Au metallogenic province. Magmatism and hydrothermal activity at Coroccohuayco is polyphased, and lasted from 41 to 35 Ma (Chelle-Michou et al. 2014, 2015b). The geochemical and petrological features of the Coroccohuayco magmatic suite have previously been described in Chelle-Michou et al. (2015a) and are summarized below.

Fig. 1

a Geological map of the Coroccohuayco deposit, Peru. The main skarn body is located below the sill-shaped gabbrodiorite complex at an average of 200 m depth. Adapted from Chelle-Michou et al. (2014). b Location of the Andahuaylas–Yauri Batholith and of the Tintaya–Coroccohuayco mining district

Magmatic activity started at 40.5–40.2 Ma with the emplacement of a heterogeneous sill-shaped body of gabbro and diorite termed the gabbrodiorite complex (Fig. 1). Using mineralogical and geochemical criteria, four phases could be identified within this complex: a gabbrodiorite, a gabbrodiorite “cumulate”, a leuco-gabbrodiorite and subordinate anorthosite. The first two phases are by far the most voluminous (> 95 vol%) and will be investigated in the present study. Both phases are made of euhedral normally zoned plagioclase (An90–30), poikilitic hornblende, Fe–Ti oxides (magnetite and ilmenite, both with sub-solidus exsolution lamellae), and interstitial quartz ± K-feldspar ± biotite (Fig. 2a, b). Resorbed clinopyroxene and/or orthopyroxene is often found in the core of poikilitic hornblende. Accessory minerals consist of apatite, zircon and occasional titanite and magmatic sulfides. Compared to the gabbrodiorite, the gabbrodiorite “cumulate” has more abundant hornblende and pyroxene, and less plagioclase (more calcic on average), is less silicic (ca. 48 wt% SiO₂ versus 51 wt%), has lower REE, Zr and P₂O₅ abundances and features a positive Eu anomaly. Chelle-Michou et al. (2015a) concluded that the gabbrodiorite “cumulate” represents an immature cumulate of early crystallized mineral phases (high-An plagioclase, pyroxenes) with an interstitial liquid that was depleted in incompatible elements compared to that of the gabbrodiorite. Signs of sub-solidus hydrothermal alteration are seldom observed in the gabbrodiorite complex and only the least altered samples were considered for this study.

Fig. 2

Back-scattered electron SEM images showing typical occurrences of amphibole and apatite in a, b the gabbrodiorite complex and c, d the porphyries. Amp amphibole, ap apatite, bio biotite, mt magnetite, pl plagioclase, qtz quartz, ttn titanite

After a nearly 5 Ma-long gap, magmatic activity resumed at 35.6 Ma with the successive emplacement (as stocks and dikes) of the hornblende and hornblende–biotite porphyries, both of dacitic composition (Fig. 1), and the coeval formation of the Fe–Cu–Au porphyry–skarn mineralization (Chelle-Michou et al. 2015b). This major magmatic–hydrothermal event was closely followed by the emplacement of rhyodacite porphyry dikes (Fig. 1). Despite being affected by a pervasive and destructive alteration of mafic minerals, these dikes crosscut the mineralization and the first two porphyries. All the porphyries feature a similar mineralogy dominated by An30–10 plagioclase, hornblende, biotite, magnetite and K-feldspar phenocrysts (Fig. 2c, d). The groundmass (46–56 vol%) is dominated by a microcrystalline patchwork of plagioclase, quartz and K-feldspar. Accessory minerals consist of titanite, apatite and zircon. No magmatic sulfide or sulfate phase could be observed in the porphyries. With the timing of emplacement, the porphyries evolve to more silicic compositions (from 63 to 68 wt% SiO₂) and develop an increasingly higher Sr/Y signature (from 50 to 110). Geochemical modeling has suggested that the chemistry of the porphyries results from a long-lived evolution within a deep crustal hot zone dominated by crystal fractionation, followed by crustal assimilation in the mid to upper crust. High-precision U–Pb zircon dating of the rhyodacite revealed that it resulted from the remelting of a proto-pluton emplaced at 36.1 Ma (Chelle-Michou et al. 2014). It has been inferred that this melting event was contemporaneous with the emplacement of the porphyries and was triggered by the emplacement and degassing of a large pluton in the upper crust (Chelle-Michou et al. 2014, 2015a).

Analytical methods for apatite

Prior to analysis, apatite was identified on thin sections and imaged by backscattered electron (BSE) microscopy. Selected apatite crystals were further imaged by “cold” optical cathodoluminescence (CL) to reveal internal zoning. Apatite chemistry was determined on a JEOL^® JXA 8200 electron microprobe equipped with five wavelength-dispersive spectrometers at the University of Lausanne (Switzerland). Analysis of apatite is known to be problematic due to the migration of halogens during analysis, depending on the crystallographic orientation of the apatite with respect to the electron beam (Stormer et al. 1993; Goldoff et al. 2012; Stock et al. 2015). To accurately measure both halogens (Cl and F) and trace elements (e.g., La, Ce, Y, Sr) in apatite, we successively employed a low-intensity (LI) and a high-intensity (HI) analytical protocol. Only a representative subset of apatite crystals analyzed with the LI method was subsequently analyzed with the HI method. A representative selection of apatite data is presented in Table 1 and the complete dataset is given in the Supplementary Material 1.

Table 1 Representative apatite composition from the Coroccohuayco magmatic suite

The LI analytical routine was designed to optimize halogen measurement (minimize diffusion) following the method proposed by Goldoff et al. (2012) which includes a 10 kV acceleration voltage, a 4 nA electron beam current and a 10 µm spot diameter. These settings were shown to minimize halogen migration even when the electron beam was parallel to the apatite c axis (Goldoff et al. 2012). The HI method was optimized for the measurement of the trace elements and includes a 15 kV acceleration voltage, 40 nA electron beam current and a 15 µm spot diameter. In both cases, F and Cl were analyzed first. The details of each analytical setup are presented in Supplementary Material 2.

In LI conditions, detection limits are typically in the range of ~ 200–300 ppm for Na, Mg, S and F, ~ 800–900 ppm for La, Ce Fe and Sr, ~ 500 ppm for Y, and ~ 120 ppm for Cl (Supplementary Material 2). HI conditions yield detection limits of ~ 50–150 ppm for Na, Fe S, Si and Cl, ~ 250–300 ppm for La, Ce and Y, and ~ 500 ppm for F and Sr (Supplementary Material 2). The analytical accuracy and precision were estimated by repeated analyses of the Durango apatite during each analytical session. Our microprobe data for the Durango apatite show good agreement with published values for all elements (Supplementary Material 2; Young et al. 1969). The precision and accuracy of analyses are typically ≤ 1% for Ca and P, and ≤ 6% for F and Cl irrespective of the method used. Relative analytical precision for the most enriched trace elements in the Durango apatite (S, Na, Si, La and Ce) was generally around 10–30% for LI and 3–10% for HI. In turn, measurements of low-concentration trace elements (Fe, Mg, Y and Sr) have lower precisions around 30–50%. Mn concentration of the Durango apatite being similar to the limit of detection with the HI method, the accuracy and precision of Mn analyses in apatite from Coroccohuayco (more enriched than the Durango apatite) cannot be evaluated. Nevertheless, the good precision and accuracy of all other elements suggest that Mn analyses are likely reliable.

Comparison of high- and low-intensity analytical methods

Overall, both analytical techniques show good accuracy on the Durango apatite standard. As expected, the HI method has lower limits of detection for the trace elements we investigated compared to the LI method (Supplementary Material 2). Interestingly, both methods accurately measure the halogen concentrations of the Durango apatite (Fig. 3). However, this apatite standard corresponds compositionally almost to the pure fluorapatite pole, a composition that is not always representative of our samples (Fig. 3). A comparison of the halogen concentrations of apatite from Coroccohuayco analyzed with both techniques reveals that the HI method systematically returns higher F concentrations than the LI method (by ca. 15%) while the Cl concentration is equivalent (Fig. 3), irrespective of the orientation of the crystal. This is similar to observations by Stock et al. (2015) who reports F surface enrichment of apatite exposed to EMP electron beam. Due to the well-documented halogen diffusion in apatite (Stormer et al. 1993; Goldoff et al. 2012; Stock et al. 2015), we consider the concentrations measured with the LI method as more accurate in addition to being more precise. No such systematic difference between the LI and HI method could be observed for the other elements.

Fig. 3

Triangular plots of molar proportion of Cl, F and OH in the hydroxyl site of apatite from Coroccohuayco, Peru. a Data acquired with the LI method. b Data acquired with the HI method. Colored fields in b show the contours of the results from the same apatite grains analyzed with the LI method. Inset with gray background shows the results from repeated measurements of the Durango apatite using both methods compared to the published values of Young et al. (1969)

Mineral chemistry

Apatite

Apatite formulae were calculated on the basis of 16 cations. OH was calculated by difference, assuming that the F–Cl–OH site is completely filled.

Apatite grains are essentially homogeneous in terms of F and Cl content even for those showing zoned CL textures (Fig. 3). We could not identify any systematic difference in halogen concentration between apatite hosted in hornblende and apatite hosted in anhydrous phases (plagioclase, groundmass, quartz). Halogen contents from apatites of the gabbrodiorite complex and the porphyries plot in two markedly different fields (Fig. 3). There is also a general tendency of decreasing the molar Cl proportion of apatite with increasing host-rock silica content (Fig. 3). Apatite from the gabbrodiorite complex has constant molar OH proportion (~ 40%), while F concentration increases (from ~ 0.4 to ~ 1.2 wt%) and Cl concentration decreases (from ~ 3.4 to ~ 1.9 wt%, with only few outliers) from the least to the most siliceous sample. In the porphyries, apatite has an invariably low Cl concentration (< 0.9 wt%) and falls along an F–OH exchange line. Apatite from the hornblende porphyry has Cl concentration of ~ 0.5 wt% and F concentration of 2.2–3.0 wt%. Apatite from the hornblende–biotite porphyry has lower Cl (~ 0.2 wt%) and higher F concentration (3.0–3.5 wt%). Finally, most analyses of apatite from the rhyodacite yield F concentration similar to those from the hornblende porphyry, but comparatively lower Cl concentration (~ 0.3 wt%). Few apatite grains from the rhyodacite define an F-rich group (fluorapatite proportion > 80%).

Sulfur concentrations in apatite from the gabbrodiorite complex are always below 0.1 wt% SO₃ (i.e., < 0.015 S pfu; Fig. 4a–d) and most of the time below the limit of detection. In contrast, apatite from the porphyries yield S concentrations that are always above this value, with a median of ~ 0.2 wt% SO₃ (~ 0.028 S pfu) for both the hornblende and hornblende–biotite porphyry, and of ~ 0.3 wt% SO₃ (~ 0.041 S pfu) for the rhyodacite (Fig. 4a–d). In the rhyodacite and, to a lesser extent, in the hornblende–biotite porphyry, few analyses have yielded high sulfur concentrations over 0.5 wt% SO₃ and up to 1.6 wt% SO₃. Sulfur has been proposed to enter the apatite crystal structure mainly in the oxidized form S⁶⁺ by replacing P⁵⁺ through a charge-balanced coupled substitution possibly involving Na⁺, Si⁴⁺, REE³⁺ and Y³⁺ cations (Rouse and Dunn 1982; Liu and Comodi 1993; Tepper and Kuehner 1999; Parat et al. 2002). A recent S XANES study has shown that minor amounts of S⁴⁺ and S²⁻ can also enter the structure of apatite as a function of oxygen fugacity (Konecke et al. 2017). However, due to the expected low abundance of S⁴⁺ and S²⁻ in magmatic apatite (likely << 300 ppm), we will assume that all S we analyzed is in the form of S⁶⁺ ions. The possible exchange reactions are:

$${\text{S}}^{ 6+ } + {\text{Na}}^{ + } \Leftrightarrow {\text{P}}^{ 5+ } + {\text{Ca}}^{ 2+ } \left( {\text{Liu and Comodi 1993}} \right),$$

(1)

$${\text{S}}^{ 6+ } + {\text{Si}}^{ 4+ } \Leftrightarrow 2 {\text{P}}^{ 5+ } \left( {\text{Rouse and Dunn 1982}} \right),$$

(2)

$${\text{Si}}^{ 4+ } + 2 {\text{Na}}^{ + } + 2 {\text{S}}^{ 6+ } + 4 {\text{REE}}^{ 3+ } \Leftrightarrow 4 {\text{P}}^{ 5+ } + 5 {\text{Ca}}^{ 2+ } \left( {{\text{Parat et al}}.\,{ 2}00 2} \right),$$

(3)

$${\text{S}}^{ 6+ } + {\text{Na}}^{ + } + {\text{Si}}^{ 4+ } + {\text{REE}}^{ 3+ } \Leftrightarrow 2 {\text{P}}^{ 5+ } + 2 {\text{Ca}}^{ 2+ } \left( {\text{Tepper and Kuehner 1999}} \right).$$

(4)

Fig. 4

Possible sulfate exchange reactions for per formula unit cations and sulfur in apatite from Coroccohuayco, Peru. Data in the left column (plots a, c, e and g) have been acquired with the LI method and data in the right column (plots b, d, f and h) with the HI method. R ² coefficient of determination of a fixed 1:1 model (solid black line) for the data; r correlation coefficient of an origin-constrained linear regression through the data; s slope of this linear regression. Numbers in parentheses were calculated for a subset of the data having Na⁺ < 0.05, corresponding to the gray field in a and b. Numbers in brackets were calculated for a subset of the data having Na⁺ > 0.05. Dashed lines represent the origin-constrained linear regression through all the data. Negative coefficients of determination indicate that the 1:1 model provides a very poor description of the data

Among these, reaction (1) provides the best explanation for the compositional variability of apatite from Coroccohuayco (Fig. 4). Indeed, Eq. (1), that is, a 1:1 relationship between S⁶⁺ and Na⁺, yields the best (closest to 1) coefficient of determination (R ²) for our data and a slope (s) closest to 1 for an origin-constrained linear regression through the data (LI: R ² = 0.68, s = 1.04; HI: R ² = 0.80, s = 1.15; Fig. 4a, b). However, a number of analyses, mainly from the rhyodacite, show high apatite Na⁺ content that cannot be explained by S⁶⁺ substitution alone (see apatite with 0.20 > Na⁺ > 0.06 pfu for S⁶⁺ ~ 0.05 pfu on Fig. 4a, b). When only points with Na⁺ > 0.05 pfu are considered, reaction (3) yields the best statistics for our data (LI: R ² = 0.49, s = 0.95; HI: R ² = 0.74, s = 1.04; Fig. 4e, f). In turn, when only points with Na⁺ < 0.05 pfu are considered, reaction (1) still yields the best statistics for our data (LI: R ² = 0.46, s = 1.05; HI: R ² = 0.52, s = 1.14; Fig. 4a, b).

Other trace elements (considering only the HI analyses) in apatite from Coroccohuayco show less contrasted behavior between the gabbrodiorite and the porphyries, even though apatite CL images of porphyry apatites reveal more complex zoning than those in the gabbrodiorite (Figs. 5, 6, 7). The average FeO concentrations are similar in both groups (median at 0.08 wt%), while MnO concentrations are slightly lower in apatites from the gabbrodiorite compared to those in the porphyries (medians of 0.08 and 0.12 wt%, respectively) resulting in median Mn/Fe ratios of 1.1 and 1.4, respectively. Similarly, Sr was more often below detection limit in apatites from the gabbrodiorite than in those of the porphyries. In turn, REE₂O₃ (La, Ce and Y) are on average slightly more concentrated in apatite from the gabbrodiorite with respect to those from the porphyries (median La₂O₃ = 0.09 wt%, Ce₂O₃ = 0.16 wt% and Y₂O₃ = 0.04 wt% for the gabbrodiorite and median La₂O₃ = 0.07 wt%, Ce₂O₃ = 0.13 wt% and Y₂O₃ = 0.03 wt% for the porphyries).

Fig. 5

CL image and chemical composition of apatite grains within the gabbrodiorite (sample 10CC09). Gray fields correspond to the average limit of detection of the LI (light gray) and HI (dark gray) methods for the corresponding trace element. The error bars on the side of each plot correspond to the average 2σ analytical uncertainty of the corresponding compound or ratio

Fig. 6

CL image and chemical compositional profiles on apatite grains within the hornblende–biotite porphyry (sample 11CC54). Gray fields correspond to the average limit of detection of the LI (light gray) and HI (dark gray) methods for the corresponding trace element. The error bars on the side of each plot correspond to the average 2σ analytical uncertainty of the corresponding compound or ratio

Fig. 7

CL image and chemical compositional profiles on apatite grains within the rhyodacite (sample 11CC17). Gray fields correspond to the average limit of detection of the LI (light gray) and HI (dark gray) methods for the corresponding trace element. The error bars on the side of each plot correspond to the average 2σ analytical uncertainty of the corresponding compound or ratio

In detail, microprobe profiles through apatite show little chemical zoning in grains from the gabbrodiorite and the hornblende–biotite porphyry, consistent with the limited zoning observed on CL images (all values overlap within analytical error; Figs. 5, 6). Instead, subhedral to anhedral grains with patchy CL textures in both rock units show noisy chemical patterns (Figs. 5, 6a). Nevertheless, profiles on apatite from the rhyodacite reveal much more complex zoning patterns (Fig. 7). In the rhyodacite, apatite grains that show concentric CL zoning have chemistries comparable to apatite from the hornblende–biotite porphyry (of both the patchy and concentric zoning types; Figs. 6, 7a). The blue cores are slightly enriched in SO₃ (up to 0.4 wt%) and to a lesser extent in REEs compared to the blue-green overgrowth (although mostly overlapping within uncertainty). In turn, apatite grains from the rhyodacite that show dissolution/overgrowth textures on CL images return the highest sulfur concentrations (> 0.5 wt% SO₃) and display complex zoning with no consistency from one grain to another (even for grains in contact; Fig. 7b, c). For example, the biggest apatite on Fig. 7b has a S-rich rim, while the smaller grain has an S-rich core. In both cases, this S-rich domain corresponds to darker and bluer CL response as well as higher Sr concentrations (> 0.20 wt% SrO). However, in the bigger grain, the blue-green core, which has SO₃ concentration around 0.2 wt%, is also anomalously enriched in Na (Na/S > 2) and Y (Y₂O₃ > 0.15 wt%; but not in La and Ce), features which are not observed in the smaller grain. In apatite grains shown in Fig. 7c, the high S concentrations again correspond to CL darker and bluer domains. These domains also have low Mn/Fe ratios (< 0.8) and Na/S ratios around 1. In turn the CL greener domains have comparatively lower S concentrations, Na/S ~ 2 and Mn/Fe ~ 1. REE are low (< 0.15 wt% REE₂O₃) and essentially overlapping within uncertainty across the different CL zones (Fig. 7c).

Amphibole

Amphibole chemical data are taken from Chelle-Michou et al. (2015a; see representative amphibole compositions Table 2) and include 235 analyses from all rock units at Coroccohuayco (including 107 from the gabbrodiorite complex and 128 from the porphyries) with the exception of the rhyodacite where no unaltered amphibole could be found. Amphibole formulae were calculated on the basis of a 13-cation normalization following the guidelines of Giesting and Filiberto (2014). According to the classification of Leake et al. (1997), most amphiboles from Coroccohuayco are magnesio-hornblende (58%) and a lesser proportion are edenite (19%; only in the porphyries), tschermakite (13%; only in the gabbrodiorite complex) and magnesio-hastingsite (11%).

Table 2 Representative amphibole composition from the Coroccohuayco magmatic suite.

In both rock units, Al_tot mostly varies from 2.0 to 0.8 pfu, and a distinct group of high-Al amphibole (Al_tot from 1.8 to 2.4 pfu) is also present in the porphyries (Fig. 8). Variations in Al_tot are mostly accounted for by the edenite exchange reaction, while the Al-tschermak substitution plays only a minimal role in these variations (Fig. 8a, b). In contrast, for the high-Al amphiboles, variations of Al_tot are strongly controlled by the Al-tschermak substitution rather than by the edenite substitution.

Fig. 8

Data are from Chelle-Michou et al. (2015a)

Amphibole composition in per formula unit. a Edenite exchange. b Al-tschermak exchange. c Cl vs Al_tot.

In the gabbrodiorite complex, amphibole Cl contents are scattered and vary from ca. 0.1 to 0.4 wt% (0.02–0.08 pfu; Fig. 8c). In detail, amphibole with Al_tot > 1.8 pfu and Al_tot < 1.1 pfu (mostly from the ‘gabbrodiorite cumulate’) tend to have a more restricted and low Cl concentration of 0.01–0.04 pfu. In turn, the most scattered Cl concentrations (0.02–0.08 pfu) correspond to Al_tot of 1.2–1.6 pfu. Amphiboles from the porphyries generally show lower and more restricted Cl concentrations of 0.04–0.13 wt% (ca. 0.01–0.03 pfu) which positively correlate with Al_tot, except for the high-Al group (Fig. 8c).

Profiles through amphibole crystals (Fig. 9) reveal that (1) temperature-sensitive elements (Al, ^A[Na + K| and Ti) can vary greatly within a single crystal with no regular core–rim trend, but that high values correspond to brighter zones in BSE images, (2) crystal-scale Cl variations are much more subtle, but correlate with temperature-sensitive elements (see also Fig. 8c) and (3) the variability of these elements in amphibole is smaller in single crystals than at the scale of the sample.

Fig. 9

Data are from Chelle-Michou et al. (2015a)

BSE image and chemical compositional profiles on amphibole crystals within a the gabbrodiorite and b the hornblende porphyry. The error bar for the Cl plot corresponds to the average 2σ analytical uncertainty and that for the temperature plot is that the thermometer uncertainty of ± 24 °C (see Ridolfi and Renzulli 2012). Analytical uncertainty for the temperature-sensitive elements (Al_tot, ^A[Na + K] and Ti) is smaller than the size of the symbol

Crystallization conditions of minerals

Amphibole

Intensive parameters (P, T, ƒO₂, H₂O_melt) at the time of amphibole crystallization were estimated based on amphibole composition (Chelle-Michou et al. 2015a) using the empirical formulations of Ridolfi and Renzulli (2012). Despite having distinct compositions (probably reflecting different magma compositions; Fig. 8; Table 2), amphiboles from both the gabbrodiorite complex and the porphyries record similar pressure, temperature and melt water content estimates of 250–100 MPa, 900–750 °C and 5 ± 1 wt%, respectively. Oxygen fugacities obtained from amphibole of the gabbrodiorite complex were NNO ± 1 (where NNO is the Ni–NiO oxygen buffer) and from NNO + 1 to NNO + 2 for the porphyries. Despite debates on the accuracy of the calculated parameters using these empirical calibrations (e.g., Walker et al. 2013; Erdmann et al. 2014), Chelle-Michou et al. (2015a) used independent mineralogical, chemical and thermodynamic constraints to argue that they represent overall reasonable estimates of intensive parameters for the magmas in equilibrium with amphibole at Coroccohuayco (see below). Importantly, the predominance of the edenite exchange reaction in amphibole from Coroccohuayco supports the temperature-controlled compositional variations with minimal influence from pressure variations (Fig. 8a, b).

To test the accuracy of the estimated pressure and temperature as determined by the empirical formulation of Ridolfi and Renzulli, Chelle-Michou et al. (2015a) used these P–T estimates to calculate the composition of plagioclase that would theoretically be in equilibrium with amphibole using the thermodynamic amphibole–plagioclase thermobarometer of Holland and Blundy (1994). For the gabbrodiorite complex, the estimated plagioclase composition always remarkably matches the measured composition of the plagioclase rims within each sample, which is consistent with the poikilitic texture of amphibole in these samples. In turn, estimated plagioclase composition for the porphyries was always higher than the measured one (estimated An30–60 vs measured An10–30, respectively). However, using the measured plagioclase and amphibole compositions with the thermobarometric formulation of Holland and Blundy (1994) in conjunction with the Al-in-hornblende barometer of Anderson and Smith (1995) resulted in a restricted near-solidus temperature range around 700 °C and a large pressure range of 400–100 MPa (Chelle-Michou et al. 2015). This is inconsistent with the well-developed edenite exchange vector and the lack of tschermak exchange in amphibole from Coroccohuayco (Fig. 8a, b). This is also inconsistent with the crystallinity of the porphyries (~ 50% crystals, ~ 50% groundmass) showing that the dacitic magma was at ca. 800–850 °C at the time of porphyry emplacement. These observations suggest that the pressure and temperature estimates using the empirical formulation of Ridolfi and Renzulli (2012) represent reasonable values for the porphyries. The increase in oxygen fugacity from the gabbrodiorite complex to the porphyries is supported by a mineralogical change of the Ti phase from ilmenite to titanite and by the increasing zircon Ce anomaly (Chelle-Michou et al. 2014, 2015a). Finally, the estimated melt H₂O concentration is consistent with the facts that basic to silicic arc magmas are hydrous and that magmatic water saturation at 250–100 MPa is around 6–4 wt% (e.g., Baker and Alletti 2012). The observations that (1) magma crystallinity at the time of amphibole saturation in the gabbrodiorite was around 50–60 vol% (ca. 60 vol% plagioclase with 30 vol% of interstitial amphibole; Chelle-Michou et al. 2015a) and that (2) the porphyries are representative of an ore-forming magmatic–hydrothermal system further support that the magma was fluid saturated at the time of amphibole crystallization throughout the Coroccohuayco magmatic suite (gabbrodiorite complex and porphyries). It is worth mentioning that the bulk of the crystal cargo of the porphyries (including plagioclase, amphibole and apatite) likely formed in an upper crustal magmatic system emplaced at 100–250 MPa and that magma was subsequently transferred to higher crustal levels (in stocks and dikes) at the time of mineralization (at around 25 MPa according to Maher 2010) where rapid cooling caused the porphyritic texture.

Calculations for the high-Al amphiboles from the porphyries result in higher pressures (500–1600 MPa), temperatures (900–1000 °C) and H₂O_melt (7–12 wt%; Chelle-Michou et al. 2015a). However, due to the lack of external constraints for these amphiboles, the robustness and accuracy of these intensive parameters should be taken with much caution. We can only mention that the predominance of the Al-tschermak substitution in these amphiboles and their high Al_tot (1.8–2.4 apfu) support their pressure-controlled compositional variations and that they crystallized at mid- to lower crustal depth. However, these amphibole crystals may have been sampled from deep crustal proto-plutons and would not bear information on the magma from which the porphyries crystallized.

Due to intra-crystal chemical variations in amphibole (Fig. 9), the estimated temperature record within a single crystal can vary up to 150 °C (70 °C on average). While the small intra-crystal variations (< 70 °C) may be explained by the uncertainty associated with the calibration of thermometer (± 24 °C, 1σ; Ridolfi and Renzulli 2012), larger variations likely record some temperature fluctuations during mineral crystallization.

Apatite

In the gabbrodiorite complex, euhedral to subhedral apatite is usually found enclosed in hornblende oikocrysts (enclosing euhedral plagioclase, Fig. 2b), while anhedral grains tend to fill the space between euhedral plagioclase crystals (Fig. 2a). It is noteworthy that subhedral and anhedral apatite grains have similar compositions. These features suggest that apatite co-crystallized with hornblende. Therefore, similar crystallization conditions (100–250 MPa, 750–900 °C, ƒO₂ of NNO ± 1 and fluid saturated) may be postulated for apatite in the gabbrodiorite complex. This temperature range can be confirmed by calculating the apatite saturation temperature (AST) for the estimated liquid composition at the time of apatite saturation (Harrison and Watson 1984), that is, the time of hornblende saturation (from petrographic observations). Based on the whole-rock composition (Supplementary Material 3), we recalculated the composition of the liquid by assuming that the magma was 50–60% crystalline with a mineral assemblage consisting of 88% of plagioclase (with an average An60–70 composition), 8% of magnetite, 2% of clinopyroxene (diopside) and 2% of high-temperature hornblende (> 900 °C) as suggested by petrographic observations, modal mineralogy and mineral chemistry (Chelle-Michou et al. 2015a). This approach is justified by the observation that the ca. 31 vol% of hornblende present in the gabbrodiorite is poikilitic and encloses plagioclase (63 vol%, An90–An30), resorbed clinopyroxene (0.5 vol%) and Fe–Ti oxides (5 vol%; Chelle-Michou et al. 2015a). This results in AST in the range of 800–870 °C, consistent with hornblende thermometry.

In the porphyries, apatite occurs as inclusions in all mineral phases and in the groundmass, and displays euhedral to subhedral habitus (Fig. 2c, d). This suggests that apatite crystallized close to the liquidus in these rocks. Assuming that the whole-rock chemistry approximates the composition of the liquid at the time of apatite crystallization, we calculate AST (Harrison and Watson 1984) in the range of 895–915 °C (Supplementary Material 3). These temperatures are indeed close to the water-saturated liquidus of dacitic magmas in the upper crust (900–950 °C; Scaillet and Evans 1999; Blundy and Cashman 2001; Costa et al. 2004). This is also similar to the highest crystallization temperature recorded by some low-Al amphibole (those with Al_tot ~ 1.6 pfu) in the porphyries which are around 900 °C (see Chelle-Michou et al. 2015a).

Some apatites from the rhyodacite show dissolution/overgrowth textures (Fig. 7b). This is consistent with previous results showing that this rock was emplaced as a result of proto-pluton remelting under near-zircon saturated conditions (this rock contains mostly antecrystic zircon and very little autocrystic ones; Chelle-Michou et al. 2014). Chelle-Michou et al. (2014) proposed that this remelting event was the consequence of the establishment of a long-lived and large thermal anomaly in the crust culminating with the emplacement of a large volume dacitic magma that sourced the ore-forming fluids of the Coroccohuayco deposit. Under these conditions, melting of a calc-alkaline proto-pluton or of the surrounding crust (sediments, volcanic rocks, older pluton) would have produced a peraluminous interstitial liquid (A/CNK > 1, where A/CNK is the Al₂O₃/[CaO + Na₂O + K₂O] molar ratio) (Patiño Douce 1997). Such melt composition has been shown to dramatically increase apatite solubility compared to metaluminous melts with similar SiO₂ and P₂O₅ concentrations (Pichavant et al. 1992). This may provide an explanation for the dissolution textures observed in some apatite grains from the rhyodacite. Grains that lack dissolution/overgrowth textures and instead show concentric zoning are likely crystallized from a newly intruded dacitic magma. The slightly contrasted trace element composition of grains with dissolution/overgrowth textures (high SO₃ > 0.5 wt% and locally high Y₂O₃ > 0.10 wt%) and concentrically zoned grains (SO₃ ~ 0.2 wt% and Y₂O₃ < 0.10 wt%) could also be consistent with this hypothesis. Yet, in the absence of more precise analyses including an extended suite of trace elements (e.g., other REEs, U, Th, etc.) or of direct evidence for a peraluminous melt, this hypothesis cannot be tested further.

Sulfur concentration of the melt

Arc basalts typically contain hundreds to thousands ppm of dissolved sulfur (e.g., Wallace 2005; Wallace and Edmonds 2011) and the basaltic melt at the source of the gabbrodiorite complex probably had comparable S concentrations. Yet, the limited occasional presence of magmatic sulfide in the gabbrodiorite suggests that the melt was on the low side of that expected for arc basalts (probably within 300–1000 ppm). Apatite from the gabbrodiorite complex systematically returns very low sulfur concentrations (< 0.1 wt% SO₃). These low values may either (1) reflect low magmatic sulfur content of the basaltic magma or (2) ƒO₂ conditions at which the dominant sulfur specie is S²⁻ (Jugo et al. 2010; Baker and Moretti 2011) and thus cannot enter the apatite structure in high amounts (Parat et al. 2011b; Konecke et al. 2017). At the time of apatite saturation (> 850 °C), the interstitial melt likely was fluid saturated and a fraction of the sulfur would have partitioned into the degassing magmatic fluid. Fluid/melt partition coefficients for sulfur in basaltic to andesitic melts at around NNO range from 1 to ca. 800 [see compilation in Webster and Botcharnikov (2011); corresponding to bulk S partition coefficient from 0.05 to 40 assuming 5 wt% H₂O in the melt] such that the sulfur concentration in the interstitial fluid-saturated melt may have increased or decreased upon fluid saturation and crystallization. Therefore, the melt sulfur concentration at apatite saturation in the gabbrodiorite complex remains unknown and the hypothesis that low S concentration in apatite could reflect low melt S concentration cannot be tested. On the other hand, the oxidation state of a silicic melt exerts a first-order control on sulfur speciation: from FMQ (where FMQ is the fayalite–magnetite–quartz oxygen buffer; ca. NNO-0.7) to FMQ + 2 (ca. NNO + 1.3) the dominant sulfur species rapidly changes from S²⁻ to S⁶⁺ (Jugo et al. 2010; Botcharnikov et al. 2011). Therefore, the low S content of apatite of the gabbrodiorite complex is also consistent with previous work showing that it corresponds to a magma in which S occurred mostly in its reduced form at NNO ± 1 (Chelle-Michou et al. 2014, 2015a).

In contrast, moderate (~ 0.2 wt% SO₃) to high (> 0.5 wt% SO₃) sulfur concentrations are recorded in apatite from the porphyries. These values are consistent with the higher oxidation state of the associated magma (NNO + 1 to NNO + 2; Chelle-Michou et al. 2014, 2015a). Using a set of natural and experimental apatite/melt partitioning data for andesitic to rhyolitic melts, Parat et al. (2011b) calibrated the following empirical non-Henrian partitioning relationship for sulfur between apatite and melt:

$${\text{S}}_{\text{apatite}} \left( {{\text{wt}}\% } \right)\; = \; 0.0629\; \times \; {\text{lnS}}_{\text{melt}} \left( {{\text{wt}}\% } \right)\; + \;0.4513.$$

(5)

This equation is constrained up to 0.1 wt% S in the melt (ca. 0.3 wt% S in apatite). When applied to apatite from the porphyries (both zoned and unzoned), the large majority of the points result in sulfur concentrations of 20–40 ppm for the melt in equilibrium with apatite (Fig. 10a). Alternatively, Peng et al. (1997) proposed an experimental calibration of S partitioning between apatite and melt that is controlled by temperature only. At AST (i.e., ~ 900 °C), the apatite/melt partition coefficient for S is 6 and increases at lower temperatures. Using a fixed value of 6, the computed S melt concentrations are mainly between 100 and 200 ppm for the three porphyries (Fig. 10b) and represent a maximum as lower values would be expected at lower temperatures. In both cases, few scattered points from S-rich apatite domains result in much higher apparent S melt concentrations (Fig. 10) and are discussed independently below. One should note that at upper crustal pressure and at fO₂ ranging from NNO + 1 to NNO + 2, sulfate (S⁶⁺) would not be the only S species and that some amount of reduced sulfur may also be present (Jugo et al. 2010; Botcharnikov et al. 2011; Matjuschkin et al. 2016). Therefore, because apatite mainly incorporates sulfate ions (S⁶⁺) in its lattice, the melt sulfur concentration we obtain is likely a minimum value and only accounts for the concentration of the sulfate ions in the melt.

Fig. 10

Probability density of estimated S concentration of the melt based on apatite from the porphyries. a Estimate using the non-Henrian partitioning function of Parat et al. (2011b). b Estimate using a fixed partition coefficient of 6, which is calculated from the temperature-dependent partition coefficient calibration of Peng et al. (1997) at 900 °C. o. r. outside range, LI low-intensity EMPA method, HI high-intensity EMPA method

S-rich apatite domains

Going from the hornblende porphyry to the rhyodacite, an increasing proportion of points shows higher S values, which even fall outside the calibration range. These are very scattered and seem unlikely to reflect very high melt sulfur concentrations, as the oxidized dacitic melt would be anhydrite saturated at few hundred ppm of S (certainly less than 500 ppm S; Baker and Moretti 2011). Similar S-rich apatites (SO₃ > 0.5 wt%) have been reported in a number of natural systems (Streck and Dilles 1998; Parat et al. 2002, 2011a; Streck et al. 2007; Chambefort et al. 2008; Van Hoose et al. 2013), but could not be synthesized experimentally and remain enigmatic. Their common association with anhydrite-saturated magmas suggests that they might have crystallized from abnormally S-enriched melt pockets (Parat et al. 2011a, b). Van Hoose et al. (2013) also proposed that S-rich apatites from Pinatubo may result from sulfur-fluxing events caused by a degassing underplated body of basalt. However, magmatic anhydrite could not be observed at Coroccohuayco and high S domains of apatite show no trace element similarity or consistency from one grain to another (Fig. 7), suggesting that no uniform process can account for their formation. The only two common characteristics of S-rich apatite domains from Coroccohuayco are their presence in grains showing dissolution/overgrowth textures and their bluer CL response (Fig. 7).

As already mentioned, the dissolution of apatite would be readily facilitated in peraluminous melts (Pichavant et al. 1992). Furthermore, given the hydrous character of the magma at Coroccohuayco, it is likely that sulfur and water fluxing accompanied melting of preexisting lithologies. Therefore, we suggest that the dissolution/overgrowth texture, the variable trace element systematics among different grains and the zoning of apatite grains with S-rich domains (Fig. 7b, c) might be consequences of the partial melting of various apatite-bearing crustal lithologies (proto-plutons, sediments; with apatite of various chemistries) and subsequent crystallization under a high S flux. In this view, apatite cores with chemistry unlike any other apatite in the same rock (e.g., in Fig. 7b, c; possibly including some S-rich cores with various trace element abundances) may be xenocrystic in origin. Partial melting of crustal lithologies promoted apatite dissolution, and sulfur from the volumetrically dominant water-rich dacitic magma would have readily fluxed into the peraluminous melt pocket and promoted the crystallization of S-rich apatite rims upon cooling. This model is consistent with the finding that the porphyries (from the emplacement of the hornblende porphyry to the emplacement of the rhyodacite) record increasing sediment assimilation, proto-pluton cannibalism and even remelting for the rhyodacite (Chelle-Michou et al. 2014, 2015a).

Chlorine concentration of the melt

Estimates from apatite

As noted by Boyce et al. (2014), simple Nernst apatite/melt partition coefficients for Cl cannot be used to estimate the melt Cl concentration. This is because, in apatite, Cl, F and OH occupy the same crystallographic site and their abundance is controlled by apatite stoichiometry, which implies that they cannot be treated in the same way as trace elements. Here, we make use of the recently calibrated thermodynamic apatite/melt chlorine partitioning model of Li and Hermann (2017) using experimental data from Webster et al. (2009) at 200 MPa and 900 °C. We argue that the experimental calibrant conditions are reasonably close to those inferred at the time of apatite crystallization at Coroccohuayco and that the thermodynamic parameters can be applied to determine the Cl melt content in equilibrium with apatite. According to Li and Hermann (2017):

$$\normalsize {\text{Cl}}_{\text{melt}} \left( {{\text{wt}}\% } \right)\; = \;\frac{{X_{\text{Cl}}^{\text{ap}} }}{{X_{\text{OH}}^{\text{ap}} }}\frac{1}{{Kd_{\text{Cl - OH}}^{\text{ap - melt}} }} \times 10.79,$$

(6)

where $X_{{\rm{Cl}}}^{{\rm{ap}}}$ and $X_{{\rm{OH}}}^{{\rm{ap}}}$ are the mole fractions of chlorapatite and hydroxylapatite, respectively, and

$$Kd_{{{\text{Cl}}{-}{\text{OH}}}}^{{{\text{ap}}{-}{\text{melt}}}} \; = \;{\text{e}}^{{\left( {25.81 + \left( {X_{\text{Cl}}^{\text{ap}} - X_{\text{OH}}^{\text{ap}} } \right) \times 17.33} \right)\; \times \;\frac{{10^{3} }}{8.314 \times T}}} ,$$

(7)

with the temperature (T) in K. We have computed the Cl melt concentration at temperatures of 850–800 °C, and 900–850 °C for apatite from the gabbrodiorite complex and from the porphyries, respectively. These temperatures correspond to the most likely crystallization temperature of apatite within these rocks.

Using this method, we obtain Cl melt concentrations of ca. 0.60 ± 0.10 wt% for the gabbrodiorite complex, and ranging from 0.3 to 0.1 wt% for the porphyries (Fig. 11a). Results for the rhyodacite are the most scattered and do not define a clear normally distributed population as for the other samples. The effect of the chosen temperature on the calculated concentration is minimal for apatites from the porphyries, but can affect the results by up to 0.1 wt% for those from the gabbrodiorite complex (Fig. 11a). It is noteworthy that despite having very different Cl concentrations (average of Cl content of 3.4 ± 0.1 wt% in sample 10CC61, 2.2 ± 0.3 wt% in sample 10CC55 and 1.9 ± 0.3 wt% in sample 10CC09), apatites from the three samples of the gabbrodiorite complex record very similar melt Cl concentrations. Our results further suggest that these large variations of apatite Cl content in the gabbrodiorite can result from variable apatite crystallization temperatures consistent with bulk sample SiO₂ content (lower in sample 10CC61 than in sample 10CC09; Figs. 3, 11a) and/or from small variations in the Cl concentration of the interstitial melt at the time of apatite crystallization (higher in sample 10CC61 than in sample 10CC09).

Fig. 11

Melt Cl concentrations estimates based on a apatite and b amphibole. AST apatite saturation temperature

Estimates from amphibole

Various studies have attempted to retrieve the magma Cl content from amphibole composition (e.g., Sato et al. 2005; Zhang et al. 2012; Giesting and Filiberto 2014). These methods rely on the calibration of the partitioning model for OH/Cl between amphibole and melt. Here, we use the most recent formulation of Giesting and Filiberto (2014) that was calibrated on 39 amphibole analyses of various composition and crystallized under various conditions:

$$K_{\text{Cl}} \; = \;\frac{{\left( {X_{\text{Cl}} /X_{\text{OH}} } \right)_{\text{amphibole}} }}{{\left( {\left[ {\text{Cl}} \right] /\left[ {\text{OH}} \right]} \right)_{\text{melt}} }},$$

(8)

$$\ln K_{\text{Cl}} { = }\frac{6.59 \text{K}}{{{\text{Na}}\; + \; {}_{{}}^{\left[ A \right]} { \boxdot }}}\; - \;0.679 {\text{Mg}}\; + \;0.487{}_{{}}^{{\left[ {\text{VI}} \right]}} {\text{Fe,}}$$

(9)

where $X$ is the mole fraction of an anion in the W site of amphibole, $\left[ {{\rm{Cl}}} \right]$ and $\left[ {{\rm{OH}}} \right]$ are the mole fractions of the designated anions in the melt on a one-oxygen basis, and $\text{K}$, ${\rm{Na}}$, ${}_{{}}^{\left[ A \right]} { \boxdot }$, ${\rm{Mg}}$, and ${}^{{\rm{VI}}}{\rm{Fe}}$ are the amounts of each component in the amphibole in apfu. Using Eqs. 8 and 9, we obtain ([Cl]/[OH])_melt in equilibrium with amphibole at the time of its crystallization.

[OH]_melt can be determined independently using available knowledge on the speciation of water in silicate melts. The speciation of water is controlled by the dissociation reaction (Stolper 1982; Zhang 1999; Zhang and Ni 2010):

$${\text{H}}_{ 2} {\text{O}}_{m} \left( {\text{melt}} \right) + \text{O} \left( {\text{melt}} \right) \Leftrightarrow 2{\text{OH}} \left( {\text{melt}} \right),$$

where ${\text{{H}}_{2}}{\text{{O}}_m}$ refers to the molecular H₂O dissolved in the melt. The equilibrium constant of this reaction is

$$K_{2} = \frac{{\left[ {\text{OH}} \right]^{ 2} }}{{\left[ {{\text{H}}_{ 2} {\text{O}}_{m} } \right]\left[ {\text{O}} \right]}},$$

(10)

where $\left[ {{{\rm{H}}_{\rm{2}}}{{\rm{O}}_m}} \right]$, $\left[ {{\rm{OH}}} \right]$ and $\left[ {\rm{O}} \right]$ are the molar fractions of molecular H₂O, hydroxyl group (not bounded with H) and bridging O atom dissolved in the melt, respectively. For the gabbrodiorite (of basaltic compositions), we use the ${K_2}$ temperature-dependent basalt calibration of Lesne et al. (2011) whereas for the porphyries (of dacitic to rhyodacitic compositions) we use the ${K_2}$ temperature-dependent dacite calibration of Liu et al. (2004) recommended by Zhang and Ni (2010). In both cases, we have used the amphibole crystallization temperatures obtained by Chelle-Michou et al. (2015a) to calculate the ${K_2}$ relevant to each amphibole analyses. In addition, the relation of the different species of water can be expressed as follows (Stolper 1982; Zhang 1999; Zhang and Ni 2010):

$$\left[ {{\text{H}}_{ 2} {\text{O}}_{t} } \right] = \frac{{{\text{C}}/18.015}}{{{\text{C}}/18.015\; + \;\left( {1 - {\text{C}}} \right)/{\text{W}}}},$$

(11)

$$\left[ {{\text{H}}_{ 2} {\text{O}}_{t} } \right] = \left[ {{\text{H}}_{ 2} {\text{O}}_{m} } \right] + {\raise0.7ex\hbox{${\left[ {\text{OH}} \right]}$} \!\mathord{\left/ {\vphantom {{\left[ {\text{OH}} \right]} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}},$$

(12)

$$\left[ {\text{O}} \right]{ + }\left[ {{\text{H}}_{ 2} {\text{O}}_{m} } \right]{ + }\left[ {\text{OH}} \right]{ = 1},$$

(13)

where ${\rm{C}}$ is the mass fraction of water in the melt, ${\rm{W}}$ is the molar mass of the dry silicate melt and $\left[ {{{\rm{H}}_{\rm{2}}}{{\rm{O}}_t}} \right]$ is the molar fraction of total H₂O in the melt. For each amphibole analysis, ${\rm{C}}$ was assumed to be equivalent to the one calculated from amphibole chemistry (Chelle-Michou et al. 2015a) and is always close to the theoretical value at water saturation. For the porphyries, we use an average value of $W$ (33.6 g/mol) calculated from the whole-rock composition. For the gabbrodiorite complex, we estimated the composition of the melt at the time of amphibole saturation (see above) and obtained an average $W$ of 36.1 g/mol. Combining Eqs. 10, 12 and 13, we can derive $\left[ {{\rm{OH}}} \right]$ as a function of ${K_2}$ and $\left[ {{{\rm{H}}_{\rm{2}}}{{\rm{O}}_t}} \right]$ (see Zhang et al. 2012):

$$\left[ \text{OH} \right] = 2\left[ {{\text{H}}_{ 2} {\text{O}}_{t} } \right] + \frac{{8\left[ {{\text{H}}_{ 2} {\text{O}}_{t} } \right] + K_{2} - 2\left[ {{\text{H}}_{ 2} {\text{O}}_{t} } \right]K_{2} - \sqrt {K_{2} } \sqrt {16\left[ {{\text{H}}_{ 2} {\text{O}}_{t} } \right] - 16\left[ {{\text{H}}_{ 2} {\text{O}}_{t} } \right]^{2} + K_{2} - 4\left[ {{\text{H}}_{ 2} {\text{O}}_{t} } \right]K_{2} + 4\left[ {{\text{H}}_{ 2} {\text{O}}_{t} } \right]^{2} K_{2} } }}{{K_{2} - 4}}.$$

(14)

Subsequently, $\left[ {{\rm{OH}}} \right]$ can be substituted in Eq. 8 to determine the molar and mass fractions of Cl in the melt in equilibrium with amphibole.

Melt Cl concentrations obtained from amphibole are plotted against the estimated temperature in Fig. 11b. For the gabbrodiorite complex, melt Cl concentration at ca. 975 °C is 0.17 ± 0.03 wt% and gradually increases to 0.37 ± 0.11 wt% at ca. 875 °C. Upon further cooling, the melt Cl concentration remains constant. In contrast, melt Cl concentration for the porphyries remains remarkably constant at 0.10 ± 0.03 wt% from 900 to 775 °C. Cl concentrations obtained from the high-Al amphiboles decrease from 0.16 wt% at 1000 °C to 0.03 wt% at 950 °C. However, the absence of edenite exchange in these high-Al amphiboles suggests that this temperature trend might be an artifact. Nevertheless, the calculated Cl melt concentration is fairly insensitive to temperature and similar values are obtained for the high-Al amphiboles if a fixed temperature of 900 °C is used.

Effect of halogen diffusion and hydrothermal alteration on the Cl and S record

Post-mineral crystallization diffusion and hydrothermal alteration need to be considered if we are to use minerals to estimate the evolution of melt properties during the evolution of the magmatic system. Indeed, both processes would obscure or even overwrite the original record. Hydrothermal experiments conducted on apatite and amphibole have shown that chlorine is a fast-diffusive element in both minerals, with diffusion coefficients that are orders of magnitude higher than for the main crystal-forming cations [4.2 × 10⁻¹⁶ and 2.8 × 10⁻¹⁵ m²/s at 800 °C and 1 GPa for Cl in apatite and amphibole, respectively; Brenan (1994), Su et al. (2015)]. This suggests that at magmatic temperature, any initial Cl zoning acquired during crystal growth should fade away and homogenize within weekly to yearly timescales (Boyce and Hervig 2008; Sato et al. 2017).

The lack of crystal-scale chlorine zoning in apatite and the limited chlorine variability in amphibole from Coroccohuayco are consistent with their plutonic (gabbrodiorite complex) to subvolcanic (porphyries) origin, whereby they have been subjected to a long annealing process during magmatic and sub-solidus cooling. If Cl has not been significantly exchanged with a surrounding phase (fluid, melt or Cl-bearing mineral) after the mineral crystallized, the Cl concentration measured on each point of a given crystal should represent an average of the Cl concentration in the entire crystal.

In the gabbrodiorite “cumulate”, the preservation of both high-T (> 900 °C) amphibole crystals that record an average low Cl melt concentration (ca. 0.17 wt%) and lower-T (< 900 °C) amphibole crystals that record an average Cl concentration of ca. 0.37 wt% in the same samples (Fig. 11b) suggests that (1) post-crystallization Cl exchange with a surrounding liquid or solid phase was limited. Yet, some amphibole crystals record intra-crystal scatter (of Cl and temperature) that cannot be explained by thermometer calibration or analytical uncertainties (Fig. 9). The observation that results from these grains fall within the array defined by the more chemically homogenous amphibole crystals (Fig. 11), suggesting that diffusion could not entirely erase the original record. This is at odds with the large diffusion coefficients for Cl that would rather suggest that Cl in amphibole would homogenize quicker than in apatite. It highlights the need for a better understanding of halogen diffusion in amphibole.

Despite that only fresh-looking amphiboles and apatites were selected for the present study (within relatively unaltered samples), the effect of potentially unrecognized sub-solidus hydrothermal alteration during the porphyry–skarn mineralization may be evaluated. The available fluid inclusion record at Coroccohuayco documents the presence of high-salinity brines during the mineralization (30–61 wt% NaCl_eq, average of ca. 45 wt% NaCl_eq) with homogenization temperatures ranging from > 650 to 170 °C (Maher 2010). If these fluids would have interacted with the already crystallized apatite and amphibole hosted within the porphyries and the gabbrodiorite complex, these minerals would have readily been dramatically enriched in Cl along mineral boundaries, cleavages or fractures [see for example the hydrothermal experiments of Brenan (1994) and Su et al. (2015)].

To our knowledge, no data on the diffusion of sulfur in apatite are available so far. However, due to the incorporation of sulfur in apatite through a coupled substitution (see above), sulfur is expected to diffuse several orders of magnitude slower than Cl in apatite. Therefore, by comparison with Cl and due to the presence of S zoning in some apatite crystals (see Figs. 6, 7), we conclude that post-crystallization diffusion and hydrothermal alteration did not affect the apatite record in our samples.

Chlorine insights into the petrologic evolution of magmas

Estimates of melt chlorine concentration using apatite and amphibole show a wide range of values of 0.1–0.7 wt%, as well as distinct behaviors depending on the mineral used for the calculation (Fig. 11). It is worth noting that these numbers are within the range of Cl melt concentrations of arc magmas (0.01–0.85; Aiuppa et al. 2009). Overall, estimates based on amphibole fall in the lower range or significantly below those based on apatite. While values of 0.2–0.6 wt% (estimated from both apatite and amphibole) seem reasonable for the gabbrodiorite complex (compared to arc basalts and andesite with values up to 0.85 wt%; Aiuppa et al. 2009), values of 0.1 wt% for the porphyries obtained from amphibole are on the low range of typical values for dacite (0.01–0.3 wt%). Indeed, on using Cl fluid/melt partition coefficients between 4.5 and 20 (corresponding to pressures of 100 and 200 MPa, respectively; Zhang et al. 2012), they correspond to a fluid salinity of ~ 2.0 ± 1.3 wt% NaCl_eq (i.e., assuming all Cl⁻ complexed with Na⁺: with ${\rm{NaC}}{{\rm{l}}_{{\rm{eq}}}}{\rm{ = C}}{{\rm{l}}_{{\rm{melt}}}}\times{\rm{D}}_{{\rm{Cl}}}^{{\rm{fluid/melt}}}{{ \times }}{m_{{\rm{NaCl}}}}{\rm{/}}{m_{{\rm{Cl}}}}$, where m refers to the molar masses) that is unusually low for pristine high-temperature single-phase magmatic fluids of porphyry copper deposits (typically, 3–10 wt% NaCl_eq; Kouzmanov and Pokrovski 2012). In turn, Cl melt concentrations estimated from apatite (0.1–0.3 wt%) result in fluid salinities (1–10 wt% NaCl_eq) that are more compatible with the salinity of fluids of porphyry systems.

The plausible causes of this discrepancy between the apatite- and amphibole-based Cl melt concentration estimates might involve (1) systematic measurement errors for F in amphibole, (2) inaccurate calibration of one of the equilibrium constants of the reactions involved (crystal–melt exchange reaction, dissociation of water in the melt) and/or (3) inaccuracy of the estimated temperature and H₂O melt concentration. We conducted sensitivity tests by varying the H₂O melt concentration of ± 1 wt%, the temperature of amphibole crystallization of ± 50 °C and by considering that the amphibole contains 0.1 wt% of F (instead of 0). The results were always within 15% of those we report in Fig. 10, suggesting that the discrepancy would rather come from the calibration of some of the equilibrium constants. Melt Cl concentrations estimated from apatite are probably reasonable estimates for both rock units, but additional constraints are necessary to confirm these results and to understand the cause of the discrepancy between apatite and amphibole estimates. Regardless of the absolute Cl melt concentrations, relative changes from one rock type to another may shed some light on the petrologic processes at stake during magma cooling, crystallization and fluid exsolution.

In the gabbrodiorite complex, few early high-T (> 900 °C) amphiboles record an increase of Cl melt concentration from 0.17 to 0.37 wt% with cooling (Fig. 11b). This likely results from the progressive crystallization of the fluid-undersaturated magma which caused the concurrent enrichment of H₂O, Cl and other incompatible elements (e.g., Zr, P) in the residual melt. This conclusion confirms earlier thoughts that the basaltic magma initially was fluid understaturated (with ~ 3 wt% H₂O in the melt) and became water saturated (with ~ 5 wt% H₂O) at the time at which most of the amphibole started to crystallize (see discussion in Chelle-Michou et al. 2015a). As the magma kept on cooling, amphibole records a relatively stable Cl melt concentration of 0.37 ± 0.11 wt% down to 750 °C (Fig. 11b). In three samples from the gabbrodiorite complex, apatite records subequal Cl melt concentration of ca. 0.60 wt% (at temperatures of 850–800 °C), small variations of which (± 0.10 wt%) can fully be explained by varying temperatures of apatite crystallization (Fig. 11a). Following the previous line of reasoning, whereby the initial basaltic magma was fluid undersaturated, the initial melt had 0.3–0.4 wt% Cl.

In the porphyries, apatite records an apparent decrease of Cl melt concentration with the relative timing of emplacement of the rocks (Fig. 11a). The largest difference is between the hornblende and the hornblende–biotite porphyries where the Cl concentration estimated from apatite (850–900 °C) drops by 30% (from 0.3 to 0.2 wt%). The hornblende porphyry and the slightly more evolved hornblende–biotite porphyry were suggested to have been sourced from an isotopically homogeneous deep crustal hot zone where they acquired their slightly distinct chemistry through crystal fractionation (Chelle-Michou et al. 2015a). In the deep crust, where the magma is likely fluid understaturated, crystal fractionation should cause an increase in melt Cl concentration rather than the observed decrease.

Upon further cooling, amphibole records a very stable Cl melt concentration of ~ 0.10 wt%, two to three times smaller than that determined from apatite (Fig. 11). We modeled the melt Cl evolution of a fluid-saturated felsic magma during cooling and outgassing at 100–200 MPa using the fluid/melt partition coefficient of Zhang et al. (2012) and bulk crystal/melt partition coefficients between 0 and 0.5 (Fig. 12). During magmatic cooling, the competing effect of magma crystallization (increase of Cl melt concentration) and fluid exsolution (decrease of Cl melt concentration), and the pressure dependence of Cl fluid/melt partition coefficient, may cause Cl melt concentration to decrease or increase. Accordingly, at 100 MPa melt, Cl enrichment is expected upon cooling, while Cl depletion is expected at 200 MPa (Fig. 12; see also Cline and Bodnar 1991). It results in average Cl melt concentrations for a fluid-saturated magma emplaced at 100–200 MPa, such as those investigated here, remaining approximately constant during crystallization. This is consistently recorded in the amphibole from the porphyry and possibly provides an external pressure constraint on the emplacement depth of the source pluton at Coroccohuayco.

Fig. 12

Model for the evolution of the relative Cl concentration of the melt for a the porphyries and b the gabbrodiorite complex. Gray fields represent the predicted Cl melt concentration computed at 100 and 200 MPa using the pressure-dependent fluid/melt partition coefficient of Zhang et al. (2012) and bulk mineral/melt Cl partition coefficients between 0 and 0.5. Cl_ini is the initial melt Cl concentration (at melt fraction of 1)

In addition to the effect of pressure, the solubility of Cl in the silicate melt tends to decrease with evolving melt composition (e.g., Webster 2004). Therefore, in the course of magma cooling and evolution of the interstitial melt, the Cl melt concentration would readily decrease upon Cl saturation. Such behavior is not recorded in our data, suggesting that interstitial melt evolution had little influence on the behavior of Cl in the melt, at least down to temperatures of ca. 750 °C for the gabbrodiorite and ca. 800 °C for the porphyries (Fig. 11).

Mass balance constraints on the genesis of the Coroccohuayco deposit

The S and Cl melt concentrations determined above can be used to derive mass balance constraints on the minimum volume of magma required to have sourced magmatic–hydrothermal fluids, Cl, S and Cu to the Coroccohuayco porphyry–skarn deposit. In addition to the concentration of these elements in the source magma, this exercise requires some estimates of the total inventory of S, Cl and Cu present in or required to form the deposit.

Given the ca. 3 Mt of contained Cu of the Coroccohuayco deposit (Chelle-Michou et al. 2015b) and assuming that all this copper is contained in chalcopyrite (which is a reasonable assumption based on drill core logging information), the deposit hosts a minimum of 3 Mt of sulfur in association with copper. Based on mine staff core logging, a chalcopyrite:pyrite proportion of 3:2 can be estimated which adds another 2 Mt of sulfur to the total amount. Assuming that the 5 Mt of reduced S (in the form of H₂S) required for the precipitation of sulfide minerals (i.e., pyrite and chalcopyrite) were formed by disproportionation of SO₂ gas (according to the reaction: 4SO₂ + 4H₂O = H₂S + 3HSO₄ ⁻ + 3H⁺; e.g., Kouzmanov and Pokrovski 2012) a minimum of 20 Mt of S should have been degassed by the cooling sub-porphyry pluton.

A similar calculation can be made for chlorine. Chlorine is the main ligand for Na, K, Fe, Cu, Pb and Zn in hydrothermal fluids, and the required amount of chlorine should account for the transport of these elements. At Coroccohuayco, the skarn body is of the order of 100 Mt (Chelle-Michou et al. 2015b). According to drill core logging information, the skarn is largely dominated by garnet, pyroxene and magnetite (> 80%; the rest being clay minerals, carbonates, amphibole and epidote) in garnet:pyroxene:magnetite proportions of 2:1:1. Maher (2010) determined that skarn garnet is dominated by andradite, while pyroxene is a mixture of diopside and hedenbergite. For the sake of simplification, we will assume that only hedenbergite was present. Using these constraints, 35 Mt of metallic iron (Fe) is present within the skarn, with an additional 5 Mt of Fe in sulfides (see above), totaling up to 40 Mt of Fe in the deposit (Fig. 13). Assuming that this iron was exclusively sourced by the magmatic–hydrothermal fluid (i.e., no Fe in the limestone protolith of the skarn), 51 Mt of Cl was necessary to transport iron as FeCl₂ complex. Another 3 Mt of Cl is required to transport the known copper mass of the deposit as CuCl₂ ⁻ complex. The total mass of Na, K, Pb, and Zn transported in the ore-forming fluid has not been estimated at Coroccohuayco. However, we can estimate their probable amount by comparison with other porphyry systems. Median values for single-phase fluid inclusions at porphyry systems (Kouzmanov and Pokrovski 2012) show that K and Na are typically 2 and 3.7 times more enriched than Fe, while the concentrations of Zn and Pb only correspond to 16 and 5% that of Fe, respectively. Using these values, and considering that these cations are transported as KCl, NaCl, ZnCl₃ ⁻ and PbCl₃ ⁻, another 312 Mt of Cl is required. Under the assumptions we have made, a total of 366 Mt of chlorine are required to form the Coroccohuayco deposit (Fig. 13).

Fig. 13

Estimates of the minimum magma volumes based on S, Cu and Cl mass balance constrained from the Coroccohuayco deposit, Peru. The pie charts show the speciation (mineral or complex) of the elements that are constrained by drill core observations (S, Cu, Fe) and by assuming similar intercationic ratio (e.g., Na/Fe, K/Fe) as fluid-inclusion data from porphyry systems worldwide (for Cl). Arrows indicate that the masses of Cl complexes with Cu and Fe derived from the estimated masses of Cu and Fe in the mineral deposit. Cpy chalcopyrite, gt andradite garnet, mt magnetite, px hedenbergite pyroxene, py pyrite

To compute the mass transfer of volatile and fluid-mobile elements (i.e., S, Cl and Cu) from the cooling pluton to the overlying porphyry–skarn deposit, we used the magma outgassing model of Chelle-Michou et al. (2017) for a fluid-saturated magma with 5 wt% of water. This model considers stepwise degassing of the magma at successive fluid percolation thresholds over the course of magma cooling and crystallization. To quantify uncertainties of the outputs, this model uses a Monte Carlo approach allowing to compute 100,000 solutions by varying simultaneously and randomly all the input parameters (such as starting composition and partition coefficient) within their reasonable range of values. Starting S and Cl concentrations were those estimated from apatite and were varied from 20 to 200 ppm for S (depending on the partition coefficient used; Fig. 10) and from 0.2 to 0.3 wt% for Cl (Fig. 11), respectively. Initial melt Cu concentrations were assumed to be 20–50 ppm as commonly advocated for such intermediate arc magmas (Cline and Bodnar 1991; Steinberger et al. 2013; Chiaradia 2014). Fluid/melt partition coefficients for S were computed from the calibration of Masotta et al. (2016) using the whole-rock composition of the porphyries and ranged from 2 to 15. To account for the evolution of the interstitial melt during cooling, we extend this range to 50. Fluid/melt partition coefficients for Cl were 4.5–20 (calculated from Zhang et al. 2012 at 100 and 200 MPa), while those for Cu were computed from the salinity of the degassed fluid according to Tattitch and Blundy (2017).

Within the range of input parameters, we determine that a minimum of 43–365 km³ (median of 81 km³), 33–131 km³ (median of 60 km³) and 60–169 km³ (median of 91 km³) of magma is required to source the 20 Mt of S, 3 Mt of Cu and 366 Mt of Cl to the Coroccohuayco deposit, respectively (Fig. 13). Magma volumes calculated using S, Cu and Cl mass balance constraints from the ore deposit at Coroccohuayco compare very well to each other and suggest that a volume of magma in the order of 100 km³ most likely sourced the deposit (Fig. 13). It is also noteworthy that these volumes are in the range of those estimated from field exposure for the Luhr Hill Granite (~ 65 km³) that sourced porphyry copper deposits from the tilted Yerington District which has a very similar Cu endowment of ~ 4.1 Mt of Cu (Cline and Bodnar 1991; Dilles and Proffett 1995).

In contrast to the figures above, high-precision zircon U–Pb dates and thermal modeling returned a volume of 500–2000 km³ for the pluton below Coroccohuayco (Caricchi et al. 2014). Another volume estimate can be made considering that the ore-related magmatic system assembled over a maximum of 100 ka (Chelle-Michou et al. 2015b). Assuming typical magma fluxes of 0.001 to 0.01 km³/a in magmatic arc setting (de Saint Blanquat et al. 2011), a maximum magma volume of 100 to 1000 km³ can be estimated (see also Chelle-Michou et al. 2017). The differences between mass balance and geochronology-based volume estimates may indicate that (1) only a small fraction of the total budget of Cu, Fe and S could have been extracted and precipitated, and/or (2) other deposits in the immediate vicinity of Coroccohuayco (e.g., Tintaya, Ccatun Pucara, Quechua and Antapaccay with a total of 13 Mt of Cu; Chelle-Michou et al. 2015b) may have been sourced by the same body of magma at depth (corresponding to a minimum of 143–570 km³ using the same constraints as above).

Conclusions

Available partitioning models based on apatite and amphibole have been used to retrieve the S and Cl melt concentrations of magmas from the Coroccohuayco magmatic suite. We show that the estimated absolute concentrations may vary up to a factor of 3, depending on the partitioning model or the mineral that is used. This highlights the strong need for a better understanding of the partitioning of S and Cl between magma, minerals and fluids for a range of compositions and P–T conditions. Despite the large uncertainties associated with our results, we show that S and Cl data from apatite and amphibole can provide useful information on the volatile budget and evolution of magmas.

The sulfur record in apatite from Coroccohuayco is consistent with the evolution of the magmatic system from being dominated by S²⁻ (reduced) at ~ 40 Ma to being dominated by S⁶⁺ (oxidized) at the time of porphyry emplacement and ore formation. Estimated initial melt S concentrations of 20–200 ppm for the porphyry magmas imply that a minimum of 43 to 365 km³ (median of 81 km³) of magma is required to source the Coroccohuayco deposit with its known amount of S (~ 5 Mt). This volume estimate is compatible with the volume required to explain the Cu endowment of the deposit (3 Mt; 33–131 km³, median of 60 km³). These data suggest that no specific S enrichment is required to form this economic porphyry copper deposit. This view contrasts with findings from other systems where critical amounts of S are thought to have been sourced by co-magmatic basalts (Keith et al. 1997; Hattori and Keith 2001; Maughan et al. 2002; Halter et al. 2002, 2005; Nadeau et al. 2010, 2016; Steinberger et al. 2013; Blundy et al. 2015). Nevertheless, this concurs with the lack of evidence for mafic magma associated with the porphyries at Coroccohuayco (Chelle-Michou et al. 2015a). Furthermore, the similarity of the minimum magma volume estimate based on Cl (60–169 km³) with those based on Cu (33–131 km³) and S (43–365 km³), suggests that the amount of Cl in the magma is at least as critical as the amount of S and Cu to form a porphyry deposit. In other words, magma with high Cu (> 100 ppm) and S (> 500 ppm) content, but normal Cl content (ca. 3000 ppm) would not necessarily have an enhanced metallogenic potential compared to those that formed the Coroccohuayco deposit.

More than the amount of S in the magma, the shift from reduced (NNO ± 1) to oxidized magma (NNO + 1 to NNO + 2) probably was a critical factor for the genesis of the Coroccohuayco deposit. While sulfide saturation in the lower crust inevitably drives the amount of Cu down during magmatic evolution of calc-alkaline magmatic suites (Chiaradia 2014), the oxidation state of sulfur can dramatically change upon magma ascent and decompression (Matjuschkin et al. 2016). Indeed, for a magma having ƒO₂ buffered around NNO + 1 to NNO + 2 such as the ore-forming porphyries at Coroccohuayco, magmatic sulfur is dominantly a reduced species at lower crustal pressures (Matjuschkin et al. 2016), but is dominantly in the form of more oxidized sulfates at upper crustal pressures. This contrasts with magmas buffered at around NNO such as those of the gabbrodiorite complex where sulfur is dominantly in reduced form throughout the thickness of the crust. We suggest that the oxidized character of sulfur at upper crustal pressure (100–200 MPa), where the sub-porphyry plutons typically assemble and degas (Sillitoe 2010), facilitates exsolution of S and Cu into the magmatic fluid rather than their sequestration into magmatic sulfides.

Using available partitioning models for apatite and amphibole, we were unable to determine consistent melt Cl concentrations from both minerals. While estimates based on apatite seem to provide more reasonable absolute values in the order of 1000 s of ppm, estimates based on amphibole are lower but present more convincing relative variations of Cl melt concentration as a function of temperature. Cl data confirm that the basaltic magma at the origin of the gabbrodiorite complex was initially fluid undersaturated and that the melt Cl content increased with magma cooling until ca. 900 °C. At this point, the Cl content remained constant, consistent with modeling of magma cooling and fluid exsolution. For the porphyries, the Cl melt concentration remains constant all along the entire cooling path. This confirms that the felsic magma was initially fluid saturated, and that magma emplacement cooling, crystallization and degassing took place at 100–200 MPa (Chelle-Michou et al. 2015a).