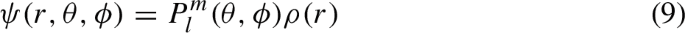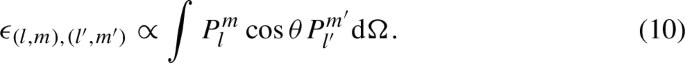Abstract
This paper re-evaluates the formative year of quantum mechanics—from Heisenberg’s first paper on matrix mechanics to Schrödinger’s equivalence proof—by focusing on the role of radiation in the emerging theory. We argue that the radiation problem played a key role in early quantum mechanics, a role that has not been taken into account in the standard histories. Radiation was perceived by the main protagonists of matrix and wave mechanics as a central lacuna in these emerging theories and continued to contribute to the theoretical development and conceptual clarification of quantum mechanics. Studying the interplay between quantum mechanics and radiation, the paper provides an account of (a) how quantum mechanics was able to connect to its empirical basis in spectroscopy and (b) how Schrödinger’s equivalence proof emerged from his explorative calculations on the emission of radiation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The emergence of matrix and wave mechanics in 1925/1926 marks a central turning point in the history of twentieth-century physics. New quantum mechanical equations of motion replaced both classical mechanics and the old quantum theory with its many riddles and anomalies. As a result, quantum mechanics promised a comprehensive theory of atomic and molecular spectroscopy, based on the calculation of atomic and molecular energy levels.
Given the major successes of this approach, it is easy to forget that these energy levels were, at least in 1926, not directly accessible through experiment. Rather they required the observation of spectral radiation and the translation of spectral data into information on energy levels and quantum states. Without an account of the emission and absorption of radiation, the promising theory remained detached from its empirical basis and was essentially incomplete. This raises the following questions: How was quantum mechanics ultimately able to provide a description of the emission of radiation and thus make contact with its primary empirical domain? How did matrix and wave mechanics expand beyond their original focus on atomic structure and manage to incorporate radiation?
Surprisingly, these seemingly basic questions have hardly, if at all, been addressed in the standard history of quantum mechanics. Much brilliant scholarship has focused on the formal elaboration of quantum mechanics and on the emergence of the interpretation debate.Footnote 1 Here, the story begins with the creation of matrix and wave mechanics and the equivalence proof by Schrödinger and Pauli. This proof marks the central turning point,Footnote 2 both initiating the formalization of a unified theory of quantum mechanics and providing a common battleground, where rival claims and philosophical views concerning the physical meaning of the evolving theory were pitted against each other.Footnote 3
Throughout this story, the physics of radiation hardly plays a role. The emission and absorption of radiation and the interaction between light and matter, crucial as these were to the old quantum theory—e.g., in the theory of Bohr, Kramers, and Slater (BKS)—appear to have vanished with the quantum revolution.Footnote 4 We believe this is ultimately because the focus of the historiography of quantum mechanics was largely set by philosophical investigations into the “foundations of quantum mechanics”.Footnote 5 Without much discussion, radiation was here largely neglected as an issue without foundational relevance. It appears that radiation was tacitly seen as a mere “application,” which could be delegated to the domain of quantum field theory, a subject that has recently engendered rich philosophical analysis of its own, without, however, feeding back into the analysis of quantum mechanics proper.Footnote 6
In recent years, the often foundational role of applications in quantum theory has finally moved into the focus of historiography.Footnote 7 These extensions of quantum historiography have led to important insights, e.g., into the role of the many-body problem in shaping concepts like tunneling or the incorporation of the exclusion principle into quantum mechanics. We attempt to do something similar for radiation theory by showing how quantum mechanics came to incorporate the emission of radiation and how the associated scheme for calculating transition probabilities arose.
However, this paper is meant to be more than an addition to a newly emerging perspective. By considering the often ignored question of radiation, we seek to reevaluate the early formative period of quantum mechanics in 1925/1926, which is arguably the core of the quantum revolution. Examining the relationship between radiation and quantum mechanics during this period provides novel insights into the genesis of the equivalence proof, a hallmark of traditional histories of quantum mechanics.
Putting the focus on radiation is not just a matter of historiographical interest or an analytical trick. As we shall see, it is anchored in historical developments and the views of the historical actors. For them, radiation was in fact a central topic, shaping their motivations, expectations and work in 1925/1926. Equally important, it played a crucial role in the development of quantum mechanics as a theoretical framework. We thus need to provide a properly historicized formulation of our initial questions and situate radiation within the historical development of quantum theory.
Throughout the 1920s, the relation between radiation and quantum mechanics was an uneasy one. On the one hand, quantum theory could not do without radiation, since radiation phenomena—ranging from spectroscopy and optics, over the photoelectric and Compton effects to black-body radiation—provided a rich and varied empirical basis as well as key insights for developing a quantum theory of atoms and molecules. On the other hand, radiation and its interaction with matter, more than any other physical process, laid bare a central tension and intractable challenge for the conception of quantum systems that emerged with Bohr’s model of the atom in 1913.
This dilemma persisted throughout the history of the old quantum theory. As we have argued elsewhere, it was instrumental for the development of matrix and wave mechanics in 1925/1926, but it was not directly resolved in the process. From this perspective, the properly historicized formulation of our initial questions is as follows: How did early quantum mechanics address this tension? To what extent did it break with or continue the development of the old quantum theory? What happened with the radiation problem, with all its phenomenological importance and conceptual intractability, as the dust of the quantum revolution began to settle in 1925/1926?
In answering these questions, we begin in Sect. 2 by situating early matrix and wave mechanics within the discussion of the radiation problem in the old quantum theory of the Bohr model. Here we establish that, all other transformations aside, the highly ambiguous status of radiation persisted in the newly emerging theories. The continuing tension between its empirical omnipresence and its theoretical fragility shaped the formative period of quantum mechanics. In Sects. 3 and 4, we thus analyze the early struggles with this tension in matrix and wave mechanics and discuss the respective research agendas of Born, Jordan and Schrödinger.
Our goal here is to follow the development of the two formulations of quantum mechanics as symmetrically as we can and to analyze the exploratory research on radiation in both cases.Footnote 8 This is not an easy task, since the source material is widely different for the two cases. For Born and Jordan’s formative work on matrix mechanics, we have neither notebooks nor letters. Apart from limited, secondary glimpses in Heisenberg’s letters to Pauli, the most substantial sources are the published papers. These seminal papers (Zur Quantenmechanik and Zur Quantenmechanik II) present matrix mechanics as a rather complete mathematical framework and do not provide a genetic account of initial motivations or thought processes. Whatever Born and Jordan’s conceptual and mathematical explorations may have been, all we have to go by are comparatively polished arguments and a program for future theoretical development. However, Born and Jordan’s research program for a new radiation theory remained rather sketchy; their arguments on the radiation process were still exploratory and preliminary in character, especially when compared with the more consolidated exposition and application of matrix mechanics. This unfinished character provides some glimpses into the unresolved tensions and the main obstacles in extending matrix mechanics to the electromagnetic field.
We are in a much better position when it comes to wave mechanics. Just as in the case of Born and Jordan, the importance of the radiation problem is already apparent in Schrödinger’s published work.Footnote 9 However, his notebooks in the AHQP and his correspondence, which can now be studied comprehensively thanks to the edition of the late Karl von Meyenn, allow us to review his exploratory phase of theorizing in much more detail. Following Schrödinger’s twists, turns and inconsistencies, we can here appreciate and uncover the full and crucial importance of the radiation problem as a phenomenological and conceptual challenge for Schrödinger’s work.Footnote 10 Indeed, we can see that the interplay between mechanics and radiation theory was the key to the further elaboration of wave mechanics.
This interplay, we will argue in Sect. 5, worked both ways and led to two major advances in the development of quantum mechanics. On the one hand, it became the starting point for Schrödinger’s equivalence proof. On the other hand, it established a procedure for calculating the amplitudes of radiative transitions, a method that would nowadays be considered a semi-classical dipole approximation. As such, the interplay between radiation and quantum mechanics proved essential for the consolidation of quantum mechanics as a theory of atomic structure.
We can thus study how quantum mechanics was reconnected to its empirical basis in spectroscopy. Simultaneously, this story will have larger implications for the ways in which we should account for the quantum revolution. First, it shows that the equivalence proof did not emerge solely—as the standard account implies—as a means to translate between two abstract mathematical frameworks. Rather, its origins lay in Schrödinger’s exploratory research on radiation. Second, the approximate character of the new radiation mechanism calls into question the extent to which quantum mechanics actually settled its affairs with radiation during its formative period.
2 Radiation where art thou? The formative period of matrix and wave mechanics
Contrary to what the term quantum revolution suggests, quantum mechanics inherited many of its key concepts from what is usually called the old quantum theory—along with some of its tools and most of its problems. In particular with regards to radiation, quantum mechanics is best understood as part of the overall development of quantum physics during the 1910s and 1920s. We thus begin by looking at the old quantum theory and its relation to radiation, sketching its modes of theorizing and its challenges, and by asking how quantum mechanics abandoned or adapted the radiation theory of its precursor.
This means, first of all, revisiting the Bohr model, which provided the blueprint for the conceptualization of physical systems in the old quantum theory. Quantum systems, i.e., atoms and molecules, were thought to exist in stationary states, in which they did not radiate. These states existed in isolation from one another and there was no way to combine two such states; in other words, there was no anticipation of the superposition principle, which would become so central to quantum mechanics later on. The only connection between two states was through discrete transitions. Atoms and molecules could change from one state to another by making discontinuous transitions, which involved the emission or absorption of radiation according to the energy-frequency condition \(\Delta E=h\nu .\)
This description, which we call the state-transition model, entailed (and in fact relied on) a separation between quantum systems and the radiation field, thus introducing a central tension within the theory. This tension played a key role not only in the old quantum theory but also in quantum mechanics. According to Bohr, atoms in their stationary states did not interact dynamically with the electromagnetic field (or with other systems, for that matter); external fields could cause shifts in the energy levels (as in the Stark or Zeeman effect), but there was no exchange of energy between the field and the effectively isolated quantum system. Such a dynamical loss or gain of energy through radiation was replaced by singular transitions, in which energy was lost to (or taken from) some external reservoir, ultimately leaving the system in a different but equally isolated state.Footnote 11
The separation between a quantum system and its environment was not an accidental feature of the state-transition model. It was reluctantly introduced by Bohr as “a horrid assumption” to ensure the stability of the stationary state and thus functioned as one of the pillars of the state-transition model. As such, it had a huge impact on the development of quantum theory, particularly on its radiation-theoretical side. It implied a radical break with classical electrodynamics and ultimately left Bohr’s theory with nothing but a single equation for determining the frequency of a spectral line. After abandoning the classical framework and its radiation mechanism, there was initially no clear theoretical pathway for developing the description of radiative transition processes beyond this frequency condition.
Such a pathway emerged only gradually in light of the analysis of atomic spectra. The most important advance in this regard was the formulation of selection rules, which required that certain transitions, which would have been in keeping with energy conservation, simply did not occur. To Bohr, this implied that the possibility of transitions needed to be restricted in certain cases and led him to formulate the correspondence principle in 1918. This principle postulated a correspondence between the motion of a quantum system (as described by the Fourier coefficients of the Bohr orbits) and the occurrence of transitions (as described by Einstein’s transition probabilities). It would thus allow for an explanation of the selections rules by connecting a zero transition probability to the vanishing of the corresponding Fourier coefficient.
The correspondence principle quickly moved beyond the explanation of selection rules and became the starting point for a more detailed description of radiation. On a purely formal level, as Bohr emphasized, it re-established a connection between radiation and the motion of charges, an integral element of classical electrodynamics eliminated by the original state-transition model. The correspondence principle thereby raised the prospect of determining the intensity (and polarization) of radiation from an underlying “corresponding” motion. This correspondence between motion and radiation made the description of transition processes considerably more sophisticated. The correspondence principle became the core idea of radiation theory in the Bohr model.
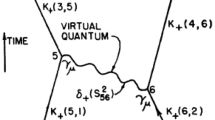
Building on this idea, physicists, most importantly Bohr and his assistant Hendrik Antoon Kramers, revitalized some of the tools of classical radiation theory. In particular, they obtained the intensity of a spectral line and the transition probability of the quantum system from the classical dipole radiation of a moving charge. Since this was difficult to square with the state-transition model, Bohr and Kramers introduced a separate theoretical space in which classical radiation theory could still be operational while leaving the state-transition model untouched. The radiation produced in an actual quantum transition was to be formally compared with the radiation of this hypothetical classical radiator. We have referred to this hypothetical radiator, and to the approach in general, as the Ersatzstrahler or substitute radiator.Footnote 12 The Ersatzstrahler brought just enough classical radiation theory into the old quantum theory to calculate the intensity of spectral lines while still effectively keeping the quantum system in dynamical isolation.
In 1923/1924, Bohr and Kramers saw the opportunity to extend this picture by building on certain elements of dual theories, which tried to reconcile Einstein’s light quanta with the continuous field of Maxwell electrodynamics. Such theories had been developed by de Broglie and Slater and combined corpuscular light quanta with an energyless guiding field. Incorporating the idea of energyless waves into the Ersatzstrahler approach, Bohr, Kramers, and Slater (BKS) developed a theory in which distant atoms interacted in space and time through what was now called virtual radiation, emitted and absorbed by virtual oscillators. The virtual radiation did not transport energy but only induced transition probabilities, implying a merely statistical correlation of transitions in different atoms and hence merely approximate conservation of energy and momentum.Footnote 13
The main goal of BKS was to develop a dynamical theory of the coupling between matter and radiation, which would reunite quantum atoms and electromagnetic radiation in an overarching spatio-temporal picture, taking the quantum atom out of its dynamical isolation.
This grand reunification of matter and radiation was abandoned rather soon, when the main prediction of BKS, statistical energy conservation, was disproven by the Bothe–Geiger experiments, leading to the conclusion that BKS theory was a complete failure. As we have argued in Blum and Jähnert (2022), this failure of BKS left research on radiation in disarray in 1925. Its main lesson for any future quantum theory of the coupling between matter and radiation was the need for correlations that were at least as strong as in the classical theory, in particular through microscopic conservation of energy and momentum.
As this constraint could not be reconciled with wave-particle duality at the time, physicists, in particular Heisenberg and Schrödinger, set aside the problem of coupling as insurmountable for the moment. Instead, they (re)focused their attention on describing isolated quantum systems and developed matrix and wave mechanics, respectively. In both cases, this meant establishing a new kinematic framework for describing the motion of quantum systems (Heisenberg’s x matrix and Schrödinger’s wave functions). The new kinematic frameworks drew on the abandoned radiation theories but were embedded into the dynamical framework of analytical mechanics—not electrodynamics.
In the period between Heisenberg’s first paper on matrix mechanics (July 1925) and Schrödinger’s second communication on wave mechanics (February 1926), the two theories successfully engaged with some of the paradigmatic problems of the old quantum theory, determining energy levels and spectra for the harmonic oscillator, the rotator, and the hydrogen atom. Matrix mechanics, having had a 6-month head start, also tackled the Stark and Zeeman effects as well as dispersion theoryFootnote 14 and developed the necessary approximation schemes (like perturbation theory) and formal techniques (like coordinate transformations, action-angle variables) for the mechanical part of theory.
Looking at these developments, the retreat from the problem of coupling and the development of new mechanical frameworks, it is easy to disregard the relation between radiation and the state-transition model entirely and to focus instead on the elaboration of quantum mechanics. But, as we argued in the introduction, there are good reasons not to do this and instead follow up on the relation between quantum mechanics and radiation.
As we thus depart from the standard history of quantum mechanics, the first thing to notice is that the emergence of the new mechanical frameworks was paralleled by significant losses in the description of the emission of radiation by quantum systems.Footnote 15 In the case of matrix mechanics, the failure of BKS not only led to a retreat from the problem of coupling but to the abandonment of the Ersatzstrahler approach. In May 1925, on verge of formulating his Umdeutung, Heisenberg wrote to his fellow post-doc Ralph Kronig:
[T]he word “Ersatzstrahler” has taken [...] the meaning: “a sloppy application of the correspondence principle that cannot be understood”; I ask you sincerely to eliminate this word, which, for me, evokes memories of wartime substitute jam (Kriegs-Ersatzmarmelade), etc.Footnote 16
In keeping with this statement, Heisenberg’s Umdeutung eschewed the notion of a classical Ersatzstrahler. Heisenberg’s alternative was to directly take the transition amplitudes and frequencies as the kinematic variables describing quantum systems. In his new kinematics, the notion of position famously changed from that of classical trajectory, represented by a Fourier series, into a quantum description in terms of arrays of two-index quantities (transition amplitudes) obeying, as Born and Jordan quickly realized, the rules of matrix algebra.
Conceptually speaking, the shift from the original correspondence approach and the Ersatzstrahler to Heisenberg’s new kinematics meant describing quantum systems through their transitions rather than through their states. Radiation frequencies and intensities were to be obtained directly from the equations of motion, without the need to specify a state emitting the radiation through some sort of mechanism. Matrix mechanics thus seemingly had radiation built into its foundations, and the primary challenge of the theory appeared to be the solution of the mechanical equations of motion.
It was at this point that difficulties started emerging. It soon became clear that the matrix equations of motion could be directly solved only in a handful of simple cases. In those cases, the empirical regularities obtained in the old quantum theory could be recaptured. In particular, it was possible to reestablish the various selection rules, which had played a key role in the creation of the correspondence principle. For systems governed by selection rules (primarily purely harmonic systems, such as the harmonic oscillator, the rotator, or the precessional motion associated with the Zeeman effect), most transitions were forbidden and the corresponding matrix elements vanished, reducing the matrix products in the equations of motion to just one or two terms.Footnote 17 In these cases, the matrix equations could thus be greatly simplified and solved.
While matrix mechanics could handle these systems, which had been characterized as multiply periodic in the old quantum theory (Bohr 1923, 120), its applicability turned out to be severely limited in more general cases. Here, matrix mechanics should be considered more of a program—still requiring major computational, if not conceptual, innovation—rather than a complete theory.Footnote 18 When there were no selection rules, the x matrix had rows and columns full of nonzero elements. The matrix products involved in the equations of motion thus contained infinite sums, making it impossible to extract equations for single matrix elements that could be solved in isolation. Instead, one had to solve the dynamical equations for the entire matrix and all possible transition amplitudes.
In some cases, it was possible to start from a simple harmonic system, introduce the more complicated dynamics as a perturbation and then solve the equation of motion iteratively. This was the approach taken by Heisenberg in the Umdeutung to treat the anharmonic oscillator; it was further formalized in Born and Jordan’s first paper on matrix mechanics. This approach, however, was not always applicable. In particular, it could not be used for the paradigmatic system of the old quantum theory: the hydrogen atom. The orbital motion of the electrons was not harmonic, and the 1/r Coulomb potential of the nucleus could not be Taylor-expanded as a harmonic potential plus small anharmonic perturbations.
In the Dreimännerarbeit, Born, Jordan and Heisenberg devised a general method for solving the matrix equations of motion, which was supposed to transcend these limitations. It consisted in finding a transformation matrix S (the “principle-axes transformation” or Hauptachsentransformation) that diagonalized the Hamiltonian, giving the energy levels \(W_n\) of the states. In principle, this procedure amounted to a complete solution of the equations of motion, providing the energy levels and the transition probabilities in one go.Footnote 19
In practice, however, it turned out to be far less powerful than anticipated. We know of only one example of a concrete application of the Hauptachsentransformation: Heisenberg and Jordan’s treatment of the anomalous Zeeman effect (Heisenberg and Jordan 1926), a spin-off from the Dreimännerarbeit. When Pauli finally turned to the hydrogen atom he set aside this technique and used what Heisenberg would call the “actual” way of solving the equations of motion:
I am always angry, when I hear the theory only referred to as matrix physics and for a while I seriously considered completely removing the word matrix from the paper and replacing it by something else, such as “quantum-theoretical quantity.” (Incidentally, matrix is probably one of the stupidest mathematical words there is). I also do not know whether one should not entirely throw out the principle-axes transformation; because you have shown for hydrogen how one actually has to integrate [the equations of motion], and everything else is thus only formal stuff after all.Footnote 20
Heisenberg was not alone in this assessment. Even Dirac, one of the champions of the newly emerging (algebraic) formalism, concluded that the principle-axes transformation “do[es] not appear to be of great practical value” (Dirac 1926a, 565). The hope to completely solve the equations of motion and thus also obtain transition probabilities thus remained unfulfilled.
With respect to radiation, Pauli’s “actual” integration method did not improve the situation. In his work on the hydrogen problem, Pauli employed an ingenious method based on conserved quantities. The classical Kepler problem had a large number conserved quantities, namely energy, angular momentum, and the somewhat esoteric Laplace–Runge–Lenz vector, which was related to the eccentricity of the orbit.Footnote 21 Pauli could show that these three quantities were also conserved in matrix mechanics. From the equations of motion, he then extracted relations that involved only these conserved quantities, and thus only diagonal matrices. These relations could be solved, yielding the energy levels of the hydrogen atom as the elements of the diagonal energy matrix.
This, however, was not a complete solution of the hydrogen atom, since the relations between the conserved quantities necessarily contained less information than the original matrix equations of motion. As Pauli explicitly conceded, this loss was evident in the fact that “the coordinates (i.e., the transition probabilities), however, [had] been eliminated” from his relations. As a result, the intensities of the hydrogen atom remained undetermined yet again.Footnote 22
This was more then a minor desideratum. While praising Pauli for his results on hydrogen, Heisenberg saw the need for further improvement. He hoped (in vain) that Dirac’s treatment of the hydrogen atom, published in March 1926, would get closer to the transition probabilities and thus to a truly complete solution.Footnote 23
It is thus safe to say that the relationship between matrix mechanics and radiation was neither settled nor of marginal interest. Heisenberg’s fundamental assumption—identifying the elements of the x matrix with the emission amplitudes—allowed matrix mechanics to reproduce the most important spectroscopic regularities, the selection rules. However, the procedures leading to these results were not generalizable, even to a paradigmatic system such as the hydrogen atom. What emerged were the drawbacks of the theory’s departure from the state-transition model of the old quantum theory, in particular from the notion of a state. In matrix mechanics, there was no notion of a single trajectory or state. This implied, first of all, that solving the dynamical equations was forbiddingly difficult. One could not find “a” solution to the equations of motion and generalize from there (as in classical mechanics). Without a concept of state, the theory’s description of the system through the totality of its transitions forced physicists to directly find “the” (most general) solution to the equation of motion.Footnote 24 Furthermore, it was not clear how one could connect the emission of radiation to a specific state of the atom—a major gap in the description of radiation processes.
If matrix mechanics already had a hard time coming to grips with radiation, the situation for wave mechanics was even more precarious.Footnote 25 In his first communication, in which he presented his time-independent wave equation (Schrödinger 1926a), Schrödinger showed that one could obtain the energy values (and the corresponding eigenfunctions) of the hydrogen atom from his wave equation. The next step would, of course, be to extract the frequencies of spectral lines from these energy levels, i.e., to reconstruct the frequency condition and thus account for the emission of radiation.
This step, however, could not be taken solely on the basis of the wave equation, and Schrödinger was unable to extend the formalism to include radiation. Instead he resorted to a qualitative physical description of the atom to account for the emission of radiation. This description is not only markedly different from later interpretations of wave mechanics but also provides key insights into Schrödinger’s conceptualization of the wave function and his thinking about radiation. For Schrödinger, wave mechanics suggested that there was “an oscillatory process in the atom” (Schrödinger 1926a, 372), described by the solution of the wave equation \(\Psi .\) The eigenvalues of his equation were then related to the frequencies of this oscillatory process.Footnote 26 This was a natural picture in Schrödinger’s approach, with far reaching implications: it was not to be expected that the atom at any given moment was oscillating in just one eigenmode; rather, the generic solution for such an oscillating system was “a potpourri of its proper vibrations,” i.e., a superposition of eigenmodes (Schrödinger 1926a, 375).
This, Schrödinger realized, implied a potential departure from the state-transition model of the old quantum theory in several respects. On the one hand, if one were to identify the eigenmodes of wave mechanics with the stationary states of the Bohr model, it would suggest that the atom would not be in one of these states but rather in a superposition of stationary states. Schrödinger flirted with this total deconstruction of the state-transition model, but he shied away from fully endorsing it. On the other hand, and more importantly, it presented an opportunity to implement a radiation mechanism in his new scheme, using the possibility of superpositions. It was now possible to re-imagine the emission of radiation as a continuous process, where “energy wanders over from one normal mode to another” (Schrödinger 1926a, 374). In this manner, the radiation frequencies and the frequency condition emerged naturally: when two eigenmodes were in superposition, they would—in full analogy with acoustics—generate a beat; and the frequency of this beat would be given by the difference between the two proper frequencies, i.e., precisely by the observed spectroscopic frequencies.
This new qualitative picture was Schrödinger’s starting point for thinking about radiation in wave mechanics: radiation was produced as energy flowed from one eigenmode to the other.Footnote 27 The separation between mechanical motion and radiation had been a central feature of the Bohr Model, and Schrödinger was now trying to undo it. Where Heisenberg had negated the problem of relating mechanical motion and emitted radiation by eliminating the former, Schrödinger was postulating a return to a direct connection between (wave-)mechanical motion and radiation through the beat frequency.
Schrödinger’s wave mechanics challenged the notion of stationary state through the possibility (or rather plausibility) of arbitrary superpositions. And it appeared to allow for a novel continuous description of transitions. Schrödinger considered this undermining of the state-transition model to be a definite conceptual advance. As late as November 1926, he criticized Born for being shackled to the concepts of states and transitions, which had “acquired citizenship in our thinking over the last twelve years [i.e., since the Bohr Model]”. Schrödinger argued that this adherence prevented Born from properly engaging with the attempts to “escape from this way of thinking [Denkschema].”Footnote 28
The further formalization of this picture was, however, far from straightforward. He soon abandoned this approach to radiation, not least because it was scrutinized and criticized by Sommerfeld, Wien and later Lorentz.Footnote 29 While they were the first and generally enthusiastic recipients of wave mechanics, all three thought that Schrödinger’s beat picture was little more than window dressing for ad-hoc formal manipulations.
While this criticism is certainly warranted, Schrödinger’s arguments in the first communication highlight most clearly that wave mechanics, even more so than matrix mechanics, had lost key theoretical conceptions of the old quantum theory and, with it, the ability to account for empirical regularities of spectroscopy. There was no transition process, no frequency condition, no correspondence principle, no Ersatzstrahler, let alone transition amplitudes (or matrix elements), in early wave mechanics. Schrödinger was painfully aware that he needed something, anything, to replace them. His ill-fated beat interpretation shows how essential it appeared to incorporate radiation into the new mechanical theory: even the most obviously hand-waving speculation was preferable to leaving radiation aside entirely.
Matrix and wave mechanics, each in their specific way, were thus struggling in coming to terms with radiation. They did so against the backdrop of an established radiation-theoretical tradition, comprised of the state-transition model, the correspondence principle, the Ersatzstrahler, a wealth of empirical regularities in spectroscopy, and the major conceptual challenge posed by the refutation of BKS. As we will see, neither Heisenberg, Born, and Jordan nor Schrödinger entertained the idea of simply neglecting radiation but rather saw it as a major lacuna, central to the future development of quantum theory.
3 More correct than physical theories have a right to be: radiation in early matrix mechanics
As we have just seen, radiation had been incorporated into matrix mechanics through Heisenberg’s initial assumption. Transition probabilities were obtained directly as solutions to the equations of motion. This was possible in some simple cases where one could indeed obtain radiative intensities by solving the mechanical equations of motion. But matrix mechanics failed to deliver for more complex systems, and there was no generally applicable method for obtaining transition probabilities within the mechanical framework.
In this section, we will analyze the ambiguous manner in which matrix mechanics dealt with radiation. First, we will consider the attempts to provide a new mechanism for the emission of radiation, designed to replace the Ersatzstrahler and to clarify Heisenberg’s foundational assumption. Then, we will analyze the attempts to finally resolve the “problem of coupling,” which had arisen in the wake of BKS theory, i.e., the problem of how to couple a fully dynamical electromagnetic field to a (now matrix-mechanical) atomic quantum system.
We can find both approaches, intimately linked yet clearly discernible, in Born and Jordan’s earliest work on matrix mechanics. As mentioned in the introduction to this paper, the only historical sources we have here are the published papers, in particular Born and Jordan’s first paper on matrix mechanics (Born and Jordan 1925), in which they were mostly concerned with laying the mathematical foundations of matrix mechanics, as well as the Dreimännerarbeit (Born et al. 1926). In the final section of both of these papers, Born and Jordan discussed the relation between matrix mechanics and radiation and sketched a comprehensive research program for a new radiation theory.
This program was still in the earliest stages. The arguments are exploratory and preliminary in character, especially when compared with the more consolidated exposition and application of the mechanical framework. This unfinished character serves as a reminder that Born and Jordan were presenting a research program, not a fully elaborated theory; this allows us to catch some glimpses of the unresolved tensions between the intuitions of the old quantum theory—where a quantum system always was in a certain state—and the new formalism, where a quantum system was defined only through its transitions. We will also be able to pinpoint some of the main obstacles in extending matrix mechanics to the electromagnetic field.
3.1 Heisenberg’s fundamental assumption and the Ersatzstrahler
While Heisenberg’s fundamental assumption that the transition probabilities are to be identified with the elements of the position matrix was taken as a given in most works on matrix mechanics, Born and Jordan took issue with it already in their first paper on the subject:
According to Heisenberg, the squared absolute values \(|q(nm)|^2\) of the elements \({\textbf{q}}\) should determine the transition probabilities, if \({\textbf{q}}\) are Cartesian coordinates. In closing [this paper], we want to explain how this assumption can be justified from general considerations. This makes it necessary to consider how the fundamental equations of electrodynamics are to be reinterpreted according to the new theory. (Born and Jordan 1925, 883)
Born and Jordan were willing to accept Heisenberg’s assumption. After all, it had provided the heuristic starting point for constructing the new theory. But they believed the assumption was in need of a justification that would rely only on foundational elements of the new formalism: Hamiltonian dynamics in matrix form and the commutation relations. In Born and Jordan’s view, these elements should suffice to extend the framework to cover electrodynamics and to derive not just energy conservation and Bohr’s frequency condition, but also Heisenberg’s assumption.Footnote 30
Approaching this task, Born and Jordan viewed the emission process as an energy transfer from a quantum system to the electromagnetic field. For this specific problem, they argued, one did not yet need a full-fledged matrix formulation of electrodynamics. The energy transfer would be governed by the same equation as in classical theory; the only difference being that all dynamical variables, including the fields, would appear as matrices.Footnote 31 Taking the charge e times Heisenberg’s matrix X to “represent the electric moment which excites the wave,”Footnote 32 they obtained for the total energy radiated per second:
This looked exactly like the classical expression, which had also been used in the correspondence tradition to calculate the intensity of spectral lines. On a formal level, there was thus continuity between matrix mechanics and the old quantum theory. But in the old quantum theory, the emitting dipole had been the classical Ersatzstrahler; the matrix X, by contrast, was no longer supposed to represent the motion of the radiating system in a particular state and could thus not be interpreted in a classical manner.
Instead, X was now a matrix involving all possible transitions and all states. In consequence, even an individual matrix element of the matrix \({\ddot{X}}^2,\) which was supposed to represent a single radiation process, would involve the amplitudes for many possible transitions. From Eq. 1, one could thus not claim that radiation with a particular intensity was emitted by a system making a particular transition from one state to another.Footnote 33
Born and Jordan’s strategy was now to “diagonalize” \({\ddot{X}}^2\) by considering only time averages. This meant that the off-diagonal elements, which were taken to be periodic functions, would vanish, leaving only the diagonal elements associated with an individual state n:
where \(\nu (nk)\) is the frequency associated with the transition from n to k.
Throwing away the off-diagonal elements meant a considerable simplification of the initial expression. Its primary importance was, however, that it allowed Born and Jordan to interpret the resulting expression in terms of the state-transition model. The diagonal element associated with the state n could now be interpreted as the intensity of the radiation emitted by the atom in that state. However, the expression for the diagonal elements still involved all matrix elements \(X_{nk},\) corresponding to all possible transitions departing from the state n. Since this included cases where \(k>n,\) it also contained transitions to higher-energy states that did not occur spontaneously, as was necessary to account for Heisenberg’s initial assumption.
This was ultimately not satisfactory for Born and Jordan, leading them to conclude:
Here, we can not yet give a complete theory of emission, from which one could necessarily deduce the association of single terms in this series with the stationary states; for this, a detailed investigation would be necessary of how the radiation reacts back onto the oscillator, i.e., a theory of damping. (Born and Jordan 1925, 887)
As this quote shows, Born and Jordan expected that a new radiation theory would have to give “the association of single terms in this series with the stationary states.” In other words, they still sought a conceptualization of the radiation process in terms of the original state-transition model; one in which a quantum system in a definite state emitted radiation during a transition. Such a theory would require not only a complete description of matter and the radiation field, but also a description of the interaction between matter and the radiation, including, in particular, the back-reaction of the emitted radiation on the material system.
Born and Jordan were nowhere near such a description and they knew it. Nonetheless, they saw the possibility to take one further step. This was the justification of Heisenberg’s initial assumption that “the radiation was indeed determined by the quantity [\(|X(nk)^2|]\)”, if only “in a purely formal manner.”Footnote 34 To this end, Born and Jordan considered the sum of all the diagonal elements of \({\ddot{X}}^2,\) i.e., the trace of the matrix in modern parlance. This gave a double sum over all states, i.e., a sum over all transitions. The double series could then be rearranged, so that it only involved transitions from a higher to a lower state:
This expression could now be read as the sum over the intensities of the radiation emitted by the atom in all possible states. Each of the summands in brackets could then be associated with the radiation emitted in a single state n:
To each state n is associated the radiation corresponding to all transitions with \(k<n,\) each one with the intensity known from classical theory. This is in accord with experience, if one assumes that the indices n are ordered according to increasing energies \(W_n.\) Thus, Heisenberg’s assumption is justified in the limited sense indicated above. (Born and Jordan 1925, 888).
We observe that, in the first paper on matrix mechanics, Born and Jordan did not simply accept Heisenberg’s assumption that radiation was built into matrix mechanics. They believed that the connection between radiation and the X matrix should and could be substantiated. Rather than assuming that the transition amplitudes themselves were kinematic properties, they posited that the role of the new kinematic quantities as transition amplitudes was something that could be derived. To achieve this goal, they considered dipole radiation, the paradigmatic example for classical theories of emission, within the new framework of matrix mechanics. The ultimate goal for a complete theory of radiation was still the picture of a system in a particular state emitting radiation. But this goal remained out of reach, and Born and Jordan fell short of providing a definite interpretation of the matrix elements. It remained unclear how to move beyond the old Ersatzstrahler approach.
3.2 The return of the coupling problem
These results—the justification of Heisenberg’s assumption and the description of the emission process in matrix mechanics—preliminary and incomplete as they were, were only the starting point for a far more ambitious program: to construct a quantum description of the electromagnetic field, a fully dynamical theory of quantum electrodynamics. In this theory, electrodynamics as whole, just like mechanics, would be transformed into a quantum theory through the use of multiplication rules and quantum conditions. While these rules might differ significantly from those used in the construction of quantum mechanics, quantum mechanics and electrodynamics would be integrated within an overarching quantum framework.
This was a grand program for the future. In their first attempts, Born and Jordan explicitly deferred the issue of multiplication rules and quantum conditions for the electromagnetic field to a later date and instead focused on questions where they did not come into play. One thing that appeared to be within reach was the conservation of energy and momentum, a central issue in view of the recent failure of BKS.
Born and Jordan were able to prove energy conservation for the electromagnetic field (in the absence of charges) without having to explicitly invoke the unknown quantum conditions.Footnote 35 This in turn implied that one could speak, in the new framework, of an atom transferring energy to the field.Footnote 36 Born and Jordan’s justification of Heisenberg’s foundational assumption then relied on the idea that this energy transfer was governed by the same equation as in classical theory, again independently of the quantum conditions.
With these forays into radiation theory, Born and Jordan felt they could transfer “a good deal” of the formalism of Maxwell’s equations into the framework of matrix mechanics.Footnote 37 Yet, the hardest parts were still to come, as one would have to formulate quantum conditions for the electromagnetic field and then find a truly dynamical theory of radiation in which both the source and the radiation were described by quantum matrices.
In Jordan’s view, the next step towards quantizing electrodynamics was to describe the electromagnetic field by itself as a quantum system. A prerequisite for such a formulation would be a matrix mechanics of continua, and the simplest model for a continuous system was a vibrating string. In the Dreimännerarbeit, Jordan thus sought to find a quantum description of a vibrating string.Footnote 38 The string could be treated with the methods of matrix mechanics by regarding it (through a Fourier transformation) as an infinite set of harmonic oscillators, each corresponding to a vibrational mode of the string. Each harmonic oscillator individually could then be quantized following the matrix-mechanical formalism.
The resulting quantum theory of the vibrating string displayed several striking characteristics that were indeed to be required of an eventual quantum theory of electrodynamics: discrete energy quanta obeying Bose–Einstein statistics and thus Planck’s law, as well as energy fluctuations showing wave-particle duality in a form first derived by Einstein for thermal radiation in 1909. This latter result, in particular, was considered essential by both Heisenberg and Jordan. Heisenberg highlighted the fact that “Einstein’s light quantum theory emerged entirely from the calculation of the mean square fluctuations” and stipulated that one should be able to find “the essential features of the light quantum theory” in matrix mechanics through “an analysis of the precise reason, why the new theory leads to the correct fluctuation formula.”Footnote 39 In other words, all the pieces seemed to be there already, it just was not clear how they fit together.
For Jordan, the implications were somewhat different and even more specific: the fluctuation formula for the vibrating string resulted from quantizing that system using the same quantization procedures used in mechanics. Thus, in order to obtain the fluctuation formula in electrodynamics, the radiation field would also have to be quantized according to that very same procedure.Footnote 40 Jordan thus felt confident that the quantization procedures already established were widely applicable.
The quantization of the electromagnetic field had further conceptual implications. In Jordan’s treatment, the vibrating string (or, by analogical extension, the radiation field in the black-body cavity) was now a quantum system in a stationary state. But it could hardly jump from one state to another by emitting radiation—it was, after all, radiation itself. However, as Bacciagaluppi et al. (2017) have shown, the radiation field was still seen as performing transitions, which now involved the exchange of energy between subsections of the string (subvolumes of the cavity). This extension of the state-transition model to the electromagnetic field pushed it well beyond its original formulation. For material quantum systems, the idea had always been that the system was in a certain state, in which energy was constant. In the case of the electromagnetic field, there was now the picture of transitions and thus energy flow occurring between the various subsystems, while the system as a whole remained in a stationary state.Footnote 41
Jordan’s treatment and his results were seen as a promising start and ultimately provided a way to introduce a notion of change into the theory (not just with respect to radiation, but also for material systems). But the question of how energy flowed from one subsystem to another was hardly answered. Moreover, there was no indication how a quantized field could be coupled to matrix-mechanical atoms performing radiative transitions. Formulating such a quantum theory of the electromagnetic field and its interaction with matter was indeed a formidable problem. On a formal level, one was dealing with a relativistic continuum theory (far more complex than Jordan’s vibrating string). Even in classical physics, this theory was still relatively new and had not undergone a century’s worth of mathematical formalization. In particular, there was no Hamiltonian formulation of Maxwellian electrodynamics, which one could then try to quantize according to the new formalism. Moreover, there was no consistent classical theory of the coupling of the electromagnetic field to atomistic charged matter. On the empirical level, one had to tackle a set of phenomena (both classical optics and quantum phenomena such as thermal radiation or the Compton effect), which were unrelated to the spectroscopic experiments that had given rise to matrix mechanics and therefore required the integration of new concepts (wave-particle duality in all its facets).
In light of these difficulties, the development of a full-blown quantum field theory was considered to be beyond the scope of matrix mechanics in 1925, as was aptly summarized by Born, Heisenberg, and Jordan in the introduction to Zur Quantenmechanik II:
Even though we would like to conclude from the mathematical uniformity and simplicity of the theory here attempted that it already represents essential features of the actual circumstances of the problem of atomic structure, one still has to call to mind that the theory cannot yet provide a solution to the principal difficulties of quantum theory. The forces that correspond to the radiation damping of the classical theory are not yet integrated into the theory, and there are only vague hints towards the connection between the problem of coupling and the quantum mechanics here attempted. (Born et al. 1926, 559)
Born, Jordan and Heisenberg thus clearly considered the problem of the interaction between matter and the radiation field as an integral and still unresolved challenge for the new quantum mechanics. They were cautiously optimistic that the new theory already contained the core ideas necessary for a quantum description of atomic systems. They were sure, however, that this did not suffice to solve “the principal difficulties of quantum theory,” which lay in the “problem of coupling.” This problem encompassed the general issue of coupling two quantum systems. In BKS theory, the coupling between two quantum atoms—be it in collision or scattering processes (Bohr 1925), be it in correlations between transitions in distant atoms—had been mediated by an essentially classical field. With Jordan’s vision of a quantum field theory of electrodynamics, the interaction between an atomic quantum system and the quantum electromagnetic field became the paradigmatic instance of the problem of coupling.
The problem of coupling thus resurfaced rather quickly after the emergence of matrix mechanics and figured prominently in the assessment of the theory’s frontiers. Pauli, Heisenberg and Bohr agreed on this assessment and identified the problem of coupling and the integration of radiation into the new quantum mechanical formalism as a central desideratum of the new theory.Footnote 42 Bohr actually argued that the emerging quantum mechanics could not possibly provide a complete solution until the issue was resolved:
As concerns the future possibilities for developing quantum mechanics, my views are very similar to yours. The problem of coupling among transitions is entirely outside the scope of Heisenberg’s line of attack [...] I do not see through the mathematical problem clearly enough to formulate my view on this point [...] precisely; but you will recognize my general point of view when I doubt that one has come to a complete treatment of any aspect of the problem before one has solved all aspects. How should we be able to make use of Heisenberg’s great effort to make further progress, if it was more “correct” than physical theories have the right to be?Footnote 43
For Bohr, the advent of matrix mechanics had not changed the situation for the radiation problem; it was still as pressing as it had been for BKS. Matrix mechanics provided a new and promising description of quantum systems undergoing transitions. However, it still described these quantum systems and their transitions in isolation from their surroundings. Without the explicit formulation of a coupling mechanism, whatever matrix mechanics appeared to be saying about the radiation problem was more correct than it had the right to be.
This underscores the main point we want to make in this section: for the pioneers of matrix mechanics, radiation was an integral and highly challenging part of the theory. As we saw, radiation was to some extant genetically built into matrix mechanics through core interpretative assumptions and the state-transition model. The theory could thereby account for the most important spectroscopic regularities, such as selection rules, and thus adequately describe empirical data. At the same time, the actual computation of intensities posed a formidable problem once the theory was extended to physical systems as complex as the hydrogen atom. Furthermore, in trying to elaborate a mechanism for emission, one ran into what appeared to be the limits of the state-transition model.
In addition to these formal and conceptual difficulties, the problem of coupling as formulated in BKS resurfaced. As the historical actors came to realize, matrix mechanics was conceptually still well within the tradition of the Bohr model, as it did not describe how quantum systems coupled to the electromagnetic field. This problem would have to be solved by integrating electrodynamics and matrix mechanics. How this integration was to be achieved was an open question. Born and Jordan believed one would have to describe the electromagnetic field as a quantum system with states and transitions. This would mean finding appropriate quantum conditions to fit quantum electrodynamics into the already completed framework of matrix mechanics. Bohr agreed that some sort of integration was necessary, but this might not just be a matter of finding quantum conditions for electrodynamics. He believed that a grand solution for all aspects of the problem was needed and thought that partial solutions, like the matrix-mechanical description of isolated systems, would eventually be revised.
4 Rules that take the place of the correspondence principle: Schrödinger and the radiation problem
While matrix mechanics had a hard time grappling with radiation, the situation for wave mechanics was still more precarious. As we have seen in Sect. 2, wave mechanics did not come with a radiation mechanism of its own, nor did Schrödinger really accept the idea of discrete transitions between stationary states. It is thus no surprise that Schrödinger struggled with radiation, both on a conceptual level and on the level of quantitative predictions.
This struggle continued through February and March, as Schrödinger prepared his second and third communications and worked out his equivalence proof. During this time, he consistently grappled with the radiation problem in his publications and, even more so, in his correspondence and private notebooks. In this section, we will analyze this process and connect it to the more formal public presentation of wave mechanics. While Schrödinger set out to present wave mechanics as a full-fledged mechanical theory in his second and third communications, we will see him exploring different pathways with respect to radiation. Like Born and Jordan, he pursued two different goals, searching for ways to (a) to calculate spectral frequencies and intensities and (b) to integrate wave mechanics and electrodynamics into an overarching theory in order to solve the “problem of coupling.”Footnote 44
His first line of inquiry began with the application of wave mechanics to the Stark effect. Here, as we will show, Schrödinger obtained serendipitous insights into the formal representation of selection rules and intensities in wave mechanics. These insights led him to his first attempt to formulate the relationship between his theory and matrix mechanics in a notebook later entitled “Intensities, Parallels to Heisenberg and Lanczos.”
Schrödinger’s second line of inquiry concerned the integration of wave mechanics into classical electrodynamics, documented in the notebook later entitled “Coupling, Very Old.” We will show how Schrödinger developed various speculative ideas on the radiation mechanism in wave mechanics, which eventually started to coalesce into a program for integrating wave mechanics and classical electrodynamics. These two separate lines of inquiry converged in early March in Schrödinger’s work on the equivalence proof, which also provided a partial solution to the radiation problem in wave mechanics, allowing him to describe the intensity of spectral lines through the classical radiation of an oscillating dipole.
4.1 Calculational exploration and programmatic vistas: two approaches to radiation
In January 1926, as detailed in Sect. 2, Schrödinger had completed his first communication and was entertaining the idea of associating radiation with beats. While preparing the second communication, he outlined his research agenda for the immediate future to Arnold Sommerfeld:
The next most important task seems to be, apart from the calculation of important special cases such as the Stark and Zeeman effects and the relativistic Kepler problem, the establishment of a rule for intensity and polarization, which is to take the place of the correspondence principle. Since I believe that the \(\psi \)-function actually describes the processes in the atom that are the cause of the emission of light, it has to provide all the relevant information [on the intensity and polarization of radiation]. One has to study the intensity beats when two proper vibrations are excited simultaneously, as well as their (the beats’) spatial distribution.Footnote 45
For Schrödinger, the extension of wave mechanics to special cases like the Stark effect was merely a question of calculational work. Conceptual advances were needed first and foremost in the field of radiation. These advances, Schrödinger anticipated, would move away from the correspondence principle, inseparably linked as it was to the state-transition model. Instead, the new approach would elaborate the idea of spectral radiation as a beat phenomenon.
In the following weeks, Schrödinger made no headway in his conceptual work on the radiation process. His straightforward calculational work, on the other hand, turned out to be more rewarding. Following what he called the “path of least resistance,” Schrödinger developed a wave-mechanical treatment of the Stark effect. A slight modification of the hydrogen atom problem with an external electric field added as a small disturbance, it required the development of a wave-theoretical version of perturbation theory. This turned out to be “beautiful, easy” and “gave [Schrödinger] great joy.”Footnote 46
The treatment of perturbations in wave mechanics drew from Lord Rayleigh’s 1894 work on acoustics and vibrating strings, which provided a wave-theoretical perturbation theory for one-dimensional objects, such as a slightly inhomogeneous vibrating string. Schrödinger extended this perturbation method to the vibrations of matter waves in three-dimensional space. The effect of an external electric field on the hydrogen atom could then be treated as a small perturbation of a physical system whose unperturbed dynamics were already solved.Footnote 47
Initially, the goal of this exploration was to improve and test the mechanical part of Schrödinger’s theory. It involved only static external fields and no radiation. Nonetheless, as we will see, it was here that Schrödinger developed the central insight into how basic spectroscopic regularities, in the form of selection rules, would be obtained in wave mechanics, ultimately laying the groundwork for describing the intensity of spectral lines.Footnote 48
This development was serendipitous in the best sense of the word, involving a mixture of calculational exploration, some surprising results made possible by rather accidental choices, as well as the recognition and creative interpretation of formal patterns. To reconstruct Schrödinger’s path and the leaps that he made in the process, we thus have to delve into the technical content of his notebooks. Schrödinger began with the wave equation for the Stark effect, i.e., for an electron in a hydrogen atom with an externally applied electric field F:
Here, the perturbation \(eFz=e F r \cos {\theta }\) involved the coordinate \(\theta \) (polar angle), which did not appear in the unperturbed wave equation. This resulted in a lifting of the degeneracy of the unperturbed case, thereby providing an explanation for the splitting of the energy levels in the Stark effect.Footnote 49
Solving the new wave equation within his perturbation theory, Schrödinger arrived at an equation for calculating both the energy splittings \(\lambda \epsilon _l = E_{kl}^{*} - E_k\) and the coefficients \(\kappa _{li}\) that described how exactly the perturbation lifted the degeneracy:Footnote 50
where
Finding the perturbed energy eigenvalues then boiled down to evaluating the integrals \(\epsilon _{ji},\) which Schrödinger referred to as the “perturbation parameters” in his notebook.Footnote 51
Overall, the derivation was a rather straightforward generalization of Schrödinger’s original calculation of the energy levels of the hydrogen atom. There was no reason for Schrödinger to expect any new insights into the radiation process from it; or to expect that the expression for the perturbation parameters, an integral over two different wave functions, had any physical significance beyond perturbation theory.
This changed when Schrödinger calculated the perturbation parameters \(\epsilon _{ji}\) explicitly for the case of hydrogen. Here, he obtained integrals of the form:
where \(P_l^m\) and \(P_{l'}^{m'}\) are spherical harmonics, which appear in the unperturbed eigenfunctions of the hydrogen atom, and \(\cos {\theta }\) is the factor in the external perturbation that depends on the polar angle. Evaluating this integral, Schrödinger found that it vanished, except for the case where the quantum numbers labeling the unperturbed hydrogen wave functions were related as \(m=m'\) (equal magnetic quantum numbers for both) and \(\vert l - l' \vert = 1\) (azimuthal/orbital quantum numbers differing by one unit).Footnote 52
This result was, in a certain sense, entirely accidental, emerging from the interplay between the unperturbed wave functions and the specific form of the perturbation, namely, the interaction with the constant external electric field. Nonetheless, the vanishing of the integral gave rise to far-reaching considerations: the conditions \(m=m'\) and \(\vert l - l' \vert = 1,\) for which the integral was non-zero, were identical to the well-established selection rules in the Stark effect. Selection rules, as mentioned in Sect. 2, were typically interpreted as statements about intensities being zero within the tradition of the state-transition model and the correspondence principle. The reproduction of such rules (or rather, of conditions formally analogous to them) appears to have been highly suggestive to Schrödinger. When he announced his Stark effect calculations in the aforementioned letter to Sommerfeld, he wrote:
I believe that one always needs two \(\psi \)-oscillations with different n in superposition in order for emission to occur through their joint action. There must be conditions that prevent emission even when there is a combination of two proper vibrations with different frequencies (selection principle). This must somehow be related to the integral over the product of the two functions or more precisely over the product of one function with the derivative of the other.Footnote 53
We see here a fusion of two distinct elements: on the one hand, Schrödinger’s concept of radiation as a beat phenomenon (“two \(\psi \)-oscillations with different n in superposition”) and, on the other hand, the “integral over the product of the two [wave] functions” which appeared in his Stark effect calculations. The alignment between the two went beyond the reproduction of selection rules: a product of two wave functions was certainly in keeping with Schrödinger’s picture of two simultaneously excited eigenfunctions. But that was as far as Schrödinger’s physical picture went: the specific formal expression he was exploring for the spectral intensities was suggested by the Stark effect perturbation parameters, not by an elaboration of the beat picture.
To put it more abstractly, we see here the interplay between mechanical theorizing and radiation theory at work. Within the mechanical part of his theory, Schrödinger developed the new calculational tool of perturbation theory and tentatively established a phenomenological connection with the radiation process via the selection rules. He then started to explore whether this connection could be generalized to provide an expression for spectral intensities, thus laying the groundwork for a radiation theory within wave mechanics.
Initially, Schrödinger appears to have believed that the formal hints obtained from the selection rules merely pointed in a general direction: two wave functions would somehow have to be combined under an integral to yield intensities. In his notes, we see him pursuing—in a very formal manner, without considering possible physical interpretations—the various ways of doing this. This exploration appears on a couple of loose notes at the beginning of his notebook later entitled “Intensities, Parallels to Heisenberg and Lanczos.”Footnote 54 Schrödinger began by noting that the energy eigenvalue \(\epsilon _n\) belonging to the eigenfunction \(\psi _n\) could be obtained as
where the explicit example given is that of the harmonic oscillator, although the last expression is more general, with \(L(\psi )\) the differential operator of the Schrödinger equation acting on a wave function \(\psi .\) Schrödinger remarked:
Intensities (Transition Probabilities)
Crazy theorem: The eigenvalue itself is equal to the integral over a certain quadratic differential form constructed from one eigenfunction. The transition probability then appears to be the integral over the corresponding bilinear form, constructed from two eigenfunctions.Footnote 55
Schrödinger’s first attempt was thus to combine the two wave functions in the expression for the intensities by copying an analogous expression for the energy eigenvalues, only now using two different eigenfunctions \(\psi _n\) and \(\psi _m.\) When this approach did not work, Schrödinger next considered the expression mentioned in his letter to Sommerfeld, which involved the product of one wave function with the derivative of the other.Footnote 56 However, in the actual notebook (presumably in late February or early March 1926, soon after the letter to Sommerfeld), Schrödinger eventually turned to an integral of the form:
which involved not just the two eigenfunctions but also a factor of the coordinate z. He thus adopted an expression that was not just inspired by, but was actually equal to, the one for the perturbation parameters in the Stark effect, where he had first encountered the tantalizing selection rules.
It is important to note how Schrödinger conceived of this expression at this point and how different his conception was from that of modern quantum mechanics: Schrödinger did not identify this expression as the dipole transition amplitude, as modern quantum mechanics would do. Such an interpretation was absent from Schrödinger’s work at this stage and only clearly appeared with the equivalence proof and the third communication. At this point, Schrödinger interpreted the expression as directly providing the intensities (or probabilities).Footnote 57
Schrödinger labeled the calculations that followed as “dogmatic.” This somewhat unusual terminology is elucidated by Schrödinger’s publications, where “dogmatic” is used in the sense of “formal” or “mathematical” and in opposition to “physical.” Schrödinger thus considered the expressions for the intensities as stemming mainly from formal insights rather than from his more physical picture of radiation as a beat phenomenon.Footnote 58
The calculations that followed show that Schrödinger was still unsure about the expression of Eq. 12; after all, there was no physical motivation, no radiation mechanism underwriting this specific weighted integral. The purely formal expressions were supported solely by the ease with which they accounted for the selection rules in hydrogen. Confidence in the intensity expression thus stood on shaky ground, exacerbated by the fact that evaluating the non-vanishing integrals turned out to be a tedious exercise of crunching numbers and combining spherical harmonics and Laguerre polynomials. Without additional means to check the adequacy of the numerical expressions he obtained, Schrödinger became rather frustrated with calculating the intensities for specific transitions. He commented on his work in a private, yet unveiled, display of quotidian antisemitism: “But now we want to develop a general method of evaluating such products, otherwise one will become an old Jew.”Footnote 59
This brings us to the second line of inquiry, which Schrödinger pursued in parallel to his work on the intensities in the Stark effect. Here, as we mentioned in the beginning of this section, Schrödinger approached the radiation problem from a more programmatic and more physical perspective. This line of inquiry remained largely separate from his work on the Stark effect and was developed in a different notebook. In hindsight, this separation is striking, since Schrödinger even discussed the two approaches in the same letters, but without linking them. In the aforementioned letter to Sommerfeld of 20 February 1926, in particular, he first introduced his formal ideas for the intensity calculation and then segued to his programmatic ideas on electrodynamics. Disconnected from each other, the intensity formulas remained purely “dogmatic” expressions for specific spectral lines, without an underlying physical radiation process. The program of developing a new radiation theory was a general one, not yet geared towards explaining or quantifying specific physical processes.
Taking a bird’s-eye view of theoretical frameworks, Schrödinger envisioned a program of fusing his wave mechanics with Maxwellian electrodynamics:
The \(\psi \)-oscillations are of course not electromagnetic oscillations in the old sense. There has to be some kind of coupling between the two [matter waves and electromagnetic waves], which corresponds to the coupling of the field vectors and the current density four-vector in the Maxwell–Lorentz equations. Here the \(\psi \)-oscillations correspond to the current density four-vector, i.e., the current density needs to be replaced by something that is derived from the function, for example the four-dimensional gradient of \(\psi .\) But this is all mere fantasy, I have not really contemplated it yet at all.Footnote 60
Even though he was still in the earliest stages of conceiving a fusion of wave mechanics and electrodynamics, Schrödinger already had very specific ideas. He proposed that Maxwell’s equations be coupled to the Schrödinger equation by replacing the current-density four-vector in Maxwell’s equations with an expression involving the wave function \(\psi .\) This did not mean, as he wrote in a letter to Planck 6 days later, that “those \(\psi \)-vibrations are mass vibrations in the sense of ordinary mechanics.” At the time, Schrödinger did not envision the wave function merely as a continuous charge-current distribution. Rather, he sought to establish an entirely new foundation for “all of mechanics and electrodynamics” on the basis of his new wave function.Footnote 61
Schrödinger’s attempt at implementing this program can be found in the notebook “Coupling, Very Old.” In the first half of this notebook, he explored the expression for the current-density four-vector that he had floated in the letter to Sommerfeld, namely that it was equal to the gradient of the wave function, \(\partial _{\mu } \psi .\) He plugged this expression into the usual continuity equation for electric charge and obtained a differential equation for \(\psi ,\) which turned out to be simply the classical three-dimensional wave equation. This is not the Schrödinger equation, but it is quite close. Schrödinger hoped that he could slightly modify the expression for the current and then obtain the Schrödinger equation instead. “In this manner, the wave equation becomes a consequence of Maxwell’s equations. As continuity equation” (p. 3).
This approach did not yield the desired result. Schrödinger thus revisited his key heuristic in developing wave mechanics, pursuing a “new attempt to set up Hamilton’s principle,” which would provide the dynamics of both the wave function and the electromagnetic field. But this time, even Hamilton’s principle failed to provide any new insights (p. 16). Then, two pages later, Schrödinger abruptly starts exploring a charge-density quadratic in the wave function, without further reference to Hamilton’s principle or to his earlier attempts at constructing a linear current-density four-vector.Footnote 62 As we will argue in the following section, there is a substantial time gap between these two entries. After the failure of Hamilton’s principle, Schrödinger set aside his attempts at unifying wave mechanics and electrodynamics for a while. He only returned to the problem (and the notebook) after the equivalence proof had provided him with essential new elements.
We use this opportunity to take stock: by late February 1926, Schrödinger had found a scheme for “dogmatically” determining intensities, without an underlying physical radiation mechanism; in parallel, he had started thinking about a larger program for integrating wave mechanics into classical electrodynamics, albeit without achieving any breakthroughs. The two approaches remained separate from each other; there was no physical picture to connect them.
In both cases, Schrödinger’s approach relied on the interplay between radiation theory and mechanical theorizing. In the case of the Stark effect, this interplay was serendipitous: the application of the wave-mechanical framework to a specific problem led to insights into the formal representation of intensities. In the case of Schrödinger’s program for a new electrodynamics, he explicitly sought to employ this interplay: first, he tried to derive the (mechanical) wave equation from the (electrodynamic) continuity equation, then he explored a reformulation of Hamilton’s principle that would directly unify wave mechanics and electrodynamics. But, as spring approached, Schrödinger had gotten nowhere with his more programmatic attempts; and his formal recipe for calculating intensities, though promising, still lacked a firm foundation.
5 Radiation theory and the equivalence proof
Matrix and wave mechanics had approached the problem of radiation from different starting points: due to Heisenberg’s pathway to Umdeutung and its (partial) adherence to the state-transition model, matrix mechanics inherently included elements of radiation theory and could account for important spectral regularities. Born and Jordan sought to extend the scope of matrix mechanics by developing a quantum electrodynamics in analogy to quantum mechanics and by conceptualizing the electromagnetic field as a quantum system. Schrödinger’s wave mechanics, by contrast, was initially at a complete loss when it came to radiation and had to undergo a phase of exploratory research before it could account for selection rules and come up with a recipe for calculating intensities. At the same time, Schrödinger sought to integrate wave mechanics and electrodynamics into a new unified description of matter and radiation, where Maxwell’s equations could remain largely unchanged.
Despite these differences, the overall conceptual situation and research agendas were quite similar for both theories. For Born and Jordan, as well as for Schrödinger, the radiation problem appeared in two distinct forms: as the immediate problem of calculating spectral intensities—the original project of the correspondence principle—and as the more general problem of combining atoms and radiation in a unified dynamical framework—the problem of coupling, as first posed by BKS.
As concerns the first problem, both matrix and wave mechanics had made some headway in reproducing spectroscopic regularities. But they had also, each in their own ways, departed from the state-transition model, which had been used to structure spectroscopic data in the old quantum theory. Consequently, several concepts and calculational tools were no longer available, hampering the treatment of radiation. Matrix mechanics was unable to fully describe radiation without the notion of a state; wave mechanics did not possess the notion of transition and could only come up with a “dogmatic” (and still unpublished) calculational scheme. As for the more general problem of coupling, the situation was no better: neither had Born and Jordan managed to incorporate the electromagnetic field into quantum mechanics, nor had Schrödinger managed to incorporate wave mechanics into Maxwellian field theory. Overall then, Schrödinger as well as Born and Jordan had to regard their approaches to radiation as highly tentative.
In March 1926, this situation changed considerably with the emergence of the equivalence proof. The proof gave rise not only to the idea that matrix and wave mechanics were two formulations of a single quantum mechanics. It also established a new, general recipe for calculating transition probabilities and a new physical picture for the emission of radiation, which changed the relation between quantum mechanics and radiation for good.
In the historiography of quantum mechanics, there is so far no detailed account of how Schrödinger came up with the equivalence proof. Consequently, the close connection between the equivalence proof and radiation has gone unnoticed. The search for the proof is generally seen as self-evidently motivated by the puzzling contrast between the concordant empirical predictions, the different formulations and the diverging physical assumptions of matrix and wave mechanics. The bridge connecting the two theories is taken to be first and foremost a mathematical one: equivalence rests on the relation between matrix algebra and differential operators, as developed in the famous mathematics textbook of Courant and Hilbert. All physicists needed to do was to identify and exploit this pre-existing connection. Then they were well on their way to transformation theory and the Hilbert space formalism of von Neumann. The equivalence proof is thus interpreted as the starting point for the clarification of the mathematical structure underlying quantum mechanics.Footnote 63
While this picture is clear and straightforward at first glance, it is rather unsatisfactory upon closer inspection, particularly when looking at Schrödinger’s pathway to the equivalence proof. In a letter to Wien of 22 February, Schrödinger did state that he firmly believed in a deep connection between matrix and wave mechanics and that he had discussed the matter extensively with Hermann Weyl. However, when even a mathematician of Weyl’s caliber was unable to find the connection, Schrödinger gave up searching for it by means of abstract mathematics. This is illustrated by an entry from one of his early notebooks: a single-page attempt entitled “Connection to Born and Heysenberg [sic],” which breaks off with the words “I cannot do anything with this.” Evidently, the abstract mathematical approach to equivalence did not provide a suitable starting point for Schrödinger.Footnote 64
Moreover, as Jürgen Renn pointed out, the mathematical road to equivalence essentially invokes a Platonist conception of nature, in which the mathematical structures underlying physical reality are taken to be pre-existing, independent of scientific inquiry. If one accepts this (strong) statement, he argued,
[it] would remain astounding that this supposedly pre-existing mathematical structure had no essential heuristic function for either of the two theories and was not discovered at all until so long after they were formulated. (Renn 2009, 16)
While Renn found the standard history to be implausible at this point, he found the alternative to be equally problematic. If the equivalence of matrix and wave mechanics was to be explained genetically, Renn argued, it should be considered a genuine puzzle for the history of science: How could the two theories turn out to be equivalent given their entirely different starting points and pathways?
Building on Renn’s work, we argued elsewhere that the resolution to this puzzle lies in the interplay between mechanics and radiation theory, which led both Heisenberg and Schrödinger to develop their new kinematics (the x matrix and the wave function, respectively). Continuing this line of argument, we will argue in the following that the actual equivalence proof—and with it the realization that these kinematics were interrelated—did not originate from the confident exploitation of well-established mathematical knowledge. Rather, the proof was a result of the continued interplay between radiation and mechanics.
The simultaneous emergence of the equivalence proof and of Schrödinger’s new radiation mechanism will thus not appear as a curious side note. Rather, we want to argue that the two were genetically connected: Schrödinger developed the equivalence proof as a result of his exploratory theorizing on radiation in wave mechanics, and the proof in turn stabilized his theory of radiation.
5.1 “Deciphering the mysterious matrix elements”: radiation and the road to equivalence
In February 1926, we saw Schrödinger hesitant and unsure about the radiation process. By 9 March, his statements on the status of wave mechanics and its connection to the radiation process became much more confident. His thoughts on the radiation process consolidated into a new intuitive picture, which became known as the charge density interpretation of the wave function. Schrödinger would defend this interpretation, against the statistical interpretation, for more than a year.Footnote 65
The essential step in this consolidation was, as we will now show, the establishment of the explicit connection between his theory and matrix mechanics. For Schrödinger, the equivalence proof and new radiation mechanism were intimately linked. As Schrödinger wrote to Planck on 11 March, 2 days after completing his proof:
I have been pondering the relation to Born–Heisenberg–Jordan for a long time. I obtained it the day before yesterday. On a mathematical formal level they are almost identical. The eigenvalues are the same [...] I can calculate every matrix element I am interested in [...] from the eigenfunctions of the boundary value problem. That is very pleasant.
In my opinion, however, some of these matrix elements can be interpreted more intuitively [anschaulicher] than as “transition probabilities.” For example: in my theory, the elements of the matrix of a Cartesian coordinate of the hydrogen electron appear as the actual amplitudes of an actually existing electrical moment of the atom. This electrical moment actually undergoes periodic, sinusoidal changes in time, with the emission frequency.Footnote 66
Linking the equivalence proof directly to his intuitive interpretation of quantum mechanics, Schrödinger was confident that his translation between matrices and wave functions was not merely mathematical, but that it led to a new physical picture of the radiation process. We will spell out this connection in the following, reconstructing Schrödinger’s thought process through his correspondence and his notebooks.
The first clue is in a letter from Schrödinger to Gregor Wentzel in May 1926. Here, Schrödinger remarked:
I noticed the schematic occurrence of selection rules from integrals over spherical harmonics a pretty long time ago, even before I knew the precise connection to Heisenberg. It was my first hint [Fingerzeig] for deciphering the mysterious matrix elements.Footnote 67
This is the first instance we are aware of in which Schrödinger described the thought process that we have analyzed above. As he clearly stated, his serendipitous discovery of the selection rules had not only preceded the equivalence proof but actually provided the “first hint” for “deciphering the mysterious matrix elements.”
By further analyzing Schrödinger’s notebooks, we can substantiate Schrödinger’s comment in the letter to Wentzel and spell out in more detail how this first hint ultimately led to the equivalence proof. Our starting point is our earlier reconstruction of the Schrödinger’s work on the Stark effect. As we have seen, the serendipitous appearance of selection rules had led Schrödinger to his formal expression for the intensity. Matrix mechanics, of course, identified the intensities with the elements of Heisenberg’s X matrix. This was the connection that Schrödinger exploited to establish the connection between Heisenberg’s theory and his own. In his notebook later entitled “Intensities, Parallels to Heisenberg and Lanczos,” he segued from his intensity calculations in the Stark effect into a study of the relation to matrix mechanics based on the intensity expression. Here, Schrödinger began directly by identifying Heisenberg’s X matrix with his expression for the intensities (Eq. 12):Footnote 68
He then went on to construct the momentum matrix in a similar manner as
where the derivative \(\frac{\partial \psi }{\partial x}\) was associated with the momentum,Footnote 69 in analogy to the coordinate q in the Eq. 13 (p. 15). Here \(\psi \) is the wave function describing the state of the atom, which Schrödinger at this point still took to involve several eigenfunctions in superposition. It appears here in addition to the two eigenfunctions \(\varphi _{i,k}.\)
This notebook entry is illuminating because this is not how Schrödinger eventually managed to prove the equivalence of wave and matrix mechanics. We can thus confidently date the respective notebook entry before the final proof. Equally important, it allows for a plausible reconstruction of Schrödinger’s initial thought process: he first established the connection between matrix elements and wave functions on a phenomenological level, the level of intensities. This immediately gave him the recipe for constructing the position matrix.
Schrödinger proceeded to construct the P matrix in full analogy. Here the phenomenological basis was missing, as matrix mechanics had not yet connected the P matrix to an observable quantity.Footnote 70 It is thus not surprising that Schrödinger’s first attempt was a failure and that the specific form of the P matrix remained in flux. Only its general structure as an integral over two eigenfunctions \(\varphi _{i,k}\) was fixed; what would take the role of the x appearing in the integral expression for the X matrix was still open. It took Schrödinger a few more days of intense workFootnote 71 to arrive at a different expression for the momentum matrix. The expression \(\partial \psi /\partial x\) was replaced by the differential operator \(\frac{h}{2 \pi i} \frac{\partial }{\partial x}\) acting on one of the eigenfunctions (p. 21).
This approach turned out to be successful. From this point onward, Schrödinger was able to follow a more formal path. With the x and p matrices in hand, the entire kinematics of matrix mechanics could be recast in terms of wave functions. In particular, Schrödinger could reconstruct the commutation relations, the multiplication rule, and the rules for partial differentiation. This was the first step in the equivalence proof, which Schrödinger characterized in his published paper as follows:
I will now first [...] show how to assign to each function of the position and momentum variable a matrix, such that these matrices at least obey the formal calculation rules [...] of Born and Heisenberg. This assignment of matrices to functions is general, it does not take into account the specific mechanical system, but is the same for all mechanical systems. (Schrödinger 1926e, 735)
Schrödinger had thus established a connection between the new kinematics of matrix and wave mechanics: the kinematic relations of matrix mechanics (in particular, the commutation relations) could be satisfied by matrices constructed from an arbitrary system of orthogonal wave functions \(\varphi _i.\)
The second step in the equivalence proof was to connect wave mechanics to the dynamical equations of matrix mechanics.Footnote 72 Schrödinger could then show that matrices constructed from a specific system of orthogonal functions, namely the eigenfunctions of his wave equation, also solved the equations of motion in matrix mechanics. This then completed the “equivalence proof” between wave and matrix mechanics.Footnote 73
The fully developed equivalence proof set out to show that there was, as Schrödinger put it in his letter to Planck, “mathematically almost entire equivalence.” Our reconstruction shows, however, that the equivalence proof did not emerge from a purely mathematical assessment, disconnected from questions of physical content and interpretation. Schrödinger did not start by exploiting the relation between matrix algebra and the theory of differential operators. Instead, he first established an isolated connection between wave mechanics and matrix mechanics on a phenomenological level, i.e., by equating the respective representations for the intensities of both theories. This particular connection through the intensities was motivated by and developed in Schrödinger’s work on the radiation process and relied on the existence of an expression for the intensity in both matrix and wave mechanics. It was only when this connection was formed that mathematical theorizing took over.
The interplay between radiation theory and mathematical theorizing thus continued to play a key role and went both ways. In the case of the Stark effect, a formal recipe for the radiation intensities had emerged from the application of the wave-mechanical framework. The expressions for the intensities, in turn, provided the key ingredient for the mathematical elaboration of that very framework and for its integration with matrix mechanics.
5.2 The equivalence proof and Schrödinger’s charge density interpretation
The emergence of the equivalence proof was not the last step in the complex, bi-directional interplay between radiation theory and the wave-mechanical formalism. As we have already seen in the letter to Planck, the equivalence proof led to a reconceptualization of the radiation process, which finally connected Schrödinger’s two disparate approaches to radiation.
This connection manifests itself in Schrödinger’s notebook “Coupling, Very Old.” As we have already discussed, Schrödinger had here developed his initial ideas of deriving the wave equation from the electromagnetic continuity equation and of constructing a variational formulation of a coupled theory of matter and electromagnetic waves. Then, in the middle of the notebook, he dropped this approach and instead focused on the emission of radiation.
As we will see, this was a fresh start, which resulted from the equivalence proof and the new direction it provoked in Schrödinger’s thinking about radiation in wave mechanics. In the notebook, Schrödinger began by posing the following question: “Can one consider \(\psi \frac{\partial \psi }{\partial t}\) as a density?” Answering this question, Schrödinger investigated whether the spatial integral of \(\psi \frac{\partial \psi }{\partial t},\) i.e., the charge, was a conserved quantity. This, he soon showed, was indeed the case for the slightly generalized expression \(\psi \frac{\partial \overline{\psi }}{\partial t} +\overline{\psi } \frac{\partial \psi }{\partial t},\) where the bar denotes complex conjugation.Footnote 74
While his new expression for the charge density satisfied this minimal requirement, it was fundamentally incompatible with his original program of equating the wave equation with the continuity equation. Since the new charge density was a non-linear expression in \(\psi ,\) the continuity equation was non-linear as well. It could thus no longer be connected to the linear wave equation.
This was a sizeable shift in Schrödinger’s attempted integration of wave mechanics and electrodynamics. He was no longer trying to derive the wave equation; instead, the wave equation was taken as given, and the wave functions provided the starting point for the construction of a charge density. The wave functions thus became classical sources of the electromagnetic field, their novelty as a description of atomic systems notwithstanding.
The following notebook pages show why this shift had become attractive in the wake of the equivalence proof: Schrödinger next constructed a dipole moment from his new expression for the charge density, thereby establishing a direct connection with the consolidated expression for the intensities and the X matrix:Footnote 75
Writing \(\psi \) as a superposition of eigenfunctions, he found that this dipole moment was equal to a sum of partial dipole moments, each of which oscillated with one of the spectral frequencies of the system. These partial dipole moment thus oscillated with the correct frequencies observed in the electromagnetic radiation. It could thus be thought of as producing radiation according to classical electrodynamics. The amplitude of this dipole moment was now given by the position matrix element \(x^{k l}\) and, as Schrödinger would argue, one could thus explain “their decisive influence on the intensity and polarization ... of the emitted radiation.”(Schrödinger 1926e, 756).
For Schrödinger, this new physical picture of the atom and its radiation process marked the key advance of the equivalence proof, above and beyond the improved calculational capabilities. He stressed the importance of this picture in both his equivalence paper and in his letters to Lorentz, Planck and Born,Footnote 76 arguing that it provided an interpretation applicable to both wave and matrix mechanics:
[...] one can actually calculate all of the Heisenberg matrix elements – in which one might be interested on the assumption [Vermutung] that they determine “transition probabilities” or “line intensities” [...]. Incidentally, these matrix elements or quantities closely related to them receive a completely intuitive [anschauliche] interpretation in wave mechanics, namely as amplitudes of the partial oscillations of the electric moment of the atom. The intensity and the polarization of the emitted light can thus be understood on the basis of the Maxwell-Lorentz theory. (Schrödinger 1926e, 736)
For Schrödinger, the new picture of an oscillating charge-density was an important step in moving away from the unintuitive state-transition model. The elements of the X matrix and his expression for the intensity did not have to be interpreted as describing the transition between two states. Rather, they were to be identified as amplitudes of an oscillating electric dipole, created by two simultaneously excited eigenfunctions.Footnote 77
In summary, we can understand both Schrödinger’s equivalence proof and his charge density interpretation as the result of his attempt to introduce a radiation process into wave mechanics. Our analysis shows that Schrödinger initially had no clear idea of how to deal with the complete absence of a radiation mechanism in wave mechanics. In his further work on wave mechanics, he pursued two main approaches: a programmatic one of combining wave mechanics with classical electrodynamics, and a pragmatic one of exploring the mechanical aspects of his theory. It was the latter approach that first gave him a “dogmatic,” i.e., phenomenological, description of intensities. This phenomenological description was initially separated from his attempts to find a more physical description of the radiation mechanics. But it ultimately led Schrödinger to the equivalence proof and subsequently to his charge density interpretation of the wave function. With the equivalence proof and the Stark effect intensities, radiation had been effectively incorporated into wave mechanics, and the theory could now be regarded as an empirically testable account of atomic structure. The gap between the mechanical description of quantum systems and the empirical basis of atomic spectra had been closed.
5.3 The return of the Ersatzstrahler
Schrödinger’s pathway to the equivalence proof and his physical interpretation of it do not appear in standard histories of quantum mechanics, and it is tempting to cast them aside as short-lived or idiosyncratic, along with Schrödinger’s interpretation of quantum mechanics.Footnote 78 However, Schrödinger’s conception of matrix elements and intensities was neither superfluous nor short-lived. Rather, it remained an indispensable aid for the quantum-mechanical description of radiative transition processes, making it possible to teach and apply quantum mechanics without having to deal with the vagaries of quantum field theory. At the same time, Schrödinger’s charge density interpretation was explicitly rejected: one calculated the dipole radiation according to Schrödinger’s recipe, but interpreted it as a transition probability within the state-transition model.
This incorporation and reinterpretation of Schrödinger’s radiation theory emerged almost immediately after the publication of Schrödinger’s equivalence proof and the paper on the Stark effect. In private correspondence with Pauli, Heisenberg trashed Schrödinger’s physical interpretation but accepted the greater applicability of wave mechanics. He argued that the main advantage of Schrödinger’s work was the possibility to “actually calculate matrix elements.”Footnote 79 Schrödinger’s approach precisely filled the gap that we observed in the structure of matrix mechanics: one no longer had to find the entire matrix that solved the equations of motion in one go; rather, one could now construct individual matrix elements from the wave functions of the respective states.
But Schrödinger’s construction of matrices from wave functions provided more than a much-needed calculational tool. His interpretation of it in terms of radiation was just as influential. This can be seen if we take into account that in the spring of 1926, a second version of the equivalence proof by Pauli was already circulating in letters. Unlike Schrödinger’s version, it had made no immediate claims about the radiation process and formulated equivalence in a purely formal manner. While such a purely formal reading of equivalence was thus available, Schrödinger’s radiation-theoretical reading of equivalence was widely adopted. Even Pauli anticipated that the matrices, written as integrals over two wave functions, would ultimately be connected to “difference tones (beats) of the de Broglie radiation.”Footnote 80 In Copenhagen, the equivalence proof was interpreted as relevant to radiation theory,Footnote 81 and Bohr would count Schrödinger’s radiation theory as one of the major achievements in wave mechanics in his seminal paper “The Quantum Postulate and the Recent Development of Atomic Theory”:
In addition, Schrödinger could associate with the solutions of the wave equation a continuous distribution of charge and current [...] the superposition of two characteristic solutions corresponds to a continuous vibrating distribution of electric charge, which on classical electrodynamics would give rise to an emission of radiation, illustrating instructively the consequences of the quantum postulate and the correspondence requirement regarding the transition process between two stationary states formulated in matrix mechanics. (Bohr 1928, 586)
Such acknowledgements notwithstanding, Bohr, and other quantum physicists with him, was not willing to follow Schrödinger in his departure from the original state-transition model. Instead, they integrated Schrödinger’s interpretation of the matrix elements into the state-transition model and the tradition of the correspondence principle. They did this by bringing back the idea of the Ersatzstrahler, which had been the central tool for dealing with radiative transitions in the old quantum theory.
This tool, as we saw in Sect. 2, had made it possible to conceive of quantum systems in terms of the state-transition model while describing the radiation process in more detail using classical radiation theory. All one had to do was to assume that the radiation emitted in a discrete transition could be formally compared with the classical radiation of the hypothetical Ersatzstrahler.Footnote 82
The same logic was now invoked in quantum mechanics. This can already be gleaned from Bohr’s somewhat vague remarks cited above. Here, Bohr acknowledged that Schrödinger’s charge distribution “on classical electrodynamics would give rise to an emission of radiation” but continued that this would only serve as an illustration for the “transition process between two stationary states.”
In practice, this meant that physicists kept the state-transition model and considered quantum systems to be in one state, characterized by the wave function \(\psi _n.\) The transition of such a system to another state \(\psi _m\) would be described by Schrödinger’s charge density interpretation; the intensity of the transition was calculated from the classical radiation emitted by said charge density. Schrödinger’s oscillating charge density effectively replaced the Ersatzstrahler.
This picture, which we would nowadays call “semi-classical,” is particularly evident in a paper by John C. Slater, published in November 1926. Here, Slater, as one of the creators of BKS theory, stated:
Radiation and absorption of light by atoms can be treated by replacing the atoms by a set of oscillators, whose natural frequencies are the frequencies of quantum transitions, as has been shown by the writer in a previous paper. By means of Schrödinger’s wave mechanics, it is possible to place the theory on a more satisfactory foundation than was possible before, at the same time changing the physical ideas to some extent. [...] we have \(\psi \overline{\psi }= \sum _{nm}c_n\overline{c_m}- e^{2\pi i(E_n-E_m)t/h}u_nu_m.\) The term with indices n, m represent an amount of charge oscillating with the frequency \((E_n-E_m)/h,\) and are to be identified with the oscillator connected with this transition frequency of the atom. (Slater 1927, 7–8)
Keeping well within the tradition of the correspondence principle discussed above, Slater argued that radiation was to be “treated by replacing the atom by a set of oscillators.” These (virtual) oscillators were “connected” to the transition processes and served as a classical substitute for the actual physical processes described by the state-transition model. As Slater saw it, Schrödinger’s construction of the matrix elements was a crucial step forward in developing this picture. It offered an explicit mathematical expression for the substitute oscillations in quantum mechanics.
Interpretations such as Slater’s clearly did not endorse Schrödinger’s idea of simultaneously excited eigenfunctions and a continuous radiation process. But they also departed from the approach of matrix mechanics, which we discussed in Sects. 2 and 3. With the return of the Ersatzstrahler, transition probabilities were again determined from an underlying physical model, which connected the kinematic description of the states, i.e., the wave functions, to the transitions by means of classical radiation theory. This was a return to the conceptualization of the state-transition model in the old quantum theory; Heisenberg’s idea of turning the transition probabilities themselves into the fundamental kinematic properties had been abandoned just one year after its inception.
The modernized Ersatzstrahler, on the other hand, made a rather successful comeback. In his fourth communication on wave mechanics (submitted in June 1926), Schrödinger introduced the time-dependent Schrödinger equation and extended his perturbation theory to cover time-dependent external fields, with the express aim of using it to develop a dispersion theory. Schrödinger was able to reproduce the Kramers–Heisenberg formula. And in the time-dependent version of his theory, the partial charge distributions now manifestly oscillated precisely with the required transition frequency.Footnote 83 In addition, Dirac, Klein, and Slater could show that the Ersatzstrahler picture was sufficient to treat all spontaneous and induced transitions, as well as the Compton effect, and to derive Planck’s law using an updated version of Einstein’s 1916 derivation.Footnote 84 These results showed that the modernized Ersatzstrahler of wave mechanics was able to reproduce essentially all the radiation-related elements in the empirical domain of quantum theory.
This picture became an integral part of the presentation of quantum mechanics in early textbooks and played a crucial role whenever quantum mechanics had to deal with transition processes and the emission of radiation. To see this, we consider two early textbook expositions, Wolfgang Pauli’s contribution to Müller-Pouillets Lehrbuch der Physik of 1929 and Max Born’s Matter and Radiation of 1932.Footnote 85
Predating even Dirac’s authoritative “Principles of Quantum Mechanics,” Pauli’s article is one of the first presentations of quantum mechanics in textbook format—and, from a modern perspective, a rather unorthodox one. It was meant as an update to Pauli’s 1926 Handbuch der Physik article “Quantentheorie,” which was famously outdated upon publication. The treatment of the old quantum theory was left essentially unchanged, but Pauli now provided an “addendum” on the new quantum mechanics. Here, he started off with de Broglie’s matter waves and Schrödinger’s wave mechanics and only then moved on to matrix mechanics and the more abstract formulation of transformation theory, all the while paying close attention to the empirical results of spectroscopy.
Pauli first showed how to obtain the energy levels as the most elementary description of the atomic states. The full potential of quantum mechanics, he continued, was however only reached when turning to the eigenfunctions, rather than just the eigenvalues. The key to unlocking this potential was Schrödinger’s calculational scheme for the transition probabilities (Pauli 1929, 1827). Pauli then went on to construct the matrices and transition amplitudes from the wave functions, singling them out as quantities that oscillated with Bohr’s transition frequencies. It is his interpretation of the resulting expression that deserves a closer look. For Pauli in 1929, the actual radiation mechanism of quantum mechanics was still unknown (despite or maybe because of his and Heisenberg’s current struggles to formulate a quantum electrodynamics). All he was sure of was that Schrödinger’s charge density interpretation was untenable and that the radiation mechanism would definitely not be describable “on the basis of classical electrodynamics.”Footnote 86
While Pauli thus rejected Schrödinger’s interpretation, he still considered the scheme for calculating transition probabilities an indispensable element of quantum mechanics and placed it within the framework of the correspondence principle and the Ersatzstrahler:
According to Bohr’s correspondence principle, it is thus to be expected that, in general, the partial oscillations [...] determine the transition probabilities. In contrast to the earlier quantum theory, this determination is now quantitative and takes place according to the equation:
$$\begin{aligned} h\nu ^n_m A^n_m=\frac{4e^2}{3c^3}(2\pi \nu ^n_m)^4 {|r^n_m|}^2 \end{aligned}$$[This equation] expresses that the intensity of light of the frequency \({\nu ^n_m}\) per atom in the state n is equal to the radiation intensity, which an oscillation of the amplitude \({x^n_m}, {y^n_m}, {z^n_m}\) would emit per unit time according to classical electrodynamics.Footnote 87
Following Slater, Pauli simply replaced the Ersatzstrahler with Schrödinger’s oscillating charge densities, thereby providing a genuinely “quantitative” formulation of the correspondence relation. For Pauli, the correspondence approach was at its core still the same as in the old quantum theory: the transition probabilities are quantitatively determined from the hypothetical classical radiation process of an Ersatzstrahler, as if the partial oscillations of the atom’s electric moment in the state n actually caused the emission of radiation.
Our second example comes from Max Born, who gave a series of lectures on modern physics entitled “Matter and Radiation” at the Technische Hochschule Berlin in 1932, just one year before he had to flee Germany. Born’s lectures were intended as a broad overview on modern physics for electrical engineers, aiming to keep technical and industrial applications in touch with basic research. Covering kinetic gas theory, canal rays, wave-particle duality, atomic spectra, etc., Born also presented a sketch of matrix and wave mechanics, using the core elements that would later come to be associated with the Copenhagen interpretation: Heisenberg’s original observability principle, wave-particle duality, the uncertainty relations and, of course, Born’s own statistical interpretation of the wave function.
When Born came to discuss the radiation process in quantum mechanics, this familiar assemblage hardly played a role. Instead, Born returned to wave mechanics as formulated in 1926 and used Schrödinger’s picture of the radiation process. He introduced Schrödinger’s expression for the charge density and showed that one could use it (a) to understand why stationary states did not radiate and (b) to define a “transition density” which determined the radiation emitted in a combination of two different states. Finally, he summarized the situation thus:
One thus obtains emission of radiation in wave mechanics by calculating—purely according to the correspondence principle [rein korrespondenzmäßig]—the radiation of an oscillating dipole according to classical electrodynamics. In this manner, one automatically obtains only those lines in the spectrum whose frequency matches an oscillation frequency between two states in the atom. (Born 1933, 105)
Taken alone, this quote might suggest that it was perfectly acceptable—at least for electrical engineers—to treat the wave functions as a radiating source within the framework of classical electrodynamics. Born was thus quick to dispel Schrödinger’s interpretation by adding:
One may not conclude from this that both states n and m are excited simultaneously during emission; rather there is a virtual presence of both. For the spontaneous emission of a spectral line, the upper state has to be excited in some way; the emission is a process (oscillation of a corresponding virtual resonator) that accompanies the jump to the lower quantum state. (Born 1933, 105)
In order to make Schrödinger’s interpretation palatable, Born thus also returned to the notion of virtuality developed in BKS. He argued that the two wave functions in the dipole moment only had a “virtual presence.” In the actual (quantum) world, spontaneous emission would still take place according to the original state-transition model with an atom in the upper state and a discontinuous transition to the lower state.
The examples of Pauli and Born are important here because they highlight the continued relevance of Schrödinger’s scheme for quantum mechanics, in applications and in connecting the theory to its empirical basis. Pauli and Born certainly took a position in the interpretation debate closer to Heisenberg, Bohr or Dirac. But they saw Schrödinger’s scheme for calculating transition probabilities as an essential part of quantum mechanics, which could not be motivated or easily understood in a first-principles approach. Rather, the scheme could be much better understood within the context of the correspondence principle and the picture of the Ersatzstrahler, which provided students with some (admittedly pragmatic or even shaky) physical intuition.
5.4 The problem of coupling and early debate on quantum electrodynamics
The Ersatzstrahler provided a pragmatic solution to the radiation problem within quantum mechanics. Schrödinger, Born and Dirac all conceived it as an effective description. Already in 1926, the ultimate goal was to develop a consistent quantum theory of matter and radiation, which tackled the elusive “problem of coupling.”
As we have seen in Sect. 3, Born, Jordan and Heisenberg, as well as Bohr and Pauli, had regarded this problem as a central lacuna for matrix mechanics before the advent of Schrödinger’s wave mechanics. With the charge density interpretation and the equivalence proof in hand, Schrödinger also returned to the coupling problem and identified it as the “cardinal question” for the future development of quantum theory:
A question of particular importance, maybe even the cardinal question of the entire atomic dynamics, is the question of the coupling between the atomic dynamical behavior and the electromagnetic field or that which has to take its place. It is not only relevant for the complex of dispersion, resonance and secondary radiation and the natural width of spectral lines; the identification [Bezeichnung] of certain dynamical quantities of the atom as emission frequencies, line intensities etc. only receives more than a dogmatic meaning when the coupling is described mathematically in some form. (Schrödinger 1926e, 753)
As the problem of coupling thus appeared to be relevant for extending the empirical domain of a future quantum theory and for a deeper understanding of “dynamical quantities of the atom,” Schrödinger discussed the two options which had emerged during the formative period of quantum mechanics:
The matrix representation of atomic dynamics has led to the conjecture that the electromagnetic field has indeed to be represented differently, namely matrix-like, to formulate the coupling mathematically. Wave mechanics shows that there is no compulsion to do so at any rate[.] The mechanical field scalar (denoted \(\psi \)) has every aptitude to enter even into the unchanged Maxwell–Lorentzian equations amongst the field vectors and as “sources” of them; just as the electrodynamical potentials enter into the coefficients of the wave equation, which determines the mechanical field scalar. (Schrödinger 1926e, 753)
Directly contrasting the programs of wave and matrix mechanics, Schrödinger correctly identified Born and Jordan’s core physical idea as the description of the electromagnetic field as a quantum system. It presented a physical entity in its own right, which manifested itself through its excited states. As we have seen, Born and, in particular, Jordan envisioned this conception of the electromagnetic field as part of a new quantum electrodynamics.Footnote 88
In contrast to this approach, Schrödinger was now confident enough to proclaim publicly that his charge density interpretation showed the road ahead. Ultimately, it would lead to the resolution of the cardinal question of quantum theory through the integration of wave mechanics and classical electrodynamics into a new field theory. In this new theory, matter waves would be used to construct a current density four-vector in the fully relativistic setting and then enter into the inhomogeneous Maxwell equations. The classical electromagnetic fields thus produced would, in turn, enter the wave equation, creating a new but ultimately classical field theory.
While differing substantially on how to achieve it, Schrödinger and Born and Jordan thus agreed that electrodynamics and the new mechanics needed to be integrated into a single, dynamical theory. Their competing research agendas would continue to evolve into to the 1930s. Both ran into considerable conceptual difficulties—sooner in Schrödinger’s case, somewhat later in the case of Dirac, Jordan, Pauli and Heisenberg. This marks the next stage in the relation between quantum mechanics and radiation, raising the question of when and how quantum mechanics cut its ties with radiation, turning radiation into a specific problem to be dealt with in quantum electrodynamics and thus ending the productive interplay between the two bodies of knowledge in the 1920s.
Readers of Blum and Jähnert (2022) may recognize here that we are thus postponing an answer to our initial question. Initially, we asked how quantum mechanics could become an empirically successful theory, capable of extension to new domains and amenable to an axiomatic formulation, while the knowledge that went into it came in large part from a theory of radiation, haunted by unresolved conceptual problems. We asked this question knowing that radiation provided a crucial input for the creation of quantum mechanics, while anticipating the ultimate separation between quantum mechanics and quantum field theory.
Looking at the formative period of quantum mechanics, we can now see that the eventual split between quantum mechanics and quantum electrodynamics was not in place with the creation of quantum mechanics and that this is not just a matter of timing. For all the reasons detailed in this paper, the interplay between radiation and mechanics was a necessary and integral part of the development of quantum mechanics. Separation was not yet an option in the formative period of quantum mechanics.
6 Conclusions
We have argued that the radiation problem played a key role in early quantum mechanics, a role that has not been taken into account in the standard histories of quantum mechanics. It was perceived by the main protagonists of matrix and wave mechanics as a central lacuna of the emerging theories: radiation remained the main contact point with empirical (spectroscopic) phenomena; it lay at the heart of the interpretation of the theory’s formal elements and it continued to be a central conceptual challenge.
We have seen that neither Heisenberg, Born, and Jordan nor Schrödinger entertained the idea of simply neglecting radiation or relegating it to a future quantum theory of radiation. Radiation thus continued to contribute to the theoretical development and conceptual clarification of quantum mechanics. Indeed, our main protagonists saw it as an integral and unresolved issue within quantum mechanics.
The historical actors approached these issues against the backdrop of the well-established, albeit patchy radiation-theoretical tradition of the old quantum theory. In time, they realized that the abandonment of key elements, in particular the picture of a quantum system in a particular state emitting radiation and the Ersatzstrahler method, was a costly move. It became clear that these elements could not be simply cast aside but needed to be replaced or adapted—otherwise, quantum mechanics would remain incomplete.
Like in the old quantum theory, the search for a new radiation mechanism directly informed their thinking about the mechanical foundations of the new theory and vice versa. The most striking instance of this bi-directional interplay is Schrödinger’s exploratory work and the resulting quasi-simultaneous establishment of the equivalence proof and of a new radiation mechanism.
The importance of this interplay is the main result of this paper. Quantum mechanics, we see perhaps better than ever, was forged and crafted here in the nitty-gritty details of working through physical phenomena. Exploratory calculations aimed at the integration of radiation were important stepping stones for the elaboration of quantum mechanics. This exploratory phase of theorizing, which is accessible to us in Schrödinger’s research notebooks and letters,Footnote 89 gradually led to calculational recipes and provided the starting point for something as abstract as the equivalence proof.
This reconstruction, we believe, provides an alternative and indeed a much better understanding of the equivalence proof and its emergence. It should be considered neither as the discovery of mathematical structures in nature, nor even as the discovery of a common structure underlying matrix and wave mechanics. Rather, we see it as Schrödinger actively constructing a bridge to matrix mechanics by singling out precisely those expressions that could serve as Heisenberg’s matrices.
This bridge did not emerge by sifting through the essentially infinite variety of mathematical expressions that could be constructed from the wave function, to most of which we would, even today, not assign any physical interpretation. Rather, Schrödinger was guided by empirical regularities, the selection rules. These rules, our analysis shows, played a crucial role, as they formally encoded empirical knowledge.Footnote 90 They thus allowed Schrödinger to recognize those elements of the formalism that could provide insights into its interpretation and further development, leading to the equivalence proof.
In turn, the equivalence proof and the now-consolidated framework of a unified quantum mechanics provided a more or less stable basis for integrating the expressions for radiation intensities that Schrödinger had started out with. This marked a return to the Ersatzstrahler picture, updated to the new atomic dynamics.
Just as in the old quantum theory, the Ersatzstrahler was seen as a pragmatic solution, which would be referred to as “semi-classical” today. The development of a comprehensive theory of light and matter was still anticipated. But the Ersatzstrahler allowed the historical actors to reconnect quantum mechanics to its experiential base and provided a first, sustainable resolution to the radiation problem for isolated quantum systems.
At this point, the formative period of quantum mechanics came to a close, ushering in a new phase of consolidation, phenomenological extension and interpretational debates. In this new phase, radiation lost some of its immediate relevance for the foundations of quantum mechanics. Radiation began to be perceived as a mere application, its details to be ironed out by applying quantum mechanics rather than revising it.
Another way to look at this formative period and its conclusion is to consider the development of the radiation problem in early quantum mechanics on its own. Here, we see a rather striking continuity with respect to the old quantum theory. For radiation, the development of matrix and wave mechanics did not present a complete rupture. Rather it was a short disruption, which ended when quantum mechanics reconnected to the research tradition of the correspondence principle and introduced a modernized version of the Ersatzstrahler. Meanwhile, the elusive problem of coupling remained unresolved.
Data availability statement
There is no further data associated to this publication.
Notes
For general overviews on the history of quantum mechanics, see Jammer (1966), Darrigol (1992, 2009), Hendry (1984), Mehra and Rechenberg (1982, 1987) as well as Duncan and Janssen (2019). The prehistory and genesis of both matrix and wave mechanics has been treated extensively. For a review of the literature as well as for our own take, see Blum et al. (2017) as well as Blum and Jähnert (2022). For more detailed discussions of early matrix mechanics, see Beller (1983b) and Bonk (1994). Discussions of wave mechanics beyond its genesis are limited primarily to interpretational issues; the formal elaboration has been briefly sketched in Joas and Lehner (2009) and Schrödinger’s theory of the Stark effect has been presented in Duncan and Janssen (2014).
The history of the interpretation debate deals with the fierce debate between Schrödinger and the Göttingen–Copenhagen community in the year 1926, Born’s probabilistic interpretation, Heisenberg’s uncertainty paper and Bohr’s complementarity, culminating at the 1927 Solvay Conference and the divergence between the adherents of the Copenhagen spirit and its dissenters. The literature on the interpretation debate is too numerous and varied to be discussed in detail here. The following rather canonical list should suffice: Bacciagaluppi and Valentini (2009), Beller (1983a, 1983b, 1990, 1992, 1999), Bitbol and Darrigol (1992), Bitbol (1996), Camillieri (2005, 2006, 2007a, 2007b), Cushing (1991), MacKinnon (1980), De Regt (1997a, 1997b, 1999), De Regt and Dieks (2005), Wessels (1979, 1980, 1983), Howard (2004) as well as Freire et al. (2022).
The few works on radiation in early quantum mechanics deal with Jordan’s work on wave-particle duality and quantum statistics, which will be seen to play a rather small role in the developments discussed in this paper.
The extant historiography traces the formal development of quantum mechanics from the development of transformation theory by Jordan and Dirac to the Hilbert-Space formalism of David Hilbert, Lothar Nordheim, and John von Neumann and the axiomatization of quantum mechanics. See Jammer (1966), Lacki (2000, 2004) as well as Duncan and Janssen (2009, 2013).
This may be exemplified by Jammer’s three-page chapter on applications. Here, one can beautifully see radiation being excluded from the main narrative as an application and delegated to the domain of quantum field theory. Similar observations apply to van der Waerden’s influential anthology on quantum mechanics, Van der Waerden (1967), which explicitly excluded quantum electrodynamics.
On applications, see in particular James and Joas (2015). They argued that the “applications” of quantum mechanics to the many-body problem in fact sparked essential conceptual developments and introduced core concepts such as exchange, tunneling and indistinguishability, which shaped the developments in quantum statistics and solid-state physics. In a similar manner, Duncan and Janssen (2007), Seth (2010), Renn (2009), Jähnert (2019) and Blum and Jähnert (2022), analyzed the practice of theory in the old quantum theory and showed, in different ways, that research on specific physical problems was a central driving force for the conceptual development of the 1920s. The conceptual impact of applications to radiation has been studied by Lehner (2011), Duncan and Janssen (2008) and Bacciagaluppi et al. (2017) in an isolated case study, namely Pascual Jordan’s derivation of Einstein’s fluctuation formula.
We use exploratory research here in the sense articulated by Friedrich Steinle (2005, 2016): as a phase where research is characterized by the absence of a secure theoretical foundation and considerable conceptual uncertainty, if not by a conceptual void. In such phases, the search for and the interpretation of empirical regularities (in our case, selection rules) often plays a crucial role as researchers tinker with their apparatus and vary parameters without clearly articulated expectations for the result. Steinle initially coined the term to describe experimental research but emphasized its applicability to theoretical practices. As such, the concept has been applied to mathematical theorizing, modeling and computer simulations, Gelfert (2016).
This was first noted in Linda Wessels’ unpublished dissertation, Wessels (1975). Wessels astutely recognized the importance of radiation for Schrödinger’s interpretation. However, she only followed the published papers. Looking at Schrödinger’s working notebooks and letters changes the picture significantly, as we will show in Sect. 5.
As we discussed in Blum and Jähnert (2022), this led to a split in the old quantum theory between a mechanical description of quantum states and a radiation-theoretical description of transitions. This split allowed the historical actors to explore different strategies of theorizing. On the one hand, there was mechanical model building using analytical mechanics and quantum conditions, a practice usually described as the old quantum theory. On the other hand, there was the attempt to develop a more detailed description of radiative transition processes, a description that went beyond the energy-frequency relation. For more detailed reconstructions of the old quantum theory and its many facets, see the literature in Footnote 1.
Jähnert (2019), and Blum and Jähnert (2022, 2024). The construction of this Ersatzstrahler in the old quantum theory was a two-step process: first, a suitable average of the Fourier coefficients in the initial and final states of the quantum system was constructed; then, this averaged Fourier coefficient was translated into an intensity (and a transition probability) by imagining it as the amplitude of a harmonic oscillator, radiating according to classical theory.
For a more detailed discussion of the notion of virtuality in BKS, see Blum and Jähnert (2024).
The applications of matrix mechanics appeared as part of the foundational papers Born et al. (1926), Born and Jordan (1925) and Heisenberg (1925) and in subsequent papers focusing on particular applications: Heisenberg and Jordan (1926), Pauli (1926), Mensing (1926), Tamm (1926) and Dennison (1926). The applications of wave mechanics up to the equivalence proof are contained in Schrödinger’s first two communications: Schrödinger (1926a, 1926b). At first glance, dispersion would clearly appear to be part of radiation theory. However, in the matrix-mechanical treatment of dispersion theory, just like in the old quantum theory, the radiation field was not a coherent dynamical entity. The incoming radiation was modeled as a time-dependent, external perturbation, without dynamics of its own. It was entirely disconnected from the scattered radiation; the latter only appeared implicitly through the perturbed transition probabilities of the dispersing atomic system. The dynamics of the electromagnetic field were thus not involved at all (Born et al. 1926, 571f).
This situation evokes the notion of a so-called Kuhn (1996, 103–110) loss, i.e., the idea that problems solved in one paradigm could no longer be solved in another, or the associated idea that a new theory loses the possibility to account for previously solved problems, see Midwinter and Janssen (2013, 140–141) for further discussion. There are subtle questions to be addressed here: Does the switch from the old quantum theory to quantum mechanics qualify as paradigm shift with respect to radiation? Was the description of radiation in the old quantum theory a theory in a strong sense? We doubt that the answer to either question can be a clear yes, and the notion of Kuhn losses thus does not seem to be directly applicable. We would like to emphasize that (a) the losses to be considered in this paper are losses of concepts and tools and (b) whatever successes had been achieved in describing the emission of radiation in the old quantum theory, they were seen as provisional by the historical actors. The loss of particular solutions was thus viewed as far less problematic than the conceptual void that had opened up.
Heisenberg to Kronig, 21 May 1925 (Archive for the History of Quantum Physics (AHQP) Mf 16 Sect. 6).
The paradigmatic case of the harmonic oscillator was treated in detail in Born and Jordan (1925). Intensity formulas for precessional motion had already been established just before the creation of quantum mechanics by Ralph Kronig and Helmut Hönl using correspondence arguments; reproducing these equations had been an important touchstone for Heisenberg (1925, 892). Rotating molecules were treated by Mensing (1926), Tamm (1926), and Dennison (1926).
The unfinished nature of matrix mechanics has long been known. It was stressed, both on a conceptual and on a computational level by Beller (1983b, 25ff.), who raised several of the points we address in the following. For the unfinished nature of early matrix mechanics, see also Bonk (1994). Still, it tends to be downplayed, cf. Heilbron and Rovelli (2023), who argue that the theory was nonetheless complete as a theoretical framework regardless of its shortcomings in application.
On the role of such transformations in the further development of quantum mechanics and on their relation to classical canonical transformations, see Duncan and Janssen (2009).
Heisenberg to Pauli 16 November 1925 in Hermann et al. (1979, 255).
See Pauli (1926) and, for a modernized presentation of Pauli’s approach, Valent (2002). The Laplace–Runge–Lenz vector has a rather convoluted history with several rediscoveries, which has been explored for the nineteenth century by Goldstein (1975). A thorough discussion in the history of quantum physics is still missing. The vector had been used in the old quantum theory by Lenz (1924), and this was Pauli’s source. Since the hydrogen atom is easily solved in the old quantum theory (as is the Kepler problem in classical mechanics), the Laplace–Runge–Lenz vector was only relevant in that context when dealing with perturbations (electric and magnetic fields).
Pauli (1926, 346).
Heisenberg to Dirac 9 April 1926, Paul A. M. Dirac Papers, Florida State University Special Collections and Archives, Box 34, Folder 08.
For a discussion of the changing notion of a state in matrix mechanics see Blum et al. (2017), as well as Bacciagaluppi et al. (2017). See also Beller (1983b), where this situation is discussed primarily in relation to later claims by the practitioners of matrix mechanics in the debate with Schrödinger.
While the literature on the genesis of wave mechanics is extensive, see Hanle (1977), Wessels (1979), Wessels (1983), Bitbol and Darrigol (1992), Bitbol (1996), Joas and Lehner (2009) and Renn (2009), the challenges posed to wave mechanics by radiation have not been discussed in detail. This is a surprising omission since Schrödinger’s struggles with radiation are directly related to his interpretations of wave mechanics. The most in-depth reconstruction of this relation is given in Linda Wessels’ unpublished PhD Thesis (Wessels 1975) on Schrödinger’s interpretation of wave mechanics. Wessels rightly focuses her discussion on Schrödinger’s attempts to work out a radiation mechanism and distinguishes between Schrödinger’s beat interpretation and his charge density interpretation. She also identified the equivalence proof as a major turning point of the story. In reconstructing the development, however, Wessels followed the chronology given by Schrödinger’s publications. By also using Schrödinger’s notebooks and linking them to letters, we have come up with a different chronology, which allows us to analyze the interplay between formal elaboration and physical interpretation. Following Wessels, Schrödinger’s interpretation was further discussed by Bitbol (1996, 55–59). Bitbol focused in particular on the inconsistency of Schrödinger’s charge density interpretation and contrasted it with Born’s probabilistic interpretation.
Schrödinger (1926a, 373–374). Schrödinger anticipated that the time-dependent equation would contain second time derivatives, just like the usual wave equation. In that case, the calculated eigenvalues of the time-independent equation were proportional to the squares of the mechanical frequency. This would have implied that electrons bound in the hydrogen atom with negative energies would oscillate with imaginary frequencies. To solve this problem, Schrödinger introduced a large constant C to shift the zero point of the energy scale and thus make all of the energies positive. The energy-frequency relation could then be approximated as
$$\begin{aligned} \nu \propto \sqrt{C+E} \approx \sqrt{C} + \frac{1}{2 \sqrt{C}} E. \end{aligned}$$The large constant term \(\sqrt{C}\) from the energy-frequency relation could then be canceled in the difference tones of the beats. By the time of the second communication, Schrödinger had resolved this difficulty and obtained the direct proportionality of energy eigenvalues and frequencies “without noticeable artificiality” (Schrödinger 1926b, 497).
Indeed, the beat interpretation of radiation appeared in Schrödinger’s very first letter on wave mechanics to Wilhelm Wien (Schrödinger to Wien, 27 December 1925 in Meyenn 2011, 163–164). Here, Schrödinger announced that he was working on a “new atomic theory,” in which “there really is an oscillatory (or rather a beat) process, which has the frequency we observe in the spectroscope.”
Schrödinger to Born 2 November 1926 (von Meyenn 2011, 329).
For the argument that Heisenberg’s assumption needs to be derived, see Born and Jordan (1925, 860).
The central problem for Born and Jordan’s original program of matrix electrodynamics was to find commutation relations for the fields. For the problem of emission, they were able to bracket this issue by formulating the emission process in terms of the “Hertz vector” (Hertz electric vector potential). This quantity is directly proportional to the moment of the emitting dipole, so that the unknown commutation relations of quantum electrodynamics did not come into play. For more background on Born and Jordan’s argument, see the discussion of the Hertz vector given in Essex (1977).
Born and Jordan (1925, 887).
See Bacciagaluppi et al. (2017).
Born and Jordan (1925, 888).
The reason is that the electromagnetic field in vacuum can be decomposed into uncoupled harmonic oscillators, one for each mode. To prove energy conservation for a quantum harmonic oscillator, it is sufficient to use the equations of motion (which are assumed to be the same as in the classical theory); the commutation relations need not be invoked explicitly.
See Born and Jordan (1925, 884), where they identify the proof of energy conservation as the means by which Heisenberg’s assumption can be justified.
Born and Jordan (1925, 884).
Born et al. (1926, 606–615).
Heisenberg to Pauli 16 November 1925 in Hermann et al. (1979, 255–256).
Jordan to Schrödinger, dated “August 1927” in Meyenn (2011, 431).
Bohr to Pauli, 25 November 1925 in Hermann et al. (1979, 268–269).
These two pathways were developed in separate notebooks and were largely independent of each other. The corresponding notebooks, “Intensities, Parallels to Heisenberg and Lanczos” and “Coupling, Very Old,” are contained in AHQP Mf 41 Sect. 2. and AHQP Mf 41 Sect. 4, respectively. The central letter, which mentions both approaches, is Schrödinger to Sommerfeld 20 February 1926 in Meyenn (2011, 179).
Schrödinger to Sommerfeld, 29 January 1926, in Meyenn (2011, 171).
All quotes from Schrödinger to Sommerfeld 20 February 1926 in Meyenn (2011, 179).
This calculation was published in Schrödinger (1926c) and was developed in the notebooks AHQP M/f 40, “Eigenwertproblem des Atoms I. Starkeffekt” (Sect. 4) and “Eigenwertproblem des Atoms II” (Sect. 6), cf. Meyenn (2011, 878). For a more comprehensive presentation of this calculation, see Duncan and Janssen (2014).
While the issue of selection rules is a standard topic within the history of the old quantum theory, essential for the development of the correspondence principle and for elaborating the role of the conservation of angular momentum in quantum theory, it plays virtually no role in the historiography on wave mechanics. A brief reminder may thus be in order: in the state-transition model, selection rules describe the (im)possibility of certain transitions. In the simplest case, they state that the quantum number associated with a simple harmonic motion can only change by \(\pm 1\) or 0 during a transition (there are no such rules for anharmonic motions). These rules were typically interpreted in terms of intensities: a disallowed transition was a transition with vanishing intensity. Selection rules were associated with a rich phenomenology, such as doublet and triplets in the fine structure, the doublet bands in molecular spectra, or the triplets and doublets in the Zeeman effect. Selection rules thus had to be accounted for in some way, even if, like Schrödinger, one rejected the underlying state-transition model. For more on the role of selection rules in the old quantum theory, see Assmus (1992), Borrelli (2009, 2011), Bokulich (2009) as well as Jähnert (2019).
In the unperturbed problem, the non-dependence on \(\theta \) implied full rotational invariance and thus the existence of a set of \(\alpha \) wave functions \(u_{ki}\) (\(i=1,\ldots ,\alpha \)) all belonging to one single degenerate energy eigenvalue \(E_k.\) The perturbation then lifted this degeneracy, introducing \(\alpha \) distinct energy eigenvalues \(E_{kl}^{*},\) where the asterisk signifies a perturbed quantity and not, as is now common, the complex conjugate. The wave functions \(u^{*}_{kl}\) belonging to these split energy eigenvalues were (to first order) linear combinations of the degenerate wave functions of the unperturbed problem, i.e.

where the \(\kappa \) are unknown coefficients that described how exactly the perturbation lifted the degeneracy.
The key step was to expand both the perturbed energies and the perturbed wave functions in a power series in the expansion coefficient \(\lambda = F/(e/a_0^2),\) where \(a_0\) is the Bohr radius, so that the expansion coefficient gives a measure of how small the external field is compared to the average Coulomb field of the nucleus.
“Eigenwertproblem des Atoms II” (AHQP M/f 40, Sect. 6), p. 29. The perturbation parameters defined a set of linear equations from which one could obtain the non-degenerate energy values of the perturbed system. Essentially, the functional eigenvalue problem of the original Schrödinger equation was thereby reduced to an eigenvalue problem for the perturbation parameters \(\epsilon _{ji}\) in the finite-dimensional vector space spanned by the formerly degenerate wave function \(u_{ki}.\) The eigenvalues thus obtained then determined the non-degenerate energy values of the perturbed system.
This calculation is in the notebook entitled “Eigenwertproblem des Atoms II.” Here, Schrödinger calculates the perturbation parameters in the Stark effect. The generic wave functions \(u_{ki}\) of Eq. 7 are replaced by
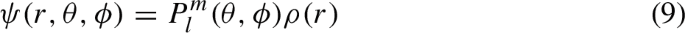
where \(\rho \) is a function of the radius r (which is the same for all the degenerate wave functions), \(P_l^m (\theta , \phi )\) are the spherical harmonics, and the index pair (l, m) (replacing the general index i) is identified with the orbital and magnetic quantum numbers of the hydrogen atom. Hence, the perturbation parameters were determined by a (weighted) integration over a product of spherical harmonics:
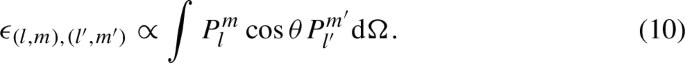
Due to the orthogonality relations of the spherical harmonics, this integral vanishes unless \(m=m'\) and \(\vert l - l' \vert = 1.\)
Schrödinger to Sommerfeld 20 February 1926 in Meyenn (2011, 179).
Schrödinger [“Loose Notes”] AHQP (M/f 40, Sect. 7). While these notes are undated, they show Schrödinger exploring the possibility of combining a wave function with the derivative of another, and can thus be directly linked to his letter to Sommerfeld.
Ibd. “Verrückter Satz: Der Eigenwert selbst ist gleich dem Integral über eine gewisse quadratische Differenzialform gebildet von einer Eigenfunktion. Die Übergangswahrscheinlichkeit ist offenbar das Integral der betreffenden Bilinearform gebildet von den zwei Eigenfunktionen.”
Schrödinger immediately realized that simply replacing one of the \(\psi _n\) by \(\psi _m\) in Eq. 11 would give zero for all transition probabilities. He thus concluded that the differential operator L would have to be replaced by something else, e.g., by the simple \({\textrm{d}}/{\textrm{d}}x.\) For the harmonic oscillator, Schrödinger found, the integral with the differential operator \({\textrm{d}}/{\textrm{d}}x\) led to non-vanishing intensities only for \(\vert m-n \vert = 1,\) thus reproducing the selection rule for the harmonic oscillator. For the rotator, however, he obtained selection rules that were so restrictive as to allow no transitions at all. While he thus obtained some promising results in selection rules for the harmonic oscillator, Schrödinger realized that this approach could not be generalized.
See Schrödinger [“Intensities, dogmatically”] AHQP (40.7). In his notebook, he identified the integral with the “Ausstrahlung” (emission).
See Schrödinger (1926e, 753–754) for Schrödinger’s use of “dogmatic” in the sense of “formal”.
“Wir wollen aber jetzt eine allgemeine Methode entwickeln, solche Produkte auszuwerten, weil man sonst ein alter Jud wird.” AHQP, M/f 41-2, p. 3 (notebook) or 5 (MF). Ironically it was the 26-year old Wolfgang Pauli, born into a Jewish family and a friend of Schrödinger, who established the closed-form expressions for the Stark multiplet intensities and provided Schrödinger with the solution. Schrödinger published these results as an addendum to the third communication on the Stark effect, giving full credit to Pauli. Schrödinger (1926c, 489–490).
Schrödinger to Sommerfeld 20 February 1926 in Meyenn (2011, 179).
Schrödinger to Planck 26 February 1926 in Meyenn (2011, 190).
For Schrödinger’s use of and indebtedness to Hamilton’s principle, see Joas and Lehner (2009).
For examples for the traditional reading of the equivalence proof, see Jammer’s standard account (Jammer 1966, 270–273) and for more recent reiterations Madrid Casado (2008), de Gosson (2014), Purrington (2018, 83–84), or Golub et al. (2023, 128–138). The motivation for the proof has also been taken for granted in historical accounts that were otherwise well-informed, e.g., Joas (2022, 181), Jähnert and Lehner (2022) and Duncan and Janssen (2023, sect. 14.5). It should be noted that this motivation of equivalence is not far fetched. It resonates with the very first sentences of Schrödinger’s equivalence paper (Schrödinger 1926e, 734). And Sommerfeld and Schrödinger had indeed concluded that there had to be a connection between the two theories because of the agreement in predictions (Sommerfeld to Schrödinger 3 February 1926 and Schrödinger to Wien 22 February 1926 in Meyenn 2011, 174–175 and 186, respectively). But, and this is of course one of the main findings of this paper, this belief in the existence of a mathematical connection was not sufficient to actually find the proof, at least in Schrödinger’s case.
See “Eigenwertproblem des Atoms III” AHQP 40, Sect. 7. The notebook contains material marked for the second communication and was probably written in February 1926, around the same time as Schrödinger’s letter to Wien (Schrödinger to Wien, 22 February 1926, in von Meyenn (2011), 186). See also Duncan and Janssen (2023, 454), who also highlight the contrast between Schrödinger’s frustration with the equivalence proof and his successful proof a few of days later.
Schrödinger to Planck, 11 March 1926, in Meyenn (2011, 194).
Schrödinger to Wentzel, 11 May 1926, in Meyenn (2011, 226).
The reader should note the shift in Schrödinger’s reading of this expression: what used to be an expression for the intensities/transition probabilities was now an expression for the transition amplitudes. Since his entire motivation for this expression lay in the selection rules, this was an easy move. After all, for disallowed transitions, both the amplitude and the probability should be zero.
This was how momentum had appeared in a variational formulation of wave mechanics introduced in notes added in proof to the first Mitteilung (Schrödinger 1926a, 376).
Matrix mechanics did not provide an interpretation for the P matrix, neither in terms of physical processes in the atom, nor in terms of spectroscopic observables. Its introduction was motivated solely by Born and Jordan’s formal transfer of Heisenberg’s matrix mechanics into the framework of Hamiltonian mechanics (Blum et al. 2017). This asymmetry between position and momentum persisted well beyond the establishment of the equivalence proof. While Schrödinger later highlighted the physical interpretation of the X matrix as the Fourier components of the dipole moment of the atom, the interpretation of the P matrix remained unclear. At one point, Schrödinger speculated that the momentum matrix was related to higher multipole moments: “For I interpret these ‘transition probabilities’ as real ‘components of the electric [dipole] moment of the molecule’, entirely in the usual sense, where the charge is distributed over space as described by one of the eigenfunctions. The whole construct can then act not only as a ‘linear antenna’ but also as a ‘loop antenna’. This last component of the radiation may be non-negligible. Translated into the language of your theory, this would probably mean that it is not just the matrix elements [\(X_{mn}\)], but also the \(P_{mn}\) that determine the ‘transition probability.”’ Schrödinger to Born, 15 April 1926 in Meyenn (2011, 210).
This work is chronicled in the notebook “Intensities, Parallels to Heisenberg and Lanczos” (AHQP Mf 41 Sect. 2). It involved several false starts and was briefly interrupted by a newly published paper by the Hungarian mathematician and physicist Cornelius Lanczos (1926), which had been written before the advent of wave mechanics and set out to provide a field-theoretical interpretation of matrix mechanics. Schrödinger only learnt about it on 7 March from Max Planck, as well as from his own assistant Erich Fues. He ultimately discarded Lanczos’ approach as going in the wrong direction and continued his feverish hunt for the equivalence proof, following his original radiation-theoretical considerations. See Planck to Schrödinger, 8 March 1926, and Schrödinger to Planck, 11 March 1926, in Meyenn (2011, 193–196).
As an intermediate step, Schrödinger had to establish a prescription on how to fix the order of matrix products, a problem that appeared in Hamiltonians containing terms of the form px.
Schrödinger appears to have originally favored the inclusion of a time derivative in the expression for the charge density, because it could then easily be extended to a relativistic charge-current four-vector \(\psi \partial _{\mu } \overline{\psi } +\overline{\psi } \partial _{\mu } \psi .\) In Schrödinger (1926d, 117), he would eventually settle on an expression for the charge density that did not include the time derivative, i.e., on the expression \(\overline{\psi } \psi ,\) and would characterize the original use of the time derivative as a “mistake” (Fehlgriff), without, however, explaining where it fell short. The matter appears to be quite trivial: the expression for the charge density that includes the time derivative is actually zero if use is made of the time-dependent Schrödinger equation.
The reader will note that Schrödinger had by now reached the conclusion that the frequency of his matter waves would be proportional to the energy E not just approximately, but exactly, cf. footnote 26. This conclusion was first published in Schrödinger (1926b, 106), submitted on 23 February 1926, 3 days after the quoted letter to Sommerfeld.
See Schrödinger to Planck, 11 March 1926; Schrödinger to Lorentz, 30 March 1926; Schrödinger to Born, 15 April 1926. See Meyenn (2011, 195, 204–5, 211, respectively).
At this point, Schrödinger still took the simultaneous excitation of different eigenfunctions for granted. The first instances of doubt appeared at a later stage, as a reaction to Born’s statistical interpretation of the wave function, see Schrödinger to Joos 17 November 1926 (von Meyenn 2011, 347).
See Jammer (1966, 300-1), where Schrödinger’s charge density interpretation is not mentioned and his interpretation attempt in terms of wave packets is discarded due to the fact that many-body systems can only be described in 3N dimensional phase space.
Heisenberg to Pauli, 8 June 1926, in Hermann et al. (1979, 328).
Pauli to Jordan, 12 April 1926, in Hermann et al. (1979, 319). From the context it is clear that the somewhat unusual term “de Broglie radiation” simply refers to matter waves. Unfortunately, there are no extant sources that would allow a reconstruction of how Pauli arrived at his proof.
Klein (1927).
For a detailed analysis of this mode of formal comparison, see Blum and Jähnert (2024).
Schrödinger (1926d).
Pauli (1929, 1831).
Pauli (1929, 1832, our emphasis).
Lehner (2011).
In this paper, we have demonstrated this for Schrödinger’s equivalence proof; however, the same is true for Heisenberg’s pathway to Umdeutung, where exploratory calculations based on intensity schemes segued into the search for a new quantum kinematics. See Blum et al. (2017).
The crucial role of selection rules in mediating between empirical data and theoretical descriptions has hitherto not been analyzed in sufficient depth in philosophy of science. Norton (2021) calls attention to this role in his current project on the “Large-Scale Structure of Inductive Inference”.
References
Assmus, A.J. 1992. The molecular tradition in early quantum theory. Historical Studies in the Physical and Biological Sciences 22: 209–231.
Bacciagaluppi, G., and A. Valentini. 2009. Quantum theory at the crossroads. Reconsidering the Solvay conference. Cambridge: Cambrige University Press.
Bacciagaluppi, G., E. Crull, and O.J. Maroney. 2017. Jordan’s derivation of blackbody fluctuations. Studies in History and Philosophy of Modern Physics 60: 23–34.
Beller, M. 1983a. The genesis of interpretations of quantum physics, 1925–1927. Ann Arbor: UMI.
Beller, M. 1983b. Matrix theory before Schrödinger: Philosophy, problems, consequences. Isis 74: 469–491.
Beller, M. 1990. Born’s probabilistic interpretation: A case study of concepts in flux. Studies in History and Philosophy of Science 21: 563–88.
Beller, M. 1992. The birth of Bohr’s complementarity: The context and the dialogues. Studies in History and Philosophy of Science 23: 147–180.
Beller, M. 1999. Quantum dialogue. The making of a revolution. Chicago: University of Chicago Press.
Bitbol, M. 1996. Schrödinger’s philosophy of quantum mechanics. Dordrecht: Kluwer.
Bitbol, M., and O. Darrigol, eds. 1992. Erwin Schrödinger: Philosophy and the birth of quantum mechanics. Gif-sur-Yvette: Editions Frontières.
Blum, A.S., and M. Jähnert. 2022. The birth of quantum mechanics from the spirit of radiation theory. Studies in History and Philosophy of Modern Physics 99: 125–147.
Blum, A.S., and M. Jähnert. 2024. Real virtuality and actual transitions: Historical reflections on virtual entities before Quantum Field Theory. Perspectives on Science 32: 329–349.
Blum, A.S., M. Jähnert, J. Renn, and C. Lehner. 2017. Translation as heuristics. Heisenberg’s turn to matrix mechanics. Studies in History and Philosophy of Modern Physics 60: 3–22.
Bohr, N. 1923. Über die Anwendung der Quantentheorie auf den Atombau. I. Die Grundpostulate der Quantentheorie. Zeitschrift für Physik 13: 117–165.
Bohr, N. 1925. Über die Wirkung von Atomen bei Stößen. Zeischrift für Physik 34: 142–157.
Bohr, N. 1926. Atomtheorie und Mechanik. Die Naturwissenschaften 14: 1–10.
Bohr, N. 1928. The quantum postulate and the recent development of atomic theory. Nature 121: 580–590.
Bokulich, A. 2009. Three puzzles about Bohr’s correspondence principle, 1–24. http://philsci-archive.pitt.edu/archive/00004826/01/3Puzzles-BohrCP-Bokulich.pdf. Accessed 16 June 2023.
Bonk, T. 1994. Bemerkungen zur Interpretation, Bestätigung und Progressivität der frühen Matrizenmechanik. Zeitschrift für allgemeine Wissenschaftstheorie 25: 1–15.
Born, M. 1933. Moderne Physik: Sieben Vorträge über Materie und Strahlung. Berlin: Springer.
Born, M., and P. Jordan. 1925. Zur Quantenmechanik. Zeitschrift für Physik 34: 858–888.
Born, M., W. Heisenberg, and P. Jordan. 1926. Zur Quantenmechanik II. Zeitschrift für Physik 35: 557–615.
Borrelli, A. 2009. The emergence of selection rules and their encounter with group theory: 1913–1927. Studies in the History and Philosophy of Modern Physics 40: 327–337.
Borrelli, A. 2011. Angular momentum between physics and mathematics. In Mathematics meets physics, ed. K.-H. Schlote and M. Schneider, 395–440. Frankfurt am Main: Verlag Harri Deutsch.
Camillieri, K. 2005. Heisenberg and the transformation of Kantian philosophy. International Studies in the Philosophy of Science 19 (3): 271–287.
Camillieri, K. 2006. Heisenberg and the wave-particle-duality. Studies in the History and Philosophy of Modern Physics 37: 298–315.
Camillieri, K. 2007a. Bohr, Heisenberg and the divergent viewpoints of complementarity. Studies in the History and Philosophy of Modern Physics 38: 514–528.
Camillieri, K. 2007b. Indeterminacy and the limits of classical concepts: The turning point in Heisenberg’s thought. Perspectives on Science 15 (2): 176–199.
Cushing, J.T. 1991. Quantum theory and explanatory discourse: Endgame for understanding? Philosophy of Science 58 (3): 337–358.
Darrigol, O. 1992. From c-numbers to q-numbers: The classical analogy in the history of quantum theory. Berkeley: University of California Press.
Darrigol, O. 2009. A simplified genesis of quantum mechanics. Studies in History and Philosophy of Modern Physics 40: 151–166.
de Gosson, M.A. 2014. Born–Jordan quantization and the equivalence of the Schrödinger and Heisenberg pictures. Foundations of Physics 44: 1096–1106.
De Regt, H.W. 1997a. Erwin Schrödinger, Anschaulichkeit, and quantum theory. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics 28 (4): 461–481.
De Regt, H.W. 1997b. Pauli versus Heisenberg: A case study of the heuristic role of philosophy. Foundations of Science 4: 405–426.
De Regt, H.W. 1999. Ludwig Boltzmann’s Bildtheorie and scientific understanding. Synthese 119 (1): 113–134.
De Regt, H.W., and D. Dieks. 2005. A contextual approach to scientific understanding. Synthese 144: 137–170.
Dennison, D.M. 1926. The rotation of molecules. Physical Review 28: 318–333.
Dirac, P.A.M. 1926a. Quantum mechanics and a preliminary investigation of the hydrogen atom. Proceedings of Royal Society of London. Series A 110: 561–579.
Dirac, P.A.M. 1926b. Relativity quantum mechanics with an application to Compton scattering. Proceedings of the Royal Society, Series A 111 (758): 405–423.
Duncan, A., and M. Janssen. 2007. On the Verge of Umdeutung in Minnesota: Van Vleck and the correspondence principle. Parts I and II. Archive for History of Exact Sciences 61: 553–624, 625–671.
Duncan, A., and M. Janssen. 2008. Pascual Jordan’s resolution of the conundrum of the wave-particle duality of light. Studies in History and Philosophy of Modern Physics 39: 634–666.
Duncan, A., and M. Janssen. 2009. From canonical transformations to transformation theory, 1926–1927: The road to Jordan’s Neue Begründung. Studies in History and Philosophy of Modern Physics 40: 352–362.
Duncan, A., and M. Janssen. 2013. (Never) mind your p’s and q’s: Von Neumann versus Jordan on the foundations of quantum theory. European Physical Journal History 38: 175–259.
Duncan, A., and M. Janssen. 2014. The trouble with orbits: The Stark effect in the old and the new quantum theory. Studies in History and Philosophy of Modern Physics 48: 68–83.
Duncan, A., and M. Janssen. 2019. Constructing quantum mechanics volume 1: The Scaffold: 1900–1923. Oxford: Oxford University Press.
Duncan, A., and M. Janssen. 2023. Constructing quantum mechanics volume 2: The Arch: 1923–1927. Oxford: Oxford University Press.
Essex, E.A. 1977. Hertz vector potentials of electromagnetic theory. American Journal of Physics 45 (11): 1099–1101.
Freire, J.O., G. Bacciagaluppi, O. Darrigol, T. Hartz, and C. Joas, eds. 2022. The Oxford handbook of the history of quantum interpretations. Oxford: Oxford University Press.
Gelfert, A. 2016. How to do science with models: A philosophical primer. Cham: Springer.
Goldstein, H. 1975. Prehistory of the “Runge–Lenz’’ vector. American Journal of Physics 43: 737–738.
Golub, R., S. Lamoreaux, and S. Lamoreaux. 2023. The historical and physical foundations of quantum mechanics. Oxford: Oxford University Press.
Hanle, P.A. 1977. The coming of age of Erwin Schrödinger: His quantum statistics of ideal gases. Archive for History of Exact Sciences 17: 165–192.
Heilbron, J.L., and C. Rovelli. 2023. Matrix Mechanics mis-prized: Max Born’s belated nobelization. European Physical Journal H 48: 11.
Heisenberg, W. 1925. Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. Zeitschrift für Physik 33 (1): 879–893.
Heisenberg, W., and P. Jordan. 1926. Anwendung der Quantenmechanik auf das Problem der anomalen Zeemaneffekte. Zeitschrift für Physik 37 (4–5): 263–277.
Hendry, J. 1984. The creation of quantum mechanics and the Bohr–Pauli dialogue. Studies in the history of modern science, vol. 14. Dordrecht: Springer.
Hermann, A., K. von Meyenn, and V.F. Weisskopf, eds. 1979. Wissenschaftlicher Briefwechsel mit Bohr, Einstein, Heisenberg u.a., vol. 1, 1919–1929. New York: Springer.
Howard, D. 2004. Who invented the Copenhagen interpretation? A study in mythology. Philosophy of Science 71: 669–682.
Jähnert, M. 2019. Practicing the correspondence principle in the old quantum theory: A transformation through application. Archimedes. Dordrecht: Springer.
Jähnert, M., and C. Lehner. 2022. The early debates about the interpretation of quantum mechanics. In The Oxford handbook of the history of quantum interpretations, ed. J.O. Freire, G. Bacciagaluppi, O. Darrigol, T. Hartz, and C. Joas, 173–201. Oxford: Oxford University Press.
James, J., and C. Joas. 2015. Subsequent and subsidiary? Rethinking the role of applications in establishing quantum mechanics. Historical Studies in the Natural Sciences 45: 641–702.
Jammer, M. 1966. The conceptual development of quantum mechanics. New York: McGraw-Hill.
Joas, C. 2022. Foundations and applications: The creative tension in the early development of quantum mechanics. In The Oxford handbook of the history of quantum interpretations, ed. J.O. Freire, G. Bacciagaluppi, O. Darrigol, T. Hartz, and C. Joas, 173–201. Oxford: Oxford University Press.
Joas, C., and C. Lehner. 2009. The classical roots of wave mechanics: Schrödinger’s transformation of the optical-mechanical analogy. Studies in History and Philosophy of Modern Physics 40: 338–351.
Klein, O. 1927. Elektrodynamik und Wellenmechanik vom Standpunkt des Korrespondenzprinzips. Zeitschrift für Physik 41: 407–442.
Klein, O. 1928. Zur fünfdimensionalen Darstellung der Relativitätstheorie. Zeitschrift für Physik 46 (3–4): 188–208.
Kuhn, T.S. 1996. The structure of scientific revolution, 3rd ed. Chicago: The University of Chicago Press.
Lacki, J. 2000. The early axiomatizations of quantum mechanics: Jordan, von Neumann and the continuation of Hilbert’s program. Archive for History of Exact Sciences 54: 279–318.
Lacki, J. 2004. The puzzle of canonical transformations in early quantum mechanics. Studies in History and Philosophy of Modern Physics 35: 317–344.
Lanczos, C. 1926. Über eine feldmäßige Darstellung der neueren Quantenmechanik. Zeitschrift für Physik 35: 812–830.
Lehner, C. 2011. Mathematical foundations and physical visions: Pascual Jordan and the field theory program. In Mathematics meets physics: A contribution to their interaction in 19th and the first half of the 20th century, 272–292. Frankfurt am Main: Verlag Harri Deutsch.
Lenz, W. 1924. Über den Bewegungsverlauf und die Quantenzustände der gestörten Keplerbewegung. Zeitschrift für Physik 25: 197–207.
MacKinnon, E.M. 1980. The rise and fall of the Schrödinger interpretation. In Studies in the foundations of quantum mechanics, ed. Suppes, Patrick, 1–58. East Lansing: University of Chicago Press.
Madrid Casado, C.M. 2008. A brief history of the mathematical equivalence between the two quantum mechanics. Latin-American Journal of Physics Education 2: 152–155.
Mehra, J., and H. Rechenberg. 1982. The historical development of quantum theory, vol. 3: The formulation of matrix mechanics and its modifications 1925–1926. New York: Springer.
Mehra, J., and H. Rechenberg. 1987. The historical development of quantum theory. Vol. 5. Erwin Schrödinger and the rise of wave mechanics. Part 2. The creation of wave mechanics: Early responses and applications. New York: Springer.
Mensing, L. 1926. Die Rotations-Schwingungsbanden nach der Quantenmechanik. Zeitschrift für Physik 36 (11): 814–823.
Midwinter, C., and M. Janssen. 2013. Kuhn losses regained: Van Vleck from spectra to susceptibilities. In Research and pedagogy: A history of quantum physics through its textbooks, Chapter 7, ed. M. Badino, and J. Navarro, 133–196. Berlin: Max-Planck-Gesellschaft zur Förderung der Wissenschaften.
Muller, F.A. 1997. The equivalence myth of quantum mechanics. Studies in the History and Philosophy of Modern Physics 28: 219–247.
Norton, J.D. 2021. Mutually supporting evidence in atomic spectra [draft], 1–19. https://sites.pitt.edu/~jdnorton/homepage/cv.html#material_large/. Accessed 16 June 2023.
Pauli, W. 1926. Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik. Zeitschrift für Physik 36 (5): 336–363.
Pauli, W. 1929. Allgemeine Grundlagen der Quantentheorie des Atombaus. In Müller-Pouillets Lehrbuch der Physik, 1709–1842. Braunschweig: Friedrich Vieweg u. Sohn.
Perovic, S. 2008. Why were matrix mechanics and wave mechanics considered equivalent? Studies in the History and Philosophy of Modern Physics 39: 444–461.
Purrington, R.D. 2018. The heroic age: The creation of quantum mechanics 1925–1940. Oxford: Oxford University Press.
Renn, J. 2009. Schrödinger and the genesis of wave mechanics. In Erwin Schrödinger—50 years after, ed. W.L. Reiter and J. Yngvason, 9–36. Zürich: European Mathematical Society.
Schrödinger, E. 1926a. Quantisierung als Eigenwertproblem (Erste Mitteilung). Annalen der Physik 79: 361–376.
Schrödinger, E. 1926b. Quantisierung als Eigenwertproblem (Zweite Mitteilung). Annalen der Physik 79: 486–527.
Schrödinger, E. 1926c. Quantisierung als Eigenwertproblem (Dritte Mitteilung). Annalen der Physik 80: 437–490.
Schrödinger, E. 1926d. Quantisierung als Eigenwertproblem (Vierte Mitteilung). Annalen der Physik 81: 109–139.
Schrödinger, E. 1926e. Über das Verhältnis der Heisenberg-Born-Jordanschen Quantenmechanik zu der meinen. Annalen der Physik 79 (4): 143–165.
Seth, S. 2010. Crafting the quantum. Arnold Sommerfeld and the practice of theory, 1890–1926. Cambridge: MIT Press.
Slater, J.C. 1927. Radiation and absorption in Schrödinger’s theory. Proceeding National Academy of Sciences 13: 7–12.
Steinle, F. 2005. Explorative Experimente: Amperé, Faraday und die Ursprünge der Elektrodynamik. Stuttgart: Franz Steiner Verlag.
Steinle, F. 2016. Exploratory experiments: Amperé, Faraday and the origins of electrodynamics. Pittsburgh: University of Pittsburgh Press.
Tamm, I. 1926. Zur Quantenmechanik des Rotators. Zeitschrift für Physik 37: 685–698.
Valent, G. 2002. The hydrogen atom in electric and magnetic fields: Pauli’s article. American Journal of Physics 71: 171–175.
Van der Waerden, B.L., ed. 1967. Sources of quantum mechanics: With a historical introduction. Amsterdam: North-Holland.
Van der Waerden, B.L. 1997. From matrix mechanics and wave mechanics to unified quantum mechanics. Notices of the AMS 44 (3): 323–328.
von Meyenn, K., ed. 2011. Eine Entdeckung von ganz außerordentlicher Tragweite: Schrödingers Briefwechsel zur Wellenmechanik und zum Katzenparadoxon, vol. 1. Heidelberg: Springer.
Wessels, L. 1975. Schrödinger’s interpretation of wave-mechanics. Ph.D. thesis, Indiana University, Bloomington.
Wessels, L. 1979. Schrödinger’s route to wave-mechanics. Studies in History and Philosophy of Science 10: 311–40.
Wessels, L. 1980. What was Born’s statistical interpretation? PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association 2: 187–200.
Wessels, L. 1983. Erwin Schrödinger and the descriptive tradition. In Springs of scientific creativity: Essays on founders of modern science, ed. R. Aris, H.T. Davis, and R.H. Stuewer, 254–278. Minneapolis: University of Minnesota Press.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Neither of the authors is aware of any conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Blum, A., Jähnert, M. Quantum mechanics, radiation, and the equivalence proof. Arch. Hist. Exact Sci. (2024). https://doi.org/10.1007/s00407-024-00334-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00407-024-00334-4