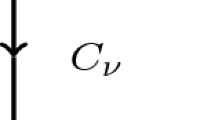“The language of Dirac’s theory of radiation”: the inception and initial reception of a tool for the quantum field theorist

Abstract

In 1927, Paul Dirac first explicitly introduced the idea that electrodynamical processes can be evaluated by decomposing them into virtual (modern terminology), energy non-conserving subprocesses. This mode of reasoning structured a lot of the perturbative evaluations of quantum electrodynamics during the 1930s. Although the physical picture connected to Feynman diagrams is no longer based on energy non-conserving transitions but on off-shell particles, emission and absorption subprocesses still remain their fundamental constituents. This article will access the introduction and the initial reception of this picture of subsequent transitions (PST) by conceiving of concepts, models, and their representations as tools for the practitioners. I will argue for a multi-factorial explanation of Dirac’s initial, verbally explicit introduction: the mathematical representation he had developed was highly suggestive and already partly conceptualized; Dirac was philosophical flexible enough to talk about transitions when no actual transitions, according to the general interpretation of quantum mechanics of the time, occurred; and, importantly, Dirac eventually used the verbal exposition in the same paper in which he introduced it. The direct impact of PST on the conception of quantum electrodynamical processes will be exemplified by its reflection in diagrammatical representations. The study of the diverging ontological commitments towards PST immediately after its introduction opens up the prehistory of a philosophical debate that stretches out into the present: the dispute about the representational and ontological status of the physical picture connected to the evaluation of the perturbative series of QED and QFT.

This article will focus on the verbal representation of the model that was, and partly still is, underlying the perturbative evaluation of quantum electrodynamical (QED) phenomena. I will engage with Paul Dirac’s initial introduction of a verbally explicit description of the light-matter interaction in terms of temporally ordered transition subprocesses, each accompanied by an emission or absorption of a photon, even though these subprocesses did not refer to actual but to (in modern terminology) virtual transitions. I will ask why it was Paul Dirac, and not someone else, who introduced this kind of representation. I will discuss its impact on other representational formats and the plethora of stances physicists took towards the verbal explication immediately after Dirac’s introduction. The basic idea behind my exploration is an understanding of theory as practice and of concepts, their representations and the models they figure in as tools for practitioners. As I will use it frequently, I will abbreviate the analytical term “verbal representation of the model” with “verbal model” and, if I refer to the late 1920s and 1930s specifically, I will follow one of the actors and call it “das Bild ‘aufeinander folgender’ Übergänge” (Kockel 1937, 162) or, the “picture of ‘successive’ transitions” (PST for short).

Even though the conception of processes in terms of PST partly differs from the physical picture connected to Feynman diagrams, I want to start out with a quick look at these diagrams as it can serve to introduce the overarching topic of this article: The use of physical reasoning in the evaluation of abstract mathematical procedures within theoretical physics, especially when a direct connection between physical language and real-world process is not warranted or called into doubt by the actors themselves. Feynman diagrams, or more to the point, their interpretation, can exemplify how a processual language and the concepts figuring in it can have a constructive function, how they can be considered tools for the quantum field theorist.

Surely, there is no doubt that Feynman diagrams are an extraordinarily useful tool in the everyday business of quantum field theorists. Even philosophers who deny Feynman diagrams any ontological or representational status acknowledge the tool character of the diagrammatic technique.¹ In the following, however, I do not want to focus on the representational format of diagrams but on the processual language, i.e. the physical reasoning that can be used to construct them.

Fig. 1

The first Feynman diagram Feynman published by him in 1949. Taken from (Feynman 1949, 772)

When Richard Feynman introduced his readers to the first Feynman diagram published by himself (see Fig. 1) he did so with a physical interpretation: The electrons (note the arrow of time on the left) would travel some way, one of them would emit and the other absorb a “virtual quantum,” not obeying the relativistic energy–momentum relation, in principle unobservable and represented by the squiggly line in the middle. The virtual photon itself would travel from the point where it was emitted to the point where it will be absorbed and, thereby, it would mediate the interaction between the two electrons. Then, the electrons would go off to infinity without further interaction.²

According to the mainstream of the philosophical literature on Feynman diagrams and virtual particles, such a picturesque description has no realistic or physical content.³ As the conclusion of the arguments goes, Feynman diagrams (at least a single diagram on its own) should not be conceived of as a representation of a physical process but of a mathematical structure, a term in an infinite perturbative series of contributions to the calculation of one single physical effect. No more, no less.

And actually, starting from their introduction in the late 1940s, Feynman diagrams were not necessarily interrelated with a physical interpretation. They can perform their function as calculational aids through their topological features and an accompanying set of rules for drawing and translating them into mathematical expressions. David Kaiser (2005, especially the first section of chapter 5) has termed the divide between physical interpretation and mere topological evaluation the Feynman (physical interpretation)–Dyson(topological constructs) split in reference to the historical protagonists who first exemplified these stances.

The Feynman–Dyson-split still resonates in the different stances towards the diagrams in perturbative evaluations. While Mandl and Shaw (1984, 56) note in their textbook that “the reader must be warned not to take this pictorial description of the mathematics as a literal description of a process in space and time,” Peskin and Schroeder (1995, 3) encourage their reader “[to] imagine a process that can be carried out by electrons and photons, draw a diagram, and then use the diagram to write down the mathematical form of the quantum-mechanical amplitude for that process to occur.” But these two points of view are not mutually exclusive. For example, Mandl and Shaw (1984, 54–55) use a physical and processual description to introduce the idea of Feynman diagrams right before their warning and thereby point towards the role of the physical reasoning this article is concerned with.

If we take Peskin’s and Schroeder’s above-mentioned encouragement at face value, the constructive process does not start with the diagram but with the physical reasoning underlying it; the diagrams are the representational format in which this reasoning is cast to translate it into mathematical expressions. Feynman himself opened and ended his own physical interpretation by noting that it “will permit us to write down the higher order terms” and that “the correct terms of higher order in $e^2$ or involving larger numbers of electrons (interacting with themselves or in pairs) can be written down by the same kind of reasoning” Feynman (1949, 773). In this sense, the interpretation in terms of processes, the storyline that is connected to a diagram or to the respective term in the perturbative series, is more than a mere interpretation. This story and the method of telling it have a tool character and are used for what a lot of every-day tools are used for: construction.

Certainly, Feynman’s version of QED constituted a digression from QED as it was practiced and conceived of in the 1930s.⁴ His space-time diagrams show similarities to Minkowski diagrams or bubble chamber pictures rather than to diagrams that were used in the theoretical evaluation of QED before the late 1940s.⁵ Feynman’s application of diagrammatical techniques further had its roots in his struggle with the Dirac equation and Feynman’s main goal was a physical understanding suitable for the elimination of the divergences plaguing QED.⁶ Yet part of the physical picture connected to the diagrams, the storyline of subsequent acts of emission and absorption processes, is older than the diagrammatical technique. As is well known, even before the invention of Feynman diagrams there was a mode of physical reasoning applied to evaluate QED and it served the same purpose as the story connected to a Feynman diagram today. PST, as introduced by Paul Dirac in 1927, was used by physicists, albeit knowing of its possibly fictional character, to construct mathematical representations of the phenomena they were investigating. In the following, I will engage with this mode of reasoning. More to the point, I will engage with the verbal representation of it, the language physicists used in their practice.

The approach I will take has been heavily influenced by pragmatic accounts of conceptual development. In the literature on the history and philosophy of science, the understanding of concepts as tools for researchers has proven a valuable angle for understanding scientific practice and its development.⁷ Similarly, nearly from the onset of the so-called practice turn in the mid-1980s, it has been argued that representations, whatever form they might take, should not be conceived of as mere depictions but as “means for doing things, tools for intervening” (Soler et al. 2014, 23).⁸

To clarify, I want to point out that a model or a concept and their representations are not equivalent in my understanding. When I refer to a representation, I always mean something concrete, specific and manifest that has been written down in some way by the historical actors. A model or a concept, on the other hand, come in different representations. Each representation enables specific inferences to be drawn, but also entails specific constraints on thinking possibilities. Such constraints might be internal, dictated by the representational format itself.⁹ But the constraints can also be externally dictated by other representations that the actors considered to describe the same model.¹⁰

As in the example of Feynman diagrams, I will conceive of the whole interpretation of the mathematical structures, i.e. the verbal expressions in which they are cast, as a tool for the respective physicists. The concepts, or rather their representations, involved in the interpretation have a tool character themselves due to the role they play. As the notion of a virtual particle is an indispensable ingredient when trying to imagine and express the processes Feynman diagrams purport to portray, the notion of “virtual transitions” and “intermediate states,” unbound by energy conservation, were an integral part of the conception of quantum electrodynamical processes during the 1930s. In this sense, the following will both be a story of the application of the verbal model and the application of the concepts used to spell it out. I believe that one cannot be told without the other.

In the first section of this article, I will engage with the initial proposal of the verbal model of the perturbative evaluation of quantum electrodynamics by Paul Dirac in 1927. To fully apprehend this introduction, I will revisit the technical and conceptual environment Dirac was working in, his general outlook on (the concepts of) quantum theory and the use he made of PST. Since part of the answer to the question why it was specifically Dirac who introduced PST is the high suggestiveness of Dirac’s mathematical framework, I cannot avoid engaging with a few technicalities.

The second section will outline some of the initial reactions to Dirac’s introduction of PST. I will exemplify its impact on diagrammatic representations and the range of stances towards PST: from ascribing the occurring intermediate states a temporal dimension and using their occurrence for inferences on the existence of physical entities to clear denotation as fiction. I will close this article with a conclusion and an outlook on the use of PST during the 1930s.

1 Dirac’s verbal model for the scattering of light

In his second paper on QED, communicated in April 1927, Dirac introduced his reader to the scattering of light from an atom in the following way:

“[...] radiation that has apparently been scattered can appear by a double process in which a third state, n say, with different proper energy from m [final state] and k [initial state] plays a part. If initially all the b’s [the quantum amplitudes of the states] vanish except $b_k$, $b_n$ [the amplitude of the intermediate state] gets excited on account of transitions from state k by an amount proportional to $v_{nk}$ [the matrix element of the interaction between radiation field and matter], and although it must itself always remain small, a calculation shows that it will cause $b_m$ to grow continually with the time at a rate proportional to $v_{mn}v_{nk}$. The scattered radiation thus appears as the result of two processes $k\rightarrow n$ and $n\rightarrow m$, one of which must be an absorption and the other an emission, in neither of which is the total proper energy even approximately conserved.”¹¹

Up to that point, such a verbally explicit and temporally ordered account of the scattering of light in terms of subsequent energy non-conserving or “virtual”¹² transitions to and from intermediate or “virtual” states was (nearly) absent from the papers dealing with this effect.¹³ This is all the more striking as similar mathematical structures to the ones Dirac presented in his solution were already known at the time.

Shortly before the publication of Heisenberg’s Umdeutungs-paper, Anthony Kramers and Werner Heisenberg (Kramers and Heisenberg 1925) had developed an account of dispersion, the Kramers–Heisenberg [KH]formula, which became, as Lacki et al. (1999, 462) phrased it, “un passage obligé” for all following versions of quantum mechanics: Born et al. (1926), Schrödinger (1926), and Klein (1927) all rederived this formula in the respective theoretical and conceptual framework. Whether a classical perturbative evaluation was performed that was then translated into quantum theory through the correspondence principle (Kramers and Heisenberg) or whether the material part of the system was treated quantum mechanically from the start, the solution for the intensity of the secondary radiation always contained something of the general structure

$$\begin{aligned} \left\| \sum _n \frac{x_{kn}y_{nm}}{E_m-E_n}\right\| ^2, \end{aligned}$$

(1)

where $x_{kn}$ and $y_{nm}$ are the “characteristic amplitudes”¹⁴ in Kramers and Heisenberg’s terminology, or, in the later conception, the dipole matrix elements between the two states k and n.

Fig. 2

The graphical display provided by Kramers and Heisenberg for the derivation (diagram on the left) and the evaluation (the two diagrams on the right) of the KH formula. Taken from Kramers and Heisenberg (1925, 694, 699)

As the initial (m) and final (k) states of the processes were connected through the third level n and as the squares of the operators $x_{nk}$ were and are interpreted as proportional to the probability of a transition between the states n and k occurring, an interpretation in terms of transitions suggests itself. Kramers and Heisenberg even provided diagrams to visualize the mathematical structures above, but in a rather abstract action-variable space and without an explicit temporal dimension (see Fig. 2).¹⁵ A verbal description of such formulas in terms of transitions from state m over n to k is lacking, not only in Kramers’ and Heisenberg’s paper but also in the later rederivations of the formula.

The most explicit description I came across prior to Dirac’s was given by Wolfgang Pauli in 1925. In his discussion of the KH formula, the atom made a “detour through a third state.”¹⁶ Nevertheless, Pauli would no longer use this interpretation of the KH formula in his Handbuch-article Pauli (1926) published shortly afterwards.¹⁷ The derived mathematical structures were certainly suggestive but for more than 2 years the practitioners did not describe their results in a temporally ordered fashion of subsequent transitions when dispersion was discussed.

And there are good reasons why such a description should be avoided. To some extent, it contradicts the general interpretation of quantum theory in neglecting the differentiation between quantum amplitudes and probabilities.¹⁸ As you can directly see from Formula (1), the sum over different combinations of matrix elements is squared and refers to a probability or the intensity of the emitted radiation. If we were to identify the matrix elements in Formula (1) with quantum jumps, several processes not conserving energy in the intermediate steps would contribute to the observable phenomenon at once. It is the differentiation between the quantum amplitudes and their squares, the probabilities, that makes a simple interpretation impossible. And it is this differentiation, an important and non-trivial one, that will concern us in the following.

And this brings the question guiding this first section into sharper focus: Why did Dirac eventually, and contrary to prior (and some later) descriptions, start to talk in a specific way about the structures he encountered? More to the point: why did Dirac choose not only to name the structures, but to describe them in terms of temporally ordered subprocesses at least suggesting some kind of causal connection between them and thereby setting “the basic language and concepts characteristic of the modern conception [...]” (Lacki et al. 1999, 484). To engage with this question, we need to take a closer look at the conceptual and technical framework Dirac developed prior to his quantum electrodynamical account of dispersion.

1.1 Dirac’s technical and conceptual background

The output of the young Cambridge physicist in the years 1925 through 1928 was, to say the least, outstanding. Dirac made a long lasting contribution to quantum theory in these years: from an alternative formulation of matrix mechanics (his q-number algebra); through his technical foundation of quantum mechanics (his transformation theory) and the first applications of quantum electrodynamics; to his relativistic description of the electron, just to name the most influential of his achievements. By early 1926, he had made a name for himself in the community of quantum physicists and his work had gathered wider attention.¹⁹

The following contextualization will focus on the aspects of Dirac’s work which I deem important to understand his invocation of PST. One of the most important aspects of his technical framework is his time-dependent perturbation theory. But, as I will argue, the conceptual framework of his radiation theory, kind of the prototype of QED in the 1930s, and the specific way of its perturbative evaluation played an important role for his invocation.

1.1.1 Time-dependent perturbation theory (Dirac 1926)

In mid-1926 and after some persuasion by Werner Heisenberg,²⁰ Dirac took up Schrödinger’s wave function in his On the Theory of Quantum Mechanics and developed a version of time-dependent perturbation theory. In this mode of evaluating the formulas, the question was not how the energy levels of the system were altered due to the perturbation but how the occupation of unperturbed states changed over time.²¹

As was common for Dirac, he treated the problem first in most general terms.²² Dirac evaluated an arbitrary system, described by the Hamiltonian $H_0$, and considered the respective problem to be solvable. Then he introduced a time-dependent external perturbation V starting to act at some moment $t=0$. Using the most general solution, a superposition of eigenstates $\psi =\sum _n c_n\psi _n$, Dirac showed that the wave function of the perturbed system could be expressed in the following way:

$$\begin{aligned} \psi (t)=\sum _n b_n(t)\psi _n, \end{aligned}$$

(2)

where the $\psi _n$ are the unperturbed wave functions and the $b_n$, the new expansion coefficients, are time dependent. Their initial values $b_n(0)$ are given by the coefficients of the unperturbed problem and their temporal development is governed by the following equation:

$$\begin{aligned} i\hbar {\dot{b}}_m=\sum _n V_{mn}b_n, \end{aligned}$$

(3)

where the $V_{mn}$ are the matrix elements of the perturbation between the two unperturbed states m and n.

The unperturbed states of the system referred to energy eigenstates of the atoms under study. Yet, as Dirac was not interested in the behaviour of a single atom but an assembly of similar ones, he did not normalize the sum of the squares of the coefficients $c_n$ and $b_n(t)$ to one but rather to the number of atoms in the respective state. Hence, in Dirac’s initial presentation $\Vert b_n(t)\Vert ^2$ corresponded to the number of atoms in the state n after the perturbation had been acting on this assembly for a time t.

Whether one follows Dirac’s conception of an assembly of atoms or interprets the square of the coefficients as the probability of finding one atom or system in a given state,²³ this perturbative scheme came with a particular understanding: In contrast to time-independent perturbation theory, Dirac did not ask about the influence of the perturbation on the energy levels of the system. Rather, according to the mathematical modelling, the focus lies on the temporal development of the coefficients of the unperturbed states. Which states couple depends on the structure of the perturbation, i.e. which matrix elements of the perturbation $V_{mn}$ are non-zero. The perturbation energy is further not directly part of the system’s energy, but causes alterations in its behaviour. In his papers on radiation theory, Dirac would therefore introduce the term “proper energy” to refer to the energy of the unperturbed part of the system (or, equivalently, to the energy of the total system minus the interaction energy).

Dirac applied his new way of performing perturbative calculations directly in the same paper for a derivation of the Einstein coefficients for induced emission and absorption (Dirac 1926, 675–677). The specifics of this semi-classical evaluation are not important for our purpose. But there is a methodological step which Dirac incorporated here that I will refer to later on. He already indicated how a second order perturbative calculation must be carried out: A first approximation is derived by plugging in the initial values $c_n$ into Eq. (3) and then integrating it with respect to t. For a second approximation, these time-dependent values are re-introduced into Eq. (3). Hence, Dirac essentially described an iterative procedure for the construction of higher order terms.

1.1.2 Radiation theory (Dirac 1927b, c)

Shortly after finishing the paper introducing his version of time-dependent perturbation theory, Dirac went to Copenhagen (September 1926 until early February 1927) and subsequently to Göttingen (until June 1927). Although Dirac was ever more strongly integrated into the circles of quantum physicists, he kept his habit of mostly working on his own. In Copenhagen, Dirac developed the so-called transformation theory,²⁴ which provided rules for quantizing any dynamical system and provided the formal basis for Heisenberg’s uncertainty paper. The transformation theory was also one of the pillars of Dirac’s radiation theory, which he developed in Copenhagen and which we shall address now.²⁵

Essentially, when constructing quantum electrodynamics, Dirac applied quantization to the wave functions, or rather to the coefficients of his perturbation theory, again. Dirac started out with an assembly of bosons and showed that the temporal development of the coefficients could be cast in an Hamiltonian form with the canonical variables $b_r$ and $b_r^{\dagger }$. As before, $N_r$, the number of the systems, was given by $N_r=\Vert b_r\Vert ^2=b_rb_r^*$.²⁶

Then, to use Dirac’s language, he did not treat these coefficients as c-numbers but as non-commuting q-numbers and imposed commutation relations on them, so that

$$\begin{aligned}{}[b_r,i\hbar b_s^{\dagger }]=i\hbar \delta _{rs}. \end{aligned}$$

(4)

These operators $b_r$ and $b_r^{\dagger }$ are today known, and were interpreted by Dirac, as creation and annihilation operators. Their action was expressed in the following terms (Dirac 1927c, 252):²⁷

$$\begin{aligned} b_r^{\dagger }\psi (N_1,\ldots ,N_r,\ldots )&=\sqrt{N_r+1}\psi (N_1,\ldots ,N_r+1,\ldots ) \end{aligned}$$

(5)

$$\begin{aligned} b_r\psi (N_1,\ldots ,N_r,\ldots )&=\sqrt{N_r}\psi (N_1,...,N_r-1,\ldots ) \end{aligned}$$

(6)

Hence, they raised or lowered the occupation number in the respective state r by 1.

Dirac could generalize this procedure: The second quantized bosonic assembly was coupled to an external perturbation, an atom. The Hamiltonian thereby constructed consisted, besides the proper energies, only of one additional term proportional to the product of each one annihilation and one creation operator: $H\propto H_0 + \sum _{r,s} v_{r,s} b_r^{\dagger }b_s$. Hence, it “will contribute only to those matrix elements that refer to transitions in which $N_r$ decreases by unity and $N_s$ increases by unity” (Dirac 1927c, 252). Without any detour through intermediate states, an initial photon was absorbed and the final photon created. In the same paper, Dirac already referred to such processes as “direct scattering processes” (Dirac 1927c, 263).²⁸

In the last section, Dirac left his initial conceptualization of a perturbed assembly of bosons and turned towards “the wave point of view” (Dirac 1927c, 262). By resolving the radiation into its Fourier components, the interaction between radiation and matter was, in classical theory, proportional to $\sum _r A_r{\dot{x}}$, where $A_r$ is the rth Fourier component of the vector potential and x the position variable at the location of the atom times the electric charge. After some manipulation, Dirac could describe the vector potential in terms of the number of light quanta $N_r$ and the conjugate phases $\theta _r$, which allowed him to impose the previously developed quantization rules.

The Hamiltonian Dirac derived in this “wave-theoretic” way only contained matrix elements which changed the occupation number by $\pm 1$. As he himself noted, “it would seem that there are no direct scattering processes [from this wave-theoretic point of view], but this may be due to an incompleteness in the present wave theory” (Dirac 1927c, 263). Since the emission and absorption coefficients could now be treated by this Hamiltonian and the two points of view led to the same Hamiltonians, the missing direct scattering term in the wave point of view set aside for the moment, Dirac still concluded that “there is thus a complete harmony between the wave and light-quantum descriptions of the interaction” (Dirac 1927c, 245).

Hence, in his first paper on quantum electrodynamics, Dirac had already established the notions of creation and annihilation operators acting on the occupation number of the wave functions. Furthermore, he had constructed an interaction Hamiltonian that consisted of a product of such operators. It was responsible for the “direct scattering of light.” Before turning to its counterpart, the scattering through intermediate states, I will revisit a technical aspect of the perturbative evaluation of Dirac’s radiation theory as it provides important insights into Dirac’s reasoning process.

1.1.3 “Dirac’s Mogelei” or how to arrive at sensible results in radiation theory

Today, Dirac’s method²⁹ is known as Fermi’s Golden Rule No. 2.³⁰ During the late 1920s and 1930s, it did not necessarily have a name. Once, it was discussed in private communications between Werner Heisenberg and Wolfgang Pauli as “Dirac’s Mogelei.”³¹ To find some balance between the “Golden Rule” and the “Mogelei,” I will call it Dirac’s trick. This procedure allowed Dirac and the physicists in his follow-up to construct probabilities in radiation theory that were proportional to the square of matrix elements and linear in time, as was expected by the actors.

Dirac’s trick is actually one of many intricacies of the perturbative evaluation of radiation theory,³² but studying it and its derivation will provide important insight into Dirac’s way of reasoning in connection with dispersion theory.³³ Let us follow Dirac and discuss Eq. (3) in most general terms. We can simply integrate the equation with respect to t and assume that we know that the system was initially in a specific state $b_n(0)$. This results in

$$\begin{aligned} b_m(t)=v_{mn}b_{n}(0)\frac{1-e^{i(W_m-W_n)t/\hbar }}{W_m-W_n}+\delta _{mn}. \end{aligned}$$

(7)

As Dirac noted, as long as the proper energies of the states m and n “differ appreciably,” the amplitude of the state m varies periodically with time and is small, i.e. “these stationary states are not excited to any appreciable extent” (Dirac 1927c, 258).

While it might seem strange at first that states with energies different from the initial state could be excited, the real problem occurred when Dirac tried to simply look at the transition amplitudes to a state whose energy is exactly equal to the energy of the initial state. Then the coefficient $b_m$ becomes proportional to t.³⁴ But since only the absolute square of this coefficient refers to the probability of finding the system in the respective state, this would render a quadratic time dependence. And this ran counter to any expectation. Dirac’s trick is a solution to exactly this problem.

As Dirac noted, the probability of finding the system in a state with exactly the same energy “is of no importance, being infinitesimal” (Dirac 1927c, 258). Rather, he proposed to multiply the absolute square of this coefficient with the density of states $(\Delta W_m)^{-1}$ around the energy value of the final state and to integrate over this energy range. Expressed in formulas this meant that

$$\begin{aligned} P_m(t)=\int \frac{dW_m}{\Delta W_m}\Vert b_m(t)\Vert ^2=2\int \frac{dW_m}{\Delta W_m}\Vert v_{mn}\Vert ^2\frac{1-cos[(W_m-W_n)t/\hbar ]}{(W_m-W_n)^2}. \end{aligned}$$

(8)

Dirac now substituted $x=\frac{(W_m-W_n)t}{\hbar }$ and pushed t to infinity.³⁵ The point is, that by pushing t to infinity (which is the formalization of considering “large” t), the energy peaks around the value of the initial state (see Fig. 3 for Dirac’s representations in his calculational notes)³⁶ and the integral can be evaluated to give $\pi$. This effectively renders

$$\begin{aligned} \lim _{\text {large}~t}P_m(t)\propto \frac{t\Vert v_{mn}\Vert ^2}{\Delta W_m}, \end{aligned}$$

(9)

where $W_m=W_n$, the proper energy of the initial state. Hence, a transition probability between states of the same energy, proportional to t and the square of the respective matrix element is obtained.

Fig. 3

Application and graphical representation of Dirac’s trick in the Archival Material. Taken from Dirac. General Calculations, p. 13 (see Footnote 36), courtesy of the Florida State University Libraries, Special Collections and Archives

In summary, there are essentially three things to note for Dirac’s later conceptualization of the scattering of light when it comes to this procedure. First of all, Dirac first imposed energy conservation directly and found that then the amplitude of the states would grow proportional to t. As we shall see in a moment, although Dirac correctly identified this as unexpected and reconfigured his calculation, he would use exactly this kind of reasoning in his dispersion paper to find the relevant matrix elements. Second, one can simply square Eq. (7), as Dirac did as well, to arrive at something which should be interpreted as a probability of finding the system in a state with different proper energy than the initial state. Hence, even the probability of finding the system in a state with different proper energy was, albeit fluctuating around a small value, non-zero. Only for longer times, this would reduce to energy conserving transitions.³⁷

Third, these states of different proper energy had to be incorporated into the procedure developed by Dirac to arrive at energy conservation in total and to arrive at a linear dependence on t. To some extent, Dirac had to use the energy non-conserving transitions already in first-order approximations to arrive at physically sensible results.

1.2 Dirac’s quantum theory of dispersion (Dirac 1927b)

After these preliminaries, it is time to delve into Dirac’s theory of dispersion. Dirac resolved some of the shortcomings of his prior wave theoretic treatment by starting with the relativistic classical Hamiltonian for the interaction of a charged particle with the electromagnetic field.³⁸ Expanding it and applying his previous quantization procedure, i.e. treating the number operators and their conjugated phases as non-commuting q-numbers, he derived a three part Hamiltonian:

$$\begin{aligned} H=H_0+V+D. \end{aligned}$$

(10)

$H_0$ described the proper energies of the material part of the system and the radiation field (in terms of $h\nu _r$). V and D were treated as perturbations. V was proportional to a sum over creation and annihilation operators which Dirac had already identified as connected, but not equivalent to emission and absorption processes. The last term, called D here, consisted of a product of such operators and, after some further reductions, boiled down to the direct or true scattering term Dirac had already partially discussed from his “bosonic point of view.”

To derive a dispersion formula, Dirac first applied the iterative procedure he had already used when introducing his perturbation theory: The general solution of the first order equation was plugged back into Eq. (3). To second order, this yielded (Dirac 1927b, 721):

$$\begin{aligned} i\hbar {\dot{b}}_m=d_{mk}e^{i(W_m-W_k)t/\hbar }+\sum _n\frac{v_{mn}v_{nk}}{W_n-W_k}(1-e^{i(W_n-W_k)t/\hbar })e^{i(W_m-W_n)t/\hbar }.\qquad \end{aligned}$$

(11)

Next, Dirac expanded the last term and reordered the whole equation with respect to the time-dependence.

After integration, the probability amplitude of the final state m was given by

$$\begin{aligned} b_m= & {} \left( d_{mk}-\sum _n\frac{v_{mn}v_{nk}}{W_n-W_k}\right) \frac{1-e^{i(W_m-W_k)t/\hbar }}{W_m-W_k}+ \nonumber \\&+\sum _n\frac{v_{mn}v_{nk}}{W_n-W_k}\frac{1-e^{i(W_m-W_n)t/\hbar }}{W_m-W_n}. \end{aligned}$$

(12)

Applying the exact same reasoning as he had done when developing and applying his trick in the previous paper, Dirac analysed the behaviour of this equation by simply imposing energy conservation for initial and final state at first. While the second term remained periodic, the time dependence of the first term became linear. Dirac now interpreted:

“The rate of increase [of the first term] consists of a part, proportional to $d_{mk}$, that is due to direct transitions from state k, together with a sum of parts, each of which is proportional to $v_{mn}v_{nk}$, and is due to transitions first from k to n and then from n to m, although the amplitude $b_n$ of the eigenfunction of the intermediate state always remains small.” (Dirac 1927b, 721)

Having thus identified the relevant terms for the description of dispersion,³⁹ he could simply apply his trick and derive the probability for transitions to the set of final states. Expressed in formulas this led to:⁴⁰

$$\begin{aligned} \sum \Vert b_m\Vert ^2=\frac{4\pi ^2 t}{h\Delta W_m}\left\| d_{mk}-\sum _n\frac{v_{mn}v_{nk}}{W_n-W_k}\right\| ^2. \end{aligned}$$

(13)

So far, this was actually a rather general argument about perturbation theory: the only functional attribute of the perturbing terms was that d could couple initial and final state directly, while v had to do so through the intermediate state. To connect this argument with physical processes, i.e. the scattering of light, and eventually to get into contact with the previously known and accepted KH formula, Dirac had to consider two different sequences of events. I quote in full:

“We can now take the state n [intermediate state] to be either the state $J=J'',~N_s=N_s'-1,~N_t=0~(t\ne s)$ for any $J''$⁴¹, which would make the process $k\rightarrow n$ an absorption of an s-quantum and $n\rightarrow m$ an emission of an r-quantum, or the state $J=J'',~N_s=N_s',~N_r=1,~N_t=0~(t\ne r,s)$, which would make $k\rightarrow n$ the emission and $n\rightarrow m$ the absorption.” (Dirac 1927b, 722)

With this set of intermediate states and subprocesses, verbally expressed in terms of PST, Dirac was able to rederive the KH formula in his new conceptual framework. By plugging in the specific form of the interaction matrix elements and after some smaller manipulations, the intensity of the scattered radiation was proportional to

$$\begin{aligned} I_r\propto \left\| \sum _{J''}\left( \frac{x_r(J'''J'')x_s(J''J')}{\nu (J''J')-\nu _s}+\frac{x_s(J'''J'')x(J''J')}{\nu (J''J')+\nu _s}\right) \right\| ^2. \end{aligned}$$

(14)

Here, the $J''$ refer to the variables of the atom in the intermediate state, $\nu (J''J')$ to the frequency corresponding to the energy difference between initial and intermediate state and $\nu _s$ to the frequency of the incident radiation. The two part structure, the addition of the two fractions in the brackets, was a direct consequence of Dirac’s invocation of PST as quoted above. The first fraction resulted from the imagined process of first an absorption and then an emission, the second fraction resulted from the inverse order of events.

Obviously, the quote I used to open this first section (see p. 6) and which Dirac provided in the introduction of his dispersion paper was written after he had finished his calculations. This is what all of the reasoning he had applied boiled down to. As should have become clear, Dirac’s description shifted completely to the quantum amplitude level. He noted that the amplitudes would vary periodically with the time if the initial and final states did not have the same energy. The amplitudes were then “changed only by a small extent” (Dirac 1927b, 712). If initial and final state had the same energy, Dirac stated that the amplitude would increase linearly with the time and thus the transitions became “physically recognizable” (Dirac 1927b, 712). The amount of excitation was then, in Dirac’s verbal description, proportional to the matrix element and not its square. While Dirac still applied his trick to impose energy conservation and to get reasonable results in agreement with priorly established formulas, his verbal description was no longer based on the level of probabilities, but on the level of probability amplitudes.

What Dirac did here was non-trivial and, as we shall later see, physicists clearly recognized that speaking about transitions when no actual transitions are concerned was not in harmony with the general interpretation of quantum theory at the time. Dirac had made transitions, emission and absorption processes take place on the quantum amplitude level. To some extent, he redefined what these terms actually refer to and thereby explicitly introduced what will later be called “virtual transitions” and “virtual states.” And now it is time to provide an answer to the question guiding this first section: Why did Dirac invoke such a temporally ordered sequence of events when describing his theoretical procedure? And why was it specifically Dirac who did so?

1.3 So, why was it Dirac who introduced PST?

A huge part of the material underlying my answer to the above question has already been presented. As should have become clear through the foregoing discussion, the technical and conceptual environment Dirac had developed was highly suggestive. But as will be exemplified in Sect. 2, Dirac’s conception was not unanimously accepted and applied. And this certainly raises the question why it was specifically Dirac who introduced PST. To present an answer I will first look more closely at Dirac’s introduction of the dispersion paper and the archival material connected to PST. Second, I will contextualize Dirac’s verbalization in respect to his philosophical stance towards quantum theory and the concepts involved in it. Concluding this section, I will draw together all of these aspects and try to provide a multifactorial answer to the question posed.

1.3.1 The careful introduction of PST

At first we have to note that the direct identification of matrix elements with transitions only occurred in Dirac’s paper on dispersion. In his first paper on radiation theory, mainly dealing with emission and absorption, Dirac spoke of “those matrix elements that refer to transitions” (Dirac 1927c, 252, emphasis added) or “the matrix elements associated with that transition” (Dirac 1927c, 259 emphasis added). As he noted, “the probability of a transition [...] is proportional to the square of the modulus of that matrix element of the Hamiltonian which refers to this transition” (Dirac 1927c, 261). The connection between the matrix elements and transitions was a cornerstone of the interpretation of quantum theory from its beginning. But an identification suggesting a physical process standing behind these structures was not.

When introducing PST in his paper on dispersion, Dirac was also rather careful. Shortly before engaging with the description of the processes on a quantum amplitude level, he observed:

If $V_{mn}$ are the matrix elements of the perturbing energy V [...] then each $V_{mn}$ gives rise to transitions from state n to state m; more accurately, it causes the eigenfunction representing state m to grow if that representing state n is already excited [...].” (Dirac 1927b, 711; emphasis added)

Dirac actually acknowledged himself that he was speaking somewhat loosely when invoking the transition terminology.

Fig. 4

Notes for a draft of Dirac (1927b), probably March 1927. Taken from Dirac. Early Work, p. 13 (see Footnote 42), courtesy of the Florida State University Libraries, Special Collections and Archives

Yet, the verbal description and the differentiation between direct scattering and scattering through intermediate states were cornerstones of his exposition. In early notes on the dispersion paper, Dirac wrote (see Fig. 4): “state how coeft. [coefficient] $v_{rs}$ in perturbation terms gives [emphasized and added] direct transitions $r\rightarrow s$ when there is no change of energy. Describe dispersion effect   Scattering terms.”⁴² When drafting the relevant passage, Dirac would wrestle with the exact formulation for framing the “dispersion effect” (see Fig. 5). He noted that “$a_n$ [the amplitude of the intermediate state] gets excited [scribbled out: at the expense of $a_m$; by transitions from $m'$] on account of the existence of $a_{m'}$ by an amount proportional to $v_{nm'}$ [...].”⁴³ Dirac certainly chose his words with care at this stage and the version he settled for in the draft (“on account of the existence”) was rather uncontroversial. Since the amplitude of the initial state was set equal to one from the beginning, this is a straightforward extrapolation. In the published paper, contrary to this draft, Dirac would nevertheless choose the transition terminology.

Fig. 5

Draft of Dirac (1927b), probably late March 1927. Dirac, Early Work, p. 11 (see Footnote 42), courtesy of the Florida State University Libraries, Special Collections and Archives

When it comes to the specifics of his route towards PST, the archival material only holds minor indications. Dirac’s notes are scattered over different folders, temporally unordered while obviously stretching over several years. He only took sparse annotations to the calculations and some are on the back of prior drafts. Worst of all, there are bigger gaps in the material which make a coherent reconstruction next to impossible.

Some of the calculations and drafts are nearly equivalent to the published version.⁴⁴ Others simply back up what was clearly the case: For example, Dirac explicitly used the wave function in occupation number representation in his drafts while such a representation, although obviously guiding his work, is nearly completely lacking in the dispersion paper.⁴⁵ Yet, there are a few pages that actually point towards conceptual issues and exemplify the strong grasp the ideas Dirac had developed already had on his thinking. One of them is reproduced in Fig. 6.

Fig. 6

Second-order perturbative calculation. Taken from Dirac, Early Work, p. 92 (Footnote 42), courtesy of the Florida State University Libraries, Special Collections and Archives

Although the notation is a little bit different,⁴⁶ up until the third line of the sheet the calculation is equivalent to the presentation in the publication. The break with his published paper occurs at the second equal sign in line three and is then carried through the whole calculation: Dirac did not split his formulas according to the time-dependence of the corresponding matrix elements, but rather in terms of direct scattering and processes through intermediate states.

There are two ways of temporally locating this calculation in Dirac’s derivation process. On the one hand, we might interpret this calculation as an attempt at treating resonance scattering. Dirac kept all terms of Eq. (12), including the ones he dropped in his calculation of dispersion. In the lower part of the draft, Dirac further applied his trick to the energy range of the intermediate states. Since this procedure was essentially a way of ensuring energy conservation, this points to an interpretation of the sheet as an attempt of treating resonant scattering.

On the other hand, had Dirac already derived the KH formula, so had he finished his dispersion theoretic treatment, which he nearly certainly did before developing an account of resonant scattering, he would have noted that he needed to group the terms differently, namely corresponding to their time dependence. As already noted, this is how he would present his calculations in the published paper.

Although I am not able to temporally locate this calculation exactly, it nevertheless provides an important insight: The ordering of the terms according to the temporal development was not guiding Dirac’s evaluation at this point, although he had already developed a firm grasp on the application of his trick. It was the distinction between direct scattering processes and scattering through intermediate states that led Dirac’s derivation of the probabilities of observable results in his radiation theory. When Dirac performed the above calculation, the conception based on a quantum amplitude level structured his evaluations.

The still existent notes by Dirac himself, taken in the period from early February to early April 1927, thus point towards the important role the verbal exposition of dispersion had for Dirac and to the influence of the conceptualization on early calculations of the effects. In particular, they highlight the role of the differentiation between direct scattering and scattering through intermediate states. Still, they do not provide any clues as to why Dirac chose to connect the calculations with PST. For this reason, as well as to finally have all the arguments needed for a coherent interpretation in place, we need to engage with Dirac’s philosophical stance towards theoretical physics and its concepts.

1.3.2 Dirac’s philosophical stance towards quantum theory

The best-known aspects of Dirac’s approach to theoretical physics are certainly his striving for mathematical beauty⁴⁷ and the method of “playing with equations.”⁴⁸ Both of these aspects were certainly part of Dirac’s development of radiation theory. Dirac remembered that, in coming up with the quantization procedure, he was simply playing with equations. The archival material suggests that he often simply tried things out to see where they lead when evaluating his radiation theory as well. One aspect of mathematical beauty, the formulation of the problem in most general but equivalently simple terms and then shifting focus to the actual application, is also mirrored in Dirac’s approach to perturbation theory. Yet, neither of these points help in answering the question guiding this section.

However, Dirac’s methodology included a standpoint that is connected to the above two guidelines and which might actually be used for an explanation: Dirac himself has called it “Eddington’s principle of identification.”⁴⁹ In most general terms, it states that the mathematics of the theory should be developed and evaluated before any physical interpretation and then, in a second step, the quantities referring to physical properties should be identified. Most explicitly, Dirac used this kind of reasoning in his argument for magnetic monopoles (Dirac 1931). But, as Olivier Darrigol (1993, 331–333) argued, it also guided Dirac’s application and interpretation of Schrödinger’s wave function in his 1926 paper. To understand how such a standpoint might be applied to explain Dirac’s invocation of PST, we need to briefly discuss the results of Dirac’s evaluation of resonant scattering.⁵⁰

In the last section of the paper on dispersion, Dirac demonstrated that in the case of resonance between the incoming frequency and the frequencies of the material system, the most relevant part of the scattered light was due to actual emission and absorption processes, connected to the squares of the respective probability amplitudes. Actual counterparts to Dirac’s virtual transitions existed that described the scattering of light when the energy of the impinging radiation was fitting. As is necessary for the principle of identification to apply, in the case of dispersion there was further no theoretical hindrance in conceiving of such counterintuitive events as energy non-conserving transitions. From this point of view, an “anything that can happen, will happen” attitude seems to fit Dirac’s reasoning process.

And even though the identification with actual processes in the case of resonance might have enhanced the suggestiveness of Dirac’s framework, there is one obstacle for invoking this kind of argument as an explanation of PST. Since the principle of identification aims at associating mathematical structures with physical objects or processes, a close look at the structures Dirac identified with transitions in dispersion theory is important. And this is where a problem occurs: The mathematical elements describing dispersion on the one hand and the ones describing resonant scattering on the other were not equivalent. The starting point of Dirac’s mathematical and verbal description of dispersion was the first part of Eq. (12) while resonant scattering was represented by its second part. Actually, the parts describing dispersion were also part of the final results on resonant scattering in Dirac’s paper, but due to the dominance of the second part of Eq. (12) they could, according to Dirac’s argument, be neglected. The two mathematical elements existed side by side. Although a direct identification of matrix elements with transitions might have become more suggestive, an implementation of the principle of identification seems (at least to me) on shaky grounds.

Rather, I would argue that Dirac’s explicit verbalization is not due to a general philosophical stance but to Dirac’s flexibility when it came to such. Dirac is often portrayed, and described himself, as a philosophically uninclined physicist. In the most prominent discussions about the interpretation of quantum mechanics, as for example the EPR-paradox, Dirac remained silent. The focus on philosophical issues, as it was most distinctly represented by Niels Bohr, and the obsessive care to keep the conceptual framework as clean as possible were to some extent foreign to Dirac’s style of work.

Dirac’s research practice shows a rather instrumentalistic outlook on quantum theory and the concepts involved in it. In most general terms, he did not care much about the ontological implications the handling of the theory had.⁵¹ As long as the theory was internally consistent and its predictions cohered with the empirical results, everything was fine for Dirac. As Max Born, contemporary of Dirac and his host in Göttingen in 1927, once pointedly described Dirac’s stance:

“They [physicists like Dirac] say: the existence of a mathematically consistent theory is all we want. It represents everything that can be said about the empirical world; we can predict with its help unobserved phenomena, and that is all we wish. What you mean by an objective world we don’t know and don’t care.”⁵²

Dirac’s disinterest in issues he considered mostly philosophical came with a rather flexible attitude towards the principles guiding the interpretation of quantum mechanics from its start. This can best be exemplified by recourse to a principle that is directly connected to Dirac’s introduction of PST: the observability principle. It stated that only quantities in principle observable could be counted as genuine concepts of quantum theory. It was clearly expressed in Heisenberg’s Umdeutungs paper and was basic pillar of the interpretation of quantum theory in the following years. Dirac himself referred to the principle all throughout his scientific career.⁵³ An analysis of his actual research practice nevertheless shows that this was not much more than lip service.

As Helge Kragh observed, “he [Dirac] did not hesitate to propose quantities that seemed to have only the slightest connection to observables” (Kragh 1990, 264). Kragh’s prime example was the hypothetical negative energy world proposed by Dirac in 1942 to cure some of the problems QED was facing at the time.⁵⁴ Andrea Oldofredi and Michael Esfeld (Oldofredi and Esfeld 2019) also argued that Dirac’s work was not guided by the observability doctrine. One of their examples is the sea of negative energy electrons introduced by Dirac in 1930. As their argument goes, these entities were from a theoretical point of view unobservable by construction.

Some smaller annotations in Dirac’s writings actually indicate that he considered a careful introduction of unobservable concepts tenable in theoretical physics. In his first lecture notes on quantum theory, we find a passage by Dirac which was an obvious attack on Schrödinger’s conception of the wave function actually representing an electrical density. In this passage, Dirac explicitly stated that “one may introduce auxiliary quantities not directly observable for the purpose of calculation; but variables not observable should not be introduced merely because they are required for the description of the phenomena according to ordinary classical notions.”⁵⁵ In a strange twist of reasoning, he made a similar statement in his paper on the many-time formalism (Dirac 1932). Therein, he upheld the observability doctrine as one of the basic pillars of the interpretation of quantum theory, yet, as he commented, “strictly speaking, it is not the observable quantities themselves (the Einstein A’s and B’s) that form the building stones of Heisenberg’s algebraic scheme, but rather certain more elementary quantities, the matrix elements, having the observable quantities as the squares of their moduli” (Dirac 1932, 456; emphasis added).

All in all, Dirac was a physicist who was neither hindered in his methodology by some strict application of the observability principle, nor was he concerned with the ontological implications of his theoretical framework. The point is, that others were and I consider this one of the reasons why physicists would shy away from talking about transitions when no “actual transitions” occurred.

1.4 An interim conclusion

Now it is time to put everything together and present my whole argument as to why it was Dirac who introduced PST, i.e. a verbal representation of the scattering of light in terms of temporally ordered and energy non-conserving subprocesses taking place on a quantum amplitude level at least suggesting some kind of causal connection between these processes.

First of all, Dirac developed an extremely suggestive technical and conceptual framework. The amplitudes and probabilities of energy non-conserving transitions were, albeit small, non-zero and fluctuating. Energy was conserved for the whole process by application of Dirac’s trick, but only by pushing time to infinity. The role of the interaction, serving to introduce alteration in the system’s behaviour and not as altering the energy levels of the system, allowed for a possible explanation of energy non-conservation.⁵⁶ Shifting the focus on the quantum amplitudes was suggested by the creation and annihilation operators working on this level of theory and by the differentiation between direct scattering and scattering through intermediate states.

Secondly, Dirac did not only interpret the equations in terms of processes and leave it at that. He actually used PST. To reproduce the structure of the KH formula, Dirac had to invoke two different sequences of events: Either first an absorption occurred and then an emission or the other way around. Since energy conservation was not imposed on the virtual transitions, there was no theoretical hindrance in conceiving of the second, quite counter-intuitive sequence of events. The storyline Dirac came up with was used, and through it the relevant matrix elements and their specific combinations could be constructed. From the first time it was explicitly expressed, the picture of subsequent transitions, emission and absorption subprocesses as well as the concepts figuring in it served as tools for the construction of mathematical representations, which were, in a second step, evaluated further. The verbalization was used to bridge the gap between an abstract mathematical representation of perturbation theory and the physical process to be calculated.

Thirdly, this intricate interplay between mathematical techniques, previously established conceptualizations and, finally, the direct application from which, according to my argument, PST emerged, would not have led any physicist to provide such an exposition. Even after the introduction of PST, some physicists would show reluctant in accepting this kind of framing. But Dirac was philosophically flexible enough (and I consider this, from a pragmatic point of view and in the given circumstances, a good thing) not to worry too much about strict philosophical guidelines of interpretation. After all, the reference to a sequential occurrence of transitions on a quantum amplitude level, when no actual transitions occurred, was retrospectively a huge step, specifically in that it provided a language suitable for the theoretical treatment of quantum electrodynamical processes and was consequently used in the majority of the evaluations of QED in the 1930s.

2 The impact of PST: representational alterations and (meta-)physical implications

Dirac’s invocation of PST did not directly cause any open philosophical dispute. But, when discussing specific problems, physicists took stances, either implicitly or explicitly, towards the verbal model Dirac had proposed. All the reflections I am about to discuss were given in the derivation and interpretation of the light–matter interaction and the second order processes that it entails, both relativistically and non-relativistically.

Since all of the formulas and their derivation in radiation theory included intermediate states, I will not order the following section in respect to the physical effects. Rather, two different consequences of the establishment and use of PST will structure the following. The first subsection will engage with the reflection of Dirac’s verbal model in the medium of diagrams. The second subsection is devoted to the different stances towards the reality of the storyline of PST and centres around one of its most important direct consequences: It motivated Dirac to develop the idea of the Dirac sea.

2.1 Alterations in diagrammatical representations: the inclusion of an ordered sequence of events

Both examples of diagrammatical representations I am about to discuss have a common feature: the explicit inclusion of an ordered sequence of events in the representational format. Yet, both of them differ appreciably in the way this was achieved and to the effects they described. The background of the first example was the experimental observation of the so-called Raman effect. This particular instance of the scattering of light from an atom or molecule had been predicted by Adolf Smekal (1923) and was put on firmer theoretical ground by Kramers and Heisenberg in their dispersion paper. In most general terms, the Raman effect consists of the occurrence of components in the secondary radiation which exhibit a discrete frequency shift from the primary radiation. This frequency shift is proportional to the energy difference between two stationary states of the scattering atom or molecule ($\Delta \nu =\frac{1}{h}(E_n-E_m)$). It was observed by C.V. Raman⁵⁷ and independently by Landsberg and Mandelstam (1928) in early 1928.

Although the Raman effect was soon celebrated as clear evidence for quantum theoretic predictions, its further empirical evaluation led to some dispute about its conceptualization, mainly amongst experimentalists.⁵⁸ An integral part of this discussion was the mounting evidence that the frequency shift did not necessarily correspond to absorption frequencies in the infra-red. Rather, the alteration in frequency was proportional to the difference between two absorption frequencies of the scattering medium: The selection rules, hence, were not equivalent to the ones for regular absorption of energy by the scattering medium.

One of the most decisive experimental proofs of this effect was provided by Franco Rasetti (1929), who was working at CalTech in Pasadena at the time. At Rasetti’s home institute in Rome, Eduardo Amaldi and Emilio Segrè (Amaldi and Segrè 1929) noted the (partial) confusion in the empirical literature and explained the occurrence of the unexpected frequency shifts, i.e. the apparent independence of Raman lines from infrared absorption lines, including a lengthy exposition of PST. In a subsequent paper, Eduardo Amaldi (1929) investigated the problem further and cast his reasoning into a diagrammatical representation depicted in Fig. 7.

Fig. 7

Graphical representations of Dirac’s verbal description in a paper explaining the Raman effect. Taken from Amaldi (1929, 878–879)

At the time, energy-level diagrams were still the most common way of representing atomic phenomena in quantum theory. Other diagrams, such as the ones by Kramers and Heisenberg (see Figure 2) or Ralph Kronig’s term scheme diagrams, as discussed by Martin Jähnert (2019, Section 7.2), were rather static in nature. But Amaldi chose to depict the process in a different fashion. The diagrams in Fig. 7 are read from left to right in the order initial, intermediate and final state. The a’s refer to the probability amplitudes of the respective states of the whole system, atom/molecule and radiation field. The indexes refer to the state of the atom (first index) and to the occupation of the components of the radiation field (all following indices). As Amaldi discussed both the Stokes and the anti-Stokes case of the Raman effect, two initial and final states occur in each diagram. The upper diagram represents first an absorption, note the index $n_{a}-1$ on the amplitude of the intermediate state, and a subsequent emission of a different quantum, represented by the index $1_b$ on the amplitude of the final state. The lower diagram refers to the process in which first an emission and then an absorption occurs.

While Amaldi’s representation digressed from the more traditional version of diagrammatical formats by representing an ordered sequence of events, also in energy-level diagrams an order was indicated in the follow-up of PST. In Göttingen, where Dirac had finished his dispersion paper, Maria Göppert-Mayer, at the time a doctoral student of Max Born, explained the physical effects predicted by the KH formula through the invocation of energy-level diagrams.⁵⁹ Kramers and Heisenberg already noted that their formula described, besides dispersion and the later to be called Raman effect, a third mechanism which is today called double emission. There is a certain probability that an atom will irradiate two different radiation components, as long as the sum of the frequencies corresponds to the energy difference between initial and final state of the process. In the course of writing an introduction to radiation theory for the textbook by Pascual Jordan and Max Born (Born and Jordan 1930, Chapter 7), Göppert-Mayer found that the inverse process, the simultaneous absorption of two photons, was also described by the KH formula. Its detailed evaluation became part of her dissertational research.

Fig. 8

Graphical representation of Dirac’s verbal description in an energy-level diagram. Taken from Göppert-Mayer (1931, 284)

In her published dissertation as well as in initial communication of the results, Göppert-Mayer used the structural analogy of Raman scattering, double emission and double absorption to explain the “synergy of two light quanta in one elementary act.”⁶⁰ The corresponding term scheme diagrams are reproduced in Fig. 8. They represent from left to right: the Stokes and anti-Stokes case of the Raman effect, double emission and double absorption. n and m are the initial/final states of the atom (depending on which process you are looking at). k is an arbitrary other state of the material system, the intermediate state. The solid lines represent photons: pointing upwards means absorption and pointing downwards emission. The dashed lines represent “the behaviour of the atom” (Göppert 1929, 932). The arrow at the end of the dashed lines indicates the sequence of events. The photon lines are not ordered. Any sequence of emission and absorption processes must be included in the theoretical description. Göppert-Mayer’s diagrams abstract from this permutation of the emission and absorption subprocesses and thereby allow her to depict the Raman-effect, double emission and double absorption each within a single diagram.

The impact of Amaldi’s and Göppert-Mayer’s diagrammatical representations on the further development of quantum theory was certainly limited. As a matter of fact, up until 1937 representations resembling Amaldi’s diagrams in structure were not used by physicists, at least I did not find any prior to a paper on nuclear physics by Gregor Wentzel (1937).⁶¹ Furthermore, I could not find any direct connection between Amaldi’s representation and Wentzel’s. But I did not choose to discuss these diagrams for their impact on the further development of diagrammatical techniques. Rather, I chose these two examples to exemplify the impact of the verbal representation on other representational formats. Contrary to previously established diagrammatical representations, they both included an ordered sequence of events. Dirac’s invocation of PST and its use by other physicists led to an alteration in another representational format.

In both cases the diagrams served a didactic purpose: Amaldi chose the specific diagrammatical representation to make the theoretical description of Raman scattering more accessible to his readers; Göppert-Mayer used the diagrams to visualize the analogical structure of the Raman effect and the other double processes. Even though the diagrams were not used for calculations, they served as tools for the respective actors.

All the same, Göppert-Mayer acknowledged that what she represented in the diagrams was not what was actually happening to the atom, but rather a language suitable to describe, compare and evaluate the theoretical modelling. The processes she subsumed under the headline of the “synergy of two light quanta in one elementary act” behave “as if two processes, neither of which satisfies the energy law, occur in one act.”⁶² The explanatory function of the physical language and the corresponding diagrammatical representation was in Göppert-Mayer’s own assessment not warranted by its direct description of real-world processes. And thereby we are directly led to the topic of the second subsection: the stances physicists took towards the reality/physicality of PST.

2.2 “A certain degree of reality”⁶³: PST between formal and physical

Maria Göppert-Mayer was not the only one who commented on the reality of PST. When John van Vleck (1929) investigated specific cases of selection rules for the Raman effect, he noted that the KH formula “involves the amplitudes connected with transitions to what we shall term the ‘intermediate’ states [...]” (van Vleck 1929, 754). He noted that “it is to be clearly understood that the term ‘intermediate’ relates merely to the position of a state such as b in the products in [the formula] [...]” (van Vleck 1929, 754).⁶⁴ To Van Vleck, the intermediate character was a mathematical one. Similarly, C. V. Raman noted that “the introduction of the third level C [the intermediate state] is merely a mathematical device.” Since energy is normally not conserved in a transition to an intermediate state, it “is a purely virtual one which cannot actually occur” (Raman 1929, 790). According to Yakov Illich Frenkel (1929, 758), who proposed to conceive of scattering as a two part process of actual transitions, “the usual assumption [...] does not regard the state n [intermediate state] as ‘really’ occurring [...].”

The above quotes are certainly indicative of a general trend of conceiving of virtual transitions as not corresponding to physical phenomena. Yet, the most decisive impact of PST was connected to the relativistic description of the electron, the Dirac equation, and its interpretation.⁶⁵ Both in the inception and the interpretation of what came to be known as the Dirac sea, the theoretical description of scattering played an important role.⁶⁶ And its invocation led some actors to see more in PST than a verbal model of mathematical structures.

2.2.1 Virtual negative energy states: beyond the purely formal

In 1928, Dirac (1928) came up with a relativistic wave equation which cured some of the problems of prior relativistic descriptions (foremost the negative probabilities), proved experimentally suitable and naturally included the spin of the electron. For the following discussion, two aspects of the Dirac equation are important. On the one hand, a problem of prior relativistic wave equations remained.⁶⁷ The Dirac equation still entailed negative energy solutions. Theoretically, there was no hindrance for positive energy electrons to fall into negative energy states which posed a severe problem: Not only were negative energy states never observed, but electrons in such states would behave in all kinds of physically unexpected ways. On the other hand, Dirac’s starting point was a wave equation which included the operators linearly. Hence, the quadratic terms of the vector potential, which were responsible for the “direct” or “true” scattering, were no longer included in the theoretical description.

Werner Heisenberg was the first one to note that the direct scattering terms no longer occurred and that they were replaced by another mechanism. In a letter to Wolfgang Pauli in late July 1928, he communicated his finding that the combination of matrix elements corresponding to transitions to and from negative energy states would lead, in the respective approximation, to the Thomson scattering formula. Hence, the scattering of light from a free electron was now theoretically connected to such “crazy transitions.”⁶⁸ Even though Heisenberg presented his conclusions at a lecture in Copenhagen, and it was therefore known in parts of the community, it did not lead to any further investigations right away. For example, Oskar Klein and Yoshio Nishina still rejected negative energy states as “physically not meaningful”⁶⁹ in their semi-classical derivation of the relativistic scattering of light resulting in what is known as the Klein–Nishina formula.⁷⁰ Only when the scattering of light from an atom and a free electron, both described relativistically, was reevaluated within the framework of Dirac’s radiation theory, the occurrence of negative energy states as intermediate states spurred further conceptual development. This reevaluation was carried out and communicated to Dirac by the Swedish physicist and expert in the theoretical description of light scattering, Ivar Waller.⁷¹

Through the study of the correspondence between Waller and Dirac, Karl Grandin (2008, 202–208) showed that it was the necessity of including negative energy states as virtual or intermediate states in radiation theory that would lead Dirac to take these negative energy solutions more seriously. In late 1929, Dirac was obviously still unaware of Werner Heisenberg’s finding. When Ivar Waller first communicated the necessity of including negative energy intermediate states to Dirac, a conclusion Waller had independently arrived at, Dirac still believed that there had to be some kind of mistake in Waller’s calculation.⁷² Only after redoing the calculation himself, Dirac came to the conclusion that negative energy states were necessary in the theoretical description.⁷³ Directly afterwards and apparently within a few days, Dirac came up with the idea of what is today known as the Dirac sea, i.e. filling all the negative energy states with an infinity of electrons. Only deviations from this uniform distribution should be considered to be observable. Through Pauli’s exclusion principle, positive energy electrons could no longer fall into the abyss of negative energy.⁷⁴

Waller’s communication of the calculational results to Dirac motivated the latter to take another look at negative energy solutions, and thereby create the first quantum theoretical conception of anti-particles, namely as holes in this sea.⁷⁵ In one letter Waller also indicated the importance of the description in terms of subsequent transitions in connection with radiation theory. He explicitly compared the role of the intermediate states in Dirac’s description and in semi-classical calculations, which Ivar Waller called the “density method”:

“By using the density method these [intermediate states] enter more formally in the calculation, so the difficulty [i.e. the occurrence of negative energy states as intermediate states] is perhaps not so serious there.”⁷⁶

From a draft of the letter, we know what Waller meant by “more formally”: “the corresponding eigenfunctions only play the mathematical role of certain terms in an expansion in eigenfunctions.”⁷⁷

As Dirac did not initially believe in the correctness of Waller’s calculation, Waller, to mitigate the problem, would retract the above statement in a second letter and note that also in radiation theory the intermediate states “play a rather formal role, as long as resonance effects do not occur.”⁷⁸ Yet, Ivar Waller as one of the leading experts on the calculation of scattering in quantum theory initially considered the intermediate states of radiation theory as something that went beyond the purely formal or mathematical. But Waller did not go as far as calling them physical. Dirac and Igor Tamm took this step.

2.2.2 The physicality of intermediate states

Dirac communicated his idea of the Dirac sea both to Ivar Waller and, in a well-known correspondence, to Niels Bohr.⁷⁹ As Bohr was initially reluctant to accept the relevance of negative energy states, Dirac argued that a “scattering process is really a double transition” and that “the intermediate state [...] lasts only a very short time.”⁸⁰ Since intermediate states of negative energy were necessary for a consistent description of scattering, Dirac considered them to be physical: “If one says the states of negative energy have no physical meaning, then one cannot see how the scattering can occur.”⁸¹ Hence, Dirac proposed, in addition to the temporal order of the events of emission and absorption processes, a finite temporal dimension of the intermediate state. Further, from the occurrence of the negative energy states as intermediate states he concluded the physicality of these states. Dirac pushed the virtual states into physical terrain.

Igor Tamm, since a shared stay at Leiden and Leipzig in 1928 well acquainted with Dirac, had independently discovered that negative energy states occurred as intermediate states in the relativistic description of light scattering.⁸² Without knowing about Dirac’s statements to Bohr, Tamm came to a similar conclusion. In a letter to Dirac, he noted that the occurrence of negative energy states as intermediate states “proves the physical relevance of these states [of negative energy].”⁸³ In one of his subsequent papers, Tamm noted that “scattering of a light quantum through matter consists according to the Dirac theory, as is well known, of a sequence of two elementary processes, namely of the absorption of the impinging and the emission of the scattered light quantum.”⁸⁴ I emphasized the term “elementary process” in this quote as it, or the equivalent “elementary act,” was conventionally used, see for example Göppert-Mayer’s statements above, to refer to processes which we today call real processes, i.e. something which can directly be connected to a probability (and not to probability amplitudes).

Dirac’s and Tamm’s comments are not only interesting as they suggest a physical interpretation of PST, or at least show how PST spurred physical conclusions. Actually, the argumentative structure they used was further and is still applied. Both, Tamm and Dirac, inferred the physicality of negative energy states from their occurrence as intermediate or virtual states. In the case of Heisenberg, Waller, Dirac and Tamm the occurrence of negative energy states was a consequence of the calculation. During the late 1930s and early 1940s physicists already took the liberty to propose new kinds of states, not yet observed by experiment, and included them as virtual states to make sense of as yet unexplained empirical observations.⁸⁵ In contemporary physics the same argumentative structure is applied: hypothetical fields are introduced and their physical existence is probed by the effects virtual particles of these fields would have on the experimental results.⁸⁶ Although all of these instances differ in the motivation to introduce new kinds of states or particles,⁸⁷ they share a common feature: In each case the step from virtual to physical is taken.⁸⁸

2.2.3 Non-invocation and refutation: physicists close to Copenhagen

As should have become clear through the above examples, some physicists took the intermediate states and the corresponding description by Dirac very seriously, at least more seriously than in semi-classical methods.⁸⁹ But there is another side to the story. Some physicists clearly used notions and methods along the lines of Dirac but refused to apply or only reluctantly applied a verbal description (at least in publication). Wolfgang Pauli and Werner Heisenberg’s work on quantum electrodynamics is one such an example (Heisenberg and Pauli 1929, 1930). As Cathryn Carson has noted, they “did not give much of a verbal description, however, largely allowing the calculation to stand on its own” (Carson 1996, 112).⁹⁰ Victor Weisskopf applied Dirac’s kind of description until spending half a year in Copenhagen with Niels Bohr and then going on to Zürich to become Pauli’s assistant. In his famous paper on the self-energy of the electron (Weisskopf 1934), there was no verbalization or visualization of any kind. But, when discussing matters with Heisenberg in correspondence, Weisskopf explicitly used the notion of intermediate states to explain the difference between the self-energy of the photon and the electron.⁹¹

In total, it is noticeable that, on the one hand, physicists who are normally portrayed as rather pragmatic (e.g. Dirac, Heitler, Fermi)⁹² applied Dirac’s description explicitly in their papers, while, on the other hand, physicists who were closely associated with the Copenhagen institute and who defined themselves (or were defined by others) as philosophically inclined (e.g. Bohr, Pauli, Heisenberg, Weisskopf, Rosenfeld)⁹³ did not represent intermediate states and the corresponding processes verbally.⁹⁴ The most explicit refutation of the physical interpretation of PST I came across after Dirac had proposed his idea of the Dirac sea, was given by a close acquaintance of Niels Bohr, Léon Rosenfeld. In a lecture held in February 1931 at l’Institut Herni Poincaré, he commented on the description of double transitions as follows:

“First of all, the negative energy states play an important, although purely formal, role in the theory of dispersion. One knows that the dispersion formula [...] includes a summation over all the energy states the diffusing body is capable of. In a pictorial fashion, but which is not justified by the general precepts of the physical interpretation of quantum mechanics, one can say that the phenomenon of diffusion consists of a double transition of the diffusing body [...].”⁹⁵

Stances were obviously split concerning the question whether or not one should use such an explicit description in terms of subsequent transitions, emission and absorption subprocesses, and whether this in some way or another cohered with physical reality.⁹⁶ Nevertheless, PST had an impact on how physicists represented scattering phenomena in other representational formats and, eventually, it made its way into the everyday work of the majority of the physicist community. The most popular introductory texts to QED during the 1930s, published by Fermi (1932) and Heitler (1936), explicitly used this kind of verbal model. Today this kind of description is still, just in a modern form, part of the practice of quantum field theorists. The basic building blocks of Feynman diagrams remain emission, absorption, pair annihilation or creation subprocesses. And thereby, PST remains a part of the tool kit of the quantum field theorist.

3 Reflection and outlook

In the foregoing discussion, I used the idea that concepts and the models they figure in come in different representations and these representations are closely related to the actual theoretical practice of the historical actors. Specifically, I focused on the emergence and the initial reception of what I called PST, i.e. the verbally explicit description of the light–matter interaction in terms of subsequent and temporally ordered virtual (modern terminology) transitions.

I argued that this representation was first provided by Paul Dirac because of three interrelated reasons. First of all, he came up with a mathematical modelling that had a highly suggestive character within the priorly established conceptual framework. Secondly, Dirac was philosophical flexible enough to explicitly express what he saw in the formulas. As indicated, in particular physicists who are generally portrayed as philosophically motivated did not express PST (at least at first). Thirdly, Dirac put PST to work in his dispersion paper. To rederive the KH formula, different orders of subprocesses had to be envisioned and superimposed. From its beginning, PST functioned as a tool for the quantum field theorist.

I showed how the verbally explicit description in terms of subprocesses had direct impact on other representational formats: New diagrammatical representations were developed, while traditional ones were modified to exhibit the ordered sequence of events explicitly. The idea of subprocesses did not only exhibit a “less formal” character in radiation theory, its physical interpretation was also closely related to the development of the Dirac sea. Nevertheless, in the immediate aftermath of Dirac’s introduction of PST, stances stretched from the physical reading by Dirac and Tamm over Waller’s “less formal” to Göppert-Mayer’s “as if”, Leon Rosenfeld’s “not warranted” or a complete lack of mention in Heisenberg and Pauli’s QED papers.

In my eyes, we can draw two immediate conclusions from the illustration of these stances. On the one hand, it shows that the Feynman–Dyson split and the philosophical debate about the ontological and representational status of Feynman diagrams, emerging in the 1950s and stretching into the present, has a rather lengthy prehistory. Starting with its introduction, physicists positioned themselves towards the use and the metaphysical implications of the physical picture that still underlies the diagrammatical technique (all the difference set aside for the moment). On the other hand, the ontological commitments of actors did, for the greater part, not interfere with the application of PST. Whether it was conceived of as a representation of mathematical structures or a representation of physical processes, the actors used the verbal model as a tool, not only for didactic purposes but also for calculational ones.

In this practice, physicists followed Dirac’s initial presentation: While the derivation of the abstract perturbative series was mostly a mathematical, albeit non-trivial business, PST was invoked when constructing the specific matrix elements describing the investigated effects. Each sequence of events that would lead from the respective initial to the respective final state through subsequent virtual transitions was thereby envisioned. Which states would couple through which subprocesses was dictated by the matrix elements of the interaction energy. The exposition of perturbation theory and its application in Heitler’s influential textbook (Heitler 1936) is a point in case, as are higher order calculations performed during the 1930s.⁹⁷ In all of these cases, the “method [...] of intermediate states”⁹⁸ was applied.

Fig. 9

Tabular display of the possible sequences of subprocesses theoretically describing the creation of a pair and a photon from two photons. Taken from Kockel (1937, 167)

During the 1930s, the prime mode of representation of this kind of reasoning was a verbal one. The well-known example of Hans Euler’s term scheme diagrams for light-by-light scattering, as discussed by Adrian Wüthrich (2010, Section 2.1), were accompanied by a tabular display listing all possible sequences of events in verbal terms. Bernhard Kockel, who was deeply involved in Euler’s calculations, did not invoke any diagrams to discuss the third-order effects he was investigating for his dissertation. He presented his reasoning with PST through tables in which each possible sequence of events was portrayed in verbal terms (see Fig. 9). Also in papers dealing with meson physics, the application of PST was often presented verbally to the readers.

Through this observation and the taken focus, my contribution also aims at enriching the collection of representational formats discussed in the historiography of QED. Diagrammatical representations currently occupy a rather prominent place. Although this focus is understandable due to the prominence of Feynman diagrams in post-WWII particle physics, it does not necessarily do justice to the practices of the physicist of the 1930s. A study of PST indicates that the diagrams of the 1930s were often post hoc representations, if the language used was cast into a diagrammatical representation at all.

In conclusion, I want to emphasize that PST as a representational format has a certain degree of independence of other representations: It can neither be reduced to the mathematical representation of the theory nor is it equivalent, although closely related, to the method of Feynman diagrams. On the one hand, PST performed a rather specific function in the theoretical evaluation of the 1930s: It bridged the gap between the abstract perturbative series and the matrix elements describing the effect to be evaluated. Even if this step might have been taken through a purely mathematical representation, the fact remains that actors did not do so. The specific language which Dirac introduced facilitated this task considerably, and as such exhibited its tool character.

On the other hand, although Feynman diagrams perform exactly the same function in perturbative evaluations, they do not allow for the same conclusions. Historical actors constructed processes through the invocation of PST that we can directly discard through the usage of Feynman diagrams.⁹⁹ Feynman’s version of QED does not only differ in the physical picture that is underlying its representation (i.e. a space-time approach vs. a state-transition model) and the physical properties of its concepts,¹⁰⁰ but it differs, through the diagrammatical representation, in the conclusions that can be extracted from the physical interpretation of the perturbative series. As such, the approach taken in this paper highlights a well-known aspect of the shift that occurred in QED in the late 1940s, namely the refinement of the theoretical tool kit through the introduction of different representational formats.