Abstract
This paper addresses an article by Felix Klein of 1886, in which he generalized his theory of polynomial equations of degree 5—comprehensively discussed in his Lectures on the Icosahedron two years earlier—to equations of degree 6 and 7. To do so, Klein used results previously established in line geometry. I review Klein’s 1886 article, its diverse mathematical background, and its place within the broader history of mathematics. I argue that the program advanced by this article, although historically overlooked due to its eventual failure, offers a valuable insight into a time of crucial evolution of the subject.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
For geometry not only illustrates and facilitates, it also has the privilege of invention in these investigations. Felix Klein (1879b, p. 253)
1 Introduction
The early work of Felix Klein is today known for two main achievements: First, his Erlangen Program, whose credo
Given a manifoldness and a group of transformations of the same; to develop the theory of invariants relating to that group. (Klein [1872] 1893, p. 219)Footnote 1
is well known to historians and mathematicians alike. And second, his Lectures on the Icosaehdron (Klein 2019b) in which half a century of mathematical research on the general polynomial equation of degree 5—the general quintic—is summarized under the geometrical banner of the Icosahedron. Two years later, Klein published a today forgotten paper entitled “On the theory of general equations of degree six and seven” (“Zur Theorie der allgemeinen Gleichungen sechsten und siebenten Grades”, 1886) in which he extended his geometrical interpretation of the general quintic to equations of degree 6 and 7:
The theory of the equations of the fifth degree, which I brought into coherent presentation in my “Lectures on the Icosahedron etc.” (Teubner 1884), allows not only, as I have indicated at various points, a transmission to equations of degree four, but also an extension to equations of degree six and seven. It is the purpose of the following lines to define the main features of this extension. Its aim subsumes under the general ideas which I have set out in Klein 1879b for the solution of arbitrary algebraic equations. It differs from them, however, by the concrete form of the geometric-algebraic process to be used, which uses individual moments present only at \(n=6\) and \(n=7\). (Klein 1886, 499–500)
These “general ideas” can be summarized as the principle to find for any class of polynomial equations some canonical geometrical equationsFootnote 2 to which it can be reduced, and subsequently to solve all polynomial equations of that class by the solution of the geometrical one. The interesting cases are those polynomials that cannot be solved directly by algebraic means. In the language of Galois theory, these are the equations whose associated Galois group (over some specified domain of rationality) is unsolvable. For those equations, also the corresponding canonical geometrical equation cannot be solved algebraically, but once a solution is found by other means (borrowing from analysis, differential equations, ...), the solution of the original equation easily follows. This idea extends the theory of algebraic theory beyond the “limits” of Galois theory; and Paul Gordan, Klein’s closest collaborator in the early stage of research on this topic, therefore called this enterprise jocularly the Hypergalois Theory.Footnote 3 Emphasizing the extensive social dimension of Klein’s theory—Klein entrusted many of his students with particular problems arising from his “general idea”, and promoted his theory on many occasions—the term Hypergalois Program might be appropriate to describe the broader implications.Footnote 4 The principles of the Hypergalois Program were most explicitly stated in the above-mentioned (Klein 1879b), and repeated in Klein (2019a). However, Klein’s motivation for a geometrical treatment of algebraic equations was already present at a much earlier stage (Klein 1871), during which even the core idea of Klein’s 1886 article was already developed.
In this sense, Klein’s 1886 article can be said to have three historical roots: Klein (1871) sets the most important mathematical background; Klein’s successful treatment of the general quintic (which was mathematically completed already in Klein (1877), but only popularized in the Lectures on the Icosahedron) provides the motivation for Klein’s renewed interested in the equations of degree 6 and 7; and Klein (1879b) sets the programmatic framework of this and subsequent works. The 1886 article itself was not very influential in mathematical terms, mainly because a “better” geometrical interpretation for equations of degree 6 was unexpectedly found soon after. At the same time, its importance for the Hypergalois Program cannot be overestimated in terms of the renewal of interest in equations of higher degree. The Hypergalois Program eventually failed, but the research questions it opened paved the way for a number of discoveries and conceptual novelties that were indispensable for the transformation that mathematics (especially group theory) underwent at the turn of the 20th century.
In the present paper, my aim is to take Klein’s article of 1886 as a testimonial and driving force of these profound transformations. This is achieved in two different ways: in Sect. 2, I locate the paper within the broader historical landscape of the Hypergalois Program: I first discuss the three historical roots mentioned above in Sects. 2.1, 2.2, and 2.3. Then, I outline the position of the paper within the theory of the equation of degree 6 (Sect. 2.4), and finally present some more general implications (Sect. 2.5). Section 3 is devoted to a more detailed reconstruction of the mathematical content of the paper itself, and follows more or less its original setup: From the presentation of Klein’s general idea (Sect. 3.1), via the construction of the representations of \(A_7\) and \(S_6\) (Sects. 3.2, 3.3), to some additional elaborations on accessory irrationalities (Sect. 3.4), covariants (Sect. 3.5), and possible generalizations to higher degrees (Sect. 3.6). A summary (Sect. 3.7) compares the results to Klein’s earlier achievements with respect to the quintic equation. As literature especially on the topic of line geometry is scarce, a special attention is given to it throughout the section. A short conclusion follows in Sect. 4. Sections 2 and 3 approach the same topic from two different angles, and can be read more or less independently from each other. However, I believe that our understanding of Klein’s mathematical thinking can benefit if both the “macro”/historical and the “micro”/mathematical content of his publication are understood side by side.
2 The Hypergalois Program
2.1 The beginnings
The 19th century was the century of classical algebraic geometry, with their practitioners interested in certain geometrical configurations, and in the corresponding equations whose solutions would yield these configurations. Hölder (1899, p. 518), and more recently, François Lê (2015) calls them the geometrical equations:
For a given geometrical situation, one may say that the corresponding geometrical equation is the algebraic equation ruling the configuration. For instance, for the nine inflection points of a cubic curve, we have the nine inflection points equation, which is the algebraic equation of degree 9 having the abscissas of the inflection points for its roots. (Lê 2015, pp. 317–318)
It was, however, only in 1871 that Felix Klein first uttered the idea to interpret the general polynomial equation geometrically:
[Klein] went on and announced his general and fundamental principle: to conceive every algebraic equation as a geometrical equation, embodying the roots of an equation in geometrical objects and replacing the substitutions of the roots by transformations of the space. [\(\dots \) T]his articulation between algebra and geometry revealed two main leitmotivs of Klein: to bring geometry to the fore because of the intuition it allowed and to stress the importance of transformation groups. (ibid., 336)
Particularly, Klein perceived the solutions of a polynomial equation of degree n as n points in \((n-2)\)-dimensional projective space, \(\mathbb {P}^{n-2}\), which allowed him to consider the permutations of the roots as transformations of space.Footnote 5 In \(\mathbb {P}^{n-2}\), there exists a unique linear transformation of space for every permutation of n given points—thus the choice of dimension. In a modern formulation, the depiction of a finite group as a group of transformation of space is called a finite group representation, and the particular representation in \(\mathbb {P}^{n-2}\) is nothing but the projectivization of the so-called standard representation

The group \(S_n\) was defined above as the permutation group of the solutions of a polynomial equation, i.e., as the Galois group of the equation. Klein thus achieved an interpretation of the Galois group of a degree n polynomial as a group of linear transformations of projective space of dimension \((n-2)\). This allowed him to bring together two notions that are considered typical representatives of nineteenth century mathematics: resolvents in the theory of algebraic equations on the one hand, and covariants as a central concept of invariant theory and geometry on the other. Klein interpreted the solutions \(x_i\) of an algebraic equation of degree n as points in space \(\mathbb {P}^{n-2}\), and the Galois group of the equation as the corresponding group of space transformations which permute these points. Applying the transformations \(S_n\) to any given point \(y_0\in \mathbb {P}^{n-2}\) yields in general n! points \(y_0,y_1,\dots ,y_{n!}\). Its geometrical equation
is invariant with respect to the configuration of roots \(x_i\), meaning that it does not change its value when the \(x_i\) are permuted. This makes g(y) a covariant of \(f(x)=0\), because any transformation of x (meaning a symmetric transformation in \(x_0,\dots ,x_n\)) leads to a “compatible” transformation of y, and one can easily calculate the effect of the one to the other. Algebraically speaking, g(y) is a Galois resolvent of f(x) (see Footnote 6). It now might happen that we chose \(y_0\) in a way that some of the \(y_i\) coincide. Then, the polynomial g(y) becomes the power of a polynomial of lower degree. It then corresponds to a special resolvent of \(f(x)=0\), namely one which can be used to algebraically simplify the initial equation \(f(x)=0\).Footnote 6 Therefore, we can just consider the resolvents of an algebraic equation \(f(x)=0\) as the covariants of \(f(x)=0\) when viewed as a geometrical equation. For the cases \(n=3,4\), this treatment yields an intuitive geometrical interpretation of the resolvents that were already known for centuries. For the case \(n=6\), a further simplification can be made by representing the roots \(x_i\) not as points, but as the so-called linear line complexes. This line-geometrical account was brought to perfection in Klein (1886), as is discussed in Sect. 3, especially Sect. 3.3.
The central idea just outlined could be interpreted as the “birth” of the Hypergalois Program, at least of those parts of it that bring together geometry, algebra, and invariant theory. However, the 1871 paper only establishes a principal connection between the two concepts of resolvents and covariants, and does not yet describe how an algebraic equation can practically be turned into a geometric configuration. It also does not give any hints as to how to proceed after such a geometric configuration would be achieved.
2.2 The icosahedron and the general quintic equation
In the years following the 1871 publication, these questions were taken up for the general quintic (Klein 1875, 1877), for which the icosahedron played a crucial role. In fact, if we are to believe the closing paragraph of Klein (1875), it was Klein’s study of the covariants of the icosahedron that accidentally led him to spot a connection to the theory of the quintic equation, not the other way around. This approach is also manifested in the Lectures on the Icosahedron, whose first half considers the invariant theory of the icosahedron without any reference to the quintic equation at all. However, during the second half of the book, Klein’s attitude seems to shift in the other direction. In one passage, he remarked that the “proper” approach to study the quintic equation might have to abandon the primacy of the icosahedron:
I believe that we shall be enabled to develop the general theory of form-problemsFootnote 7 algebraically, and in such wise that our reduction of equation of the fifth degree to the icosahedron appears as a mere corollary, and does not need to be established in a special manner. (Klein, [1884] 2019b, pp. 281–282)Footnote 8
Klein strengthened this idea in the 1886 article:
The fact that the group in question is identical with the otherwise known group of icosahedral substitutions appears to be coincidental and insignificant. In fact: if the group of linear transformations of z were not already known elsewhere, all its properties could be taken from the definitions of the group given in (1), (2). (Klein 1886, p. 501)
In the following outline of Klein’s theory of the icosahedron, I follow this approach and focus on the application of Klein’s icosahedron to the solution of the quintic equation only. I also restrict myself to those considerations that find analogues in Klein’s 1886 paper, and omit the others.Footnote 9
We are given a quintic equation in which the coefficients of \(x^4\) and of \(x^3\) vanish
Klein called such an equation a principal equation, which has the advantage that its roots \(x_1,\dots ,x_5\) satisfy two additional identities
Let us consider an ordered list of solutions \((x_1,x_2,x_3,x_4,x_5)\) as a point in homogeneous 4-space, \({(x_0\!:\!x_1\!:\!x_2\!:\!x_3\!:\!x_4)\in \mathbb {P}^4}\). In this sense, solving the equation means to find the yet “hidden” coordinates of this point.Footnote 10 The first of the two identities above says that this point lies on a hypersurface
We introduce a new coordinate system \(\pi _0,\dots ,\pi _4\) with \(\pi _k = \frac{1}{5}(1,\varepsilon ^{4k},\varepsilon ^{3k},\varepsilon ^{2k},\varepsilon ^k)\) (and \(\varepsilon \) being a fifth root of unity), with the effect that \(\mathcal {H}\) consists of exactly those points for which its first coordinate \(\pi _0\) vanishes.Footnote 11 The second identity says that within \(\mathcal {H}\), our point lies on a quadratic surface, which we can directly write in terms of our new coordinates \(\pi _i\)
Klein called this surface, defined by the condition \(p_1p_4+p_2p_3=0\) (in \(\pi \)-coordinates), the principal surface (“Hauptfläche”). Geometrically, such a surface is commonly known as a (complex) hyperboloid.Footnote 12 As in the case of the hyperboloid in real space (see Fig. 1), also a complex hyperboloid contains two families of lines, or reguli (Sg. regulus); let us call them \(\mathcal {L}_1\) and \(\mathcal {L}_2\). Two lines from the same regulus are parallel in \(M_2^{(2)}\), while two lines from different reguli meet each other in a point in \(M_2^{(2)}\).Footnote 13 If we parametrize \(\mathcal {L}_1\) and \(\mathcal {L}_2\) with one (homogeneous) parameter each, say \(\lambda =(\lambda _1\!\!:\!\lambda _2)\) and \(\mu =(\mu _1\!\!:\!\!\mu _2)\), we get an isomorphism that maps a point \(p=(p_1\!\!:\!\!p_2\!\!:\!\!p_3\!\!:\!\!p_4)\) (in \(\pi \)-coordinates) to the parameters of the two lines on \(M_2^{(2)}\) it is incident with (see, again Fig. 1)
Families of lines on a hyperboloid. F maps a point p (marked orange) to the coordinates \((\lambda ,\mu )\) of the lines incident with p (marked red). The code for this graphic was partly taken from the user maphy-psd of the website texwelt.de, see https://texwelt.de/fragen/18796
We can choose a parametrization \(\lambda ,\mu \), such that \((\lambda ,\mu )=((-p_1\!\!:\!\!p_2),(p_3\!\!:\!\!p_4))\); its inverse \(F^{-1}\), today called a Segre embedding, accordingly maps \((\lambda ,\mu )\) to \(p=(\lambda _1\mu _1\!:\!-\lambda _2\mu _1\!:\!\lambda _1\mu _2\!:\!\lambda _2\mu _2)\).
We now want to understand what happens under permutation of the roots: If we interpret, as above, a listing of the roots \((x_1,x_2,x_3,x_4,x_5)\) as the homogeneous coordinates of \(\mathbb {P}^4\), then a permutation of the roots amounts to a permutation of coordinates. Thus, in a representation-theoretic formulation, we obtain the projectivization of the standard representation of \(S_5\) in \(\mathbb {P}^4\) (see Sect. 2.1). Since the equations \(\sum _{i=0}^4 x_i=0\) and \(\sum _{i=0}^4 x_i^2=0\) are invariant under such permutation of coordinates, \(S_5\) acts on \(M_2^{(2)}\) as a whole. Linear transformations map lines to lines; therefore, \(S_5\) merely permutes the lines of \(M_2^{(2)}\). Specifically, one can show that even permutations \(\sigma \in A_5\) permute the lines within their families, and odd permutations \(\sigma \in S_5{\setminus } A_5\) interchange the lines of \(\mathcal {L}_1\) with those of \(\mathcal {L}_2\). We consider \(\mathbb {P}^1_{(1)}\) as a Riemann sphere; this is a sphere whose points are identified with complex numbers. This can be done by stereographically projecting the complex numbers (viewed as a plane) onto a sphere, where the “north pole” of the sphere is identified with \(\infty \) (see Fig. 2).
The stereographical projection between the (usual) representation of complex numbers z on a plane, and its representation \(z'\) on the Riemann sphere. The code for this graphic was partly taken from the users Subhajit Paul and Torbjørn T of the website stackexchange.com; see https://tex.stackexchange.com/questions/538970
It can then be shown that the 60 permutations of lines \(\mathcal {L}_1\), when viewed as complex numbers, and thus as points of the Riemann sphere, are realized by rotations of the sphere. As rotations of the Riemann sphere are special kinds of projectivities of \(\mathbb {P}^1\) (which are generally called Möbius transformations), we could say that we found a representationFootnote 14

Now, the icosahedron comes in: If we inscribe an icosahedron into the sphere, it can be shown that this group is exactly the group of rotations which leave the icosahedron invariant!Footnote 15 We can therefore call the above group of rotations the icosahedral group.
To summarize: The map \(F:M_2^{(2)}\rightarrow \mathbb {P}^1\) which sends points of the quadratic surface \(M_2^{(2)}\subset \mathbb {P}^4\) to points of the Riemann sphere is such that a permutation of the coordinates of the argument \(x\in M_2^{(2)}\) results in the application of an icosahedral rotation of the image \(\lambda =F(x)\). In a modern formulation, we would say that F is \(A_5\)-equivariant with respect to the (projectivized) standard representation in \(\mathbb {P}^4\) and the icosahedral representation in \(\mathbb {P}^1\); or, that the following diagram commutes:

We can also note that the permutations of the coordinates \(x_i\) act diagonally on \(\mathbb {P}^1_{(1)}\) and \(\mathbb {P}^1_{(2)}\); thus, we only need to consider the above action on \(\mathbb {P}^1_{(1)}\) and the other one follows by a multiplication by a constant.
We see in Sect. 3.7 how this representation can be used to reduce a principal quintic equation to some canonical icosahedral equation, but let us for conclude with a remark on the general quintic equation: It was known already for centuries that a general equation can be brought into principal form by a linear and quadratic Tschirnhaus transformation. Today, a Tschirnhaus transformation of a polynomial f(x) is usually considered as a polynomial transformation of the variable x to some new variable y, leading to a new polynomial g(y) with “favorable” properties such as the vanishing of some coefficients. In Klein’s time, a Tschirnhaus transformation was more generally considered as a parallel transformation of the roots \(x_i\) of \(f(x)=0\). These are spanned by the following basis transformation:Footnote 16
where \(s_j\) are the elementary symmetric polynomials and thus deducible from the coefficients \(a_i\) of the given equation. By the way, taken alone, the first basis transformation makes the coefficient \(a_1\) vanish, the second one makes the coefficient \(a_2\) vanish, and so forth. To make both coefficients vanish, a combination of both basis transformations is necessary, which can be calculated by some quadratic equation. Therefore, every general quintic equation can easily be reduced to a principal equation. If a quintic equation is already in reduced form \(x^5+a_2 x^3+a_3x^2+a_4x+a_5=0\), we can interpret its ordered solution as a point in \(\mathcal {H}\), and the Tschirnhaus transformation becomes a map that moves this point onto \(M_2^{(2)}\). The square root that appears when solving the quadratic equation above finds a geometrical interpretation in the fact that any geometrical construction (which happens parallel in all coordinates) performing such a map cuts the quadratic surface \(M_2^{(2)}\) at two points. We therefore do not arrive at a uniquely defined map from any point in \(\mathcal {H}\) to one point on \(M_2^{(2)}\) and after F to one point in \(\mathbb {P}^1_{(1)}\), but only a correspondence. The analogy of this idea for the higher degree equations is discussed in Sect. 3.5.
All these considerations, as will be seen in the next section, were successfully transferred to the theory of equations of degree 6 and 7 in Klein’s 1886 article. Specifically, Klein achieved both:
-
the construction of some representation of \(S_6\) and \(A_7\) in three-dimensional space \(\mathbb {P}^3\), analogous to the one-dimensional \(\mathbb {P}^1_{(1)}\) here (see Sects. 3.1–3.3); and
-
the calculation of a covariance between a solution \((x_0\!\!:\!\dots :\!\!x_{n-1}\)) of a reduced equation and a point in \(\mathbb {P}^3\), analogous to the Tschirnhaus transformation followed by the map F here (see Sect. 3.5).
What Klein could not transfer was the second half of the icosahedral theory, in which the above considerations were used to bring a given quintic equation into a canonical form, called the icosahedral equation. For this reason, I omit these considerations in this section. However, they are shortly addressed within the broader historical framework of Klein’s Hypergalois Theory in the following subsection.
2.3 Modular equations
After the theory of the general equation of degree 5 was virtually completed in the late 1870s, it seemed only natural to ask for analogous theorems for other classes of polynomials, i.e., polynomials with the same degree and the simple Galois group. Of course, such analogs appear more interesting when the resulting canonical equation can actually be solved by one or the other non-algebraic method. For the icosahedral group  , this is possible by the local inversion of the icosahedral equation by modular equations. This approach can be generalized to two other cases, the linear group
, this is possible by the local inversion of the icosahedral equation by modular equations. This approach can be generalized to two other cases, the linear group  of order 168, and the linear group
of order 168, and the linear group  of order 660. The special status of these three simple groups was already known to Galois who showed that
of order 660. The special status of these three simple groups was already known to Galois who showed that  (p prime) acts non-trivially on a set of p (or less) elements only for \(p\le 11\), and this action can be used in the theory of modular equations.Footnote 17 Klein considered the modular equation of degree 7 in Klein (1879a) and shortly after found a geometrical representation of the group
(p prime) acts non-trivially on a set of p (or less) elements only for \(p\le 11\), and this action can be used in the theory of modular equations.Footnote 17 Klein considered the modular equation of degree 7 in Klein (1879a) and shortly after found a geometrical representation of the group  in three (complex) dimensions, namely as the automorphism group of the Klein quartic (Klein 2001). The Klein quartic is given by the equation
in three (complex) dimensions, namely as the automorphism group of the Klein quartic (Klein 2001). The Klein quartic is given by the equation
As with the icosahedron before, one is interested in the graded \(\mathbb {C}\)-algebra  of invariants with respect to this automorphism group. Here, Klein left the explicit calculations to Gordan who published five papers on the topic in the following 5 years. Klein tackled the task an equation of degree 7 (or degree 8) with Galois group isomorphic to
of invariants with respect to this automorphism group. Here, Klein left the explicit calculations to Gordan who published five papers on the topic in the following 5 years. Klein tackled the task an equation of degree 7 (or degree 8) with Galois group isomorphic to  to the canonical equation thus established in the aforementioned articles. The theory can be said to have been successfully completed in 1885, although it never received the prominence of the theory of the icosahedron.Footnote 18 In the same spirit, also the above-mentioned group
to the canonical equation thus established in the aforementioned articles. The theory can be said to have been successfully completed in 1885, although it never received the prominence of the theory of the icosahedron.Footnote 18 In the same spirit, also the above-mentioned group  was considered (Klein 1879c), but the absence of a low-dimensional representation seems to have hindered further progress (cf. the modern 1995). This completes the list of Galois groups whose equations are solvable by modular equations. Klein, however, had no intention to stop at this point, but instead sought for a generalization of his methods to other Galois groups. This point of view was first made explicit in Klein (1879b) (see Sect. 1), which one can therefore take as the starting point of the Hypergalois Theory as a systematic research program:
was considered (Klein 1879c), but the absence of a low-dimensional representation seems to have hindered further progress (cf. the modern 1995). This completes the list of Galois groups whose equations are solvable by modular equations. Klein, however, had no intention to stop at this point, but instead sought for a generalization of his methods to other Galois groups. This point of view was first made explicit in Klein (1879b) (see Sect. 1), which one can therefore take as the starting point of the Hypergalois Theory as a systematic research program:
In my presentation, I have given the principles such a form that they not only solve the problem of equations with 168 substitutions, which is the first problem to be considered, but also make it possible to see how to treat similar problems with any higher equations and, what is more important, how to set them up. The resulting general method for treating higher equations (which will of course still be open of manifold development) includes both the solution of cyclic equations by root symbols and the Kroneckerian treatment of equations of the fifth degree. One can regard my method virtually as a generalization of the latter. (Klein 1879b, p. 252)
As for the first problem—the construction of some canonical Galois resolvent—Klein remarked:
The general method which I propose for the rational transformation of the algebraic equations consists simply in this, that I first search for the smallest number \(\mu \) for which an isomorphism of the desired kind between the permutations of the x and linear substitutions of the \(y_1\dots y_\mu \) is possible, and that I then replace the equation \(f(x)=0\) with the “problem of the y”. (ibid., p. 257)
This outline also indicates a shift of attention in Klein’s program: The geometrical considerations of the groups  and
and  were motivated by successful treatment of the case
were motivated by successful treatment of the case  . What holds these groups together is their special status with respect to modular equations. Therefore, the solvability of some canonical equation by analytic means came to the foreground, and the geometrical interpretations only followed afterward. When the modular equations “did their job” as much as they could (the next subsection shows that this assessment might not be quite correct, though), the picture was reversed, with the geometrical interpretation forming the starting point.
. What holds these groups together is their special status with respect to modular equations. Therefore, the solvability of some canonical equation by analytic means came to the foreground, and the geometrical interpretations only followed afterward. When the modular equations “did their job” as much as they could (the next subsection shows that this assessment might not be quite correct, though), the picture was reversed, with the geometrical interpretation forming the starting point.
Under this new credo, the overall aim remained the same, but the steps toward achieving this aim changed their order: First came the geometrical interpretation, then the calculation of the invariants (which are covariants with respect to the Galois group of the original equation), and only then the local solutions to them. Klein called the whole of this problem the form problem, and already in the Lectures on the Icosahedron explained its central position in his theory of equations:
The formulation of this problem [how to reduce equations with identical Galois groups to one another] has a certain importance for we obtain thereby at the same time a general program for the further development of the theory of equations. Among the form-problems or equation-systems with isomorphic groups, we have already above described as the simplest that which possesses the smallest number of variables. If therefore, any equation \(f(x)=0\) is given, we will first investigate what is the smallest number of variables with which we can construct a group of linear substitutions which is isomorphous with the Galois group of \(f(x)=0\). Then we shall establish the form problem or the equation-system which appertains to this group, and then seek to reduce the solution of \(f(x)=0\) to this form problem or equation-system, as the case may be. (Klein, [1884] 2019b, p. 138)
For a given Galois group, the “simplest” form problem was later called the normal problem. One condition for being “simple” is the above-mentioned minimization of its dimension, i.e., we are looking for a faithful representation

with n as small as possible. A second condition is that the representation and the resulting invariants and covariants have as easy or intuitive values as possible, which is usually achieved by choosing a suitable coordinate system or by relying on geometrical intuition, or both. I cannot go into the details of the historical achievements here, but it is clear that working on the normal problem starts with finding the minimal-degree faithful representation. The importance of this first step could be seen, for example, at the occasion of the famous Evanston Colloquium of 1894, when Klein repeated the principles of the program to a more general mathematical audience:
Let us consider the very general problem: a finite group of homogeneous linear substitutions of \(\mathrm {n}\) variables being given, to calculate the values of the \(\mathrm {n}\) variables from the invariants of the group.
This problem evidently contains the problem of solving an algebraic equation of any Galois group. [\(\dots \) A]mong the problems having isomorphic groups we consider as the simplest the one that has the least number of variables, and call this the normal problem. This problem must be considered as solvable by series of any kind. The question is to reduce the other isomorphic problems to the normal problem. (Klein 1894, pp. 72–73)
And further:
The reduction of the equation of the fifth degree to the icosahedron problem is evidently contained in this as a special case, the minimum number of variables being two. (ibid.)
In this spirit, it is only natural that the results of Klein’s 1886 paper were considered a major step in the development of the Hypergalois Program. Additionally, the groups \(A_6\) and \(S_6\) were crucial to the general equations of degree 6, and thus provided the first step toward a real generalization of Klein’s icosahedron. I show in the next subsection how Klein’s paper fits into this story.
2.4 The general sextic equation
The general equation of degree 5 was one of the dominating forces of development both in algebra and analysis for the better of part of the 19th century, that is, at least until the publication of the Lectures on the Icosahedron in 1884. The class of equations to naturally consider next, the sextic equation, on the other hand, was only of marginal interest throughout the history. We already witnessed in Sect. 2.1 an early interest of Klein into the sextic equation, whose Galois group \(S_6\) was there geometrically realized as a group of permutations of six linear complexes (see Sect. 3.3). What is more, if we assume the sextic equation in principal form like the quintic before
then the roots \(x_i\) again fulfill some relations \(\sum x_i=0\) and \(\sum x^2_i=0\); and the second relation can be said to define a quadratic line complex, whose focal surface is a Kummer surface, i.e., a surface of degree four with 16 nodal points lying on 16 planes (see Rowe (2019, p. 8)). The automorphism group of the resulting configuration is a 16-cover of the group \(S_6\). In short, the theory of the sextic can be approached by a closer study of this configuration, which thus plays a similar role to the icosahedron or the Klein quartic. However, being more concerned with the latter two geometrical objects, Klein did not return to the theory for a while.
Instead, it seems to have been due to the early work of the geometer and Klein student Giuseppe Veronese that the group \(A_6\) and the general equation of degree 6 came back into Klein’s agenda, as he remarked in a footnote in the Lectures on the Icosahedron 13 years later:
If we wished to treat equations of the sixth degree in an analogous sense, it would be necessary, after adjunction of the square root of the discriminant, to start from that group of 360 linear transformations of space which I have established in Bd. iv of the Math. Ann., l.c., [Klein (1871)] and to which latterly Signor Veronese has returned from the side of geometry [Veronese (1882b)]. (Klein, [1884] 2019b, p. 139n)
Veronese, who studied mathematics in Zurich and Rome, visited Klein in 1880–1881 in Leipzig (2003, p. 100; 2021, p. 154), and wrote the aforementioned geometrical approach during the end of his stay there. He had worked on the topic already in Veronese (1877), when he used Pascal’s Hexagramme Mystique to approach the group \(A_6\) geometrically. In later works (Veronese 1882a, b), Veronese combined the two available geometrical interpretations of \(A_6\)—Pascal’s Hexagramme Mystique and Klein’s use of the Kummer surface—but did not link them to the theory of equations.
Such a link seems to have been discussed first in Klein’s seminars in Leipzig during the years 1884–1886, as at least two of his students recounted: The first student was the American mathematician Frank Nelson Cole, who stayed as a student of Klein in Leipzig between 1883 and 1885 and participated at Klein’s seminars in Summer 1884 and Winter 1884/85. After his return to Harvard University, Cole devoted his Ph.D. thesis to A Contribution to the Theory of the General Equation of the Sixth Degree. This thesis was effectively supervised by Felix Klein and shortly after published in the American Journal of Mathematics. We can read in its introduction:
The subject of the present article was suggested to me by Prof. Klein, when I was a student in his Seminar at Leipzig, and I wish here to acknowledge my great indebtedness to him for valuable advice and suggestion, which have been of the greatest use to me. The fundamental idea of the entire treatment of the subject is due to him, as I have indicated below, and he might claim many of the particular methods involved as his own, if he should consider them worthy of such recognition. (Cole 1886, p. 265)
Cole started with a short review of Klein’s Lectures on the Icosahedron, which he believed to have completed the theory of the quintic equation:
While the theory of the equation of the fifth degree is thus completed in all directions, that of the sixth degree is only just begun. (ibid., p. 266)
His method to treat the sextic followed the proposition of the footnote in Klein’s Lecture on the Icosahedron (see above), in whose spirit Cole proceeded:
The method proposed by Klein for the solution of the general equation of any degree is perfectly analogous to this. We have to seek a group of linear substitutions which shall be isomorphic with the group of n! permutations belonging to the equation. Functions of the roots must then be found which undergo these linear transformations when the roots are permuted; and finally, corresponding differential equations must be obtained and their solutions studied. (ibid., p. 269)
As for the first task:
What is the smallest number of variables for which a group of linear equations is isomorphic with the 720 permutations of six elements? There is no such group for one or two variables. There is, however, such a group for three variables, or, if we write our linear transformation in homogeneous form, for four variables, of which the ratio of three of the fourth will then be transformed by a non-homogeneous transformation. This group of transformations is best known under the geometrical form in which its theory has been treated in connection with the remarkable surface of the fourth order and class known as Kummer’s surface. (ibid., pp. 270–271)
Unfortunately, Cole’s dissertation ends in a heap of long-winded calculations, and does not permit a conclusion. His closing paragraph contains the announcement of further research on the sextic, together with the promise to calculate some coefficients missing in the dissertation. We can only imagine the hardship Cole faced on the calculations when reading his complaints in his letter exchange with Klein (also see Parshall and Rowe 1994, pp. 192–197):
I feel quite exhausted from the arduous work of this year. Especially the calculations were too much for me, as I spent for almost six months ten hours daily on them. ([UBG] Cod. Ms. F. Klein 8: 476; a letter from Cole to Klein, 26 May 1886)
The second student to work on the sextic equation, Wilibald Reichardt was not much luckier. He visited Klein’s seminar of the summer term of 1885 in Leipzig (during which time he was also famulus, a sort of assistant, of Klein) and reported that Klein proposed to geometrically interpret the group \(S_6\) as some symmetry group of a Kummer surface, just as Cole did before (Reichardt 1885, p. 28). Reichardt followed that route and published an extended article on the topic (Reichardt 1886), but seems to have given up on the topic thereafter.Footnote 19
This was the situation in late 1886, when Klein used similar line-geometric ideas to calculate transformation groups of projective complex space that are isomorphic to \(S_6\) and \(A_7\), respectively. In a modern terminology, we would say that Klein was the first to explicitly calculate the generators of some faithful projective representations

(which are furthermore irreducible). In the historical context just described, it does not take much creativity to imagine the real intention behind the publication of this (admittedly, mathematically not very advancing) paper: It is reasonable to assume that Klein wanted to bring a fresh impetus to the theory of the sextic equations, provide some solid ground from which his students could more easily depart, and also demonstrate some personal involvement in the topic, which would certainly boost the motivation of his students. Klein’s mentioning of both Reichardt’s and Cole’s work in a footnote of the 1886 article, together with his announcement to come back to their results at a later stage, support this view (Klein 1886, p. 499n). And finally, it did not seem to cost Klein too much effort to produce his results: He did not start working on the paper before September 1886, and had finished it already in October.Footnote 20 In this sense, I believe that Klein’s decision to publish a 34 pages strong paper in his Mathematische Annalen was guided more by programmatic than by purely mathematical considerations.
A similar conclusion can be drawn with respect to Klein’s communication with fellow mathematicians after the publication of his paper, in which he encouraged his students to further study the general sextic. I could find two examples of such engagement: First, Klein naturally sent copies of his article to Cole who in return expressed his wish to work with Klein on the topic in Summer 1887, at which time he saw a chance to visit Germany.Footnote 21 However, severe mental conditions prevented him from any kind of mental effort for at least a year.Footnote 22 Only in October 1889, did he find the strength to return to mathematical productivity, resulting in an paper on subgroups of  (Cole 1890), an area of interest that could be said to vaguely fit into the scope of finding faithful representations of least degree.Footnote 23
(Cole 1890), an area of interest that could be said to vaguely fit into the scope of finding faithful representations of least degree.Footnote 23
A second mathematician to pick up the topic was Klein’s student Heinrich Maschke who spent the spring and summer of 1888 on the attempt to connect Klein’s paper with his own research on Borchardt moduli, and thus covered similar terrain as Cole. In a letter to Klein dated to the 16 February 1888, Maschke outlined this connection, concluding:
The solution of the equation of the 6th degree thus results in the following: Calculation of the Borchardt moduli from a form of 6th order, all of whose [five] invariants having given values. ([UBG] Cod. Ms. F. Klein 10: 936; a letter from Maschke to Klein, 16 February 1888)
Some months later, Maschke managed to simplify Klein’s representation of \(A_7\) further. Maschke also recognized that a second, similar, representation can be easily constructed. This anticipated the modern result that \(2.A_7\) (the result of the lift from  ) has two irreducible representations of dimension 4.Footnote 24 With the representation thus simplified, it was easier to approach the task of finding its covariants:
) has two irreducible representations of dimension 4.Footnote 24 With the representation thus simplified, it was easier to approach the task of finding its covariants:
With this, this problem has also been taken so far that I can approach the immediate setting up of the form system. ([UBG] Cod. Ms. F. Klein 10: 938; a letter from Maschke to Klein, 4 July 1888)
Maschke furthermore published a small note on a configuration of 140 lines in space which are permuted by Klein action of \(A_7\) on \(\mathbb {P}^3\) (Maschke 1889, 1890), but soon turned to other form-theoretic questions, and a complete treatment of the sextic equation has not been achieved on this way. Thus, at the Evanston Colloquium of 1894 that we discussed already in the last subsection, Klein could only point to his old 1886 article with respect to the achievements on the general equation of degree 6 and 7 (Klein 1894, p. 74).
Unbeknownst to Klein during that time, progress was on the way, and in fact already started in 1889 with the publication of the Danish mathematician Herman Valentiner, who just found a ternary substitution group (a subgroup of  ) of order 360 (Valentiner 1889). Valentiner recognized that his group contained the icosahedron group \(A_5\) as a subgroup, but only some 6 years later, the Swedish mathematician Anders Wiman (1865–1959) showed that this group is isomorphic to the group of even permutations of six elements, \(A_6\)! This came as a surprise even more so as Jordan (1878) had already ruled out any ternary substitution group other than the then-known ones (although the falsity of his claim was already established when Klein showed the existence of a ternary
) of order 360 (Valentiner 1889). Valentiner recognized that his group contained the icosahedron group \(A_5\) as a subgroup, but only some 6 years later, the Swedish mathematician Anders Wiman (1865–1959) showed that this group is isomorphic to the group of even permutations of six elements, \(A_6\)! This came as a surprise even more so as Jordan (1878) had already ruled out any ternary substitution group other than the then-known ones (although the falsity of his claim was already established when Klein showed the existence of a ternary  that Jordan also missed, cf. (Wiman 1899, p. 529)). Wiman did not doubt that his result would be of interest to Klein, and wrote him on 18 November 1895:
that Jordan also missed, cf. (Wiman 1899, p. 529)). Wiman did not doubt that his result would be of interest to Klein, and wrote him on 18 November 1895:
Hereby I am sending you a treatise “On a simple group of 360 plane collineations” of 33 pages. The group in question is holohedrally isomorphic to the group of even permutations of 6 things, and it seems to be that a representation of this group in the plane has not yet been known. As I believe that the subject offers at least some interest, I am taking the audacity to ask for a place of the treatise in the Mathematische Annalen. ([UBG] Cod. Ms. F. Klein 12: 355; a letter from Wiman to Klein, 18 November 1895)
Naturally, Klein met Wiman’s (or better: Valentiner’s) discovery with enthusiasm and not only approved the result for publication, but also immediately asked Wiman to use it for an advancement of the theory of the sextic equation.Footnote 25 One explanation why the representation was so long overlooked lies in the fact that unlike all finite linear groups considered before, the representation  does not lift to a double cover in
does not lift to a double cover in  , but to a triple cover
, but to a triple cover

known today as the Valentiner group. I might also point out here that Valentiner’s and Wiman’s discoveries conclude the list of ternary substitution groups, and that Klein’s representation of the group of even permutations of seven letters,  , was indeed optimal. Naturally, Wiman’s result triggered new hope for a genuine theory of equations of degree 6 (although not of degree 7), which arose immediately: Only months after Wiman’s first publication, Robert Fricke, who is today almost exclusively known as Klein’s closest collaborator, answered positively the question whether Klein’s invariant theory of
, was indeed optimal. Naturally, Wiman’s result triggered new hope for a genuine theory of equations of degree 6 (although not of degree 7), which arose immediately: Only months after Wiman’s first publication, Robert Fricke, who is today almost exclusively known as Klein’s closest collaborator, answered positively the question whether Klein’s invariant theory of  generalizes to \(A_6\).Footnote 26 Also, the today unknown Muscovite Leonid Lachtin (today transcribed as Lahtin), unaware of Fricke’s results, found a canonical equation of degree 6, solvable by linear differential equations of third order, which he assumed to be the analog of Klein’s icosahedral resolvent. (Lachtin 1899, 465n). Finally, Klein, “under the impulses of [his] old friend Mr. Gordan” turned back with new enthusiasm to the theory of the general sextic:
generalizes to \(A_6\).Footnote 26 Also, the today unknown Muscovite Leonid Lachtin (today transcribed as Lahtin), unaware of Fricke’s results, found a canonical equation of degree 6, solvable by linear differential equations of third order, which he assumed to be the analog of Klein’s icosahedral resolvent. (Lachtin 1899, 465n). Finally, Klein, “under the impulses of [his] old friend Mr. Gordan” turned back with new enthusiasm to the theory of the general sextic:
But this is only a beginning; I hope that his continued efforts will succeed in clarifying the subject in every respect as fully as we have been able to do in the past with the theory of equations of the fifth degree. (Klein, [1905] 2019a, p. 2)
However, a number of publications on the topic in the following yearsFootnote 27 could not save the theory of the equation of degree 6 from oblivion, and today, the history of the sextic equation remains forgotten. All in all, the success in treating the general sextic equation came too late, and was already drowned by a new approach to algebra that valued general theories over particular results. The latest contribution to the Hypergalois theory of the sextic was made by Robert Fricke, whose Lehrbuch der Algebra (1924/26/28) might be the historically last treatise to solely employ Klein’s approach to algebra.Footnote 28
2.5 The legacy of the Hypergalois Program
There was a second major discovery by Wiman, which ironically might have contributed to the demise of the Hypergalois Program: Already during the Evanston Colloquium, Klein wondered whether the group \(A_8\)—the Galois group of the general equation of degree 8 (after adjoining a square root) and thus the next natural “candidate” to consider—possessed a low-dimensional representation similar to the (then-known) cases of \(n\le 7\), or whether “the equation of the eight degree was its own normal problem”, i.e., whether no faithful representation in less than seven homogeneous coordinates (i.e., less than six dimensions) existed. Wiman (1897b) soon after showed that the latter was indeed the case, a result that he soon generalized to arbitrary dimensions: for \(n\ge 8\), there exists no faithful representation of \(A_n\) in less than six dimensions (Wiman 1897a). In other words, the representations

which stood at the heart of Klein’s theory on the quintic, sextic, and septic, were by no means the beginning of a general series, but rather a list of exceptions that could not be extended to \(n\ge 8\). The disappointment connected with this insight is summarized in a letter that Wiman sent to Klein on 2 January 1898:
Here as everywhere everything has to proceed lawfully; to those laws the beautiful \(G_{60}\), \(G_{360}\), \(G_{2520}\) [the presentations of \(A_{5,6,7}\)] must be allowed to subordinate; thus they probably only form the first members of a whole chain of interesting collineation groups, and the corresponding reduction of the general equation of degree n to normal equations must be achievable by uniform principles, i.e., yield a general theory. What could be found out famously destroyed this beautiful construction; a law really existed, but the interesting cases, after which the draft was sketched, proved themselves as exceptions. ([UBG] Cod. Ms. F. Klein 12: 359; a letter from Wiman to Klein, 2 January 1898)
Wiman, in close collaboration with Maschke, continued research on the topic for another year, but eventually decided that it was time to move to the more promising area of discontinuous infinite groups, another branch of mathematics invented by Klein. Looking back, he laconically comments:
It is strange that I have almost always had a headache when I was busy with my now terminated work. This may well be due to the fact that I was in spaces of too high a dimension. In a mere four-dimensional space I hope that I will feel at home. ([UBG] Cod. Ms. F. Klein 12: 361; a letter from Wiman to Klein, 27 November 1898)
If we could ask Maschke the same question, he might have given us a different answer though: His involvement in the Hypergalois Program quickly led to a focus of research on the purely group-theoretic considerations of linear substitution groups, i.e., of (linear or projective) group representations. Indeed, Maschke soon made a contribution to the newly emerging representation theory which guaranteed remembrance of his name until today: The Maschke theorem (1899) states that every given group representation splits is a direct sum of the so-called irreducible representations. In this sense, there does exist a “general law” behind the representations of \(A_5,A_6,A_7\) that Wiman was looking for, as they were all irreducible faithful representations of minimal degree. This result could hardly be satisfying in terms of the Hypergalois Program, but it demonstrates that the efforts made throughout the years were not in vain. Also other representation-theoretic results can be traced directly to Klein’s program. Among them was the concept of the Schur multiplier (Schur 1904) which was but a pre-mature version of the second cohomology group of a group. In two subsequent papers, Schur also showed—using the result from Cole (1893) that  —that the Schur multiplier of \(S_n\) and \(A_n\) is 2 except for \(A_6,A_7\), where it is 6 (Schur 1907, 1911). We can understand this result as the deeper reason for the discrepancy between the Valentiner group and the usual double covers of the groups in question. (Also, \(A_7\) has a triple cover like the Valentiner group.) We should also note that Schur’s results stemmed from his interest in projective representations, which were (and still are) much less considered than the usual linear representations. It is not hard to draw the line to Klein’s insistence on projective geometry during the whole of the Hypergalois Program.
—that the Schur multiplier of \(S_n\) and \(A_n\) is 2 except for \(A_6,A_7\), where it is 6 (Schur 1907, 1911). We can understand this result as the deeper reason for the discrepancy between the Valentiner group and the usual double covers of the groups in question. (Also, \(A_7\) has a triple cover like the Valentiner group.) We should also note that Schur’s results stemmed from his interest in projective representations, which were (and still are) much less considered than the usual linear representations. It is not hard to draw the line to Klein’s insistence on projective geometry during the whole of the Hypergalois Program.
The general impact of Klein’s Program for the development of representation theory is described by Hawkins:
Klein himself and the mathematicians directly associated with him in the execution of his program were concerned with representations by collineation groups and with the representation of specific groups rather than with the creation of a general theory of such representations. But it is not difficult to imagine how suggestive their work might appear, especially to someone aware of the developments taking place in Lie’s theory of groups and the theory of hypercomplex systems. (Hawkins 1972, p. 269)
Hawkins particularly points out the influence of Klein on the work Maschke, but also on William Burnside and Theodor Molien.
A second influence of the Hypergalois Program on modern mathematics can be found in Klein’s and his colleagues increasing understanding of exceptionality in group theory. This includes the plain discovery of exceptional isomorphisms or behavior, but more importantly the recognition of such objects or properties as exceptional, and the consequential search for root causes of these exceptions. The following list shall only provide an overview of what has been achieved (often as mere “side products”) within the Hypergalois Program:
-
The isomorphism between \(A_5\) and the symmetry group of the icosahedron was already known to Hamilton. Many other exceptional isomorphisms, such as
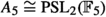 ,
, 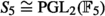 ,
, 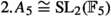 , were probably first systematically studied in the context of Klein’s icosahedron.Footnote 29
, were probably first systematically studied in the context of Klein’s icosahedron.Footnote 29 -
Likewise, the exceptional subgroup structure of the groups
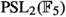 ,
, 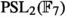 and
and 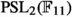 was already known to Galois, but were consequently employed within the Hypergalois Program. Klein himself did not recognize the set-theoretic identities (not as groups!) with “his” symmetry group of the platonic solids:
was already known to Galois, but were consequently employed within the Hypergalois Program. Klein himself did not recognize the set-theoretic identities (not as groups!) with “his” symmetry group of the platonic solids: 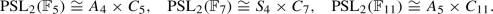
Today, these identities appear as part of the so-called McKay correspondences, and continue to be of mathematical interest (Kostant 1995).
-
As we saw in Footnote 14 and 38, Klein was the first to systematically use the exceptional isomorphisms of linear groups
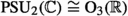 and
and 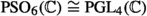 .
. -
In his dissertation, Cole recognized that \(S_6\) has two families of subgroups isomorphic to \(S_5\): one family of six subgroups that fixes one element, and one exceptional family of “twisted” \(S_5\subset S_6\):
As a result of the presence of this exceptional group, all equations of the sixth degree are connected in pairs, the roots of the two equations of each pair belonging respectively to the ordinary and the extraordinary groups of 120 permutations. (Cole 1886, pp. 269–270)
-
Wiman showed that the representations of \(A_5,A_6,A_7\) which were central to the Hypergalois Program are in fact exceptional representations.
-
Schur showed that the existence of the Valentiner group was the consequence of the exceptional Schur cover of \(A_6\) (together with \(S_6,A_7,S_7\)).
Unfortunately, no historical account on the history of exceptional isomorphisms seems to exist (the otherwise very interesting (Stillwell 1998) do not cover them), but it would surely be interesting to obtain certainty on Klein’s influence in this respect.
Finally, it should be noted that the Hypergalois Program had a much wider range of influence than the two topics mentioned in this subsection. Their selection was purely based on the direct connection to Klein’s 1886 article.
3 Klein’s projective representations
Having outlined the historical background and implication of Klein’s 1886 article, the current section aims to reconstruct the mathematical content of the article. The article consists of an introduction and three main parts, which are further subdivided into 11 paragraphs; and in the following subsections, my aim is to reconstruct at least the main ideas of all paragraphs from a perspective that mimics Klein’s own attempt to present his theory as a natural continuation of his previous icosahedral mathematics: In Sect. 3.1, I introduce the general approach that is taken in Klein’s paper (reflecting Klein’s §1–4); this is followed by a demonstration of Klein’s construction of the representations of \(A_7\) (Sect. 3.2) and \(S_6\) (Sect. 3.3) (both §5–6). A short “interlude” on Klein’s interest in so-called accessory irrationalities (Sect. 3.4, §7) is followed by an analysis of Klein’s calculation of the covariants (Sect. 3.5, §8–10). Finally, I briefly consider Klein’s thoughts on the possibility of generalizing his theory to equations of arbitrary degree (Sect. 3.6, §11). One can see already that Klein’s paper does not attempt to generalize the whole of his previous icosahedral mathematics: The deployment of some canonical invariant, the reduction of the general equation to such invariant, and finally the analytic solutions were not discussed in Klein’s 1886 article.
For easy comparison with the original article, I keep Klein’s enumeration of equations and most of his variable notation, while at the same time adapting his notation to ease readability.Footnote 30
3.1 The general theory
We are given a general reduced equation of degree 6 or 7, respectively
Then, its solutions \(x_i\) fulfill the two additional identities
When viewed as a “solution space” \(\mathbb {P}^{n-1}\), the first identity singles out a hyperspace of dimension \((n-2)\), while the second identity defines a quadratic manifold \(M_{n-3}^{(2)}\) of dimension \(n-3\) within that hyperspace. This is completely analogous to the case \(n=5\) (Sect. 2.2). As \(M_2^{(2)}\), also the quadratic surfaces \(M_3^{(2)}\) and \(M_4^{(2)}\) are generated by some family or families of linear subspaces, and Klein notes (without proof), that \(M_3^{(2)}\) contains a three-parameter family of lines, while \(M_4^{(2)}\) contains two three-parameter families of planes.Footnote 31 We want to denote the families of lines by \(\mathcal {E}\) and the two families of planes by \(\mathcal {E}_1\) and \(\mathcal {E}_2\). All of them are isomorphic to \(\mathbb {P}^3\), and thus can be parametrized by four homogeneous coordinates
It is clear that \(M_3^{(2)}\) can be represented as a hyperspace of \(M_4^{(2)}\), and in fact, the family \(\mathcal {E}\) is nothing but the cut of \(\mathcal {E}_1\) with the hyperplane that cuts out \(M_3^{(2)}\), and coincides with the cut of \(\mathcal {E}_2\) with that said hyperplane. In this sense, we can restrict attention for now to the case \(n=7\), and later consider \(n=6\) as a special case thereof.Footnote 32 In analogy to the case \(n=5\) (Sect. 2.2), once a parametrization of \(\mathcal {E}_1\) and \(\mathcal {E}_2\) is defined, the permutations of the seven coordinates \(x_i\) permutes the planes in both families, and thus define linear transformations of some \(\mathbb {P}_{(1)}^3\times \mathbb {P}_{(2)}^3\). And just as before, the even permutations of \(A_7\) permute planes within one family (say, \(\mathcal {E}_1\)), while the odd permutations will permute the two families. In a modern notation, this established the desired representation  . However, it is so far completely unclear how a suitable parametrization of the subspace \(\mathcal {E}_1\) should look like, and thus how an explicit matrix representation (or, in Klein’s time: a system of linear equations) can be established! (In the case \(n=5\) the map F was quickly found by invariant-theoretic considerations, which I do not cover here.)
. However, it is so far completely unclear how a suitable parametrization of the subspace \(\mathcal {E}_1\) should look like, and thus how an explicit matrix representation (or, in Klein’s time: a system of linear equations) can be established! (In the case \(n=5\) the map F was quickly found by invariant-theoretic considerations, which I do not cover here.)
This problem is overcome by borrowing some theorem of line geometry, a topic that Klein covered extensively in his Ph.D. thesis and in a couple of subsequent papers, but did not develop much during the late 1870s and 1880s. Especially in the context of the theory of equations, Klein thus seemed to feel obliged to provide a short justification:
If this way appears strange to some algebraist, it is worth recalling that everything we know about linear spaces in three- and four-times extended quadratic manifolds was originally developed on this exact way. (Klein 1886, pp. 504–505)
To understand exactly how Klein wants to use line-geometric results in this context, we have to go a little into the most important concepts, especially since historico-mathematical literature on this niche topic is scarce.Footnote 33 In projective space \(\mathbb {P}^3\), points and planes are famously dual, meaning that planes form a dual space \((\mathbb {P}^3)^*\) which can be described by plane coordinates.Footnote 34 This leaves us with lines (the dual of a line is again a line) for which we might ask if a useful coordinatization of them also exists. Julius Plücker, Klein’s former Ph.D. supervisor, answered this question positively: For a given line, he took two distinct points \(z=(z_1\!:\!z_2\!:\!z_3\!:\!z_4)\) and \(z'=(z_1'\!:\!z_2'\!:\!z_3'\!:\!z_4')\) lying on it, and defined its six today so called Plücker coordinates as follows:
Elementary calculations reveal that the Plücker coordinates of a given line are (up to a common scalar) independent from the particular choice of the points z and \(z'\); thus, the term coordinate is justified. The coordinates also fulfill the Plücker equation
Conversely, any sixtuple \(p=(p_1{:}p_2{:}p_3{:}p_4{:}p_5{:}p_6)\) satisfying the Plücker equation form the Plücker coordinates of a line. In other words, there is a one-to-one correspondence between the lines of \(\mathbb {P}^3\) and the points of the quadratic surface
The quadric \(\mathcal {Q}\) later became known as the Klein quadric,Footnote 35 and the bijection
is today called the Klein correspondence. In his inaugural dissertation (Klein 1868), Klein made a number of interesting observations about the behavior of Plücker coordinates. One of them concerns linear transformations (i.e., projectivities) of Plücker coordinates, concluding that any sixtuple of homogeneous coordinates satisfying some non-degenerate quadratic form can be used as a coordinatization of lines: a projectivity of Plücker coordinates \((p_1,\dots ,p_6)\mapsto (x_0,\dots ,x_5)\) transforms the Plücker equation \(\mathcal {P}(p_1,\dots ,p_6)=0\) to some non-degenerate quadratic equation \(\Omega (x_0,\dots ,x_5)=0\). Conversely, any non-degenerate quadratic form in six homogeneous variables can be obtained from the Plücker equation by a suitable transformation of Plücker coordinates, and therefore defines a coordinatization of lines.
Back to our reduced equation of degree 7, we can also treat its solutions \(x_0,\dots ,x_6\) as such coordinates, with the quadratic equation \(\Omega (x_0,\dots ,x_6)=\sum _{i=0}^{6} x_i^2=0\) holding between them. That we have seven coordinates instead of six poses no problem, because we can eliminate one variable with the equation \(\sum _{i=0}^6 x_i=0\). But as this would disturb the symmetry of the exposition, Klein decided to keep all \(x_0,\dots ,x_6\) as superfluous line coordinates between which the additional relation \(\sum _{i=0}^6 x_i=0\) is assumed. In effect, we can interpret the solution space of the reduced equation of degree 7 as the space of lines in \(\mathbb {P}^3\).Footnote 36 In this interpretation, the quadratic manifold \(M_4^{(2)}\) is nothing but the above Klein quadric \(\mathcal {Q}\) in x-coordinates! Most remarkably, this construction already provides a parametrization of our family \(\mathcal {E}_1\) above, as one can show that there is an isomorphism between the latter and the original point space \(\mathbb {P}^3\). Unfortunately, Klein commented on this astonishing situation rather too concisely:
Indeed, the points of space, as it is not necessary to explain here, understood as bundles of lines, correspond exactly to the triple infinite \(R_2\) [= planes] of the first kind, which are contained in the \(M_4^{(2)}\) defined through (8) (while the planes of spaces, understood as planes of lines, correspond to the triple infinite \(R_2\) of the second kind). (Klein 1886, p. 505)
I therefore want to use the remainder of this section to elaborate a little more on this topic. The Klein correspondence \(\kappa \) between lines in \(\mathbb {P}^3\) and points on \(\mathcal {Q}\) can be extended to points and planes of \(\mathbb {P}^3\) as well: a point \(z\in \mathbb {P}^3\) is incident with a two-parameter family of lines, \(\mathcal {L}_z\). Under \(\kappa \), this family maps to a two-dimensional manifold in \(\mathcal {Q}\), and it can be verified that this manifold forms in fact a plane. Slightly abusing our notation, we call this plane \(\kappa (z)\). Similarly, a plane \(A\subset \mathbb {P}^3\) is incident with a two-parameter family of lines \(\mathcal {L}_A\), which also maps to a plane in \(\mathcal {Q}\), and which we call \(\kappa (A)\). In fact, we can show that any plane contained in \(\mathcal {Q}\) is the image of either a point or a plane in \(\mathbb {P}^3\) under \(\kappa \). This establishes two families of planes in \(\mathcal {Q}\), which are just the above \(\mathcal {E}_1\) and \(\mathcal {E}_2\) (in new coordinates). Naturally, both families are isomorphic to \(\mathbb {P}^3\). We can also convince ourselves that all incidence relations between points, lines, and planes in \(\mathbb {P}^3\) can be formulated in terms of lines, and in fact translate to incidence relations in \(\mathcal {Q}\).Footnote 37 In this sense, the Klein correspondence \(\kappa \) extends to an incidence-preserving isomorphism between the geometry of \(\mathbb {P}^3\) and the geometry of \(\mathcal {Q}\) as follows:
In particular, the planes in \(\mathcal {E}_1\) can be parametrized by the coordinates of their corresponding point in \(\mathbb {P}^3\).
3.2 The representation of \(A_7\)
Analogous to the case \(n=5\) discussed in Sect. 2.2, we now want to investigate the effect of a permutation of the line coordinates \(x_i\) on the planes \(\mathcal {E}_1\). With the above isomorphism between \(\mathcal {E}_1\) and \(\mathbb {P}^3\) in mind, this is the same as asking the effect of a permutation of line coordinates to the underlying space \(\mathbb {P}^3\). Here, a second theorem from Klein’s inaugural dissertation, reformulated in Klein’s 1886 article, is helpful:
[... E]very linear substitution of line coordinates \(\xi _1\dots \xi _6\), which transforms the quadratic form \(\Omega \) [...] into itself, means a collineation or a dualistic transformation of space; namely the first or the second, depending on whether the associated substitution determinant, whose square necessarily equals 1, is equal to \(+1\) or \(-1\). (ibid., p. 507)
This result can be translated as follows: The group of projectivities of line coordinates leaving a quadratic form invariant (a special case being: projectivities of Plücker coordinates leaving the Plücker equation invariant) is called the projective (general) orthogonal group, because it is the projecitivization of the (general) orthogonal group,  . The latter
. The latter  splits into (six-dimensional) rotations \(\text {SO}_6(\mathbb {C})\) with determinant \(+1\) and reflections with determinant \(-1\). In even dimensions, this distinction is upheld under projectivization of the linear group, i.e., also
splits into (six-dimensional) rotations \(\text {SO}_6(\mathbb {C})\) with determinant \(+1\) and reflections with determinant \(-1\). In even dimensions, this distinction is upheld under projectivization of the linear group, i.e., also  splits into projective “rotations”
splits into projective “rotations”  and “reflections”
and “reflections”  . The above theorem then states that a “rotation” corresponds to a projectivity of \(\mathbb {P}^3\) and vice versa, and we can convince ourselves that this correspondence preserves group multiplication and thus forms an isomorphism:Footnote 38
. The above theorem then states that a “rotation” corresponds to a projectivity of \(\mathbb {P}^3\) and vice versa, and we can convince ourselves that this correspondence preserves group multiplication and thus forms an isomorphism:Footnote 38

Specifically, the permutations of line coordinates \(x_0,\dots ,x_6\) correspond to projectivities and dualities of the underlying space \(\mathbb {P}^3\), namely the former for the even permutations \(A_7\), and the latter for the odd permutations. We thus achieve a projective representation

Compared to the projectivization of the standard representations,  , this is a reduction of dimensionality by 2; the improvement is in this sense as “good” as the one achieved by the icosahedral representation of \(A_5\).
, this is a reduction of dimensionality by 2; the improvement is in this sense as “good” as the one achieved by the icosahedral representation of \(A_5\).
In the remainder of this section, let us reconstruct Klein’s explicit calculation of this representation. The first calculation concerns the transformation of our line coordinates \(x_i\) to the usual Plücker coordinates \(p_{jk}\) (§5). This is necessary, because the relations between \(\mathbb {P}^3\) (and thus: \(\mathcal {E}_1\)) and line coordinates are given in Plücker coordinates, while our intended permutations of line coordinates cannot simply be taken to be transformations of Plücker coordinates, because they would not leave the Plücker equation invariant. Practically, we are looking for a transformation that maps the quadratic form of line coordinates, \(\sum _{i=0}^{6} x_i^2=0\), to the Plücker equation \(p_1p_4+p_2p_5+p_3p_6=0\). As for the case \(n=5\) (Sect. 2.2), we start with a rotation of our coordinate system by introducing new coordinates (Eq. 15) \(\pi _i=(1,\gamma ^i,\gamma ^{2i},\gamma ^{3i},\gamma ^{4i},\gamma ^{5i},\gamma ^{6i})\), where \(\gamma \) is a 7th (primitive) root of unity. Again, this makes the first coordinate \(\pi _0\) vanish for all points on the quadric. We solve this system of equations for \(x_i\), (Eq. 23), \(x_i=\left( \gamma ^{-i}\pi _1+\gamma ^{-2i}\pi _2+\dots +\gamma ^{-6i}\pi _6\right) /7\), and plug the values into the quadratic equation \(\sum _{i=0}^6 x_i=0\). This gives us
which looks almost like our Plücker equation! (A great example of Klein’s careful preparation that makes almost all actual calculation superfluous.) All we have to do is a small redefinition (Eq. 25) \(\pi _6=p_1, \pi _1=p_2,\dots \), which gives usFootnote 39
The second step is to use these equations to calculate how the permutations of the \(x_i\) effect the Plücker coordinates. To do so, it is enough to calculate the same for some generating elements, Klein took here \(S=(0123456)\) and \(T=(34)\). For S, the resulting transformation is
(We cover T below.) The third step consists in finding the corresponding projectivity or duality. As S is even, it will be of the former kind, and “one can easily see” that this is achieved by the representationFootnote 40
Finally, the fourth step is to normalize the matrix up to a multiple \(\pm 1\), the significance of which becomes transparent in Sect. 3.4. In the case above, the matrix already has determinant \(\pm 1\), so we are done. The permutation \(T=(34)\), is odd and corresponds to a duality. As the formulas for T turn out to be more complicated than the ones for S (so I guess), Klein simplified the case by referring to the “geometrical meaning” (ibid., p. 514) of the permutation: T leaves invariant those lines for which \(x_3-x_4=0\). A family of lines determined by one linear equation such as this one is called a linear (line) complex.Footnote 41 It has some interesting properties: all lines of a linear complex that pass through a fixed point lie in one plane and vice versa. Thus, a complex defines a duality between points and planes which is furthermore self-inverse and therefore called a polarity. What is more, this polarity leaves all the lines of the complex invariant! As T is a self-inverse (\(T^2=Id\)) duality leaving the linear complex \(x_3-x_4=0\) invariant, it must be the polarity with respect to that complex. The equation of this polarity is established if we take the defining linear equation, in this case \(x_3-x_4=0\), bring it into Plücker coordinates, substitute \(p_1=z_1z'_2-z_2z'_1,\dots \), and order everything by \(z'\) and z:
For any given z, the points \(z'\) form a plane with plane coordinates A (by definition of the concept of plane coordinates). In this sense, A is the matrix (defined up to a scalar) representing the duality which corresponds to T. All that is left to do is to normalize the matrix. To do so, Klein did not calculate the determinant manually, but plugged in some specific values for \(z,z'\) to ease the calculation. It turned out that the scalar \(\pm 1/\sqrt{7}\) will do. With the projectivity corresponding to S and the duality corresponding to T established, we have a proper representation (i.e., a group of projectivities) for exactly those products of S’s and T’s in which T occurs an even number of times. This establishes our  .
.
3.3 The special case of \(S_6\)
The case \(n=6\) was carried out in principle analogously to the above calculation, but with one additional improvement: the linear equation \(\sum _{i=0}^{n-1} x_i=0\) (which was used for \(n=7\) to interpret the seven variables \(x_0,\dots ,x_7\) as line coordinates) was not yet “used” in the case \(n=6\). Geometrically, this equation singles out a linear complex (just as the one defined by T above), which Klein called the unit complex. The polarity with respect to this complex can be shown to be given by the equation
where \(w=(w_1{:}w_2{:}w_3{:}w_4)\) can be understood either as a plane which is mapped to a point, or as a point mapped to a plane. Any duality, as we saw, corresponds to a linear transformation of lines, which is in this case given by the self-inverse
The latter leaves the lines of the linear complex element-wise invariant. The solutions of the principal equation of degree 6 fulfill the equation \(\sum _{i=0}^5 x_i=0\), thus are represented by lines on the unit complex, and thus left invariant by the polarity above. As any solution of a reduced sextic is represented by a line at the unit complex, we can at liberty apply the transformation u without changing the solution. In particular, we can concatenate u to any linear transformation which corresponds to a duality, resulting in a product of two dualities, that is, a projectivity. In short, concatenating u is a tool to make permutations \(S_6{\setminus } A_6\) correspond to projectivities! This establishes a representation of the whole of \(S_6\) as a group of projectivities in \(\mathbb {P}^3\)

In a modern formulation, we would speak of a “twist in the sign” of \(S_6\).Footnote 42 Klein used this trick for both \(S=(012345)\) and \(T=(12)\) (which are both odd and therefore correspond to dualities). The corresponding normalizes projectivities are
with \(\gamma \) being a primitive sixth root of unity.
3.4 Accessory irrationalities
At the end of the second part, Klein devoted an extra paragraph “About the necessity of the double signs, which arise in the substitution formulas of the z” (§7). Klein’s aim in this paragraph was to show that there cannot exist a representation

whose projectivization is the above calculated projective representation  . Put differently, the projective representation of G necessarily lifts to a non-trivial cover in the space of linear transformations. This is shown by reference to the subgroup \(V_4\subset S_6,A_7\), from which we know from the Lectures on the Icosahedron that its representation
. Put differently, the projective representation of G necessarily lifts to a non-trivial cover in the space of linear transformations. This is shown by reference to the subgroup \(V_4\subset S_6,A_7\), from which we know from the Lectures on the Icosahedron that its representation  necessarily lifts to a double cover
necessarily lifts to a double cover  . Therefore, also for
. Therefore, also for  , we must pass to some (non-trivial) cover in
, we must pass to some (non-trivial) cover in  . This is probably also the reason why Klein normalized his representations
. This is probably also the reason why Klein normalized his representations  (where A are the above matrices corresponding to \(S,T\in S_6,A_7\)); as in this way, we directly obtain the representations of the generators of the double covers in
(where A are the above matrices corresponding to \(S,T\in S_6,A_7\)); as in this way, we directly obtain the representations of the generators of the double covers in  (where \(+A\) and \(-A\) are now distinct elements). What he seemed to have missed was the fact that the matrices iA and \(-iA\) are distinct elements in
(where \(+A\) and \(-A\) are now distinct elements). What he seemed to have missed was the fact that the matrices iA and \(-iA\) are distinct elements in  which also project to the same transformation, we have therefore also the possibility of a 4-cover.Footnote 43
which also project to the same transformation, we have therefore also the possibility of a 4-cover.Footnote 43
Klein’s discussion on these particularities stemmed from his interest in accessory irrationalities, of which the above situation is just a geometrical interpretation. These irrationalities occur in the process of solving equations, when the radical extension created in the process of solving an equation is strictly larger than the splitting field in which the roots lie. A notorious example is the case of an (irreducible) cubic equation with real coefficients. Its roots are always real, but the process of finding them still requires the use of complex numbers. Also the solution of the general quintic equation in terms of the icosahedral equation involves one additional square root. It was to Klein’s great pleasure that he could prove what Kronecker only guessed, namely that this irrationality is in fact unavoidable.Footnote 44 In this example, the accessory irrationalities find a geometric interpretation in terms of the double cover, because the subsequent problem of solving an equation that is geometrically given necessitates a switch from homogeneous to affine coordinates.Footnote 45
The general problem of accessory irrationalities was more easily treatable with the development of the modern, field-theoretic approach to Galois theory during the 1880s and 1890s by works of Heinrich Weber, Richard Dedekind, and Otto Hölder.
In fact, Hölder was motivated to work in this modern setting precisely because of the better way in which it could treat accessory irrationality, a work that was suggested to him by Felix Klein.Footnote 46
3.5 Tschirnhaus transformations and covariants
We are now turning to the third part of Klein’s 1886 paper, which he devoted to the search for covariants between the “solution space” of an equation of degree \(n=6,7\) and the space \(\mathbb {P}^3\), on which \(S_6,A_7\) act as calculated above. We remember this procedure from the case \(n=5\), where first a Tschirnhaus transformation maps a general solution to one that is interpreted as a point on the principal surface \(M_2^{(2)}\), from where it is mapped to some \(\lambda \in \mathbb {P}^1_{(1)}\) via F.
For \(n=6,7\), the idea is a bit different because instead of points on \(M_2^{(2)}\) and parameters of their generators (i.e., the planes in \(\mathcal {E}_1\)), we consider lines and points in projective 3-space. As in the case of \(n=5\), Klein here considered not only solutions of a principal equation, but slightly more generally solutions of a reduced equation, i.e., an equation were merely the second coefficient \(a_1\) vanishes, and for whose solutions we thus have
A tuple \((x_0\!:\!\ldots :\!x_{n-1})\) can then not anymore be understood as the coordinates of a line, but—what is good enough—as the coefficients of a linear equation between line coordinates, i.e., as a three-parameter family of lines, we called a linear complex (Sect. 3.2). If, accidentally, \(\sum _{i=0}^{n-1} x_i^2=0\) does hold, the linear complex is called a special linear complex and singles out exactly those lines which meet the line with coordinates \((x_0\!:\!\ldots :\!x_{n-1})\), and our original intuition is restored.Footnote 47
Thus, for a reduced equation of degree \(n=6,7\), the task is to find a point \(z\in \mathbb {P}^3\) that is covariant with the linear complex \((x_0\!:\!\ldots :\!x_{n-1})\) in the way that a permutation of coordinates of \(x_i\) corresponds to the application of the above representation on z. The principal idea to find such covariant point is to take a small detour, and first to obtain two linear complexes \(x'\) and \(x''\) via two Tschirnhaus transformations from x, such that \(x'\) and \(x''\) respect the additional identities
The left and the right identity say that both complexes are special linear complexes, and can therefore be interpreted as coordinates of two lines; the middle identity then states that the two lines are coplanar, i.e., that they intersect in a point which we call z. As both \(x'\) and \(x''\) stem from x by Tschirnhaus transformations, they are covariant to x and thus also the point z is. This is not only a beautiful construction of a covariant point z, but also produces, as Klein remarked, “the most general point z covariant to the complex x” (ibid., p. 529).
Unfortunately, the beauty faded when Klein proceeded with the construction of explicit formulas for the complexes \(x',x''\) and the point z (§9, I omit most of the calculations): For the first Tschirnhaus transformation \(x_i\mapsto x_i'\), Klein chose a quadratic map
(he doesn’t have to write “\(x_i-s_1/n\)”, because already \(s_1=\sum x_i=0\)) for which he set the task to find a \(\lambda \), such that \(\sum x_i'^2=0\) will hold. Plugging Eq. (52) into \(\sum x_i'^2=0\) gives a quadratic equation in \(\lambda \), which one can solve for \(\lambda \). Klein denoted the square root that appears in this quadratic equation by \(W'\), it represents a first accessory irrationality (see Sect. 3.4). Similarly, by a quite long calculation, a Tschirnhaus transformation \(x_i\rightarrow x_i''\) can be found, such that \(\sum x_i''^2=0\) and simultaneously \(\sum x_i'x_i''=0\) hold. Also here, a coefficient \(\lambda \) has to be calculated from a quadratic equation, and, “oddly enough” (p. 527) the obtained second square root \(W''\) does not involve the previously calculated \(W'\). To summarize:
It is clear that we cannot avoid the occurrence of two accessory square roots even if we determine \(\lambda ',\lambda ''\) in a different way, provided we stick to the use of ordinary methods. Whether it is at all impossible to satisfy the equations (50) without any involvement of accessory irrationalities remains to be seen. The fact that the accessory irrationalities cannot be completely avoided has already been emphasized in §7. (ibid., p. 527)
Having calculated the two special linear complexes \(x'\) and \(x''\), which can be interpreted as coplanar lines, Klein proceeded with the calculation of their intersection. For some reason or another, Klein did not use the elementary formula to calculate the intersection of two lines given in Plücker coordinates Lindemann and Clebsch (1891, p. 49). Instead, he took a third line x (not to be confused with our initial x), set a system of equations which forces x to cut both \(x'\) and \(x''\), then replaced the Plücker coordinates of x by the coordinates of two points lying on x (\(p_{12}=z_1z_2'-z_2z_1',\dots \)), ordered the resulting system according to the coordinates of z, and finally asked for a solution z of the system that would hold independently of the choice of the other point, \(z'\). Then, this point z is the intersection of \(X'\) and \(X''\). Klein did not finish the calculations (which, according to him would require to give up the symmetry of the calculations), and instead concluded the paragraph on covariants with the observation that the values of z linearly depend on the “three-termed determinants of the Lagrange expression \(\Pi ,\Pi '\)” (ibid., p. 530) (\(\Pi \) and \(\Pi '\) are the Plücker coordinates of \(X'\) and \(X''\)), compared to the direct linear dependence of the similar analogous expressions in his Lectures on the Icosahedron.
3.6 Generalizations
In the last paragraph of his article (§11), Klein discontinued his considerations of equations of degree six and seven, and provided a short outlook on equations of arbitrary degree n. Klein was not very explicit here, but the general idea seems to be the following: We interpret the space \(\mathbb {P}^{n-1}\) as the projectivized root space of the general equation of degree n. The roots of the reduced equations, i.e., those equations for which the coefficient of \(x^{n-1}\) already vanished, lie on a hypersurface isomorphic to \(\mathbb {P}^{n-2}\). The permutations of the roots are realized as permutations of the coordinates of \(\mathbb {P}^{n-1}\) and thus also act (faithfully) on the hypersurface \(\mathbb {P}^{n-2}\). If in the equation not only the coefficient of \(x^{n-1}\), but also of \(x^{n-2}\), vanishes, the solution lies on a quadratic (hyper-)surface of dimension \(n-3\)
Take \(\nu =\left\lfloor {n/2}\right\rfloor \), then \(M_{n-3}^{(2)}\) contains a family of linear subspaces of dimension \(\nu -2\), which Klein called \(R_{\nu -2}\). If n is even, these are already the maximal linear subspaces; if n is odd, there are two additional families of subspaces of dimension \(\nu -1\), \(R_{\nu -1}^{(1)}\) and \(R_{\nu -1}^{(2)}\), which meet in \(R_{\nu -2}\).Footnote 48 The idea is to single out one such space for any given solution \((x_1,\cdots ,x_n)\) of the equation. To do so, we again take a number of related Tschirnhaus transformations, namely \(\nu -1\) many. For \(n=4,5\), we had one single transformation; for \(n=6,7\), we had two transformations in terms of linear complexes. These relations are, as before, \(\sum x_i'x_j''=0\) for any two (not necessarily distinct) transformations \(X'\) and \(X''\). As Tschirnhaus transformations are covariant with respect to the action of \(S_n\), so is the linear subspace thus singled out.
However, as Klein added, this generalization cannot be fruitfully carried any further, because the actual calculations of the covariants depended on function-theoretic (for \(n=4,5\), i.e., \(\nu =2\)) or line-geometric (\(n=6,7\), i.e., \(\nu =3\)) grounds which do not generalize:
But for \(\nu >3\) such special tools fail and we will have to answer the question about the most appropriate definition of the resulting linear spaces by parameters, as well as about the behavior of these parameters at the possible permutations of x, in a direct, algebraic way. I would like to reserve the right to come back to this on occasion, and for the time being I will limit myself to referring to Mr. Lipschitz’s investigations on orthogonal substitutions (Lipschitz 1880, 1886), which I will have to use in the process. (ibid., pp. 531–532)
3.7 Summary
To summarize the above reconstruction of Klein’s 1886 article, we can say that Klein succeeded to construct some “optimal” representations  by use of the exceptional isomorphism between special orthogonal transformations of \(\mathbb {P}^5\) and linear transformations of \(\mathbb {P}^3\). Klein also outlined the construction of some correspondence between the “hidden” roots of an equation of degree 6 or 7 and a point in \(z\in \mathbb {P}^3\), and although the general idea is quite simple, the calculations appear long-winded and could not be finished. What has not been achieved at all was the employment of this geometrical construction for the purpose of actually solving an equation of degree 6 and 7. To understand what such a treatment would look like, let me quickly come back to the icosahedron: We define a polynomial on \(\mathbb {P}^1\) that is invariant under the \(A_5\)-action by the icosahedral symmetries, i.e., that maps all 60 points that are identified by the \(A_5\)-action to one and the same point. This 60-cover of \(\mathbb {P}^1\)
by use of the exceptional isomorphism between special orthogonal transformations of \(\mathbb {P}^5\) and linear transformations of \(\mathbb {P}^3\). Klein also outlined the construction of some correspondence between the “hidden” roots of an equation of degree 6 or 7 and a point in \(z\in \mathbb {P}^3\), and although the general idea is quite simple, the calculations appear long-winded and could not be finished. What has not been achieved at all was the employment of this geometrical construction for the purpose of actually solving an equation of degree 6 and 7. To understand what such a treatment would look like, let me quickly come back to the icosahedron: We define a polynomial on \(\mathbb {P}^1\) that is invariant under the \(A_5\)-action by the icosahedral symmetries, i.e., that maps all 60 points that are identified by the \(A_5\)-action to one and the same point. This 60-cover of \(\mathbb {P}^1\)
can be explicitly calculated by considering the image of the special points: Under \(A_5\), the 12 vertices, the 20 midpoints of the faces, and the 30 midpoints of the edges of the icosahedron, are permuted among themselves. With the points of the vertices given (Sect. 2.2), it is easy to construct a polynomial f of order 12 whose solutions are thus just these points. Also a polynomial H of order 20 and a polynomial T of order 30 could be calculated elementarily, but Klein more elegantly used results from invariant theory to see that H is in fact just the Hessian of f, while T is the Jacobian of f and H. (These are just the “special covariants” of Sect. 2.2.) Then, the map
sends the vertices to \(\infty \), the face midpoints to 0, and the edge midpoints to 1, the latter can be seen by the relation \(T^2=-H^3+1728f^5\) (Klein 2019b, p. 62). Geometrically speaking, the special points above divide the icosahedron into 120 fundamental triangles, and it can be observed that q sends 60 of them to the “northern hemisphere” of the Riemann sphere and the other 60 fundamental triangles to the “southern hemisphere” (see Fig. 3), while the edges and among them the special points are sent to the equator.
In a modern formulation, one can say that Klein calculated the graded \(\mathbb {C}\)-algebra \(\mathbb {C}(z_1\!\!:\!z_2)^{A_5}\) which is generated by the invariants f, T, H between which the above syzygy (a term that goes back to Cayley and was popularized by Hilbert) holds.
If we are now given any particular reduced quintic equation \(x^5+\alpha x^2+\beta x+\gamma =0\) with an ordered list of “hidden” solutions \((x_0\!:\!x_1\!:\!x_2\!:\!x_3\!:\!x_4)\) and map it via F to some \(\lambda \in \mathbb {P}^1\), then \(u=q(\lambda )\) will be invariant under the permutations \(A_5\) of the \(x_i\). Thus, u will be symmetric in the solutions \(x_i\), and can thus be calculated from the coefficients \(\alpha ,\beta ,\gamma \) and the square root of the discriminant \(\Delta \) alone!Footnote 49 We can then pass to affine coordinates \(z=z_1,z_2=1\) and write the above q as the icosahedral equation
which can be solved by the analytic methods. It is sufficient to note here that these analytic methods use the fact that \(A_5\) is isomorphic to  and thus acts on the projective line with six points (\(0,1,2,3,4,\infty \)) (also see Sect. 2.3). The big achievement of this whole complicated construction is that every reduced quintic equation can be transformed to a single equation, with only one variable parameter.Footnote 50
and thus acts on the projective line with six points (\(0,1,2,3,4,\infty \)) (also see Sect. 2.3). The big achievement of this whole complicated construction is that every reduced quintic equation can be transformed to a single equation, with only one variable parameter.Footnote 50
None of this had been achieved for the case \(n=6,7\), at least not in Klein’s 1886 paper. The analogue of the above map q would result in the construction of some \(G=S_6,A_7\)-invariant
for which a calculation of the field of invariants \(\mathbb {C}(z_0\!:\!z_1\!:\!z_2\!:\!z_3)^G\) would be necessary. Later work in the theory of quarternary forms shows that attempts in such directions were made; it is however not possible to give closer attention to them within the scope of the present work.
4 Conclusion
This article covered a number of mathematical topics and a comparatively wide range of time, from Klein’s inaugural dissertation of 1868 until the turn of the 20th century. Nevertheless, I attempted to restrict attention to those works that are in direct connection to the main historical event of this article, namely Felix Klein’s publication “On the theory of general equations of degree six and seven” of 1886. Its roots lie in two branches of mathematics that are today almost forgotten, namely line geometry and Klein’s geometrical theory of equations. Likewise, the paper only influenced a relatively small branch of research, and only for a short period of time.
At the same time, the transience of Klein’s research ideas was not clear at all during that time (“[The theory] of the sixth degree only just begun.” (Cole 1886, p. 266)), and hope in a late success only vanished slowly (“But this is only a beginning.” (Klein 2019a, p. 1)). The examination of Klein’s article within the context of its time offers the modern reader an authentic insight into algebraic thinking at a time of rapid change in the subject matter. Also, the importance of Klein’s program for the development and (maybe more important) for the popularization of Galois theory itself—similarly underestimated in the classical accounts—is worth being discussed (remember Klein’s influence on Hölder’s modern formulation of Galois theory, Sect. 3.4. In this sense, I can only support Gray’s (2019) recent attempt of a “rehabilitation” of Klein as a Galois theorist:
Klein not only presented a detailed account of the ‘Galois theory’ of polynomial equations, he argued polemically for his view as the ‘right’ one. He pushed for an autonomous theory of equations grounded in an analysis of their ‘Galois groups’ and independent of the theory of elliptic and modular functions (a field he certainly saw as important). This vision contributed to the Göttingen vision of contemporary mathematics, in which Gauss, Riemann, and Galois took pride of place, with its hierarchy of values that emphasized the role of concepts in determining what to calculate. In the 1870s and 1880s, when many regarded abstract group theory as too abstract, Klein’s promotion of the subject was louder than anyone else’s, and helped create the 20th century definition of Galois theory. (Gray 2019, p. 22).
But not only did Klein’s efforts promote his own vision of Galois theory, they additionally (and somewhat ironically) helped in the development of the field-theoretic Galois theory we know today. Also in theory of groups itself, the impact of Klein’s Hypergalois Program cannot be underestimated. The particularist approach of the Hypergalois Program, which relies on mathematical “accidents” and low-dimensional geometrical intuition instead of general principles, is often considered either irrelevant or even counter-progressive for the development of “abstract”, “axiomatic” or “structural” understanding of group theory.Footnote 51 Klein’s distaste against a solely axiomatic teaching of group theory and his tireless advocacy for intuition in mathematics and unification of unconnected mathematical branches can easily lead to the impression that Klein was, after all, a hindrance or at least a force of delay in the development of modern algebra.Footnote 52 This view is for example taken, at least with respect to the Hypergalois Program, by Wussing (2007), who was interested in the success of group theoretical publications only with respect to their contributions toward an abstraction, or axiomatization of the concept. In this broad-scale narrative, the Hypergalois Program thus played an only marginal role:
[A]ll these extremely impressive papers [of the Hypergalois Program] had done little to extend and deepen the new conceptual content of a group. This was because Klein and his fellow workers in this area relied on isomorphisms between groups of isometries and permutation groups, and thus stayed within the conceptual environment of (finite) permutation groups. (Wussing, [1969] 2007, pp. 208–209)
In fact, the opposite is the case: Klein’s involvement with particular problems, specific interesting groups, and unexpected connections between mathematical theories might not reflect the “spirit” of modern mathematics as we have it today, but were essential ingredients to sharpen the mathematical community’s understanding on which algebraic concepts and properties were worth following and which were not. In other words, Klein was an important source (if not, at least for some time, the most important one) to direct his fellow mathematicians’ interest in the right direction, which in turn led them to formulate the right concepts.Footnote 53 Wiman’s discovery about the exceptionality of the representations of \(A_5,A_6,A_7\), which led to the invention of the Schur multiplier and ultimately (although indirectly) to the concept of cohomology, is only one example of such unintended influence.
Such motivation-based reading of mathematical innovation might be unusual (although it does exist, for example in Schlimm (2008)). However, especially in the case of Klein’s Hypergalois Program (see Footnote 4), it offers an enriching narrative, and contributes to a better understanding of the becoming of modern mathematics.
Notes
Here and below, italics are always Klein’s. Translations into English are mine, except where (as in this case) a published English translation exists. Years in square brackets refer to the original (usually German) publication.
The term appeared in printed form in Klein’s Collected Works (Klein 1922, p. 261) and in The Development of Mathematics in the 19th Century (Klein 1926, p. 90), and was rediscovered in (Gray, [1986] 2008, p. 77). Among the unpublished material, the term appeared in Klein’s manuscript for his algebra lecture in Summer 1886 in Göttingen: “Error [to believe], as if the whole question were exhausted with the Galois scheme. The ‘Hypergalois’ Theory must find on least one month’s time.” ([UBG], Cod. Ms. F. Klein 14J). Digitally available at https://resolver.sub.uni-goettingen.de/purl?DE-611-HS-3206860.
The term Program is chosen not only for the analogy with the Erlangen Program (and many other mathematical programs) that are staged around a common methodological, sometimes even metaphysical, basis, but also to indicate the possibility of a socio-historical analysis in terms of a scientific research program (Lakatos 1978), or more specifically, a mathematical research program (Corfield 2012).
About this terminology: Given a vector space V, we denote its projectivization by \(\mathbb {P}(V)\). If \(V=\mathbb {C}^{n+1}\), its projectivization \(\mathbb {P}(\mathbb {C}^{n+1})\) is abbreviated by \(\mathbb {P}^n\), and we talk about n-dimensional projective complex space. This diction is justified because we can think about \(\mathbb {P}^{n}\) as an affine space \(\mathbb {C}^n\) extended by additional elements at infinity. We typically write the elements of \(\mathbb {P}^n\) as homogeneous coordinates \(z=(z_1\!\!:\!z_2\!:\!\dots \!:\!z_n)\) which are only defined up to a scalar. For example, the projectivization of \(V=\mathbb {C}^2\) is the complex projective line \(\mathbb {P}^1\) which can be identified with the usual complex numbers extended by a point at infinity:
$$\begin{aligned}\mathbb {P}^1=\{(z_1\!\!:\!z_2)\mid z_{1,2}\in \mathbb {C},(z_1,z_2)\ne (0,0)\}=\{(z_1/z_2\!\!:\!1)\mid z_{1,2}\in \mathbb {C},z_2\ne 0\}\cup \{(1\!\!:\!0)\}\cong \mathbb {C}\cup \{\infty \}\end{aligned}$$Thus, we can freely switch between homogeneous coordinates \((z_1\!\!:\!z_2)\) and non-homogeneous \(z=z_1/z_2\).
In general, a resolvent of a polynomial \(f(x)=0\) is a polynomial \(g(y)=0\) whose coefficients rationally depend on the coefficients of f, and whose solutions yield the solutions of \(f(x)=0\) by some auxiliary equation. Algebraically, if \(f(x)=0\) has Galois group G, then the auxiliary equation has Galois group \(H\lhd G\), and the resolvent itself has Galois group isomorphic to G/H. The above Galois resolvent is thus an extreme case where H is the trivial group; it therefore does not simplify the problem algebraically. But as we saw, it is also the most general case, in that it subsumes the “special” resolvents.
The so-called form problem considers the reduction of a polynomial equation to some homogeneous polynomial equation, where the polynomial is called a form and can be studied be methods of invariant theory.
Page numbers refer to the second English edition of 1913, which are provided in square brackets in the 2019 edition.
A short completion of the theory is provided in Sect. 3.7. Among the excellent reconstructions of Klein’s icosahedron are the classic (Fricke 1926), the modern (Slodowy 1986), the more elementary (Shurman 1997), the lighthearted (Eschenburg and Hefendehl-Hebeker 2000; Eschenburg 2017), and the historically most complete (Tobies 2021), especially pp. 286–291. Slodowy’s account is repeated in the introduction of his edition of Klein’s Lectures on the Icosahedron (Klein 1993), and translated into English in Klein (2019b).
This looks analogous to the approach in Klein (1871), but here an ordered solution is represented by only one point in \(\mathbb {P}^3\), not five points.
In the underlying affine space \(\mathbb {C}^5\), this is but a rotation of the coordinate system.
The notation hyperboloid is unambiguous, because in complex (hyper-)space, all non-degenerate quadratic surfaces of equal dimension are equivalent. We see in Sects. 3.1 and 3.6 that in general, the root space of a reduced equation of degree n is a quadratic manifold of dimension \(n-3\), i.e., some \(M_{n-3}^{(2)}\). Finally, let me emphasize that the notation \(M_d^{(k)}\) to indicate a surface of dimension d and order k is due to Klein, and still in use today.
From a purely incidence-geometric point of view, such a geometry is called a “generalized quadrangle”, see Beutelspacher and Rosenbaum (2013), p. 156.
In abstract terms, one can say that the existence of this representation is due to the exceptional isomorphism
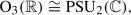
which allows us to view rotations of Euclidean three-space,
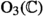 , as a special kind of Möbius transformations,
, as a special kind of Möbius transformations, 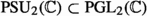 . I come back to this point in Sect. 2.5
. I come back to this point in Sect. 2.5Klein inscribes the icosahedron, such that its 12 vertices lie on the south pole 0, the north pole \(\infty \), and 10 other specified points on two different latitudes. The calculations of the symmetries of the icosahedron in terms of transformations of the Riemann sphere are an elementary, but little revealing task. Historically, it was already known to Hamilton (1856) that the symmetry group of the icosahedron is isomorphic to \(A_5\).
This result was generalized in a study on the subgroup structure of
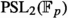 by Gierster (1881), who expressed his gratitude to Klein for his “multiple stimulation and support” for that article.
by Gierster (1881), who expressed his gratitude to Klein for his “multiple stimulation and support” for that article.Reichardt finished his Ph.D. in 1887 under the supervision of Felix Klein and Sophus Lie (who took Klein’s position in Leipzig after Klein’s departure to Göttingen in 1886). He published a second article on Kant’s synthetical a priori and its importance to philosophy of mathematics in 1888, but was not academically active thereafter.
In a letter to Hurwitz dated 31 August 1886, Klein announced that he would start working on the “equations of 6th degree” the following day ([UBG] Cod. Ms. Math. Arch. 77: 160; a letter from Klein to Hurwitz, 31 August 1886). The information on the completion in October 1886 is taken from the published paper itself (Klein 1886, p. 543).
See ([UBG] Cod. Ms. F. Klein 8: 477; a letter from Cole to Klein, 12 March 1887).
See ([UBG] Cod. Ms. F. Klein 8: 478; a letter from Cole to Klein, 22 October 1887) and ([UBG] Cod. Ms. F. Klein 8: 479; a letter from Cole to Klein, 22 March 1889). Also, other students of Klein, by name Oskar Bolza, Otto Hölder, and Max Born, reported mental exhaustion as a direct consequence of the workload provided by Klein (Thiele 2018, pp. 84–85). Cole is less direct here, but the exhaustion from working on the coefficients of his covariants is obvious.
This work was (among others) followed by a very enlightening review of the first volume of Klein’s Lectures on the Theory of Elliptic Modular Functions as well as the production of a complete list of simple (non-Abelian) groups up to order 660. The systematic search for simple groups of small order was mainly advanced by Otto Hölder, and demonstrates an increasing interest in group theory from a completely abstract point of view (see Gallian 1976).
In fact, the representations given in the Atlas of Finite Groups (http://brauer.maths.qmul.ac.uk/Atlas/v3/) look almost like Maschke’s result.
See ([UBG] Cod. Ms. F. Klein 12: 356; a letter from Wiman to Klein, 28 November 1895).
Wiman (1896) appeared in Mathematische Annalen 47(4), which was distributed in 11 August 1896. Fricke dates his publication to 5 September of the same year.
In its second volume, Fricke also provided a new representation of \(A_6\) as a principal congruence subgroup of level 3 over some ring of integers:
$$\begin{aligned} A_6\cong \text {PSL}_2\left( \mathbb {Z}\left[ \frac{1+\sqrt{5}}{2}\right] \right) /\sim ,\qquad g\sim h:\Leftrightarrow g\equiv h \mod 3 \end{aligned}$$This representation would potentially enable a solution of the sextic equation in terms of modular equations similar to Klein’s quintic (see Sutherland 2019), but it is beyond my capabilities to verify this claim.
It seems that Klein was also aware of Schläfli’s (then little known) result that the diversity of regular polyhedra in three (and four) dimensions was an exceptional situation, and did not generalize to higher dimensions. He subsequently did not seek to generalize his Icosahedron to polyhedra of higher dimensions.
Particularly, I added missing indices, introduced round brackets for homogeneous coordinates, and replaced systems of linear equations with matrix representation.
Klein denotes the maximal linear subspaces of some \(M_d^{(2)}\) by \(R_\nu \), where \(\nu \) represents their dimension. In this case: “\(M_3^{(2)}\) contains \(\infty ^3\) many \(R_1\); \(M_4^{(2)}\) contains two families of \(\infty ^3\) many \(R_2\)” (Klein 1886, p. 503). Today, we would call \(\nu +1\) the index of the quadratic manifold. A non-singular quadratic manifold in projective space \(\mathbb {P}^{d}\) has index d/2 or \((d+1)/2\), depending on whether d is even (in which case the quadric is called parabolic) or odd (in which case it is called hyperbolic. In real projective space, also elliptic quadrics of index \((d-1)/2\) exist for odd d. (cf. Beutelspacher and Rosenbaum 2013, p. 147)
Also in Klein’s generalization to arbitrary degrees (§11, see Sect. 3.6), the geometrical treatment of the equation of degree 2k is treated as a special case of the one of degree \(2k+1\).
A plane A in \(\mathbb {P}^3\) can be described as the set points \(x=(x_1\!:\!x_2\!:\!x_3\!:\!x_4)\) satisfying a linear equation
$$\begin{aligned}A_1x_1+A_2x_3+A_3x_3+A_4x_4=0\end{aligned}$$It is then only natural to refer to the coefficients \((A_1\!:\!A_2\!:\!A_3\!:\!A_4)\) as the plane coordinates of A.
Not to be confused with the Klein quartic of Sect. 2.3! The Klein quadric \(\mathcal {Q}\) is indeed the Grassmannian \(\mathbf{Gr} (2,\mathbb {C}^4)\) of 2-dimensional subspaces of \(\mathbb {C}^4\).
Thus, an ordered list of solutions of any particular equation of degree 7 can be interpreted as one particular line in \(\mathbb {P}^3\). Klein’s approach here is more general, in that the coefficients of his equations are completely undetermined.
For example, two points are distinct in \(\mathbb {P}^3\), \(z_1\ne z_2\), if and only if they only have one line in common, i.e. if and only if the planes \(\kappa (z_1)\) and \(\kappa (z_2)\) meet in a single point. (This is possible, because \(\mathcal {Q}\) is a quadratic manifold in \(\mathbb {P}^5\), not the whole \(\mathbb {P}^5\).) The same holds for planes A, B. Similarly, a point z not incident with a plane A, \(z\notin A\), have no line in common; thus, the planes \(\kappa (z)\) and \(\kappa (A)\) do not meet at all. On the other hand, if z is incident with A, \(z\in A\), they share a one-parameter family of lines (those lines in A that go through z); thus, \(\kappa (z)\) and \(\kappa (A)\) will meet in a line. In other words, two planes from the same family \(\mathcal {E}_i\) will either coincide or have a single point in common, while two planes from distinct families have either an empty intersection or meet in a line. Similar observations can be made about incidence relations between points and lines, lines and lines, and planes and lines.
Likewise, the “reflections” correspond to dualities in \(\mathbb {P}^3\). Today, this isomorphism is considered exceptional (see Footnote 14), because it does not generalize to arbitrary dimensions. I will come back to this point in Sect. 2.5.
All Plücker coordinates are mapped to multiples of themselves, so it makes sense to try to achieve such transformation by also mapping projective coordinates \(z_i\) to multiples of themselves. As the whole projectivity is only defined up to a scalar, we can take one multiplication at liberty, and choose \(z_1\mapsto z_1\). As \(p_1=z_1z_2'-z_2z_1'\) maps to \(\gamma p_1\), we better map \(z_2\mapsto \gamma z_2'\). From \(p_2=z_1z_3'-z_3z_1'\) and \(p_2\mapsto \gamma ^4 p_2\) we likewise infer \(z_3\mapsto \gamma ^4 z_3\), and from \(p_3=z_1z_4'-z_4z_1'\) and \(p_3\mapsto \gamma ^2 p_3\) we deduce \(z_4\mapsto \gamma ^2 z_4\). We then check that these transformations also yield the desired transformations \(p_4\mapsto \gamma ^6 p_4\), \(p_5\mapsto \gamma ^3 p_5\), and \(p_6\mapsto \gamma ^5 p_6\).
On the history of the theory of linear complexes, see again (Rowe 2019).
As this technique had virtually no impact on the subsequent development of the Hypergalois Program, I decided not to go into the details any further.
However, this extension of \(G=S_6,A_7\) by \(\{Id_4,i\cdot Id_4,-Id_4,-i\cdot Id_4\}\cong \mathbb {Z}_4\) partially splits, for it is already induced by Klein’s double cover. I am grateful to Alain Genestier for pointing out and clarifying this detail.
For the more personal story behind Kronecker’s and Klein’s rivalry, see Tobies (2021, p. 289).
For the quintic, this is shortly explained in Slodowy (1993, p. xvii).
For further discussion, see the fourth chapter of Nicholson (1992), “A Transitional Period for Galois Theory” (p. 37–59), which treats the subject with great care.
We could therefore think about special linear complexes as the dual of lines, and general linear complexes as the dual of some (imaginary) general lines. However, I never found such a line of thought in either Klein’s or other contemporaries’ work.
We could also say more efficiently: \(M_{n-3}^{(2)}\) has one (for n even) or two (for n odd) families of linear subspaces of maximal dimension \(\left\lfloor {(n-3)/2}\right\rfloor \); also see Footnote 31. Klein also remarked (albeit not using this fact any further) that the dimensionality of such family itself is \(\nu (\nu -1)/2\). This gives us for \(n=4\) a one-dimensional space of points; for \(n=5\) two one-dimensional spaces of lines; for \(n=6\) a three-dimensional space of lines; for \(n=7\) two three-dimensional spaces of planes.
The explicit formulas (which are too long to repeat here) can be found in Eschenburg and Hefendehl-Hebeker (2000), 17f..
Klein later described this achievement as analogous to the solution of pure equations \(x^n=A\) by logarithms (Klein 2019a, p. 3).
For a practice-based account on these notions, see Marquis (2014).
The following reference might be one of the most-quoted statements of Klein: “This abstract formulation [of the group axioms] is excellent for the working out of proofs but it does not help one find one new ideas and methods ...In general, the disadvantage of that method is that it fails to encourage thought.” (Klein 1926, pp. 335–336), as in (Wussing 2007).
Mehrtens’s characterization of Klein as a proponent of a “counter-modern” vision of mathematics (“Gegenmoderne”), oppositional and at the same time essential for the formation of modern mathematics, goes into a similar direction (Mehrtens 1990, p. 328).
References
Beutelspacher, A. and Rosenbaum, U. 2013. Projektive Geometrie: Von den Grundlagen bis zu den Anwendungen. Vol. 41. vieweg studium; Aufbaukurs Mathematik. Vieweg.
Coble, A.B. 1911. An application of Moore’s cross-ratio group to the solution of the sextic equation. Transactions of the American Mathematical Society 12 (3): 311–325.
Coble, A.B. 1911. The reduction of the sextic equation to the Valentiner form-problem. Mathematische Annalen 70 (3): 337–350.
Cole, F.N. 1886. A contribution to the theory of the general equation of the sixth degree. American Journal of Mathematics 8 (3): 265–286.
Cole, F.N. 1890. On rotations in space of four dimensions. American Journal of Mathematics 1: 191–210.
Cole, F.N. 1893. Simple groups as far as order 660. American Journal of Mathematics 15 (4): 303–315.
Corfield, D. 2012. Narrative and the rationality of mathematical practice. In Circles Disturbed. The Interplay of Mathematics and Narrative, Chap. 9, ed. A. Doxiadis and B. Mazur, 241–272. Princeton: Princeton University Press. https://doi.org/10.23943/princeton/9780691149042.003.0009.
Eschenburg, J.-H. 2017. Sternstunden der Mathematik. Berlin: Springer.
Eschenburg, J.-H., and L. Hefendehl-Hebeker. 2000. Die Gleichung 5. Grades: Ist Mathematik erzählbar? Mathematische Semesterberichte 47 (2): 193–220. https://doi.org/10.1007/s005910070003.
Fricke, R. 1924/26/28. Lehrbuch der Algebra. Berlin: Vieweg & Sohn.
Fricke, R. 1926. Lehrbuch der Algebra II. Berlin: Vieweg & Sohn.
Gallian, J.A. 1976. The search for finite simple groups. Mathematics Magazine 49 (4): 163–180.
Gierster, J. 1881. Die Untergruppen der Galois’schen Gruppe der Modulargleichungen für den Fall eines primzahligen Transformationsgrades. Mathematische Annalen 18 (2): 319–365.
Gordan, P. 1905. Die partiellen Differentialgleichungen des Valentinerproblems. Mathematische Annalen 61 (4): 453–526.
Gordan, P. 1909. Über eine Kleinsche Bilinearform. Mathematische Annalen 68 (1): 1–23.
Gray, J. 1982. From the history of a simple group. The Mathematical Intelligencer 4 (2): 59–67. https://doi.org/10.1007/bf03023483.
Gray, J. [1986] 2008. Linear differential equations and group theory from Riemann to Poincaré. Modern Birkhäuser Classics, 2nd ed. Basel: Birkhäuser. https://doi.org/10.1007/978-1-4899-6672-8.
Gray, J. 2019. 19th century Galois theory. In: Serva di due padroni: Saggi di Storia della Matematica in onore di Umberto Bottazzini. Ed. by A. Cogliati. EGEA spa. Chap. 6, pp. 97–128.
Hamilton, W.R. 1856. Memorandum respecting a new system of roots of unity. The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science 12 (4): 446.
Hashagen, U. 2003. Walther von Dyck (1856–1934): Mathematik. Technik und Wissenschaftsorganisation an der TH München: Franz Steiner Verlag.
Hawkins, T. 1972. Hypercomplex Numbers, Lie Groups, and the Creation of Group Representation Theory. Archive for History of Exact Sciences 8 (4): 243–287.
Hawkins, T. 1989. Line geometry, differential equations and the birth of Lie’s theory of groups. In Ideas and their Reception, 274–327. Oxford: Elsevier.
Hölder, O. 1899. Galois’sche Theorie mit Anwendungen. In Encyklopädie der mathematischen Wissenschaften mit Einschluß ihrer Anwendungen Arithmetik und Algebra Erster Teil, 481–518. Erster Band: Teubner.
Jordan, M.C. 1878. Mémoire sur les équations différentielles linéaires à intégrale algébrique. Journal für die reine und angewandte Mathematik 84: 89–215.
Klein, F. 1868. Ueber die Transformation der allgemeinen Gleichung des zweiten Grades zwischen Linien-coordinaten auf eine canonische Form. Georgi: Druck von C.
Klein, F. 1871. Ueber eine geometrische Repräsentation der Resolventen algebraischer Gleichungen. Mathematische Annalen 4 (2): 346–358 (GMA II, L, 262–274).
Klein, F. 1875. Ueber binäre Formen mit linearen Transformationen in sich selbst. Mathematische Annalen 9 (2): 183–208 (GMA II, LI, 275–301).
Klein, F. 1877. Weitere Untersuchungen über das Ikosaeder. Mathematische Annalen 12 (4): 503–560 (GMA II, LIV, 321–384, with additional commentaries).
Klein, F. 1879. Ueber die Erniedrigung der Modulargleichungen. Mathematische Annalen 14 (3): 417–427 (GMA III, LXXXIII, 76–89).
Klein, F. 1879. Ueber die Auflösung gewisser Gleichungen von siebenten und achten Grade. Mathematische Annalen 15 (2): 251–282 (GMA II, LVII, 390–425).
Klein, F. 1879. Ueber die Transformationen elfter Ordnung der elliptischen Functionen. Mathematische Annalen 15 (3–4): 533–555 (GMA III, VXXXVI, 140–168).
Klein, F. 1886. Zur Theorie der allgemeinen Gleichungen sechsten und siebenten Grades. Mathematische Annalen 28: 499–522 (GMA II, LVIII, 439–472).
Klein, F. [1872] 1893. A comparative review of recent researches in geometry. Bulletin of the American Mathematical Society 2(10): 215–249.
Klein, F. 1894. Lectures on mathematics. (The Evanston Colloquium). American Mathematical Soc.
Klein, F. 1921. Gesammelte Mathematische Abhandlungen. Erster Band: Liniengeometrie. Grundlegung der Geometrie. Zum Erlanger Programm. Ed. by R. Fricke and A. Ostrowski. Springer (GMA I).
Klein, F. 1922. Gesammelte Mathematische Abhandlungen. Zweiter Band: Anschauliche Geometrie. Substitutionsgruppen und Gleichungstheorie. Zur Mathematischen Physik. Ed. by R. Fricke and H. Vermeil. Springer (GMA II).
Klein, F. 1923. Gesammelte Mathematische Abhandlungen. Dritter Band: Elliptische Funktionen, insbesondere Modulfunktionen. Hyperelliptische und Abelsche Funktionen. Riemannsche Funktionentheorie und autormorphe Funktionen. Ed. by R. Fricke, H. Vermeil, and B. Bessel-Hagen. Springer (GMA III).
Klein, F. 1926. Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert. Vol. 1. Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen 24. Springer.
Klein, F. 1993. Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade. Ed. by P. Slodowy. Birkhäuser.
Klein, F. 2001. On the Order-Seven Transformation of Elliptic Functions. In: The Eightfold Way: The Beauty of Klein’s Quartic Curve. Ed. by S. Levy. Vol. 35. Mathematical Sciences Research Institute Publications. Cambridge University Press, pp. 287–331. Originally “Ueber die Transformation siebenter Ordnung der elliptischen Functionen”. Mathematische Annalen 14 (3): 428–471 (1879) (GMA III, LXXXIV, 90–135).
Klein, F. [1905] 2019a. About the Solution of the General Equation of Fifth and Sixth Degree. Trans. by A. Sutherland. In: arXiv preprint arXiv:1911.02358. Originally “Über die Auflösung der allgemeinen Gleichungen, fünften und sechsten Grades” in Journal für reine und angewandte Mathematik 129, pp. 151–180 (1905); reprinted in Mathematische Annalen 61 (1): 50–71 (1905) (GMA II, LXI, 481–502).
Klein, F. [1884] 2019b. Lectures on the Icosahedron and the Solution of Equations of the Fifth Degree. Ed. by L. Ji. Classical Topics in Mathematics 5. Higher Education Press. Originally Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade (1884); Translation by Georg Gavin Morrice in 1888/1913 (reprinted 1956/2007). 2nd German edition with a new introduction and commentary by Peter Slodowy (1993). The current edition (2019) comprises of Morrice’s translation (1913) and a new translation of Slodowy’s introduction and commentary by Lei Yang.
Kostant, B. 1995. The graph of the truncated icosahedron and the last letter of Galois. Notices of the AMS 42 (9): 959–968.
Kraft, H. 2006. A result of Hermite and equations of degree 5 and 6. Journal of Algebra 297 (1): 234–253.
Kraft, H. and Procesi, C. 2000. Classical invariant theory, a primer. In: Lecture Notes, Version.
Lachtin, L. 1899. Die Differentialresolvente einer algebraischen Gleichung 6ten Grades mit einer Gruppe 360ster Ordnung. Mathematische Annalen 51 (3): 463–472.
Lakatos, I. 1978. The Methology of Scientific Research Programmes.https://doi.org/10.1017/cbo9780511621123.
Lê, F. 2015. The “Geometrical Equations’’: Forgotten premises of Felix Klein’s Erlanger Programm. Historia Mathematica 42 (3): 315–342. https://doi.org/10.1016/j.hm.2014.11.002.
Levy, S., ed. 2001. The Eightfold Way: The Beauty of Klein’s Quartic Curve, vol. 35. Cambridge: Mathematical Sciences Research Institute Publications, Cambridge University Press.
Lindemann, F., and A. Clebsch. 1891. Vorlesungen über Geometrie unter besonderer Benutzung der Vorträge von Alfred Clebsch, vol. 2. Stuttgart: Teubner.
Lipschitz, R. 1880. Principes d’un calcul algébrique qui contient comme espèces particulières le calcul des quantités imaginaires et des quaternions. In: Comptes Rendus hebdomadaires des séances de l’Académie des sciences 91, pp. 619–621, 660–664.
Lipschitz, R. 1886. Untersuchungen über die Summen von Quadraten. Bohn: M. Cohen & Sohn (F. Cohen).
Marquis, J.-P. 2014. Mathematical abstraction, conceptual variation and identity. In Methodology and Philosophy of Science—Proceedings of the 14th International Congress (Nancy), ed. S.H. Ogic, et al., 299–321. London: College Publications.
Maschke, H. 1889. Ueber eine merkwürdige Configuration gerader Linien im Raum. In: Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts- Universität zu Göttingen 1889.14, pp. 384–388.
Maschke, H. 1890. Ueber eine merkwürdige Configuration gerader Linien im Raum. Mathematische Annalen 36 (2): 190–215.
Maschke, H. 1899. Beweis des Satzes, dass diejenigen endlichen linearen Substitutionsgruppen, in welchen einige durchgehends verschwindende Coefficienten auftreten, intransitiv sind. Mathematische Annalen 52 (2–3): 363–368.
Mehrtens, H. 1990. Moderne Sprache Mathematik. Frankfurt: Suhrkamp.
Nicholson, J. 1992. Otto Hölder and the Development of Group Theory and Galois Theory. PhD thesis. Merton College, Oxford.
Parshall, K.H., and Rowe, D.E. 1994. The emergence of the American mathematical research community. In History of Mathematics 8, ed. J.J. Sylvester, F. Klein, and E.H. Moore, 1876–1900. London: American Mathematical Society, London Mathematical Society. https://doi.org/10.2307/2687058.
Reichardt, W. 1885. Ein Beitrag zur Theorie der Gleichungen sechsten Grades. In: Berichte über die Verhandlungen der Küniglich Sächsischen Gesellschaft der Wissenschaften zu Leipzig, vol. 37. Mathematisch-Physische Classe, pp. 419–426.
Reichardt, W. 1886. Ueber die Normirung der Borchardt’schen Moduln der hyperelliptischen Functionen vom Geschlechte p = 2. Mathematische Annalen 28 (1): 84–98.
Rowe, D.E. 1989. The early geometrical works of Sophus Lie and Felix Klein. In Ideas and their Reception, ed. D.E. Rowe and J. McCleary, 208–273. New York: Academic.
Rowe, D.E. 2019. Klein, Lie, and their early Work on Quartic Surfaces. In Serva di due padroni: Saggi di Storia della Matematica in onore di Umberto Bottazzini, ed. A. Cogliati, 171. Evanston: EGEA spa.
Schlimm, D. 2008. On abstraction and the importance of asking the right research questions: Could Jordan have proved the Jordan-Hölder Theorem? Erkenntnis 68 (3): 409–420. https://doi.org/10.1007/s10670-008-9108-z.
Schur, I. 1904. Über die Darstellung der endlichen Gruppen durch gebrochen lineare Substitutionen. Journal für die reine und angewandte Mathematik 127: 20–50.
Schur, I. 1907. Untersuchungen über die Darstellung der endlichen Gruppen durch gebrochene lineare Substitutionen. Journal für die reine und angewandte Mathematik 132: 85–137.
Schur, I. 1911. Über die Darstellung der symmetrischen und der alternierenden Gruppe durch gebrochene lineare Substitutionen. Journal für die reine und angewandte Mathematik 139: 155–250.
Shurman, J. 1997. Geometry of the Quintic. Oxford: Wiley.
Slodowy, P. 1986. Das Ikosaeder und die Gleichungen fünften Grades. In Arithmetik und Geometrie, 71–113. Berlin: Springer. https://doi.org/10.1007/978-3-0348-5226-5_3.
Slodowy, P. 1993. Einführung in die Thematik der “Ikosaederbuches”. In Vorlesungen über das Ikosaeder, ed. F. Klein, viii–xxviii. Boston: Birkhäuser.
Stillwell, J. 1998. Exceptional objects. The American Mathematical Monthly 105 (9): 850–858.
Sutherland, A. J. 2019. On Klein and Fricke’s Modular Solution of the Sextic. University Presentation. https://sites.uci.edu/alexsutherland/files/2019/05/Advancement-to-Candidacy-Slides.pdf.
Thiele, R. 2018. Felix Klein in Leipzig, 2nd ed. Leipzig: Edition am Gutenbergplatz.
Tobies, R. 2021. Felix Klein. In Visions for Mathematics, Applications, and Education. Vita Mathematica 20, ed. M. Mattmüller. Boston: Birkhäuser. https://doi.org/10.1007/978-3-662-58749-2.
Valentiner, H. 1889. De endelige Transformations-Gruppers Theori. Avec un résumé en français. Vol. 2. Bianco Lunos.
Veronese, G. 1877. Nuovi teoremi sull’hexagrammum mysticum. Atti della Beale Accademia dei Lincei 3 (1): 649–703.
Veronese, G. 1882. Interprétations géométriques de la théorie des substitutions de n lettres, particulièrement pour n = 3; 4; 5; 6, en relation avec les groupes de l’Hexagramme mystique. Annali di Matematica Pura ed Applicata 11 (1): 93–236.
Veronese, G. 1882. Sui gruppi (\(P\))360, (\(\Pi \))360 della figura di sei complessi lineari di rette due a due in involuzione. Annali di Matematica Pura ed Applicata 11 (1): 284–290.
Wiman, A. 1896. Ueber eine einfache Gruppe von 360 ebenen Collineationen. Mathematische Annalen 47 (4): 531–556.
Wiman, A. 1897a. Note über die symmetrischen und alternierenden Vertauschungsgruppen von n Dingen. In: Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch- Physikalische Klasse 1897.2, pp. 191–197.
Wiman, A. 1897b. Note über die Vertauschungsgruppen von acht Dingen. In: Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse 1897.1, pp. 55–62.
Wiman, A. 1899. Endliche Gruppen linearer Substitutionen. In: Encyklopädie der mathematischen Wissenschaften mit Einschluß ihrer Anwendungen. Vol. Erster Band: Arithmetik und Algebra. Erster Teil. Teubner, pp. 522–554.
Wussing, H. [1969] 2007. The Genesis of the Abstract Group Concept. A Contribution to the History of the Origin of Abstract Group Theory. Dover Publications, Mineola.
Acknowledgements
I would like to express my gratitude to Prof. Alain Genestier for his comments and corrections on the mathematical side of the paper, and to Gerhard Heinzmann for making this exchange possible. I also thank Günther Eder, Eduardo Giovannini, Inger Bakken Pedersen, Georg Schiemer, and Renate Tobies for helpful comments. Finally, I would like to thank Bärbel Mund on behalf of the Manuscript Department at the University Library of Göttingen for her support during my archival work. The current paper is my own work, and no one else is responsible for any mistakes in it.
Funding
Open access funding provided by University of Vienna. Research on this article was funded by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant agreement no. 715222).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author states that there is no conflict of interest.
Archival material
All used archival materials stem from the Niedersächsische Staats- und Universistätsbibliothek Göttingen, Handschriftenabteilung [UBG], particularly from the Klein Nachlass. (Digitally available at: http://hans.uni-goettingen.de/nachlaesse/Klein.pdf.)
Additional information
Communicated by Jeremy Gray.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Heller, H. Felix Klein’s projective representations of the groups \(S_6\) and \(A_7\). Arch. Hist. Exact Sci. 76, 431–470 (2022). https://doi.org/10.1007/s00407-022-00290-x
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00407-022-00290-x







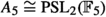 ,
, 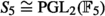 ,
, 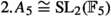 , were probably first systematically studied in the context of Klein’s icosahedron.
, were probably first systematically studied in the context of Klein’s icosahedron.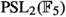 ,
, 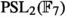 and
and 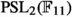 was already known to Galois, but were consequently employed within the Hypergalois Program. Klein himself did not recognize the set-theoretic identities (not as groups!) with “his” symmetry group of the platonic solids:
was already known to Galois, but were consequently employed within the Hypergalois Program. Klein himself did not recognize the set-theoretic identities (not as groups!) with “his” symmetry group of the platonic solids: 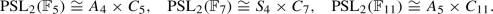
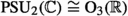 and
and 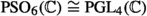 .
.
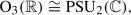
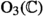 , as a special kind of Möbius transformations,
, as a special kind of Möbius transformations, 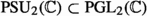 . I come back to this point in Sect.
. I come back to this point in Sect. 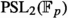 by Gierster (
by Gierster ( ; some of them published in Levy (
; some of them published in Levy ( ; I come back to this point in Sect.
; I come back to this point in Sect.