Abstract
Peirce wrote in late 1901 a text on formal logic using a special Dragon-Head and Dragon-Tail notation in order to express the relation of logical consequence and its properties. These texts have not been referred to in the literature before. We provide a complete reconstruction and transcription of these previously unpublished sets of manuscript sheets and analyse their main content. In the reconstructed text, Peirce is seen to outline both a general theory of deduction and a general theory of consequence relation. The two are the cornerstones of modern logic and have played a crucial role in its development. From the wider perspective, Peirce is led to these theories by three important generalizations: propositions to all signs, truth to scriptibility, and derivation to transformability. We provide an exposition of such proposed semiotic foundation for logical constants and point out a couple of further innovations in this rare text, including the sheet of assertion, correction as a dual of deduction and the nature of conditionals as variably strict conditionals.
Similar content being viewed by others
Notes
The references are to the Papers of Charles S. Peirce, as catalogued by Richard Robin (Peirce 1967).
We thank the reviewer for raising this point on the relevance of Dragon Logic to the foundations of mathematics.
These years are indicative only, given the constantly evolving nature of Peirce’s explorations. For example, higher-order logic was algebraically investigated in his 1885 “On the Algebra of Logic: A Contribution to the Philosophy of Notation” paper (Peirce 1885) though presented in its graphical outfit beginning in 1898.
There are only a few references and hints to them in his other published papers from the early twentieth century, such as the “Some Amazing Mazes” series (Peirce 1908c, d, 1909a). The second Monist paper “Issues of Pragmaticism” (Peirce 1905c) makes one reference; the first, “What Pragmatism Is”, does not (Peirce 1905a). Nor does the published version of the “Neglected Argument for the Reality of God” (Peirce 1908b) refer to EGs.
Sometimes, and especially in relation to Peirce’s model-building games, these roles are split so that the Grapheus and the Interpreter are playing separate roles (Pietarinen 2013). Hilpinen (1982) first identified Peirce’s semantics as a species of the game-theoretic one. On games in logic, see e.g. Pietarinen (2003); Majer et al. (2009).
Similar textual evidence for the game-theoretic interpretation occurs in numerous places, see e.g. R 238, R S-64 and the references in Pietarinen (2003).
Such modifications and extensions of ‘classical’ logic may necessitate modifications to the structural rules of the graphical (sequent) calculus, such as taking the sheet of assertion to be a vector space.
For some further work and applications along the lines, Peirce had set out to do see, for example, Bellucci and Pietarinen (2020); Bellucci et al. (2014); Pietarinen (2010, 2012, 2019); Sowa (2006); Zalamea (2012). For details on Peirce’s deductive logic, see the collection of Houser et al. (1997). Hilpinen (2004) gives a good overview of Peirce’s logic.
Peirce’s preferred spelling.
See also R 516, On the Basic Rules of Logical Transformation, for similar definitions of ‘scriptible’ and ‘transformable’ in the context of the graphical method of the logic of existential graphs.
In the language of existential graphs, a graph that is not scriptible would be one that is surrounded by an oval, or a cut, such as
 . But the cut itself is only a boundary and not something that strictly speaking can be scribed on the sheet. Hence, cuts alone are to be considered to be unscriptible, while enclosures (cuts and their contents) are scriptible.
. But the cut itself is only a boundary and not something that strictly speaking can be scribed on the sheet. Hence, cuts alone are to be considered to be unscriptible, while enclosures (cuts and their contents) are scriptible.Or, one might add, possibly those of adaptive forms of reasoning as well (see e.g. Batens 2004). Moreover, one might be led to wonder whether Peirce had here hit upon an example of a form of reasoning which is none of the three of deduction, induction or abduction. Unless we interpret correction in strictly classical terms of being about negation in the classical sense and not about strong negation or negation as a ‘stopping rule’, ‘failure’ or similar interpretations familiar from non-classical logic and logic programming, or unless we embed correction and non-monotonic consequence into abductive reasoning, we might tentatively conclude that he might well have. In that case, the question remains why he seemed to have forgotten this 1901 invention of his when he in his later writings insisted that there are reasonable—though not conclusive—arguments that establish the presence of three and only three kinds of reasoning (see e.g. R 855–R 856, 1911; Peirce 2019–2021, LoF 1).
For Peirce, and especially as we move towards the last decade of his life, necessary consequences do not exhaust what deduction consists of. Deduction is split into logical analysis (definition) and demonstration. Later he grew increasingly convinced that deduction ought to be characterized in terms of compulsive rather than necessary inferences:
I have hitherto defined [deduction] as necessary reasoning; and no doubt much, perhaps most, possibly all deduction is necessary. But on reviewing the subject for this talk, it seems to me more correct to define Deduction as compulsive reasoning. Retroduction seduces you. Induction appeals to you as a reasonable being. But Deduction first points to the premises and their relation, and then shakes its fist in your face and tells you “Now by God, you’ve got to admit the conclusion”. I beg your pardon, with all my heart, I meant to say, “Now by the eternal world forces spiritual and personal [illeg.]”. Necessary reasoning is reasoning from the truth of whose premises it not only follows that the conclusion is true, but that it would be so under all circumstances. (R 754)
Deduction may be characterized as compulsive rather than necessary in that there is no room for living doubt that the conclusion follows from the premises.
A few years later still, in the Logic Notebook notes from February 1909, Peirce would famously present a sketch of his systems of triadic logic, whose underlying ideas have thus been simmering in the meaning of conditionals, among others, for quite some time.
[R 9, p. 5, Alt.] Let a formal definition be a definition, not of the signification of a sign, but of all the necessary relations between different applications of it. I will proceed to give formal definitions of two
 relations which may be represented by the signs for dragon’s head and tail turned upon their side, and the latter altered slightly, thus:
relations which may be represented by the signs for dragon’s head and tail turned upon their side, and the latter altered slightly, thus:
 ,
,
 . Parentheses round the last two of three signs are omitted. Thus, we write ú
. Parentheses round the last two of three signs are omitted. Thus, we write ú
 à for ú(
à for ú(
 à).
à).We begin with the study of the former relation, which we will first take in a singular sense.
Whatever is written without any indication to the contrary is supposed to be written on a “sheet of assertion” and to be held for true, applicable, justified, etc. [p. 6]

The other definition may be postponed.
Theorem I. Whatever a may be, á
 à.
à.Proof. For whatever u may be, if ú
 à, then ú
à, then ú
 à.
à.The mathematician will say, with some disdain, that most of my “theorems” are corollaries; while some of my corollaries, by a liberal construction of the term, might be dignified with the title of theorems. I wish to say, therefore, that I have to propose, in future, to make a scientific distinction between two classes of mathematical inferences, to one of which the name ‘corollarial’ may be properly applicable, and to the other that of ‘theorematic’. But this distinction is not yet thoroughly worked out, so that, while I attempt to apply it here, I may very likely have given the wrong titles to some of the propositions.
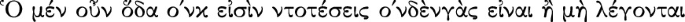
. (\(\mathrm{o}\upnu \updelta \acute{\upvarepsilon }\upnu \) is the reading of the two best MSS.; and perhaps \(\uplambda \acute{\upvarepsilon }\upgamma \mathrm{o}\upnu \uptau \upalpha \upiota \) is one of Apellicon’s conjectures for \(\uplambda \acute{\upvarepsilon }\upgamma \mathrm{o}\upnu \upsigma \upiota \). But that need not be).
 is the sign of Taurus. The more the form of the character approaches mine, the better.
is the sign of Taurus. The more the form of the character approaches mine, the better. and
and
 are the signs for first quarter and last quarter of the Moon.
are the signs for first quarter and last quarter of the Moon.[Alt., p. 6\(\frac{1}{2}\)]...[scripti]ble to an unscriptible sign; where I speak of the entire sign. I shall use conjunctions ‘If
 then
then
 ’, strictly to express the permissibility of a deduction. Therefore, if the sign, i, is unscriptible, ‘If i, then x’ will express a necessarily [sic., contingently] permissible deduction; if the sign, e, is a scriptible sign, ‘If y, then e’ will express a necessarily permissible deduction. Further, this sort of transformation is possible upon the sheet of assertion; so that, supposing ‘If i, then e’ to express a permissible transformation (necessary or contingent), then supposing i to be written on the sheet of assertion, e may also be written. The necessary and sufficient condition of the necessity of a correction is that it should proceed from a sign which need not be written to a sign that must be written.
’, strictly to express the permissibility of a deduction. Therefore, if the sign, i, is unscriptible, ‘If i, then x’ will express a necessarily [sic., contingently] permissible deduction; if the sign, e, is a scriptible sign, ‘If y, then e’ will express a necessarily permissible deduction. Further, this sort of transformation is possible upon the sheet of assertion; so that, supposing ‘If i, then e’ to express a permissible transformation (necessary or contingent), then supposing i to be written on the sheet of assertion, e may also be written. The necessary and sufficient condition of the necessity of a correction is that it should proceed from a sign which need not be written to a sign that must be written.[Alt., p. 7] ...[scripti]ble to an unscriptible sign, where I refer to the entire sign. I shall strictly confine my use of the conjunctions ‘If
 then
then
 ’ to the expression of the permissibility of deductions. A deduction, if permissible, may be performed on the sheet of assertion. That is, whatever
’ to the expression of the permissibility of deductions. A deduction, if permissible, may be performed on the sheet of assertion. That is, whatever
 signs i and e may be, supposing ‘If i, then x’, and supposing i to be
signs i and e may be, supposing ‘If i, then x’, and supposing i to be
 scriptible, e will also be scriptible. Supposing e to be scriptible, then, whatever sign x may be, ‘If x, then e’. Supposing i to be unscriptible, whatever sign y may be, ‘If i then
scriptible, e will also be scriptible. Supposing e to be scriptible, then, whatever sign x may be, ‘If x, then e’. Supposing i to be unscriptible, whatever sign y may be, ‘If i then
 ’. In a correction, the crossing out of the original sign is supposed to signify the condemnation of it as bad. Consequently, the necessary and sufficient condition of the permissibility of a correction will be that
’. In a correction, the crossing out of the original sign is supposed to signify the condemnation of it as bad. Consequently, the necessary and sufficient condition of the permissibility of a correction will be that
 it should proceed from an unscriptible to a scriptible sign. A correction cannot normally be performed on the sheet of assertion, because there will be no occasion for it, but its permissibility may be expressed upon the sheet of assertion or elsewhere. I will use the words ‘Not
it should proceed from an unscriptible to a scriptible sign. A correction cannot normally be performed on the sheet of assertion, because there will be no occasion for it, but its permissibility may be expressed upon the sheet of assertion or elsewhere. I will use the words ‘Not
 but
but
 ’ to express the permissibility of a correction. Consequently, [p. 8] ‘Not(Not i, but e), but x’, where x is a sign entirely vague, will be scriptible or not, in agreement with ‘If e, then i’; although the latter does not directly express all that the former expresses; and ‘If (if e, then i), then y’, where y is a sign entirely general, will be scriptible or not, in agreement with ‘Not i, but e’; although the former expresses an alternative that the latter does not leave open. Since the rules of the notation, which is what I am to consider, are all general, I shall have little occasion for the form of proposition ‘Not
’ to express the permissibility of a correction. Consequently, [p. 8] ‘Not(Not i, but e), but x’, where x is a sign entirely vague, will be scriptible or not, in agreement with ‘If e, then i’; although the latter does not directly express all that the former expresses; and ‘If (if e, then i), then y’, where y is a sign entirely general, will be scriptible or not, in agreement with ‘Not i, but e’; although the former expresses an alternative that the latter does not leave open. Since the rules of the notation, which is what I am to consider, are all general, I shall have little occasion for the form of proposition ‘Not
 , but
, but
 ’. I shall have much occasion to use the form ‘If
’. I shall have much occasion to use the form ‘If
 , then
, then
 ’, not only in its simple form, but also in the form ‘If (if i, then e), then e’. This will be bad, untrue, or unsriptible, if, and only if, ‘If i, then e’ is scriptible while e is unscriptible. But that ‘If i, then e’ should be scriptible although e is unscriptible, requires that i should be unscriptible, lest the passage from i to e should be from the scriptible to the unscriptible. Therefore, ‘If (if i, then e), then e’ is scriptible if and only if i or e (one or [p. 9] other or both) is scriptible. I shall write, whatever i and e may be, ‘either i or e’ to express this; that is, ‘If i then either i or e’, and ‘If e, then either i or e’; and ‘either i or e’ is not scriptible unless so necessitated to be scriptible. The proposition ‘either i or e’ is thus vague, insofar as it does not declare i nor e, but only some one (or both) of the two.
’, not only in its simple form, but also in the form ‘If (if i, then e), then e’. This will be bad, untrue, or unsriptible, if, and only if, ‘If i, then e’ is scriptible while e is unscriptible. But that ‘If i, then e’ should be scriptible although e is unscriptible, requires that i should be unscriptible, lest the passage from i to e should be from the scriptible to the unscriptible. Therefore, ‘If (if i, then e), then e’ is scriptible if and only if i or e (one or [p. 9] other or both) is scriptible. I shall write, whatever i and e may be, ‘either i or e’ to express this; that is, ‘If i then either i or e’, and ‘If e, then either i or e’; and ‘either i or e’ is not scriptible unless so necessitated to be scriptible. The proposition ‘either i or e’ is thus vague, insofar as it does not declare i nor e, but only some one (or both) of the two.By the above convention, this means
 .
. is the sign of Taurus. Get a type that looks as near a Bull’s head as may be. [This annotation reads as an instruction to the typesetter or printer suggests that Peirce might in fact have contemplated to have this earlier version of the manuscript to be typeset or published, possibly along with his other Minute Logic drafts.]
is the sign of Taurus. Get a type that looks as near a Bull’s head as may be. [This annotation reads as an instruction to the typesetter or printer suggests that Peirce might in fact have contemplated to have this earlier version of the manuscript to be typeset or published, possibly along with his other Minute Logic drafts.][The segment that follows here may be discontinuous with the above pages, as
 is used without its definition.]
is used without its definition.][Alt.] Scholium. To one who attaches an absolute value to logical analysis it is a most important fact that a state of knowledge is possible from which the logician [p. 19] could not deduce the idea that anything is false. It is a Garden-of-Eden stage of development in which there is no knowledge of logical Evil; and since Truth, logical Good, consists merely in freedom from falsity, there can be no distinct knowledge of logical Good; although the idea is present in every idea. Though it does not concern me, as a logician to say so, I cannot doubt that every mind passes through this stage of development. If this be true, there must have been such a historical stage of society. For a society is a mind. What is true of logical evil must be true of moral and all other evil; for all are but varieties of logical evil. Therefore, the outline of the story of the Garden of Eden must be true. I have said that no pure logician could ever deduce from such knowledge the idea of falsity. But the Serpent was bound to appear in the guise of the mathematical mind, and suggest falsity. [p. 20] Now the false is no sooner named, than it manifestly exists. For if nothing else is false, it is so. I attribute this dire rôle to the Mathematician, because the precise difference between logical and mathematical thought is that the logician merely analyses the conceptions already had, while the mathematician looks at the situation and produces new conceptions. Whoever started the calumny that the Old Serpent is the “father of lies” must have been one of these flat unraised spirits who would call it a lie to say that a sphere is a ruled surface, or that all spheres have one circle in common.
[Alt.] ...call in question. It is analogous to those public facts of which a law-court will “take cognizance”, without any proof.
Axiom. Something is non-scriptible.
Proof. For suppose this false. Then it is not scriptible on the sheet of assertion; and consequently, it is something non-scriptible, contrary to the hypothesis. Thus, we are driven to admit the axiom.
Although this demonstration is conclusive, it is not a deduction from any of our definitions, which allow the supposition that everything is scriptible. In point of fact, anything can be written on a scrap of paper; none of our definitions forbid it. Nor does the notation provide any means of writing anything contrary to the rules of the notation. It is not until we arbitrarily invent a sign which we define as being non-scriptible that we then create something that is non-scriptible. The “proof” rests upon the observation that [p. 23] the term “non-scriptible”, which the notation had not afforded us any means of writing, is of such a character that as soon as it is admitted among the number of signs there comes to be something non-scriptible. Before that was done, the axiom was not demonstrable. It therefore involves a new premiss, which is, strictly speaking that it is possible to invent a non-scriptible sign. Given that [as] its objective expression, it becomes “something is non-scriptible”, which ought therefore to be accepted as an axiom, the “proof” of which, though formally necessary, involves a petitio principii.
[Peirce changed \(\Diamond \) in the later versions of this paper to
 .]
.]
References
Aristotle. 1831. Aristoteles Graece. Two volumes, ed. Theodor Waitz. Leipzig: Georg Reimer. (Peirce’s Library, the item currently at Johns Hopkins University, JHU) [Peirce mentions Aristotle’s Posterior Analytics. Peirce also listed as his volume “Aristotelis opera, with the commentaries of Averroes, usually referred to in the middle ages as the Commentator, simply. Venice, 1489. Gothic character. 2 vols folio”.]
Aristotle. 1844–1846. Aristotelis Organon graece, ed. Theodor Waitz. Lipsiae: Sumtibus Hahnil. (Peirce’s Library, JHU) [A later edition that Peirce also owned.]
Batens, D. 2004. Extending the realm of logic. The adaptive-logic programme. In Alternative logics. Do sciences need them?, ed. P. Weingartner, 149–164. Berlin: Springer.
Bellucci, F. 2017. Peirce’s speculative grammar: Logic as semiotics. New York: Routledge.
Bellucci, F., and A.-V. Pietarinen. 2016. Existential graphs as an instrument for logical analysis. Part 1: Alpha. The Review of Symbolic Logic 9 (2): 209–237. https://doi.org/10.1017/S1755020315000362.
Bellucci, F., and A.-V. Pietarinen. 2017. From Mitchell to Carus: 14 years of logical graphs in the making. Transactions of the Charles S. Peirce Society 52 (4): 539–575. https://doi.org/10.2979/trancharpeirsoc.52.4.02.
Bellucci, F., and A.-V. Pietarinen. 2020. Notational differences. Acta Analytica 35: 289–314. https://doi.org/10.1007/s12136-020-00425-1.
Bellucci, F., X. Liu, and A.-V. Pietarinen. 2020. On linear existential graphs. Logique et Analyse 251: 261–296. https://doi.org/10.2143/LEA.251.0.3288641.
Bellucci, F., A.-V. Pietarinen, and F. Stjernfelt, eds. 2014. Peirce: 5 questions. Copenhagen: VIP/Automatic Press.
Bobrova, A., and A.-V. Pietarinen. 2019. Thoughts, things and logical guidance. In Peirce and Husserl: Mutual insights on logic, mathematics and cognition. Logic, epistemology, and the unity of science, vol. 46, ed. M. Shafiei and A.-V. Pietarinen. Cham: Springer. https://doi.org/10.1007/978-3-030-25800-9_3.
Clark, G. 1997. New light on Peirce’s iconic notation for the sixteen binary connectives. In Studies in the logic of Charles S. Peirce, ed. N. Houser, D. Roberts, and J. Van Evra, 304–333. Indianapolis, IN: Indiana University Press.
Dekker, P. 2001. Dynamics and pragmatics of ‘Peirce’s Puzzle’. Journal of Semantics 18: 211–241.
Dipert, R. 1995. Peirce’s underestimated place in the history of logic: A response to Quine. In Peirce and contemporary thought, ed. K.L. Ketner, 32–58. New York: Fordham University Press.
Dipert, R. 2004. Peirce’s deductive logic: Its development, influence, and philosophical significance. In The Cambridge companion to Peirce, ed. C. Misak, 257–286. Cambridge, MA: Cambridge University Press.
Euclid. 1883–1916. Euclidis Opera Omnia, ed. J. L. Heiberg and H. Menge, 8 volumes. Lipsiae: B. G. Teubneri. (Peirce’s Library.)
Fisch, M.H. 1982. Peirce’s place in American life. Historica Mathematica 9: 265–287.
Fisch, M.H. 1986. Peirce, semeiotic, and pragmatism: Essays by Max H. Fisch, ed. K.L. Ketner and C.J.W. Kloesel. Bloomington and Indianapolis, IN: Indiana University Press.
Gentzen, G.K.E. 1934. Untersuchungen über das logische Schließen. I. Mathematische Zeitschrift 39 (2): 76–210.
Hamblin, C.L. 1967. One-valued logic. Philosophical Quarterly 17: 38–45.
Hilpinen, R. 1982. On C. S. Peirce’s theory of the proposition: Peirce as a precursor of game-theoretical semantics. The Monist 65 (2): 182–188.
Hilpinen, R. 2004. Peirce’s logic. In Handbook of the history of logic. Vol. 3: The rise of modern logic from Leibniz to Frege, ed. Dov M. Gabbay and John Woods, 611–658. Amsterdam: Elsevier.
Hilpinen, R. 2009. Conditionals and possible worlds: On C. S. Peirce’s conceptions of conditionals and modalities. In The Development of Modern Logic, ed. L. Haaparanta, 551–561. Oxford: Oxford University Press.
Hintikka, J. 1996. The place of C. S. Peirce in the history of logical theory. In The rule of reason: The philosophy of Charles Sanders Peirce, ed. J. Brunning and P. Forster, 13–33. Toronto: University of Toronto Press.
Houser, N., D. Roberts, and J. Van Evra, eds. 1997. Studies in the logic of Charles S. Peirce. Bloomington: Indiana University Press.
Kent, B. 1987. Charles S. Peirce: Logic and the classification of the sciences. Kingston: McGill-Queen’s University Press.
Lewis, C.I. 1918. A survey of symbolic logic. Berkeley: University of California Press.
Lewis, D. 1973. Counterfactuals. Oxford: Blackwell Publishing.
Ma, M. 2018. Peirce’s logical graphs for Boolean algebras and distributive lattices. Transactions of the Charles S. Peirce Society 54 (3): 320–340.
Ma, M., and A.-V. Pietarinen. 2017a. Proof analysis of Peirce’s alpha system of graphs. Studia Logica 105 (3): 625–647.
Ma, M., and A.-V. Pietarinen. 2017b. Graphical sequent calculi for modal logics. Electronic Proceedings in Theoretical Computer Science 243: 91–103. https://doi.org/10.4204/EPTCS.243.7.
Ma, M., and A.-V. Pietarinen. 2017c. Gamma graph calculi for modal logics. Synthese 195: 3621. https://doi.org/10.1007/s11229-017-1390-3.
Ma, M., and A.-V. Pietarinen. 2018a. Peirce’s calculi for classical propositional logic. Review of Symbolic Logic 13 (3): 509–540.
Ma, M., and A.-V. Pietarinen. 2018b. A graphical deep inference system for intuitionistic logic. Logique et Analyse 245: 73–114.
Ma, M., and A.-V. Pietarinen. 2018c. A weakening of alpha graphs: Quasi-Boolean algebras. In Diagrammatic representation and inference. Diagrams 2018. Lecture Notes in Computer Science, vol. 10871, ed. P. Chapman, G. Stapleton, A. Moktefi, S. Perez-Kriz, and F. Bellucci, 549–564. Cham: Springer.
Majer, O., A.-V. Pietarinen, and T. Tulenheimo. 2009. Introduction to logic and games. In Games: Unifying logic, language, and philosophy, ed. O. Majer, A.-V. Pietarinen, and T. Tulenheimo, ix–xxiii. Dordrecht: Springer.
Mitchell, O..H. 1883. On a new algebra of logic. In Studies in logic, by members of Johns Hopkins University, ed. C.S. Peirce, 72–106. Boston: Little, Brown & Company.
Mill, John Stuart. 1846. A System of Logic, Ratiocinative and Inductive. New York. (Peirce’s Library) [Peirce mentions “the first edition of his System of Logic, Ratiocinative and Inductive, published in March, 1843” (LoF 3), and that “Mill’s went through 9 editions (though with the advantage of containing no special novelty)” (LoF 3). Peirce’s copy at Houghton is the heavily annotated edition A System of Logic, Ratiocinative and Inductive: being a connected view of the principles of evidence and the methods of scientific investigation. Longmans, Green, and co., 1886 (London), knows as “People’s edition”.]
Moore, M., ed. 2010. New essays on Peirce’s mathematical philosophy. Chicago: Open Court.
Peirce, C.S. 1880. On the algebra of logic. American Journal of Mathematics 3 (1): 15–57. (Reprinted in: C.J.W. Kloesel (ed.), Writings of C.S. Peirce: A Chronological Edition, Vol. 4, Bloomington, IN: Indiana University Press, 1989, pp. 163–209.)
Peirce, C.S., ed. 1883. Studies in logic by members of the Johns Hopkins University. Boston: Little, Brown, and Co.
Peirce, C.S. 1885. On the algebra of logic: A contribution to the philosophy of notation. American Journal of Mathematics 7 (2): 180–196.
Peirce, C.S. 1891a. Algebra of the copula [Version 1]. In Writings of Charles S. Peirce. Vol. 8 (1890–1892), pp. 210–211. Indiana University Press, 2010.
Peirce, C.S. 1891b. Algebra of the copula [Version 2]. In Writings of Charles S. Peirce. Vol. 8 (1890–1892), pp. 212–216. Indiana University Press, 2010.
Peirce, C.S. 1893a. Grand logic. Division I. Stecheology. Part I. Non relative. Chapter VIII. The algebra of the copula (R 411).
Peirce, C.S. 1893b. Grand logic. Chapter XI. The Boolean calculus (R 417).
Peirce, C.S. 1893c. Grand logic. Book II. Division I. Part 2. Logic of relatives. Chapter XII. The algebra of relatives (R 418).
Peirce, C.S. 1894. Letter to Francis C. Russell. (R L 387).
Peirce, C.S. 1896. The regenerated logic. The Monist 7 (1): 19–40.
Peirce, C.S. 1896-7. On logical graphs. (R 482). In LoF 1, 211–261.
Peirce, C.S. 1897b. The logic of relatives. The Monist 7(2)(January): 161–217. (Reprinted in CP 3.456–552).
Peirce, C.S. 1898. On existential graphs, F4 (R 484). In LoF 1.
Peirce, C.S. 1900. Letter to Christine Ladd-Franklin, November 9, 1900 (R L 237). In LoF 3/2.
Peirce, C.S. 1901. New elements (Kaina stoicheia) (R 517). Houghton Library. (Reprinted in NEM IV, pp. 235–263; EP 2, pp. 300–324).
Peirce, C.S. c.1901a. A proposed logical notation (R 530). In LoF 1.
Peirce, C.S. c.1901b. On the first principles of logical algebra (R 515). In LoF 1.
Peirce, C.S. c.1901c. On the basic rules of logical transformation (R 516). In LoF 1.
Peirce, C.S. 1902. Minute logic. Chapter III. The simplest mathematics (Logic III) (R 430). In LoF 1.
Peirce, C.S., and C. Ladd-Franklin. 1902. Symbolic logic, or algebra of logic. In Dictionary of philosophy and psychology, vol. 2, ed. James Mark Baldwin, 640–651. London: Macmillan and Co., Ltd. In LoF 3/2.
Peirce, C.S. 1903a. Logical tracts. No. 1. On existential graphs (R 491). In LoF 2/1.
Peirce, C.S. 1903b. Logical tracts. No. 2. On existential graphs, Euler’s diagrams, and logical algebra (R 492). In LoF 2/1.
Peirce, C.S. 1903c. Some topics of logic bearing on questions now vexed (The Lowell Lectures of 1903). Lecture II(b) (R 455-456, R S-29, R S-33). In LoF 2/2.
Peirce, C.S. 1903d. Some topics of logic bearing on questions now vexed (The Lowell Lectures of 1903). Lecture III(c) (R 464). In LoF 2/2.
Peirce, C.S. 1903e. Syllabus of some topics of logic bearing on questions now vexed (The Lowell Lectures of 1903) (R 478). In LoF 2/2.
Peirce, C.S. 1905a. What pragmatism is. The Monist 15 (2)(April): 161–181. (Reprinted in CP 5.411–437).
Peirce, C.S. 1905b. A logical analysis of some demonstrations in high arithmetic (D) (R 253). In LoF 1.
Peirce, C.S. 1905c. Issues of pragmaticism. The Monist 15 (4)(October): 481–499. (Reprinted CP 5.438–463).
Peirce, C.S. 1906. Prolegomena to an apology for pragmaticism. The Monist 16(4) (October): 492–546. Errata: The Monist 17(1) (January), 1907, p. 160. (Reprinted in CP 4.530–572).
Peirce, C.S. 1908a. One, two, three (R 905). In LoF 3/1.
Peirce, C.S. 1908b. A neglected argument for the reality of God. Hibbert Journal 7: 90–112. (Reprinted in CP 6.452–485; EP 2, pp. 434–450).
Peirce, C.S. 1908c. Some Amazing Mazes. The Monist 28(2), pp. 227–241. (Reprinted in CP 4.585–593).
Peirce, C.S. 1908d. Some amazing mazes (Conclusion). Explanation of curiosity the first. The Monist 28 (3): 416–464. (Reprinted in CP 4.594–642).
Peirce, C.S. 1909a. Some amazing mazes, a second curiosity. The Monist 29 (1): 36–45. (Reprinted CP 4.643–646).
Peirce, C.S. 1931–1966. The collected papers of Charles S. Peirce, 8 vols., ed. by C. Hartshorne, P. Weiss and A.W. Burks, Cambridge: Harvard University Press. Cited as CP followed by volume and paragraph number.
Peirce, C.S. 1967. Manuscripts in the Houghton Library of Harvard University. Identified by Richard Robin, Annotated Catalogue of the Papers of Charles S. Peirce, Amherst: University of Massachusetts Press, 1967, and The Peirce Papers: A supplementary catalogue. Transactions of the C. S. Peirce Society 7 (1971), pp. 37–57. Cited as R followed by manuscript number.
Peirce, C.S. 1976. The new elements of mathematics by Charles S. Peirce, 4 vols., ed. by C. Eisele, The Hague: Mouton. Cited as NEM followed by volume and page number.
Peirce, C.S. 1982-. Writings of Charles S. Peirce: A chronological edition. 7 vols., ed. E.C. Moore, C.J.W. Kloesel et al. Bloomington: Indiana University Press. Cited as W followed by volume and page number.
Peirce, C.S. 1998. The essential Peirce. Volume II, ed. by Peirce Edition Project. Bloomington: Indiana University Press. Cited as EP 2 followed by page number.
Peirce, C.S. 2010. Philosophy of mathematics: Selected writings, ed. M. Moore. Bloomington: Indiana University Press. Cited as PoM.
Peirce, C.S. 2020. Charles S. Peirce. Semiotic writings, ed. F. Bellucci, Berlin & Boston: De Gruyter. Cited as SW followed by page number.
Peirce, C.S. 2019–2021. Logic of the future: Writings on existential graphs, A.-V. Pietarinen, Vol.1: History and Applications, 2019; Vol. 2/1: The Logical Tracts; 2/2: The 1903 Lowell Lectures; Vol.3/1: Pragmaticism; Vol.3/2: Correspondence. De Gruyter (2019–2021). Cited as LoF followed by volume and page number.
Pietarinen, A.-V. 2001. Most even budged yet: Some cases for game-theoretic semantics in natural language. Theoretical Linguistics 27 (1): 20–54.
Pietarinen, A.-V. 2003. Peirce’s game-theoretic ideas in logic. Semiotica 144 (14): 33–47.
Pietarinen, A.-V. 2006a. Signs of logic: Peircean themes on the philosophy of language, games, and communication. Dordrecht: Springer.
Pietarinen, A.-V. 2006b. Interdisciplinarity and Peirce’s classification of the sciences: A centennial reassessment. Perspectives on Science 14 (2): 127–152.
Pietarinen, A.-V. 2007. Game theory and linguistic meaning. (Current Research in the Semantics/Pragmatics Interface 18). Oxford: Elsevier Science.
Pietarinen, A.-V. 2010. Peirce’s pragmatic theory of proper names. Transactions of the Charles S. Peirce Society 46 (3): 341–363.
Pietarinen, A.-V. 2012. Why is the normativity of logic based on rules? In The normative thought of Charles S. Peirce, ed. Cornelis De Waal and Kristof P. Skowronski, 172–184. Fordham: Fordham University Press.
Pietarinen, A.-V. 2013. Logical and linguistic games from Peirce to Grice to Hintikka. Teorema 33 (2): 121–136.
Pietarinen, A.-V. 2015a. Two papers on existential graphs by Peirce. Synthese 192: 881–922.
Pietarinen, A.-V. 2015b. Signs systematically studied: Invitation to Peirce’s theory. Sign Systems Studies 43 (4): 372–398. Recent Studies on Signs: Commentary and Perspectives, pp. 616–650; [Division of Signs, by Charles Peirce], pp. 651–662.
Pietarinen, A.-V. 2019. Semeiotic completeness in the theory of signs. Semiotica: Journal of the International Association for Semiotic Studies/Revue de l’Association Internationale de Sémiotique 228: 237–257.
Pietarinen, A.-V., F. Bellucci, A. Bobrova, N. Haydon, and M. Shafiei. 2020. The blot. Lecture Notes in Artificial Intelligence, vol. 12169, 225–238. Cham: Springer.
Pietarinen, A.-V., and F. Stjernfelt. 2021. Semiotics of mathematics and logic. In Bloomsbury companion of semiotics, ed. J. Pelkey. London: Bloomsbury Publishing.
Pratt, V. 1992. Origins of the calculus of binary relations. In Proceedings of seventh annual IEEE symposium on logic in computer science, Vol. 1, 248–254.
Putnam, H. 1982. Peirce the logician. Historia Mathematica 9: 290–301.
Roberts, D.D. 1973. The existential graphs of Charles S. Peirce. The Hague: Mouton.
Riemann, Bernhard. 1854/1867. “Über die Hypotheses, welche der Geometrie zu Grunde liegen”. Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen 13, 132–152. [Riemann’s inaugural lecture read in 1854 and published in 1867.]
Sanford, D.H. 1989. If P then Q: Conditionals and the foundations of reasoning. London: Routledge.
Shin, S.-J. 2002. The iconic logic of Peirce’s graphs. Cambridge, MA: MIT Press.
Short, T. 2007. Peirce’s theory of signs. Cambridge, MA: Cambridge University Press.
Stalnaker, R.C. 1968. A theory of conditionals. In Studies in logical theory, ed. N. Rescher, 98–112. Oxford: Blackwell.
Stjernfelt, F. 2007. Diagrammatology. Dordrecht: Springer.
Sowa, J. 2006. Peirce’s contributions to the 21st century. In Proceedings of the 14th international conference on conceptual structures. Lecture Notes in Computer Science, vol. 4068, 54–69.
Wadding, Luke (ed.). 1639. Scotus, Duns. Ioannis Duns Scoti Opera Omnia. Twelve Volumes. London: Laurent Durand. (Peirce’s Library, JHU) [Peirce owned Volumes 1–4 of Duns Scotus’s Opera Omnia, together with at least thirteen other 15th, 16th and early 17th century works by Scotus (JHU). Thomas of Erfurt’s Tractatus de modis significandi sive Grammatica Speculativa is included in Volume 1 of the Wadding edition.]
Wolff, Christian. 1713. Vernünfftige Gedancken Von den Kräfften des menschlichen Verstandes Und ihrem Richtigen Gebrauche In Erkäntnißder Wahrheit. Halle im Magdeburgischen Renger Halle, Saale Halle. [Peirce’s citation was to “Vernünftige Gedanken von den Kräften des menschlichen Verstanden, 1710” (LoF 1). Peirce owned at least thirteen volumes of Wolff’s works, current provenance at JHU.]
Zalamea, F. 2012. Peirce’s logic of continuity: A mathematical and conceptual approach. New York: Docent Press.
Zellweger, S. 1997. Untapped potential in Peirce’s iconic notation for the sixteen binary connectives. In Studies in the logic of Charles S. Peirce, ed. N. Houser, et al., 334–386. Indianapolis, IN: Indiana University Press.
Zeman, J. 1964. The graphical logic of Charles S. Peirce, Ph.D. thesis, University of Chicago.
Acknowledgements
We thank Jukka Nikulainen for equipping his LaTeXpackage EGpeirce with all the special symbols that occur in the copy text, namely

,

,

,

,

and

. He is also to be thanked for making a wealth of other Peirce-specific signs available in that package. The documentation of EGpeirce.sty has the details. Transcriptions are published by the kind permission of Harvard University’s Houghton Library. Last, our thanks go to the reviewers of the journal for their precise comments that have much helped in our efforts not only in improving the presentation of the work but also in order to make better sense of the status of Peirce’s logic as it obtained at the turn of the century.
Funding
Work (Ma Minghui) supported by Chinese National Funding of Social Sciences (Grant No. 18ZDA033) and (Ahti-Veikko Pietarinen) by Estonian Research Council’s Personal Research Grant PUT 1305 (“Abduction in the Age of Fundamental Uncertainty”, 2016–2018, the Basic Research Program at the National Research University Higher School of Economics, and Chinese National Funding of Social Sciences “The Historical Evolution of Logical Vocabulary and Research on Philosophical Issues” (Grant No. 20& ZD046).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare they have no financial or non-financial interests.
Additional information
Communicated by Jeremy Gray.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
[On the Foundations of Mathematics], R 9, R 11, R 501, c.1901
[R 9, p. 1] §1. A sign is not a real thing. The same sign may occur or as we may say,
 can be uttered, over and over again. We may call these things embodying the same sign replicas of it. They need not be alike as things. Man, homo,
can be uttered, over and over again. We may call these things embodying the same sign replicas of it. They need not be alike as things. Man, homo,
 \(\upnu \!\uptau \!\uprho \!\mathrm{o}\!\uppi \!\mathrm{o}\!\varsigma \) are the same sign. A sign is
\(\upnu \!\uptau \!\uprho \!\mathrm{o}\!\uppi \!\mathrm{o}\!\varsigma \) are the same sign. A sign is
 intended to correspond to a real thing or fact, or to something relatively real; this object of the sign may be the very sign itself, as when a map is precisely superposed upon that which it maps. It is a perfection in a sign if it separately represent its object; in which case it becomes a proposition and is true or false. A sign is also
intended to correspond to a real thing or fact, or to something relatively real; this object of the sign may be the very sign itself, as when a map is precisely superposed upon that which it maps. It is a perfection in a sign if it separately represent its object; in which case it becomes a proposition and is true or false. A sign is also
 intended to determine, in a mind or elsewhere, a sign of the same object; this interpretant of the sign may be the very sign itself, but as a general rule it will be different. It is a perfection in a sign separately to signify its intended interpretant. If it does this, it becomes an argumentation or [p. 2] argument. (Some pedants insist on the former word; but the very best usage supports the latter.)
intended to determine, in a mind or elsewhere, a sign of the same object; this interpretant of the sign may be the very sign itself, but as a general rule it will be different. It is a perfection in a sign separately to signify its intended interpretant. If it does this, it becomes an argumentation or [p. 2] argument. (Some pedants insist on the former word; but the very best usage supports the latter.)
§2. A sign must, from the nature of it, be applicable to different objects, supposing there happen to exist any such objects. This [is] true even of a proper name. Phillip of Macedon may stand for Phillip drunk, or for Phillip sober, or for the collective Phillip. But, from a special point of view, a sign may be regarded as proper to a single object. If a sign is apt to represent many things, the option as to what single thing it shall be taken to represent may be reserved by the utterer of it, to whom it naturally belongs, in which case it may be said to be used vaguely, or not definitely. The utterer may, however, transfer this option to the interpreter, in which case the sign may be said to be used generally, or not individually. Obviously the option cannot, in the same respect, at once lie with both parties. Hence, a sign cannot be at once vague and general in the same respect. It may, [p. 3] however, be both definite and individual, and in that case may be said to be used singularly. ‘Man’ is used vaguely in ‘Some man sins’; generally, in ‘Every man sins’; singularly, in ‘This man sins’. If we put Roman lower-case letters for ordinary signs, we may put an acute accent over a letter, as á, to show that it is taken generally; a grave accent, à, to show that it is used vaguely; and a circumflex, â, to show that it is used singularly.
§3. Let us use the sign of the moon’s first quarter,
 , to signify a dyadic relation, and
, to signify a dyadic relation, and
 for its converse. Thus, â
for its converse. Thus, â
 ê might mean ‘Socrates loves Plato’. Then we shall have,
ê might mean ‘Socrates loves Plato’. Then we shall have,

But á
 è may be understood in two senses. For here the utterer is to determine the object of e; the interpreter that of a. The utterer is essentially a defender of his own [p. 4] proposition and wishes to interpret it so that it will be defensible. The interpreter, not being so interested, and being unable to interpret it fully without considering to what extreme it
è may be understood in two senses. For here the utterer is to determine the object of e; the interpreter that of a. The utterer is essentially a defender of his own [p. 4] proposition and wishes to interpret it so that it will be defensible. The interpreter, not being so interested, and being unable to interpret it fully without considering to what extreme it
 may reach, is relatively in a hostile attitude, or looks for the interpretation least defensible. Whichever of the two makes his choice of the object he is to choose, after the other has made his choice, is supposed to know what that choice was. This is an advantage to the defence or attack, as the case may be. If we enclose the earlier choice in parenthesis (á
may reach, is relatively in a hostile attitude, or looks for the interpretation least defensible. Whichever of the two makes his choice of the object he is to choose, after the other has made his choice, is supposed to know what that choice was. This is an advantage to the defence or attack, as the case may be. If we enclose the earlier choice in parenthesis (á
 )è will signify more than á(
)è will signify more than á(
 è). We may omit the parentheses from the last.
è). We may omit the parentheses from the last.
§4. For purposes of logical criticism, vague and general signs are to be treated as substitutes for singulars.

§5. Let a formal definition be defined as a definition, not of the peculiar qualitative signification, or flavour, of its definitum, but of the essential relations between different applications of it.Footnote 19 I proceed to give formal definitions establishing a system of notation, beginning with a certain sign of relation,
 (a “dragon’s head” turned on its side), and since, to begin with, this is to be taken in a singular sense, a circumflex accent shall surmount it. We shall be supposed to be provided with a certain blank sheet, to be called the “sheet of assertion”; in connection with this we are to be supposed to have a certain purpose, which remains vague, so that the writing of any given sign on the sheet of assertion may or may not accord with that purpose, but the purpose does not require any entire sign to be written. Whether or not any or every sign rendered possible by the system of notation may be written, as an entire sign, on the [p. 6] sheet of assertion conformably to the purpose, remains to be seen.
(a “dragon’s head” turned on its side), and since, to begin with, this is to be taken in a singular sense, a circumflex accent shall surmount it. We shall be supposed to be provided with a certain blank sheet, to be called the “sheet of assertion”; in connection with this we are to be supposed to have a certain purpose, which remains vague, so that the writing of any given sign on the sheet of assertion may or may not accord with that purpose, but the purpose does not require any entire sign to be written. Whether or not any or every sign rendered possible by the system of notation may be written, as an entire sign, on the [p. 6] sheet of assertion conformably to the purpose, remains to be seen.
A sign that may be so written as an entire sign will be termed scriptible, good, true, etc. Otherwise, it will be unscriptible, bad, false, etc. The mere writing of the sign, as an entire sign, conformably to the purpose of the notation is to be considered as, in effect, conclusive evidence that it is scriptible. This establishes a relation between propositions which we may really judge to be true concerning the notation, and signs which we may imagine to be written conformably to our imagined purpose upon the imagined sheet of assertion. In order that a notation should have an algebraic character, it must be that under certain conditions transformations should be permitted. Such transformation may either leave the original sign standing and add another, in which case it may be called a deduction, or it may involve the
 crossing-out of the first sign, in which case, it may be called a correction. The necessary and sufficient condition of the permissibility of a deduction is that it should not proceed from a scriptible [p. 7] to an unscriptible sign; where I refer to the entire sign. I shall strictly confine my use of the conjunctions ‘If
crossing-out of the first sign, in which case, it may be called a correction. The necessary and sufficient condition of the permissibility of a deduction is that it should not proceed from a scriptible [p. 7] to an unscriptible sign; where I refer to the entire sign. I shall strictly confine my use of the conjunctions ‘If
 then
then
 ’ to the permissibility of deductions. But it is to be observed that I do not here
’ to the permissibility of deductions. But it is to be observed that I do not here use confine the word deduction to logical deductions, but extend it to all statements of consequences. That is to say the consequent may be true if the antecedent is true, merely as a matter of fact, not necessarily by virtue of the logical form, or because an analogous deduction would be true in every universe to which the language would be applicable at all. Ordinarily deductions are general with respect to their antecedent. Thus to say, ‘If a man is ill, he will be excused from business’, is to give the interpreter a right to apply the remark to any case of a man’s being ill that he can find. Being general, it is, in the same respect, definite. The utterer does not reserve to himself any right to limit the breadth of application of the antecedent. But in speaking of  , the generality of the deduction disappears. [p. 8] The antecedent refers to a single event or state of things without any reference to analogous cases. Therefore, we cannot say, as a universal rule, that a deduction is general with respect to its antecedent, but only that it is definite. In an ordinary conditional proposition, there is a tacit implication that there is some reason for the consequence, which is not stated. In
, the generality of the deduction disappears. [p. 8] The antecedent refers to a single event or state of things without any reference to analogous cases. Therefore, we cannot say, as a universal rule, that a deduction is general with respect to its antecedent, but only that it is definite. In an ordinary conditional proposition, there is a tacit implication that there is some reason for the consequence, which is not stated. In
 respect to the reason of the antecedent, the proposition is vague. But this is not necessarily so: the reason may be fully stated in the antecedent. All that can be said universally, is that the interpreter is not allowed to
respect to the reason of the antecedent, the proposition is vague. But this is not necessarily so: the reason may be fully stated in the antecedent. All that can be said universally, is that the interpreter is not allowed to
 attribute to the utterer such reason as he likes. In respect to the reason of the antecedent, the proposition is individual. In regard to the consequent, the interpreter is at liberty to single out by abstraction any of the elements of the meaning of the consequent. ‘If a man is ill he will be excused from business’. To be excused, he must be a moral being. Therefore, the interpreter may take the sentence as implying that if a man is ill, he remains a moral being. But since the [p. 9] consequent may conceivably be unanalyzable, we can only say that it is definite in its logical depth. For so far as it [is] indefinite in this respect, it is meaningless; as ‘If a man is ill he has some resemblance to an excused man’. On the other hand in its application to an object, the consequent retains its natural vagueness. ‘If a man is ill, he is excused etc.’ does not say what individual man he is. But since, it may be definite in that respect, we can only say that it confers no liberty of choice of the object upon the inter[preter] [end]
attribute to the utterer such reason as he likes. In respect to the reason of the antecedent, the proposition is individual. In regard to the consequent, the interpreter is at liberty to single out by abstraction any of the elements of the meaning of the consequent. ‘If a man is ill he will be excused from business’. To be excused, he must be a moral being. Therefore, the interpreter may take the sentence as implying that if a man is ill, he remains a moral being. But since the [p. 9] consequent may conceivably be unanalyzable, we can only say that it is definite in its logical depth. For so far as it [is] indefinite in this respect, it is meaningless; as ‘If a man is ill he has some resemblance to an excused man’. On the other hand in its application to an object, the consequent retains its natural vagueness. ‘If a man is ill, he is excused etc.’ does not say what individual man he is. But since, it may be definite in that respect, we can only say that it confers no liberty of choice of the object upon the inter[preter] [end]
[p. 6\(\frac{1}{2}\)]


Corollary 1. Whatever a may be,

For putting a for e in Clause 2,

But putting a for i in Clause 1,

Corollary 2. From Clause 1 and Clause 2, whatever i, a, e, may be,

[Corollary 3. Crossed out.]
[p. 7]
Theorem I. If e be such that, whatever x may be,  , then e.
, then e.
Proof
For assume that, whatever x may be,  . Then I have only to prove e. Let x be
. Then I have only to prove e. Let x be  . Then, by hypothesis,
. Then, by hypothesis,  ; whence, by Clause 3, if
; whence, by Clause 3, if  then e; whence, by Corollary 1, e. \(\square \)
then e; whence, by Corollary 1, e. \(\square \)
Theorem II. Whatever a and e may be, in case, whatever x may be,

 will be scriptible.
will be scriptible.
Proof
For suppose a and e to be any such things that, whatever x may be, if  then
then  . Then, I have only to show that
. Then, I have only to show that  . Let x be a. Then, by hypothesis, if
. Let x be a. Then, by hypothesis, if  then
then  ; whence, by Corollary 1,
; whence, by Corollary 1,  . \(\square \)
. \(\square \)
Theorem III. Whatever i and a may be, in case, whatever x may be,

 will be scriptible.
will be scriptible.
Proof
For suppose i and a to be any such things that, whatever x may be, if  then
then  . Then I have only to show that
. Then I have only to show that  . Let x be a. Then, by hypothesis, if
. Let x be a. Then, by hypothesis, if  , then
, then  ; whence, by Corollary 1,
; whence, by Corollary 1,  . \(\square \)
. \(\square \)
[p. 8]
Theorem IV. Whatever i, a, e may be, if

then

Proof
For suppose i, a, e, to be any such things that  . Then I have only to show that
. Then I have only to show that  . By Clause 1,
. By Clause 1,
-
(No. 1) If e, then
 .
. -
(No. 2) If
 , then
, then  . By Clause 2,
. By Clause 2, -
(No. 3) Either i or
 .
. -
(No. 4) Either a or
 . By Clause 3,
. By Clause 3, -
(No. 5) If i and
 , then
, then  .
. -
(No. 6) If a and
 , then e. By (No. 5) and the hypothesis,
, then e. By (No. 5) and the hypothesis,
if i, then  ; whence, by (No. 3), either
; whence, by (No. 3), either  or
or  ; whence by (No. 6), either
; whence by (No. 6), either  or if a then e; whence by (No. 1), if a, then
or if a then e; whence by (No. 1), if a, then  ; whence, by (No. 2), if a, then
; whence, by (No. 2), if a, then  ; whence, by (No. 4),
; whence, by (No. 4),  . \(\square \)
. \(\square \)
[p. 9]
Theorem V. Whatever i, a, e may be, if  , then either i or e.
, then either i or e.
Proof
For suppose i, a, e to be any such things that  . Then I have only to show that either i or e. By Clause 3, if
. Then I have only to show that either i or e. By Clause 3, if  and
and  , then e; whence, by the hypothesis, if
, then e; whence, by the hypothesis, if  then e. But by Clause 2, either i or
then e. But by Clause 2, either i or  ; whence either i or e. \(\square \)
; whence either i or e. \(\square \)
Theorem VI. Whatever i, a, e may be, if  , then
, then  .
.
Proof
For suppose i, a, e to be any such things that  . Then I have only to show that
. Then I have only to show that  . By Clause 1,
. By Clause 1,
-
(No. 1) If a, then
 .
. -
(No. 2) If e, then
 . By Clause 2,
. By Clause 2, -
(No. 3) Either a or
 . By Clause 3,
. By Clause 3, -
(No. 4) If
 and
and  , then e.
, then e.
By (No. 4) and the hypothesis, if  then e; whence by (No. 1), if a then e; whence, by (No. 3), either
then e; whence by (No. 1), if a then e; whence, by (No. 3), either  or e; whence by (No. 2),
or e; whence by (No. 2),  . \(\square \)
. \(\square \)
[p. 10]
Theorem VII. Whatever i, a, e may be, if either e or both i and  , then
, then  .
.
Proof
For, by Clause 1, if e then  . Consequently, it will be sufficient to prove that if i and
. Consequently, it will be sufficient to prove that if i and  then either e or
then either e or  . For this purpose, assume that i, a, e are any such things that; (1), i; and (2),
. For this purpose, assume that i, a, e are any such things that; (1), i; and (2),  . Then I have only to show that either e or
. Then I have only to show that either e or  . By Clause 2,
. By Clause 2,
-
(No. 1) Either
 or
or  . By Clause 3,
. By Clause 3, -
(No. 2) If a and
 , then e.
, then e. -
(No. 3) If i and
 , then a.
, then a.
By (No. 2) and the second assumption, if a then e; whence, by (No. 3), if i and  , then e; whence, by the first assumption, if
, then e; whence, by the first assumption, if  then e; whence by (No. 1) either e or
then e; whence by (No. 1) either e or  . \(\square \)
. \(\square \)
Corollary 3. Hence, à fortiori, if both  and either i or e, then
and either i or e, then  .
.
Scholium. This is the most difficult of all the theorems of this section and may be considered as the key to the subject.
[p. 11]
Theorem VIII. Whatever i and a may be, if i then  .
.
Proof. For, by Theorem VII, whatever i, a, e may be, if both i and  then
then  . Let e be a. Then, if both i and
. Let e be a. Then, if both i and  , then
, then  ; whence, by Corollary 1, if i then
; whence, by Corollary 1, if i then  .Footnote 20
.Footnote 20
Corollary 4. By Clause 2, either i or  . But by Clause 1, if e then
. But by Clause 1, if e then  . Hence, if from i follows e then
. Hence, if from i follows e then  .
.
Corollary 5. If  , then
, then  . For, by Theorem VIII, if
. For, by Theorem VIII, if  , then from i follows
, then from i follows  ; whence, by Corollary 4, if
; whence, by Corollary 4, if  , then
, then  ; whence, by Theorem IV, if
; whence, by Theorem IV, if  , then
, then  .
.
[p. 12]
Corollary 6. From Corollary 5, it follows, by Clause 3, that if  and
and  , then
, then  .
.
Corollary 7. From Corollaries 6 and 4, it follows that if  , then
, then  .
.
Scholium. All that logical criticism is concerned about is to secure the reasoner against passing from a true premiss, or antecedent, to a false conclusion, or consequent. All that is meant, therefore, in this paper by ‘If x, then y’ is that in passing from x, as antecedent, to y, as consequent, the reasoner will be so secure. That is, that y cannot be false and x true at the same time. Thus, the conditional proposition has a different meaning from ordinary conditional propositions. For an ordinary conditional proposition refers to a general range of possibilities of the fulfillment of the antecedent condition, from which the interpreter is at liberty to select any case he likes (under assumptions supposed to be agreed upon, although they are commonly more or less vague), and the truth of the consequent is guaranteed by the asserter in every case. But Scotus [Wadding 1639] and other logicians consider a kind of conditional that occasionally [p. 13] occurs in ordinary speech, and which they term a “conditional proposition de inesse”. This does not refer to any general range of possibilities, but only to a definite and individual state of things. Everything written on our “sheet of assertions” in the present paper is supposed to represent a definite and individual universe, “the Truth”; so that when a conditional proposition, say ‘If i, then e’ is written on the sheet, no illative connection is implied between i and e, which should mean that throughout a general range of possibilities the truth of anything analogous to i would be accompanied by the truth of something corresponding to e, but all that is meant is that taking the universe of Truth in the state in which it happens to be, although i may not be true (or applicable, or justifiable, or whatever is the appropriate variety of scriptibility), and should it not be so, nothing whatever is said about e, yet provided i is true, the interpreter may be sure that e is true. That is in passing from i to e, one would not pass from truth to falsity. For example, [p. 14] considered as a proposition de inesse, it would be true to say that ‘If 6 is not divisible by 3, it is a prime number’, or ‘If a quadratic equation has two roots, a quadrangle has two dimensions’, or ‘If 7 is greater than 8, then 8 is greater than 7’. Perhaps it may aid to reconcile the reader to such language to call attention to a feature of conditionals of the ordinary kind. The proposition that ‘If a sensible man were, under ordinary circumstances to deliberately dash a full inkstand upon his library floor, he would voluntarily ruin his carpet (supposing the room to be carpeted)’ is certainly true, since an inkstand thrown on such a floor would inevitably ruin the carpet; and a sensible man would know this; so that if he did it, he would do it voluntarily. At the same time no sensible man would, under any ordinary circumstances, voluntarily ruin his library carpet. From this it follows that ‘If a sensible man were, under ordinary circumstances, deliberately dash a full inkstand upon his library floor, he would so do it, or at least design so to do it as not to ruin his carpet, for he would not voluntarily ruin his carpet’, for if a man [p. 15] were to do such a thing, he would be out of his senses. Here, then, are two contradictory propositions both true at once. This is possible because they refer to general conditions, and generals are not subject to the principle of contradiction. The truth is that no sensible man under ordinary circumstances would throw a full inkstand on his library floor. What reconciles us to a conditional proposition with a false antecedent is that, though it does not apply in the particular contingency, there are a great many cases where the general principle does apply; and in those cases it is true; and the utterer, disclaiming all attempt to find out whether the present case is one of those, but throwing the determination upon the interpreter, states what the interpreter will find when he meets such a case, if he ever does. Now the conditional de inesse is merely the limiting case when the general class of cases referred to is but a single state of things. The
 asserter still
asserter still
 refuses all responsibility for the antecedent. That is the concern of the interpreter. He simply guarantees him against all danger of passing from truth to falsity.
refuses all responsibility for the antecedent. That is the concern of the interpreter. He simply guarantees him against all danger of passing from truth to falsity.
[p. 16] But such a proposition perplexes the ordinary interpreter, because in ordinary conditionals it is left to the interpreter’s good sense, to guess what is the class of analogous cases to which the antecedent is meant to apply, and consequently, when he meets with a conditional de inesse, he straightway casts about for such a class of cases, although no such class is referred to. In these propositions, ‘If A is true, then B is true’ practically amounts merely to saying that ‘Either A is not true or B is true (or both)’; the only difference being that the conditional makes no positive suggestion that A may not be true.

Clause 1. Whatever i and e may be, if \(i=e\) and i, then e.
Clause 2. Whatever i and e may be, if \(i=e\) and e, then i.
Clause 3. Supposing that if i then e, and if e then i, then, whatever i and e may be, \(i=e\).
[p. 17]
Corollary 8. If i then  . For assume, first, that i and e are any such things that if i then e. Then, since by Clause 2 of the Definition of
. For assume, first, that i and e are any such things that if i then e. Then, since by Clause 2 of the Definition of  , either i or
, either i or  , it follows that either e or
, it follows that either e or  . But, by Clause 1 of the same Definition, if e then
. But, by Clause 1 of the same Definition, if e then  . Hence e. Thus, it is proved that
. Hence e. Thus, it is proved that
-
(No. 1) Supposing that if i then e, it follows that
 .
.
Secondly, assume that i and e are any such things that  . Then, by Clause 3 of the Definition of
. Then, by Clause 3 of the Definition of  , it follows that if i, then e. Thus, it is proved that, whatever i and e may be
, it follows that if i, then e. Thus, it is proved that, whatever i and e may be
-
(No. 2) Supposing that
 , it follows that if i then e.
, it follows that if i then e.
From (No. 1) and (No. 2), taken together with Clause 3 of the Definition of =, the corollary follows.
Scholium. The explanation of the meaning of the word postulate (
 \(\acute{\upiota }\uptau \upvarepsilon \upmu \upalpha \)) given by Aristotle (1831, 1844) (who must have had some acquaintance with mathematics to be admitted into the school of Plato, and must there have become familiar with the language of mathematics, [p. 18] as his writings show that he was with their discussions of that time) entirely agrees with the usage of Euclid in the following century, and with the established meaning of the word in English and in French. Aristotle, as is explained by Johannes Philoponus, draws an insignificant distinction between a postulate and a hypothesis, which latter word he uses in several allied senses, but disregarding idle distinctions, we may say that Aristotle gives to the word postulate the precise signification which Riemann attached to hypothesis when he wrote “Über die Hypotheses welche der Geometrie zu Grunde liegen” (Riemann 1854/1867). The point about which Aristotle is most particular is that a postulate is not evidently true. The distinction which he makes between hypothesis, or supposition, in one of its senses, and postulate, in its only sense, is that the interpreter will already believe a hypothesis and will have no positive belief in a [p. 19] postulate. Two millennia of familiarity with the postulates of geometry seem to have bred in us a traditional and almost natural belief in most of them. Any close student of the first book of the Elements will, I believe, agree with me that Euclid purposely throws his fifth postulate (the one about parallels) into a form intended to bring about its non-evident character. This, then, is the meaning which we ought to attach to the word postulate. It is the only meaning upon which good usage, in English and French, can remain or ever be fixed. The Germans, under the influence of Baron Christian Wolff (1713), commonly attach to the word Postulat an abusive meaning of considerable antiquity; that of an indemonstrable practical proposition. Germans, generally, do not seem to feel that there is any such thing as the ethics of terminology. The mathematico-logical sense of the [p. 20] word axiom
\(\acute{\upiota }\uptau \upvarepsilon \upmu \upalpha \)) given by Aristotle (1831, 1844) (who must have had some acquaintance with mathematics to be admitted into the school of Plato, and must there have become familiar with the language of mathematics, [p. 18] as his writings show that he was with their discussions of that time) entirely agrees with the usage of Euclid in the following century, and with the established meaning of the word in English and in French. Aristotle, as is explained by Johannes Philoponus, draws an insignificant distinction between a postulate and a hypothesis, which latter word he uses in several allied senses, but disregarding idle distinctions, we may say that Aristotle gives to the word postulate the precise signification which Riemann attached to hypothesis when he wrote “Über die Hypotheses welche der Geometrie zu Grunde liegen” (Riemann 1854/1867). The point about which Aristotle is most particular is that a postulate is not evidently true. The distinction which he makes between hypothesis, or supposition, in one of its senses, and postulate, in its only sense, is that the interpreter will already believe a hypothesis and will have no positive belief in a [p. 19] postulate. Two millennia of familiarity with the postulates of geometry seem to have bred in us a traditional and almost natural belief in most of them. Any close student of the first book of the Elements will, I believe, agree with me that Euclid purposely throws his fifth postulate (the one about parallels) into a form intended to bring about its non-evident character. This, then, is the meaning which we ought to attach to the word postulate. It is the only meaning upon which good usage, in English and French, can remain or ever be fixed. The Germans, under the influence of Baron Christian Wolff (1713), commonly attach to the word Postulat an abusive meaning of considerable antiquity; that of an indemonstrable practical proposition. Germans, generally, do not seem to feel that there is any such thing as the ethics of terminology. The mathematico-logical sense of the [p. 20] word axiom
 is a secondary one. In general, it means approval, especially general approval, or what is approved or generally approved. Aristotle, in the same chapter X of the first Posterior Analytics just cited, speaks of
is a secondary one. In general, it means approval, especially general approval, or what is approved or generally approved. Aristotle, in the same chapter X of the first Posterior Analytics just cited, speaks of
 and Euclid (1883) calls them
and Euclid (1883) calls them
 A contemporary of Euclid was Zeno, the founder of the stoic school; among the stoics
A contemporary of Euclid was Zeno, the founder of the stoic school; among the stoics
 meant a judgment of common sense, which seems to be an English translation of the phrase. Doubtless
meant a judgment of common sense, which seems to be an English translation of the phrase. Doubtless
 was in this phrase understood to refer to the unanimity of men about such a judgment. (To a stoic
was in this phrase understood to refer to the unanimity of men about such a judgment. (To a stoic
 would mean no more than a proposition.) When Aristotle speaks of ‘common axioms’, the word ‘common’ must have the same meaning, since he refers to the expression as a familiar one. Otherwise, one might gather from what Aristotle says that the axioms are called common as being used in [p. 21] different branches of science. Very significant of the meaning attached by Aristotle to the word axiom is the remark of this true prince of logicians (76b16) which, though half-expressed, in the style of the Analytics, I understand to mean that a science does not fail in conclusiveness by omitting distinctly to note an axiom. For the axiom being self-evident, even when it is not noted it remains evident that the premisses cannot be true without the conclusion being true. It is to the sense of a principle to which this remark applies that the word axiom ought to be restricted.
would mean no more than a proposition.) When Aristotle speaks of ‘common axioms’, the word ‘common’ must have the same meaning, since he refers to the expression as a familiar one. Otherwise, one might gather from what Aristotle says that the axioms are called common as being used in [p. 21] different branches of science. Very significant of the meaning attached by Aristotle to the word axiom is the remark of this true prince of logicians (76b16) which, though half-expressed, in the style of the Analytics, I understand to mean that a science does not fail in conclusiveness by omitting distinctly to note an axiom. For the axiom being self-evident, even when it is not noted it remains evident that the premisses cannot be true without the conclusion being true. It is to the sense of a principle to which this remark applies that the word axiom ought to be restricted.
Concerning Definition, also, Aristotle in this chapter makes a very essential remark, which acute logicians [Mill (1846) among them] have failed to give heed, to the effect that a definition does not assert the existence of anything.Footnote 21
[p. 22]

Axiom. Something is scriptible.
Scholium. Consider the following argument: By Corollary 1,  is scriptible. Ergo, Something is scriptible.
is scriptible. Ergo, Something is scriptible.
This is unexceptionable reasoning. Yet since Corollary 1 is based exclusively upon a definition, it must not be understood to assert, or imply, the existence of anything, while the Axiom does distinctly assert existence. Corollary 1 does assert, or imply, that  is scriptible. It simply writes
is scriptible. It simply writes  , and then, the reasoner observes that
, and then, the reasoner observes that  is written. When the argument says, ‘By Corollary 1,
is written. When the argument says, ‘By Corollary 1,  is scriptible’, this is true in the sense of ‘By observation of Corollary 1, etc.’ This does not affect the validity of the argument. For if a reasoner were not permitted to observe facts about his premisses which those premisses do not themselves [p. 23] assert, no mathematical reasoning would be possible; not even
is scriptible’, this is true in the sense of ‘By observation of Corollary 1, etc.’ This does not affect the validity of the argument. For if a reasoner were not permitted to observe facts about his premisses which those premisses do not themselves [p. 23] assert, no mathematical reasoning would be possible; not even

As Aristotle well says, a science can reach its conclusions with perfect logic without referring to axioms or being distinctly aware of them. The only use that the expression of an axiom series is that of rendering the why of the conclusion, the source of it, more intelligible. When Aristotle calls axioms indemonstrable, he must not be understood to mean that an argument concluding an axiom is necessarily a bad argument. For every argument which proceeds from sound premisses and is of such a kind that no argument of its kind could have true premisses and a false conclusion, is a good argument. Therefore, an argument is not a petitio principii, nor has it any logical fault, merely because it assumes something [p. 24] absolutely self-evident. This follows from the very purpose of logical criticism, and not to recognize its truth is to be in imminent danger of falling into perhaps the most pestilential of all the swamps of metaphysics. Every axiom, therefore, is essentially capable of proof, provided anybody can be found who does not already see the truth of it. But it is quite true that there can be no real proof of what is not doubted, and therefore, so far as an axiom is self-evident, Aristotle is quite right in calling it indemonstrable. But it is possible that a man should be in a state of mind in which he cannot apprehend the meaning of an axiom; and for him it may be proved. [p. 25]

Postulate. Something is unscriptible.
Scholium. The following argument might be proposed to prove this postulate:
For suppose it false. Then something is false, or unscriptible, contrary to the hypothesis. Therefore, the falsity of the postulate being impossible, it must be true.
This argument rests upon an entirely different sort of basis from the argument which proves the above axiom. For though the conclusion of this argument necessarily follows from the premiss; this premiss is quite undeniable, yet the argument is, as the reader assuredly perceives, a petitio principii.
For any argument which proceeds from a premiss such that a consistent opposition to its conclusion can be maintained by not accepting [p. 26] that premiss, and in no other way, is a petitio principii. Now a person who does not admit that anything is unscriptible is in one or other of two states of mind; namely, either the conceptions of falsity and of denial are unintelligible to him, or he holds that the system of signs to which “anything” refers does not contain any false or unscriptible sign nor afford any means of constructing such a sign. But in either of these cases he will not admit that there is any sign that signifies that ‘Something is unscriptible’. But this is the essential premiss of the argument proposed to prove that something really is unscriptible. Moreover, if the person who should maintain that everything is scriptible were to admit that premiss, his position would at once become untenable. Consequently, the argument fulfils all the conditions of a petitio principii.
[p. 27] Were the proposition under consideration an axiom, it might perhaps be absurd to say that any argument concluding it was a petitio principii. But it is not an axiom: it is a postulate. For, antecedently to the admission of this proposition, the notation afforded no means of expressing any proposition that is necessarily false nor any means of denying any proposition expressible. Consequently, were the single letters restricted to signifying propositions necessarily true,—a restriction contrary to no convention of the notation, antecedently to the present proposition,—it would not have been true for the universe of signs of this system that ‘Something is unscriptible’. Far from being self-evident, therefore, this proposition is a convention distinctly added to the conventions of the algebra.
This circumstance opens a line of thought which [p. 28] it is proper for me to notice, although it does not precisely concern me as a logician. We see, from the example of this notation, that a state of mind is conceivable which should be capable of making judgments and yet should not have any such ideas as falsity and denial. Does such a state of mind exist? It is very nearly, if not quite, the state of mind of a horse. The phrase “horse sense” testifies to the general conviction of those who are acquainted with horses that they make judgments. But we rarely, if ever, observe in the horse, what is common enough in the dog, a state of doubt and deliberation as to whether
 an idea is true or not. But admitting that there is such a state of mind, is it not presumable that every human mind passes through such a state in its development? It appears to be the [p. 29] state of mind of a baby at about the epoch of its first attempts to speak. If, however, we once admit that this is an inevitable stage in the development of every mind that develops sufficiently to make judgments at all, then we shall be forced to suppose that there was historically such a state of society. For society is a mind. We must, then, suppose that men once spoke without being distinctly aware of what they were doing, and without, ordinarily at least, thinking that a proposition could be denied or be false. Of course, now and then, it must have been forced upon them; so that this stage of linguistic development must have been brief. What we thus see reason to conjecture was true of the conception of logical evil, must have been true at some time of evil generally, and to a much later state of moral evil. Thus, the legend (or should we not say the philosophical hypothesis?)—of the Garden of Eden seems likely to have [p. 30] had a historical basis.
an idea is true or not. But admitting that there is such a state of mind, is it not presumable that every human mind passes through such a state in its development? It appears to be the [p. 29] state of mind of a baby at about the epoch of its first attempts to speak. If, however, we once admit that this is an inevitable stage in the development of every mind that develops sufficiently to make judgments at all, then we shall be forced to suppose that there was historically such a state of society. For society is a mind. We must, then, suppose that men once spoke without being distinctly aware of what they were doing, and without, ordinarily at least, thinking that a proposition could be denied or be false. Of course, now and then, it must have been forced upon them; so that this stage of linguistic development must have been brief. What we thus see reason to conjecture was true of the conception of logical evil, must have been true at some time of evil generally, and to a much later state of moral evil. Thus, the legend (or should we not say the philosophical hypothesis?)—of the Garden of Eden seems likely to have [p. 30] had a historical basis.
As far as logical evil, at any rate, is concerned, the mere question of whether anything is false, was no sooner put, than the
 suggestion itself would have created something false. This was the Serpent in the Garden of Eden. He took the
suggestion itself would have created something false. This was the Serpent in the Garden of Eden. He took the
 shape of a mark of interrogation. Less fancifully, we may say that his dire rôle was enacted by the Mathematical Thought; since the precise difference between the Logician and the Mathematician is that while the former merely analyses the conception we already have, the latter so scrutinizes the relations of the signs already used, as to observe facts about them that had escaped notice, and thus introduces new conceptions. Whoever started the calumny that the ‘Old Serpent’ is the father of lies must have been one of those flat, unraised spirits who would call it a Deliberate lie to say that a sphere is a ruled surface, or that there is a single circle in which all spheres intersect.
shape of a mark of interrogation. Less fancifully, we may say that his dire rôle was enacted by the Mathematical Thought; since the precise difference between the Logician and the Mathematician is that while the former merely analyses the conception we already have, the latter so scrutinizes the relations of the signs already used, as to observe facts about them that had escaped notice, and thus introduces new conceptions. Whoever started the calumny that the ‘Old Serpent’ is the father of lies must have been one of those flat, unraised spirits who would call it a Deliberate lie to say that a sphere is a ruled surface, or that there is a single circle in which all spheres intersect.
[p. 31]
✋ n.b. Although it has been judged well to introduce this postulate immediately upon the Definition of
 , and to discuss its nature, yet it will be ignored, until certain properties of
, and to discuss its nature, yet it will be ignored, until certain properties of
 and
and
 that do not depend upon it have been developed, lest the true character of these should be observed.
that do not depend upon it have been developed, lest the true character of these should be observed.
Corollary 9.
 = ‘Something is scriptible’. For by Clause 1 of the Definition of
= ‘Something is scriptible’. For by Clause 1 of the Definition of  , if ‘Something is scriptible’, then
, if ‘Something is scriptible’, then

 ‘Something is scriptible’. Hence, since evidently something is scriptible, it follows that
‘Something is scriptible’. Hence, since evidently something is scriptible, it follows that

 ‘Something is scriptible’; whence, by Clause 3 of the Definition of
‘Something is scriptible’; whence, by Clause 3 of the Definition of  , if
, if
 then ‘Something is scriptible’. On the other hand, by the Definition of
then ‘Something is scriptible’. On the other hand, by the Definition of
 , if ‘Something is scriptible’, then
, if ‘Something is scriptible’, then
 . Hence, by Clause 3 of the Definition of = follows the proposition.
. Hence, by Clause 3 of the Definition of = follows the proposition.
Corollary 10.
 = ‘Everything is scriptible’. For, by Clause 2 of the Definition of
= ‘Everything is scriptible’. For, by Clause 2 of the Definition of  , Either everything is scriptible or ‘Everything is scriptible’
, Either everything is scriptible or ‘Everything is scriptible’
 . But evidently, if everything is scriptible, ‘Everything is scriptible’
. But evidently, if everything is scriptible, ‘Everything is scriptible’
 is scriptible. [p. 32] Hence ‘Everything is scriptible’
is scriptible. [p. 32] Hence ‘Everything is scriptible’
 ; and by Clause 3 of the Definition of
; and by Clause 3 of the Definition of  , if everything is scriptible then
, if everything is scriptible then
 . But by the Definition of
. But by the Definition of
 , if
, if
 then everything is scriptible. Hence, by Clause 3 of the Definition of =, the proposition follows.
then everything is scriptible. Hence, by Clause 3 of the Definition of =, the proposition follows.
Corollary 11. If anything is scriptible (as it evidently is), then whatever a may be, a =

 .
.
For, by Clause 3 of the Definition of  , if
, if

 and if
and if
 then a. But, by the Definition of
then a. But, by the Definition of
 , if anything is scriptible, then
, if anything is scriptible, then
 . Hence, if anything is scriptible and if
. Hence, if anything is scriptible and if

 , then a. But by Clause 1 of the Definition of
, then a. But by Clause 1 of the Definition of  , if a then
, if a then

 . Whence, by Clause 3 of the Definition of =, follows the proposition. [p. 33]
. Whence, by Clause 3 of the Definition of =, follows the proposition. [p. 33]
Corollary 12.  = Either i or e =
= Either i or e =  . For, by Theorem V, if
. For, by Theorem V, if  then either i or e; and by Theorem VII if either e or both i and
then either i or e; and by Theorem VII if either e or both i and  then
then  . But, by the Definition of
. But, by the Definition of
 ,
,

 . Hence if either e or i, then
. Hence if either e or i, then  ; and in the same way, if either e or i, then
; and in the same way, if either e or i, then  .
.
Corollary 13.  = Either i or e =
= Either i or e =  . For, by Clause 3 of the Definition of
. For, by Clause 3 of the Definition of  , if
, if  and
and  , then e. But, by Clause 2 of the same Definition, Either i or
, then e. But, by Clause 2 of the same Definition, Either i or  . Hence, if
. Hence, if  then either i or e. But, by Theorem VII, if either e or
then either i or e. But, by Theorem VII, if either e or  then
then  . But, by Corollary 1,
. But, by Corollary 1,  . Hence if either i or e then
. Hence if either i or e then  ; and in like manner
; and in like manner  . Hence by Clause 3 of the Definition of = follows the proposition.
. Hence by Clause 3 of the Definition of = follows the proposition.
Appendix B
[Alternative draft version, R 11, R 501, c.1901]
[R 11, p. 1] A sign is supposed to have an object or meaning, and also to determine an interpretant sign of the same object. It is convenient to speak as if the sign originated with an utterer and determined its interpretant in the mind of an interpreter.
If a sign allows no latitude, either to utterer or to interpreter, as to what object or meaning it shall be regarded as
 representing, it may be called a singular sign. Let us use the Roman capitals to represent singular signs. If a sign allows a latitude of choice to the utterer, in certain respects and within certain limits, as to what its object or meaning shall be, it may be called vague, or non-determinate. Let us use the Greek minuscules to represent vague signs. If a sign allows a latitude of choice [p. 2] to the interpreter, within certain limits and in certain respects, as to what its object or meaning shall be regarded as being, it may be called general, or non-individual. Let us use the Italic lowercase letters to represent general signs. It is evident that no sign can be at once vague and general in the same respect. For as long as the determination of the meaning depends upon the choice of one party, the other must follow it, or they will be at cross-purposes; the sign will fail to function as such.
representing, it may be called a singular sign. Let us use the Roman capitals to represent singular signs. If a sign allows a latitude of choice to the utterer, in certain respects and within certain limits, as to what its object or meaning shall be, it may be called vague, or non-determinate. Let us use the Greek minuscules to represent vague signs. If a sign allows a latitude of choice [p. 2] to the interpreter, within certain limits and in certain respects, as to what its object or meaning shall be regarded as being, it may be called general, or non-individual. Let us use the Italic lowercase letters to represent general signs. It is evident that no sign can be at once vague and general in the same respect. For as long as the determination of the meaning depends upon the choice of one party, the other must follow it, or they will be at cross-purposes; the sign will fail to function as such.
Let
 stand for any dyadic relation, and
stand for any dyadic relation, and
 for its converse.Footnote 23 Then if A
for its converse.Footnote 23 Then if A
 B, also B
B, also B
 A; if Socrates loves Plato, Plato is loved by Socrates. Likewise, if A
A; if Socrates loves Plato, Plato is loved by Socrates. Likewise, if A
 \(\beta \), then \(\beta \)
\(\beta \), then \(\beta \)
 A; if Socrates loves some man, some man is loved by Socrates. Further ifA
A; if Socrates loves some man, some man is loved by Socrates. Further ifA
 b, then b
b, then b
 A; if Socrates loves every man, every man is loved by Socrates. So also \(\alpha \)
A; if Socrates loves every man, every man is loved by Socrates. So also \(\alpha \)
 \(\beta \) = \(\beta \)
\(\beta \) = \(\beta \)
 \(\alpha \) and a
\(\alpha \) and a
 b = b
b = b
 a.
a.
But a
 \(\beta \) may be understood in two senses. For here the utterer is to determine the meaning of one sign, the interpreter [R 501, p. 3] of the other. Whichever of the two has the last choice is supposed to know what the previous determinations were. Consequently, the utterer, who is essentially a defender of his own utterance, has an advantage in choosing last, while the interpreter, as not being necessarily a defender of that which he interprets, but rather a critic, and quasi-opponent, is as such, at a relative disadvantage. Consequently,
\(\beta \) may be understood in two senses. For here the utterer is to determine the meaning of one sign, the interpreter [R 501, p. 3] of the other. Whichever of the two has the last choice is supposed to know what the previous determinations were. Consequently, the utterer, who is essentially a defender of his own utterance, has an advantage in choosing last, while the interpreter, as not being necessarily a defender of that which he interprets, but rather a critic, and quasi-opponent, is as such, at a relative disadvantage. Consequently,  is easier to defend, or signifies less than
is easier to defend, or signifies less than  .
.
The key of the whole subject is in the above. Especially it will be observed that vague and general signs are, from the point of view of logical criticism, to be treated as mere substitutes for singular signs.


[R 9, p. 5]
§5. Let a formal definition be defined as a definition, not of the qualitative signification of its definitum, but of the essential relations between different applications of it. I proceed to give formal definitions establishing a system of notation, beginning with a certain sign of relation,
 (a “dragon’s head” turned on its side), and since, to begin with, this will be taken in a singular sense, a circumflex accent will be written over it. We shall be supposed to be provided with a certain blank sheet, called the “sheet of assertion”; a purpose is vaguely supposed. But whether or not every sign rendered possible by the system of notation may be written on this sheet as an entire sign remains to be seen. A sign that may be so written will be termed scriptible, or good, or true, etc. The mere writing of a sign, as an [R 501, p. 6] entire sign, conformably to the supposed purpose of the notation, is to be considered as, in effect, conclusive evidence that it is scriptible. If any two signs, i and e, are of such natures (formal
(a “dragon’s head” turned on its side), and since, to begin with, this will be taken in a singular sense, a circumflex accent will be written over it. We shall be supposed to be provided with a certain blank sheet, called the “sheet of assertion”; a purpose is vaguely supposed. But whether or not every sign rendered possible by the system of notation may be written on this sheet as an entire sign remains to be seen. A sign that may be so written will be termed scriptible, or good, or true, etc. The mere writing of a sign, as an [R 501, p. 6] entire sign, conformably to the supposed purpose of the notation, is to be considered as, in effect, conclusive evidence that it is scriptible. If any two signs, i and e, are of such natures (formal
 and material) that passage might always be made from the former to the latter, without passing from a scriptibleFootnote 24 to an unscriptible sign, i is said to be transformable into e, and then only ‘If i, then e’ becomes scriptible. It is evident that such a sign is general. If any two signs, i and e, are of such a nature, that whatever sign x be taken, supposing ‘If i, then x’ to be scriptible and ‘If e, then x’ to be scriptible, it will always be the case that x is scriptible, then, and then only, ‘Either i or e’ becomes scriptible. It is evident that such a sign is vague. [p. 6]
and material) that passage might always be made from the former to the latter, without passing from a scriptibleFootnote 24 to an unscriptible sign, i is said to be transformable into e, and then only ‘If i, then e’ becomes scriptible. It is evident that such a sign is general. If any two signs, i and e, are of such a nature, that whatever sign x be taken, supposing ‘If i, then x’ to be scriptible and ‘If e, then x’ to be scriptible, it will always be the case that x is scriptible, then, and then only, ‘Either i or e’ becomes scriptible. It is evident that such a sign is vague. [p. 6]


Theorem I. Something can be written on the sheet of assertion.
Proof
For each clause of the above definition is so written. \(\square \)
Scholium. It cannot be proved or disproved that there is anything that cannot be written on the sheet of assertion.
In place of Theorem I, we may substitute,
Theorem I\(^\prime \). Whatever a may be,  .
.
Proof
Putting a for e in Clause 2, unless  is scriptible, a is so. But in that case, by Clause 1, putting a in place of e,
is scriptible, a is so. But in that case, by Clause 1, putting a in place of e,  is again scriptible. \(\square \)
is again scriptible. \(\square \)
Theorem II. Whatever a, e, i may be, if  is scriptibleFootnote 25 then
is scriptibleFootnote 25 then  is scriptible.
is scriptible.
[p. 7]
Theorem I. If, whatever x may be,  , then e.
, then e.
Proof
For if, whatever x may be,  , then, putting
, then, putting  for x,
for x,  will be scriptible. Whence, by Clause 3, putting
will be scriptible. Whence, by Clause 3, putting  for i,
for i,

Whence, by Corollary 1, e will be scriptible. \(\square \)
Corollary 4. By Corollary 1, something is scriptible. Indeed, either clause of the definition, since it holds good, is scriptible.

Footnote 26 is scriptible; or, more briefly,
is scriptible; or, more briefly,

Scholium. It can neither be proved nor disproved that anything is not scriptible. The following sign therefore can never be written by itself on the sheet of assertion.

Clause 1. Whatever a may be

Clause 2. If, whatever x may be, x is scriptible,
 is scriptible.
is scriptible.
[p. 8]
Definition of =.
Clause 1. Whatever i and e may be,

Clause 2. Whatever i and e may be,

Clause 3. Supposing, that if i then e and if e then i, we have
\(i=e\).
Scholium. A conditional proposition, expressing that if certain conditions are or were to be fulfilled, a certain consequent is or would be the case, usually refers to a general range of possibilities, and giving the interpreter liberty to imagine any case of the fulfillment of the condition, expresses that under assumptions supposed to be accepted, though they are usually more or less vague, the truth of the consequent would have to be admitted. But Scotus and other logicians consider a form of “conditional proposition de inesse”, [p. 9] which does not refer to any general range of possibilities, but to a definite and individual state of things. Everything written on our sheet of assertions is supposed to
 represent a definite and individual universe, “the Truth”, so that when a conditional proposition is written on the sheet, say ‘If i, then e’, no illative connection between i and e is expressed that would imply that throughout a whole general range of possibilities the truth of i (where it is true) is accompanied with that of e, but all that is meant is that taking the universe of Truth as it happens to be, although i may not be true (applicable, justifiable, etc.), and should that be the case, nothing is said about e, yet i being true e will as a matter of fact be true also. All that is meant is that, in proceeding from i to e, we should not be proceeding from the scriptible to the unscriptible. As a proposition de inesse, it is true that ‘if 7 is divisible by 3, it is a prime number’. For this proposition confines itself to the actual state of things, and since 7 is not divisible by 3, it really says [p. 10] nothing. Now a proposition is true so far as it is not false. It may contribute to a clear apprehension of the matter to compare the proposition about the number 7 with this: ‘If a sensible man were (under ordinary circumstances) to throw a full inkstand upon his library floor, he would voluntarily spoil his carpet (supposing the room were carpeted)’. This is true, since an inkstand thrown on such a floor would certainly ruin the carpet; and a sensible man would know this beforehand; so that if he did it, he would do it voluntarily. At the same time, no sensible man would, under any ordinary circumstances voluntarily spoil his carpet. Consequently it is true that ‘If a sensible man were, under ordinary circumstances, to throw a full inkstand upon his library floor, he would not voluntarily
represent a definite and individual universe, “the Truth”, so that when a conditional proposition is written on the sheet, say ‘If i, then e’, no illative connection between i and e is expressed that would imply that throughout a whole general range of possibilities the truth of i (where it is true) is accompanied with that of e, but all that is meant is that taking the universe of Truth as it happens to be, although i may not be true (applicable, justifiable, etc.), and should that be the case, nothing is said about e, yet i being true e will as a matter of fact be true also. All that is meant is that, in proceeding from i to e, we should not be proceeding from the scriptible to the unscriptible. As a proposition de inesse, it is true that ‘if 7 is divisible by 3, it is a prime number’. For this proposition confines itself to the actual state of things, and since 7 is not divisible by 3, it really says [p. 10] nothing. Now a proposition is true so far as it is not false. It may contribute to a clear apprehension of the matter to compare the proposition about the number 7 with this: ‘If a sensible man were (under ordinary circumstances) to throw a full inkstand upon his library floor, he would voluntarily spoil his carpet (supposing the room were carpeted)’. This is true, since an inkstand thrown on such a floor would certainly ruin the carpet; and a sensible man would know this beforehand; so that if he did it, he would do it voluntarily. At the same time, no sensible man would, under any ordinary circumstances voluntarily spoil his carpet. Consequently it is true that ‘If a sensible man were, under ordinary circumstances, to throw a full inkstand upon his library floor, he would not voluntarily
 ruin his carpet’; for if a man were to do such a thing, he would not be a sensible man. Here there area two contradictory propositions true at the same time, which is possible because they refer to general conditions, and generals are not subject to the principle of contradiction. The truth is that no sensible man under ordinary circumstances [p. 11] would throw a full inkstand upon his library floor, and thus, these two propositions are quite similar to that concerning the number 7, except that they are supported by general reasons and consequently refer to a general range of possibilities. In ordinary speech conditionals de inesse are rare, and they perplex the non-logician because he attempts to interpret them as referring to some general principle or reason. In logic they are quite indispensable to any thorough analysis of reasoning.
ruin his carpet’; for if a man were to do such a thing, he would not be a sensible man. Here there area two contradictory propositions true at the same time, which is possible because they refer to general conditions, and generals are not subject to the principle of contradiction. The truth is that no sensible man under ordinary circumstances [p. 11] would throw a full inkstand upon his library floor, and thus, these two propositions are quite similar to that concerning the number 7, except that they are supported by general reasons and consequently refer to a general range of possibilities. In ordinary speech conditionals de inesse are rare, and they perplex the non-logician because he attempts to interpret them as referring to some general principle or reason. In logic they are quite indispensable to any thorough analysis of reasoning.
Corollary 5. Whatever i and e may be

For by Clause 2 of the definition of  , putting i in place of a, either
, putting i in place of a, either  or i. But if i and ‘If i, then e’, then e, when by Clause 1 of the same definition, putting e in place of a,
or i. But if i and ‘If i, then e’, then e, when by Clause 1 of the same definition, putting e in place of a,  . Thus, supposing ‘If i, then e’ to be scriptible, so is
. Thus, supposing ‘If i, then e’ to be scriptible, so is  . On the other hand by Clause 3 of the same definition, if
. On the other hand by Clause 3 of the same definition, if  is scriptible, so is ‘If i then e’. Hence, in Clause 3 of the definition of =, putting ‘If i, then e’ [p. 12] in place of i, and
is scriptible, so is ‘If i then e’. Hence, in Clause 3 of the definition of =, putting ‘If i, then e’ [p. 12] in place of i, and  in place of e, we have the proposition enunciated.
in place of e, we have the proposition enunciated.
Scholium. Since our definition of  is purely formal, it follows that, in a conditional proposition de inesse, the ‘If
is purely formal, it follows that, in a conditional proposition de inesse, the ‘If
 then
then
 ’ has a purely formal signification.
’ has a purely formal signification.
Theorem II. Whatever a, e, i may be, if

then

Proof
For assume

Then I have only to prove  . [p. 13] Hence, we have
. [p. 13] Hence, we have

But substituting a for i in the same clause, we have

Whence

But in Clause 2 of the same Definition, substituting  for e we have
for e we have

Hence

But in Clause 1 of the same Definition, substituting e for a, we have

Hence

But in the same clause substituting  for a and a for i, we have
for a and a for i, we have

Hence

[p. 14]
Theorem III. Whatever i, a, e may be,

Proof
For assume

Then I have only to prove that either i or e.
By Clause 2 of the Definition of 

By Clause 3 of the same Definition

Whence by the assumption

Whence by the result of Clause 2,
Either i or e. \(\square \)
[p. 15]
Theorem IV. Whatever i, a, e may be,

Proof
For assume

Then I have only to prove that  .
.
By Clause 1 of the Definition of  ,
,
-
(A) If a then
 ,
, -
(B) If e then
 .
.
By Clause 2 of the same Definition,
-
(C) Either a or
 .
.
By Clause 3 of the same Definition,
-
(D) If
 and
and  then e.
then e.
By (D) and the assumption
-
If
 , then e.
, then e.
Whence, by (A),
-
If a, then e.
Whence, by (C),
-
Either
 or e.
or e.
Whence, by (B),
-
 . \(\square \)
. \(\square \)
[p. 16]
Theorem V. Whatever i, a, e may be,

Proof
I will first prove that if i and  , then either e or
, then either e or  . For assume
. For assume
-
(A) i
-
(B)
 .
.
Then, I am to prove that either e or  .
.
By Clause 1 of the Definition of  ,
,
-
(C) If e then
 .
.
By Clause 2 of the same Definition,
-
(D) Either
 or
or  .
.
By Clause 3 of the same Definition,
-
(E) If a and
 , then e
, then e -
(F) If i and
 , then a.
, then a.
By (E) and (B)
-
If a, then e.
By this and (F)
-
If i and
 , then e.
, then e.
[p. 17] By this and (A)
-
If
 , then e.
, then e.
By this and (D)
-
Either e or
 .
.
I have thus proved that if both i and  , we get the result. But this is also true if e is true. Hence, it is true if either e or both i and
, we get the result. But this is also true if e is true. Hence, it is true if either e or both i and  . Now from this, with (C), we have
. Now from this, with (C), we have

Corollary 6. Hence, à fortiori, if both  and either i or e, then
and either i or e, then  .
.
Corollary 7. Hence, if  then
then  . For, by Theorem V, if
. For, by Theorem V, if  and if i then
and if i then  ; or by Corollary 5, if
; or by Corollary 5, if  then
then  ; or by Theorem II, if
; or by Theorem II, if  , then
, then  .
.
Corollary 8. From Corollary 7, by Theorem II: If  and
and  , then
, then  .
.
Corollary 9. From Corollary 8, we have: If  , then
, then  .
.
[p. 18]Footnote 27
Corollary 10. 
 = If a then everything is scriptible. For Clause 2 of the Definition of
= If a then everything is scriptible. For Clause 2 of the Definition of  gives
gives

Whence, if we assume
If a then everything is scriptible
we have

But in Clause 1, putting
 and a for i, we get
and a for i, we get

From these two, it follows that

On the other hand, assuming this, Clause 3 gives

Scholium. A postulate
 as explained by Aristotle and as plainly understood by Euclid, is a hypothesis
as explained by Aristotle and as plainly understood by Euclid, is a hypothesis
 essential to a deductive theory, with the truth or falsity of which the utterer of the theory does not concern himself. When Riemann [p. 21] wrote about “die Hypotheses welcher zu Grunde der Geometrie liegen”, he used the word hypothesis precisely in the sense in which Euclid understood
essential to a deductive theory, with the truth or falsity of which the utterer of the theory does not concern himself. When Riemann [p. 21] wrote about “die Hypotheses welcher zu Grunde der Geometrie liegen”, he used the word hypothesis precisely in the sense in which Euclid understood
 This is shown both by Aristotle’s distinct statement that a postulate is not necessarily true but must be admitted before the propositions of geometry can be proved, and also by Euclid’s pains in putting his fifth postulate into a shape in which its non-evidence should be striking. The German use of ‘Postulat’, as an indemonstrable practical proposition, may be very ancient; but it was brought into common use by Christian Baron Wolff. The English and French languages have, on the contrary, always followed the original and more useful meaning. An axiom, called
This is shown both by Aristotle’s distinct statement that a postulate is not necessarily true but must be admitted before the propositions of geometry can be proved, and also by Euclid’s pains in putting his fifth postulate into a shape in which its non-evidence should be striking. The German use of ‘Postulat’, as an indemonstrable practical proposition, may be very ancient; but it was brought into common use by Christian Baron Wolff. The English and French languages have, on the contrary, always followed the original and more useful meaning. An axiom, called
 by Aristotle, and by Euclid by the term
by Aristotle, and by Euclid by the term
 which afterward passed into stoical terminology, is a deliverance of common sense which nobody will [p. 22] call in question.Footnote 29 It is analogous to those public facts of which a law court will “take cognizance” without evidence.
which afterward passed into stoical terminology, is a deliverance of common sense which nobody will [p. 22] call in question.Footnote 29 It is analogous to those public facts of which a law court will “take cognizance” without evidence.
Definition of \(\Diamond \).Footnote 30
Whatever there may be that is unscriptible is \(\Diamond \).
Axiom. Something is unscriptible.
Scholium. The following demonstration might be suggested:
Something is unscriptible. For suppose this to be false. Then, it is not scriptible. For suppose this to be false. Then, it is not scriptible, and consequently something is unscriptible, contrary to the hypothesis. The hypothesis must, therefore, be rejected, and we are forced to admit that something is unscriptible.
This argument is conclusive, but it is a petitio principii. For anybody who should maintain that everything is scriptible would mean by ‘everything’ either everything which he could conceive or everything that could be expressed in the notation used. In the one case, he would have no such conception as denial [p. 24] or falsity; in the other, he would point out that the notation provides no means of expressing that ‘something is unscriptible’ or of denying anything. Consequently, this person would in the one case pronounce the
 ‘unscriptible’ unintelligible and in the other would say that it was not within the universe of signs intended. In either case he would deny that merely uttering this proposition afforded any proof of the truth of it. In this he would be right: the proposed demonstration begs the question.
‘unscriptible’ unintelligible and in the other would say that it was not within the universe of signs intended. In either case he would deny that merely uttering this proposition afforded any proof of the truth of it. In this he would be right: the proposed demonstration begs the question.
It is true that the instant that the definition which I have connected with the axiom by a brace, to show that they are logically simultaneous, is admitted, so that there is a sign for the unscriptible, admitted to have that meaning, it becomes evident that there is something unscriptible. But a sound logic cannot admit the monstrous doctrine that a definition can declare the existence of anything. Although the propo- [end; version abandoned or remaining pages have not survived]
[p. 23] ...demonstration proposed begs the question.
It is only when a sign for the non-scriptible is introduced into the notation and is admitted to have that meaning, that it becomes evident that something is non-scriptible. A mere definition may create the sign, but a definition does not, according to sound logic, declare the existence of anything. For that purpose, positive observation is required. In this case, the substance of that observation is evident. It ought, therefore, to be termed an axiom.
Corollary 11.


 = the unscriptible, or false. For
= the unscriptible, or false. For
 signifies that everything is scriptible; since this could not be proved, it was before not positively scriptible. But the Axiom renders it non-scriptible. This proves that
signifies that everything is scriptible; since this could not be proved, it was before not positively scriptible. But the Axiom renders it non-scriptible. This proves that
 is unscriptible. But to prove that
is unscriptible. But to prove that
 = the unscriptible it must further be proved that whatever is unscriptible is
= the unscriptible it must further be proved that whatever is unscriptible is
 . That is, if Z is unscriptible
. That is, if Z is unscriptible 
 . But this follows from Clause 2 of the Definition [end, fragment abandoned]
. But this follows from Clause 2 of the Definition [end, fragment abandoned]
[The following bibliography includes Peirce’s references occurring in the text of Appendices A and B, with details, when known, of their provenance.]
Rights and permissions
About this article
Cite this article
Ma, M., Pietarinen, AV. Peirce’s Dragon-Head Logic (R 501, 1901). Arch. Hist. Exact Sci. 76, 261–317 (2022). https://doi.org/10.1007/s00407-021-00285-0
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00407-021-00285-0





 . But the cut itself is only a boundary and not something that strictly speaking can be scribed on the sheet. Hence, cuts alone are to be considered to be unscriptible, while enclosures (cuts and their contents) are scriptible.
. But the cut itself is only a boundary and not something that strictly speaking can be scribed on the sheet. Hence, cuts alone are to be considered to be unscriptible, while enclosures (cuts and their contents) are scriptible. relations which may be represented by the signs for dragon’s head and tail turned upon their side, and the latter altered slightly, thus:
relations which may be represented by the signs for dragon’s head and tail turned upon their side, and the latter altered slightly, thus:
 ,
,
 . Parentheses round the last two of three signs are omitted. Thus, we write ú
. Parentheses round the last two of three signs are omitted. Thus, we write ú
 à for ú(
à for ú(
 à).
à).
 à.
à. à, then ú
à, then ú
 à.
à.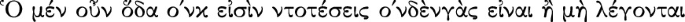
 is the sign of Taurus. The more the form of the character approaches mine, the better.
is the sign of Taurus. The more the form of the character approaches mine, the better. and
and
 are the signs for first quarter and last quarter of the Moon.
are the signs for first quarter and last quarter of the Moon. then
then
 ’, strictly to express the permissibility of a deduction. Therefore, if the sign, i, is unscriptible, ‘If i, then x’ will express a necessarily [sic., contingently] permissible deduction; if the sign, e, is a scriptible sign, ‘If y, then e’ will express a necessarily permissible deduction. Further, this sort of transformation is possible upon the sheet of assertion; so that, supposing ‘If i, then e’ to express a permissible transformation (necessary or contingent), then supposing i to be written on the sheet of assertion, e may also be written. The necessary and sufficient condition of the necessity of a correction is that it should proceed from a sign which need not be written to a sign that must be written.
’, strictly to express the permissibility of a deduction. Therefore, if the sign, i, is unscriptible, ‘If i, then x’ will express a necessarily [sic., contingently] permissible deduction; if the sign, e, is a scriptible sign, ‘If y, then e’ will express a necessarily permissible deduction. Further, this sort of transformation is possible upon the sheet of assertion; so that, supposing ‘If i, then e’ to express a permissible transformation (necessary or contingent), then supposing i to be written on the sheet of assertion, e may also be written. The necessary and sufficient condition of the necessity of a correction is that it should proceed from a sign which need not be written to a sign that must be written. then
then
 ’ to the expression of the permissibility of deductions. A deduction, if permissible, may be performed on the sheet of assertion. That is, whatever
’ to the expression of the permissibility of deductions. A deduction, if permissible, may be performed on the sheet of assertion. That is, whatever
 signs i and e may be, supposing ‘If i, then x’, and supposing i to be
signs i and e may be, supposing ‘If i, then x’, and supposing i to be
 scriptible, e will also be scriptible. Supposing e to be scriptible, then, whatever sign x may be, ‘If x, then e’. Supposing i to be unscriptible, whatever sign y may be, ‘If i then
scriptible, e will also be scriptible. Supposing e to be scriptible, then, whatever sign x may be, ‘If x, then e’. Supposing i to be unscriptible, whatever sign y may be, ‘If i then
 ’. In a correction, the crossing out of the original sign is supposed to signify the condemnation of it as bad. Consequently, the necessary and sufficient condition of the permissibility of a correction will be that
’. In a correction, the crossing out of the original sign is supposed to signify the condemnation of it as bad. Consequently, the necessary and sufficient condition of the permissibility of a correction will be that
 it should proceed from an unscriptible to a scriptible sign. A correction cannot normally be performed on the sheet of assertion, because there will be no occasion for it, but its permissibility may be expressed upon the sheet of assertion or elsewhere. I will use the words ‘Not
it should proceed from an unscriptible to a scriptible sign. A correction cannot normally be performed on the sheet of assertion, because there will be no occasion for it, but its permissibility may be expressed upon the sheet of assertion or elsewhere. I will use the words ‘Not
 but
but
 ’ to express the permissibility of a correction. Consequently, [p. 8] ‘Not(Not i, but e), but x’, where x is a sign entirely vague, will be scriptible or not, in agreement with ‘If e, then i’; although the latter does not directly express all that the former expresses; and ‘If (if e, then i), then y’, where y is a sign entirely general, will be scriptible or not, in agreement with ‘Not i, but e’; although the former expresses an alternative that the latter does not leave open. Since the rules of the notation, which is what I am to consider, are all general, I shall have little occasion for the form of proposition ‘Not
’ to express the permissibility of a correction. Consequently, [p. 8] ‘Not(Not i, but e), but x’, where x is a sign entirely vague, will be scriptible or not, in agreement with ‘If e, then i’; although the latter does not directly express all that the former expresses; and ‘If (if e, then i), then y’, where y is a sign entirely general, will be scriptible or not, in agreement with ‘Not i, but e’; although the former expresses an alternative that the latter does not leave open. Since the rules of the notation, which is what I am to consider, are all general, I shall have little occasion for the form of proposition ‘Not
 , but
, but
 ’. I shall have much occasion to use the form ‘If
’. I shall have much occasion to use the form ‘If
 , then
, then
 ’, not only in its simple form, but also in the form ‘If (if i, then e), then e’. This will be bad, untrue, or unsriptible, if, and only if, ‘If i, then e’ is scriptible while e is unscriptible. But that ‘If i, then e’ should be scriptible although e is unscriptible, requires that i should be unscriptible, lest the passage from i to e should be from the scriptible to the unscriptible. Therefore, ‘If (if i, then e), then e’ is scriptible if and only if i or e (one or [p. 9] other or both) is scriptible. I shall write, whatever i and e may be, ‘either i or e’ to express this; that is, ‘If i then either i or e’, and ‘If e, then either i or e’; and ‘either i or e’ is not scriptible unless so necessitated to be scriptible. The proposition ‘either i or e’ is thus vague, insofar as it does not declare i nor e, but only some one (or both) of the two.
’, not only in its simple form, but also in the form ‘If (if i, then e), then e’. This will be bad, untrue, or unsriptible, if, and only if, ‘If i, then e’ is scriptible while e is unscriptible. But that ‘If i, then e’ should be scriptible although e is unscriptible, requires that i should be unscriptible, lest the passage from i to e should be from the scriptible to the unscriptible. Therefore, ‘If (if i, then e), then e’ is scriptible if and only if i or e (one or [p. 9] other or both) is scriptible. I shall write, whatever i and e may be, ‘either i or e’ to express this; that is, ‘If i then either i or e’, and ‘If e, then either i or e’; and ‘either i or e’ is not scriptible unless so necessitated to be scriptible. The proposition ‘either i or e’ is thus vague, insofar as it does not declare i nor e, but only some one (or both) of the two. .
. is the sign of Taurus. Get a type that looks as near a Bull’s head as may be. [This annotation reads as an instruction to the typesetter or printer suggests that Peirce might in fact have contemplated to have this earlier version of the manuscript to be typeset or published, possibly along with his other Minute Logic drafts.]
is the sign of Taurus. Get a type that looks as near a Bull’s head as may be. [This annotation reads as an instruction to the typesetter or printer suggests that Peirce might in fact have contemplated to have this earlier version of the manuscript to be typeset or published, possibly along with his other Minute Logic drafts.] is used without its definition.]
is used without its definition.] .]
.] .
. , then
, then  . By Clause 2,
. By Clause 2, .
. . By Clause 3,
. By Clause 3, , then
, then  .
. , then e. By (No. 5) and the hypothesis,
, then e. By (No. 5) and the hypothesis, .
. . By Clause 2,
. By Clause 2, . By Clause 3,
. By Clause 3, and
and  , then e.
, then e. or
or  . By Clause 3,
. By Clause 3, , then e.
, then e. , then a.
, then a. .
. , it follows that if i then e.
, it follows that if i then e. ,
, .
. .
. and
and  then e.
then e. , then e.
, then e. or e.
or e. .
.  .
. .
. or
or  .
. , then e
, then e , then a.
, then a. , then e.
, then e. , then e.
, then e. .
.