Introduction

Hindfoot varus or valgus malalignment is a recognized cause of persisting foot and ankle disability and may result in degenerative joint disease [1]. Several authors have reported medial or lateral sliding calcaneal osteotomies (CO) to correct the malalignment [2–5]. For this correction, surgeons recommend an osteotomy angle in the sagittal plane of 45° relative to the plantar surface of the foot sole (Fig. 1a) [2, 6–8]. This angle does not appear to be based on some sort of mechanical calculation. After displacement in a medial or lateral direction, the posterior calcaneal fragment is fixed by means of screws or a plate in order to secure the position and stimulate the healing [5]. The postoperative treatment consists of a prolonged non-weight bearing cast for 6–8 weeks [3, 7, 9, 10]. Early weight bearing mobilization increases blood flow and reduces muscle atrophy [11, 12], improves the range of motion [13], results in earlier rehabilitation [14–16], and leads to a higher proportion of patients having a symmetrical gait postoperatively [17]. Therefore, early weight bearing mobilization is favorable. Reduction of shear forces on the osteotomy in the sagittal plane could be important in order to prevent secondary displacement and may accommodate earlier weight bearing mobilization.

Fig. 1
figure 1

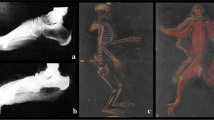
a In this specimen a calcaneal osteotomy (CO) was performed whereby an osteotomy angle was used of approximately 45° relative to the foot sole. A anterior calcaneal fragment, B posterior calcaneal fragment. b After performing a CO the foot was dissected. The plantar apeunorosis (PA) and Achilles tendon (AT) insert on the posterior calcaneal fragment. Both structures carry forces during gait and may cause shear forces on the posterior calcaneal fragment

Full size image

Shear forces depend on external loads (reaction forces from the floor acting upon the foot) and internal loads (forces acting inside the foot). The calcaneus supports the highest loads during the second half of the stance phase [18, 19]. Therefore, it is likely that shear forces on the osteotomy are also highest during this part of the stance phase. The purpose of this study was to determine whether there is a mechanism that may explain that the foot geometry has an effect on the loading of the posterior calcaneus and thus on the shear forces, and as a result may indicate a preferred CO angle for different foot types, which minimizes these shear forces. This has been executed by setting up a simple clinically interpretable model which incorporates the most dominant factors.

Materials and methods

To set up the simplified model, the following assumptions were made:

  • The foot is considered to be a segmented solid coplanar system in the sagittal plane of the foot (Fig. 2).

    Fig. 2
    figure 2

    a Sagittal T1-weighted MRI study of a foot that is modeled as a system of two trusses, at the apex connected by a hinge and stabilized by two wires representing the plantar aponeurosis (PA) and the long plantar ligament (PL). The ground reaction force at the forefoot (Ff) is balanced by the joint contact force (Fc) and the Achilles tendon (AT) force (Fat). b The free body diagram of the posterior calcaneal fragment in a calcaneal osteotomy (CO). The forces acting on the posterior calcaneal fragment in the second half of the stance phase are the PA force (Fpa), the AT force (Fat), and the force in the osteotomy plane (Fop). If the force ratio (Fpa/Fat) and the directions of PA and AT are known, then the direction of the resultant force (Fop) can be calculated. If the CO is performed perpendicular to Fop, the shear force in the osteotomy plane is theoretically zero. Angle β is the angle between the footsole and PA. c The free body diagram of the posterior truss of the foot model. From the moment balance of moments around the center of the distal talus point C the force ratio (Fpa/Fat) can be determined. An assumption needs to be made for the direction and magnitude of the force in the PL (Fpl) relative to Fpa. The force ratio (Fpa/Fat) is then depending on the direction of the PA, PL and AT and the moment arms l1 of Fat, l2 of Fpa and l3 of Fpl. The ratio (l2/l1) is a relative measure for the height of the foot arch

    Full size image

  • The center of rotation of the ankle joint is fixed, modeling the ankle joint as a single degree of freedom hinge.

  • Dominant loads in the second half of the stance phase act in the sagittal plane.

  • All analyses are limited to static equilibrium poses in the sagittal plane.

  • Muscle and ligaments can only generate a pulling force in the direction of their fiber orientation.

  • The end of the Achilles tendon is fixed.

The locations of the insertions of the plantar aponeurosis (PA) and the Achilles tendon (AT) on the posterior calcaneal fragment were identified after a regular osteotomy (Fig. 1a). Five cadaver feet were dissected after performing a CO in 45° relative to the plantar surface of the foot sole (Fig. 1a). In all specimens the PA and the AT were inserted on the posterior calcaneal fragment (Fig. 1b). On the anterior calcaneal fragment, the long plantar ligament (PL) was inserted.

The posterior calcaneal fragment is acted upon by three forces in the second half of the stance phase, where ground reaction force is on the forefoot. The forces on the posterior calcaneal fragment are the PA force (F pa), the AT force (F at) and the force in the osteotomy plane (F op) (Fig. 2a, b). Theoretically, the shear force in the osteotomy plane is zero in the plane perpendicular to the resultant force of the PA and AT forces (Fig. 2b). From the force balance follows:

$$ \Upsigma F_{x} = 0:\quad F_{{{\text{op}}x}} - F_{\text{pa}} - F_{\text{at}} { \cos }\alpha = 0, $$
(1a)
$$ \Upsigma F_{y} \, = \,0:\quad F_{{{\text{op}}y}} - F_{\text{at}} { \sin }\alpha = 0, $$
(1b)

where F opx and F opy are the x- and y-components of the force in the osteotomy plane F op; α is the angle between the PA and AT. The x-axis is assumed to be parallel to F pa. From Eq.1a,b the ratio of F opx and F opy can be derived:

$$ \begin{gathered} \left( {F_{{{\text{op}}x}} / \, F_{{{\text{op}}y}} } \right)\, = \,\left( {F_{\text{pa}} + F_{\text{at}} { \cos }\alpha } \right)/F_{\text{at}} { \sin }\alpha , \hfill \\ \,\quad \quad \quad \quad \; = \left( {\left( {F_{\text{pa}} / \, F_{\text{at}} } \right) + { \cos }\alpha } \right)/{ \sin }\alpha \hfill \\ \end{gathered} $$
(2)

The angle γ between the PA and the osteotomy plane follows from

$$ \gamma = {\text{atan}}\left( {F_{{{\text{op}}x}} /F_{{{\text{op}}y}} } \right). $$
(3)

The CO angle is found by correcting γ by the angle β between the foot sole and the PA. For calculating the CO angle are required the ratio of F pa and F at and the directions of PA and AT.

The directions of the PA and AT were measured on 58 MRIs in neutral ankle position. All MRIs were made in the period of 2009–2010. The MRIs were made for various indications of foot pathology. Excluded were those for suspected PA and AT pathologies and for foot deformities beyond what can be considered as within the normal physiological range. The directions were determined on the sagittal MRI slide at the level of the fourth metatarsal bone, in which the PA, PL and AT structures are seen. Custom software written in MatLab (Release 2007b, Mathworks, Natick, MA) was used to mark ten points on the PA and AT from which the force directions were calculated with a least squares linear fit.

The ratio of the forces F pa and F at was experimentally determined by Erdemir et al. [20]. They measured the F pa and F at during the simulated stance phase of walking in seven cadaver feet. The correlation coefficient between F pa and F at ranged between r = 0.86 and r = 1.00, depending on the specimen. Because the highest forces are present at the second half of the stance phase, only the data were included for the phase where F at was ≥1.0 body weight. This occurred between 56 and 91% of the stance phase (Fig. 3).

Fig. 3
figure 3

Mean calculated musculoskeletal forces of the Achilles tendon (F at) and plantar aponeurosis (F pa) during the stance phase of walking (data adapted from Erdemir et al. [20]). The shaded surface in the graph represents the fraction of the stance phase where the Achilles tendon force is ≥1.0 body weight

Full size image

Custom software written in MatLab was used to calculate the CO angle for which the shear force is zero (Fig. 2b). Because of the variable determination of the force directions of the PA and AT which affects the calculation of the CO angle, the measurements were performed by two different examiners to calculate the interobserver reliability. To calculate the intraobserver reliability, measurements were performed twice by one examiner.

In the 58 MRIs in which the force direction of the PA and AT was measured, the force ratio was used from each of the seven specimens as measured by Erdemir et al. (Table 1) [20]. Based on the force direction of the PA, and AT, and the force ratio between both structures seven vector directions of the force in the osteotomy plane (F op) were calculated on each MRI. In all MRIs the CO angle relative to the foot sole was determined by calculating a perpendicular line to F op (Fig. 4).

Table 1 The force ratios of the plantar apeunorosis (PA) over the Achilles tendon (AT) in seven cadaver feet for the stance phase and where the AT force is greater than one time body weight (data adapted from Erdemir et al. [20])
Full size table
Fig. 4
figure 4

Custom software routines written in MatLab (Mathworks, Natick, MA) were used to calculate the calcaneal osteotomy (CO) angle with the lowest shear forces on sagittal T1-weighted MR image at the level of the fourth metatarsal bone. The plantar apeunorosis (PA) and the Achilles tendon (AT) were marked with ten points to calculate the force direction. Based on the force direction of the PA, and AT, and the 7 different force ratios (F pa/F at) between these structures (data adapted from Erdemir et al. [20]), the resultant force in the osteotomy plane (F op) was calculated. The CO angle relative to the foot sole was determined by the line CO that is perpendicular to F op

Full size image

As stated, the variation of the ratio (F pa/F at) between specimens may be related to the geometry of the hindfoot. The presence of a mechanism that could explain this was evaluated by elaborating the two-dimensional static force analysis to the complete foot. The foot is modeled as a system of two trusses, at the apex connected by a hinge and stabilized by two wires representing the PA and the PL (Fig. 2a). During the second half of the stance phase, the ground reaction force F f is acting on the fore foot which is balanced by the joint reaction force F c and the AT force F at. From the free body diagram of the hindfoot (Fig. 2c), it follows that the moment caused by F at should be balanced by the moment of the PA force (F pa) and of the PL force (F pl):

$$ \Upsigma M_{\text{c}} = 0:F_{\text{pa}} l_{ 2} + F_{\text{pl}} l_{ 3} + F_{\text{at}} { \cos }\alpha l_{ 2} - F_{\text{at}} { \sin }\alpha l_{ 2} = 0, $$
(4)

where l 1, l 2 and l 3 are the moment arms (Fig. 2c).

The ratio between F pa and F pl was 1, relying on the predictions by Giddings et al. from 56 to 91% of the stance phase [21], i.e.

$$ F_{\text{pl}} = F_{\text{pa}} $$
(5)

By combining Eq. 4 and 5 it follows:

$$ \left( {F_{\text{pa}} /F_{\text{at}} } \right) = \left( {{ \sin }\alpha \, l_{ 1} - { \cos }\alpha \, l_{ 2} } \right)/\left( {l_{ 2} + l_{ 3} } \right) $$
(6)

Formula 6 indicates that the F pa/F at ratio in this simplified clinically interpretable model is solely dependent on the foot geometry defined by l 1, l 2 and l 3 and angle α. This force model was applied to the 58 MRI sagittal slices using custom software written in MatLab to determine the moment arms. The length of the hindfoot (l 1) was the distance between the line fitted through points marking the AT and the center of the circle fitted through the points marking the talus roll [22, 23]. The height of the hindfoot (l 2) was the distance between the line fitted through points marking the PA and the talus roll center (Fig. 2c). The moment arm l 3 of the PL (l 3) was the distance between the line fitted through points marking the PL and the talus roll center. Measurements of the directions of the PA, PL, and AT, and the talus roll were performed by two different examiners and twice by one examiner to calculate the intra- and inter-observer reliability of the calculated ratio (F pa/F at).

Statistics

All statistics were performed with SPSS (version 16.0, SPSS Inc; Chicago, IL, USA). The CO angle measurements were presented as mean and standard deviation (SD). To make a distinction between variation due to force direction (N = 58) and force ratio (N = 7), for each force ratio the variation of the CO angle was calculated. The square root of the mean of these variations indicated the variability of the measurements due to the variation of the force directions. For each force direction, we performed the same procedure and calculated the variability of the measurements due to the variation of the force ratio.

To assess the reliability, Intraclass Correlation Coefficients (ICC) was used. An ICC of 0.85 or higher indicates good reliability (p < 0.01) [24–26]. The limits of agreement were calculated for repetitive measurements of the individual examiner and amongst the examiners.

The correlation between the CO angle and the foot geometry was performed with a linear regression analysis.

Results

Based on the force ratios in seven different foot specimens of the PA and AT, mean 0.55 (SD 0.19) [20], and the force direction of the PA and AT determined on 58 MRIs, a mean osteotomy angle of 32.6° relative to the plantar foot sole was calculated, with a standard deviation of 7.9°. The standard deviations due to the variation of the force ratio and the force direction were 8.0° and 2.6°, respectively.

Based on two-dimensional static force analysis of the hindfoot, a mean force ratio of 0.54 (SD 0.08) was determined between the PA and AT, and a mean osteotomy angle of 33.0° (S.D. 4.0°) was calculated. Linear regression analysis revealed that CO angle and the geometric ratio between l 2 and l 1 were well correlated (r = 0.90) (Fig. 5). In a pes planus foot geometry the CO angle was higher, while in a pes cavus foot geometry the CO angle was lower (Fig. 6).

Fig. 5
figure 5

a Linear regression analysis revealed that the CO angle and the relative height of the foot arch (l2/l1) were well correlated (r = 0.90). In a pes cavus foot geometry the ratio l2/l1 was higher and the mean CO angle (33°) was smaller. In a pes planus foot geometry the ratio l2/l1 was smaller and the mean CO angle was higher

Full size image
Fig. 6
figure 6

Sagittal T1-weighted MRI study of an ankle, in which the force ratio (F pa/F at) of the plantar apeunorosis (PA) and Achilles tendon (AT) was determined based on a two-dimensional static force analysis of the hindfoot (Fig. 2c) . In a pes cavus foot geometry (a) the force ratio (F pa/F at) was smaller compared to a pes planus foot geometry (b). Using the individual force ratio measured on MRI-scan, (a) and the actual force directions of the PA and AT an osteotomy angle of 27° was determined in this pes cavus foot geometry. In the pes planus foot geometry (b) the osteotomy was 37°

Full size image

The measurements of the force direction of the PA and AT on MRI gave an intra- and interclass correlation coefficient of 0.93 and 0.92 for the calculated CO-angle. The limits of agreement were ±2.0° for repeated measurement by one examiner and ±2.2° between the examiners. The calculation of the force ratio of the PA and AT based on the static force analysis from geometry measurements on 58 MRIs gave an intra- and interclass correlation coefficient of both 0.94.

Discussion

The purpose of this study was to determine whether the foot geometry may have an effect on the loads on the calcaneus and as a consequence on the preferred CO angle in performing a calcaneal correction osteotomy. On the basis of a published in vitro experimental study by Erdemir et al. in 2004 [20] combined with a two-dimensional static force analysis, a mean osteotomy angle relative to the horizontal plane was determined to be 33°(± 8)° in a small group of lower leg preparations (N = 7). The force analysis on the posterior calcaneal fragment shows that variation of the osteotomy angle is primarily determined by the variation of the ratio of the PA force and the AT force [20], and that the effect of variation of the force direction of the PA and AT, as taken from anatomical measurements on MRI-scans of a population of patients (N = 58), was negligible relative to the effect of the PA-AT force ratio.

From the two-dimensional static force analysis of the hindfoot, it is concluded that the PA-AT force ratio may be primarily determined by the geometry of the length-height ratio of the hindfoot. In this simplified clinically interpretable model, the moment equilibrium around the centre of rotation of the ankle joint explains this mechanism as the multiplication of the force with its moment arm determines the share in loading. Using the length-height ratio as measured on MRI-scans of a population of patients (N = 58) and corrected for the actual force direction of the PA and AT, a similar mean osteotomy angle of 33°(± 4)° was determined as determined with data from Erdemir et al. in 2004 [20]. More specifically, the simplified model indicates that in pes planus foot geometry, the angle should be higher than the mean and contrary in pes cavus foot geometry, the angle should be smaller (Fig. 6).

With the assumption that reduction of shear forces in the osteotomy plane is important in order to accommodate earlier weight bearing mobilization and prevents secondary displacement, the simplified clinically interpretable model indicates that a preferable CO-angle can be calculated based on geometric measurements on MRIs. Although, non-union of the osteotomy is rare, delayed or non-union does occur after a CO [27–29]. Additionally, over- or under-correction of the posterior calcaneal fragment is reported in several studies [3, 9, 30]. This might be a result of inadequate preoperative planning, inadequate fragment fixation perioperatively, or as a result of secondary displacement postoperatively. The propose model might be used to aid in planning and prevent secondary displacement. We do realize that in the operation room a patient specific CO angle based on the foot geometry is not always anatomically feasible (Fig. 4). In that case, the CO angle should be performed as close as possible to the calculated CO angle in consideration to the ankle anatomy i.e. lateral plantar nerve, the medial nerve, and the plantar artery.

We are well aware that the proposed model is a simplification of the actual situation, but contains the most important elements and therefore is useful to explain the relationship between loading and foot geometry. In this study, it was assumed that the center of rotation of the ankle joint and the end of the AT were fixed, modeling the ankle joint as a single degree of freedom hinge where the ankle joint reaction force is acting. The extent to which the location of this hinge moves during normal gait is still the subject of some debate. Anthropometric data suggest that the talocrural joint can be considered to be a single-axis joint [31], although in vivo kinematic analysis suggests that the center of rotation does move somewhat within the sagittal plane during weight bearing activities [32]. In vivo MRI of ankle motion demonstrated a significant increase in the AT moment arm and small variations in the location of the center of rotation within the talar body during passive dorsiflexion from 10° to passive plantarflexion of 40° [33]. However, within the range of normal ankle motion during stance (5° in dorsiflexion to 17° in plantarflexion [34]), the study of Rugg et al. did not show significant changes in the tendon moment arm length or the location of the center of rotation [33]. So we are confident that the hinge single axis joint is a good model for our intended purpose. Furthermore, the effect of heel strike on the osteotomy was not taking into account. For walking and at heel strike, the calcaneus supports a load of approximately one time body weight [18, 19], while during the second half of the stance phase the force in the AT is three to four times the body weight [20, 21, 35–38]. Therefore, it was assumed that the osteotomy angle should primarily be determined by the maximum loading condition. Finally, in the two-dimensional static force analysis of the hindfoot, we considered the forces in the PA and PL as being representative of the tension in all the underlying ligamentous structures. The force ratio between PA and PL was taken from a more elaborate biomechanical model presented by Giddings et al. [21]. This assumed constant ratio may change in case of extreme pes planus foot geometry because of the failed arch support. The described model is a simple two-dimensional model used to explain the underlying mechanism of the influence of the foot geometry on the force ratio between the PA and AT, which may help the orthopaedic surgeon to understand the influence of the foot geometry on the force ratio between the PA and AT. A limitation is that this model is not validated in a 3D model or experimental study. However, the mechanism of the relative foot height (l 2 /l 1 ) will still be key for the magnitude of the moment arm of the PA and AT in a 3D model or experimental study. A higher moment arm of the PA results in a smaller PA force. The smaller ratio (F PA/F AT), leads to a smaller CO angle.

In conclusion, foot geometry, in particular the relative foot height is a determinant for the optimal CO angle in performing the sliding calcaneal correction osteotomy. In a pes planus foot geometry the CO angle should be higher than the mean CO angle of 33°, while in a pes cavus foot geometry the CO angle should be lower.