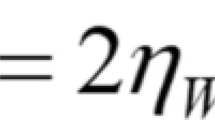Elastic and shear-thinning effects in contraction flows: a comparison

Abstract

The flow through a 4:1 planar contraction has  been investigated using different rheological models having the same shear viscosity, namely, the inelastic Carreau-Yasuda model (CY), the enhanced Bautista-Manero-Puig (eBMP), and the exponential version of the Phan-Thien/Tanner (PTT). Noticeable discrepancies were observed with the CY model and the eBMP in terms of the velocity profiles along the centerline and in the exit channel (near the end of the geometry) normal to the flow direction. Transient planar extensional viscosity shows a large effect on vortex dynamics although the effect of transient and steady elongation on pressure drop seems negligible. Simulation results allowed gathering that pressure drop is largely influenced by the shear-thinning behavior of the fluid, noticeably affected by elasticity, and less by extensional viscosity.

Graphical Abstract

Introduction

Computational fluid dynamics (CFD) is now an essential tool for analyzing fluid flow problems; in some cases, it considerably reduces the need for experiments, and in other situations, it allows determining the degree of the effect of some variable or parameter in complex flows, for which a theoretical solution would be challenging, if possible, at all. In rheology, the study of the flow of highly viscous and viscoelastic materials is of the essence. Excellent reviews and perspectives on this topic have been reported by Owens & Phillips(2002), Keunings (2000), and Walters & Webster (2003).

The so-called Boger fluids have attracted much attention of rheologists. This type of liquids shows a nearly constant shear viscosity but exhibiting large elasticity, which can be noticeable in terms of extensional viscosities and nonzero normal stress differences in simple shear flow. Effects of elasticity on such fluids have been studied by (Nigen & Walters (2002), Campo-Deaño et al. (2011), Binding & Walters (1988), Rothstein & McKinley (2001), Pérez-Camacho et al. (2015), Tamaddon-Jahromi et al. (2016), Aguayo et al. (2008)) among others. The Newtonian model corresponds to the inelastic class of constitutive equations, while the Boger, a highly elastic fluid, requires a viscoelastic model capable of reproducing the nearly constant shear viscosity with high levels of elasticity. Then, in a comparison between a Newtonian and a Boger fluid through the same geometry and flowrate, elasticity would be responsible for the differences between the results of both fluids. However, the difficulty to determine the influence of elasticity for liquids exhibiting shear-thinning behavior consists in the requirement of two fluids with the same shear viscosity response but just one being elastic. Experimentally, this would be problematic, although from the computational rheology perspective, the high flexibility of the Carreau-Yasuda (CY) model to adjust shear-thinning viscosity data gives an opportunity to make such a study. The viscoelastic constitutive equation is the enhanced version of the Bautista-Manero-Puig (eBMP) model (Boek et al. 2005), which is a model capable of reproducing shear-thinning fluids with the first and second Newtonian plateaus and including viscoelasticity. To have two fluids with the same shear response, the shear viscosity predicted by the eBMP model was fitted using the CY constitutive equation.

The Carreau-Yasuda equation is a non-Newtonian inelastic model, with five adjustable parameters, two of which corresponding to the first and second Newtonian regions of the shear viscosity curve, and the other three parameters give great flexibility to modify the degree of thinning and the shear-rate at which the thinning starts (Bird et al. 1987). In contrast to the most recognizable non-Newtonian model, i.e., the Power-Law equation, the Carreau-Yasuda viscosity is bounded between the first and second Newtonian regions and can effectively fit many sets of viscosity data (Morrison 2001).

The CY model has been extensively used for a variety of fluids; for example, based on a finite volume implementation, Kumar et al. (2019) used the CY constitutive equation to model the flow of blood through carotid arteries. Tabakova et al. (2014) employed the original Carreau model (for this original version, the $a$-parameter is fixed to 2, where for the Carreau-Yasuda, this parameter can be adjusted to a better fit) for a theoretical analysis of oscillatory flow of blood in a tube. Also, the CY model was implemented with a lattice Boltzmann method to study oscillatory flows (Boyd et al. 2007). Furthermore, Kadyirov et al. (2023) examined the effect of ultrasonic treatment on crude oils; the results of the study were expressed in terms of the CY adjustment parameters. High pressure rheological tests of Polymer-based oil mixtures were carried out to study the performance of viscosity index improvers (Cusseau et al. 2018). The non-Newtonian models used were the Zhang and the Carreau-Yasuda equations. Another study of viscosity modifiers for multigrade oils was made by Marx et al. (2018), where the temperature superposition shift factor allowed to employ the models (Carreau-Yasuda, Powell-Eyring, Cross) at different temperatures. The model was also used by Le et al. (2009) to fit the viscosities of hyperbranched polymer melts computed from Non-Equilibrium Molecular Dynamics. The CY fit gave consistency to the computed results and allowed a more detailed analysis in that study. Although the model has been extensively used, it is to note that by modeling viscoelastic fluids with this inelastic equation, the effect of elasticity is not considered, and this is one of the objectives of this research, to give an idea of the error if elasticity is ignored.

For the viscoelastic model, the enhanced Bautista-Manero-Puig (eBMP) model is considered here. The original BMP model was introduced by Bautista et al. (1999) to model worm-like micellar viscoelastic solutions. The BMP models consist basically of two equations: the first one, an Oldroyd-B model for stress evolution, and the second one, a Fredrickson equation to account for the effect of the construction/destruction by flow of the micelles; even though the model was capable to successfully reproduce in a qualitative manner the complex response of such micellar solutions, it suffered a major drawback, it presented a discontinuous extensional viscosity. By a stability analysis, Boek et al. (2005) developed an enhanced version, now with a continuous extensional viscosity behavior. The model was able to represent shear thinning and also shear thickening fluids; by choosing the parameters, the model can vary the level of extension hardening. An important feature of this improved version of the BMP model is that by keeping the product of the parameters that control the formation and destruction of micelles constant, different transient evolutions towards the same stable material functions can be produced. Such an uncommon characteristic of the model was used to show that, two different eBMP fluids, with exactly the same steady shear and extensional viscosities and also, the same first normal stress difference in shear, reach two different steady-state pressure drops and vortex sizes in (4:1 and 8:1) contraction flows; the variations are due to the different transient evolutions of the two fluids (Pérez-Salas et al. 2023).

Besides the eBMP viscoelastic model, the exponential version of the Phan-Thien/Tanner model is also considered here. The model was derived from network theory (Phan-Thien & Tanner 1977) and is capable of reproducing the behavior of shear thinning and extension hardening fluids. Since its publication, the model has been extensively employed in numerical simulations (see Alves et al. (2021), Aboubacar et al. (2002), Ferrás et al. (2014) Afonso et al. 2011, Alves et al. (2004)), theoretical analyses (Akbar & Nadeem 2015) Pérez-Salas et al. (2019), Pérez-Salas et al. (2021), Arcos et al. (2012)) and experimental measurements (Chougale et al. (2018), Dietz (2015), and Ramiar et al. (2017)).

Contraction flows have attracted the attention of several research groups since this type of flows allow the study of the stability of constitutive models and the comparative evaluation of the numerical methods implemented. For example, Bschorer & Brunn (1996) studied a 4:1 planar contraction, comparing four non-Newtonian models (Carreau, Criminale-Ericksen-Filbey, White–Metzner and Oldroyd 4-constant constitutive equations). In their analysis, they concluded that, for a better reproduction of flow phenomena, shear-thinning (pseudoplasticity) alone is not enough, and elasticity must be considered. The effect of the contraction ratio ($CR$) was investigated by (Alves et al. 2004), by varying $CR$ to values up to $100$. One result from their research is the absence of lip-vortices for $CR=4$ for a linear PTT with moderate hardening ($\varepsilon =0.25$) fluid. In addition, Lee et al. (2004) presented a comparison among several viscoelastic models using a Finite Element procedure. The studied models were the White–Metzner, upper convected Maxwel, Giesekus, Larson, Leonov, FENE-P and the upper convected Phant-Thien/Tanner (PTT) equations, considering both linear and exponential versions. In their results they concluded that the PTT model was among the most stable rheological equations as the limit Deborah number was higher than several of the other models. In Pérez-Salas et al. (2023), the effect of the transient evolution of rheometrical functions were studied in steady contraction flows, employing the eBMP model.

In this research, a numerical comparison between inelastic and viscoelastic models is presented but considering the shear-thinning phenomena. For the CFD simulations, the RheoTool software (Pimenta & Alves 2022) has been used, which is an open-source simulator. For each comparison presented here, two fluids were selected, one elastic and the other inelastic, but having the same shear-thinning viscosity, this will help us to identify how important the role of elasticity is, when a reduction in viscosity is presented by the fluids. The selected inelastic model was the Carreau-Yasuda equation, for its great capability to reproduce adequately shear viscosity data, and for the viscoelastic fluids the eBMP model, and to further study the effect of elasticity, the simplified PTT model was also used.

Governing and rheological equations

For the flow system under consideration, the continuity (mass conservation) equation for an incompressible fluid is:

$$\nabla \bullet \underline{v}=0.$$

(1)

The momentum equation, ignoring the effects of any external force (gravity) can be written as:

$$\rho \left(\frac{\partial \underline{v}}{\partial t}+\underline{v}\bullet \nabla \underline{v}\right)=-\nabla p+\nabla \bullet \underset{\_}{\underset{\_}{\tau }}$$

(2)

In eqs. (1) and (2), $v$ is the velocity vector, $\rho$ the density, $p$ is pressure, $t$ is time and $\tau$ is the total stress tensor. The expression for the total stress tensor depends on the selected rheological model; here we employed the Carreau-Yasuda, the enhanced Bautista-Manero-Puig and the Phan-Thien/Tanner constitutive models.

The Carreau-Yasuda model implemented in RheoTool (Pimenta & Alves 2022) is given in Eq. (3):

$$\eta ={\left({\eta }_{0}-{\eta }_{\infty }\right)\left[1+{\left(k \dot{\gamma }\right)}^{a}\right]}^{\frac{n-1}{a}}+{\eta }_{\infty }.$$

(3)

The model parameters are (Morrison (2001), Javed et al. (2021)):

• ${\eta }_{0}$ is the first Newtonian region (${\eta }_{0}={\eta |}_{\dot{\gamma }\to 0}$),

• ${\eta }_{\infty }$, the second Newtonian region, ${(\eta }_{\infty }={\eta |}_{\dot{\gamma }\to \infty })$,

• $n$ is a power-law-like parameter, which describes the slope of the shear-thinning zone,

• $k$, which is a parameter related to the shear-rate value where the thinning starts,

• $a$ is a shape parameter to model adequately the different shapes of the start of the thinning zone.

For the enhanced BMP model, viscoelastic stress evolution is given by (Pimenta & Alves 2022), (Boek et al. 2005):

$$\underset{\_}{\underset{\_}{{\tau }_{p}}}+{\lambda }_{rlx} \underset{\_}{\underset{\_}{{\stackrel{\nabla }{\tau }}_{p}}}=2 {\eta }_{p}\underset{\_}{\underline{d}},$$

(4)

Equation (4) is the Oldroyd-B model, and it is coupled by the fluidity ($\varphi ={\eta }^{-1}$) given by Eq. (5):

$$\frac{\partial \varphi }{\partial t}+\underline{v}\bullet \nabla \varphi =\frac{1}{{\lambda }_{s}}\left( {\varphi }_{0}-\varphi \right)+{k}_{\infty } \underset{\_}{\underset{\_}{{\tau }_{p}}} :\underset{\_}{\underline{d}}.$$

(5)

The Upper-convected derivative in Eq. (6), is defined as:

$$\underset{\_}{\underset{\_}{{\stackrel{\nabla }{\tau }}_{p}}}=\frac{\partial }{\partial t}\left( \underset{\_}{\underset{\_}{{\tau }_{p}}}\right)+\underline{v}\bullet \nabla \underset{\_}{\underset{\_}{{\tau }_{p}}}-{\left[\nabla \underline{v}\right]}^{T}\bullet \underset{\_}{\underset{\_}{{\tau }_{p}}}-\underset{\_}{\underset{\_}{{\tau }_{p}}}\bullet \left[\nabla \underline{v}\right],$$

(6)

and the model considers a Newtonian solvent contribution. Then, the solvent and total stresses are expressed as:

$$\underset{\_}{\underset{\_}{{\tau }_{solv}}}=2{\eta }_{solv}\underset{\_}{\underline{d}},$$

(7)

$$\underset{\_}{\underset{\_}{\tau }}=\underset{\_}{\underset{\_}{{\tau }_{solv}}}+\underset{\_}{\underset{\_}{{\tau }_{p}}}.$$

(8)

In Eqs. (4) to (8) ${\tau }_{p}$, ${\tau }_{solv}$ and $\tau$ are the viscoelastic and solvent contributions, and the total stress (required in Eq. 2), respectively. $\varphi$ is the fluidity, $d=\frac{1}{2}\left(\nabla \underline{v}+{\left[\nabla \underline{v}\right]}^{T}\right)$ is the rate-of-deformation tensor, and $v$ is the velocity vector. Additionally, ${G}_{0},{\eta }_{solv}$ and ${\eta }_{T}$ are the relaxation modulus, solvent viscosity, and total viscosity, respectively, ${k}_{\infty }$ is the parameter controlling the destruction of micelles and ${\lambda }_{s}$ is the structural time for the formation of micelles. The viscoelastic relaxation time is given by ${\lambda }_{rlx}$. $Uc$, $H$ are the characteristic velocity (average) and height, both taken at the inlet of the geometry and $L$ is the characteristic length of the geometry.

The main differences between the original BMP and the eBMP models are that the later splits the stress into a viscoelastic and a purely viscous contribution, as expressed in Eq. (8) and the other is that the $k$-parameter, is divided by ${\eta }_{\infty }$ in the original model; however, in the resulting equations of the enhanced version, both parameters ($k/{\eta }_{\infty }$) appears as a “single parameter” (Boek et al. 2005). Therefore, in Eq. (5), it is defined as ${k}_{\infty }=k/{\eta }_{\infty }$. For the analysis, we needed to add to RheoTool code the eBMP model, as mentioned in Pérez-Salas et al. (2023).

The Phan-Thien/Tanner model implemented in RheoTool (Pimenta & Alves 2022) is:

$$f \underset{\_}{\underset{\_}{{\tau }_{p}}}+{\lambda }_{rlx} \underset{\_}{\underset{\_}{{\stackrel{\nabla }{\tau }}_{p}}}=2 {\eta }_{p}\underset{\_}{\underline{d}}.$$

(9)

With the function $f$ for the exponential version:

$$f=exp\left(\frac{\varepsilon {\lambda }_{rlx}}{{\eta }_{p}} tr\left[\underset{\_}{\underset{\_}{{\tau }_{p}}}\right]\right).$$

(10)

As mentioned earlier, with the eBMP model, it is possible to have two (or infinite) number of fluids with different transient evolution but arriving at the same steady response, as long as the product $\left({\lambda }_{s}{ k}_{\infty }\right)$ is kept constant.

For the eBMP model, two degrees of extension hardening fluids were chosen, one is a strong hardening (SH) fluid, and the other, a low hardening (LH) case. The term “strong” and “low” hardening refers to the fluid response to planar extensional flow, which for the SH fluid, the extensional viscosity maximum value is almost one decade larger than the viscosity at low extension rates, and in turn, the LH corresponds to a fluid where the maximum viscosity is somehow difficult to detect. Figure 1 shows the shear and extensional viscosity for the eBMP low and strong hardening fluids and the corresponding CY fit to shear viscosity. In addition, to determine the effect of transient rheological functions in this steady-state flow, for each eBMP level of extension hardening, two fluids were studied, one monotonic and the other, overshoot. The “monotonic” and “overshoot” names correspond to the path exhibited by their transient responses, which as it can be seen in Fig. 2 (a,b and d) the monotonic fluids reach their steady state values directly, without any maxima or minima, in contrast to the overshoot case, which follows a path with at least one peak value but, it is important to note that both reach the same value at long times. Then at this point, there are two SH eBMP fluids (one monotonic and one overshoot), similarly two LH fluids and two CY fluids, one matching the SH and the other for the LH case. All the simulated fluids have the same zero-shear-rate and infinite shear-rate viscosities.

Fig. 1

Steady shear and planar extension viscosities for the eBMP low and strong hardening fluids and their correspondent Carreau-Yasuda fit

Fig. 2

Transient viscosities and first normal stress difference for the eBMP model: a) transient shear and planar extensional viscosities for the low hardening fluid; b) transient shear and planar extensional viscosities for the strong hardening fluid; c) steady first normal stress difference; and d) transient first normal stress difference

Transient and ${N}_{1}$ rheometric functions are presented in Fig. 2 where 2a and 2b show the transient path of the monotonic and overshoot cases towards steady shear and extensional viscosities. The steady first normal stress difference (${N}_{1}$) is portrayed in Fig. 2c and its dynamic evolution (${N}_{1}^{+}$) in 2d. In the steady case Figs. 1 and 2c, there is no difference between the monotonic and overshoot fluids; they overlay completely.

Simulation setup

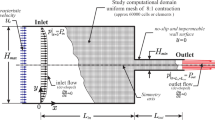
The flow geometry is a planar 4:1 abrupt contraction with a length before the contraction of $40 {H}_{min}$ and after the contraction of $20 {H}_{min}$. The simulations were carried out in RheoTool (Pimenta & Alves 2022), which is a tool from the open-source software OpenFOAM®. Boundary conditions implanted for the simulation are (see Fig. 3):

• At inlet, flat velocity profile, zero stress and zero pressure gradient.

• At wall, no-slip and impermeable condition for velocity, zero pressure gradient and linear extrapolation for stress.

• Fully developed flow at exit.

Fig. 3

Boundary conditions for the 4:1 contraction geometry

The channel length at inlet is long enough for the flow to achieve fully developed conditions before the contraction.

The simulator is based on the finite volume method and our mesh is regular (see Fig. 4). The mesh consists of 21,951 quadrilateral cells with local refinement near the reduction in the flow area.

Fig. 4

Meshing, zoom of the contraction zone and schematic representation of the flow geometry

Mesh independence test

Figure 5 displays the mesh independence test; to this end, three structured meshes with local refinement near the contraction were analyzed, namely: coarse (M1) with 11,991 cells, medium-refined (M2) with 16,000 cells and a refined mesh (M3) with 21,951 cells. The test was carried out with ${\tau }_{xx}$ for the eBMP, strong hardening with overshoot fluid at $Q/{Q}_{0}=500$. Figure 5a contains the plot for the profile at some distance before but near the contraction zone ($\underline{x}=0.49$; the contraction is located at $\underline{x}=0.5$), and Fig. 5b shows the centerline profile. It is possible to discern that the coarse mesh presents some discrepancies, while the medium and refined exhibit almost the same results; nevertheless, here we opted for the refined mesh (M3).

Fig. 5

Mesh independence test in terms of ${\tau }_{xx}$, for the coarse (M1), medium refined (M2) and refined (M3) meshes: a) at a position before but near the contraction, b) at centerline

Results

The Results section is divided into two parts, the first considering only the eBMP (low and strong hardening) and its corresponding Carreau-Yasuda match. For the second part, the Phan-Thien/Tanner model is also considered and a comparison between the eBMP and PTT is presented.

Bautista-Manero-Puig vs. Carreau-Yasuda models

A first analysis of the effect of elasticity is performed by comparing the eBMP and CY models with the same shear viscosity response. First, the velocity profiles at a position near the exit of the geometry were analyzed. Figure 6 shows such profiles. From these, it can be observed the gradual evolution of the viscoelastic fluids (eBMP strong hardening) from an almost Newtonian response at $Q/{Q}_{0}=1$ (which corresponds to a Weissenberg number of $0.01$, defined by $We={\lambda }_{rlx} {U}_{c}/H$), to a flattened velocity profile at $Q/{Q}_{0}=50$ (strong hardening, Fig. 6b). For larger values of flowrate, the eBMP fluids return to an almost parabolic, i.e., Newtonian profile; however, the velocity profile for inelastic CY-fluid maintains the flattened shape at both scenarios. Note also that CY for $Q/{Q}_{0}\ge 200$, the flow is nearly the so-called plug flow. Very similar observations trends and observations can be made to the low hardening case, and for this reason the corresponding plots are in the Appendix (fig. A1).

Fig. 6

Velocity profiles near the exit of the geometry, strong hardening fluid at different flowrates: a) $Q/{Q}_{0}=1$; b) $Q/{Q}_{0}=50$; c) $Q/{Q}_{0}=200$ and d)$Q/{Q}_{0}=500$

The next variable to analyze is the $\underline{U}$ at centreline. From Fig. 7, it can be observed that at the lowest flowrate, none of the fluids exhibits a peak value in centerline velocity but as the flowrate increases, the elastic fluids reach a maximum value exactly at the position of the contraction ($\underline{x}=0.5$). The increasing in the peak value with elasticity has been reported previously by Oliveira et al. (2007), but for an axysimmetric case. The Carreau-Yasuda fluid also exhibits a peak but is hardly noticeable and for the Newtonian case, it seems that it arrives to its final values in a monotonic fashion. In addition, note that the eBMP fluid with the transient response with overshoots, requires longer distances (residence time) to reach an asymptotic value. Again, similar comments can be said for the low hardening fluid (fig. A2), except that for the eBMP with overshoots no maximum is found.

Fig. 7

Velocity profiles at centerline, strong hardening fluid at different flowrates: a) $Q/{Q}_{0}=1$; b) $Q/{Q}_{0}=50$; c) $Q/{Q}_{0}=200$ and d)$Q/{Q}_{0}=500$

Now, in terms of pressure-drop ($\Delta P$), made dimensionless by dividing it by $Pc={\eta }_{p} {U}_{c} L/{H}_{max}^{2}$, the differences are more dramatic; for the eBMP strong hardening fluid, pressure-drop values are significantly lower than the corresponding inelastic CY fluid, even though their viscosity curves are essentially the same. Then, a first comment is that elasticity reduces the pressure-drop required for the flow through the contraction. In addition to this, shear-thinning has a much larger effect on pressure, as the Newtonian fluid exhibits extremely high values compared to both the inelastic and viscoelastic shear-thinning fluids (see Table 1). Again, as pointed out Pérez-Salas et al. (2023), the $\Delta P$ for eBMP monotonic fluids are smaller than for the overshoot case, but such differences are of smaller magnitude than those gathered by comparing elastic to inelastic scenarios. Table 2 in the Appendix contains similar data for the low hardening fluid, where same comments apply noting that discrepancies in $\Delta P$ for the overshoot and monotonic eBMP fluids are smaller.

Table 1 Non-dimensional pressure-drop vs. flowrate for the strong hardening fluid

Streamlines are shown in Fig. 8 for the case of strong hardening; from this figure, it can be deduced that in the Newtonian fluid the vortex size remains almost independent of the flow rate, unlike the Carreau-Yasuda and monotonic eBMP, where the corner vortices start with almost the same size as the Newtonian fluid; however, as the flowrate increases, these corner vortices almost vanish at $Q/{Q}_{0}=500$. For the eBMP overshoot, the vortex dynamics is somehow different; first, the corner vortex starts with the same size as the other fluids, then a reduction in size is observed as flowrate increases but for further increments in flowrate, the vortex is extremely large, reaching the contraction zone. Focusing on the vortex behavior for the low hardening case (fig. A3), similar comments apply for the CY and eBMP monotonic but for the overshoot, the vortices much smaller than those for the strong hardening fluid; such a statement agrees with the explanation that vortices are a stress relief mechanism, which for this low hardening fluids, there is no need to generate large vortices. In these simulations, no lip-vortices appear, which is in agreement with the results for the linear PTT presented in (Alves et al. 2004) for the 4:1 contraction ratio.

Fig. 8

Streamlines and vortex dynamics for strong hardening fluids

As shown in Tables 1 and Table 2 in the Appendix, the pressure-drop computed with the eBMP model is significantly lower than the one corresponding to an inelastic fluid with the same viscosity. From these results, it seems that the extensional viscosity is not a critical flow parameter. For example, even considering the strong hardening fluid, we have that $\Delta {P}_{eBMP}\ll \Delta {P}_{CY}$. Also, for all cases, the Newtonian $\Delta P$ is considerably larger than for the other fluids, an observation confirmed by the results of Oliveira et al. (2007), where they found that pressure-drop from Newtonian is much larger than that for an Oldroyd-B (an elastic fluid with constant shear viscosity), which in turn is larger than $\Delta P$ for a linear PTT model with moderate level of extension-hardening and displaying shear-thinning. By comparing only the eBMP monotonic and overshoot fluids, we obtain that the overshoot transient evolution, which corresponds to a higher extensional viscosity (at least for some short period of time before both fluids reach the same steady rheological properties) produces an increase in pressure-drop of about 30% compared to the monotonic case. A similar comment applies to the low hardening, but as the extensional viscosity both steady and transient are considerably lower than of strong hardening, the increase in pressure-drop from monotonic to overshoot is now ~ 15%. From data of Sarkar & Gupta (2001), similar conclusions can be drawn. In their research, they tested a modified Carreau-Yasuda model coupled with an extensional viscosity equation and, they reported that by increasing the level of strain-hardening, a moderate increase in pressure-drop was observed. However, such increments in $\Delta {P}_{eBMP}$ from monotonic to overshoot seem to fade when compared to the much larger values reported for the inelastic CY simulations.

Bautista-Manero-Puig and Phan-Thien/Tanner

To further analyze the influence of elasticity, simulations with the simplified Phan-Thien/Tanner model considering only the exponential version were performed. For such a comparison, two sets of PTT parameters (i.e., two new fluids) were chosen, trying to match as close as possible the strong and low hardening eBMP fluids (only the overshoot versions); unfortunately, there are some regions where both models differ in behavior (see Fig. 9).

Fig. 9

Steady shear and planar extension viscosities for the viscoelastic eBMP and PTT models and their correspondent Carreau-Yasuda fit: a) steady shear viscosity; b) planar elongational viscosity

The criterion to choose the PTT parameters is that both models must have the same relaxation time (${\lambda }_{rlx}=1$) and both reach the same ${\eta }_{ext}$-peak value. In addition to the two new PTT fluids, a Carreau-Yasuda fit for each one was considered; CY-eBMP corresponds to the CY fit of the enhanced Bautista-Manero-Puig model and the CY-PTT is the Carreau-Yasuda parameters matching the Phan-Thien/Tanner shear viscosity.

By including the PTT model in the comparison, we confirmed that including elasticity in the modelling, a further decrease in pressure-drop is obtained; however, the level of decrease seems to depend heavily on the selected model. Still, the evidence allows identifying that shear-thinning is the main influence on pressure-drop across the geometry; this conclusion is supported additionally by a comparison of the Carreau-Yasuda fits for the eBMP and the PTT, where a small change in the shear viscosity trend (see CY-PTT and CY-eBMP in Fig. 9a) provokes a significant variation in pressure drop for this inelastic model (see CY-PTT and CY-eBMP in Fig. 10a and b). This comment applies for both the strong and low hardening cases.

Fig. 10

Pressure-drop for the eBMP, PTT and CY models: a) strong hardening, b) low hardening

The dominant type of deformation presented in this complex flow can be determined by the flow classification parameter, ${d}_{fc}$, which was introduced by Astarita (1979), and modified by Mompean (2002). The parameter varies continuously between $-1$ and $1$ with three values to highlight:

$${d}_{fc}=\left\{\begin{array}{cc}-1,& \text{rigid body rotation}\\ 0,& \text{shear deformation}\\ 1,& \text{extensional deformation}\end{array}\right.$$

(11)

An evaluation of this flow classification parameter is presented in Fig. 11 for $Q/{Q}_{0}=50$. This is the flow value for which the flattened profiles between CY and both eBMP models are closest to each other (see Fig. 6b). In Fig. 11, rigid body rotation or (${d}_{fc}=-1$)-case corresponds to the color blue, shear-deformation (${d}_{fc}=0$) is in grey, and the extensional dominant deformation (${d}_{fc}=1$) is in red. As expected, the centerline is a zone where pure extensional flow is reached, the exit channel region is dominated by simple shear flow, except in the centerline. In the region before the reduction of the area, a complex mixture of the three types of movement occurs: around the centerline a red region develops just before entering the contraction, but as the fluid enters to the exit channel two small regions of rigid body rotation appears. In the corners, the three movements are gathered in a complex fashion. One major difference that can be appreciated for the eight fluids shown in Fig. 11 is the shape or extent of the extensional deformation just before the contraction. The four Carreau-Yasuda fluids exhibit essentially the same extension dominated zone, and the size of this zone is smaller than for the viscoelastic fluids, except perhaps the PTT low hardening case. The eBMP (overshoot versions) low hardening fluid exhibits a very large zone of elongation, but we need to recall that the extensional viscosity peak value is quite low. For the strong hardening fluid, the eBMP zone for extension is smaller than for the low hardening. This could be the result of the vortex stress mechanism relief. Considering now the PTT fluid, the low hardening fluid resembles the response of the CY models, except in the zones of the corner vortices. Finally, for the strong hardening PTT, a very sharp transition from extension to shear is noted before the contraction, also, the fluid shows a very large zone of this elongational flow which appears to reach (almost) the geometry walls before the area reduction point. It is worth noting that the PTT SH fluid, which corresponds to the larger area of extensional deformation is the case for which larger pressure drops are obtained for the viscoelastic fluids but still lower than its inelastic version. There is qualitatively agreement between the shape of the extension dominated zone presented in Fig. 11 for the PTT low hardening and the flow classification parameter contour plot (linear PTT) obtained in (Afonso et al. 2011), taking into account that both models present a moderate or low extension hardening. However, one aspect to point out from our results is that the flow classification parameter (${d}_{fc}$) depends significantly on the rheological model.

Fig. 11

Flow classification parameter

Conclusions

A series of simulations to analyze the effect of elasticity and shear-thinning in the flow through abrupt changes in the geometry have been performed. Results reveal that the velocity at the exit channel and along the centerline are quite different from the inelastic and viscoelastic situations. The flattening effect of shear-thinning is more pronounced and sustained for the inelastic fluids, while for the viscoelastic, the flattening occurs at intermediate flows, but the profile is gradually recovering a Newtonian parabolic-type as the flowrate increases.

For the center line, elasticity manifests itself in maximum values at the position where contraction begins; those peaks are absent for Newtonian and Carreau-Yasuda fluids. The effect of the transient evolution in rheological properties is manifested in noticeable differences in pressure-drop, minor in velocity profiles and radically in vortex dynamics, the latter is explained in terms of significative discrepancies in values of extensional viscosity and vortex growth mechanism to relief stress in the flow.

It was confirmed that elasticity contributes to a further decrease in pressure-drop although the ratios of such a reduction are extremely dependent on the selected viscoelastic model. From the comparisons among both viscoelastic models and the inelastic one, it can be concluded that the main cause of the pressure-drop reduction is the shear-thinning alone. Elasticity contributes further but not as significative. As final comment, the evidence suggests that extensional viscosity does not play an important role in pressure-drop when comparted to shear-thinning, only in vortex dynamics through the transient (${\eta }_{ext}^{+}$) extension evolution.

Appendix

Figures 12, 13 and 14

Tables 2, 3 and 4

Fig. 12

Velocity profiles near the exit of the geometry, Low Hardening fluid at different flowrates: a) $Q/{Q}_{0}=1$; b) $Q/{Q}_{0}=10$; c) $Q/{Q}_{0}=50$ and d)$Q/{Q}_{0}=200$

Fig. 13

Velocity profiles at centreline, Low Hardening fluid at different flowrates: a) $Q/{Q}_{0}=1$; b) $Q/{Q}_{0}=10$; c) $Q/{Q}_{0}=50$ and d)$Q/{Q}_{0}=200$

Fig. 14

Streamlines and vortex dynamics for low hardening fluids

Table 2 Non-dimensional pressure-drop vs. flowrate for the low hardening fluid

Table 3 Model parameters for the eBMP fluids and the corresponding CY fit

For the simulations carried out here, ${H}_{max}=0.025 m$ and the minimum average velocity (the one that defines ${Q}_{0}$ is ${v}_{{0}_{in}}=0.00002495 m/s$

Table 4 Model parameters for the PTT fluids and the corresponding CY fit