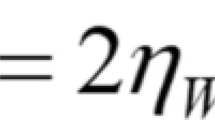Introduction

The flow through contraction geometries has generated great scientific interest over the years. It has been studied from experimental, numerical, and theoretical viewpoints. This type of flow is complex due to the simultaneous presence of shear and elongative strain near the entrance of the reduction in area. In industry, flows through contractions are important in polymer processing operations such as extrusion or mold injection, inkjet printing (Lee et al. 2014), and more recently in the field of additive manufacturing (Petrie 1995), where the performance of the manufacturing process greatly depends on the material rheology to improve the flow reliability and the performance of the deposition (Van Waeleghem et al. 2022). According to Owens and Phillips (2002), the first experimental work on contraction geometries was reported by Tordella (1957), who studied the instability of extruded polymers through capillaries. In general, experimental studies have concentrated on visualizing vortex dynamics, and measuring pressure drop, particle trajectories, and centerline velocity (Owens and Phillips 2002). Since the work of Nguyen and Boger (1979), who used highly elastic fluids with nearly constant shear viscosity, allowing any shear-thinning effect to be removed experimentally, a large part of this research has been focused on the so-called Boger fluids (see, e.g., references) (Boger et al. 1986; Boger 1987; Yesilata et al. 1999; Rothstein and McKinley 2001; Nigen and Walters 2002; Pérez-Camacho et al. 2015).

Considering shear-thinning viscoelastic fluids in contraction flows, White and Kondo (1977) concluded after evaluating a vast collection of experimental data that, for polymer melts to exhibit vortices, a rapid rise in extensional viscosity is needed. Besides vortex growth, the appearance of lip vortices, and thus their evolution, has generated considerable research interest, for example, Evans and Walters (1989) performed experiments to visualize vortex dynamics in planar contractions for shear-thinning viscoelastic fluids (polyacrylamide aqueous solutions). From their experiments, they concluded that for abrupt 2:1 and 4:1 contraction ratios, the salient corner vortex growth was the dominant phenomenon, in contrast to the lip vortex; however, for their less viscous fluids, lip vortex was observed, for which it is assumed that inertia is responsible to keep the salient and lip vortices apart. Excellent reviews on the subject, regarding Boger and shear-thinning fluids, can be found in the works of White et al. (1987) and Owens and Phillips (2002). The research in this area has continued, for example, Lee et al. (2014) studied the flow in 3D rectangular contractions of viscoelastic liquids showing moderate shear thinning. According to their results, as the elasticity number increases, the vortex evolves from lip to corner vortex, then a divergent flow occurs followed by vortex growth where the dynamics depend on the aspect ratio. In addition, Pérez-Camacho et al. (2015) conducted an experimental study for an axisymmetric contraction–expansion, analyzing Boger and elastic shear-thinning fluids. According to these authors, fluids showing similar \({N}_{1}\) will exhibit comparable vortex sizes.

It is clear that the relationship between fluid rheology and vortex dynamics is complex. In this context, our results will show that transient rheology may be necessary to achieve a better understanding of the phenomenon. This seems to agree with White et al. (1987), who express the idea that vortex growth is controlled by the transient extensional viscosity of the fluids.

In the literature, contraction flows have also been studied from numerical and theoretical perspectives. Obtaining analytical solutions to study complex flows has been the subject of several researchers, for example, pulsatile flow (Fernández et al. 2021), electroosmotic flow (Goswami and Chakraborty 2011), and uniform potential flow (Crowdy 2006), to mention a few. Therefore, as the flow that is evaluated in this work is a mixture of shear and elongational deformations, there are several analytical approximations that can be used to represent such a complex flow. As example, Cogswell (1972) derived an approximation to the flow through dies, he might be the first to acknowledge the relevance of extensional viscosity in contractions and separate shear and extensional deformations for the analysis. Years later, Binding (1988; 1991) presented an improved approximation that was used to estimate the extensional viscosity of some polymer solutions. Lubansky and Matthews (2015) tackled the case for Boger fluids in contractions, obtaining good qualitative agreement in vortex lengths and in pressure-drop calculations. More recently, Pérez-Salas et al. (2019, 2021) obtained approximations of the flow in hyperbolic contractions using the simplified Phan-Thien/Tanner model, with satisfying results when compared to simulations.

From the numerical point of view, the 4:1 contraction has been often used as a benchmark problem (Owens and Phillips 2002; Alves et al. 2021). Several authors have contributed to this subject matter. For instance, Debbaut and Crochet (1988) showed that extensional effects are responsible of vortex growth in 4:1 circular contractions. Aboubacar et al. (2002) simulated the flow of Oldroyd-B and Phan-Thien/Tanner models across 4:1, sharp and rounded, contractions. By analyzing an Oldroyd-B fluid, Sato and Richardson (1994) captured the presence of a lip-vortex which disappears as the simulation moves forward in time. López-Aguilar and Tamaddon-Jahromi (2020) also simulated the flow of Boger fluids to reproduce experimental streamlines reported in literature for abrupt axisymmetric geometries. Reviews on this topic can be found in (White et al. 1987; Owens and Phillips 2002; Alves et al. 2021). As mentioned before, contraction flows together with the Oldroyd-B model, which is an option to represent Boger fluids, have been frequently used for benchmarking numerical methods and their implementation. This is due to challenges produced by the sharp corner and to the unbounded extensional viscosity of the selected rheological equation. In their review of numerical methods for viscoelastic flows, Alves et al. (2021) showed the existing level of discrepancy between various numerical algorithms when computing vortex lengths considering data before 2003; however, recent comparisons of some numerical implementations shows a much larger level of agreement.

Concerning wormlike micellar (WLM) solutions, Hashimoto et al. (2006) studied the behavior of wormlike micellar solutions in a 11:1 axisymmetric contraction geometry using flow visualization. They concluded that the flow can be classified into four regions: The first one is obtained at a low flow rate in which there is a Newtonian response of the fluid; in the second, time independent vortices appear which increase in size as the flow rate increases; in the third region, the vortices are unsteady, they present fluctuations, and in the last one, the flow becomes turbulent. Lutz-Bueno et al. (2015) studied the flow of WLM solutions made of cetyl trimethylammonium bromide (CTAB) and sodium salicylate (NaSal) in abrupt contraction geometries. They followed the micelles alignment using small angle neutron scattering (SANS). They found that vortex formation of these solutions depends on the fluid elasticity, which in turn depends on concentration. At low flow rates, shear deformation is dominant, and the flow increases; extension becomes more important, which is reflected in the flow pattern, and in micelles deformation. In another study, Hwang et al. (2017) investigated the flow of these WLM solutions (linear and branched chains) around a sharp microfluidic band by visualization; they observed the flow behavior as the Weissenberg number (We) increased. From their experiments, no vortices were observed at low flow rates, however, as the \(We\) increases a critical value is reached around \(We=6\) to \(8\). At this stage, stable lip vortex formation is observed; these vortices remain time independent up to a value of \(We=20\). Values higher than \(We=20\) and up to \(41\), the lip vortex becomes unsteady and changes its length with time. Jafari Nodoushan et al. (2021) conducted a study of flow stability of WLM solutions. They tested three concentrated solutions of CTAB and NaSal in a rectangular 8:1 contraction geometry. They found that for the least concentrated fluid, vortices appear only as function of elasticity, while for the other two, more concentrated solutions, vortex dynamics, and their stability depend on the shear-banding phenomena of these solutions.

Regarding transient effects, Webster et al. (2004) tested the influence of the type of inlet boundary conditions, time-dependent and static, for the Oldroyd-B fluid in contraction geometries. They found a large impact in the evolution of vortex patterns; however, once the simulations in both scenarios reach the steady state, the results were exactly the same. From experimental observations, Boger et al. (1986) concluded that steady and dynamic shear data are insufficient to explain the evolution of vortices, in consequence, extensional viscosity needs to be taken into account. When evaluating experimental data to find the origin of vortices in planar and axisymmetric flows, a similar conclusion was obtained by White et al. (1987). These authors concluded that elasticity based on shear properties is less significant and transient extensional viscosity is more important in explaining vortex dynamics. Recently, Davoodi et al. (2022) compared the response of the simplified linear Phan-Thien/Tanner and the FENE-P models. For such a comparison, the steady rheological behavior of both models was matched by making the sPTT extension controlling parameter \(\varepsilon\) equal to \(1/{L}^{2}\), where \({L}^{2}\) is the extensibility parameter of the FENE fluid. In this matching procedure, they obtained the same shear, both \({\eta }_{s}\) and \({N}_{1}\), and the same extensional viscosity, \({\eta }_{e}\). For the transient rheological behavior, \({\eta }_{e}^{+}\) follows very similar values for both models, this with respect to time and for all Weissenberg (\(We\)) numbers considered. Nevertheless, some differences (less than 7% in \(\eta /{\eta }_{0}\)) were found in the transient shear viscosity \({\eta }_{s}^{+}\), where for a value of \(We=5\), the FENE-P model predicts a small overshoot for \(\dot{\gamma }t\sim 7\) units. Clearly, as \(We\) increases, the overshoot increases considerably and shifted to larger \(\dot{\gamma }t\) values. In opposite, both models give the same results for values of \(We\le 2\). Also, the sPTT transient shear viscosity shows a very small overshoot for values of \(We\ge 20\). In their analysis, Davoodi et al. (2022) obtained just some slight differences between steady-state results for vortex length and the streamlines near the re-entrant corner.

In this research, we obtain very different vortex trends and pressure drops by simulating the flow of the enhanced BMP model. Two sets of parameters were chosen to obtain exactly the same steady state response but following very different paths for transient rheological functions. One set of parameters shows at least one overshoot in shear and extensional viscosities, and in the first normal stress differences, while the second set of parameters produces a monotonic increase from rest to the steady values.

Rheological model

To represent the rheological behavior of viscoelastic micellar solutions, Bautista et al. (1999) were the first that introduced the Bautista-Manero-Puig (BMP) model. Later, Boek et al. (2005) presented an enhanced version, where an instability in the extensional viscosity is removed. For this work, since the transient response in a viscoelastic flow through an abrupt contraction is analyzed, the enhanced version of the BMP model is implemented using RheoTool, which is an opensource software based on OpenFOAM®. In this case, the version of the existing model in the software was updated following the model proposed by Boek et al. (2005); in addition, the following assumptions and limits of study are considered to build the numerical analysis.

  1. 1)

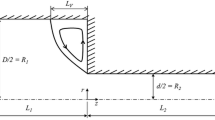
    The study domain (mesh) is mainly represented by two sections, one that precedes the contraction and the other after it. For the first case, \({L}_{in}\) represents the distance required to avoid any effect of the contraction on the flow, with which a developed flow can be assumed for the initial point of study. Similarly, \({L}_{out}\) is the length that allows the flow to reach the condition of fully developed flow after the contraction (see Fig. 1). It is worth mentioning that the first section is greater than \({L}_{in}\) for the computational mesh; this is because the software needs an extra length to generate a developed flow at the starting point of the analysis. This procedure has already been used and validated in previous works (Pérez-Salas et al. 2019, 2021; Bishko et al. 1999).

  2. 2)

    Two geometries were built for the study, with contraction ratios of 4:1 and 8:1 between the two cross sections (\({H}_{max}/{H}_{min}\)). Furthermore, three different mesh densities were evaluated: a low density with about 8000 cells (M1), an intermediate one with approximately 60,000 cells (M2), and a high density one where close to 150,000 cells (M3) were used. After evaluating the results obtained, it was determined that the intermediate mesh (M2) is the most appropriate to carry out the numerical evaluations (see Fig. 2). As an additional test of the quality of the selected working mesh (M2), Fig. 3 presents quite similar lip vortices comparted to the observed for the most refined mesh (M3), showing in turn that these types of vortices are not a numerical/computational mesh refinement phenomenon in the present work.

  3. 3)

    Non-slip conditions and nonpermeable surfaces in the entire contraction contour were assumed (\(\underline{u}=0\)). Moreover, the outlet pressure in the contraction is the atmospheric pressure (\({\left.p\right|}_{x={L}_{in}+{L}_{out}}={P}_{out}\)), and the inlet pressure (\({\left.p\right|}_{x=0}={P}_{in})\) is calculated after proposing the characteristic velocity (\({u}_{c}\)). The above follows the theoretical formulation reported in Pérez-Salas et al. (2019, 2021), where the value of \({u}_{c}\) is employed to define the corresponding value of the Weissenberg number (\(We)\), relationship that is explained in detail later.

Fig. 1
figure 1

Schematic representation of one of the contractions built for the study. Here, the main physical characteristics of the flow and the chosen mesh density (for the contraction 8:1) are shown. The mesh is uniform and grid-like

Full size image
Fig. 2
figure 2

Analysis of mesh independence in terms of dimensionless pressure drop along the contractions. a In the case of 4:1 contraction, three meshes with different densities were evaluated, and b in the case of 8:1 contraction, two meshes were evaluated

Full size image
Fig. 3
figure 3

Analysis of mesh independence in terms of lip-vortex behavior, for the 4:1 contraction, \(We=2\). Monotonic fluid. a Medium (M2) mesh and b most refined (M3) mesh

Full size image

Here, we consider the enhanced version of the BMP model (Boek et al. 2005), which consists of an Oldroyd-B equation for the polymeric stress evolution coupled with an equation that accounts for the fluidity (inverse of viscosity), in terms of the formation and destruction of micellar structures.

To express the model equations in dimensionless form, \(H,{U}_{c}\) and \(H/{U}_{c}\) are the characteristic length, velocity, and time, respectively. Stress is dimensionless by \(\frac{{U}_{c}}{\left({\varphi }_{0}H\right)}\); and the fluidity is \(\varphi ={\eta }_{T}/{\eta }_{p}\). Then, the dimensionless equations for the rheological model are expressed as follows:

For the case of the polymeric stress evolution:

$$\varphi\underline{\underline{\tau}}_p+\;W\;e\;\underline{\underline{\overset\nabla\tau}}_p=\nabla\underline v\;+\;\left[\nabla\underline v\right]^T,$$
(1)

where the fluidity \(\varphi\) and the upper-convected Maxwell derivative of the polymeric stress tensor, \({\underline{\overset\nabla{\underline\tau}}}_p\), are given by the following expressions:

$$\frac{\partial\varphi}{\partial t}+\underline v\cdot\nabla\varphi=\frac1\omega\left(\varphi_0-\varphi\right)+\xi\underline{\underline{\tau}}_p\;:\;\underline{\underline d};$$
(2)

and

$${\underline{\underline{\overset\nabla\tau}}}_p=\frac\partial{\partial t}(\underline{\underline{\tau}}_p)+\underline u\cdot\nabla{\underline{\underline{\tau}}}_p-\left[\nabla\underline u\right]^T\cdot{\underline{\underline{\tau}}}_p-{\underline{\underline{\tau}}}_p\cdot\left[\nabla\underline u\right],$$
(3)

respectively. In addition, the Newtonian solvent contribution (\({\underline{{\underline\tau}}}_{solv}\)) is defined as follows:

$${\underline{\underline{\tau}}_{solv}}=\frac2{\varphi_{solv}}\underline{\underline d},$$
(4)

Therefore, the total stress tensor (\({\underline{{\underline\tau}}}\)) is determined by the following:

$$\underline{\underline\tau}={\underline{\underline{\tau}}_{solv}}+{\underline{\underline\tau}}_p.$$
(5)

In previous equations, \(\underline{\underline{d}}\) represents the strain tensor and \(\underline{u}\) is the velocity vector. Also, the zero shear-rate fluidity and high shear-rates fluidity, together with the kinetic parameters for structure construction and for the destruction of micellar structures, and the dynamic viscosities of the polymer and Newtonian solvent are defined by \({\varphi }_{0}\), \({\varphi }_{\infty }\), \(\lambda\), \(k\), \({\eta }_{p}\), and \({\eta }_{solv}\), respectively. In addition, \({G}_{0}\) is the relaxation modulus, \(\stackrel{.}{\epsilon }\) is the extensional rate, and \(\stackrel{.}{\gamma }\) is shear rate.

By expressing the equations in dimensionless terms, the following numbers were defined:

$$We=\frac{{\eta }_{T} {U}_{c}}{{G}_{0} H},\omega ={\lambda }_{s} \frac{{U}_{c}}{H},\xi =k {{\eta }_{T}}^{2}\frac{{U}_{c}}{H},\hspace{2mm} and\hspace{2mm} {\varphi }_{solv}=\frac{{\eta }_{T}}{{\eta }_{solv}}$$

In these definitions, \(We\) is the Weissenberg number; \(\omega\) and \(\xi\) represent the dimensionless terms for construction and destruction of micelles, respectively; and \({\varphi }_{solv}\) corresponds to the Newtonian viscosity contribution. Note that in all these equations \({\varphi }_{0}\) and \({\varphi }_{\infty }\) are dimensionless.

On the other hand, after considering a 2D Cartesian coordinate system in the contraction (\(x,y\)), as illustrated in Fig. 1, the equations for time-evolving material functions are for a simple shear flow:

$$\begin{array}{c}\frac{d{{\tau }_{p}}_{xx}}{dt}=-\frac{1}{We}{{\tau }_{p}}_{xx}+2\stackrel{.}{\gamma }{{\tau }_{p}}_{xy},\\ \frac{d{\tau }_{xy}}{dt}=\frac{1}{We}\left(\stackrel{.}{\gamma }-\varphi {{\tau }_{p}}_{xy}\right),\\ \begin{array}{c}\frac{d\varphi }{dt}=\frac{1}{\omega }\left({\varphi }_{0}-\varphi \right)+\xi \stackrel{.}{\gamma } {{\tau }_{p}}_{xy},\\ {{\eta }_{shear}}^{+}=\frac{{{\tau }_{p}}_{xy}}{\stackrel{.}{\gamma }}+\frac{1}{{\varphi }_{solv}},\\ {{N}_{1}}^{+}={{\tau }_{p}}_{xx}.\end{array}\end{array}$$
(6)

And for elongational flow:

$$\begin{array}{c}\frac{d{{\tau }_{p}}_{xx}}{dt}=-\left(\frac{1}{We}\varphi -2\stackrel{.}{\epsilon }\right){{\tau }_{p}}_{xx}+\frac{2}{We}\stackrel{.}{\epsilon },\\ \begin{array}{c}\frac{d{{\tau }_{p}}_{yy}}{dt}=-\left(\frac{1}{We}\varphi +\stackrel{.}{\epsilon }\right){{\tau }_{p}}_{yy},\\ \frac{d\varphi }{dt}=\frac{1}{\omega }\left({\varphi }_{0}-\varphi \right)+\xi \stackrel{.}{\epsilon }\left({{\tau }_{p}}_{xx}-{{\tau }_{p}}_{yy}\right),\\ {{\eta }_{ext}}^{+}=\frac{{{\tau }_{p}}_{xx}-{{\tau }_{p}}_{yy}}{\stackrel{.}{\epsilon }}+\frac{3}{{\varphi }_{solv}}.\end{array}\end{array}$$
(7)

In these expressions, \({\eta }_{s}^{+}\), \({N}_{1}^{+}\), and \({\eta }_{e}^{+}\) are the transient shear viscosity, the transient first normal stress difference, and the transient extensional viscosity, respectively.

As was mentioned previously, two sets of model parameters are used to conduct the transient response analysis (see Table 1). Here, the names of the cases are according to their transient rheological response, namely, monotonic or overshoot. However, as can be observed when comparing both cases, the product of the structural kinetic parameters (\(\omega \xi\)) is the same (\(\approx 0.2808\)), which ensures the same steady-state rheology for both fluids.

Table 1 Enhanced BMP non-dimensional model parameters
Full size table

In Fig. 4, the steady and dynamic responses of the enhanced BMP model used in the present work are shown. As mentioned before, the steady response is identical for both fluids; therefore, only one case is plotted. We can see that the fluids exhibit a moderate extension-hardening followed by an extension-softening behavior. The shear viscosity presents the first and second Newtonian plateaus and a shear-thinning zone (see Fig. 4a). For the case of the first normal stress difference, it rises to an asymptotic value for \({\lambda }_{relax} \dot{\gamma }\ge 8\) (see Fig. 4b), where \({\lambda }_{relax}={\eta }_{p}/{G}_{0}\) represents the relaxation time. Besides, for the transient functions, we can see that shear properties exhibit the overshoot for \({\lambda }_{relax} \dot{\gamma }>1\) (see Fig. 4c and d), while for the extensional viscosity, the overshoot is not only present at \({\lambda }_{relax }\stackrel{.}{\epsilon }=1\), but also the peaks are of larger magnitude than those observed for shear properties.

Fig. 4
figure 4

Rheometric functions of the enhanced BMP model: a steady shear and extensional viscosities, b steady first normal stress difference, c transient shear viscosity, d transient First normal stress difference, and e transient extensional viscosity. Symbols and dotted lines correspond to the overshoot and monotonic fluids, respectively

Full size image

Results

As previously detailed in the basic aspects of mesh construction, the simulations start from rest with a flat velocity profile. Similar to Pérez-Salas et al. (2019, 2021) and Bishko et al. (1999), the entrance channel is large enough to let the velocity profile evolves to a fully developed condition before interacting with the contraction (start point of the study).

To corroborate the good performance of the numerical scheme solution, a mesh independence test was carried out successfully. Similarly, the implemented model was tested with an analytical solution for the Poiseuille flow between parallel plates (Aguayo-Vallejo 2006). Assuming a value of \(We=2.0\), where it is defined as \(We={U}_{c} {\lambda }_{relax}/{H}_{max}\) 22,23, the velocity profile from the analytical procedure and from the model in RheoTool is presented in Fig. 5. From this figure, we can infer that the rheological model was well encoded. Furthermore, the results show that both sets of parameters produce the same steady-state values for Poiseuille flow, in which the flow area is constant; therefore, no Lagrangian effects appear, as occurs in a contraction flow.

Fig. 5
figure 5

Velocity profile for the Poiseuille flow; comparison between the analytical solution and the implemented model considering a value of \(We=2.0\), both monotonic and overshoot cases

Full size image

From the most relevant results obtained in the numerical evaluations, the pressure-drop (\(\Delta P=p-{P}_{out}\)) computations are shown in Fig. 6. In this figure, the resulting values were made non-dimensional using the pressure-drop of a Newtonian fluid (\(\Delta {P}_{Newt}\)) computed at the lowest flow rate (characteristic velocity, \({u}_{c}\)) analyzed here. It can be gathered from these results that for increasing \(We\) values, the pressure drops (\(\Delta P\)) recorded by the cases of monotonic and overshoot fluids are different. In all evaluations, the overshoot fluid exhibits larger pressure values than those from the monotonic fluid.

Fig. 6
figure 6

Non-dimensional pressure-drops: a 4:1 contraction and b 8:1 contraction

Full size image

In addition, another observation that can be gathered from Fig. 6 is that the dimensionless pressure is larger for the 4:1 contraction than those displayed by the 8:1 geometry. The fact that \(\Delta P/\Delta {P}_{Newt}\) is larger for the 4:1 contraction can be explained by considering that for the 8:1 case, the shear-rate would reach higher values compared to the 4:1 situation; this higher deformation-rate means a higher degree of viscosity reduction of the fluid; therefore, the pressure-drops decreases.

To simplify the comparison of the pressure-drop result, Fig. 7 shows the normalized pressure-drop (\({\Delta P}_{max}/\Delta {P}_{Newt}=({P}_{in}-{P}_{out})/\Delta {P}_{Newt}\)) at different elasticity levels. Here, we can notice that for larger values of \(We\), increasing differences between the monotonic and the overshoot fluids are obtained. The fluid with the overshoots in the rheometrical functions seems to dissipate more energy.

Fig. 7
figure 7

Normalized pressure-drop \({\Delta P}_{max}/{\Delta P}_{Newt}\) at different \(We\): a 4:1 contraction and b 8:1 contraction

Full size image

In the same context, the differences in the steady state of the two fluids are more noticeable when the vortex patterns are compared, as is illustrated in Fig. 8, for the 4:1 contraction and in Fig. 9 for the 8:1 geometry. For the 4:1 contraction, the overshoot fluid presents much larger vortices compared to those of the monotonic fluid. No lip vortex can be gathered for the overshoot case, and the corner vortex becomes larger at increasing Weissenberg. Quite a different trend is observable for the monotonic scenario for which the corner vortices tend to disappear for the simulated \(We\) increments. In addition, for this monotonic case, a lip vortex seems to emerge at \(We=1.5\), and it becomes more noticeable at \(We=2.\) The same behavior is obtained in the 8:1 geometry for the overshoot liquid but amplified. For this case, the corner vortices are quite large, while for the monotonic scenario, the corner vortex seems very small, and the lip vortex appears at \(We=0.5\) and becomes larger with elasticity. As an additional comment, it is to note that for the largest Weissenberg number simulated here (\(We=2\)), the monotonic fluid required approximately half of the time to reach the steady flow.

Fig. 8
figure 8

Vortex behavior with respect to \(We\), for the 4:1 contraction

Full size image
Fig. 9
figure 9

Vortex behavior with respect to \(We\), for the 8:1 contraction

Full size image

Conclusions

As mentioned before, Davoodi et al. (2022) simulated two different constitutive models (sPTT and FENE-P) with the same steady properties, very similar shear transient values at least for \(We<20\), and for the time evolving extensional viscosity, both models follow a monotonic increase in this property where the FENE-P fluid reaches the steady state some small time before the sPTT. As consequence of such similarities, Davoodi et al. (2022) reported very similar vortex size values between both models. Here, due to the much more significant variations in transient rheology of the two selected set of parameters of the enhanced BMP model, we report visible differences in pressure-drop and most significant differences in vortex dynamics.

By observing the material functions time evolution (Fig. 4), it can be argued that even with the differences in \({\eta }_{s}^{+}\) and in \({N}_{1}^{+}\) between the monotonic and the overshoot cases, these differences may seem somehow small to cause distinct patterns in the vortex dynamics, as those obtained in this work. Therefore, our observations let us to infer, as White et al. (1987) mentioned, that the dominant effect in vortex evolution is the extensional deformation, because it is in \({\eta }_{e}^{+}\) where the separation in the two fluids is more significant; in fact, for some instances, there is an order of magnitude of difference. In addition, the results exposed here seem to agree with the remark of White and Kondo (1977) that a rapid rise in extensional viscosity is needed for polymer melts to exhibit vortices. Here, both fluids presented vortices, but the overshoot fluid, where the extensional viscosity grows much faster, is the fluid exhibiting larger vortices.

This research shows significant differences in steady-state simulations results for fluids exhibiting exactly the same steady rheology but with separate trends in transient response. The fluid with the overshoot in dynamic material functions presents larger pressure drops and large corner vortices, while, for the monotonic fluid, corner vortices are small and lip vortices may become significant when increasing elasticity.