Introduction

The scarcity of reliable shear flow data of unentangled polymers in the nonlinear-viscoelastic regime has made the understanding and modelling of shear flow behaviour of unentangled polymers challenging. A set of rare transient data reported by Santangelo and Roland et al. (2001) in the nonlinear range of shear rates on a monodisperse unentangled polystyrene melt (PS13K) was recently modelled by Ianniruberto and Marrucci (2020) using Brownian dynamics simulation of Fraenkel chains representing the Rouse modes, and empirically adding the effect of the glassy modes (Inoue et al. 1991). Ianniruberto and Marrucci (2020) based their model on the assumption of flow-induced reduction of the monomeric friction coefficient in continuation of earlier modelling of elongational flow of unentangled and entangled polymers (Ianniruberto 2015; Ianniruberto et al. 2019; Matsumiya et al. 2018; Park and Ianniruberto 2017). As in the case of elongational flow, they fitted the functional expression of the monomeric friction coefficient reduction to the steady-state viscosity data, albeit in the case of shear flow, a different functional expression had to be used in order to achieve an agreement with the shear data.

To separate Rouse modes and glassy modes, Ianniruberto and Marrucci relied on the mastercurves of storage and loss modulus as reported by Santangelo and Roland (2001) over a frequency range from 10−4 to 102 rad/s, despite the thermorheological complexity and the breakdown of time-temperature superposition in the vicinity of the glass transition temperature. Polymers exhibit distinct temperature dependencies for the segmental relaxation (α-relaxation) time and the terminal flow relaxation time (Ngai and Plazek 1995; Plazek 1965; Roland et al. 2001; Santangelo and Roland 1998). Plazek et al. (1993) showed the breakdown of the conventional Rouse model for low molecular weight polymers near the glass transition temperature when there is a stronger temperature dependence of the segmental relaxation time compared to the terminal relaxation time. The rationalisation of deviations in thermorheological simplicity can be achieved through the use of the coupling model (CM) (Ngai and Plazek 1995; Robertson and Rademacher 2004). The CM (Ngai 1979, Ngai and White 1979) is an approach to relate the dynamical relationship between systems, and it was used to express correlations between different segmental chain dynamics processes with different temperature-dependent shift factors. Plazek and Ngai (1991) showed that the coupling parameter nα increases with the steepness index, S. The steepness index or fragility index m of a polymer is the characterisation of the temperature-dependent gradient of viscosity or structural relaxation time near the glass transition temperature Tg and the degree to which the system is non-Arrhenius (Angell 1985; Dalle-Ferrier et al. 2016). Santangelo and Roland (1998) demonstrated through a series of dynamic mechanical and calorimetric measurements of polystyrene that Tg and the fragility of PS increase with increasing molecular weight.

A different and novel approach for modelling the nonlinear rheology of unentangled polymers, which does not rely on the hypothesis of friction coefficient reduction, was recently developed by Narimissa and Wagner (2020). The model is based on a single integral constitutive equation, a Rouse-type relaxation modulus, and it considers the orientation and stretch of polymer strands representing the relaxation modes of Rouse chains. The use of a history integral avoids pre-averaging of orientation and stretch. Stretch is limited by a finite conformational stretch parameter. Narimissa and Wagner (2020) found good agreement between model predictions and experimental data for start-up and steady-state elongational flow of monodisperse unentangled polystyrene PS27K and poly(p-tert-butylstyrene) PtBS53 melts as investigated by Matsumiya et al. (2018) and qualitative agreement with stress relaxation after the stop of elongation. The extension thickening and extension thinning observed are caused by a finite stretch in combination with strand orientation. The model features a scaling exponent for high Weissenberg number (\( Wi=\dot{\varepsilon}{\tau}_R \)) elongational flows with elongation rate \( \dot{\varepsilon} \) and Rouse time τR of ηE ∝ Wi−1/2 in agreement with experimental evidence. The scaling is a consequence of the specific structure of the Rouse relaxation modulus with G(t) ∝ t−1/2 for t < τR in combination with strand orientation and finite stretch. The same scaling exponent was predicted by Colby et al. (2007) for high Weissenberg number (\( Wi=\dot{\gamma}{\tau}_R \)) shear flows with shear rate \( \dot{\gamma} \). Furthermore, Narimissa and Wagner (2020) demonstrated that the shear viscosity data of two unentangled polystyrene melts investigated by Stratton (1972) are in nearly quantitative agreement with model prediction assuming only orientation of strands in shear flow with no stretch.

The objective of this paper is to analyse the set of steady and transient data reported by Santangelo and Roland (2001) in the nonlinear range of shear rates of an unentangled PS melt (PS13K) by using the single integral constitutive equation approach developed by Narimissa and Wagner (2020) for Rouse melts. We compare model predictions with the steady-state, stress growth (start-up), and stress relaxation data after start-up shear flow of PS13K and assess the universality of steady shear flow of Rouse melts.

Experimental

Materials

The shear rheological modelling of this study was conducted on previous data released by Santangelo and Roland (2001) on a linear atactic polystyrene (PS13K) melt with a molar mass of 13.7 kDa and polydispersity index of 1.1. PS13K melt is considered unentangled because its molar mass is less than the critical molar mass for entanglements M < Mc ≅ 2Me, with Mc = 31.2 kDa (Fetters et al. 2007).

Rheological measurements

The linear viscoelastic oscillatory shear measurements were conducted on PS13K by an ARES (TA Instrument) shear rheometer using parallel-pate geometry fixture at several temperatures ranging from 5 to 45 °C above its glass transition temperatures with a reference temperature of 104.7 °C. The samples were raised to approximately 130 °C and pre-sheared at 0.01 rad/s before being relaxed for 1 h at each of the measurement temperatures. Steady-state, stress growth, and stress relaxation measurements after start-up shear flow were also performed with the same rheometer and with parallel-plate fixture at a temperature of 104.7 °C. For further details about the measurements, please refer to Santangelo and Roland (2001).

Modelling approach

Narimissa and Wagner (2020) presented a novel modelling approach for the elongational flow of unentangled polymer melts based on a single integral constitutive equation and a Rouse-type relaxation modulus. They made use of the fact, as shown by Lodge and Wu (1971), that the modes of Rouse chains can be considered an ensemble of virtual viscoelastic “strands” with relaxation times τi = τR/i2 and creation rates Gn/τi, where τR is the Rouse stress relaxation time, i the mode index, and Gn = nkBT a modulus depending on the number density of chains, n, and kBT the thermal energy. Each Rouse chain can be represented by nK viscoelastic strands, where nK is the number of Kuhn steps per chain, and at any time, there exist n times nK strands per volume. Creation rates and relaxation times are not affected by the flow, and, at the instance of strand creation (at time t’), strands possess an isotropic distribution function. In the following, we present the main equations of our novel single integral constitutive equation approach for shear flow of unentangled polymer melts (for more details, see Narimissa and Wagner 2020).

We express the relaxation modulus G(t) of unentangled Rouse melts by the sum over the number of Kuhn steps nK,

$$ G(t)=\sum \limits_{i=1}^{n_K}{G}_i(t)={G}_n\sum \limits_{i=1}^{n_K}\exp \left(-t/{\tau}_i\right) $$
(1)

As shown by Lodge and Wu (1971) (see their eq. 5.17) and widely overlooked ever since, the constitutive equation of the Rouse model is fully equivalent to the rubberlike-liquid equation,

$$ \sigma (t)={\int}_{-\infty}^tm\left(t-t\hbox{'}\right)\;{\mathbf{C}}^{-\mathbf{1}}\left(t,t\hbox{'}\right) dt\hbox{'} $$
(2)

σ(t) is the extra stress tensor, and C−1(t, t') the relative Finger strain tensor. The memory function is obtained from Eq. (1) by

$$ m\left(t-t\hbox{'}\right)=\sum \limits_i\frac{\partial {G}_i\left(t-t\hbox{'}\right)}{\partial t\hbox{'}}=\sum \limits_i\frac{G_n}{\tau_i}\exp \left[-\left(t-t\hbox{'}\right)/{\tau}_i\right] $$
(3)

At the instant of strand creation (at time t′), strands are characterised by an isotropic distribution function of normalised end-to-end vectors u(t'). At the observation time t, the unit vectors u are deformed to vectors u', which follow from the affine deformation hypothesis (with F−1(t, t') being the relative deformation gradient tensor) as,

$$ \mathbf{u}\hbox{'}\left(t,t\hbox{'}\right)={\mathbf{F}}^{-1}\left(t,t\hbox{'}\right)\bullet \mathbf{u}\left(t\hbox{'}\right) $$
(4)

The Finger strain tensor C−1(t, t')can then be expressed by

$$ {\mathbf{C}}^{-\mathbf{1}}\left(t,t\hbox{'}\right)=3\left\langle \mathbf{u}\hbox{'}\left(t,t\hbox{'}\right)\mathbf{u}\hbox{'}\Big(t,t\hbox{'}\Big)\right\rangle $$
(5)

The bracket denotes an average over an isotropic distribution of unit vectors u(t') at time t′ and can be obtained by a surface integral over the unit sphere,

$$ \left\langle \kern0.5em \right\rangle \equiv \frac{1}{4\pi}\oiint \left[\right]\kern0.5em \sin \theta \kern0.5em d\theta \kern0.5em d\varphi $$
(6)

It is important to note that the stress tensor of the Rouse model can be expressed in terms of a history integral of the Rouse modes as given by Eq. (2) while for the stress tensor, the one-to-one correlation of the Rouse modes or viscoelastic strands to a specific location along the polymer chain is irrelevant. The modelling approach of Narimissa and Wagner (2020) is based on this mesoscopic level of coarse-graining. In order to find a more realistic nonlinear viscoelastic constitutive equation, they retained the linear-viscoelastic spectrum of the Rouse model but consider a different nonlinear strain measure. Instead of the affine deformation hypothesis of Lodge and Wu (1971), they assumed that strands are oriented (“affine rotation”, orientation tensor S) and stretched from the time of their creation (at time t′) up to time t of observation, when the stress is measured. Stretch ratios fi are independent of orientation, yet dependent on relaxation times. Only strands which still exist at time t and have not yet relaxed contribute to the stress. The use of history integral avoids pre-averaging of orientation and stretch; i.e. both are relative quantities depending on observation time t, and time t’ of creation of viscoelastic strands. Therefore, the multi-mode extra stress tensor of the model is given as,

$$ \sigma (t)=5\sum \limits_i{\int}_{-\infty}^t\frac{\partial {G}_i\left(t-t\hbox{'}\right)}{\partial t\hbox{'}}{f}_i^2\left(t,t\hbox{'}\right)\mathbf{S}\left(t,t\hbox{'}\right) dt\hbox{'} $$
(7)

Equation (7) is formally equivalent to the stress tensor of the HMMSF model (Narimissa and Wagner 2016), and the decoupling of stretch and orientation has also been successfully applied in the rheological modelling of entangled melts (see e.g. Narimissa and Wagner (2019)). S is the relative second-order orientation tensor with dependence on t and t′ understood,

$$ \mathbf{S}=\left\langle \frac{\mathbf{u}\hbox{'}\mathbf{u}\hbox{'}}{u{\hbox{'}}^2}\right\rangle $$
(8)

and u '  = |u'| indicating the length of the vector u'. The orientation tensor S requires a normalisation factor of 5 in Eq. (7) instead of 3 as in Eq. (5).

Narimissa and Wagner (2020) showed that quantitative agreement with the shear viscosity curves presented by Stratton (1972) and Colby et al. (2007) for two unentangled polystyrene melts can be achieved by assuming fi ≡ 1. This means that due to the rotational component of shear flow, strands are only oriented but not stretched in shear flow, and the extra stress tensor in shear flow depends exclusively on the relaxation spectrum and the orientation tensor S,

$$ \sigma (t)=5\sum \limits_i{\int}_{-\infty}^t\frac{\partial {G}_i\left(t-t\hbox{'}\right)}{\partial t\hbox{'}}\mathbf{S}\left(t,t\hbox{'}\right) dt\hbox{'} $$
(9)

We remark that although according to Eq. (9) strands are not stretched in shear flow, this does not exclude that the length of the end-to-end vector of chains may increase due to conformational rearrangements of strands during flow, as e.g. seen in nonequilibrium molecular dynamics (NEMD) simulations of unentangled or mildly entangled polymers in shear flow (see e.g. Baig et al. (2010) and Kim et al. (2010)). We also note that a frame-indifferent formulation of the constitutive Eqs. (7) and (9) can be obtained by considering the “flow strength” or “rotationality” of deformation as e.g. discussed recently by Narimissa and co-workers (Narimissa et al. (2020), but as the focus of this contribution is on shear flow, we refrain from doing so here.

We will now compare predictions of Eq. (9) with the data set of Santangelo and Roland (2001) on the monodisperse unentangled polystyrene melt PS13K.

Comparison between model predictions and data

Linear-viscoelastic characterisation

Figure 1 shows the master curves of storage (G′) and loss (G″) modulus at a reference temperature of 104.7 °C as reported by Santangelo and Roland (2001). In order to test the credibility of the reported LVE master curve, one must consider the glass transition temperature (Tg) of PS13K and carefully investigate the difference between the Tg and the testing temperature (i.e. Tref = 104.7 °C). According to an earlier publication of Santangelo and Roland (1998), Tg of PS13K can be estimated as 93 °C (see eq. 2 of Santangelo and Roland (1998)). However, Santangelo and Roland (2001) reported a different Tg for their PS13K when they noted that their measurements were conducted at 17.1° above the Tg of their samples; hence, Tg of PS13K = 104.7 °C−17.1 K = 87.6 °C. Both reported values of Tg indicate that the testing temperature is considerably close to the glass transition temperature of PS13K. According to Ngai and co-workers (Ngai 2011; Ngai and Plazek 2007; Ngai et al. 1997), at temperatures sufficiently higher than Tg, the steady-state recoverable compliance Js of unentangled polymers is well predicted by the conventional Rouse model; however, Js shows significant decrease as the test temperatures approach Tg. This drop in recoverable compliance is even more accentuated in the case of low molecular weight unentangled polymers when e.g. Plazek and O'Rourke (1971) and Gray et al. (1977) reported a 30-fold drop in Js for a polystyrene with M = 3400 Da within 30 K of its glass transition temperature. Therefore, in both entangled and unentangled systems, the thermorheological simplicity (TRS) of the polymeric systems becomes invalid when the test temperature is in the vicinity of Tg of samples. In the case of PS13K, whether the test temperature is 17.1 K (Santangelo and Roland (2001)) or 11.7 K (Santangelo and Roland 1998) above the glass transition temperature, the TRS of the dynamic shear tests is highly questionable, and it is likely that thermorheological complexity (TRC) (Ngai et al. 1997) is the governing scenario in these measurements. Therefore, we conclude that the credibility of the reported master curves of G′ and G″ over 6 decades in frequency is questionable. We also note that Matsumiya et al. (2018) reported considerable scatter in their master curves for G′ and G″ of PS27K with a molar mass of 27 kDa when their testing temperature (115 °C) was in the vicinity of the glass transition temperature (94 °C). Furthermore, the terminal slope of G′ in the experimental data of Santangelo and Roland (2001) is less than 2 which as explained before could be due to the shifting errors caused by TRC. Based on creep-compliance measurements, Santangelo and Roland (2001) rule out the alternative explanation that this effect may be caused by a small high molar mass fraction in PS13K.

Fig. 1
figure 1

Storage (G′) and loss (G″) moduli of PS13K at 104.7 °C (symbols) as reported by Santangelo and Roland (2001). Segmental relaxation fitted by a stretched exponential function (dotted lines), Eq. (10). Terminal relaxation fitted by effective Rouse relaxation (continuous lines), Eq. (1), with Gn = 8.1 × 105Pa and τR = 12s

Full size image

According to the coupling model (CM) of Ngai et al. (1997), the glassy and Rouse modes cannot be separated in the vicinity of glass transition temperature as they are combined; hence, the molecular units are densely packed together and the understanding of their interactions would require the solution of a “many-body” problem at different length scales and in several viscoelastic relaxation zones. The occurrence of these many-body interactions at temperatures in the vicinity of Tg causes the inseparability of the Rouse and glassy modes.

The many-body interactions lead to a slowdown in the relaxation process, which can be described by a “stretched exponential” relaxation function,

$$ G(t)={G}_0\exp \left[-{\left(t/{\tau}_{\alpha}\right)}^{\left(1-{n}_{\alpha}\right)}\right] $$
(10)

As indicated in Fig. 1 by dotted lines, the segmental relaxation regime of the master curves of storage (G′) and loss (G″) modulus of PS13K can be fitted by the Fourier transforms of Eq. (10) with modulus G0 = 4.6 × 108Pa, characteristic time τα = 6.6 × 10−3s, and interaction parameter nα = 0.5. At the reference temperature of 104.7 °C, the segmental relaxation considerably affects the terminal relaxation regime. As segmental relaxation and Rouse relaxation are coupled with nonlinear effects, they cannot be separated by assuming simple additive superposition. In characterising the linear-viscoelastic terminal behaviour of PS13K, we therefore use the strategy of fitting the terminal regime of G′ and G″ by a so-called effective Rouse relaxation modulus. In other words, we assume that in the vicinity of Tg (at the occurrence of TRC), the terminal behaviour of the melt is determined by effective Rouse modes which are influenced by many-body interactions as described by Ngai et al. (Ngai et al. 1987; Ngai et al. 1997), and not by “free” Rouse modes. These effective Rouse modes in the terminal regime result from the interactions between free Rouse modes and glassy modes, and indubitably, those effective Rouse modes cannot describe the intermediate/high-frequency behaviour. Figure 1 (continuous lines) shows the best fit of the effective Rouse relaxation modulus to the terminal behaviour of loss and storage modulus of PS13K at 104.7 °C by IRIS software (Winter and Mours 2006) according to Eq. (1) with the material parameters Gn = 8.1 × 105Pa and τR = 12s. (nK is taken as 40 as conventionally used by IRIS.) It is important to note that these parameter values define the zero-shear values of viscosity (η0) and the first normal stress coefficient (ψ10) of PS13K according to the following relations,

$$ {\lim}_{\omega \to 0}{G}^{\hbox{'}\hbox{'}}={G}_0^{\hbox{'}\hbox{'}}={\eta}_0\omega =\frac{\pi^2}{6}{G}_n{\tau}_R\omega \Rightarrow {\eta}_0=16.0\kern0.5em MPa\kern0.5em s $$
(11)
$$ {\lim}_{\omega \to 0}G\hbox{'}={G}_0^{\hbox{'}}=\frac{\psi_{10}}{2}{\omega}^2=\frac{\pi^4}{90}{G}_n{\tau}_R^2{\omega}^2\Rightarrow {\psi}_{10}=253\kern0.5em MPa\kern0.5em {s}^2 $$
(12)

Both obtained values in Eqs. (11) and (12) agree very well with the zero-shear data (η0 and ψ10) of PS13K in steady shear flow as depicted in Fig. 2. It must be reiterated that the difference between the calculated parameters of effective Rouse modes in this study (i.e. Gn = 8.1 × 105Pa and τR = 12s) and the “free” Rouse modes assumed by Ianniruberto and Marrucci (2020) for the same PS13K samples (i.e. Gn = 2.3 × 105Pa and τR = 24s) is due to the many-body interactions in the vicinity of Tg.

Fig. 2
figure 2

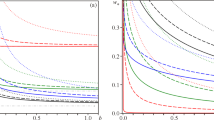
Modelling (blue lines) of shear viscosity η (top) and first normal stress coefficient ψ1 (bottom) data of PS13K (open symbols) as reported by Santangelo and Roland (2001)

Full size image

Shear viscosity and 1st normal stress coefficient

Figure 2 shows the modelling (blue lines) of shear viscosity η and first normal stress coefficient ψ1 data of PS13K (open symbols) through constitutive Eq. (9) with the relaxation modulus according to Eq. (1) and the material parameters Gn = 8.1 × 105Pa and τR = 12s as obtained from fitting the terminal behaviour of G′ and G″. An Excellent agreement is achieved between model prediction and steady shear viscosity data as reported by Santangelo and Roland (2001). Considering the difficulties involved with the measurement of the first normal stress difference N1, the model shows quite reasonable agreement with the first normal stress coefficient (ψ1) data. It should be noted that although the measurements were made in parallel-plate geometry with inhomogeneous shear flow, the steady-state data were corrected in Santangelo and Roland (2001) by using the Weissenberg−Rabinowitsch (Bird et al. 1987) procedure that transforms the parallel disk data into the true material functions.

As shown by Narimissa and Wagner (2020), the shear viscosity η of unentangled melts is given through Eq. (9) as,

$$ \eta =\frac{\sigma_{12}}{\dot{\gamma}}=\frac{5}{\dot{\gamma}}\sum \limits_{i=1}^{n_K}\underset{-\infty }{\overset{+\infty }{\int }}\frac{\partial {G}_i\left(t-t\hbox{'}\right)}{\partial t\hbox{'}}{S}_{12}\left(t,t\hbox{'}\right) dt\hbox{'} $$
(13)

with σ12 as shear stress and S12 as the 12-component of the orientation tensor. If scaled by the zero-shear viscosity and represented as a function of Weissenberg number \( Wi=\dot{\gamma}{\tau}_R \) (with shear strain \( \gamma =\dot{\gamma}\kern0.5em t \)), the normalised shear viscosity is universal for unentangled melts, i.e. independent of Gn and τR,

$$ \frac{\eta }{\eta_0}=\frac{30}{\pi^2{Wi}^2}\sum \limits_{i=1}^{n_K}\underset{-\infty }{\overset{+\infty }{\int }}{i}^2\exp \left[-{i}^2\left(\gamma -\gamma \hbox{'}\right)/ Wi\right]\kern0.5em {S}_{12}\left(\gamma, \gamma \hbox{'}\right)\kern0.5em d\gamma \hbox{'} $$
(14)

and approaches a scaling of Wi−1/2 at sufficiently high Wi. This universal master curve (continuous line) as plotted in Fig. 3 agrees with the data of Stratton (1972) for two Rouse melts with M = 10.5 kDa and M = 9.8 kDa (full symbols), and it also agrees perfectly with the data of Santangelo and Roland (2001) for PS13K (open symbols). The scaling of Wi−1/2 (dotted line in Fig. 3) at sufficiently high Weissenberg numbers is a consequence of the specific structure of the Rouse spectrum with G(t) ∝ t−1/2 for t < τR and the decreasing contribution of the long relaxation times to the shear stress with increasing shear deformation due to a decreasing S12 component of the orientation tensor. Colby et al. (2007) also reported the same scaling exponent and explained it through the contribution of only shorter relaxation modes to the shear stress at higher shear rates within shear-thinning regime.

Fig. 3
figure 3

Normalised viscosity η/η0 as a function of Weissenberg number \( Wi=\dot{\gamma}{\tau}_R \). Data from Stratton (1972) for two Rouse melts M = 10,500 Da and M = 19,800 Da (full symbols) and Santangelo and Roland (2001) for PS13K (open symbols). Full continuous line is the prediction of Eq. (14), and dotted line indicates the scaling of at high Wi

Full size image

We note that the universal master curve of the shear viscosity can be used to determine the parameters of the effective Rouse relaxation modulus. With the experimental value of η0 = 16.0MPa for PS13K, the best fit of the normalised shear viscosity data is obtained, if the shear rate is scaled to Weissenberg number Wi with a Rouse time of τR = 12s. From η0 = (π2/6)GnτR, the modulus Gn is then given by \( {G}_n=\frac{6}{\pi^2}\frac{\eta_0}{\tau_R}\approx 8.0\cdot {10}^5 Pa \). Accordingly, τR is smaller and Gn is higher than the corresponding values given by Ianniruberto and Marrucci (2020) for the parameters of the hypothetical “free” Rouse model. This is due to the combined effect of Rouse modes and glassy modes in the vicinity of the glass transition temperature Tg.

Apparent stress growth coefficients for shear stress and first normal stress difference

Figure 4 shows the comparison between model predictions (continuous lines) with the data of the apparent shear stress growth coefficient \( {\eta}_{app}^{+}(t) \) and the first normal stress growth coefficient \( {\psi}_{1 app}^{+}(t) \) of PS13K (open symbols). Due to the inhomogeneous nature of shear flow in parallel-plate geometry used by Santangelo and Roland (2001), they reported the shear rate \( {\dot{\gamma}}_R=0.14{s}^{-1} \) measured at the outer radius R of the parallel plates for their transient measurements. To compare predictions with the apparent stress growth data of shear stress and first normal stress difference, we follow Ianniruberto and Marrucci (2020). They showed that the relation between the apparent and the true stress growth coefficients is given by

$$ {\eta}_{\mathrm{app}}\left({\dot{\gamma}}_R,t\right)=4\underset{0}{\overset{1}{\int }}\eta \left(x{\dot{\gamma}}_R,t\right){x}^3 dx $$
(15)
$$ {\psi}_{1\kern0em \mathrm{app}}\left({\dot{\gamma}}_R,t\right)=4\underset{0}{\overset{1}{\int }}{\psi}_1\left(x{\dot{\gamma}}_R,t\right){x}^3 dx $$
(16)

where x = r/R is the nondimensional radial coordinate and both equations reduce to identities when the material quantities are shear rate independent.

Fig. 4
figure 4

Comparison between model predictions (continuous lines) and the experimental data (open symbols) of shear stress growth coefficient \( {\eta}_{app}^{+}(t) \) and first normal stress growth coefficient \( {\psi}_{1 app}^{+}(t) \) of PS13K as reported by Santangelo and Roland (2001). Continuous lines are predictions of Eqs. (15) and (16) for \( {\dot{\gamma}}_R=0.14{s}^{-1} \), while long-dotted lines are model predictions of Eq. (9) for a homogeneous shear rate of \( {\dot{\gamma}}_R=0.14{s}^{-1} \), respectively. Dotted lines are model predictions for the zero-shear stress growth coefficients \( {\eta}_0^{+}(t) \) and \( {\psi}_{10}^{+}(t) \)

Full size image

Predictions of Eqs. (15) and (16) for \( {\dot{\gamma}}_R=0.14{s}^{-1} \) (continuous lines) are compared with experimental data in Fig. 4. Predictions of the stress growth coefficients by assuming homogeneous shear flow with \( {\dot{\gamma}}_R=0.14{s}^{-1} \) (Eq. (9)) are also shown (long-dotted lines), which due to shear thinning, they are below the predictions of Eqs. (15) and (16). We note that as a consequence of the power of (r/R)3 in Eqs. (15) and (16), mainly the shear rates close to the rim at r = Rof the parallel plates dominate the stress growth coefficients. By restricting Eq. (15) to the steady-state viscosity \( \eta \left(\dot{\gamma}\right) \) and taking into account the − 1/2 scaling of the viscosity in the shear-thinning region at \( {\dot{\gamma}}_R=0.14{s}^{-1} \) (Figs. 2 and 3), we find immediately from Eq. (15) that the effective shear rate for the steady-state shear viscosity is \( {\dot{\gamma}}_{eff}=0.14{\left(\frac{7}{8}\right)}^2{s}^{-1}=0.107{s}^{-1} \); i.e. the apparent shear viscosity \( {\eta}_{app}\left({\dot{\gamma}}_R\right) \) is equal to the viscosity \( \eta \left({\dot{\gamma}}_{eff}\right) \) that would be obtained in the case of a homogeneous shear rate \( {\dot{\gamma}}_{eff} \). Indeed, the prediction of Eq. (15) and prediction of the steady-state shear viscosity for a homogeneous shear rate of \( {\dot{\gamma}}_{eff}=0.107{s}^{-1} \) agree within line width.

While model predictions are in fair agreement with the experimental data in the steady-state regime, the start-up predictions of the shear viscosity are delayed relative to the experimental data, while the rise of the first normal stress growth coefficient is predicted to be faster than seen experimentally. However, as seen in Fig. 2, significant nonlinear effects are evident for shear rates greater than 0.05 s−1, which may lead to the formation of flow instabilities such as shear banding, wall slip, and most importantly edge fracture (Costanzo et al. 2016; Tanner and Keentok 1983), while normal stress difference measurements may be additionally hampered by limited compliance of the rheometer (Meissner et al. 1989; Schweizer et al. 2008). Santangelo and Roland (2001) did not account for those flow instabilities in their measurements; hence, the accuracy of their data may be compromised. On the other hand, these deviations between model and data may also indicate limitations of the assumption of the effective Rouse model due to the complex interactions of Rouse modes and glassy modes in the vicinity of the glass transition temperature.

Apparent stress relaxation of shear stress and first normal stress difference

Model predictions of the apparent shear stress relaxation coefficient \( {\eta}_{app}^{-}(t) \) and the first normal stress relaxation coefficient \( {\psi}_{1 app}^{-}(t) \) of PS13K following steady flow at a shear rate of \( {\dot{\gamma}}_R=0.14{s}^{-1} \)as calculated by Eqs. (15) and (16) are shown in Fig. 5 (continuous lines) and are compared to experimental evidence (symbols). Also, predictions of the stress relaxation coefficients by assuming homogeneous shear flow with \( {\dot{\gamma}}_R=0.14{s}^{-1} \) are shown (long-dotted lines), which due to shear thinning, they are again below the predictions of Eqs. (15) and (16). We note that Santangelo and Roland (2001) used a logarithmic time scale for \( {\psi}_{1 app}^{-}(t) \), but plotted the data on a linear time scale (Figure 5 of Santangelo and Roland (2001)), and as explained in the previous section, they did not account for the possible effects of flow instabilities such as edge fracture. Nevertheless, model predictions are in reasonable qualitative agreement with the data of both the shear stress relaxation coefficient and the first normal stress relaxation coefficient.

Fig. 5
figure 5

Comparison between model predictions (continuous lines) and experimental data (open symbols) of shear stress relaxation coefficient \( {\eta}_{app}^{-}(t) \) and first normal stress relaxation coefficient \( {\psi}_{1 app}^{-}(t) \) of PS13K as reported by Santangelo and Roland (2001). Continuous lines are predictions of Eqs. (15) and (16) for \( {\dot{\gamma}}_R=0.14{s}^{-1} \), while long-dotted lines are model predictions of Eq. (9) for a homogeneous shear rate of \( {\dot{\gamma}}_R=0.14{s}^{-1} \), respectively

Full size image

Conclusions

The nonlinear shear rheology of unentangled polymer melts in the vicinity of the glass transition temperature is determined by an inseparable combination of Rouse and glassy modes (Ngai et al. (Ngai et al. 1987, Ngai et al. 1997)). The molecular units are densely packed together, and the understanding of their interactions would require the solution of a “many-body” problem at different length-scales. In characterising the linear-viscoelastic terminal behaviour of PS13K at the reference temperature of Tref = 104.7 °C, therefore, we have fitted the terminal regime of G′ and G″ by an “effective” Rouse relaxation modulus resulting from the interactions between Rouse modes and glassy modes. Based on this linear-viscoelastic characterisation, the nonlinear shear rheology of PS13K was modelled by the use of a single integral constitutive equation. As shown by Narimissa and Wagner (2020), viscoelastic strands representing the Rouse modes are only oriented in shear flow, but not stretched. An excellent agreement is observed between model predictions and the steady shear viscosity data, and good agreement with first normal stress coefficient data is achieved. In particular, the shear viscosity data agree quantitatively with the universal master curve predicted by Narimissa and Wagner (2020) for unentangled melts and approach a scaling of Wi−1/2 at sufficiently high Weissenberg numbers Wi. Some deviations between model predictions and data are seen for stress growth and stress relaxation, which can be attributed to limitations of the experiments, but may also indicate limitations of the assumption of the effective Rouse model due to the complex interactions of Rouse modes and glassy modes in the vicinity of the glass transition temperature.