Efficient inference and learning of a generative model for ENSO predictions from large multi-model datasets

Abstract

Historical simulations of global sea-surface temperature (SST) from the fifth phase of the Coupled Model Intercomparison Project (CMIP5) are analyzed. A state-of-the-art deep learning approach is applied to provide a unified access to the diversity of simulations in the large multi-model dataset in order to go beyond the current technological paradigm of ensemble averaging. Based on the concept of a variational auto-encoder (VAE), a generative model of global SST is proposed in combination with an inference model that aims to solve the problem of determining a joint distribution over the data generating factors. With a focus on the El Niño Southern Oscillation (ENSO), the performance of the VAE-based approach in simulating various central features of observed ENSO dynamics is demonstrated. A combination of the VAE with a forecasting model is proposed to make predictions about the distribution of global SST and the corresponding future path of the Niño index from the learned latent factors. The proposed ENSO emulator is compared with historical observations and proves particularly skillful at reproducing various aspects of observed ENSO asymmetry between the two phases of warm El Niño and cold La Niña. A relationship between ENSO asymmetry and ENSO predictability is identified in the ENSO emulator, which improves the prediction of the simulated Niño index in a number of CMIP5 models.

1 Introduction

1.1 General background

Understanding of the features and drivers of natural climate variability or of the response of the climate system to anthropogenic greenhouse gases forcing are needed for risk and impact studies across ecosystems and society. The development of Earth Systems Models (ESMs) has underlined much of the research in climate sciences to understand and predict the evolution of climate variability since the mid 1970 s with Manabe et al (1975) pioneering work. ESMs have been used to study the dynamics of sub-seasonal, to annual and decadal climate variability (Robertson et al 2020) – for instance to assess how sea surface temperature (SST) anomalies may affect surface air temperature multiscale spatial and temporal variability, or how decadal variability responds to anthropogenic greenhouse forcing.

However, in spite of important progress, uncertainties on the evolution of climate dynamics at regional or global scales, and sub-seasonal to decadal timescales have remained large. For instance, the range of equilibrium climate sensitivity to a twofold increase in carbon dioxide concentration has increased from the estimates of the Coupled Climate Model Intercomparison Project Phase 5 (CMIP5, Taylor et al 2012) with a range of 2.0–4.7 K to a wider range of 1.8–5.5 K for CMIP6 models (Flynn and Mauritsen 2020). The large range of estimates derives from model uncertainty linked to the diversity of parameterizations between models, such as differences in prescribed forcings across models as shown in Fyfe et al (2021) and scenario uncertainty (Hawkins and Sutton 2009). Indeed, ESMs include physical parameterizations of unresolved scales. These parameterizations are often based on uncertain empirical or theoretical relations. The sensitivity of climate model outputs to parameterization has led to refer to model tuning as an “art and science” (Hourdin et al 2017).

The current technological paradigm in ensemble climate prediction is to account for systematic model errors by averaging the outputs of independently performed simulations with different ESMs. This generally leads to a reduced error in the ensemble mean (Reichler and Kim 2008) and more reliable predictions (Palmer et al 2004). Because the models differ strongly in their parameterizations of unresolved physical processes, Palmer et al (2004) demonstrate an enhanced reliability and skill of the multi-model ensemble over a more conventional single-model ensemble approach. The operational predictions used by the climate research community rely on multi-model ensembles. For instance, the Copernicus Climate Change Services (C3S 2023) provides sub-seasonal to seasonal forecasts up to six months ahead and the North American Multi-Model Ensemble (NMME 2023) provides forecasts for up to 12 months.

However, in the face of the large present and persistent inter-model uncertainties and the need to assess potential impacts and risks today, several alternative approaches have also been suggested. Mauritzen et al (2017) argues that the expert-based selection of a subset of models depending on the question asked is a more appropriate strategy. Qasmi and Ribes (2022) suggest instead a statistical approach to constrain multi-model temperature outputs with global and local historical observational data to reduce uncertainties in local and regional projections. Tools like the ESMValTool address the need for fast and comprehensive diagnostics and performance metrics for analyzing and evaluating large multi-model ensembles, including grouping and selecting ensemble members by user-defined criteria (Eyring et al 2020).

Recently, as well, machine learning and neural network-based techniques have been suggested in this field to understand and forecast low to high-frequency climate processes. The emergence of physically constrained machine-learning-techniques has in particular shown promise to generalize beyond the training data used (Irrgang et al 2021; Kashinath et al 2021).

In this manuscript, we propose a methodological approach to provide a unified access to the diversity of ESM dynamics in order to go beyond the current technological paradigm of simple model averaging. The variational auto-encoder (VAE) is a universal, state-of-the-art neural network (NN)-based machine learning approach (Kingma and Welling 2014) that is not limited to any specific kind of data and allows for representation learning with many applications in computer vision (Higgins et al 2017; Chen et al 2018; Dosovitskiy and Djolonga 2020), natural language processing (Bowman et al 2015) and other fields (Hafner et al 2021). In this manuscript, we introduce a VAE architecture that allows to disentangle the complexity inherent to large climate datasets and that helps us extract underlying generic properties shared by an ensemble of ESMs. Here, the underlying objective is to build an ESM emulator requiring a minimum of expert-based fine tuning and customization.

In this manuscript, in order to illustrate the performance of the proposed VAE-based approach to build an emulator, we focus on El Niño Southern Oscillation (ENSO). ENSO is a well studied alternation of warm El Niño and cold La Niña SST anomalies in the Eastern tropical Pacific and represents the strongest year-to-year fluctuation of the global climate system, affecting global climate, marine and terrestrial ecosystems, fisheries and human activities (Timmermann et al 2018). Tang et al (2018) identify ESM model systematic error as probably the most challenging issue in ENSO prediction. Hope et al (2016) compares characteristics of ENSO spectra with models from the CMIP5 and show that no single model completely reproduces the instrumental spectral characteristics. Beobide-Arsuaga et al (2021) shows that ENSO uncertainty is large and that the sign of future variation of its amplitude is still unknown in both CMIP5 and the more recent CMIP6 outputs.

1.2 Subject of the study

We focus on studying the dynamics of monthly global temperature fields, represented as gridded global SST with a particular focus on the ENSO. The challenge of the task of one-to-two year prediction of the mixed deterministic and stochastic components of ENSO dynamics is addressed. Here, we present the formulation of a VAE deep-learning model allowing to derive a future path of an ENSO index (e.g. Niño 3.4 index) based on past observations and ESM simulations of global SSTs. The model is trained on an ensemble of CMIP5 historical runs of global SST and Niño 3.4. The objective is to build an emulator that is able to capture the diversity of the CMIP5 ensemble dynamics in the ENSO region. The proposed emulator is a much simpler model that reproduces the behavior of the ensemble of ESMs by training on sufficiently long simulations of the latter. The emulator is compared with historical observations of SST data (e.g. NOAA Extended Reconstructed Sea Surface Temperature, ERSST, Huang et al, 2017) and is shown to provide a skillful emulator of observed ENSO dynamics.

The manuscript is organized as follows: In Sect. 2, we first give a brief overview of the data used in this study and then present general principles of the VAE and the variant that we propose here. In Sect. 3, we present further details on the architecture of the NNs used to build the VAE. In Sect. 4, we illustrate the generative capabilities of the VAE and compare its statistical properties with those of observed ENSO dynamics. A summary of the results concludes the paper in Sect. 5, and the Appendix provide technical details about model configuration and model training.

1.3 Related work

In recent years, there has been an increasing interest in developing deep-leaning techniques for ENSO modeling and prediction.

Ham et al (2019) present a deep learning-based ENSO forecast framework in which separate convolutional neuronal networks (CNNs) are trained independently for each target season and forecast lead month, resulting in an ensemble of 276 different models (23 lead months $\times$ 12 target seasons). In subsequent studies different variants of deep learning architectures are presented by combining CNNs with recurrent neural networks (RNNs) (Mahesh et al 2019; Broni-Bedaiko et al 2019), but similarly trained separately for each target season or lead month. Given resulting inconsistencies in the seasonal characteristics of the ENSO predictions of this approach, Ham et al (2021) suggested an all-season variant of their previous model that combines all lead months and target seasons. To account for seasonal variability, they add an auxiliary task to the model in which the model is trained to predict the target months.

While we also adopt a similar all-season approach the proposed model also provides information about the season as an additional input that allows the VAE to condition its prediction on the season. We choose a conditioning method similar to Dosovitskiy and Djolonga (2020), which allows us to generate outputs of the VAE that correspond to the information provided as additional input.

Moreover, Ham et al (2021) suggest to average predictions over a deep ensemble of 40 independently trained all-season model. Instead, we propose to combine the VAE approach with a batch-ensemble technique (Wen et al 2020), which is a more parameter-efficient variant of the deep ensemble technique (Lakshminarayanan et al 2017).

In the ENSO forecast framework of Ham et al (2019), the CNNs use SST data on a global grid as input. In contrast, Yan et al (2020) focus on scalar data as input, which they first decompose into empirical modes and then feed into a one-dimensional CNN with causal convolutions that operates in the time domain. This hybrid approach is similar in structure to our approach in that we also use causal convolutions in the VAE. However, the proposed model uses principal components (PCs) of global SST as input that allows us to infer information on spatiotemporal aspects of ENSO. Hassanibesheli et al (2022) develop another hybrid approach using echo state networks to predict the low-frequency variability of different ENSO indices, which is combined with estimates of high-frequency variability using past-noise forecasting (Chekroun et al 2011).

Our work differs from previous deep learning approaches primarily in that we aim to develop a generative model of ENSO dynamics. Trained on a variational auto-encoding objective, the proposed VAE combines an inference model with a generative model. In this way, we can derive information about the distribution of generative factors from the data and make predictions about the ENSO dynamics based on samples of the various latent factors. In this way, the proposed model can act as an investigative tool for discovery and assist in theoretical advances (Irrgang et al 2021; Kashinath et al 2021).

2 Methodology

In this section, we first give a brief overview of the data used in this study. Next, we present the general principles of the VAE and discuss more recent variants that improve the learning of disentangled latent factors. Finally, we present our variant of VAE in which we combine the auto-encoding objective with a prediction task.

2.1 Data

The coupled general circulation climate model simulations analyzed in this study are from the fifth phase of the Coupled Model Intercomparison Project (CMIP5, Taylor et al 2012). We use monthly global SST anomalies from historical simulations over the 1865–2005 period. One run of each of the CMIP5 models is taken and interpolated onto a regular $5^\circ \times 5^\circ$ global grid between $55^\circ {S}$ and $60^\circ {N}$.

To compute a single set of empirical orthogonal functions (EOFs) common to all CMIP5 models, the covariance matrices of the SST anomalies are averaged before the eigendecomposition. Then, the SST anomalies are projected onto the resulting EOFs to obtain an ensemble of principal components (PCs). In the present work, the leading $S=20$ PCs are used as input to the VAE, capturing about 80% of the total variance in the ensemble of SST anomalies. To give the same weight to the PCs, they are further normalized to have the same variance and scaled so that their total variance matches one. In addition, the corresponding time series of monthly SST anomalies averaged over the Niño 3.4 region ($170^\circ {W}-120^\circ {W}$, $5^\circ {S}-5^\circ {N}$) are provided along with the PCs as input to the VAE.

For comparison purposes, historical observations of monthly global SST data are taken from the fifth version of the NOAA Extended Reconstructed Sea Surface Temperature (ERSST, Huang et al 2017). We use SST anomalies over the same 1865–2005 period projected onto the CMIP EOFs to obtain ERSST PCs. Similarly, the corresponding time series of monthly SST anomalies, averaged over the Niño 3.4 region, is obtained from ERSST and provided along with the ERSST PCs as input to the VAE.

2.2 Variational auto-encoding

Fig. 1

Overview of the model components. The model is a combination of a VAE, with its encoder (left) and decoder (middle), and a second decoder for prediction (right). An example of the input ${\textbf{x}}$ to the encoder (blue) and the resulting ensemble of stochastic reconstructions $\hat{\textbf{x}}$ and predictions $\hat{\textbf{y}}$ (orange) are shown below the corresponding model parts. With a prior ${\mathcal {N}}(0,{\textbf{I}})$ over the latent space, the encoder approximates a posterior ${\mathcal {N}}(\varvec{\mu },\textrm{diag}(\varvec{\sigma }^{2}))$, which is used by the two decoders to stochastically estimate the input ${\textbf{x}}$ and prediction target ${\textbf{y}}$ (blue)

The VAE combines variational inference with deep learning and provides a probabilistic approach to describe observations in the latent space (Kingma and Welling 2014, 2019). The VAE encoding and decoding methodology provides a computationally efficient way to a) infer information about latent variables from observations and b) to approximate the difficult-to-compute probability density functions (PDFs) that underlie the complex nonlinear ENSO dynamics in the multi-model CMIP ensemble.

To achieve this, the VAE is trained on samples from the multi-model dataset ${\mathcal {D}}=\{{\mathcal {D}}_{m}\}_{m=1}^{M}$ that combines the M different historical simulations, ${\mathcal {D}}_{m}=\{{\textbf{x}}_{m}(n)\}_{n=1}^{N}$, each providing N training samples (cf. Fig. 1). In the following, we omit the indices m and n when referring to a random sample ${\textbf{x}}={\textbf{x}}_{m}(n)$ from the entire multi-model dataset ${\mathcal {D}}$.

Auto-encoding The encoder q, parameterized by a neuronal network (NN) with parameters $\phi$, approximates the PDF of the latent space ${\textbf{z}}$ conditional on the sample ${\textbf{x}}$,

$$\begin{aligned} q_{\phi }({\textbf{z}}|{\textbf{x}}). \end{aligned}$$

(1)

The decoder p, parameterized by a second NN with parameters $\theta$, approximates the PDF of the sample ${\textbf{x}}$ conditional on the latent space ${\textbf{z}}$,

$$\begin{aligned} p_{\theta }({\textbf{x}}|{\textbf{z}}). \end{aligned}$$

(2)

In jointly optimizing the parameters of the encoder and decoder, the VAE learns to find stochastic mappings between a high-dimensional input space ${\textbf{x}}$, whose distribution is typically complicated, and a low-dimensional latent space ${\textbf{z}}$, with a distribution that is comparatively much simpler.

Generative model The VAE combines an inference model with a generative model. The inference model, represented here by the encoder, approximates the true but difficult-to-compute (intractable) posterior, $p({\textbf{z}}|{\textbf{x}})\approx q_{\phi }({\textbf{z}}|{\textbf{x}})$. The generative model then learns a joint distribution $p_{\theta }({\textbf{x}},{\textbf{z}})$ between input space and latent space, which allows us to continuously generate new unseen data in input space while sampling from the latent space. The generative model is typically factorized as

$$\begin{aligned} p_{\theta }({\textbf{x}},{\textbf{z}})=p_{\theta } ({\textbf{z}})p_{\theta }({\textbf{x}}|{\textbf{z}}), \end{aligned}$$

(3)

with a prior distribution $p_{\theta }({\textbf{z}})$ over the latent space and the decoder $p_{\theta }({\textbf{x}}|{\textbf{z}})$ in Eq. (2). The prior is taken from a family of densities whose parameter can be easily optimized; cf. Sect. 2.4.

Evidence lower bound The optimization objective of the VAE is the evidence lower bound (ELBO) (Kingma and Welling 2014, 2019),

$$\begin{aligned} {\mathcal {L}}_{\textrm{ELBO}}({\textbf{x}})&= \mathbb {E}_{q_{\phi }({\textbf{z}}|{\textbf{x}})}\left[ \log \left( \frac{p_{\theta } ({\textbf{x}},{\textbf{z}})}{q_{\phi }({\textbf{z}}|{\textbf{x}})}\right) \right] , \end{aligned}$$

(4a)

$$\begin{aligned}&\le \mathbb {E}_{q_{\phi }({\textbf{z}}|{\textbf{x}})}\left[ \log p_{\theta }({\textbf{x}})\right] . \end{aligned}$$

(4b)

The ELBO in Eq. (4a) puts a lower bound on the marginal likelihood (4b). The expectation on the rhs of Eqs. (4a) and (4b) is formally defined using samples ${\textbf{z}}$ from the approximate posterior $q_{\phi }({\textbf{z}}|{\textbf{x}})$, taken into account the samples from the entire dataset ${\textbf{x}}\in {\mathcal {D}}$. In practice, though, the VAE is optimized using stochastic gradient descent, in which the expectation in minibatches ${\mathcal {M}}\subset {\mathcal {D}}$ is used (Goodfellow et al 2016).

Maximizing Eq. (4a) allows us to jointly optimize the parameters $\theta$ and $\phi$ of the encoder and decoder, improving at the same time the two aspects we are interested in (see e.g. Kingma and Welling 2019, Sect. 2.2):

• 1. The inference model improves in the approximation of the true posterior distribution (of the data-generating factors).

• 2. The generative model improves in its ability to generate more likely (more realistic looking) data.

If we use the factorization of the generative model in Eq. (3), the ELBO in Eq. (4a) can be rewritten as the sum of two terms,

$$\begin{aligned} {\mathcal {L}}_{\textrm{ELBO}}({\textbf{x}})&= \mathbb {E}_{q_{\phi }({\textbf{z}}|{\textbf{x}})}\left[ \log p_{\theta }({\textbf{x}}|{\textbf{z}})\right] + \mathbb {E}_{q_{\phi }({\textbf{z}}|{\textbf{x}})}\left[ \log \left( \frac{p_{\theta } ({\textbf{z}})}{q_{\phi }({\textbf{z}}|{\textbf{x}})}\right) \right] , \end{aligned}$$

(5a)

$$\begin{aligned}&= \mathbb {E}_{q_{\phi }({\textbf{z}}|{\textbf{x}})}\left[ \log p_{\theta }({\textbf{x}}|{\textbf{z}})\right] - \textrm{KL}\left( q_{\phi }({\textbf{z}}|{\textbf{x}})\Vert p_{\theta }({\textbf{z}})\right) . \end{aligned}$$

(5b)

The first term in Eq. (5b) is the log-likelihood of the training samples ${\textbf{x}}$ and is a measure of the reconstruction quality of the decoder $p_{\theta }({\textbf{x}}|{\textbf{z}})$. The second term in Eq. (5b) is the Kulback-Leibler (KL) divergence and acts as a regularization term on the encoder. Minimizing $\textrm{KL}\left( q_{\phi }({\textbf{z}}|{\textbf{x}})\Vert p_{\theta }({\textbf{z}})\right)$ keeps the approximate posterior $q_{\phi }({\textbf{z}}|{\textbf{x}})$ in the proximity of the prior $p_{\theta }({\textbf{z}})$.

Thus, the VAE is trained to find a trade-off between a close approximation of the samples from the training data, ${\textbf{x}}\in {\mathcal {D}}$, by the decoder and the amount of information in terms of KL divergence that the encoder needs to form the aggregated posterior $q_{\phi }({\textbf{z}})$,

$$\begin{aligned} q_{\phi }({\textbf{z}})=\frac{1}{NM} \sum _{{\textbf{x}}\in {\mathcal {D}}}q_{\phi }({\textbf{z}}|{\textbf{x}}). \end{aligned}$$

(6)

2.3 Disentangled representations

In order to be more flexible in balancing decoding and encoding objectives, Higgins et al (2017) introduce an adjustable hyper-parameter $\beta$ that scales the KL term in Eq. (5b). They show that with a carefully chosen $\beta$, this so-called $\beta$-VAE improves the learning of an interpretable representation of the independent generative factors of the data.

Rolinek et al (2019) show that part of this improvement can be attributed to the specific implementation design of a diagonal covariance in the encoding NN; cf. Sect.  2.4 for implementation details. Although an increase of $\beta$ promotes (local) independence and disentanglement in the latent space, it comes at the cost of a potentially undesirable increase in stochasticity in the model-generated data, i.e. an increase in blurriness, for which the VAE has often been criticized.

Total correlation Instead of scaling up the entire KL divergence in Eq. (5b), Chen et al (2018) suggest a further decomposition of the KL divergence. They show that one component that proves particularly important in learning a disentangled representation is the total correlation (TC). The TC quantifies the statistical dependence between the different dimensions $z_{k}$ of ${\textbf{z}}\in \mathbb {R}^{K}$ and is defined as

$$\begin{aligned} {\mathcal {L}}{}_{\textrm{TC}}({\textbf{x}})=\textrm{KL} \left( q_{\phi }({\textbf{z}}) \parallel \prod _{k}q_{\phi }(z_{k})\right) . \end{aligned}$$

(7)

In minimizing the TC loss in Eq. (7), the encoder is forced to find statistically independent factors in the aggregated posterior. Chen et al (2018) provide a minibatch version of the sampled TC that approximates the aggregated posterior $q_{\phi }({\textbf{z}})$ and its marginal distributions $q_{\phi }(z_{k})$ in a minibatch ${\mathcal {M}}$ when optimizing the VAE with stochastic gradient descent.

Batch ensemble Despite the success of VAE and its variants in efficiently learning interpretable disentangled representation in large datasets, there is generally no guarantee of success for finding isolated compositional factors in real-world data. For example, Locatello et al (2019) show that the quality of disentanglement is strongly influenced by randomness in the form of initial values of the model parameters and the training run. To reduce this undesired influence, Duan et al (2020) propose to train an ensemble of multiple VAEs that are initialized and trained independently. They argue that disentangled representations are similar and entangled representations are different in its own way, and propose a comprehensive ranking algorithm that quantifies the quality of disentanglement in an ensemble of VAEs.

Instead of performing exhaustive training of an ensemble of independent VAEs, we rely here on the principle of a batch ensemble (Wen et al 2020). The members in a batch ensemble share most of their parameters and can be efficiently trained in parallel by combining them into a minibatch. The minibatch is augmented with different ensemble members that are given the same data, so their individual parameters are jointly optimized along with the shared parameters in each step of the stochastic gradient descent.

More generally, the ensemble approach attempts to mitigate the problem that NNs are typically under-specified by the data ${\mathcal {D}}$. In the case of the encoder, for example, we can have many different settings of parameters $\phi$ that all perform equally well, and the posterior that we want to compute is

$$\begin{aligned} q({\textbf{z}}|{\textbf{x}},{\mathcal {D}})=\int q_{\phi }({\textbf{z}}|{\textbf{x}})p(\phi |{\mathcal {D}})\textrm{d}\phi . \end{aligned}$$

(8)

Rather than placing everything on a single set of parameters, we want to marginalize the parameters $\phi$ (Wilson and Izmailov 2020). In this context, Wen et al (2020) show that batch ensembles can indeed compete in performance with other ensembling techniques, for example, even compared to typical deep ensembles (Lakshminarayanan et al 2017) on out-of-distribution tasks.

We note that the TC affects the diversity of ensemble members as training progresses. Since different members are jointly optimized on the same data, minimizing TC leads to an increase in the diversity of the parameters $p(\phi |{\mathcal {D}})$.

Cross entropy To increase the diversity in the data generating process as well, i.e., to avoid overfitting the training data, we add a loss term inspired by the contrastive learning approach of Radford et al (2021).

Let $\hat{\textbf{x}}$ be a sample from the decoder $p_{\theta }({\textbf{x}}|{\textbf{z}})$. We first compute the cosine similarity between all pairs $\hat{\textbf{x}}_{i}$ and $\hat{{\textbf{x}}}_{j}$ in a minibatch. In this symmetric matrix, we then seek to reduce the similarity for negative pairs ($i\ne j$). In doing so, we follow Radford et al (2021) and continue to normalize the rows of the cosine similarity matrix using the softmax function. This normalization provides the probability distributions, which we finally use to calculate the categorical cross entropy ${\mathcal {L}}_{\textrm{CE}}(\hat{\textbf{x}})$ with the diagonal $i=j$ as target labels.

Since different members of the batch ensemble are jointly optimized with the same data ${\textbf{x}}$, minimizing the cross entropy ${\mathcal {L}}_{\textrm{CE}}(\hat{\textbf{x}})$ on samples $\hat{\textbf{x}}$ increases diversity in the data generation process and prevents the ensemble of decoders from placing everything on a single set of parameters. Similar to the encoder case in Eq. (8), we can have many different settings of the parameters $\theta$ with similar data likelihood, and the data distribution we want to model is

$$\begin{aligned} p({\textbf{x}}|{\textbf{z}},{\mathcal {D}})=\int p_{\theta }({\textbf{x}}|{\textbf{z}})p(\theta |{\mathcal {D}})\textrm{d}\theta . \end{aligned}$$

(9)

Instead of a local maximum-likelihood approximation, the data distribution we want to approximate could be more complex in nature, so that functional diversity in Eq.  (9) is important for a good approximation (Wilson and Izmailov 2020). Based on our experience with the CMIP data, we find that with the minimization of ${\mathcal {L}}_{\textrm{CE}}(\hat{{\textbf{x}}})$, the reproduction of ENSO asymmetry in the generative part of the VAE improves (not shown).

2.4 Gaussian approximation

For various practical considerations, the approximate posterior of the encoder is often parameterized in the form of a factorized Gaussian distributions,

$$\begin{aligned} q_{\phi }({\textbf{z}}|{\textbf{x}})={\mathcal {N}}\left( {\textbf{z}};\varvec{\mu }, \textrm{diag}(\varvec{\sigma }^{2})\right) , \end{aligned}$$

(10)

with mean $\varvec{\mu }$ and a diagonal covariance matrix, $\textrm{diag}(\varvec{\sigma }^{2})$.

The encoder NN, which is typically implemented as a deterministic feed-forward NN (cf. Fig. 1), returns a tuple of parameters representing the mean, $\varvec{\mu }$, and diagonal of the covariance matrix, $\textrm{diag}(\varvec{\sigma }^{2})$, of the factorized Gaussian in Eq. (10), i.e.,

$$\begin{aligned} (\varvec{\mu },\varvec{\sigma }^{2})=\textrm{Encoder}_{\phi }({\textbf{x}}). \end{aligned}$$

(11)

The encoder therefore learns the parameters of the distribution of ${\textbf{z}}$ conditioned on input ${\textbf{x}}$.

In the combination of a simple factorized Gaussian posterior with a Gaussian prior, $p_{\theta }({\textbf{z}})={\mathcal {N}}(0,{\textbf{I}}),$ the KL divergence in Eq. (5b) can then be computed component-wise in closed form as, cf. Kingma and Welling (2014),

$$\begin{aligned} \textrm{KL}\left( q_{\phi }({\textbf{z}}|{\textbf{x}})\Vert p_{\theta }({\textbf{z}})\right) =\frac{1}{2}\sum _{k=1}^{K}\mu _{k}^{2} +\sigma _{k}^{2}-\log \sigma _{k}^{2}-1, \end{aligned}$$

(12)

where $\mu _{k}$ and $\sigma _{k}^{2}$ denote the k-th components of $\varvec{\mu }$ and $\varvec{\sigma }^{2}$, respectively.

The decoder NN, which is likewise implemented as a deterministic feed-forward NN (cf. Fig. 1), samples from the approximate posterior,

$$\begin{aligned} {\textbf{z}}&\sim {\mathcal {N}}\left( \varvec{\mu },\mathrm {diag(}\varvec{\varvec{\sigma }}^{2})\right) , \end{aligned}$$

(13a)

$$\begin{aligned} \hat{{\textbf{x}}}&= \textrm{Decoder}_{\theta }({\textbf{z}}), \end{aligned}$$

(13b)

and provides stochastic estimates $\hat{{\textbf{x}}}$ of the input ${\textbf{x}}$. The reconstruction error in Eq. (5b) is approximated by the mean square error,

$$\begin{aligned} \mathbb {E}_{q_{\theta }({\textbf{z}}|{\textbf{x}})}\left[ \log p_{\theta }({\textbf{x}}|{\textbf{z}})\right] \simeq -\mathbb {E}_{q_{\theta }({\textbf{z}}|{\textbf{x}})}\left\| {\textbf{x}}-\hat{{\textbf{x}}}\right\| {}^{2}. \end{aligned}$$

(14)

which maximizes the likelihood on Gaussian-distributed data. For the sake of simplicity, the dispersion of the Gaussian distribution is omitted in Eq. (14), i.e. we only consider the mean of $p_{\theta }({\textbf{x}}|{\textbf{z}})$ when optimizing the parameters $\theta$ of the decoder NN.

Since we would like to optimize the ELBO objective with stochastic gradient descent, Kingma and Welling (2014) introduce a so-called reparameterization trick. To that end, the sampling from the posterior in Eq. (13a) is externalized by an auxiliary random process $\varvec{\varepsilon }\sim {\mathcal {N}}(0,{\textbf{I}})$ as

$$\begin{aligned} {\textbf{z}}=\varvec{\mu }+\varvec{\varvec{\sigma }}\odot \varvec{\varvec{\varepsilon }}, \end{aligned}$$

(15)

with $\odot$ the element-wise product.

In this way, the encoder NN in Eq. (11) receives as input ${\textbf{x}}$ and returns the parameters $\varvec{\mu }$ and $\varvec{\sigma }^{2}$ of the approximate posterior in Eq. (10). Sampling from the approximate posterior in Eq. (13a) is then performed by sampling from the auxiliary random process $\varvec{\varepsilon }$ in Eq. (15). The random sample ${\textbf{z}}$ is then used as input to the decoder NN in Eq. (13b) to provide a stochastic estimate $\hat{{\textbf{x}}}$ of the input ${\textbf{x}}$, cf. Fig. 1.

2.5 VAE and forecasting

In addition to the auto-encoding task, a second decoder NN with parameters $\eta$ is trained jointly to approximate the conditional PDF between ${\textbf{z}}$ and a prediction target ${\textbf{y}}$:

$$\begin{aligned} p_{\eta }({\textbf{y}}|{\textbf{z}}) \end{aligned}$$

(16)

Similarly to the first decoder NN, the random sample ${\textbf{z}}$ from the approximate posterior in Eq. (15) is used as input to the second decoder NN, cf. Fig. 1,

$$\begin{aligned} \hat{{\textbf{y}}} = \textrm{Decoder}_{\eta }({\textbf{z}}), \end{aligned}$$

(17)

and provides a stochastic estimate $\hat{{\textbf{y}}}$ of the prediction target ${\textbf{y}}$. The prediction error is also approximated by the mean square error,

$$\begin{aligned} \mathbb {E}_{q_{\theta }({\textbf{z}}|{\textbf{x}})}\left[ \log p_{\eta }({\textbf{y}}|{\textbf{z}})\right] \simeq -\mathbb {E}_{q_{\theta }({\textbf{z}}|{\textbf{x}})}\left\| {\textbf{y}}-\hat{{\textbf{y}}}\right\| {}^{2}, \end{aligned}$$

(18)

and jointly minimized with the auto-encoding objective. Similar to the first decoder, we also try to increase the diversity in the batch ensemble of forecasts and minimize the cross entropy loss ${\mathcal {L}}_{\textrm{CE}}(\hat{\textbf{y})}$ in a minibatch of predictions $\hat{\textbf{y}}$.

In summary, parameters $\theta$, $\phi$, and $\eta$ are optimized by minimizing the total loss

$$\begin{aligned}{} & {} {\mathcal {L}}{}_{\theta ,\phi ,\eta }({\textbf{x}},{\textbf{y}}) =\mathbb {E}_{q_{\theta }({\textbf{z}}|{\textbf{x}})}\left\| {\textbf{x}}-\hat{{\textbf{x}}}\right\| {}^{2}+\alpha \,\mathbb {E}_{q_{\theta }({\textbf{z}}|{\textbf{x}})}\left\| {\textbf{y}}-\hat{{\textbf{y}}}\right\| {}^{2}\nonumber \\{} & {} \quad +\beta \left[ \textrm{KL}\left( q_{\phi }({\textbf{z}}|{\textbf{x}})\Vert p_{\theta }({\textbf{z}})\right) +\gamma \,{\mathcal {L}}_{\textrm{TC}}({\textbf{x}}) \right. \nonumber \\{} & {} \quad \left. +\delta _{x}{\mathcal {L}}_{\textrm{CE}}(\hat{{\textbf{x}}})+\delta _{y}\, {\mathcal {L}}_{\textrm{CE}}(\hat{\textbf{y}})\right] . \end{aligned}$$

(19)

The first and second terms of Eq. (19) represent the reconstruction and prediction error, respectively. The remaining term of Eq. (19), on the other hand, represent the various regularization penalties for the model. A summary of their individual scaling parameters used in the ENSO modeling application is provided in Appendix . At training time, we apply an annealing scheme to the regularization strength in which we gradually increase the scale $\beta$ (Bowman et al 2015). In this way, the model can initially encode a maximum amount of information, but is then forced to find a more compact, disentangled representation that approximates the diversity in the data.

Figure 1 provides an overview of the different components of the model as well as of their interaction. Below each of the model components, an example of the data is shown to illustrate the general flow of data within the model. In each step of the stochastic gradient descent, a minibatch ${\mathcal {M}}$ of pairs ${\textbf{x}}$ and ${\textbf{y}}$ is drawn from the multi-model dataset ${\mathcal {D}}$. Next, independent random samples are drawn from the auxiliary process $\varvec{\varepsilon }$ for each of the pairs and used to obtain ${\textbf{z}}$ from the approximate posterior in Eq. (15). Provided as input to the decoder NNs, stochastic estimates $\hat{{\textbf{x}}}$ and $\hat{{\textbf{y}}}$ in Eqs. (13b) and (17), respectively, are finally obtained. The encoder receives as input a sample ${\textbf{x}}\in \mathbb {R}^{L\times (S+1)}$ from the CMIP data in Sect. 2.1, combining values of the leading S PCs with Niño 3.4 SST in a sliding time window of length L. These are the observations of the last L month before a given time t, which are used as input to the encoder NN to approximate the posterior ${\mathcal {N}}(\varvec{\mu },\textrm{diag}(\varvec{\sigma }^{2}))$ at time t. A new sample is drawn from the posterior at time t, ${\textbf{z}}={\textbf{z}}(t)$, and provided as input to the two decoder NNs. While the first decoder NN provides estimates $\hat{\textbf{x}}$ of the past observations ${\textbf{x}}$, the second decoder NN is used to make future predictions $\hat{\textbf{y}}$ for the following F months of the Niño 3.4 index in ${\textbf{y}}$.

The minibatch is augmented with different ensemble members that are given the same data ${\textbf{x}}$ and ${\textbf{y}}$ (not shown), but optimized with different random samples $\varvec{\varepsilon }$ from the auxiliary process. This provides an additional source of diversity in the data generation process insofar as the minimization of the total correlation loss ${\mathcal {L}}_{\textrm{TC}}$ and the cross entropy losses ${\mathcal {L}}_{\textrm{CE}}$ in Eq. (19) increase the diversity in the batch ensemble.

3 Model architecture of encoder and decoder NNs

Fig. 2

Architecture of the encoder NN (left) and the decoder NN (right). The figure shows the case of $B=2$ blocks. Examples of the input data ${\textbf{x}}$ to the encoder and the decoder output $\hat{\textbf{x}}$ are shown below the corresponding parts. The encoder and decoder consist of multiple blocks combining causal convolutional layers and temporal resampling by pixel shuffling (blue boxes) to aggregate and distribute temporal information. Auxiliary information on the index m of the CMIP model from which the sample ${\textbf{x}}_{m}\in {\mathcal {D}}_{m}$ was taken and the temporal information ${\textbf{s}}(t)$ are used to modulate features in the encoder and decoder NNs by FiLM layers (green boxes). Only the first decoder NN for reconstruction is shown, cf. Fig. 1. The second decoder NN used for forecasting (not shown here) has the same structure as the first decoder NN, but differs only in the output size $F \times 1$ and keeps the temporal order, i.e. has no reverse layer

The following section provides a more detailed description of the implementation of the encoding and decoding NNs. A detailed schematic representation of the architectures of the two NNs and the different elements we find in each of them is shown in Fig. 2.

Both the encoder and decoder are implemented as residual networks (He et al 2016a) that process their input through a stack of residual units. In this framework, the output of the residual unit $f_{l}$ is combined with the input $x_{l}$ to the unit, $x_{l+1}=f_{l}(x_{l})+x_{l}$. These skip connections improve signal propagation from one unit to another leading to easier optimization. We use a variant of full pre-activation (He et al 2016b) in which the convolutional layers are preceded by a batch-normalization layer and the activation function. For the latter, we use the sigmoid linear unit or SiLU, a specific case of the swish activation function.

In the convolutional layers, we use causal convolutions to ensure that temporal dependencies are modeled in the right order; cf. e.g. van den Oord et al (2016). However, by reversing the temporal order in the output of the decoder, the temporal dependencies are modeled in an anti-causal order in the convolutional layers. The features that we extract from the convolutional layers are then used as input to a multilayer perceptron (MLP), from which we obtain the mean and variance of the posterior. Although the MLP is not causal, we see that past observations in ${\textbf{x}}$, at time $t+\tau$ with $-L\le \tau <0$, are modeled with latent samples ${\textbf{z}}(t)$ drawn at time t from the posterior, cf. Fig. 1. In this way, the encoder aggregates information from an interval of past observations to form the posterior, which the first decoder NN uses to model the past observations. In the second decoding NN used for forecasting, the output is not reversed, so the prediction target ${\textbf{y}}$, at time $t+\tau$ with $0\le \tau < F$ is modeled in the forward direction in the convolutional layers, cf. Fig. 1.

To capture temporal dependencies on different time scales, the data is resampled in each of the B residual blocks as shown in Fig. 2, i.e., sub-sampled at half the sampling rate in the encoder and up-sampled at twice the sampling rate in the decoder. To efficiently resample the data, we use here a parameter-free variant of a pixel shuffling originally proposed in the context of image super-resolution (Shi et al 2016). Some illustrative examples of the pixel-shuffle algorithm in the encoder and decoder are shown in Fig. 2. In the encoder, pairs of temporally adjacent elements are stacked, which reduces the sampling rate by half and doubles the number of channels in each of the B blocks, i.e. ${\textbf{x}}:R^{L\times C}\mapsto R^{\frac{L}{2}\times 2C}$. In the decoder, these stacks are redistributed again by splitting the channels into half and then filling temporally adjacent pairs with the respective elements, i.e. ${\textbf{x}}:R^{L\times C}\mapsto R^{2L\times \frac{C}{2}}$. Therefore, resampling by pixel shuffling preserves the number of elements in ${\textbf{x}}$ and thus the total amount of information. The cost, however, is the exponential growth in the number of channels, which limits it to a few resampling steps. Since the output of residual block B has a shape $\frac{L}{2^{B}}\times 2^{B}C$, the number of parameters in the convolutional layers likewise grows exponentially with the number of blocks. To keep the number of parameters in the convolutional layers manageable, we use here only a few blocks, e.g., $B \le 3$.

In the encoder, an initial convolutional layer with kernel size 1 embeds the input with $S+1$ channels into an initial number of C channels, which is used as input to the stack of B residual blocks. The features that we extract from the stack are then used as input to an MLP, from which we obtain the mean and variance of the posterior. In this MLP, we have a first fully-connected (FC) layer with $K'$ units and the hyperbolic tangent as nonlinearity, from which we obtain the mean and variance through a pair of FC layers with K units each.

In the decoder, a sample from the latent space is used as input to an MLP in which we combine a pair of FC layers with $K'$ and $L \cdot C$ units, respectively, with a hyperbolic tangent in the middle. The output of the MLP is then used as input to the stack of B residual blocks, while a final convolutional layer with kernel size 1 provides the desired number of output channels.

Forecasting In the first decoder NN, the number of output channels is the same as the number of input channels to the encoder NN, cf. Fig. 1. However, in the second decoder NN used for forecasting, we only consider one output channel, the Niño 3.4 SST, so we choose a smaller number of embedding channels $C'<C$ in the convolutional layers. This reduces the number of parameters not only in the convolutional layers, but also in the MLP, where the second FC layer has $F\times C'$ units in the second decoder NN. On the other hand, the two decoders in Fig. 1 are of the same structure, and we have omitted the second decoder in Fig. 2. Note that the time is reversed only in the first decoder NN used for reconstruction.

Feature-wise linear modulation (FiLM) Based on auxiliary information, the computation in the stack of residual blocks is influenced by so-called FiLM layers. Introduced as a general-purpose conditioning method, FiLM layers influence neural network computation via a simple, Feature-wise Linear Modulation (FiLM, Perez et al 2018). In their FiLM layers, the auxiliary input is first transformed to match the number of features (channels) C of the FiLM-ed input by a pair of FC layers with C units each. The output of the two FC layers is then used to scale and shift the features in the FiLM-ed tensor. In the present context, this allows the encoder and decoder NNs to condition their computation on auxiliary information. Here we condition the NNs on two types of information: a) temporal information on the current month and b) ensemble information on the current ensemble member.

To encode temporal information on the current month at time t, we combine sine and cosine functions of different frequencies,

$$\begin{aligned} {\textbf{s}}(t)=\left\{ \left( \sin \bigg(2\pi \frac{k}{12}t\bigg),\cos \bigg(2\pi \frac{k}{12}t\bigg)\right) ,\quad k=1,2,\dots ,6\right\} . \end{aligned}$$

(20)

The functions are sampled at frequencies of the discrete Fourier transform and form a system of orthogonal functions. For illustration, the monthly values of the first six components of the temporal encoding are shown in Fig. 2. The set of periodic functions in the vector ${\textbf{s}}(t)$ of size 12 is then used as input to a FC layer with P units to obtain the conditioning information for the FiLM layers. In this way, the encoder and decoder NNs can learn seasonal variations of the feature-wise scale and bias parameters in the FiLM layers specific to each month of the year.

To encode information about the current ensemble member, we draw a random number from a categorical distribution, where the different categories represent different members of the batch ensemble. As shown in Fig. 2, sampling from the categorical distribution is implemented by categorical reparameterization with Gumbel-Softmax (Jang et al 2017), which allows the NN to optimize the parameters of the categorical distribution with stochastic gradient descend. Instead of selecting the batch ensemble members at random (Wen et al 2020), we make the selection process itself dependent on auxiliary information. For the latter, we use the index m of the CMIP model from which the sample ${\textbf{x}}_{m}\in {\mathcal {D}}_{m}$ was taken. This means that the integer index m is first one-hot encoded into a binary vector ${\textbf{m}}\in \mathbb {R}^{M}$, with a single high (one) bit at the m-th position, and then used as input to a FC layer with E units to learn the parameters of the categorical distribution. A sample from the distribution with E categories is then used as input to a second FC layers with P units and added to the temporal encoding. This way, the model can learn an optimal combination of the two types of information.

Conditioning on index m allows the encoder and decoder to learn a distribution of the feature-wise scale and bias parameters in the FiLM layers specific to each of the m CMIP models. In learning distributions $p(\phi |{\mathcal {D}}_{m})$ in the encoder and $p(\theta |{\mathcal {D}}_{m})$ in the decoder, we attempt to marginalize parameters, although quite simplistically, in the approximation of the posterior in Eq. (8) and the data distribution in Eq. (9), respectively.

In our experiments with the CMIP data, optimizing on the TC and CE terms in Eq. (19) prevents the model from collapsing to a single category in the Gumbel Softmax and helps mitigate the risk of overfitting the data. On the other hand, setting the batch ensemble size E to a value smaller than M, i.e., $E<M$, encourages more general inter-model solutions common to different CMIP models.

A summary of the model configuration and related parameters can be found in Appendix A.

4 ENSO modeling

An important aspect of the ENSO dynamics is the asymmetry between the two phases of warm El Niño and cold La Niña. While there is significant differences in the observed spatial pattern, amplitude and duration of the two phases (e.g. Dommenget et al 2012), climate models still underestimate the degree of the observed ENSO asymmetry (Dommenget et al 2012; Zhang and Sun 2014; Zhao and Sun 2022).

Given the wide range in the simulation of ENSO events in the climate models, some of which are more realistic than others, we will first assess the extent to which the VAE can disentangle the complexity inherent in the large CMIP5 dataset. We hence extract the underlying generic properties that are shared among an ensemble of climate models and build an emulator of ENSO dynamics, which we will subsequently study then in greater detail. We will demonstrate the various generative capabilities of the ENSO emulator and evaluate its ability to reproduce various key features of the observed ENSO asymmetry.

4.1 Latent-space dynamics

We start by analyzing properties of the latent space. In doing so, we sort the latent dimensions, $k=1\dots K$, in descending order with respect to their KL divergence in Eq. (12), averaged over all samples from ${\mathcal {D}}$. Just as is common practice to order principal components by their contribution to the variance, we rank the latent dimensions according to their contribution of encoding information in the posterior, cf. Burgess et al (2018) for a similar approach.

Fig. 3

Phase-space properties of the latent space spanned by the leading two latent dimensions, $z_{0}\times z_{1}$. The latent variables are aggregated over the entire CMIP5 dataset to form the aggregated posterior. a Samples ${\textbf{z}}$ from the aggregated posterior. The different colors refer to different types of ENSO events. The phase-space is divided into small bins, and in each bin, the b decoder output of Niño 3.4 SST corresponding to samples ${\textbf{z}}$ and the c temporal dynamics estimated by finite-time differences of consecutive samples ${\textbf{z}}$ (arrows) is averaged; see text for more details. The arrows are colored according to the speed of rotation around the origin. For reference, ${\textbf{z}}$-values derived from the ERSST dataset at El Niño and La Niña events are shown (red and blue triangles). The contours in all three panels correspond to regression of the decoder output of Niño 3.4 SST on $z_{0}\times z_{1}$ based on k-nearest neighbors

Figure 3 summarizes statistical properties of the aggregated posterior in the latent space $z_{0}\times z_{1}$, spanned by the leading two latent variables $z_{0}$ and $z_{1}$ of the input ${\textbf{z}}\in \mathbb {R}^{K}$ to the decoder. Given the diversity of the CMIP ensemble, we will see that the VAE has found a remarkable simple abstraction of the ENSO dynamics in this subspace.

In Fig. 3a, we see that the posterior is centered at the origin, i.e., close to the prior. The samples are dense with no apparent gaps or isolated regions, which allows us to randomly sample from the posterior during data generation.

To gain a first insight into the generative properties of the decoder, we show in Fig. 3b the averaged decoder output of Niño 3.4 SST while sampling from the posterior. We consider here the average of the last three months out of the window of L months that are returned by the decoder; cf. again Fig. 1. In Fig. 3b we observe a smooth, continuous picture in the averaged decoder output that separates positive and negative SST. There is a visible skewness amplitude, with a notably larger magnitude of positive Niño 3.4 SST, which is consistent with observed ENSO asymmetry. This is interesting that many CMIP5 models on which the VAE is trained underestimate this asymmetry in ENSO amplitude (Zhang and Sun 2014). Later in Sect. 4.5, we will show that the VAE is indeed able to reproduce observed ENSO asymmetry.

Given the clear picture that the decoder shows in Fig. 3b, we can easily define distinct regions in the latent space that represent different types of ENSO. We rely here on a non-parametric form of a regression, based on k-nearest neighbors, that approximates a mapping from $z_{0}\times z_{1}$ to the decoder output as the target. Since we are interested in a sufficiently smooth approximation, we use a fairly extensive number of neighbors on the order of about 100. In all panels of Fig. 3, we have added contours of the resulting regression model.

To define different types of ENSO, we follow the common classification scheme by Niño 3.4 SST temperature values T, cf. e.g. Dommenget et al (2012):

• strong El Niño ($T>1^\circ {C}$),

• weak El Niño ($0.5^\circ {C}<T<1^\circ {C}$),

• weak La Niña ($-1^\circ {C}<T<-0.5^\circ {C}$),

• strong La Niña ($T<-1^\circ {C}$).

The result of this ENSO classification procedure is shown in Fig. 3a, with different colors assigned to the different categories. We note that the asymmetry in the magnitude of Niño 3.4 SST in Fig. 3b is also reflected in an asymmetry of the posterior. In Fig. 3a, the posterior has a positive skewness with a longer tail for strong El Niños, which means that the VAE gives more weight to this part of the posterior in terms of higher KL divergence.

To understand the dynamical aspects in the latent space $z_{0}\times z_{1}$, we obtain estimates of first-order time derivatives from consecutive samples, ${\textbf{z}}={\textbf{z}}(t)$, of the posterior using the Savitzky-Golay filter (Savitzky and Golay 1964). The estimates are averaged within small bins, and the resulting vector field is shown in Fig. 3c. We see that the temporal dynamics are dominated by a single large vortex that is characterized by a clockwise motion around the origin. The magnitude apparently depends on the ENSO strength and phase indicating the presence of non-linear dynamics. The phase speed ranges from about 0.1 to 0.3 cycles per year, which corresponds to a period of about 3 to 10 years. This is consistent with the wide range of observed periods of motion of ENSO (Timmermann et al 2018). It is interesting to note that the VAE reveals an asymmetry in the phase speed between transitions from El Niño to La Niña (upper right quadrant) and from La Niña to El Niño (lower left quadrant). The transitions from strong El Niño to La Niña are particularly pronounced in the vortex, indicating a more deterministic behavior with improved predictability, which contrasts with the more diffuse picture we see in the transition from La Niña to El Niño. Later in Sect.  4.4, we will see that the VAE found the transition from El Niño to La Niña to be more predictable, which is consistent with observations (Timmermann et al 2018).

To briefly test the robustness of the VAE, especially the universality of the latent space with respect to changes in the input distribution, we use samples from the ERSST dataset as input. In Fig. 3c, we show the resulting z-values that correspond to observed El Niño and La Niña events since 1920. Although ERSST data were not used during model training, we find a robust separation between observed El Niño and La Niña events, which is a good indicator for the zero-shot skill of the VAE. Note that there is no index m associated with the ERSST data, and the z-values presented here are averages over various random numbers m. Variations of m, however, do not affect the quality of separation (not shown).

4.2 Global patterns

To get an overview of the spatiotemporal dynamics associated with the different ENSO clusters in Fig. 3a, we aggregate the decoder output corresponding to the leading S PCs, cf. again Fig. 1.

Fig. 4

Spatiotemporal SST composites obtained by averaging the decoder output over samples from different clusters of the aggregated posterior, as defined in Fig. 3a. Shown are SST composites from samples of the cluster of a–d strong El Niño and e–h strong La Niña. The sum of the two SST composites is shown in i–l. Note the different scale in the right column

In this subsection, we analyze the average SST over samples from the different ENSO clusters. For this reason, the PCs generated in each ENSO cluster are first averaged and then multiplied with the corresponding EOFs to obtain SST composites; cf. again Sect. 2.1 for details of the initial EOF analysis.

In Fig. 4, we show the resulting SST composites at various time lags $\tau \in \{-L,\dots ,-1\}$ that correspond to the different positions in the decoder output $\hat{{\textbf{x}}}$ of length L; cf. again Fig. 1. In Figs. 4a–d, the composites from samples of the cluster of strong El Niño is shown, and compared with the composite of strong La Niña in Figs. 4e–h. Given the diversity of modeled ENSO dynamics in CMIP, it is remarkable that the VAE draws a picture of the dynamics that is consistent with the different phases that we see in the composite evolution of observed El Niño and La Niña events; see for example Timmermann et al (2018) and Fig. 1 therein. The cyclical character that we have already seen in the latent space of the VAE is likewise reflected in the SST composites. For example at $\tau =-16$ months in Figs. 1a and e, we can distinguish slightly negative or positive SST values in the Niño 3.4 region prior to the onset of El Niño and La Niña, respectively.

However, in addition to the cyclical nature, the VAE has identified notable differences in the two SST composites. At $\tau =-11$ months, for example, the SST composite has a rather neutral character ($T\approx 0$) at the onset to a strong El Niño (Fig. 4b), while there is still a persistent positive anomaly in Niño 3.4 SST at the onset to a strong La Niña (Fig. 4f).

To highlight differences in the two SST composites, we show in Figs. 4i–l the sum of the two SST composites. At all values of the time lag $\tau$, we see a notable spatial asymmetry that is to a large extent characterized by a stable spatial pattern over time. The asymmetry appears strongest in earlier phases and reaches its maximum at $\tau =-16$ months (Fig. 4i); i.e., the maximum lag considered here. Just before the mature phase at $\tau =-1$ (Fig. 4l), the asymmetry pattern in the Tropical Pacific is consistent with the spatial asymmetry that we observe between strong El Niños and strong La Niñas (Kang and Kug 2002; Dommenget et al 2012). In a comparison with coupled ESM simulations from the CMIP3 database, Dommenget et al (2012) show that a similar ENSO asymmetry is found in only a few models. Since many of the CMIP5 models still underestimate ENSO asymmetry (Zhang and Sun 2014), it is therefore interesting to note that the VAE shows a spatial pattern similar to the observed one. We will see in Sect. 4.5 that, in fact, few of the CMIP5 models used for model training have a comparable magnitude in ENSO asymmetry, and that the VAE has given greater weight to these models in the posterior.

4.3 Precursors of strong ENSO

To quantify the relevance of the patterns in the SST composites of the VAE, we will next test the significance of the SST values.

Fig. 5

Probability of SST values from samples of strong ENSO being greater than SST values from samples of weak ENSO at different time lags $\tau$ prior to a strong ENSO. Probabilities of a–e strong El Niño compared with weak El Niño and f–j strong La Niña compared with weak La Niña. In all panels, only probabilities that are significant at the 10% and 90%-level from an approximation with a normal distribution are shown

As before, the part of the decoder output corresponding to the leading S PCs is obtained and SST maps are generated by the product of the PCs with the EOFs. However, instead of comparing the average of the SST values in the different SST composites, we next compare their distribution. At each grid point and time lag separately, we compare the generated SST values from samples of strong ENSO with the ones from samples of weak ENSO and test whether:

• 1. SST values from samples of strong El Niño are statistically significantly greater than SST values from samples of weak El Niño and

• 2. SST values from samples of strong La Niña are statistically significantly lower than SST values from samples of weak La Niña.

Following the non-parametric Mann–Whitney U test (Mann and Whitney 1947), the probabilities of success in the two tests are determined and their significance levels are approximated by a normal distribution centered around $p=0.5$.

In Fig. 5 we show the results of the two tests at the various time lags $\tau$. As in the previous section, the time lag $\tau \in \{-L,\dots ,-1\}$ correspond to the different positions in the decoder output $\hat{{\textbf{x}}}$ of length L. In Figs. 5a–e we show the results for the first test on El Niño, and in Figs. 5f–j the results for the second test on La Niña.

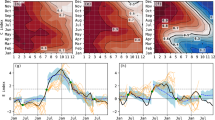
The spatial asymmetry in the SST composites of strong El Niño and strong La Niña is likewise reflected here. For large time lags, for example at $\tau =-16$ months, there is no significant precursor signal in the SST values prior to a strong El Niño (Fig. 5a). This means that a strong El Niño is not necessarily preceded by a La Niña. However, prior to a strong La Niña at $\tau =-16$ months, there is a significant pattern of positive SST values along the equatorial tropical Pacific (Fig. 5f), which means that a strong La Niña is more likely preceded by an El Niño than a weak La Niña.

This asymmetric picture that the VAE shown here at $\tau =-16$ months is consistent with the asymmetric forcing of ENSO events: while strong El Niño events are mostly wind driven and less predictable, strong La Niña events are mostly driven by the depth of the thermocline and therefore more predictable (Dommenget et al 2012; Timmermann et al 2018). In the latter case, however, we find other regions with significant SST differences (Fig. 5f) that could also be potential sources of predictability for strong La Niña events; for example, a positive phase of the Indian Ocean Dipole (IOD), which has been shown to often precede La Niña events (Izumo et al 2010).

The asymmetry in the ENSO dynamics is also reflected in the later growth patterns to a mature ENSO event. Prior to a strong El Niño, at time lags of about $\tau =-6$ months, we already observe a significant increase in the SST values along the equatorial Pacific (Fig. 5c). The equatorial Pacific warm water volume is known to be an essential parameter in the ENSO cycle (Meinen and McPhaden 2000) and indicative of potentially developing El Niño conditions (Timmermann et al 2018). In the picture here, we see indeed an increase in the likelihood for the development of an El Niño event, with a further strengthening in the Eastern Pacific (Fig. 5d). During the mature phase, finally, we observe a highly significant spatial asymmetry between the distribution of strong and weak El Niño events (Fig. 5e). This shift of strong El Niño events towards the Eastern tropical Pacific that we observe here is consistent with observed ENSO asymmetry (Dommenget et al 2012).

Prior to a strong La Niña, we observe no significant SST patterns at time lags of about $\tau =-6$ months (Fig. 5h) and differences emerge only later at time lags of about $\tau =-3$ months (Fig. 5i). On the other hand, we find no clear spatial asymmetry between strong and weak La Niña events along the equatorial Pacific (Fig. 5j), although there is some weak evidence of observed ENSO asymmetry in La Niña (Dommenget et al 2012).

4.4 ENSO predictions

Fig. 6

Dynamics of past and future Niño 3.4 SST generated from samples of different ENSO clusters of the aggregated posterior. Reconstructions $\hat{{\textbf{x}}}$ of past observations ($\tau <0$) and predictions $\hat{{\textbf{y}}}$ of future values ($\tau \ge 0$) are obtained by sampling the output of the first and second decoder, respectively; cf. Fig. 1. The samples correspond to the clusters of a strong El Niño, b strong La Niña, c weak El Niño, and d weak La Niña, as defined in Fig. 3a. In all panels, the mean of the reconstruction (bold dashed lines) and prediction (bold solid lines), as well as different percentiles of the distribution are shown (green shading). The corresponding probability p of the reconstruction and prediction of Niño 3.4 SST values falling into different ENSO categories is likewise shown in all panels (inset axes)

We next examine the extent to which the asymmetry is also reflected in the predictions of Niño 3.4 SST. To this end, we sample from the different ENSO clusters in the posterior and generate trajectories of past and future Niño 3.4 SST from the corresponding output of the first and second decoder of the VAE, respectively; cf. Fig. 1.

Figure 6 shows the mean and various quantiles of the distribution of trajectories generated in the different ENSO clusters. In all panels, we observe noticeable differences not only in the mean SST, but also the distribution. To study the transition dynamics linking the two ENSO phases, we also determine the probability p that the generated Niño 3.4 trajectory falls into the different ENSO categories, as defined in Sect. 4.1. The resulting temporal patterns of p are also shown in Fig. 6. First, note that in all panels, the ENSO category from which the latent samples are taken is also the most likely one at $\tau \approx 0$, i.e., as we would expect based on the definition of ENSO clusters in Sect. 4.1.

On the other hand, there are significant variations in the transition dynamics between the different ENSO clusters. In Fig. 6a, for example, we see that the probability of La Niña one year after a strong El Niño event ($\tau \gtrsim 12$ months) tends to be higher than the probability one year before ($\tau \lesssim -12$ months). However, the opposite pattern emerges for strong La Niñas, as shown in Fig. 6b. Here, the probability of El Niño one year after a strong La Niña event is noticeably smaller, while the probability of El Niño one year before a strong La Niña event is higher.

The picture that the VAE draws is fairly consistent with observed transitions, in which strong El Niño events are followed by La Niña events and strong La Niña events are preceded by El Niño events (Dommenget et al 2012; Timmermann et al 2018). This again suggests some asymmetry in the driving forces of strong El Niño and La Niña events found by the VAE in the CMIP5 ensemble, and which is consistent with the picture found by Dommenget et al (2012) in four of the CMIP3 models. Between weak El Niño and La Niña, though, the differences in Figs. 6c and d are rather marginal, indicating that asymmetries become more pronounced with increasing strength.

This asymmetry in the transition dynamics between El Niño and La Nina explains the asymmetry in the posterior that we have already identified in Fig. 3. Since transitions from El Niño to La Niña appear more regular in Fig. 6, they are also more pronounced and regular in the vortex of Fig. 3c. This clearly highlights the ability of the VAE to learn reasonable stochastic mappings between a high-dimensional input space, whose distribution is typically complicated, and a low-dimensional latent space, whose distribution is relatively simple and much easier to interpret.

Prediction of simulated ENSO Next, we will evaluate the ability of the VAE to reproduce the asymmetry in the transition dynamics between El Niño and La Niña in the CMIP5 ensemble. To this end, we also obtain SST composites from trajectories of Niño 3.4 SST from the individual CMIP5 models. For this purpose, we select all pairs of CMIP5 data, ${\textbf{x}}$ and ${\textbf{y}}$, such that the corresponding samples ${\textbf{z}}$ from the posterior $q_\phi ({\textbf{z}}|{\textbf{x}})$ fall into the different ENSO clusters, cf. again Fig. 3a. The resulting SST composites of the CMIP ensemble are shown in Fig. 7.

Fig. 7

Similar to Fig. 6, but with data from the CMIP5 ensemble. The SST composites are obtained from pairs of past observations ${\textbf{x}}$ and the corresponding future ${\textbf{y}}$ from the CMIP5 dataset. The pairs are selected such that the corresponding samples ${\textbf{z}}$ from the posterior $q_\phi ({\textbf{z}}|{\textbf{x}})$ fall into the clusters of a strong El Niño, b strong La Niña, c weak El Niño, and d weak La Niña, as defined in Fig. 3a

In all panels of Fig. 7, we see that the distribution of SST values in the CMIP5 ensemble is fairly consistent with the generated distribution of SST values in the VAE (Fig. 6). In particular the distribution of past observations ${\textbf{x}}$ ($\tau <0$) is well reproduced by the VAE, which is consistent with the fact that the VAE is trained on maximizing the data likelihood of ${\textbf{x}}$ in the CMIP5 ensemble. In the distribution of future SST values ${\textbf{y}}$ ($\tau \ge 0$), however, we see some differences emerge. In particular at much larger lead times ($\tau > 15$ month), the VAE tends to underestimate the probability of strong ENSO events, which shows the limits of the VAE in the long-term prediction of ENSO in the CMIP5 ensemble. Still, at lead times of up to about 15 months, the VAE is able to predict fairly well the distribution of future SST values in the CMIP5 simulations; especially the asymmetry in the future distribution of SST values following strong El Niño and strong La Niña events in Fig. 7a and b, respectively, is well reproduced by the VAE, cf. again Fig. 6a and b.

Prediction of observed ENSO Finally, we will evaluate the ability of the VAE to make predictions about the observed ENSO dynamics. In Fig. 3, we have already seen a clear separation between observed El Niño and La Niña events from the ERSST dataset in the latent space of the VAE. In a next step, we will use these ${\textbf{z}}$-values to generate trajectories of Niño 3.4 SST from the corresponding output of the two decoders. For this purpose, we first select all pairs of ERSST data, ${\textbf{x}}$ and ${\textbf{y}}$, at observed El Niño and La Niña events in the 1920–2005 period, respectively. Next, corresponding samples ${\textbf{z}}$ from the posterior $q_\phi ({\textbf{z}}|{\textbf{x}})$ are drawn and used as input to the two decoders, so that we can finally generate trajectories of past and future Niño 3.4 SST from the corresponding output of the first and second decoder, respectively.

Fig. 8

Observed dynamics of past and future Niño 3.4 SST from the ERSST dataset in comparison with predictions from the VAE. In the upper panels, SST composites of past observations ${\textbf{x}}$ ($\tau <0$) and the corresponding future ${\textbf{y}}$ ($\tau \ge 0$) are obtained from samples of the ERSST dataset in the 1920–2005 period at observed a El Niño and b La Niña events. In the lower panels, the corresponding reconstructions $\hat{{\textbf{x}}}$ and future predictions $\hat{{\textbf{y}}}$ from the VAE are shown for observed c El Niño and d La Niña events. In all panels, the mean of the Niño 3.4 SST (bold lines), different percentiles of the distribution (green shading), and the 5%–90%-percentile range (orange, dash-dotted) are shown. The corresponding probability p of the Niño 3.4 SST values falling into different ENSO categories is likewise shown in all panels (inset axes)

In Fig. 8, we show the resulting output of the two decoders (lower panels), which we compare with the observed Niño 3.4 SST in the ERSST dataset (upper panels). We see that the VAE is able to reproduce the observed dynamics of past and future Niño 3.4 SST fairly well. In particular the distribution of past observations ${\textbf{x}}$ ($\tau <0$) is well reproduced by the VAE, which demonstrates the robustness of the VAE with respect to changes in the input distribution and its ability to generalize to unseen data. For example, the VAE is able to reproduce the seasonality in the SST variability that we can observe in the ERSST dataset; see the percentile range in Fig. 8a and b, which is well reproduced by the VAE in Fig. 8c and d. Note that $\tau =0$ corresponds to December of the year of the observed El-Niño and La-Niña events and that the SST variability, which is particularly pronounced in the boreal winter (e.g. Timmermann et al 2018), peaks at a multiple of 12 months.

However, when comparing the distributions of future SST values ($\tau \ge 0$), differences become more apparent. The fact that the VAE tends to underestimate the probability of strong ENSO events in simulated ENSO is also reflected here. In comparison to the SST composites of observed El Niño events (Fig. 8a), for example, we see that the VAE tends to underestimate the probability of strong La Niña events at lead times of $\tau \approx 12$ months (Fig. 8c). However, the seasonality in the SST variability is still reproduced at lead times of up to about 18 months and only becomes underestimated at much larger lead times of about 24 months (Fig. 8c); i.e. the VAE tends to predict the SST as more neutral at very large lead times.

When compared to the picture we see for observed La Niña events (Fig. 8b), the VAE tends to predict the SST as more neutral and therefore underestimates SST variability already at shorter lead times of $\tau \approx 12$ months (Fig. 8d). This illustrates that the prediction performance drops more significantly after observed La Niña events, but this is consistent with a similar decrease in the prediction performance after simulated La Nina events; see again Fig. 6b and d, in which the VAE tends to predict the SST at large lead times more neutrally than is observed in the CMIP5 ensemble in Fig. 7b and d, respectively.

4.5 ENSO asymmetry

In Sect. 4.2, we demonstrated that the VAE found a clear pattern of a spatial asymmetry between strong El Niño and strong La Niña events along the equatorial Pacific; cf. again Fig. 4l. Since underestimation of ENSO asymmetry remains a common limitation in CMIP5 models (Zhang and Sun 2014), we will evaluate the ability of the VAE to reproduce the magnitude of observed ENSO asymmetry and compare it with the CMIP5 ensemble used for model training.

Fig. 9

ENSO asymmetry as a function of the El Niño strength. ENSO asymmetry, on the vertical axis, is defined as the east–west difference along the equatorial Pacific in the sum of the SST composites of the two ENSO phases; El Niño strength, on the horizontal axis, is defined as the average of the Niño 3.4 SST in El Niño condition. The threshold $T_{c}$ to define the two ENSO phases is varied to illustrate the relationship between El Niño strength and ENSO asymmetry. Values of observed ENSO asymmetry in the ERSST observational dataset (blue solid line) are compared with modeled ENSO asymmetry with (1) the VAE (green solid line), (2) the individual CMIP5 historical runs (light orange lines), and (3) the aggregated CMIP5 ensemble (brown dashed line). The modeled ENSO asymmetry in the VAE, with the top-8 CMIP5 models removed from the aggregated posterior, is also shown (red solid line). The corresponding CMIP5 models that rank in the top 8 in terms of KL divergence are highlighted in bold

To quantify the spatial asymmetry along the equatorial Pacific that we find in the sum of the SST composites of Fig. 4l, we follow the analysis of Dommenget et al (2012) and consider in a next step its difference between the eastern equatorial Pacific ($140^\circ {W}-80^\circ {W}$, $5^\circ {S}-5^\circ {N}$) and the western equatorial Pacific ($140^\circ {E}-160^\circ {W}$, $5^\circ {S}-5^\circ {N}$). Since the VAE is trained on PCs, we would need to account for any potential bias that the EOF analysis has on the SST. This means that we also average the PCs in each of the historical CMIP5 runs under either El Niño or La Niña conditions, which are then multiplied with the corresponding EOFs to determine their SST composites. We thus closely follow the procedure used to obtain SST composites from the decoder output of the VAE; cf. Sect. 4.2.

Since the strength of modeled ENSO dynamics varies widely across the CMIP5 models (Zhang and Sun 2014), we repeat the analysis with different values of the thresholds $T_{c}$ to define ENSO conditions in each of the model runs, i.e., we obtain the Niño 3.4 index $T_{\textrm{nino}}$ from the 3-month average of Niño 3.4 SST, and consider the model to be in El Niño or La Niña condition whenever $T_{\textrm{nino}}>T_{c}$ or $T_{\textrm{nino}}<-T_{c}$, respectively. For reference, we repeat the analysis on the ERSST dataset in the same time interval of 1865–2005.

In Fig. 9, we show the resulting values of the ENSO asymmetry as a function of the El Niño strength for various values of $T_{c}$. Within the CMIP5 ensemble, we find a considerable diversity between the individual models that ranges from models with a strong asymmetry to models with a weak or even no asymmetry. In comparison with the ERSST dataset, the picture supports the findings of Zhang and Sun (2014) in that underestimation of observed ENSO asymmetry still remains a pervasive challenge in CMIP5.

Similarly, we also vary the threshold $T_{c}$ defining El Niño and La Nina clusters in the latent space of the VAE. However, this time we do not distinguish between strong and weak ENSO while sampling from the posterior. The ENSO asymmetry that we obtain from the resulting SST composites of the VAE is also shown in Fig. 9. In contrast to the mixed picture that we observe in the CMIP5 ensemble, the asymmetry in the VAE is remarkably close to the observed ENSO asymmetry over a wide range of the El Niño strength. This is even more remarkable in comparison to a simple ensemble average, which is often used to combine different CMIP runs. In Fig. 9 we also show the ENSO asymmetry that results from combining all historical runs into a single long run. However, as can be seen, the asymmetry in this simple ensemble average is clearly below the observed ENSO asymmetry.

To understand the improvement that we see in the VAE over a simple ensemble average, we next rank the various CMIP runs in order of their contribution of encoding information in the posterior. That is, for each CMIP dataset ${\mathcal {D}}_{m}$ separately, we average the corresponding KL divergence in the two clusters of a strong El Niño and a strong La Niña in Fig. 3a. The CMIP runs with the highest KL divergence contribute most to the aggregated posterior and possibility also to the underlying data generation process that the VAE has learned. To better understand their contribution, we will focus on the CMIP runs with the highest KL divergence and explore their dynamics in more detail.

The CMIP runs that rank in the top 8 in terms of KL divergence are highlighted in bold in Fig. 9. It appears that most of these models show a well-developed asymmetry in their ENSO dynamics that scales similarly to the observed asymmetry with increasing strength of El Niño. However, we also see that in a some of these models the ENSO dynamics appears to be much stronger in magnitude and asymmetry than it is observed. It is interesting to note that these models already account for about 50 % of the total KL divergence in the two ENSO clusters, indicating a strong focus of the VAE on only a few models in these parts of the posterior.

Finally, to quantify the extent to which the top 8 models contribute to the ENSO asymmetry in the SST composites of the VAE, we have removed their samples from the aggregated posterior. As expected, the resulting asymmetry in the modified SST composites is significantly lower, as shown in Fig. 9, and is comparable to the asymmetry we find in the SST composite of a simple ensemble average of all CMIP runs.

4.6 ENSO predictability

To understand the rationale behind the focus on a few CMIP models in the construction of the posterior, we must keep in mind that the model in Fig. 1 has been trained on different objectives: (1) reconstruct past observations, (2) predict the corresponding future, and (3) efficiently encode the information needed to solve the first two objectives. In the pure auto-encoder setting (objectives 1 and 3), the model is trained on a reconstruction-information trade-off, which means that the model will try to optimally encode information in the posterior while still being able to reconstruct the past observations as good as possible. In the prediction setting (objectives 2 and 3), the model is trained on a prediction-information trade-off, which means that the model will try to optimally encode information in the posterior while still being able to predict the future as good as possible. In both settings, the regularization term ensures an optimal encoding of information in the posterior that is most relevant to jointly solve the two tasks (1) and (2). In particular, this means that pairs of training samples ${\textbf{x}}$ and ${\textbf{y}}$, which are easier to model, will be given more weight in the posterior in the form of a higher KL divergence. Vice versa, pairs of training samples that are more difficult to model will have a lower KL divergence.

In view of the strong focus on the ENSO region in the design of the training data (cf. Fig. 1), it is therefore likely that training samples from CMIP models, which are easier to model in terms of their ENSO dynamics, are given more weight in the posterior. To better understand the particular focus on CMIP models with enhanced ENSO asymmetry, we will show in the following that the VAE has identified a useful relationship between ENSO asymmetry and ENSO prediction that helps to jointly solve the two tasks.

Fig. 10

Same as Fig. 6, but with samples taken from the clusters of a, c strong El Niño and b, d strong La Niña. Samples are from a-b the aggregated posterior, which is restricted to the CMIP5 models that rank in the top 8 in Fig. 9, and c-d the aggregated posterior, in which the top 8 models are excluded

To see this effect, we repeat the analysis from Sect. 4.4 in two mutually exclusive variants, where we

• 1. Restrict the aggregated posterior to the top 8 CMIP models and

• 2. Exclude the top 8 models from the aggregated posterior.

As before, we generate trajectories of past and future Niño 3.4 SST from the output of the first and second decoder of the VAE. In Fig. 10 we compare the SST composites of the two variants for strong El Niño (Fig. 10a, c) and strong La Niña (Fig. 10b, d).

At a time lag of $\tau \approx 0$, we see that in all variants the most likely ENSO category still matches the cluster from which we sample, although the likelihood is slightly lower in the second variant (Fig. 10c, d). This reduction is consistent with Fig. 9 in that we remove CMIP models with a particularly strong El Niño from the composite in the second variant.

However, at other time lags, there are noticeable differences in the distribution of the trajectories generated in the two variants. In Fig. 10a, for example, the probability of a La Niña following a strong El Niño is very pronounced in the first variant and much larger than in the second variant Fig. 10c. This shows that for the first variant, transitions from El Niño to La Niña are more regular and thus more predictable, which explains why the VAE attributes more weight to these CMIP models given their higher KL divergence. This increase in regularity is also reflected in the dynamics preceding a La Niña, where the probability of El Niño preceding a strong La Niña is higher in the first variant (Fig. 10b) than in the second variant (Fig. 10d).

Interestingly, the differences are less pronounced in the opposite transition from La Niña to El Niño. The probability of an El Niño following a strong La Niña is only slightly more enhanced in the first variant (Fig. 10b) than in the second variant (Fig. 10d). This suggests that dynamical aspects driving the transition from El Niño to La Niña are more pronounced in the CMIP models used in the first variant, which enhances the predictability of the more thermocline depth-driven La Niña events. In the opposite transition, the picture is less clear maybe due to the more stochastic nature of the problem and a lower predictability of the more wind-driven El Niño events.

The relationship between asymmetry and predictability identified by the VAE in the CMIP ensemble may be related to the different flavors of ENSO (Dommenget et al 2012; Timmermann et al 2018). Jeong et al (2012), for example, have shown that the evolution of the canonical Eastern Pacific (EP) type of El Niño is more predictable than the evolution of the central Pacific (CP) type.

Although these are not distinct types rather than two modes of a continuum (Johnson 2013), we will analyze next the extent to which the difference in predictability between the two variants in Fig. 10 is also reflected in the spatial structure of the equatorial Pacific SST. We therefore repeat the analysis in Sect. 4.3 using the two variants of the posterior.

In the first variant, where we restricted the posterior to the top 8 models, there are no notable changes in the spatiotemporal structure of the probability distribution, and the picture (not shown) is very similar to that of Fig. 5. During the mature phase of a strong El Niño (Fig. 5e), the SST distribution peaks in the Eastern Pacific, which suggests that strong El Niño events are more likely to be of EP type in the first variant, and hence leads to a stronger ENSO asymmetry as discussed in Fig. 9

Fig. 11

Same as Fig. 5, but with samples from the aggregated posterior, in which the top 8 models are excluded

In the second variant, where the top 8 models are excluded from the posterior, we observe indeed notable differences (Fig. 11); e.g., a flattening in the SST distribution along the equatorial Pacific in the mature phase of a strong El Niño (Fig. 11e). In this variant, the likelihood to observe a strong El Niño of EP type is less pronounced and similar to the CP type. In the onset phase at a time lag of $\tau =-6$ months (Fig. 11c), there is no longer a significant pattern of increased SST values along the equatorial Pacific; i.e. a signal indicative of potentially developing El Niño conditions, which we found to be significant in Fig. 5c. The rather flat distribution in the flavor of strong El Niño events along with the lack of potential trigger signals could therefore be a source of uncertainty for the VAE in modeling the evolution of El Niño and therefore explain why the VAE assigns a lower KL divergence to these CMIP models.

In the mature phase of strong La Niña events (Fig. 11j), the changes that we see in the second variant are rather marginal compared to the full composite in Fig. 5j. Instead, differences become more apparent at a time lag of $\tau =-16$ months (Fig. 11f) in that there is no longer a significant pattern indicating a possible precursor signal before a strong La Niña; i.e., in contrast to the potential precursors that we saw in various regions of Fig. 5f.

The lack of a precursor signal before a strong La Niña is consistent with a decrease in regularity we observed in the transition from El Niño to La Niña in the second variant (Fig. 10d). Instead, we see that the probability of an El Niño preceding a strong La Niña in the second variant (Fig. 10d) is comparable to the probability of an El Niño preceding a weak La Niña in the full composite (Fig. 6d). This suggests that (non-linear) dynamical aspects driving a strong La Niña are less developed in the second variant and therefore may have contributed to an underestimation of ENSO asymmetry in these CMIP models. However, the extent to which the potential precursors that we see in various regions of Fig. 5f are independent in nature or rather manifestations of a common underlying mechanism is not clear from the present analysis.

5 Summary

We have analyzed historical simulations of global sea-surface temperature (SST) from the fifth phase of the Coupled Model Intercomparison Project (CMIP5, Taylor et al 2012). To provide a unified access to the diversity of simulations in the large multi-model dataset and go beyond the current technological paradigm of simple ensemble averaging, we proposed a state-of-the-art deep learning approach based on the concept of a variational auto-encoder (VAE, Kingma and Welling 2014).

In the VAE-based approach, a generative model of global SST is trained in combination with an inference model that aims to solve the problem of learning a joint distribution over the data generating factors. Parameterized by neuronal networks (Fig. 2), we have shown that this variational deep-learning approach enables efficient learning of stochastic mappings between global SST, whose distribution is typically complicated, and a low-dimensional latent space, whose distribution is relatively simple (Fig. 3).

We focused on El Niño Southern Oscillation (ENSO) and presented a generative model to emulate ENSO. The ENSO emulator has been shown to reproduce several aspects of observed ENSO asymmetry between the two phases of warm El Niño and cold La Niña, such as a spatial asymmetry between their SST composites in the equatorial Pacific (Fig. 4) that is still underestimated by many CMIP5 models (Zhang and Sun 2014).

We further analyzed the predictions of the VAE about the distribution of global SST in different ENSO regimes and tested the statistical significance of the SST composites to identify precursors of strong ENSO events (Fig. 5). It appears that the ENSO asymmetry between strong El Niño and strong La Niña was also reflected in the evolution of global SST (Fig. 5). Prior to a strong La Niña (Fig. 5f), the VAE found different regions with significant SST patterns that could be potential sources of predictability for strong La Niñas, e.g., positive SST values along the equatorial Pacific, indicating that a strong La Niña is likely to be preceded by an El Niño event, or a positive phase of the Indian Ocean Dipole, which has been shown to often precede La Niña events (Izumo et al 2010). However, prior to a strong El Niño, the VAE found no precursor in global SST (Fig. 5f), which is consistent with the mostly wind driven and less predictable nature of strong El Niño events (Dommenget et al 2012; Timmermann et al 2018).

Furthermore, a combination of the VAE with a forecasting model was proposed (Fig. 1) to provide predictions about the future path of the Niño 3.4 SST (Fig. 6). The proposed model identified an asymmetry in the transitions between El Niño and La Niña that is consistent with observed transitions, e.g., that strong El Niño events are followed by La Niña events (Dommenget et al 2012; Timmermann et al 2018).

The ability of the VAE to make predictions about the observed ENSO dynamics, taken from the fifth version of the NOAA Extended Reconstructed Sea Surface Temperature (ERSST, Huang et al 2017), was further evaluated. Although the VAE was not trained with the ERSST dataset, it was able to reproduce the statistical properties of the observed Niño 3.4 SST quite well (Fig. 8). It was shown that the prediction performance decreases more significantly after observed La Niña events than after observed El Niño events (Fig. 8). This is consistent with a similar decrease in the prediction performance of the VAE (Fig. 6) for simulated La Niña events of the CMIP5 ensemble (Fig. 7).

Since underestimation of ENSO asymmetry remains a common problem in CMIP5 models (Zhang and Sun 2014), we have evaluated the ability of the VAE to reproduce the magnitude of observed ENSO asymmetry and compared it with the CMIP5 ensemble used for training. While we found a considerable diversity of models with a strong asymmetry to models with a weak or even no asymmetry in the CMIP5 ensemble, the asymmetry in the VAE simulation is remarkably close to the observed ENSO asymmetry over a wide range of the El Niño strengths (Fig. 9). To understand the improvement in the VAE over a simple ensemble average, we ranked the various CMIP runs in order of their importance and found a strong focus of the VAE on only a few models with a strong asymmetry (Fig. 9).

Finally, to understand the rationale behind higher weighting performed by the VAE on models with a strong asymmetry, we analyzed different variants of the posterior and their impact on the predictability of ENSO. It was shown that the VAE has identified a useful relationship between ENSO asymmetry and ENSO predictability that improves the prediction of the simulated Niño index in a number of CMIP5 models with strong ENSO asymmetry (Fig. 11). In CMIP5 models with a weak ENSO asymmetry, on the other hand, the VAE was less certain in modeling the evolution to a strong El Niño (Fig. 11). A possible connection with the different ENSO types was discussed, supporting the findings of Jeong et al (2012) that the evolution of the canonical eastern Pacific (EP) type of El Niño is more predictable than the evolution of the central Pacific (CP) type.

In summary, we have shown that the VAE approach is capable of disentangling the complexity inherent to large climate datasets and helps us extract the underlying general properties shared by an ensemble of ESMs. The VAE is a universal, state-of-the-art machine learning approach that enables efficient learning of a skillful ESM emulator that can serve as an investigative tool for discovery and assist in theoretical advances (Irrgang et al 2021; Kashinath et al 2021).

Appendix A: Model configuration and training

The appendix summarizes the model configurations of the encoder, decoder, and forecast NNs discussed in detail in Sect. 3. A summary of the exact values we have chosen here for the different parts in the NNs can be found in Table 1. In this configuration, the final model in Fig. 1 has about 162 k trainable weights.

Table 1 Summary of model configurations of encoder, decoder, and forecast NNs as described in section 3 and shown in Figs. 1 and 2

The model weights are optimized using the Adam optimizer (Kingma and Ba 2014) and a learning rate of $10^{-3}$. They are optimized on the objective in Eq. (19) with stochastic gradient descend on mini-batches of size $N_{{\mathcal {M}}}$. The mini-batches are augmented with r different members sampled from the batch ensemble so that the different members are jointly optimized on the same data. The model weights are optimized for 20 epochs on the data ${\mathcal {D}}$, using all available data from historical simulations in the period 1865–2005, cf. Sect. 2.1. A summary of the training parameters can be found in Table 2.

Table 2 Overview of the training configuration used in stochastic gradient descent and the corresponding scale parameters of the different loss terms in Eq. (19)

In our experience, the proposed VAE model is not very sensitive to the choice of the parameters determining the configuration of the encoder, decoder, and forecast NNs (listed in Table 1). Note that the number of model parameters even exceeds the number of training samples in ${\mathcal {D}}$ (listed in Table 2). Instead, a proper choice of the regularization turns out to be more crucial (listed in Table 2). As motivated in Sect.  2.3, the various regularization objectives help the VAE to learn a disentangled representation of the data generating factors and to mitigate the problem of overfitting to the training data. The choice of the regularization parameters in Table 2 is not straightforward and requires some experimentation to find a proper balance between a good fit to the training data and a good generalization to unseen data. We have not run any systematic experiments to find the optimal regularization parameters, which in case of learning disentangled representations is not straightforward (e.g. Locatello et al 2019; Duan et al 2020). Instead, we have chosen to slowly increase the strength of the regularization during model training by annealing the parameter $\beta$ in Table 2. This is a common strategy in VAEs (Bowman et al 2015) and allows us to explore trade-off effects between a good fit and generalization. More generally, the choice of the regularization parameters in Table 2 and the annealing scheme is not unique and can be further explored in future work (e.g. Fu et al 2019; Sankarapandian and Kulis 2021). Dosovitskiy and Djolonga (2020), for example, further extend the idea and explore a whole spectrum of trade-offs with the $\beta$-VAE along a rate-distortion curve (Alemi et al 2018; Burgess et al 2018).