1 Introduction

Midlatitude ocean–atmosphere interaction is widely considered to be an important source of decadal to interdecadal climate variability (Nakamura et al. 1997; Pierce et al. 2001; Zhong et al. 2008; Kelly et al. 2010; Kwon et al. 2010; Liu and Di Lorenzo 2018). However, the mechanism responsible for the midlatitude ocean–atmosphere interaction remains unclear for a long time, primarily because compared with the strong atmospheric forcing on the ocean (Hasselmann 1976; Seager et al. 2001; Nonaka et al. 2006, 2008; Qiu et al. 2014; Yao et al. 2017), whether and in what way the midlatitude ocean affects the atmosphere have not been fully understood (Kushnir and Held 1996; Liu and Di Lorenzo 2018).

The typical dynamical structure of the midlatitude ocean–atmosphere system anomalies is different from that of the tropical ocean–atmosphere system. Corresponding to a basin-scale cold (warm) SST anomaly, the atmospheric geopotential height aloft shows a consistent low (high) anomaly in the vertical direction throughout the troposphere (Palmer and Sun 1985; Kushnir and Lau 1992; Kushnir et al. 2002; Deser et al. 2004; Fang and Yang 2016; Wang et al. 2017; Sun et al. 2018; Wills and Thompson 2018; Tao et al. 2020). This structure, also called the equivalent barotropic cold/trough (warm/ridge) structure, cannot be explained by the thermal-driven circulation theory that is applicable in the tropics. In the middle latitudes, on one hand, the SST-induced diabatic heating is relatively weak and mainly confined to the lower troposphere due to the stable atmospheric stratification. On the other hand, the midlatitude atmosphere is strongly baroclinic, and the synoptic transient eddy activities are vigorous, featuring storm tracks (Hoskins and Valdes 1990; Chang and Orlanski 1993; Chang et al. 2002; Kushnir et al. 2002; Nakamura et al. 2004, 2008; Nakamura and Shimpo 2004; Ren et al. 2007, 2010; Small et al. 2008; Sampe et al. 2010; Chu et al. 2013; Liu et al. 2014; Okajima et al. 2022). The systematical transportations of heat, moisture and momentum by transient eddies can in turn drive and maintain the midlatitude mean atmospheric circulations (Chang and Orlanski 1993; Chang et al. 2002; Ren et al. 2010; Sampe et al. 2010; Xiang and Yang 2012; Nie et al. 2013, 2014; Fang and Yang 2016; Wang et al. 2017; Tao et al. 2020). Therefore, the midlatitude atmospheric circulation is both thermal- and transient eddy-driven, and the midlatitude SST anomalies can affect the atmosphere by changing both the diabatic heating and the transient eddy feedback (Nakamura et al. 2004, 2008; Nonaka et al. 2009; Taguchi et al. 2009, 2012; Sampe et al. 2010; Hotta and Nakamura 2011; Fang and Yang 2016; Tao et al. 2020, 2022).

In the past two decades, an increasing number of studies based on high-resolution observational data and high-resolution numerical model revealed that the midlatitude oceans can actively influence the atmosphere, especially over the oceanic frontal zones (Kushnir et al. 2002; Feliks et al. 2004, 2007, 2011; Minobe et al. 2008; Small et al. 2008; Taguchi et al. 2009; Sampe et al. 2010; Czaja and Blunt 2011; Smirnov et al. 2015; Wills and Thompson 2018; Yook et al. 2022). The midlatitude large-scale oceanic front zone is the region with the strongest SST gradient, and also associated with strongest SST variability. It not only corresponds to the intense air-sea heat exchange, but is also closely related to the atmospheric baroclinicity and transient eddy activities (Nakamura et al. 2004; Nakamura and Shimpo 2004; Nakamura and Yamane 2009, 2010; Taguchi et al. 2009; Sampe et al. 2010; Fang and Yang 2016; Tao et al. 2020). The SST variation in oceanic frontal zone, which usually shows large-scale pattern, is accompanied with the intensity change and meridional movement of the atmospheric baroclinic zone as well as the in-phase changes of the upper westerly jet and storm tracks (Nakamura et al. 2004; Nakamura and Shimpo 2004; Nakamura and Yamane 2009, 2010; Taguchi et al. 2012). Therefore, the midlatitude oceanic frontal zone is the key region of ocean–atmosphere interaction.

Our previous work Fang and Yang (2016) investigated the features and dynamics of North Pacific ocean–atmosphere anomalies associated with the Pacific Decadal Oscillation (PDO). Based on observational study and quantitative dynamical diagnosis, a positive feedback mechanism for midlatitude unstable air-sea interaction in the North Pacific was hypothesized. In the hypothesis, the PDO-related SST anomaly is mainly forced by the surface heat flux and Ekman current advection induced by anomalous atmospheric westerly. Then, the basin-scale SST anomaly tends to change the direction of air-sea heat flux exchange and the intensity of the subtropical oceanic front of North Pacific, resulting in the anomalies of both diabatic heating and transient eddy thermal and dynamical forcing. The transient eddy dynamical forcing that dominates the total atmospheric forcing tends to produce an equivalent barotropic atmospheric circulation response that intensifies the initial surface westerly anomaly. Hence the midlatitude air-sea interaction, in which the oceanic front and atmospheric transient eddy feedback are the indispensable, can provide a positive feedback mechanism for the development and maintenance of PDO-related anomalies in the midlatitude North Pacific ocean–atmosphere system. This hypothesis has been confirmed by the later observational, theoretical and modeling studies (Wang et al. 2017; Chen et al. 2020; Tao et al. 2020, 2022; Zhang et al. 2020; Fang et al. 2022).

However, the above midlatitude ocean–atmosphere interaction mechanism is proposed based on the simultaneous correlation of seasonal-mean data that is already an equilibrium state after air-sea adjustment. The detailed interaction processes, especially the oceanic feedback process to the atmosphere, needs to be further revealed and verified from the observation. Furthermore, during the wintertime, there actually exist two oceanic frontal zones in the midlatitude North Pacific, i.e., the subtropical frontal zone (STFZ) and the subarctic frontal zone (SAFZ). The latter, formed by the convergence of warm Kuroshio current and cold Oyashio current, is much stronger than the former and could exist all the year round (Nakamura et al. 1997; Nakamura and Kazmin 2003; Wang et al. 2017). Previous studies revealed that the air-sea interaction near the SAFZ is particularly intensive over the North Pacific during the winter (Nakamura et al. 2008; Sampe et al. 2010; Frankignoul et al. 2011; Yao et al. 2017, 2018; Wills and Thompson 2018). The cross-frontal differential heat flux in SAFZ effectively offsets the relaxing effect of transient eddies, acting to maintain the near-surface baroclinicity and anchor the storm track, which is called the oceanic baroclinic adjustment mechanism (Nakamura et al. 2008; Sampe et al. 2010). Frankignoul et al. (2011) found the SST anomaly in SAFZ could excite downstream curl response in the eastern North Pacific, which causes subsequent westward-propagating Rossby waves impacting the whole gyre circulation. However, what are the evolution characteristics of the ocean–atmosphere system anomalies associated with the SAFZ during the winter, how does the midlatitude ocean–atmosphere interaction contribute to them, and what are the specific physical processes of ocean–atmosphere interaction? These issues remain to be further explored based on observational study.

In the present study, we focus on the anomalies of the North Pacific ocean–atmosphere system associated with SAFZ variability during the wintertime. A lead-lag regression analysis with high-resolution data is applied to identify the evolution characteristics of the SAFZ-related air-sea anomalies. Based on the diagnoses of the oceanic mixed-layer temperature tendency equation and the atmospheric quasi-geostrophic potential vorticity (QGPV) equation, the ocean–atmosphere interaction processes and their roles in the development and evolution of the air-sea anomalies are examined. It is found that the unstable ocean–atmosphere interaction mechanism proposed by Fang and Yang (2016) also works in the issues we discuss. It helps to maintain the atmospheric anomalies throughout the winter season.

The manuscript is organized as follows. Section 2 introduces the data and methods. Evolution characteristics of the air-sea variable anomalies associated with the SAFZ are investigated in Sect. 3. The corresponding ocean–atmosphere interaction processes are explored in Sect. 4. Section 5 is devoted to the conclusions and discussion.

2 Data and methods

The analyzed data used in the present study are from the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA5 hourly reanalysis products, with a horizontal resolution of 0.25° longitude × 0.25° latitude. The surface variables include sea surface temperature (SST), sea level pressure (SLP), sensible heat flux (SHF) and latent heat flux (LHF) (positive denoting upward). The multi-level variables include geopotential height (hereafter denoted by Z), air temperature, wind field and relative vorticity from 100 to 1000 hPa. Other oceanic data including sea water potential temperature, potential density, velocity, mixed-layer depth (MLD), and wind stress are from the Simple Ocean Data Assimilation (SODA) version 3.4.2 5-day reanalysis products (Carton et al. 2018), with a spatial resolution of 0.5° longitude × 0.5° latitude. In our study, the hourly ERA5 data has been processed into daily-mean, and the SODA data has also been interpolated into daily data before analysis. Our study focuses on the boreal winter (December–February) from 1980 to 2020, linear trend and seasonal cycle (daily climatological mean) are removed for all the data.

The atmospheric baroclinicity is represented by the maximum Eady growth rate (EGR) (Eady 1949; Lindzen and Farrell 1980) as \(\sigma_{BI} = 0.3098 \cdot \left| f \right| \cdot \left| {\frac{\partial u}{{\partial z}}} \right|/N\), where f is the Coriolis parameter, u the zonal wind, and \(N = \left( {g\frac{\partial \ln \theta }{{\partial z}}} \right)^{1/2}\) the Brunt-Väisälä frequency.

3 Evolution of the ocean–atmosphere anomalies associated with the SAFZ-SST variability

The large-scale North Pacific SAFZ refers to the belt-shaped region of strongest meridional SST gradient located around 40°N (Fig. 1a) in the northwestern Pacific. It is mainly composed by the western boundary warm Kuroshio current at 35°N, the cold Oyashio current at about 40°N, and their eastward extension areas. In the wintertime North Pacific, SAFZ is also the region of strongest SST variability (Fig. 1b), and it corresponds to intense upward heat flux transport from the ocean (Fig. 1c). The atmospheric circulation over the North Pacific is characterized by deep westerly jet stream with its maximum value at about 200 hPa (Fig. 5a). The jet core locates near 32°N, south of the SAFZ, and the corresponding surface Aleutian Low (AL) lies north of the SAFZ (Fig. 1d). Accompanied by the westerly jet, the midlatitude atmosphere shows strong baroclinicity (Fig. 5b), and the synoptic transient eddies stimulated by baroclinic instability develop vigorously, favoring North Pacific storm track. The core of the storm track in the lower troposphere and the poleward transient eddy heat transport are highly correlated to the strong oceanic front (Fig. 1e). Previous researches based on global climate model (GCM) numerical simulations (Nonaka et al. 2009; Taguchi et al. 2009; Sampe et al. 2010) have suggested that the heat supply from the ocean around the frontal zone helps to maintain an atmospheric baroclinic zone and thereby acts to anchor a storm track.

Fig. 1
figure 1

Wintertime (DJF) climatological mean states of a SST (℃; contours) and its meridional gradient (10–5 ℃/m; shaded), b standard deviation (SD) of SST, c turbulent heat flux (THF; W/m2; positive denoting upward), d SLP (hPa; shaded) and the zonal wind at 200 hPa (U200; m/s; contours; positive denoting westerly), and e meridional transient eddy heat flux (℃·m/s). The dashed box in (a) refers to the region of 37.5°–44.5°N, 144°–172°E for the definition of SAFZ-SST index

Full size image

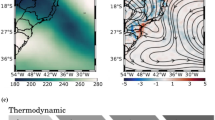
To demonstrate the SST variability associated with the SAFZ, we define an index by averaging the wintertime (DJF) SST anomaly within the region of 37.5°–44.5°N, 144°–172°E (Fig. 2a), hereafter called the SAFZ-SST index. The SAFZ-SST index is standardized and a 7-day running mean is performed to remove the synoptic disturbance. The regressed SST anomaly displays a large-scale pattern with a warming anomaly in the western-to-central midlatitude North Pacific and a surrounding cooling anomaly along the west coast of North America continent and in the subtropical North Pacific (Fig. 2b). Resultantly, the meridional SST gradient on the north (south) side of SAFZ increases (decreases) (Fig. 2b), conductive to the poleward displacement of SAFZ. Such SAFZ-related SST variability is an interannual mode with a main period of about 2–3 years, but it shows insignificant correlation with ENSO (r = 0.0374) (Nakamura et al. 1997; Nakamura and Yamagata 1999; Frankignoul et al. 2011; Wills and Thompson 2018), representing an independent midlatitude oceanic mode of the North Pacific.

Fig. 2
figure 2

Definition of the wintertime (DJF) SAFZ-SST index. a SAFZ-SST index defined by averaging the SST anomalies within the region indicated by the dashed box in Fig. 1a (i.e., 37.5°–44.5°N, 144°–172°E). The index is standardized and a 7-day running mean is applied to remove the synoptic disturbance. b Simultaneous regression of SST (℃) onto the SAFZ-SST index, with corresponding zonal mean meridional gradient of SST (10–6 ℃/m) within 144°–172°E attached on the right side. Stippling in shaded and red color in line indicate statistical significance at the 95% confidence level based on the two-tailed Student’s t test. The effective degrees of freedom are calculated after Bretherton et al. (1999)

Full size image

Figure 3 exhibits the lead-lag regression of SST, surface turbulent heat flux (THF, sum of SHF and LHF), SLP and Z200 anomalies onto the SAFZ-SST index during the wintertime. Note that in the present study, we use “leading phase” (“lagging phase”) to denote the time when regressed variables lead (lag) the SAFZ-SST index. The specific days for variables leading or lagging the SAFZ-SST index are shown on the right side of the panel. For example, “− 30 days” (“ + 30 days”) on the right side of the panel (Fig. 3) denotes regressed anomalies leading (lagging) the SAFZ-SST index by 30 days. As shown by Fig. 3a–f, the SST anomaly is prominent and persistent during the whole winter season. It enhances in the leading phase, reaches the maximum at 0 day, and weakens gradually in the lagging phase.

Fig. 3
figure 3

Lead-lag regression of a–f SST (℃), g–l THF (W/m2), m–r SLP (hPa), and s–x geopotential height at 200 hPa (Z200; m) onto the SAFZ-SST index. Negative (positive) number on the right side denotes the number of days leading (lagging) the SAFZ-SST index. Stippling indicates statistical significance at the 95% confidence level based on the two-tailed Student’s t test

Full size image

However, the associated THF anomaly undergoes a phase reversal (Fig. 3g–l). In the leading phase, the warm SST anomaly corresponds to a downward THF anomaly in the SAFZ (Fig. 3g–h), while in the lagging phase, the warm SST anomaly is related to an upward THF anomaly (Fig. 3j–l). The relative contributions of oceanic and atmospheric anomalies to the anomalous THF can be quantified based on the decomposition of bulk formulas (see Appendix). It is illustrated that the downward heat flux anomaly in the leading phase is dominated by the atmospheric anomalies while the upward heat flux anomaly in the lagging phase is determined by the SST anomaly. Hence, the change of relationship between SST anomaly and THF anomaly suggests that the atmosphere forces the ocean in the leading phase while the ocean turns to force the atmosphere in the lagging phase.

The corresponding atmospheric circulation anomalies also show obvious variation during the wintertime. There is a strong positive SLP anomaly to the north of 40°N, indicating a weakened AL, and a week negative SLP anomaly in its south in the leading phase (Fig. 3m–n). The positive anomaly peaks at about − 15 day, then decays rapidly and retreats to the north after 0 day. Meanwhile, the negative SLP anomaly is enhanced and moves northward with two centers located in the western and eastern midlatitude North Pacific respectively (Fig. 3p). It should be noted that the positive SLP anomaly is strengthened again at + 45 day after being largely reduced, and the negative anomaly moves eastward, forming a dipole structure (Fig. 3q–r). Similar characteristics can be also found in the evolution of Z200 anomalies (Fig. 3s–x), which confirm the equivalent barotropic structure in the vertical direction of midlatitude atmospheric anomalies.

Clues of ocean–atmosphere interaction can be found in the evolution of oceanic and atmospheric anomalies associated with the SAFZ-SST variability. The dominant role between ocean and atmosphere in the interaction process changes from the leading phase to the lagging phase. The ocean seems to be passive in the leading phase but later starts to force the atmosphere firstly by driving upward heat flux. Then, what cause the changes of SST anomalies and atmospheric anomalies, and how the ocean feedbacks on the atmosphere, especially why the atmospheric anomaly is re-enhanced, will be analyzed in detail below.

4 Ocean–atmosphere interaction processes associated with the SAFZ-SST variability

Here we diagnose the oceanic mixed-layer temperature tendency equation and the atmospheric QGPV equation respectively to further understand the mechanism of ocean–atmosphere interaction during the evolution process.

4.1 Mechanism responsible for the variation of SST anomalies

Following Qiu (2000) and Yao et al. (2017), the mixed-layer temperature tendency equation can be written as

$$ \frac{\partial T}{{\partial t}} = \frac{{Q_{net} }}{{\rho c_{p} h}} - {\mathop{V}\limits^{\rightharpoonup}}_{ek} \cdot \nabla T - \frac{{\left. {w_{e} } \right|_{z = - h} \left( {T - \left. T \right|_{z = - h} } \right)}}{h}, $$
(1)

where T denotes the mixed-layer temperature, \(\rho\) the sea water density, \(c_{p}\) the specific heat capacity of sea water, h the MLD, \(Q_{net}\) the net surface turbulent heat flux, \({\mathop{V}\limits^{\rightharpoonup}}_{ek}\) the Ekman advection velocity, and \(w_{e}\) the vertical entrainment velocity. According to the equation, three types of physical processes can lead to the change of SST, i.e., the net surface turbulent heat flux, the horizontal Ekman advection driven by surface wind stress, and the vertical entrainment. Note that the advection of geostrophic flow, which is proven to be unimportant by previous studies (Fang and Yang 2016; Yao et al. 2017; Tao et al. 2022), has been neglected in the equation.

Figure 4 shows the evolution of SST tendencies induced by the three terms, respectively. The THF-induced SST anomaly in SAFZ also reverses between leading and lagging phases (Fig. 4a–f), similar as the THF anomaly (Fig. 3g–l). In the leading phase, the heat is transported from the atmosphere to the ocean over SAFZ region (Fig. 3g–h), and thus the SST tends to be increased there (Fig. 4a–b). When the ocean is warmer than the atmosphere at the air-sea interface, the ocean starts to heat the atmosphere in turn (Fig. 3j–l). So in the lagging phase, the SST in SAFZ is decreased due to heat release to the atmosphere (Fig. 4d–f). On the other hand, the westward wind stress on the south side of the positive SLP anomaly can drive northward oceanic Ekman flow. They transport warm water to the midlatitude North Pacific, leading to warm SST anomaly there (Fig. 4g–i). However, SST anomaly induced by the Ekman advection anomaly is strong in the leading phase, but greatly abates in the lagging phase (Fig. 4j–l), consistent with the evolution of SLP anomaly (Fig. 3m–r). By contrast, the wind-driven vertical entrainment always reduces the SST anomaly in the western-to-central North Pacific, but its influence on SST anomaly is always small and can be ignored (Fig. 4m–r).

Fig. 4
figure 4

As Fig. 3, but for the SST tendencies (10–7 ℃/s) induced by (a–f) net turbulent heat flux, g–l Ekman advection, and m–r vertical entrainment, respectively

Full size image

Through the diagnosis of mixed-layer temperature tendency equation, we can find that the Ekman advection dominates the total forcing term in the leading phase and its distribution pattern is similar as that of the SST anomaly. At this time, the atmosphere forces the upper ocean mainly by driving Ekman advection, and the warm SST anomaly increases. While in the lagging phase, the ocean turns to feedback on the atmosphere, and the ocean-induced upward heat flux damps SST itself gradually.

4.2 Mechanism responsible for the variation of atmospheric circulation anomalies

The midlatitude atmosphere follows quasi-geostrophic dynamics. Following Fang and Yang (2016), the time-mean atmospheric QGPV equation can be written as

$$ \begin{gathered} \left( {\frac{\partial }{\partial t} + \overline{{{\mathop{V}\limits^{\rightharpoonup}}_{h} }} \cdot \nabla } \right)\left[ {\frac{1}{f}\nabla^{2} \overline{\phi } + f + \frac{\partial }{\partial p}\left( {\frac{f}{{\overline{\sigma }_{1} }}\frac{{\partial \overline{\phi } }}{\partial p}} \right)} \right] \hfill \\ \begin{array}{*{20}c} {} & { = \underbrace {{ - f\frac{\partial }{\partial p}\left( {\frac{{\overline{\alpha } }}{{\overline{\sigma }_{1} }}\frac{{\overline{Q}_{d} }}{{\overline{T} }}} \right)}}_{{F_{1} }}} \\ \end{array} \underbrace {{ - f\frac{\partial }{\partial p}\left( {\frac{{\overline{\alpha } }}{{\overline{\sigma }_{1} }}\frac{{\overline{Q}_{eddy} }}{{\overline{T} }}} \right)}}_{{F_{2} }} + \underbrace {{\overline{F}_{eddy} }}_{{F_{3} }}, \hfill \\ \end{gathered} $$
(2)

where the overbar denotes the time mean (7-day mean is used in this study), \({\mathop{V}\limits^{\rightharpoonup}}_{h}\) is the geostrophic wind, \(\phi\) the geopotential, T the air temperature, \(\alpha\) the specific volume, and \(\sigma_{1}\) the static stability parameter. \(\overline{Q}_{d}\) is the time-mean diabatic heating that can be diagnosed as the residual of the thermodynamic equation (Christy 1991; Yanai and Tomita 1998), \(\overline{Q}_{eddy} = - \nabla \cdot \overline{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V^{\prime}}_{h} T^{\prime}}} - \frac{{\partial \overline{{\omega^{\prime}T^{\prime}}} }}{\partial p} + \frac{R}{{c_{p} p}}\overline{{\omega^{\prime}T^{\prime}}}\) and \(\overline{F}_{eddy} = - \nabla \cdot \overline{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V^{\prime}}_{h} \zeta^{\prime}}}\) are defined as the time-mean transient eddy heating and transient eddy vorticity forcing, which are caused by the convergence of heat and vorticity flux transports by transient eddies, respectively. The frictional dissipation term has been omitted. From the perspective of QGPV dynamics, there are three PV forcing sources that can change the time-mean atmospheric circulation: the diabatic heat forcing (F1), the transient eddy heat forcing (F2), and the transient eddy vorticity forcing (F3). The latter two terms represent the transient eddy thermal and dynamical feedback on the mean flow, respectively.

Wintertime climatological mean states of the three PV sources as well as the zonal wind (U) and EGR averaged between 150°E and 170°W are shown in Fig. 5. As we mentioned before, the ocean–atmosphere heat exchange is strong over oceanic frontal zones, and the ocean always heats the atmosphere in winter on average. However, the \(\overline{Q}_{d}\) is relatively weak compared with that in tropics (Zhang et al. 2012) and is confined to the middle-to-lower troposphere with a maximum at 700 hPa (Fig. 5c). Meanwhile, the transient eddies that generate in the region of large atmospheric baroclinicity transport heat and vorticity flux northward systematically. The transient eddy heat and vorticity flux both converge north of the SAFZ, producing positive \(\overline{Q}_{eddy}\) and \(\overline{F}_{eddy}\) with maxima at 250–300 hPa (Fig. 5d, e). \(\overline{Q}_{eddy}\) offsets \(\overline{Q}_{d}\) to some extent and \(\overline{F}_{eddy}\) maintains the eddy-driven westerly jet at around 40°N. Our previous works (Fang and Yang 2016; Wang et al. 2017; Tao et al. 2020) have proved that \(\overline{F}_{eddy}\) plays the dominant role in the generation and maintenance of the equivalent barotropic atmospheric geopotential anomaly.

Fig. 5
figure 5

Latitude-altitude sections of the wintertime (DJF) climatological mean states of a zonal wind (U; m/s), b Eady growth rate (EGR; 10–5 s−1), c diabatic heating (\(\overline{Q}_{d}\); 10–6 K/s), d transient eddy heating (\(\overline{Q}_{eddy}\); 10–6 K/s), and e transient eddy vorticity forcing (\(\overline{F}_{eddy}\); 10–11 s−2), which are averaged between 150°E and 170°W. Corresponding zonal mean meridional gradient of SST (10–5 ℃/m; red line) is attached in the lower panel of (a–e)

Full size image

Using the successive over-relaxation (SOR) method, we can numerically solve Eq. 2 to obtain the geopotential tendencies (\(\frac{{\partial \overline{\phi } }}{\partial t}\)) induced by the three PV forcing terms, respectively (Lau and Holopainen 1984), which denote the initial atmospheric responses to the forcing terms. The lead-lag evolutions of the anomalies of \(\overline{Q}_{d}\), \(\overline{Q}_{eddy}\) and \(\overline{F}_{eddy}\) (Fig. 6 and continued) as well as their causing geopotential tendencies (Fig. 7 and continued) further reveal their different roles in influencing the atmosphere. Consistent with the evolutions in Fig. 3m–x, the regressed Z anomalies develop and peak at about-15 day, then start to decay and largely weaken in lagging phase whereas enhance again at + 40–45 days (Fig. 6a–d).

Fig. 6
figure 6figure 6

Latitude-altitude sections of the wintertime (DJF) lead-lag regression of a–d geopotential height (Z; m), e–h diabatic heating (\(\overline{Q}_{d}\); 10–6 K/s), i–l transient eddy heating (\(\overline{Q}_{eddy}\); 10–6 K/s), and m–p transient eddy vorticity forcing (\(\overline{F}_{eddy}\); 10–11 s−2) upon the SAFZ-SST index, which are averaged between 150°E and 170°W. Negative (positive) number on the top of panel denotes the number of days leading (lagging) the SAFZ-SST index. Stippling indicates statistical significance at the 95% confidence level based on the two-tailed Student’s t test. As in this figure, but for the lag regression from + 30 day to + 45 day (at 5-day interval)

Full size image
Fig. 7
figure 7figure 7

As Fig. 6, but for the geopotential tendencies (10−4 m2/s3) induced by e–h diabatic heat forcing (F1), i–l transient eddy heat forcing (F2), and m–p transient eddy vorticity forcing (F3), respectively. As in this figure, but for the lag regression from + 30 day to + 45 day (at 5-day interval)

Full size image

It can be proved that during the whole evolution process, the change of Z is determined by the three forcing terms to a great extent while the effects of advection and diffusion are secondary (Lau and Holopainen 1984). In the leading phase, since the atmosphere heats the ocean over SAFZ region, the \(\overline{Q}_{d}\) anomaly is negative in the lower level (Fig. 6e–g). It tends to induce geopotential low anomaly below 400 hPa and thus acts to reduce the positive Z anomaly in lower troposphere (Fig. 7e–g). Meanwhile, the atmospheric baroclinicity is significantly decreased in the baroclinicity zone and SAFZ (violet lines in Fig. 8a–c). Therefore, the transient eddy activities are suppressed and both the \(\overline{Q}_{eddy}\) and \(\overline{F}_{eddy}\) are decreased over SAFZ (Fig. 6i–k, m–o). However, the atmospheric response to \(\overline{Q}_{eddy}\) anomaly shows a geopotential low anomaly in the middle-to-upper troposphere (Fig. 7i–k), which also damps the positive Z anomaly as \(\overline{Q}_{d}\) does. In contrast, the \(\overline{F}_{eddy}\) anomaly tends to produce equivalent barotropic atmospheric response with a geopotential high anomaly north of 40°N and a geopotential low anomaly south of 40°N (Fig. 7m–o), acting to maintain the initial atmospheric circulation anomaly.

Fig. 8
figure 8

Lead-lag regression of meridional SST gradient (10–6 ℃/m; red line) and EGR at 850 hPa (10–5 s−1; violet line) onto the SAFZ-SST index, which are averaged between 144–172°E and 150°E–170°W, respectively. Values exceed 0.05 signifies statistical significance at the 95% confidence level based on the two-tailed Student’s t test, and the dashed line marks the center of SAFZ

Full size image

Taken overall, the contribution of thermal forcing, including the diabatic heat forcing and the transient eddy heat forcing, exceeds that of the dynamic forcing, and thus leads to the damping of Z anomaly after-15 day (Fig. 7). It should be noted that the change of atmospheric baroclinicity in the leading phase doesn’t match well with that of the SST gradient (Fig. 8a–c), indicating that the transient eddy feedback is also mostly determined by the atmospheric process. Therefore, the atmosphere plays a dominant role in the leading phase and results in a self-damping effect.

When it comes to the lagging phase, the warm upper ocean in SAFZ region starts to stimulate upward heat flux anomaly (Fig. 3j–l), and the \(\overline{Q}_{d}\) anomaly also reverses from negative to positive in the lower atmosphere (Fig. 6h and continued e–h). Influenced by the oceanic thermal forcing, the atmospheric baroclinic zone begins to be synchronized with the SAFZ, i.e., the low-level atmospheric baroclinicity increases in the north of SAFZ while weakly decreases in the south (Fig. 8d–h). Compared to the leading phase, the positive baroclinicity region originally in the north of SAFZ moves southward and occupies above the SAFZ. At this time, the changes of atmospheric baroclinicity and the associated transient eddy activities are dominated by the ocean. The enhanced atmospheric baroclinicity then leads to stronger transient eddy heat and vorticity transport, thus \(\overline{Q}_{eddy}\) and \(\overline{F}_{eddy}\) anomalies become to be positive over SAFZ (Fig. 6l, p and continued i–l, m–p). The atmospheric geopotential height response to \(\overline{Q}_{d}\) anomaly always shows baroclinic structure in the vertical direction (Fig. 7h and continued e–h), and the response to \(\overline{Q}_{eddy}\) anomaly, which partly cancels the contribution of \(\overline{Q}_{d}\), always decays the Z anomaly (Fig. 7l and continued i–l). Only the \(\overline{F}_{eddy}\)-induced atmospheric response is equivalent barotropic (Fig. 7p and continued m–p). Its negative value around 40°N tends to cause the enhancement and northward movement of the negative Z anomaly in the south, and its positive value near 50°N helps to reinforce the positive Z anomaly in the north. Therefore, the transient eddy dynamical forcing, which dominantly contributes to the maintenance and northward shift of the atmospheric circulation anomalies, is the main way for the ocean to affect the atmosphere in the lagging phase.

It should be pointed out that compared with the strong atmospheric forcing in the leading phase, the oceanic feedback on the atmosphere in the lagging phase is relatively weak. It takes approximately a month for the oceanic influence to be identified visibly by the re-enhancement of Z anomalies at + 40–45 days.

4.3 Ocean–atmosphere interaction processes over the SAFZ

Through the above analysis, it can be seen that the generation and evolution of SAFZ-SST variability during the wintertime is accompanied with clear local ocean–atmosphere interaction processes. The initial anticyclonic surface wind anomaly associated with the weakened AL forces a large-scale warm SST anomaly in midlatitude North Pacific by increasing downward heat flux and driving northward Ekman flow. With the increase of SST anomaly, the direction of air-sea heat flux exchange reverses and the ocean starts to heat the atmosphere. Meanwhile, the warm SST anomaly increases the SST gradient in the north part of SAFZ. The upward THF anomaly helps to synchronize the change of low-level atmospheric baroclinicity to that of the SAFZ, and the transient eddy activities are changed correspondingly. Though all the ocean-induced diabatic heating, transient eddy heating and transient eddy vorticity forcing are enhanced over SAFZ, the last physical process plays the most important role in shifting and maintaining the equivalent barotropic atmospheric circulation anomalies. Our study also provides observational evidence for the unstable ocean–atmosphere interaction mechanism in middle latitudes proposed by Fang and Yang (2016).

5 Conclusions and discussion

Different from the thermal-driven tropical atmosphere, the midlatitude atmospheric circulation is generally thermal- and transient eddy-driven. On time-mean scale, the atmospheric forcing sources include direct diabatic heating and indirect transient eddy thermal and dynamical forcing. Recent research works have indicated that the midlatitude oceanic frontal zones are the key regions of ocean–atmosphere interaction. The thermal condition of midlatitude ocean in frontal zones can affect the atmosphere efficiently by changing both the diabatic heating and the transient eddy feedback (Nakamura et al. 2004; Taguchi et al. 2012; Fang and Yang 2016; Tao et al. 2020).

In the North Pacific, a mechanism of unstable ocean–atmosphere interaction associated with the STFZ is proposed to explain the development and maintenance of the PDO-related atmospheric anomalies (Fang and Yang 2016). In this study, we further investigate the SAFZ-related SST variability and the corresponding anomalies of ocean–atmosphere system in winter. The associated ocean–atmosphere interaction processes and their roles in the development and evolution of the air-sea anomalies are examined through observational and theoretical analyses.

The SST variability in SAFZ shows a large-scale pattern with a warming anomaly in the western-to-central midlatitude North Pacific and a surrounding cooling anomaly in its positive phase. It is an interannual midlatitude oceanic mode of the North Pacific that is independent of ENSO. Lead-lag regression analysis illustrates that the SST anomaly can persist during the whole winter season, and its corresponding atmospheric circulation anomalies display a strong positive SLP anomaly (weakened AL) to the north of 40°N and a week negative SLP anomaly in its south in the leading phase. The positive anomaly peaks at about − 15 day, then decays rapidly and retreats to the north, while the negative SLP anomaly is enhanced and moves northward in the lagging phase. The dipole-type SLP anomaly is reinforced again at + 45 day and then lasts in the rest of winter. Similar characteristics can be also found in the evolution of Z anomalies at different levels, appearing an equivalent barotropic structure in the vertical direction.

Based on the diagnoses of the oceanic mixed-layer temperature tendency equation and the atmospheric QGPV equation, it can be found that the wintertime evolution of SAFZ-related oceanic and atmospheric anomalies is accompanied with local ocean–atmosphere interaction processes. In the leading phase, the anticyclonic surface wind anomaly associated with the weakened AL drives downward heat flux and northward Ekman flow anomalies, leading to a large-scale warm SST anomaly in midlatitude North Pacific. During this time, both the diabatic heating and the transient eddy activities are dominated by the atmosphere. The thermal forcing including diabatic heating and transient eddy heating dominate the total atmospheric forcing and significantly decay the initial atmospheric circulation anomalies.

With the increase of SST anomaly, the heat flux exchange at air-sea interface reverses in the lagging phase, indicating that the ocean starts to heat the atmosphere. In addition to increasing the diabatic heating, the warm SST anomaly strengthens the SST gradient in the north part of SAFZ, and the upward THF anomaly helps to synchronize the change of low-level atmospheric baroclinicity to that of the SAFZ. As a result, the transient eddy heating and transient eddy vorticity forcing are both enhanced over SAFZ. Mainly forced by the transient eddy vorticity forcing, the equivalent barotropic atmospheric circulation anomalies maintain and slightly shift northward.

Therefore, during the processes of air-sea interaction, the atmosphere forces the ocean in the leading phase while the ocean turns to force the atmosphere in the lagging phase. Although compared with the atmospheric forcing on the ocean, the feedback of the ocean is weak and requires a relatively long time for adjustment (nearly 1 month), it can still be clearly identified in the observation. It is the feedback effect of the ocean on the atmosphere that enables the atmospheric anomalies to be maintained throughout the winter, and even has a cross-seasonal impact on the downstream and subtropical regions. Our study further provides observational evidence for the unstable ocean–atmosphere interaction mechanism in middle latitudes proposed by Fang and Yang (2016).

Our study mainly focuses on the local ocean–atmosphere interaction processes associated with SAFZ-SST variability in the North Pacific basin, but issues like what causes the initial AL anomaly and how about the potential influence of local system on the surrounding regions, still need further discussion. As a tentative exploration, we analyze the anomalous 200 hPa Z and the T-N wave activity flux (T-N WAF) (Takaya and Nakamura 2001) in the Northern Hemisphere (Fig. 9). The initial atmospheric circulation anomaly exhibits a large-scale pattern of the positive phase of Arctic Oscillation (AO). The positive Z anomaly is strongest in the North Pacific, corresponding to the weakened AL. In the leading phase, the correlated wave energies are largely dispersed from the AL center into the North America, Arctic region and subtropical North Pacific (Fig. 9a–c), demonstrating potential influence from the North Pacific ocean–atmosphere system to downstream and Arctic region. It is also found that the anomalous center of atmospheric circulation shifts to the North Atlantic region in the lagging phase, transitioning from the positive phase of AO into the positive phase of North Atlantic Oscillation (NAO) (Fig. 9d–f), consistent with the finding of Zhang et al. (2020). The local ocean–atmosphere interaction associated with SAFZ provides energy support for the atmospheric anomaly in the North Pacific and its impact on the downstream and subtropical regions. More research based on observation and numerical experiments will be carried out to verify the mechanism of ocean–atmosphere interaction in the midlatitude North Pacific and its connection with the Arctic and North Atlantic regions.

Fig. 9
figure 9

Lead-lag regression of Z200 (m; shaded) and its corresponding T-N wave activity flux (T-N WAF; m2/s2; vectors) in Northern Hemisphere. Stippling indicates statistical significance at the 95% confidence level based on the two-tailed Student’s t test. Vectors with magnitude below 0.03 m2/s2 were masked out

Full size image

In addition, our study emphasizes the SAFZ-SST anomaly impacting on the large-scale atmospheric circulation over the North Pacific. However, its potential influence on the storm track and upper jet stream, which is also a prominent climatic phenomenon in the North Pacific, e.g., the “midwinter activity minimum” of the storm track (Nakamura and Sampe 2002; Nakamura et al. 2004), remains to be further studied. Besides, as the global warming and climate crisis worsen, some insignificant factors in the past may show up and make an impact on the atmospheric circulation, e.g., the anthropogenic factor (Liu and Di Lorenzo 2018). Future study also needs to consider about the influence from climate change.