1 Introduction

Observational studies have revealed that there is a significant decadal variability in the midlatitude North Pacific ocean–atmosphere system (Trenberth 1990; Graham et al. 1994; Minobe 1997; Mantua et al. 1997; Enfield and Mestas-Nunez 1999; Zhu and Yang 2003; Fang et al. 2006). The decadal mode of North Pacific SST anomalies, also known as the Pacific Decadal Oscillation (PDO), is well correlated with the atmospheric circulation anomalies that exhibit an equivalent barotropic structure in the vertical direction, with geopotential lows (highs) above cold (warm) water (Kushnir et al. 2002; Namias and Cayan 1981; Fang and Yang 2016). Such an equivalent barotropic cold/trough (warm/ridge) structure is the typical feature of midlatitude climate variabilities on decadal time scale (Cayan 1992; Deser and Blackman 1993).

Usually, to generate an oscillation, a positive feedback mechanism is needed to make the initial perturbation to develop, and a delayed negative feedback mechanism is also needed for the phase transition. For PDO, the negative feedback mechanisms are attributed to be those slow upper-ocean adjustment processes involving the oceanic gyre (Latif and Barnett 1994; Fang et al. 2006), the subduction (Gu and Philander 1997), and the oceanic Rossby wave propagation (Qiu et al. 2007), in which the decadal time scale of PDO is determined by the adjustment period, while the positive feedback mechanism is considered to be the local large-scale ocean–atmosphere interaction in the middle latitudes (Latif and Barnett 1994, 1996; Latif 1999; Miller and Schneider 2000; Robertson 1996; Zorita and Frankignoul 1997). Though a number of observations, theoretical analyses and GCM simulations have provided evidence for the active feedback of extratropical SST on large-scale atmospheric circulation (Saravanan and McWilliams 1997, 1998; Neelin and Weng 1999; Latif and Barnett 1996; Liu and Wu 2004; Zhong et al. 2008; Zhu et al. 2008; Fang and Yang 2011), the mechanism responsible for the midlatitude unstable air–sea interaction remains unclear, which is primarily because the processes by which the midlatitude sea surface temperature (SST) anomaly affects the seasonal-mean atmospheric anomaly have not been fully understood.

Different from the tropical atmospheric circulation that is mainly driven by the SST-related convective diabatic heating, the midlatitude atmospheric circulation is both thermally- and eddy-driven. Since the atmospheric stratification in the middle latitudes is stable, the SST-induced diabatic heating is relatively weak and mainly confined to the lower troposphere. On the other hand, the midlatitude atmosphere is strongly baroclinic, and the synoptic transient eddies are active, particularly over the midlatitude oceanic frontal zones, featuring storm tracks (Ren et al. 2010; Chu et al. 2013; Liu et al. 2014; Nakamura et al. 2004; Small et al. 2008; Wang et al. 2017). The transient eddies can systematically transport heat and momentum, driving and maintaining mean atmospheric circulations in the middle latitudes via the nonlinear eddy-to-mean flow feedback (Ren et al. 2010; Xiang and Yang 2012; Zhang et al. 2012; Nie et al. 2013, 2014). From the perspective of quasi-geostrophic potential vorticity (QGPV) dynamics, the seasonal-mean potential vorticity (PV) sources include the diabatic heating, the transient eddy heating, and the transient eddy vorticity forcing (Fang and Yang 2016). The latter two items caused by the convergence of the heat and vorticity transport by transient eddies, respectively, can be considered as indirect forcing sources of atmospheric circulation. Therefore, the midlatitude SST anomalies can affect the atmosphere by changing both the diabatic heating and the transient eddy forcing.

Fang and Yang (2016) identified the features of those PV sources associated with PDO and quantitatively diagnosed their effects on the atmospheric anomalies. Based on their analyses, a positive feedback mechanism for midlatitude unstable air–sea interaction in the North Pacific was hypothesized as follows. An initial midlatitude surface westerly anomaly accompanied by intensified Aleutian low tends to force a negative SST anomaly by increasing upward surface heat fluxes and driving southward Ekman current anomaly. Then, the basin-scale SST cooling tends to increase the meridional SST gradient in its southern flank, thus enhancing the subtropical oceanic front. In adjustment to the enhanced oceanic front, the low-level atmospheric baroclinicity tends to be strengthened, and more transient eddies are generated, resulting in enhanced meridional thermal and momentum transportations. Although all the diabatic heating, transient eddy heating and transient eddy vorticity forcing are increased during these processes, only the atmospheric response to the transient eddy vorticity forcing tends to be barotropic. The vorticity forcing that dominates the total atmospheric forcing tends to produce an equivalent barotropic atmospheric low pressure that intensifies the initial anomalies of the midlatitude surface westerly and Aleutian low. Therefore, the midlatitude air–sea interaction, in which the oceanic front and the atmospheric transient eddy are the indispensable ingredients, can provide a positive feedback mechanism for the development and maintenance of the observed decadal anomalies in the midlatitude North Pacific ocean–atmosphere system. This hypothesis has been confirmed by the later observational and modeling studies (Wang et al. 2017, 2019; Tao et al. 2020; Zhang et al. 2020).

Since atmospheric transient eddy dynamical forcing-driven midlatitude unstable air–sea interaction is recognized as a crucial positive feedback for the maintenance of the extratropical decadal variabilities, our recent theoretical work (Chen et al. 2020, hereinafter CFY2020) has characterized such an interaction through building an analytical midlatitude barotropic atmospheric model coupled to a simplified upper oceanic model. In the analytical coupled model, the atmospheric component is governed by the barotropic QGPV equation with transient eddy vorticity forcing which is parameterized to be linearly proportional to the second-order meridional derivative of SST anomaly in terms of observational analyses. It is found that the oceanic Rossby wave stimulated by air–sea coupling can be unstable within a wide range of wavelengths. The configuration structure of the most unstable mode is similar to that of the observed decadal variability. Although both surface diabatic heating and transient eddy vorticity forcing can cause unstable mode, the latter plays a dominant role. The results provide a theoretical support for the eddy-driven midlatitude unstable air–sea interaction hypothesis.

Note that a simplified assumption of the barotropic atmosphere is used in CFY2020. In reality, both diabatic heating and transient eddy vorticity forcing for the atmosphere have vertical variations. Studies using linear baroclinic model show that the atmospheric response is sensitive to the vertical structure of the idealized heat source. In response to the low-level heating, the atmosphere tends to produce a barotropic low-pressure response, while to the mid-level heat source, the atmospheric response tends to be baroclinic (Qiu et al. 2014; Hoskins and Karoly 1981; Fang and Yang 2011). The influence of vertical distribution of the transient eddy vorticity forcing on the atmospheric response remains to be clarified.

In the present study, the atmospheric component of the analytical midlatitude coupled air–sea model in CFY2020 is extended to a two-layer baroclinic quasi-geostrophic model, and the oceanic component remains to be a 1.5-layer upper ocean model. The vertical structures of diabatic heating and transient eddy vorticity forcing are both taken into account to further explore their relative contributions to midlatitude unstable air–sea interaction. The rest of the paper is organized as follows. Description of the analytical coupled model is presented in Sect. 2. The dynamical features of midlatitude air–sea coupled mode and the relative contributions of diabatic heating and transient eddy vorticity forcing with different vertical profiles are examined in Sects. 3 and 4, respectively. A comparison of the results from current model with those from previous model is presented in Sect. 5. Influences of other processes and factors such as the oceanic adjustment processes, the air–sea coupling intensity and the background atmospheric flow on the unstable coupled mode are discussed in Sect. 6. The final section is devoted to conclusions and discussion.

2 An extended analytical midlatitude coupled air–sea model

Figure 1 shows a schematic diagram of the extended analytical coupled air–sea model used in this study. The atmospheric component is a two-layer baroclinic quasi-geostrophic model with a shallow boundary layer. The oceanic component remains to be a quasi-geostrophic upper-ocean model, as in CFY2020, which consists of a constant-depth mixed layer, a thin entrainment layer, and a thermocline layer. Both the atmosphere and the ocean are governed by their respective quasi-geostrophic potential vorticity (QGPV) equations on a midlatitude beta plane.

Fig. 1
figure 1

Schematic diagram of vertical structure of the analytical midlatitude coupled air–sea model and corresponding variables

Full size image

For the atmosphere, the diabatic heating can occur both at the top of boundary layer (surface heating, \({Q}_{s}\)) and between the two layers (mid-level heating, \(Q\)). The transient eddy vorticity forcing (\({F}_{eddy}\)) exists in both layers. Since the adjustment time scale of the atmosphere is much shorter than that of the ocean, the atmospheric fluctuations are assumed to be a steady-state response to the forcing sources. Under these considerations, seasonal mean QGPV equations for the two atmospheric layers can be written as,

$$J\left({\overline{\psi }}_{1},{\overline{q} }_{1}\right)+r{\nabla }^{2}{\overline{\psi }}_{1}={\overline{F} }_{eddy1}-\frac{g{H}_{a}\overline{Q}}{2f{L }_{a}^{2}},$$
(1)
$$J\left({\overline{\psi }}_{2},{\overline{q} }_{2}\right)+r{\nabla }^{2}{\overline{\psi }}_{2}={\overline{F} }_{eddy2}+\frac{g{H}_{a}\left(\overline{Q }-{\overline{Q} }_{s}\right)}{2f{L}_{a}^{2}},$$
(2)

where the overbar denotes seasonal mean, \(q\) is the potential vorticity defined by

$${\overline{q} }_{1}={\nabla }^{2}{\overline{\psi }}_{1}+\beta y-\frac{1}{{L}_{a}^{2}}\left({\overline{\psi }}_{1}-{\overline{\psi }}_{2}\right),$$
(3)
$${\overline{q} }_{2}={\nabla }^{2}{\overline{\psi }}_{2}+\beta y+\frac{1}{{L}_{a}^{2}}\left({\overline{\psi }}_{1}-{\overline{\psi }}_{2}\right).$$
(4)

\(\psi\) is the streamfunction, \(J\left(a,b\right)=\frac{\partial a}{\partial x}\frac{\partial b}{\partial y}-\frac{\partial a}{\partial y}\frac{\partial b}{\partial x}\) the Jacobian operator, \({L}_{a}=({N}_{a}{H}_{a})/(2f)\) the atmospheric baroclinic Rossby radius of deformation with \({N}_{a}\) the atmospheric Brunt-Väisälä buoyancy frequency and \({H}_{a}\) the depth of the free troposphere. In this model, seasonal mean atmospheric anomalies are driven by PV sources due to diabatic heating [the second terms on the right hand of Eqs. (1) and (2)] and due to transient eddy vorticity forcing (\({\overline{F} }_{eddy}\)). The PV sources due to diabatic heating is proportional to the vertical gradient of diabatic heating, while \({\overline{F} }_{eddy}=-\nabla \cdot \overline{{\vec{V}_{h} ^{\prime } \zeta ^{\prime}} }\), representing the seasonal mean convergence of vorticity transport by synoptic transient eddies (denoted by primes). \(r{\nabla }^{2}\overline{\psi }\) represents the damping effect that is proportional to the relative vorticity, and \(r\) is the diffusive coefficient with a characteristic time scale taken as \({r}^{-1}=5\) days (Pedlosky 1970).

The atmospheric basic state is assumed to be a horizontally uniform zonal flow with vertical shear. Then, seasonal mean atmospheric streamfunction can be expressed as a sum of a part determined by the basic flow (climatological mean) and a perturbation (seasonal anomaly) like \({\overline{\psi }}_{1}={\psi }_{1}-{U}_{1}y\), \({\overline{\psi }}_{2}={\psi }_{2}-{U}_{2}y\). Further, atmospheric perturbations can be decomposed into barotropic and baroclinic components defined as

$$\widehat{\psi }={\psi }_{1}+{\psi }_{2}; \stackrel{\sim }{\psi }={\psi }_{1}-{\psi }_{2},$$
(5)
$$\widehat{U}={U}_{1}+{U}_{2}; \tilde{U }={U}_{1}-{U}_{2}.$$
(6)

Then the barotropic and baroclinic PV perturbation equations can be linearized about the basic state, respectively, as.

$$\widehat{U}\frac{\partial }{\partial x}{\nabla }^{2}\widehat{\psi }+\widehat{\beta }\frac{\partial \widehat{\psi }}{\partial x}+\tilde{U }\frac{\partial }{\partial x}{\nabla }^{2}\stackrel{\sim }{\psi }+2r{\nabla }^{2}\widehat{\psi }=2{F}_{eddy1}+2{F}_{eddy2}-\frac{g{H}_{a}{Q}_{s}}{f{L}_{a}^{2}},$$
(7)
$$\begin{aligned} & \hat{U}\frac{\partial }{\partial x}\left\{ {\nabla^{2} \tilde{\psi } - \frac{2}{{L_{a}^{2} }}\tilde{\psi }} \right\} + \tilde{\beta }\frac{{\partial \hat{\psi }}}{\partial x} + \tilde{U}\frac{\partial }{\partial x}\nabla^{2} \hat{\psi } + \hat{\beta }\frac{{\partial \tilde{\psi }}}{\partial x} + 2r\nabla^{2} \tilde{\psi } \hfill \\ & \quad = 2F_{eddy1} - 2F_{eddy2} - \frac{{2gH_{a} Q}}{{fL_{a}^{2} }} + \frac{{gH_{a} Q_{s} }}{{fL_{a}^{2} }}, \hfill \\ \end{aligned}$$
(8)

where \(\widehat{\beta }=2\beta\), and \(\stackrel{\sim }{\beta }=2\tilde{U }/{L}_{a}^{2}\). Accordingly, the right-hand terms in Eqs. (7) and (8)  represent their seasonal anomalies. It should be noted that the surface diabatic heating and the atmospheric transient eddy vorticity forcing in each layer drive the barotropic and baroclinic components together, whereas the mid-level heating only acts on the baroclinic component.

As assumed in CFY2020, the anomalous transient eddy vorticity forcing is parameterized to be proportional to the second-order meridional derivative of SST anomaly. Thus here the forcing in the upper layer is specified to be equal to that in the barotropic model (CFY2020), i.e., \({F}_{eddy1}=\gamma {\partial }^{2}{T}_{1}/\partial {y}^{2}\), with \({T}_{1}\) representing the sea surface temperature anomaly. Meanwhile, following Shutts (1987) and Fang and Yang (2011), the mid-level heating is prescribed to have the form of Newtonian relaxation of the atmospheric potential temperature perturbation at middle level \({\theta }_{a}\) to a radiative–convective equilibrium temperature anomaly \({\theta }_{a}^{*}\), given by

$$Q=-{\gamma }_{a}\left(\frac{{\theta }_{a}}{{\theta }_{ao}}-\frac{{\theta }_{a}^{*}}{{\theta }_{ao}}\right)=-{\gamma }_{a}\left(\frac{2f}{g{H}_{a}}\stackrel{\sim }{\psi }-\frac{{\theta }_{a}^{*}}{{\theta }_{ao}}\right),$$
(9)

where \({\theta }_{a}\) can be converted into \(\stackrel{\sim }{\psi }\) using the thermal wind relation, \({\theta }_{ao}\) is a typical value of \({\theta }_{a}\), \({\gamma }_{a}\) is the atmospheric air–sea heat exchange parameter, and \({\theta }_{a}^{*}\) is set to be the function of SST anomaly. For simplicity, it is assumed that \({\theta }_{a}^{*}={T}_{1}\).

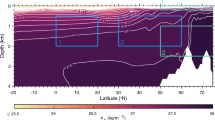
Based on the observational analysis on vertical distributions of the anomalous diabatic heating and transient eddy vorticity forcing over the North Pacific region (Fig. 2b and c, quoted from CFY2020), the surface heating is estimated to be twice as large as that of the mid-level heating (\({Q}_{s}={\delta }_{1}Q\), \({\delta }_{1}=2\)), and the transient eddy vorticity forcing in the lower atmosphere is estimated to be 0.2 times of that in the upper atmosphere (\({F}_{eddy2}={\delta }_{2}{F}_{eddy1}\), \({\delta }_{2}=0.2\)). Then, Eqs. (7) and (8) can be rewritten as

$$\begin{aligned} & \hat{U}\frac{\partial }{\partial x}\nabla^{2} \hat{\psi } + \hat{\beta }\frac{{\partial \hat{\psi }}}{\partial x} + \tilde{U}\frac{\partial }{\partial x}\nabla^{2} \tilde{\psi } + 2r\nabla^{2} \hat{\psi } \hfill \\ & \quad = 2\gamma \left( {1 + \delta_{2} } \right)\frac{{\partial^{2} }}{{\partial y^{2} }}T_{1} + \frac{{2\gamma_{a} \delta_{1} }}{{L_{a}^{2} }}\left( {\tilde{\psi } - \frac{1}{{r_{a} }}T_{1} } \right), \hfill \\ \end{aligned}$$
(10)
$$\begin{gathered} \hat{U}\frac{\partial }{\partial x}\left\{ {\nabla^{2} \tilde{\psi } - \frac{2}{{L_{a}^{2} }}\tilde{\psi }} \right\} + \tilde{\beta }\frac{{\partial \hat{\psi }}}{\partial x} + \tilde{U}\frac{\partial }{\partial x}\nabla^{2} \hat{\psi } + \hat{\beta }\frac{{\partial \tilde{\psi }}}{\partial x} + 2r\nabla^{2} \tilde{\psi } \hfill \\ \quad \quad = 2\gamma \left( {1 - \delta_{2} } \right)\frac{{\partial^{2} T_{1} }}{{\partial y^{2} }} + \frac{{2\gamma_{a} \left( {2 - \delta_{1} } \right)}}{{L_{a}^{2} }}\left( {\tilde{\psi } - \frac{1}{{r_{a} }}T_{1} } \right), \hfill \\ \end{gathered}$$
(11)

where \({r}_{a}\equiv (2f{\theta }_{ao})/(g{H}_{a})\).

Fig. 2
figure 2

Latitude-altitude sections of regressed wintertime (DJF) anomalies (shaded) upon the standardized PDO index during 1960–2010 for a geopotential height (units: \(m\)), b diabatic heating (units: \(\mathrm{K}/\mathrm{day}\)), and c transient eddy vorticity forcing (units: \({10}^{-10}{\mathrm{s}}^{-2}\)), averaged between \(150 ^\circ \mathrm{E}\) and \(150 ^\circ \mathrm{W}\), in which the black contours in (b, c) represent their corresponding climatologies, and the dots indicate the regions passing the student t-test at 95% significant level. A corresponding meridional distribution of regressed sea surface temperature anomalies (units: \(\mathrm{K}\)) is shown in the lower panel of (a). This figure is quoted from CFY2020

Full size image

The oceanic component of the coupled model keeps the same as in CFY2020 and Fang and Yang (2011). The upper-layer motion represented by the first baroclinic Rossby mode is controlled by a linear QGPV equation with a rest basic state driven by the curl of the surface wind stress. The evolution of SST is determined by physical processes including horizontal advection, vertical entrainment and heat exchange at air–sea interface. The governing equations for the ocean are given by

$$-\frac{1}{{L}_{o}^{2}}\frac{\partial {\psi }_{o}}{\partial t}+\beta \frac{\partial {\psi }_{o}}{\partial x}=\alpha {\nabla }^{2}\left(\frac{\widehat{\psi }}{2}-\stackrel{\sim }{\psi }\right),$$
(12)
$$\frac{\partial {T}_{1}}{\partial t}={c}_{1}{\psi }_{o}-{c}_{2}{T}_{1}-{c}_{3}{W}_{e}+{c}_{4}\frac{\partial {\psi }_{o}}{\partial x}+{c}_{4}\frac{H-{H}_{1}}{H}{v}_{s}-{\gamma }_{o}\left({T}_{1}-{r}_{a}\stackrel{\sim }{\psi }\right),$$
(13)

where \({\psi }_{o}\) is the upper-layer oceanic geostrophic streamfunction, \({L}_{o}\) the oceanic baroclinic Rossby radius of deformation. \({c}_{1}, {c}_{2}, {c}_{3}\) and \({c}_{4}\) are all positive coefficients relevant to advection and entrainment processes, and \({\gamma }_{o}\) the oceanic air–sea heat exchange parameter.

Equations (10)–(13) constitute the final closed equations for the coupled air–sea model. Compared with the coupled model used in Fang and Yang (2011), the role of the atmospheric transient eddy dynamical feedback is introduced in the present model. Also, the coupled model with barotropic atmosphere used in CFY2020 can be regarded as a special case of the present model.

3 Dynamical features of the midlatitude unstable coupled modes

Atmospheric and oceanic perturbations are assumed to be limited within a channel of [0, \(\uppi\)] in \(y\) direction and satisfy the standard plane wave solution in \(x\) direction with the form

$$\left(\widehat{\psi }, \stackrel{\sim }{\psi },{\psi }_{o},{T}_{1}\right)\propto {e}^{i\left(kx-\sigma t\right)}sinly,$$
(14)

where \(\sigma\) is the complex frequency, \(k\) and \(l\) are the horizontal wavenumbers in \(x\) and \(y\) directions, respectively. Substituting (14) into Eqs. (10)–(13), we obtain the following dispersion relations of the coupled modes

$$\begin{aligned}{\sigma }_{\pm }& =\frac{1}{2}\left\{{\omega }_{r}-i{c}_{2}-i{\gamma }_{o}+\frac{\left[2\gamma {l}^{2}\left(1+{\delta }_{2}\right)+\frac{2{\gamma }_{a}{\delta }_{1}}{{L}_{a}^{2}}\frac{1}{{r}_{a}}\right]\left[{\gamma }_{o}{r}_{a}-\left[{c}_{3}^{{\prime }}f{K}^{2}+{c}_{4}^{{\prime }}\left({r}_{s}k+fl\right)i\right] \frac{\alpha \left(\frac{\mu }{2}+1\right)}{\left({f}^{2}+{r}_{s}^{2}\right)}\right]}{\mu k\left(-\widehat{U}{K}^{2}+\widehat{\beta }-\frac{2r{K}^{2}}{ik}\right)+\tilde{U}{kK}^{2}+\frac{2{\gamma }_{a}{\delta }_{1}}{{L}_{a}^{2}i}}\right\}\\ & \quad \pm i{\left\{-\frac{1}{4}{\left({\omega }_{r}+i{c}_{2}+i{\gamma }_{o}-\frac{\left[2\gamma {l}^{2}\left(1+{\delta }_{2}\right)+\frac{2{\gamma }_{a}{\delta }_{1}}{{L}_{a}^{2}}\frac{1}{{r}_{a}}\right]\left[{\gamma }_{o}{r}_{a}-\left[{c}_{3}^{{\prime }}f{K}^{2}+{c}_{4}^{{\prime }}\left({r}_{s}k+fl\right)i\right]\frac{\alpha \left(\frac{\mu }{2}+1\right)}{\left({f}^{2}+{r}_{s}^{2}\right)}\right]}{\mu k\left(-\widehat{U}{K}^{2}+\widehat{\beta }-\frac{2r{K}^{2}}{ik}\right)+\tilde{U}{kK}^{2}+\frac{2{\gamma }_{a}{\delta }_{1}}{{L}_{a}^{2}i}}\right)}^{2} \right.}\\ & \quad \left. -\left({c}_{1}+{c}_{4}ik\right)\frac{\alpha{K}^{2}{L}_{o}^{2}\left(\frac{\mu}{2}+1\right)\left[2\gamma{l}^{2}\left(1+{\delta}_{2}\right)+\frac{2{\gamma }_{a}{\delta }_{1}}{{L}_{a}^{2}}\frac{1}{{r}_{a}}\right]}{\left[\mu ik\left(-\widehat{U}{K}^{2}+\widehat{\beta }-\frac{2r{K}^{2}}{ik}\right)+\tilde{U}ik{K}^{2}+\frac{2{\gamma }_{a}{\delta }_{1}}{{L}_{a}^{2}}\right]} \right\}^\frac{1}{2}, \end{aligned}$$
(15)

where \({\omega }_{r}\equiv -k\beta {L}_{\mathrm{o}}^{2}\), indicating the frequency of free oceanic baroclinic Rossby wave, \({K}^{2}={k}^{2}+{l}^{2}\), representing the square of total wavenumber, \({c}_{3}^{{{\prime}}}={c}_{3}(H-{H}_{1})\) and \({c}_{4}^{{{\prime}}}={c}_{4}(H-{H}_{1})/{H}_{1}\), which are both positive coefficients, and

$$\mu =\frac{\tilde{U }{K}^{2}+\widehat{U}{K}_{a}^{2}-\widehat{\beta }+\frac{2r{K}^{2}}{ik}+\frac{2\gamma {l}^{2}{L}_{a}^{2}{r}_{a}}{{\gamma }_{a}{\delta }_{1}}\left(-\widehat{U}{K}_{a}^{2}+\widehat{\beta }-\frac{2r{K}^{2}}{ik}+\frac{2{\gamma }_{a}{\delta }_{1}}{{L}_{a}^{2}ik}\right)}{\widehat{U}{K}^{2}-\widehat{\beta }+\frac{2r{K}^{2}}{ik}+\tilde{U }{K}^{2}-\stackrel{\sim }{\beta }+\frac{2\gamma {l}^{2}{L}_{a}^{2}{r}_{a}}{{\gamma }_{a}{\delta }_{1}}\left(-\tilde{U }{K}^{2}+\stackrel{\sim }{\beta }\right)},$$
(16)

measuring the relative strength of barotropic and baroclinic modes as \(\widehat{\psi }=-\mu \stackrel{\sim }{\psi }\).

The two solutions of (15) correspond to two coupled modes caused by midaltitude air–sea interaction. The real part of \(\sigma\) represents the frequency of the coupled mode and the imaginary part the growth rate of the amplitude of coupled mode. The coupled mode is unstable if the imaginary part of \(\sigma\) is positive. For calculating \(\sigma\), values of all parameters are taken to be the same as in CFY2020 (see Table 1), except for the basic zonal wind speeds which are set to be \({U}_{1}=17{\mathrm{m\,s}}^{-1}\) and \({U}_{2}=8{\mathrm{m\,s}}^{-1}\) for upper and lower atmosphere, respectively. The frequency and growth rate of the two coupled modes can be calculated as a function of zonal wavelength. The frequency curve of the first mode (the blue line in Fig. 3a) is very close to that of the free oceanic Rossby wave (the red line), indicating that the first coupled mode (\({\sigma }_{+}\)) is essentially a coupled oceanic Rossby wave mode modified by air–sea interaction. The coupled oceanic Rossby wave mode propagates westward and is unstable over the whole range of zonal wavelengths (Fig. 3b). The other coupled mode (\({\sigma }_{-}\)) corresponds to an eastward-propagating decaying mode since its growth rate is always negative within the entire range of zonal wavelengths (Figure not shown). Because the focus in this study is mainly on the unstable air–sea interaction, the damping mode will no longer be discussed below.

Table 1 Standard values of parameters used in the coupled air–sea model
Full size table
Fig. 3
figure 3

a Frequency and b growth rate of the coupled oceanic Rossby wave mode as a function of zonal wavelength. The red line in (a) denotes the frequency of free oceanic Rossby wave

Full size image

The most unstable coupled Rossby wave mode occurs at the wavelength around 9900 km (Fig. 3b), with a frequency of 0.78 per year (Fig. 3a) corresponding to a period at about 8 years, which is close to that of the observed decadal variability (~ 10 years, Qiu et al. 2007). Figure 4 shows the spatial phase relationships between the SST anomaly (shading) and the upper- and lower-layer atmospheric streamfunction anomalies as well as the upper-oceanic streamfunction anomalies (contours) for the most unstable coupled mode. The upper- and lower-layer atmospheric streamfunction anomalies are both in phase with the SST anomaly, indicating that the atmospheric response to the SST anomaly is equivalent barotropic with highs (lows) over warm (cold) water (Fig. 4a and b). In addition, the wind-driven upper oceanic streamfunction anomaly has a slight eastward phase shift relative to SST and atmospheric streamfunction anomalies, indicating the importance of the meridional advection process in determining the SST variation. Such a phase relationship between atmospheric and oceanic anomalies is quite consistent with that of the observed decadal variability (Fig. 5c and d). These results suggest that midlatitude air–sea interaction through atmospheric thermal and transient eddy dynamical feedback can produce an unstable coupled oceanic Rossby wave mode on decadal time scale with equivalent barotropic cold trough/warm ridge structure.

Fig. 4
figure 4

Spatial phase relationships between the characteristic SST (shaded) and a upper-layer atmospheric streamfunction, b lower-layer atmospheric streamfunction, and c upper-oceanic streamfunction anomalies (contours) for the fastest-growing coupled oceanic Rossby mode, given a fixed meridional wavelength at 6400 km. The largest amplitude of the SST anomaly is specified as 2 K

Full size image
Fig. 5
figure 5

Spatial phase relationships between the characteristic SST (shaded) and a barotropic atmospheric streamfunction and b upper-oceanic streamfunction anomalies (contours) for the fastest-growing coupled oceanic Rossby mode in CFY2020. The observed wintertime SST anomalies (shaded, units: degree in \(K\)) together with vertical integration of atmospheric streamfunction anomalies (contours, units: \({10}^{-4}{\mathrm{m}}^{2}{\mathrm{s}}^{-1}\)) and upper-oceanic streamfunction anomalies (contours, units: \({10}^{-4}{\mathrm{m}}^{2}{\mathrm{s}}^{-1}\)), regressed on the standardized PDO index, are shown in (c) and (d), respectively. This figure is quoted form CFY2020

Full size image

Note that, according to the form of plane wave solutions used above in this study, all the variables are required to be in phase in \(y\) direction. Thus the meridional phase shift as shown in Fig. 5c and d cannot be obtained. If the form of plane wave solutions is assumed as \(\propto {e}^{i(kx+ly-\sigma t)}\), the meridional phase shift among SST, atmospheric and oceanic streamfunction anomalies can be examined.

4 Roles of diabatic heating and transient eddy vorticity forcing

4.1 Role of diabatic heating with different vertical profiles

In this coupled model, diabatic heating and atmospheric transient eddy vorticity forcing are the two PV sources that jointly affect the seasonal-mean atmospheric anomaly. To examine the relative contributions of different PV sources in destabilizing the coupled oceanic Rossby wave mode, the transient eddy vorticity forcing term is firstly removed by setting \(\gamma =0\) in Eqs. (10) and (11), and only diabatic heating is kept. Three heating profiles are investigated, respectively: surface heating only (\({Q}_{s}\ne 0,Q=0\)), mid-level heating only (\({Q}_{s}=0,Q\ne 0\)), and both surface and mid-level heating (\({Q}_{s},Q\ne 0\)).

The dispersion relation curves (frequencies) of all the three cases are almost the same as the free oceanic Rossby wave, shown in Fig. 6a, c and e. This indicates that the frequency of the oceanic Rossby wave has little been affected by the air–sea coupling. However, the instability appears to be sensitive to the heating profiles. When the surface heating is only considered, the coupled oceanic Rossby mode can destabilize over the entire range of wavelengths (Fig. 6b) with growth rate that has a significant reduction compared with the standard full PV sources case (Fig. 3b), and the most unstable mode shifts to a shorter wavelength at around 8500 km. When the mid-level heating is only considered, the coupled oceanic Rossby mode becomes a weak damping mode. By comparing the phase relationships of atmospheric and oceanic variables for the two cases (Fig. 7), we can find that the atmospheric anomalies for the two cases are nearly out of phase, relative to the same negative SST anomalies. The atmospheric response to the surface cooling induced by cold SST anomaly shows an equivalent barotropic low above cold water anomaly (Fig. 7a and c), similar to the situation in the standard case but with an eastward phase shift relative to SST anomalies. The surface low pressure further sustains the cyclonic oceanic flow and enhances the cold SST anomaly by transporting cold water (Fig. 7e), thus forming a positive air–sea feedback, indicating that the coupled Rossby wave mode is a growing mode. However, in the case of the negative SST anomaly-induced mid-level cooling, the upper-layer atmospheric streamfunction exhibits a high anomaly response just over the negative SST anomaly (Fig. 7b), while the high anomaly of the lower-layer atmospheric streamfunction leads that of the upper layer by nearly \(\pi /2\) phase (Fig. 7d). The surface high pressure tends to weaken the cyclonic oceanic flow and thus reduce the cold SST anomaly. In this case, the coupled Rossby wave mode decays gradually.

Fig. 6
figure 6

Frequency (upper panels) and growth rate (lower panels) of the coupled oceanic Rossby wave mode as a function of zonal wavelength corresponding to the surface diabatic heating-only case (left panels), the mid-level heating-only case (mid panels), and the both surface and mid-level heating case (right panels), respectively. Red lines in upper panels denote the frequency of free oceanic Rossby wave

Full size image
Fig. 7
figure 7

As in Fig. 4, but for the surface diabatic heating only (left panels) and the mid-level diabatic heating only (right panels)

Full size image

When the surface and mid-level heating are both included, the results are very similar to that of the surface heating only case (Fig. 6f), indicating that the contribution of diabatic heating to the unstable air–sea coupled mode is dominated by the surface heating. Mid-level heating that tends to cause baroclinic atmospheric response does not cause any unstable coupled mode while surface heating always generates the instability. Figure 10a shows the variation of unstable growth rate with zonal wavelength and surface heating intensity. Here the mid-level heating is fixed and the surface heating is modified continuously by changing \({\delta }_{1}\). It can be seen that, corresponding to the fastest-growing mode, the stronger the surface heating is (the larger \({\delta }_{1}\) is), the more unstable the coupled mode emerges.

4.2 Role of transient eddy vorticity forcing with different vertical profiles

By setting \({\gamma }_{a}=0\) in Eqs. (10) and (11), the diabatic heating is neglected. Atmospheric transient eddy vorticity forcing becomes the only PV source of the atmosphere. Also, three vertical profiles of the transient eddy vorticity forcing are discussed: the forcing occurring only in the lower troposphere (\({F}_{eddy2}\ne 0, {F}_{eddy1}=0\)), only in the upper troposphere (\({F}_{eddy2}=0, {F}_{eddy1}\ne 0\)), and in both layers (\({F}_{eddy2}, {F}_{eddy1}\ne 0\)).

In all the three cases, the oceanic Rossby wave mode is unstable over the entire range of wavelengths (Fig. 8). However, in the lower-layer forcing-only case, the instability of the coupled mode is very weak. Growth rate of the most unstable mode is only 0.02 per year, and corresponding wavelength and period are 8800 km and 7.67 years, respectively (Fig. 8b and e). In the upper-layer forcing-only case, growth rate of the most unstable mode is greatly increased, corresponding to a longer wavelength of 9900 km and a longer period of 8.17 years (Fig. 8a and d). The spatial phase relationship between the atmospheric streamfunction and SST anomalies (Fig. 9a and c) is much closer to that in the standard case (Fig. 3a and b). When the transient eddy vorticity forcings at both layers are considered, growth rate is similar to that in the upper-layer forcing-only case, but the most unstable growth rate is increased slightly with a zonal wavelength of around 10,200 km and a period of 8.34 years (Fig. 8c and f). From the above results, it can be concluded that the upper-layer transient eddy vorticity forcing plays a dominant role in producing unstable air–sea interaction mode.

Fig. 8
figure 8

As in Fig. 6, but for the transient eddy vorticity forcing in the upper layer only (left panels), lower layer only (mid panels), and both layers (right panels), respectively. Note that the green lines in the lower panels indicate the associated growth rate when the transient eddy vorticity forcing in the lower layer is increased to be equal to that in the upper layer

Full size image
Fig. 9
figure 9

As in Fig. 4, but for the transient eddy vorticity forcing only in the upper layer (left panels) and only in the lower layer (right panels)

Full size image

It should be mentioned that, in the present study, the lower-layer transient eddy vorticity forcing is set to be 0.2 times of that of upper layer (\({\delta }_{2}=0.2\)) according to the observational analysis. If we assume the magnitudes of the forcing at both layers are equal (\({\delta }_{2}=1\)), which is equivalent to the setting in the barotropic atmospheric model (CFY2020), then the unstable growth rate is enhanced greatly no matter whether the upper-layer forcing is considered or not (as shown by the green lines in Fig. 8e and f). Under this setting, the contribution of individual lower-layer vorticity forcing on the unstable mode has overtaken that of individual upper-layer forcing (Fig. 8d and e), suggesting that the lower-layer vorticity forcing causes instability more effectively. This is also illustrated by Fig. 10b, in which the upper-layer forcing is fixed and the lower-layer forcing is changed continuously. With the increase of low-layer forcing, the unstable growth rate increases, and the fastest-growing mode moves to longer wavelengths slightly. This result can be explained by Eqs. (7) and (8). According to the relationship between transient eddy vorticity forcing and SST anomalies, a cold SST anomaly causes positive vorticity forcing in both layers. The lower-layer forcing \({F}_{eddy2}\) makes the same contribution to the barotropic component of the atmosphere as the upper-layer forcing \({F}_{eddy1}\) does. But for the baroclinic component, \({F}_{eddy2}\) tends to decrease the baroclinic component by offsetting the contribution of \({F}_{eddy1}\), indicating that the lower-layer atmospheric response of geopotential low anomaly becomes stronger which strengthens the cold SST anomaly more effectively through driving cyclonic oceanic flow.

Fig. 10
figure 10

Growth rate of the coupled oceanic Rossby wave mode as a function of the zonal wavelength versus a the ratio of surface-to-mid-level heating (\({\delta }_{1}\), here the mid-level heating is fixed and the surface heating is enhanced with increase of \({\delta }_{1}\)), and b the ratio of lower-layer-to-upper-layer transient eddy vorticity forcing (\({\delta }_{2}\), here the upper-layer forcing is fixed and the lower-layer forcing is enhanced with increase of \({\delta }_{2}\)), respectively

Full size image

Although either diabatic heating or transient eddy vorticity forcing can lead to a destabilized oceanic Rossby wave mode with similar equivalent barotropic structure of atmospheric anomaly, the latter has a larger contribution to the unstable growth rate (Figs. 3b, 6f, and 8f). This demonstrates again that atmospheric transient eddy dynamical feedback plays a crucial role in unstable midlatitude air–sea interaction, as pointed out by previous studies (Fang and Yang 2016; CFY2020).

5 Comparison with the results of coupled model with barotropic atmosphere

In CFY2020, since the atmosphere is assumed to be barotropic, only the surface diabatic heating that occurs at the top of boundary layer and the transient eddy vorticity forcing with no vertical variation can have effect. Nevertheless, as expressed by Eqs. (1) and (2) in the present baroclinic atmospheric model, surface diabatic heating acts only on the lower-layer atmosphere, whereas mid-level heating affects both lower- and upper-layers but with opposite effect. Thus they both contribute to the baroclinic component, but their contributions can offset each other to some extent, as expressed in Eq. (8), while the surface diabatic heating only affects the barotropic component as expressed in Eq. (7). Moreover, if the transient eddy vorticity forcing is unchanged in vertical direction (i.e., \({F}_{eddy1}= {F}_{eddy2}\)), as in the barotropic model, it will only impact on the barotropic atmospheric component. Otherwise, when the transient eddy vorticity forcings in the two layers are not equal, their difference will cause baroclinic atmospheric response. Above analysis indicates that if \(U\) and \({F}_{eddy}\) have no vertical change the barotropic component of atmosphere in our study is equivalent to the barotropic atmosphere model used in CFY2020.

Compared with the results of CFY2020 in which the atmosphere is assumed to be barotropic, the period of the most unstable mode in this study becomes longer, and the associated SST and atmospheric streamfunction anomalies are exactly in phase (Fig. 4), which is more consistent with the observation (Fig. 5c and d), instead of a slight phase shift in \(x\) direction in the barotropic atmospheric model (Fig. 5a and b). Another striking difference is on the growth rate for the most unstable mode which is largely reduced (Fig. 11a) in the present model when the vertical profiles of diabatic heating and transient eddy vorticity forcing are taken to be close to the observed. One reason is due to the offset effect by the mid-level diabatic heating (Fig. 11b), and other reason is due to the smaller lower-layer transient eddy vorticity forcing (Fig. 11c). As mentioned in Sect. 3, because the vertical structures of atmospheric PV sources and basic flow are more realistic in the present baroclinic model, the associated period and spatial configuration patterns of the atmospheric and oceanic anomalies for the unstable coupled mode coincide with the observation much better.

Fig. 11
figure 11

Comparison of growth rate of the coupled oceanic Rossby wave mode derived in our study (blue lines) with that derived in CFY2020 (orange lines) when a both diabatic heating and transient eddy vorticity forcing are considered, b the diabatic heating is only considered, and c the transient eddy vorticity forcing is only considered

Full size image

6 Contributions of other processes and factors

6.1 Relative roles of oceanic entrainment and advection processes

As expressed in Eq. (12), the oceanic processes determining SST evolution include horizontal advection, vertical entrainment and air–sea flux exchange, which represent the oceanic adjustment to the atmospheric forcing. Relative roles of different oceanic processes in destabilizing coupled oceanic Rossby wave mode are examined below.

Since air–sea flux exchange just stimulates very weak damping mode (figure not shown), main processes emphasized here are entrainment and advection. Figure 12 shows the growth rate as a function of wavelength for the coupled oceanic Rossby wave mode for three cases: full processes, entrainment-only, and advection-only, respectively. It can be found that both entrainment and advection have contributions to the unstable coupled mode. When the wavelength is shorter than 10,000 km, total unstable growth rate is contributed primarily from advection, while within the wavelength range beyond 10,000 km, it is contributed jointly from advection and entrainment.

Fig. 12
figure 12

Growth rate as a function of wavelength for the coupled oceanic Rossby wave mode with SST evolution determined by a full oceanic processes, b entrainment process-only, and c advection process-only. Note that a is the same as Fig. 3b

Full size image

6.2 Influence of coupling strength and basic zonal flows

The unstable coupled mode may be influenced by two kinds of critical parameters, coupling coefficients (\({\gamma }_{a}\) and \(\gamma\)) determining the coupling strength between ocean and atmosphere through thermal and dynamical processes, and background zonal wind speeds in the two atmospheric layers (\({U}_{1}\) and \({U}_{2}\)). In the standard case, values of these parameters are set as: \(\gamma =11.2{\mathrm{s}}^{-2}{\mathrm{m}}^{2}{\mathrm{K}}^{-1}\), \({\gamma }_{a}=8\times {10}^{-7}{\mathrm{s}}^{-1}\), \({U}_{1}=17{\mathrm{m\,s}}^{-1}\), and \({U}_{2}=8{\mathrm{m\,s}}^{-1}\). The influence of air–sea coupling strength and basic zonal flows on unstable air–sea interaction is estimated by changing those parameters.

Figure 13 shows the variation of growth rate for the most unstable Rossby wave mode with zonal wavelength versus dynamical coupling coefficient (\(\gamma\)), thermal coupling coefficient (\({\gamma }_{a}\)), upper-layer basic zonal wind speed (\({U}_{1}\)), lower-layer basic zonal wind speed (\({U}_{2}\)), and vertical wind shear (\({\tilde{U }={U}_{1}-U}_{2}\)), respectively. The growth rate for the standard case is marked by “\(\times\)” in the figure. It can be seen from Fig. 13a and b that the coupled oceanic Rossby wave is always unstable within the entire range of air–sea coupling parameters. With an increase of coupling strength, no matter dynamical coupling or thermal coupling, the instability of the coupled mode is enhanced. However, compared with the thermal coupling (Fig. 13b), the influence of transient eddy dynamical feedback intensity is much more prominent, because the amplitude of growth rate is much larger and the corresponding unstable wavelength range is much wider (Fig. 13a). When the air–sea coupling is strengthened, the SST anomaly can force the atmosphere more strongly, especially through transient eddy vorticity forcing, thus the coupled mode becomes more unstable.

Fig. 13
figure 13

As in Fig. 10, but for a the dynamical coupling coefficient (\(\gamma\)), b thermal coupling coefficient (\({\gamma }_{a}\)), c the upper-layer background zonal wind speed (\({U}_{1}\)), d the lower-layer background zonal wind speed (\({U}_{2}\)), and e the vertical wind shear (\({U}_{1}-{U}_{2}\)), respectively

Full size image

The intensity and the vertical shear of basic zonal wind are also crucial factors determining the unstable growth. When basic zonal wind speed in the upper layer is larger than that in the lower layer (\({U}_{1}>8{\mathrm{m\,s}}^{-1}\)), the unstable growth rate decreases with increase of \({U}_{1}\) (Fig. 13c). Conversely, when basic zonal wind speed in the lower layer is less than that in the upper layer (\({U}_{2}<17{\mathrm{m\,s}}^{-1}\)), the unstable growth rate increases with increase of \({U}_{2}\) (Fig. 13d). In other words, the larger the vertical wind shear, the weaker the instability (Fig. 13e). When basic zonal wind speeds in both layers are equal, as in the barotropic model, the unstable growth rate reaches its maximum (Fig. 13e). That is because the vertical wind shear tends to weaken the barotropic atmospheric response by vorticity advection and thus is not conducive to the unstable coupled mode.

7 Conclusions and discussion

Midlatitude air–sea interaction is one of the crucial sources for decadal climate variabilities. However, mechanism responsible for the midlatitude air–sea interaction remains unclear primarily due to a lack of deep understanding on how the midlatitude SST can affect the atmosphere. Generally, it is believed that the midlatitude SST may affect the atmosphere through diabatic heating, as in the tropics. But such a thermally-driving mechanism fails to explain observed equivalent barotropic structure of decadal atmospheric anomalies.

The atmosphere features strong baroclinicity in the midlatitudes where synoptic eddies accompanied with jet stream develop vigorously, and heat and momentum transports by those transient eddies can in turn feedback onto the midlatitude mean flow. The eddy-to-mean flow feedback has been found to be a key approach for midlatitude SST to affect the atmosphere by a number of recent studies (Wang et al. 2017, 2019; Tao et al. 2020). Atmospheric transient eddy dynamical forcing (TEDF)-driven midlatitude unstable air–sea interaction has recently been recognized as a crucial positive feedback for the maintenance of the extratropical decadal variabilities (Fang and Yang 2016; Chen et al. 2020). Our recent theoretical work by Chen et al. (2020) has characterized such an interaction through building an analytical midlatitude barotropic atmospheric model coupled to a simplified upper oceanic model.

As a theoretical development, this study extends the analytical coupled air–sea model of Chen et al. (2020) to including a two-layer quasi-geostrophic baroclinic atmospheric model and then identifies the roles of vertical distributions of atmospheric TEDF and diabatic heating in midlatitude unstable air–sea interaction. In the extended coupled model, both the atmospheric and oceanic perturbations satisfy quasi-geostrophic dynamics and are governed by their respective linearized QGPV equations on a midlatitude beta plane. A linearized mixed layer temperature equation is considered to describe the SST evolution. The ocean is driven by the anomalous wind stress of the atmosphere and in turn forces the atmosphere through diabatic heating and atmospheric transient eddy vorticity forcing. The diabatic heating is specified at the top of atmospheric boundary layer and at the mid-level of two-layer atmosphere, which is linearly dependent of SST anomaly. The transient eddy vorticity forcing in each layer is parameterized to be proportional to the second-order meridional derivative of SST anomaly. Based on observation, the surface heating is set to be twice of the mid-level heating and the transient eddy vorticity forcing in the lower layer is 0.2 times of that in the upper layer for the standard case.

Analytical solutions of the model show that the midlatitude air–sea coupling with more realistic vertical profiles of atmospheric TEDF and diabatic heating destabilizes the oceanic Rossby wave mode that propagates westward over the entire range of zonal wavelengths, in which the most unstable or the fastest-growing coupled mode occurs at the wavelength of around 9900 km, with a period of nearly 8 years. For this mode, atmospheric streamfunction anomalies in the two layers are both in phase with SST anomaly, with atmospheric lows (highs) over cold (warm) water. Correspondingly, the oceanic streamfuction anomalies also exhibit a cyclonic (anticyclonic) anomaly which is slightly shifted to east of the cold (warm) SST anomaly. Thus the unstable coupled mode exhibits an equivalent barotropic cold trough (warm ridge) structure, quite similar to the observed feature of decadal climate variability.

Figure 14 illustrates a schematic diagram of the phase relationships among atmospheric and oceanic variables for the most unstable coupled oceanic Rossby wave mode in the midlatitudes. If there is an initial cold (warm) SST anomaly in the north (south), it induces a strong surface cooling (warming) and a weak mid-level cooling (warming), leading to a positive (negative) PV source in both atmospheric layers. Meanwhile, the above SST anomaly pattern tends to give rise to a larger meridional SST gradient and thus a stronger low-level atmospheric baroclinicity. Atmospheric synoptic eddies become more active, causing positive (negative) transient eddy vorticity forcing (also, PV source) in the north (south) for both layers. Therefore, through both diabatic heating and transient eddy dynamical forcing, the initial cold (warm) SST anomaly generates an in-phase equivalent barotropic atmospheric low (high) anomaly over the SST anomaly. The surface low (high) pressure anomaly tends to drive the upper oceanic Rossby wave and generate a cyclonic (anticyclonic) upper oceanic flow anomaly with a slight eastward phase shift relative to the SST anomaly, which thus further amplify the initial cold (warm) SST anomaly mainly through oceanic advection process. Consequently, the amplitude of the oceanic Rossby wave grows due to the air–sea coupling.

Fig. 14
figure 14

Schematic diagram of the phase relationships among atmospheric and oceanic variables for the most unstable coupled oceanic Rossby wave mode in the midlatitudes

Full size image

Relative roles of diabatic heating and transient eddy vorticity forcing with different vertical profiles in destabilizing the coupled oceanic Rossby wave are analyzed. A SST anomaly can induce in-phase surface and mid-level diabatic heating as well as an opposite-phase transient eddy vorticity forcing in both layers of the atmosphere. The surface heating favors the barotropic atmospheric response, while the mid-level heating always excites the baroclinic atmospheric response. In the observation, the surface heating is larger than the mid-level heating, the contribution of diabatic heating on the unstable coupled mode is dominated by the surface heating. On the other hand, the transient eddy vorticity forcing at each layer can force barotropic atmospheric response and induce unstable coupled mode, while the lower-layer forcing can affect the unstable mode more effectively by weakening the baroclinic response. However, in the standard case, since the transient eddy vorticity forcing at the lower layer is much smaller than that in the upper layer, the upper-layer transient eddy vorticity forcing makes more prominent contribution to the unstable growth rate. Although either diabatic heat forcing or transient eddy vorticity forcing can generate unstable coupled oceanic Rossby wave alone, the transient eddy dynamical feedback plays a much more important role.

Besides the SST-induced forcing on the atmosphere, the oceanic adjustment processes driven by the atmospheric windstress anomaly, which mainly include advection and entrainment, can also affect the unstable coupled mode. When SST is adjusted by the advection process alone, the coupled oceanic Rossby wave with zonal wavelength shorter than 10,000 km tends to be unstable. When the entrainment process is considered alone, the unstable coupled mode occurs within a wider range of wavelengths (> 10,000 km). Moreover, the influences of air–sea coupling strength and background zonal wind speed on the unstable coupled mode are also examined. When air–sea coupling (either dynamical coupling or thermal coupling) is strengthened, the instability of the coupled mode is enhanced. But the effect of dynamical coupling through transient eddy vorticity forcing is more significant. For the basic zonal wind speed, its barotropic part favors the growth of coupled mode, whereas its baroclinic part determined by the vertical wind shear tends to decay the coupled mode.

Compared with the results derived from CFY2020 in which the atmospheric component is barotropic, the spatial configuration structure and period of the unstable coupled mode in this study are more consistent with the observation, although the growth rate of the unstable coupled mode becomes smaller due to the mid-level atmospheric heating and the TEDF with vertical varation which both tend to contribute to baroclinic atmospheric response and check the instability.

It should also be mentioned that there are three PV sources in the atmospheric QGPV equation due to diabatic heating, transient eddy heating and transient eddy vorticity forcing, respectively (Fang and Yang 2016). The PV source due to transient eddy heating is proportional to the vertical gradient of transient eddy heating (\({Q}_{eddy}\)) that represents the convergence/divergence of heat flux transported by transient eddies. Transient eddy heating that has the same dimension as diabatic heating can be seen as an indirect heat source of the atmosphere, reflecting the transient eddy thermal forcing on the atmosphere. The magnitude of transient eddy heating is comparable with that of diabatic heating, and it is mainly confined to the middle of the troposphere (Fig. 2c in CFY2020). Hence in the barotropic model, it vanishes after vertical integration. In the present study, it is not explicitly expressed in the coupled model. However, since it is equivalent to a mid-level heating, the increased mid-level heating or decreased surface heating (i.e., decreased \({\delta }_{1}\) in Fig. 10a) in this study can be equivalent to the case that the transient eddy heating is considered in the coupled model. At this time, the growth rate of the most unstable coupled mode is decreased a little due to the enhancement of baroclinic atmospheric response induced by transient eddy heating.