Drivers of low-frequency Sahel precipitation variability: comparing CMIP5 and CMIP6 ensemble means with observations

Abstract

Phases 5 and 6 of the Coupled Model Intercomparison Project (CMIP5 and CMIP6) both grossly underestimate the magnitude of low-frequency Sahel rainfall variability; but unlike CMIP5, CMIP6 mean historical precipitation does not even correlate with observed multi-decadal variability. We demarcate realms of simulated physical processes that may induce differences between these ensembles and prevent both from explaining observations. We partition all influences on simulated Sahelian precipitation variability into (1) teleconnections from sea surface temperature (SST); (2) atmospheric and (3) oceanic variability internal to the climate system; (4) the SST response to external radiative forcing; and (5) the “fast” (not mediated by SST) precipitation response to radiative forcing. In a vast improvement from previous ensembles, the mean spectral power of Sahel rainfall in CMIP6 atmosphere-only simulations is consistent with observed low-frequency variance. Low-frequency variability is dominated by teleconnections from observed global SST, and the fast response only hurts the performance of simulated precipitation. We estimate that the strength of simulated teleconnections is consistent with observations using the previously-established North Atlantic Relative Index (NARI) to approximate the role of global SST, and apply this relationship to the coupled ensembles to infer that both fail to explain low-frequency historical Sahel rainfall variability mostly because they cannot explain the observed combination of forced and internal variability in North Atlantic SST. Yet differences between CMIP5 and CMIP6 in mean Sahel precipitation and its correlation with observations do not derive from differences in NARI, but from the fast response or the role of other SST patterns.

1 Introduction

The semi-arid region bordering the North African Woodlands and the Sahara Desert, known as the Sahel, received much scientific attention since it experienced dramatic rainfall variability in the second half of the twentieth century. Sahel rainfall variability has been linked to remote radiative drivers, or “forcings”, including volcanic eruptions as well as anthropogenic aerosol (AA) and greenhouse gas (GHG) emissions (Ackerley et al. 2011; Biasutti 2013; Biasutti and Giannini 2006; Biasutti et al. 2008; Bonfils et al. 2020; Dong and Sutton 2015; Giannini and Kaplan 2019; Haarsma et al. 2005; Haywood et al. 2013; Hirasawa et al. 2020; Hua et al. 2019; Iles and Hegerl 2014; Kawase et al. 2010; Marvel et al. 2020; Polson et al. 2014; Undorf et al. 2018; Westervelt et al. 2017). Nevertheless, because computational models generally cannot account for the full observed variability, the magnitude and importance of the observed responses to these driving factors—relative to each other and to variability internal to the climate system (Sutton and Hodson 2005; Ting et al. 2009; Zhang and Delworth 2006)—are still widely debated (Biasutti 2019).

Recently, Herman et al. (2020, hereafter H20) investigated the causes of observed Sahel precipitation variability using the Coupled Model Intercomparison Project phase 5 (CMIP5, Taylor et al. 2012), which is the first multi-model ensemble to include “Detection-Attribution” simulations aimed at separating the effects of the radiative forcing agents mentioned above. Rather than focusing on the specific behavior of any individual model—which may outperform other models in one metric but underperform in another—they employ a multi-model mean (MMM) to identify a more robust “central tendency” of the ensemble (Mote et al. 2011). They show that, while the MMM variance might be somewhat damped relative to the forced response in individual simulations, the MMM of historical Sahel precipitation matches observed historical precipitation better than simulated precipitation from any individual model in CMIP5. H20 find that AA and volcanic aerosols—but not GHG—are responsible for forcing simulated Sahelian precipitation that correlates well with observations, with AA alone responsible for the low-frequency component of simulated variability. This conclusion appeared consistent with previous claims that global AA emissions—which originate mostly in the Northern Hemisphere, and which increased until the 1970s and then decreased until 2000 in response to clean air initiatives (Klimont et al. 2013; Smith et al. 2011)—caused multi-decadal variability in Sahel precipitation via changes in Northern Hemisphere surface temperature (Ackerley et al. 2011; Haywood et al. 2013; Hwang et al. 2013; Undorf et al. 2018), or specifically via multidecadal variability in North Atlantic SST (the Atlantic Multidecadal Variability, AMV; Booth et al. 2012; Hua et al. 2019). However, H20 also find that, like previous simulations, the CMIP5-simulated rainfall response to forcing (given by the MMM) has too little low-frequency power relative to observations, and simulated internal variability is unable to account for this difference.

H20 do not examine in depth the pathways through which any given forcing agent affects Sahel precipitation. Thus, they do not determine whether the discrepancy between the CMIP5 simulations and observations represents a quantitative underestimate of aerosol indirect effects and related feedbacks, or a qualitative inability of the models to simulate the observed climate response to forcing or observed modes of internal variability. The distinction is crucial if we are to trust these models’ projections of future Sahelian rainfall.

A first investigation into the mechanisms of forced Sahel precipitation variability should focus on sea surface temperature (SST). Early Sahel climate variability research (Folland et al. 1986; Giannini et al. 2003; Knight et al. 2006; Palmer 1986; Zhang and Delworth 2006) and more recent studies (Okonkwo et al. 2015; Parhi et al. 2016; Park et al. 2016; Pomposi et al. 2015, 2016; Rodríguez-Fonseca et al. 2015 and references therein) used atmospheric simulations with prescribed global SST to demonstrate causal “teleconnections” between remote SST in a number of ocean basins and Sahel precipitation, and used observational statistics to show the importance of these teleconnections. Unfortunately, like coupled simulations, atmospheric simulations have also historically failed to explain the full magnitude of observed Sahel precipitation variability (e.g. Scaife et al. 2009). Thus, while the dominant role of global SST over local land-use practices in driving the pacing of observed twentieth century Sahel rainfall variability is unquestioned (Biasutti 2019), it has not yet been possible to rule out simultaneous (and potentially important) roles for solely-atmospheric responses to global radiative forcing that are in-phase with observed SST variability.

Since the publishing of H20, new coupled and atmosphere-only simulations became available from phase 6 of the Coupled Model Intercomparison Project (CMIP6, Eyring et al. 2016), in which many models have an improved representation of physical processes and newly implemented biogeochemical cycles as well as higher resolution (Masson-Delmotte et al. 2021). In coupled models, these changes have reportedly resulted in greater (and perhaps unrealistic) sensitivity to GHG (Forster et al. 2020; Zelinka et al. 2020) but little change in the representation of summer monsoons (Fiedler et al. 2020), though in this paper we identify and explore some notable differences in the historical evolution of Sahel rainfall. Atmosphere-only simulations in CMIP5 used both prescribed SST and remote radiative forcing simultaneously, and only covered the last couple decades of the twentieth century, making it previously impossible to examine multi-decadal SST-forced variability using CMIP. CMIP6 for the first time includes an ensemble of atmosphere-only (“AMIP”) simulations long enough to capture the observed period of multi-decadal Sahel precipitation variability, with and without simultaneous radiative forcing. This new ensemble will allow us to robustly analyze the simulated response to realistic SST in CMIP and in observations.

Here, we extend the methodology of H20 by using the well-established dependence of Sahel precipitation on global SST in combination with the CMIP6 atmosphere-only simulations to examine the mechanisms of Sahel precipitation variability in observations and in the CMIP ensembles in more depth. We decompose the simulated effects of individual external forcing agents (F) and internal climate variability on low-frequency Sahel precipitation variability (P) into five path components, presented in Fig. 1: (1) teleconnections that communicate variations in SST to variations in precipitation (indicated by the arrow $\overrightarrow{\mathrm{t}}$); (2) the “fast” atmospheric and land-mediated effect of external forcing (F) on precipitation ($\overrightarrow{\mathrm{f}}$); (3) the expression of atmospheric internal variability (IV_a) as precipitation variability ($\overrightarrow{\mathrm{a}}$); (4) the effect of forcing on SST ($\overrightarrow{\mathrm{s}}$); and (5) the expression of internal variability in the coupled climate system (IV_o) as SST variability ($\overrightarrow{\mathrm{o}}$). The path $\mathrm{F}\to \mathrm{SST}\to \mathrm{P}$ is the “slow,” SST-mediated effect of forcing on precipitation. While the atmospheric response to forcing is not more rapid than teleconnections or atmospheric internal variability, we prefer to label this term the “fast response to forcing” rather than employing the other commonly used label—the “direct response”—in order to avoid terminology confusion with the “direct” effect of aerosols (which contributes to the “fast response” to forcing in combination with the "indirect effect" of aerosols).

Fig. 1

Causal diagram relating external forcings (F), atmospheric (IV_a) and oceanic internal variability (IV_o), sea surface temperatures (SST), and Sahel precipitation (P) via directional causal arrows. Unobserved variables that are not explicitly measured and their causal effects are presented with dashed lines, while observed variables are presented with solid lines

To this point, characterization of these path components in observations remains controversial. Firstly (top of diagram), separating the SST response to forcing ($\overrightarrow{\mathrm{s}}$) from SST variability internal to the climate system ($\overrightarrow{\mathrm{o}}$) has proven difficult. In particular, there is significant debate over whether observed AMV is a response to external forcing (Booth et al. 2012; Chang et al. 2011; Hua et al. 2019; Menary et al. 2020; Rotstayn and Lohmann 2002) or mainly an expression of internal variability in the Atlantic Meridional Overturning Circulation (AMOC, Han et al. 2016; Knight et al. 2005; Qin et al. 2020; Rahmstorf et al. 2015; Sutton and Hodson 2005; Ting et al. 2009; Yan et al. 2019; Zhang 2017; Zhang et al. 2016; Zhang et al. 2013) that is underestimated in models (Yan et al. 2018). This debate has been hard to resolve partially because internal variability in AMOC and aerosol forcing may have coincided by chance in the twentieth century (Qin et al. 2020). Next, examine the bottom of the diagram. The effect of the observed SST field on Sahel precipitation $(\overrightarrow{\mathrm{t}})$ can be directly estimated using atmosphere-only simulations, but while these simulations capture the pattern of observed Sahel precipitation variability, many fail to capture its full magnitude (Biasutti 2019; e.g. Hoerling et al. 2006; Scaife et al. 2009). This could reflect an underestimate in climate models of the strength of SST teleconnections $(\overrightarrow{\mathrm{t}})$, which could be resolution dependent (Vellinga et al. 2016); or of land-climate feedbacks that amplify the teleconnections, such as vegetation changes (Kucharski et al. 2013). But it could also reflect a significant additional role in the observations for a fast response to forcing ($\overrightarrow{\mathrm{f}}$) that drives (Bretherton and Battisti 2000) and confounds the SST-forced signal $[\mathrm{P}\leftarrow \mathrm{F}\to \mathrm{SST}\to \mathrm{P}$; see Pearl et al. (2016) for notation] or coincides with it by chance.

We will not be able to resolve all of these uncertainties, but if coupled simulations or the new atmospheric simulations from CMIP6 can explain either precipitation or SST variability in observations, then this exercise should simultaneously shed light on the drivers of observed variability (where the forced response and simulated internal variability jointly explain the observations) and the realms of common shortcomings of CMIP models (where simulations fail to explain observations). We continue to use the MMM to understand the forced response in both observations and simulations. While model improvement efforts also benefit from model-specific analysis, we believe it is most urgent to identify and address model biases that are common across Model Intercomparison Projects because they prevent the ensemble from giving accurate mean and uncertainty estimates in future projections.

To examine the path components in coupled simulations, we need a parsimonious characterization of the relationship between SST and Sahel precipitation. The scientific literature has linked Sahelian precipitation to many ocean basins, including the equatorial Pacific Ocean, the Indian Ocean, the North and South Atlantic Oceans, and the Mediterranean Sea (Rodríguez-Fonseca et al. 2015). Observed Mediterranean SST correlates with observed Sahel precipitation mainly at high frequencies (not shown), which are not the focus of this study. Giannini et al. (2013) summarize the influence of the other relevant ocean basins in a single index, defined as the difference between average SST in the North Atlantic (NA) and in the Global Tropics (GT), and termed the North Atlantic Relative Index (NARI). Warming of NA is argued to increase the moisture supply to the Sahel, destabilizing the column from the bottom up (Giannini and Kaplan 2019), while warming of GT is expected to stabilize the column by causing upper tropospheric warming throughout the tropics (Chou and Neelin 2004; Giannini 2010). Thus, an increase in NARI is expected to wet the Sahel while a decrease is associated with drying. Giannini and Kaplan (2019, hereafter GK19) identify NARI as the dominant SST indicator of twentieth century Sahel rainfall in observations and CMIP5 simulations. Others have preferred to summarize the teleconnected SST as an Interhemispheric Temperature Difference, linking Sahel rainfall to energetically-driven shifts in the Intertropical Convergence Zone (Donohoe et al. 2013; Kang et al. 2009; Kang et al. 2008; Knight et al. 2006; Schneider et al. 2014). The two indices are sufficiently correlated at the low frequencies of interest here (r = 0.89 in observations, 0.79 in CMIP5, and 0.98 in CMIP6 for periods of > 20 years; see Fig. 4 and relevant discussion for motivation of this choice) that it is difficult to separate their potential effects on Sahel precipitation. We prefer NARI because the mechanisms associated with it are predictive rather than diagnostic (but see Sect. 5 for a discussion of the choice). Here, we choose to use NARI together with the assumption of linearity to approximate the full slow response as the product of the NARI response to external forcing and the strength of the NARI-Sahel teleconnection.

This paper is organized as follows: Sect. 2 provides details on the simulations and observational data used in this analysis while Sect. 3 discusses the methods. In Sect. 4.1, we update H20’s analysis to CMIP6, examining the total response to forcing (all paths from F to P) and to internal variability (all paths from IV to P). We then evaluate the performance of the CMIP6 AMIP simulations, decomposing them into the path components from the bottom half of Fig. 1$(\overrightarrow{\mathrm{t}}$, $\overrightarrow{\mathrm{f}}$, and $\overrightarrow{\mathrm{a}}$) in Sect. 4.2, and focusing on the NARI teleconnection in Sect. 4.3. Section 4.4 decomposes coupled simulations of NARI into the path components from the top half of Fig. 1 ($\overrightarrow{\mathrm{s}}$ and $\overrightarrow{\mathrm{o}}$), while Sect. 4.5 evaluates the consistency of the NARI teleconnection established in Sect. 4.3 with coupled simulations. Finally, in Sect. 4.6, we use simulated NARI and the simulated NARI teleconnection to decompose the total response of Sahel precipitation to external forcing in coupled simulations (examined in Sect. 4.1) into NARI-mediated and residual components. We discuss whether the residual is consistent with a fast response in Sect. 5 before concluding in Sect. 6. Table 1 contains descriptions of all acronyms we use throughout the paper.

Table 1 Definition of all acronyms used in this paper

2 Data

We examine twentieth century Coupled Model Intercomparison Project simulations from CMIP5 (Taylor et al. 2012) and CMIP6 (Eyring et al. 2016), including “historical” simulations forced with all sources of external radiative forcing (ALL) and “pre-Industrial control” (piC) simulations in which all external forcing agents are held constant at pre-Industrial levels. We additionally examine “Detection and Attribution” simulations (Gillett et al. 2016) forced with AA alone, natural forcing alone (NAT, which includes volcanic aerosols as well as solar and orbital forcings), and GHG alone. Finally, we also examine CMIP6 amip-piForcing (amip-piF) simulations (Webb et al. 2017), in which atmospheric models are forced solely with observed SST, and CMIP6 amip-hist simulations (Zhou et al. 2016), which are forced with observed SST and historical ALL radiative forcing. Our calculations begin in 1901 and extend to the end of the simulated period: 2003 for CMIP5 and 2014 for CMIP6.

In H20, we used all models available through the International Research Institute (IRI) and Lamont-Doherty Earth Observatory (LDEO) Climate Data Library for each forcing subset. Here, in order to provide a more stringent comparison of the effects of different forcing agents, we exclude models from the coupled ensemble if no AA, GHG, or ALL simulations for that model (or a related model from the same institution) were available on the IRI/LDEO Climate Data Library (for CMIP5) or on Pangeo’s CMIP6 Google Cloud Collection (for CMIP6) as of May 4, 2022. For the AMIP ensemble, all existing CMIP6 amip-piForcing simulations were downloaded from the Earth System Grid Federation website, and models were excluded if there was not at least one available amip-piForcing simulation or if there was no amip-hist simulation available on Pangeo’s CMIP6 Google Cloud Collection. Tables S1–S3 enumerate the simulations used in this analysis.

Precipitation observations are from the Global Precipitation Climatology Center (GPCC, Becker et al. 2013) version2018, and SST observations are from the National Oceanic and Atmospheric Administration’s (NOAA) Extended Reconstructed Sea Surface Temperature, Version 5 (ERSSTv5, Huang et al. 2017).

We analyze precipitation over the Sahel (12°–18° N and 20° W–40° E), and the SST indices of GK19: the North Atlantic (NA, 10°–40° N and 75°–15° W), the Global Tropics (GT, ocean surface in the latitude band 20° S–20° N), and the North Atlantic Relative index (NARI, the difference between NA and GT). All indices are spatially- and seasonally-averaged for July–September.

3 Methods

In defining the causal diagram in Fig. 1, we have explicitly assumed that external forcing does not affect internal variability. This may not be completely justified (e.g. Ham 2017), but is standard practice in model-based attribution methods that go beyond simple comparison. Such methods typically further assume (implicitly or explicitly) that observations and simulations are the sum of externally forced climate signals and independent internal climate variability. This allows the researcher to define the simulated response to forcing and internal variability using an ensemble of simulations with differing initial conditions (Hegerl and Zwiers 2011). Our formulation additionally assumes that precipitation variability does not affect simultaneous or following atmospheric or oceanic internal or forced variability—a simplification that precludes the possibility of vegetation feedbacks. While these might be relevant for the real world, we assume they are of secondary importance in the CMIP ensembles analyzed here, which do not include dynamic vegetation.

We define the response of a climate variable to a set of radiative forcing agents as the multi-model mean (MMM) of that variable over a set of historical simulations which prescribe that forcing agent. The MMM filters out intermodel differences and internal variability (which is independent across simulations), leaving an ensemble consensus response to forcing (which is dependent on the common radiative forcing applied to every model). We calculate the MMM as a 3-tiered weighted average over (1) individual simulations (runs) from each model, (2) models from each research institution, forming the Institution Mean (IM), and (3) institutions in that ensemble. Details of the weighting are provided in H20; the results are robust to differences in weighting. Time series are not detrended, and anomalies are calculated relative to the period 1901–1920 unless otherwise noted.

To evaluate the performance of the simulations relative to observations, we compute correlations (r), which capture similarity in frequency and phase, and root mean squared errors standardized by the standard deviation of observations (sRMSE), which measure yearly differences in magnitude between the simulated MMM and observations. The MMM time series are usually smoothed with a 20-year lowpass filter before calculating these statistics, and this is notated (•)_LF. We chose to divide high- and low-frequencies at a period of 20 years because that is the border between low- and high-power variance in observations (see Fig. 4). An sRMSE of 0 represents a perfect match between the simulated MMM and observations, and 1 would result from comparing the observations with a constant time series.

To gauge uncertainty in the smoothed MMM estimates of the forced signals and associated metrics, we resample the institution means (output of tier two) with replacement to calculate a set of perturbed MMMs (details in H20), yielding probability distribution functions (PDF) of the MMMs and of the values of each metric. Due to the finite number of simulations, these PDFs underestimate the true magnitude of the uncertainty. We evaluate significance by applying a randomized bootstrapping technique, which increases the effective sample size, to the smoothed piC simulations with one significant improvement over H20: instead of using just one subset of each piC simulation at a random offset to calculate the model means (tier 1 of the MMM) in each bootstrapping iteration, we take enough subsets to match the number of that model’s historical runs. Done this way, the confidence intervals calculated using piC simulations accurately represent noise in the forced MMMs. PiC PDFs from the same ensemble associated with different experiments differ slightly because a different number of simulations are available for different subsets of forcing agents (see Table S2).

We perform a residual consistency test, which compares the power spectra (PS) of individual simulations (not smoothed) to that of observations, with one significant modification over H20: we calculate the PS using the multi-taper method. Confidence intervals for the PS for observations and MMMs are given by the multi-taper method, without accounting for the uncertainty in the MMMs themselves. Mean PS by model are pictured with colors according to climatological rainfall bias given by those simulations. The multi-model mean of these PS is calculated using the three tiers from the definition of the MMM, but without weights, since spectral power is not attenuated when averaging PS. The power spectrum of observed Sahel rainfall is used to justify the choice of 20 years for the low-pass filter.

4 Results

4.1 Changes in CMIP6: total precipitation response to forcing and internal variability

In this section, we compare observed Sahelian precipitation to simulated forced and internal precipitation variability.

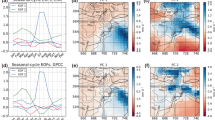
We begin by examining forced variability. The multi-model mean (MMM) over coupled simulations filters out atmospheric and oceanic internal variability ($\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{o}}$), leaving the fast and slow precipitation responses to external radiative forcing ($\overrightarrow{\mathrm{f}}$ and $\mathrm{F}\to \mathrm{SST}\to \mathrm{P}$; see methods for a discussion of the MMM). Figure 2 compares observed Sahelian precipitation anomalies to the simulated response to four sets of forcing agents (colors) in CMIP5 (dotted curves) and CMIP6 (solid curves). To highlight the primarily low-frequency simulated precipitation response to slowly-varying anthropogenic emissions, the anthropogenic aerosols (Fig. 2b, “AA,” magenta) and greenhouse gases (Fig. 2d, “GHG,” green) MMMs are smoothed with a 20-year lowpass filter and contrasted with smoothed observations (black). Natural forcing (Fig. 2c, “NAT,” brown and red), on the other hand, is dominated by sporadic and non-periodic short-lived volcanic episodes, some of which are highlighted on the x ordinates. Spectral decomposition of any kind assumes that all components of the time series are periodic, so the simulated and observed responses to volcanic eruptions will necessarily be split between the apparent “high-frequency” and “low-frequency” components. Because the episodes are short-lived, we find it visually more helpful to compare the NAT MMMs to high frequency observed precipitation variability (grey), calculated by subtracting the low-pass filtered time series from the full time series. ALL simulations with all three forcing agents (Fig. 2a, blue) include both episodic and low-frequency forced variability, and so their MMMs are visually compared to the full observed precipitation variability (light grey) in addition to the smoothed version. The figure also presents the bootstrapping 95% confidence intervals of the forced MMMs (blue, magenta, red/brown, and green shaded areas) and of MMMs over randomly-shifted CMIP5 and CMIP6 preindustrial control (piC) simulations (dotted and solid black lines, respectively). These dotted and dashed lines represent the magnitude of noise deriving from coincident internal variability in the MMMs; differences between panels arise from varying numbers of simulations for the different forcing subsets (see Methods and Table S2) and from smoothing in some panels.

Fig. 2

Observed high (grey) and low-frequency (black) Sahelian precipitation anomalies and MMM simulated precipitation anomalies (colored) from CMIP5 (dotted bold curves) and CMIP6 (solid bold curves) forced with ALL (a, blue), AA (b, magenta), NAT (c, brown/red), and GHG (d, green). The colored shaded areas surrounding the MMMs denote the bootstrapping confidence intervals, and the horizontal black lines mark the confidence intervals of randomized bootstrapped MMMs from CMIP5 (dotted) and CMIP6 (solid) piC simulations, representing the magnitude of noise in the MMMs. For AA (b) and GHG (d), which cause low-frequency precipitation variability, simulations are smoothed over 20 years before taking the MMM and are visually compared to smoothed observations. Because volcanic forcing in NAT (c) causes short-lived episodic precipitation variability, we present observed high-frequency precipitation variability in grey. We also make note of hemispherically asymmetric volcanic forcing from Haywood et al. 2013 on the x ordinates, where a negative sign denotes an eruption that cooled the northern hemisphere more than the southern hemisphere while a positive sign denotes the opposite, aligning with the sign of the expected Sahel precipitation response to the eruption. The ALL MMM (a) includes both episodic and low-frequency forced variability, and so we present the full observed precipitation variability (light grey) in addition to the smoothed version (black). This panel additionally shows the sum of the smoothed AA and GHG MMMs for CMIP5 (auburn dotted-dashed curve) and CMIP6 (amber dashed curve). The label shows the standardized root mean squared error of the CMIP6 MMM with observations at low-frequency (sRMSE_LF)

Though we sometimes visually present “high-frequency” variability to clarify the impact of volcanic eruptions on total as well as apparent “low-frequency” variability, only low-frequency (LF) correlation and sRMSE statistics are presented. This means that the statistic was calculated after smoothing the MMM and observations, and the confidence interval and significance level are calculated by repeating the statistic on the smoothed bootstrapped MMMs of forced and piC simulations, respectively. Significance in the context of this paper means that the performance of the forced response is separable from unforced noise in the performance statistic.

The CMIP6 MMM is less successful than CMIP5 at producing a forced dry interval in the second half of the century that compares to the observed drought in the 1970s and 80s (Fig. 2a). To understand why, we examine the individual forcing experiments. In the AA experiments (Fig. 2b), CMIP6 looks similar to CMIP5—precipitation declines in the mid-century and then recovers in response to clean air initiatives, preceding the timing of observed variability by about 10 years—but the drought is not quite as strong. There are some differences in the NAT experiments between CMIP5 and CMIP6 (Fig. 2c), but the largest MMM variations in both ensembles are interannual episodes that are clearly associated with volcanic eruptions, most notably following El Chichón in 1982. In the GHG experiments (Fig. 2d), CMIP6 shows anomalous wetting after 1970 that wasn’t present in CMIP5.

The changes in the single forcing experiments are reflected in the ALL MMM (Fig. 2a): while CMIP5 reaches peak drought in 1982—close to the observed precipitation minimum—CMIP6 dries very little and only until 1970, after which it displays an anomalously wetter climate than CMIP5 through the end of the century. But while the precipitation responses to different forcing agents appear to add linearly in CMIP5 (compare the auburn dotted-dashed curve to the blue dotted curve), the late century wetting in CMIP6 is larger than the sum of GHG and AA wetting (amber dashed curve; including NAT does not help). This effect is robust to differences in model availability for the different sets of forcing agents. Thus, in the ALL MMM, CMIP6 displays slightly less drying from AA compared to CMIP5, more wetting from GHG, and additional wetting after 1990 from a non-linear interaction between forcings.

As a result of these changes, the response to forcing in CMIP6 is a poor match to observations. At low frequencies, the correlation between the CMIP6 ALL MMM and observations is statistically indistinguishable from 0, and, while the sRMSE_LF between observations and the ALL MMM in CMIP5 ($0.88\pm 0.04)$ is significantly better than a constant prediction (1) or noise in the MMM, the sRMSEs for all CMIP6 MMMs are equivalent to or worse than noise ($\ge$ 0.96, see panel titles). The poor correlation for CMIP6 makes it clear that amplifying the simulated precipitation response to forcing will not help explain observed precipitation.

H20 showed that the CMIP5 ALL MMM (dotted blue curve) better reproduces observed Sahelian precipitation than individual ALL institution means (IMs). This is not true for CMIP6, whose MMM performance is a closer match to the median of the Institution Mean (IM) performances (not pictured). Though it does not perform better than the IMs, the MMM seems an accurate representation of the behavior of the individual IMs and the ensemble as a whole. In Fig. 3, smoothed individual simulations are presented in grey, with 95% of the yearly precipitation anomalies falling within the dotted black curves. IMs are presented in cyan, and the institution that performs best in correlation and sRMSE (MRI) is presented in green. The smoothed MMM is presented in blue, and compared to smoothed observations (obs), in black. The major characteristics of the MMM generally apply to the IMs: none of the IMs capture the observed pluvial, all of the IMs show wetting at the end of the century despite almost none producing any drought at all, and those IMs that do produce a late-century rainfall minimum reach minimum precipitation earlier than observations. MRI appears to outperform the other IMs in part because the drought is later than the others (but still earlier than observed), and also in part because the difference in magnitude between the late-century drying and wetting is smaller than the other IMs. But its performance statistics are not distinct from the performance distributions over all IMs in CMIP6 (not pictured), and it still differs strongly from observations, with no simulated pluvial and with a drought and a recovery that are weaker than observations and some (or most) of the other IMs. Thus, the discrepancy between the MMM and observations is much larger than the difference between models, and we continue to use the MMM to represent the response to forcing in CMIP6.

Fig. 3

Low-frequency Sahel precipitation anomalies from individual ALL simulations (“runs”, grey), Institution Means (IMs, cyan), and the MMM (blue) compared to observations (black). The best-performing IM (MRI) is highlighted in green. The 95% range of runs is outlined in dotted black curves

Atmospheric and oceanic internal variability ($\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{o}}$) are not anchored in time, so they do not survive in the MMM, and will generally not align between the observed time series and any given individual simulation; thus, we must compare observations to the ensemble of individual simulations. One way to target low-frequency internal variability would be to compare the observed time series to the 95% range of smoothed individual simulations, outlined in dotted black curves in Fig. 3. This span clearly does not encompass the observed pluvial between 1925 and 1965 nor the precipitation minimum in the 1980s. A more quantitative approach is presented in Fig. 4, which compares the power spectra (PS) of individual piC simulations (colored brown to turquoise by model climatological rainfall) to the observed PS (solid black) and the PS of the ALL-residual (observations minus the ALL MMM, dotted-dashed black) to determine whether simulated internal variability can explain observed precipitation variability on its own or in combination with the simulated response to forcing, respectively. In the observations and the residual, variance at periods longer than about 20 years (low-frequency) is roughly 5 times as large as the high-frequency variance. Low-frequency variability in the piC simulations is smaller than, and inconsistent with, either observed or residual variability. Moreover, it is similar in magnitude to simulated high frequency variability. If the observed low-frequency variability is internal, then this suggests that internal variability in simulated Sahel rainfall derives mostly from atmospheric ($\overrightarrow{\mathrm{a}}$), rather than oceanic ($\overrightarrow{\mathrm{o}}$), internal variability, or that simulated oceanic internal variability is too white (Eade et al. 2021). Because the shape of the spectrum is wrong, even a bias correction that inflates simulated internal variability would not bring simulations and observations into alignment.

Fig. 4

PS of observed Sahelian precipitation (solid black curve) and the residual of observations and the ALL MMM (dotted-dashed black curve) and associated 95% confidence intervals (grey shading), compared to the model-average PS of individual piC simulations. Mean piC PS are colored by the average yearly piC precipitation by model, where brown simulations are drier than observed, grey simulations match observed yearly precipitation, and turquoise simulations are wetter than observed

We must conclude that no linear combination of the simulated forced MMM (which is a poor match to observations at low frequencies) and simulated internal variability (which has insufficient low-frequency variance) in the coupled CMIP6 ensemble can explain observed low-frequency Sahel variability during the twentieth century. Thus, model deficiency in the CMIP ensemble cannot be limited to the simulation of climate feedbacks which amplify—but do not otherwise change—the simulated response to forcing: the CMIP6 ensemble displays a fundamental inability to simulate the evolution of the observed Sahelian precipitation response to forcing, the magnitude of observed low-frequency internal variability, or both. To identify the proximate cause of this failure, in the next three sections we examine each causal path component identified in Fig. 1.

4.2 AMIP simulations: the response to SST, atmospheric internal variability, and the fast response to forcing ( $\overrightarrow{t}$ , $\overrightarrow{a}$ , and $\overrightarrow{f}$ )

To isolate the effect of SST on the Sahel ($\overrightarrow{\mathrm{t}}$), we examine precipitation in the CMIP6 amip-piForcing simulations, which force atmosphere-only models with the observed SST history (containing both internal, $\overrightarrow{\mathrm{o}}$, and forced, $\overrightarrow{\mathrm{s}}$, oceanic variability) and constant preindustrial external radiative forcing (no $\overrightarrow{\mathrm{f}}$). The MMM of simulated Sahel precipitation filters out atmospheric internal variability ($\overrightarrow{\mathrm{a}}$), leaving the precipitation response to the entire observed SST field (although the reliability of the prescribed SST is still investigated; see Chan and Huybers 2021; Chan et al. 2019). At all frequencies (Fig. 5a), the amip-piF MMM (orange) is a much better match to observations (black) than the coupled MMMs are. Though the amip-piF MMM still doesn’t accurately capture many observed interannual episodes (notably including the precipitation minimum in 1984 and the local minimum in 1972), it captures much of the magnitude of observed low-frequency variability, even including wetting between the 1920s and the early 1960s, which is missing from the coupled MMM. A smoothed low-frequency comparison can be seen in Fig. 5d. When smoothed, the amip-piF MMM achieves very high correlation (r_LF = 0.94, CI = [0.90, 0.95]) and low sRMSE_LF (0.40, CI = [0.37, 0.52]) with observations. The main source of low-frequency sRMSE (which would ideally be 0) appears to be due to the influence of the dry episodes of 1972 and 1984 on the smoothed observed time series in the 70s and 80s.

Fig. 5

Sahelian precipitation anomalies in observations (black) and simulations (colored) from CMIP6 atmospheric models forced with observed historical SST alone (a, amip-piF, orange) and with observed historical SST and all historical external forcing agents (b, amip-hist, dark green). The shaded areas denote the bootstrapping confidence intervals about the simulated MMMs. Panel a additionally displays observed NARI anomalies (light blue, right ordinates). The right ordinates for panel a are scaled by the inverse of the simulated amip-piF teleconnection strength (see Sect. 4.3) so that, when read on the left ordinates, NARI represents its predicted impact on precipitation. Panel c compares observed precipitation at all frequencies (grey) and at high frequencies (black) to the mean implied simulated fast component in AMIP simulations (amip-hist minus amip-piF, purple). As in Fig. 2, panel c denotes hemispherically asymmetric volcanic eruptions, where the pictured sign denotes the sign of the expected Sahelian precipitation response to the eruption. Panel titles show the correlation (r_LF) and sRMSE_LF of simulated MMMs with observations at low frequencies. Panel d shows the low-pass filtered versions of panels a–c

Could the difference between the MMM and observations be explained by simulated random atmospheric internal variability? Fig. 6a compares the PS of observations (black) to that of the amip-piF MMM (dashed orange) and to the mean over the individual-simulation PS (solid orange). The 95% confidence intervals for the PS of the observations and of the amip-piF MMM are displayed in grey and orange shading. The PS of the amip-piF MMM contains only SST-forced variability ($\overrightarrow{\mathrm{t}}$), while the mean over the individual simulation PS contains atmospheric internal variability in addition ($\overrightarrow{\mathrm{a}}$). Atmospheric white noise gives the mean of PS slightly more power at all frequencies, and thus it falls within the grey shaded area and is not statistically distinguishable from the observed PS (black). Unlike previous generations of AMIP experiments (e.g. Scaife et al. 2009), when combined with atmospheric internal variability, global SST causes Sahel precipitation variability consistent with the full magnitude of observed variability at all frequencies. This substantial low-frequency power can only be achieved when atmospheric internal variability aligns with the high-performing MMM, and thus would place observed variability within the range of individual simulations. This suggests that CMIP6 atmospheric models successfully capture observed teleconnections to SST that are important at low frequencies.

Fig. 6

PS of observed Sahelian precipitation (bold black) and associated 95% confidence interval (grey shading) compared to the PS of amip-piF simulations (a) and amip-hist simulations (b). As in Fig. 5, mean PS by model are colored by average yearly precipitation, where brown is drier than observed, grey is observed, and turquoise is wetter than observed. The mean of the model PS is displayed in bold orange for amip-piF (a) and in bold green for amip-hist (b, the MMM PS is below the observed PS in both cases). The bold dashed lines show the PS of the MMMs with associated 95% confidence intervals (colored shaded areas). The amip-piF MMM is repeated in (b) to facilitate comparison

Could the discrepancy be better explained by the atmospheric response to forcing? The “fast” atmospheric and land-mediated precipitation response to ALL in the CMIP6 AMIP ensemble ($\overrightarrow{\mathrm{f}}$) can be estimated by subtracting the MMM of amip-piF simulations (Fig. 5a, orange) from that of amip-hist simulations (Fig. 5b, green), the latter of which are forced with historical SST and historical external radiative forcing. This estimate (Fig. 5c, purple) gives us the natural direct effect (as opposed to the 'controlled direct effect'; Pearl 2022) of radiative forcing on Sahel precipitation given observed SST. (If the atmospheric responses to radiative forcing and SST do not add linearly, then the natural direct effect might not be independent of SST, and thus may be different in coupled models.)

Low frequency variability in the AMIP “fast” MMM (Fig. 5d, purple) is likely mostly due to anthropogenic emissions. It displays a small wet undulation centered at 1960 and a wetting trend after 1985. It does not perform well relative to observed low-frequency variability on its own (r = 0.01, sRMSE = 1.05), suggesting that it is not the dominant driver of observed variability. Additionally, it only hurts the performance of the amip-hist MMM (green) relative to amip-piF (orange) by keeping simulated precipitation too wet in recent decades—low-frequency correlation reduces from 0.94 (CI = [0.90, 0.95]) to 0.85 (CI = [0.66,0.96]), sRMSE is increased from 0.40 (CI = [0.37, 0.52]) to 0.55 (CI = [0.31,0.77]), and the spectral properties of the precipitation MMM are virtually unchanged (Fig. 6b, green)—suggesting that the AMIP “fast” MMM may be an inaccurate representation of the observed fast response to radiative forcing.

Short-lived episodic variability in the AMIP “fast” MMM (Fig. 5b) is likely to be associated with volcanic eruptions, noted on the x ordinates, obscured by noise from both sets of AMIP simulations. Though part of the observed response to these volcanic eruptions will exist in the “low-frequency” component, most of the low-frequency variability that dominates total observed precipitation variability (grey) is not volcanic and would inhibit comparison with the mostly-flat “fast” MMM. Instead, we compare the “fast” response to observed “high-frequency” precipitation variability (black), which will clarify the timing (though not the full magnitude) of observed episodes of precipitation variability that may be a response to volcanic eruptions. Indeed, the total fast response appears to match the sign and timing of observed episodes near the marked eruptions, notably including the observed precipitation minimum in 1984. This suggests that the actual observed precipitation minimum in 1984—which is not well-captured by the amip-piF MMM (Fig. 5a)—is at least partially a fast response to the eruption of El Chichón in 1982. The “low-frequency” component of the fast response to the eruption of El Chichón might have helped lessen the gap between the amip-piF low-frequency MMM (Fig. 5d, orange) and observations (black) around 1980, but the benefit of this fast volcanic drying is overwhelmed in the fast (purple) and amip-hist (green) MMMs by the unrealistic anthropogenic fast wetting trend.

The high performance of the AMIP MMMs suggests that the principal deficiency in reproducing observed low-frequency Sahelian precipitation variability in coupled models stems from a failure to simulate the observed combination of forced and internal variability in SST or from corruption of the simulated teleconnections in coupled models (due to e.g., variations in model basic state and patterns of SST variability). The reduced performance of the amip-hist MMM relative to the amip-piF MMM at low frequencies suggests that a secondary deficiency might arise from an overzealous fast wetting response to anthropogenic emissions.

4.3 The NARI teleconnection: AMIP simulations and observations ( $\overrightarrow{t}$ )

We next examine Sahel teleconnections to SST in more depth. Observed NARI is presented in Fig. 5a in light blue on the right ordinates. NARI correlates reasonably with SST-forced Sahelian precipitation at all frequencies in the amip-piF MMM (orange, left ordinates; $\mathrm{r }= 0.60,\mathrm{ CI}=[\mathrm{0.42,0.62}]$), but this still leaves 64% of total variance unexplained, suggesting influences from SST variations elsewhere or non-linear or non-stationary effects (Losada et al. 2012). A low-frequency comparison of NARI with simulated precipitation can be seen in Fig. 5d (r_LF = 0.72$,\mathrm{ CI}=[\mathrm{0.54,0.81}]$). It is clear that NARI matches the timing and sign of observed (black) and simulated (orange and green) low-frequency Sahel precipitation variability, but no linear teleconnection with NARI can explain the full magnitude of the simulated drought (orange), because NARI in the 1980s is in the same range as in the beginning of the century.

Let’s assume that the NARI teleconnection is linear at all frequencies (as claimed by GK19) and unconfounded by the influence of SST changes in other ocean basins (correlating NARI and amip-piF MMM precipitation with globally-varying MMM SST, not shown, suggests that candidates for confounders are limited to ocean basins north of the area covered by NARI or the Interhemispheric Temperature Difference; we will revisit this assumption in the Discussion). Then we can measure the strength of the NARI teleconnection by the regression coefficient of the amip-piF precipitation MMM, which contains only SST-forced variability, on NARI. This calculation yields a regression slope of $0.87\pm 0.26\frac{\mathrm{mm}}{\mathrm{day}*^\circ \mathrm{C}}$. This value is affected by both high- and low-frequency variability, which is appropriate if the teleconnection is, indeed, linear. The left ordinates in Fig. 5a and d are scaled relative to the right ordinates by this teleconnection strength so that, when read on the left ordinates, the light blue curve represents the expected precipitation response to NARI. This view highlights how NARI captures the timing of simulated low-frequency variability, even though it fails to explain the full magnitude of simulated dry anomalies after 1975. In the rest of this paper, we use the NARI teleconnection as the preferred linear representative of the simulated influence of SST on Sahel precipitation in the twentieth century.

The teleconnection strength that we calculated from the amip-piF MMM is not directly comparable to observations, because the latter includes the fast precipitation response to forcing, which can in theory confound estimates of the teleconnection. A more direct comparison can be drawn between the apparent teleconnection strength in the amip-hist MMM ($0.93\pm 0.41$) and in observations (1.04). The consistency lends credence to our previous suggestion that simulated SST teleconnections to Sahel rainfall appear to have the appropriate strength in CMIP6, at least in the AMIP MMM.

4.4 Forced and internal SST variability in coupled simulations ( $\overrightarrow{s}$ and $\overrightarrow{o}$ )

We now examine simulation of forced ($\overrightarrow{\mathrm{s}}$) and internal ($\overrightarrow{\mathrm{o}}$) SST variability in the coupled ensembles. Figure 7 compares observations (black and grey) to the simulated coupled SST response to forcing ($\overrightarrow{\mathrm{s}}$)—represented by MMM anomalies (colors)—for NARI (right column) and its constituent ocean basins: the North Atlantic (NA, left column) and the Global Tropics (GT, middle column). The horizontal dotted and solid black lines show the bootstrapping 95% confidence intervals of the piC simulations for statistical significance for CMIP5 and CMIP6, respectively, while the colored shaded areas denote uncertainty in the CMIP5 and CMIP6 MMMs. As above, CMIP5 MMM anomalies are presented in dotted curves and CMIP6 in solid curves, color-coded according to their forcing. We observed that the simulated North Atlantic and tropical SST responses to external forcing are quite similar in CMIP5 and CMIP6.

Fig. 7

Observed high- (grey) and low-frequency (black) SST anomalies (°C relative to 1901–1920) and simulated SST anomalies from CMIP5 (dotted curves) and CMIP6 (solid curves) for the North Atlantic (NA, left column), the Global Tropics (GT, middle column), and the North Atlantic Relative Index (NARI, right column) when forced with ALL (blue, top row), AA (magenta, second row), NAT (brown/red, third row), and GHG (green, bottom row). As in Fig. 2, the shaded areas mark the bootstrapping confidence intervals, and the horizontal black lines mark the confidence intervals of randomized bootstrapped MMMs from CMIP5 (dotted) and CMIP6 (solid) piC simulations, representing the magnitude of noise in the MMMs. AA (second row) and GHG (last row) simulations are smoothed over 20 years and compared to smoothed observations (black) or a smoothed residual (orange) between observed SST (black) and simulated GHG-forced SST (green, bottom row) in that basin. NAT simulations are compared to high-frequency observed variability and are presented relative to the 1920–1960 mean, between volcanic eruptions. The y labels show the number of institutions that were used for each subset of forcing agents in CMIP6 (N, see Table S2), and for all panels, the subplot titles display the correlation (r_LF) and sRMSE_LF between the smoothed MMM and smoothed observations (or GHG residual) for CMIP6. Panel a additionally displays the sum of simulated NA forced with AA and GT (burgundy dashed curve)

CMIP5 and CMIP6 historical MMMs are unable to capture observed NARI (Fig. 7c, grey), which shows strong multi-decadal variability (black) throughout the century. In the ALL MMM (top row, blue), the temporal evolution of NARI (Fig. 7c) matches the observations at low frequencies with some skill, and significantly better than noise in the MMM (r_LF = 0.46, CI = [0.39, 0.51]; sRMSE_LF = 0.89 $\pm 0.03$ for CMIP6), but fails to capture the observed multi-decadal NARI warm period between 1925 and 1970. Moreover, its NA (Fig. 7a) and GT (Fig. 7b) components are a poor match to the observed marked multi-decadal variability in NA and the roughly linear warming trend in GT. For NA, the match between observations and the ALL-forced response is better in the later part of the record, but worse in the first half. During the period prior to 1960, according to the MMMs from both CMIP ensembles, GHG warming (Fig. 7j, green) masks AA cooling (Fig. 7d, magenta) to produce a roughly constant temperature in the ALL MMM (Fig. 7a, blue). The simulated cold episode in 1964 is due to the eruption of Agung in 1963 (Fig. 7g, brown and red), and it is only after the mid 1960s that increased GHG warming overtakes stagnating AA cooling to produce pronounced warming in fairly good accord with observations. The simulated response to external radiative forcing cannot explain much of the observed low-frequency variability in NA (Fig. 7a, black), especially the anomalously warm period between 1930 and 1960. In both CMIP5 and CMIP6 ALL simulations, the MMMs of GT (Fig. 7b, blue) are anomalously colder than observations between 1960 and 2000. This behavior is reminiscent of the inaccurate simulation of global SST in HadGEM2-ES, as pointed out by Zhang et al. (2013), who questioned the claims of Booth et al. (2012) that observed AMV was externally forced. This period coincides with a cluster of volcanic eruptions (Fig. 7h) that possibly affect GT too strongly in simulations. It is also the period when simulated AA cooling (Fig. 7e, magenta) is the strongest and not yet compensated by GHG warming (Fig. 7k, green). These correspondences lead us to question whether the match of simulated and observed NARI in this period happens due to compensating errors across different ocean basins and between the responses to different radiative forcing agents.

Examining all types of experiments (all rows), we see that coupled simulations cannot reproduce realistic low-frequency mean variability in the North Atlantic (left column) or in NARI (right column) no matter what forcing is applied. GHG (Fig. 7l) and NAT (Fig. 7i) both produce little variability in NARI. AA forcing (second row, magenta)—which had appeared to explain the timing of observed low-frequency Sahel precipitation variability in H20—does produce some low-frequency NARI variability (Fig. 7f), but it does not capture the warm period between 1925 and 1970 or correlate significantly with observations. Moreover, it derives from simulated NA and GT that do not match observations. Specifically, AA do not cause oscillatory variability in NA. Instead, they cause nearly monotonic cooling throughout the century in NA (Fig. 7d) and also in GT (Fig. 7e) with especially steep declines in SST between ~ 1940 and 1980. Though legislation to curb pollution reduced global AA loading in the northern hemisphere after 1970 (Hirasawa et al. 2020; Klimont et al. 2013; Smith et al. 2011), its effect in both CMIP ensembles is to halt the cooling of NA, not to cause actual warming. This is consistent with estimates of the hemispheric difference in total absorbed solar radiation in AA simulations in CMIP6, which level off—but do not decrease—after 1970 (Menary et al. 2020). We summarize the discrepancy between observations and simulations by noting that, while observed multidecadal variability in NARI derives from multidecadal variability in NA, simulated multidecadal variability in the AA-forced NARI MMM (Fig. 7f) comes from the fact that AA-forced cooling in NA precedes the cooling in GT.

In observations, the warming response to GHG dominates regional averages such as NA and GT, so the AA-forced MMMs are best compared to an observed “GHG-residual” (that is, the observations minus the GHG-forced MMM, presented in orange instead of black), which represents our best estimate of the sum of observed oceanic internal variability and the observed response to aerosols (the response to natural forcing is assumed to be small). These estimates (Fig. 7d and e, orange) differ greatly from the simulated response to AA, especially in the mid-century warm anomalies, which maximize as simulated AA (magenta) begin to cool NA and GT. Observational estimates may be too high between 1940 and 1945 (Chan and Huybers 2021), but while correcting this bias would address the warm period in GT and reduce the magnitude of the warm period in NA, it could not explain the magnitude or duration of the warm period in NA. Inaccuracies in the simulated response to GHG forcing—which is small in the first half of the century—are unlikely to be the cause of this discrepancy. If the observed Atlantic Multidecadal Variability is externally forced, then volcanic aerosols (Fig. 7g)—which cool NA during the reference period for our anomaly calculations—would have to play a much larger role in forcing observed NA variability than suggested by the CMIP ensembles.

Could internal SST variability ($\overrightarrow{\mathrm{o}}$) instead explain the difference between the simulated response to forcing and observations in these ocean basins? In Fig. 8, we present the mean PS of SST indices for piC simulations from each CMIP6 model (colder than observed models are in blue and warmer than observed models are in red). We compare these PS to the PS for observed SST (solid black), the GHG-residual (dotted-dashed black), and/or the ALL-residual (dotted black), omitting PS for time series with dramatic trends. Simulated internal variability in most of the CMIP6 models used in this study does not match residual or observed low-frequency variability in NA (Fig. 8a), GT (Fig. 8b), or NARI (Fig. 8c). In CMIP5, climatological NA and GT are colder and internal variability at all frequencies is larger than in CMIP6, but no model shows an increase in spectral power at low frequencies for any of these SST indices (not shown). There are, however, three CMIP6 models that produce low-frequency internal variability in NA consistent with observations—in order of decreasing power at 50 years: CNRM-ESM2-1 p1 (pink), IPSL-CM6A-LR p1 (blue), and CNRM-CM6-1 p1 (grey)—suggesting that observed variability may be internal. Certainly, either the simulated SST response to forcing, simulated oceanic internal variability, or both, are not well represented in the CMIP ensembles.

Fig. 8

PS of observed SST (bold solid black), observed SST minus the GHG MMM (dotted-dashed black), observed SST minus the ALL MMM (dotted black) and associated 95% confidence intervals (black shading) in NA (a), GT (b), and NARI (c), compared to the PS of piC simulations. Similar to Fig. 5, mean PS by model are colored by average SST, where blue is colder than observed, grey is observed, and red is warmer than observed

Though simulated MMM SST is inconsistent with observations, it may still contribute to the relatively high correlation of the CMIP5 AA MMM with observations. While the correlation of the AA NARI MMM with observations is not significant on its own, it is still positive (r_LF = 0.27, CI = [− 0.09, 0.55] for CMIP5), and it shares many of its shortcomings with simulated precipitation: neither capture the observed warm/wet period from the 1920s to the 1960s and both reach their minimum in temperature/rainfall about 10 years before the observed minimum. Though we have argued that SST is a more important driver of Sahel rainfall variability than the fast response to radiative forcing in observations and AMIP simulations, the fast response in coupled simulations may mask the differences between the NARI-mediated precipitation response to AA in CMIP5 and observed rainfall changes, giving the appearance of a partially right result, but for the wrong reasons. Additionally, because there are only minor differences in the ALL NARI MMM between CMIP5 and CMIP6 (Fig. 7c), the difference in mean simulated Sahel rainfall between CMIP5 and CMIP6 must derive from some combination of changes in the fast response to forcing, the nature of the NARI-Sahel teleconnection, and variability in other SST basins.

4.5 The NARI teleconnection in coupled simulations

Now that we have examined NARI in the coupled ensemble, we may investigate the ensemble's representation of the NARI teleconnection with Sahel precipitation. Though the estimate of the teleconnection strength from the amip-piF MMM is much more likely to be causal than estimates from coupled simulations that are confounded by external radiative forcing, we cannot automatically assume that it represents teleconnections in the coupled models. First, differences between observed and simulated mean state global SST (Richter and Tokinaga 2020; Wang et al. 2014) may affect the mechanism and strength of the atmospheric teleconnection. Second, while GK19 already showed NARI is dominant in CMIP5, changes in simulated global SST variability may mean that NARI is not the dominant SST driver of precipitation variability in CMIP6. Finally, changes in the atmospheric models themselves between CMIP5 and CMIP6 could cause differences in the teleconnection unrelated to SST.

Do the teleconnections in coupled simulations appear consistent with that in the amip-piF MMM? Calculating the teleconnection strength in coupled simulations is difficult: the relationship between SST and precipitation in historical simulations is confounded by radiative forcing, and SST variability in the (unforced) piC simulations is small and varies from simulation to simulation. Thus, there is no guarantee that NARI is the prominent driver of precipitation variability in the piC simulations. Furthermore, piC simulations must be treated individually, leaving the teleconnection obscured by atmospheric internal variability. The teleconnection strengths calculated from individual piC simulations are, therefore, generally smaller and less certain than the amip-piF teleconnection strength. Nevertheless, the amip-piF teleconnection strength does fall within the estimated range for CMIP5 ($0.5\pm 0.6\frac{\mathrm{mm}}{\mathrm{day}*^\circ \mathrm{C}}$) and CMIP6 ($0.3\frac{\mathrm{mm}}{\mathrm{day}*^\circ \mathrm{C}}, \mathrm{CI}=[-\mathrm{0.1,0.9}]$) piC simulations. (These estimates of the teleconnection strength are unrelated to model performance, not shown.) As a second test, we compare the confounded teleconnection strength from the amip-hist MMM ($0.9 \frac{\mathrm{mm}}{\mathrm{day}*^\circ \mathrm{C}}, \mathrm{CI}$ = [0.6,1.4]) to that of bootstrapped MMMs over the coupled ALL simulations in CMIP5 ($0.96\pm 0.56 \frac{\mathrm{mm}}{\mathrm{day}*^\circ \mathrm{C}}$) and CMIP6 ($1.5\pm 0.3 \frac{\mathrm{mm}}{\mathrm{day}*^\circ \mathrm{C}}$). The confounded teleconnection strength in the CMIP6 amip-hist MMM is consistent with that in CMIP5, but it is smaller than, and inconsistent with, that in CMIP6, falling outside the 95% confidence interval. This may be because NARI variability in the coupled ensemble is smaller relative to the magnitude of external radiative forcing than it is in the amip-hist ensemble. If this is the cause for the apparent inconsistency in confounded teleconnection strengths between the two ensembles, we may still confirm the NARI teleconnection strength indirectly in CMIP6 by showing that the fast response to forcing implied by the NARI teleconnection is consistent with the mean fast response from the amip-hist simulations.

4.6 Fast and slow responses to forcing in coupled simulations ($\overrightarrow{\mathrm{f}}$ and $\mathrm{F}\to \mathrm{SST}\to \mathrm{P}$)

Under the assumption that the dominant simulated path of SST influence on the Sahel is captured by a linear relationship with NARI, we estimate the slow response to forcing in coupled simulations as the simulated NARI MMM scaled by the teleconnection strength derived from amip-piF MMM ($0.87\frac{\mathrm{mm}}{\mathrm{day }^\circ \mathrm{C}}$, Sect. 4.3), so that a warm (cold) NARI predicts a wet (dry) Sahel. In Fig. 9, simulated NARI (as in Fig. 7, right column) is displayed on the left ordinates in light blue (CMIP6, left) and turquoise (CMIP5, right). On the right ordinates are the total simulated precipitation responses to forcing (as in Fig. 2), colored by forcing agents. The right ordinates are scaled by the teleconnection strength so that, when read on the right ordinates, simulated NARI represents the estimated slow component of the precipitation response to forcing.

Fig. 9

Simulated Sahel precipitation (right ordinates, same as Fig. 2) MMMs (bold solid and dotted curves) at various frequencies and associated 95% confidence intervals (shaded areas) in CMIP5 (right column) and CMIP6 (left column) when forced with ALL (blue, top row), AA (magenta, second row), NAT (brown/red, third row), and GHG (green, bottom row), compared to simulated NARI (left ordinates, thin light blue and turquoise curves, same as Fig. 7). The right ordinates are scaled such that a 1 °C change in NARI corresponds to a 0.87 mm/day change in precipitation, given by the teleconnection strength in the CMIP6 amip-piF MMM (see Sect. 4.3)

Simulated precipitation matches the estimated slow response in CMIP6 relatively well: The phase of simulated precipitation anomalies in the CMIP6 ALL (Fig. 9a), AA (Fig. 9b), and NAT (Fig. 9c) MMMs match the estimated NARI-driven slow responses throughout the century, and the magnitudes of the anomalies also match throughout the century in the NAT MMM (Fig. 9c) and until 1980 in the AA (Fig. 9b) and ALL (Fig. 9a) MMMs. But after 1980, the ALL (Fig. 9a), AA (Fig. 9b), and GHG (Fig. 9d) MMMs all experience increases in precipitation beyond our estimate of the slow response. In CMIP5, the timing of simulated precipitation anomalies still mostly matches anomalies in the estimated slow response, but the ALL (Fig. 9e) and AA (Fig. 9f) MMMs experience drying after 1950 that is larger than can be explained by our NARI-based estimated slow response to forcing. The discrepancies between the total and NARI-mediated responses, which we’ll denote P_nonNARI, account for most of the difference in simulated forced precipitation between CMIP5 and CMIP6.

Is P_nonNARI consistent with the mean simulated fast response in the AMIP simulations? Time series for these differences are displayed in Fig. 10 in a fashion similar to Fig. 2, and are compared to the fast response obtained as the difference between amip-hist and amip-piF simulations (purple, as in Fig. 5c). Mean P_nonNARI in the CMIP6 (solid curves) ALL ensemble (Fig. 10a, blue) is consistent with the sum of wetting from P_nonNARI in the AA (Fig. 10b) and GHG (Fig. 10d) MMMs. It doesn’t capture the simulated fast wetting in between 1950 and 1970, but does capture the fast wetting after 1980, and matches the AMIP fast response significantly better than noise (sRMSE_LF = 0.46, CI = [0.40, 0.77]). These consistencies give us confidence that P_nonNARI describes the mean fast response in CMIP6 coupled simulations with all subsets of radiative forcing agents, and that NARI is sufficient to summarize the effect of SST on Sahel rainfall in the MMM from the CMIP6 coupled ensemble.

Fig. 10

Compares the MMM fast Sahelian precipitation response to forcing in AMIP simulations (thin purple curve, as in Fig. 5c) to P_nonNARI MMMs (precipitation − 0.87*NARI; the difference between the colored and light blue curves in Fig. 9) in coupled CMIP5 (bold dotted curves) and CMIP6 (bold solid curves) simulations forced with ALL (a, blue), AA (b, magenta), NAT (c, brown/red), and GHG (d, green), displayed as in Fig. 2

P_nonNARI in CMIP5 (dotted curves), on the other hand, doesn’t resemble the mean fast response from CMIP6 AMIP simulations at all. In the ALL MMM (Fig. 10a, turquoise), P_nonNARI dries from the 1940s to the end of the record, and is composed of drying centered at 1970 from the AA MMM (Fig. 10b, magenta) and drying after 1980 from the GHG MMM (Fig. 10d, green). Whether P_nonNARI in CMIP5 is also consistent with a fast response to forcing in CMIP5 (which we cannot directly estimate) or is a response mediated by SST in ocean basins other than the Atlantic cannot be firmly established by this analysis, but we offer our perspective below.

5 Discussion: P_nonNARI in CMIP5 and CMIP6

The interpretation of the P_nonNARI response to GHG as a fast response is more consistent with theory in CMIP6 than in CMIP5, as it is generally accepted that the fast response of the Sahel to GHG is wetting (Biasutti 2013; Gaetani et al. 2017; Giannini 2010; Haarsma et al. 2005; Mutton et al. 2022). Though basic physical theory links increased (reduced) aerosol concentrations to decreasing (increasing) rainfall via fast surface cooling (warming) and increasing (decreasing) optical depth of the atmosphere (Allen and Ingram 2002; Rosenfeld et al. 2008), the observed and simulated fast responses are difficult to predict because reflective and absorbing aerosols may have different fast effects, and because the concentrations of aerosols vary greatly in space and time and are affected by circulation patterns which differ between models and observations (Hirasawa et al. 2022; Liu et al. 2018). One could propose storylines for the P_nonNARI responses to AA in CMIP5 and CMIP6, but these storylines cannot be confirmed without a thorough analysis of the ensemble in the style of (Hirasawa et al. 2022), who found evidence of late-century fast drying due to African black carbon emissions in the Community Atmosphere Model 5 – a phenomenon which does not appear to be prominent in the MMM for either CMIP ensemble. But even if the simulated P_nonNARI MMM does not successfully capture the fast response to forcing in the observed climate system, the good match between P_nonNARI in the coupled CMIP6 ensemble and the estimated mean fast response in amip-hist simulations increases our confidence that P_nonNARI in CMIP6 reflects a simulated fast response to forcing, that NARI is a sufficient linear representative of the effect of SST on Sahel rainfall in CMIP6, and that the strength of the teleconnection in the coupled MMM is the same as in the AMIP MMM.

The same cannot be said for CMIP5. We calculated the correlation of P_nonNARI with SST in CMIP5 and CMIP6 (not shown) and found it to be uniformly negative in CMIP5 (consistent with the result of GK19 for the twentieth century, but not the 21st) aside from the subpolar North Pacific and Atlantic basins (which are most strongly correlated with NARI at low frequencies), giving us confidence that P_nonNARI in CMIP5 is not an artifact of using the wrong strength for the NARI teleconnection. The same calculation is uniformly positive in CMIP6, reflecting the prominence of global warming in simulated SST and opposite trends in P_nonNARI. Uniform warming would not appear as part of NARI, and Sahel drying in response to uniform warming is strong in models that simulate a deeper ascent profile, but weak otherwise (Hill et al. 2017), so it is possible that newer parameterizations and higher resolution have changed the sensitivity to this forcing in the latest generation of models. Nevertheless, the inconsistency in the sign of this relationship means further investigation is needed to reach a conclusion.

Additionally, we correlated the difference between CMIP6 and CMIP5 in MMM SST with the corresponding difference in MMM Sahel rainfall. The pattern (emerging at low frequencies) is also reminiscent of the simulated global warming pattern, but now includes anomalies of the opposite sign in the subpolar North Atlantic – in the region where models simulate a so-called warming hole in response to GHG and AA (i.e. Baek et al. 2022). Martin et al. (2014) suggest that, unlike the North Atlantic south of 40°N, variability in the subpolar North Atlantic is not well-connected to Sahel precipitation variability, so the connection to P_nonNARI might be confounded by the fast effect of the imposed anthropogenic forcings or by its relationship to NA. Insignificant correlations between SST in this region and Sahel precipitation at all frequencies in the amip-piF MMM would support this view, at least when observed SST variability is involved. Nevertheless, it is intriguing that an index summarizing the warming hole pattern (the difference between the North Atlantic box 60°–15°W by 50°–65°N and the area 60°S–60°N) is well correlated at low frequencies not only with the difference in Sahel rainfall between CMIP5 and CMIP6 (r_LF = 0.71), but also with P_nonNARI in each ensemble (r_LF = 0.78 in CMIP5 and r_LF = 0.86 in CMIP6). Whether there is a causal connection between the strength of the warming hole in the coupled models and P_nonNARI could be tested by targeted simulations, and this is left for future work. In any case, the simulated forced warming hole pattern differs from observed in a manner similar to NARI: it does not capture the observed warm period in the first half of the century, and then cools too little and too early followed immediately by warming in the second half of the century (not shown); thus, our assessment that a deficient simulation of low-frequency SST variability is the primary reason for CMIP’s poor Sahel precipitation variability still stands.

6 Summary and conclusions

In this paper, we decompose Sahelian precipitation from atmospheric (“AMIP”) simulations into (1) teleconnections from sea surface temperature (SST), (2) atmospheric noise, and a (3) fast, atmospheric- and land-mediated response to forcing. We then calculate a linear regression coefficient between the North Atlantic Relative Index (NARI)—an index of the warming of the North Atlantic relative to the Global Tropics—and the AMIP Multi-Model-Mean (MMM) and employ it to decompose coupled simulations into (1) forced NARI variability, (2) internal NARI variability, and (3) forced precipitation variability not explained by a linear relationship with NARI (P_nonNARI). Treating NARI as a representative for Sahel teleconnections from global SST allows comparison of the components from AMIP and coupled simulations. We examine these components in order to determine which are responsible for differences in the simulation of Sahel rainfall between the 5^th and 6^th generations of the Coupled Model Intercomparison Project (CMIP) and which are to blame for the inconsistency of both ensembles with observed Sahel precipitation variability.

When forced with observed SST alone, mean precipitation from CMIP6 atmospheric simulations captures the evolution of observed low-frequency variability quite well (r_LF = 0.94, CI = [0.90, 0.95]; sRMSE_LF = 0.40, CI = [0.37, 0.52]), and—when combined with atmospheric white noise—these simulations are also able to explain the full spectral power of observed low-frequency variability. This is a welcome improvement from previous generations of climate models, and allows us to use the simulations to make claims about observed variability as well as the shortcomings of the simulations.

Including radiative forcing alongside observed SST in the AMIP simulations mostly acts to increase mean wetting in the second half of the century and notably worsens the MMM sRMSE (0.55, CI = [0.31, 0.77]), suggesting that the mean simulated fast response is incorrect while the observed fast component is small and plays a secondary role to SST-forced precipitation variability. Nevertheless, even with the inclusion of the fast response, atmospheric models forced by observed SST capture much of the observed Sahel rainfall variability. This leads us to conclude that observed precipitation variability is mostly a response to global SST, and that the failure of coupled simulations to explain observed low-frequency Sahel precipitation variability must be due mainly to an incorrect response to SST, either because of incorrect teleconnections or deficiencies in reproducing observed forced and internal SST variability.

Using the AMIP ensemble, we summarize simulated Sahel teleconnections from global SST as a linear relationship of $0.87\pm 0.26\frac{\mathrm{mm}}{\mathrm{day}*^\circ \mathrm{C}}$ with NARI (a relationship that explains about 48% of low-frequency, and 36% of the total, variance in the simulated precipitation response to observed global SST given by the AMIP MMM) and verify that this simulated teleconnection strength is consistent with observations. This estimate is consistent with the coupled CMIP ensembles, meaning that—to the extent that NARI is representative of simulated teleconnections in the AMIP and coupled simulations—the main deficiency of CMIP coupled simulations for explaining observed low-frequency precipitation variability is likely in explaining observed SST variability.

Indeed, simulated mean low-frequency NARI variability is different and much smaller than observed, with the latter mostly coming from low-frequency variability in North Atlantic SST (NA). In both CMIP5 and CMIP6, anthropogenic aerosols (AA) cause a cooling trend and GHG cause a warming trend, but no combination of forcing agents produces a decadal-scale oscillation in NA. The resulting NARI-mediated slow response to external radiative forcing is to dry the Sahel slightly in the 60s and to wet it immediately afterwards; this does not, in isolation, explain the timing or magnitude of the observed drought or recovery. Only three CMIP6 models (out of 25 CMIP5 and 30 CMIP6 models) are able to generate internal SST variability commensurate to the residual (the difference between total and radiatively forced) low-frequency variability. If we trust these three models, one possible interpretation is that observed SST variability is mostly an expression of internal climate variability that is poorly simulated in the other CMIP models. However, even these three models cannot explain observed precipitation variability; and it is not clear physically that we should trust them more than the other models. We must conclude that the CMIP coupled ensembles as a whole are inconsistent with observed low-frequency SST and precipitation variability, and that it is impossible to determine from these ensembles whether the latter is mainly the expression of a response to forcing, oceanic internal variability, or both.

How do we reconcile our results with those using coupled simulations to support claims that the observed Atlantic Multidecadal Variability (AMV) is externally forced (Bellomo et al. 2018; Booth et al. 2012; Hua et al. 2019; Murphy et al. 2017)? The discrepancy can be explained because these studies examine only one or two models (Booth et al. 2012) or subtract a linear trend from simulated NA before comparing to observations (Bellomo et al. 2018; Hua et al. 2019; Murphy et al. 2017), thus aliasing non-linear simulated global warming and inducing artificial low-frequency variability in the simulated AA-induced monotonic decreasing step function (Baek et al. 2022 demonstrated this effect in CESM1). Furthermore, our results for the CMIP5 and CMIP6 ensembles are consistent with the findings of Zhang et al. (2013) for the model used by Booth et al. (2012), showing that simulated multidecadal variability in the North Atlantic is often associated with unrealistic multidecadal variability in global (tropical) SST. This does not preclude a role for external forcing in observed AMV: observational evidence may still suggest an important role for volcanic aerosols (Birkel et al. 2018) that is poorly captured in simulations, and AA and GHG may still contribute some forced cooling and warming, respectively, to observed AMV in the second half of the century. But a prominent role for internal variability cannot yet be dismissed, as suggested by Yan et al. (2018), who—consistent with our analysis—find that most models do not capture observed AMOC variability. These results cast doubt on claims that AA caused observed AMV based on attribution studies employing CMIP ensembles.

With nearly identical forced NARI variability and similar teleconnection strengths, the difference in Sahel precipitation between CMIP5 and CMIP6 is likely due to P_nonNARI, which contains the fast response to forcing and slow responses mediated by other SST patterns. Because forced NARI variability in the coupled simulations is small relative to observations throughout the century, P_nonNARI has a larger relative effect on the evolution and performance of the MMMs from coupled simulations than on those from AMIP simulations. The CMIP6 MMMs underperform relative to CMIP5 because P_nonNARI includes substantial fast wetting responses to increasing GHG and decreasing AA that are comparable in magnitude to the NARI-related component and consistent with the detrimental fast response in that ensemble’s AMIP MMM. In contrast, P_nonNARI in CMIP5 is drying that may be a fast response to anthropogenic emissions or a slow response to global warming and forced changes in the subpolar North Atlantic.

P_nonNARI plays an important role in CMIP5 because it delays the drought from the NARI-mediated slow response to forcing and increases its strength, causing simulated precipitation to correlate well with observed precipitation even though simulated SST—which is the primary driver of observed precipitation variability—is incorrect. We conclude that CMIP5 MMM Sahel precipitation correlates with historical observations despite not reproducing the physical phenomena that were most important for the Sahel in the twentieth century. Thus, while both CMIP5 and CMIP6 suggest that historical AA emissions had a larger effect on observed Sahel precipitation variability than GHG, it is premature to conclude that AA were the dominant influence on observed variability based on attribution studies using CMIP (e.g. Hua et al. 2019; Polson et al. 2014; Undorf et al. 2018).

This work has shown that, while there has been progress in the simulation of the Sahel’s response to global SST, much remains uncertain in our understanding and simulation of the pathways of Sahel multi-decadal variability, especially in the characterization of Sahel teleconnections and the simulation of low-frequency variability in North Atlantic SST. Differing mechanisms can lead to similar time evolutions in observations and simulations; to avoid this pitfall, future work should focus on evaluating in more detail the hypothesized pathways of the Sahel response to anthropogenic emissions and oceanic internal variability in individual models as well as the CMIP ensembles in order to further categorize model performance and improve predictions of the future.