1 Introduction

The Indian Ocean Dipole (IOD) is a major aspect of climate variability that develops from coupled air–sea interactions in the tropical Indian Ocean. A positive IOD event brings about warm and cold sea surface temperature (SST) anomalies (SSTAs) in the tropical western and southeastern Indian Ocean, respectively, while a negative IOD event does the opposite (Saji et al. 1999; Webster et al. 1999). Such IOD events significantly influence variabilities in oceanic processes (Chen et al. 2015, 2016a, b; Liu et al. 2015), the Indian Ocean carbon cycle (Valsala et al. 2020), and climate over the Indian Ocean rim and remote countries by altering ocean–atmosphere circulations (Saji and Yamagata 2003; Cai et al. 2014; Xu et al. 2020; Zhang et al. 2021). Therefore, academic research on the triggering and development mechanisms of IOD is considered worthwhile.

Occurrences of IOD mostly result from the forcing of the El Niño–Southern Oscillation (ENSO) in the tropical Pacific Ocean (Fischer et al. 2005; Zhang et al. 2015; Fan et al. 2017; Stuecker et al. 2017), as well as local air–sea interaction in the tropical Indian Ocean (Saji et al. 1999; Webster et al. 1999; Rao and Behera 2005). Meanwhile, numerous studies have revealed triggering mechanisms independent of the ENSO. For instance, employing coupled simulation, Fischer et al. (2005) suggested that anomalous Hadley circulation over the eastern Indian Ocean and Maritime Continent during the boreal spring could trigger the IOD. According to Wang et al. (2016), a springtime rainfall deficit in Indonesia could stimulate a positive IOD through local surface wind response. The occurrence of an extreme positive IOD in 2019 has been associated with a record-breaking inter-hemispheric pressure gradient between Australia and the South China Sea after May (Lu and Ren 2020) and thermocline warming in the tropical southwestern Indian Ocean during March–May (Du et al. 2020). Other triggers also significantly contribute to the development of the IOD, such as a preceding subtropical IOD (Feng et al. 2014; Huang et al. 2021), subtropical high pressure in the Southern Hemisphere (Zhang et al. 2020), preceding December Laptev Sea Ice (Chen et al. 2021), and spring–summer north tropical Atlantic SSTAs (Zhang et al. 2022). Further, the Asian summer monsoon plays a crucial role in the triggering and development of IOD (Drbohlav et al. 2007; Krishnan and Swapna 2009). Summer monsoon circulation over the tropical Indian Ocean provides a favorable background condition for the development of the IOD (Annamalai et al. 2003; Xiang et al. 2011). Early onset of the Bay of Bengal summer monsoon triggers a positive IOD by inducing the equatorial easterly wind anomaly (Sun et al. 2015). The strong Northwest Pacific summer monsoon and South China Sea summer monsoon facilitate the growth of a positive IOD event (Kajikawa et al. 2003; Huang and Shukla 2007; Zhang et al. 2018, 2019). Recently, Jiang et al. (2022) have indicated the role of different South Asian summer monsoon anomalies in modulating the SSTA pattern during IOD development. Strong or weak South Asian summer monsoon conditions induce stronger SSTA amplitudes in the eastern and western poles of the IOD, respectively.

The influence of mid–high latitude atmospheric circulation over the Northern Hemisphere on the IOD is not well investigated and understood. However, several studies have indicated that anomalous mid–high latitude circulation remarkably influences the subtropical and tropical climate (Gong et al. 2011; Chen et al. 2014; Cui et al. 2015; Oshika et al. 2015; Yu et al. 2021). For example, the spring Arctic Oscillation (AO) strongly affects the subsequent East Asian summer monsoon and ENSO by modulating atmospheric circulation over the western North Pacific (WNP; Nakamura et al. 2006, 2007; Gong et al. 2011; Chen et al. 2014). Winter AO/North Atlantic Oscillation (NAO) affects the simultaneous tropical Indian Ocean precipitation, as well as the following summer SSTAs and monsoon circulation (Gong et al. 2014, 2017a, b). Similarly, the NAO crucially influences both the East Asian and the South Asian summer monsoon through a downstream Rossby wave propagation (Wu et al. 2009; Cui et al. 2015; Yu et al. 2021).

Considering the key role of the winter–spring AO/NAO on the subsequent ENSO and the Asian summer monsoon and the close linkage between the ENSO as well as the Asian summer monsoon and the IOD, it is reasonable to infer that the preceding winter–spring AO/NAO could influence the development of a subsequent IOD. The key question to be answered in our study is whether a preceding NAO could affect the following IOD. If yes, what are the possible physical mechanisms? What is the relative importance of ocean dynamic processes and atmospheric thermal forcing in the process of an NAO affecting the following IOD? To address these questions, we conducted preliminary statistical analysis and found a significant relationship between the March NAO and the subsequent summer and autumn IOD (Fig. 1a). However, the correlations between the NAO of other months in the boreal winter–spring and the IOD were insignificant (Fig. 1a). Therefore, the objective of this study was to investigate the influence of the March NAO on the development of the subsequent IOD.

Fig. 1
figure 1

a Correlation between the North Atlantic Oscillation (NAO) index and 3-month averaged Indian Ocean Dipole (IOD) index. Gray dashed and solid lines indicate the 95% and 99% confidence levels, respectively. b Standardized time series of the March NAO index (bars) and September–October–November (SON) averaged IOD index (orange line) for the period 1950–2020. Gray dashed lines represent ± 1 standard deviation

Full size image

In Sect. 2, we present the data, methodology, and model, and the relationship between the NAO and IOD is shown in Sect. 3. The possible mechanisms through which the March NAO influences the subsequent IOD are discussed in Sect. 4, and our investigation of the ocean mixed-layer heat budget is presented in Sect. 5. A summary of the study is presented in Sect. 6.

2 Data, methodology, and model

2.1 Data

We used the Extended Reconstructed Sea Surface Temperature V5, a global SST dataset from the US National Oceanic and Atmospheric Administration. The horizontal resolution of the dataset is 2° × 2° (Huang et al. 2017). Atmospheric circulation variables (e.g., wind fields and geopotential height), precipitation, mean surface, top heat flux, mean total precipitation, and evaporation rate were obtained from the European Center for Medium-Range Weather Forecasts (ECMWF) Reanalysis V5 dataset, with 1° × 1° horizontal resolution (Hersbach et al. 2020). These datasets contain the monthly mean values for the period 1950–2020. The monthly sea surface height (SSH) dataset (1° × 1°; 1958–2017) was acquired from ECMWF Ocean Reanalysis System 4 (Balmaseda et al. 2013).

To calculate the mixed-layer heat budget equation, we obtained the pentad potential temperature, and horizontal and vertical velocities from the National Centers for Environmental Prediction (NCEP) Global Ocean Data Assimilation System (GODAS) at 40 levels (Behringer and Xue. 2004). The daily surface heat flux dataset was obtained from newly developed Trop-Flux products (Kumar et al. 2012). Following Mao and Wang (2018), all GODAS variables were interpolated to 1° × 1° horizontal resolution and the Trop-Flux products were converted into pentad datasets. After removing linear trends, a 2–9-year bandpass Lanczos filter was used to extract the interannual signal (Yu et al. 2021).

2.2 Methodology

We employed several indexes in this study. Differences in area-averaged SSTAs between the tropical western (10° S–10° N, 50°–70° E) and tropical southeastern (10° S–0°, 90°–110° E) Indian Ocean (TSEIO) were defined as the IOD index (Saji et al. 1999). An IOD event was identified when the September–October–November (SON) averaged IOD index was greater than 1 standard deviation. The Niño3.4 index was defined as area-averaged SSTAs in the Niño3.4 region (5° N–5° S, 120°–170° W; Trenberth 1997). The Indian Ocean basin mode (IOBM) index was calculated from area-averaged SSTAs in the tropical Indian Ocean (20° S–20° N, 40°–100° E; Guo et al. 2018). The NAO index was calculated as the difference in the regionally zonal-averaged sea level pressure (SLP) anomaly over the North Atlantic region from 80° W to 30° E between 35° N and 65° N (Li and Wang 2003). A positive NAO event was defined when the NAO index in March was greater than 1 standard deviation.

A horizontal wave-activity flux based on a zonally varying basic flow was applied to reflect the propagation of Rossby wave energy. The horizontal flux in the pressure coordinate system is expressed as follows (Takaya and Nakamura 2001):

$$W = \frac{P}{{2|\overline{{\overrightarrow {V} }} |}}\left\{ {\begin{array}{*{20}c} {\overline{u} (\varphi_{x}^{^{\prime}2} - \varphi_{{}}^{^{\prime}} \varphi_{xx}^{^{\prime}} ) + \overline{v} (\varphi_{x}^{^{\prime}} \varphi_{y}^{^{\prime}} - \varphi_{{}}^{^{\prime}} \varphi_{xy}^{^{\prime}} )} \\ {\overline{u} (\varphi_{x}^{^{\prime}} \varphi_{y}^{^{\prime}} - \varphi_{{}}^{^{\prime}} \varphi_{xy}^{^{\prime}} ) + \overline{v} (\varphi_{y}^{^{\prime}2} - \varphi_{{}}^{^{\prime}} \varphi_{yy}^{^{\prime}} )} \\ \end{array} } \right.$$
(1)

where the overbar and primes denote the time mean of the period 1950–2020 and time anomalies, respectively. \(P\), \(\overrightarrow {V} = (u,v)\), and \(\varphi\) represent the pressure, horizontal wind velocity, and stream function, respectively. The subscripts x and y represent the derivatives in the zonal and meridional directions, respectively.

Vertically integrated diabatic heating (Q1) is defined as follows (Boer 1986; Trenberth and Solomon 1994):

$$Q_{1} = R_{T} - F_{S} + L(P - E)$$
(2)

where RT indicates net downward radiation at the top of atmosphere, including the mean top net shortwave and longwave radiation flux; FS is net surface heat flux, defined as the sum of the mean surface latent and sensible heat flux, and net longwave and shortwave radiation flux; L represents the latent heat owing to evaporation, 2.5 × 106 J kg–1; P and E indicate the precipitation rate and surface evapotranspiration, respectively.

The mixed-layer heat equation (Li et al. 2002; He et al. 2019) is:

$$\overline{{\frac{\partial T}{{\partial t}}}} = \frac{{Q_{net} - Q_{p} }}{{\rho C_{p} h}} - \overline{{u\frac{\partial T}{{\partial x}}}} - \overline{{v\frac{\partial T}{{\partial y}}}} - \overline{{w\frac{\partial T}{{\partial z}}}} + R$$
(3)

where \(\overline{()} = \frac{1}{h}\int_{ - h}^{0} {dz}\) indicates the vertical mean values over the mixed layer; the mixed–layer depth h is approximately 45 m in the tropical Indian Ocean (Du et al. 2005; He et al. 2019); T is the potential temperature; u, v, and w are the zonal, meridional, and vertical currents, respectively; the downward net surface heat flux Qnet is defined as the sum of the net downward shortwave and longwave radiation flux, and latent and sensible heat flux; and Qp is shortwave penetration through the mixed-layer depth. Following Paulson and Simpson (1977), the solar radiation penetration parameterization scheme is:

$$Q_{p} = SW \times (r \times e^{{ - \frac{h}{L1}}} + (1 - r) \times e^{{ - \frac{h}{L2}}} )$$
(4)

where SW is downward shortwave radiation at the sea surface, r = 0.67, L1 = 1, and L2 = 17 (Dong et al. 2007). The density of seawater ρ is 1 026 kg m−3, and its specific heat Cp is 3 986 J kg−1 K−1. R in (4) is the residual term, such as the unresolved subgrid-scale turbulence and the neglected horizontal diffusion (Du et al. 2005; Yue et al. 2021).

We employed several statistical methods in our study, including linear correlation, partial correlation, regression, partial regression, and singular value decomposition (SVD; Li and Lu 2017; Zhang et al. 2018; Xia et al. 2019; Liu et al. 2020). The two-tailed Student's t-test was used to evaluate the statistical significance of the results.

2.3 Model

The linear baroclinic model (LBM) was used to examine the response of atmospheric circulation to prescribed diabatic heating (Watanabe and Kimoto 2000; Watanabe et al. 2002). Reanalysis data from NCEP1 were used as the model input. The model generally reaches a steady state at approximately 10 days (Watanabe and Jin 2003); therefore, each experiment integrated 30 days. The averaged results of days 15–30 showed a steady response to idealized diabatic heating.

3 Relationship between NAO and IOD

The spatiotemporal correlation analysis between the March NAO and subsequent IOD indicated that the correlation becomes significant in late spring, reaches a peak (0.46) in summer, and decreases quickly in winter (Fig. 1a). Considering the possible effects of the preceding winter–spring ENSO and IOBM on the IOD (Guo et al. 2015), we conducted partial correlation analysis by excluding the effect of ENSO and IOBM, as shown in Table 1. The correlation between the March NAO and the subsequent IOD remained nearly unchanged, suggesting that the preceding ENSO and IOBM had little influence on the relationship between the NAO and IOD. Accordingly, the influence of preceding winter–spring ENSO and IOBM were disregarded in the subsequent analysis. The same result (not shown) is presented for the NAO index derived from the time series of the leading Empirical Orthogonal Function of SLP anomalies over the Atlantic sector (20°–80° N, 90° W–40° E; Hurrell and Deser 2009).

Table 1 Correlation and partial correlation between the March NAO and June–July–August (JJA) and SON-averaged IOD index during 1950–2020
Full size table

Figure 1b shows the normalized time series of the March NAO index and SON-averaged IOD index. There are 11 (8) positive (negative) IOD events during the period 1950–2020, including 1961, 1967, 1972, 1982, 1991, 1994, 1997, 2002, 2006, 2015, 2019 (1960, 1975, 1996, 1998, 2005, 2010, 2016, 2020). This result is largely consistent with that of previous studies (Du et al. 2013; Endo and Tozuka 2016; Jiang et al. 2022). Just over the half (54%) of the positive IOD events coincide with the positive March NAO events, including 1961, 1967, 1982, 1994, 1997, and 2019.

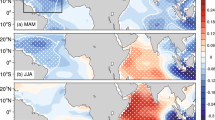
As shown in Fig. 2, the relationship between the March NAO and IOD was verified by comparison of bimonthly regression maps of the March NAO against the tropical Indian Ocean and Pacific Ocean SSTAs and surface wind anomalies from spring to autumn. As regards the positive phase of the March NAO, significant negative SSTAs (i.e., regression coefficients) occur across the tropical Indian Ocean, accompanied by northerly wind anomalies from the continent during March–April (Fig. 2a). Southeasterly wind anomalies off Sumatra and easterly wind anomalies over the equatorial Indian Ocean start developing during May–June. Correspondingly, significant positive SSTAs replace negative SSTAs in the tropical western Indian Ocean, and negative SSTAs in the TSEIO gradually intensify (Fig. 2b). The east–west SST gradient promotes IOD development, attaining a peak during September–October (Fig. 2b–d). The seasonal evolution of the March NAO-associated SSTAs in the tropical Indian Ocean well repeats the development features of the IOD, as was described in previous studies (Saji et al. 1999; Zhang et al. 2018). Positive SSTAs spread across the tropical eastern Pacific Ocean during May–October, however, they are insignificant at the 90% confidence level (Fig. 2b–d). To further verify the role of the March NAO on the SSTAs in the tropical Indian Ocean, we conducted additional partial regression analysis. After excluding the simultaneous ENSO signal, the insignificant positive SSTAs in the tropical eastern Pacific Ocean disappears, but the dipole SSTA pattern in the tropical Indian Ocean is still established and significant during May–October (Fig. R1a–d). When the simultaneous IOD signal is excluded, the dipole SSTA pattern in the tropical Indian Ocean and the insignificant positive SSTAs in the tropical eastern Pacific both do not develop (Fig. R1e–h). These spatiotemporal results suggest that the March NAO has a robust relationship with the following IOD. A possible physical mechanism linking the March NAO and subsequent IOD is revealed in the following section.

Fig. 2
figure 2

Bimonthly averaged regression of sea surface temperature anomalies (shading, units: °C) and 10 m wind anomalies (vectors, units: m s–1) against March NAO index for a March–April (MA), b May–June (MJ), c July–August (JA), and d September–October (SO). Stippling indicates the 90% confidence level. Only wind vectors significant at the 90% confidence level are shown. Dark-blue contours represent the 3000 m topographic height

Full size image

4 Possible mechanisms of March NAO influencing subsequent IOD

4.1 Atmospheric circulation associated with March NAO from spring to summer

Geopotential height and wave-activity flux anomalies at 300 hPa associated with the March NAO indicate that a steady Rossby wave extends from the North Atlantic to the WNP (i.e., the east of Japan) along the poleward side of the subtropical westerly jet (Fig. 3a). The geopotential height in the mid–high latitude at 500 and 850 hPa present a similar pattern, suggesting an equivalent barotropic structure, particularly the WNP cyclone (Fig. 3a–c). The WNP low-level cyclonic circulation prevails from spring to summer, and the center shifts equatorward during May–June (Figs. 2a, b, 3c, d). These findings correspond with those from Hu et al. (2021), and they demonstrated that the equatorward displacement of the WNP cyclone induced by the positive March AO favors the early onset of the South China Sea summer monsoon. Previous studies have indicated the role of the WNP atmospheric circulation anomalies on the development of IOD (Kajikawa et al. 2003; Huang and Shukla 2007). Therefore, it is inferred that the WNP circulation anomalies linked to the March NAO are a key connection between the March NAO and subsequent IOD. The memory of atmospheric circulation is short (Gong et al. 2011) and a consequent question is what are the maintenance mechanisms of cyclonic circulation from spring to summer.

Fig. 3
figure 3

a Regression of 300-hPa geopotential height anomalies (shading, unit: gpm) and wave-activity flux (vectors, unit: m2 s–2) against March NAO index in March. Green contours represent 300 hPa climatological zonal wind larger than 20 m s–1 (contour interval: 10 m s–1), indicating the location of a westerly jet. The red dashed line indicates the Rossby wave path. b and c as for the shading in a, but for 500 hPa and 850 hPa, respectively. d As for c, but for May–June (MJ) averaged regression. Only geopotential height anomalies significant at the 90% confidence level are shown. Dark-blue contours represent the 3000-m topographic height

Full size image

During March–April, northeasterly wind anomalies to the northwestern side of the WNP cyclonic circulation induce significant negative SSTAs by strengthening the climatological trade wind and transporting dry and cold air southward (Figs. 2a, 4a). Southwesterly and easterly wind anomalies in the southeastern and northern flanks of the cyclone, respectively, reduce the mean wind, thereby promoting warm SSTAs (Figs. 2a, 4a). In association with anomalous atmospheric circulation, a significant tripole SSTA pattern becomes established locally. This pattern is characterized by cold SSTAs in the central pole (20°–40° N, 120°–180° E) and warm SSTAs in the northern and southern poles. Warm SSTAs in the southern pole extend toward the eastern North Pacific, bearing some resemblance to the Pacific Meridional Mode (Fig. 2a; Chiang and Vimont 2004; Fan et al. 2021). The net surface heat flux pattern, which is dominated by latent heat flux, bears a close resemblance to the WNP SSTA pattern, indicating that net surface heat flux dominates the formation of the SSTA pattern during March–April (Figs. 2a, S2). Further, cyclonic circulation promotes cooling by upwelling linked to increased Ekman pumping (Gong et al. 2011; Chen et al. 2014). The conclusion is, therefore, that WNP cyclonic circulation causes the observed SSTA pattern through wind–evaporation–SST (WES) feedback and Ekman pumping.

Fig. 4
figure 4

Bimonthly averaged regression of precipitation (shading, unit: mm) and 850 hPa wind (vectors, units: m s–1) anomalies against March NAO index for a March–April (MA), b May–June (MJ), and c July–August (JA). d–f As for a–c, but for diabatic heating anomalies (shading, units: W m−2). Gray stippling indicates the 90% confidence level. Only wind vectors significant at the 90% confidence level are shown. Dark-blue contours represent the 3000 m topographic height

Full size image

We further examined the feedback of SST on atmospheric circulation. Warm SSTAs in the subtropical WNP contribute to the ascending motion and convection development, accompanying significant above-normal precipitation and diabatic heating in the southern and eastern flanks of the cyclone during March–April (Figs. 2a, 4a, d). Following the Sverdrup vorticity balance along the subtropics (Liu et al. 2001; Rodwell and Hoskins 2001), an anomalous cyclonic circulation is generated over the northwestern side of the heating region, which, in turn, sustains the WNP cyclonic circulation. Therefore, the air–sea positive feedback over the subtropical WNP maintains low-level cyclonic circulation from spring to summer (Figs. 2a–c, 3c–d, 4a–c; Gong et al. 2011). Moreover, Rossby wave response associated with positive diabatic heating has the strongest westerly wind to the south of the heating center (Gill 1980; Hu et al. 2021); accordingly, warm SSTAs and cyclonic circulations develop equatorward (Fig. 2a–c, 3c–d, 4a–c). The next question that needs to be answered is how the WNP cyclone triggers the IOD.

We conducted SVD analysis of SLP anomalies over the northern Atlantic (defined as the left field) and SSTAs over the WNP (defined as the right field) during March to further reveal the relationship between the March NAO and March WNP SSTAs (Fig. 5). The first leading mode (SVD1), explaining 54% of the total co-variance, presents an evident dipole SLP pattern (i.e., a typical NAO mode) over the northern Atlantic and a tripole SSTA pattern over the WNP, which are in good agreement with the regression pattern associated with the March NAO (Figs. 2a, 3a–c, 5a, b). The individual variances explained by this mode for SLP and for SST is 46% and 12%, respectively. The correlation coefficient between the time series of the expansion coefficients of the left and right fields is 0.50, which exceeds the 99% confidence level. The above analysis suggests that a robust relationship does exist between the March NAO and WNP tripole SSTA pattern (Fig. 5c).

Fig. 5
figure 5

a Left and b right homogeneous fields of the first leading singular value decomposition mode for sea level pressure over the northern Atlantic (left field) and sea surface temperature over the western North Pacific (WNP; right field). c Standardized time coefficients of left (red) and right (black) homogeneous fields

Full size image

Additionally, the Rossby wave train associated with the March NAO propagates southeastward and reaches the northern Arabian Sea and neighboring areas, contributing to an equivalent barotropic anticyclone locally (Fig. 3a–c). Gong et al. (2014) have indicated that the AO influences precipitation in the tropical Indian Ocean by an analogous path of wave-activity during the boreal winter. The enhanced Arabian High brings stronger northerly wind over the southeastern Arabian Sea, inducing significant negative SSTAs and below-normal precipitation during March–April (Figs. 2a, 4a). In turn, the negative precipitation anomalies over the southeastern Arabian Sea maintain the anticyclone. The anomalous SST and precipitation pattern over the Arabian Sea during March–April favor the weakening of the summer monsoon in the tropical western Indian Ocean during May–June. This is verified by May–June averaged regression of surface wind and SST against the March–April precipitation index derived by area-averaging precipitation anomalies over the 0°–10° N, 60°–80° E region (not shown).

4.2 Roles of atmospheric circulation over the WNP on IOD development

Here, we discuss the roles of the WNP anomalous cyclone associated with the March NAO in the occurrence and development of the IOD. During May–June, with the onset of the Asian summer monsoon, the WNP cyclone maintenance enhances the cross-equatorial southerly wind, which turns into southeasterly and southwesterly winds off Sumatra–Java and to the north of the equator, respectively, aided by the Coriolis force (Figs. 2b, 4b; Zhang et al. 2018; Lu and Ren 2020). The increased lower-level southerly wind brings abundant moisture to the WNP, favorable for the development of local precipitation and cyclonic circulation. In contrast, the southeasterly wind off Sumatra–Java promotes cooling, which suppresses local convection and induces below-normal precipitation. Correspondingly, strong surface convergence and upper-level divergence are observed over the WNP during May–June, with the opposite occurring over the TSEIO (Fig. 6a, b). Concurrently, anomalous local meridional circulation becomes established with the ascent over the WNP and descent over the TSEIO and Maritime Continent (Fig. S3a). As indicated by Zhang et al. (2018), the development of a south–north precipitation dipole, featuring above-normal precipitation over the WNP and below-normal precipitation over the TSEIO and Maritime Continent, is conducive to northward lower-level and southward upper-level wind, suggesting an enhanced local meridional circulation. In turn, such enhancement reinforces the south–north precipitation dipole (Figs. 4b, 6a, b, S3a). This positive feedback is favorable for reinforcing the related anomalous circulation and precipitation during May–August, particularly for the TSEIO southeasterly wind (Figs. 4b, c, 6a–d, S3a, b). In conclusion, the WNP anomalous cyclone is beneficial to the development of southeasterly wind anomalies and cooling over the TSEIO.

Fig. 6
figure 6

a Bimonthly averaged regression of 200 hPa velocity potential (shading, units: 106 m2 s–1) and divergence wind (vectors, units: m s –1) against March NAO index for May–June (MJ). b As for a, but for 850 hPa. c, d As for a, b, but for July–August. Gray stippling indicates the 90% confidence level. Only wind vectors significant at the 90% confidence level are shown. Dark-blue contours represent the 3000 m topographic height

Full size image

It is known that the southeasterly wind anomalies off Sumatra–Java during May–June are key triggers for the IOD (Saji et al. 1999; Li et al. 2003; Cai et al. 2013; Lee et al. 2022). The significant southeasterly wind anomalies off Sumatra, superimposed on the climatological southeasterly wind, enhance WES feedback, inducing upward latent heat flux transport and contributing to the cooling and depressed convection over the TSEIO (Figs. 2b, 4b; Xie and Philander 1994; Li et al. 2003; Cai et al. 2013). Moreover, the enhancement of the southeasterly wind over the TESIO strengthens coastal upwelling and shoaling of the thermocline, promoting cooling through positive wind–thermocline–SST feedback (Figs. 2b, 7b; Saji et al. 1999; Cai et al. 2013). As a Rossby wave response of negative diabatic heating over the TSEIO, two anticyclonic circulations develop over its northwestern and southwestern regions along with the anomalous easterly wind over the equatorial Indian Ocean (Gill 1980). This anomalous equatorial easterly wind forces the warm water to accumulate westward (Figs. 2b, 4b, e). Furthermore, significant easterly and northerly wind anomalies appear in the south of the Arabian Sea and off the East Africa during May–June, respectively, suggesting a weakened summer monsoon (Figs. 2b, 4b; Yu et al. 2021; Jiang et al. 2022). Such wind anomalies weaken the WES feedback and coastal upwelling off the East Africa, further inducing significant positive SSTAs over the tropical western Indian Ocean (Fig. 2b). During July–August, the southeasterly wind anomalies off Sumatra–Java become stronger, accompanied by the enhancement of local meridional circulation between the TSEIO and WNP (Figs. 2c, 4c, S3b). Moreover, the east–west SST gradient in the tropical Indian Ocean strengthens the easterly wind anomalies over the equatorial Indian Ocean, leading to further warming of the western pole and cooling of the eastern pole. Consequently, a typical dipole mode is established in autumn (Fig. 2d).

Fig. 7
figure 7

Bimonthly averaged regression of sea surface height anomalies (units: m) against March NAO index for a March–April (MJ), b May–June (MJ), c July–August (JA), and d September–October (SO), respectively. Gray stippling indicates the 90% confidence level

Full size image

The oceanic wave associated with surface wind anomalies is another important factor in IOD development (Yuan and Liu 2009; Wang and Yuan 2015; Effy et al. 2020). We examined the thermocline variation represented by the SSH, as was used in Rao and Behera (2005) and Wang et al. (2016). On the one hand, the local southeasterly wind anomalies off Sumatra uplift the thermocline locally (Murtugudde et al. 2000; Rao et al. 2002). On the other hand, forced by equatorial easterly wind anomalies, the upwelling Kelvin waves propagate eastward, shoaling the thermocline over the eastern Indian Ocean and contributing to local cooling (Figs. 2b–d, 4b, c, 7b–d, S4b; Murtugudde et al. 2000; Rao et al. 2002). Meanwhile, the anticyclone wind stress curl excites the downwelling Rossby waves propagating westward, which are stronger in the southern than in the northern Indian Ocean, subsequently deepening the thermocline and facilitating warming over the western Indian Ocean (Figs. 2b–d, 4b, c, 7b–d, S4a, and S4c; Xie et al. 2002; Effy et al. 2020).

4.3 LBM numerical experiment

We conducted LBM experiments to verify the feedback role of precipitation on atmospheric circulation. The heating region was determined according to the precipitation pattern associated with the March NAO. As regards the WNP above-normal precipitation during March–April, the key positive heating source is situated over a region (8°–16° N, 125°–160° E) with its center at 12° N and 142.5°E (Figs. 4a, d, 8a). The area-averaged diabatic heating profile has a maximum of approximately 0.65 K day–1 at the sigma of 0.45, with the same value used as input for the LBM (not shown). The results show that a cyclone is stimulated over the northwest of the heating region and extends meridionally as noted in the observation (Figs. 2a, 3c, 4a, 8d). The strongest westerly wind anomalies are observed on the southern flank of the cyclone, beneficial to the equatorward development of cyclone (Fig. 8d). Such circulation indicates that the WNP above-normal precipitation during March–April, in turn, favors the development and equatorward shift of the cyclone.

Fig. 8
figure 8

a Location of March–April (MA) averaged above-normal precipitation-related diabatic heating source over the WNP at the sigma of 0.45 in the linear baroclinic model (LBM). d Response of 850 hPa stream function (shading, 106 m2 s–1) and wind (vectors, m s–1) for 15–30-day averaged results in the LBM. b and e As for a and d, but for May–June–July–August (MJJA) averaged above-normal precipitation-related diabatic heating source over the WNP. c and f As for b and e, but for below-normal precipitation-related diabatic heating source over the Maritime Continent

Full size image

The heating source corresponding to the WNP precipitation pattern during May–August is located a region at 5°–20° N, 150°–180° E. The heating center at 12.5° N and 165° E is located more eastward than in March–April, and the area-averaged diabatic heating profile has a maximum of 0.5 K day–1 at the sigma of 0.45 (Figs. 4a–f, 8a, b). The results indicate that a zonally extending cyclone develops over the WNP, agreeing well with the observation (Figs. 2b, c, 3d, 4b, c, 8e). The heating source linked to below-normal precipitation over the TSEIO and Maritime Continent during May–August is situated over a region at 10° S–5° N, 90°–130° E, with its center at 2.5° S and 110° E. The minimum of the area-averaged diabatic heating profile is approximately − 0.6 K day–1 at the sigma of 0.45 (Fig. 4b, c, e, f). As a Rossby wave response, anticyclonic circulations appear in the northwestern and southwestern sides of the heating region. Correspondingly, anomalous southeasterly and easterly winds develop off Sumatra and the equatorial Indian Ocean, respectively, which are favorable for the development of the IOD (Fig. 8c, f). The low pressure can be noted over the WNP, suggesting the role of negative precipitation anomalies over the Maritime Continent on the cyclones over the WNP. Although the LBM experimental results do not exactly support this observation owing to a lack of feedback from the LBM, the feedback role of precipitation on the local atmospheric circulation is confirmed.

5 Ocean mixed-layer heat budget associated with March NAO

To investigate the relative contribution of the net surface heat flux and ocean dynamic process associated with the March NAO to IOD development, we diagnosed the ocean mixed-layer heat budget equation. First, each term in the heat budget equation was calculated, after which we conducted regression analysis against the March NAO. The evolution and peak of forcing, defined as the sum of zonal, meridional, and vertical advection, and the net surface heat flux, show consistence with the mixed-layer temperature (MLT) tendency. This finding is similar to the results of Hong et al. (2008a, b). The result is verified by correlation coefficients of 0.85 and 0.79 between forcing and the MLT tendency for the eastern and western poles of the IOD, respectively (Fig. 9). As stated in Sect. 2, some residuals can probably be ascribed to the coarse temporal and spatial resolution of the datasets, different data sources for ocean and heat flux, and uncertainties in parameterization (Huang et al. 2010).

Fig. 9
figure 9

Regression of mixed-layer temperature (MLT) anomalies (right axis) and mixed layer heat budget (left axis) against March NAO index. MLT anomalies (black, unit: °C), MLT tendency (blue, unit: °C month–1), and forcing (red, unit: °C month–1), defined as the sum of zonal, meridional, and vertical advection, and net surface heat flux, are shown in a and c. The correlation coefficient in a and c represents the relationship between the MLT tendency and forcing. The zonal (red), meridional (blue), and vertical (black) advection, and net surface heat flux (purple) are shown in b and d. Results in a and b represent the area-averaged values of the eastern pole of the IOD (IOD-E), and c and d the western pole of the IOD (IOD-W). The results derive from the pentad dataset, with 18–657 pentad bandpass filtering

Full size image

As the eastern pole of the IOD, the negative MLT tendency starts developing from May, attains a peak during August, and turns positive during October–December. Cold MLT anomalies prevail during the entire IOD development phase, and are the strongest during September–October, agreeing with the SSTAs (Figs. 2a–d, 9a). Determining the contributions of different components to the MLT tendency, we found that the cold MLT tendency primarily results from negative 3-D ocean advection during the development stage of IOD, particularly negative vertical ocean advection (Fig. 9a, b). The net surface heat flux shows a weak positive contribution during mid-June–September, as the large positive downward shortwave radiation flux offsets the negative latent heat flux and longwave radiation flux, suggesting the dominance of negative SST–cloud–radiation feedback (Hong et al. 2008b) over positive WES feedback (Figs. 9b, S5a). After October, strong positive net surface heat flux, resulting from positive net shortwave radiation flux, latent heat flux, and sensible heat flux, plays a key role in damping the cold MLT anomalies of the eastern pole (Figs. 9a, b, S5a). Our finding agrees with the results of previous studies (Li et al. 2002; Sun et al. 2014; Jiang et al. 2022).

As the western pole of the IOD, the positive MLT tendency develops during April–mid-June and September–December, mainly resulting from positive vertical ocean advection (Fig. 9c, d). During July–August, negative meridional and zonal ocean advection and net surface heat flux induce the negative MLT tendency, weakening warm MLT anomalies (Fig. 9c, d). Therefore, the warmest MLT anomalies occur in June and December (Fig. 9c). Negative net surface heat flux during May–September and October–December result from negative latent heat flux and negative net downward shortwave radiation flux, respectively (Figs. 9d, S5b). The development of both eastern and western poles is dominated by the ocean process, particularly vertical ocean advection. However, net surface heat flux has adverse effects on the MLT anomalies of the eastern and western poles during their development stages.

6 Summary

This study demonstrated a significant correlation between the March NAO and the subsequent boreal summer and autumn IOD, even after the removal of preceding winter–spring ENSO and IOBM signals. Focusing on the importance of WNP air–sea interaction, we revealed the triggering mechanism of the March NAO for the subsequent IOD through the reanalysis data and LBM simulation, as shown schematically in Fig. 10.

Fig. 10
figure 10

Schematic diagram of the March NAO influencing the IOD. a Regression of 300 hPa geopotential height anomalies (shading, unit: gpm) against March NAO index in March. A and C denote the anomalous anticyclone and cyclone, respectively. The red dashed line indicates the Rossby wave path. b Shading over the WNP and tropical Indian Ocean indicates the SST anomalies during March–April and September–October, respectively. The red solid and dashed elliptic circles represent WNP low-level cyclonic circulation during March–April and May–August, respectively. The blue solid elliptic circle represents the low-level anticyclonic circulation over the Arabian Sea during March–April. The black vertical circulation represents anomalous local meridional circulation, which ascends over the WNP and descends over the TSEIO during May–August. Gray and red vectors denote the mean climatological wind and upwelling in the TSEIO and the condition corresponding to the positive March NAO, respectively. The gray and red curve denotes the depth of the mean thermocline in the tropical Indian Ocean and the depth corresponding to the positive March NAO, respectively

Full size image

First, a strong March NAO induces equivalent barotropic cyclonic circulation over the WNP through a steady Rossby wave. The anomalous low-level cyclone stimulates a tripole SSTA pattern over the WNP by changing the surface heat flux and Ekman pumping in the ocean. The SSTAs, in turn, contribute to the development and equatorward displacement of cyclonic circulation by inducing anomalous precipitation and diabatic heating. Such air–sea positive feedback maintains the cyclone over the subtropical WNP from early spring to summer.

Subsequently, anomalous WNP cyclonic circulations and precipitation during May–August reinforce southeasterly wind off Sumatra and cooling of the IOD eastern pole through local meridional circulation, which ascends over the subtropical WNP and descends over the TSEIO and Maritime Continent. Concurrently, equatorial easterly wind anomalies and northerly wind anomalies off the East Africa induce warming of the IOD western pole.

Finally, WES and wind–thermocline–SST positive feedback contribute to the development of the IOD in summer and autumn. The Arabian Sea anomalous anticyclone, associated with a southeast-propagating Rossby wave induced by the March NAO, is also important to IOD development. Moreover, thermocline shoaling, which results from eastward upwelling Kelvin waves and local upwelling, facilitates cooling over the TSEIO. Thermocline deepening, resulting from westward downwelling Rossby waves, is beneficial to warming in the tropical western Indian Ocean, particularly in the southwest of the ocean. The diagnosis of a MLT heat budget indicates that the ocean dynamic process associated with the March NAO contributes more to the development of the IOD than does the net surface heat flux.

Our results indicated the influence of mid–high latitude circulation anomalies over the Northern Hemisphere on the occurrence of the IOD. This finding could provide a new cue to improve the seasonal prediction of the IOD. In future, we aim to improve our understanding of this physical process by employing the air–sea coupled model.