On the choice of TLS versus OLS in climate signal detection regression

Abstract

Total least squares (TLS) or multivariate orthogonal regression is widely used as a remedy for attenuation bias in climate signal detection or “optimal fingerprinting” regression. But under some circumstances it overcorrects and imparts an upward bias, as well as generating extremely unstable and imprecise coefficient estimates. While there has been increasing attention paid recently to the validity of TLS-based confidence intervals, there has been no corresponding examination of coefficient bias problems. This note explains why they are pertinent and presents a Monte Carlo simulation to illustrate the hazards of using TLS in a signal detection application without testing whether the modeling context makes it a suitable choice. TLS is not automatically preferred over OLS even when explanatory variables are believed to contain random errors. Notably it can be sufficiently biased to cause false positives when explanatory signals are negatively correlated, and the bias gets worse as the signal-noise ratio on the explanatory variables rises. Additionally TLS should not be used on its own for climate signal detection inferences since if the no-signal null is true, TLS is generally inconsistent whereas OLS attenuation bias disappears.

Introduction

When the explanatory variable in a univariate regression model is measured with error the ordinary least squares (OLS) slope coefficient is biased downwards, a phenomenon called attenuation bias (Wooldridge 2020). Orthogonal regression provides a correction in the univariate regression case (Carroll and Ruppert 1996; Allen and Stott 2003) argued that since signal vectors generated by climate models contain model noise this could bias coefficient estimates towards the null hypothesis and potentially thwart signal detection in fingerprinting regressions. They proposed Total Least Squares (TLS), the multivariate extension of orthogonal regression (Gleser 1981), as a remedy. It has been widely used in the climate literature ever since.

Properties of TLS estimators that are straightforward in the single-variable case do not necessarily carry over to the multivariate case, however. Consider, for instance, the direction of bias in OLS in a two-variable regression $y=Wb+e$ where y is a zero-mean vector of observations, $W=X+U$, X consists of two columns of zero-mean unobserved explanatory variables, U consists of two columns of zero-mean observational errors on X, and e is a vector of errors on the observations in y. Assume the columns of U are independent of each other and of e. Then according to Fuller (1987, p. 107) the orthogonal regression estimator is $\tilde{b}={\left({M}_{WW}-{S}_{UU}\right)}^{-1}{M}_{Xy}$ where ${M}_{WW}={W}^{T}W$, ${S}_{UU}$ is a diagonal, unbiased estimator of the covariance matrix of U and ${M}_{Wy}={W}^{T}y$. If we denote the OLS estimator as $\widehat{b}={M}_{WW}{M}_{Wy}$ then in the univariate case it would be immediate that $\widehat{b}<\tilde{b}$ but not in the two-variable case. It can be shown (see Appendix) that if ${\left({m}_{11}{m}_{22}-{m}_{12}^{2}\right)}^{-1}>0$ ${\widehat{b}}_{1}<{\tilde{b}}_{2}$ only if ${m}_{12}{s}_{22}/\left({m}_{22}{s}_{11}\right)<{\tilde{b}}_{1}/{\tilde{b}}_{2}$ where ${m}_{ij}$ and ${s}_{ij}$ denote, respectively, the elements of ${M}_{WW}$ and ${S}_{UU}$. Thus even in the simplest two-variable case the relative size of the OLS coefficient depends on the relative magnitudes of all the elements of ${M}_{WW}$ and ${S}_{UU}$ and on the relative size of the two TLS coefficients. Allowing for non-zero correlation between U and e makes the comparison even more ambiguous.

Claims about the validity of TLS coefficient estimates, especially consistency and unbiasedness, typically require strong assumptions about unobservable error terms. As noted in Carroll and Ruppert (1996) in a univariate orthogonal regression there are five sufficient statistics available in the sample and six parameters to estimate, so identification of the slope parameter b requires a normalizing assumption on the ratio of the unknown error variances. The need for a normalizing assumption carries over to the multivariate case, making the fit of the model sensitive to arbitrary choices of units (a problem noted earlier in Samuelson 1942). Fuller (1987, p. 164) points out that the TLS slope estimator is a ratio of two random variables, and such ratios are typically biased estimators of the ratio of the expectations. Gleser (1981) provides a thorough treatment of the consistency properties of the TLS estimator under the assumption that the error variances in the explanatory variables are equal and homoscedastic. If this assumption does not hold, he emphasizes (p. 43) that no strongly consistent estimator exists.

Carroll and Ruppert (1996) also point out that if in the univariate case the regression model is underspecified, TLS overcorrects for attenuation bias. The usual model form for TLS implies that if the measurements were exact all the data would lie exactly on the regression line. This may be reasonable in laboratory experiments but in most other applications it is more realistic to suppose that there are potential specification errors (such as omitted variables) in addition to measurement noise, and even correctly measured observations would not lie exactly on the regression line. If this is true of the model being estimated TLS introduces an upward bias on the slope coefficients. In practice there is no way to tell without additional testing if an implementation of TLS is correcting or overcorrecting for attenuation bias. The simulations shown herein will provide many cases of overcorrection and upward bias in TLS coefficients.

Inference regarding a zero-slope null hypothesis is also a problem in TLS regressions. Under a chosen normalization the formula for the TLS slope coefficient $\tilde{b}$ (see Fuller 1987 Eq. 1.3.7) contains in the denominator the covariance between the dependent variable and the observed independent variable. Under the hypothesis $b=0$ this term is also zero and the estimator $\tilde{b}$ is thus undefined. If the variance of the dependent variable is sufficiently small relative to that of the independent variable it is reasonable to set $\tilde{b}=0$, but not otherwise (see Fuller 1987 p. 32). Hence the existence of well-defined confidence intervals depends on unobservable variance ratios and therefore cannot be guaranteed. The conditionality is not a problem in experimental settings in which a single treatment is paired with a single response variable, a zero value in the denominator of $\tilde{b}$ can be ruled out a priori and the information necessary to estimate the variance ratio can be collected experimentally. These conditions do not hold in signal detection contexts.

Before proceeding we should take note of some conflicting terminology regarding the “noise” associated with regression variables. In classical OLS regression modeling (e.g. Davidson and MacKinnon 2004) the random component is usually called the “error term” or the regression “disturbance”, and it denotes the unexplained portion of the dependent variable, which includes measurement error. It is assumed to be a zero-mean random variable, thereby allowing the tools of testing and inference to follow from applications of central limit theorems and asymptotic analysis. Models with error terms on the explanatory variables are called errors-in-variables (EIV) models (e.g. Gleser 1981) and the typical justification is measurement error (as indicated by the title of Fuller 1987), allowing EIV methods to also employ asymptotic analysis. But in the signal detection context there is no measurement error since it is the observable output of a climate model. Instead the justification is “sampling uncertainty” (Allen and Stott 2003) associated with chaotic internal variations in models, whereby the same model rerun with nearly identical initial conditions would yield slightly different signal vectors. The notional unobserved “signal” is therefore an underlying deterministic process that would be identical across model runs, and the “error” is not a classical stochastic process but an additive deterministic chaotic realization. Whether chaotic variations of this kind should be treated as stochastic processes subject to standard asymptotic theory is an interesting question but is beyond the scope of this analysis. We will follow standard practice in assuming that the additive “noise” on explanatory variables is a random disturbance term and model it herein accordingly.

Theoretical treatments of TLS and EIV estimators generally focus on cases in which the underlying variances are known or the relative variances can be strongly restricted. In practice there is no way to tell from a sample of observations alone whether the conditions supporting strong consistency hold. Econometricians thus prefer to deal with the problem of randomness in the explanatory variables using the instrumental variables method due to the fact that consistency can be established based on testable properties of the data (Fuller 1987; Davidson and MacKinnon 2004), but this option has never been used in optimal fingerprinting.

The purpose of this study is to explore using Monte Carlo analysis how these issues may affect parameter estimation in the specific context of signal detection models. I will show through comparisons with OLS that even when attenuation bias exists TLS is not automatically the preferred option, and many cases it exhibits worse performance than OLS. I focus primarily on the coefficient bias issue rather than on the question of confidence interval estimation, although the simulations will reveal the relative inefficiency of TLS estimators. Obtaining valid TLS standard errors and confidence intervals is difficult due to the nonlinearity of the estimator and the dependence on identifying assumptions regarding the unknown error variances (Fuller 1987). DelSole et al. (2019) provide a thorough review of some of the main approaches to construction of confidence intervals in signal detection models and they propose a method that relies on a Wilke’s deviance statistic associated with the maximized likelihood function which, under certain conditions, can be shown to have a known (${\chi }^{2}$) distribution. However they also note that this approach may fail to yield closed confidence regions when the explanatory variables are collinear, so they also suggest use of a bootstrap methodology due to Pešta (2013). Trenary et al. (2020) compare bootstrap TLS confidence intervals to those derived using likelihood-based methods taking account of classical and regularized covariance matrix estimation methods within a fingerprinting context in which potential sources of model error are ruled out. It is beyond the scope of the current paper to resolve the variance estimation problem, instead I will use Monte Carlo simulations of the point estimates to characterize the coefficient distributions.

Signal detection using TLS

In what follows a bold-face letter (e.g. X) denotes a vector or matrix, a variable with a single numerical subscript (e.g. ${x}_{1}$) denotes a column of a matrix and a lower-case variable (e.g. ${x}_{i,j}$) with two subscripts i, j refer to the i, jth element of the corresponding matrix. We estimate a linear model in which a dependent variable y is regressed on explanatory variables ${x}_{1}, \dots ,{x}_{k}$ where the sample size is N. The model is thus.

$$\mathbf{y}=\mathbf{X}\mathbf{b}+\mathbf{e}$$

(1)

where e is the regression error term, or the component of y not explained by the columns of X which is assumed to be a homoscedastic random variable with $E\left(\mathbf{e}|\mathbf{X}\right)=0$. Classical fingerprinting following Allen and Tett (1999) involves using a pre-whitening operator formed as the truncated Moore-Penrose pseudo-inverse of a noise covariance matrix from a climate model preindustrial control run. The method of Ribes et al. (2013) generates the matrix weights using a full-rank regularized inverse. Because the weights are stochastic this step introduces potential consistency problems (McKitrick 2021) but we will ignore these and assume the regression error in Eq. (1) is homoscedastic and independent of X. Suppose we cannot observe X directly, instead we observe $\mathbf{W}=\mathbf{X}+\mathbf{U}$ with elements ${w}_{i,j}$where U is an $N\times k$ matrix of column-wise zero-mean error terms. The OLS estimator ${\widehat{\mathbf{b}}}_{OLS}={\left({\mathbf{W}}^{\mathbf{T}}\mathbf{W}\right)}^{-1}{\mathbf{W}}^{\mathbf{T}}\mathbf{y}$ is a biased and inconsistent estimator of b (Davidson and MacKinnon 2004, p. 313). TLS regression coefficients can be found using the algorithm presented in Gleser (1981) and Markovsky and Van Huffel (2007). Denote the singular value decomposition of the $N\times (k+1)$ matrix $\left[\mathbf{W} \mathbf{y}\right]$ as $\mathbf{V}\varvec{\Sigma }\mathbf{H}$. The final column of H is denoted ${H}_{k+1}$, and has elements ${h}_{1,k+1},\dots , {h}_{k+1,k+1}$. Then the k elements of the TLS solution vector ${\widehat{\mathbf{b}}}_{TLS}$ are:

$${\widehat{\mathbf{b}}}_{TLS}\left(i\right)= \left(-\frac{{h}_{i,k+1}}{{h}_{k+1,k+1}}\right), i=1, \ldots ,k$$

(2)

The Gauss-Markov theorem implies that if e in Eq. (1) satisfies the classical assumptions (Koop 2008), which include the absence of randomness in W, ${\widehat{\mathbf{b}}}_{OLS}$ is the most efficient estimator of b. Thus we expect to find Eq. (2) yields coefficients with higher variances than those of ${\widehat{\mathbf{b}}}_{OLS}$. Ideally, ${\widehat{\mathbf{b}}}_{TLS}$ trades off some efficiency for correction of bias induced by the random errors. As we will see in the Monte Carlo simulations the TLS tradeoff is not always advantageous: efficiency is always lost but new and potentially worse biases are introduced except under specific conditions. This is especially the case if the model is underspecified, in which case OLS and TLS are both biased and inefficient. For instance if the true model is

$$\mathbf{y}=\mathbf{X}\mathbf{b}+\mathbf{Q}\mathbf{d}+\mathbf{e}$$

(3)

and we estimate $\mathbf{y}=\mathbf{W}\mathbf{b}+\mathbf{e}$ instead then even if $\mathbf{W}=\mathbf{X}$ unless W and Q are uncorrelated OLS will be affected by omitted variable bias (OVB). This is also true of TLS, and we will furthermore find evidence of bias in TLS even if W and Q are uncorrelated.

Numerical example

Independent signals and noise

To make the Monte Carlo simulation resemble an optimal fingerprinting exercise we consider the $k=2$ case and use $N=200$ pseudo-observations. Many signal detection regressions have much smaller sample sizes due to the limited degrees of freedom in climate model preindustrial control run covariances. Assume there are two model-generated explanatory signal or response pattern variables denoted ${x}_{1}$ and ${x}_{2}$ and an observational target denoted y. We can think of y as being a spatial pattern of observed temperature changes and the ${x}_{j}$’s as the simulated patterns from climate models run using, respectively, anthropogenic and natural forcings. Inferences about the elements of b imply detection of the corresponding signal as a causal factor on observations.

The first simulated signal pattern is constructed as a uniform random draw plus a spatial pattern that reaches minimum in the middle of the sample and a maximum at the start and finish:

$${x}_{1i}=\left|\text{cos}\left(\pi *\frac{i}{N}\right)\right|+{v}_{1i}$$

where $i=1,\dots ,N$ and ${v}_{1i}$ are draws from a uniform distribution with bounds $\pm \sqrt{12}/2$ in order to yield an expected variance of 1. If the data are assumed to be arranged spatially from north to south the signal can be thought of as a latitude-dependent warming pattern that reaches a maximum in the polar regions.

The second signal pattern is defined as

$${x}_{2i}={v}_{2i}$$

where ${v}_{2i}$ are draws from a uniform distribution with an expected variance of 1. Define three error vectors ${u}_{j} \sim N \left(\text{0,1}\right)$, $j=(1, 2, y)$, representing independent zero-mean Gaussian noise terms associated with, respectively, the two explanatory variables and the dependent variable. We observe the noise-contaminated signals ${w}_{j}={x}_{j}+{u}_{j}/s$ $(j=\text{1,2}$) where s is a parameter we will use to scale the variance of ${u}_{j}$ relative to that of ${x}_{j}$. All variables are zero-centered then we construct pseudo-observations ${y}_{i}^{0}$ using:

$${y}_{i}^{0}=\beta {x}_{1i}+0.5{x}_{2i}+{u}_{iy}$$

using an assumed true value of $\beta$ which will be, in turn, 0.0, 0.5 or 1.0. Note that the coefficient on ${x}_{2}$ is always 0.5, so in the $\beta =1$ case the construction of ${y}_{i}^{0}$ would imply ${x}_{1}$ is the dominant influence on y. The reader can think of ${x}_{2}$ informally as the pseudo-natural forcing signal and ${x}_{1}$ as the pseudo-anthropogenic forcing signal.

We also construct additional model variables ${q}_{1}$ and ${q}_{2}$, both of which are independent uniform random numbers with bounds $\pm \sqrt{12}/2$, with ${q}_{2}$ additionally including the additive term ${x}_{1}/4$ to induce a partial correlation between ${q}_{2}$ and ${x}_{1}$, thus ${q}_{2}=U\left[-\frac{\sqrt{12}}{2},\frac{\sqrt{12}}{2}\right]+{x}_{1}/4$. Each will represent an omitted variable in the regression model, with the latter constructed so that it partially overlaps the response pattern ${x}_{1}$. Since ${q}_{1}$ is uncorrelated with ${x}_{1}$ and ${x}_{2}$ its omission is expected to cause inefficiency but not bias in OLS estimation. Omission of ${q}_{2}$ will cause both bias and inefficiency. Pseudo-observations ${y}_{i}^{q1}$ and ${y}_{i}^{q2}$ are formed using

$${y}_{i}^{q1}=\beta {x}_{i1}+0.5{x}_{i2}+{q}_{i1}+{u}_{iy}$$

and

$${y}_{i}^{q2}=\beta {x}_{i1}+{0.5x}_{i2}+{q}_{i2}+{u}_{iy}.$$

Estimation is done by applying both OLS and TLS to the regression models.

$${y}_{i}^{0}=\beta {w}_{i1}+\alpha {w}_{i2}+{e}_{i}$$

(4)

$${y}_{i}^{q1}=\beta {w}_{i1}+\alpha {w}_{i2}+{e}_{i}$$

(5)

and

$${y}_{i}^{q2}=\beta {w}_{i1}+\alpha {w}_{i2}+{e}_{i}.$$

(6)

The constant term is omitted in each case. Note that the differences between these regression equations and the true models arise from the reliance on the observed (but noisy) ${w}_{i}$’s and the presence or absence of the ${q}_{i}$’s in the y terms A researcher running a signal detection regression does not know which of the three models he or she has run since it is not possible to tell whether ${y}_{i}^{0}$, ${y}_{i}^{q1}$ or ${y}_{i}^{q2}$ was used. Equation (4) assumes the variables are measured with noise but the model is correctly specified. This can be thought of as the most optimistic assumption about the regression model. Equation (5) assumes the model omits a single uncorrelated explanatory variable, which is more realistic though still optimistic. Equation (6) assumes the model omits a single explanatory variable that partly correlates with ${x}_{1}$. We will confine the discussion to the resulting distributions of $\widehat{\beta }$.

The above simulations were each run 20,000 times and both the OLS and TLS estimates of $\beta$ were saved. Four versions of each regression were run based on different assumptions about the noise terms. In one pair $s=2$, which means that each draw of the error component in ${w}_{i}$ is, on average, half the magnitude and one-quarter the variance of the underlying signal ${x}_{i}$. The reasoning is that we assume a certain minimum level of data quality: if $s=1$ the explanatory variable is as much noise as it is signal, which seems overly pessimistic. We refer to $s=2$ as the low signal-to-noise in ${x}_{i}$ case, or ‘low $SN{R}_{x}$’. In the high $SN{R}_{x}$ case we set $s=5$, so the error draw is one-fifth the magnitude and its variance is one-twenty fifth that of ${x}_{i}$. Note that the high $SN{R}_{x}$ case approaches the no-EIV case and under our set-up we should thus expect OLS to approach unbiasedness. These two cases were run with no scaling on ${u}_{y}$, the error term on the observations. Then they were repeated using ${u}_{y}/2$ thus shrinking the noise on the dependent variable to have one-quarter the variance of the observed signal.

As noted the researcher does not does not know which of Eqs. (4), (5) or (6) has been estimated. Neither does the researcher know the true value of $\beta$, the $SN{R}_{x}$ or the scaling on ${u}_{y}$, although using climate model ensemble means rather than individual runs to construct the ${x}_{i}$’s would bring us closer to the higher $SN{R}_{x}$ case. Since the existence and magnitudes of biases will vary considerably across the values of the simulation parameters, this illustrates the challenge of interpreting coefficient estimates.

Correlated signals and noise

It is reasonable to suppose that the signal variables ${x}_{1}$ and ${x}_{2}$ will not be strictly independent. If, for instance, ${x}_{1}$ is the anthropogenic forcing pattern and ${x}_{2}$ is a natural forcing pattern dominated by volcanic aerosols they may be negatively correlated. To check, forcing patterns (anthropogenic GHG and natural) were obtained from nine climate models archived as part of the Fifth Coupled Model Intercomparison Project (CMIP5) archive and were taken as-is from the Koninklijk Nederlands Meteorologisch Instituut Climate Data Explorer site (van Oldenborg 2016). The signals were defined as linear temperature trends over the 1950–2005 interval by grid cell associated with each forcing pattern, and for each model the correlation between the anthropogenic and natural forcing signal patterns were computed. All nine correlations were negative with magnitudes ranging from − 0.29 to − 0.91. It would also be reasonable to suppose that the noise terms ${u}_{1}$ and ${u}_{2}$ are positively correlated since signal patterns from a common model will share the same underlying model-generated weather variability, however we will ignore this and assume they are independent. The above simulations are therefore re-run replacing ${x}_{2}$ with

$${x}_{2i}={v}_{2i}+c{x}_{1i}$$

where c is a constant. The resulting covariance between ${x}_{1}$ and ${x}_{2}$ will be $E\left({x}_{1}{v}_{2}\right)+c{\sigma }_{1}^{2}$ where ${\sigma }_{1}^{2}$ is the variance of ${x}_{1}$.

Results

Independent signals and noise

Low $SN{R}_{x}$, no ${u}_{y}$ scaling

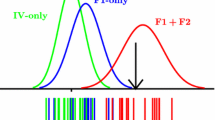
The results are summarized in the top three panels of Fig. 1 and the first three columns of Table 1. The blue curves in Fig. 1 are Normal densities using the mean and variance of the OLS estimates of $\widehat{\beta }$ and the red curves are the same from using TLS. The solid line is the distribution of $\widehat{\beta }$ from Eq. (4), dashed is from (5) and dotted is from (6). The true value of $\beta$ is as indicated. The first three columns of Table 1 report, for the low $SN{R}_{x}$ case, the bias $(Mean \widehat{\beta }-true \beta )$ and empirical one-sided 95% confidence interval widths (97.5th percentile of $\widehat{\beta }-median \widehat{\beta })$, as well as the fraction of the $\widehat{\beta }$ values exceeding 1.0, which measures the p-value on a test of model consistency or $\beta =1$. The latter three columns report the same for the high $SN{R}_{x}$ case.

Fig. 1

$\widehat{\beta }$ distributions without scaling on ${u}_{y}$; $N=200$. Blue: OLS; Red: TLS. Solid: Eq. (4); dashed: Eq. (5); dotted: Eq. (6)

Table 1 Distributions of $\beta$ with no variance scaling on y.$N=200$

Note that in this case attenuation bias is multiplicative whereas OVB is additive. Since the ${x}_{i}$’s and the noise components are uncorrelated we can estimate the univariate attenuation bias factor using the standard formula $var\left({x}_{1}\right)/(var\left({x}_{1}\right)+var\left({u}_{1}\right))$ (Wooldridge p. 311), which in the low $SN{R}_{x}$ case is $1/1.25=0.80$. In the topmost panel of Fig. 1, with a true value of $\beta =0.0$, the OLS estimators from Eqs. (4) and (5) are unbiased because the attenuation effect is multiplicative, with a slight efficiency loss in the latter case. In Eq. (6) the OLS estimator is biased upwards by 0.20 due to OVB. The application of TLS causes a dramatic increase in the variances. The estimates from Eqs. (4) and (5) are unbiased, but in Eq. (6) there is a larger upward bias (+ 0.29) than in the OLS case. Consequently, the severe loss of efficiency has no payoff in terms of relative reduction of bias.

The OLS pattern changes somewhat as the true value of $\beta$ increases to 0.50. Now Eqs. (4) and (5) exhibit the expected attenuation bias with the OLS coefficient biased downward by 0.09 in each case. But Eq. (6) still imparts a + 0.20 omitted variable bias in the other direction, with the result that the net bias becomes + 0.11 in that case. TLS remains inefficient and is now biased as well, but in a different way than OLS. Using Eqs. (4) and (5) the distribution is still very wide and the mean is displaced upward by just under + 0.1, which in Eq. (6) is combined with the OVB to yield an overall + 0.41 bias. While the upward bias from Eqs. (5) and (6) are expected due to model error it is somewhat unexpected to observe that Eq. (4) yields a biased TLS estimator as well. However, as discussed in the introduction, other than in the univariate case the literature only provides assurances of asymptotic unbiasedness under restrictive conditions on the sample variances. In this case the conditions do not hold, but this could not have been determined in advance by a researcher. When Eq. (6) is estimated and true $\beta =0.5$ the TLS bias rises to + 0.41. In the case of both Eqs. (5) and (6) the combination of bias and inefficiency means we would fail to reject a false null of $\beta =1$.

When the true $\beta =1$ the attenuation biases in the OLS Eqs. (4) and (5) become − 0.19 as expected, which is large enough to reject a true null of model consistency since $\beta =1$ is outside the 95% confidence interval. The omitted variable bias in Eq. (6) is + 0.21 so the two biases cancel out. What appears to be an unbiased OLS coefficient in that example is in fact two mutually offsetting biases, but of course in practice one can’t guarantee such a fortuitous outcome. TLS in Eqs. (4) and (5) now exhibit a bias equal in magnitude but of opposite sign to that under OLS, and in the case of Eq. (6) the combined bias is now + 0.46, with nearly the entire distribution exceeding 1.0.

Summarizing, only when true $\beta =0$ and there is no OVB does TLS yield an unbiased estimator, but OLS does as well in those cases, and it is more efficient. When true $\beta >0$, OLS is biased downwards and TLS is biased upwards. When OVB is present the TLS estimator is biased to a greater magnitude than OLS. In this configuration of variances there is no case in which TLS is preferred to OLS.

High $SN{R}_{x}$, no ${u}_{y}$ scaling

In the high $SN{R}_{x}$ case (s = 5, bottom three panels in Fig. 1) the OLS attenuation bias coefficient is now much smaller, i.e. $\frac{1}{1+\frac{1}{25}}\cong 0.962$ so we encounter a bias of approximately only − 0.04 when true $\beta =1$. In other words, there is still an attenuation bias on OLS but in practical terms it is too small to matter much. When true $\beta =0.0$ OLS is unbiased in Eqs. (4) and (5) and there is only a minor efficiency loss due to OVB. The OVB becomes slightly larger (+ 0.24) than in the low $SN{R}_{x}$ case however, and since the attenuation bias is smaller the result is a larger upward shift in the $\widehat{\beta }$ distributions in all three models compared to the low $SN{R}_{x}$ case. The small attenuation bias on OLS emerges when $\beta =0.5$ and 1.0, namely − 0.02 and − 0.04 respectively.

The TLS distributions remain inefficient with confidence interval widths at least twice the size of OLS. Also the bias magnitudes are not reduced by the increased signal strength: indeed they become slightly larger. Equations (4) and (5) still yield unbiased estimates when the true $\beta =0$ but under higher values of $\beta$ the biases grow by 0.02–0.04. Thus in all cases examined thus far OLS is a better option than TLS. Both estimators suffer bias problems, but as the signal-noise ratio in the explanatory variables increases OLS converges onto its true value while TLS does not. Both estimators suffer particularly large OVB in Eq. (6). It is worth noting that successfully detecting and remediating OVB would be more difficult under TLS because of the large variance estimates.

Downscaling${u}_{y}$

The low and high$SN{R}_{x}$ experiments were re-run replacing ${u}_{y}$ with ${u}_{y}/2$ so the variance of the error on the dependent variable shrinks by a factor of 4, making it the same magnitude as that on ${x}_{i}$ in the low $SN{R}_{x}$ case. Setting the noise variances equal across all variables coincides with a typical normalizing assumption in theoretical analyses of TLS estimation (e.g. Allen and Stott 2003), and in this case we will observe TLS is unbiased for Eq. (4) [although not for (5) or (6)]. Note that a researcher would not be able to measure the error variance on y independently of estimating the regression model itself so this change does not represent a methodological option, instead it represents an alternative conjecture regarding the unknown relative noise variances of the data.

The results are in Fig. 2 and Table 2. The OLS results remain qualitatively the same, with the combined effects of attenuation bias and OVB the same as before, but the variances are now smaller and the distributions are narrower. The empirical confidence interval widths are now virtually identical in the low and high $SN{R}_{x}$ cases. The TLS variances shrink considerably compared to the unscaled ${u}_{y}$ case. In the low $SN{R}_{x}$ case TLS in Eq. (4) now yields an unbiased estimator for all three values of $\beta$, although it remains uniformly less efficient than OLS. A comparison between Figs. 1 and 2 shows that the efficiency loss can be very sensitive to the variance of the error term of the dependent variable, which is not directly measurable.

Fig. 2

$\widehat{\beta }$ distributions after scaling ${u}_{y}$ down by half, $N=200$. Legend as for Fig. 1

Table 2 Distributions of $\beta$ with ¼ variance scaling on y. $N=200$

In the high $SN{R}_{x}$ case the noise variances are no longer equal and Eq. (4) yields an upwardly-biased TLS estimate when true $\beta >0$. Note that an improvement in the signal-noise ratio on the ${x}_{i}$’s is associated with an increase in the TLS upward bias. Equation (5) yields a biased estimate for both OLS and TLS which worsens as true $\beta$ gets larger. In the high $SN{R}_{x}$ case the magnitude of the bias on TLS equals or exceeds that on OLS under all values of $\beta$. Under Eq. (6) TLS continues to exhibit both a large upward bias and inefficiency.

Table 3 summarizes some distributional results by showing the 0.975 percentile value of the slope coefficient for Eq. (4) when true $\beta =0$. Because the attenuation bias is multiplicative and there is no OVB in this case the distributions of estimates from both methods are correctly zero-centred so the OLS entry indicates the start of the region in which a Type I error would occur. The relative inefficiency of TLS implies that a part of its distribution overlaps the Type I region and a larger critical value is needed to reject the zero null. In the upper left cells, corresponding to no variance scaling on y and low $SN{R}_{x}$ the OLS 2.5% upper tail starts at 0.127 whereas the TLS 2.5% upper tail begins at 0.434, which is about 3.4 times higher. In all cases the TLS upper tail cut-off point is higher than that for OLS, with the smallest gap in the lower right grouping, with the variance on ${u}_{y}$ downscaled and high $SN{R}_{x}$.

Table 3 97.5th percentile of $\widehat{\beta }$ when true $\beta =0$ using Eq. (4)

Discussion of results thus far

The estimator comparisons are summarized in Table 4. The rows are grouped by true value of $\beta$ and within each group, the rows correspond to whether the model is correctly specified (no OVB), missing an uncorrelated explanatory variable (OVB-1) or missing a correlated explanatory variable (OVB-2). The preferred estimator is the one shown and the ground for the preference is indicated in brackets. (e) indicates that one is more efficient than the other, but neither one is materially less biased. (b) denotes that one is less biased than the other but both are about equally efficient. (b,e) indicates that the preference is based on grounds both of bias and efficiency improvements.

Table 4 Preferred estimators. Term in brackets denotes basis of preference: b – reduced bias, e – increased efficiency

TLS is preferred in only 4 of 36 cases, and in one there is no clear preference. If the researcher has no information at all about which cell best describes the information set and the true model, OLS is a safer choice. If specific conclusions depend on using TLS rather than OLS the researcher needs to make the case why the conditions support using TLS. The difficulty is that the case may depend on the relative sizes of unobservable variances. As the variance of the error term on ${x}_{1}$ goes from high to low the preference moves unambiguously towards OLS. This accords with theory since the rationale for TLS is the presence of errors in the explanatory variables, and the smaller these are, the closer we get to conditions that guarantee OLS is unbiased and efficient. But even within the low $SN{R}_{x}$ case, note that the preference moves unambiguously towards OLS as the variance on y increases (compare column 2 to column 1). This is because consistency properties of ${\widehat{\mathbf{b}}}_{TLS}$ depend on the relative variances of the dependent and independent variables. While the researcher may have reason to believe the data set belong to the low $SN{R}_{x}$ category (for instance if the signals are from individual climate models rather than ensemble averages) there is no information within the sample itself that would tell a researcher whether the data belong to the high or low ${u}_{y}$ variance group.

Likewise the preference moves unambiguously towards OLS as the true $\beta$ approaches zero. This raises an important point about signal detection: rejection of the zero null on $\beta$ cannot be conditional on the decision to use TLS, since if the null were true we would not choose TLS. Signal detection can only be based on TLS results if it is confirmed using OLS. Unfortunately it is rare for researchers report results from both TLS and OLS estimation, which means readers cannot tell if published signal detection results were consistent with the estimator choice.

Finally the preference moves unambiguously towards OLS as the likelihood of OVB-2 rises. This cannot be ruled in or out merely by inspecting the estimation results. It needs to be specifically tested for and ruled out using information from outside the original information set (see, e.g. Davidson and MacKinnon 2004). However the construction of informative F tests for this purpose would be undermined by the greatly inflated variances from TLS estimation. Hence such tests would be better constructed using OLS variances.

Several authors have noted that optimal fingerprinting coefficients can be very unstable and even sensitive to the choice of which climate model is used to generate the internal variability covariance matrix (see Jones et al. 2013, 2016 for examples). The instability typically takes the form of extremely wide confidence intervals. Examining the 72 distributions in Figs. 1 and 2, if the TLS standard errors are very large but those of OLS are not, it is likely we are in a Fig. 1-type information set, in which the error variance on y is large enough that OLS would be preferred. If the OLS and TLS coefficient variances are reasonably similar we are probably looking at a case more like Fig. 2 in which TLS will be preferred unless $SN{R}_{x}$ is high, in which case TLS overcorrects and OLS is preferred.

It is noteworthy that the biases in OLS and TLS tend to go in opposite directions. More specifically, the bias in TLS is always $\ge 0$ in these experiments, although there was nothing in the set-up that suggested a priori this would be the outcome. The derivation in the Appendix reveals that unlike OLS the TLS slope coefficient depends on unbiased error variance estimates, which are themselves difficult to obtain. Consequently biased variances will introduce biases in the slope coefficients. This has numerous implications even if the bias does not affect the binary decision of whether a signal is detected or not. The magnitudes of signal scaling coefficients are themselves important because they are used in the computation of transient climate response (TCR) magnitudes (Jones et al. 2016) and Transient Response to Cumulative Emissions (TCRE) magnitudes (Gillett et al. 2013) which, in turn, are important for estimating future warming rates and potential carbon budgets for compliance with policy goals such as the Paris targets (Nijsse et al. 2020). A systematic upward bias in the signal coefficients would result in a downward bias on the Paris-compliant carbon budget.

Correlated signals and noise

We consider the case with $c=-0.15$ which implies a correlation of about − 0.2 between ${w}_{1}$ and ${w}_{2}$. This parameter value is well below the range (– 0.29 to – 0.91) computed from the CMIP5 sample noted above and is therefore a conservative magnitude. It was also chosen to avoid the “weak signal” regime in DelSole et al. (2019) which refers to highly correlated signals which creates problems for constructing confidence intervals. Setting c to 0.9, for instance, causes the TLS results to become degenerate and uninformative. The chosen parameter value is small enough to belong to the “strong signal” regime, in the sense that ${w}_{1}$ and ${w}_{2}$ are still largely independent, but large enough to provide interesting contrasts with the uncorrelated case.

The results are summarized in Tables 5 and 6; Figs. 3 and 4, which follow the formats of Tables 1 and 2 and Figs. 1 and 2. Figure 3 shows the results for the unscaled ${u}_{y}$ case. The OLS confidence intervals are wider by a negligible amount but the TLS ones become considerably wider. The biases noted previously retain their respective signs and become larger. In all six panels in Fig. 3, OLS imparts a downward bias and TLS imparts an upward bias regardless of the estimation [Eqs. (4), (5) or (6)]. Interestingly OLS exhibits an additive negative bias so its distribution is centered slightly below zero even when true $\beta =0$. Moving from the low $SN{R}_{x}$ to the high $SN{R}_{x}$ case we can see that the OLS bias shrinks but—as before—the TLS bias gets larger.

Table 5 Distributions of $\beta$ with no variance scaling on y and $c=-0.15$.$N=200$

Table 6 Distributions of $\beta$ with ¼ variance scaling on y. $N=200$

Fig. 3

Same as Fig. 1 but with correlated signals

Fig. 4

Same as Fig. 2 but with correlated signals

Of particular note, when the true value of $\beta =0$, in the low $SN{R}_{x}$ case under Eq. (6) and in the high $SN{R}_{x}$ case with all three estimation equations the TLS distribution is centered so far above zero that the lower 2.5% bound is itself above zero and we therefore have a Type I error, or a false signal detection. In the OLS case a false detection would occur for Eq. (6) at the 10% significance level in the low $SN{R}_{x}$ case and at 5% in the high $SN{R}_{x}$ case.

Figure 4 shows the results with the variance on ${u}_{y}$ scaled down so the noise variances are equal on all variables. OLS retains its downward bias in the low $SN{R}_{x}$ case using Eqs. (4) and (5) whereas TLS is unbiased using Eq. (4). The omission of an uncorrelated explanatory variable (Eq. 5) does not change the OLS estimator but does impart an upward bias on TLS. Both OLS and TLS yield Type I errors in the Eq. (6) case, and in the high $SN{R}_{x}$ case TLS does additionally in the Eq. (5) case.

Focusing on the case where the true $\beta =0$, between Figs. 4 and 5 OLS exhibits a Type I error in four of the 12 cases (whenever Eq. (6) is used) and TLS exhibits a Type I error in in seven of the 12 cases. Additionally, both OLS and TLS tend to be more likely to reject a true null hypothesis in the higher $SN{R}_{x}$ case, because the variance shrinks more quickly than the bias. Also, in the high $SN{R}_{x}$ case the positive bias increases on TLS but not on OLS. With the exception of the low $SN{R}_{x}$ case with ${u}_{y}$ variance scaled down, TLS exhibits an upward bias exceeding the downward bias on OLS.

Overall, as with uncorrelated signals, when the explanatory signals are negatively correlated TLS compares unfavourably to OLS in most cases. Except when there is no model misspecification (Eq. 4) and the error terms all have equal variances TLS is biased, inefficient and prone to false positives. Even if the true $\beta >0$ the TLS coefficient magnitude is biased upward. Since there is no way for the researcher to tell which specific case is being observed OLS in general would be a safer choice but if it suspected that we are in a low $SN{R}_{x}$ regime with no OVB it should be assumed that OLS underestimates $\beta$ and results from using a single signal vector should be compared to those from an ensemble average of signal vectors.

Conclusions

Figures 1, 2, 3 and 4 present 72 parameter distributions for each (OLS, TLS) estimator which might describe the underlying data generating process from which a fingerprinting coefficient estimate was drawn. Unless the researcher takes specific steps to ascertain which one is most relevant there could be serious problems with interpretation. Some steps are straightforward, such as checking if the signal patterns are uncorrelated. Others are more difficult, such as testing for omitted variables bias. In the absence of specific evidence supporting use of TLS it should not be a default option. OLS imparts a downward bias in the coefficient estimate except in the uncorrelated signals case when true $\beta =0$, or when a correlated explanatory variable is omitted from the model. As $SN{R}_{x}$ rises the attenuation bias becomes small and less likely to interfere with a valid signal detection inference. The assumption that TLS is always less biased than OLS is incorrect in the multiple regression context or even in the single-variable case when the model is underspecified. The simulations herein show that overcorrection is ubiquitous in the multivariate case, and in some cases, for instance if the signal patterns are negatively correlated the upward bias can be severe enough to routinely yield false positives. Even when an upward bias is not large enough to yield a false positive, it would still lead to downward bias in TCRE-based carbon budget applications. Also the bias gets worse as the signal-noise ratio on the explanatory variable strengthens, which is opposite to intuition.

For testing the specific hypothesis of whether an anthropogenic signal coefficient is zero (“detection”) TLS is especially unreliable since the coefficient is typically undefined under the null. This problem does not arise with OLS and in the uncorrelated signals case the attenuation bias goes to zero, so anthropogenic signal detection results can be based on, or should at least be confirmed with, OLS. If it is believed a priori that $\beta >0$ and the signals and noise terms are believed to be independent, OLS will still be preferred if the dependent variable is relatively noisy or if the explanatory variables are known to contain a relatively small error component, or if omitted variable bias has not been ruled out. These decisions cannot be made based only on information in the sample itself or from TLS results alone. At a minimum readers need to compare TLS and OLS results to assess whether conditions supporting use of TLS might be present, and ideally should be shown tests for the presence of OVB based on OLS variances.

If OLS generally biases low and TLS generally biases high, what should a researcher do? Optimal fingerprinting methodology would benefit from use of the instrumental variable method, which is a feasible and commonly-used tool in econometrics for dealing with randomness in explanatory variables which has well-established consistency properties (Fuller 1987; Davidson and MacKinnon 2004).

Appendix

Comparison of TLS estimator $\tilde{b}={\left({M}_{WW}-{S}_{UU}\right)}^{-1}{M}_{Wy}$ and OLS estimator $\widehat{b}={M}_{WW}^{-1}{M}_{Wy}$:

$${(M}_{WW}-{S}_{UU})\tilde{b}={M}_{Wy}$$

$${\Rightarrow M}_{WW}\tilde{b}-{S}_{UU}\tilde{b}={M}_{Wy}$$

$$\Rightarrow \tilde{b}-{M}_{WW}^{-1}{S}_{UU}\tilde{b}={M}_{WW}^{-1}{M}_{Wy}=\widehat{b}$$

$$\Rightarrow (I-{M}_{WW}^{-1}{S}_{UU})\tilde{b}={M}_{WW}^{-1}{M}_{Wy}=\widehat{b}$$

Assume a 2 variable case and denote $\delta ={\left({m}_{11}{m}_{22}-{m}_{12}^{2}\right)}^{-1}$. Note ${M}_{WW}^{-1}=\left[\begin{array}{cc}{\delta m}_{22}& -\delta {m}_{12}\\ -{\delta m}_{12}& \delta {m}_{11}\end{array}\right]$.

Then if ${S}_{UU}$ is diagonal

$$\left(I-{M}_{WW}^{-1}{S}_{UU}\right)=\left[\begin{array}{cc}{1-\delta m}_{22}{s}_{11}& \delta {m}_{12}{s}_{22}\\ \delta {m}_{12}{s}_{11}& 1-\delta {m}_{11}{s}_{22}\end{array}\right]$$

and

$$\left[\begin{array}{c}{\widehat{b}}_{1}\\ {\widehat{b}}_{2}\end{array}\right]=\left[\begin{array}{c}\left({1-\delta m}_{22}{s}_{11}\right){\tilde{b}}_{1}+{\delta {m}_{12}{s}_{22}\tilde{b}}_{2}\\ \delta {m}_{12}{s}_{11}{\tilde{b}}_{1}+\left(1-\delta {m}_{11}{s}_{22}\right){\tilde{b}}_{2}\end{array}\right]$$

Taking the first row: ${\widehat{b}}_{1}={\tilde{b}}_{1}+\delta \left({{m}_{12}{s}_{22}{\tilde{b}}_{2}-m}_{22}{s}_{11}{\tilde{b}}_{1}\right)$ and if we assume $\delta >0$ we obtain

$${\widehat{b}}_{1}<{\tilde{b}}_{1}\iff \frac{{m}_{12}{s}_{22}}{{m}_{22}{s}_{11}}<\frac{{\tilde{b}}_{1}}{{\tilde{b}}_{2}}$$

as stated.