Abstract
Interannual oscillatory modes, atmospheric and oceanic, are present in several large regions of the globe. We examine here low-frequency variability (LFV) over the entire globe in the Community Earth System Model (CESM) and in the NCEP-NCAR and ECMWF ERA5 reanalyses. Multichannel singular spectrum analysis (MSSA) is applied to these three datasets. In the fully coupled CESM1.1 model, with its resolution of \(0.1 \times 0.1\) degrees in the ocean and \(0.25 \times 0.25\) degrees in the atmosphere, the fields analyzed are surface temperatures, sea level pressures and the 200-hPa geopotential. The simulation is 100-year long and the last 66 yr are used in the analysis. The two statistically significant periodicities in this IPCC-class model are 11 and 3.4 year. In the NCEP-NCAR reanalysis, the fields of sea level pressure and of 200-hPa geopotential are analyzed at the available resolution of \(2.5 \times 2.5\) degrees over the 68-years interval 1949–2016. Oscillations with periods of 12 and 3.6 years are found to be statistically significant in this dataset. In the ECMWF ERA5 reanalysis, the 200-hPa geopotential field was analyzed at its resolution of \(0.25 \times 0.25\) degrees over the 71-years interval 1950–2020. Oscillations with periods of 10 and 3.6 years are found to be statistically significant in this third dataset. The spatio-temporal patterns of the oscillations in the three datasets are quite similar. The spatial pattern of these global oscillations over the North Pacific and North Atlantic resemble the Pacific Decadal Oscillation and the LFV found in the Gulf Stream region and Labrador Sea, respectively. We speculate that such regional oscillations are synchronized over the globe, thus yielding the global oscillatory modes found herein, and discuss the potential role of the 11-year solar-irradiance cycle in this synchronization. The robustness of the two global modes, with their 10–12 and 3.4–3.6 years periodicities, also suggests potential contributions to predictability at 1–3 years horizons.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and motivation
Interannual and interdecadal oscillations with a regional extent have been found in several areas of the Earth’s oceans and atmosphere. In and near the North Atlantic basin, such oscillations have been identified in many observational studies, including in the oceans’ temperature field and in the atmosphere’s geopotential fields (e.g., Bjerknes 1964; Deser and Blackmon 1993; Dettinger et al. 1995; Hurrell and Van Loon 1997; Moron et al. 1998; Da Costa and Colin de Verdiére 2002; Feliks et al. 2010; Jajcay et al. 2016). The extent to which these oscillations are due to purely oceanic (Dijkstra and Ghil 2005; Berloff et al. 2007, and references therein) purely atmospheric (e.g., Frankignoul and Hasselmann 1977; Frankignoul et al. 1997) or coupled (Vannitsem et al. 2015, and references therein) processes is still a matter of controversy (Dijkstra and Ghil 2005; Ghil and Robertson 2000; Clement et al. 2015; Zhang et al. 2016; Srivastava and DelSole 2017).
Over and near the Pacific Ocean basin, the Pacific Decadal Oscillation (PDO) was extensively studied; see, for instance, the Newman et al. (2016) review. These authors affirm that, in all likelihood, the PDO is not due to a single mechanism but rather to the combination of several different basin-scale processes. The spatial patterns corresponding to these processes are not identical and their characteristic time scales are quite different, but they all project strongly onto the PDO pattern; see also Chao et al. (2000).
Newman et al. (2016) identify three eigenmodes that represent dynamical processes with maxima in the northern, central tropical–northern subtropical, and eastern tropical Pacific, respectively; similar patterns from various analyses have been reported elsewhere (e.g., Barlow et al. 2001; Chiang and Vimont 2004; Guan and Nigam 2008; Compo and Sardeshmukh 2010. The first eigenmode represents largely North Pacific dynamics, while the latter two represent interannual-to-decadal tropical dynamics driving North Pacific variability. Among the proposed mechanisms, several authors (e.g., Deser et al. 1999; Seager et al. 2001; Schneider and Cornuelle 2005; Zhang and Delworth 2015; Wills et al. 2019 suggest that the PDO is primarily an extratropical phenomenon caused by an integrated response to prior Aleutian Low wind stress forcing, while other studies suggest that it represents the long-lived remnants of ENSO variability (e.g.,Zhang et al. 1997; Vimont 2005; Newman et al. 2016,).
In this paper, we focus on significant oscillations with periods in the interannual-to-interdecadal, 2–15-years band studied, for instance, by Moron et al. (1998). Several studies reported oscillations in this band in sea surface temperatures (SSTs), as well as in land surface and atmospheric temperatures. Deser et al. (2002), for instance, addressed decadal recurrence of above-normal sea ice extent anomalies in the Labrador Sea and associated below-normal SSTs in the North Atlantic basin (NAB), with a 1–3-years persistence of these anomalies. They attributed a major role to atmospheric forcing but admitted that the year-to-year SST persistence in the subpolar NAB could not be simulated with a slab mixed-layer ocean. In a rather different spirit, Clement et al. (2015) and Srivastava and DelSole (2017) suggested that the Atlanitic Multidecadal Oscillation and PDO are mainly the oceans’ response to stochastic forcing by the mid-latitude atmospheric circulation, while Zhang et al. (2016) vigorously rebutted the claims of Clement et al. (2015).
Curry and McCartney (2001) and Eden and Jung (2001) showed observational evidence of interannual-to-interdecadal variability in the intensity of the North Atlantic gyre circulation related to the atmospheric North Atlantic Oscillation (NAO) patterns. Eden and Jung (2001), moreover, provided evidence for interdecadal variability in the surface net heat flux forcing associated with the NAO governing interdecadal changes of the North Atlantic circulation. Feliks et al. (2011), though, found a 10.5-years periodicity in the Atlantic SSTs along the North Atlantic Drift near the Grand Banks that affected the atmospheric circulation above. Muller et al. (2013) analyzed average global land surface temperatures and found a significant oscillation with a period of 9-10 yr that correlates well with their Atlantic SST index, while the period is quite close to that of Feliks et al. (2011).
Kondrashov et al. (2005) studied the Nile River water level records for 1–300 years and found statistically significant interannual oscillations with periodicities of 2.2, 4.2 and 7 years. The two shorter ones were attributed to precipitation anomalies over the Ethiopian Plateau due to the effect of the Southern Oscillation on the African easterlies, while the latter was linked to NAO influences. Feliks et al. (2010, 2013) showed that a 2.7-years and a 7–8-years oscillation is present over the NAB, Middle East, the Indian subcontinent and the Tropical Pacific, and that the separate regional modes are synchronized at these two periodicities, at least in part.
Whatever the origin of these oscillations, understanding the complex interactions between the ocean and the overlying atmosphere is crucial for the prediction of the climate system’s LFV (Kushnir et al. 2002; Czaja et al. 2003; Hurrell et al. 2003; Visbeck et al. 2003; Liu 2012; Vannitsem et al. 2015; Pierini et al. 2016). The physics behind the climate’s LFV is still far from elucidated and there are basic questions such as: is the ocean causing the variability and if so, in what regions, and how does it influence the atmosphere? Atmospheric LFV with similar broad periodicities is often found thousands of kilometers away, largely over the land, as in Feliks et al. (2010, 2013, 2016). While the results of Feliks et al. (2004, 2007, 2011) suggest that it is the interannual variability of oceanic thermal fronts, such as the Gulf Stream or Kuroshio front, that give rise to atmospheric LFV above the fronts and further downwind, the amplitude of this LFV is smaller by an order of magnitude than the variance of the synoptic-scale weather systems and of the intraseasonal variability.
Previous studies concentrated on regional or, at most, hemispheric aspects of interannual variability, albeit including teleconnection effects. The purpose of this paper is to examine global modes of interannual variability. We find that two such modes are statistically significant and have periods of 10–12 yr and roughly 3.5 yr. Both are, in fact, consistent with some of the previously described regional modes. The exact mechanism for the way that these two global climate modes arise has to be left for further studies but it seems to be consistent with their being synchronized by propagating waves in the atmosphere and oceans.
Most previous studies used low-resolution general circulation models (GCMs) or highly idealized ones that lacked many important processes in the ocean and the atmosphere. In this paper, we use the Community Earth System Model (CESM: Hurrell et al. 2013; Small et al. 2014), an IPCC-class GCM with a resolution of \(0.1 \times 0.1\) degrees in the ocean and \(0.25 \times 0.25\) degrees in the atmosphere, as recommended by Feliks et al. (2004, 2007) and improved upon by Minobe et al. (2008). Such high resolution is necessary to resolve the ocean’s internal dynamics, particularly in the western boundary currents and their eastward-jet extension, like the Gulf Stream and North Atlantic Drift, as well as resolving the air–sea fluxes and the atmospheric dynamics in regions of narrow SST fronts, cf. Small et al. (2008). The results obtained by analyzing a CESM 100-years simulation are then confronted with those afforded by a study of the NCEP-NCAR reanalysis (Kalnay et al. 1996; Kistler et al. 2001) and of the ECMWF ERA5 reanalysis (Hersbach et al. 2020).
A number of previous papers studied also global modes of variability in the observations or reanalyses on the interannual-to-interdecadal time scale. Thus, Moron et al. (1998) used MSSA to examine the U.K. Meteorological Office’s MOHSST5 data base of SSTs over the 1901–1994 time span and found several interannual oscillations associated with the El Niño–Southern Oscillation (ENSO) and the NAB, as well as an irregular trend with 1910–1940 and 1975–1994 warming and 1940–1975 cooling, especially in the northern hemisphere; see also Ghil and Vautard (1991). The change in trend was preceded in both 1940 and 1975 by the appearance of a small anomaly of opposite sign in the North Atlantic, south of Greenland (Moron et al. 1998, Fig. 3, panels 1936–1940 and 1976–1980).
De Viron et al. (2013) used a comprehensive set of 25 climate indices; their set encompassed not only scalar indices associated with climate variability in large regions, like ENSO or the PDO, but also some that have been associated with much smaller areas, like Sahel rainfall. The various indices extended over time spans of 50–60-years lengths. These authors found that four leading principal components (PCs) captured most of the variability in their dataset; the spectral analysis of these PCs was limited to the shortest interannual modes, namely those associated with ENSO, because of the limited length of their dataset.
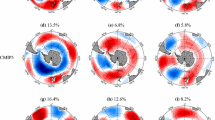
Finally, Kravtsov (2017) and Kravtsov et al. (2018) focused on the differences between decadal and multidecadal climate variability in simulations produced by IPCC-class models from the Coupled Model Intercomparison Project Phase 5 (CMIP5: Taylor et al. 2012), on the one hand, and in a number of datasets, such as the indices used by De Viron et al. (2013) and others, and two distinct reanalyses, 20CRv2 (Compo et al. 2011) and ERA-20C (Poli et al. 2016). They did find in the observational datasets a global stadium wave (GSW), which was not present in the model simulations nor was it similar to the decadal wave found in this paper. Gavrilov et al. (2020a) took another look at this GSW by introducing a novel analysis method of the data, based on Linear Dynamical Modes (LDMs).
In Sect. 2, we present the CESM model and its 100-years simulation, as well as the MSSA methodology. The CESM simulation is studied in Sect. 3, emphasizing oscillatory modes in the 2–15-years band. In Sect. 5, we ascertain that the spatio-temporal pattern and the dynamics of the 11-years oscillatory mode is not an artifact of the MSSA methodology and that it can be obtained directly from the data. In Sect. 4, we present the NCEP-NCAR reanalysis and ECMWF ERA5 reanalysis and their interannual oscillations. A summary and conclusions follow in Sect. 6, where we also attempt to address (a) the differences between our results and those of Kravtsov et al. (2018) and Gavrilov et al. (2020b); and (b) the potential role of the solar cycle in the decadal mode described in this paper.
The Electronic Suplementary Material (ESM) complements the information in the paper’s main text. It consists of three short animations for northern hemisphere fields extracted from the CESM model’s simulation:
-
(i)
The 11-years oscillatory mode in the surface temperatures (STs);
-
(ii)
The 11-years oscillatory mode in the 200-hPa geopotential field; and
-
(iii)
The 3.4-years oscillatory mode in the 200-hPa geopotential field.
2 Dataset and methodology
2.1 The Community earth system model (CESM)
CESM is a state-of-the-art, fully coupled ocean–atmosphere GCM (Hurrell et al. 2013). The version used herein is CESM1.1; see also Small et al. (2014). The model components are the Community Atmosphere Model (CAM5), with the Spectral Element dynamical core and 27 vertical levels, and the Community Land Model (CLM4), both with a horizontal resolution of horizontal resolution of \(0.25 \times 0.25\) degrees, which permits mesoscale systems, coupled with the Parallel Ocean Program (POP2) with 62 vertical levels and the Community Ice CodE (CICE), both with a horizontal resolution of \(0.1 \times 0.1\) degrees, These resolutions permit the inclusion of mesoscale systems in the atmosphere and resolve many of the mesoscale eddies in the ocean.
CESM was run for 100 year from an initial state for year 2000 and a short, one-year ocean-ice spin-up from the Gouretski and Koltermann (2004) climatology, based on the World Ocean Circulation Experiment (WOCE) results and other data. Present-day greenhouse gas conditions—e.g., a fixed 367 ppm \(\hbox {CO}_2\) concentration—were used.
The coupled run performed ocean–atmosphere coupling every 6 hr and its atmospheric fields equilibrated to a statistically near–steady state in about 33 years. The subsurface fields in the ocean were still experiencing some climate drift, but the SSTs equilibrated, too, after the CESM run’s first 50 years, as documented in Small et al. (2014, Fig. 1b). The reanalysis datasets studied in Sect. 4 are 68-years and 71-years long, for the NCEP-NCAR and ERA5 reanalysis, respectively; hence, we analyzed the last 66 years of the CESM model simulation using the methodology of the next subsection. The residual SST drift did not seem to affect the LFV in the atmospheric fields that we analyzed.
2.2 Multivariate singular spectrum analysis (MSSA)
To identify complex patterns of spatio-temporal behavior in the CESM simulation summarized above, we rely here on MSSA, which provides an efficient and robust tool to extract dynamics from short, noisy time series. MSSA relies on the classical Karhunen–Loève decomposition of stochastic processes into data-adaptive orthogonal functions. Broomhead and King (1986) introduced MSSA into dynamical system analysis as a robust version of the Mañé–Takens idea to reconstruct the underlying dynamics from a time-delayed embedding of time series; see Ghil et al. (2002) and Alessio (2015, Ch. 12) for a comprehensive overview of the methodology and of related spectral methods. Groth et al. (2017) present some of the algorithmic details that have proven useful in applying MSSA to high-dimensional climatic problems.
The MSSA method essentially diagonalizes the lag-covariance matrix \(\mathbf{M}\) of one or more climatic fields to yield a set of orthogonal eigenvectors and the corresponding eigenvalues. The eigenvectors are referred to as space-time empirical orthogonal functions (ST-EOFs), while the eigenvalues equal the variance that is captured in the direction of a given ST-EOF. The projection of the original data onto the ST-EOF yields the corresponding PCs. A key feature of the MSSA approach is that oscillatory behavior is detected by the presence of so-called oscillatory pairs, that is, ST-EOFs with approximately equal eigenvalues and fundamental frequencies (Vautard and Ghil 1989; Ghil and Vautard 1991; Plaut and Vautard 1994).
To improve the separability of distinct frequencies, we rely here on a subsequent varimax rotation of the ST-EOFs (Groth and Ghil 2011). The presence of oscillatory pairs, though, is not sufficient to reliably identify nearly periodic deterministic behavior in the underlying dynamics. Allen and Smith (1996) provided, therefore, a Monte Carlo–type test against a null hypothesis of red noise for the statistical significance of one or more oscillatory modes, while Allen and Robertson (1996) suggested a multi-channel extension thereof to MSSA. A more rigorous significance test for the multivariate, high-dimensional case considered herein was formulated by Groth and Ghil (2015) and applied to coupled ocean–atmosphere interannual variability by Groth et al. (2017). It is the latter form of the significance test for high-dimensional MSSA that was used throughout the present paper.
3 Interannual oscillatory modes in the CESM model’s simulation
To find the coupled oscillatory modes in the CESM simulation, we examine the global surface temperatures (STs) over sea and land, the sea level pressures (SLPs) and geopotential heights at 200 hPa. Note that CESM does not contain a prognostic equation for the temperature of the interface between the atmosphere and sea or atmosphere and land. Hence, the STs in CESM are computed, over the oceans as well as over the continents, by equating the heat fluxes at each grid point on either side of the interface with the atmosphere.
These three fields represent therewith the land, the sea and the lower and upper layers of the atmosphere. The resolution we used in our ST analysis was about \(0.5 \times 0.5\) degrees, while it was about \(1.0 \times 1.0\) degrees for the SLP and 200 hPa fields. The fact that the resolution cannot be exactly uniform is due to the presence of different horizontal grids near the surface in the atmosphere and in the oceans, which requires interpolation. We normalize each field by its variance so as to analyze the three of them together.
To remove the strong seasonal cycle in the data, we first calculated monthly averages from the daily values. We then applied a 12-month moving-average filter to the monthly time series so obtained. Feliks et al. (2013) examined the response function of this filter and showed that the amplifying or damping of the periodicities longer than 3 years is very small. Next, we derived annually sampled time series by simply taking all 66 January values from this smoothed time series and checked that the results are almost the same as those reported below when taking another month of the year.
MSSA was then applied with a window width of \(M = 20\) years. In constructing the lag-covariance matrix \(\mathbf{M}\), copies of the available time series are lagged by multiples of 1 years, and the maximum lag equals the method’s window width M, i.e., the matrix \(\mathbf{M}\) is \(M \times M\). This window width is about 1/3 of the length of the time series, as recommended by Vautard and Ghil (1989). The methodology is by now pretty standard in the climate sciences (e.g., Krishnamurthy 2019) and there are many sources for the the algorithmic details (Ghil et al. 2002; Alessio 2015; Groth et al. 2017, and references therein). Only the signals significant at the two-sided 95% level are analyzed further below.
3.1 The CESM model’s decadal mode
The MSSA spectrum of the combined global fields is shown in Fig. 1 together with error bars that indicate the 95% confidence interval with respect to a null hypothesis of red noise. Oscillations with periods of 11 and 3.4 years emerge as statistically significant and are analyzed below. There several points around 0.05 cy/year and below that appear as statistically significant, but these points are associated with periods of 20 years and longer. Since the total length of the time series is \(N = 66\) years, the oscillatory modes corresponding to these points cannot be resolved correctly since they only satisfy—marginally or not at all—the Vautard and Ghil (1989) criterion of \(N \ge 3M\).
Spectral analysis of the time series of the global ST, SLP and 200-hPa fields, as found in the CESM model simulation, after detrending and by using MSSA with a window width \(M = 20\) years, after subtracting the seasonal cycle and applying varimax rotation for better frequency separation (Groth and Ghil 2015; Groth et al. 2017). The estimated variance of each mode in the dataset is shown as a filled red square, while lower and upper ticks on the error bars indicate the \(5{\mathrm{th}}\) and \(95{\mathrm{th}}\) percentiles of a red-noise process constructed from a surrogate data ensemble of 100 time series. Each of the surrogates has the same variance and lag-one auto-correlation as the original record. The surrogate time series were produced by projecting the first 40 principal components (PCs) of the MSSA analysis onto the basis vectors of a red-noise process
The oscillatory mode captured by the ST-EOFs (3,4) pair has a period of 11 years and accounts for 6% of the interannual variance, after subtracting the seasonal signal. Phase composites of the corresponding reconstructed components (RCs: Ghil and Vautard 1991; Ghil et al. 2002), denoted by RCs (3,4), are shown in Figs. 2, 5 and 6, for the ST, 200 hPa and SLP fields, respectively. In each of these three figures, the cycle has been divided into eight phase categories, following Moron et al. (1998).
Composites of the 11-years mode of global STs found in the CESM model simulation, in eight phase categories, displayed clockwise and labeled by the epoch at the middle of the category; color bar in degrees Celsius. These composites are based on the MSSA pair (1,2), which captures 6% of the interannual variance. The mean ST field in the middle panel has contour interval (CI) = 2 K
In the ST field of Fig. 2, north of 25 N, the 11-years oscillatory mode is dominated by a superposition of wavenumbers 1–3 in the zonal, east–west direction, with alternating, large-scale warm and cold anomalies. These waves are propagating eastward and poleward around the globe.
For example, the very extensive warm anomaly occurring in phase 4.1 years at longitudes (40 E–320 E) and latitudes (20 N–75 N) shrinks substantially and can be found in phase 6.9 years mainly north of 70 N and over North America. The cold anomaly located in phase 4.1 years at longitudes (70 E–200 E) and latitudes (20 N–40 N) propagates to longitudes (40 E–320 E) and latitudes (40 N–75 N) in phase 8.2 years. So, in phase 9.6 years, the warm and cold anomalies have switched their places with respect to the phase at 4.1 years. This mode is found over vast regions of the Arctic Ocean and the surrounding high-latitude land areas. It would thus appear that the interaction of sea ice with the ocean, atmosphere and land surfaces plays a large role in this oscillation. The propagation of the ST of this mode in most of the northern hemisphere is shown in the animation in Online Resource 1.
The 11-years oscillations in STs over the North Pacific display a tongue-and-horseshoe pattern. This pattern is similar to PDO patterns found in previous studies (e.g.,Newman et al. 2016; Kren et al. 2016). Comprehensive reviews of the different processes that affect the PDO can also be found in Miller and Schneider (2000) and Alexander et al. (2010).
In our results, though, a warm tongue is found in phases 9.6–2.8 years; it starts developing at 144 W over Japan, and it propagates northeastward. Later, as the tongue reaches the West Coast of North America, the warm anomaly deforms to a horseshoe shape, in phases 2.8–5.5 years. During the latter phases, a cold tongue develops in the western mid-latitudes of the Pacific Ocean; thus, in phases 4.1 years and 5.5 years, a cold tongue in the western basin coexists with a warm horseshoe in the east.
The tongue and horseshoe described herein are spatial features that do appear in the second and third eigenmodes of the PDO, as obtained by Newman et al. (2016); see their Figs. 6b and 6d, respectively. But there are significant differences in the evolution of their modes and ours, and the succession of changes in shape, extent, location and polarity of these features, as shown in Fig. 2 here, cannot be represented by a linear combination,whose coefficients change in time, of the Newman et al. (2016) patterns in their Figs. 6b and 6d; the latter were derived by using a methodology that emphasizes variability in the North Pacific ocean basin, while ours is evenhandedly global.
Thus, for instance, in phases 6.9 years and 1.4 years of our Fig. 2, only a very small tongue is present in the western North Pacific; this state cannot be described by a weighted sum of the second and third eigenmodes of Newman et al. (2016): the second one (their Fig. 6b) has a very large tongue, while the third one (their Fig. 6d) has only a negligible amplitude in the western basin and cannot erase therewith the large area and strength of the second mode there. Hence the North Pacific features of our global 11-years oscillatory mode seem to provide a different picture of the decadal component of the PDO than the Newman et al. (2016) combination of regional mechanisms.
Turning now to the North Atlantic sector, the 11-years oscillatory mode in the Labrador Sea has a warm ST anomaly in the phases 1.4 years–4.1 years and a cold one in phases 6.9 years–9.6 years. We will show further below that the temperatures in the Labrador Sea at depth of 5 m lack these anomalies and are thus led to conclude that this oscillation is probably due to changes in sea ice cover. This mode in our results seems to agree in the Atlantic sector with the decadal variations described by Deser et al. (2002). The latter authors used a simple ice–ocean mixed layer model forced with observed air temperature and wind fields and found that large-scale atmospheric thermodynamic forcing could account for much of the ice extent and SST evolution, but that the year-to-year persistence of SST anomalies in the subpolar Atlantic could not be explained in the absence of an active ocean.
There is a close connection, though, between the eastward propagation of the global decadal mode herein and the temperature anomaly in the Gulf Stream region, as seen in Fig. 2. To highlight this connection, Fig. 3 zooms into the Gulf Stream area within the curvilinear rectangle (35 N–46 N, 287 E–310 E). A cold anomaly is observed in phases 1.4 years–5.5 years, and a warm anomaly in phases 6.9 years–11 years. Further to the northeast in the domain (46 N–60 N, 320 E–330 E), a warm anomaly is observed in phases 2.8 years–5.5 years, and a cold anomaly in phases 8.2 years–11 years as the oscillatory 11-years mode propagates eastward.
Composites of the 11-years mode of global STs shown in Fig. 2, but zooming over the North Atlantic basin (NAB) in the Gulf Stream area (35 N–46 N, 287 E–310 E), in eight phase categories. This area encompasses both the Cape Hatteras and Great Banks regions (CHR and GBR), as defined by Feliks et al. (2011); see text for details
This spatial pattern and the eastward propagation in the NAB resemble the oscillatory modes found by Groth et al. (2017) in their MSSA investigation of the SST field from the Simple Ocean Data Assimilation (SODA: Carton and Giese 2008; Giese and Ray 2011) reanalysis. A. Groth and colleagues found highly significant oscillatory modes with periods in the 7.7–13 years band. Similar oscillatory patterns have already been reported in the analysis of instrumental SST records for the NAB. Sutton and Allen (1997) had identified already in their analysis of shipboard observations a northward propagation of SST anomalies Their dominant spectral peak, though, was centered at 12–14 years in the SST power spectrum.
Feliks et al. (2011) found in the Cape Hatteras and Great Banks regions—CHR = (34 N–43.5 N, 75 W–60 W), where the Gulf Stream front associated with the subtropical gyre separates from the coast, and GBR = (42 W–50 N, 55 W–35 W), where the Gulf Stream front diverges abruptly due to the confluence between the subtropical and subpolar gyres—oscillatory modes with periods of 8.5 and 10.5 years, respectively. Siqueira and Kirtman (2016) used SODA data and an older high-resolution model, namely CCSM4. They repeated the analyses of Feliks et al. (2011) over the same two regions, CHR and GBR, by applying MSSA to SODA data and to CCSM4 simulations; the latter used the current IPCC horizontal resolution and the higher resolution recommended by Feliks et al. (2004, 2007) and implemented by Minobe et al. (2008). Not surprisingly, Siqueira and Kirtman (2016) found the same oscillatory modes in the SODA dataset and the high-resolution simulation, but not in the lower-resolution one. The present results suggest that these near-decadal oscillatory modes in the NAB are, like the PDO in the North Pacific, a manifestation of the 11-years global mode in the Atlantic sector.
In the southern hemisphere, the 11-years global mode is prominent mainly in the Antarctic Circumpolar Current (ACC) and over Antarctica. The spatial pattern of this anomaly in STs is a standing oscillation whose wavelength is about 120 degrees of longitude; it has large amplitudes near 220 E and 340 E. These two “crests” of a wavenumber-3 wave correspond, roughly, to the Ross and Weddell Seas, which suggests an influence of sea ice formation and melting. A prominent feature of the global oscillation—which is quite visible in Fig. 2 at a larger map scale than the one printed here—occurs at the confluence of the Brazil and Malvinas Currents (308 E, 38 S); compare Olson et al. (1988). Over the southern tip of South America, a weak cooling is apparent in phase 2.8 years, and a weak warming at 8.2 years, over land only. Overall, the amplitude of the 11-years global mode in and near the Arctic and the Antartica is about 1.5 K, i.e. the peak-to-peak change in STs at the highest latitudes is over 3 K.
To confirm the effect of sea ice extent on decadal ST variability, we examine separately the oscillatory modes in the oceans at 5 m depth, as a proxy for the SST field. The statistically significant oscillatory modes in this field (spectrum not shown) are about the same as in the coupled analysis discussed thus far. We plot in Fig. 4 the 11.5-years oscillatory mode; the difference between peak periodicities at 11 and 11.5 years is not significant for a dataset that is only 66 years long. Still, no substantial SST variability is present in or near the Labrador Sea, thus confirming the role of the sea ice in giving rise to the ST variability noted in Fig. 2.
Composites of the 11.5-years mode of global SSTs, given here by the temperature at a 5-m depth in the CESM model. Same panels and color bar units as in Fig. 2
The amplitude of the decadal SST mode in the ACC is also dramatically smaller than for the decadal ST mode. These high-latitude differences in amplitude of the decadal mode, for the SST vs. the ST field, are obviously due to the fact that the ST field is influenced by sea ice much more than by the temperatures at a depth of 5 m. The anomalies of the SST proxy field in ocean areas where sea ice does not form look very similar to the ST anomalies, in particular so in the North Pacific, where the tongue-and-horseshoe pattern discussed above is clearly visible.
The spatio-temporal pattern of the 11-years oscillatory mode in the atmosphere is mapped in Fig. 5 for the 200-hPa geopotential field. The main spatial aspect of this pattern can be described as hemispheric level curves of the anomalies. Each such level curve appears to be a combination of zonal wavenumbers 1–3, and it propagates from the subtropics toward the poles, i.e. northward in the northern hemisphere and southward in the southern one. The amplitude of the meanders in these level curves increases as the associated anomalies approach the pole, where the largest anomaly amplitude is observed.
As in Fig. 2 but for 200-hPa geopotential. The green solid line shows the approximate position of a specific hemispheric level curve in the northern hemisphere, in each phase of the oscillatory mode; its southern-hemisphere counterpart is shown as a solid magenta line. The dashed green and magenta lines indicate the position of the same level curves one 11-years period later; see text for details. Color bar is in geopotential meters (gpm) for the phases of the oscillation, as well as for the mean field in the middle panel
In Fig. 5, the green solid line shows the approximate position of one specific global anomaly curve in the northern hemisphere in each phase of the decadal oscillation. Thus, in phase 9.6 years, the solid green line is found between 25 N and 30 N, and it is rather zonal, with fairly small-amplitude meanders. As one progresses through the later phases, the northward propagation of the green line is prominent, and the propagation speed is different at different longitudes, leading to larger and larger meanders. At phase 8.2 years, the level curve we have been following is close to the North Pole and, when reaching phase 9.6 years again, it is indicated by the dashed green line.The position of this level curve, one 11-years period later, is also shown by the dashed green line at the 11-years phase and, finally, at 1.4 years, when it has reached the North Pole. The east- and northward propagation of this mode over most of the northern hemisphere is shown by the animation in Online Resource 2.
The magenta solid line in Fig. 5 shows the approximate position of a similar level curve in the southern hemisphere. In phase 9.6 years, the magenta solid line is found between 20 S and 40 S. Here the southward propagation is faster than in the northern hemisphere, so that in the 5.5-years phase, the level curve is already quite close to Antarctica and, in the 6.9–9.6 years phases, it meanders all over Antarctica.
The poleward propagation of the decadal oscillatory mode at 200 hPa and the increase in its meandering amplitude needs further study. There is a suggestive analogy with the work of Hoskins and Karoly (1981) on long Rossby waves of zero frequency, in which the energy of the long waves propagates poleward and eastward. As it stands, however, this work cannot explain the dynamics of the oscillatory modes herein since the timescale for the atmospheric circulation to adjust to changes in forcing is less than 1 years; hence, the propagation from one phase of the decadal mode to the next cannot be thought of as a consequence of the group velocity of stationary Rossby waves.
More generally, though, James and James (1989), among others, have shown that ultra-low frequencies can play an important role in interannual atmospheric variability. Clarifying these issues will certainly require additional work.
The spatio-temporal evolution of the 200-hPa field in Fig. 5 does exhibit some of the well-known features of northern hemisphere LFV, as summarized, for instance, by Kren et al. (2016). Prominent among these is the Pacific North American (PNA) pattern, which consists of four centers of action: near Hawaii, over the North Pacific, over Alberta, and over the Gulf Coast of the United States Wallace and Gutzler (1981). The positive phase of the PNA pattern is similar to the positive phase of the PDO, with a strong Aleutian Low, strong ridging over western Canada, and anomalously lower pressure over the eastern United States (e.g., Chen and Trenberth 1988).
Kren et al. (2016) examined the atmospheric oscillations associated with the PDO in a 200-years preindustrial control simulation of the Whole Atmosphere Community Climate Model, with greenhouse gas concentrations fixed at year-1850 levels. Many aspects of the model simulation studied and of the methodology applied to study it are different from those used here. As a result, these authors obtain, by concentrating on the tongue-and-horseshoe area of the PDO—see their Figs. 1 and 3c—a dominant periodicity in the 15–20-years band, as in the SST analysis of Chao et al. (2000). Still, many features found in our 11-years global mode do agree with those apparent in their longer-period PDO variability.
The spatio-temporal pattern of the SLP field in Fig. 6 is most prominent in the extratropical latitudes of both hemispheres. The poleward and eastward propagation and the intensification of the anomalies as they near the poles are evident. For example, the low-pressure anomaly over the North Pacific in phase 2.8 years propagates eastward so that at phase 6.9 years it is situated over the North American West. Later still, in the 11-years and 1.4-years phases, this negative anomaly is centered over the Canadian Archipelago and the Labrador Sea.
As in Fig. 5 but for the SLP field. Color bar is in hPa for the phases of the oscillation, as well as for the mean field
This propagation pattern in SLP has a lot in common with the one apparent in the 200-hPa field of Fig. 5. The global decadal mode found herein appears therewith to have a predominantly barotropic vertical structure, as is the case of intraseasonal LFV in the atmosphere (e.g., Hoskins and Pearce 1983).
3.2 The CESM model’s 3.4-years mode
The 3.4-years oscillatory mode of Fig. 1 is captured by ST-EOFs (16, 18) and it contains 3% of the interannual variance, while ST-EOF 17 is associated with a trend-like variability. The phase composites of the ST field in RCs (16,18) are shown in Fig. 7.
Composites of the 3.4-years mode of global ST, in eight phase categories. These composites are based on MSSA pair (16,18), which captures 3% of the interannual variance. Same panels as in Fig. 2 and middle panel identically the same
In the Tropical Pacific, warm and cold tongues in ENSO’s El Niño vs. La Niña phases are prominent. La Niña begins in phase 0.8 years in the eastern Tropical Pacific and the cold tongue extends westward till phase 1.7 years, accompanied by a westward propagation and meridional broadening of the most intense cold anomaly. Likewise, El Nĩno starts in phases 2.5 years and 3.4 years and the warm tongue also extends westward, along with a shift of the strongest warm anomaly. The periodicity of 3.4 years corresponds roughly to ENSO’s quadrennial mode (Jiang et al. 1995a), also referred to sometimes as ENSO’s low-frequency mode (Ghil et al. 2002).
In the northern hemisphere, mid- and high-latitude ST anomalies propagate northeastward, as was the case for the 11-years oscillatory mode. This propagation is pronounced over Asia, Europe, North Africa and the Arabian Peninsula. In the southern hemisphere, a standing oscillation is prominent over Australia and Antarctica, somewhat similar to Fig. 2, although the dominant wavenumber here seems to be 2, rather than 3.
In the atmosphere, the 3.4-years oscillatory mode in the geopotential at 200 hPa is plotted in Fig. 8. North of 30 N and south of 30 S this mode is characterized by level curves with a hemispheric extent, as in Fig. 5, with each level curve again dominated by wavenumbers 1–3 and traveling north- and eastward. The east- and northward propagation of this mode over most of the northern hemisphere is apparent in the animation of Online Resource 3.
Starting in the northern hemisphere with the phase at 1.3 years, the solid green line lies close to 25 N. Again, as the anomaly propagates northward, increasingly large meanders form. In the 0.8-years phase, the anomaly’s northernmost meander almost touches the North Pole and later, having returned to phase 1.3 years, the dashed green line indicate the position of this level curve after one 3.4-years period: at year 1.3 + 3.4 = 4.7, this anomaly reaches the North Pole and subsequently disappears.
The propagation of similar anomalies in the southern hemisphere is indicated again by the evolution from panel to panel of the magenta lines, first solid and then dashed. In the 2.1-years phase, the solid magenta line is found betwen 15 S and 35 S and its meanders amplify at it propagates poleward. In phase 1.7 years the anomaly is close to the South Pole and later, in the 2.1-years phase, the dashed magenta line indicate the position of this anomaly after one full period. Finally, in the 2.5-years phase, the anomaly reaches the South Pole.
The SLP component of the 3.4-years oscillatory mode is shown in Fig. 9. In spite of the difference in periodicity, several features of the SLP evolution are quite similar to those in Fig. 6: the most extensive and strongest anomalies are in the extratropics, propagate northeastward and intensify as they approach the poles. Note, though, that in the 11-years mode the southern and northern hemispheres are in phase, cf. Fig. 6, while in the 3.4-years mode the hemispheres are in phase opposition, cf. Fig. 9.
The amplitude of this mode is much smaller in the tropics over both the Pacific and Atlantic oceans, although the ST field in the Pacific Ocean has large-amplitude ENSO tongues along the equator; see again Fig. 7. Over the tropical Indian Ocean the 3.4-years SLP mode has fairly strong anomalies, mainly south of the equator. The spatio-temporal patterns of this mode in both the SLP field and at 200 hPa in the tropics are quite similar, i.e. this oscillatory mode has a significant barotropic component, like the decadal one.
4 Interannual oscillatory modes in the two reanalyses
In this section, we compare the global oscillatory modes found above in the CESM model’s 100-years simulation with global oscillatory modes found in the NCEP–NCAR reanalysis (Kalnay et al. 1996; Kistler et al. 2001) and in the ECMWF ERA5 reanalysis (Hersbach et al. 2020). The NCEP-NCAR reanalysis was used first, at its horizontal resolution of \(2.5 \times 2.5\) degrees over the 68-years interval from January 1949 to December 2016. The ERA5 reanalysis was then used at the much higher horizontal resolution of \(0.25 \times 0.25\) degrees over the 71-years interval from January 1950 to December 2020.
4.1 Interannual oscillatory modes in the NCEP-NCAR reanalysis
We restricted here the study to the monthly averages of the geopotential field at 200 hPa, since the surface features, such as the SLP field, have finer structure than the upper tropospheric ones and are not very well captured by the \(2.5 \times 2.5\) degree resolution of this reanalysis. Note also that the availability of the data for the surficial fields changes in time over the reanalysis interval (Kalnay et al. 1996, Sec. 4d). Moreover, Kistler et al. (2001) explicitly attach lower credence to fields like the surface fluxes—which are mostly determined by the NCEP model, rather than by observations—and which have to be used in determinining the ST field in the reanalysis.
In order to remove the strong seasonal cycle in the data, we applied a 12-month moving-average filter. Next, we obtained an annually sampled time series by taking all January values from this smoothed time series and checked that the results are almost the same as those reported below when taking another month of the year (not shown).
MSSA was applied to this annually sampled time series with a window width of \(M = 20\) years. The four leading modes of ST-EOFs capture the lowest-frequency components, that is, those with periods longer than M, including a nonlinear trend (Ghil et al. 2002, and references therein), and account for 37% of the interannual variance. We then removed the long-term trend captured by the RCs (1–4). Next, we applied MSSA to the prefiltered data with a window width of \(M = 20\) years. As for the CESM model simulation, only those oscillatory signals significant at the two-sided 95% level are analyzed further below.
The MSSA spectrum of the global 200-hPa fields is shown in Fig. 10 together with error bars that indicate the 95% confidence interval with respect to a red-noise null hypothesis. Oscillations with 12-years and 3.6-years periods are found to be statistically significant and are analyzed below. These two oscillatory modes have almost the same periods as found in the CESM model simulations and described in the previous section; more precisely, the differences in periodicity between 12 and 11 years, and between 3.6 and 3.4 years, are not significant given the limited length of the two datasets, of 68 and 66 years.
Spectral analysis of the global geopotential 200-hPa field, as found in the NCEP-NCAR reanalysis, and by using MSSA with a window width of \(M = 20\) years; please see text for detrending the time series, subtracting the seasonal cycle, and varimax rotation. The graphical conventions and significance methodology are as in Fig. 1
The 12-years oscillatory mode in the reanalysis is captured by ST-EOFs (3,4) and it accounts for roughly 6% of the interannual variance: this is about the same fraction as for the 11-years mode of the CESM simulation, cf. Sect. 3a. It turns out, though, to be slightly smaller than the 6% variance associated with the 3.6-years oscillatory mode in the reanalysis, captured here by ST-EOFs (1,2). In the CESM simulation, the variance fraction associated with the 3.4-years mode is only 3% and it is captured by ST-EOFs (16,18).
Phase composites of the corresponding RCs (3,4) are shown in Fig. 11. Their level curves in the extratropics of both hemispheres are dominated by wavenumbers 1–3, as in the CESM simulation’s 11-years mode (Fig. 5); they propagate poleward and their meanders increase in amplitude as they reach the poles.
Composites of the 12-years mode of global geopotential at 200 hPa, as found in the NCEP-NCAR reanalysis; panel ordering as in Fig. 2, color bars as in Fig. 5. These composites are based on MSSA pair (3,4), which captures 6% of the interannual variance. Same convention for the green and magenta solid and dashed lines as in Fig. 5
The 3.6-years oscillatory mode, captured by ST-EOFs (1,2), accounts for 6% of the interannual variance. Phase composites of the corresponding RCs (1,2) are shown in Fig. 12. The key features of this mode again resemble those of the 3.4-years mode in Fig. 8. In particular, wavenumber 1 reaches the poles—at phase 2.7 years for the North and South Poles—while the shorter waves do not reach them.
4.2 Interannual oscillatory modes in the ERA5 reanalysis
For comparison purposes with the preceding NCEP-NCAR reanalysis, we only studied here, too, the monthly averages of the geopotential field at 200 hPa. The same 12-month moving-average filter as above was applied to the data and an annually sampled time series was obtained by taking all January values from this smoothed time series. As before, we checked that the results are almost the same as those reported below when taking another month of the year (not shown).
We applied MSSA to this annually sampled time series with the same window width of \(M = 20\) years. This time, it is the eight leading modes of ST-EOFs that capture the lowest-frequency components trend (Ghil et al. 2002, and references therein), and they account for 65% of the interannual variance. We then removed the long-term trend captured by RCs (1–8). Next, we applied MSSA to the prefiltered data with a window width of \(M = 20\) years. As for the CESM model simulation and for the NCEP-NCAR reanalysis, only the oscillatory signals significant at the two-sided 95% level with respect to a red-noise null hypothesis are analyzed further below.
The MSSA spectrum of the global 200-hPa fields is shown in Fig. 13, together with error bars that indicate this 95% confidence interval. Oscillations with 10-years and 3.6-years periods are found to be statistically significant and are analyzed below. These two oscillatory modes have almost the same periods as found in the CESM model simulations and in the NCEP-NCAR reanalysis; more precisely, the differences in periodicity between 10, 11 and 12 years, and between 3.6 and 3.4 years, are not significant given the limited length of the datasets, of 71, 68 and 66 years.
Spectral analysis of the global geopotential 200-hPa field, as found in the ERA5 reanalysis, and by using MSSA with a window width of \(M = 20\) years; please see text for detrending the time series, subtracting the seasonal cycle, and varimax rotation. The graphical conventions and significance methodology are as in Fig. 1
The 10-years oscillatory mode in the ERA5 reanalysis is captured by ST-EOFs (1,2) and it accounts for roughly 3.5% of the interannual variance: this is about 60% of the fraction for the 11-years mode of the CESM simulation and for the 12-years mode of NCEP-NCAR reanalysis, cf. Sects. 3.1 and 4.1, respectively. The 3.6-years oscillatory mode, captured here by ST-EOFs (3,4), accounts for roughly 3% of the interannual variance. This fraction is about the same as the 3.4-years mode in the CESM simulation and it equals about half the fraction for the 3.6-years mode of the NCEP-NCAR reanalysis; see Sects. 3.2 and 4.1, respectively.
Phase composites of the corresponding RCs (1,2) are shown in Fig. 14. As in the CESM simulation’s 11-years mode (Fig. 5), the anomalies propagate poleward and their amplitude increases as they approach the North Pole. The anomalies in the southern hemisphere, though, do not reach the South Pole in the ERA5 reanalysis, unlike the result for the CESM simulation and the NCEP-NCAR reanalysis in Figs. 5 and 11, respectively.
The 3.6-years oscillatory mode, captured by ST-EOFs (3,4), accounts for 3% of the interannual variance. Phase composites of the corresponding RCs (3,4) are shown in Fig. 15. The key features of this mode again resemble those of the CESM 3.4-years mode in Fig. 8 and of the NCEP-NCAR 3.6-years mode in Fig. 12.
In the 3.6-years mode of the NCEP-NCAR and ERA5 reanalyses, the hemispheres are in phase, cf. Figs. 12 and 15, respectively, while in the CESM model’s simulation, the 3.4-years mode’s opposite southern and northern hemispheres are in phase opposition, cf. Fig. 8. The cause of these differences between the two reanalyses, on the one hand, and the CESM model’s simulation, on the other, requires further study.
Overall, there is good agreement between the spatio-temporal behavior of the decadal and the shorter interannual mode in the two reanalyses. Clearly, all three datasets show a decadal, 10–12-years mode, and a shorter interannual, 3.4–3.6-years mode. Still, the two hemispheres are in phase in the two reanalyses’ interannual mode, but in opposite phases in the decadal mode. The differences noted among the three datasets will, no doubt, stimulate further efforts for their explanation.
5 Verification and solar-cycle correlations
5.1 Verification with raw data
In order to verify whether the spatio-temporal patterns of the decadal modes in the CESM simulation and the NCEP-NCAR reanalysis are not an artifact of the MSSA methodology, we used several tests. First, we showed in Sects. 3.1 and 4 that all three decadal modes, with their 10–12-years periodicities, were significant at the two-sided 95% level. In this section, we show that the associated patterns of climate variability can be extracted more directly from the raw data as well. To show this, we start by computing the 11-years cycle from the CESM simulation, by using only a scalar index of this mode and not the MSSA’s ST-EOFs.
The scalar index we use is the PC of the first traditional, purely spatial EOF (S-EOF) of the reconstructed 11-years oscillatory mode. This index is labeled S-PC1, it contains 73% of this mode’s variance, and we denote the normalized versions of S-PC1 and of its time derivative by \((c(t), c^{\prime }(t))\); see Moron et al. (1998, Appendix) for further details. The amplitude A(t) and phase \(\theta (t)\) are given by the polar transform
The cycle is then divided into \(M = 8\) phase categories, \(1 \le m \le M\), by using \((m - 1) (\pi /4) \le \theta (t) \le m(\pi /4)\) and the average over the raw maps associated with phase m is the appropriate composite \(\mathbf{C}_m\). Thus, there is no longer any filtering involved in constructing the eight composites, only a selection of the time intervals over which the averaging is done.
In Fig. 16, the 11-years cycle of the CESM simulation’s ST field is shown in the eight categories. This cycle’s spatio-temporal evolution is very similar to that of Fig. 2. Likewise, the 11-years cycle of the geopotential at 200 hPa is plotted in Fig. 17, and its spatio-temporal evolution is very similar to that of Fig. 5. From these two comparisons, it is clear that the spatio-temporal evolution of this coupled oscillatory mode is not an artifact of the MSSA analysis.
Same as in Fig. 2 but for ST composites based on S-PC1 of the MSSA pair (3,4) and the CESM-simulated field evolution; see text for details. No filtering through the MSSA ST-EOFs has been used in this compositing. The mean ST field in the middle panel has contour interval (CI) = 2 K
We also calculated the correlations between S-PC1 of the 11-years mode and the raw ST field at any given grid point: the results appear in Fig. 18. The largest correlations observed in the northern hemisphere occur in the latitude belt 45 N–75 N, where strong propagating anomalies were present in Figs. 2 and 16; these large correlations are visible over both continents and oceans. In the southern hemisphere, the correlations are largest over the ACC, which is also consistent with the active propagating anomalies in the 45 S–62 S latitude belt apparent in Figs. 5 and 17.
To ascertain in yet another way that this 11-years oscillatory mode is truly global—rather than merely a teleconnection that decays away from a particular regional mode, like the NAO or the PDO—we computed the correlations between the S-PC1 and the ST time series at each CESM grid point. From the correlation map in Fig. 18, and the ESM animations Online Resource 1, 2 and 3, it is quite clear that the model’s decadal oscillatory mode is of global extent, being quite active in several regions of both hemispheres, over land as well as over water.Footnote 1
In a similar vein to the compositing done in Figs. 16 and 17 for the CESM simulation, we computed the S-PC1 for the MSSA pair (3,4) associated with the 12-years mode of the 200-hPa geopotential evolution in the NCEP-NCAR reanalysis. Based on this scalar index, we composited the raw 200-hPa maps into eight phase categories, plotted in Fig. 19. Visually, the agreement with the corresponding panels in Fig. 11 is excellent.
Same as Fig. 17 but for the 12-years mode in the NCEP-NCAR reanalysis, with no ST-EOF–based filtering. See text for details
Likewise, we also computed the S-PC1 for the MSSA pair (1,2) associated with the 10-years mode of the 200-hPa geopotential evolution in the ERA5 reanalysis. As for the NCEP-NCAR reanalysis in Fig. 19, we composited the raw 200-hPa maps from ERA5 into eight phase categories, plotted in Fig. 20. Visually, the agreement with the corresponding panels in Fig. 14 is very good.
Same as Fig. 17 but for the 10-years mode in the ERA5 reanalysis, with no ST-EOF–based filtering. See text for details
Finally, not content with the good visual agreement between the pairs of figures, we computed the Pearson correlation coefficient r,Footnote 2 phase by phase, between the MSSA-based and the raw composites. The results are listed in Table 1.
All three sets of panel-to-panel correlations are fairly high, and thus consistent with the visual-inspection results. The NCEP-NCAR reanalysis correlations, r (NCEP 200 hPa), are more uniformly high than those for the CESM simulation correlations, where especially low correlations appear for phases 2, 4 and 11 of the filtered-to-raw correlations of the 200-hPa geopotential field. Like in CEMS simulation the reanalysis correlations, r (ERA5 200 hPa), are not uniform especially low correlations appear for phases 0, 3 and 5 of the filtered-to-raw correlations.
To test the null hypothesis of the correlations in Table 1 being due to mere chance, we evaluated the p-value of a one-sided, right-tail test for the entire evolution of each field of interest, i.e., of the 200-hPa geopotential and the ST field in the CESM simulation, as well as of the 200-hPa geopotential in the NCEP-NCAR and ERA5 reanalyses. This test involves, in each case, all eight maps that describe the full evolution of the decadal mode.
Both r- and p-values were computed using Python’s “scipy.stats” module and the three (r, p) pairs appear in the table’s bottom row; they are for the 200-hPa geopotential and the ST field in the CESM simulation, along with the 200-hPa geopotential in the NCEP-NCAR reanalysis. The r-values are nearly identical for the three pairs, in spite of the less regular map-by-map behavior of the CESM simulation pairs, and the null hypothesis can be rejected with very high confidence.
5.2 Solar-cycle correlations
The results so far still leave the question wide open of what the origin of this decadal mode—with its period of 11 years in the CESM simulation and 12 years in the NCEP-NCAR reanalysis — might be. The synchronization of several regional modes with slightly shorter or longer periodicities—such as the NAO and PDO —may be due either to internal coupling between them or to external forcing. An obvious mechanism for such forcing is the solar cycle, with its somewhat irregular 11-years periodicity.
In Fig. 21, we take a look at the evolution of total solar irradiance (TSI: Coddington et al. 2016) (black dashed curve) and the decadal mode, plotted in blue for the CESM simulation in panel (a) and in red for the NCEP-NCAR reanalysis in panel (b). The maximal correlation between the two curves in panel (a) is of \(r = 0.84\) for a mean lag of 2 years, while in panel (b) it is \(r = -0.53\) for a zero mean lag. The p-values in both cases are practically null.
Solar cycle and its relation to the decadal mode. a Total solar irradiance (TSI: Coddington et al. 2016) (black dashed curve) and the decadal mode (blue solid curve) in the CESM simulation; and b TSI and the decadal mode (red solid curve) in the NCEP-NCAR reanalysis. Starting date of the CESM run in panel a is shifted to match the solar cycle. Units on the y-axis are nondimensional
We note that, in panel (a), the two curves start in phase and stay so for the first three cycles but greater irregularity in the relationship occurs for the latter three cycles. In panel (b), given the greater length of the decadal mode in the reanalysis, the solar cycle starts out behind of the climatic 12-years mode but gradually moves ahead over the interval of comparison, with the mean lag ending up as zero.
The present study was undertaken with no intention whatsoever to attempt relating multiannual climate variability with the solar 11-years cycle, but the very high correlations apparent in Fig. 21 oblige us to inspect more closely the potential physical causes of such a relationship. The topic has been quite controversial for a long time: on the one hand, the relative regularity of solar activity appeals to one’s attributing to it substantial weather and climate effects on a decadal scale; on the other, the very small changes in solar irradiance actually reaching the terrestrial troposphere and the high noise levels arising from weather and shorter-lived climate variability made incontrovertible evidence of a link hard to ascertain.
In 1978, Siscoe (1978) stated in a short review paper that “During the past century over 1000 articles have been published claiming or refuting a correlation between some aspect of solar activity and some feature of terrestrial weather or climate. Nevertheless, the sense of progress that should attend such an outpouring of ’results’ has been absent for most of this period. The problem all along has been to separate a suspected Sun–weather signal from the characteristically noisy background of both systems.” He proceeded, though, to indicate that, finally, some progress was being made.
The effect of solar activity changing the ozone concentration in the stratosphere—and hence the ultraviolet fraction of solar irradiance reaching the troposphere—is pretty well established observationally (e.g., Keckhut et al. 2005). Shindell et al. (1999) also showed in a GCM with a well-resolved stratosphere that this “top–down” effect can result in measurable changes in the troposphere as well.
White and Liu (2008) documented the presence of a solar-cycle signal in the upper ocean on a global scale. This observational result stimulated a number of papers (Meehl et al. 2008, 2009; White and Liu 2008) to propose an alternative to the stratospheric, top-down approach. In this alternative, “bottom-up” approach, the minute variations in solar irradiance of roughly 0.2 \(\hbox {Wm}^{-2}\) peak-to-peak amplitude (e.g., Meehl et al. 2009) affect air–sea coupling and are amplified at the surface in the relatively cloud-free areas of the subtropics.
Misios et al. (2016) have confirmed the presence of such a mechanism in a subset of CMIP-5 models that show a statistically significant global mean warming of about 0.07 K in their multi-model mean. This warming penetrates to a depth of 80–100 m in the ocean, in agreement with the White et al. (1997) observations, it is more pronounced in the western Tropical Pacific and the Arctic, and it lags the maximum of solar irradiance by 1–2 years on average.
Now the fascinating aspect of the CESM simulation used throughout this paper is that it is a perpetual year-2000 run, with no interannual TSI variability whasoever, while the features of the global decadal mode described in Sect. 3 agree very well with the the same mode in the NCEP-NCAR reanalysis of Sect. 4. In fact, Meehl et al. (2008)—who studied an earlier version of the CESM model used herein, but with solar-cycle forcing—mention an anomalous Rossby wave activity somewhat reminiscent of the substantial anomalies in both the 200-hPa field and the SLP field herein of Figs. 5 and 9, respectively.
Of course, the timing of the S-PC1 scalar time series in Fig. 21a is perfectly arbitrary and has been chosen to optimize the correlation with the TSI cycle, yielding the previously mentioned value of \(r = 0.84\) for a 2 years mean lag and \(p = 10^{-5}\). This result shows: (i) the limitations of purely statistical inference of causality, no matter how good the correlations r(X, Y) of two phenomena X and Y and how low the associated p values, cf. Siscoe (1978); and (ii) the fact that the global decadal mode present in both reanalyses, where interannual TSI variability has done its job, as well as in the CESM run, where it has not, must be largely a manifestation of the climate system’s intrinsic variability.
6 Concluding remarks
6.1 Summary
We studied in this paper the interannual variability in a high-end coupled ocean–atmosphere model, the CESM1.1 model (Hurrell et al. 2013; Small et al. 2014), and in the NCEP-NCAR (Kalnay et al. 1996; Kistler et al. 2001) and ERA5 (Hersbach et al. 2020) reanalyses. A 100-years CESM simulation was carried out at a horizontal resolution of \(0.1 \times 0.1\) degrees in the ocean and \(0.25 \times 0.25\) degrees in the atmosphere, and its last 66 years were analyzed. The global fields used in this analysis were the surface temperatures (STs) over sea and land, the sea level pressures (SLPs) and geopotential heights at 200 hPa, as well as the ocean temperatures at 5-m depth, which represent a proxy for the sea surface temperatures (SSTs). Together, these fields provide good insights into the coupled variability of the atmosphere, ocean and land surface.
The main analysis tool was multichannel singular spectrum analysis (MSSA), a nonparametric, data-adaptive method for time series analysis (Alessio 2015; Ghil et al. 2002). We used it to obtain the power spectrum of the three datasets, namely the CESM model simulation and the two reanalyses—cf. Figs. 1, 10 and 13, respectively—as well as the spatio-temporal patterns of the statistically significant global oscillatory modes. These patterns were studied in Sect. 3, Figs. 2, 3, 4, 5, 6, 7, 8, 9, for the CESM model, and in Sect. 4, Figs. 11, 12, 14 and 15 for the two reanalyses.
Two global oscillatory modes were found to be significant at the 95% level in the CESM simulation. Their periods are 11 years and 3.4 years, respectively. In the atmosphere, both the decadal and the interannual mode have common characteristics, as seen from the evolution of their spatio-temporal patterns. These patterns are characterized at 200 hPa by level curves of the anomalies that are of hemispheric extent and present at middle and high latitudes, outside the belt extending from 30 N to 30 S; see Fig. 5 for the decadal mode and Fig. 8 for the interannual one.
These level curves are dominated by zonal wavenumbers 1–3 and they propagate east- and poleward, with meanders that increase in amplitude as they do so. Wavenumber 1 reaches the pole in either hemisphere, while the shorter waves do not. One can visualize the propagation of this feature as that of a “smoke ring” floating through the Earth’s atmosphere but with a decreasing mean radius as it draws nearer to a pole, while its meandering becomes more-and-more pronounced.
The ST field is plotted in Figs. 2 and 7 for the 11-years and the 3.4-years mode, respectively. North of 30 N, the spatio-temporal evolution is similar to that of the 200 hPa field, i.e. the anomalies propagate northeastward, and their amplitudes increase as they approach the North Pole. Over the North Pacific, two features prominent in the ST field’s decadal oscillations here are well known from previous studies, namely the tongue in the western Pacific and the horseshoe in the eastern Pacific (Miller and Schneider 2000; Alexander et al. 2010; Newman et al. 2016).
Due to the ability of the MSSA methodology to follow the propagation of spatial patterns in time and space (Plaut and Vautard 1994; Ghil et al. 2002; Groth et al. 2017), we showed that the tongue that develops in the western Pacific propagates eastward, as part of the global mode plotted in Fig. 2. As the anomaly reaches the eastern Pacific, it intensifies and expands, spreading out along the West Coast of North America and its spatial pattern becomes horseshoe-shaped. This evolution was not found in previous analyses using only stationary-EOF tools.
In the Tropical Pacific, the 3.4-years oscillatory mode in STs includes a strong ENSO signal (Fig. 7), which is not present in the 11-years oscillatory mode (Fig. 2 for the STs and Fig. 4 for the SSTs). A warm tongue develops in the eastern Tropical Pacific along the equator during the El Niño phase of the 3.4-years mode; it extends westward, accompanied by a westward propagation of the most intense warm anomaly. During the La Niña phase, it is a cold tongue that evolves in the same way. In fact, this 3.4-years period is fairly close to ENSO’s quasi-quadrennial or low-frequency periodicity (Jiang et al. 1995a; Ghil et al. 2002).
The evolution of the SLP field within the decadal and interannual modes appears in Figs. 6 and 9, respectively. Over the tropical Pacific and Atlantic, the SLP anomalies in both modes are quite small—in spite of the large ENSO anomalies in the STs of the 3.4-years mode—while over the tropical Indian Ocean they are stronger.
In the extratropics, the SLP evolution is quite similar to that of the 200-hPa field, in both modes; compare with Figs. 5 and 8, respectively. This similarity suggests that both modes are predominantly barotropic, which is not surprising, since baroclinicity is greatly reduced by the so-called barotropic or third adjustment—so named because it occurs on slower time scales than the hydrostatic (first) and geostrophic (second) adjustment (Hoskins and Pearce 1983, and references therein). The time for this third adjustment is of the order of a few tens of days (e.g., Lau and Nath 1987, Figs. 3–6) and hence atmospheric LFV is predominantly barotropic already on the intraseasonal time scale (Ghil et al. 1991) and thus, a fortiori, on the interannual one.
Both the decadal and the interannual oscillatory modes were also found in the NCEP–NCAR and ERA5 reanalyses, as shown in Figs. 11 and 12 and in Figs. 14 and 15, respectively. The two reanalyses have very different resolutions: \(2.5 \times 2.5\) degrees for the NCEP-NCAR reanalysis, which covered the 68-years interval from January 1949 to December 2016, and \(0.25 \times 0.25\) degrees over the 71-years interval from January 1950 to December 2020. In spite of these differences, the results of our study are quite similar for the three datasets. The characteristics of the three datasets and the periodicities obtained are summarized in Table 2.
There are two statistically significant oscillatory modes in all three datasets: a decadal and a shorter interannual mode. Note that the 11-years periodicity of the CESM-simulated decadal mode lies between the two values obtained from the NCAR-NCEP and ERA5 reanalysis, of 12 years and 10 years, respectively. The relative differences of 1/12 and of \(0.2/3.6 = 1/18\) in periodicity between the pairs of modes are both physically of no consequence and statistically not significant.
Comparison of Fig. 11 with Fig. 5 and of Fig. 12 with Fig. 8 showed that the spatio-temporal patterns of the decadal and interannual modes, respectively, have quite similar characteristics in both the CESM simulation and the NCEP-NCAR reanalysis, even though there are large differences between the NCEP model used in the latter and the CESM model. The same statement holds for the ERA5 reanalysis, with minor changes seen in comparing Figs. 14 and 15 with Figs. 11 and 12, respectively. It thus appears that—for both the decadal and the interannual variability of the upper troposphere—the anomaly level curves of hemispheric extent observed in all six above-mentioned figures are characterized by wavenumbers 1–3 being dominant and propagating northeastward; see also the three animations in the Electronic Suplementary Material.
6.2 Discussion of global modes
We have seen that the two low-frequency modes described herein, decadal (11–12-years periodicity) and interannual (3.4–3.6-years periodicity), have regional features that agree with those described in previous work, namely the NAO in the Atlantic sector, the PDO in the extratropical Pacific one, and ENSO in the Tropical Pacific. The main question raised by the results presented herein is, How are these various types of regional, ocean basin–scale types of variability synchronized into participating in the two global modes studied in the present paper?
The phenomenon of entrainment or frequency locking between an internal oscillation of a nonlinear system and an external, periodic forcing has been known for a long time (Stoker 1950; Minorsky 1962), as has the frequency locking of two or more nonlinear oscillators with distinct frequencies. Ghil and Childress (1987, Ch. 12, and references therein) have systematically applied these concepts to Quaternary glaciations in the presence of astronomical forcing.
More recently, the broader concept of synchronization of chaotic oscillators has attracted considerable attention (e.g., Boccaletti et al. 2002; Duane et al. 2017) and been applied to the atmospheric and climate sciences (Duane and Tribbia 2001, 2004; Feliks et al. 2010, 2013; Groth and Ghil 2011; Groth et al. 2017, among others). The obvious conjecture in the present context is that the synchronization of regional modes into global ones is due, on the one hand, to ocean–atmosphere–sea ice coupling and, on the other, to the propagation of Rossby waves with very low frequency within the atmosphere. The role of the sea ice, for instance, was evident in the discussion of substantial ST anomalies in the Labrador Sea and the subantarctic waters (Fig. 2) in the absence of notable SST anomalies there (Fig. 4).
Still it is not clear what determines the period of each one of the two global modes: (i) is it the ocean or the atmosphere; and (ii) what is the relative contribution of the various basin-scale regions? One possible train of thought is that the decadal mode is mainly a compromise between near-decadal periodicities in the Atlantic, of 7–13 years (Feliks et al. 2011; Siqueira and Kirtman 2016; Groth et al. 2017, and references therein), and longer ones in the Pacific, of 17–20 yr (Chao et al. 2000). The interannual mode, in turn, is due mainly to the quasi-quadrennial ENSO oscillation synchronized with other nonlinear oscillators, like the South Asian and Southeast Asian monsoon systems (Jin et al. 1994; Tziperman et al. 1994; Jiang et al. 1995a; Ghil and Robertson 2000; Ghil et al. 2002).
Finally, the variance of these global modes is rather small, not exceeding 10% of total interannual variance. Still, they can be useful tools in predicting changes in year-to-year large-scale features, as is certainly the case for the Tropical Pacific and regions teleconnected to it (e.g., Barnston et al. 2012), while longer-range predictions that rely on the decadal mode might require more detailed assessment (e.g., Plaut et al. 1995).
All this being said, we are left with the rather puzzling quandary of the difference between the present results and those of Kravtsov et al. (2018, and references therein): (i) the global decadal mode we find herein, in the CESM simulation and the two reanalyses, does not resemble their GSW; while (ii) these authors do find the GSW in the NCEP-NCAR reanalysis they have relied upon but not in the CMIP5 simulations.
Kravtsov et al. used the same time series analysis methodology, MSSA (Ghil and Vautard 1991; Plaut and Vautard 1994; Plaut et al. 1995; Ghil et al. 2002), as done in the present paper, although there might be some technical details that differ. In fact, their GSW bears some similarity to the multidecadal variability described in previous work by Ghil et al. (e.g., Ghil and Vautard 1991; Plaut et al. 1995; Moron et al. 1998; Chao et al. 2000); see, in particular, see, in particular, (1998, Fig. 3). Moreover, the LDM decomposition of Gavrilov et al. (2020b) found some of their leading LDMs to be associated with regional patterns concentrated either in the Atlantic or the Pacific Ocean.
Concerning the absence of the GSW from the CMIP5 simulations (Kravtsov 2017, Table 1) analyzed by Kravtsov and colleagues, this might be due to the ensemble averaging, which probably included models with insufficient horizontal resolution. Recall, once more, that Feliks et al. (2004, 2007) concluded—by using detailed horizontal resolution experiments in simplified atmospheric models—that a resolution of 50 km or better was necessary to reproduce the effect of oceanic SST fronts, like the Gulf Stream or the Kuroshio, on the atmosphere above and downstream. This conclusion was verified in GCMs with uniformly high resolution by Minobe et al. (2008) and in a GCM with suitable zooming-in over the Gulf Stream region by Brachet et al. (2012), who thus confirmed the role of this mechanism in climatic LFV.
6.3 Discussion of Sun-climate effects
Both the groups of Meehl et al. (2008, 2009) and of Liu et al. (1990, 2008, 2012) concentrated on Sun-climate effects upon the Pacific basin’s quasi-decadal variability, with an emphasis on the Tropical Pacific. The latter group started its study with a relatively simple delayed-action oscillator (Graham et al. 1990) and emphasized this oscillator’s resonant response to solar-cycle forcing (White and Liu 2008) in follow-up work with the Fast Ocean-Atmosphere Model (FOAM) fully coupled ocean-atmosphere GCM.
The picture here is somewhat more complex: The decadal-scale evolution of the tongue in the western Tropical Pacific and of the horseshoe in the eastern Pacific do actively participate in our global mode. But we have clearly shown that other large areas of the globe are quite active in this mode. In particular, Fig. 3 illustrated the decadal evolution of gyre-mode–type features in the northwestern sector of the North Atlantic that had been studied over a full hierarchy of oceanic and atmospheric models and several data sets by Feliks et al. Jiang et al. (1995b) through Feliks et al. (2011) and on to Feliks et al. (2016); see the Dijkstra and Ghil (2005) review and recent observational confirmation by Groth et al. (2017).
It appears therewith that separate North Atlantic, Pacific, and high-latitude modes synchronize to give rise to a global decadal mode, as described in Sect. 3 where solar activity was absent and discussed in Sect. 6.2. It is this global mode of purely internal variability that responds resonantly in nature to the very small and somewhat irregular 11-years solar forcing, and it is this resonant response of the intrinsic global decadal mode of Sect. 4 that yields the amplitude and pattern of the mode we found in the reanalysis studied in Sect. 4.
In order to provide further insights into interannual climate LFV and the solar cycle’s role therein, it will be necessary (i) to apply advanced time series analysis tools to both GCM simulations and observational datasets; and (ii) to use a full hierarchy of climate models—from the simplest conceptual models to IPCC-class GCMs (e.g., Ghil 2001, 2019; Held 2005)—to ascertain the mechanisms that give rise to the global oscillatory modes identified and described herein.
Notes
Srivastava and DelSole (2017) used a similar argument in determining the global character of their predictability-maximizing modes, by demonstrating their effectiveness in global, rather than merely local, prediction. A key distinction with respect to our approach is that these authors did not discriminate between the dominant periodicities of their modes, while we do, which further strengthens our argument.
The Pearson correlation coefficient, or Pearson’s r, is a perfect illustration of Stigler’s law (Stigler 1980), which states that no scientific discovery is named after its original discoverer.
References
Alessio SM (2015) Digital signal processing and spectral analysis for scientists: concepts and applications. Springer, Berlin
Alexander M et al (2010) Extratropical air-sea interaction, sea surface temperature variability, and the Pacific decadal oscillation. Climate dynamics: why does climate vary? Geophys Monogr 189:123–148
Allen MR, Robertson AW (1996) Distinguishing modulated oscillations from coloured noise in multivariate datasets. Clim Dyn 12(11):775–784
Allen MR, Smith LA (1996) Monte Carlo SSA: detecting irregular oscillations in the presence of colored noise. J Clim 9:3373–3404
Barlow M, Nigam S, Berbery EH (2001) Enso, pacific decadal variability, and us summertime precipitation, drought, and stream flow. J Clim 14(9):2105–2128
Barnston AG, Tippett MK, Heureux ML, Li S, DeWitt DG (2012) Skill of real-time seasonal ENSO model predictions during 2002–2011—is our capability improving? Bull Am Meteorol Soc 93(5):631–651. https://doi.org/10.1175/BAMS-D-11-00111.1
Berloff P, Hogg AM, Dewar W (2007) The turbulent oscillator: a mechanism of low-frequency variability of the wind-driven ocean gyres. J Phys Oceanogr 37(9):2363–2386
Bjerknes J (1964) Atlantic air–sea interaction. In: Landsberg HE, Van Mieghem J (eds) Advances in geophysics, advances in geophysics, vol 10. Elsevier, pp 1–82. https://doi.org/10.1016/S0065-2687(08)60005-9
Boccaletti S, Kurths J, Osipov G, Valladares DL, Zhou CS (2002) The synchronization of chaotic systems. Phys Rep 366(1–2):1–101. https://doi.org/10.1016/S0370-1573(02)00137-0
Brachet S, Codron F, Feliks Y, Ghil M, Le Treut H, Simonnet E (2012) Atmospheric circulations induced by a mid-latitude SST front: a GCM study. J Clim 25:1847–1853. https://doi.org/10.1175/JCLI-D-11-00329.1
Broomhead DS, King GP (1986) On the qualitative analysis of experimental dynamical systems. In: Sarkar S (ed) Nonlinear phenomena chaos. Adam Hilger, Bristol, pp 113–144
Carton JA, Giese BS (2008) A reanalysis of ocean climate using simple ocean data assimilation (SODA). Mon Weather Rev 136(8):2999–3017. https://doi.org/10.1175/2007MWR1978.1
Chao Y, Ghil M, McWilliams JC (2000) Pacific interdecadal variability in this century’s sea surface temperatures. Geophys Res Lett 27(15):2261–2264
Chen SC, Trenberth KE (1988) Orographically forced planetary waves in the Northern Hemisphere winter: steady state model with wave-coupled lower boundary formulation. J Atmos Sci 45(4):657–681
Chiang J, Vimont D (2004) Analogous Pacific and Atlantic meridional modes of tropical atmosphere-ocean variability. J Clim 17(21):4143–4158
Clement A, Bellomo K, Murphy LN, Cane MA, Mauritsen T, Rädel G, Stevens B (2015) The Atlantic multidecadal oscillation without a role for ocean circulation. Science 350(6258):320–324
Coddington O, Lean J, Pilewskie P, Snow M, Lindholm D (2016) A solar irradiance climate data record. Bull Am Meteorol Soc 97(7):1265–1282
Compo GP, Sardeshmukh PD (2010) Removing enso-related variations from the climate record. J Clim 23(8):1957–1978
Compo GP, Whitaker JS, Sardeshmukh PD, Matsui N, Allan RJ, Yin X, Gleason BE, Vose RS, Rutledge G, Bessemoulin P et al (2011) The twentieth century reanalysis project. Quart J R Meteorol Soc 137(654):1–28
Curry RG, McCartney MS (2001) Ocean gyre circulation changes associated with the north Atlantic oscillation. J Phys Oceanogr 31(12):3374–3400
Czaja A, Robertson AW, Huck T (2003) The role of Atlantic ocean-atmosphere coupling in affecting North Atlantic Oscillation variability. In: Hurrell JW, Kushnir Y, Ottersen G, Visbeck M (eds) The north atlantic oscillation: climatic significance and environmental impact, geophysical monograph, vol 134. American Geophysical Union, Washington, D.C., pp 147–172
Da Costa ED, Colin de Verdiére A (2002) The 7.7-year North Atlantic Oscillation. Quart J R Meteorol Soc 128(581):797–817
De Viron O, Dickey JO, Ghil M (2013) Global modes of climate variability. Geophys Res Lett 40(9):1832–1837. https://doi.org/10.1002/grl.50386
Deser C, Blackmon M (1993) Surface climate variations over the North Atlantic Ocean during winter: 1900–1989. J Clim 6(9):1743–1753
Deser C, Alexander MA, Timlin MS (1999) Evidence for a wind-driven intensification of the kuroshio current extension from the 1970s to the 1980s. J Clim 12(6):1697–1706
Deser C, Holland M, Reverdin G, Timlin M (2002) Decadal variations in Labrador Sea ice cover and North Atlantic sea surface temperatures. J Geophys Res Oceans 107(C5):3035. https://doi.org/10.1029/2000JC000683
Dettinger MD, Ghil M, Keppenne CL (1995) Interannual and interdecadal variability in united states surface-air temperatures, 1910–1987. Clim Change 31(1):35–66. https://doi.org/10.1007/BF01092980
Dijkstra H, Ghil M (2005) Low-frequency variability of the large-scale ocean circulation: a dynamical systems approach. Rev Geophys 43(3):RG3002. https://doi.org/10.1029/2002RG000122
Duane GS, Tribbia JJ (2001) Synchronized chaos in geophysical fluid dynamics. Phys Rev Lett 86(19):4298
Duane GS, Tribbia JJ (2004) Weak Atlantic-Pacific teleconnections as synchronized chaos. J Atmos Sci 61(17):2149–2168
Duane GS, Grabow C, Selten F, Ghil M (2017) Introduction to focus issue: synchronization in large networks and continuous media-data, models, and supermodels. Chaos 27(126):601. https://doi.org/10.1063/1.5018728
Eden C, Jung T (2001) North atlantic interdecadal variability: oceanic response to the north atlantic oscillation (1865–1997). J Clim 14(5):676–691
Feliks Y, Ghil M, Simonnet E (2004) Low-frequency variability in the midlatitude atmosphere induced by an oceanic thermal front. J Atmos Sci 61(9):961–981
Feliks Y, Ghil M, Simonnet E (2007) Low-frequency variability in the midlatitude baroclinic atmosphere induced by an oceanic thermal front. J Atmos Sci 64(1):97–116
Feliks Y, Ghil M, Robertson AW (2010) Oscillatory climate modes in the Eastern Mediterranean and their synchronization with the North Atlantic Oscillation. J Clim 23(15):4060–4079
Feliks Y, Ghil M, Robertson AW (2011) The atmospheric circulation over the North Atlantic as induced by the SST field. J Clim 24(2):522–542
Feliks Y, Groth A, Robertson AW, Ghil M (2013) Oscillatory climate modes in the Indian Monsoon, North Atlantic, and Tropical Pacific. J Clim 26(23):9528–9544
Feliks Y, Robertson AW, Ghil M (2016) Interannual variability in North Atlantic weather: data analysis and a quasigeostrophic model. J Atmos Sci 73(8):3227–3248
Frankignoul C, Hasselmann K (1977) Stochastic climate models, part ii application to sea-surface temperature anomalies and thermocline variability. Tellus 29(4):289–305
Frankignoul C, Müller P, Zorita E (1997) A simple model of the decadal response of the ocean to stochastic wind forcing. J Phys Oceanogr 27(8):1533–1546
Gavrilov A, Kravtsov S, Mukhin D (2020a) Analysis of 20th century surface air temperature using linear dynamical modes. Chaos Interdiscip J Nonlinear Sci 30(12):123110
Gavrilov A, Kravtsov S, Mukhin D (2020b) Analysis of 20th century surface air temperature using linear dynamical modes. Chaos Interdiscip J Nonlinear Sci 30(12):123110
Ghil M (2001) Hilbert problems for the geosciences in the 21st century. Nonlinear Process Geophys 8(4/5):211–211
Ghil M (2019) A century of nonlinearity in the geosciences. Earth Space Sci 6(7):1007–1042
Ghil M, Childress S (1987) Topics in geophysical fluid dynamics: atmospheric dynamics, dynamo theory, and climate dynamics. Springer, Berlin, Heidelberg (Reissued in pdf, 2012)
Ghil M, Robertson AW (2000) Solving problems with GCMs: General circulation models and their role in the climate modeling hierarchy. In: Randall DA (ed) General circulation model development: past, present and future. Academic Press, New York, pp 285–325
Ghil M, Vautard R (1991) Interdecadal oscillations and the warming trend in global temperature time series. Nature 350(6316):324–327. https://doi.org/10.1038/350324a0
Ghil M, Kimoto M, Neelin JD (1991) Nonlinear dynamics and predictability in the atmospheric sciences. Rev Geophys 29(S1):46–55
Ghil M, Allen MR, Dettinger MD, Ide K, Kondrashov D, Mann ME, Robertson AW, Saunders A, Tian Y, Varadi F, Yiou P (2002) Advanced spectral methods for climatic time series. Rev Geophys 40(1):1–41. https://doi.org/10.1029/2000RG000092
Giese BS, Ray S (2011) El Niño variability in simple ocean data assimilation (SODA), 1871–2008. J Geophys Res Oceans. https://doi.org/10.1029/2010JC006695
Gouretski V, Koltermann KP (2004) WOCE global hydrographic climatology. Berichte des BSH 35, pp 1–52
Graham NE, White WB, Pares-Sierra A (1990) Low frequency ocean-atmosphere interactions in the tropical pacific. In: Jiping C, Young J (eds) Air-Sea Interaction in the Tropical Western Pacific, China Ocean Press, Beijing, pp 457–484
Groth A, Ghil M (2011) Multivariate singular spectrum analysis and the road to phase synchronization. Phys Rev E 84(036):206. https://doi.org/10.1103/PhysRevE.84.036206
Groth A, Ghil M (2015) Monte carlo singular spectrum analysis (SSA) revisited: detecting oscillator clusters in multivariate datasets. J Clim 28(19):7873–7893. https://doi.org/10.1175/JCLI-D-15-0100.1
Groth A, Feliks Y, Kondrashov D, Ghil M (2017) Interannual variability in the North Atlantic ocean’s temperature field and its association with the wind stress forcing. J Clim 30(7):2655–2678
Guan B, Nigam S (2008) Pacific sea surface temperatures in the twentieth century: an evolution-centric analysis of variability and trend. J Clim 21(12):2790–2809
Held IM (2005) The gap between simulation and understanding in climate modeling. Bull Am Meteorol Soc 86(11):1609–1614
Hersbach H, Bell B, Berrisford P, Hirahara S, Horányi A, Muñoz-Sabater J, Nicolas J, Peubey C, Radu R, Schepers D et al (2020) The ERA5 global reanalysis. Quart J R Meteorol Soc 146(730):1999–2049
Hoskins BJ, Karoly DJ (1981) The steady linear response of a spherical atmosphere to thermal and orographic forcing. J Atmos Sci 38(6):1179–1196
Hoskins BJ, Pearce RP (eds) (1983) Large-scale dynamic processes in the atmosphere. Academic Press, London, New York
Hurrell JW, Van Loon H (1997) Decadal variations in climate associated with the North Atlantic Oscillation. In: Diaz HF, Beniston M, Bradley RS (eds) Climate change at high elevation sites. Reidel, Dordrecht, pp 69–94
Hurrell JW, Holland MM, Gent PR, Ghan S, Kay JE, Kushner PJ, Lamarque JF, Large WG, Lawrence D, Lindsay K et al (2013) The community earth system model: a framework for collaborative research. Bull Am Meteorol Soc 94(9):1339–1360
Hurrell J, Kushnir Y, Ottersen G, Visbeck M (2003) An overview of the North Atlantic Oscillation. In: Hurrell JW, Kushnir Y, Ottersen G, Visbeck M (eds) The north atlantic oscillation: climatic significance and environmental impact, no. 134 in Geophysical Monograph, American Geophysical Union, pp 1–36
Jajcay N, Hlinka J, Kravtsov S, Tsonis AA, Paluš M (2016) Time scales of the European surface air temperature variability: the role of the 7–8 year cycle. Geophys Res Lett 43(2):902–909
James IN, James PM (1989) Ultra-low-frequency variability in a simple atmospheric circulation model. Nature 342(6245):53–55
Jiang N, Neelin JD, Ghil M (1995) Quasi-quadrennial and quasi-biennial variability in the equatorial Pacific. Clim Dyn 12(2):101–112
Jiang S, Jin FF, Ghil M (1995) Multiple equilibria, periodic, and aperiodic solutions in a wind-driven, double-gyre, shallow-water model. J Phys Oceanogr 25(5):764–786
Jin FF, Neelin JD, Ghil M (1994) El Niño on the devil’s staircase: annual subharmonic steps to chaos. Science 264:70–72
Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, Gandin L, Iredell M, Saha S, White G, Woollen J et al (1996) The NCEP/NCAR 40-year reanalysis project. Bull Am Meteorol Soc 77(3):437–471
Keckhut P, Cagnazzo C, Chanin ML, Claud C, Hauchecorne A (2005) The 11-year solar-cycle effects on the temperature in the upper-stratosphere and mesosphere: part i-assessment of observations. J Atmos Solar-terrestrial Phys 67(11):940–947
Kistler R, Kalnay E, Collins W, Saha S, White G, Woollen J, Chelliah M, Ebisuzaki W, Kanamitsu M, Kousky V et al (2001) The NCEP-NCAR 50-year reanalysis: monthly means CD-ROM and documentation. Bull Am Meteorol Soc 82(2):247–268
Kondrashov D, Feliks Y, Ghil M (2005) Oscillatory modes of extended Nile River records (AD 622–1922). Geophys Res Lett 32(10):L10–702. https://doi.org/10.1029/2004GL022156
Kravtsov S (2017) Pronounced differences between observed and CMIP5-simulated multidecadal climate variability in the twentieth century. Geophys Res Lett 44(11):5749–5757
Kravtsov S, Grimm C, Gu S (2018) Global-scale multidecadal variability missing in state-of-the-art climate models. NPJ Clim Atmos Sci 1(1):34. https://doi.org/10.1038/s41612-018-0044-6
Kren AC, Marsh DR, Smith AK, Pilewskie P (2016) Wintertime northern hemisphere response in the stratosphere to the Pacific Decadal Oscillation using the whole atmosphere community climate model. J Clim 29(3):1031–1049
Krishnamurthy V (2019) Predictability of weather and climate. Earth Space Sci 6(7):1043–1056
Kushnir Y, Robinson WA, Bladé I, Hall NMJ, Peng S, Sutton R (2002) Atmospheric GCM response to extratropical SST anomalies: synthesis and evaluation. J Clim 15(16):2233–2256
Lau NC, Nath MJ (1987) Frequency dependence of the structure and temporal development of wintertime tropospheric fluctuations-comparison of a GCM simulation with observations. Mon Wea Rev 115:251–271
Liu Z (2012) Dynamics of interdecadal climate variability: a historical perspective. J Clim 25(6):1963–1995
Meehl GA, Arblaster JM, Branstator G, Van Loon H (2008) A coupled air-sea response mechanism to solar forcing in the pacific region. J Clim 21(12):2883–2897
Meehl GA, Arblaster JM, Matthes K, Sassi F, van Loon H (2009) Amplifying the pacific climate system response to a small 11-year solar cycle forcing. Science 325(5944):1114–1118
Miller AJ, Schneider N (2000) Interdecadal climate regime dynamics in the North Pacific Ocean: theories, observations and ecosystem impacts. Prog Oceanogr 47(2–4):355–379
Minobe S, Kuwano-Yoshida A, Komori N, Xie SP, Small RJ (2008) Influence of the Gulf Stream on the troposphere. Nature 452(7184):206
Minorsky N (1962) Nonlinear oscillations. Van Nostrand, Princeton
Misios S, Mitchell DM, Gray LJ, Tourpali K, Matthes K, Hood L, Schmidt H, Chiodo G, Thiéblemont R, Rozanov E et al (2016) Solar signals in cmip-5 simulations: effects of atmosphere-ocean coupling. Quart J R Meteorol Soc 142(695):928–941
Moron V, Vautard R, Ghil M (1998) Trends, interdecadal and interannual oscillations in global sea-surface temperatures. Clim Dyn 14(7):545–569
Muller RA, Curry J, Groom D, Jacobsen R, Perlmutter S, Rohde R, Rosenfeld A, Wickham C, Wurtele J (2013) Decadal variations in the global atmospheric land temperatures. J Geophys Res Atmos 118(11):5280–5286
Newman M, Alexander MA, Ault TR, Cobb KM, Deser C, Di Lorenzo E, Mantua NJ, Miller AJ, Minobe S, Nakamura H et al (2016) The Pacific decadal oscillation, revisited. J Clim 29(12):4399–4427
Olson DB, Podestá GP, Evans RH, Brown OB (1988) Temporal variations in the separation of Brazil and Malvinas Currents. Deep Sea Res Part A Oceanogr Res Pap 35(12):1971–1990
Pierini S, Ghil M, Chekroun MD (2016) Exploring the pullback attractors of a low-order quasigeostrophic ocean model: the deterministic case. J Clim 29(11):4185–4202
Plaut G, Vautard R (1994) Spells of low-frequency oscillations and weather regimes in the Northern Hemisphere. J Atmos Sci 51(2):210–236. https://doi.org/10.1175/1520-0469(1994)051<0210:SOLFOA>2.0.CO;2
Plaut G, Ghil M, Vautard R (1995) Interannual and interdecadal variability in 335 years of Central England temperature. Science 268:710–713
Poli P et al (2016) ERA-20C: an atmospheric reanalysis of the twentieth century. J Clim 29(11):4083–4097
Schneider N, Cornuelle BD (2005) The forcing of the pacific decadal oscillation. J Clim 18(21):4355–4373
Seager R, Kushnir Y, Naik NH, Cane MA, Miller J (2001) Wind-driven shifts in the latitude of the kuroshio-oyashio extension and generation of sst anomalies on decadal timescales. J Clim 14(22):4249–4265
Shindell D, Rind D, Balachandran N, Lean J, Lonergan P (1999) Solar cycle variability, ozone, and climate. Science 284(5412):305–308
Siqueira L, Kirtman BP (2016) Atlantic near-term climate variability and the role of a resolved gulf stream. Geophys Res Lett 43(8):3964–3972
Siscoe GL (1978) Solar-terrestrial influences on weather and climate. Nature 276(5686):348–352
Small RJ et al (2008) Air–sea interaction over ocean fronts and eddies. Dyn Atmos Oceans 45:274–319
Small RJ, Bacmeister J, Bailey D, Baker A, Bishop S, Bryan F, Caron J, Dennis J, Gent P, Hsu H, Jochum M, Lawrence D, Muñoz E, diNezio P, Scheitlin T, Tomas R, Tribbia J, Tseng Y, Vertenstein M (2014) A new synoptic scale resolving global climate simulation using the community earth system model. J Adv Model Earth Syst 6(4):1065–1094. https://doi.org/10.1002/2014MS000363
Srivastava A, DelSole T (2017) Decadal predictability without ocean dynamics. Proc Natl Acad Sci 114(9):2177–2182
Stigler SM (1980) Stigler’s law of eponymy. Trans N Y Acad Sci 39(1 Series II):147–157
Stoker JJ (1950) Nonlinear vibrations in mechanical and electrical systems. Wiley, New York
Sutton R, Allen MR (1997) Decadal predictability of north atlantic sea surface temperature and climate. Nature 388(6642):563
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93(4):485–498
Tziperman E, Stone L, Cane MA, Jarosh H (1994) El Nino chaos: overlapping of resonances between the seasonal cycle and the Pacific ocean-atmosphere oscillator. Science 264(5155):72–74
Vannitsem S, Demaeyer J, De Cruz L, Ghil M (2015) Low-frequency variability and heat transport in a low-order nonlinear coupled ocean-atmosphere model. Physica D: Nonlinear Phenomena 309:71–85
Vautard R, Ghil M (1989) Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series. Physica D: Nonlinear Phenomena 35(3):395–424
Vimont DJ (2005) The contribution of the interannual enso cycle to the spatial pattern of decadal enso-like variability. J Clim 18(12):2080–2092
Visbeck M, Chassignet EP, Curry RG, Delworth TL, Dickson RR, Krahmann G (2003) The ocean’s response to North Atlantic Oscillation variability. In: Hurrell JW, Kushnir Y, Ottersen G, Visbeck M (eds) The North Atlantic Oscillation: climatic significance and environmental impact, no. 134 in geophysical monograph, Wiley Online Library, pp 113–145
Wallace JM, Gutzler DS (1981) Teleconnections in the geopotential height field during the northern hemisphere winter. Mon Weather Rev 109(4):784–812
White WB, Liu Z (2008) Resonant excitation of the quasi-decadal oscillation by the 11-year signal in the sun’s irradiance. J Geophys Res Oceans 113:C01002
White WB, Lean J, Cayan DR, Dettinger MD (1997) Response of global upper ocean temperature to changing solar irradiance. J Geophys Res Oceans 102(C2):3255–3266
Wills RC, Battisti DS, Proistosescu C, Thompson L, Hartmann DL, Armour KC (2019) Ocean circulation signatures of north pacific decadal variability. Geophys Res Lett 46(3):1690–1701
Zhang L, Delworth TL (2015) Analysis of the characteristics and mechanisms of the pacific decadal oscillation in a suite of coupled models from the geophysical fluid dynamics laboratory. J Clim 28(19):7678–7701
Zhang Y, Wallace JM, Battisti DS (1997) Enso-like interdecadal variability: 1900–1993. J Clim 10(5):1004–1020
Zhang R, Sutton R, Danabasoglu G, Delworth TL, Kim WM, Robson J, Yeager SG (2016) Comment on “The Atlantic Multidecadal Oscillation without a role for ocean circulation”. Science 352(6293):1527–1527
Acknowledgements
Y. Feliks acknowledges the hospitality of the National Center for Atmospheric Research (NCAR) in Boulder, Colo., during two sabbatical months in Fall 2017; it is at that time that the present work was started. Discussions with many colleagues, at NCAR and at UCLA, have helped crystallize the authors’ ideas on the methodology and the results. In particular, it is a pleasure acknowledge the exchanges with Gokhan Danabasoglu and Jerry Meehl on the 11-years solar cycle in various CESM versions. Careful and constructive comments from an anonymous reviewer have helped improve the final version of this paper. The high-resolution CESM data for the run we used is available from: https://www.earthsystemgrid.org/dataset/ucar.cgd.asd.hybrid_v5_rel04_BC5_ne120_t12_pop62.html. Computing and data storage resources, including the Cheyenne supercomputer (doi:10.5065/D6RX99HX),were provided by the Computational and Information Systems Laboratory (CISL) at NCAR. The CESM project is supported primarily by the National Science Foundation (NSF). This material is based upon work supported by the National Center for Atmospheric Research, which is a major facility sponsored by the NSF under Cooperative Agreement No. 1852977. The present paper is TiPES contribution #7; this project has received funding from the EU’s Horizon 2020 research and innovation programme under grant Agreement No. 820970, and it helps support the work of M. Ghil. Work on this paper has also been supported by the EIT Climate-KIC; EIT Climate-KIC is supported by the European Institute of Innovation & Technology (EIT), a body of the European Union.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
The 11-years oscillatory mode in the CESM simulation's surface temperatures (STs) (mp4 262 KB)
The 11-years oscillatory mode in the CESM simulation's 200-hPa geopotential field (mp4 368 KB)
The 3.4-years oscillatory mode in the CESM simulation's 200-hPa geopotential field (mp4 374 KB)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Feliks, Y., Small, J. & Ghil, M. Global oscillatory modes in high-end climate modeling and reanalyses. Clim Dyn 57, 3385–3411 (2021). https://doi.org/10.1007/s00382-021-05872-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-021-05872-z