Introduction

Climate variability exists across a large spectrum of temporal and spatial scales (Mitchell Jr. 1976; Huybers and Curry 2006; Franzke et al. 2020; Rodgers et al. 2021). In this paper, we outline a hierarchy of conceptual climate models that serves both as physical and statistical null hypotheses when studying the subset of internal climate variability that exists on subseasonal-to-decadal timescales. We here focus our discussion primarily on variability of sea surface temperature (SST)—a key control on global rainfall patterns (Ropelewski & Halpert 1987; Xie et al. 2010) and numerous marine ecosystems (Smale et al. 2019), amongst many other things—however, the concepts discussed here can be applied widely to many components of the climate system.

On subseasonal-to-decadal timescales, so-called modes of climate variability are ubiquitous phenomena that are typically defined empirically and have received much attention since the pioneering work of Walker (Walker 1925, 1928), who identified and named the North Atlantic Oscillation, the North Pacific Oscillation, and the Southern Oscillation. Here we use the term mode loosely, referring generally to coherent patterns of spatio-temporal variability in the climate system (and not solely to eigenmodes of the climate system), some of which exhibit strong seasonality. The most prominent of these modes is the El Niño-Southern Oscillation (ENSO), a phenomenon characterized by large-scale inter-annual vacillations of SST anomalies in the eastern tropical Pacific and coherent variations in the strength of the trade winds with maximum variance in boreal winter (Stein et al. 2014; Chen & Jin 2020), which together arise from a coupled instability of the tropical Pacific ocean–atmosphere system (Carrillo 1892; Walker 1925; Bjerknes 1969; Wyrtki 1985; Zebiak and Cane 1987; Jin 1997; Battisti et al. 2018; Jin et al. 2020). While ENSO itself is confined to the tropical Pacific, its impacts can be traced across the globe (Ropelewski and Halpert 1987; Lau and Nath 1996; McPhaden et al. 2006; Taschetto et al. 2020; Callahan and Mankin 2023; Liu et al. 2023) and form the basis of operational seasonal forecasting (Cane et al. 1986; Trenberth et al. 1998).

Over recent decades, much research has been conducted to identify similar modes of variability in the climate system, both in the tropics and extratropics (Deser et al. 2010; Di Lorenzo et al. 2015; Newman et al. 2016; Stuecker 2018; Cai et al. 2019; Power et al. 2021; Capotondi et al. 2023), often aimed at improving climate predictions from subseasonal to decadal timescales (Meehl et al. 2021). These include (but are not limited to) the Indian Ocean Dipole (IOD; Saji et al. 1999; Webster et al. 1999), the Indian Ocean Basin (IOB) mode (Xie et al. 2009, 2016), North Tropical Atlantic (NTA) variability (Enfield 1996; Ham et al. 2013), Atlantic Niño (Zebiak 1993), the Atlantic and Pacific Meridional Modes (AMM/PMM; Vimont et al. 2001; Chiang & Vimont 2004; Di Lorenzo et al. 2015; Battisti et al. 2018; Stuecker 2018), the Interdecadal Pacific Oscillation (IPO; Zhang et al. 1997; Power et al. 1999, 2021; Capotondi et al. 2023), the Pacific Decadal Oscillation (PDO; Mantua et al. 1997; Minobe 1997; Newman et al. 2016; Di Lorenzo et al. 2023), and the Northern Gulf of Alaska Oscillation (NGAO; Hauri et al. 2021). The potential interactions of these modes and the implication of these interactions on climate predictability are active fields of research (Cai et al. 2019; Wang 2019). Here we focus our discussion on modes of variability that involve fluxes (of heat, moisture, and/or momentum) between the ocean and atmosphere (Cronin et al. 2019) and have clear SST signatures. In the remainder of this paper we will argue the case that these modes of variability can be primarily understood as oceanic responses to stochastic forcing and/or ENSO that are oftentimes facilitated or modulated by different feedbacks, such as the Bjerknes feedback (Bjerknes 1969), Wind-Evaporation-SST feedback (Xie and Philander 1994; Karnauskas 2022), and/or SST-(low)cloud feedback (Norris and Leovy 1994; Tanimoto and Xie 2002; Clement et al. 2009; Bellomo et al. 2015). We will not discuss primarily atmospheric modes such as the Arctic Oscillation, the North Atlantic Oscillation, or the North Pacific Oscillation [for a recent review of those the reader is referred to Williams et al. (2017)]. Neither will we discuss multi-decadal-to-centennial variability associated with changes in the strength of the Atlantic Meridional Overturning Circulation [for a recent review the reader is referred to Zhang et al. (2019)].

One of the most important revelations in climate research has been that much of climate variability—except for ENSO—can be understood to first order as a system with a characteristic damping timescale that integrates stochastic forcing (Hasselmann 1976). As a result, much of the observed SST variability (Fig. 1) in many regions of the global oceans [apart from the tropical Pacific and regions where ocean currents are vigorous (Hall and Manabe 1997; Frankignoul et al. 2002; Kohyama et al. 2021)], can be explained by a local linear stochastic model that formulates SST variations as the result of the ocean mixed layer integrating local air–sea fluxes associated with random atmospheric variability (Frankignoul and Hasselmann 1977). Support for the applicability of this stochastic model for climate variability can be found in the observed lead/lag correlation structure between heat fluxes and SST (Frankignoul and Hasselmann 1977; von Storch 2000; Wu et al. 2006; Kirtman et al. 2012).

Fig. 1
figure 1

Spatial pattern of the observed SST anomaly standard deviation [K] during 1982–2021 using high spatial resolution monthly data (Reynolds et al. 2007)

Full size image

This stochastic climate model that has been proposed both in one-dimensional (Hasselmann 1976; Frankignoul and Hasselmann 1977) and multi-dimensional forms (Hasselmann 1988) that can be used as a statistical null hypothesis, against which one needs to evaluate whether these statistical modes of variability—identifiable empirically in observations and climate model simulations—can be explained solely by the oceanic integration of atmospheric noise or if indeed they offer potential predictability beyond damped persistence (Hasselmann 1988; Penland 1989; Penland and Sardeshmukh 1995; Zhao et al. 2019, 2020).

Here we present a hierarchy of null hypotheses (both from a physical and statistical perspective) for climate variability based on the original Hasselmann model and various extensions, focusing on those proposed in recent years. We will present examples of how one can apply this model hierarchy to identify the dynamics underlying observed climate variability. Recent research has shown that three players and their interactions are instrumental in generating much of the observed SST variability, including many modes of variability: the thermal inertia of the ocean mixed layer, the El Niño-Southern Oscillation, and the seasonal cycle.

Building a hierarchy of conceptual climate models

A white atmosphere and a red ocean

The chaotic nature of atmospheric motions results in fast decorrelation timescales of atmospheric variables (Lorenz 1963), yielding an essentially white spectrum (i.e., power is distributed equally across all timescales; Fig. 2a, c). By separating the fast variations of weather from the slow variations of climate—analogous to Brownian motion (Einstein 1905; Langevin 1908; Uhlenbeck and Ornstein 1930)—Hasselmann (1976) derived the following stochastic differential equation, in which climate variations [here: SST, but with applications for many other variables such as upper-ocean heat content (Frankignoul and Hasselmann 1977), sea surface salinity (Hall and Manabe 1997), sea-ice concentration (Lemke et al. 1980), or soil moisture (Delworth & Manabe 1988; Olson et al. 2021)] arise from the integration of white noise:

$$\frac{dT}{dt}=-\lambda T+\sigma \xi$$
(1)

where T denotes SST anomalies [K], \(\xi\) is white noise with Gaussian distribution of zero mean and unit variance Footnote 1, \(\sigma\) is the noise amplitude [K month−1], and λ a linear damping term [month−1] that prevents unbounded growth [for detailed discussions on the derivation and history as well as applications such as the detection and attribution of the forced climate change signal (Hasselmann 1979, 1997) the reader is referred to von Storch et al. (2000), Franzke et al. (2022), von Storch (2022), and Heimbach (2022) among othersFootnote 2]. Here we are using the original formulation in which the heat fluxes \(Q (={Q}_{T}+{Q}_{\xi })\), ocean mixed layer depth HML, ocean heat capacity cp, and ocean density ρ are implicit in the damping rate as local linear temperature feedback (\(\lambda T= \frac{{Q}_{T}}{{H}_{ML}{c}_{p}\rho })\) and noise term inferred from the residual \((\sigma \xi = \frac{{Q}_{\xi }}{{H}_{ML}{c}_{p}\rho }\)). For applications of the model with those variables and parameters being explicit see for instance Frankignoul and Hasselmann (1977) and Hall and Manabe (1997).

Fig. 2
figure 2

Examples of white and red noise: sea level pressure (SLP) and sea surface temperatures (SSTs). a Leading EOF of detrended monthly SLP anomalies in the North Pacific (between 20 and 60°N; area-weighted) during 1959–2022 displayed as regression coefficients in physical units [hPa per standard deviation] using ERA5 reanalysis (Hersbach et al. 2020), capturing variability of the Aleutian Low. b Leading EOF of detrended monthly SST anomalies in the North Pacific (between 20 and 60°N; area-weighted) during the same time period displayed as regression coefficients in physical units [K per standard deviation] using ERSSTv5 data (Huang et al. 2017), capturing the characteristic PDO pattern. c Power spectral density [PSD; using the Multi-Taper Method (MTM) with 3 tapers and nfft = 1024 (Thomson 1982)] of the normalized leading principal components (PCs) of North Pacific SLP anomalies (grey line) and North Pacific SST anomalies (black line) corresponding to the EOFs shown in a, b, respectively. The AR(1) fit (solid orange and red lines) as well as the 99% confidence levels (CL; dashed orange and red lines) for potential spectral peaks were calculated from the respective percentile at each frequency of 10,000 power spectra generated from discrete AR(1) processes with the same lag(-1) autocorrelation r and data length as the respective PC time series (\({\lambda }^{-1}=\sim 8.1\) months for SST PC1 and \({\lambda }^{-1}=\sim 0.7\) months for SLP PC1). The SLP PC1 spectrum is almost white (i.e., characterized by a very fast decorrelation timescale) whereas the SST PC1 exhibits a Lorentzian spectrum (i.e., red at high frequencies and white at low frequencies). The predicted -2 power law slope in log–log space of red noise at high frequencies is indicated by the thin black line. The vertical dashed grey lines indicate the frequencies beyond which the spectra are expected to be approximately white for each \(\lambda\)

Full size image

The power spectrum of T resulting from integration of Eq. 1 is given by: \(P\left(\omega \right)=\frac{{\sigma }^{2}}{{\lambda }^{2}+{\omega }^{2}}\), being determined by the variance of the white noise forcing \({\sigma }^{2}\) [K2 month−2], the damping rate λ, and the angular frequency ω. This Lorentzian spectrum (Hasselmann 1976; Pelletier 1997; Franzke et al. 2020) has two regimes (Fig. 2c): at high-frequencies (ω > λ) the T spectrum is proportional to 1/ω2 (i.e., red or Brownian noise) whereas at low-frequencies (ω < λ) the T spectrum has constant power independent of frequency, i.e., it is white (P(ω) ~ 1/λ2). The value of the damping rate λ determines both the transition point between the two regimes (indicated by the vertical grey lines in Fig. 2c) as well as the value of the variance plateau at low frequencies. As was mentioned previously, in regions where ocean dynamics are important (due to either strong vertical and/or horizontal advection), this local stochastic view of climate may not be appropriate (Frankignoul 1985; Hall & Manabe 1997). The discrete analogue of Eq. 1 is a Markov process, specifically an autoregressive model of order 1 (AR(1); e.g., von Storch and Zwiers (1999)): \({T}_{n+1}=r{T}_{n}+\sigma {\epsilon }_{n}\) [for a derivation refer for instance to Wettlaufer and Bühler (2015)].Footnote 3 Here, n is a discrete time step index, r [unitless] the fraction of anomalies that is retained at the next time step (that can be related to the damping time scale via \(r={e}^{-\lambda \Delta t}\); see also footnoteFootnote 4), and \(\sigma {\epsilon }_{n}\) discrete white noise [K]. Note that the discretized noise term is not truly white, but instead is white noise integrated over a sampling interval \(\Delta t\) (Penland 1989, 1996).

The above model can be applied not only to model SST anomalies (or other variables) at a given grid point, but also applied to model the temporal evolution and variance of climate indices that describe large-scale modes of variability, such as the aforementioned PDO (Schneider and Cornuelle 2005; Newman et al. 2016). A simple example for the PDO index in discrete form would be: \({\mathrm{PDO}}_{n+1}= r{\mathrm{PDO}}_{n}+\sigma {\epsilon }_{n}\) [see Fig. 2b for the characteristic PDO pattern obtained via Empirical Orthogonal Function (EOF) decomposition (Lorenz 1956)]. However, how one exactly defines a mode of climate variability—with the EOF decomposition being a potential and popular tool—and whether that choice is reasonable strongly depends on the specific question at hand [see for instance discussion in Monahan et al. (2009)].

The temporal evolution of climate variables in response to stochastic forcing and their manifestation in spatial patterns—such as the PDO—can be more generally formalized via a multi-dimensional extension of Eq. 1 (or its discrete analogue) leading to the following stochastically forced linear systemFootnote 5 (Hasselmann 1988): \(\frac{d\mathbf{x}}{dt}=\mathbf{L}\mathbf{x}+ \sigma \xi\), where x is a multi-dimensional state vector, L a multi-dimensional (finite) linear operator, and \(\sigma \xi\) again is referring to white noise forcing that now can have spatial patterns as well. In fact, it can be easily observed that not just climate but also its forcing, i.e., atmospheric variability, manifests itself in spatial patterns (e.g., Walker 1925, 1928).

This formalism is utilized in the Principal Oscillation Pattern (POP) analysis (Hasselmann 1988; von Storch et al. 1995), closely related to Linear Inverse Models (LIMs; Penland 1989, 1996; Penland and Sardeshmukh 1995; Xu et al. 2022). The reader is referred to the extensive literature (e.g., von Storch et al. 1995; Ghil et al. 2002; Penland 2007; Schmid 2010; Tu et al. 2014; Franzke et al. 2022; Heimbach 2022) for discussions on the different aspects of dimensionality reduction [e.g., via Principal Interaction Patterns (Hasselmann 1988)], time discretization, and linearization (around a basic state) of the underlying high-dimensional nonlinear dynamical system based on data and the subtle differences between the POP and LIM frameworks.

The POPs are the eigenmodes of the discretized linear reduced system that can be calculated from data (via a lagged covariance matrix), such as observables of the climate system or Earth system model output (Hasselmann 1988; von Storch et al. 1995; Ghil et al. 2002). When constructing the linear system, the state vector x is typically a subspace (e.g., composed of many EOFs) of a high-dimensional data set. The state vector can also encompass multiple physical variables if one is interested in their covariance (e.g., SSTs and sea surface height). Note that the POP/LIM formalism can allow for nonnormal growth to occur (e.g., Penland and Sardeshmukh 1995; Martinez-Villalobos et al. 2018).Footnote 6 It is important to emphasize that EOFs do not necessarily correspond to the eigenmodes of a dynamical system (e.g., North 1984), in fact, they are only exactly the same if the linear operator L is normal and the noise forcing has no spatial structure [see for instance discussion in Monahan et al. (2009)].

While EOF modes do not necessarily correspond to the eigenmodes of the underlying dynamical system, they can nevertheless be a very useful tool to define coherent spatio-temporal patterns of climate variability. First, identifying the principal axes of variability and thereby the orthogonal patterns that explain most of the variance can help develop understanding of the underlying physics driving the variability (Monahan et al. 2009). Second, data dimensionality reduction via a number of leading EOFs ensures that the fraction of total variance explained is maximized in the subset (Monahan et al. 2009), which can be a very useful attribute when constructing a reduced linear system. Let us further consider the following brief example to illustrate the practical utility of EOFs: When applying an EOF decomposition to SST anomalies in the tropical Indian Ocean one obtains the aforementioned IOB mode and IOD patterns as the two leading EOF modes (i.e., they explain the largest fractions of the total variance). The case can be made that the IOB mode and IOD are both physically and societally relevant as they are associated with large-scale reorganizations of tropical convection and associated atmospheric circulation changes, thereby impacting precipitation in countries surrounding the Indian Ocean and beyond (e.g., Saji and Yamagata 2003; Xie et al. 2016).

As discussed by Tu et al. (2014) and Brunton and Kutz (2019), the time evolution of a nonlinear dynamical system can be described by an infinite-dimensional linear operator—the Koopman operator (Koopman 1931)—which advances measurement functions of the system’s state. In practice, obtaining a finite-dimensional approximation of the Koopman operator and determine its eigenmodes is not trivial and a field of active research (e.g., Brunton and Kutz 2019). One approach is the recently proposed Dynamic Mode Decomposition (DMD), which is closely related to the POP/LIM framework and has been applied in many different areas of data science and control theory (e.g., Schmid 2010; Tu 2013; Tu et al. 2014; Franzke et al. 2022; Heimbach 2022). It can be argued that Koopman operator theory provides a foundation for the applicability of the linear POP/LIM framework to many problems, as POPs/LIMs can capture the essential dynamics of the underlying high-dimensional nonlinear dynamical system if one is able to construct a reasonable reduced system (although choosing the right subset for a reduced system is not trivial, see for instance the discussion in Hasselmann (1988)).Footnote 7

Beyond a red ocean: the El Niño-Southern Oscillation (ENSO)

Next, we discuss climate variability beyond this stochastic view of climate. The most prominent mode of variability in the climate system is ENSO, which has its dynamical origin in an instability of the coupled ocean–atmosphere system in the tropical Pacific. Specifically, the fast positive Bjerknes feedback [perturbations in SST, trade winds, and thermocline tilt reinforcing each other (Bjerknes 1969)] together with the slow negative feedback associated with the adjustment of the equatorial Pacific ocean heat content due to anomalous Sverdrup transport (Wyrtki 1985), lead to vacillations between periods of anomalously warm eastern equatorial Pacific SSTs and weak trade winds (i.e., El Niño) and periods of anomalously cold eastern equatorial Pacific SSTs and strong trade winds (i.e., La Niña). ENSO can be isolated empirically from observational data and/or high-dimensional coupled climate models either as the leading oscillatory (or weakly damped; see discussion in Jin (2022) on near-criticality) eigenmode of the coupled tropical ocean–atmosphere system—or under an alternative hypothesis arising from a combination of several leading damped modes under nonnormal growth (Penland and Sardeshmukh 1995). For the latter, the aforementioned POP/LIM framework is an often-employed tool (Xu and von Storch 1990; von Storch et al. 1995; Kleeman 2011; Gehne et al. 2014). The simplest deterministic conceptual model, derived from a high-dimensional intermediate complexity climate model (Zebiak and Cane 1987), which succinctly captures the essential dynamics of the tropical Pacific air–sea coupled system, is the ENSO recharge oscillator (Jin 1997), a system of two coupled ordinary differential equations (ODEs):

$$\frac{d{T}_{\mathrm{ENSO}}}{dt}={a}_{11}{T}_{\mathrm{ENSO}}+ {a}_{12}h$$
(2a)
$$\frac{dh}{dt}={a}_{21}{T}_{\mathrm{ENSO}}+ {a}_{22}h$$
(2b)

Here, TENSO are SST anomalies associated with ENSO—typically averaged over a geographical box in the eastern equatorial Pacific, such as the Niño3.4 region—and h are thermocline depth anomalies in either the western equatorial Pacific or zonally averaged over the whole equatorial Pacific [see discussion in Jin et al. (2020)]. In its simplest formulation (Burgers et al. 2005), aij are constant coefficients that can be obtained empirically from either observations or climate model simulations, yielding a system of two linear ODEs. One of the solutions of this system is a limit cycle, characterized by periodic oscillations with TENSO and h being in quadrature, similar to what is being seen in observations (Meinen and McPhaden 2000). Nonlinearities, non-constant coefficients (more on this later), and multiplicative noise can be included in the recharge oscillator framework to account for the observed spatio-temporal complexity of ENSO (Timmermann et al. 2018; Jin et al. 2020; Jin 2022). The largely oscillatory nature of ENSO leads to distinct spectral peaks on interannual timescales above the AR(1) background spectrum (i.e., what would be obtained by integrating Eq. 1), displaying variance at these timescales that is significantly larger than what would be expected from the null hypothesis of stochastic climate variability (e.g., Rodgers et al. (2021); Fig. 3a, c, d).

Fig. 3
figure 3

The El Niño-Southern Oscillation (ENSO) and its Combination Mode. a EOF1 (ENSO) and b EOF2 (ENSO Combination Mode) of ERA5 (Hersbach et al. 2020) detrended joint u and v 10 m wind monthly anomalies displayed as regression coefficients in physical units following the methodology and applied to the same spatial domain (100°E–60°W, 10°S–10°N; area-weighted; normalized PCs regressed on the anomalies over the larger domain shown here) as described in Stuecker et al. (2013). Shading is the zonal wind component. c Power spectral density [PSD; using the Multi-Taper Method (MTM) with 5 tapers and nfft = 1024 (Thomson 1982)] of the normalized leading two principal components (PCs) of the ERA5 10 m wind anomalies EOF analysis. The confidence level (CL) for spectral peaks was calculated from the respective percentile at each frequency of 10,000 power spectra generated from discrete AR(1) processes with the same lag(-1) autocorrelation r and data length as the respective PC time series (\({\lambda }^{-1}=\sim 4.3\) months for PC1 and \({\lambda }^{-1}=\sim 2.6\) months for PC2). The time series representing the C-mode (spectrum in yellow line) was created using Eq. 4 with TENSO = PC1 following Stuecker et al. (2013). The grey boxes represent the approximate frequency range of ENSO (fE) and the near-annual combination tones (1-fE and 1 + fE). d The same as c but for the normalized leading two PCs of the same EOF analysis (same domain) applied to surface wind stress monthly anomalies (the Combination Mode is reflected in the second PCs of 10 m surface winds as well as in wind stress; see results in Stuecker et al. (2013) and McGregor et al. (2012)) from a 1000-year preindustrial control simulation of the CESM2 climate model (using 7 instead of 5 tapers). The EOF patterns are not shown but are very similar to the ERA5 patterns (explained variance: 18% and 12% for EOF1 and EOF2; \({\lambda }^{-1}=\sim 6.8\) months for PC1 and \({\lambda }^{-1}=\sim 2.2\) months for PC2)

Full size image

The pacemaker of the climate system: the seasonal cycle

The third member and pacemaker of the trio is the seasonal cycle. Changes in insolation due to the seasonal cycle drive large seasonal variations in climate. These large amplitude signals are immediately evident when contrasting the SST climatology in different calendar months.Footnote 8 It is critical to recognize that these seasonal variations in the mean state can interact with climate variability in nontrivial (i.e., non-additive) ways, which we will discuss in the following sections.

Extension of the stochastic climate model to include the seasonal cycle

In this section, we will discuss the role that the seasonal cycle plays in stochastic climate variability. De Elvira and Lemke (1982) and Ortiz and De Elvira (1985) added two important extensions to the stochastic climate model of Hasselmann (1976), leading to a first-order linear stochastic differential equation with a non-constant (i.e., time dependent) coefficient:

$$\frac{dT}{dt}=-\left[{\lambda }_{0}+{\lambda }_{ac}\mathrm{cos}\left({\omega }_{ac}t-{\phi }_{1}\right)\right] T+ \widetilde{\sigma }\xi$$
(3)

The first extension is the addition of an idealized sinusoidal seasonal cycle with angular frequency \({\omega }_{ac}=\frac{2\pi }{12 \mathrm{months}}\) and phase \({\phi }_{1}\) to the damping rate (with λ0 being a constant coefficient and λac its seasonal modulation). This is motivated by the fact that both the efficiency of SST anomaly thermodynamic damping and the ocean mixed layer depth (and thereby its inertia) exhibit strong seasonal cycles. The second extension is the addition of a seasonal cycle in the amplitude of the atmospheric noise forcing (\(\widetilde{\sigma }\xi \sim [{\gamma }_{0}+{\gamma }_{ac}\mathrm{cos}\left({\omega }_{ac}t-\phi \right)]\xi\)). De Elvira and Lemke (1982) investigated three cases, one with only seasonality in the damping rate included, one with only seasonality in the noise forcing included, and the third case in which both are included. They found that both seasonal modulations critically reshape the covariance functions and power spectra of the slow climate variable (here: SST). The seasonal cycle of the ocean mixed layer depth is implicitly included in the damping rate seasonal cycle in Eq. 3. However, Deser et al. (2003) found that it is necessary add an additional term that mimics the seasonal entrainment process in the Hasselmann model to reproduce the observed partial “re-emergence” of SST anomalies in a given winter season that were generated during the previous winter.

Similarly, the multi-dimensional POP/LIM extension of the stochastic climate model can also be modified to a cyclo-stationary POP/LIM that includes a seasonal cycle in either the linear operator and/or the noise forcing: \(\frac{d\mathbf{x}}{dt}=\mathbf{L}\mathbf{x}+ \widetilde{\sigma }\xi\), with \(\mathbf{L}={\mathbf{L}}_{0}+{\mathbf{L}}_{ac}\) and/or \(\widetilde{\sigma }\) having a seasonal modulation (Blumenthal 1991; von Storch et al. 1995; OrtizBeviá 1997; Shin et al. 2020; Chen and Jin 2021; Chen et al. 2021; Vimont et al. 2022; Kido et al. 2023). The reader is directed to these references for more detailed discussions on cyclo-stationary POPs/LIMs and their different applications.

Seasonal cycle interactions with ENSO: the combination mode leading to an upscale frequency cascade

Next, we discuss one key aspect of ENSO’s interaction with the seasonal cycle. ENSO affects climate globally, primarily through atmospheric teleconnections (Walker 1925; Ropelewski and Halpert 1987; Karoly 1989; Lau and Nath 1996; Alexander et al. 2002; Taschetto et al. 2020). Importantly, these impacts are not the same in each calendar month at a given location—in fact, they can even reverse in sign in different seasons. To account for this seasonal modulation, one can write the impact of ENSO SST anomalies on an atmospheric variable y (i.e., variables that adjust at fast timescales of less than a month, as generally true for the atmospheric response to tropical SST forcing) at a given location [or also on climate indices describing coherent spatio-temporal patterns with fast adjustment timescales, such as the Aleutian Low index (e.g., Fig. 2a) or the aforementioned North Pacific Oscillation] in the following general form (Stuecker et al. 2013, 2015a, 2015b):

$$y=\left[{\beta }_{0}+{\beta }_{ac}\mathrm{cos}\left({\omega }_{ac}t-{\phi }_{2}\right) \right]{T}_{\mathrm{ENSO}}$$
(4)

where the coefficients β0 and βac are measures of the linear and seasonally modulated ENSO impacts, respectively. The seasonally modulated impacts are the so-called ENSO Combination Mode (Stuecker et al. 2013), named after the characteristic near-annual timescales (combination tones) that arise from the interannual ENSO signal interacting with the seasonal cycle. A simple illustration can be made by approximating ENSO as a perfect sinusoidal cycle: \({T}_{\mathrm{ENSO}}= \mathrm{cos}\left({\omega }_{\mathrm{E}}t\right)\), with an angular frequency of \({\omega }_{\mathrm{E}}= \frac{1}{5}\frac{2\pi }{12 \mathrm{months}}\) (i.e., a 5-yr ENSO cycle). Any multiplication of the ENSO signal and the seasonal cycle leads to the following difference and sum terms: \(\mathrm{cos}\left({\omega }_{\mathrm{E}}t\right)\mathrm{cos}\left({\omega }_{ac}t\right)=\frac{1}{2}\left\{\mathrm{cos}\left(\left[{\omega }_{ac}-{\omega }_{\mathrm{E}}\right]t\right)+\mathrm{cos}(\left[{\omega }_{ac}+{\omega }_{\mathrm{E}}\right]t)\right\}\), which for the ENSO period stated above of 5 years are associated with timescales of 15 months and 10 months, respectively. As ENSO has a broad spectral peak of ~ 2–7 years in nature and due to the existence of higher-order nonlinearities, its interaction with the seasonal cycle leads to deterministic variability on a wide range of higher frequencies, leading to an upscale ENSO frequency cascade (Stuecker et al. 2015a). Due to this mechanism, the atmospheric background spectrum in many regions of the world includes ENSO-related deterministic variance across a wide range of timescales [from sub-annual to interannual-(Stuecker 2015; Stuecker et al. 2015a)]. As expected from the above considerations, changes in ENSO’s spatial pattern and dominant timescale—either due to decadal variations and/or secular trends (McPhaden et al. 2020)—also lead to related changes in the ENSO Combination Mode (Ren et al. 2016; Jiang et al. 2020).

This interaction between the seasonal cycle and ENSO is an important driver of climate variability across the globe. The ENSO Combination Mode was first discovered to be manifested in the second Empirical Orthogonal Function of surface wind anomalies in the tropical Pacific (Stuecker et al. 2013), which is a meridionally antisymmetric atmospheric circulation pattern that includes the southward shift of anomalous winds from the equator that accelerates the termination of El Niño events and contributes to ENSO’s seasonal synchronization (McGregor et al. 2012; Stuecker et al. 2013; Abellán and McGregor 2015; Abellán et al. 2017; Iwakiri and Watanabe 2021) as well as a characteristic anomalous low-level circulation feature in the Western North Pacific (WNP; Stuecker et al. 2013, 2015b, 2016). Figure 3 shows the spatial patterns of the leading two EOFs of surface wind anomalies in the tropical Pacific from the latest ERA5 reanalysis data (Hersbach et al. 2020). EOF1 (Fig. 3a) describes the variations in the Walker cell during El Niño and La Niña, and its corresponding principal component (PC1) is highly correlated with TENSO (Stuecker et al. 2013, 2015b). EOF2 (Fig. 3b) is the ENSO Combination Mode wind pattern with pronounced variance at the near-annual combination tone frequencies (red line in Fig. 3c) that have high coherence with the spectrum of the theoretical Combination Mode (yellow line in Fig. 3c) derived from Eq. 4. Statistical significance of the spectral peaks can be further improved by looking at longer data, for instance using 1000 years of a preindustrial control experiment with the CESM2 climate model (Fig. 3d) or the preindustrial control experiment of the GFDL CM2.1 climate model (Stuecker et al. 2013).

Whereas both the difference (1-fENSO) and sum (1 + fENSO) tone are statistically significant at the 99% confidence level (compared to an AR(1) null hypothesis) in the CESM2 data, only the difference tone is statistically significant at the 95% confidence level in the ERA5 reanalysis. That the sum tone is not statistically significant at this level in the ERA5 reanalysis can likely be explained by the following: First, the shorter time period (~ 60 years) of ERA5 data compared to the CESM2 data (1000 years). Indeed, it has been shown that the spectrum at the combination tone frequencies shows a large amplitude range when subsampling a long climate model control simulation in shorter sections (that have by chance varying ENSO variance) with a data length comparable to typical reanalysis products [see Fig. 3b in Stuecker et al. (2015b)]. Second, the different amplitude of the difference and sum tones could be partially explained by the representation of nonlinear processes in climate models [see discussion in Stuecker et al. (2013), Stuecker et al. (2015b), and Stuecker et al. (2016)].

Beyond this wind pattern, the Combination Mode is ubiquitous in many of ENSO’s global impacts, including but not limited to extreme latitudinal swings of the South Pacific Convergence Zone (Stuecker et al. 2013), extreme sea level events in the tropical Pacific (Widlansky et al. 2014), the Pacific Meridional Mode (Stuecker 2018), climate impacts over East Asia (Zhang et al. 2016b; Zheng et al. 2020) including extreme Yangtze river flooding events (Zhang et al. 2016a), precipitation in the Niño3.4 region (Fukuda et al. 2021; Rodgers et al. 2021), the Pacific North-American (PNA) teleconnection pattern (Hu et al. 2023), and synchronized spatial shifts of the Hadley and Walker circulations (Yun et al. 2021b). The ENSO Combination Mode is also detectable in eigenmodes of Indo-Pacific SSTs obtained via nonlinear Laplacian spectral analysis (Slawinska and Giannakis 2017; Giannakis and Slawinska 2018) and transfer/Koopman operator analysis (Froyland et al. 2021).

One key climate impact of ENSO—and its conduit to the East Asian monsoon system (Wang et al. 2000; Zhang et al. 2016a)—is the aforementioned anomalous low-level atmospheric circulation in the WNP. During the evolution of an El Niño event, the anomalous WNP low-level circulation typically undergoes a rapid transition from cyclonic to anticyclonic (establishing the so-called North-West Pacific Anticyclone: NWP-AC) in boreal fall to winter [and vice versa during La Niña events (Stuecker et al. 2015b)]. This rapid phase reversal of ENSO-induced climate anomalies—while the ENSO SST anomalies remain of the same sign—can only be explained by the ENSO Combination Mode [refer to Eq. 4 above and Stuecker et al. (2015b)]. Indeed, spectral analysis clearly shows the characteristic near-annual enhanced variance (relative to the expected white atmospheric and Lorentzian oceanic background spectra depending on the variable in question) associated with the combination tones in the observed WNP wind, sea level pressure, and thermocline fields (Wang et al. 1999; Stuecker et al. 2015b, 2016).

Moreover, targeted atmospheric general circulation model experiments with different prescribed idealized ENSO and seasonal cycle phasing demonstrate that the rapid phase transitions and near-annual spectral peaks in the anomalous WNP circulation are the result of the deterministic ENSO Combination Mode and cannot be explained otherwise (Stuecker et al. 2015b). Later applied diagnostic decompositions such as a moist static energy budget for the NWP-AC formation during El Niño events (Wu et al. 2017) as well as a momentum budget analysis for the aforementioned anomalous southward wind shift during ENSO events (Gong and Li 2021) further confirm that the Combination Mode—that is, ENSO’s interaction with the seasonal cycle—is responsible for both phenomena (Stuecker et al. 2013, 2015b), albeit not recognized by Wu et al. (2017) and Gong and Li (2021) in their discussion of the results.

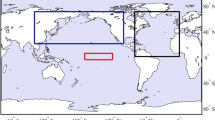
The persistence of the anomalous NWP-AC into post-El Niño boreal summer—when its effect on the East Asian monsoon system is most critical—is due to a confluence of three processes, (i) the Combination Mode induced fast transition to La Niña and associated anomalous anticyclonic low-level wind anomalies in the WNP (Stuecker et al. 2015b), (ii) local air–sea interactions in the WNP (Wang et al. 2000; Stuecker et al. 2015b), and (iii) remote air–sea interactions in the Indian Ocean (Watanabe and Jin 2002; Xie et al. 2009, 2016; Stuecker et al. 2015b; Xie and Zhou 2017)—see Fig. 4 for a detailed schematic.

Fig. 4
figure 4

© American Meteorological Society. Used with permission

Schematic of the impacts of El Niño and its Combination Mode during a composite El Niño event. Highlighted are the mechanisms associated with El Niño and its Combination Mode that regulate the anomalous low-level circulation in the Indo-Pacific with emphasis on the anomalous low-level North-West Pacific Anticyclone (NWP-AC). The seasonal climatological extent of the warm pool (temperatures above 27.5 °C) is displayed by gray shading, and the seasonal climatological surface wind field is displayed by vectors. Idealized sea surface temperature anomalies are indicated by red (positive) and blue (negative) shading. The anomalous low-level anticyclones (AC) and cyclones (C) are indicated by ellipses. a Quasi-symmetric circulation response during the developing El Niño year (June-July–August: JJA(0) to September–October–November: SON(0)) due to the quasi-symmetric warm pool background state. b Antisymmetric circulation response during the El Niño peak phase (in December-January–February: DJF) and following boreal spring (March–April-May: MAM(1)) due to the seasonal warm pool migration to the Southern Hemisphere (antisymmetric background state). c) Persistence of the anomalous NWP-AC until boreal summer after an El Niño event (June-July–August: JJA(1)). The symmetric anticyclone response due to eastern equatorial Pacific cooling (blue shading), a weak antisymmetric Combination Mode response, local air–sea feedback (cooling on the eastern flank of the NWP-AC and warming on the western flank), and the delayed Indian Ocean warming (capacitor effect) contribute to the persistence and amplification of the anomalous NWP-AC until JJA(1). Figure and modified caption from Stuecker et al. (2015b).

Full size image

Seasonal cycle interactions with ENSO: seasonally varying growth rate

The seasonal cycle plays not only a key role in modulating ENSO’s impacts—as we discussed in the previous section—but also in the fundamental ENSO dynamics due to its impact on the air–sea coupling strength in the tropical Pacific [the reader is referred to Timmermann et al. (2018) and Jin et al. (2020) for recent reviews]. This effect can be parameterized in the recharge oscillator model by considering a seasonally dependent SST growth rate instead of a constant coefficient in Eq. 2: \({a}_{11}=-[{r}_{0}+{r}_{ac}\mathrm{cos}\left({\omega }_{ac}t-{\phi }_{3}\right) ]\), where the coefficients r0 and rac are the constant and seasonally modulated parts of the growth rate. This seasonal modulation of the growth rate leads again to the emergence of combination tones in the solutions of the seasonally modulated recharge oscillator (An and Jin 2011; Stein et al. 2014), that can also be detected in ENSO SST anomalies in the different Niño regions (Jin et al. 1996; Stein et al. 2014). Importantly, this seasonal modulation of the growth rate is critical to reproduce the observed seasonal synchronization of ENSO (von Storch et al. 1995; Thompson and Battisti 2000; Stein et al. 2014; Chen and Jin 2020, 2021; Jin et al. 2020).

Putting it all together: the ocean integrating seasonally modulated ENSO and noise forcing

So far, we discussed the deterministic ENSO model (Eq. 2) as the most succinct physics-based model explaining the observed SST variability in the tropical Pacific, whereas the original stochastic climate model (Eq. 1) and its extension that considers seasonal modulations (Eq. 3) can explain much of the SST variance in the extratropics (aside from regions of strong ocean currents). Moreover, we discussed that ENSO has far reaching climate impacts that are also seasonally modulated (Eq. 4).

To consider these ENSO impacts on SST variance outside the tropical Pacific [note that also extensions of Eq. 1 that include remote ENSO forcing but not any effects of seasonality exist, refer for instance to Newman et al. (2016) for a recent review] we further extend the seasonally modulated stochastic climate model (Eq. 2) by including remote seasonally modulated ENSO forcing [Eq. 4; (Stuecker et al. 2017b)]:

$$\frac{dT}{dt}=-\left[{\lambda }_{0}+{\lambda }_{ac}\mathrm{cos}\left({\omega }_{ac}t-{\phi }_{1}\right)\right] T + \left[{\beta }_{0}+{\beta }_{ac}\mathrm{cos}\left({\omega }_{ac}t-{\phi }_{2}\right) \right]{T}_{\mathrm{ENSO}} + \widetilde{\sigma }\xi$$
(5)

This equation can be applied as both a model for local SST variations and/or modes of climate variability (for the latter the growth rate can include non-local feedbacks). Stuecker et al. (2017b) applied the above model to describe the temporal evolution of the IOD index (with T representing the IOD index). Here, the growth rate of the IOD (\({\lambda }_{0}+{\lambda }_{ac}\mathrm{cos}\left({\omega }_{ac}t-{\phi }_{1}\right)\)) has a pronounced seasonal cycle with a relatively strong positive feedback between SSTs, winds, and thermocline depth—akin to the Bjerknes feedback in the tropical Pacific (Bjerknes 1969)—during a few calendar months, leading to a weakly damped system during these months. During the rest of the calendar year the air–sea coupled feedback is weak, leading to a highly damped system during the remainder of the year (Stuecker et al. 2017b). Note that the absence of strong ocean memory in the Indian Ocean—unlike the recharge/discharge process in the tropical Pacific (Wyrtki 1985; Jin 1997)—is the justification for describing the IOD in a stochastic-deterministic model (SDM) framework (Eq. 5) instead of describing it as an oscillatory system like ENSO.

Stuecker et al. (2017b) demonstrated that the observed IOD characteristics, such as its power spectrum (including combination tones) and lead/lag cross-correlation with ENSO, can be accurately captured by the above model. For instance, the fact that growth rates of the IOD and ENSO have different phasing leads to the SST variance for the IOD being maximized in boreal fall while for ENSO it is maximized in boreal winter. Due to the different phasing of these growth rates, both the observed IOD index as well as the solution to Eq. 5 exhibit a maximized positive correlation when the IOD is leading ENSO by ~ 3 months and a maximized negative correlation when the IOD is leading ENSO by ~ 14–16 months. The latter has been hypothesized to help predict ENSO conditions in the next year based on the IOD conditions in the present year (Izumo et al. 2010; Jourdain et al. 2016). However, this statistical relationship can also be explained by the IOD being forced by ENSO (Eq. 5) without a feedback from the IOD back to ENSO (Stuecker et al. 2017b). Indeed, it has been shown that the model as formulated in Eq. 5 using state-of-the-art operational ENSO forecasts as input on the right-hand-side has better predictive skill for the IOD than operational IOD forecasts, demonstrating that all the effective predictive skill for the IOD arises from ENSO (Zhao et al. 2019, 2020). While about 2/3 of the observed IOD events are attributable to ENSO, the remaining 1/3 are likely due to noise forcing that might not be predictable beyond subseasonal timescales (Stuecker et al. 2017b). We acknowledge that it is possible that a feedback of the IOD on ENSO exists. However, this additional level of complexity in the model hierarchy would need to be tested against the null hypothesis of a one-way forcing as formulated in Eq. 5. For instance, one would need to demonstrate that a two-way coupling between ENSO and the IOD is necessary to reproduce the observed ENSO statistics and predictability.

Given the substantial importance of the IOD SST pattern for precipitation variability in the Indo-Pacific region (Ashok et al. 2003, 2004; Saji and Yamagata 2003; Zhang et al. 2021b) and remaining deficiencies in the simulation of many ENSO characteristics (Bayr et al. 2019; Planton et al. 2021) as well as remaining uncertainties in projected future ENSO changes (Cai et al. 2021; Stevenson et al. 2021; Wengel et al. 2021; Yun et al. 2021a; Maher et al. 2023), the above results point to an urgent necessity to refocus attention on model improvements in simulating ENSO—as well as its forcing of other climate phenomena—to improve societally-relevant seasonal predictions as well as regional future climate projections.

To explore how biases and changes in ENSO characteristics affect the statistical ENSO/IOD relationships, we can use different simulated ENSO time series—resulting from different parameters that control ENSO characteristics—from a version of the ENSO recharge oscillator model (a nonlinear extension of Eq. 2 with state-dependent noise included) as input for the stochastic-deterministic (i.e., including both stochastic and deterministic components) IOD model (Eq. 5). Jiang et al. (2021) used this approach to show that the pacing of ENSO (quantified by two metrics describing ENSO periodicity and regularity) determines the statistical inter-basin relationship between ENSO and the IOD across 40 CMIP6 models. Moreover, the observed “nonstationarity” (here referring to variations on decadal timescales) of this statistical relationship can be succinctly explained by decadal changes of ENSO characteristics. Thus, Jiang et al. (2021) conclude that this evidence points towards a largely one-way forcing of ENSO on the IOD, which is in agreement with the finding that nearly all the effective predictability of the IOD in operational seasonal forecast systems results from ENSO (Zhao et al. 2019, 2020).

Equation 5 can be applied to many other climate phenomena across the globe. Another example is SST variability in the NTA region (Zhang et al. 2021a). Zhang et al. (2021a) demonstrate that the statistical lead–lag relationship between ENSO and the NTA is also consistent with a one-way forcing of the NTA by ENSO once ENSO autocorrelation and seasonal modulations are considered. Furthermore, as for the ENSO/IOD case, it is shown that inter-model spread in ENSO characteristics (here: ENSO periodicity) and in the ENSO/NTA statistical relationship across 46 CMIP6 models is consistent with ENSO being a one-way driver in this relationship. The statistical relationship between ENSO and the NTA continues to hold in a projected warming climate, emphasizing the continuing potential of ENSO as the dominant source of seasonal-to-interannual predictability even in regions outside the tropical Pacific. Similarly, the same framework can also be applied to examine the relationship between ENSO and the Atlantic Niño phenomenon (Jiang et al. 2023).

Layered systems with different timescales: the effect of double integration

The original stochastic climate model (Eq. 1) can be extended to systems in which one variable Ψ1 with a characteristic damping rate λ1 integrates stochastic forcing (i.e., white noise), and then in turn Ψ1, characterized by a Lorentzian spectrum, is the forcing of another variable Ψ2 with its own damping rate λ2 (Kilpatrick et al. 2011; Di Lorenzo and Ohman 2013)Footnote 9:

$$\frac{d{\Psi }_{1}}{dt}=-{\lambda }_{1}{\Psi }_{1}+\sigma \xi$$
(6a)
$$\frac{d{\Psi }_{2}}{dt}=-{\lambda }_{2}{\Psi }_{2}+{\Psi }_{1}$$
(6b)

In Di Lorenzo and Ohman (2013), the above system is applied to explain the ocean ecosystem response to random weather forcing, with Ψ1 being an index describing Pacific decadal climate variability driven by stochastic forcing associated with variability of the Aleutian Low, and Ψ2 being a zooplankton species. This double linear integration of variables with different timescales (λ1 ~ 1/6 months−1 and λ2 ~ 1/24 months−1 in this case) leads to a steeper slope in the power spectrum of Ψ2 than for Ψ1 (-4 slope in log–log space instead of a -2 slope for a single integration Kilpatrick et al. 2011; Di Lorenzo and Ohman 2013); and thus enhanced variance at lower frequencies.

Similarly, ENSO impacts can be integrated in such a layered system consisting of variables with different damping timescales. Using a modification of this system (Eq. 6) but taking into account seasonally modulated ENSO impacts, i.e., the ENSO Combination Mode (Eq. 4), Kim et al. (2021) formulated the null hypothesis for ENSO-induced (neglecting stochastic forcing ξ for simplicity) vegetation variability in eastern Africa as follows:

$$y=\left[{\beta }_{0}+{\beta }_{ac}\mathrm{cos}\left({\omega }_{ac}t-{\phi }_{2}\right) \right]{T}_{\mathrm{ENSO}}$$
(7a)
$$\frac{d{\Psi }_{1}}{dt}=-{\lambda }_{1}{\Psi }_{1}+y$$
(7b)
$$\frac{d{\Psi }_{2}}{dt}=-{\lambda }_{2}{\Psi }_{2}+{\Psi }_{1}$$
(7c)

Here, y are ENSO-induced precipitation anomalies, Ψ1 the burned land area, and Ψ2 the leaf area index (a common metric for vegetation), all spatially averaged over eastern Africa. Further, λ1 is the inverse recovery timescale for land area after wild fires and λ2 is the inverse timescale characterizing vegetation resilience (Kim et al. 2021). It was shown that this model reproduces the key temporal characteristics of ENSO-induced vegetation variability in a high-complexity land model (the Community Land Model).

The ENSO combination mode concept applied to higher frequency transients

A final application of the climate trio framework that we will discuss in this paper is the goal of explaining the variability of higher frequency deterministic transients such as tropical instability waves (Boucharel and Jin 2019; Xue et al. 2020) and coastal wave energy (Boucharel et al. 2021). As discussed earlier, the original stochastic climate model (Eq. 1) and its extensions are founded on a scale separation between the slow climate variable and the fast fluctuations described in the noise term (Hasselmann 1976; von Storch 2022). In these formulations, the aforementioned deterministic transients are not explicitly considered and are part of the noise term. However, if one is interested in the dynamics of a specific higher frequency transient, one needs to consider their modulation by lower-frequency deterministic processes such as the annual cycle and ENSO. The time evolution of such transients (denoted here by Z) can be written as a damped oscillator forced by noise:

$$\frac{dZ}{dt}=\left[-\left({\lambda }_{0}+\frac{2i\pi }{\tau }\right)+A+B \right]Z+ \sigma \xi$$
(8)

where λ0 is the damping rate for the respective phenomena, τ their return period, and the A and B terms are associated with the seasonal cycle and ENSO, respectively. Slightly different formulations are used in the two examples mentioned here, for details the reader is referred to Boucharel and Jin (2019), Xue et al. (2020), and Boucharel et al. (2021). Note that the exact definition of a transient Z and its separation from the noise term depends on the phenomenon under consideration and should be carefully justified by the physical problem at hand.

With this general model we can quantify the combined effect of ENSO and the seasonal cycle (and their interactions) on these transients, leading to the recognition that much of their observed variance can be explained by them. Taking these interactions into account is critical as recent high-resolution coupled climate model experiments demonstrated the important role that tropical instability waves play in projected future ENSO changes (Wengel et al. 2021). Promise exists of the applicability of this framework to other transients in the climate system, including atmospheric noise patterns such as westerly wind bursts (Xuan et al. 2023) that play an important role in triggering El Niño events and can be parameterized as multiplicative noise in the recharge oscillator framework (Levine and Jin 2017; Jin et al. 2020).

Conclusions

Here we presented how the three key players in climate variability on subseasonal-to-decadal timescales—the thermal inertia of the surface ocean (or other slow climate variables), ENSO, and the seasonal cycle—and their interactions can be described and quantified in a hierarchy of conceptual climate models (summarized in Fig. 5). Much of the observed variance of key climate variables such as SST can be explained by the interactions of this climate trio. In addition, much of the statistical properties of different empirical modes of climate variability and their interactions can be understood with this hierarchy, including covariances, lead/lag correlations, and power spectra. Beyond this, the same model framework can be applied to understand the statistical properties of many transients in the climate system, such as tropical instability waves. Therefore, careful attention needs to be paid when formulating appropriate null hypotheses for investigating observed and simulated climate variability. There are several other extensions and numerous applications of the stochastic climate model not covered in this review (e.g., Benzi et al. 1982, 1983; Frankignoul et al. 1997; Barsugli and Battisti 1998; Bretherton and Battisti 2000; Qiu 2003; Zhang 2017; Larson et al. 2018; Martinez-Villalobos et al. 2018; Proistosescu et al. 2018; Laurindo et al. 2022; Patrizio and Thompson 2022). These include the role of wind-forced oceanic Rossby waves on non-local low-frequency climate variability (Frankignoul et al. 1997; Qiu 2003), stochastic resonance (Benzi et al. 1982, 1983; Franzke et al. 2022), and explicit feedback of SST anomalies back on the atmospheric dynamics (Barsugli and Battisti 1998; Bretherton and Battisti 2000). We refer the reader to the above references for more information on these extensions.

Fig. 5
figure 5

Summary of the building blocks in the conceptual model hierarchy. The symbols used in the equations are defined in the main text. Red font is used in the equations to indicate seasonal processes

Full size image

The relationships identified here that are attributable to the climate trio warrant great caution when (i) processing climate data prior to statistical analysis and (ii) investigating potential causal links between different modes of variability. Regarding the former, due to an upscale frequency cascade, much of ENSO’s deterministic signal is spread across subseasonal-to-interannual timescales for many climate variables in many geographical regions (Stuecker 2015; Stuecker et al. 2015a). Therefore, any temporal filtering—as it is often done in climate research—should only be applied with great caution, as one can easily remove critical parts of the deterministic signal (Stuecker et al. 2016). Regarding the latter, seasonal modulations with different phases lead to statistical lead/lag relationships between different climate phenomena that can be misleading. For instance, the lead/lag cross correlation between ENSO and the IOD is maximized when the IOD is leading ENSO by ~ 3 months. Critically, this statistical relationship does not imply any causality. In fact, a one-way forcing of the IOD by ENSO can reproduce this cross correlation due to their growth/damping rates having different phases (Stuecker et al. 2017b).

Due to ENSO’s intricate interplay with the other two climate players, it is likely that we are currently not recognizing and utilizing all the available information of ENSO’s far reaching imprints on the climate system. A better understanding of the seasonally modulated (and potentially integrated) impacts of ENSO on different modes of variability, different geographical regions, and various transients should lead to improved predictability in these subsystems on subseasonal-to-decadal timescales. Both climate model experiments with idealized sinusoidal ENSO forcing (Stuecker et al. 2015a, 2015b, 2017a, 2017b; Kim et al. 2021) and large ensembles that can help to maximize the signal-to-noise ratio in analyses (Rodgers et al. 2021) will be valuable tools for delineating these impacts and can be directly incorporated into the conceptual model framework presented here.

Not discussed here but of equal importance are the imprints that ENSO can have (in addition to the double integration mechanism) on low-frequency variability via nonlinear rectification (Jin et al. 2003; Rodgers et al. 2004; Hayashi et al. 2020; Park et al. 2020; Liu et al. 2022). Thus, both effective upscale (Stuecker et al. 2015a) and downscale (Jin 2022) ENSO frequency cascades exist in the climate system. Importantly, the fact that ENSO has nonlinear rectified effects on the climate systems means that reducing uncertainties in projected ENSO variance changes should in turn help constrain low frequency mean state changes in the tropical Pacific (Hayashi et al. 2020).

In summary, uncovering ENSO’s full rich imprints in the climate system holds exciting promise for improving our process-level understanding of regional climate variability in many parts of the Earth system, narrowing future regional climate projections, as well as utilizing the improved understanding for more skillful subseasonal-to-decadal climate predictions.