1 Introduction

The Atlantic Niño and the weaker Atlantic Niño-II dominate interannual variability in the equatorial Atlantic (Zebiak 1993; Keenlyside and Latif 2007; Ding et al. 2010; Lübbecke et al. 2018; Okumura and Xie 2006). These phenomena peak respectively in boreal summer and November–December. They both exhibit dynamics similar to the much stronger El Niño Southern Oscillation (ENSO), but coupled ocean–atmosphere interactions are less pronounced (Jansen et al. 2009; Lübbecke and McPhaden 2013) and positive and negatives events are more symmetric (Lübbecke and McPhaden 2017). Like ENSO, they also have important climatic impacts (Okumura and Xie 2006; Lübbecke et al. 2018; Foltz et al. 2019; Losada et al. 2010).

Unlike with ENSO, little skill has been demonstrated in predicting equatorial Atlantic variability (Stockdale et al. 2006, 2011; Richter et al. 2018; Barreiro et al. 2005). The low predictability can be partly explained by the strong seasonal modulation of coupled ocean–atmosphere interactions in this basin and the greater influence of largely stochastic wind variability (Richter et al. 2014a; Richter and Doi 2019; Nnamchi et al. subm.). Furthermore, thermodynamic ocean–atmosphere interaction and a range of other mechanisms contribute to equatorial Atlantic variability (Lübbecke et al. 2018; Nnamchi et al. 2015; Brandt et al. 2011; Richter et al. 2013); and most of these mechanisms may be less predicable than ENSO like dynamics.

Model error is also a potential cause for poor prediction skill. In particular, the tropical Atlantic biases in state-of-the-art models are much larger than the amplitude of the interannual variability (Richter et al. 2014b). They are characterised by a large warm SST bias (up to \(8\,^{\circ }\text{C}\) in the southeast tropical Atlantic), a too deep thermocline in the eastern Atlantic (Richter et al. 2014b), a cyclonic surface wind bias in the Angola–Benguela Frontal Zone and a southward shift of the intertropical convergence zone (ITCZ) (Richter et al. 2012). These biases cause an underestimation of the thermocline feedback (Deppenmeier et al. 2016) and an overestimation of thermodynamic ocean–atmosphere interaction (Jouanno et al. 2017); and reducing them enhances the simulation of dynamical ocean–atmosphere interaction and Atlantic Niño variability (Ding et al. 2015a, b; Dippe et al. 2018; Harlaß et al. 2018). Furthermore, Dippe et al. (2019) show that reducing this bias improves the prediction of Atlantic Niño variability, although prediction skill remains poor—i.e. only beating marginally persistence for May start and beating persistence by 0.1 for August start up to 4 lead month.

Unfortunately, improvements in simulating tropical Atlantic climate have been only moderate during the past 20 years (Davey et al. 2002; Richter et al. 2012; Toniazzo and Woolnough 2014). There is a greater understanding of the causes of tropical Atlantic biases: The equatorial Atlantic SST biases are linked to too weak trade winds in boreal spring (Richter and Xie 2008; Wahl et al. 2011; Voldoire et al. 2019); whereas southeastern tropical Atlantic bias has been related to the misrepresentation of (1) the persistent low level cloud cover (Zuidema et al. 2016), (2) along shore coastal winds (Xu et al. 2014a; Koseki et al. 2018) and (3) coastal upwelling (Xu et al. 2014b). Several studies have shown that increasing atmospheric model resolution can reduce tropical Atlantic biases, especially in the southeastern Atlantic (Small et al. 2015; Milinski et al. 2016; Harlaß et al. 2018), whereas de la Vara et al. (2020) have shown improvements from increasing oceanic model resolution. While detecting the cause of the bias and formulating a solution that is computationally tractable is most desirable, the remaining bias even in the computationally demanding systems (e.g., Harlaß et al. 2018) is still large (about 2–3 \(^{\circ }\text{C}\)). Thus, the tropical Atlantic warm bias is likely to remain a problem for seasonal prediction for a while to come.

Flux correction and anomaly coupling are alternate approaches that mitigate climatological biases and their impacts, and thereby enhance predictions. In flux correction a fixed numerical correction is added to the exchanged fluxes (Sausen et al. 1988), while in anomaly coupling the variables used to compute air–sea fluxes are corrected (Kirtman et al. 1997). Although neither approach guarantees an improved simulation of variability, anomaly coupling has been shown effective in improving the simulation and prediction of equatorial Atlantic interannual variability (Ding et al. 2015a; Dippe et al. 2018, 2019). A drawback with both approaches is that estimating effective numerical corrections is difficult, because coupled feedbacks in the tropics can strongly amplify errors (Neelin and Dijkstra 1995). This is particularly problematic when the corrections are estimated from uncoupled ocean general circulation model (GCM) and atmospheric GCM simulations. To overcome this, Toniazzo and Koseki (2018) developed an iterative approach to estimate the anomaly coupling corrections from a coupled GCM simulation. They applied their approach to the Norwegian Earth system model (NorESM; Bentsen et al. 2012), which has tropical Atlantic biases comparable to those of the models from the Coupled Model Intercomparison Project 5 (CMIP5) (Koseki et al. 2018; Toniazzo and Koseki 2018). Their technique alleviated the SST and precipitation biases in the tropical Atlantic (and elsewhere) without damping too much the variability.

In this study, we aim to use Toniazzo and Koseki (2018) improved technique to assess whether current model biases limit seasonal prediction skill in the equatorial Atlantic. This work is based on the Norwegian Climate Prediction Model (NorCPM, Counillon et al. 2014, 2016), which combines the NorESM and the ensemble Kalman filter (EnKF, Evensen 2003) data assimilation method. We will use NorESM in its standard and anomaly coupled configurations. NorCPM aims to provide long-term reanalyses and seasonal-to-decadal climate predictions. NorCPM demonstrated good skill in controlling the upper ocean heat content in the equatorial and north Pacific, the north Atlantic subpolar gyre region and the Nordic Seas seas by assimilating surface temperature anomalies (SSTAs, Counillon et al. 2016). In Wang et al. (2019) NorCPM with assimilation of SST reaches skill comparable to the top-performing prediction systems of the North American Multi Model ensemble (NMME, Kirtman et al. 2014) in most regions, but performance in the tropical Atlantic—were the model has large biases—were found to be poor. One can thus expect anomaly coupling to be particularly beneficial there, by correcting the model bias, improving the representation of the dynamics and enhancing the prediction skill.

This paper is organised as follow. Section 2 presents the Norwegian climate prediction model, in its standard and anomaly coupled configurations. We then assess the impact of the anomaly coupling on the accuracy of a reanalysis for the period 1980–2010 (Sect. 4), and on the skill of retrospective hindcasts of Atlantic Niño variability (Sect. 5).

2 Norwegian climate prediction system and experimental design

2.1 The Norwegian Earth system model

The NorESM (Bentsen et al. 2012) is a global fully coupled model for climate simulations. It is based on the Community Earth System Model version 1.0.3 (CESM1, Vertenstein et al. 2012), a successor to the Community Climate System Model version 4 (CCSM4, Gent et al. 2011). Unlike in the Community Atmosphere Model (CAM4, Neale et al. 2010), the atmospheric component (CAM4-OSLO) features advanced aerosol chemistry schemes (Kirkevåg et al. 2013). The ocean component (Bentsen et al. 2012) is an updated version of the isopycnal coordinate ocean model MICOM (Bleck et al. 1992). This study uses the medium-resolution NorESM1-ME (Tjiputra et al. 2013), which has the capability to be fully emission driven and has contributed output to CMIP5. External forcings used here comply with CMIP5’s historical experiment (see Bentsen et al. 2012 for details). The atmosphere and land components are configured on a \(2^\circ\) finite-volume grid that has a latitude longitude resolution of \(1.9^\circ \times 2.5^\circ\). The atmosphere component uses 26 hybrid sigma-pressure levels with a model top at approximately 3 hPa. The horizontal resolution of the ocean and sea-ice model is approximately \(1^\circ\), but is enhanced in the meridional direction about the equator and enhanced in both zonal and meridional directions at high latitudes. The ocean uses 51 isopycnal layers and two layers for representing the bulk mixed layer with time-evolving thicknesses and densities. We refer to this configuration as CTRL. The NorESM CTRL has climatological SST, precipitation, and wind biases in the tropical Atlantic that are typical of CMIP5 models (Koseki et al. 2018).

Fig. 1
figure 1

The first row is the precipitation bias (in mm per day) of the mean of a 5 ensemble member free running versions (i.e. without assimilation) of CTRL (a) and ACPL (b) calculated against GPCP V2.3 for the period 1980–2010. The second row (panels c and d) is the same for SST against HadISST2

Full size image

2.2 The anomaly coupled version of NorESM

The anomaly coupling technique developed by Toniazzo and Koseki (2018) allows to substantially reduce such biases, through correcting the SST and wind stress exchanged between the ocean and atmosphere models at each coupling steps. The corrections in the anomaly coupling vary in space and time according to a monthly climatology. They compensate for biases that arise when the coupled surface fluxes of energy and momentum act to cause systematic departures of local SSTs from the observed surface climatology. The correction thus represents a compensation for the difference between the sea-surface climatology of the observations and that of the (standard) model simulations. In this sense the model thus becomes anomaly coupled (hereafter “ACPL”) i.e., the ocean model receives wind stress consisting of atmosphere model simulated anomalies added to the observed climatology—and likewise for SST received by the atmosphere. The corrections are calculated in coupled mode according to an iterative scheme that allows to account for the effect of coupled feedbacks. For details of this procedure, including the target climatology, the reference observation data set, and a validation of the resulting simulated climatology, see Toniazzo and Koseki (2018). Note that we do not use Toniazzo and Koseki (2018)’s proposed global energy conservation scheme. The global energy imbalances are globally uniform and within \(\pm 1\,\text{W/m}^2\) that is generally small compared to regional physical flux anomalies. While this may become important for inter-annual or slower modes of variability, we do not expect its inclusion to substantially alter seasonal predictions and the findings of our paper. Furthermore, we did not identify strong regional climate drifts in our seasonal predictions system (not shown).

The impact of anomaly coupling on SST and precipitation in our model configuration for the period 1980–2010 is now depicted (Fig. 1). For precipitation we calculate the bias against the Global Precipitation Climatology Project monthly precipitation (GPCP) Version 2.3 dataset (Adler et al. 2003). In the tropical Atlantic anomaly coupling dramatically reduces the SST and precipitation biases. Although the scope of the paper focuses is in the tropical Atlantic, it is worth mentioning that the SST bias in the tropical Pacific is not fully eliminated by anomaly coupling (Fig. S1 for a global assessment). The remaining bias can be related to the fact that (1) the bias of the individual components (here in the ocean model MICOM) is not reduced by the anomaly coupling (2) the flux correction term was trained with constant external forcing, while we are now verifying the performance with transient forcing.

Although anomaly coupling corrects the mean bias for our region of interest, it does not guarantee an improved simulation of variability. We illustrate this by presenting the standard deviation of equatorial Atlantic SST anomalies as a function of calendar month from observations and free running simulations with the standard and anomaly coupled configurations of NorESM (Fig. 2). The seasonality of equatorial Atlantic SST variability provides insights into the model’s performance in capturing the timing of Atlantic Niño variability. The standard version of NorESM shows a marked seasonal peak in variability along the equator in July while in observations the peak is reached a month earlier and is weaker. With ACPL, the maximum occurs in June as in the observation but is a little weaker and displaced to the east. In the standard NorESM the strong SST variability persist until the end of the year while in the observation it decays rapidly during September before showing a second weaker peak during November–December associated with the Atlantic Niño-II phenomena (Okumura and Xie 2006). Again, the ACPL model better captures this secondary maximum in SST variability, although it is slightly too far to the east compared to the observations and a little too strong. Overall, the anomaly coupled model simulates more realistic variability compared to the standard version of NorESM.

Fig. 2
figure 2

The annual cycle of SST standard deviation along the equator in the observation (HadISST2) and in free running versions of CTRL and ACPL. The simulated standard deviations are estimated for the period 1980–2010 using five members for both CTRL and ACPL

Full size image

2.3 Reanalyses and seasonal hindcasts experiment description

The Norwegian Climate prediction model (Counillon et al. 2014, 2016; Wang et al. 2019) assimilates observations with the EnKF. Here, we assimilate SST and hydrographic profiles as described in Counillon et al. (2014, 2016) and Wang et al. (2017). The SST data is from the HadISST2 data set (HadISST2.1.0.0, Rayner et al., personal communication) that provides an ensemble of reconstruction of SST for the period 1850–2010. We assimilate the ensemble mean and use the ensemble spread, which varies in space and time, to quantify the accuracy of the observational data set, as is needed for the data assimilation. The hydrographic profiles are from EN4.1.1 (Gouretski and Reseghetti 2010). The observation error is estimated as described in Karspeck (2016) and the localisation radius varies with latitudes as described in Wang et al. (2017). The entire ocean state vector is updated; that is we update the temperature, salinity, and layer thickness of all vertical layers. We employ the aggregation method (Wang et al. 2016) for layer thickness. It is a cost-efficient modification of the linear analysis update in data assimilation (DA) for physically constrained variables, which ensures that the analysis satisfies physical bounds without changing the expected mean of the update and thus avoid introducing a drift.

Two 30 member reanalyses are performed with CTRL and ACPL configurations for the period 1980–2010. The initial conditions for both reanalyses are branched in 1980 from the two corresponding ensemble historical simulations. These two ensemble historical simulations are produced by selecting random initial condition from a stable preindustrial simulations and integrating the ensemble from 1850 to 2005 using CMIP5 historical forcings and there after the RCP8.5 is used (Taylor et al. 2012). CTRL historical ensemble simulations of 30 members have been performed for a previous study (Counillon et al. 2016, data set available on https://doi.org/10.11582/2019.00035). As producing such initial conditions is computationally expensive, ACPL historical simulation is performed differently: using the anomaly coupled configuration with fixed monthly climatological correction, we perform a 5 ensemble member simulation from 1850 to 2010; the other 25 ensemble members are spawned from these 5 members, by perturbing the SST of the initial condition in January 1970 with \(0.1\,^\circ \text{C}\) spatially white noise and then integrating these 25 members to 1980. The resulting ensemble spread in the near surface and intermediate ocean depths of the 30 member ACPL simulation has comparable amplitude to that of CTRL (not shown); and thus it should satisfy a well balanced EnKF (i.e. error versus ensemble spread) for seasonal prediction.

We perform anomaly assimilation; that is the climatological monthly mean for the observations and the model are removed before comparing the two. This option was preferred over full field assimilation for several reasons. First handling model bias in DA is a real challenge because it is designed to correct random, zero-mean errors, i.e. the model and observations are assumed (erroneously) to be unbiased. As a result, the analysis state with full field assimilation will still include part of the bias (Dee 2005) and yields a too strong reduction of ensemble spread (Anderson 2001). Second, full field assimilation can produce a large shock as the model often drifts back rapidly to its own climatology (or attractor). Third, when models are attracted to their biased climatology, full field assimilation will cause recurrent corrections of the model bias, and yield a transfer of bias to the non-observed variables (via the multivariate updates). All of these can lead to a slow degradation of the performance of the data assimilation system during the analysis period (Dee 2005). For anomaly assimilation we used the climatological reference period 1980–2010, a period that is sufficiently long for sampling the variability of the tropical Atlantic and during which there is enough data to estimate the observed climatology accurately. Note that for the hydrographic profiles (Gouretski and Reseghetti 2010), the climatological mean is calculated from the EN4 objective analysis (Good et al. 2013), because profile data are too sparse and heterogeneously distributed to estimate a trustworthy climatology. The monthly climatological mean of the model is estimated from the historical ensemble for the period 1980–2010. For CTRL it is calculated from 30 members, while for ACPL it is calculated from only 5 members.

We assimilate data every month and only update the ocean component. The other components (atmosphere, sea ice and land) adjust dynamically between the assimilation cycle. In the reanalysis and hindcasts, we apply the same external forcing as in the historical simulations. We assess the prediction skill based on hindcasts (i.e. retrospective predictions). Seasonal hindcasts start on the 15th of January, April, July and October each year during 1985–2010. In total, there are 104 hindcasts (26 years with 4 hindcasts per year). Each hindcast runs 9 realisations (ensemble members) for 13 months. Initial conditions are taken from the first 9 members of the 30 ensemble member reanalyses. Note that this choice has no influence on the results, because with the EnKF all members are equally likely.

3 Validation data sets and metrics

For validation of the reanalysis, we use the independent sea surface height (SSH) altimetry data and the EN4 objective analysis (Good et al. 2013). Monthly sea surface height (SSH) anomalies (i.e., sea level anomalies) are computed from the Global ARMOR3D L4 Reprocessed dataset (http://marine.copernicus.eu, available from 1993 to present) produced by Ssalto/Duacs and distributed by AVISO with support from the Centre National D’Études Spatiales. The product is gridded to a resolution of \(1^\circ\) for comparisons with our coarser model data.

The EN4 objective analysis is not independent from our reanalysis because it uses the same raw observations (i.e. the EN4 hydrographic profiles, Gouretski and Reseghetti 2010) to construct the 4-dimensional reconstruction. However, this comparison is of interest because objective analysis and model reanalysis are different by construction. Objective analysis provides a 4D interpolation of the observations without dynamical constraints and reverts to climatology when no data are available—as every monthly estimate minimises the error locally in space and time based on the available observations. Model reanalysis on the contrary use available observations to correct the state of a dynamical model and provide a dynamical reconstruction (Murphy 1993). An advantage of reanalyses is that they propagate dynamically the improvements of sparse observations to the unobserved regions (Storto et al. 2019), but in a region where the biases are very large (such as in the tropical Atlantic) the growth of the model error within the assimilation cycle may become quantitatively larger than the benefit. The DA settings used in NorCPM favour dynamical consistency at the expenses of accuracy. Namely, (1) we use anomaly assimilation to minimise dynamical adjustment post assimilation; (2) we add a representativity error term to the observation error to ensure that the ensemble DA system remains reliable (i.e. ensemble spread matches the error of the ensemble mean); and (3) we use the k-factor formulation (Sakov et al. 2012) in which observational error is artificially inflated if the assimilation pushes the update beyond two times the ensemble spread.

For validating the hindcasts, we focus on the performance in predicting the ATL3 index (SST anomalies averaged over the region \(20^{\circ }\text{W}\) to 0\(^{\circ }\) and \(3^{\circ }\text{S}\) and \(3^{\circ }\text{N}\)), which is a good indicator of the Atlantic Niño (Zebiak 1993). We have also analysed the performance of hindcasts for the ATL2 SST index (15\(^{\circ }\text{W}\)–\(5^{\circ }\text{W}\), \(3^{\circ }\text{S}\)–\(3^{\circ }\text{N}\)), an indicator of the Atlantic Niño II that occurs during November–December (Okumura and Xie 2006). The area of both indices is marked on Fig. 5. We benchmark the performance of the two predictions systems against the persistence forecast and hindcasts from the North American Multimodel Ensemble (Kirtman et al. 2014, https://www.earthsystemgrid.org/search.html?Project=NMME). Note that for comparing the skill of NorCPM with NMME, we use NOAA OI-SST V2 (Reynolds et al. 2002), which differs from the data set used for assimilation (HadISST2), making the comparison fairer. The validation was also repeated with other data set HADISSTV1.1 (Rayner et al. 2003) with similar results (not shown).

The NMME is a multi-model seasonal forecasting system that consists of several coupled climate models from US and Canadian modelling centres. We select 13 NMME systems that provide SST hindcasts from 1985 to 2010 (Table 1). All NMME hindcasts start on the first day of each month and are 8–12 months long. The NorCPM hindcasts start 15 days earlier than the NMME hindcasts, but make use of monthly average to perform a centered analysis. As an example, our hindcasts starting on the 15th of April have assimilated monthly average April data and is compared to the hindcasts of NMME starting on the first of May; it will be referred to as May hindcast in the following for simplicity. The ensemble size ranges from 6 to 24 among the NMME models. Here, we use the first 9 ensemble members of each NMME model (except for CCSM3 that only provides 6 ensemble members) to have a comparable ensemble size to NorCPM. The NMME hindcast data are provided as monthly means with a horizontal resolution of \(1^\circ \times 1^\circ\).

The performance of the model reanalyses and hindcasts are assessed by calculating anomaly correlation coefficient (ACC) and root mean square error (RMSE). Statistical significance is estimated by a Students t-test at the significance level of 5%. The degrees of freedom are estimated from the auto-correlation (equation 8.7, p.149 Von Storch and Zwiers 1999). We also assess the reliability of our ensemble prediction systems for the ATL3 index. Reliability refers to the property of the ensemble spread to match the accuracy of the ensemble mean (Eq. 1). There are advanced formulation for checking the reliability of an ensemble system using a probabilistic Attributes Diagrams (Corti et al. 2012), but here we will only assess the reliability of the total variance. When calculating the RMSE with imperfect observations, one should account for observational error variance in the reliability budget analysis (e.g., Sakov et al. 2012; Rodwell et al. 2016) and ensure that the error variance of the ensemble mean matches the sum of the variance of the ensemble (\(\sigma _{ens}\)) and the observation error variance (\(\sigma _{obs}\)). For this purpose, we use the HadISST2, because it provides a more accurate estimate of the observation error than the OI-SST V2, and it is the product assimilated in ACPL and CTRL reanalyses and thus is the data set for which the reliability relation should be satisfied:

$$\begin{aligned} \text{RMSE}=\sqrt{\sigma _{obs}^2 +\sigma _{ens}^2}. \end{aligned}$$
(1)
Table 1 Brief description of NorCPM and 13 NMME models used in this paper
Full size table

4 Reanalysis

Here we investigate the accuracy of the reanalyses performed with CTRL and ACPL configurations of NorCPM that are used to initialise the hindcasts (Sect. 5) for the period 1985–2010. The correlations in the tropical Atlantic are substantially higher than in CTRL (Fig. 3). It should be noted that both reanalyses are able to constrain monthly variability of upper \(200\,\text{m}\) ocean heat content over much of the globe (Fig. S2) and correlations are mostly very similar exception made of our area of interest. There are also some difference in the tropical Pacific: ACPL yields an improved representation of the variability in the western part, but causes a slight degradation in the central part, where the bias is amplified (see Figure S1).

The improvements in the tropical Atlantic from anomaly coupling are related to Atlantic Niño variability (Fig. 3). In particular, the signature of the Atlantic Niño is absent in the performance of CTRL reanalysis for upper ocean heat content, while it is marked by correlations exceeding 0.5 in ACPL. The discrepancies in correlation coefficient are also clearly visible in the reanalysis performance for subsurface temperature variability at the equator and for SSH. The tropical Atlantic can be approximated as a 1.5 layer system, (i.e., an active less dense layer over a much thicker and denser inactive layer), and SSH variations are closely related to the thickness of the upper layer and thermocline-depth variations (Wyrtki and Kendall 1967; Rebert et al. 1985). The pattern of correlation coefficient improvement in SSH in the tropical Atlantic and in temperature at 150–200 m depth in the eastern equatorial Atlantic are consistent with a better representation of the thermocline variations linked to Atlantic Niño variability in ACPL compared to CTRL. Correlation with the upper 200 m ocean salt content is also improved in ACPL (not shown). These results suggest that by improving the dynamical representation in our model, we are able to make more efficient use of the observations to provide a dynamical reconstruction. In the supplementary material, one can see that similar results are found for RMSE (Fig. S4), where we present the difference of correlation and RMSE to better highlight the improvements.

Fig. 3
figure 3

First row shows the pointwise de-seasoned (with the mean seasonal cycle removed) correlation of monthly \(200\,\text{m}\) ocean heat content of EN4 objective analysis with CTRL (a) and ACPL (b). The second row (c, d) shows the temperature correlation in the vertical along the tropical Atlantic band (between \(3^{\circ }\text{S}\) and \(3^{\circ }\text{N}\)), the third row (e, f) the same for SSH correlation. Correlations that are not significant (at significance level of 5%) are masked. The last row shows the averaged correlation and RMSE of temperature within the top 200 m in the equatorial band over calendar months (between \(3^{\circ }\text{S}\) and \(3^{\circ }\text{N}\))

Full size image

In the last row of Fig. 3, we present the seasonal variability of the averaged correlation and RMSE of the temperature in the upper 200 m of the ocean in the equatorial band. A more detailed verification can be found in the supplementary with the spatial and vertical correlation at the starting months of the four seasonal hindcasts (see Figure S5). ACPL reanalysis performs better than CTRL reanalysis from May to October, with the greatest improvements in August and September. The improvements coincide with ACPL’s better representation of equatorial SST variability, while in CTRL there is excessive variability from July to November (Fig. 2). ACPL reanalysis performs slightly better in January and December, coinciding with the better representation of the secondary maximum in equatorial SST variability in ACPL. There are no improvements in February to April, when the simulated variability is weak in both models, in reasonable agreement with the observations.

5 Hindcasts

The performance of ACPL and CTRL hindcasts in predicting the ATL3 SST index is assessed in terms of anomaly correlation and RMSE, and their skill is compared against that of the NMME forecasting systems (Fig. 4). Considering all four start dates (Fig. 4a), CTRL performs very poorly and is less skilful than the NMME systems and most of the time than persistence. ACPL improves on CTRL. Up to forecast lead month 3, ACPL shows skill comparable to the NMME system, though it does not beat persistence. From forecast lead month 4 onward, ACPL beats persistence and is as skilful as the best models of the NMME system. The improvements seem at least partially explained by the improved accuracy of the initial SST conditions (denoted with a square on the y-axes in Fig. 4 and calculated from the monthly averaged of the reanalyses). However, the skill of all the models is low, and no model has a correlation skill above 0.5 after month lead month 4. Next we investigate how the skill varies with start month.

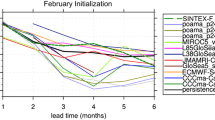
For hindcasts started from February, ACPL achieves a correlation skill larger than 0.5 at 4 months lead time (i.e., in May), a skill that is better than all NMME systems. CTRL and NNME hindcasts do not beat persistence during the first 4 months. Thereafter the skill of all systems is low. Interestingly, the performance of the SST initial condition (marked with the squares) is indiscernible between CTRL and ACPL, but the accuracy of the initial 200 m heat content is improved in ACPL (see Fig. 3 and Fig. S5). A good subsurface initialisation can remerge to the surface when the shoaling of the thermocline occurs. The evolution of skill in ACPL may also be related to the behaviour of the model during the hindcast integration. The strong drop in skill of ACPL in June coincide with the boreal summer peak in equatorial SST variability (Fig. 2) and there is a rapid drop of skill in June for all start dates, which resemble the spring predictability barrier in May in the tropical Pacific.

Accordingly, for May starts, there is initially some large improvements for ACPL compared to CTRL prediction system, but the performance drops again very quickly and is poorer than in most NMME systems and persistence. This is disappointing because June corresponds to the time when Atlantic equatorial variability and its impact are at their maximum. Also, one would expect to achieve skilful predictions when starting from May (as few NMME systems do). It should be acknowledged that the NMME systems achieving skill for May start (CMC1-CanCM3, CMC1-CanCM4, and NASA-GMAO) assimilate data in the atmospheric component. In NorCPM, we only initialise the ocean of these hindcasts on the 15th of April—i.e. 15 days prior to the effective start date (May 1st). We notice that ensemble members diverge rapidly during that time and that the variability of the ensemble mean flattens (not shown). This suggests that further initialisation of the atmospheric component and moving the assimilation closer to the effective start date can be important for improving prediction skill at this time of large internal atmospheric variability (Richter and Doi 2019). It is also possible that updating the ocean without the atmosphere component can introduce some imbalances (Penny and Hamill 2017), enhance the stochasticity of the atmosphere and accelerate the ensemble dispersion.

For the August starts, ACPL shows good improvement compared to CTRL for hindcasts. ACPL hindcasts sustain correlation skill between 0.4–0.6 up to 7 months lead time (February). Similarly, the RMSE of ATL3 in ACPL is reduced compared to CTRL. The skill relates to good subsurface initialisation that remerge to the surface when the second shoaling of the thermocline occurs, and it is tied to the seasonal cycle. The November–December upwelling is also associated with a shoaling thermocline and local weak intensification of the trade winds that drive upwelling. The thermocline anomalies partly originate from reflected Kelvin waves, and so from off-equatorial heat content anomalies (e.g. Fig. S5). Thus, the predictability comes from the propagation of anomalous heat content anomalies, which represent a modulation of the seasonal cycle and that become expressed as SST anomalies in November–February, when there is a local upwelling. In contrast, CTRL hindcasts have rapid drop in correlation skill during the first 2 months and this is followed by a recovery of skill to a level similar to ACPL at lead month 7. In CTRL, the upwelling seasons is very strong and delayed, this could explain why the SST anomalies are erroneous in the period before November. Many of the NMME models, ACPL and CTRL show relatively high skill in January and February, which indicates that this mechanism is highly predictable. The skill in February is larger in CTRL than in ACPL. In NorCPM, there is an overly strong ENSO teleconnection with equatorial Atlantic in February. In observations the correlation between in Nino3.4 and ATL3 is around 0.2 in February while in CTRL it is 0.4 and in ACPL it is 0.5. As a result, in NorCPM there is a spurious ENSO signal superposed on the observed low-frequency signal, degrading the ACPL prediction for ATL3 more so than CTRL. It is interesting to notice that beyond June month, RMSE is reducing with lead time. This occurs for all start dates, and can be seen as a consequence of interannual variability getting weaker in these seasons.

For November starts, the initial SST condition is improved in ACPL compared to CTRL, but the performance of the two systems quickly converge and are similar to that of the NMME, until April of the following year—suggesting that the system is dynamically relatively stable prior to May. The highest skill of all systems is found in January–February as a reemergence of subsurface anomaly. In May and June, ACPL system achieves better performance than that of NMME systems and CTRL, and its skill approaches that achieved from May start.

Fig. 4
figure 4

The first row shows the skill in predicting ATL3 SST in terms of a correlation and b RMSE for the different prediction systems considering all start dates. CTRL is indicated by the blue solid line, ACPL with the red solid line, persistence by the dashed black, and the different models comprising the NMME system by the other thin coloured lines. The following rows show the skill of hindcasts started in c, d February, e, f May, g, h August and i, j November. The squares on the y-axes indicate the accuracy of the monthly averaged ATL3 index in ACPL and CTRL reanalyses (i.e. lead month 0). The skill is calculated using NOAA OISST V2. A circle is added for CTRL and ACPL when correlations are significant at a 5% significance level. Legend for the NMME system is shown in Fig. S3

Full size image

It is encouraging that ACPL system shows some skill in predicting the second equatorial SST variability maximum occurring in November–December from August starts. This variability is related to the Atlantic Niño phenomenon, which is centred on the ATL2 region (within 15\(^{\circ }\text{W}\)–\(5^{\circ }\text{W}\); \(3^{\circ }\text{S}\)–\(3^{\circ }\text{N}\), Okumura and Xie 2006). We further assess the skill of August started hindcasts in predicting such events. ACPL hindcasts capture the variability of the ATL2 SST index in November–December quite well with a correlation of around 0.5. We do not show the skill in predicting the ATL2 index as a function of lead time, as ATL2 and ATL3 are very similar and prediction skill is nearly identical to the one shown in Fig. 4g. For comparison with (Okumura and Xie 2006), we do show predictions of the ATL2 index in November–December (left panel of Fig. 5). ACPL is substantially more skilful than CTRL that has correlation skill around 0. The difference in correlation skill between ACPL and CTRL for November–December average calculated against NOAA OISST shows that ACPL improves the representation of the variability in the equatorial band (right panel of Fig. 5).

Fig. 5
figure 5

Left is the time series of the ATL2 in November–December from NOAA OISST (in black) and from ACPL hindcasts started in August (red line, ensemble mean); the shading represents the ensemble envelope (min and max). Right is the pointwise correlation difference between ACPL and CTRL for November–December predicted SST. The green box shows the ATL3 region and the blue box shows the ATL2 region

Full size image

In Fig. 6, we show the evolution of the reliability (meaning satisfying Eq. 1) of the ensemble prediction systems as function of lead month for the ATL3 SST index. The standard deviation of observation error is about \(0.1\,^{\circ }\text{C}\). In both systems the estimated error is slightly lower than the RMSE. This is typical with the ensemble DA method, because DA assumes that models are unbiased (Dee 2005). This assumption is not satisfied even with anomaly assimilation, because it only correct the climatological bias while assimilation assumes that any error type is random, which can also influence the higher moments (e.g. variance, skewness, kurtosis). Breaking this assumption results in a spurious reduction of the ensemble spread (Anderson 2001; Raanes et al. 2019). The dispersion is much improved in ACPL compared to CTRL, in particular at analysis time when discrepancies between RMSE and estimated error is marginal. It is reassuring that assimilation with a prediction system that uses a model with reduced bias improves this property. However, the ensemble spread does not grow at the same pace as the RMSE suggesting that the climatological correction term causes an artificial damping of the variability. By contrast, the RMSE in CTRL at the first lead month is not lower than in the rest lead month while the spread is reduced by assimilation. This suggests that assimilation in CTRL does not reduce substantially the error compared to climatological level but mostly reduces the ensemble spread. At 12 month lead time, the reliability is recovered in CTRL.

In Fig. 6, we assess how the probability density function of the ATL3 in ACPL and CTRL are aligned with the observations using a quantile–quantile plot of the index. In CTRL prediction system, the regression line is very well aligned although it tends to slightly overestimate the low values of ATL3. In ACPL, the prediction system underestimates the low values and the high value causing a tilt in the regression lines. We find very comparable results when breaking down the analysis for the different seasonal hindcasts or for hindcasts at different lead time (not shown).

Fig. 6
figure 6

In the left panel we assess the reliability of the ensemble prediction systems for the ATL3 index using HadISST2. The RMSE of persistence, ACPL and CTRL hindcasts are plotted with plain lines at different lead months. The dashed red and blue lines represent the estimated error (i.e. \(\sqrt{\sigma _{ens}^2+\sigma _{obs}^2}\), where \(\sigma _{ens}\) is the ensemble spread and \(\sigma _{obs}\) is the observation error). In the right-hand panel, we show the quantile–quantile graph of ATL3 predictions (all lead times) against observations

Full size image

6 Conclusions

Coupled Earth system models have very large biases and the impact of these on the prediction skill is yet to be determined. Here we investigate this issue for the tropical Atlantic, because this is a region where current models exhibit large biases compared to the amplitude of interannual variability and have demonstrated low prediction skill. Furthermore, several previous studies have reported an influence of model biases on the simulated variability and prediction skill in this region (Ding et al. 2015a; Dippe et al. 2018, 2019).

To investigate this question, we have used the anomaly coupled method of Toniazzo and Koseki (2018) in the NorESM model. The method has been shown to effectively reduce the systematic biases in the simulated tropical climatology of SST, wind stress and precipitation (Toniazzo and Koseki 2018). We compare performance of reanalyses and hindcasts with two versions of the NorCPM, one using the standard version of NorESM (CTRL) and one using the anomaly coupled version of NorESM (ACPL). With both configurations, we assimilate SST and ocean temperature and salinity profile data with the EnKF, and we perform 12 month long seasonal predictions, with 9 ensemble members, and initiated once per season. We focus on the period 1985–2010, and we compare of prediction skill against that of the North American Multi-model Ensemble.

We show that reducing the climatological biases in the tropical Atlantic improves the ocean reanalysis. Using a model with reduced bias allows the data assimilation to find a better dynamical reconstruction that satisfies the observations and their likelihood. The benefits are largest from June to November when simulated equatorial variability is most improved by anomaly coupling.

We also show that the performance of the prediction system for the Atlantic Niño index (ATL3) is greatly enhanced in ACPL compared to CTRL. Beyond 3 months lead time, ACPL hindcasts reaches skill comparable to the better NMME systems and beats persistence. We show that the skill is most improved when the simulated variability and the initial condition are improved, i.e. during the second half of the calendar year. For certain lead times and validity dates, notable in May from February initialisation, the ACPL system shows better skill than the entire NMME system. The skill however rapidly drops in June, which corresponds to the start date with largest potential impact but also to the most challenging one. We speculate that poor skill at that times is related to the poor accuracy of the atmospheric state in our system, which is not initialised. We plan to move the assimilation close to the effective start date of the hindcast and further initialise the atmospheric state.

The reliability of the ensemble prediction system is well improved initially with ACPL, as the perfect model hypothesis in the data assimilation better holds. However, the reliability degrades with integration time as ACPL causes an artificial damping of the variability. In fact, the distribution of Atlantic Niño with ACPL is found to underestimate the low and high values.