Abstract
Sea surface temperature (SST) biases in the tropical Atlantic are a long-standing problem among coupled global climate models (CGCMs). They occur in equilibrated state, as well as in initialised seasonal to decadal simulations. The bias is typically characterised by too high SST in upwelling regions and associated errors of wind and precipitation. We examine the SST bias in the state-of-the-art CGCM EC-Earth by means of an upper ocean heat budget analysis. Horizontal advection processes affect the SST bias development only to a small extent, and surface heat fluxes mostly dampen the warm bias. Subgrid-scale upper ocean vertical mixing is too low in EC-Earth when compared to estimates from reanalysis data, potentially giving rise to the warm bias. We perform sensitivity experiments to examine the effect of enhanced vertical mixing on the SST bias in quasi equilibrium present day climate and its impact on projected climate change. Enhanced mixing in historical simulation mode (\({\text {MixUp}}_{pr}\)) reduces the SST bias in the tropical Atlantic compared to the control experiment (\({\text {Control}}_{pr}\)). Associated atmospheric biases of precipitation and surface winds are also reduced in \({\text {MixUp}}_{pr}\). We further perform climate projections under the RCP8.5 emission scenario (\({\text {Control}}_{fu}\) and \({\text {MixUp}}_{fu}\)). Under increasing greenhouse gas forcing, the tropical Atlantic warms by up to \(4.5\,^{\circ }{\text {C}}\) locally, and maritime precipitation increases in boreal winter and spring. We show that the vertical mixing parameterisation influences future climate. In \({\text {MixUp}}_{fu}\), SSTs remain \(0.5\,^{\circ }{\text {C}}\) colder in boreal winter and spring, but increase with the same amplitude in summer and fall. The strength and location of the projected intertropical convergence zone also depends on the ocean vertical mixing efficiency. The rain band moves southward in summer, and its strength increases in winter in \({\text {MixUp}}_{fu}\) as compared to \({\text {Control}}_{fu}\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The importance of the tropical Atlantic to climate variability is evident from the sizable impacts it asserts on the surrounding continents. Tropical Atlantic sea surface temperatures (SST) are related to precipitation over Africa (Rouault et al. 2003; Okumura and Xie 2004), the Indian Summer Monsoon (Kucharski et al. 2009), as well as to drought and rainfall in the Brazilian Norderste region (Nobre and Shukla 1996; Pezzi and Cavalcanti 2001; Giannini et al. 2004; Yoon and Zeng 2010), and precipitation over equatorial South America (Crespo et al. 2019). The tropical Atlantic modulates the North Atlantic Oscillation (NAO) (Okumura et al. 2001; Haarsma and Hazeleger 2007), influences heat waves in Europe (Cassou et al. 2005) and precipitation in North America (Kushnir et al. 2010).
Yet, SST biases in the tropical Atlantic are a longstanding problem among state-of-the-art coupled global climate models (CGCMs). They commonly feature a large southeastern warm bias off the coast of southwest Africa, which extends along the equator (Wang et al. 2014). This bias might deteriorate climate predictions and projections in the TA and surrounding regions (Stockdale et al. 2006; Richter et al. 2018). The origins of this bias are not fully understood, even though the question has received considerable attention (see for example Wahl et al. 2011; Richter et al. 2012; Patricola et al. 2012; Exarchou et al. 2017; Koseki et al. 2018; Prodhomme et al. 2019, and references therein). Several studies point to westerly wind biases along with misrepresented Amazonian precipitation as its main cause (Wahl et al. 2011; Richter et al. 2012; Voldoire et al. 2014). Indeed, the important role of wind stress at the ocean surface has recently been underlined by Wen et al. (2017) and Voldoire et al. (2019). Enhancing the atmospheric model resolution can improve the simulation of the wind field and thereby the simulation of tropical Atlantic variabilty (Milinski et al. 2016; Harlaß et al. 2018).
Ma et al. (1996) link stratocumulus cloud cover to the cold tongue bias in the Pacific and Bellomo et al. (2015) show that local cloud feedbacks are equally important in the tropical Atlantic. Huang et al. (2007) and Hu et al. (2008) have linked low cloud cover to bias development in he NCEP coupled forecast system (CFS). Non-locally, Mechoso et al. (2016) link cloud forcing in the Southern Ocean to bias development in the tropical Atlantic. Hourdin et al. (2015) point to the role of evaporation and near surface relative humidity, and Hu et al. (2011) note the importance of a correctly simulated cloud liquid water path. Whether deficient low cloud cover in the southeastern tropical Atlantic forces the bias or is a result thereof remains under discussion (Large and Danabasoglu 2006; Xu et al. 2014a; Richter 2015). Recent reviews by Lübbecke et al. (2018) and Cabos et al. (2019) summarise the numerous potential origins of the tropical Atlantic biases.
While atmospheric biases may partly explain the warm SST bias, the ocean model also contributes. Increased ocean resolution often leads to improvements in the tropical Atlantic (Seo et al. 2006; Doi et al. 2012; Small et al. 2014). However, part of the warm SST bias remains, even when forcing eddy-resolving ocean models with reanalysis wind stress (Xu et al. 2014b). The authors of the latter study discuss the influence of the biased equatorial thermocline on ocean dynamics. The position of the thermocline is connected to large parts of SST variability in the tropical Atlantic, for example via the Bjerknes Feedback, which causes the leading mode of inter-annual variability (Keenlyside and Latif 2007; Deppenmeier et al. 2016), as well as contributing to the seasonal cycle (Burls et al. 2011). The important role of smaller scale ocean processes, especially of turbulent mixing, has been pointed out by Hazeleger and Haarsma (2005), Hummels et al. (2014), Polo et al. (2015), and Planton et al. (2018). In the tropical Pacific, insufficient vertical mixing has been proposed as a possible candidate for causing the warm biases in ocean models from observational analysis (Moum et al. 2013). Model representation of vertical mixing might play an important role in the tropical Atlantic, as well.
The development of biases in coupled climate models, rather than the equilibrated bias, can be studied from ensembles of initialised hindcast simulations. For these experiments, the model components for the atmosphere and the ocean are initialised with estimates of the observed state, for example, constructed from reanalysis data. Choosing an initialisation date in the past allows one to study the development of the bias by tracing the simulation’s deviations from observations (Toniazzo and Woolnough 2014; Huang et al. 2007; Vannière et al. 2013; Gaetani and Mohino 2013; Voldoire et al. 2019). Assuming the initialisation shock is small (Balmaseda and Anderson 2009), possible feedbacks leading to the biases can be followed and their origins untangled. This is not possible with data from an equilibrated climate model simulation.
In this study, we use initialized seasonal hindcasts to study the origin of the warm bias in the tropical Atlantic by means of a heat budget analysis. From this analysis, we form a hypothesis that places upper ocean vertical mixing at the center of the warm bias development. To test this hypothesis we perform a climate mode sensitivity experiment with altered parameterizations initialized from equilibrated biased model state, as well as a control experiment with the unchanged version of the climate model EC-Earth 3.2.3 (climate mode simulations).
The tropical Atlantic region is relevant for science and society, hence there is considerable interest in how tropical Atlantic climate will react to the global increase of greenhouse gas (GHG) concentrations. Projected climate change and model sensitivity to GHG forcing has been investigated globally and regionally. In the tropical Atlantic, climate models do not agree on the response to increasing GHG. Precipitation changes are particularly uncertain. While some models project drying above the tropical Atlantic and on the surrounding continents, especially of the Sahel region, others project wetting of the North African subcontinent (Held et al. 2005; Cook and Edward 2006; Biasutti et al. 2008).
The mechanism by which the rainfall patterns in and around the tropical Atlantic change are the result of tropical Atlantic SST forcing as well as direct response to enhanced GHG concentrations (Biasutti et al. 2008; Mohino et al. 2011; Biasutti 2013). Cook and Edward (2006) suggest that temperature change in the Gulf of Guinea is an important indicator for rainfall shifts connected to the West African Monsoon (WAM). Rodríguez-Fonseca et al. (2011) stress the importance of the background state to reliably simulate the WAM variability.
Present day climate model biases impact the projected future climate, especially in the tropics (Breugem et al. 2006; Good et al. 2009; Ashfaq et al. 2011; Zhou and Xie 2015). To investigate the climate change signal in EC-Earth and its dependence on the present day bias, we continue the experiments into the 21st century. We analyse the impact of enhanced mixing on the tropical Atlantic climate change response to rising greenhouse gas forcing.
The data used in this study is described in Sect. 2. The results are presented in Sect. 3, first from the seasonal hindcasts (Sect. 3.2) and then the sensitivity experiments (Sect. 3.3), and placed in context in Sect. 4.
2 Data and methodology
To identify the origin of the SST bias, we construct an upper ocean heat budget from an ensemble of seasonal hindcasts. Each seasonal hindcast is initialised from an estimate of the observed state constructed from reanalysis data on the first of May between 2000 and 2009. The reanalysis products chosen for the initialisation are based on the ocean and atmosphere models native to EC-Earth, ORAS4 (Balmaseda et al. 2013) (NEMO), and ERA-Interim (Dee et al. 2011) (IFS). This choice is made to reduce the initialisation shock. While the reanalyses include assimilated data, the underlying dynamical model is the same as the CGCM used in this study. Our simulations focus on boreal summer, when the tropical Atlantic cold tongue develops, and model biases grow concurrently. The hindcasts are integrated over 4 months, from the 1st of May until the 31st of August. Repeating the experiment four times starting form perturbed atmospheric initial states leads to an ensemble of five members for each year. The ensemble is generated with EC-Earth version 3.2.1. The model is based on EC-Earth2.2 (Hazeleger et al. 2010, 2012) with updated atmosphere, ocean, sea ice [modeled by LIM3 (Vancoppenolle et al. 2008)], and aerosol components. It consists of the NEMO ocean engine version 3.3 using the ORCA1 grid and 46 vertical levels (ORCA1L46) (Madec et al. 2011) and IFS cycle 36r4 with triangular truncation at truncation at wavenumber 255 and 91 vertical levels up to 5 hPa (T255L91, Riddaway, Newsletter ECMWF 2010). The individual components are coupled via OASIS3 (Valcke 2013).
We use surface heat and radiative fluxes from TropFlux (Kumar et al. 2012), ERA-Interim (Dee et al. 2011), and the Simple Ocean Data Assimilation 3 (SODA3) (Carton et al. 2018), wind stress from ERA-Interim (Dee et al. 2011) and the ECMWF ocean reanalysis system 4 (ORAS4, (Balmaseda et al. 2013)) to construct a reanalysis upper ocean heat budget. We calculate heat budgets for two regions in which the SST bias is large in the seasonal hindcasts as well as in the equilibrated control experiment (Figs. 2, 3): off the Angolan–Namibian coast, (AN regionbox, \(4^{\circ }\,{\text {E}}\)–\(11^{\circ }\,{\text {E}}\), \(6^{\circ }\,{\text {S}}\)–\(18^{\circ }\,{\text {S}}\)), and underneath the ITCZ (ITCZ box, \(25^{\circ }\,{\text {W}}\)–\(8^{\circ }\,{\text {W}}\), \(2^{\circ }\,{\text {N}}\)–\(5^{\circ }\,{\text {N}}\)). For both of those regions, a sizable SST bias develops within 3 months in the seasonal hindcast. The boxes are indicated by the boxes in Fig. 3. The differences between the model and reanalysis budgets are used to study the development of the SST bias.
Seasonal hindcasts are costly, therefore we use comparatively cheap climate mode simulations to test our hypotheses in an equilibrated situation. For the climate mode simulations we use the CMIP6 version of EC-Earth3, consisting of LIM3, NEMO3.6 with the ORCA1 grid with 75 vertical levels, and IFS cycle 36r4 with T255L91. The resolution in the atmosphere and the horizontal resolution of the ocean are identical to the one in the seasonal hindcasts, but the ocean model in EC-Earth3 features more vertical levels. We generate one member for each sensitivity experiment. The historical simulations \({\text {Control}}_{pr}\) and \({\text {MixUp}}_{pr}\) start from spun up conditions (500 years) in 1950 and are forced with CMIP5 historical forcing (1950–2010). The climate projections \({\text {Control}}_{fu}\) and \({\text {MixUp}}_{fu}\) under RCP8.5 forcing (Riahi et al. 2011) start in 2010 from the simulated states of \({\text {Control}}_{pr}\) and \({\text {MixUp}}_{pr}\). These experiments are continued until the end of the century (2099). For evaluation of future climate we use the period between 2070 and 2099, for evaluation of the present climate we use data from 1979 to 2009. The present climate period begins in line with the availability of reliable reanalysis data, and ends before RCP8.5 forcing is applied. The setup of the MixUp experiments is explained in more detail in Sect. 3.3.1, and the experiments are listed in Table 1.
3 Results
3.1 Biases in the historical simulation and seasonal hindcasts
The annual tropical Atlantic SST bias in EC-Earth closely resembles the bias of other CMIP5 models (Taylor et al. 2012) in equilibrium state (Wang et al. 2014, Fig. 1a). It extends from the western coast of Africa into the tropical Atlantic Ocean, close to the equator (Fig. 1a). In May, June, July, and August, when the annual equatorial cold tongue develops and the southeastern tropical Atlantic cools (Fig. 1d), the bias is even larger (Fig. 1b). The CGCM is not able to produce sufficiently strong cooling during boreal summer and displays a bias with root mean square errors on the order of 1– 2 °C in the ITCZ and AN boxes (Table 2), locally the biases are even larger. While these biases are smaller than those of other CGCMs (Toniazzo and Woolnough 2014), their spatial pattern is very similar.
Climate mode EC-\({\text {Earth}}_{\mathrm {Control}}\) sea surface temperature bias with respect to ERA-Interim in present climate for the period of 1979–2009. Annually averaged bias in a, and the heightened summer time bias in the months May, June, July, August in b. Values below significance at 90% level have been left white. c, d The climatological SST from ERA-Interim for annually, and in MJJA, respectively. Contours in panel d show the EC-\({\text {Earth}}_{\mathrm {Control}}\) MJJA SST bias, which follows the structure of the cooling in ERA-Interim, contour lines in \(1\,^{\circ }{\text {C}}\)
Since the atmosphere and ocean in the tropics are strongly coupled, CGCM biases in one component affect the wider climate system. Therefore, we examine the seasonally stratified biases of SST, wind and precipitation in the control simulation.
Throughout all seasons, south-eastern tropical Atlantic SSTs are too high (Fig. 2), in line with Figs. 1 and 3. The maximum SST bias moves northward towards the cold tongue region along the equator from boreal winter to summer. Its extent along the equator is greatest in spring, albeit with a smaller amplitude than in winter and summer.
In DJF and MAM, the SST bias displays a meridional dipole structure, with too warm waters in the southern hemisphere and too cold waters in the northern hemisphere (Fig. 2). The location of the ITCZ is associated to the SST bias via the temperature gradient control on the ITCZ (Biasutti et al. 2003, 2006). As a consequence, the ITCZ is located too far south in EC-Earth compared to reanalysis data, following the band of high SSTs. In JJA and SON, the warm bias south of the equator is confined to the east of the basin. A cold bias in the west leads to a meridionally tripolar bias structure. In these seasons, the positive precipitation bias is confined to the warm region in the southeast. The accumulated precipitation bias across the basin is negative in SON and DJF, when basin wide precipitation is underestimated by 23% and 16%, respectively. In MAM and JJA, the bias is more of a shift, and the underestimation is small (3% and 6%, respectively).
Concurrent with the ITCZ bias, there is a surface wind bias in all seasons in EC-Earth Control. The wind bias is mostly directed towards the warm SST bias, which leads to a southward wind bias across the equator. The strength of the surface wind bias varies with the season. Surface winds in the eastern equatorial Atlantic (ATL3 box, \(25^{\circ }\,{\text {W}}\)–\(0^{\circ }\,{\text {E}}\), \(3^{\circ }\,{\text {N}}\)–\(^{\circ }\,{\text {S}}\)) are underestimated by more than 50% in boreal winter, and by about 40% in spring. Western equatorial Atlantic surface winds are well reproduced during most of the year, but are underestimated by more than 40% in spring. Richter et al. (2012) show that weak equatorial easterlies in boreal spring are responsible for the warm equatorial SST bias in the Geophysical Fluid Dynamics Laboratory (GFDL) model. In a later study, Richter et al. (2014) link deep convection and the free troposphere to these wind biases. The effect of wind stress on the equatorial and southeastern Atlantic SST biases has been tested using 5 CGCMs by Voldoire et al. (2019). While improved wind stress reduces the bias in most models, the effects are smaller in some models than in others. The Cerfacs and Centre National de Recherches Météorologiques (CNRM) earth system models, for example, react strongly to improved equatorial wind stress, while the effect is less pronounced in the Institut Pierre Simon Laplace (IPSL) model and EC-Earth, which is used in this study. Voldoire et al. (2019) demonstrates that wind stress forcing cannot explain the SST bias in EC-Earth, especially in the southeastern Atlantic (see Fig. 12 in their study). We hence study the origin of the warm SST bias in EC-Earth with an upper ocean heat budget analysis on the seasonal hindcast data set.
Three months after initialisation, i.e. in July, a bias pattern emerges that is very similar to the equilibrium bias (Fig. 3). The amplitude is weaker, likely due to slow adjustment time scale of the ocean, but we can assume that the physical mechanisms responsible for the fast developing bias also contribute to the equilibrated bias . EC-Earth performs better than most climate models in the tropical Atlantic Voldoire et al. (2019). For instance, it does not exhibit the notorious double ITCZ structure many other models suffer from (Huang et al. 2004; Biasutti et al. 2006; Deser et al. 2006; Breugem et al. 2006, 2007; Lin 2007; Adam et al. 2016, 2018; Zuidema et al. 2016), although it produces rainfall too far to the south of observed values (see Fig. 2).
3.2 Upper ocean heat budget
We calculate two sets of heat budgets, one from the ORAS-4/flux dataset and one from model output, per box (see Fig. 3 for the boxes), and subtract them from each other to form bias development budgets. The upper ocean heat budgets are constructed according to the following equation
In Eq. (1), \(\partial _t T_s\) is the temperature evolution in the upper mixed layer approximated by the SST evolution, Q is the net surface flux into the mixed layer, assuming that the entire solar radiation flux is absorbed in the mixed layer, u, v, and w are the horizontal and vertical velocities (w is calculated from the horizontal divergence of u and v). \(\rho _w\) is the density of seawater, \(c_p\) its heat capacity, and h is the mixed layer depth according to a temperature threshold (\(T \le SST - 0.1\)). This compares well to the mixed layer depth obtained from a density threshold (not shown). R is the residual comprising all subgrid-scale terms (and, in the case of the reanalysis budget, true residual, because this dataset is not necessarily energy conserving, see discussion below). We use three flux products for the reanalysis budgets, SODA3 (Carton et al. 2018), ERA-Interim (Dee et al. 2011), and TropFlux (Kumar et al. 2012), to estimate the contribution of the net heat flux Q into the ocean. The spread among these products is reflected in error bars in Fig. 4. The error in Q introduces and error in the residual, which is reflected in the error bars on R.
In the AN box, the SST bias rises monotonously throughout the first 2 months of the simulation (Fig. 4a). Excess incoming shortwave radiation has been named as a possible explanation of the bias (Huang et al. 2007; Hu et al. 2008). In our case, the net surface fluxes immediately dampen the bias. A positive shortwave radiation bias eventually develops, but only after 2 weeks into the simulation (not shown). This occurs after an initial SST bias has already been formed.
Sea surface temperature bias development budget for the EC-Earth seasonal hindcasts. Panels a and b show the time integrated contributions to the SST bias evolution derived from to the upper ocean heat budget (Eq. 1), for the AN and the ITCZ box respectively (see Fig. 3 for the boxes). The components contributing to the warm bias are mean horizontal advection (UV), mean vertical advection (W), the net surface heat flux into the well mixed layer (Q), and the residual (R). Error bars on Q and R reflect the uncertainty of the net heat flux into the ocean derived from three different reanalysis products. The latter contains subgrid-scale and short timescale processes that are parameterised in the model and not available from reanalysis data. Panels c and d show the seasonal hindcast subsurface temperature bias development for the two boxes with respect to ORAS4
The heat budget shows that, in the first 2 months, mean upwelling contributes little to the bias. Horizontal advection does not contribute to the fast response bias, either. The subgrid-scale processes, captured in the residual, are the only large positive contribution to the SST bias. This term encompasses all processes that are not explicitly solved in the numeric climate model. These processes consist of vertical mixing, diffusion, mesoscale eddies, and horizontal turbulent processes. Among those terms, turbulent vertical mixing is likely the most important one. Observations show that horizontal and vertical diffusion are both smaller by an order of magnitude (Foltz et al. 2003), and lateral subduction is expected to be small in regions with a horizontally homogeneous mixed layer depth such as in the tropics. In regions where tropical instability waves (TIWs) are present the mesoscale eddy transports can be sizable (Hazeleger et al. 2001), but these regions are closely confined to the equatorial region and likely do not penetrate the southeastern part of the tropical Atlantic (Jochum et al. 2004).
The ocean column in the AN region shows approximately monotonous warm bias development (Fig. 4c). A small bias throughout the ocean column develops as quickly as within the first month of the simulation. In the following months, the bias grows in the well mixed surface layer, down to 20–40 m. In July it reaches its maximum at the surface, and in August it spreads through the upper 50 m.
The SST bias in the ITCZ region develops in two stages. In the first 2 month after initialisation, the bias remains relatively small (less than \(0.5\,^{\circ }{\text {C}}\)). During this time, there is a slight contribution of excess net surface heat flux (Q), as well as of the residual in June (see Fig. 4b). In July, the net heat flux becomes negative, and dampens the bias. After the initial onset of the bias by Q and the residual, the residual becomes the sole large positive contribution to the SST bias, similar to the development in the AN box. The residual comprises errors from potentially not closing heat budget for the reanalysis data, as well as assimilation increments. It is therefore not only composed of physical processes. However, given its magnitude (\(>2\,^{\circ }{\text {C}}\)), we believe it to contain some physical meaning. In the absence of large positive contributions of surface flux heating, this suggests that one or more subgrid-scale processes cooling the ocean surface are weaker in the CGCM than in ORAS4. Underneath the ITCZ we can expect an impact of mesoscale and smaller scale processes (e.g. TIWs), but vertical mixing is expected to play a more prominent role (Foltz et al. 2003). The upper ocean heat budget analyses for both AN and ITCZ suggest that subgrid-scale processes play a dominant role in the bias development in the seasonal hindcast simulations.
An uncertainty on the heat budget is the use of only one ocean reanalysis (ORA). A study by Zhu et al. (2012) highlights differences in the leading empirical orthogonal functions of heat content variability in the tropical Atlantic, though the authors also find commonalities among the six ORAs they use. A more recent study by Balmaseda et al. (2015) involving more ORAs find that the available datasets agree largely on tropical mixed layer depth and the upper ocean heat content. The latter study reports differences between the ORAs mostly in the deep ocean, which is not considered in the present study. Furthermore, the heat budget constructed from the reanalsyis and flux product dataset are not closed, but include a true residual because they are not constructed to conserve energy among them. However, given the large size of the residual, we assume that a significant part of it stems from parameterized ocean products. We hypothesise that vertical mixing is the most important among the processes contributing to the residual, and that it is underestimated in coupled global climate model simulations. This leads us to performing sensitivity experiments with heightened ocean vertical mixing.
3.3 Sensitivity experiments
3.3.1 Setup of the enhanced vertical mixing experiments MixUp
Turbulent motion acts on such small time and length scales that it cannot be resolved in global climate models, and hence has to be parameterized. Therefore, turbulent coefficients are defined in analogy to molecular diffusion and viscosity which act on the gradients of temperature, salt and momentum to mimic turbulent motion.
The vertical eddy diffusivity coefficient \(A_{vt}\) acts on the temperature field according to the diffusive operator \(D_{vt}\):
The temperature T and the height of the layer z along the vertical index k are resolved in the model, the vertical eddy diffusivity coefficient \(A_{vt}\) needs to be prescribed or calculated from resolved variables.
In the ocean component of EC-Earth, NEMO (Madec et al. 2015), several methods are available to compute the vertical diffusivity coefficients. It can be chosen as constant, dependent on the local Richardson number, or calculated with a turbulence closure scheme. In this study, we use the turbulent kinetic energy (TKE) scheme. This scheme was first introduced by Bougeault and Lacarrere (1989) in the atmosphere, adapted for use in the ocean by Gaspar et al. (1990), and introduced into OPA, the former version if NEMO, by Blanke and Delecluse (1993). It has been adapted and extended by Madec et al. (1988). In the following, we describe the employed TKE scheme following the description of the NEMO documentation (Madec et al. 2015).
The TKE scheme employs the prognostic equation for the turbulent kinetic energy \({\bar{e}}\):
In Eq. (3) t is time, h is the depth of the ocean layer, defined in the vertical along z, u and v are the zonal and meridional velocities. In all cases in this study, the Prandtl number, set as a function of the Richardson number Ri (\(P_{rt} = 1\) for \(Ri \le 0.2\)) is \(P_{rt} = 1\), and hence \(A_{vt} = A_{vm} \cdot l_{mxl}\) in Eq. (4) is the mixing length scale. Both \(l_{\epsilon }\) and \(l_{mxl}\) are dependent on the square root of the turbulent kinetic energy and the Brünt–Väisälä frequency
Note that \(N^2\) is calculated from temperature T and salinity S and thermal and haline expansion coefficients \(\alpha\) and \(\beta\) which are functions of T and S. \(l_{\epsilon }\) and \(l_{mxl}\) are additionally bound by physical reasoning about the vertical length scale they can achieve. In the surface layer this scaling takes into consideration the penetration depth of turbulent kinetic energy due to wind stress forcing.
In Eq. (3) the first term on the right hand side expressed turbulence production due to vertical shear, the second term is the destruction of turbulence due to stratification, the third term represents the vertical diffusion of turbulent kinetic energy, and the last term its Kolmogorov dissipation (Kolmogorov 1941).
Apart from the turbulence generation by vertical shear, Langmuir cells (LC) and internal wave breaking (IWB) give rise to turbulent kinetic energy, and at the surface TKE is injected into the ocean column by the magnitude of the local wind stress \(|\tau |\)
where \(\rho _0\) is the reference density defined as \(1035\,{\text { kg/m}}^3\). For more detail on the implementation of the parameterization schemes we refer to Madec et al. (2015).
In this study we test the effect of enhanced vertical mixing on the tropical Atlantic. In the most straightforward manner, this can be achieved by increasing \(A_{vt}\). To keep the model’s parameterization scheme and allow the mixing coefficient to react to the available turbulence kinetic energy, we do not prescribe \(A_{vt}\), but instead allow the model to calculate the coefficient according to its algorithms, but enforce enhancement of \(A_{vt}\) as described below.
Testing different parameters in 3D setting is costly. Instead we performed a number of sensitivity experiments with a coupled single column version of EC-Earth (Hartung et al. 2018), to determine which parameter changes should be made to enhance vertical mixing in the ocean (Deppenmeier et al. 2020). Based on these experiments, we increase \(C_{diff}\) in Eq. (4), which determines the turbulent eddy diffusivity coefficient, from the reference value of 0.1–0.5. \(C_{diff}\) is constrained by the mixing efficiency \(\gamma\), according to
Observational estimates for \(\gamma\) differ (Gaspar et al. 1990, and references therein). The value chosen for this study is larger than suggested by the measurements, which allow for \(C_{diff} = 0.3\). We chose to enhance \(C_{diff}\) drastically to study the effect of enhanced mixing and reduced warm surface layer formation.
The increase of \(C_{diff}\) can be understood as an enhanced model efficiency to use the available turbulent kinetic energy to mix the ocean column. We maintain the physical reasoning behind the TKE calculation, while strongly strengthening the mixing capability. We call the resulting sensitivity experiment MixUp. We also perform an unaltered experiment to compare to, named Control. These model simulations are first performed in historical climate mode, i.e. with prescribed historical estimates of greenhouse gas and aerosol concentrations as well as land use as described in Data and Methodology section. Secondly, we extend the experiments to future climate projections under RCP 8.5 to investigate the impact of enhanced vertical mixing on climate change projections of the tropical Atlantic region. The resulting set of experiments is \({\text {Control}}_{pr}\) and \({\text {Control}}_{fu}\), and the corresponding sensitivity experiments MixUppr and MixUpfu.
3.3.2 Impact of enhanced vertical mixing on present day climate
The amplification of vertical heat and momentum exchange in the ocean column driven by turbulent kinetic energy successfully reduces the present day SST bias in the southeastern tropical Atlantic, both annually and in MJJA (Fig. 5).
Panel a shows the sea surface temperature bias in EC-\({\text {Earth}}_{\mathrm {MixUp}}\) with respect to ERA-Interim for the period May–August in present climate (1979–2009). Panel b shows the difference between the sensitivity experiment EC-\({\text {Earth}}_{MixUp}\) and the control experiment in the same period. Note the different scales of the colorbars. Values below significance at 90% levels have been left white
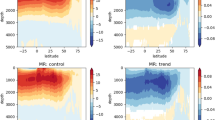
Along the equator, between 3\(^{\circ }\) N and 3\(^{\circ }\) S, the warm bias is reduced in \({\text {MixUp}}_{pr}\), especially in boral spring (Fig 6). Between February and April, \({\text {Control}}_{pr}\) features an artificial central Atlantic warm pool, which is reduced in \({\text {MixUp}}_{pr}\) (Fig 6, top row). In boreal summer, when the cold tongue extends along the equator in observations, the control simulation misplaces the center of the cold water to the west and underestimates the strength of the cooling. This leads to a warm bias in the cold tongue region (eastequatorial). The artifical westerward extension of the simulated cold tongue causes a cold bias in the western part of the basin (Fig. 6, bottom row). Both biases are reduced in \({\text {MixUp}}_{pr}\). Similarly, the strong bias close to the coast of Africa is reduced.
Monthly stratified sea surface temperature along the equator (\(3^{\circ }\)N–3\(^{\circ }\)) in present climate (1979–2009) for a ERA-Interim, b EC-\({\text {Earth}}_{\mathrm {Control}}\), and c EC-\({\text {Earth}}_{\mathrm {MixUp}}\). d, e Biases of EC-\({\text {Earth}}_{\mathrm {Control}}\) and EC-\({\text {Earth}}_{\mathrm {MixUp}}\) with respect to ERA-Interim
3.3.3 Subsurface ocean changes
The enhanced ocean vertical mixing efficiency impacts temperatures at the sea surface and below. In the AN box, the upper 25 m are cooler in \(\hbox {MixUP}_{pr}\) than in \(\hbox {Control}_{pr}\) throughout the year (Fig. 7a, significant at 90% level from November to June). The cooling is stronger in boreal winter and spring (DJF and MAM) than in summer and autumn (JJA and SON). Below the first 25 m, the subsurface ocean warms, displaying a maximum warming signal between 30 and 60 m.
Difference between the \(\hbox {MixUp}_{pr}\) and \(\hbox {Control}_{pr}\) in the upper ocean column in AN. The left panel depicts the box average change in temperature for each month of the year, the center panel the amplification of the vertical eddy diffusivity parameter \(A_{vt}\). The right hand panel shows temperature difference throughout the year with depth in colours, and the isopycnals in contours [1000-x \(\hbox {kg/m}^3\)]. The solid lines are the isopycnals in the control experiment, the dashed lines the isopycnals in the sensitivity experiment
The turbulent vertical mixing coefficient \(\hbox {A}_{vt}\) is increased strongly in the upper 50 m in \(\hbox {MixUp}_{pr}\) with respect to \(\hbox {Control}_{pr}\) (Fig. 7b). In JJA the enhanced mixing extends down to the upper 100 m of the ocean column, deeper than in DJF, when the changes are confined to the upper 50 m. The varying depths coincide with the seasonal cycle of the mixing layer depth, which is deeper in austral winter summer than in austral summer.
Enhanced vertical mixing in the upper 100 m explains the surface cooling, as well as the warming directly underneath the cooler layer. Heat is redistributed vertically in the well mixed layer, transported away from the surface, and then accumulates at the bottom of the well mixed layer. From here it cannot directly be distributed deeper into the column by fast mixing processes, due to the barrier of the thermocline. The mixing coefficient \(\hbox {A}_{vt}\) decreases rapidly with depth (not shown). Hence, a dipole structure develops, with cooler water in the upper and warmer water in the lower part of the well mixed layer. The large amplitude of the warm signal is also partly due to it coinciding with its proximity to the thermocline.
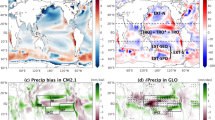
Another possible contribution to the subsurface warming is advection of warm water along isopycnals due to a change in outcrop location to warmer surface waters. When the outcrop location of the density surface moves toward warmer surface waters, these warmer waters will be subducted and transported along the isopycnal. In \(\hbox {MixUp}_{pr}\), the \(1025\,\hbox {kg/m}^3\) isopycnal outcrops closer to the equator than in \(\hbox {Control}_{pr}\) (see Fig. 8, grey line is the outcrop of \(\hbox {Control}_{pr}\) and the black line the outcrop of \(\hbox {MixUp}_{pr}\)). Surface waters are warmer at the outcrop location in \(\hbox {MixUp}_{pr}\) than in \(\hbox {Control}_{pr}\). North of the outcrop, the the \(1025\hbox { kg/m}^3\) isopycnal is warmed in \(\hbox {MixUp}_{pr}\) compared to \(\hbox {Control}_{pr}\), especially over the southeastern part of the tropical Atlantic basin (Fig. 8). We choose this isopycnal because of its proximity to the subsurface warm bias. The changes are larger in the southern subtropical Atlantic and to the west of the AN box, but part of the subsurface warming signal can be caused by warm water advected along the isopycnal into the AN box.
Difference of ocean temperature along the \(1025\, \hbox {kg/m}^3\) isopycnal between EC-\({\text {Earth}}_{MixUp}\) and EC-\({\text {Earth}}_{Control}\). The \(1025\, \hbox {kg/m}^3\) isopycnal is chosen for its location at the center of the warming signal between the two experiments (Figs. 7, 10). Grey and black lines show the outcrop location of the 1025 \(\, \hbox {kg/m}^3\) isopycnal for the control and sensitivity experiment, respectively
From the bottom of the well mixed layer, where the additional heat has accumulated, diffusion allows heat to penetrate into the deeper ocean on long timescales. The minimum value for the vertical eddy diffusivity in the ocean model is \(1.2\times 10^{-5}\, \frac{m^2}{s}\) . The temperature gradient between the depth of the maximum warming at 50 m and the maximum depth at which we still observe warming (1 km), is approximately \(20\,^{\circ }\hbox {C}\). According to the law of diffusion, \(\frac{\varDelta T}{\varDelta t} = -A_{vt} \times \frac{\varDelta T}{\varDelta z^2}\), after 45 years of runtime an ocean column of 950 m below the maximum warming could have warmed by \(\approx 0.4\,^{\circ }\hbox {C}\). This is the order of magnitude of warming that we observe below the well mixed layer and thermocline.
In the ITCZ box surface temperatures in \(\hbox {MixUp}_{pr}\) cool less in comparison to \(\hbox {Control}_{pr}\) than in the AN box (Figs. 9, 10). The upper 15–20m cool slightly throughout boreal spring and the beginning of summer (Fig. 10a), although the signal is not statistically significant. Below the cooled upper layer there is a warming of subsurface water. The maximum of this subsurface warming lies below the layer in which vertical mixing is enhanced (Fig. 10b). Because the mean enhanced mixing does not penetrate this layer, it seems that remote processes such as advection of warmer subducted water along the isopycnal, rather than vertical mixing, play a dominant role. The warm signal closely follows the seasonal cycle of the depth of isopycnals in these layers. Ventilation along the isopycnal is known to reach the equatorial currents from the subtropical gyre via the Brazil Current (Hazeleger et al. 2003). Water from the subtropical Atlantic reach the ITCZ box through subsurface advection along isopycnals and may cause warming through the same subduction and along-isopycnal advection mechansim as described above (Fig. 8). Shoaling plays a smaller role than in the AN box (average shoaling in ITCZ box at \(1025\,\hbox { kg/m}^3\): 6.7 m, in the AN box: 8.7 m).
Differences in the upper ocean column between the sensitivity and the control experiments in the ITCZ box. The left panel depicts the box average change in temperature for each month of the year, the center panel the amplification of the vertical eddy diffusivity parameter \(A_{vt}\). The right hand panel shows temperature difference throughout the year with depth in colours, and the isopycnals in contours [1000-x\(\, \hbox {kg/m}^3\)]. The solid lines are the isopycnals in the control experiment, the dashed lines the isopycnals in the sensitivity experiment
3.3.4 Impact of enhanced vertical mixing on the atmosphere in present day climate
Coupled to SST changes, the atmospheric circulation responds to the parameterization change. In boreal winter and spring, cooler SST in the southern part of the tropical Atlantic lead to a larger meridional SST gradient in \(\hbox {MixUp}_{pr}\). In line with the increased gradient, cross equatorial winds strengthen in those seasons, which reduces the inital southerly wind bias seen in \(\hbox {Control}_{pr}\) (Figs. 2, 11). Simultaneously, the northeastern part of the ITCZ strengthens and the spurious southern part of the ITCZ lessens. Precipitation and wind biases lessen similarly in spring. The fomer negative precipitation bias of up to 4 mm/day in \(\hbox {Control}_{pr}\) is halved in \(\hbox {MixUp}_{pr}\), and greatly reduced in spatial extent. In DJF, the basin wide cumulative negative precipitation bias reduces from 16 to 5%. Similarly, the strength and extent of the southern part of the model ITCZ reduces beneficially by up to 3 mm/day. In boreal fall, surface temperatures north of the simulated ITCZ are cooled in \(\hbox {MixUp}_{pr}\), which increases the meridional SST gradient between the ITCZ and to the north of it. The position of the ITCZ and the interhemispheric SST gradient are closely linked, as demonstrated by Zhang and Delworth (2005), among others, and more recently by Green et al. (2017) and Moreno-Chamarro and Marshall (2019). In case of cooling in the northern hemisphere, the ITCZ is shifted to the south (Zhang and Delworth 2005). In \(\hbox {MixUp}_{pr}\), the cooling of the northern hemisphere traps the ITCZ and it remains too far south. The ITCZ in \(\hbox {MixUp}_{pr}\) is narrower than in \(\hbox {Control}_{pr}\), which leads to a larger negative bias in the north and a stronger positive bias at the center of the simulated ITCZ. In the southwest of the tropical Atlantic, the positive alongshore wind bias at the coast of Brazil increases, but the bias west off the African coast is reduced, even though SSTs change only slightly.
Seasonally stratified sea surface temperature differences between EC-\({\text {Earth}}_{\mathrm {Control}}\) and EC-\({\text {Earth}}_{\mathrm {MixUp}}\) in present day climate in colours, differences of the wind vectors (arrows) and precipitation (mm/day) in contours. The control experiment is subtracted from the sensitivity experiment, such that negative (positive) values show decreased (increased) temperature and precipitation in MixUp compared to the control. Only changes significant at 90% level are shown
Throughout boreal summer and fall, SST increase along the equator in \(\hbox {MixUp}_{pr}\) compared to \(\hbox {Control}_{pr}\) (Fig. 11). Locally, the westerly surface wind bias reduces. To the south of the warmer sea surface, the northerly wind bias is reduced slightly. Above, and slightly north of, the region of increased SST precipitation is increased in the sensitivity experiment. In summer and fall, the ITCZ moves northward in ERA-interim (Fig. 2). In both the control and the sensitivity simulations, the seasonal displacement of the warm band is smaller than observed (shown for \(\hbox {Control}_{pr}\) in Fig. 2, not explicitly shown for \(\hbox {MixUp}_{pr}\)). In summer and autumn, the strength of the ITCZ is overestimated in both simulations. In the increased ocean vertical mixing experiment, the ITCZ is even stronger than in \(\hbox {Control}_{pr}\), which leads to a larger positive precipitation bias.
Summarising, in winter and spring the circulation and precipitation patterns, along with SST, are improved in \(\hbox {MixUp}_{pr}\). In boreal summer and fall there are improvements in the circulation and SST, but not in the location and strength of the ITCZ. Especially in fall the ITCZ is captured better by the control experiment.
Our analysis shows how sensitive the coupled system is to the choice of ocean vertical mixing parameterization. There are substantial differences between \(\hbox {MixUp}_{pr}\) and \(\hbox {Control}_{pr}\) in present day climate. In the following section, we investigate the effect of enhanced vertical ocean mixing on projected future climate.
3.3.5 Tropical Atlantic climate change
In this section, we investigate the tropical Atlantic climate change response to RCP8.5 (Riahi et al. 2011) in EC-Earth, and its dependence on the ocean vertical mixing efficiency. We first focus on the signal common to the control and the sensitivity experiment, before highlighting the differences.
As a response to increasing GHG forcing, tropical Atlantic SST increase locally by up to \(4.5\,^{\circ }\hbox {C}\) at the end of the century (Fig. 12). The ATL3 box (\(20^{\circ }\,\hbox {W}\)–\(0^{\circ }\,\hbox {E}\), \(3^{\circ }\,\hbox {S}\)–\(3^{\circ }\,\hbox {N}\)) warms by \(3.6\,^{\circ }\hbox {C}\) in the control and \(3.9\,^{\circ }\hbox {C}\) in the sensitivity experiment. The warming in the Atlantic is comparable to other CGCMs, CMIP5 models warm on average 3–\(4\,^{\circ }\hbox {C}\) (Team et al. 2014). The warming is basin wide, but it is intensified along the equator and in the east, where the equatorial cold tongue is located, especially in summer and fall. Tropical Atlantic surface winds weaken, and precipitation increases above warmer sea surface in the west. In spring, the ITCZ shifts northward, in line with enhanced warming of the sea surface on the northern hemisphere and the associated enhanced interhemispheric temperature gradient.
The subsurface ocean also warms. In the AN box, warming signal gradually decreases with depth below 50 m (Fig. 13a). In boreal spring and early summer, the subsurface warming peaks between 20 and 50 m below the surface. At this depth the temperature gradient is steepest in present day climate (Fig. 9), leading to a large warming signal when the mixed layer deepens. Surplus warming at the top of the column stabilises the ocean column. The turbulent eddy diffusivity coefficient is decreased in the future (Fig. 13b in austral summer, d all year) compared to present climate, in line with enhanced upper ocean stratification.
In the ITCZ box, the subsurface warming consists of two parts: near the surface, in the upper 50 m, and below the thermocline, between 70 and 200 m (Fig. 14a). The warming in the upper 50 m can be explained directly by warming of the overlying atmosphere, due to enhanced GHG forcing. Warmer surface temperatures stabilise the upper ocean, again reducing the eddy diffusivity (Fig. 14b). The subsurface warming below the region where turbulent mixing is active, on the other hand, cannot be explained by local influences. The subsurface warming is likely due to advection of remotely subducted warmer water.
To summarise, in both experiments, the sea surface and subsurface warm, winds weaken, and tropical precipitation increases. However, there are significant differences between \(\hbox {Control}_{fu}\) and \(\hbox {MixUp}_{fu}\). In the following, we compare the differences between the two simulations at the end of the century.
Both the SST response and the increase of tropical Atlantic precipitation are dependent on the vertical mixing parametrisation (Fig. 15). The projected SST signal is stronger in the \(\hbox {MixUp}_{fu}\) than in the control experiment (Fig. 12). Locally, the amplification of the warming signal reaches \(1\,^{\circ }\hbox {C}\), a considerable fraction of the warming (\(4.5\,^{\circ }\hbox {C}\)). Slight equatorial warming of \(\hbox {MixUp}_{fu}\) compared to \(\hbox {Control}_{fu}\) is enough to increase local rainfall intensity in boreal winter (Fig. 15). In spring, it is notably colder in the southern hemisphere in \(\hbox {MixUp}_{fu}\) than in \(\hbox {Control}_{fu}\). We speculate that this leads to a WES-type feedback (Chang et al. 1997), which enhances southerly cross-equatorial winds and shifts the ITCZ to the north (indicated by strengthened cross equatorial winds and shifted precipitation in Fig. 15). In summer, this signal is reversed. The southern hemisphere is warmer in \(\hbox {MixUp}_{fu}\), and northerly winds are stronger, shifting the ITCZ to the south. This signal prevails in fall, albeit with a weaker amplitude. In both seasons, future precipitation over Africa is weaker in the enhanced ocean mixing experiment.
Seasonally stratified differences in sea surface temperature, wind vectors, and precipitation (mm/day) between EC-\({\text {Earth}}_{\mathrm {MixUp}}\) and EC-\({\text {Earth}}_{\mathrm {CE}}\) as before in Fig. 11, but for future climate (2070–2099)
The seasonal cycle is suppressed along the equatorial band in the sensitivity experiment (Fig. 16a, b). The differences along the equator are enhanced in future climate as compared to present day climate (Fig. 16c, d).
Sea surface temperature (colours) and precipitation (contours every 2 mm/day) in future climate (2070–2099) along the equator (\(3^{\circ }\)N–3\(^{\circ }\)) for EC-\({\text {Earth}}_{\mathrm {Control}}\) and EC-\({\text {Earth}}_{MixUp}\), and the differences between the two experiments (contours indicate 1 mm precipitation differences)
Returning to the subsurface, large differences between the two simulations also exist there. In the AN box, the subsurface warming in \(\hbox {MixUp}_{fu}\) (Fig. 13c) is stronger and extends to greater depths than in \(\hbox {Control}_{fu}\) (Fig. 13a). Due to the stronger vertical mixing, more heat is transported downwards from the surface. Note that while the vertical eddy diffusivity in \(\hbox {MixUp}_{fu}\) decreases at the end of the century (Fig. 13d, Fig. 14d), the decrease is a factor two smaller than the differences between the two experiments in present day climate (Figs. 7b, 10b). Mixing is still stronger in \(\hbox {MixUp}_{fu}\) than in \(\hbox {Control}_{fu}\) at the end of the century.
Ocean temperatures in the ITCZ box increase more in \(\hbox {MixUp}_{fu}\) than in \(\hbox {Control}_{fu}\), especially in boreal summer and fall (Fig. 14). Below the thermocline, the warming is amplified throughout the year.
4 Summary and discussion
EC-Earth, like most other state-of-the-art coupled global climate models, suffers from fast developing and persistent warm SST biases in the eastern and east-equatorial tropical Atlantic (Richter and Xie 2008; Wang et al. 2014; Richter et al. 2018, and others). These biases are present in the equilibrated state in climate simulations (Fig. 2), as well as in simulations initialised from estimates of the observed states after only 2–3 months of runtime (Fig. 3).
We analyse the upper ocean mixed layer heat budget from EC-Earth and ORAS4/TropFlux data for two regions displaying large SST biases and shallow mixed layer depths, and compared the individual contributions to the sea surface temperature evolution (Fig. 4). We deduct that unresolved subgrid-scale processes play a large role in the fast development of the tropical Atlantic warm bias in EC-Earth. Ocean vertical mixing is an important component of these small-scale processes which exerts sizable influence on SST, especially in regions where the mixed layers is shallow (Foltz et al. 2003; Planton et al. 2018, and others). We increase the ocean vertical mixing efficiency in a historical climate simulation and in a climate projection with RCP 8.5 to test the system’s sensitivity to the representation of this turbulent process.
The present day climate SST bias in the tropical Atlantic is reduced under enhanced mixing (Fig. 5). Following the SST improvement, atmospheric biases in precipitation and winds also decrease (Fig. 11). EC-Earth suffers from relatively small atmospheric biases in the tropical Atlantic compared to other CGCMs (Fig. 2). However, it simulates excess precipitation to the south of the ITCZ, similarly to other models (Biasutti et al. 2006; Breugem et al. 2006; Lin 2007, and others), and it suffers from a weak (zonal) wind bias. Cross equatorial winds as well as precipitation are beneficially increased under enhanced mixing (Fig. 11). In spring, the west equatorial easterlies are strengthened. Though the bias is reduced at 90% statistical significance, a bias remains in the MixUp experiment. Its structure is similar to the Control bias.
Subsurface ocean temperatures are also affected by the enhanced mixing. Off the coast of Angola and Namibia, in the AN box, the difference between \(\hbox {MixUp}_{pr}\) and \(\hbox {Control}_{pr}\) manifests as a vertical dipole in the upper 50–75 m of the ocean column. The depth coincides with the layer in which vertical eddy diffusivity is active. The dipole likely develops due to heat redistribution in the mixed layer. Enhanced mixing transports heat to the bottom of the thermocline, from where it can only reach the deeper ocean via slow diffusion processes. Apart from this local effect, advection along isopycnals might transport warmer water to layers at or below thermocline depth (Fig. 8). A combination of local and remote effects likely play a role in warming the water at the bottom of the mixed layer in this region.
In the ITCZ box, the surface cooling in \(\hbox {MixUp}_{pr}\) is weaker than in the AN box with respect to \(\hbox {Control}_{pr}\). Vertical eddy diffusivity increases in the upper 40 m of the ocean column. Below the slightly cooled surface layer, and below the layer in which \(A_{vt}\) increases, \(\hbox {MixUp}_{pr}\) is warmer than \(\hbox {Control}_{pr}\). The warm signal follows the \(1025\,\hbox {kg/m}^3\) isopycnal closely, which suggests advective processes along this isopycnal (Fig. 8a). In both boxes, the ocean is warmed down to 1 km. This deep warming is attributed to a slow vertical diffusion processes.
We further investigate projected climate change under the RCP8.5 forcing scenario in EC-Earth by performing two climate projection experiments, \(\hbox {Control}_{fu}\) and \(\hbox {MixUp}_{fu}\). In both experiments, the tropical Atlantic warms, winds weaken and maritime precipitation increases. While there are similarities between the two projections, the climate change signal is sensitive to the vertical mixing parameterization. SST and maritime precipitation increase more in the \(\hbox {MixUp}_{fu}\) than in \(\hbox {Control}_{fu}\). \(\hbox {MixUp}_{fu}\) remains cooler than \(\hbox {Control}_{fu}\) in winter and spring. In boreal summer and fall, \(\hbox {MixUp}_{fu}\) is warmer than \(\hbox {Control}_{fu}\), especially in the southern hemisphere.
Subsurface climate change also dependends on the vertical mixing parametrisation, especially in the AN box. In \(\hbox {MixUp}_{fu}\) the entire upper ocean column is warmed almost uniformly, while in \(\hbox {Control}_{fu}\) the largest warming can be seen at the depth of the thermocline.
In this study we highlight the large impact of ocean vertical mixing on the coupled system. In both present day, as well as future climate, enhanced vertical mixing influences the ocean (sub)surface, and the atmospheric circulation. Changes at the sea surface are especially large in regions where the mixed layer is shallow. Further research and collaboration between modelers and observationalists are necessary to better constrain the important control that vertical ocean mixing asserts on the climate system.
References
Adam O, Schneider T, Brient F, Bischoff T (2016) Relation of the double-itcz bias to the atmospheric energy budget in climate models. Geophys Res Lett 43(14):7670–7677
Adam O, Schneider T, Brient F (2018) Regional and seasonal variations of the double-itcz bias in CMIP5 models. Clim Dyn 51(1–2):101–117
Ashfaq M, Skinner CB, Diffenbaugh NS (2011) Influence of SST biases on future climate change projections. Clim Dyn 36(7–8):1303–1319
Balmaseda M, Anderson D (2009) Impact of initialization strategies and observations on seasonal forecast skill. Geophys Res Lett 36:1
Balmaseda MA, Mogensen K, Weaver AT (2013) Evaluation of the ECMWF ocean reanalysis system ORAS4. Q J R Meteorol Soc 139(674):1132–1161
Balmaseda M, Hernandez F, Storto A, Palmer M, Alves O, Shi L, Smith G, Toyoda T, Valdivieso M, Barnier B et al (2015) The ocean reanalyses intercomparison project (ORA-IP). J Oper Oceanogr 8(sup1):s80–s97
Bellomo K, Clement AC, Mauritsen T, Rädel G, Stevens B (2015) The influence of cloud feedbacks on equatorial Atlantic variability. J Clim 28(7):2725–2744
Biasutti M (2013) Forced sahel rainfall trends in the CMIP5 archive. J Geophys Res Atmos 118(4):1613–1623
Biasutti M, Battisti DS, Sarachik ES (2003) The annual cycle over the tropical Atlantic, South America, and Africa. J Clim 16(15):2491–2508. https://doi.org/10.1175/1520-0442(2003)016<2491:TACOTT>2.0.CO;2
Biasutti M, Sobel A, Kushnir Y (2006) Agcm precipitation biases in the tropical Atlantic. J Clim 19(6):935–958
Biasutti M, Held IM, Sobel AH, Giannini A (2008) Sst forcings and sahel rainfall variability in simulations of the twentieth and twenty-first centuries. J Clim 21(14):3471–3486
Blanke B, Delecluse P (1993) Variability of the tropical Atlantic ocean simulated by a general circulation model with two different mixed-layer physics. J Phys Oceanogr 23(7):1363–1388
Bougeault P, Lacarrere P (1989) Parameterization of orography-induced turbulence in a mesobeta-scale model. Mon Weather Rev 117(8):1872–1890
Breugem WP, Hazeleger W, Haarsma R (2006) Multimodel study of tropical Atlantic variability and change. Geophys Res Lett 33:23
Breugem WP, Hazeleger W, Haarsma RJ (2007) Mechanisms of northern tropical Atlantic variability and response to CO2 doubling. J Clim 20(11):2691–2705
Burls N, Reason C, Penven P, Philander S (2011) Similarities between the tropical Atlantic seasonal cycle and ENSO: an energetics perspective. J Geophys Res Oceans 116:C11
Cabos W, de la Vara A, Koseki S (2019) Tropical Atlantic variability: observations and modeling. Atmosphere 10(9):502
Carton JA, Chepurin GA, Chen L (2018) SODA3: a new ocean climate reanalysis. J Clim 31(17):6967–6983
Cassou C, Terray L, Phillips AS (2005) Tropical Atlantic influence on European heat waves. J Clim 18(15):2805–2811
Chang P, Ji L, Li H (1997) A decadal climate variation in the tropical Atlantic ocean from thermodynamic air–sea interactions. Nature 385(6616):516–518
Cook KH, Edward KV (2006) Coupled model simulations of the west African monsoon system: 20th century simulations and 21st century predictions. J Clim Citeseer 20:20
Crespo LR, Keenlyside N, Koseki S (2019) The role of sea surface temperature in the atmospheric seasonal cycle of the equatorial Atlantic. Clim Dyn 52(9–10):5927–5946
Dee D, Uppala S, Simmons A, Berrisford P, Poli P, Kobayashi S, Andrae U, Balmaseda M, Balsamo G, Bauer P et al (2011) The era-interim reanalysis: configuration and performance of the data assimilation system. Q J R Meteorol Soc 137(656):553–597
Deppenmeier AL, Haarsma RJ, Hazeleger W (2016) The Bjerknes feedback in the tropical Atlantic in CMIP5 models. Clim Dyn 20:1–17
Deppenmeier, A-L et al (2020) The Southeastern Tropical Atlantic SST bias investigated with a coupled atmosphere-ocean single column model at a PIRATA mooring site. J Clim. https://doi.org/10.1175/JCLI-D-19-0608.1
Deser C, Capotondi A, Saravanan R, Phillips AS (2006) Tropical Pacific and Atlantic climate variability in CCSM3. J Clim 19(11):2451–2481. https://doi.org/10.1175/JCLI3759.1
Doi T, Vecchi GA, Rosati AJ, Delworth TL (2012) Biases in the Atlantic ITCZ in seasonal–interannual variations for a coarse-and a high-resolution coupled climate model. J Clim 25(16):5494–5511
Exarchou E, Prodhomme C, Brodeau L, Guemas V, Doblas-Reyes F (2017) Origin of the warm eastern tropical Atlantic SST bias in a climate model. Clim Dyn 20:1–22
Foltz GR, Grodsky SA, Carton JA, McPhaden MJ (2003) Seasonal mixed layer heat budget of the tropical Atlantic ocean (1978–2012). J Geophys Res Oceans 108:C5
Gaetani M, Mohino E (2013) Decadal prediction of the sahelian precipitation in CMIP5 simulations. J Clim 26(19):7708–7719
Gaspar P, Grégoris Y, Lefevre JM (1990) A simple eddy kinetic energy model for simulations of the oceanic vertical mixing: tests at station papa and long-term upper ocean study site. J Geophys Res Oceans 95(C9):16,179–16,193
Giannini A, Saravanan R, Chang P (2004) The preconditioning role of tropical Atlantic variability in the development of the enso teleconnection: implications for the prediction of nordeste rainfall. Clim Dyn 22(8):839–855
Good P, Lowe JA, Rowell DP (2009) Understanding uncertainty in future projections for the tropical Atlantic: relationships with the unforced climate. Clim Dyn 32(2–3):205–218
Green B, Marshall J, Donohoe A (2017) Twentieth century correlations between extratropical sst variability and ITCZ shifts. Geophys Res Lett 44(17):9039–9047
Haarsma RJ, Hazeleger W (2007) Extratropical atmospheric response to equatorial Atlantic cold tongue anomalies. J Clim 20(10):2076–2091
Harlaß J, Latif M, Park W (2018) Alleviating tropical Atlantic sector biases in the kiel climate model by enhancing horizontal and vertical atmosphere model resolution: climatology and interannual variability. Clim Dyn 50(7–8):2605–2635
Hartung K et al (2018) An EC-Earth coupled atmosphere-ocean single-column model (AOSCM. v1_EC-Earth3) for studying coupled marine and polar processes. Geosci Model Dev 11(10):4117–4137
Hazeleger W, Haarsma RJ (2005) Sensitivity of tropical Atlantic climate to mixing in a coupled ocean-atmosphere model. Clim Dyn 25(4):387–399
Hazeleger W, de Vries P, van Oldenborgh GJ (2001) Do tropical cells ventilate the indo-Pacific equatorial thermocline? Geophys Res Lett 28(9):1763–1766
Hazeleger W, de Vries P, Friocourt Y (2003) Sources of the equatorial undercurrent in the Atlantic in a high-resolution ocean model. J Phys Oceanogr 33(4):677–693
Hazeleger W, Severijns C, Semmler T, Ştefăănescu S, Yang S, Wang X, Wyser K, Dutra E, Baldasano JM, Bintanja R et al (2010) Ec-earth: a seamless earth-system prediction approach in action. Bull Am Meteorol Soc 91:10
Hazeleger W, Wang X, Severijns C, Ştefănescu S, Bintanja R, Sterl A, Wyser K, Semmler T, Yang S, Van den Hurk B et al (2012) Ec-earth v2. 2: description and validation of a new seamless earth system prediction model. Clim Dyn 39(11):2611–2629
Held I, Delworth T, Lu J, Findell Ku, Knutson T (2005) Simulation of sahel drought in the 20th and 21st centuries. Proc Natl Acad Sci 102(50):17,891–17,896
Hourdin F, Găinusă-Bogdan A, Braconnot P, Dufresne JL, Traore AK, Rio C (2015) Air moisture control on ocean surface temperature, hidden key to the warm bias enigma. Geophys Res Lett 42(24):10–885
Hu ZZ, Huang B, Pegion K (2008) Low cloud errors over the southeastern Atlantic in the NCEP CFS and their association with lower-tropospheric stability and air–sea interaction. J Geophys Res Atmos 113:D12
Hu ZZ, Huang B, Hou YT, Wang W, Yang F, Stan C, Schneider EK (2011) Sensitivity of tropical climate to low-level clouds in the NCEP climate forecast system. Clim Dyn 36(9–10):1795–1811
Huang B, Schopf PS, Shukla J (2004) Intrinsic ocean–atmosphere variability of the tropical Atlantic ocean. J Clim 17(11):2058–2077
Huang B, Hu ZZ, Jha B (2007) Evolution of model systematic errors in the tropical Atlantic basin from coupled climate hindcasts. Clim Dyn 28(7–8):661–682
Hummels R, Dengler M, Brandt P, Schlundt M (2014) Diapycnal heat flux and mixed layer heat budget within the Atlantic cold tongue. Clim Dyn 43(11):3179–3199
Jochum M, Malanotte-Rizzoli P, Busalacchi A (2004) Tropical instability waves in the Atlantic ocean. Ocean Model 7(1–2):145–163
Keenlyside NS, Latif M (2007) Understanding equatorial Atlantic interannual variability. J Clim 20:131–142. https://doi.org/10.1175/JCLI3992.1
Kolmogorov AN (1941) Equations of turbulent motion in an incompressible fluid. Dokl Akad Nauk SSSR 30:299–303
Koseki S, Keenlyside N, Demissie T, Toniazzo T, Counillon F, Bethke I, Ilicak M, Shen ML (2018) Causes of the large warm bias in the angola-benguela frontal zone in the norwegian earth system model. Clim Dyn 50(11–12):4651–4670
Kucharski F, Bracco A, Yoo J, Tompkins A, Feudale L, Ruti P, Dell’Aquila A (2009) A gill-matsuno-type mechanism explains the tropical Atlantic influence on African and Indian monsoon rainfall. Q J R Meteorol Soc 135(640):569–579
Kumar BP, Vialard J, Lengaigne M, Murty V, McPhaden M (2012) Tropflux: air–sea fluxes for the global tropical oceans-description and evaluation. Clim Dyn 38(7–8):1521–1543
Kushnir Y, Seager R, Ting M, Naik N, Nakamura J (2010) Mechanisms of tropical Atlantic SST influence on north American precipitation variability*. J Clim 23(21):5610–5628
Large W, Danabasoglu G (2006) Attribution and impacts of upper-ocean biases in CCSM3. J Clim 19(11):2325–2346
Lin JL (2007) The double-ITCZ problem in IPCC AR4 coupled GCMS: ocean–atmosphere feedback analysis. J Clim 20(18):4497–4525. https://doi.org/10.1175/JCLI4272.1
Lübbecke JF, Rodríguez-Fonseca B, Richter I, Martín-Rey M, Losada T, Polo I, Keenlyside NS (2018) Equatorial Atlantic variability-modes, mechanisms, and global teleconnections. Wiley Interdiscip Rev Clim Change 9(4):e527
Ma CC, Mechoso CR, Robertson AW, Arakawa A (1996) Peruvian stratus clouds and the tropical Pacific circulation: a coupled ocean–atmosphere GCM study. J Clim 9(7):1635–1645. https://doi.org/10.1175/1520-0442(1996)009<1635:PSCATT>2.0.CO;2
Madec G, Rahier C, Chartier M (1988) A comparison of two-dimensional elliptic solvers for the barotropic streamfunction in a multilevel OGCM. Ocean Model 78:1–6
Madec G, et al (2011) Nemo ocean engine
Madec G, et al (2015) Nemo ocean engine
Mechoso CR, Losada T, Koseki S, Mohino-Harris E, Keenlyside N, Castaño-Tierno A, Myers TA, Rodriguez-Fonseca B, Toniazzo T (2016) Can reducing the incoming energy flux over the southern ocean in a CGCM improve its simulation of tropical climate? Geophys Res Lett 43(20):11–057
Milinski S, Bader J, Haak H, Siongco AC, Jungclaus JH (2016) High atmospheric horizontal resolution eliminates the wind-driven coastal warm bias in the southeastern tropical Atlantic. Geophys Res Lett 43(19):10–455
Mohino E, Janicot S, Bader J (2011) Sahel rainfall and decadal to multi-decadal sea surface temperature variability. Clim Dyn 37(3):419–440. https://doi.org/10.1007/s00382-010-0867-2
Moreno-Chamarro E, Marshall J, Delworth T (2019) Linking ITCZ migrations to AMOC and north Atlantic/Pacific SST decadal variability. J Clim 20:20
Moum JN, Perlin A, Nash JD, McPhaden MJ (2013) Seasonal sea surface cooling in the equatorial Pacific cold tongue controlled by ocean mixing. Nature 500(7460):64
Nobre P, Shukla J (1996) Variations of sea surface temperature, wind stress, and rainfall over the tropical Atlantic and south America. J Clim 9(10):2464–2479
Okumura Y, Xie SP (2004) Interaction of the Atlantic equatorial cold tongue and the African Monsoon*. J Clim 17(18):3589–3602
Okumura Y, Xie SP, Numaguti A, Tanimoto Y (2001) Tropical Atlantic air–sea interaction and its influence on the nao. Geophys Res Lett 28(8):1507–1510
Patricola CM, Li M, Xu Z, Chang P, Saravanan R, Hsieh JS (2012) An investigation of tropical Atlantic bias in a high-resolution coupled regional climate model. Clim Dyn 39(9–10):2443–2463
Pezzi L, Cavalcanti I (2001) The relative importance of ENSO and tropical Atlantic sea surface temperature anomalies for seasonal precipitation over south America: a numerical study. Clim Dyn 17(2–3):205–212
Planton Y, Voldoire A, Giordani H, Caniaux G (2018) Main processes of the Atlantic cold tongue interannual variability. Clim Dyn 50(5–6):1495–1512
Polo I, Lazar A, Rodriguez-Fonseca B, Mignot J (2015) Growth and decay of the equatorial Atlantic sst mode by means of closed heat budget in a coupled general circulation model. Front Earth Sci 3:37
Prodhomme C, Voldoire A, Exarchou E, Deppenmeier AL, García-Serrano J, Guemas V (2019) How does the seasonal cycle control equatorial Atlantic interannual variability? Geophys Res Lett 20:20
Riahi K, Rao S, Krey V, Cho C, Chirkov V, Fischer G, Kindermann G, Nakicenovic N, Rafaj P (2011) Rcp 8.5-a scenario of comparatively high greenhouse gas emissions. Clim Change 109(1–2):33
Richter I (2015) Climate model biases in the eastern tropical oceans: causes, impacts and ways forward. Wiley Interdiscip Rev Clim Change 6(3):345–358
Richter I, Xie SP (2008) On the origin of equatorial Atlantic biases in coupled general circulation models. Clim Dyn 31(5):587–598
Richter I, Xie SP, Wittenberg AT, Masumoto Y (2012) Tropical Atlantic biases and their relation to surface wind stress and terrestrial precipitation. Clim Dyn 38(5–6):985–1001
Richter I, Behera SK, Doi T, Taguchi B, Masumoto Y, Xie SP (2014) What controls equatorial Atlantic winds in boreal spring? Clim Dyn 43(11):3091–3104
Richter I, Doi T, Behera SK, Keenlyside N (2018) On the link between mean state biases and prediction skill in the tropics: an atmospheric perspective. Clim Dyn 50(9–10):3355–3374
Rodríguez-Fonseca B, Janicot S, Mohino E, Losada T, Bader J, Caminade C, Chauvin F, Fontaine B, García-Serrano J, Gervois S et al (2011) Interannual and decadal SST-forced responses of the west African monsoon. Atmos Sci Lett 12(1):67–74
Rouault M, Florenchie P, Fauchereau N, Reason CJC (2003) South east tropical Atlantic warm events and southern African rainfall. Geophys Res Lett 30:5. https://doi.org/10.1029/2002GL014840
Seo H, Jochum M, Murtugudde R, Miller AJ (2006) Effect of ocean mesoscale variability on the mean state of tropical Atlantic climate. Geophys Res Lett 33:9
Small RJ, Bacmeister J, Bailey D, Baker A, Bishop S, Bryan F, Caron J, Dennis J, Gent P, Hm Hsu et al (2014) A new synoptic scale resolving global climate simulation using the community earth system model. J Adv Model Earth Syst 6(4):1065–1094
Stockdale TN, Balmaseda MA, Vidard A (2006) Tropical Atlantic SST prediction with coupled ocean-atmosphere gcms. J Clim 19(23):6047–6061
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93:4
Team CW, Pachauri R, Meyer Le (2014) Climate change 2014: synthesis report. contribution of working groups i, ii and iii to the fifth assessment report of the intergovernmental panel on climate change. IPCC p 151p
Toniazzo T, Woolnough S (2014) Development of warm sst errors in the southern tropical Atlantic in CMIP5 decadal hindcasts. Clim Dyn 43(11):2889–2913
Valcke S (2013) The OASIS3 coupler: a european climate modelling community software. Geosci Model Dev 6(2):373–388
Vancoppenolle M, Fichefet T, Goosse H, Bouillon S, Beatty CK, Morales Maqueda M (2008) Lim3, an advanced sea-ice model for climate simulation and operational oceanography. Mercator Ocean Q Newsl 28:16–21
Vannière B, Guilyardi E, Madec G, Doblas-Reyes FJ, Woolnough S (2013) Using seasonal hindcasts to understand the origin of the equatorial cold tongue bias in CGCMS and its impact on ENSO. Clim Dyn 40(3–4):963–981
Voldoire A, Claudon M, Caniaux G, Giordani H, Roehrig R (2014) Are atmospheric biases responsible for the tropical Atlantic SST biases in the CNRM-CM5 coupled model? Clim Dyn 43(11):2963–2984
Voldoire A, Exarchou E, Sanchez-Gomez E, Demissie T, Deppenmeier AL, Frauen C, Goubanova K, Hazeleger W, Keenlyside N, Koseki S et al (2019) Role of wind stress in driving SST biases in the tropical Atlantic. Clim Dyn 20:1–24
Wahl S, Latif M, Park W, Keenlyside N (2011) On the tropical Atlantic SST warm bias in the kiel climate model. Clim Dyn 36(5–6):891–906
Wang C, Zhang L, Lee Sk WuL, Mechoso CR (2014) A global perspective on CMIP5 climate model biases. Nat Clim Change 4(February):201–205. https://doi.org/10.1038/NCLIMATE2118
Wen C, Xue Y, Kumar A, Behringer D, Yu L (2017) How do uncertainties in NCEP R2 and cfsr surface fluxes impact tropical ocean simulations? Clim Dyn 49(9–10):3327–3344
Xu Z, Chang P, Richter I, Tang G (2014a) Diagnosing southeast tropical Atlantic sst and ocean circulation biases in the CMIP5 ensemble. Clim Dyn 43(11):3123–3145
Xu Z, Li M, Patricola CM, Chang P (2014b) Oceanic origin of southeast tropical Atlantic biases. Clim Dyn 43(11):2915–2930
Yoon JH, Zeng N (2010) An Atlantic influence on amazon rainfall. Clim Dyn 34(2–3):249–264
Zhang R, Delworth TL (2005) Simulated tropical response to a substantial weakening of the Atlantic thermohaline circulation. J Clim 18(12):1853–1860
Zhou ZQ, Xie SP (2015) Effects of climatological model biases on the projection of tropical climate change. J Clim 28(24):9909–9917
Zhu J, Huang B, Balmaseda MA (2012) An ensemble estimation of the variability of upper-ocean heat content over the tropical Atlantic ocean with multi-ocean reanalysis products. Clim Dyn 39(3–4):1001–1020
Zuidema P, Chang P, Medeiros B, Kirtman BP, Mechoso R, Schneider EK, Toniazzo T, Richter I, Small RJ, Bellomo K et al (2016) Challenges and prospects for reducing coupled climate model sst biases in the eastern tropical Atlantic and Pacific oceans: the US clivar eastern tropical oceans synthesis working group. Bull Am Meteorol Soc 97(12):2305–2328
Acknowledgements
The authors would like to thank the two anonymous reviewers for their constructive criticism and suggestions. This study was supported by the EU FP7/2007–2013 PREFACE Project under Grant agreement 603521.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Deppenmeier, AL., Haarsma, R.J., LeSager, P. et al. The effect of vertical ocean mixing on the tropical Atlantic in a coupled global climate model. Clim Dyn 54, 5089–5109 (2020). https://doi.org/10.1007/s00382-020-05270-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-020-05270-x