Abstract
Seasonal forecasts of rainfall are considered the priority timescale by many users in the tropics. In East Africa, the primary operational seasonal forecast for the region is produced by the Greater Horn of Africa Climate Outlook Forum (GHACOF), and issued ahead of each rainfall season. This study evaluates and compares the GHACOF consensus forecasts with dynamical model forecasts from the UK Met Office GloSea5 seasonal prediction system for the two rainy seasons. GloSea demonstrates positive skill (r = 0.69) for the short rains at 1 month lead. In contrast, skill is low for the long rains due to lack of predictability of driving factors. For both seasons GHACOF forecasts show generally lower levels of skill than GloSea. Several systematic errors within the GHACOF forecasts are identified; the largest being the tendency to over-estimate the likelihood of near normal rainfall, with over 70% (80%) of forecasts giving this category the highest probability in the short (long) rains. In a more detailed evaluation of GloSea, a large wet bias, increasing with forecast lead time, is identified in the short rains. This bias is attributed to a developing cold SST bias in the eastern Indian Ocean, driving an easterly wind bias across the equatorial Indian Ocean. These biases affect the mean state moisture availability, and could act to reduce the ability of the dynamical model in predicting interannual variability, which may also be relevant to predictions from coupled models on longer timescales.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
East Africa is a region that is highly vulnerable to rainfall variability, as consistent rainfall is vital for crops and livestock. Extreme events such as the 2010-11 year long drought have major effects on society, and flooding events can occur even in years of water scarcity, such as in 2018, when heavy boreal spring rains followed the severe drought conditions of late 2017 (http://fews.net/east-africa). Seasonal prediction of these events, if skilful, can therefore provide users with information to mitigate or avoid humanitarian disasters.
Equatorial East Africa experiences two rainfall seasons per year, commonly termed the long rains, occurring from March to May (MAM), and the short rains, occurring from October to December (OND). The long rains have higher total rainfall (Camberlin and Wairoto 1997), and are more reliable, and so coincide with the main growing season (Camberlin and Philippon 2002), whilst the short rains have a much larger interannual variability (Hastenrath et al. 1993; Nicholson 1996). The two rainfall seasons lie within the seasonal reversals of the Somali Jet (Okoola 1999), are observed to be dynamically different (Camberlin and Wairoto 1997), and are classically attributed to the motion of the Intertropical Convergence Zone (e.g. Okoola 1998; Mutai and Ward 2000).
The correlation between the major modes of sea surface temperature (SST) variability and East African rainfall is different in the two rainfall seasons, and as such, the predictability of rainfall is different in the long and short rains (Camberlin and Philippon 2002). The short rains have been linked to variability within the Pacific Ocean, with Rodhe and Virji (1976) observing similar periodicities in East African rainfall variability to those observed for El Niño-Southern Oscillation (ENSO). Many studies since (e.g. Nicholson and Entekhabi 1986; Ogallo 1988; Nicholson 1996; Nicholson and Kim 1997; Indeje et al. 2000), have investigated the role and mechanism of ENSO in influencing East African rainfall, through its effect on the Walker Circulation. More recently, a mode of variability within the Indian Ocean, termed the Indian Ocean Dipole (IOD), has been linked to East African rainfall variability (Saji et al. 1999; Webster et al. 1999; Black et al. 2003; Marchant et al. 2007; Ummenhofer et al. 2009). The positive phase of the IOD is often found to occur simultaneously with El Niño, and as such, several authors have investigated the dependence of this mode on El Niño. The general consensus is that whilst El Niño modulates the IOD and is favourable for the evolution of an IOD event (Black et al. 2003), the IOD is an independent mode of variability from ENSO (Saji and Yamagata 2003; Yamagata et al. 2004; Behera et al. 2005; Bahaga et al. 2015). There are years where the IOD occurs under neutral ENSO conditions, such as in 1961 when a strong positive IOD event took place in absence of anomalies in the Pacific Ocean, causing heavy rains in East Africa (Saji et al. 1999).
A major source of moisture variability for East African rainfall during the short rains originates from the flow over the Indian Ocean (Hastenrath et al. 2011). These zonal winds are described as being part of a Walker circulation cell (Hastenrath et al. 1993; Hastenrath 2000). Areas of ascent and descent lie over Indonesia and East Africa respectively, with a mean state of near-surface westerlies and upper level easterlies over the Indian Ocean. Years with near-surface easterly anomalies coincide with upper level westerly anomalies, increased ascent over East Africa and higher rainfall (Hastenrath et al. 1993; Yamagata et al. 2004; Hastenrath 2007). These anomalies are driven by a positive IOD, which drives high near-surface pressure in the eastern Indian Ocean and low pressure in the west.
Meanwhile, predictability during the long rains is less well understood (Camberlin and Philippon 2002), with several studies demonstrating that the season is not strongly constrained by SST variability (e.g. Ogallo 1988; Liebmann et al. 2014). Nicholson (2014) suggested that this is likely to be because El Niño is in transition during this time of year, a phenomenon referred to as the spring predictability barrier (Torrence and Webster 1998). Several authors have suggested that atmospheric phenomena could control the interannual variability in this season (Philippon et al. 2002; Nicholson 2014, 2015), with Pohl and Camberlin (2006a, b) showing that the Madden-Julian Oscillation (MJO; Madden and Julian 1971, 1972) plays an important role, as well as Indeje and Semazzi (2000) identifying a possible contribution from the Quasi-Biennial Oscillation (QBO; Ebdon 1960; Reed et al. 1961), although the underlying mechanism is not well described.
Real time forecasts of seasonal rainfall in East Africa have been made for several decades, with reasonable success over the short rains, initially based upon statistical methods linking SST variability and rainfall (e.g. Farmer 1988; Mutai et al. 1998). More recently, statistical forecasts of the long rains have also been produced. Nicholson (2014, 2015) used several variables including zonal and meridional wind fields at several pressure levels, as well as sea level pressure (SLP) values, to create models with strong correlations (up to 0.76) for February predictors, and also noted that using atmospheric fields improved statistical models of the short rains. Vellinga and Milton (2018) meanwhile created a multiple linear regression model for the long rains (defined in this study as March to April) using February to March MJO amplitude, QBO from September to November of the previous year, and an area of Indian Ocean SSTs close to the coast of Somalia in the Arabian Sea, finding a correlation with the first principal component of the long rains of 0.77, with the largest contribution generally coming from the MJO amplitude.
In recent years, dynamical models have advanced greatly, and have become increasingly used to produce seasonal forecasts. Batté and Déqué (2011) evaluated the ENSEMBLES project multi-model ensemble of seasonal forecasts over Africa, finding mixed results over East Africa, with the model performing better during the short rains than the long rains. Bahaga et al. (2016) also evaluated a multi-model ensemble with models sourced from North America and Asia over the short rains at 1 month lead. Models that could better forecast the Indian Ocean Dipole were found to have better skill, with the multi-model ensemble achieving a correlation of 0.44 between observed and forecast rainfall, increasing to 0.67 when using only the models that had significant skill when evaluated individually. Although Nicholson (2017) noted that statistical forecasts generally outperform dynamical forecasts in this region, the latter are constantly improving, with ever increasing resolution, and improved representation of physical processes. The skill of statistical models in producing real time forecasts is also often overestimated due to the method of their construction, with common mistakes being overfitting the model, and using too many predictors or unphysical predictors. They also often fail to consider the nonstationary relationship between rainfall and the predictors. Such nonstationary relationships of teleconnections to East African rainfall in particular have been highlighted by Clark et al. (2003), Bahaga et al. (2019). To best meet user needs, a combination of statistical and dynamical methods is often most appropriate (Doblas-Reyes et al. 2013).
Supported by the World Meteorological Organisation (WMO), consensus seasonal forecasts are produced by Regional Climate Outlook Forums (RCOFs) for many locations around the world (Ogallo et al. 2008). The Greater Horn of Africa Climate Outlook Forum (GHACOF), organised by the Intergovernmental Authority on Development (IGAD) Climate Prediction and Applications Centre (ICPAC), has been issuing seasonal consensus forecasts for East Africa since 1998. GHACOFs are held three times per year, in the lead up to the long and short rains, and the summer rainfall season. For the long rains, GHACOFs are typically held in mid February (lead time less than 1 month), whilst for the short rains, they are typically held late in August (lead time greater than 1 month). For the summer rainfall season, the GHACOF is typically held in the second half of May. The WMO has also fostered coordination among centres running operational dynamical seasonal forecast systems, so-called Global Producing Centres for Long-Range Forecasts (GPCs), with a specific objective to increase access and use of the model outputs in regional forecasting activities (Graham et al. 2011). Details of the GHACOF process will be presented in Sect. 2.3.
As well as producing the forecasts, RCOFs have been praised as an excellent opportunity for networking and information sharing between nations within the region, and within the different stakeholder groups (Ogallo et al. 2008; Mwangi et al. 2014). Success stories of GHACOF forecasts having positive impact on the region have been recorded, such as a bumper harvest in 2009, where, based upon information from the GHACOF forecast, Kenya Red Cross distributed extra seeds to farmers across Kenya, leading to enhanced stores of grain (Graham et al. 2012), and in 2002, where forecasts of below normal rainfall in Ethiopia were acted upon to relieve food insecurity (Patt et al. 2007; Hellmuth et al. 2007).
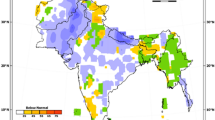
Example GHACOF consensus seasonal forecast for rainfall for OND 2015. The different coloured regions represent regions with different forecast probabilities. The column of three numbers in each region gives the probability of the total rainfall amount for the season being within the upper, middle, and lower tercile with respect to climatology. Colours indicate regions where the issued forecast is the same. As described in the GHACOF statement: grey indicates the region is usually dry during this season, yellow indicates regions likely to receive near normal to below normal rainfall, green indicates regions likely to receive above normal to near normal rainfall, blue indicates regions likely to receive near normal to above normal rainfall
An evaluation of the GHACOF consensus forecasts was performed by Mason and Chidzambwa (2008) for 10 years of forecasts, as part of an RCOF review by the WMO. The forecasts were found to have positive skill but observed some notable biases that were also common to the West Africa and southern Africa RCOFS. In particular, forecast probabilities for the near average category were found to be systematically too high, indicating a tendency to “hedge” to average conditions. Current assessment of GHACOF includes an evaluation of each individual forecast’s performance using a form of hit score (http://rcc.icpac.net/index.php/long-range-forecast/verification-products), and an analysis of the performance of the previous forecast at the following GHACOF event.
Comparisons between consensus and dynamical forecasts are few and far between. Mwangi et al. (2014) investigated whether European Centre for Medium-Range Weather Forecasts (ECMWF) seasonal forecasting system product 4 (SYS-4) can provide additional information, however, no statistical side-by-side comparison has been produced. Additionally, biases within dynamical models are well known, and regularly documented, such as in the Coupled Model Intercomparison Project Phase 5 (CMIP5; Taylor et al. 2012) and Phase 3 (CMIP3; Meehl et al. 2007) models (Yang et al. 2015; Li and Xie 2014; Richter et al. 2016), however, their origins, and their effects on the models ability to produce skilful forecasts is rarely considered. In operational models, mean state biases are linearly removed from the forecast models using hindcasts (Troccoli 2010). A recent study by Hirons and Turner (2018) demonstrated that biases in the CMIP5 models’ mean states can drastically influence their ability to correctly represent the atmospheric response to anomalies from the mean state, whilst a study by Delsole and Shukla (2010) suggested that models whose mean state are most similar to the observations have a tendency to demonstrate higher skill.
As part of its GPC output the UK Met Office issues monthly-updating seasonal forecasts with global coverage and with a focus on RCOF regions including the Greater Horn of Africa using the dynamical forecast system: Global Seasonal Forecasting System Version 5 (GloSea5; MacLachlan et al. 2015). Skill maps to assist in use of the forecast are also published (https://www.metoffice.gov.uk/research/climate/seasonal-to-decadal/gpc-outlooks). In this paper a detailed assessment of the ability of GloSea in predicting the rainfall seasons over East Africa is presented and for the first time, a quantitative comparison of skill between forecasts from a dynamical model and the GHACOF consensus forecasts is made. This analysis goes beyond that of Mason and Chidzambwa (2008), by using a larger period of assessment, and considering the impact of the skill conditional on a remote driver of rainfall. A secondary objective is to investigate the sources of rainfall biases within GloSea, to understand whether these biases could have a negative effect on the model’s prediction skill.
The structure of the rest of the paper will be as follows: Sect. 2 will introduce the data used for this study, and analysis methodologies. Section 3.1 will evaluate the climatology and interannual variability of GloSea. A statistical comparison of the forecast skill of GloSea and GHACOF forecasts will be presented in Sect. 3.2. Section 3.3 will consider the drivers of variability in the short rains, and their effects on skill within both GloSea and GHACOF, whilst Sect. 3.4 will discuss and investigate the origin of biases of rainfall within the short rains in GloSea. Section 4 summarises the key findings.
2 Data and methodology
2.1 Verification data
The observational rainfall data used in this study is Global Precipitation Climatology Project (GPCP) version 2.3 (Adler et al. 2003), a monthly rainfall dataset from 1979 to present, that combines observations from rain gauges and several satellite datasets. This is gridded onto a \(2.5^{\circ } \times 2.5^{\circ }\) resolution grid. This commonly used dataset covers the study period and region with both land and ocean rainfall estimates.
Sea surface temperature (SST) observations are obtained from the Hadley Centre Sea Ice and Sea Surface Temperature (HadISST) dataset (Rayner et al. 2003). HadISST provides monthly mean data at \(1^{\circ } \times 1^{\circ }\) resolution. For comparison with wind climatologies, the European Centre for Medium-Range Weather Forecasts (ECMWF), interim reanalysis (ERA-Interim; Dee et al. 2011) is used. Mean sea level pressure data use the National Centers for Environmental Prediction-National Center for Atmospheric Research (NCEP-NCAR) reanalysis (Kalnay et al. 1996).
2.2 Seasonal forecast model
The forecast system used in this study is the UK Met Office Global Seasonal Forecast System 5 (GloSea5; MacLachlan et al. 2015). The core of GloSea5 is the Hadley Centre Global Environmental Model version 3 (HadGEM3; Hewitt et al. 2011), with atmosphere resolution \(0.833^{\circ } \times 0.556^{\circ }\), with 85 atmospheric levels. The ocean resolution is \(0.25^{\circ } \times 0.25^{\circ }\). The higher ocean resolution improves predictions of sea surface temperature anomalies in the Tropical Pacific, as tropical instability waves can be better resolved, and improves mid-latitude ocean biases (Scaife et al. 2011). The seasonal forecast model runs for 210 days from initialisation. An operational hindcast is produced in parallel and is used to bias correct the forecast. Further details of the GloSea5 system and the previous version (GloSea4) are discussed in MacLachlan et al. (2015) and Arribas et al. (2011) respectively.
This study makes use of operational hindcasts produced in parallel to the forecast, covering the period 1993–2015. Hindcasts are run 4 times per month (1st, 9th, 17th, 25th of each month) with three ensemble members initialised per start date. Members initialised on the same date differ by stochastic physics (Bowler et al. 2009). Three months preceding each rainfall season are used: December, January, February for the long rains, and July, August, September for the short rains, giving a total of 36 ensemble members available for each season. When gridpoint to gridpoint comparison with observational data is needed, GloSea is interpolated onto a \(2.5^{\circ } \times 2.5^{\circ }\) resolution grid. The word forecast will be used from here on to refer to the GloSea hindcasts in the evaluation. This is because the evaluation treats the hindcasts as forecasts, and provides consistency when referring to both GloSea and GHACOF.
The full 36 members are used only in results investigating effects of ensemble size and lead time on model behaviour. For results investigating the forecast skill of the system, and in comparison with the GHACOF forecasts, a smaller ensemble is used to represent a forecast initialised with 1 month lead time. To create this 1 month lead forecast, three start dates centred around the first of the month prior to the start of the season are used (25th January, 1st February, 9th February for the long rains, and 25th August, 1st September, 9th September for the short rains). As 3 ensemble members are initialised per start date this produces an ensemble of 9 members. The use of members from three different dates is to create a larger ensemble, representing the skill of the central date, as there is little difference in skill between hindcasts from neighbouring weeks, and any advantage gained from the shorter lead time members will be balanced out by the longer lead time members.
2.3 GHACOF forecasts and the GHACOF process
Currently, the GHACOF process is split into two parts: a pre-COF capacity building workshop with the purpose of both producing the consensus forecast and giving training to forecasters from the East Africa member states; and the GHACOF itself, where the forecast for the season is presented to the media and representatives from climate sensitive sectors such as agriculture, energy, water resources, and health, and gives an opportunity for representatives of these sectors to interact with forecasters from East Africa as well as climate experts from around the world.
To produce the GHACOF forecast, predictions from many sources are used. ICPAC produce a seasonal forecast using the weather and research forecast (WRF; Skamarock et al. 2008) model over the Greater Horn of Africa (GHA) region, covering 11 countries. The model is driven by the NCEP Climate Forecast System version 2 (CFSv2; Saha et al. 2014). This model has an horizontal resolution of 30km, with an ensemble of up to 15 members, many of which are initialized from different dates and, more recently, some members use different convective parameterization schemes for the same initial and boundary conditions. The model domain covers all of Africa and the adjoining water bodies, which incorporate the large-scale systems that drive the weather and climate of the region. In addition to rainfall and temperature, the dynamical forecast diagnostics available to the forecasters include the onset of the rainfall season, its cessation, intervening dry and wet spells, and duration of the season, for the entire GHA region.
Predictions from global dynamical seasonal forecast models from the North American Multi Model Ensemble (NMME; Kirtman et al. 2014) are considered, as well as dynamical forecasts from the UK Met Office, Metéo-France and ECMWF. These are looked at both in their raw form, with simple mean bias correction, linear regression, and also as calibrated forecasts using the Climate Predictability Tool (CPT; Mason and Tippett 2016). A statistical model approach is also used, using the Geospatial Climate Outlook Forecasting Tool (GeoCOF; Magadzire et al. 2016) and CPT to produce multiple linear regression forecasts using predictors such as observed or GCM predicted SSTs and wind fields. Each country uses all of these data sources, as well as their own knowledge of their country’s climate, to produce a subjective forecast for their country, dividing it into zones where the forecast falls into the same probability categories. ICPAC then collate the country level forecasts together onto a map. At this point, inconsistencies at country borders are considered, with forecasters from each country giving their justification for the forecast category they have used, to come to an agreement on how to solve these inconsistencies. The forecast is presented on a map of the region (Fig. 1), displaying the probability of the seasonal rainfall tercile categories, above normal (upper tercile category), near normal (centre tercile category), and below normal (lower tercile category), in zones delineated by regions where the forecasts were the same.
2.4 Gridding of GHACOF forecasts
The rainfall outlooks produced by the GHACOF were sourced from ICPAC (http://geoportal.icpac.net/), in the form of digital shapefiles containing the different forecast probability regions for each season, starting with the first GHACOF in 1998. These forecasts were then gridded using rasterization into a \(2.5^{\circ } \times 2.5^{\circ }\) grid matching the GPCP verification data. In this way, the GHACOF forecasts can be evaluated in the same manner as a probabilistic dynamical model forecast, against a gridded comparison dataset. For direct comparison between GloSea and GHACOF the overlapping 18 year period of 1998 to 2015 is used. Regions where a climatological forecast was given due to the region being dry for that particular season were removed from the evaluation to avoid evaluating a forecast that by definition has zero skill in many of the metrics used.
2.5 Limitations of the probabilistic evaluation method
In converting the GHACOF consensus forecast into a gridded probabilistic forecast of the same format as a dynamical model forecast, and making comparison to a dynamical model, some considerations need to be made. Firstly, the GHACOF consensus forecasts, although issued in a probabilistic format, are not true probabilistic forecasts due to the subjectivity that is applied throughout their production meaning the probabilities given may not necessarily be the true probability. However, for the purposes of this study these numbers will be assumed to represent the true probability.
Another limitation is due to the resolution of the observation data to be used. Although \(2.5^{\circ } \times 2.5^{\circ }\) observation data is the most commonly used for verification of seasonal forecasts (and hence why it is used in this study) this relatively low resolution can cause problems when converting the hand drawn lines of the consensus forecast into a grid, as several grid squares are likely to cover regions split between two or even more different forecast zones, and are simply treated as the zone which has the greatest area inside the grid square. This is not necessarily representative of the forecast issued for that location, however, the lines drawn within the forecast are themselves subjective.
Finally, there are limitations related to the timing of the forecasts. These forecasts are being treated as 1 month lead time forecasts, this is to represent the time when the forecast becomes available. Whilst this is a fair comparison for the long rains, which is often released at a less than 1 month lead time (ie later than 1st February) and utilises 1 month lead dynamical model predictions, this is less favourable for the short rains forecast, which is released in late August (compared to 1st September for the 1 month lead forecast of the dynamical model). Although the availability of these forecasts is therefore often only a few days apart, the GHACOF process for the short rains utilises dynamical forecasts from August, or 2 month lead time. Consideration should also be given to the fact that older GHACOF forecasts of the short rains were issued for September to December rather than October to December, and that when issuing probabilities based on terciles, the terciles are based on the climatological normal period at the time of issue (currently 1981–2010), rather than the period used here (1998–2015: the period over which the analysis is performed).
In order to address these limitations, it must be stated that the presented analysis only represents an estimate of the true skill of the consensus forecasts. Similarly the analysis of the dynamical forecasts are only an estimate of the true forecast skill due to the differing sizes of ensembles and different availability of initialisation data between forecasts and hindcasts, and as such, statistical significance tests have not been applied to any identified differences in skill between the two forecasts. Finally, there is a level of uncertainty within the observed data used that must be taken into consideration when performing any comparison between models and observations.
Despite these limitations, the comparison between the two forecasts is an important aspect of this study, as it provides information of the ability the GHACOF forecast with respect to state of the art models, which can be used to judge the GHACOF forecasts against the predictability of the rainfall seasons that the forecasts are being issued for.
2.6 Statistical techniques
To construct the relative operating characteristic (ROC) curve (Mason 1982), thresholds of predicted probabilities for each tercile category (above, near, and below average) were selected at every 10% for GloSea due to ensemble size, and every 5% for GHACOF chosen due to the practice of issuing forecasts with probabilities rounded to the nearest 5% recommended by Mason (2013). For each threshold, if the forecast probability of a category is greater than the threshold value, it is classed as a forecast event, otherwise it is classed as a forecast non-event. The observation matching the forecast is then considered, to determine which category occurred. This produces for each threshold value a \(2 \times 2\) contingency table, whereby a forecast event that occurred in observations is a hit, a forecast non-event where the event subsequently occurred in observations is a miss, a forecast event that did not occur in the observations is a false alarm, and a forecast non-event that did not occur in the observations is a correct negative. For each contingency table the hit rate (HR), defined as \(\textit{hits/(hits} + \textit{misses)}\) and false alarm rate (FAR), defined as \(\textit{false alarms/ (false alarms} + \textit{correct negatives)}\) can then be calculated. These values are plotted with hit rate on the y-axis, and false alarm rate on the x-axis, for each threshold value. The curve passing through the points is referred to as the ROC curve, and the area under the ROC curve is the ROC score, which can be any value between 0 and 1. A line of gradient 1 passing through the origin defines the line of no skill compared to a random forecast with a ROC score of 0.5. ROC scores greater than 0.5 are therefore considered to have positive predictive skill with respect to a random forecast. Threshold values of 0% (the event is always forecast) and greater than 100% (the event is never forecast) are used to fix the curves to (1,1) and (0,0), as these threshold values will always produce hit rates of 1 and 0, and false alarm rates of 1 and 0, respectively, regardless of the forecast being evaluated.
To construct the reliability diagram (Hartmann et al. 2002), forecasts are split into bins dependent on the forecast probability of an event. For each bin, the forecasts are matched up to their corresponding observations, and the observed frequency of the event occurring is calculated for each bin. The forecast probability is then plotted against the observed frequency for each bin. A perfectly reliable forecast would have a forecast probability equal to the observed frequency in all bins, leading to a diagonal line of gradient 1, shown on the diagrams. Horizontal and vertical lines are plotted through the climatological frequency of the event (in the case of terciles, 1/3). The horizontal line corresponds to no resolution (ie the outcome is the same regardless of what was forecast), whilst the vertical line is a forecast of climatology. Another line is added bisecting the diagonal and no resolution lines, marking the line of no skill. Forecast points that lie in the region between this line and the vertical line contribute positively to the Brier skill score of the forecast.
When analysing reliability diagrams, several terms are regularly used, with their definitions as follows: over/under-confidence, meaning the line has a gradient less/ greater than one, and over/under-forecasting, meaning that the line lies mostly below/ above the diagonal line, as defined in Mason (2013).
The Heidke Skill Score (HSS; Heidke 1926) is computed using the results from an \(n \times n\) contingency table. HSS is defined as:
where \(p_{ij}\) is the probability of the i’th row and j’th column of the contingency table. This can be rewritten as:
where PC is the proportion correct, or the sum of the values on the diagonal of the contingency table, and E is the expected proportion correct for a random forecast, found by taking the sum of the probability of a forecast of event i multiplied by the probability of observing event i, for each i. HSS is a standard skill score metric, with a minimum of −1, and a maximum of 1, with a score of 0 meaning the forecast is no better than a random chance forecast.
For further information on ROC curves, reliability diagrams, and skill scores or metrics used in this study, the reader is referred to Wilks (2006).
2.7 Time series indices
For time series of area averaged rainfall over East Africa, the land area within the region (\(12^{\circ }\hbox {N--}10^{\circ }\hbox {S}\), \(30^{\circ }\hbox {E--}55^{\circ }\hbox {E}\)) is used, and is also averaged over the 3 months of March, April, and May (MAM) referred to as the East African long rains, and the 3 months of October, November, and December (OND) for the East African short rains. To represent the state of ENSO, the Niño 3.4 index is used, with its usual definition of the average SST anomaly over the region (\(5^{\circ }\hbox {N--}5^{\circ }\hbox {S}\), \(170^{\circ }\hbox {W--}120^{\circ }\hbox {W}\); Barnston et al. 1997). In particular, the time averaged Niño 3.4 index is used, with the anomaly being the average SST anomaly over OND with respect to the 1993-2015 climatological SST average over OND within this region. Similarly, two indices within the Indian Ocean are used. The Western Tropical Indian Ocean (WTIO) is the average SST anomaly over the region (\(10^{\circ }\hbox {N--}10^{\circ }\hbox {S}\), \(50^{\circ }\hbox {E--}70^{\circ }\hbox {E}\)) and the South Eastern Tropical Indian Ocean (SETIO) is the average SST anomaly over the region (\(0^{\circ }\hbox {N--}10^{\circ }\hbox {S}\), \(90^{\circ }\hbox {E--}110^{\circ }\hbox {E}\)), as defined by Saji et al. (1999), and calculated in the same manner as the Niño 3.4 index. Finally the Indian Ocean Dipole (IOD) index is calculated as the difference between the WTIO and SETIO indices, again as defined by Saji et al. (1999).
3 Results
3.1 East African climatology and interannual variability in GloSea
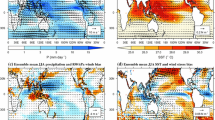
East Africa rainfall (colours) and 850 hPa wind (vectors) climatology during the short rains for an ensemble mean of 36 members for GloSea (left), GPCP rainfall and ERA-Interim winds (second column), GloSea minus GPCP/ ERA-Interim (third column), and violin plots of rainfall distributions of GloSea and GPCP, with white dots representing the mean, the thick black line the interquartile range, and the shaded areas showing the distribution, for each land gridpoint within the region (\(12^{\circ }\hbox {N--}10^{\circ }\hbox {S}\), \(30^{\circ }\hbox {E--}55^{\circ }\hbox {E}\)), for each year (right). The rows show the climatologies for OND (a–d), then October (e–h), November (i–l), December (m–p), separately
As in Fig. 2, but for the long rains (MAM)
In this section, the performance of GloSea in forecasting the climatology and interannual variability is analysed over East Africa in both rainfall seasons. The rainfall and 850 hPa wind climatology of the short rains for GloSea and observations, with relative biases, is shown in Fig. 2. Large scale patterns in both rainfall and wind vectors are captured well by GloSea, however the dominant feature is a clear wet bias, approximately 40% over land areas over OND, with an approximately 35% bias over the land areas in the region (\(12^{\circ }\hbox {N--}10^{\circ }\hbox {S}\), \(30^{\circ }\hbox {E--}55^{\circ }\hbox {E}\)) to be used in later analysis, with greatest bias over the regions with greatest rainfall. This is followed by a dry bias during the dry season, evident in December when a spatially coherent dry bias is present north of the equator, but a wet bias remains to the south. Consistent with this, the change in wind direction in GloSea from a southerly to northerly flow appears to occur too early in the season, suggesting a possible mistiming in the progression of the ITCZ. The rainfall biases based on the distributions coincidingly show a larger bias in October and November than December.
In Fig. 3, the climatology for the long rains is shown. Large scale patterns are again captured well by GloSea, however in this season an overall dry bias over land is present. The reversal of the northerly flow appears to occur too late in the season, and whilst a dry bias is present over the land points in the region (\(12^{\circ }\hbox {N--}10^{\circ }\hbox {S}\), \(30^{\circ }\hbox {E--}55^{\circ }\hbox {E}\)) in March, it has changed to a slight wet bias by May. The net effect is that the rainfall bias in this season is of relatively small magnitude, as seen in Fig. 3d. A large wet bias persists over the Indian Ocean, although moves northwards throughout the season, following the peak in rainfall.
The wet bias in the short rains, coupled with a minor dry bias in the long rains leads to a pattern where the short rains in the model provide greater rainfall than the long rains. This same error in the annual cycle of rainfall over East Africa is present in other models, as has been documented in previous studies of the CMIP3 (Anyah and Qiu 2012) and CMIP5 (Yang et al. 2015) climate models. Wet biases are found in most tropical regions in many seasonal forecast systems (Scaife et al. 2018).
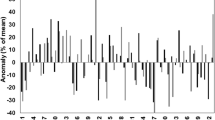
Time series of rainfall anomaly from climatology for the short rains (a) and long rains (b), for 1 month lead time forecasts from GloSea ensemble mean (solid line), ensemble members (dots, coloured by initialisation date), and GPCP (dashed line). Correlation coefficient between ensemble mean and GPCP shown at bottom of each panel
The key feature of interest within a seasonal rainfall forecast is the prediction of a rainfall anomaly over the season in comparison to climatology. Figure 4 shows the predicted rainfall anomaly for each year of the forecast period for both GloSea and observations for both rainfall seasons. During the short rains, a correlation skill of 0.69 is achieved. This result is insensitive to the exact definition of the region. The model predicts the sign of many of the extreme years correctly such as 1997 and 2006, however ensemble members do not reach the extreme values seen in observations. The ensemble mean has a standard deviation of \(0.40\,\hbox {mm day}^{-1}\), and the observations have a standard deviation of \(0.85\,\hbox {mm day}^{-1}\). Some lack of variance with respect to the observations is expected, as the ensemble mean represents the predictable part of the variance (Scaife and Smith 2018). However, the mean ensemble member standard deviation over all members and years is \(0.55\,\hbox {mm day}^{-1}\), also lower than the observations. Ensemble members should have approximately the same variance on average as the observations, to represent a possible realisation of the observations. This lack of variance explains why the ensemble members struggle to forecast the extremity of the most extreme wet or dry years (e.g. 1997, 1998, 2005, 2006). In a well calibrated forecast where each ensemble member represents a possible realization, the observations would be expected to appear as one of the extreme outer realisations in 2 out of 10 years (if treated as a 10th ensemble member then it would be expected to be the most wet 1 in 10 times, or most dry 1 in 10 times), so somewhere between 4 and 5 occurrences would be expected to happen over 23 years. This is considerably less than the 10 occurrences over the 23 years found here.
During the long rains, a correlation of 0.07 is achieved, this is insignificant at the 5% level and demonstrates that the model is unable to predict the long rains interannual variability over land, consistent with previous results based on other models (e.g. Batté and Déqué 2011; Shukla et al. 2016). There is also an apparent failure of the model in capturing anomalies in the most extreme wet (e.g. 1996, 2013) and dry (e.g. 2000, 2009) years in this season. In all years the spread of the ensemble members exceeds the spread of the observations.
Correlation skill of GloSea forecasts as a function of ensemble size for the short rains (a), and long rains (b), for randomised ensembles using all 36 members available (blue crosses) and each initialisation month consisting of 12 members (coloured crosses). Dashed lines show curve fitted to crosses of corresponding colour. Dotted line in a shows correlation of GloSea ensemble mean rainfall against a single removed ensemble member, demonstrating internal predictability
A common question within dynamical models is whether an increase in ensemble size could further improve the forecast. To examine this, the correlation coefficient of the ensemble mean with the observations as a function of ensemble size is shown in Fig. 5. To create this, for each ensemble size, ensemble members are randomly sampled to build an ensemble of the correct size, then correlated with the observations. This is repeated 10,000 times, and the mean result is taken for each ensemble size. In the short rains the curves using both all 36 members available and the 12 member sub-samples demonstrate a curve approaching an asymptote, with the curves flattening between 10 and 15 ensemble members. The small increase from 12 to 36 members indicates that a further increase in ensemble size would provide limited additional benefit, given that the current operational forecasts use an ensemble size of 42. Also demonstrated here is a monotonic increase in skill with decreasing lead time. As well as studying potential improvements from increasing ensemble size, the potential skill; the ability of the model to predict itself (as in Kumar et al. 2014; Scaife et al. 2014), is also investigated. This is achieved by replacing the observations with a single member of the ensemble, and calculating the correlation between the ensemble mean of the rest of ensemble and the single member. This is repeated for each member in the ensemble, and the mean score is taken. It is also repeated for each ensemble size, leading to the dotted line in Fig. 5. The average correlation between a single member and the ensemble is shown to be consistently lower than the correlation between the ensemble and the observations, suggesting the model can better predict the observations than itself. This phenomenon has also been found elsewhere by Eade et al. (2014), and by Scaife and Smith (2018) who note its prevalence in the extratropical Atlantic, however this is one of few tropical examples of this behaviour as models generally overestimate the predictability of tropical rainfall.
The long rains similarly demonstrate the pattern that an increase in ensemble size would have limited benefits, although for the 36 member line there is an increase in skill with ensemble size. The asymptote value for an infinitely large ensemble in this case is 0.26. In the long rains, the correlation does not increase monotonically with decreasing lead time, as was observed in the short rains. This is likely due to the limited skill at any lead time.
3.2 Forecast skill in GloSea and GHACOF
Tercile category ROC curves (a, b) and reliability diagrams (c, d) for GloSea (left) and GHACOF (right), for the short rains. Upper tercile category shown in blue, lower tercile category in red, centre tercile category in black. ROC scores inset onto curves, labelled points on ROC curves correspond to threshold value used for each point. Dashed line in a, b refers to line of no ROC skill. Dashed line in c, d refers to line of zero Brier skill, horizontal dotted line shows line of no resolution, vertical dotted line represents climatological forecast. Points lying between climatological forecast and dashed line contribute positively to Brier skill score. Size of circles demonstrate relative frequency of occurrence of the probability being forecast
In this section, a comparison is made between GloSea and GHACOF consensus forecasts. Both are regridded to \(2.5^{\circ } \times 2.5^{\circ }\), and the period 1998–2015 is used. A discussion on this process and the limitations of the comparisons made in this section was given in Sects. 2.4 and 2.5. Figure 6 shows ROC curves and reliability diagrams for both forecasts during the short rains. Both forecasts demonstrate skill for the outer categories, with the above average rainfall category being highest. GloSea demonstrates some level of skill in predicting the middle category although lower than in the outer categories, as is often the case for categorical forecasts (van den Dool and Toth 1991), and generally achieves higher scores in all categories than GHACOF at one month lead. ROC scores of two month lead forecasts of GloSea were also calculated, finding values of 0.621 and 0.567 in the above and below normal categories respectively, remaining higher than the GHACOF forecast. In the GloSea reliability diagam, there is clear evidence of forecast over-confidence in all three categories: a gradient less than 1. This means that for categories forecast with increased/decreased probability of occurrence with respect to climatology, the increase/decrease in probability is larger in magnitude than is observed. Meanwhile, the GHACOF reliability diagrams appear to show under-confidence in the outer categories, with a gradient greater than one, implying shifts in probability from climatology are on average too small.
As in Fig. 6, but for the long rains
Figure 7 shows the ROC curves and reliability diagrams for the long rains. Both GloSea and GHACOF display little skill during this season for any tercile, although ROC scores are generally greater than 0.5 by a marginal amount. The GloSea reliability diagram displays very little resolution for any category, the observed frequency being approximately the same regardless of the forecast probability. GHACOF appears to show slightly greater reliability for this season. Both of the reliability diagrams for GHACOF demonstrate a lack of forecasts landing within the 30% category. Forecasts of 30% for any category are rarely issued. This is related to the method of construction of the probabilities. In general, 40% is often taken as the starting point for the probability of the near normal category, meaning that a probability of 30% for either outer category would then result in a forecast of equal probability for both outer categories. Situations in which forecasts for both outer categories are given equal probabilities are avoided, as they are seen by users as not being a useful forecast.
In Fig. 8, a spatial map of the ROC score for each category is shown for GloSea and GHACOF for the short rains. In the outer categories there is a coherent region of higher skill over Kenya, coastal Somalia, southeast Ethiopia and northeast Tanzania, as well as over the Indian Ocean. This region is apparent in both GloSea and GHACOF, and in both outer categories. These diagrams show highest skill in the regions where the heaviest rainfall is present. ROC scores for the long rains (Fig. 9) are lower than for the short rains for both GloSea and GHACOF for all categories, and less coherently distributed in GloSea. Kenya however appears to show some evidence of positive skill in the above tercile for GloSea, and both outer categories of GHACOF. The GloSea ROC maps demonstrate that positive skill is achieved over the Indian Ocean off the coast of East Africa in both outer categories.
As in Fig. 8, but for the long rains
Although it is not good practice to interpret the probability forecasts deterministically, it is still a widespread practice (Patt et al. 2007). To explore the performance of the forecasts interpreted in this way, the probabilistic forecasts were converted into deterministic categorical forecasts whereby the forecast is assigned as the category of the highest probability of occurrence. If an outer category and centre category are equal highest (for example a split of 40,40,20 for above, near, below categories respectively), then the higher outer category is assigned. If both outer categories are equal highest then the forecast is not included in this evaluation, this removes climatological forecasts, and bimodal forecasts. Table 1 presents a contingency table evaluation of deterministic forecasts generated in this way for both GloSea and GHACOF, and for both the long and short rains. The most striking difference between the GHACOF and GloSea forecasts are the large number of forecasts in which GHACOF has the highest weighting assigned to the normal category, with 81% of forecasts being made for this category for the long rains, and 71% of forecasts being made for this category in the short rains. This is something common to the West African RCOF (Bliefernicht et al. 2018), and RCOFs elsewhere in Africa (Mason and Chidzambwa 2008). It is clear from the middle row of Table 1 that within GHACOF, as often occurs in categorical forecasts (van den Dool and Toth 1991), there is very low skill in forecasting this category: when the near normal category is forecast, observations are spread approximately equally across the three categories. The number of correct forecasts within this category falls at approximately one third (34% for both MAM and OND). GloSea has similarly equal spread across this category, although has a lower number of forecasts falling into it. Approximately 35% of near normal forecasts are correct for MAM, 40% for OND, and a total of 30% of forecasts are issued into the near normal category for MAM, and 38% for OND. This high level of hedging in GHACOF drastically lowers the hit rates for the outer tercile categories, as seen in Table 2, and thus the usefulness of the forecasts, and was identified by Mason and Chidzambwa (2008) as one of the key issues within RCOF forecasts.
Some favourable conclusions for GHACOF can however be drawn from this table. Table 2 shows that for all categories except for the above normal category in MAM, GHACOF has a higher hit rate than false alarm rate, a signal that there is positive skill coming from these forecasts. By looking at the Heidke Skill Score (HSS) for the forecasts, positive values are achieved in both seasons by both forecasts, however GloSea shows marginally higher scores in each season. It is likely that the GHACOF forecast has lower scores in this measure due to the large number of forecasts that contained highest weighting into the centre category, which could have had higher weighting towards the correct outer category than incorrect, but is instead interpreted as a forecast for the near normal category. It is again clear from Table 2, the difference in skill for forecasting between the two seasons, with higher HSS and generally greater differences between the hit rates and false alarm rates in each category for the short rains than for the long rains.
By considering within GHACOF, the forecasts of the outer categories, it is clear from Table 1 that the forecasts are in fact capable of identifying years in which an above or below average year is most likely, with many more forecasts for the correct outer category than incorrect outer category, with the exception of above normal forecasts of the long rains. These forecasts then have a property which, when considering the relative risks of an incorrect forecast compared to the return for a correct forecast, may be considered highly desirable; a low rate of forecasts with two category errors, much lower than is seen in GloSea.
Combining both GloSea and GHACOF also appears to display some complementary information. Whilst GloSea generally performs better over the previously displayed statistical measures, it appears that GloSea shows a lack of skill in predicting below average rainfall in the long rains, whilst GHACOF performs best in this category, with a higher ROC score (Fig. 7), and positive scores from the contingency table (Table 2), with this skill appearing to originate from over Kenya (Fig. 9). This is possibly due to alternative sources of predictability utilised by the forecasters that are not currently represented in GloSea, but could be related to other factors. For example the higher skill in both forecasts observed over Kenya could be related to higher observed data quality in this region. This could be due to, for example, the less complex orography over the coastal area, as satellite estimates often struggle to estimate correctly rainfall rates over steeper orography (e.g. Cattani et al. 2016; Kimani et al. 2017).
3.3 Drivers of interannual rainfall variability in the short rains
Many previous studies have shown the relationship between the East African short rains and SST anomalies in the equatorial Pacific, and more recently, Indian Ocean, as discussed in Sect. 1, in particular highlighting the importance of the El Niño-Southern Oscillation and Indian Ocean Dipole. For a model of the short rains to be successful it needs to predict correctly both the evolution of these modes of variability in the oceans, and also produce the correct atmospheric response to the predicted SST anomalies. Figure 10 shows the correlations of rainfall over East Africa within each grid point to the Niño 3.4 and IOD indices for GloSea and for observations. The spatial patterns of both indices correlations are well represented by GloSea; the model correctly represents the effect of these modes of variability on the rainfall, however some differences are noted. There is a sharp decrease in correlation running north to south through Kenya in the model in both indices, suggesting a sharp change in rainfall interannual variability here. This is not present in the observations (although some gradient does exist in the IOD map) and hints at a misplaced teleconnection, too far east in the model, as well as some possible incorrect orographic effects taking place in the model, as this north to south decrease runs down the eastern edge of the East African highlands. The region with the highest correlation to IOD in the model coincides with the region of highest skill.
Figure 11 shows the correlation of SST anomalies at each grid point with the East African short rains, in the observations and in GloSea. In both panels the large scale pattern is clear, with the strongest, coherent correlations coming from the Pacific and Indian Oceans, representing the El Niño and IOD modes of variability. The correlations within GloSea are of a smaller magnitude than within the observations, suggesting that the coupling between the ocean and atmosphere may be too weak in the model. The positive correlation in the Pacific Ocean also stretches too far west, as does the negative correlation over the eastern Indian Ocean, matching with the rainfall response to ENSO noted by MacLachlan et al. (2015) within GloSea in December to February.
As in Fig. 8, but for years with a GloSea forecast active Indian Ocean Dipole event. Positive IOD years were identified as 1994, 1997, 2006, 2007, 2011, 2012. Negative IOD years were identified as 1996, 1998, 2001, 2008, 2010
As well as capturing the correct teleconnections, the model also needs to capture the evolution of SSTs to be useful as a forecast model. To examine whether the model captures the evolution of SSTs, SST indices within the Indian and Pacific Oceans over OND were forecast with 1 month lead time. These were then compared with observations, and a 1 month persistence forecast was used as a reference forecast. This was done as high correlation scores are likely to occur even if the model doesn’t correctly model the evolution of the SSTs, due to the slowly evolving nature of SSTs. If the forecast can beat the correlation of the persistence forecast this implies that some useful information can be obtained from the forecast. The persistence forecast uses the average SST anomalies over the entire month of August, whilst the forecast is that which would be used for the 1st September, for a direct comparison. These were then compared with the observed SST anomaly over OND, as shown in Fig. 12. GloSea consistently outperformed the persistence forecast in all indices, with the most promising results being over the western Indian Ocean (WTIO) where GloSea had a correlation of 0.93 with the observations, whilst the persistence forecast had a value 0.71. GloSea also captured well the observed warming trend in the ocean in this region. This improvement over a persistence forecast also meant a notably better forecast IOD than persistence, with a correlation score for GloSea of 0.85, whilst persistence achieved 0.77. The eastern Indian Ocean and Niño 3.4 region both showed marginal improvements in comparison to persistence. Whilst there is already improved prediction compared to persistence at 1 month lead time, at longer lead times, better performance of the dynamical model against persistence is expected for the Niño 3.4 region (Graham et al. 2012). For IOD it is less clear whether this is the case, as Graham et al. (2012) found that the previous version, GloSea4, was outperformed by persistence at forecasting IOD at both short and longer lead times.
A common feature of all the SST indices within GloSea was a variance larger than the observations, as can be seen in Fig. 12. This is in contrast to lower than observed variability in rainfall, and further suggests that the coupling between SSTs and the short rains is too weak. This large variance was particularly noticeable in the SETIO index, where the standard deviation was more than double that of the observed. This region also achieved the lowest correlation score in GloSea (equal with the IOD, which is itself dependent on the SETIO forecast). Difficulty in forecasting SST evolution in this region has been highlighted previously by Lu et al. (2018).
As in Fig. 6, but for years with a GloSea forecast active Indian Ocean Dipole event. Positive IOD years were identified as 1994, 1997, 2006, 2007, 2011, 2012. Negative IOD years were identified as 1996, 1998, 2001, 2008, 2010
As well as correctly predicting rainfall, GloSea has shown that it potentially can hold value over a purely statistical forecast of rainfall by skilful prediction of the evolution of SST anomalies in the Pacific and Indian Ocean. To confirm this, multiple linear regression models were built using indices from the Pacific and Indian Ocean. A regression model was built using observed SST indices over OND to predict OND rainfall within the observations. The regression value achieved by the model utilising IOD and Niño 3.4 was 0.90, and demonstrates the dominance that these two modes of variability have over the region, during this period. Bahaga et al. (2019) demonstrated however that the correlation between these modes can fluctuate on decadal timescales, with the period used here found to have a particularly high correlation.
Building a regression model from the persisted values of IOD and Niño 3.4 achieved a regression value of 0.77. This value is actually larger than the rainfall forecast from GloSea (at 0.69), and although the difference is not significant, demonstrates the strength of a statistical forecast in this region.
Since the persistence model value is lower than the regression model using the observed SSTs, correct predictions of SST evolution may give an improvement on the persistence model. To test this, a regression model was then built using GloSea forecast SST indices of IOD and Niño 3.4 for OND. This model achieved a regression value of 0.80, bettering the persistence forecast, although again the difference is not significant at this short lead time. The fact that the observed SST regression model achieved the same score regardless of whether the Niño 3.4 index was included, whilst in the persistence model it improved the model, leads to the hypothesis that the high correlation observed between El Niño and East African rainfall is primarily through modulation of the Indian Ocean, rather than independent influence, similar to the conclusions of Behera et al. (2005), Bahaga et al. (2015). To examine whether this is the case, the partial correlation of two variables (subscript 1, 2) with the influence of a third variable (subscript 3) removed (Yule 1907; Lawrence 1976), is calculated, defined as:
where \(\rho _{ij}\) refers to the Pearson correlation coefficient of variables i and j. This value runs from − 1 to 1 as in the Pearson correlation coefficient. In particular the partial correlation of East African rainfall with the IOD with the influence of ENSO removed, \(\rho _{ri,n}\), and the partial correlation of East African rainfall with ENSO with the influence of IOD removed, \(\rho _{rn,i}\), are calculated, where the r, n, and i subscripts refer to the time series of East African rainfall, Niño 3.4, and IOD respectively. In the observations, a value of \(\rho _{ri,n}=0.82\) is found, suggesting that when the effect of ENSO is excluded, the IOD still maintains a strong relation to East African rainfall. Meanwhile a value of \(\rho _{rn,i}=0.02\) was found in the observations, suggesting that when the effect of the IOD is excluded, ENSO has very little effect on East African rainfall, supporting the hypothesis above, also suggested by Behera et al. (2005), Bahaga et al. (2015). By performing the same calculations for GloSea’s forecast SST indices against rainfall, we find values of 0.83 and − 0.06 for \(\rho _{ri,n}\) and \(\rho _{rn,i}\) respectively, suggesting GloSea does very well at capturing the relationship between the IOD, ENSO, and East African rainfall. From this, it could be suggested that when an ENSO event is forecast, if anomalies in the Indian Ocean remain small, then a response in East African rainfall should not necessarily be expected.
Given the strength of connection between SST anomalies and the short rains, and the ability of GloSea at predicting SST evolution, it should be expected that during years where an IOD or ENSO event is forecast, the capability of the model should increase (Frías et al. 2010; Pegion and Kumar 2013). To test this, both GloSea, and GHACOF forecasts were re-evaluated conditional on years where an IOD event (defined by an anomaly greater than 0.5\(^{\circ }\)C) is forecast by the model. The model forecast IOD years are used rather than observed to demonstrate the skill based on making decisions using forecast SSTs. Figure 13 shows tercile category ROC maps (as in Fig. 8) for years where GloSea has forecast an IOD event, for both GloSea and GHACOF. In both forecasts the increase in skill is clear, with both having regions along coastal East Africa above 0.8 or 0.9, with this region coinciding well with the regions of highest skill and highest correlation with IOD shown in Figs. 8 and 10. Figure 14 shows the corresponding ROC curves, and reliability diagrams for this set of forecasts. Both GloSea and GHACOF show an increased ROC score, with the above normal category scoring highest in both. GloSea again generally outperforms GHACOF in this score.
The reliability diagram for GloSea demonstrates that during these years the forecast is highly reliable, with the outer categories lying consistently close to the perfect reliability line. Some evidence of under-forecasting is present in the below normal category, with the observed frequency consistently higher than the forecast probability. There is also a hint of under-confidence in the above normal category, with a gradient greater than 1 apparent for this line. During these years the centre tercile category appears to be over-forecast.
The reliability diagram for GHACOF, although noisy, demonstrates the under-confidence of forecasts during these years in the outer terciles, with a gradient greater than one apparent. This is more evident within the above average category. The below average category demonstrates both some under-confidence, and some under-forecasting, below average years have occurred with greater probability than were forecast.
Similar results were found for years with an active ENSO event (not shown), however, in many of the years where IOD is active, ENSO was also found to be active. Years where SST anomalies in both the Niño 3.4 and the IOD index were small were also investigated. GloSea demonstrated positive skill in the outer categories in these neutral years, with a ROC score for the above (below) normal category being 0.61 (0.54). GHACOF meanwhile shows less skill in the years where neutral conditions are forecast, with ROC score for the above (below) normal category being 0.52 (0.48).
3.4 Drivers of GloSea rainfall bias in the short rains
GloSea lead time-bias relations over short rains season forecasts for a rainfall (against GPCP), b SST indices (against HadISST), c sea level pressure (against NCEP-NCAR Reanalysis), d 850 hPa equatorial zonal wind over Indian Ocean (against ERA-Interim Reanalysis). Dots on same day show ensemble members initialised at the same lead time. Vertical dashed lines mark the 1st September, August, July. Proxy IOD shows the index for model minus observations in the mean state. Mean sea level pressure west and east refer to same co-ordinates as west and east poles of IOD, whilst west minus east shows relative pressure gradient compared to observed. Zonal winds averaged over (\(5^{\circ }\hbox {N--}5^{\circ }\hbox {S}\), \(60^{\circ }\hbox {E--}90^{\circ }\hbox {E}\)). Dotted line on bottom panel shows point at which zonal average wind in box is zero
The large wet bias in GloSea over East Africa during the short rains was highlighted in Fig. 2. Whilst it is known that coupled dynamical models regularly have too much rainfall in the tropics (Li and Xie 2014; Scaife et al. 2018), this wet bias is large in size when compared to the rest of the tropics within GloSea. Although it is clear that GloSea achieves high levels of skill despite this bias, understanding the origin of this bias may be important for explaining the lack of variability in the model, and for future improvements to forecasts for this region. To understand this, the bias evolution over time was studied over a stationary period of time (the 3 months of OND) for different forecast lead times. Figure 15a shows the evolution of the rainfall bias over East Africa as a function of lead time. At all lead times there is a wet bias. There is an approximately linear increasing trend in the wet bias as lead time increases; a model drift. To understand what may be causing this, the bias as a function of lead time was plotted for several other fields. Figure 15b shows the bias-lead time relation for the SST indices over the Pacific and Indian Oceans. A cold bias is present in both the Pacific and Indian Ocean; these biases remain approximately constant in the Pacific and western Indian Ocean, however the SETIO index displays a linear decrease in temperature with increasing lead time, this region was also highlighted as the most difficult to forecast in the previous section, as well as having an unrealistically large variance within GloSea [also seen in Lu et al. (2018)]. This increasing cold bias has an impact on the sea level pressure over the eastern Indian Ocean region, seen in Fig. 15c. The bias in pressure over the western Indian Ocean remains approximately constant, whilst the pressure over the eastern Indian Ocean increases with increasing lead time, consistent with the cooler SSTs at longer lead times, generating a west to east pressure gradient.
Figure 15d shows the equatorial zonal wind bias over the Indian Ocean (\(5^{\circ }\hbox {N--}5^{\circ }\hbox {S}\), \(60^{\circ }\hbox {E--}90^{\circ }\hbox {E}\)) as a function of lead time. At all lead times there is an easterly wind bias of these zonal winds. Matching with the pressure biases, the zonal winds become more easterly (more negative in Fig. 15d) with increasing lead times, with the average wind direction within the model switching from the observed westerlies to become easterly between 40 and 50 days lead time. This wind anomaly is likely to draw more moisture toward the African continent from the Indian Ocean, as well as having an effect on the Indian Ocean Walker circulation, reproducing a positive IOD-like response within the mean state. This is likely to reduce the impact of further increases in these winds in providing moisture. Whilst this is not necessarily the case for GloSea, it could explain part of the weakened coupling between the Indian Ocean and the short rains, as well as the lack of variability in rainfall with respect to the observations.
Capturing the direction of these winds is known to be difficult for coupled models, with Hirons and Turner (2018) recently showing that the majority of CMIP5 models incorrectly capture the mean state of these winds, and the models with incorrect easterly zonal winds in the mean state struggle to capture correctly the influence of the IOD on rainfall in the short rains.
4 Conclusions
Skilful seasonal forecasts of rainfall are vitally important for many sectors in East Africa. In this study, the most widely issued operational seasonal forecast within the region, the GHACOF consensus forecast, has been evaluated against observations and compared to the UK Met Office dynamical seasonal forecast system, GloSea. In addition, physical rainfall-producing processes within the dynamical model related to the short rains season were investigated and an analysis of the origin of the model’s regional wet bias was performed.
The ability of Met Office GloSea system operational hindcasts were evaluated on their ability to predict seasonal rainfall anomalies over East Africa at 1 month lead time before the start of the two rainy seasons. GloSea demonstrates an ability to represent the climatology of the rainfall seasons well, but with a large wet bias of approximately 40% during the short rains, and a lack of interannual variability. GloSea performs much better at predicting interannual variability during the short rains than the long rains due to its ability to capture teleconnections between SST anomalies and rainfall in the short rains season, as documented by Batté and Déqué (2011), Shukla et al. (2016), Nicholson (2017). However, GloSea’s short rains forecasts can be outperformed by a statistical forecast using persisted SST anomalies from August. A similar statistical model based on GloSea’s SST forecasts can, however, outperform both GloSea’s own rainfall prediction and the aforementioned statistical forecast using persistence. The ability to better predict rainfall using GloSea’s SST field suggests that further improvements to predictions of the short rains could be made by improving the atmospheric response to the ocean state.
GloSea displayed little ability in forecasting rainfall during the long rains, with a correlation between GloSea and GPCP of 0.07, a result common to previous dynamical seasonal forecast models in this season (e.g. Batté and Déqué 2011; Shukla et al. 2016) with the potential for increases to approximately 0.25 in a larger ensemble than the ensemble of 9 members used. In both seasons it was demonstrated that an increase in ensemble size above the current operational size of 42 members would provide limited benefits, although could offer relatively larger improvements to the long rains than the short rains.
Probabilistic verification was performed on both GloSea and the GHACOF consensus forecasts. Both GloSea and GHACOF displayed positive skill in forecasting outer tercile categories of rainfall over East Africa, and promisingly, both demonstrated similar spatial patterns of skill, with a coherent region of high skill coinciding with the area most highly correlated with Indian Ocean SST anomalies during the short rains. However, in general GHACOF was outperformed by GloSea over the two seasons, with the exception of the below normal category within the long rains. The predictability here could be related to GHACOF utilising information not represented within dynamical models, and demonstrates the value of using both statistical and dynamical modelling techniques (Doblas-Reyes et al. 2013), as is done within the GHACOF forecasts.
Despite the positive skill, GHACOF demonstrated several features that are potentially harmful to the usefulness of the forecast. The stand out error is the tendency to over-forecast the near normal category of rainfall, common to RCOFs in other regions (Mason and Chidzambwa 2008; Bliefernicht et al. 2018). GHACOF regularly issue a probability of over 40% in the near normal category, and this category is issued as the highest probability category at over 70% of the forecast grid points over both seasons. Not only is it demonstrated that forecasting this category is less skilful than forecasting for the outer categories, but this tendency also undermines the use of tercile categories, as, over the period of the forecasts, the three tercile categories have not been forecast to occur equally often. This could confuse interpretation of the forecasts by user groups, who have regularly noted difficulties in understanding probabilistic forecasts. This lack of confidence also lowers the statistical resolution of the forecasts; forecasts predicting the most wet and most dry events often appear remarkably similar, with the probabilities in the outer categories often only shifting by 5 or 10%.
Another common behaviour was the tendency to avoid forecasting 30% probability, this is due to the method with which probabilities are assigned. In general a probability of 40% is used as an initial value for the near normal category, the 30% forecast is then avoided so as to ensure issuing a forecast with different probabilities for above and below normal years. In some cases however, a forecast for 30% may indeed be most appropriate. These tendencies identified within the GHACOF forecast process are performed within a risk averse strategy, and this is reflected in the low number of times where the opposite outer category was forecast as the most probable, to what subsequently occurred. Whilst this strategy of reducing the number of complete misses may be a desirable property in building trust between forecasters and users, it also reduces the utility of the forecast.
A promising result from this study is the contrasting behaviour between the dynamical forecast, which often over-confidently forecasts a wet or dry year, and the comparatively risk averse consensus forecast. A way to reduce the under-confidence issues in the GHACOF forecasts would be to give an increased confidence weighting to the dynamical forecast in scenarios where the dynamical models are known to be skilful. These results demonstrate the benefit of using a consistent comparison method for forecast evaluation, something commonly produced for dynamical forecast verification, but rarely applied elsewhere.
It was shown that in years where a driver such as the IOD is forecast as active, prediction skill of both GloSea and GHACOF is increased, however GHACOF still show evidence of under-confidence within the forecasts. This suggests that in years when a strong driver is forecast, the probabilities of the relevant outer categories of the GHACOF forecast should be more confidently forecast to reflect the increased predictability. This can be aided by the fact that GloSea outperforms persistence SST forecasts even at a 1 month lead time.
The large rainfall bias during the short rains was shown to primarily originate from the evolution of a cold SST anomaly in the eastern Indian Ocean and easterly wind anomalies across the equatorial Indian Ocean, a situation reminiscent of a positive IOD state (Saji et al. 1999). At short lead times, there is little SST bias, however an easterly wind bias forms very quickly, suggesting that the mechanism for the generation of the IOD-like state is caused by the wind bias: an easterly wind bias across the Indian Ocean causes upwelling and cooling of the eastern side of the Indian Ocean basin, reducing SSTs. This causes a higher pressure to form over the eastern IO, generating a west to east pressure gradient, further increasing the easterly wind. This positive Bjerknes feedback (Bjerknes 1969) then causes the increase in bias with increased lead time.
Recent results from Hirons and Turner (2018) demonstrate that CMIP5 models with easterly zonal winds across the Indian Ocean in the mean state fail to capture the observed moisture advection in the short rains linked to Indian Ocean SSTs, and struggle to capture the observed teleconnection patterns. This bias should be further investigated to understand what impact it has on predictions on a seasonal timescale, and whether improvements to the Indian Ocean and the Walker circulation can reduce the rainfall bias and improve predictions of the short rains.
References
Adler RF, Huffman GJ, Chang A, Ferraro R, Xie PP, Janowiak J, Rudolf B, Schneider U, Curtis S, Bolvin D, Gruber A, Susskind J, Arkin P, Nelkin E (2003) The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979-Present). J Hydrometeorol 4(6):1147–1167
Anyah RO, Qiu W (2012) Characteristic 20th and 21st century precipitation and temperature patterns and changes over the Greater Horn of Africa. Int J Climatol 32(3):347–363. https://doi.org/10.1002/joc.2270
Arribas A, Glover M, Maidens A, Peterson K, Gordon M, MacLachlan C, Graham R, Fereday D, Camp J, Scaife AA, Xavier P, McLean P, Colman A, Cusack S (2011) The GloSea4 ensemble prediction system for seasonal forecasting. Mon Weather Rev 139(6):1891–1910. https://doi.org/10.1175/2010MWR3615.1
Bahaga TK, Mengistu Tsidu G, Kucharski F, Diro GT (2015) Potential predictability of the sea-surface temperature forced equatorial east african short rains interannual variability in the 20th century. Quart J R Meteorol Soc 141(686):16–26. https://doi.org/10.1002/qj.2338
Bahaga TK, Kucharski F, Tsidu GM, Yang H (2016) Assessment of prediction and predictability of short rains over equatorial East Africa using a multi-model ensemble. Theor Appl Climatol 123(3–4):637–649. https://doi.org/10.1007/s00704-014-1370-1
Bahaga TK, Fink AH, Knippertz P (2019) Revisiting interannual to decadal teleconnections influencing seasonal rainfall in the Greater Horn of Africa during the 20th century. Int J Climatol 39(5):2765–2785. https://doi.org/10.1002/joc.5986
Barnston AG, Chelliah M, Goldenberg SB (1997) Documentation of a highly ENSO-related SST region in the equatorial pacific: research note. Atmos Ocean 35(3):367–383. https://doi.org/10.1080/07055900.1997.9649597
Batté L, Déqué M (2011) Seasonal predictions of precipitation over Africa using coupled ocean-atmosphere general circulation models: skill of the ENSEMBLES project multimodel ensemble forecasts. Tellus, Ser A: Dyn Meteorol Oceanogr 63A(2):283–299. https://doi.org/10.1111/j.1600-0870.2010.00493.x
Behera SK, Luo JJ, Masson S, Delecluse P, Gualdi S, Navarra A, Yamagata T (2005) Paramount impact of the Indian ocean dipole on the East African short rains: a CGCM study. J Clim 18(21):4514–4530. https://doi.org/10.1175/JCLI3541.1
Bjerknes J (1969) Atmospheric teleconnections from the equatorial Pacific. Mon Weather Rev 97(3):163–172. https://doi.org/10.1175/1520-0493(1969)097(0163:ATFTEP)2.3.CO;2
Black E, Slingo J, Sperber KR (2003) An observational study of the relationship between excessively strong short rains in coastal East Africa and Indian Ocean SST. Mon Weather Rev 131(1):74–94. https://doi.org/10.1175/1520-0493(2003)131(0074:AOSOTR)2.0.CO;2
Bliefernicht J, Waongo M, Salack S, Seidel J, Laux P, Kunstmann H (2018) Quality and value of seasonal precipitation forecasts issued by the West African regional climate outlook forum. J Appl Meteorol Climatol 2014:621–642. https://doi.org/10.1175/jamc-d-18-0066.1
Bowler NE, Arribas A, Beare SE, Mylne KR, Shutts GJ (2009) The local ETKF and SKEB: Upgrades to the MOGREPS short-range ensemble prediction system. Quart J R Meteorol Soc 135:767–776. https://doi.org/10.1002/qj.394
Camberlin P, Philippon N (2002) The East African March–May rainy season: associated atmospheric dynamics and predictability over the 1968–97 period. J Clim 15(9):1002–1019
Camberlin P, Wairoto JG (1997) Intraseasonal wind anomalies related to wet and dry spells during the “long” and “short” rainy seasons in Kenya. Theor Appl Climatol 58(1–2):57–69. https://doi.org/10.1007/BF00867432
Cattani E, Merino A, Levizzani V (2016) Evaluation of monthly satellite-derived precipitation products over East Africa. J Hydrometeorol 17(10):2555–2573. https://doi.org/10.1175/JHM-D-15-0042.1
Clark CO, Webster PJ, Cole JE (2003) Interdecadal variability of the relationship between the Indian Ocean zonal mode and East African coastal rainfall anomalies. J Clim 16(3):548–554
Dee DP, Uppala SM, Simmons AJ, Berrisford P, Poli P, Kobayashi S, Andrae U, Balmaseda MA, Balsamo G, Bauer P, Bechtold P, Beljaars AC, van de Berg L, Bidlot J, Bormann N, Delsol C, Dragani R, Fuentes M, Geer AJ, Haimberger L, Healy SB, Hersbach H, Hólm EV, Isaksen L, Kållberg P, Köhler M, Matricardi M, Mcnally AP, Monge-Sanz BM, Morcrette JJ, Park BK, Peubey C, de Rosnay P, Tavolato C, Thépaut JN, Vitart F (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q J R Meteorol Soc 137(656):553–597. https://doi.org/10.1002/qj.828
Delsole T, Shukla J (2010) Model fidelity versus skill in seasonal forecasting. J Clim 23(18):4794–4806. https://doi.org/10.1175/2010JCLI3164.1
Doblas-Reyes FJ, García-Serrano J, Lienert F, Biescas AP, Rodrigues LR (2013) Seasonal climate predictability and forecasting: status and prospects. Wiley Interdiscip Rev: Clim Change 4(4):245–268. https://doi.org/10.1002/wcc.217
Eade R, Smith D, Scaife A, Wallace E, Dunstone N, Hermanson L, Robinson N (2014) Do seasonal-to-decadal climate predictions underestimate the predictability of the real world? Geophys Res Lett 41(15):5620–5628. https://doi.org/10.1002/2014GL061146
Ebdon RA (1960) Notes on the wind flow at 50 mb in tropical and sub-tropical regions in January 1957 and January 1958. Q J R Meteorol Soc 86(370):540–542. https://doi.org/10.1002/qj.49708637011
Farmer G (1988) Seasonal forecasting of the Kenya coast short rains, 1901–84. J Climatol 8(5):489–497. https://doi.org/10.1002/joc.3370080505
Frías MD, Herrera S, Cofiño AS, Gutiérrez JM (2010) Assessing the skill of precipitation and temperature seasonal forecasts in Spain: windows of opportunity related to ENSO events. J Clim 23(2):209–220. https://doi.org/10.1175/2009JCLI2824.1
Graham R, Colman A, Vellinga M, Wallace E (2012) Use of dynamical seasonal forecasts in the consensus outlooks of African Regional Climate Outlook Forums (RCOFs). ECMWF Seminar on Seasonal Prediction (September) 3–7
Graham RJ, Yun WT, Kim J, Kumar A, Jones D, Bettio L, Gagnon N, Kolli RK, Smith D (2011) Long-range forecasting and the global framework for climate services. Clim Res 47(1–2):47–55. https://doi.org/10.3354/cr00963
Hartmann HC, Pagano TC, Sorooshian S, Bales R (2002) Confidence builders: evaluating seasonal climate forecasts from user perspectives. Bull Am Meteorol Soc 83(5):683–698
Hastenrath S (2000) Zonal circulations over the equatorial Indian Ocean. J Clim 13(15):2746–2756
Hastenrath S (2007) Circulation mechanisms of climate anomalies in East Africa and the equatorial Indian Ocean. Dyn Atmos Oceans 43(1–2):25–35. https://doi.org/10.1016/j.dynatmoce.2006.06.002
Hastenrath S, Nicklis A, Greischar L (1993) Atmospheric-hydrospheric mechanisms of climate anomalies in the western equatorial Indian Ocean. J Geophys Res 98(C11):20,219–20,235. https://doi.org/10.1029/93JC02330
Hastenrath S, Polzin D, Mutai C (2011) Circulation mechanisms of Kenya rainfall anomalies. J Clim 24(2):404–412. https://doi.org/10.1175/2010JCLI3599.1
Heidke P (1926) Berechnung Des Erfolges Und Der Güte Der Windstärkevorhersagen Im Sturmwarnungsdienst. Geografiska Annaler 8(4):301–349. https://doi.org/10.1080/20014422.1926.11881138
Hellmuth M, Moorhead A, Thomson M, Williams J (2007) Climate Risk Management in Africa: Learning from Practice
Hewitt HT, Copsey D, Culverwell ID, Harris CM, Hill RS, Keen AB, McLaren AJ, Hunke EC (2011) Design and implementation of the infrastructure of HadGEM3: the next-generation Met Office climate modelling system. Geosci Model Dev 4(2):223–253. https://doi.org/10.5194/gmd-4-223-2011
Hirons L, Turner A (2018) The impact of Indian Ocean mean-state biases in climate models on the representation of the East African short rains. J Clim 31(16):6611–6631. https://doi.org/10.1175/JCLI-D-17-0804.1
Indeje M, Semazzi FH (2000) Relationships between QBO in the lower equatorial stratospheric zonal winds and East African seasonal rainfall. Meteorol Atmos Phys 73(3–4):227–244. https://doi.org/10.1007/s007030050075
Indeje M, Semazzi FH, Ogallo LJ (2000) ENSO signals in East African rainfall seasons. Int J Climatol 20(1):19–46
Kalnay E et al. (1996) The NCEP/NCAR 40-year reanalysis project. Bull Am Meteorol Soc 77(3):437–472
Kimani MW, Hoedjes JC, Su Z (2017) An assessment of satellite-derived rainfall products relative to ground observations over East Africa. Rem Sens 9(5). https://doi.org/10.3390/rs9050430
Kirtman BP, Min D, Infanti JM, Kinter JL, Paolino DA, Zhang Q, Van Den Dool H, Saha S, Mendez MP, Becker E, Peng P, Tripp P, Huang J, Dewitt DG, Tippett MK, Barnston AG, Li S, Rosati A, Schubert SD, Rienecker M, Suarez M, Li ZE, Marshak J, Lim YK, Tribbia J, Pegion K, Merryfield WJ, Denis B, Wood EF (2014) The North American multimodel ensemble: phase-1 seasonal-to-interannual prediction; phase-2 toward developing intraseasonal prediction. Bull Am Meteorol Soc 95(4):585–601. https://doi.org/10.1175/BAMS-D-12-00050.1
Kumar A, Peng P, Chen M (2014) Is there a relationship between potential and actual skill? Mon Weather Rev 142(6):2220–2227. https://doi.org/10.1175/MWR-D-13-00287.1
Lawrence AJ (1976) On conditional and partial correlation. Am Stat 30(3):146–149. https://doi.org/10.2307/2683864
Li G, Xie SP (2014) Tropical biases in CMIP5 multimodel ensemble: the excessive equatorial pacific cold tongue and double ITCZ problems. J Clim 27(4):1765–1780. https://doi.org/10.1175/JCLI-D-13-00337.1
Liebmann B, Hoerling MP, Funk C, Bladé I, Dole RM, Allured D, Quan X, Pegion P, Eischeid JK (2014) Understanding recent eastern Horn of Africa rainfall variability and change. J Clim 27(23):8630–8645. https://doi.org/10.1175/JCLI-D-13-00714.1
Lu B, Ren HL, Scaife AA, Wu J, Dunstone N, Smith D, Wan J, Eade R, MacLachlan C, Gordon M (2018) An extreme negative Indian Ocean Dipole event in 2016: dynamics and predictability. Clim Dyn 51(1–2):89–100. https://doi.org/10.1007/s00382-017-3908-2
MacLachlan C, Arribas A, Peterson KA, Maidens A, Fereday D, Scaife AA, Gordon M, Vellinga M, Williams A, Comer RE, Camp J, Xavier P, Madec G (2015) Global seasonal forecast system version 5 (GloSea5): a high-resolution seasonal forecast system. Quart J R Meteorol Soc 141(689):1072–1084. https://doi.org/10.1002/qj.2396
Madden RA, Julian PR (1971) Detection of a 40–50 day oscillation in the zonal wind in the tropical Pacific. J Atmos Sci 28(5):702–708
Madden RA, Julian PR (1972) Description of global-scale circulation cells in the tropics with a 40–50 day period. Journal of the Atmospheric Sciences 29(6):1109–1123. https://doi.org/10.1175/1520-0469(1972)029\(<\)1109:DOGSCC\(>\)2.0.CO;2
Magadzire T, Harrison L, Galu G, Nsadisa F (2016) Seasonal forecasting using the GeoCOF software: GeoCOF version 2.1 manual. FEWS NET/Climate Hazards Group
Marchant R, Mumbi C, Behera S, Yamagata T (2007) The Indian Ocean dipole—the unsung driver of climatic variability in East Africa. African J Ecol 45(1):4–16. https://doi.org/10.1111/j.1365-2028.2006.00707.x
Mason I (1982) A model for assessment of weather forecasts 30
Mason S, Chidzambwa S (2008) Verification of African RCOF forecasts. https://doi.org/10.7916/D85T3SB0
Mason SJ (2013) Guidance on verification of operational seasonal climate forecasts. In: World Meteorological Organisation, Commision for Climatology XIV Technical Report
Mason SJ, Tippett MK (2016) Climate Predictability Tool version 15.3 https://doi.org/10.7916/D8NS0TQ6
Meehl GA, Covey C, Delworth T, Latif M, Mcavaney B, Mitchell JFB, Stouffer RJ, Karl ET (2007) The WCRP CMIP3 Multimodel: A new era in climate change research. Am Meteorol Soc (September) 1383–1394. https://doi.org/10.1175/BAMS-88-9-1383
Mutai CC, Ward MN (2000) East African rainfall and the tropical circulation/convection on intraseasonal to interannual timescales. Journal of Climate 13(22):3915–3939. https://doi.org/10.1175/1520-0442(2000)013<3915:EARATT>2.0.CO;2
Mutai CC, Ward MN, Colman AW (1998) Towards the prediction of the East Africa short rains based on sea-surface temperature-atmosphere coupling. Int J Climatol 18(9):975–997
Mwangi E, Wetterhall F, Dutra E, Di Giuseppe F, Pappenberger F (2014) Forecasting droughts in East Africa. Hydrol Earth Syst Sci 18(2):611–620. https://doi.org/10.5194/hess-18-611-2014
Nicholson S (1996) A review of climate dynamics and climate variability in Eastern Africa. In: The limnology, climatology and paleoclimatology of the East African lakes, CRC Press, pp 25–56
Nicholson SE (2014) The predictability of rainfall over the Greater Horn of Africa. Part I: prediction of seasonal rainfall. J Hydrometeorol 15(3):1011–1027. https://doi.org/10.1175/JHM-D-13-062.1
Nicholson SE (2015) The predictability of rainfall over the Greater Horn of Africa. Part II: prediction of monthly rainfall during the long rains. J Hydrometeorol 16(5):2001–2012. https://doi.org/10.1175/JHM-D-14-0138.1
Nicholson SE (2017) Climate and climatic variability of rainfall over eastern Africa. Rev Geophys 55(3):590–635. https://doi.org/10.1002/2016RG000544
Nicholson SE, Entekhabi D (1986) The quasi-periodic behavior of rainfall variability in Africa and its relationship to the southern oscillation. Arch Meteorol, Geophys, Bioclimatol Ser A 34(3–4):311–348. https://doi.org/10.1007/BF02257765
Nicholson SE, Kim J (1997) The relationship of the El Niño Southern Oscillation to African rainfall. International Journal of Climatology 17(2):117–135. https://doi.org/10.1002/(SICI)1097-0088(199702)17:2<117::AID-JOC84>3.0.CO;2-O
Ogallo L, Bessemoulin P, Ceron JP, Mason S, Connor S (2008) Adapting to climate variability and change: the Climate Outlook Forum process. WMO Bull 57(2):93–102
Ogallo LJ (1988) Relationships between seasonal rainfall in East Africa and the Southern Oscillation. J Climatol 8(1):31–43. https://doi.org/10.1002/joc.3370080104
Okoola RE (1998) Spatial evolutions of the active convective patterns across the equatorial eastern Africa region during northern hemisphere spring season using outgoing longwave radiation records. Meteorol Atmos Phys 66(1–2):51–63. https://doi.org/10.1007/BF01030448
Okoola RE (1999) A diagnostic study of the eastern Africa monsoon circulation during the northern hemisphere spring season. Int J Climatol 19(2):143–168
Patt AG, Ogallo L, Hellmuth M (2007) Sustainability: learning from 10 years of climate outlook forums in Africa. Science 318(5847):49–50. https://doi.org/10.1126/science.1147909
Pegion K, Kumar A (2013) Does an ENSO-conditional skill mask improve seasonal predictions? Mon Weather Rev 141(12):4515–4533. https://doi.org/10.1175/mwr-d-12-00317.1
Philippon N, Camberlin P, Fauchereau N (2002) Empirical predictability study of October–December East African rainfall. Q J R Meteorol Soc 128(585 PART A):2239–2256. https://doi.org/10.1256/qj.01.190
Pohl B, Camberlin P (2006a) Influence of the Madden–Julian Oscillation on East African rainfall. I: intraseasonal variability and regional dependency. Q J R Meteorol Soc 132(621):2521–2539. https://doi.org/10.1256/qj.05.104
Pohl B, Camberlin P (2006b) Influence of the Madden–Julian Oscillation on East African rainfall. II. March–May season extremes and interannual variability. Q J R Meteorol Soc 132(621):2541–2558. https://doi.org/10.1256/qj.05.223
Rayner NA, Paker DE, Horton EB, Folland CK, Alexander LV, Rowell DP, Kent EC, Kaplan A (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res 108(D14):4407. https://doi.org/10.1029/2002JD002670
Reed RJ, Campbell WJ, Rasmussen LA, Rogers DG (1961) Evidence of a downward-propagating, annual wind reversal in the equatorial stratosphere. J Geophys Res 66(3):813–818. https://doi.org/10.1029/JZ066i003p00813
Richter I, Chang P, Doi T, Kataoka T, Nagura M, Oettli P, de Szoeke S, Tozuka T, Xu Z (2016) An overview of coupled GCM biases in the tropics. In: Indo-Pacific Climate Variability and Predictability, pp 213–263
Rodhe H, Virji H (1976) Trends and periodicities in East African rainfall data. Monthly Weather Review 104(3):307–315. https://doi.org/10.1175/1520-0493(1976)104<0307:TAPIEA>2.0.CO;2
Saha S, Moorthi S, Wu X, Wang J, Nadiga S, Tripp P, Behringer D, Hou Y, Chuang H, Iredell M, Ek M, Meng J, Yang R, Mendez MP, van den Dool H, Zhang Q, Wang W, Chen M, Becker E (2014) The NCEP climate forecast system version 2. J Clim 27:2185–2208. https://doi.org/10.1175/JCLI-D-12-00823.1
Saji NH, Yamagata T (2003) Possible impacts of Indian Ocean Dipole mode events on global climate. Clim Res 25(2):151–169. https://doi.org/10.3354/cr025151
Saji NH, Goswami BN, Vinayachandran PN, Yamagata T (1999) A dipole mode in the tropical Indian ocean. Nature 401(6751):360–363. https://doi.org/10.1038/43854
Scaife AA, Smith D (2018) A signal-to-noise paradox in climate science. NPJ Clim Atmos Sci 1(1):28. https://doi.org/10.1038/s41612-018-0038-4
Scaife AA, Copsey D, Gordon C, Harris C, Hinton T, Keeley S, O’Neill A, Roberts M, Williams K (2011) Improved Atlantic winter blocking in a climate model. Geophys Res Lett 38(23):L23,703. https://doi.org/10.1029/2011GL049573
Scaife AA, Arribas A, Blockey E, Brookshaw A, Clark RT, Dunstone N, Eade R, Fereday D, Folland CK, Gordon M, Hermanson L, Knight JR, Lea DJ, MacLachlan C, Maidens A, Martin M, Peterson AK, Smith D, Vellinga M, Wallace E, Waters J, Williams A (2014) Skillful long range prediction of European and North American winters. Geophys Res Lett 5(7):2514–2519. https://doi.org/10.1002/2014GL059637
Scaife AA, Ferranti L, Alves O, Athanasiadis P, Baehr J, Déqué M, Dippe T, Dunstone N, Fereday D, Gudgel RG, Greatbatch RJ, Hermanson L, Imada Y, Jain S, Kumar A, MacLachlan C, , Merryfield W, Müller WA, Ren HL, Smith DM, Takaya Y, Vecchi G, Yang X (2018) Tropical rainfall predictions from multiple seasonal forecast systems. Int J Climatol pp 1–15. https://doi.org/10.1002/joc.5855
Shukla S, Roberts J, Hoell A, Funk CC, Robertson F, Kirtman B (2016) Assessing North American multimodel ensemble (NMME) seasonal forecast skill to assist in the early warning of anomalous hydrometeorological events over East Africa. Climate Dynamics pp 1–17, https://doi.org/10.1007/s00382-016-3296-z
Skamarock WC, Klemp, Joseph B, Dudhia J, Gill DO, Barker DM, Duda MG, Xiang-Yu H, Wang W, Powers JG (2008) A description of the advanced research WRF version 3. NCAR/TN-475+STR pp 1–113
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93(4):485–498. https://doi.org/10.1175/BAMS-D-11-00094.1
Torrence C, Webster PJ (1998) The annual cycle of persistence in the El Niño/Southern Oscillation. Q J R Meteorol Soc 124(550):1985–2004. https://doi.org/10.1002/qj.49712455010
Troccoli A (2010) Seasonal climate forecasting. Meteorol Appl 17(3):251–268. https://doi.org/10.1002/met.184
Ummenhofer CC, Gupta AS, England MH, Reason CJC (2009) Contributions of Indian Ocean sea surface temperatures to enhanced East African rainfall. J Clim 22(4):993–1013. https://doi.org/10.1175/2008JCLI2493.1
van den Dool HM, Toth Z (1991) Why do forecasts for near normal often fail? Weather and Forecasting 6(1):76–85. https://doi.org/10.1175/1520-0434(1991)006<0076:wdffno>2.0.co;2
Vellinga M, Milton S (2018) Drivers of interannual variability of the East African ‘Long Rains’. Quarterly Journal of the Royal Meteorological Society. https://doi.org/10.1002/qj.3263
Webster PJ, Moore AM, Loschnigg JP, Leben RR (1999) Coupled ocean–atmosphere dynamics in the Indian Ocean during 1997–98. Nature 401(6751):356–360. https://doi.org/10.1038/43848
Wilks DS (2006) Statistical methods in the atmospheric sciences, 3rd edn. Elsevier, Oxford
Yamagata T, Behera SK, Luo JJ, Masson S, Jury MR, Rao SA (2004) Coupled ocean-atmosphere variability in the tropical Indian Ocean. In: Earth’s Climate, pp 189–211. https://doi.org/10.1029/147GM12
Yang W, Seager R, Cane MA, Lyon B (2015) The rainfall annual cycle bias over East Africa in CMIP5 coupled climate models. J Clim 28(24):9789–9802. https://doi.org/10.1175/JCLI-D-15-0323.1
Yule GU (1907) On the theory of correlation for any number of variables, treated by a new system of notation. Proc R Soc Lond Ser A, Contain Papers Math Phys Char 79(529):182–193. https://doi.org/10.1098/rspa.1907.0028
Acknowledgements
This work was supported by the Natural Environment Research Council (NERC) through an industrial CASE award with the UK Met Office (grant NE/N008227/1). C. Birch, J. Marsham, and Z. Segele were supported by the UK Research and Innovation as part of the Global Challenges Research Fund, grant number NE/P021077/1 (GCRF African SWIFT). J. Marsham was also supported by the HyCRISTAL project (grant NE/M02038X/1), and by the NCAS ACREW project. A. Scaife was supported by the Joint DECC/Defra Met Office Hadley Centre Climate Programme (GA01101). R. Graham was supported by the ForPAc project within the NERC/DFID SHEAR programme, grant number NE/P000428/1. R. Graham and Z. Segele were also funded by the Weather and Climate Information Services (WISER) Support to ICPAC Project (W2-SIP). The GHACOF forecast shapefiles were provided by ICPAC, Nairobi, Kenya through http://geoportal.icpac.net. The GPCP data and NCEP/NCAR Reanalysis were provided by NOAA/ESRL PSD, Boulder, Colorado, USA, and the ERA-Interim Reanalysis data by ECMWF, Reading, UK. D. Walker would also like to thank ICPAC for the invitation to attend the GHACOF50 event and PreCOF50 Capacity Building and Training Workshop, and for the discussions that took place during this event, helping to shape this work. The authors would like to thank the two reviewers for their helpful comments, which have improved the clarity and quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Walker, D.P., Birch, C.E., Marsham, J.H. et al. Skill of dynamical and GHACOF consensus seasonal forecasts of East African rainfall. Clim Dyn 53, 4911–4935 (2019). https://doi.org/10.1007/s00382-019-04835-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-019-04835-9