1 Introduction

The tropical Indian Ocean (TIO) is a major part of the largest warm pool at the Earth’s surface, and its interaction with the atmosphere plays an important role in influencing climate on both regional and global scales. In particular, there are two dominant variability modes that exist over the TIO domain over time scales that vary from seasons to years. First, a basin-wide warming, known as the Indian Ocean Basin mode (IOBM) is the most pronounced mode and is often argued to be coupled with the El Nino-Southern Ocean (ENSO) (e.g., Weare 1979; Klein et al. 1999). The IOBM usually peaks in the boreal early spring and persists until summer following the decay of ENSO. The IOBM modifies local precipitation, the onset of the Indian summer monsoon and the Northwest Pacific anticyclone (e.g., Annamalai et al. 2005; Yang et al. 2007). The second mode, referred to as the Indian Ocean dipole mode (IOD; Saji et al. 1999), is characterised by an opposite sea surface temperature anomaly (SSTA) between the eastern and western Indian Ocean. The IOD can significantly modulate atmospheric and oceanic circulations, which induces a series of climate anomalies in many areas of the world, such as surroundings area in the Indian Ocean, southeastern Australia, eastern Africa and northeastern Asia (Clark et al. 2003; Saji and Yamagata 2003; Ashok et al. 2004; Behera et al. 2005; Cai et al. 2011). Therefore, predicting the TIO SSTA is a crucial step toward predicting the seasonal climate of these regions.

A number of studies have successfully predicted the TIO SSTA several months in advance. For example, Kug et al. (2004) used the Nino-3 index to statistically predict the basin-averaged SSTA up to 6 months in advance. For IOD predictions, current coupled climate models can make useful predictions of up to one season in advance, although some strong IOD events are predictable at longer leads (Song et al. 2008; Zhao and Hendon 2009; Shi et al. 2012; Liu et al. 2016). Some recent studies suggest that an IOD event may be more predictable when it co-occurs with El Nino event (Yang et al. 2015; Tanizaki et al. 2017; Song et al. 2018). One main issue to degrade the IOD predictability is the winter predictability barrier (WPB), i.e. the lowest prediction skill occurs when the prediction target month crosses the boreal winter (December, January and February) (e.g., Wajsowicz 2007; Feng et al. 2014a). Several studies have argued that the WPB is related to the IOD seasonality, which often reverses its sign during the winter season due to monsoon effect. The prediction of SSTA phase transition is very difficult and has usually a large error growth (e.g., Wajsowicz 2004; Feng et al. 2014a, b).

Compared with ENSO, the study of TIO modes is much more recent. In particular for the IOD, its prediction skill at current climate models is much lower than that of ENSO. There are several possible reasons for the poor skill of IOD prediction, including large model errors and inadequate initialization, which can theoretically be addressed by model development and initialization improvement by assimilation (Doi et al. 2017). On the other hand, the IOD may be intrinsically difficult to predict, which is likely due to either weak air–sea coupling in the TIO or strong stochastic processes, e.g., the impact of the Asian and Australian monsoons.

Therefore, exploring the potential predictability of the TIO modes is of interest. In particular, how much the IOD predictability upper limit is under the scenario of a perfect prediction system? A second issue is if the IOBM and IOD modes are intrinsically difficult to predict, whether there are more predictable modes in the TIO and how, if they exist, can we identify them? Liu et al. (2016) has investigated the first issue finding that the IOD potential predictability is higher than the actual prediction skill in current climate models, which suggests a room of improvement existing. However, they also observed that the IOD potential predictability is much lower than the ENSO counterpart, i.e. the IOD is intrinsically less predictable than the ENSO.

In this study, we focus on the second issue, i.e. we attempt to identify more predictable modes in the TIO. Indeed, the IOD and IOBM were defined based on the variance contribution (variability), rather than predictability itself. One may expect that the extracted dominant modes based on the predictability contribution should be more predictable. To achieve this objective, DelSole and Tippett (2009) proposed a method to optimise predictability that is integrated over all lead times, which is known as the Average Predictability Time (APT). Using this method, Jia et al. (2015) explored the most predictable modes for rainfall and surface air temperature over the continents at a seasonal time scale. By applying the APT to a comprehensive ensemble hindcast product, we aim to identify the most predictable modes of TIO SSTA and to further understand the underlying physical mechanisms and predictability sources.

This paper is organized as follow. We briefly introduce in Sect. 2 the data, including ensemble hindcast product and the observation data. Section 3 describes the method used to identify the most predictable modes. In Sect. 4, we investigate the most predictable modes, assess their actual prediction skills, and explore their possible mechanisms. The paper finishes with discussion and conclusion in Sect. 5.

2 Model and data

In this study, we use an ensemble hindcast product composed of 7 coupled models from the North American Multi-model Ensemble (NMME) phase-I (Kirtmann et al. 2014). The NMME is a multi-model forecasting system that combines state-of-art coupled models from the North American forecasting centres. All model outputs have a 1° by 1° horizontal resolution. We only selected the models with a lead time of 9 months or longer. Each model performs ensemble prediction for each calendar month between 1982 and 2010, with an ensemble size from 6 to 24 as shown in Table 1. For consistency, this study uses the ensemble prediction of up to a 9-month lead. In this study, we mainly use the multi-model ensemble (MME), which is obtained by combining all individual model ensemble members. The predicted SST anomalies are formulated with respect to the seasonal cycle of individual models. To remove the linear trend, all data is detrended. The IOBM index is defined as the SSTA averaged over the tropical Indian Ocean (40°E–100°E, 20°S–20°N). The IOD index is defined by the SSTA difference between the western Indian Ocean (10°S–10°N, 50°E–70°E) and the southeastern Indian Ocean (10°S–0°, 90°E–110°E).

Table 1 Models used in the NMME, phase I
Full size table

We use the Optimum Interpolation SST version 2 (OISSTv2; Reynolds et al. 2002) and NCEP–DOE Reanalysis 2 (NCEP II; Kanamitsu et al. 2002) as observation datasets, which include the monthly SST, the 10-m wind velocity, the shortwave radiation and the latent heat flux. The observed thermocline depth is derived from ocean temperature from the NCEP Global Ocean Data Assimilation System (GODAS; Behringer and Xue 2004).

3 Methods

The Average Predictability Time (APT) method, proposed by DelSole and Tippett (2009), is used to extract the most predictable TIO SSTA modes.

The signal-to-total ratio is widely used to measure the potential predictability in the seasonal prediction field (e.g., Tang et al. 2008a, b; Peng et al. 2009; Kumar and Hu 2014; Hu et al. 2014). For an ensemble seasonal climate prediction, the signal, which is often dominated by an external force, is almost completely quantified by the variance of the ensemble mean, while the noise induced by small perturbations is quantified with the averaged ensemble spread over all predictions (Shukla 1998; Peng et al. 2009). The total variance is the sum of the signal and noise variance, which is often referred to as the climatological variance. The total variance of the MME is the average over the total variance of each model. The potential predictability at a fixed lead time τ, is estimated with the following equation:

$$p(\tau )=\frac{{\sigma _{{signal}}^{2}(\tau )}}{{\sigma _{{total}}^{2}}},$$
(1)

where \(\sigma _{{signal}}^{2}(\tau )\) is the signal variance at a lead time τ, and \(\sigma _{{total}}^{2}\) is the total variance. Thus, p(τ) is a function of the lead time and decreases monotonically from 1 to 0.

The APT is defined as the integration of p(τ) over all lead times:

$$APT=2\sum\limits_{{\tau = 1}}^{\infty } {\frac{{\sigma _{{signal}}^{2}(\tau )}}{{\sigma _{{total}}^{2}}}} .$$
(2)

Therefore, APT is independent of the lead times but refers to the system’s inherent properties. The most predictable mode is an optimal vector q with which we can optimise the APT. Statistically, optimising the APT leads to an eigenvalue problem (Delsole and Tippett 2009):

$$\left( {2\sum\limits_{{\tau = 1}}^{\infty } {{\Sigma _{signal}}(\tau )} } \right)q=\lambda {\Sigma _{total}}q,$$
(3)

where \({\Sigma _{signal}}(\tau )\) is the signal covariance at a fixed lead time τ, \({\Sigma _{total}}\) is the total covariance, and q is a projection vector. The eigenvalue of (3) measures the potential predictability of the ensemble prediction system.

By decreasingly ordering the eigenvector according to its eigenvalue, the first eigenvector yields the most predictable mode with maximum predictability (APT1), the second eigenvector yields the second most predictable mode with the second maximum predictability (APT2), which is uncorrelated with the first one, and so on. In other words, the APT method is similar to Principal Component Analysis (PCA), except that it decomposes predictability into different components instead of decomposing the variability (variance). The APT is also closely connected to maximised signal-to-noise ratio (MSN). The main difference between the two is that the MSN maximises the signal to noise ratio at one lead time, τ, whereas the APT maximises the sum of the predictability over all lead times. More details on the APT can be found in DelSole and Tippett (2009).

In practice, the ensemble forecast is first projected onto the leading principal components (PCs) to reduce the spatial dimensions. In this study, we chose 20 PCs from the TIO SSTA and consider all predictions of up to a lead time of 9 months. We tested the APT analysis sensitivity based on the number of PCs and maximum lead time. We find that the major results are not sensitive to the parameter choice. The significance test for the APT is based on the Monte Carlo method as in Yang et al. (2013).

4 The tropical Indian SSTA prediction

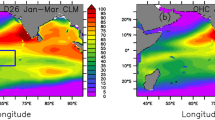
We first examine the actual prediction skill of the TIO SSTA using the MME. Figure 1 shows the SSTA correlation coefficient (ACC) for the MME predictions against the observations. As can be seen, the MME produces statistically skilful predictions (correlation > 0.5) over a large part of the TIO with up to 4–5 month lead times. Longer lead times yield predictions that distribute sporadically throughout the tropic domain. The southwest Indian Ocean region is characterised by high prediction skill where thermocline variability significantly affects changes in the SST (e.g., Masumoto and Meyers 1998; Chambers et al. 1999; Xie et al. 2002). The ACC in this region is above 0.8 at a 1-month lead and then decrease to 0.7, 0.6 and 0.5 at 3-, 6- and 9-month lead times, respectively. In addition, the MME also shows large predictability from the eastern equatorial to the central Indian Ocean, where there are strong influences from the prevailing Wyrtki Jet (Wyrtki 1973) and equatorial zonal wind. We observed all these features in the persistent prediction skill with short lead times (not shown) and they have also been found in some previous studies that used single model ensemble (e.g., Zhu et al. 2015).

Fig. 1
figure 1

Anomaly correlation coefficients (ACC) between the observations and tropical Indian Ocean sea surface temperature anomaly (SSTA) predictions in the multi-model ensemble (MME) based on all initial conditions (IC) between January 1982 and December 2010. The contour at 0.5 is highlighted

Full size image

4.1 The actual prediction of the dominant modes

Here, we evaluate the actual prediction skill of the IOBM and IOD. Figure 2 shows their ACC and root mean squared error (RMSE) in each model and in the MME, as well as their persistence skills. We observe large diversity in the IOBM prediction skill among the models. For example, the ACC for the IOBM prediction remains above 0.6 at a 9-month lead in the CFSv2 and CanCM4 but drops below 0.6 near a 5-month lead time in the other 5 models (Fig. 2a). The RMSEs of individual models are less diverse, which suggests that phase prediction is more sensitive to model biases than magnitude for the IOBM. In general, all models produce statistically skilful prediction for the IOBM (ACC > 0.5) with at least 9-month lead.

Fig. 2
figure 2

a, b ACC and c, d root mean squared error (RMSE) for the IOBM and IOD indices for the individual models, persistence and the MME

Full size image

The ACCs for the IOD predictions, however, are lower in these models, typically dropping below 0.5 at lead times of 3- to 4-month. The CCSM3 has the worst skill, yielding statistically skilful predictions at only 2-month lead times. Compared with the observed IOD index, the CCSM3 successfully predicts several of the strongest IOD events but produces too many false alarms, which results in poor skill (not shown). Comparisons with IOBM predictions reveal that IOD prediction RMSE varies significantly among these models (Fig. 2d), similar to its correlation skill. This suggests that IOD amplitude predictions are more sensitive to model biases than those of the IOBM.

The differences between the prediction skills in these models may be due to differences in model physics, the initial conditions and/or the ensemble size. To reduce model bias and formulation uncertainties, we use the MME, which is thought to holistically consider uncertainties that derive from both the initial conditions and the model uncertainties. As such, the lack of understanding about climate system behaviour in an individual model could possibly be offset by using different model framework assumptions (Palmer et al. 2004; Yan and Tang 2012). Previous studies have found that the MME is able to effectively improve predictions and perform better than any individual model (Krishnamurti et al. 1999; Hagedorn et al. 2005). Figure 2 shows that the MME does produce the best skill in this study, not only for the correlation but also for the RMSE. Thus, in the following discussion, we only focus on results from the MME unless otherwise indicated.

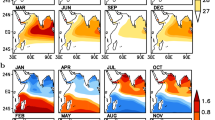
To examine seasonal variation in the IOBM and IOD prediction skills, Fig. 3 shows the ACC and RMSE values for the MME as a function of the initial month and target month. For the IOBM index, the MME is characterised by strong seasonality in both correlation and RMSE skills (Fig. 3a, c). The IOBM is the most predictable when the prediction target is in the boreal spring [i.e. March to May (MAM)] and summer, with an ACC as high as 0.5 at a 9-month lead time. However, when the prediction target is in the boreal fall, the IOBM has the lowest prediction skill, with statistically skilful prediction at only 2- to 3-month lead times. The seasonality of the IOBM prediction skill is likely linked to the fact that ENSO-induced basin-scale warming is dominant in the spring (Schott et al. 2009).

Fig. 3
figure 3

(top) ACC and (bottom) RMSE as a function of the initial month (x axis) and targeted month (y axis) for a, c the IOBM index and b, d the IOD index, based on all predictions in the MME

Full size image

The IOD index prediction skill also strongly depends on the season (Fig. 3b, d). The MME generally has high prediction skill when the prediction target is in the boreal fall [i.e. September to November (SON)], with an ACC of up to 0.5 at a 5-month lead time. The skilful predictions with the longest lead times are those initialized in June and July. This is likely because the development phase of the IOD begins usually in boreal summer, when the initial prediction conditions contain IOD precursor signals, such as zonal surface wind along the Indian Ocean equator and shallow thermoclines in the eastern Indian ocean. On the other hand, the forecast rapidly degrades in the following winter, which is known as the WPB (Wajsowicz 2004, 2007). Predictions initialized before May are also characterised by poor skill, suggesting the IOD onset is difficult to predict before May. This is also likely due to a lacking precursor signal during the IOD onset phase. A key point for IOD prediction is the need to correctly capture the precursors triggering IOD event. These prediction skill features are consistent with IOD event evolution, which develop in the summer, peak in the autumn and decay in the winter (Saji et al. 1999).

During the SON, the IOD events are well developed with maximum magnitude, when the strong signals are favourable for high predictive skill. In the following winter, the TIO exhibits a weak air–sea coupling and thermocline feedback as well as strong weather noise, which results in small SSTA variability and prediction difficulties (Feng et al. 2014a, b). The seasonal dependence of the SSTA variability also leads to the largest RMSE targeted in the autumn and the lowest in the winter, suggesting the RMSE may not be an appropriate metric to evaluate IOD predictability (Liu et al. 2016).

4.2 The most predictable mode related to IOBM

In this section, we extract the most predictable SSTA pattern by applying the APT method. By considering the strong seasonal variation in both the TIO variability and predictability, we explore the most predictable mode (APT1) for the IOBM and IOD mature season, i.e. the MAM and SON, respectively.

Figure 4a shows the leading APT mode obtained using the TIO SSTA during MAM, which corresponds to the IOBM mature phase. The most predictable mode for the TIO SST during MAM depicts a basin-wide warming, with maximum loading over the southwest IO (SWIO) region. We obtained a similar pattern using the summer and winter SSTA but the warming was relatively weak and narrow (not shown). The spatial pattern is in good agreement with the TIO SSTA teleconnection pattern with ENSO (i.e. the IOBM mode). We also conduct the same APT analysis for each model ensemble and all depict a basin-wide mode similar to Fig. 4a (not shown). A significant feature in Fig. 4a is that the SSTA predictability is not spatially uniform in the tropic domain. The SSTA has the largest predictable potential in the southwest Indian Ocean centred at 10°S and 60°E. The high ACC prediction skill in this region, as shown in Fig. 1, is reminiscent of the most predictable mode, which verifies the reliability of the APT1.

Fig. 4
figure 4

The most predictable component (APT1) for the MME SSTA targeted during MAM: a spatial pattern, b the corresponding time series of the component for observation (green), lead times of 0–4 months (blue), lead times of 5–10 months (red) and the observed IOBM index (black), c the corresponding ACC of the predictable mode (blue) and the observed IOBM index during MAM (black) as a function of the initial month. The APT1 time series for observation (green line in b) was obtained by projecting the OISSTv2 onto the spatial pattern of the APT1 (a). All time series in b are normalised

Full size image

Figure 4b shows the observed IOBM index, the predicted APT1 time series at lead time 0–4 months and 5–10 months, as well as the observed APT1 time series, where the observed APT1 time series is obtained by projecting the APT1 mode (i.e. Fig. 4a) onto the observed SSTA. It is indicated that the APT1 time series in the model and observation are consistent with the observed IOBM index, which suggests that there is a significant relationship between the APT1 mode and the IOBM.

To examine the differences between the APT1 mode and the IOBM, we calculate the actual ACC skill between the predicted index and the observed counterpart for both modes. These are calculated by projecting the predicted SSTA and observed SSTA onto the IOBM and APT1 mode, respectively. The results are shown in Fig. 4c, which indicate that the APT1 has a clear advantage when extracting the predictable component.

It is interesting to investigate the possible predictability source of the APT1. For this purpose, we regress the MAM APT1 time series to surface wind, heat flux and the thermocline depth of the same season, which can characterise the atmospheric and oceanic contributions to the APT1 (Fig. 5). Figure 5a shows that the SST pattern, as expected, has a basin-wide warming with enhanced loadings over the southwest Indian Ocean. The southward SST gradient anchors an anti-symmetrical surface wind, with anomalous northeasterlies and northwesterlies over the north and south of the equator, respectively. The wind-induced latent heat flux and cloud-induced shortwave radiation heat flux anomalies are positive over most of the basin but only significant over the northern and southeastern Indian Ocean (Fig. 5c, d). The positive flux indicates the heat transfer from the atmosphere to ocean, which warms the SST. The SWIO warming is different, compared with warming in the rest of the basin, but originates from ocean dynamics (e.g., Klein et al. 1999; Alexander et al. 2002). Figure 5b shows the depth of 20 °C isotherms, which indicates thermocline variation. Previous studies have shown that there is a thermocline ridge over the SWIO. Thus, surface temperature there is strongly influenced by thermocline variation (Schott et al. 2009). During the mature phase of El Nino, anomalous anticyclones form over the southeast TIO via a reduced Walker circulation (Alexander et al. 2002), which forces oceanic Rossby waves. The downwelling Rossby waves propagate westward and arrive at the SWIO after one season in the following spring (Xie et al. 2002). As shown in Fig. 5b, the deepened thermocline warms the SST over the SWIO, strengthens the SSTA signal there and eventually enhances the predictability. This process locally accounts for more than 50% of the explained variance in the SST variability over the SWIO (not shown), which was derived from correlation analysis with the APT1 time series. In short, the slowly varying thermocline variation, which is induced by ENSO, explains the localised SST pattern in the most predictable mode during MAM.

Fig. 5
figure 5

The regression patterns of the observed anomalous (a) SST (shaded, °C) and 10-m wind velocity (vector, m/s), b depth of the 20 °C isotherm (Z20, m), c the latent heat flux (W/m2) and d the shortwave radiation heat flux (W/m2) during MAM onto the APT1 time series for observation (green line in Fig. 4b). Positive heat flux indicates ocean warming. The contours in c, d indicate the zero line of the regression. Areas shown in colour and vectors are significant at the 95% confidence level

Full size image

4.3 The most predictable mode related to IOD

Similarly, we apply the APT method to the boreal autumn (SON) SSTA ensemble prediction, which corresponds to the IOD mature phase. The resultant APT1 mode is shown in Fig. 6a. We find that the pattern in Fig. 6 is similar to the IOD and features a west–east SSTA seesaw in the TIO with a stronger signal near Sumatra. The observed IOD index is also consistent with the observed and predicted APT1 time series, which is characterised by a good relationship between the APT mode and IOD, as shown in Fig. 6b.

Fig. 6
figure 6

The most predictable component (APT1) for the MME SSTA targeted during SON: a spatial pattern, b the corresponding time series of the component for observation (green), lead times of 0–4 months (blue), lead times of 5–10 months (red) and the observed IOD index (black), c the corresponding ACC of the predictable mode (blue) and the observed IOD index during SON (black) as a function of the initial month. The APT1 time series for observation (green line in b) was obtained by projecting the OISSTv2 onto the APT1 spatial pattern (a). All time series in b are normalised

Full size image

Figure 6c is the actual ACC skills for the IOD mode and the APT1 mode, where the indices were obtained by projecting the predicted SSTA and observed SSTA onto the IOD and APT1 mode, respectively, similar to Fig. 4c. Obviously, the APT1 mode has improved prediction skill compared with the IOD at lead times greater than 3 months because the former optimises the predictability attributes. For example, at a 9-month lead time, the APT1 has still the ACC skill above 0.5, whereas the IOD ACC is approximately 0.3. By comparing the potential predictability and the actual prediction skill, Liu et al. (2016) concluded that there is still a large room to improve IOD predictions. The APT1 mode may provide a practical approach for this purpose.

To shed light on the IOD-related APT1 mode, Fig. 7 presents the SSTA and the anomaly field of the surface winds, heat flux and thermocline depth associated with the APT1 mode, which are obtained using the projections of the APT1 time series onto these anomaly fields during the SON season. As can be seen in Fig. 7a, the SSTA pattern has a dipole similar to the IOD but with the most significant loadings in the eastern pole region. As deep convection is suppressed due to the negative SSTA, more shortwave radiation flux reaches the ocean surface and offsets SST cooling in this region (Fig. 7d). The wind anomalies are characterised by an off-equatorial anticyclone over the eastern TIO, which combine with strong zonal easterlies along the equator (Fig. 7a). Anomalous southeasterly winds over the southeast TIO lead to anomalous wind evaporation and negative latent heat flux (Fig. 7c), which is favourable for SST cooling. However, the significant latent heat flux is somehow shifted to the west of the SST cooling, while the cooling occurs along the coastal area of Sumatra. The atmosphere heat flux influences, in a limited manner, SST cooling in the eastern IOD pole.

Fig. 7
figure 7

The regression patterns for the observed anomalous (a) SST (shaded, °C) and 10-m wind velocity (vector, m/s), b Z20 (m), c the latent heat flux (W/m2) and d the shortwave radiation heat flux (W/m2) during SON onto the APT1 time series for observation (green line in Fig. 6b). The contours in c, d indicate the zero line of the regression. Areas shown in colour and vectors are significant at the 95% confidence level

Full size image

The most significant factor that results in eastern IOD pole cooling is probably the variation in the thermocline (Tanizaki et al. 2017). In general, the climatological monsoon winds are southeasterly off the Sumatra coast during the summer and autumn seasons. These forcings favour a shallow thermocline and upwelling in the southeastern IO (SEIO), which allows the upwelling of cool subsurface water (Saji et al. 1999). Through the Bjerknes positive feedback, the easterlies strengthen SEIO cooling by shoaling the thermocline there. As shown in Fig. 7b, the anomalous thermocline depth is characterised by a localised decrease over the southeastern IO, which leads to SST cooling. Similar to ENSO’s influences, in response to an off-equator anticyclone, downwelling oceanic Rossby waves are generated during the IOD events and deepen the thermocline over the central IO (Fig. 7b, Yu et al. 2005). Yet due to the climatological deep thermocline, Rossby wave processes induce limited changes in SST variation over the central IO (Fig. 7a). We conclude that the localised predictability over the eastern IOD pole mainly originates from SEIO thermocline variations, which is a component of the Bjerknes feedback.

5 Summary and discussion

The tropical Indian Ocean (TIO) plays an important role in modulating the global climate. In this study, we have investigated the seasonal predictability of the TIO SSTA using the North American Multimodel Ensemble (NMME) dataset. We first examined its actual prediction skill, in particular the skill of two dominant interannual variability modes: the Indian Ocean Basin mode (IOBM) and the Indian Ocean Dipole (IOD). Furthermore, we identified, by means of Average Predictability Time (APT), the most predictable modes (APT1) for the TIO SSTA during the mature seasons of the IOBM and IOD and analysed their underlying physical processes.

The results show that MME produces statistically skilful predictions up to 4–5 months for the entire tropical domain in these models, after which this skill quickly drops for many TIO regions. For the IOBM, all models in the NMME produce statistically skilful predictions at least 9 months in advance, although there is a large diversity among the different models. The multimodel ensemble (MME), which consists of all ensemble members, outperforms all single models and persistence. IOBM prediction skill is seasonally dependent, with the prediction target of the boreal spring yielding the best skill. In contrast, IOD prediction skill is lower in these models, with most yielding statistically skilful predictions only at lead times of 3- to 4-months. IOD predictions also show pronounced seasonal variation, with the best skills for prediction targets occurring during SON.

The two most predicable modes, i.e. the APT1s, for the TIO SSTA in spring and fall are similar to the IOBM and IOD, respectively. However, we find several significant differences between the predictability and variability modes. The APT1 in spring (MAM) shows significant signals over the southwest IO (SWIO) and displays higher prediction skill than the IOBM mode. The APT1 in MAM locally explains up to 50% of the SST variance. The enhanced localised predictability over the SWIO derives from ocean dynamics. The ENSO-induced oceanic Rossby waves slowly propagate to the SWIO region, influence the thermocline and SST there, and provide the enhanced predictability. The APT1 pattern in autumn (SON) concentrate in the southeastern IO, with limited signals over the western pole of the IOD. Although IOD events exhibit a dipole pattern, the contributions from the eastern and western pole to the IOD pattern are quite different (Saji and Yamagata 2003). IOD events are dominated by the eastern pole, where ocean upwelling is an important process. The APT1 during SON emphasizes the differences and shows large loads only in the eastern pole. Also, this APT1 mode locally accounts for up to 70% of the SST variance in the eastern pole region. This is probably because the thermocline variation in the eastern pole, by the Bjerknes feedback, can result in large SSTA variability thereby enhancing the predictability. Relative to the IOD, the APT1 during SON has high prediction skill, especially for predictions initialized before the onset of IOD events in May. The possible underlying physical mechanisms responsible for the APT1 during MAM and SON are highlighted in a schematic diagram in Fig. 8.

Fig. 8
figure 8

A Schematic showing the physical mechanisms for the most predictable SSTA modes targeted during MAM and SON

Full size image

We analysed the seasonal predictability based on the most predictable modes and underlying physical processes in the TIO. The correlations between the diagnosed predictable modes and the observations are significant for all initial times (Figs. 4c, 6c). Based on these strong correlations, we conclude that the most predictable modes found in the dynamical models also exist in the observations. These modes identify the regions that have high predictability, which may provide a practical approach to improve TIO seasonal prediction skill. The identified regions can offer useful information in determining the optimal prediction targets, and in designing the optimal observing network in the TIO region.