Abstract
High-resolution climate information provided by e.g. regional climate models (RCMs) is valuable for exploring the changing weather under global warming, and assessing the local impact of climate change. While there is generally more confidence in the representativeness of simulated processes at higher resolutions, internal variability of the climate system—‘noise’, intrinsic to the chaotic nature of atmospheric and oceanic processes—is larger at smaller spatial scales as well, limiting the predictability of the climate signal. To quantify the internal variability and robustly estimate the climate signal, large initial-condition ensembles of climate simulations conducted with a single model provide essential information. We analyze a regional downscaling of a 16-member initial-condition ensemble over western Europe and the Alps at 0.11° resolution, similar to the highest resolution EURO-CORDEX simulations. We examine the strength of the forced climate response (signal) in mean and extreme daily precipitation with respect to noise due to internal variability, and find robust small-scale geographical features in the forced response, indicating regional differences in changes in the probability of events. However, individual ensemble members provide only limited information on the forced climate response, even for high levels of global warming. Although the results are based on a single RCM–GCM chain, we believe that they have general value in providing insight in the fraction of the uncertainty in high-resolution climate information that is irreducible, and can assist in the correct interpretation of fine-scale information in multi-model ensembles in terms of a forced response and noise due to internal variability.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
To increase our ability to make predictions of changes of the climate—and associated weather—in response to anthropogenic forcing of the climate system (human induced aerosols, land use change and greenhouse gas emissions), commonly multi-model ensembles of climate simulations are explored, as provided by e.g. the modelling initiatives/projects CMIP (Meehl et al. 2000) for global climate model (GCM) simulations and CORDEX (Giorgi et al. 2009), PRUDENCE (Christensen and Christensen 2007), ENSEMBLES (Van der Linden and Mitchell 2009) and NARCCAP (Mearns et al. 2012) for dynamically downscaled model ensembles. While the application of multiple models provides an estimate of the robustness of the model results, the interpretation of the differences between the individual simulations is not straightforward (Räisänen and Palmer 2001; Tebaldi and Knutti 2007; Tebaldi et al. 2011; Deser et al. 2012a; Von Storch and Zwiers 2013). The total projected change in an individual climate simulation results from the response of the simulated climate system to anthropogenic forcing, referred to as the forced response or climate change signal, and internal variability. Internal, or natural, variability of the climate system originates from the inherent chaotic nature of atmospheric/oceanic/land surface processes and their interactions, and is unpredictable. It is always present and causes the weather and climate to be variable even when averaged over periods up to multiple decades (e.g. Kendon et al. 2008; Deser et al. 2012a, b). As long as the internal variability is large compared to the forced response, it is an irreducible source of uncertainty (noise) in the estimation of the forced response (signal) and prediction of the future climate (e.g. Räisänen 2001; Hegerl et al. 2004; Kendon et al. 2008; Hawkins and Sutton 2009; Deser et al. 2012a, b; Fischer et al. 2013; Xie et al. 2015). The relative importance of internal variability is generally larger for precipitation than for temperature, larger in the extra-tropics than in the tropics, and is particularly large for climate/weather extremes at local to regional scales (Hegerl et al. 2004; Kendon et al. 2008; Hawkins and Sutton 2009, 2011; Deser et al. 2012a; Maraun 2013; Fischer et al. 2013, 2014; Xie et al. 2015).
To be able to correctly interpret climate change projections—and differences between the members of a multi-model ensemble—in terms of the forced response and noise due to internal variability, the magnitude of the internal variability must be known. Internal variability can be estimated from single simulations (or observations) by time filtering of the results (Hawkins and Sutton 2009, 2011; Addor and Fischer 2015). However, it can be derived more accurately and straightforwardly from large ensembles performed with a single-model configuration, created by perturbation of the atmospheric initial state (e.g. Deser et al. 2012a, b). The ensemble members of such an ensemble differ due to internal variability alone.
For global climate models (GCMs) a number of these large single-model ensembles are available and have been analyzed (Selten et al. 2004; Deser et al. 2012a, b, 2014; Fischer et al. 2013, 2014; Hawkins et al. 2016). At the spatial resolution typical for GCMs it was found that much of the spread in multi-model ensembles can be explained by internal atmospheric variability, especially in the extra-tropics and for precipitation (Deser et al. 2012b, 2014; Fischer et al. 2014). Moreover, for temperature and precipitation extremes Fischer et al. (2013) and Fischer and Knutti (2014) have shown that internal variability mainly causes uncertainty in the location of changes in extremes, but that ensemble members largely agree on the fraction of the domain (globe, continents, large countries) where changes are experienced.
While simulations with GCMs provide information on large-scale patterns of climate change and variability, for impact assessments, e.g. in hydrology, agriculture and urban drainage, climate information is required on the regional or local scale. This high-resolution information can be generated by dynamical downscaling of the GCMs with regional climate models (RCMs). For Europe—the focus of our analysis—modelling efforts such as PRUDENCE, ENSEMBLES and most recently EURO-CORDEX (Jacob et al. 2014) have provided large multi-model ensembles of RCM simulations, at increasing spatial resolution (~12 km currently). Such multi-model RCM ensembles have been used extensively to explore changes in climate (extremes) over Europe (e.g. Frei et al. 2006; Fowler et al. 2007; Rajczak et al. 2013; Kjellström et al. 2013; Jacob et al. 2014; Vautard et al. 2014), and as input in hydrological models to assess changes in flood magnitude in response to climate change (e.g. Rojas et al. 2012; Alfieri et al. 2015). Taking into account more detail in topography, land-use, coastlines and smaller-scale atmospheric processes than can be resolved by GCMs and low resolution RCMs allows a better representation of the magnitude, variability and the small-scale spatial pattern of climate variables, especially for precipitation (e.g. Frei et al. 2006; Fowler et al. 2007; Maraun et al. 2010; Kotlarski et al. 2014; Prein et al. 2016; Giorgi et al. 2016). While there is more confidence in the representativeness of the climate variables, the internal variability is larger at these local (grid-cell) scales as well, limiting the predictability of the high-resolution forced response. This is especially the case for precipitation, due to the non-linear and local character of (extreme) precipitation events (Giorgi and Bi 2000; Frei et al. 2006; Fowler et al. 2007; Kendon et al. 2008; Hawkins and Sutton 2011; Fischer et al. 2013; Maraun 2013; Sieck and Jacob 2016). Remarkably, the role of internal variability in the predictability of the high-resolution forced response received relatively little attention and is consequently still rather uncertain (e.g. Kendon et al. 2010; Kjellström et al. 2011; Déqué et al. 2012).
The internal variability in the RCM is partly forced by the atmospheric flow conditions at the lateral boundaries (i.e. inherited from the GCM), but is also generated within the regional model domain. The relative importance of these two sources depends on several factors, such as the circulation type, season, and domain size (e.g. Giorgi and Bi 2000; Christensen et al. 2001; Lucas-Picher et al. 2008; Sieck and Jacob 2016). Here, we do not distinguish between internal variability generated within the domain or forced from the boundary. When mentioning single-model or initial-condition RCM-GCM ensembles we refer to an ensemble created by a single RCM, downscaling multiple members of the same GCM that differ only in their initial conditions.
Kendon et al. (2008) examine the robustness of mean and heavy precipitation changes based on a 3-member initial-condition ensemble of an RCM resolved at 50 km horizontal resolution and conclude that a much larger ensemble would be both valuable and required to fully sample the multi-decadal internal variability and predict the forced response. Kjellström et al. (2011) show that internal variability sometimes dominates over uncertainty due to model formulation. They sample internal variability from a 3-member initial-condition ensemble as well, and also Kjellström et al. argue that larger (initial-condition) ensembles would be valuable. Analyses of large high-resolution single-model RCM–GCM ensembles spanning (parts of) Europe have, to our knowledge, not been published since. The research on this subject has been limited to small single-model ensembles (Déqué et al. 2007; Kendon et al. 2008; Kjellström et al. 2011 and; Imbery et al. 2013), large single-model ensembles but analyzed over relatively small domains (Addor and Fischer 2015) and methods sampling internal variability from single simulations (inter-annual variability) (Maraun 2013; Kjellström et al. 2013).
To obtain an accurate estimate of the local-scale forced response and the relative role of multi-decadal internal variability in mean and extreme daily precipitation, we analyze a 16-member initial-condition ensemble conducted with the GCM EC-EARTH, which is regionally downscaled with the RCM RACMO2 over Western Europe and the Alps, at a resolution of 0.11° (12 km), for the period 1950–2100 (Lenderink et al. 2014 and; Lenderink and Attema 2015). The resolution is equal to the highest-resolution EURO-CORDEX simulations. Lenderink and Attema (2015) have used this ensemble in the development of a scaling approach for local precipitation extremes, and already revealed some characteristics of the ensemble mean response versus individual ensemble members for mean and extreme precipitation indices. Here we look deeper into the ‘issue’ of signal and noise, focusing on the following three questions: How robust is the high-resolution spatial response pattern? When and where does the local-scale climate change signal emerge from internal variability? Given the internal variability, how much information on the local-scale forced response is contained in individual ensemble members?
For the first two questions we use an approach similar to Kendon et al. (2008) and Deser et al. (2012a, b, 2014) to estimate the forced component of the precipitation response (the mean response across the 16-members) and internal variability (the standard deviation across the ensemble).
In part 1 of the analysis we first consider the forced response in the ‘absence’ of internal variability and analyze its characteristics. Despite the relatively large ensemble, internal variability may still affect the ensemble mean response (Hegerl et al. 2004)—a patchy spatial structure as seen in the multi-model mean response of heavy precipitation may be an indication that this indeed is the case (Vautard et al. 2014; Fischer et al. 2014; Xie et al. 2015). By testing pattern robustness through time, we test whether (small-scale) geographical features in the spatial pattern of the forced response are actual features of the forced response or originate from noise.
Internal variability is quantified in part 2 of the analysis, where we determine statistical significance of the forced response (certainty on the sign of the change) and look at emergence of the forced response (signal, S) from internal variability (noise, N), using a signal-to-noise (S/N) perspective (e.g. Hegerl et al. 2004; Giorgi and Bi 2009; Hawkins and Sutton 2009, 2011; Hawkins et al. 2016; Deser et al. 2012a, b, 2014; Kendon et al. 2008; Fischer et al. 2014).
In the last part of the analysis, concerning the information retrievable from individual ensemble members, we determine the pattern similarity between the forced response and the individual ensemble members for different levels of global warming, following Fischer et al. (2014). The pattern similarity is used as measure for the ‘predictive’ value of individual ensemble members for the forced response. The results are relevant for the correct interpretation of multi-model ensembles in terms of the forced response (signal) and internal variability (noise). As long as the predictive value of a single ensemble member for the forced response is low (i.e. the relative role of internal variability is large) (multi-model) ensemble members cannot be expected to agree on the response (Tebaldi et al. 2011).
2 Models and methodology
2.1 Models and domain
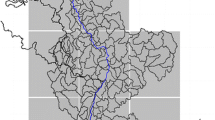
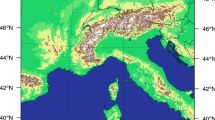
The 16-member ensemble is generated with the RCM KNMI-RACMO2 (Van Meijgaard et al. 2008, 2012) driven by the GCM EC-EARTH 2.3 (Hazeleger et al. 2012). EC-EARTH was run 16 times from 1850 to 2100, each member starting from a slightly different initial state (the 1st until the 16th of January 1850 from an initial model run), under forcing of historical emissions until 2005 and the RCP8.5 greenhouse gas concentration pathway from 2006 onwards (Riahi et al. 2007; Van Vuuren et al. 2011). Each of the EC-EARTH members was subsequently downscaled on a 0.11° (~12 km) resolved domain of 222 × 216 grid-cells (longitude × latitude), covering Western Europe including the Alps for the period 1950–2100. The lateral-boundary relaxation zone counts 16 grid-cells on all sides. The greenhouse gas and aerosol forcing in the EC-EARTH as well as in the RACMO simulations has been implemented to conform with CMIP5 prescriptions (Collins et al. 2013). The resolution of the RACMO grid matches that of the 0.11° EURO-CORDEX simulations (Jacob et al. 2014), but the domain is rotated slightly differently. The domain that is used in the analysis, spanning the region 7°W–15°E, 45°N–60°N, is shown in Fig. 1.
To evaluate whether the RACMO-EC-EARTH model chain realistically simulates part of the internal variability, we compare the simulated inter-annual variability with the corresponding variability in the gridded observational dataset E-OBS (Klein Tank et al. 2002), and in an ERA-Interim forced RACMO run in the period 1981–2010, the reference period (see below). Results of the evaluation are presented in the supplementary material (S1). Overall, we find a high similarity between simulated and observed inter-annual variability (Figs. S1.1, S1.2). Differences (small under-, respectively overestimations of the inter-annual variability in the simulations compared to observations in mean summer precipitation, respectively precipitation maxima in summer and winter, described in detail in S1) will be reflected in the multi-decadal variability, but are not expected to have considerable influence on the analyses presented in this paper.
Given the limited temporal coverage of the observational data, we cannot assess the variability on multi-decadal time scales in the observational data in similar fashion as for the simulated data (Hawkins et al. 2016). However, a large part of the internal variability on longer time scales consists of the integration of the inter-annual variability (Fischer et al. 2013; Thompson et al. 2015). If we neglect the year-to-year correlation, the variance on longer time scales is given by the year-to-year variance divided by the number of years. Indeed, in our model, the variance of 30-year mean precipitation indices is highly similar to the estimate based on the inter-annual variability in a 30-year period (see supplement, Figs. S1.4 and S1.5). This, together with the relatively good representation of inter-annual variability in the RACMO-EC-EARTH ensemble, gives confidence in the representation of the variability on longer time scales. The relation between inter-annual variability and longer term trends is further discussed by Thompson et al. (2015).
2.2 Precipitation indices, seasons, time horizons
We analyze changes in mean and extreme daily precipitation in winter (December–February, DJF) and summer (June–August, JJA) over the period 1981–2100. The analysis is restricted to the land pixels in the domain, which is where the impact of changes is predominantly felt. We adopt a relatively large set of precipitation indices to be able to evaluate how the change depends on the extremity of the event. These are mean daily precipitation (RRmean), mean annual maximum daily precipitation (RX1day) and daily precipitation with a return period (T) of 10 and 20 years (RX1dT10 and RX1dT20) in winter and summer.
The T year return values of daily precipitation intensities are estimated by fitting a Generalized Extreme Value (GEV) distribution to the annual daily precipitation maxima. The cumulative distribution function is:
and µ, σ and ξ are the location, scale and shape parameters, respectively (Coles et al. 2001). Maximum likelihood fitting is used to estimate the GEV parameters. The T year return value x T of daily precipitation can subsequently be calculated by:
R package ‘ismev’ has been used to perform the maximum likelihood fitting.
In the main part of our analysis we consider relative changes in precipitation indices in 30-year future periods relative to the reference period 1981–2100. For ensemble member i this reads:
with F being the value of the precipitation index in a future 30-year period and C the value of the index in the reference period. The three independent periods 2011–2040, 2041–2070 and 2071–2100 are referred to as early, middle and end of the twenty-first century. In these periods, the coinciding global mean temperature rise in the driving EC-EARTH simulations since the reference period is respectively 0.8, 1.9 and 3.4 °C for the ensemble mean, with a standard deviation of typically 0.05 °C between the members. Global mean warming in the reference period with respect to ‘pre-industrial times’ (1861–1890) is 0.9 °C in the EC-EARTH simulations.
Additionally, we compute the relative change in precipitation per degree global warming using the entire simulation period (1981–2100) instead of time slices. For mean and annual maximum daily precipitation this is done by a linear regression on global mean temperature from the driving EC-EARTH simulation(s), per member (120 years) and for all members at once (16 × 120 model years). The thus determined change per degree global warming is normalized with mean daily precipitation, respectively mean annual maximum daily precipitation in the reference period.
For precipitation extremes with longer return periods for the time slices method we fit a stationary GEV to the 30 (29 in DJF) maxima per 30-year period, per member. For the ‘linear regression’ method we fit a GEV to the entire simulation period per member (120 years) and all members at once (16 × 120 model years), allowing the location and scale parameters to vary with time (t) (e.g. Westra et al. 2013; Kharin and Zwiers 2005):
where y(t) is a time-varying covariate, taken as the global mean temperature in the driving EC-EARTH simulation, and µ0, σ0, α and β additional parameters that have to be determined by maximum likelihood fitting.
If changes in precipitation scale linearly with global mean temperature, linear regression using the entire simulation period filters more of the internal variability and yields a more robust estimate of the forced part of the precipitation change (Fischer et al. 2014).
2.3 Separation of forced response and internal variability
The only difference between the model runs is the initial atmospheric state in EC-EARTH, therefore the forced climate response in all members is equal and the members differ due to the internal variability only. This internal variability may originate from both the global and regional model simulations. We estimate the forced climate response (signal, S)—given the applied model chain and forcing scenario—as the ensemble mean response (Eq. 6). The standard deviation across the ensemble is used as a measure for the internal variability (noise, N, Eq. 7).
where n is the number of ensemble members (n = 16).
It should be noted that determining the forced response from the arithmetic ensemble mean over relative changes with different values in the reference period, introduces a spurious increase in the ensemble mean, as also pointed out by Sippel et al. (2017) in a slightly different context. Consider one ensemble member with a future doubling of precipitation from 1 to 2 mm/day, so a relative change of 2/1. In another ensemble member (with a different realization of internal variability) precipitation is projected to decrease from 2 to 1 mm/day. In this case, there is no systematic change between the control and future period, but the ensemble mean response of the relative change gives an artificial increase of 25%.
In practice changes are usually much smaller, and the effect in the RACMO results is typically in the order of 0.1–0.2%/°C of the climate change response. For changes in rare extremes, however, the effect is larger, up to 0.8%/°C. These error estimates and results of alternative, arguably better methods to determine the forced response are given in the supplement (S2). Here, we stick to the conventional approach as this method is commonly used in the analysis of multi-model ensembles.
2.4 Signal-to-noise and statistical significance
The signal-to-noise ratio (S/N) expresses the magnitude of the forced response (signal) compared to internal variability (noise):
To test statistical significance of the forced response we apply the t-test, allowing us to express the test statistic in terms of S/N (comparable to Kendon et al. 2008; Deser et al. 2012b). For the null-hypothesis of no change, \({H_0}:\overline {{\Delta R}} =0\), the test statistic (Y) is:
With \({\sigma _m}=\frac{{{\sigma _{\Delta R}}}}{{\sqrt {n - 1} }},\) the standard error of the ensemble mean response, this leads to:
We assume that under the null-hypothesis Y has a \(t\left( {n - 1} \right)\) distribution. Since precipitation can either increase or decrease, we consider a two-sided test, and reject \({H_0}\) when the response is larger or smaller than 95% of the possible outcomes under \({H_0}\), i.e. at the 5% significance level or smaller:
with \({t_{n - 1,0.025}}~\) the right tail critical value of the distribution. For n = 16, \({t_{n - 1,0.025}}=2.13~\) and a significant change at the 5% levelFootnote 1 is indicated by |S/N| > 0.55.
The assumption that Y has a t(n − 1) distribution implies that the sampling distribution of ΔR i , and thus \({\varepsilon _i}=\Delta {R_i} - \overline {{\Delta R}} ,~\) is normally distributed. Since we use relative differences, the distribution could be positively skewed, meaning that significant changes could be detected too early in areas with increasing precipitation and too late in areas with decreasing precipitation. In the supplement (S3) we show for a selection of grid cells the distribution of \({\varepsilon _i}\) derived from all 30-year periods, which generally is reasonably close to a normal distribution. However, we note that there is uncertainty associated with this choice. A non-parametric test, or empirical bootstrapping to estimate the distribution of Y under the null-hypothesis, could be used to explore this further.
3 Forced response
3.1 Forced response at the end of the century
We first consider the mean response over the 16 ensemble members—our estimate of the forced response due to enhanced greenhouse gas concentrations—at the end of the century. This period is chosen in order to obtain the largest signal, thereby reducing the relative impact of the internal variability, i.e. the noise component. We show the spatial pattern of the forced response in mean daily precipitation (RRmean), annual maximum daily precipitation (RX1day) and daily precipitation with a return period of 20 years (RX1dT20), for the winter and summer season (Fig. 2).
In winter we find an overall increase in mean and extreme precipitation (Fig. 2, top row). The spatial response pattern at least partially reflects orographic features like the Central Massif, the Alps, the mountain ranges of Great-Britain and the Scandinavian Mountains, with generally smaller relative increases—and even small decreases for extreme precipitation—at the (north)western flanks of the mountain ranges, where precipitation is already relatively high in the reference period. This is in agreement with the findings of Gao et al. (2006) and Jacob et al. (2014). In absolute terms (mm/day), increases are generally higher at the most western flanks of the mountain ranges (coasts of Great-Britain and Norway) than in the surrounding area. For the Alps however the windward areas with small or even opposed signal compared to the surroundings in relative terms, have a small or opposed (obviously) signal in absolute terms as well, especially for the extreme precipitation indices. Highest absolute changes in extreme precipitation are found in northern Italy, south of the Alps. Again considering relative changes (Fig. 2, top row), the forced response in mean and extreme precipitation display a very similar spatial pattern. However, the 16-member mean response in extreme precipitation has an added patchiness at the smallest scale, with locally stronger intensification. Whether the latter is a robust feature through time or rather an influence of the noise component is examined in Sect. 3.3.
In summer, the forced response in mean precipitation does not seem to be correlated with the forced response pattern in extreme events (Fig. 2, bottom row). There is a clear gradient in the forced response pattern of mean precipitation, with strong relative drying in the south and west of the domain (south-western France and United Kingdom), gradually reducing and turning into moistening in the north–east. Exceptions to this drying gradient are the high elevated areas along the west-coast of Norway and Scotland and in the Alps, where increases in mean precipitation are displayed amidst drying in the surroundings, consistent with Giorgi et al. (2016). The forced response in summer precipitation extremes shows an intensification in the majority of the domain. Annual maximum daily precipitation in summer decreases in the south and southwest of the domain, where mean summer drying is largest, but moderately increases elsewhere. A stronger intensification over a larger area is seen in the response of daily precipitation intensities with a longer return period (20 years in Fig. 2). Whereas the forced response in mean summer precipitation has a rather smooth spatial pattern with a few small-scale features at high elevated areas, the response pattern of extreme precipitation is far more patchy, especially for the longer return periods. This suggests that in the 16-member mean response of extreme precipitation in summer, the noise is not ‘filtered out’ completely.
To further examine how the forced response in mean and extreme daily precipitation relate to each other, we employ a spatial pooling approach over the entire land domain, where a spatial probability distribution function (pdf) is constructed from the response per grid cell. In Fig. 3 we plot the pdf of the response in the indices shown in Fig. 2 and add the pdf for precipitation with a return period of 10 years (RX1dT10). In winter, as to be expected from the spatial pattern, the pdfs of the forced response in mean and extreme precipitation almost completely overlap, with roughly equal median values. The right tail however is slightly increasing for more extreme precipitation (the patches with higher intensification for RX1day and RX1dT20 in Fig. 2), indicating that higher intensity events increase more strongly and in a larger part of the domain. In summer, the pdf of mean precipitation change is bimodal. This indicates that there is a rather narrow transition zone between two regimes of climate change response. Despite the decrease in mean precipitation, the extremes show a clear increase in most of the region, which is strongest for the 20-year return value. Furthermore, the spatial variability of the ensemble mean response also increases for longer return periods, as shown by the broadening of the distribution.
Spatial probability distribution of the forced response in the period 2071–2100 relative to 1981–2010, over all land points in the domain, in a winter and b summer. Shown are the pdf of mean (RRmean, black) and extreme daily precipitation [RX1day (green), RX1dT10 (blue) and RX1dT20 (red)]. The spatial median of the forced response is indicated in the right corner (number), and by the dashed vertical lines in the plots
3.2 Aggregated response as function of global warming
Having determined the forced response at the end of the century, we now examine how the forced response in mean and extreme precipitation evolves within the twenty-first century.
We plot the forced response as a function of the mean global near-surface temperature rise in the driving EC-EARTH simulations (instead of time), in order to examine whether linear scaling of the response applies [the underlying assumption in pattern scaling, see Mitchell (2003) and Tebaldi and Arblaster (2014)]. Moreover, the agreement in the response magnitude among different models is larger when the response is considered at a fixed level of global warming instead of at a fixed period in time (Fischer et al. 2014; Vautard et al. 2014), which makes our results better comparable with other model ensembles. Lastly, it links regional climate change to global mean temperature rise for which climate mitigation targets are set (Vautard et al. 2014; Seneviratne et al. 2016).
We consider the forced response in the 30-year periods starting every 10 years between 2011 (the first non-overlapping period with the reference period) and 2071, coinciding with a mean global warming in the EC-EARTH simulation ranging between 0.8 and 3.4 °C compared to the reference period. We consider the forced response aggregated over all land pixels in the domain, and plot the median and standard deviation of the pdf as function of global warming (Fig. 4). The forced responses of all precipitation indices—in spatial aggregate—scale roughly linearly with global warming for a global temperature rise larger than around 1.3 °C. In winter, mean and extreme precipitation intensify with approximately the same rate (as in Fig. 3a) with a median increase of 4.2–5.0% °C−1 (Fig. 4a). The shading around the median of the pdf of mean (grey) and 20-year precipitation extremes (red) marks the response between the 5% lowest and highest pixels in the domain. The spatial variability clearly increases with global warming. If the spatial variability would originate solely from a structural spatial pattern in the forced response, i.e. the pattern is constant through time and precipitation in every pixel scales linearly with global warming, the spatial variability is expected to increase linearly as well. For mean winter precipitation this is indeed the case, see Fig. 4 (y-axis on the right-hand side), where we plotted the spatial variability (2 times the standard deviation) as function of global warming. For precipitation extremes we see a relatively large increase between the reference period and the first independent 30-year period (ΔTglob = 0.8 °C), after which the increase in spatial variability continues linearly at a smaller rate. This indicates the presence of a noise component in the ensemble mean response.
Evolution of the forced response with global mean temperature rise for a winter and b summer. On the left y-axis (dashed lines), the spatial median of the pdf of the forced response in mean (RRmean, black) and extreme precipitation [RX1day (green), RX1dT10 (blue) and RX1dT20 (red)] are shown. The shading around the median marks the response between the 5th and 95th percentiles of the spatial distribution (so the spatial spread) for RRmean (black) and RX1dT20 (red). On the right y-axis (dotted lines) the spatial spread is shown as well, but for all indices and expressed as two times the standard deviation (std)
The decrease of the spatially aggregated response in mean summer precipitation starts off gently for low levels of global warming (Fig. 4b). After global warming reaches about 1.3 °C the decrease continues linearly at a rate of −4.8% °C−1. The intensification of summer extremes depends on the return period, and ranges for the spatial median between 1.9% °C−1 for RX1day to 4.9% °C−1 for RX1dT20. Note that there is a part of the domain in which the ensemble mean response in extreme precipitation is negative (see the red shading reaching out to lower than zero for RX1dT20 in Fig. 4b). The area with decreasing precipitation extremes is larger for less extreme events (relatively large area in the southern part of the domain for RX1day; a much smaller area with decreasing RX1dT20, recall Fig. 3b). In contrast to winter, the spatial variability of the ensemble mean response in mean summer precipitation increases faster than for precipitation extremes. This relatively large increase can be related to the expansion and strengthening of the drying gradient over the domain with global warming, see Sect. 3.3. The ensemble mean response in precipitation extremes seems to be affected by a noise component (as in winter), given the non-linear increase of the spatial variability of the ensemble mean response in precipitation extremes.
3.3 Robustness of the response pattern through time
In the following we assess the robustness of the forced response pattern through time, i.e. we test whether pattern scaling is valid (Mitchell 2003; Tebaldi and Arblaster 2014) and whether the spatial features we find in the forced response at the end of the century are actual features of the forced response or originate from internal variability (which is random ‘noise’, i.e. not robust through time).
We first consider the spatial response pattern in mean and 20-year extreme precipitation for the three independent periods 2011–2040, 2041–2070, and 2071–2100. The response is normalized by the global mean temperature rise to be able to compare the results for the different time periods. We also consider the estimate of the response based on all model years (1981–2100) determined by linear regression (lin.reg.) or a non-stationary GEV fit (GEV μ, σ ~ Tglob), with global mean temperature as dependent variable, respectively covariate (Fig. 5). When linear scaling of the forced response with global mean temperature rise is valid, this yields a more robust estimate of the forced response.
Maps of the forced response per degree global warming for RRmean (top two rows) and RX1dT20 (bottom two rows) in winter and summer. The first three columns show the estimates for the periods 2011–2040, 2041–2070 and 2071–2100, based on the 30-year time slices. The last column shows the estimates based on precipitation in the full period 1981–2100, determined by linear regression of mean precipitation on global mean temperature (lin.reg); by a GEV fit with global temperature as covariate and non-stationary location (μ) and scale (σ) parameter for RX1dT20 (GEV μ, σ ~ Tglob)
For mean precipitation the main features of the forced response pattern (overall moistening in winter, drying gradient in summer) are present in all periods (Fig. 5, top row), and the pattern similarity between the response at the end and in the middle of the century is particularly high. In winter, early in the century, the intensification of mean precipitation is generally larger per degree global warming (up to 15% °C−1 locally) than in later periods (up to 10% °C−1), but the geographic pattern with relatively small responses along the northwest oriented mountain ranges, emerging more clearly in the middle of the century, is already visible. Although we cannot exclude that the ensemble mean still contains a noise component causing this larger intensification in the first period, the initial larger increase in precipitation could be related to a stronger local warming and corresponding stronger humidity increase per degree global warming in the same period (Lenderink and Attema 2015). The response determined by linear regression (Fig. 5, right column) is almost indistinguishable from the response determined from the 30-year period at the end of the century, despite the initial faster increase in precipitation.
In summer, while in later periods almost everywhere in Western Europe summer drying is projected, the forced response early in the century displays an increase in mean precipitation in a relatively large part of the domain (eastern Germany and further to the north–east). Moreover, the projected drying in the south of the domain is not as strong as in later periods, and the spatial pattern of the response is slightly more patchy. The gradual expansion of the drying area suggests a non-linear response in mean summer precipitation. The projected summer drying over Western Europe is associated with a change in atmospheric circulation (to dominant easterly winds), governed by higher pressures over the British Isles (Lenderink et al. 2014; Haarsma et al. 2015). This is a feature of the CMIP5 ensemble, and is reproduced by the EC-EARTH ensemble. The development of the anomalous high pressures has been explained by changes in the Hadley cell circulation (CMIP5, Lau and Kim 2015) and a weakening of the Atlantic meridional overturning circulation (AMOC) (CMIP5, EC-EARTH, Haarsma et al. 2015). Under RCP8.5, CMIP5 models project a continuous weakening of the AMOC throughout the twenty-first century (Cheng et al. 2013), which might explain the gradual expansion of summer drying over time (global warming). Additionally, due to summer soil drying, a large-scale Mediterranean heat low develops (CMIP3 models, EC-EARTH), enhancing the easterly winds and thus summer drying over Europe (Haarsma et al. 2009). Despite the non-linearity according to the 30-year period differences, the forced response estimate determined by linear regression over the entire simulation period is again almost equal to the forced response based on the 30-year period difference at the end of the century.
For extreme precipitation, in both winter and summer, the response pattern early in the century is characterized by a much larger spatial heterogeneity (larger patchiness) than in the two later periods, with regions exhibiting larger increases (>15% °C−1) as well as decreases in precipitation (<−12.5% °C−1). This patchiness is a clear manifestation of the larger role of internal variability early in the century. In winter, the pattern similarity in the forced response increases in later periods. In summer, at the larger scale, there seems to appear a pattern with decreasing precipitation extremes south of the Massif Central and the Alps and increasing precipitation elsewhere, but at the pixel scale, for the time horizon applied here, small-scale features are not robust through time. The GEV fit on all members and years with global temperature as covariate gives a response in RX1dT20 with a smaller patchiness and smaller positive relative changes (in the right tail of the distribution) than the ensemble mean response based on a stationary fit in the 30-year periods per ensemble member. In summer, the absolute difference between the two estimates of the forced response in RX1dT20 is in the order of 1.7% °C−1 (see Table S2.1). This difference is partly related to the use of the 60 additional years and the linear scaling of μ and σ with mean global temperature [both methods yield a reasonably small uncertainty (Fig. S2.3)]. Partly, however, it is caused by taking the arithmetic ensemble mean of relative changes in precipitation, as introduced in Sect. 2.3 and elaborated on in supplementary material S2. The spurious increase due to the averaging method is very small for RRmean and RX1day (spatial median of the absolute increase <0.1–0.2% °C−1, hardly visible in Figs. 5 and S2.1–2), but is larger when internal variability and relative changes are larger. For RX1dT20 in summer the spurious increase is around 0.8% °C−1. The results based on the conventional method (Eq. 8) hold for all methods, but the magnitude of the response in precipitation extremes may deviate.
To quantify the pattern similarity of the forced response estimates in different time periods we calculate a simple pattern correlation (Pearson) between the ensemble mean response determined at the end of the century (‘best’ estimate of the forced response) and the ensemble mean response in earlier periods. Again, the 30-year periods starting every 10 years between 2011 and 2071 are considered. Note that the time slices partially overlap and that only one-third of the points shows fully independent results. In Fig. 6a the pattern similarity, expressed as the correlation coefficient (⍴), is plotted as a function of global temperature rise. The pattern similarity between the forced response at the end of the century and in earlier periods is relatively low early in the century, and increases for higher levels of global warming (⍴ = 0.41–0.92 early in the century, 0.58–0.98 in the middle of the century).
a Spatial correlation of the forced response at the end of the century and the forced response in earlier periods, in winter (crosses) and in summer (triangles) as function of global warming, for RRmean, RX1day and RX1dT20. b Spatial correlation between the ensemble mean response in mean precipitation and precipitation extremes (RX1day, RX1dT10, RX1dT20) as function of global warming
Whereas mean precipitation is more robust through time in summer (ρ = 0.92–0.98, early to middle of the century) than in winter (ρ = 0.72–0.90), this is the other way around for extreme precipitation. In winter, the spatial response pattern is fairly robust from the middle of the century onwards for all extreme indices, with a spatial correlation between the forced response at the end and in the middle of the century ranging between 0.83 for annual maximum daily precipitation and 0.69 for precipitation with a return period of 20 years. In summer this is 0.81, respectively 0.58. The response pattern in extreme summer precipitation with a longer return period therefore is not considered to be robust across time at the resolved resolution. We associate the lack of a robust response pattern with a high relative impact of internal variability (see also e.g. Mitchell 2003; Tebaldi and Arblaster 2014). This suggests that, at the grid-cell scale, the forced response in extreme summer precipitation has, at the end of the century, not emerged yet from internal variability. This is likely linked to the local character and unpredictable behavior of convective extreme precipitation, which contributes importantly to the precipitation extremes in summer, even in daily sums.
In the first part of this section we shortly discussed the high degree of similarity in the spatial response pattern between mean and extreme precipitation in winter. In Fig. 6b we plot the spatial correlation between the ensemble mean change in RRmean and the three extreme precipitation indices in winter and summer, as function of global warming. Not surprisingly, the spatial correlation between the ensemble mean change in mean and extreme precipitation is much higher in winter (up to ρ = 0.82 respectively 0.61 for RX1day and RX1T20 at the end of the century) than in summer (ρ = 0.64, respectively 0.23), and is lower for more extreme precipitation indices. For lower levels of global warming, the spatial correlation is lower. This indicates that the similarity in the spatial pattern of change in mean and extreme precipitation, which we see mainly in winter, is a feature of the forced climate response.
4 Emergence from internal variability
4.1 Internal variability
To illustrate the character and large role internal variability may play for different indices, we give two examples of the projected change in individual ensemble members. Figure 7 shows the total response in mean precipitation in winter in 2041–2070 according to two ensemble members with completely opposing spatial patterns. One member (15) projects strong drying south of the Alps and moistening in west-central Europe, whereas another member (13) projects strong moistening south of the Alps and drying in west-central Europe, and the ensemble mean response shows an overall moistening (Fig. 7c). Findings of Kjellström et al. (2013) and Deser et al. (2016) suggest that the opposite patterns in the individual members as shown here originate from internal variability in the large scale atmospheric circulation, associated with the North Atlantic Oscillation. For comparison, Fig. S5.1 shows the same information, but now for the driving EC-EARTH simulations. The contrasting large-scale pattern between the two members (13 and 15) is similar to the RACMO output, but the contrast is smaller (smaller increases in member 15, smaller/no decreases in member 13) and of course lacks spatial detail.
In a second example we show the change in extreme summer precipitation (RX1dT20) (Fig. 8), illustrative for the character of internal variability in (smaller-scale) precipitation extremes. The individual realizations show a highly patchy pattern, with locally considerable increases as well as decreases in high intensity precipitation, in the order of ±45% with respect to the reference period, whereas the ensemble mean response is a general increase in the order of 15% (Fig. 8c). In addition to large-scale variability, an additional spatial heterogeneity, related to the small spatial scale of (convective) extreme events in summer, can be distinguished. When larger spatial scales are considered, part of this small-scale internal variability averages out [the locally strong intensification ‘seen’ in the individual realizations can manifest itself everywhere, but not everywhere at the same time (Fischer et al. 2013)]. Again there is some similarity between the RACMO results and the driving EC-EARTH results (members 5 and 15), yet due to the patchiness of the results at spatial scales close to the grid-scale this similarity is difficult to assess (see Fig. S5.1).
Next we consider the internal variability separately from the forced response, expressed as the standard deviation across the ensemble. Opposed to what is shown by the individual ensemble members in Figs. 7 and 8, Fig. 9 gives an estimate of the spread that can be expected at a grid-cell basis. The spread in the ensemble is fairly constant through time (not shown), and we consider the internal variability at the end of the century only (Fig. 9).
Internal variability (N) in mean and extreme precipitation in winter (top row) and summer (bottom row) for the period 2071–2100 relative to 1981–2010. The maps show the internal variability in RRmean (left column) and RX1dT20 (middle). The right column shows the spatial distribution function of RRmean (black), RX1day (green), RX1dT10 (blue) and RX1dT20 (red), with the spatial median indicated by the dashed lines and in the upper right corner
The internal variability in mean winter precipitation has a clear spatial pattern, with relatively low values (5–10%) in the majority of the domain and higher values (15–30%) at the south-eastern flanks of the Alps, in the Po basin and in small areas along the south-west oriented coasts of Norway and Sweden (Fig. 9a). This captures to a large extent the difference between the two ensemble members in Fig. 7. For precipitation extremes the internal variability is larger and spatially more heterogeneous (Fig. 9b), reflecting the higher spatial variability associated with extreme events. To examine how the magnitude and spatial variability in the internal variability vary with the precipitation index, we consider the internal variability in spatial aggregate, in similar fashion as we did for the forced response in Fig. 3. Clearly, the longer the return period, the larger the internal variability of the associated precipitation event (domain median ranging between 11% for RX1day and 19% for RX1dT20), and the higher the spatial heterogeneity (Fig. 9c).
In summer, internal variability of mean precipitation is distributed more evenly over the domain than in winter, with values around 6% over the majority of the domain, but higher internal variability in the south of Sweden (around 10%) (Fig. 9d). Also in summer the internal variability of precipitation extremes is larger than in mean precipitation with a domain median ranging between 12 and 26% for RX1day and RX1dT20 respectively (Fig. 9e, f). Note that the internal variability of summer extremes is larger and features a smaller-scale patchiness than in winter.
4.2 Signal-to-noise at the end of the century
The signal-to-noise ratio provides information on the relative importance of the forced response over internal variability (one standard deviation across the ensemble) and on the significance of the projected change. Given our 16-member ensemble, for |S/N| ≥0.55 the null-hypothesis of no systematic change is rejected at the 5% significance level, based on a two sided t-test. In other words, for |S/N| ≥0.55, the forced response has statistically emerged from the noise due to internal variability and we have confidence in the direction of the change.
In Fig. 10 we show the S/N in mean and extreme precipitation at the end of the century. The grey shading marks the area where the projected change is non-significant at the 5% level. In winter, S/N is relatively large for mean precipitation (S/N >2.3 in 50%, >0.55 in 99% of the land area, Fig. 10a). Non-significant changes are found where the forced response is relatively weak (in the Alps and the Scandinavian Mountains), which is not per se where the internal variability is high. As we have seen, the forced response in extreme precipitation scales with mean precipitation, but the internal variability is much larger for precipitation events with longer return periods. The S/N in extreme precipitation therefore is smaller for more extreme events (spatial median S/N ranges between 1.8 (RX1day) and 1.0 (RX1dT20), Fig. 10b, c). The land area where changes are non-significant is larger for more extreme events, and is located where the forced response in mean precipitation is weak as well (Alps and Scandinavian Mountains, Fig. 10b). Note that while the forced response features decreases in precipitation in a small fraction of the domain (Fig. 5b), only positive changes in mean and extreme precipitation are found to be significantly different from zero (Fig. 10c).
As Fig. 9 but for the signal-to-noise ratio. The grey shading marks the area where the change is non-significant at the 5% level
In summer, the spatial pattern in S/N for mean precipitation follows the pattern of the forced response as a result of the spatially uniform internal variability (Fig. 10d). Non-significant changes are found in the north-eastern part of the domain in the transition zone of decreasing and increasing precipitation. Significant changes are predominantly negative (median S/N <−2.5), but small areas in the Alps, Scottish Highlands and Scandinavian Mountains feature significant increases in precipitation (S/N up to 2). Owing to the large internal variability, the S/N in summer precipitation extremes is rarely larger than 1.0 (median S/N ~0.6 for all extreme indices). Non-significant changes are found south of the Alps and in western France and in smaller areas scattered over the domain, without clear spatial structure (Fig. 10e). Since in summer both the internal variability and the intensification of extremes increase for more extreme precipitation, the S/N is similar for all extreme indices (Fig. 10f). The median S/N is equal, but the tail of the pdf is slightly fatter for shorter return periods.
4.3 Emergence of the forced climate response
Next we look at the development of S/N throughout the twenty-first century as function of global temperature rise, i.e. at the emergence of the forced climate response. In the reference period (1981–2010), the global temperature rise since ‘pre-industrial’ times (1861–1890) is 0.9 °C in the EC-EARTH ensemble. Note that we consider climate change—and thus emergence—with respect to this reference period, when anthropogenic changes in other variables may have already occurred as well, at least at global scales (e.g. King et al. 2015; Fischer and Knutti 2015).
Following the S/N and the fraction of the land experiencing significant changes throughout the twenty-first century (Fig. 11) we see an earlier emergence of the forced response in winter than in summer and in mean than in extreme precipitation, when aggregated over the entire domain. Locally this may be different though. In Figs. S4.1 and S4.2 we show the maps of S/N for the three independent periods 2011–2040, 2041–2070 and 2071–2100, which for example show that south of the Alps, in part of the Po basin, emergence is earliest in heavy winter precipitation (RX1day), followed by mean precipitation in summer and winter.
Evolution of S/N (left y-axis, dashed lines) and fraction of the land experiencing significant changes in mean and extreme precipitation (right y-axis, dotted lines) with global temperature rise in winter (a) and summer (b). For S/N the crosses mark the spatial median for mean (RRmean, black) and extreme precipitation [RX1day (green), RX1dT10 (blue) and RX1dT20 (red)]; the shading around the median indicates S/N between the 5th and 95th percentiles of the spatial distribution of the response for RRmean (black) and RX1dT20 (red). The light grey band around the x-axis indicates |S/N| <0.55
In winter, in the entire domain, early in the century already 89% of the land experiences significant changes in mean precipitation, reaching 99% at the end of the century (Fig. 11a). Non-significant changes early in the century are found south of the Alps and Massif Central and in the Scottish Highlands and Scandinavian Mountains, i.e. in the same locations as in later periods but covering larger areas (Figs. 10a, S4.1). For precipitation extremes the domain median S/N increases almost linearly with global warming (Fig. 11a). At the beginning of the century the forced response in RX1day is significant in more than 64% of the land area. The signal in precipitation events with longer return periods emerges later, at higher levels of global warming. For RX1dT20 the spatial median S/N reaches values above 0.55 around the middle of the century, when the global temperature rise exceeds 1.5 °C.
In summer, due to the weaker signal in a large part of the domain, the S/N is smaller and significant changes are found in only 26% of the domain early in the century, which gradually increases to 83% at the end of the century. Emergence is earliest for projected decreases in mean summer precipitation in the south-western part of the domain [France, south England (Fig. S4.2)] and for increases at the western flanks of the Scandinavian Mountains and Scottish Highlands and a few areas in the Alps. For higher levels of global warming the signal of decreasing precipitation gradually emerges from southwest to northeast. In the northeast of the domain, where increases in precipitation in earlier periods turn into decreases in later periods (recall Fig. 5), the signal does not emerge from internal variability within the simulation period. For summer extremes, S/N and the increase in S/N are relatively small for all extreme indices. Early in the century, the forced response is significant in less than 10% of the domain, and only after a global warming of approximately 2.5 °C is reached there is significant change in more than half of the land domain (RX1day to RX1dT20). Recall from Fig. 10f that, while the spatial median S/N is approximately equal for all extreme indices, the tail of the pdf is fatter for precipitation with shorter return periods, suggesting earlier emergence of changes in RX1day than in more extreme precipitation. While early in the twenty-first century the fraction of the land experiencing significant changes is indeed (slightly) larger for RX1day than for the more extreme precipitation indices, in later periods this is not the case anymore (Fig. 11b). However, where the signal has emerged, S/N is generally larger for RX1day than for RX1dT10 and RX1dT20, see Fig. S4.2.
5 Information in single ensemble members
We have seen that, while the forced response significantly emerges from internal variability over the course of the twenty-first century for all indices but extreme summer precipitation, the internal variability may cause single simulations to deviate largely from the forced response (Figs. 7, 8). When the forced response of a certain precipitation index starts to dominate over the internal variability, the response pattern in the individual simulations is expected to more closely resemble the pattern in the forced response. The pattern similarity between individual members is consequently expected to increase for higher levels of global warming and associated higher S/N as well (Fischer et al. 2014). We have calculated the pattern similarity between the forced response at the end of the century and the precipitation change in all individual ensemble members for different levels of global warming using a simple pattern correlation (Fig. 12a). It shows the amount of information on the forced response pattern that can be obtained if only a single simulation (per model) is available.
Pattern similarity between a the ensemble mean response at the end of the century (forced response) and the projected change according to an individual member and b two individual members as function of global warming, expressed as the mean Pearson correlation coefficient ρ for all combinations of ensemble members. Results are shown for winter (crosses) and summer (triangles) and for RRmean, RX1day and RX1dT20. LR shows the pattern similarity in the estimates of the response in individual ensembles members based on linear regression (RRmean and RX1day) and a non-stationary GEV fit (RX1dT20)
For low levels of global warming the pattern similarity is limited for all indices, but indeed increases for higher levels of global warming and associated higher S/N. Moreover, pattern similarity is larger for mean than for extreme precipitation, again consistent with the associated larger S/N. However, given that aggregated over the land domain, the S/N until late in the twenty-first century is smaller for mean precipitation in summer than in winter (see Fig. 11), the pattern similarity in mean summer precipitation is surprisingly high for all levels of global warming (ρ = 0.47 early in the century to 0.89 at the end of the century). Apparently, although the spread in the response still exceeds the amplitude in a large part of the domain (|S/N| <2) until late in the century, the location of the transition zone between decreasing precipitation in the south and increasing precipitation in the north–east is a consistent feature in the individual simulations. Also for extremes, based on S/N one would expect a larger difference between the pattern similarity in winter and summer, especially in RX1day. Yet, also for summer extremes there is consistency in the location of the transition zone south in the domain (Fig. 2e) in the individual members. While the inter-annual variability in mean summer precipitation in the current climate is captured rather well (S1), the inter-member spread in the pressure response in EC-EARTH (related to decreasing precipitation over Europe, see Sect. 3.3) does not span the full CMIP5 range (Lenderink et al. 2014). The rather robust response in summer precipitation may therefore be a feature of EC-EARTH, and the inter-member pattern similarity in the summer precipitation response may be smaller (or larger) in other initial-condition RCM-GCM ensembles.
Overall, even for high levels of global warming we find that individual members provide limited information on the forced response in extreme precipitation in winter (ρ = 0.50 and 0.35 for RX1day and RX1dT20 respectively, for a global warming of 3.4 °C at the end of the century) and summer (ρ = 0.49 and 0.32). For mean precipitation the pattern similarity is reasonable in winter (ρ = 0.56) and unexpectedly high in summer (ρ = 0.89). This illustrates that, when one is interested in determining the forced climate response pattern given a certain model and forcing scenario, an ensemble of simulations is required, just to ‘filter out’ internal variability. While in our ensemble the response pattern in mean summer precipitation is rather insensitive to internal variability, this does not necessarily apply for other driving GCMs as well, as discussed above.
Additionally, we plot the mean pattern similarity between all combinations of ensemble members (Fig. 12b). This can be seen as the ‘predictability’ of the real climate (forced response + internal variability) for a given single simulation in a perfect model world. It is also the upper limit of the pattern similarity that can be found between members of a multi-model ensemble (see also Tebaldi and Arblaster 2014). For high levels of global warming (end century), the pattern similarity for mean summer precipitation is still relatively large (ρ = 0.77), but for all other indices, including mean winter precipitation, internal variability results in a poor agreement on the pattern (ρ < 0.30).
To reduce the influence of internal variability and maximize the information in individual simulations we apply a linear regression of precipitation on global mean temperature over the full period (1981–2100), following Fischer et al. (2014). Under the assumption that the precipitation response scales linearly with global warming, linear regression over a longer simulation period more efficiently ‘filters’ internal variability than using time slices to determine the response. Fischer et al. (2014) show for the global domain and resolution of GCMs that the regression method results in a larger agreement in magnitude and pattern of (extreme) precipitation response estimates according to individual ensemble members compared to the time slices method. Here we examine whether this is the case for the high-resolution response in Western Europe as well.
For mean and annual maximum daily precipitation we perform per member a linear regression on global mean temperature from the driving EC-Earth member. For precipitation extremes with longer return periods we fit a non-stationary GEV distribution to the period 1981–2100 (see Methods). Recall (Fig. 5) that the forced response estimate based on linear regression is rather similar to the estimate of the forced response based on the 30-year time slices for the period 2071–2100 for mean and annual maximum precipitation in winter and summer. For extremes with longer return periods and associated higher internal variability, differences between the two methods are larger. The mean pattern similarity in the response in individual realizations based on linear regression (non-stationary GEV fit) is shown in Fig. 12a, b (LR). For RRmean and RX1day there is only a slight improvement in the agreement between the forced response and an individual simulation (Fig. 12a) and between two individual simulations (Fig. 12b) when using linear regression. For RX1dT20 a considerable amount of internal variability is filtered out, with individual simulations more closely resembling the forced response (and thus each other) than for the time slices method for the period 2071–2100. However, pattern correlations for RX1dT20 do not exceed 0.45 (Fig. 12a), respectively 0.20 (Fig. 12b) in both winter and summer and the information contained in individual simulations on the structural response pattern in precipitation extremes remains rather poor.
6 Discussion and conclusions
We have for the first time presented results of the analysis of a large single model RCM-GCM ensemble over Western Europe including the Alps for the period 1981–2100 at a resolution (0.11°) relevant for impact studies. This single-model ensemble has been investigated in terms of the ensemble mean response in mean and extreme daily precipitation in winter and summer (i.e. the estimate for the forced response or climate change signal), as well as the difference between the ensemble members, which measures internal variability (noise).
6.1 Robust small-scale geographical features
We find robust (small-scale) geographical features in the forced response of mean and annual maximum daily precipitation in winter and summer, partially reflecting the orography in the domain. In winter this also applies for more rare events (return periods up to 20 years), the pattern of which is highly correlated with the forced response in mean precipitation. In summer however, we find significant changes in a large part of the domain, but the internal variability of small-scale precipitation extremes is too large to find a robust pattern in the forced response through time. There does seem to appear a larger-scale pattern with a structural intensification of extreme summer precipitation over most of Western Europe and decreasing precipitation in northern Italy and southern France, but longer simulation periods or an even larger ensemble should confirm this.
6.2 Winter extremes scale with mean precipitation, summer extremes intensify more strongly for longer return periods
In winter, mean and extreme precipitation increase with the same rate of change with global warming, and the scaling is fairly constant throughout the century (linear scaling from the middle of the century onwards). In summer, mean precipitation not only gradually decreases with global warming, but the drying area seems to expand to the northeast as well. This indicates a non-linear response to global warming. Heavy summer precipitation generally intensifies and the spatial median scales linearly with global warming. The area with intensifying summer extremes and the rate of intensification is larger for precipitation events with longer return periods. This confirms that pattern scaling with global mean temperature (Mitchell 2003; Tebaldi and Arblaster 2014) is applicable for the high resolution spatial pattern of mean and extreme winter precipitation for the RCP8.5 emission scenario [for scenarios with strong mitigation, pattern scaling might not be as efficient (Tebaldi and Arblaster 2014)]. For mean summer precipitation the response pattern does not scale linearly over the full range of global temperature rise, and for summer extremes pattern scaling could not be confirmed due to the high noise component.
6.3 Earlier emergence in winter than in summer
In most of Western Europe, the local-scale forced response in mean and extreme precipitation emerges earlier from internal variability in winter than in summer, except for the southern and southwestern part of the domain (incl. southern England) where the signal of decreasing precipitation is strong. For extreme precipitation the difference in time of emergence is primarily caused by differences in the internal variability, which is much larger for extreme events in summer—generally convective events—than for extreme precipitation in winter associated with larger-scale systems. Moreover, the signal is weaker for moderately extreme events in summer than in winter.
Emergence occurs earlier for mean precipitation than for precipitation extremes and, in winter, earlier for extremes with shorter return periods. Our results are in qualitative terms in agreement with Kendon et al. (2008), who analyzed changes in precipitation over Europe in terms of S/N as well. Also in studies using GCMs, at the grid-cell scale, this behavior of earlier emergence in mean than in extreme precipitation is found (King et al. 2015), but when aggregated over larger areas, extreme precipitation emerges earlier from the noise than mean precipitation. This is explained by the relatively strong reduction of internal variability in spatially aggregated precipitation extremes and, globally, a larger fraction of the domain with increasing precipitation extremes than increasing mean precipitation (Fischer and Knutti 2014; Fischer et al. 2014; King et al. 2015). Whether the effect of aggregation on emergence of extremes is as large for the domain and resolution of the RACMO-EC-EARTH ensemble should be subject to further study.
6.4 Individual members are poor predictors for the forced response in precipitation extremes
Individual simulations provide rather limited information on the local-scale forced response pattern in precipitation extremes in winter and summer, even for high levels of global warming, owing to the relatively large internal variability. While individual simulations to some extent agree on the response pattern in mean winter precipitation, they show a higher level of agreement on the response pattern in mean summer precipitation. Despite a relatively low S/N in mean summer precipitation, the location of the transition zone between decreasing precipitation in the southwest and increasing precipitation in the northeast is, at least in this ensemble, rather robust. For all other precipitation indices, individual simulations (in single-model ensembles, but likewise in multi-model ensembles) cannot be expected to agree on the response pattern.
6.5 Implications
The results imply that climate change (impact) studies based on small (single or multi-model) ensembles are, in general, of little value. Although they provide insight in a small range of possible futures, the climate change signal, important for risk assessments, cannot be determined reliably. There seems to be a tendency in (hydrological) climate change impact studies to use larger multi-model ensembles of climate simulations as input (e.g. Dankers and Feyen 2009; Madsen et al. 2014; Alfieri et al. 2015), which is encouraged, although to find a statistically significant signal, the use of (multiple) single-model initial-condition ensembles may be preferable.
For the interpretation of high-resolution information in multi-model ensembles our results imply that the individual simulations should not be expected to show similar patterns in precipitation changes until late in the twenty-first century apart from mean summer precipitation. If we would like to determine and compare the forced climate response according to different models, the production of a larger number of single-model ensembles is a prerequisite, as already stated by e.g. Deser et al. (2012b) and Fischer et al. (2014) for GCMs; by Giorgi and Bi (2000) and Kendon et al. (2008) for RCMs, providing high-resolution information on the forced response.
Jacob et al. (2014) show the ensemble mean response of a subset of the 0.11° EURO-CORDEX ensemble forced with the same emission scenario as our ensemble. Interestingly, the spatial pattern in this ensemble is—by visual inspection—highly similar to the ensemble mean response of the RACMO-EC-EARTH ensemble for mean as well as heavy precipitation in winter and summer. The highest-resolution features (grid-cell scale) cannot be compared by visual inspection, but the general agreement in the response pattern suggests that much of the inter-model spread in the EURO-CORDEX ensemble originates from internal variability and that the underlying forced response agrees reasonably well across different GCMs (and RCMs).
7 Limitations and outlook
As discussed in the supplementary material, the conventional method of averaging relative changes arithmetically across members to determine the ensemble mean response in precipitation introduces a spurious positive bias in the response estimate. Using geometric means or arithmetic averaging over absolute changes does not suffer from such a spurious increase. The bias is very small for mean precipitation and moderately extreme precipitation indices, but when the internal variability is large, and both large positive and large negative changes are found in the individual simulations (extreme precipitation events in summer), the spurious increase is larger (~0.8% °C−1 in RX1dT20 in summer). Moreover, estimating the response in extremes based on a non-stationary GEV fit on the entire simulation period yields smaller positive changes than the estimate based on a stationary GEV on 30-year periods. Nevertheless, while the magnitude of the change in extreme precipitation depends on the method that is used, the main conclusions are independent of the applied method.
The conclusions drawn here are, intentionally, based on a single RCM-GCM chain. The benefit of using a single-model initial-condition ensemble is that in separating the forced response from internal variability other sources of uncertainty (model uncertainty, scenario uncertainty) are ruled out, which allows the formulation and testing of a well-posed statistical hypothesis concerning the significance of the forced response. The inter-annual variability in precipitation in our ensemble is, compared to observations, captured fairly well, which gives confidence that also the natural variability at longer time scales is adequately represented. Yet, the sensitivity of the GCM and RCM to the (external) forcing of course is model dependent, so it is not obvious how general our results are. It would be very interesting to repeat our analyses with other initial-condition ensembles in order to assess the robustness of our results.
In this study we focused on the high-resolution forced response in precipitation and examined to what extent a signal is detectable from internal variability at the local scale. Although we find that in summer, at the grid-cell scale, significant trends in extremes could not be established everywhere in the domain, not even at the end of the century under RCP8.5, this does not imply that changes in precipitation extremes are unimportant from a risk perspective considering larger areas. Aggregation of changes over larger areas (e.g. river basins) could lead to a better signal-to-noise ratio and better detectability of trends. Whether that enhances the robustness of the results and how this aggregated information can be used in e.g. climate impact and risk assessment studies is subject of further study.
Notes
For |S/N| = 0.45, the change is significant at the 10% level, 0.76 at 1% level, 0.85 at 0.5% level, 2 < 0.1% level.
References
Addor N, Fischer EM (2015) The influence of natural variability and interpolation errors on bias characterization in RCM simulations. J Geophys Res Atmos. doi:10.1038/nclimate2617
Alfieri L, Burek P, Feyen L, Forzieri G (2015) Global warming increases the frequency of river floods in Europe. Hydrol Earth Syst Sci 19(5):2247–2260. doi:10.5194/hess-19-2247-2015
Cheng W, Chiang JCH, Zhang D (2013) Atlantic meridional overturning circulation (AMOC) in CMIP5 models: RCP and historical simulations. J Clim 26:7187–7197
Christensen JH, Christensen OB (2007) A summary of the PRUDENCE model projections of changes in European climate by the end of this century. Clim Change 81:7–30. doi:10.1007/s10584-006-9210-7
Christensen OB, Gaertner MA, Prego JA, Polcher J (2001) Internal variability of regional climate models. Clim Dyn 17(11):875–887
Coles S, Bawa J, Trenner L, Dorazio P (2001) An introduction to statistical modeling of extreme values, vol 208. Springer, London
Collins M, Knutti R, Arblaster J, Dufresne J-L, Fichefet T, Friedlingstein P, Gao X, Gutowski WJ, Johns T, Krinner G, Shongwe M, Tebaldi C, Weaver AJ, Wehner M (2013) Long-term climate change: projections, commitments and irreversibility. In: Stocker TF, Qin D, Plattner G-K, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds.) Climate change 2013: the physical science basis. Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
Dankers R, Feyen L (2009). Flood hazard in Europe in an ensemble of regional climate scenarios. J Geophys Res Atmos. doi:10.1029/2008JD011523
Déqué M et al (2007) An intercomparison of regional climate simulations for Europe: assessing uncertainties in model projections. Clim Change 81:53–70. doi:10.1007/s10584-006-9228-x
Déqué M, Somot S, Sanchez-Gomez E, Goodess CM, Jacob D, Lenderink G, Christensen OB (2012) The spread amongst ENSEMBLES regional scenarios: regional climate models, driving general circulation models and interannual variability. Clim Dyn 38(5–6):951–964. doi:10.1007/s00382-011-1053-x
Deser C, Knutti R, Solomon S, Phillips AS (2012a) Communication of the role of natural variability in future North American climate. Nat Clim Change 2(11):775–779. doi:10.1038/nclimate1562
Deser C, Phillips A, Bourdette V, Teng H (2012b) Uncertainty in climate change projections: the role of internal variability. Clim Dyn 38(3–4):527–546. doi:10.1007/s00382-010-0977-x
Deser C, Phillips AS, Alexander MA, Smoliak BV (2014) Projecting North American climate over the next 50 years: uncertainty due to internal variability. J Clim 27(6):2271–2296. doi:10.1175/JCLI-D-13-00451.1
Deser C, Hurrell JW, Phillips AS (2016). The role of the North Atlantic Oscillation in European climate projections. Clim Dyn. doi:10.1007/s00382-016-3502-z
Fischer E, Knutti R (2014) Detection of spatially aggregated changes in temperature and precipitation extremes. Geophys Res Lett 41(2):547–554
Fischer EM, Knutti R (2015) Anthropogenic contribution to global occurrence of heavy-precipitation and high-temperature extremes. Nat Clim Change 5(6):560–564
Fischer E, Beyerle U, Knutti R (2013) Robust spatially aggregated projections of climate extremes. Nat Clim Change 3(12):1033–1038
Fischer E, Sedlácek J, Hawkins E, Knutti R (2014) Models agree on forced response pattern of precipitation and temperature extremes. Geophys Res Lett 41(23):8554–8562
Fowler H, Ekström M, Blenkinsop S, Smith A (2007) Estimating change in extreme European precipitation using a multimodel ensemble. J Geophys Res Atmos 112(D18)
Frei C, Schöll R, Fukutome S, Schmidli J, Vidale PL (2006) Future change of precipitation extremes in Europe: intercomparison of scenarios from regional climate models. J Geophys Res Atmos 111(D6)
Gao X, Pal JS, Giorgi F (2006) Projected changes in mean and extreme precipitation over the Mediterranean region from a high resolution double nested RCM simulation. Geophys Res Lett 33(3)
Giorgi F, Bi X (2000) A study of internal variability of a regional climate model. J Geophys Res Atmos 105(D24):29503–29521. doi:10.1029/2000JD900269
Giorgi F, Bi X (2009). Time of emergence (TOE) of GHG-forced precipitation change hot-spots. Geophys Res Lett. doi:10.1029/2009GL037593
Giorgi F, Jones C, Asrar GR (2009) Addressing climate information needs at the regional level: the CORDEX effort. WMO Bull 58(3):175–183
Giorgi F, Torma C, Coppola E, Ban N, Schär C, Somot S (2016) Enhanced summer convective rainfall at Alpine high elevations in response to climate warming. Nat Geosci. doi:10.1038/ngeo2761
Haarsma RJ, Selten F, Hazeleger W, Wang X (2009) Drier Mediterranean soils due to greenhouse warming bring easterly winds over summertime central Europe. Geophys Res Lett 36(4)
Haarsma RJ, Selten FM, Drijfhout SS (2015) Decelerating Atlantic meridional overturning circulation main cause of future west European summer atmospheric circulation changes. Environ Res Lett 10(9):094007. doi:10.1088/1748-9326/10/9/094007
Hawkins E, Sutton R (2009) The potential to narrow uncertainty in regional climate predictions. Bull Am Meteorol Soc 90(8):1095–1107. doi:10.1175/2009BAMS2607.1
Hawkins E, Sutton R (2011) The potential to narrow uncertainty in projections of regional precipitation change. Clim Dyn 37(1–2):407–418. doi:10.1007/s00382-010-0810-6
Hawkins E, Smith RS, Gregory JM, Stainforth DA (2016) Irreducible uncertainty in near-term climate projections. Clim Dyn 46(11–12):3807–3819. doi:10.1007/s00382-015-2806-8
Hazeleger W et al (2012) EC-Earth V2. 2: description and validation of a new seamless earth system prediction model. Clim Dyn 39(11):2611–2629. doi:10.1007/s00382-011-1228-5
Hegerl GC, Zwiers FW, Stott PA, Kharin VV (2004) Detectability of anthropogenic changes in annual temperature and precipitation extremes. J Clim 17(19):3683–3700
Imbery F, Plagemann S, Namyslo J (2013) Processing and analysing an ensemble of climate projections for the joint research project KLIWAS. Adv Sci Res 10(1):91–98
Jacob D et al (2014) EURO-CORDEX: new high-resolution climate change projections for European impact research. Reg Environ Change 14(2):563–578. doi:10.1007/s10113-013-0499-2
Kendon EJ, Rowell DP, Jones RG, Buonomo E (2008) Robustness of future changes in local precipitation extremes. J Clim 21(17):4280–4297
Kendon EJ, Jones RG, Kjellström E, Murphy JM (2010) Using and designing GCM–RCM ensemble regional climate projections. J Clim 23(24):6485–6503
Kharin VV, Zwiers FW (2005) Estimating extremes in transient climate change simulations. J Clim 18(8):1156–1173
King AD et al (2015) The timing of anthropogenic emergence in simulated climate extremes. Environ Res Lett 10(9):094015
Kjellström E, Nikulin G, Hansson U, Strandberg G, Ullerstig A (2011) 21st century changes in the European climate: uncertainties derived from an ensemble of regional climate model simulations. Tellus A 63:24–40. doi:10.1111/j.1600-0870.2010.00475.x
Kjellström E, Thejll P, Rummukainen M, Christensen JH, Boberg F, Christensen OB, Maule CF (2013) Emerging regional climate change signals for Europe under varying large-scale circulation conditions. Clim Res 56(2):103–119
Klein Tank AMG et al (2002) Daily dataset of 20th-century surface air temperature and precipitation series for the European Climate Assessment. Int J Climatol 22(12):1441–1453
Kotlarski S, Keuler K, Christensen OB, Colette A, Déqué M, Gobiet A et al (2014) Regional climate modeling on European scales: a joint standard evaluation of the EURO-CORDEX RCM ensemble. Geosci Model Dev 7(4):1297–1333
Lau WK, Kim KM (2015). Robust Hadley circulation changes and increasing global dryness due to CO2 warming from CMIP5 model projections. Proc Natl Acad Sci 112(12):3630–3635
Lenderink G, Attema J (2015) A simple scaling approach to produce climate scenarios of local precipitation extremes for the Netherlands. Environ Res Lett 10(8):85001. doi:10.1088/1748-9326/10/8/085001
Lenderink G, Van den Hurk BJJM, Klein Tank AMG, Van Oldenborgh GJ, Van Meijgaard E, De Vries H, Beersma JJ (2014) Preparing local climate change scenarios for the Netherlands using resampling of climate model output. Environ Res Lett 9(11):115008
Lucas-Picher P, Caya D, de Elia R, Laprise R (2008) Investigation of regional climate models’ internal va- riability with a ten-member ensemble of 10-year simulations over a large domain. Clim Dyn 31:927–940. doi:10.1007/s00382-008-0384-8
Madsen H, Lawrence D, Lang M, Martinkova M, Kjeldsen TR (2014) Review of trend analysis and climate change projections of extreme precipitation and floods in Europe. J Hydrol 519:3634–3650
Maraun D (2013) When will trends in European mean and heavy daily precipitation emerge? Environ Res Lett 8(1):014004
Maraun D et al (2010) Precipitation downscaling under climate change: recent developments to bridge the gap between dynamical models and the end user. Rev Geophys 48(3)
Mearns LO et al (2012) The North American regional climate change assessment program: overview of phase I results. Bull Am Meteorol Soc 93(9):1337–1362
Meehl GA, Boer GJ, Covey C, Latif M, Stouffer RJ (2000) The coupled model intercomparison project (CMIP). Bull Am Meteorol Soc 81(2):313–318
Mitchell TD (2003) Pattern scaling: an examination of the accuracy of the technique for describing future climates. Clim Change 60(3):217–242
Prein AF et al (2016) Precipitation in the EURO-CORDEX 0.11° and 0.44° simulations: high resolution, high benefits? Clim Dyn 46(1–2):383–412. doi:10.1007/s00382-015-2589-y
Räisänen J (2001) CO2-induced climate change in CMIP2 experiments: quantification of agreement and role of internal variability. J Clim 14(9):2088–2104
Räisänen J, Palmer TN (2001) A probability and decision-model analysis of a multimodel ensemble of climate change simulations. J Clim 14(15):3212–3226
Rajczak J, Pall P, Schär C (2013) Projections of extreme precipitation events in regional climate simulations for Europe and the Alpine region. J Geophys Res Atmos 118(9):3610–3626
Riahi K, Gruebler A, Nakicenovic N (2007) Scenarios of long-term socio-economic and environmental development under climate stabilization. Technol Forecast Soc Change 74(7):887–935
Rojas R, Feyen L, Bianchi A, Dosio A (2012). Assessment of future flood hazard in Europe using a large ensemble of bias-corrected regional climate simulations. J Geophys Res Atmos. doi:10.1029/2012JD017461
Selten FM, Branstator GW, Dijkstra HA, Kliphuis M (2004) Tropical origins for recent and future Northern Hemisphere climate change. Geophys Res Lett 31(21)
Seneviratne SI, Donat MG, Pitman AJ, Knutti R, Wilby RL (2016) Allowable CO2 emissions based on regional and impact-related climate targets. Nature 529:477–483
Sieck K, Jacob D (2016) Influence of the boundary forcing on the internal variability of a regional climate model. Am J Clim Change 5:373–382
Sippel S et al (2017) Have precipitation extremes and annual totals been increasing in the world’s dry regions over the last 60 years? Hydrol Earth Syst Sci 21:441–458. doi:10.5194/hess-21-441-2017
Tebaldi C, Arblaster JM (2014) Pattern scaling: its strengths and limitations, and an update on the latest model simulations. Clim Change 122(3):459–471
Tebaldi C, Knutti R (2007) The use of the multi-model ensemble in probabilistic climate projections. Philos Trans R Soc Lond A Math Phys Eng Sci 365(1857):2053–2075
Tebaldi C, Arblaster JM, Knutti R (2011) Mapping model agreement on future climate projections. Geophys Res Lett 38(23)
Thompson DWJ, Barnes EA, Deser C, Foust WE, Phillips AS (2015) Quantifying the role of internal climate variability in future climate trends. J Clim 28:6443–6456
Van Meijgaard E, Van Ulft LH, Van de Berg WJ, Bosveld FC, Van den Hurk BJJM, Lenderink G, Siebesma AP (2008) The KNMI regional atmospheric climate model RACMO version 2.1. Koninklijk Nederlands Meteorologisch Instituut. http://edepot.wur.nl/312258
Van Vuuren DP, Edmonds J, Kainuma M, Riahi K, Thomson A, Hibbard K, Hurtt GC, Kram T, Krey V, Lamarque J-F, Matsui T, Meinshausen M, Nakicenovic N, Smith SJ, Rose SK (2011) Representative concentration pathways: an overview. Clim Change 109:5–31
Van Meijgaard E, van Ulft LH, Lenderink G, de Roode SR, Wipfler EL, Boers R, van Timmermans RMA (2012) Refinement and application of a regional atmospheric model for climate scenario calculations of Western Europe. Technical report KVR 054/12
Van der Linden P, Mitchell JE (eds) (2009) ENSEMBLES: climate change and its impacts: summary of research and results from the ENSEMBLES project. Met Office Hadley Centre, Exeter. http://ensembles-eu.metoffice.com/docs/Ensembles_final_report_Nov09.pdf
Vautard R et al (2014) The European climate under a 2 °C global warming. Environ Res Lett 9(3):034006
Von Storch H, Zwiers F (2013) Testing ensembles of climate change scenarios for “statistical significance”. Clim Change 117(1–2):1–9
Westra S, Alexander LV, Zwiers FW (2013) Global increasing trends in annual maximum daily precipitation. J Clim 26(11):3904–3918
Xie SP, Deser C, Vecchi GA, Collins M, Delworth TL, Hall A et al (2015) Towards predictive understanding of regional climate change. Nat Clim Change 5(10):921
Acknowledgements
We thank the two reviewers for their useful comments, and our colleague Camiel Severijns for producing the 16-member EC-EARTH ensemble. This research was supported by the European Union Horizon 2020 IMPREX project, Grant agreement No 641811 (http://www.imprex.eu).
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Aalbers, E.E., Lenderink, G., van Meijgaard, E. et al. Local-scale changes in mean and heavy precipitation in Western Europe, climate change or internal variability?. Clim Dyn 50, 4745–4766 (2018). https://doi.org/10.1007/s00382-017-3901-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-017-3901-9