Abstract
Distributions of ocean mixed layer temperature trends and trends in the net heat flux from the atmosphere differ, indicating the important role of the transport of heat within the ocean for determining temperature trends. Annual-mean, linear trends in the components of the tropical ocean mixed layer heat budget for 1980–2015 are diagnosed in 4 ocean reanalyses to improve our physical understanding of multidecadal-scale SST trends. The well-known temperature trend in the tropical Pacific, with cooling in the east and warming in the west, is reproduced in each reanalysis with high statistical significance. Cooling in the east is associated with negative trends in the net heat flux from the atmosphere and enhanced equatorial upwelling related to a strengthening of the subtropical cells. Negative trends in the net heat flux also occur in the western tropical Pacific, but advective warming associated with a strengthening and shoaling of the equatorial undercurrent overwhelms these negative trends. The strengthening of the equatorial undercurrent is consistent with enhanced easterly wind stress, which is applied to the ocean reanalyses, and differential sea level trends that enhance the negative zonal height gradient across the Pacific. The Pacific North Equatorial countercurrent is also strengthening in all 4 reanalyses in association with a strengthening of the sea level trough at 10°N in the central and eastern Pacific. All 4 ocean reanalyses produce warming of 0.1–0.3 K/decade in the North Atlantic with statistical significance levels ranging from below 90–99%. The Atlantic is similar to the Pacific in having the equatorial undercurrent strengthening, but indications of shoaling are less consistent in the reanalyses and the North Equatorial Countercurrent in the Atlantic is not strengthening. Large-scale ocean mixed layer warming trends in the Indian Ocean in the reanalyses are interrupted by some regional cooling close to the equator. Net surface heat flux trends are mostly negative, indicating increasing heat fluxes from the ocean to the atmosphere. Wind stress trends applied to the ocean reanalyses are weak, but trends in the Indian Ocean equatorial undercurrent are strong. Since the Indian monsoon climate introduces strong seasonality, the annual analysis may not be adequate for studying physical processes in this ocean basin.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Cook and Vizy (2017) examined trends in the net surface heat flux from the atmosphere to the ocean from 1979 to 2015 as represented in atmospheric reanalysis. These trends are important for understanding trends in tropical and subtropical ocean temperatures, but they are far from the entire story; distributions of net surface heat flux trends do not closely resemble SST trends. Assembling a complete picture of how and why ocean mixed layer temperatures are changing as the global climate warms requires a consideration of the coupled atmosphere/ocean system. On the multi-decadal time scales of the global warming signal, understanding adjustments in the ocean mixed layer heat budget is essential.
Here we compare heat budget climatologies and trends in 4 ocean reanalyses for the 1979–2014 time period. We want to better understand how the ocean mixed layer thermodynamics and, thereby, SSTs are adjusting to global warming, and the implications for ocean mixed layer temperature trends. The primary goal is not to evaluate the accuracy of the ocean reanalyses against observations, but to compare multiple reanalyses with each other as a measure of confidence. We seek trends and processes that make physical sense, emerge as statistically significant, and are similar across reanalysis products.
Background on our current understanding of trends in the ocean mixed layer at low latitudes is provided in the following section. The ocean reanalyses used are described in Sect. 3, and the analysis methodology is presented in Sect. 4. Results are in Sect. 5, and conclusions in Sect. 6.
2 Background
To our knowledge, there have been no previous studies directly addressing the evolution of the ocean mixed layer heat budget in recent decades, but other investigations of changing SSTs and trends in elements of the ocean circulation have direct implications for heat budget trends.
In the tropical Pacific, SST trends (with ENSO anomalies removed) exhibit warming in the west with weak cooling in the east (Compo and Sardeshmukh 2010; Solomon and Newman 2012). The reduced heat flux from the ocean to the atmosphere over the cooler SSTs has been related to a slowing of the global warming signal in the early twenty-first century (Kosaka and Xie 2013; Drijfhout et al. 2014; Chen and Tung 2014; England et al. 2014; Nieves et al. 2015), and with the negative phase of the Interdecadal Pacific Oscillation (IPO; Meehl et al. 2013; Dong and Zhou 2014).
Palmer et al. (2015) compare ocean heat content linear trends in 4 ocean reanalyses with output available back to 1970. For the upper 300 m, they find that there is less agreement in the equatorial Pacific and Indian Oceans than in the rest of the world oceans. They suggest that this disagreement may be related to “end point” effects that arise when the linear trend is calculated in these regions with high interannual variability due to ENSO.
The tropical Atlantic Ocean has warmed more uniformly than the Pacific, with SSTs increasing by approximately 0.8 °C since the mid-1970’s, following temperature decreases in the 1950s and 1960s (e.g., Thompson et al. 2010; Servain et al. 2014). Hakkinen et al. (2015) report steady increases in ocean heat content south of 30°N in their analysis of reanalyses and observations for the North Atlantic, in contrast to high levels of multidecadal variability at higher latitudes as the Atlantic Multidecadal Oscillation (AMO) index transitions from negative to positive values (e.g., Ting et al. 2014; Gu et al. 2016).
Observed Indian Ocean warming is widespread and steady (e.g., Alory et al. 2007; Rao et al. 2012) with some structure related to the Interdecadal Pacific oscillation (IPO; Dong et al. 2016). In the subtropics, the warming is especially pronounced and extends from the surface to 800 m depth, while in the tropics it is underlain with cooling and a shoaling of the thermocline (Alory et al. 2007).
Changes in ocean mixed layer currents are more difficult to observe than SST trends. Luo et al. (2009) and Sen Gupta et al. (2012) simulate a strengthening of the Pacific equatorial undercurrent (EUC), especially in the central and eastern equatorial Pacific, in coupled GCM simulations of the 21st c. Luo and Rothstein (2011) report a more complicated pattern of change in model projections for the same period, with strengthening in the upper EUC balanced by weakening in the lower part of the current. Drenkard and Karnauskas (2014) examine the Simple Ocean Data Assimilation (SODA; Carton and Giese 2008) reanalysis, which assimilated SST only for the 1870–2010 time period, and find that the Pacific EUC core has intensified at a rate of 16% per century and shoaled. In boreal spring, this intensification is associated with stronger easterly wind stress and the resulting intensification of zonal pressure gradients within the ocean mixed layer. In summer, a shoaling of the EUC, i.e., intensification of the more shallow portions of the current, occur in association with weakened easterly wind stress and the resulting decrease in the downward propagation of easterly momentum.
Decadal-scale changes in the Pacific subtropical cells (STCs) have also been examined using somewhat limited observations [e.g., McPhaden and Zhang (2004)] and model simulation (e.g., Cheng et al. 2007). Easterly wind stress acting on the ocean along the equator generates meridional divergence in the Ekman layer and equatorial upwelling. The meridional overturning of the STC is completed by subtropical (25–25° latitude) subsidence and equatorward flow within the pycnocline. Possible coupling with the EUC adds zonal structure to the circulation system (Cheng et al. 2007), with implications for both meridional and horizontal advection of heat within and below the ocean mixed layer. Yang et al. (2014) examine changes in the STCs in the sparse-input version of the SODA reanalysis and suggest that the Pacific STC has strengthened over the 1900 to 2008 time period, and that this strengthening contributes to the observed cooling in the eastern tropical Pacific. This result contrasts with their analysis of the CMIP5 models, most of which produce warming trends in the eastern tropical Pacific accompanied by a decreasing intensity of the STC.
In an examination of trends in surface heat fluxes in four atmospheric reanalyses, Cook and Vizy (2017) showed that trends in the net heat flux between the atmosphere and the oceans do not explain SST trends in the tropics and subtropics. One cannot understand SST trends without a consideration of how the ocean mixed layer heat budget is adjusting as climate changes, including heat and momentum exchanges between the atmosphere and ocean.
3 Datasets
Ocean reanalyses provide a complete description of the mixed layer by combining observations with model calculations. Despite concerns about the validity of model-dependent variables and scarcity of observations in some regions, reanalyses are widely used for trend analyses; some examples are discussed in Sect. 2. Here, confidence in trends in the reanalyses is supported through statistical and physical analysis, as well as agreement among the reanalyses.
Balmaseda et al. (2015) compare climatologies and trends of ocean variables in 26 ocean reanalyses as part of ocean reanalysis intercomparison project (ORA-IP). Accuracy of the ocean reanalysis are estimated by evaluating agreement among the reanalyses and with observations. They find that the greatest uncertainties occur in the tropics, but that the surface heat fluxes are more balanced than in atmospheric reanalyses.
Annual-mean trends in the components of the ocean mixed layer heat budget are examined in ocean reanalyses for 1980–2014 from 30°S to 30°N. Multiple reanalyses are used and an examination of the climatology is included since an ability to reproduce the climatology also adds to confidence in the results, and can point to problem areas in a reanalysis. The ocean reanalysis products used are the following:
-
The NCEP/Global Ocean Data Assimilation System (GODAS; Behringer and Xue 2004). GODAS is based on the GFDL MOM.v3 model and is available at 1/3° latitude × 1° longitude resolution in the tropics on 40 vertical levels with 10 m resolution in the upper 225 m. Temperature and sea level height are assimilated, and salinity is calculated from the temperature profile with local information about temperature/salinity correlations. GODAS is forced with daily surface fluxes, winds, and fresh water fluxes (precipitation minus evaporation) derived from the NCEP2 atmospheric reanalysis. It is available from January 1979—present.
-
The GECCO2 ocean reanalysis (GECCO2; Kohl 2015). GECCO2 is available at 1° × 1° resolution, with 50 vertical levels from 1948 to 2014. Surface forcing of wind stress, heat flux, and fresh water is from the NCEP1 atmospheric reanalysis (Kalnay et al. 1996).
-
The ECMWF Ocean Reanalyses S3 (ORA-S3; Balmaseda et al. 2008). ORAS3 is provided on a variable grid, with 1° resolution refining to 0.3° at the equator, and 29 vertical levels including approximately 10 m layer thickness in the upper 200 m. Variables assimilated are temperature, salinity, and sea level. ORAS3 is forced with daily surface fluxes derived from the ERA-40 reanalysis (Uppala et al. 2005) through 2002, and thereafter from the ECMWF operational archive. Output is available from 1959 to 2011.
-
ECMWF ocean reanalyses S4 (ORA-S4; Balmaseda et al. 2013). ORAS4 is available on a 1° grid with 42 vertical levels, and 10 m layer thickness in the upper 200 m. Assimilated variables are temperature, salinity, and sea level. ORAS4 is forced with daily surface fluxes derived from the ERA-40 reanalysis until 1989, from the ERAI reanalysis (see below) from 1989 to 2009, and thereafter from the ECMWF operational archive. Output is available from 1958—present.
Since the reanalyses are of similar resolution, each is analyzed on its native grid to avoid the loss of information that comes from interpolation.
We also refer to atmospheric reanalyses to understand how trends in the ocean reanalyses may be driven. The following atmospheric reanalyses are primarily chosen because they are used to force the ocean reanalyses listed above.
-
European centre for medium-range weather forecasts (ECMWF) Reanalysis ERA-Interim (ERAI; Dee et al. 2011). ERAI is a global 6-hourly reanalysis available at 1.5° resolution from 1979–present. It is included for its relationship with the reanalyses used to drive ORA-S3 and ORA-S4.
-
Japanese 55-year reanalysis (JRA-55; Kobayashi et al. 2015). JRA-55 is a 3-hourly global reanalysis at 1.25°-resolution from 1958 to 2014. Like ERAI, JRA-55 is a second-generation reanalysis that represents the state-of-the-art, but it is not used to drive any of the ocean reanalyses used here.
-
NCEP/DOE reanalysis II (NCEP2; Kanamitsu et al. 2002). NCEP2 is a 6-hourly global reanalysis, with surface fields available at 1.9°-resolution from 1979—present. This is a first-generation reanalysis product and it is included here because it is used to drive GODAS.
-
NCEP/NCAR reanalysis I (NCEP1; Kalnay et al. 1996). This is a first generation reanalysis, included for its role in driving the GECCO2 ocean reanalysis. It uses a frozen data assimilation system for 1948—present. Horizontal resolution is about 210 km.
4 Methodology
Linear trends in annual mean values are calculated for the 1980–2014 period for GODAS and GECCO2, 1979–2011 for ORA-S3, and 1979–2010 for ORA-S4. ORA-S3 and ORA-S4 are limited by the availability of the necessary monthly averaged fields for analysis of the ocean mixed layer heat budget (see below). The linear trend is chosen despite the presence of hiatus periods in the global warming record since these are not statistically significant (Liebmann et al. 2010), and to minimize the influence of modes of natural variability on interannual to decadal time scales. The evaluation of statistical significance includes an accounting of autocorrelation using the Zwiers and von Storch (1995) two-stage table lookup test procedure. We note, however, that a statistically-significant value from a reanalysis does not mean that the value is correct, but only that the signal has emerged from the background variability as represented in the reanalysis.
Terms in the ocean mixed layer heat budget are examined. We compare annual-mean climatologies and trends of each term from the four ocean reanalyses as one element in evaluating reliability. The ocean mixed layer heat budget is
where \(C\) is the heat capacity of the ocean mixed layer,
\({c_w}\) is the specific heat of sea water, \({\rho _w}\) is mixed layer density, and h is mixed layer depth. We use \({c_w}=3993\,{\text{Jk}}{{\text{g}}^{ - 1\,}}{{\text{K}}^{ - 1}}\) and \({\rho _w}=1025\,{\text{kg}}\,{{\text{m}}^{ - 3}}\), which are valid for seawater with a salinity of 35 psu and a temperature of 293 K (20 °C). In Eq. 1, \(\theta\) is the ocean mixed layer potential temperature and \({F_{NET}}\) is the net heat flux from the atmosphere to the ocean, the net result of the absorption of solar and longwave radiative fluxes, longwave radiative emission, and evaporative and sensible cooling (and heating). The redistribution of heat within the mixed layer is accounted for by horizontal temperature advection, \({F_H}\), and vertical temperature advection, \({F_V}\). D includes numerical error as well as heat transport by diffusion and sub-grid-scale advection.
The advection terms in Eq. 1 are calculated using
and
where \(\vec v\) is the vertically-averaged mixed layer horizontal current velocity and \(W\) is the vertical velocity at the base of the mixed layer. The vertical derivative of temperature in Eq. 4 is taken from the layers immediately above and below the mixed layer base, and \(\Delta z\) is the distance between these two layers.
Various criteria are used to define ocean mixed layer depth, h, in the literature and in the reanalyses based on temperature and/or density profiles. Figure 1a, b show the GODAS and ORA-S3 reanalysis mixed layer depth climatologies, respectively. These h distributions are similar, with deepest mixed layer depths up to 100 m in the central equatorial Pacific and the subtropical Southern Hemisphere in association with mixing by strong surface winds. Four additional definitions of h are shown in Fig. 1c–f. de Boyer Montegut et al. (2004) use three definitions of mixed layer depth based on temperature alone (Fig. 1c) and density (Fig. 1d, e), and produce h distributions that are similar to the reanalyses in the eastern Pacific and Atlantic, but significantly shallower in the central ocean basins. Toyoda et al. (2015) show that monthly mean ocean mixed layer depths from de Boyer Montegut et al. (2004) are more shallow than individual observed profiles due to rapid restratification in spring and vertical resolution issues. The Naval Research Lab (Kara et al. 2003) annual mean mixed layer depth climatology is shown in Fig. 1f. It is based on density, with temperature and salinity values from the World Ocean Atlas (Levitus et al. 1994).
Estimated climatological annual mean mixed layer depth (m) from the a 1980–2014 GODAS and b 1979–2011 ORA-S3 ocean reanalysis. Observational 1941–2002 annual mean mixed layer depth climatologies from de Boyer Montegut et al. (2004) using c a temperature threshold criterion of 0.2 °C (DT02), d a density threshold criterion of 0.03 kg/m3 (DR003), and e density with a variable threshold criterion equivalent to a 0.2 °C decrease (DReqDTm02). f Naval Research Lab (Kara et al. 2003) annual mean mixed layer depth climatology constructed using monthly mean temperature and salinity climatologies from the World Ocean Atlas (Levitus et al. 1994) and a density criterion
In calculating heat capacity (Eq. 2) and horizontal temperature advection (Eq. 3), we use GODAS h values for both the GODAS and GECCO2 reanalyses, and ORAS-3 h values with the ORAS-3 and ORAS-4 reanalyses. This was necessary because estimates for h are not supplied by GECCO2 and ORA-S4. However, we recognize that these h values may be unrealistically deep, and they are somewhat arbitrary given the different definitions of mixed layer depth in use. For this reason, cross sections through the ocean are used to supplement the interpretation of trends in the ocean mixed layer heat budget.
5 Results
5.1 External forcing factors of the ocean reanalyses
Trends in the ocean mixed layer heat budget are driven by surface wind stress, net surface heat flux (\({F_{NET}}\) in Eq. 1), and fresh water flux values from atmospheric reanalyses. We neglect fresh water fluxes here because of their uncertainty in reanalyses and because halosteric trends in density are smaller than thermosteric trends (Durack and Wijffels 2010; Levitus et al. 2012) and examine the momentum and heat fluxes that are applied to the ocean reanalyses.
Figure 2a–d show \({F_{NET}}\) climatologies as provided in the four ocean reanalyses. These fields are averaged using values of \({F_{NET}}\) that have been taken from atmospheric reanalyses (see Sect. 3), applied as forcing factors in the ocean reanalyses, and provided as output. For the global mean, Valdiviesco et al. (2015) find that ocean reanalyses generally exhibit a relatively small (~4 W/m2) positive bias of net heat flux into the oceans. In many ocean reanalysis products, the assimilation increments compensate for this bias because upper ocean temperatures are assimilated (e.g., Song and Yu 2013).
Figure 2e–h are the \({F_{NET}}\) climatologies calculated using the surface heat flux terms provided in the four atmospheric reanalyses listed in Sect. 3. In the Atlantic and Pacific Oceans, there is general agreement that there is a net heat flux directed from the atmosphere into the ocean (positive values) along the equator and in the eastern ocean basins where cooler water upwells. In the subtropics, values are smaller but negative indicating a flux of heat from the ocean to the atmosphere. Heat fluxes are mostly positive in the Indian Ocean north of about 15°S, with larger values in the west where upwelling occurs off the East African coast. As discussed above, GODAS and GECCO2 are driven with \({F_{NET}}\) values from the NCEP2 and NCEP1 atmospheric reanalyses, respectively, and these fields are similar but not identical. ORA-S3 and ORA-S4 \({F_{NET}}\) values (Fig. 2c, d) are different combinations of ECMWF atmospheric reanalysis and operational analysis values (see Sect. 3), and they are consistent with the GODAS and GECCO2 climatologies (Fig. 2a, b) as well as the ERAI \({F_{NET}}\) climatology (Fig. 2g). JRA-55 is somewhat different, with more widespread negative values in all three ocean basins (Fig. 2h).
\({F_{NET}}\)trends from the 4 ocean reanalyses are shown in Fig. 3a–d, with the 90, 95, and 99% levels of confidence indicated by stippling (see figure caption). Since the \({F_{NET}}\) trends applied in the ORA-S4 reanalysis are not supplied as part of the output, we estimate it from the ERAI atmospheric reanalysis for the 1979–2010 period. Despite the similarity in the climatology (Fig. 2a–d), disagreement in the trends among the ocean reanalyses is striking. \({F_{NET}}\) trends in the atmospheric reanalyses, shown in Fig. 3e–h, are in better agreement, but with significant differences (see Cook and Vizy 2017). ERAI in Fig. 3g and JRA-55 in Fig. 3h are in good agreement, but both NCEP2 (Fig. 3e) and NCEP1 (Fig. 3f) are different from them and each other. GODAS \({F_{NET}}\) trends (Fig. 3a) are in general, but not exact, agreement with the NCEP2 \({F_{NET}}\) trends that are used to drive GODAS. Curiously, there are large differences between the NCEP1 (Fig. 3f) and GECCO2 (Fig. 3b) \({F_{NET}}\) trends, and between the ERAI (Fig. 3g) and ORA-S3 (Fig. 3c) trends. There is apparently some processing of the input from atmospheric reanalyses that leads to differences when these values are reported in the ocean reanalyses.
\({F_{NET}}\) trends from the a GODAS, b GECCO2, c ORA-S3, and d ORA-S4 ocean reanalyses, and the e NCEP2, f NCEP1, g ERAI, and h JRA-55 atmospheric reanalyses. Contour intervals are 4 W/m2-decade. Positive values indicate that the net heat flux from the atmosphere into the ocean mixed layer is increasing with time. White, green, and purple stippling denote values found statistically significant at the 90, 95, and 99% levels of confidence, respectively, after accounting for autocorrelation using the Zwiers and von Storch (1995) two-stage table lookup test procedure
The two second-generation atmospheric reanalyses, ERAI and JRA-55 (Fig. 3g, h), are in good agreement, and regions of strong statistical significance emerge. (ORA-S4 \({F_{NET}}\) values also agree with ERAI and JRA-55, but these are just ERAI \({F_{NET}}\) values for 1979–2010 as discussed above. According to ERAI and JRA-55, the net heat flux from the atmosphere to the oceans is decreasing throughout most of the tropical Pacific basin, with largest decreases near 15°S. There is a narrow region in which the heat flux trend is positive (adding heat to the oceans) in the eastern equatorial Pacific, and additional positive values off the North and South American west coasts. Pronounced zonal structure emerges in the tropical Atlantic, with warming in the east and cooling in the west. Net surface heat flux trends are negative over most of the Indian Ocean with maximum values close to the equator. Cook and Vizy (2017) discuss the components of this net surface heat flux; here, we take these values as a given forcing into the ocean mixed layer.
Another driving factor applied to ocean reanalyses is surface wind stress. The wind stress climatologies provided in the GODAS, GECCO2, and ORA-S3 ocean reanalyses (Fig. 4a–c; ORA-S4 does not supply this field) are in general agreement, with maximum values near 15° latitude in association with the steady trade wind regime and equatorial minima. Wind stress trends in the GODAS and GECCO2 reanalyses (Fig. 4d, e) are similar, but with GODAS tending to larger values. These reanalyses are driven with easterly wind stress trends in the central equatorial Pacific (near the dateline), in the eastern South Pacific (0°–30°S), in the South Atlantic (0°–30°S), and in the northern Indian Ocean. Westerly wind stress trends occur in the equatorial Pacific from 110°E to 150°E, in the northern tropical Atlantic (0°–20°N), and in the southern Indian Ocean. Pacific wind stress trends in ORA-S3 are larger and more organized than in the other two reanalyses, with a chevron of easterly trends centered on the central equatorial Pacific that are especially strong in the Southern Hemisphere.
In summary, we have examined trends in the external forcing factors applied to the ocean reanalyses, namely, the net heat flux from the atmosphere (\({F_{NET}}\)) and the surface wind stress. For \({F_{NET}}\) we find that, while the climatologies are similar, trends are dissimilar among the ocean reanalyses. \({F_{NET}}\) trends from the second-generation ERAI and JRA-55 atmospheric reanalyses are similar, with statistical significance emerging, enhancing confidence in the values and suggesting that these atmospheric reanalyses would be good choices for driving ocean reanalyses. For the surface wind stress we find that the wind stress trends applied in the GODAS and GECCO2 reanalyses are similar throughout the tropics, but those included in the ORA-S3 are not, especially in the tropical Pacific.
Disparities in \({F_{NET}}\) and wind stress trends among the ocean reanalyses do not necessarily mean that trends in the heat budget components in the ocean reanalyses are spurious because the ocean reanalysis are further constrained by the assimilation of observed variables in the ocean; trends in FNET and surface wind stress are only two factors that can generate trends in the ocean reanalyses.
5.2 Temperature trends and ocean heat storage
To understand the LHS of Eq. 1, we examine trends in ocean mixed layer potential temperatures and ocean heat storage. Figure 5a–d show ocean mixed layer temperature climatologies from the four ocean reanalyses listed in Sect. 3. They are in good agreement, with similarly-sized western Pacific warm pools and cold tongue structures in the equatorial Pacific and Atlantic Oceans.
Climatological ocean mixed layer temperatures from the a GODAS, b GECCO2, c ORA-S3, and d ORA-S4 ocean reanalyses. Contours are drawn every 2 K. Annual mean trends in ocean mixed layer temperature from the e GODAS, f GECCO2, g ORA-S3, and h ORA-S4 ocean reanalyses. Units are K/decade with contours drawn every 0.1 K/decade. White, green, and purple stippling denote values found statistically significant at the 90, 95, and 99% levels of confidence, respectively, after accounting for autocorrelation using the Zwiers and von Storch (1995) two-stage table lookup test procedure
Ocean mixed layer temperature trends are displayed in Fig. 5e–h. While there is large-scale, general agreement among the four reanalyses and with the studies of SST trends reviewed above, there are notable regional differences. All 4 reanalyses produce warming of 0.1–0.3 K/decade in the North Atlantic with statistical significance levels ranging from below 90–99%. The GODAS and GECCO2 reanalyses extend this warming into the Southern Hemisphere to 15°S, and reproduce the SST patterns of the Atlantic Multidecadal Oscillation (AMO) as the AMO index transitions from negative to positive through the analysis period (e.g., Ting et al. 2014; Gu et al. 2016). The ORA-S3 and ORA-S4 reanalyses (Fig. 5g, h) extend the warming trend farther into the Southern Hemisphere, especially in the western subtropical South Atlantic.
A large-scale zonal pattern in ocean mixed layer temperature trends emerges across the tropical Pacific in each reanalysis, with cooling in the east and warming in the west as discussed in the literature reviewed in Sect. 2. Ocean mixed layer warming in the far western Pacific emerges as more highly significant than cooling in the central and eastern equatorial Pacific. The relatively low levels of significance in the central and eastern equatorial Pacific may occur because of the region’s pronounced interannual variability due to ENSO (see also Palmer et al. 2015). The GECCO2 reanalysis has a warming trend centered on the equator in the central and eastern Pacific; there is a similar but much small region of warming in GODAS, but not in ORA-S3 and ORA-S4.
In the Indian Ocean, all 4 ocean reanalyses produce large-scale warming trends in the mixed layer of 0.2–0.4 K/decade with statistical significance at 90–95% regionally. This overall warming is interrupted by some regional cooling close to the equator, but it is not statistically significant in any of the datasets. Anomaly structure is suggestive of the Indian Ocean dipole mode in GECCO2, but only weakly in GODAS and not at all in ORA-S3 or ORA-S4.
Despite these ocean mixed layer temperature trends, the heat storage term, \(C{\raise0.7ex\hbox{${\partial \theta }$} \!\mathord{\left/ {\vphantom {{\partial \theta } {\partial t}}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{${\partial t}$}}\) in Eq. 1, is small, especially on annual-mean time scales. To estimate an upper-end value, let \(h \approx {100^{}}m\) and assume a temperature trend of 0.5 K/decade. Then, \(C{\raise0.7ex\hbox{${\partial \theta }$} \!\mathord{\left/ {\vphantom {{\partial \theta } {\partial t}}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{${\partial t}$}}\,0.6\,{\text{W}}{{\text{m}}^{ - 2}}\) while many of the terms on the right-hand-side of Eq. 1 are on the order of tens or hundreds of Wm−2. All the terms on the right-hand-side of Eq. 1 depend on the ocean mixed layer temperature directly or indirectly and the adjustment of the surface heat balance occurs on time scales that are much smaller than the annual time scale considered in this analysis.
To confirm this estimate, Fig. 6a–d display climatologies of \(C{\raise0.7ex\hbox{${\partial \theta }$} \!\mathord{\left/ {\vphantom {{\partial \theta } {\partial t}}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{${\partial t}$}}\) from the four ocean reanalyses. Values are small—less than 0.4 Wm−2 everywhere. Trends in this heat storage term, shown in Fig. 6e–h, are generally below 0.02 W/m−2-decade in all four ocean reanalyses. These values are negligible and certainly well below the accuracy of the reanalyses. Thus, trends in the annual-mean heat flux terms (i.e., the terms on the RHS of Eq. 1) can be seen as a series of mutually-adjusted equilibrium states.
\(C{\raise0.7ex\hbox{${\partial \theta }$} \!\mathord{\left/ {\vphantom {{\partial \theta } {\partial t}}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{${\partial t}$}}\) climatologies from the a GODAS, b GECCO2, c ORA-S3, and d ORA-S4 ocean reanalyses. Contour intervals are 0.05 W/m2. \(C{\raise0.7ex\hbox{${\partial \theta }$} \!\mathord{\left/ {\vphantom {{\partial \theta } {\partial t}}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{${\partial t}$}}\) trends from the e GODAS, f GECCO2, g ORA-S3, and h ORA-S4 ocean reanalyses. Contour intervals are 0.01 W/m2-decade. White, green, and purple stippling denote values found statistically significant at the 90, 95, and 99% levels of confidence, respectively, after accounting for autocorrelation using the Zwiers and von Storch (1995) two-stage table lookup test procedure
5.3 Horizontal temperature advection by ocean currents
Figure 7a–d display climatological values of the annual-mean horizontal heat flux advection term, FH, integrated over the ocean mixed layer (Eq. 3) from the four ocean reanalyses. They are in general agreement in all three ocean basins. In the central Pacific, cool-water advection (negative values) in the eastern third of the basin in the Southern Hemisphere and along the equator into the central Pacific indicates the role of the Peru Current and the North and South Equatorial Currents that are associated with the easterly surface winds in maintaining the cold tongue. Warm-water advection by the westerly North Equatorial countercurrent (NECC) is also apparent near 10°N in the Atlantic and Pacific basins. Warm-water advection in the subtropical western Pacific marks the presence of the warm western boundary currents. Magnitudes of \({F_H}\) are similar in all four reanalyses, on the order of 10–30 W/m2, in the Atlantic and Indian Ocean basins and in the subtropical Pacific. However, ORAS-3 and ORAS-4 produce stronger cool-water advection in the central equatorial Pacific than GODAS and GECCO2. This is consistent with having greater easterly surface wind stress in this region in the ORA-S3 climatology (Fig. 4c) compared with GODAS and GECCO2 (Fig. 4a, b).
\({F_H}\) climatologies from the a GODAS, b GECCO2, c ORA-S3, and d ORA-S4 ocean reanalyses. Contour intervals are 10 W/m2. \({F_H}\) trends from the e GODAS, f GECCO2, g ORA-S3, and h ORA-S4 ocean reanalyses. Contours are 4 W/m2-decade, and positive (negative) values indicate enhanced warming (cooling) of the ocean mixed layer due to changes in horizontal currents. White, green, and purple stippling denote values found statistically significant at the 90, 95, and 99% levels of confidence, respectively, after accounting for autocorrelation using the Zwiers and von Storch (1995) two-stage table lookup test procedure
\({F_H}\)trends (Fig. 7e–h) are not similar in the four ocean reanalyses. In the equatorial Pacific, GODAS and GECCO2 (Fig. 7e, f) produce positive trends east of the date line. Alone, such a trend distribution would support a weakening of the negative zonal temperature gradients across the equatorial Pacific, or an eastward retraction of the cold tongue, but the ocean mixed layer temperature trends do not reflect such changes (Fig. 5e, f). GODAS extends these positive \({F_H}\) trends westward, while GECCO2 places negative values in the western equatorial Pacific. Somewhat similar to GODAS, ORA-S3 produces positive trends along the equator flanked by negative trends, suggesting a broadening of the region of cool water advection along the equator (Fig. 7g). This is consistent with trends in the surface wind stress in ORA-S3 (Fig. 4f), which indicate a broadening of the easterly wind stress region in the central tropical Pacific. In the ORA-S4 reanalyses (Fig. 7h), \({F_H}\) trends are localized without an apparent large-scale structure.
\({F_H}\)depends on the product of two reanalyzed fields (temperature and currents; Eq. 3). Figure 5 shows that there is good agreement among the reanalyses about ocean mixed layer temperatures and trends, so we examine horizontal currents and their trends to better understand the disagreement in FH trends shown in Fig. 7e–h. Figure 8a–d show vertical cross sections of the zonal current velocity climatology at 140°W, in the tropical Pacific, from the four reanalyses; the green line marks the bottom of the ocean mixed layer as provided in the GODAS and ORA-S3 output (see Sect. 3). In all four reanalyses, the EUC is represented by westerly current maxima along the equator, with the shallower NECC located to the north. In each case, the core of the EUC is below the mixed layer. In GODAS, the upper portion of the EUC extends well into the ocean mixed layer, but not in the other three reanalyses. The shallow Pacific EUC in GODAS is associated with positive values of \({F_H}\) on the equator immediately east of the dateline (Fig. 7a). In all four ocean reanalyses, positive values of \({F_H}\) (Fig. 7a–d) occur near 10°N in the Pacific in association with the NECC (Fig. 8a–d).
Vertical cross sections of the annual mean zonal ocean current climatology (m s−1) in the Pacific at 140°W for a GODAS, b GECCO2, c ORA-S3, and d ORA-S4 ocean reanalyses. Green line denotes the climatological annual mean mixed layer depth (m) used for each ocean reanalysis (see text). Vertical cross sections of the annual mean trends in zonal ocean current (m s−1-decade) at 140°W from (3) GODAS, f GECCO2, g ORA-S3, and h ORA-S4 ocean reanalyses, with shading intervals of 0.02 m s−1-decade. Y-axis denotes depth from sea surface
Vertical cross sections of trends in the zonal current speeds at 140°W are shown in Fig. 8e–h. In each reanalysis, both the EUC and the NECC are strengthening in the Pacific. As discussed in Sect. 2, a strengthening of the Pacific EUC is projected in coupled climate models (Luo et al. 2009; Sen Gupta et al. 2012), and reported by Drenkard and Karnauskas (2014) for the SODA reanalysis for the 1871–2008 time period. The Pacific EUC has also shoaled according to the SODA reanalysis over the same period (Drenkard and Karnauskas 2014), and each of the four reanalyses examined here produce some level of shoaling as well. It is especially strong in GODAS (Fig. 8e), and associated with the positive trends of \({F_H}\) in the central tropical Pacific (Fig. 7e).
EUC zonal velocities are primarily accelerated by negative zonal pressure gradients within the ocean mixed layer generated by the westward transport of ocean water by the easterly surface winds, and decelerated by friction (Knauss 1960; McPhaden and Taft 1988). These zonal pressure gradients are directly related to zonal gradients in sea level height in the hydrostatic ocean. Figure 9a–c show tropical and subtropical sea level height climatologies from the GODAS, ORA-S3 and ORA-S4 reanalyses; this quantity is not available from GECCO2. Sea level, which is measured relative to the geoid, is assimilated in each ocean reanalysis and the climatologies are very similar (Fig. 9a–c). Across the Pacific basin, sea level in the western subtropical Pacific is about 0.7 m higher than in the eastern subtropical Pacific, with the largest zonal gradient centered near 15°S.
Sea level climatologies from the a GODAS, b ORA-S3, and c ORA-S4 ocean reanalyses. Contour intervals are 0.15 m. Sea level trends from the d GODAS, e ORA-S3, and f ORA-S4 ocean reanalyses. Contour intervals are 1.2 × 10− 2 m-decade. White, green, and purple stippling denote values found statistically significant at the 90, 95, and 99% levels of confidence, respectively, after accounting for autocorrelation using the Zwiers and von Storch (1995) two-stage table lookup test procedure
Trends in sea level height, shown in Fig. 9d–f, indicate a strengthening of zonal gradients in the tropical Pacific in all three reanalyses. In GODAS (Fig. 9d), sea level trends are negative in the eastern tropical Pacific and positive in the west, similar to the SODA trends discussed in Drenkard and Karnauskas (2014). In ORA-S3 and ORA-S4, sea level rise is small and positive in the east and larger in the west, consistent with the observational analysis of Palanisamy et al. (2015).
On global space scales, positive sea level trends are attributed about equally to steric effects due to water density trends, and to the addition of mass to the oceans as glaciers melt. This addition of mass is not strongly contributing to regional trends in the equatorial Pacific sea level gradients (Purkey et al. 2014). Thermosteric changes, however, contribute to increases in sea level in the warming western tropical Pacific and decreases in the cooling east. Halosteric sea level trends are thought to be small (e.g., Ishii et al. 2006), although recent results suggest that they may be more prominent (Durack et al. 2014). In any event, steric changes in sea level do not change zonal pressure gradients since they do not redistribute mass zonally, and they will not affect the EUC.
Regionally, changes in the wind stress can change sea level, redistribute mass, and, thereby, change zonal pressure gradients and the EUC. With easterly wind stress anomalies in the equatorial Pacific (Fig. 4), we expect higher (lower) sea levels in the western (eastern) tropical Pacific. These changes in sea levels, being associated with mass distribution, will change zonal pressure gradients and the EUC [See Purkey et al. (2014) for an in-depth diagnosis of regional and global sea level trends and the role of depth in their evaluation.]. Separation of the increasing trends in zonal sea level gradients across the tropical Pacific (Fig. 9d–f) is beyond the scope of this study. Here we note that the intensification of the Pacific EUC is consistent with increases in easterly winds stress (Fig. 4) and sea level rise (Fig. 9).
The Pacific NECC is, to first order, a geostrophic current the lies immediately south of the sea level trough at 10°N (Fig. 9a–c). At 140°W (Fig. 8), and, more generally, in the central and eastern Pacific, this trough is strengthening in the three ocean reanalysis (Fig. 9d–f). The result is a strengthening of the Pacific NECC (Fig. 8e–h).
As seen in Fig. 7e–h, Z is not trending in the tropical Atlantic basin. However, some acceleration of the easterly wind stress occurs in the Atlantic in GODAS and, more weakly, in GECCO2 (Fig. 4d, e) south of about 10°S; it is small in ORA-S3 (Fig. 4f). Sea level trends are fairly uniform across the tropical Atlantic (Fig. 9d–f), suggesting that the EUC in the Atlantic is not accelerating as it is in the Pacific. To confirm, Fig. 10 shows vertical cross sections of the zonal current velocity climatology and trends at 30°W from the 4 reanalyses. The Atlantic EUC and NECC are similar in the four reanalysis climatologies (Fig. 10a–d) and, unlike the Pacific, the EUC is located below the mixed layer depth as defined in the GODAS and ORA-S3 reanalyses so its effects are not included in the vertical averaging that produces \({F_H}\). The four reanalyses disagree about how the Atlantic EUC and NECC currents are changing (Fig. 10e–h). The Atlantic EUC is strengthening but not shoaling in GODAS, and shoaling but not strengthening in GECCO2, Ora-S3, and ORA-S4. It is weakening in ORA-S3.
Climatological vertical cross sections of the annual mean zonal ocean current (m s−1) at 30°W for a GODAS, b ORA-S3, and c GECCO2 ocean reanalyses. Green line denotes the climatological annual mean mixed layer depth (m) used for each ocean reanalysis. Vertical cross sections of the annual mean trends in zonal ocean current (m s−1-decade) at 30°W from d GODAS, e ORA-S3, and f GECCO2, with shading intervals of 0.01 m s− 1-decade. Y-axis denotes depth from sea surface
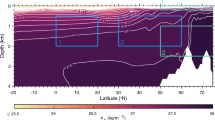
Figure 11a–d show cross-sections at 65°E of zonal ocean currents. Each reanalysis represents the Indian Ocean EUC with similar magnitudes and positions. The Indian Ocean EUC is weaker and shallower than in the Pacific and Atlantic Oceans. Trends in the Indian Ocean EUC, shown in Fig. 11e–h, are quite strong in GODAS and ORA-S3 compared with trends in the other ocean basin. In each reanalysis, there is significant meridional structure in the zonal wind trends, with positive and negative regions alternating approximately every 3°. Since there is strong seasonality in this basin in association with the Indian monsoon, a seasonal analysis in future work may shed more light on changes in this basin.
Climatological vertical cross sections of the annual mean zonal ocean current (m s− 1) at 65°E for the a GODAS, b GECCO2, c ORA-S3 and d ORA-S4 ocean reanalyses. Green line denotes the climatological annual mean mixed layer depth (m) used for each ocean reanalysis. Vertical cross sections of the annual mean trends in zonal ocean current (m s−1-decade) at 65°E from e GODAS, f GECCO2, g ORA-S3 and h ORA-S4, with intervals of 0.01 m s−1-decade. Y-axis denotes depth
5.4 Temperature advection by vertical ocean currents
The climatologies of the vertical advection of heat at the base of the ocean mixed layer, \({F_V}\), in the ocean reanalyses are shown in Fig. 12a–d. North and south of about 10° latitude in both hemispheres, \({F_V}\) values are small in the open ocean in all four ocean reanalyses. Ocean mixed layer cooling (negative values) associated with coastal upwelling extends north and south from the equator in the far eastern Pacific and Atlantic basins. The reanalyses are consistent in producing negative values along the equator in each ocean basin, denoting regions of ocean mixed layer cooling by upwelling. In the tropical Pacific, the reanalyses agree that this cooling is strongest east of the dateline, and it extends poleward along the South and North American coasts. The cooling effects of coastal upwelling are also evident off the west coast of African in the Atlantic basin but, in contrast to the Pacific, equatorial upwelling is zonally uniform. In the Indian Ocean, equatorial upwelling tends to be either centrally located (ORA-S3 and ORA-S4) or positioned in the western part of the basin (GODAS and GECCO2). Small, negative \({F_V}\) values in the subtropics may indicate the role of the STCs in the ocean mixed layer heat budget. Overall, the four reanalysis are in good agreement concerning the distribution of ocean mixed layer cooling by equatorial and coastal upwelling.
Climatology of annual mean F v from the a GODAS, b GECCO2, c ORA-S3, and d ORA-S4 ocean reanalyses, with shading intervals of 10 W m−2. F v trends from e GODAS, f GECCO2, g ORA-S3, and h ORA-S4, with shading intervals of 2 W/m2-decade. Positive (negative) values indicate enhanced warming (cooling) of the ocean mixed layer due to changes in upwelling or downwelling. White, green, and purple stippling denote trends found statistically significant at the 90, 95, and 99% level of confidence, respectively, after taking into account autocorrelation
Similar agreement among the reanalyses does not occur for \({F_V}\) trends, which are shown in Fig. 12e–h. In the Pacific, GODAS produces positive trends along the equator in the central and eastern equatorial Pacific that are flanked by negative trends to the south and, more strongly, to the north (Fig. 12e). The trends are large compared with the climatological values, and they indicate a broadening of the region of equatorial upwelling east of the dateline rather than a weakening of the STCs since most of the subsidence associated with the STCs occurs poleward of 15° latitude (see Fig. 1 in Yang et al. 2014). The GECCO2 reanalysis trends (Fig. 12f) are, in some respects, opposite to those in GODAS in the Pacific. Equatorial upwelling is strengthened in the central Pacific, with weakening in the east. ORA-S3 and ORA-S4 (Fig. 12g, h) display significant small-scale structure in \({F_V}\) trends, with no discernible or consistent pattern in the Pacific.
In summary, we find no consistency among the reanalyses in Pacific \({F_V}\) trends, and they are not in agreement with Yang et al. (2014) who reported a strengthening of the Pacific STC in the SODA reanalysis. There is also disagreement among the four ocean reanalyses on \({F_V}\) trends in the tropical Atlantic and Indian Oceans.
5.5 Sub-grid scale temperature advection—the diffusion term
The final term in the ocean heat budget is D, which is calculated as a residual in Eq. 1
D includes sub-grid-scale vertical advection and diffusion as well as numerical error. An issue that arises in the calculation of D is the source of \({F_{NET}}\) values. One choice is \({F_{NET}}\) as represented in the atmospheric reanalyses, a choice that amounts to connecting both atmospheric and ocean reanalyses for a potentially more robust examination of the surface heat budget. However, as discussed above (see Figs. 2, 3), differences among these fields precludes this approach. For consistency, we use \({F_{NET}}\) in Eq. 5 as provided in each ocean reanalysis output to calculate D. As above, the ERAI value of \({F_{NET}}\) is used as an estimate for ORA-S4 since this reanalysis does not provide FNET in its standard output.
Figure 13a–d show the D climatology for the four reanalyses. In GODAS (Fig. 13a), contributions to ocean mixed layer cooling along the equator in the Pacific with warming in the subtropics is consistent with the presence of STCs—similar to but more clearly expressed than in the GODAS \({F_V}\) field (Fig. 12a). In the Atlantic and Indian Oceans, the GODAS D field captures cooling due to coastal upwelling (in the east in the Atlantic and the west in the Indian Ocean), with warming contributions in the subtropical South Indian Ocean. The GECCO2 D climatology (Fig. 13b) is similar to the GODAS D climatology (Fig. 13a) in that diffusion strengthens and widens the region of cooling along the equator, but without well-defined warming in the subtropical Pacific. This similarity to \({F_V}\) suggests that the contributions to the D climatology from sub-grid-scale vertical heat advection are substantial.
Climatology of annual mean D from the a GODAS, b GECCO2, c ORA-S3, and d ORA-S4 ocean reanalyses, with intervals of 20 W m− 2. D trends from e GODAS, f GECCO2, g ORA-S3, and h ORA-S4, with intervals of 5 W/m2-decade. Positive (negative) values indicate enhanced warming (cooling) of the ocean mixed layer due to changes in diffusion. White, green, and purple stippling denote trends found statistically significant at the 90, 95, and 99% level of confidence, respectively, after taking into account autocorrelation
In contrast to the climatology, the trend in D from the GODAS reanalysis (Fig. 13e) is not similar to the \({F_V}\) trend (Fig. 12e). In the Pacific and Atlantic Oceans, trends in D are negative along the equator and positive off the equator to about 15° latitude. This is reminiscent of the strengthening of the STCs described by Yang et al. (2014) in the SODA reanalysis, and indicates that this strengthening occurs at unresolved space scales in the GODAS reanalysis. In the Indian Ocean, trends in D strengthen the D climatological pattern (Fig. 13a) with warming centered near 15°S and cooling (enhanced upwelling) off the Somali coast.
Trends in D from the GECCO2 and ORA-S3 reanalyses (Fig. 13f–g) are smaller than in GODAS, but with some structural similarity to the GODAS trends. For example, values tend to be negative on the equator in the Atlantic and Pacific with some tendency for positive values off the equator. ORA-S4 D trends (Fig. 13h) are similar to the GODAS trends (Fig. 13e) in the equatorial Pacific, with negative values close to the equator and positive values in much of the subtropics.
In the Indian Ocean, the D climatologies in the Southern Hemisphere (Fig. 13a–d) have a warming maximum centered near 15°S and 90°E that is similar in location and magnitude to the warming maximum in \({F_H}\) (Fig. 7a–d), the cooling maximum in \({F_{NET}}\) (Fig. 2a–d), and the easterly wind stress maximum (Fig. 4a–c). This similarity in D and \({F_H}\) suggests that D represents sub-grid-scale horizontal advection of heat in this region rather than vertical advection.
In GODAS, the region of warming in the southern Indian Ocean associated with D is strengthening at a rate up to 10 W/m2-decade (Fig. 13e) while \({F_H}\) does not have a trend in the same region. This leads to the same conclusion as for the vertical advection in the equatorial region, namely, that trends in \({F_H}\) are being expressed at unresolved space scales. Unlike the equatorial vertical advection example, however, the other 3 reanalyses do not support this conclusion in the southern Indian Ocean.
6 Summary and conclusions
Annual-mean trends in the components of the tropical ocean mixed layer heat budget since 1980 are diagnosed in 4 ocean reanalyses to improve our physical understanding of multidecadal-scale SST trends. The GODAS, GECCO2, ORA-S3 and ORA-S4 oceans reanalyses are examined. Linear trends in annual mean values are calculated, and the evaluation of statistical significance includes an accounting of autocorrelation using the Zwiers and von Storch (1995) two-stage table lookup test procedure. In addition to statistical significance, which only measures how a trend signal emerges from the background variability as represented in the individual reanalyses, confidence in trends is evaluated through physical analysis and agreement among the reanalyses in both the climatology and trends. On annual mean time scales, the heat storage term in the ocean mixed layer heat budget is very small so trends in the components of the ocean mixed layer heat budget are evaluated as a series of mutually-adjusted equilibrium states.
Ocean reanalyses apply the net heat flux from the atmosphere and surface wind stress taken from atmospheric reanalyses as forcing factors. Most ocean reanalyses are dependent on older-generation atmospheric reanalyses for their forcings (e.g., NCEP1, NCEP2, and ERA40), and these reanalyses are known to have deficiencies (Trenberth et al. 2005, 2011) that are better accounted for in newer reanalyses such as ERAI and JRA-55. Climatologies and trends in these factors are compared among the four oceans reanalyses as well as in four atmospheric reanalyses (ERAI, NCEP1, NCEP2, and JRA-55). While the net surface heat flux climatologies are in general agreement across all of these reanalysis products, heat flux trends in GODAS, GECCO2, ORA-S3, NCEP1, and NCEP2 do not agree with each other. However, the two most recent atmospheric reanalysis products (ERAI and JRA-55) are in good agreement and produce consistent, statistically-significant trends in the net surface heat flux. According to these two products, the net heat flux from the atmosphere to the oceans is decreasing throughout most of the tropical Pacific basin, with the largest decreases up to about 10 W/m2-decade in the subtropics, and increasing along the eastern equatorial Pacific and coastal upwelling regions off the North and South American west coasts. In the tropical Atlantic, net surface heat flux trends are warming the eastern basin and cooling the west, with trend magnitudes of 4–8 W/m2-decade. Net surface heat flux trends are negative over most of the Indian Ocean with largest magnitudes of about 8 W/m2-decade close to the equator. Cook and Vizy (2017) discuss the components of this net surface heat flux; here, we take these values as a given forcing into the ocean mixed layer.
Wind stress trends as provided with the GODAS, GECCO2 and ORA-S3 are similar to each other in sign but not in magnitude. Easterly wind stress trends dominate in the central equatorial Pacific (near the dateline), in the eastern South Pacific (0°–30°S), in the South Atlantic (0°–30°S), and in the northern Indian Ocean. There are westerly wind stress trends in the equatorial Pacific from 110°E to 150°E, in the northern tropical Atlantic (0°–20°N), and in the southern Indian Ocean.
Applying forcing factors derived from atmospheric models in the ocean reanalyses provides a tendency for change in the ocean mixed layer heat budget, but change can also enter the reanalysis system when values of temperature, sea level, currents, and salinity from observations are assimilated. Therefore, disagreement among the atmospheric fields used to force the ocean reanalyses does not eliminate the possibility of extracting useful information from the ocean reanalysis about multidecadal changes in the ocean mixed layer heat budget.
A summary and discussion of the findings about trends in the ocean mixed layer heat budget for each tropical ocean basin is provided below.
6.1 Tropical Pacific Ocean
A large-scale zonal pattern in ocean mixed layer temperature trends emerges across the tropical Pacific in each reanalysis, with cooling in the east and warming in the west as discussed in the literature reviewed in Sect. 2 (Fig. 5e–h). This temperature trend pattern is dissimilar to trends in the net heat flux from the atmosphere into the ocean, which is dominated by negative values (decreases in the net heat flux from the ocean to the atmosphere) throughout the basin (Fig. 3e–h).
Across the equatorial Pacific, the EUC is strengthening and shoaling in all four ocean reanalyses (Fig. 8e–h), in agreement with other studies based on coupled climate models and the SODA reanalysis and consistent with increases in easterly winds stress in the eastern Pacific (Fig. 4d–f) and differential sea level rise (Fig. 9d–f). This shoaling of the EUC introduces a dominant warming trend component in the equatorial western and central Pacific and it is influential in determining the longitudinal extent of the eastern Pacific cooling.
The Pacific NECC is strengthening in all 4 reanalyses in association with a strengthening of the sea level trough at 10°N in the central and eastern Pacific (Fig. 9d–f). The result for ocean mixed layer temperatures is a contribution to warming in the Northern Hemisphere subtropics.
Despite agreement in the climatologies of the contributions of resolved vertical motion (\({F_V}\)) to establishing ocean mixed layer temperature distributions (Fig. 12a–d), especially in upwelling regions along the equator and off the west coasts of North and South America, Pacific \({F_V}\) trends are inconsistent across the reanalyses (Fig. 12e–h). Similarity between \({F_V}\) and D climatologies, however, suggests that there are contributions to \({F_V}\) from sub-grid-scale vertical motion in the tropical Pacific. Unlike \({F_V}\) trends, D trends are coherent with agreement across reanalyses. They tend to be negative along the equator and positive off the equator to about 15° latitude. This structure is in agreement with a strengthening of the STCs described by Yang et al. (2014) in the SODA reanalysis, and indicates that this strengthening occurs at unresolved space scales in the GODAS reanalysis. This strengthening contributes to cooling ocean mixed layer and surface temperatures along the equator, especially in the central and eastern Pacific, with weaker warming tendency near 15° latitude in both hemispheres.
In summary, this analysis of the ocean mixed layer heat budget in four ocean reanalyses suggests that the observed warming trends in the western tropical Pacific are associated with a strengthening and shoaling of the EUC, while cooling trends in the eastern tropical Pacific are associated with enhanced heat fluxes from the ocean to the atmosphere. Both are related to a strengthening trend in the tropical easterly winds in the central and eastern tropical Pacific. Further support for cooling in the eastern portion of the basin is provided by a strengthening of the STCs and the associated strengthening of equatorial upwelling.
6.2 Tropical Atlantic Ocean
All 4 ocean reanalyses produce warming of 0.1–0.3 K/decade in the North Atlantic with statistical significance levels ranging from below 90–99% (Fig. 5e–h). The GODAS and GECCO2 reanalyses extend this warming into the Southern Hemisphere to 15°S, and reproduce the SST patterns of the Atlantic Multidecadal Oscillation (AMO) as the AMO index transitions from negative to positive through the analysis period (e.g., Ting et al. 2014; Gu et al. 2016). The ORA-S3 and ORA-S4 reanalyses (Fig. 5g, h) extend the warming trend farther into the Southern Hemisphere, especially in the western subtropical South Atlantic.
According to the ERAI and JRA-55 reanalyses, \({F_{NET}}\)trends have zonal structure in the tropical Atlantic, with net ocean warming in the east and cooling in the west (Fig. 3e–h). The wind stress trends applied to the ocean reanalyses (Fig. 4e–h) are easterly in the South Atlantic (0°–30°S) and westerly, but weaker, in the northern tropical Atlantic (0°–20°N).
The Atlantic is similar to the Pacific in having the EUC strengthening, but only two of the four reanalyses indicate weak shoaling. Another difference from the Pacific is that the NECC in the Atlantic is not strengthening. The result is a more zonally uniform warming in the tropical Atlantic than in the Pacific.
As was the case in the Pacific, Atlantic \({F_V}\) trends are inconsistent across the reanalyses (Fig. 12e–h) but similarity between \({F_V}\) and D climatologies (Fig. 12e–h) suggests that there are contributions to \({F_V}\) from sub-grid-scale vertical motions (D). D trends are also coherent with agreement across reanalyses in the Atlantic, and they tend to be negative along the equator and positive off the equator to about 15° latitude indicating a strengthening of the STCs (Yang et al. 2014) at unresolved space scales. This strengthening contributes to a minimum in warming along the equator.
6.3 Indian Ocean
In the Indian Ocean, all 4 ocean reanalyses produce large-scale warming trends in the mixed layer of 0.2–0.4 K/decade (Roxy et al. 2014) with statistical significance at 90–95% regionally (Fig. 5e–h). This overall warming is interrupted by some regional cooling close to the equator, but it is not statistically significant in any of the datasets. Anomaly structure is suggestive of the Indian Ocean dipole mode in GECCO2, but only weakly in GODAS and not at all in ORA-S3 or ORA-S4.
According to the ERAI and JRA-55 reanalyses, net surface heat flux trends are negative over most of the Indian Ocean with maximum values close to the equator, indicating increasing heat fluxes from the ocean to the atmosphere. Weak westerly wind stress trends occur in the southern Indian Ocean with weak easterly trends in the northern Indian Ocean.
Trends in the Indian Ocean EUC are strong in GODAS and ORA-S3 compared with trends in the other ocean basins, with positive and negative regions alternating approximately every 3° of latitude. Because of stronger seasonality in the equatorial and northern Indian Ocean associated with the monsoon, the annual analysis may not be adequate for studying physical processes. In the southern Indian Ocean, similarity between the \({F_H}\) and D terms of the heat budget suggests that warming in this region is associated with sub-grid-scale horizontal heat advection rather than vertical advection in the GODAS reanalysis, but the other three reanalyses do not support this conclusion.
This comparison among ocean reanalyses reveals a number of similarities and the emergence of statistical significance that help explain how the tropical ocean mixed layer heat budget is adjusting on the warming planet. We have retained a large scope for this project to enable a comparison among the three ocean basins in addition to the comparison among four ocean reanalyses. Next steps should include a focus on individual ocean basins, including a consideration of seasonality.
References
Alory G, Wijffels S, Meyers G (2007) Observed temperature trends in the Indian Ocean over 1960–1999 and associated mechanisms. Geophys Res Lett 34, Art. No. L02606. doi:10.1029/2006GL028044
Balmaseda MA, Vidard A, Anderson DLT (2008) The ECMWF ocean analysis system: ORA-S3. Mon Weather Rev 136:3018–3034
Balmaseda MA, Mogensen K, Weaver AT (2013) Evaluation of the ECMWF ocean reanalysis system ORAS4. QJR Meteorol Soc 139:1132–1161
Balmaseda MA, Hernandez F, Storto A, Palmer MD, Alves O et al (2015) The ocean reanalyses intercomparison project (ORA-IP). J Oper Oceanogr 8(sup1):s97
Behringer DW, Xue Y (2004) Evaluation of the global ocean data assimilation system at NCEP: The Pacific Ocean. Eighth Symposium on Integrated Observing and Assimilation Systems for Atmosphere, Oceans, and Land Surface, AMS 84th Annual Meeting, Washington State Convention and Trade Center, Seattle, Washington, pp 11–15
Carton J, Giese B (2008) A reanalysis of ocean climate using Simple Ocean Data Assimilation (SODA). Mon Weather Rev 136:2999–3017
Chen X, Tung KT (2014) Varying planetary heat sink led to global-warming slowdown and acceleration. Science 345:897–903. doi:10.1126/science.1254937
Cheng W, McPhaden MJ, Zhang D, Metzger EJ (2007) Recent changes in the Pacific subtropical cells inferred from an eddy-resolving ocean circulation model. J Phys Oceanog 37:1340–1356
Compo GP, Sardeshmukh PD (2010) Removing ENSO-Related variations from the climate record. J Clim 23:1957–1978
Cook KH, Vizy EK (2017) Multidecadal adjustment of the net surface heat flux over the tropical and subtropical oceans. Clim Dyn (submitted)
de Boyer Montegut G, Madec AS, Lazar FA, Iudicone D (2004) Mixed layer depth over the global ocean? An examination of profile data and a profile-based climatology. J Geophys Res 109:C12003
Dee DP, Uppala SM, Simmons AJ et al (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q J R Meteorol Soc 137:553–597
Dong L, Zhou T (2014) The formation of the recent cooling in the eastern tropical Pacific Ocean and the associated climate impacts: a competition of global warming, IPO, and AMO. J Geophys Res-Atmos 119:11272–11287
Dong L, Zhou TJ, Dai AG, Song FF, Wu B, Chen XL (2016) The footprint of the inter-decadal Pacific Oscillation in Indian Ocean sea surface temperatures. Sci Rep 6, Art. No. 21251. doi:10.1038/srep21251
Drenkard EJ, Karnauskas KB (2014) Strengthening of the Pacific equatorial undercurrent in the SODA reanalysis: mechanisms, ocean dynamics, and implications. J Clim 27:2405–2416
Drijfhout SS, Blaker AT, Josey SA, Nurser AJG, Sinha B, Balmaseda MA (2014) Surface warming hiatus caused by increased heat uptake across multiple ocean basins. Geophys Res Lett 41:7868–7874. doi:10.1002/2014GL061456
Durack PJ, Wijffels SE (2010) Fifty-year trends in global ocean salinities and their relationship to broad-scale warming. J Clim 23:4342–4362
Durack PJ, Wijffels SE, Gleckler PJ (2014) Long-term sea-level change revisited: the role of salinity. Env Res Lett 9(Art. No):114017
England MH, McGregor S, Spence P, Meehl GA, Timmermann A, Cai W, Gupta AS, McPhaden MJ, Purich A, Santoso A (2014) Recent intensification of wind-driven circulation in the Pacific and the ongoing warming hiatus. Nat Clim Change 4:222–227. doi:10.1038/nclimate2106
Gu G, Adler RF, Huffman GJ (2016) Long-term changes/trends in surface temperature and precipitation during the satellite era (1979–2012). Cli Dyn 46:1091–1105
Hakkinen S, Rhines PB, Worthen DL (2015) Heat content variability in the North Atlantic Ocean in ocean reanalyses. Geophys Res Lett 42:2901–2909
Ishii M, Kimoto M, Sakamoto K, Iwasaki SI (2006) Steric sea level changes estimated from historical ocean subsurface temperature and salinity analyses. J Oceanog 62:155–170
Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, Gandin L, Iredell M, Saha S, White G, Woollen J, Zhu Y, Leetmaa A, Reynolds R, Chelliah M, Ebisuzaki W, Higgins W, Janowiak J, Mo KC, Ropelewski C, Wang J, Jenne R, Joseph D (1996) The NCEP/NCAR 40-year reanalysis project. Bull Am Meteorol Soc 77:437–470
Kanamitsu M, Ebisuzaki W, Woollen J, Yang S-K, Hnilo JJ, Fiorino M, Potter GL (2002) NCEP-DOE AMIP-II Reanalysis (R-2). Bull Am Meteor Soc 83:1631–1643
Kara AB, Rochford PA, Hurlburt HE (2003) Mixed layer depth variability over the global ocean. J Geophys Res 108(C3):3079.
Knauss JS (1960) The structure of the Pacific equatorial countercurrent. J Geophys Res 66:143–155
Kobayashi S, Ota Y, Harada Y, Ebita A, Moriya M, Onoda H, Onogi K, Kamahori H, Kobayashi C, Endo H, Miyaoka K, Takahashi K (2015) The JRA-55 reanalysis: general specifications and basic characteristics. J Meteorol Soc Jpn 93:5–48.
Köhl A (2015) Evaluation of the GECCO2 ocean synthesis: transports of volume, heat and freshwater in the Atlantic. Q J R Meterol Soc 141(686):166–181, doi:10.1002/qj.2347
Kosaka Y, Xie SP (2013) Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature 501:403–405. doi:10.1038/nature12534
Levitius S, Burgett R, Boyer TP (1994) World Ocean Atlas. National Oceanic and Atmospheric Administration, Silver Spring
Levitus S, Antonov JI, Boyer TP, Baranova OK et al (2012) World ocean heat content and thermosteric sea level change (0–2000 m), 1955–2010. Geophys Res Lett. doi:10.1029/2012GL051106
Liebmann B, Dole RM, Jones C, Blade I, Allured D (2010) Influence of choice of time period on global surface temperature trend estimates. Bull Am Meteorol Soc 91:1485–1491. doi:10.1175/2010BAMS3030.1
Luo Y-Y, Rothstein LM (2011) Response of the Pacific ocean circulation to climate change. Atmos Ocean 49:235–244
Luo Y-Y, Rothstein LM, Zhang R-H (2009) Response of Pacific subtropical-tropical thermocline water pathways and transports to global warming. Geophys Res Lett 36:L04601
McPhaden MJ, Taft BF (1988) On the dynamics of the seasonal and intraseasonal variability in the eastern equatorial Pacific. J Phys Oceanogr 18:1713–1732
McPhaden MJ, Zhang DX (2004) Pacific Ocean circulation rebounds. Geophys Res Lett 31:L18301
Meehl GA, Hu A, Arblaster JM, Fasullo J, Trenberth KE (2013) Externally forced and internally generated decadal climate variability associated with the Interdecadal Pacific Oscillation. J Clim 26:7298–7310
Nieves V, Willis JK, Patzert WC (2015) Recent hiatus caused by decadal shift in Indo-Pacific heating. Science 349:532–535. doi:10.1126/science.aaa4521
Palanisamy H, Cazenave A, Delacroix T, Meyssignac B (2015) Spatial trend patterns in the Pacific Ocean sea level during the altimetry era: the contribution of thermocline depth change and internal climate variability. Ocean Dyn 65:341–356
Palmer MD, Roberts CD, Balmaseda M et al (2015) Ocean heat content variability and change in an ensemble of ocean reanalyses. Clim Dyn. doi:10.1007/s00382-015-2801-0
Purkey SG, Johnson GC, Chambers DP (2014) Relative contributions of ocean mass and deep steric changes to sea level rise between 1993 and 2013. J Geophys Res 119:7509–7522
Rao SA, Dhakate AR, Saha SK, Mahapatra S, Chaudhari HS, Pokhrel S, Sahu SK (2012) Why is Indian Ocean warming consistently? Clim Change 110:709–719. doi:10.1007/s10584-011-0121-x
Roxy MK, Ritika K, Tarray P, Masson S (2014) The curious case of Indian Ocean warming. J Clim 22:8501–8509
Sen Gupta A, Ganachaud A, McGregor S, Brown JN, Muir L (2012) Drivers of the projected changes to the Pacific Ocean equatorial circulation. Geophys Res Lett 39:L09605
Servain J, Caniaux G, Kouadio YK, McPhaden MJ, Araujo M (2014) Recent climatic trends in the tropical Atlantic. Clim Dyn 43:3071–3089
Solomon A, Newman M (2012) Reconciling disparate twentieth-century Indo-Pacific ocean temperature trends in the instrumental record. Nat Clim Change 2:691–699. doi:10.1038/nclimate1591
Song X, Yu L (2013) How much net surface heat flux should go into the Western Pacific Warm Pool? J Geophys Res Oceans 118:3569–3585
Thompson DWJ, Wallace JM, Kennedy JJ, Jones PD (2010) An abrupt drop in Northern Hemisphere sea surface temperature around 1970. Nat Lett Res 467:444–447. doi:10.1038/nature09394.
Ting M, Kushnir Y, Li C (2014) North Atlantic multidecadal oscillation: external forcing versus internal variability. J Mar Syst 113:27–38
Toyoda T, Fujii Y, Kuragano T, Kamachi M, Ishikawa Y, Masuda S, Sato K, Awaji T, Hernandez F, Ferry N, Guinehut S, Martin M, Peterson KA, Good SA, Valdivieso M, Haines K, Storto A, Masina S, Köhl A, Zuo H, Balmaseda M, Yin Y, Li Shi, Alves O, Smith G, Chang Y-S, Vernieres G, Wang X, Forget G, Heimbach P, Wang O, Fukumori I, Lee T (2015) Intercomparison and validation of the mixed layer depth fields of global ocean syntheses. Clim Dyn. doi:10.1007/s00382-015-2637-7
Trenberth KE, Fasullo JT, Smith L (2005) Trends and variability in column-integrated water vapor. Clim Dyn 24:741–758. doi:10.1007/s00382-005-0017-4
Trenberth KE, Fasullo JT, Mackaro J (2011) Atmospheric moisture transport from ocean to land and global energy flows in reanalyses. J Clim 24:4907–4924. doi:10.1175/2011JCLI4171.1
Uppala SM, Kallberg PW, Simmons AJ et al (2005) The ERA-40 reanalysis. Q J R Meteorol Soc 131:2961–3012
Valdivieso M, Haines K, Balmaseda M, Chang Y-S, Drevillon M, Ferry N, Fujii Y, Köhl A, Storto A, Toyoda T, ang X, Waters J, Xue Y, Yin Y, Barnier B, Hernandez F, Kumar A, Lee T, Masina S, Andrew Peterson K (2015) An assessment of air-sea heat fluxes from ocean and coupled reanalyses. Clim Dyn. doi:10.1007/s00382-015-2843-3
Yang CX, Giese BS, Wu LX (2014) Ocean dynamics and tropical Pacific climate change in ocean reanalyses and coupled climate models. J Geophys Res Oceans 119:7066–7077
Zwiers FW, von Storch H (1995) Taking serial correlation into account in tests of the mean. J Clim 8:336–351
Acknowledgements
Support for National Science Foundation Award 1356386 is gratefully acknowledged. We also extend our appreciation to the groups who have so carefully assembled the reanalyses and made them available, the Texas Advanced Computing Center at the University of Texas at Austin for providing the high performance computing and database resources, and to Caroline Binkley for assistance with some of the preliminary analysis.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Cook, K.H., Vizy, E.K. & Sun, X. Multidecadal-scale adjustment of the ocean mixed layer heat budget in the tropics: examining ocean reanalyses. Clim Dyn 50, 1513–1532 (2018). https://doi.org/10.1007/s00382-017-3703-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-017-3703-0