1 Introduction

The Mistral and Tramontane are mesoscale winds in southern France. Both winds are channeled through valleys and impact the hydrological cycle of the Mediterranean Sea by causing deep-water formation in the Gulf of Lion (Marshall and Schott 1999; Somot et al. 2016). The Mistral passes through the Rhône valley between the Alps and Massif Central from north to south, while the Tramontane emerges in the Aude valley between the Pyrenees and Massif Central (Fig. 1). In these constricting valleys, both cold and dry winds accelerate before they reach the Mediterranean Sea at the Gulf of Lion. They are caused by similar synoptic situations, and consequently, they often coincide (Georgelin et al. 1994; Guenard et al. 2005). Furthermore, Mistral and Tramontane winds can increase the risk and propagation of bush fires because of the dry polar air they bring to southern France (Pugnet et al. 2013).

Fig. 1
figure 1

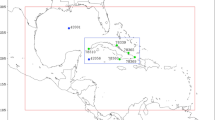
ETOPO1 (Amante and Eakins 2009) orography (shaded in red) and bathymetry data (shaded in blue) in Mistral and Tramontane regions (units are meters). Analysis areas of Mistral and Tramontane valleys (outlined in orange and turquoise, respectively) and the Gulf of Lion (outlined in gray) area shown, as well as locations of stations for gust time series in Mistral (orange symbols) and Tramontane (turquoise symbols) areas such as in the valleys (circles) and plains (triangles), and close to the coast (squares)

Full size image

In this study, a possible change in Mistral and Tramontane frequency and intensity under future climate conditions is surveyed. The frequency of occurrence and intensity of Mistral and Tramontane winds are of great interest not only for risk assessments under changing climatic conditions, but also for scientific reasons. Many case studies have dealt with Mistral and Tramontane events (e.g., Drobinski et al. 2005; Berthou et al. 2016). Obermann et al. (2016) found the sea-level pressure fields associated with an occurrence of Mistral and Tramontane to be simulated equally well in simulations with 0.088\(^\circ\)–0.44\(^\circ\) grid spacing, while higher resolution simulations perform better in terms of wind speed and wind direction. Herrmann et al. (2011) and Ruti et al. (2008) found the representation of wind speeds in the Mediterranean region to be improved by increasing the resolution of the model employed.

Numerous studies deal with near-surface wind speeds over Europe in climate projections (see Pryor et al. 2006, 2012; Rockel and Woth 2007), as well as changes in wind energy potential (e.g., Hueging et al. 2013) and loss potential due to windstorms (Pinto et al. 2012). Rockel and Woth (2007) found that the number of storm peaks (gusts greater then 8 Bft) increase over Western and Central Europe when applying the Special Report on Emissions Scenarios (SRES, Nakicenovic and Swart 2000) A2 scenario, while their number decreases over the Western Mediterranean Sea. This is consistent with the findings of Beniston et al. (2007), who found an increase in simulated 90th percentiles of surface wind speeds north of the Alps and a decrease south of the Alps in SRES A2 simulations. Najac et al. (2008, 2011) projected that the wind speeds in the Mistral and Tramontane area in 2046–2065 will be lower than those in 1971–2000 in an ensemble of SRES A1B simulations. Somot et al. (2006) found a decrease in wind stress over the Mediterranean Sea in a SRES A2 simulation, especially in the Gulf of Lion area. Hueging et al. (2013) and Nikulin et al. (2011) projected a decrease in wind energy density and maximum wind speed in regional climate simulations driven by SRES A1B global simulations. However, to the best knowledge of the authors, the frequencies of occurrence of Mistral and Tramontane events in climate models have not yet been surveyed.

In this paper, a method to estimate future Mistral/Tramontane (M/T) occurrence frequencies is presented. A classification algorithm was applied to identify sea-level pressure patterns that permit Mistral and Tramontane winds, following the approach of Obermann et al. (2016), who used empirical orthogonal functions of mean sea-level pressure fields and mapped it to Mistral and Tramontane time series derived from station observations. Regional climate model (RCM) simulations driven by ERA-Interim data (Dee et al. 2011) were used to calibrate the classification algorithm and to estimate its accuracy. Five simulations with three RCMs at 0.44\(^\circ\) grid spacing from the Med-CORDEX framework (Ruti et al. 2015) driven by global circulation models (GCMs) from the fifth phase of the Climate Model Intercomparison Project (CMIP5, Taylor et al. 2012) were then evaluated. Climate projections for two representative concentration pathways (RCPs, Moss et al. 2010) are available within the Med-CORDEX dataset (RCP4.5 and RCP8.5) and are discussed in this paper. In addition, the wind speeds during Mistral and Tramontane events are discussed.

This paper is structured as follows. The observation and simulation data are discussed in Sect. 2. Then, the methods used are explained in Sect. 3, followed by the results and discussion in Sect. 4. The last section contains a summary of this work and the conclusions.

2 Data

The data used in this study include station observations, reanalysis data, GCMs, and RCMs. Table 1 gives an overview of the GCMs and RCMs.

Table 1 GCM and RCM simulations and modeling groups
Full size table

2.1 Observational Mistral and Tramontane time series

Mistral and Tramontane time series derived from station data are used for both training and testing of the classification algorithm for identifying Mistral and Tramontane situations. The daily gust time series from 13 Météo-France stations in the Mistral and Tramontane regions (locations are shown in Fig. 1) provide gust data with wind velocities greater than 16 m/s from the dominant Mistral and Tramontane directions at each individual station. These observation data are available for the period 1981–2010. The days were tagged based on the occurrence of the two wind systems of interest. The method for Mistral and Tramontane identification is described in Obermann et al. (2016), where this method was applied to the period 2001–2009. Table 2 gives the resulting numbers of Mistral and Tramontane days in 1981–2010.

Table 2 Observed frequency of Mistral and Tramontane days in 1981–2010
Full size table

2.2 ERA-Interim

The reanalysis dataset ERA-Interim (Dee et al. 2011) is used as a forcing for the evaluation runs of the RCMs in this study. It is calculated with a grid resolution of about 80 km. Sea-level pressure fields from ERA-Interim are used together with the observational Mistral and Tramontane time series to train the classification algorithm. ERA-Interim data were provided by the European Centre for Medium-Range Weather Forecasts (ECMWF) database.

2.3 Global circulation models (GCMs)

The Earth System Model (MPI-ESM, Mauritsen et al. 2012; Giorgetta et al. 2013) of the Max-Planck-Institut für Meteorologie (Max Planck Institute for Meteorology, MPI-M) comprises the atmosphere model ECHAM6 (Stevens et al. 2013) and the ocean model MPIOM (Jungclaus et al. 2013). The two model configurations, LR (low resolution) and MR (medium resolution), differ in the number of levels in the atmosphere (LR: 47, MR: 95) and ocean grid spacing (LR: 1.5\(^\circ\), MR: 0.4\(^\circ\)).

ECHAM5, (Roeckner et al. 2003) with a grid spacing of about 0.75\(^\circ\) and 31 vertical levels, is the atmospheric component of the Centro Euro–Mediterraneo sui Cambiamenti Climatici (CMCC) Climate Model (CMCC-CM). In this model, the ocean is represented by OPA 8.2 (Madec et al. 1997) in the ORCA2 configuration (0.5\(^\circ\)–2\(^\circ\) grid spacing).

HadGEM2-ES is the earth system version of the Hadley Centre Global Environment Model version 2 (HadGEM2, The HadGEM2 Development Team: Martin et al. 2011). It has a grid spacing of 1.25\(^\circ\)–1.875\(^\circ\) in the atmosphere and 0.33\(^\circ\)–1.0\(^\circ\) in the ocean component. Simulations were done by the Met Office Hadley Centre (MOHC) and Instituto Nacional de Pesquisas Espaciais (INPE).

CNRM-CM5 (Voldoire et al. 2013) consists of the atmosphere model ARPEGE-climat v5.2 (Météo-France 2009) with a grid spacing of about 1.4\(^\circ\), 31 vertical levels, and the ocean model NEMO v3.2 (Madec 2008), with a grid spacing of 0.3–1\(^\circ\) and 43 vertical levels. The simulations used in this study were produced by the Centre National de Recherches Météorologiques/Centre Européen de Recherche et Formation Avance en Calcul Scientifique (CNRM-CERFACS).

2.4 Regional climate models (RCMs)

The regional climate simulations investigated in this study were prepared in the Med–CORDEX framework (Ruti et al. 2015) and HyMeX program (Drobinski et al. 2014), and were performed on the Med–CORDEX domain (encompassing the Mediterranean and Black Sea, as well as the surrounding land areas). Data from five different combinations of GCMs and atmosphere-only RCMs are available in the MedCORDEX database on \(0.44^\circ\) grids. In this study, the simulations are identified by the name of the RCM for ERA-Interim driven simulations. GCM driven simulations are identified by the GCM’s name followed by the name of the RCM applied.

Simulations with the COSMO-CLM (CCLM) model (see Rockel et al. 2008) were performed at two institutions: CMCC and Goethe University, Frankfurt (GUF). Simulations driven by ERA-Interim and MPI-ESM-LR were performed at GUF with CCLM4-8-18. The CCLM simulations produced by CMCC used model version CCLM4-8-19, and were driven by ERA-Interim and CMCC-CM.

RegCM4-3 (see Giorgi et al. 2012) is a hydrostatic model. The RegCM4-3 runs were performed by the International Center for Theoretical Physics (ICTP).

CNRM performed the simulations with the limited area version of ARPEGE, ALADIN version 5.2 (Colin et al. 2010; Herrmann et al. 2011) driven by ERA-Interim and CNRM-CM5.

2.5 Temporal and spatial interpolation of simulation datasets

Sea-level pressure datasets were interpolated bilinearly to a common \(0.25^\circ\) grid in the area \(-20.25\)–\(20.25^\circ\) E and 25.75–\(55.5^\circ\) N (treated in the same way as sea-level pressure fields in Obermann et al. (2016)). Unless stated otherwise, calculations are based on daily means. The mean wind speeds in Mistral and Tramontane areas were obtained by calculating spatial averages for the areas indicated in Fig. 1.

3 Methods

3.1 Sea-level pressure pattern classification

A classifying algorithm based on an empirical orthogonal function (EOF) analysis in conjunction with a Bayesian network was used to determine on which days the simulated large-scale sea-level pressure fields were likely to produce a Mistral or Tramontane event. For an introduction to Bayesian networks, see Scutari (2010). An introduction to EOF analysis can be found in von Storch and Zwiers (2001).

In this study, we follow the approach of Obermann et al. (2016), where the classification process is discussed in detail. In both cases, a similar classification algorithm is used for identifying Mistral and Tramontane days in daily mean sea-level pressure fields from Med-CORDEX regional climate simulations. Therefore, only differences between earlier work and the present approach are discussed here.

The classification algorithm consists of the following three steps: preparation of input data, structure learning and training, and processing the output. In contrast to the above-mentioned paper, the EOFs were calculated from ERA-Interim sea-level pressure fields for the time interval 1981–2010 instead of 2000–2008. Although calculated for a different time period, the resulting EOFs look very much alike. A longer time series (30 years instead of 9 as in Obermann et al. 2016) of fewer principal components (the first 50 instead of the first 100) of ERA-Interim EOFs and the observed M/T time series were used for training. Higher numbers of EOFs were tested with the 30-yr training period, but did not significantly increase the number of correctly identified M/T days. Furthermore, large numbers of EOFs would introduce noise to the classification algorithm by adding small scale variations because Mistral and Tramontane winds are mesoscale phenomena driven by sea-level pressure gradients on scales of hundreds of kilometers.

Given a set of principal components from the EOF analysis of ERA-Interim, an RCM, or a GCM, the trained Bayesian networks’ output is a number indicating if a day is likely to be a Mistral or Tramontane day or not. Values above a certain threshold were regarded as Mistral or Tramontane days, while those below the threshold were regarded as non-Mistral or non-Tramontane days. The threshold was chosen in such a way that the numbers of Mistral and Tramontane days in the overlapping time period of observed time series and simulations were the same. The thresholds were kept constant over the whole simulation period for the 1950–2100 simulations.

The proportion correct (PC) score is the percentage of days on which simulations and observations agree on the occurrence of a Mistral as well as a Tramontane event during a given time period. The mean obtained PC score (all year) for ERA-Interim was about 70\(\%\) for training periods longer than 9 years. The full 30 years of available data were used for training because the PC score varies depending on the days used for training, and an extended training period smooths possible distortions introduced by exceptional individual random samples.

3.2 Testing the classification algorithm

To get an estimate of the classification accuracy, the classification algorithm was applied to the ERA-Interim-driven RCM simulations. Figure 2 shows the number of Mistral and Tramontane days per year (i.e., from December of the previous year to November of the actual year) identified by the classification algorithm for ERA-Interim and ERA-Interim driven simulations. Correlations of simulated and observed days per year were 0.44 and higher for Mistral as opposed to 0.67 and higher for Tramontane, respectively (Table 3). Table 3 also shows the PC scores of the ERA-Interim-driven simulations with the observation Mistral and Tramontane time series as reference. The PC score reaches values between 66.6 and 70.6\(\%\) in the ERA-Interim period. The obtained PC scores of the RCMs were higher than those in the trivial cases. If all days were identified as non-Mistral and non-Tramontane days, a PC score of 64.60% would be reached. For the second trivial case, i.e., if all days were identified as Mistral and Tramontane days, the resulting PC score would be 12.61%.

Fig. 2
figure 2

Number of Mistral and Tramontane days per year in ERA-Interim, ERA-Interim-driven simulations, and observations

Full size image
Table 3 Proportion correct (PC) score, correlation, and average period length of Mistral and Tramontane events from ERA-Interim and ERA-Interim-driven RCMs for the years 1982 to 2010 (1982 to 2008 for RegCM4-3) in days
Full size table

All simulations are able to reproduce the number of M/T days per year, but the results overestimate the period length. If the Mistral and Tramontane days were distributed randomly, the average period length would be \(\approx\)1.2 days for Mistral winds and \(\approx\)1.5 days for Tramontane winds. The observed time series, however, shows higher average period lengths (1.7 for Mistral and 2.5 for Tramontane winds). The simulations overestimate the period length by 17–35%. The reason for this could be an erroneous modeling of blocking situations, which causes the simulation to change too rarely from an M/T to a non-M/T situation and vice versa. The PC score of the RCMs with ERA-Interim as reference is 81.2–83.5%, which is in agreement with the results of Sanchez-Gomez et al. (2009) on the reproduction of ERA-Interim weather regimes in RCMs.

A pair of CCLM4-21-2 simulations (one of them coupled to NEMO, Akhtar et al. 2014) was used to test the influence of coupling (not shown). The coupled run shows a slightly higher PC score than its uncoupled counterpart. The average period length is not influenced by coupling. Therefore, the coupling has a minor significant effect on Mistral and Tramontane time series obtained from sea-level pressure patterns. This is consistent with the results of Artale et al. (2010) for RegCM3 and Herrmann et al. (2011) for ALADIN simulations.

4 Results and discussion

4.1 GCM simulations

Tables 4 and 5 show the 30-yr means and standard deviations of M/T days per year for the GCMs. Values were calculated only if at least 20 years of simulation data were available for the given time period (e.g., 1981–2005 instead of 1981–2010 for the GCM simulations ending in 2005). The GCMs show no significant change in Mistral days per year between the reference period (1981–2010) and the end of the 21st century. All GCM simulations except MPI-ESM-LR showed a decrease in Tramontane days per year. Most of them show a significant decrease in Tramontane days in RCP8.5, but do not agree if the change in number of Mistral events is stronger in RCP4.5 or RCP8.5. Few periods show a significant difference in mean or variance at the 95% significance level compared to the period 1981–2010.

Table 4 Mean \(\bar{x}\) and standard deviation \(\sigma\) of GCM simulated Mistral days per year for 1981–2010 and differences expressed as \(\Delta \bar{x}\) and \(\Delta \sigma\) to the values of that period
Full size table
Table 5 Same as Table 4 but for Tramontane days in GCMs
Full size table

4.2 RCM simulations

Figure 3 shows the 30-yr running mean of M/T days per year for RCMs in the 1950–2100 period. Tables 6 and 7 give the 30-yr averages and standard deviations of windy days per year. When both the RCP4.5 and RCP8.5 scenarios are available, the mean number of windy days per year is lower in the RCP8.5 scenario than in the RCP4.5 scenario for most models. Besides HadGEM2-RegCM4-3 showing a smaller number of Mistral days in summer and a larger number in winter, the simulations agree on the distribution of windy days over the seasons (not shown).

Fig. 3
figure 3

Thirty-year running mean of Mistral and Tramontane days per year in historical runs (dashed), RCP4.5 (full lines), and RCP8.5 (dotted lines) scenarios and mean of observed Mistral and Tramontane days per year (black dots)

Full size image
Table 6 Overview analog to Table 4 but for Mistral days in RCMs
Full size table
Table 7 Overview analog to Table 4 but for Tramontane days in RCMs
Full size table

Figure 4 shows the 30-yr running mean of M/T period lengths for RCMs in the 1950–2100 period. With more than 3.5 days for Tramontane winds, HadGEM2-RegCM4-3 shows larger average period lengths than the other models, while both CCLM versions show short period lengths of less than 2 days for Mistral winds and about 2.5 days for Tramontane winds. MPIESM-RegCM4-3 and both CCLM simulations for RCP8.5 show a decrease in Tramontane period lengths over the 21st century. Nevertheless, the observed period lengths stay above the expected period lengths for the case of randomly distributed events.

Fig. 4
figure 4

Time series of 30-yr running means of Mistral and Tramontane period lengths in days. Legend as in Fig. 3

Full size image

4.3 GCM constraint on RCMs

To estimate the influence of the driving GCM on the M/T representation in RCMs, the PC score of the two setups MPI-ESM-LR-CCLM4-8-18 and CMCC-CM5-CCLM4-8-19 with the driving GCM as reference is used. These runs provide the longest time series of the models in this study, and both RCP4.5 and RCP8.5 simulations are available. The PC scores are given in Table 8. The PC score between the RCM simulations and the driving GCMs is about \(80\%\). This shows that the RCMs are constrained by the driving GCM, consistent with the results of Sanchez-Gomez et al. (2009), who found the RCMs ALADIN, CCLM, and RegCM to reproduce similar weather regimes as the driving dataset in about 70–90% of the cases. When looking at Mistral days only, the proportion of correct score reaches higher values than for Tramontane winds.

Torma and Giorgi (2014) found temperature and precipitation in RegCM simulations to be more sensitive to the applied convection scheme than to the driving GCM in some regions of the Med-CORDEX domain. Such a dependency on internal model physics could also affect pressure and wind speed. Different physics schemes, therefore, could cause RegCM4-3 and CCLM to show fewer M/T days than the driving GCMs and CNRM-CM5-ALADIN52 to show more M/T days than the driving GCMs. Furthermore, the RCMs show stronger changes than their driving GCMs for Tramontane winds. The higher agreement with GCMs in the Mistral case could be due to the fact that the Alps are more visible in coarser grids than the Pyrenees, and therefore higher resolution runs are necessary to simulate the Tramontane winds well. Another possible explanation is that pressure pattern details are less important for Mistral winds because the Alps strongly constrain them.

Table 8 PC score of CCLM runs with driving GCMs as reference
Full size table

4.4 Pressure pattern persistence

The autocorrelation of principal components time series with a lag of one or more days can be used to determine the persistence of pressure patterns. Here, we use the number of lagged days after which the autocorrelation decreases below 0.5 to evaluate the persistence of pressure patterns. For ERA-Interim, this value is 0–1 days for most principal components. Only the first three principal components show higher persistence (3, 5, and 2 days, respectively). All simulations show an increase in persistence of the second principal component in both the RCP4.5 and RCP8.5 simulations compared to the historical simulations, with RCP8.5 runs showing the highest persistence. The RCM simulations show longer persistence in several higher principal components, while the GCMs show no persistence in higher order principal components.

4.5 Wind speed changes

Figure 5 shows the mean wind speed in Mistral and Tramontane areas (both including the Gulf of Lion area, areas as indicated in Fig. 1) for M/T days and non-M/T days. The M/T days show significantly higher wind speeds than the non-M/T days for all simulations. Both RegCM4-3 simulations show a smaller difference between M/T and non-M/T days than the other RCMs. Figure 6 shows the difference in wind speed 90th percentiles between the periods 2071–2100 and 1981–2010. The Gulf of Lion region shows the largest differences. The changes in the RCP8.5 simulations are greater than those in RCP4.5.

Figure 6 shows a decrease in the wind speed 90th percentile in the Gulf of Lion for all RCM simulations. This decrease could be due to fewer Tramontane events. The two models that have more classified Mistral days in 2071–2100 (CNRM-CM5-ALADIN52 and MPI-ESM-LR-CCLM4-8-18) show a small decrease (CNRM-CM5-ALADIN52 for RCP8.5 even shows an increase) in the 90th percentile in the Mistral area. Most simulations show a decrease in the same areas as was found for SRES scenarios A1B (e.g., Najac et al. 2008, 2011) and A2 (Somot et al. 2006).

Fig. 5
figure 5

Thirty-year running mean wind speed on days with Mistral and Tramontane (upper half of figures) and without Mistral and Tramontane (lower half of figures) in the Mistral, Tramontane, and Gulf of Lion (GoL) areas. Legend as in Fig. 3

Full size image
Fig. 6
figure 6

Difference in 90th percentile of daily mean surface wind speed between the periods 2071–2100 and 1981–2010 (units are meters per second)

Full size image

4.6 Classification quality in future climate conditions

The climate could change to a state in which different types of Mistral and Tramontane winds occur that were not present in the training period and, therefore, could not be detected by the classification algorithm. The principal components of several EOFs show changes in their mean during the 21st century (data not shown), which is indicative of a change in sea-level pressure patterns. Since Mistral and Tramontane winds depend on orographic effects such as channeling, as well as pressure gradients, a spatial shift in the pressure patterns relative to the orography should lead to a different number of M/T days. If the classification algorithm happened to be erroneous and, therefore, failed to identify M/T days, there should be a drift in the wind speed during M/T days and non-M/T days to more similar values, i.e., the gap in wind speed between M/T and non-M/T days decreases. If more days with M/T were classified as non-M/T, the average non-M/T wind speed would increase, while non-M/T days classified as M/T day would lead to a decrease in M/T-day wind speed. Since the mean wind speeds during neither M/T nor non-M/T days show a large change in the 21st century, this effect appears unlikely.

5 Summary and conclusion

In this study, Mistral and Tramontane frequencies of occurrence in climate simulations ranging from 1950 to 2100 were derived from simulated sea-level pressure patterns using EOFs and a Bayesian network. The results for the ERA-Interim period show that the classification algorithm and RCMs are able to reproduce the number of Mistral and Tramontane days per year, while the period length is overestimated. This overestimation could be due to erroneous simulation of blocking situations in the models.

The five simulations with three RCMs and five GCMs in this study show only small changes in Mistral frequency in RCP4.5 and RCP8.5 projections, but a significant decrease in Tramontane frequency. Most GCMs and RCMs show a decrease in Tramontane days per year, but changes are stronger in RCM simulations. This leads to the conclusion that future climate could lead to a change in Tramontane frequency, while the average wind speed during Tramontane events is not projected to change.

The wind speed 90th percentile of RCP8.5 is lower than that of RCP4.5 for most simulations. The decrease in wind speed in the Gulf of Lion area, which was found in previous studies, could be potentially attributed to fewer Tramontane events in future climate. Since Mistral and Tramontane events are driven orographically and by pressure patterns, the classification algorithm should be able to identify possible Mistral and Tramontane situations in projections as well. It appears unlikely that these findings are due to incorrect identification of M/T situations.

On about \(80\%\) of days, the RCMs and their driving GCMs agree on the occurrence of Mistral and Tramontane winds. In this study, each RCM was driven by a different GCM. This makes it difficult to estimate how different RCMs would simulate Mistral and Tramontane winds when given the same GCM input data. Therefore, it would be interesting to run several RCMs with the same GCM forcing and to increase the ensemble size in future studies.