1 Introduction

The El Niño-Southern Oscillation (ENSO) phenomenon is the dominant climate mode on interannual timescales (typically about 2‒7 year period) with origin in the tropical Pacific. Despite recent progress, it remains a large challenge to capture the observed ENSO physical feedback mechanisms accurately with coupled general circulation models (CGCMs) (Kim and Jin 2011; Kim et al. 2014). Several metrics have been proposed to quantify the performance of CGCMs from the Coupled Model Intercomparison Project (CMIP) in capturing the observed ENSO properties. These metrics include the ENSO spatial pattern, amplitude, propagation characteristics, periodicity, meridional structure, and physical feedbacks (e.g., van Oldenborgh et al. 2005; Guilyardi 2006; Guilyardi et al. 2009; Zhang and Jin 2012; Bellenger et al. 2014).

A large part of the variability in the tropical Pacific climate system is explained by the annual cycle (AC) with a period of 1 year. Jin et al. (1994) found that the nonlinear interaction between ENSO and the Eastern Pacific AC is able to generate new timescales and explain ENSO’s irregularity. These new timescales include combinations of the annual and ENSO frequencies. This research led recently to a new understanding of how the annual cycle in the Western Pacific helps to extend ENSO’s impact. That is, Stuecker et al. (2013) found an ENSO-dependent mode of climate variability with near-annual timescales in observations and GCM simulations. This combination mode (denoted as C-mode) originates from the nonlinear atmospheric interaction of ENSO with the warm pool AC in the tropical Pacific and is characterized by distinct timescales and a spatial pattern orthogonal to the traditional linear ENSO pattern.

This atmospheric C-mode over the Pacific warm pool is associated with the seasonally modulated termination process of big El Niño events (e.g., Harrison 1987; Harrison and Vecchi 1999; Spencer 2004; Vecchi 2006; Lengaigne et al. 2006; Ohba and Ueda 2009; McGregor et al. 2012; Stuecker et al. 2013). Furthermore, it results in inter-hemispheric sea level variability in the Pacific (Widlansky et al. 2014), and is responsible for the genesis of the anomalous low-level Northwest Pacific Anticyclone (Stuecker et al. 2015). A recent study showed the notable annual-cycle modulation of the meridional asymmetry in the atmospheric response to the so-called Eastern Pacific El Niño events, in contrast to the Central Pacific El Niño and La Niña events (Zhang et al. 2015). These indicate that the C-mode plays a crucial role in directly shaping ENSO life cycle and further extending the indirect effects of ENSO on climate anomalies in the tropical Pacific to western North Pacific as well as other regions.

Since the C-mode is essential for understanding both the seasonally modulated dynamics and impacts of ENSO, we need to determine the skill of the current generation of CGCMs from the CMIP Phase 5 (CMIP5) in capturing the observed C-mode characteristics. This will provide a powerful new ENSO metric to guide future climate model development and have important implications for improving seasonal climate prediction. Note that we are assessing the atmospheric C-mode response skill of these models. Additional nonlinear processes in the ocean–atmosphere coupled system also yield combination tones in oceanic ENSO indices (Jin et al. 1994; Stein et al. 2014), which are beyond the scope of this study.

This study focuses on a CMIP5 model performance in simulating the observed C-mode as an AC-induced extension of ENSO dynamics. The remaining paper is organized as follows. In Sect. 2 we introduce the data and methods, and in Sect. 3 we show a comparison of the spatial C-mode characteristics in the CMIP5 historical and AMIP simulations with reanalysis products. In Sect. 4 we examine the relationship of simulation skills between the C-mode and ENSO, and in Sect. 5 we examine the C-mode spectral characteristics in the CMIP5 models, followed by a summary and discussion in Sect. 6.

2 Data and methods

We utilize the historical experiment simulations from 27 CMIP5 CGCMs, driven by the historical climate forcing including time-evolving atmospheric compositions, solar forcing, and land cover/land use during the period of 1850‒2005 (Taylor et al. 2012). Additionally, we use the Atmospheric Model Intercomparison Project (AMIP) experiments. The AMIP runs are conducted with the atmospheric component of the CMIP5 CGCMs (denoted as AGCMs) and forced by observed sea surface temperature (SST) and sea ice cover from 1979 to present. The historical run simulations are available for all the 27 models, while for the AMIP run simulations only 15 out of the 27 models are available. Detailed information about all the used models can be found in Table 1.

Table 1 The models used in the present study, including configurations and length of simulations
Full size table

In the present study, we use the monthly mean 10 m zonal and meridional wind velocity, and analyze the period of 1861‒2005 for the historical run experiments, in which the first 10 years of data are removed as the spin-up time of coupled model simulations, and 1979‒2008 for the AMIP runs. For comparison, we utilize the wind products from the European Centre for Medium-Range Weather Forecasts (ECMWF), including the 40 years ECMWF Reanalysis data (ERA40, 1958–2001) and the ERA-Interim data (1979–2008). The ERA40 reanalysis data has a horizontal resolution of 2.5° × 2.5° (Uppala et al. 2005), and the ERA-Interim data 1.5° × 1.5° (Dee et al. 2011). All the model and ERA-Interim data are regridded to a 2.5°× 2.5°regular grid prior to our analysis in this study.

Following Stuecker et al. (2013), in terms of the definition of the C-mode, we will first conduct an Empirical Orthogonal Function (EOF) analysis on the combined anomalous zonal and meridional 10 m wind velocities to identify the C-mode. We first perform the combined EOF analysis on the individual model wind anomalies over the tropical Pacific region (10°S‒10°N, 100°E‒60°W) and then calculate the spatial patterns by regressing the zonal and meridional wind anomalies onto the first two normalized principal components (PCs), respectively. We further average the linear regression coefficients of all the models to obtain the multi-model ensemble (MME) average of EOF patterns. Similarly, we first conduct our power spectral analysis on the individual model PCs and then make a MME average. The power spectrum for each PC time series is calculated using the Blackman–Tukey method (Blackman and Tukey 1958) with a Bartlett window size of 11 years. We apply the same approach for both the CMIP and AMIP models.

3 Simulated spatial patterns of the C-mode

First, we compare the first two MME average simulated EOF patterns of tropical Pacific surface wind anomalies with the observations, as shown in Fig. 1a, b, where the EOF patterns of regressed zonal and meridional wind anomalies are plotted on the domain (30°S–30°N) for better visualization of the large-scale features. The first EOF pattern (EOF1) of the observations shows the linear ENSO response with meridionally quasi-symmetric westerly wind anomalies over the equatorial western-central Pacific. In contrast, the observed second EOF pattern (EOF2) exhibits a meridionally anti-symmetric circulation pattern with a strong anomalous Northwest Pacific anticyclone (Fig. 1b). This pattern captures the characteristic atmospheric C-mode response (Stuecker et al. 2013, 2015). The C-mode emerges from the atmospheric nonlinear interaction of ENSO and AC in the western tropical Pacific warm pool. The weakening and southward shift of the equatorial central-Pacific westerly wind anomalies, as seen in EOF2, are responsible for fast termination of strong El Niño events (e.g., McGregor et al. 2012) and lead to development of the North-West Pacific anticyclone, which is explained by the combination mode mechanism of the ENSO–AC interaction in the tropical Pacific warm pool region (Stuecker et al. 2013).

Fig. 1
figure 1

The first and second EOF patterns of tropical Pacific surface wind anomalies (m/s) for a, b ERA40, c, d MME average of CGCMs and e, f MME average of AGCMs. Shading indicates the regressed zonal wind anomalies. All the values in (c) and (d) have been multiplied by a factor 2. Percentages of variance explained by the EOF patterns are given in parentheses

Full size image

We see that the MME averages of both the CMIP5 historical and AMIP simulations can reasonably capture the main features of the two leading EOF patterns (Fig. 1), including the strong westerly wind anomalies over the equatorial western-central Pacific for EOF1 and the strong anomalous Northwest Pacific anticyclone and the southward-shift of westerly wind anomalies over the Central Pacific for EOF2. However, compared with the observations, the first two CGCM MME average EOF patterns explain smaller percentages of the total variance of the anomalous wind fields, which are also subject to a weaker amplitude and exhibit a westward shift of the wind anomaly centers. The similarity of the AMIP MME average patterns can likely be attributed to the prescribed SST boundary forcing.

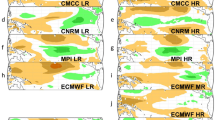
We also show the first two EOF patterns for individual CGCM models in Figs. 2 and 3, respectively. Not all the CGCMs reproduce a realistic C-mode response, however, most are able to simulate the C-mode pattern very realistically. There exhibits an obvious divergence in the simulated main features of the two EOFs for amplitude and pattern similarity to the observed EOFs. Evidently, the individual CGCMs simulated patterns tend to exhibit biases similar to the MME average, for instance a pronounced westward shift of the atmospheric response in the models compared to the observations. This is a common bias though not all of the CGCMs exhibit a strong bias, reflecting the deficiency of current CGCMs in simulating the mean state, AC, and ENSO related variability in the tropical Pacific realistically (e.g., Zhang et al. 2013; Taschetto et al. 2014; Zhang and Sun 2014). Moreover, although the MME mean of the AGCMs provides better simulations, not all the AGCMs reproduce a realistic C-mode response (not shown).

Fig. 2
figure 2

The first EOF patterns of tropical Pacific surface wind anomalies (m/s) for each CGCM. Percentages of variance explained by the EOF patterns are given in parentheses. Models are organized according to the pattern correlation of the second EOF pattern between the observations and simulations

Full size image
Fig. 3
figure 3

The same as Fig. 2, but for the second EOF

Full size image

Figure 4 shows a Taylor diagram (Taylor 2001), which displays a comparison of the first two EOF patterns between the observation and CMIP5 model simulations, to quantitatively measure the resemblance of the simulated ENSO mode and C-mode to the observation. In general, the AGCMs reproduce the first two EOFs much better than the CGCMs, and the CMIP5 models tend to simulate EOF1 better than EOF2. Compared to the observations, the AGCMs can simulate an amplitude of the two EOF patterns more similar to the observations than the CGCMs. The majority of the CGCMs underestimates the amplitude of the two leading EOFs. Notably, the MME average of the CGCMs can reproduce the C-mode pattern better than the majority of the individual CGCMs, while the MME average of the AMIP experiments reproduces it better than almost every individual AGCM. The spatial correlation coefficient of the EOF1 (EOF2) pattern of the combined zonal and meridional wind between the CGCM MME average and the observation is 0.69 (0.80). The two AGCM MME average EOF patterns are even more similar to the observations, obtaining a linear pattern correlation coefficient of 0.93 (0.92) for EOF1 (EOF2). As the SSTs are prescribed as boundary condition in the AMIP experiments, we can obtain a more realistic representation of the atmospheric response to both ENSO and AC forcing. However, even if a realistic SST AC is prescribed, this does not guarantee a realistic AC in the precipitation and diabatic heating.

Fig. 4
figure 4

Taylor diagram summarizes the comparison of the first two EOF patterns between observation and a CGCM and b AGCM simulations. The radial distance from the origin indicates the standard deviation of EOF pattern for each model normalized by the observed value. The azimuthal position denotes the correlations between the observed and simulated EOF patterns

Full size image

4 Relationship between skills of ENSO and C-mode simulations

The C-mode representation in climate models is certainly affected by the ENSO fidelity of the models. Next, we rank the CGCMs by pattern correlations between the simulated and observed EOF2 (Fig. 5). It can be seen that with the EOF2 correlations decreasing, the CGCMs overall have declined correlations for EOF1 correspondingly, implying a potential relationship between the skills of ENSO and C-mode pattern simulations. Moreover, it is noted in Figs. 2 and 3 that the models are ranked in terms of the same sequence that the pattern correlations of EOF2 decrease, clearly exhibiting some details of such a relationship. Also in Fig. 5, we can note that the MME average works to improve pattern fidelity better in EOF2 than EOF1.

Fig. 5
figure 5

Pattern correlations between the observed and CGCM simulated EOFs, where the sequence of the CGCMs has been ranked by the decrease in the EOF2 correlations

Full size image

Further, we quantify the similarity between the simulated and observed EOF patterns as a scatter plot (Fig. 6a). Both the CGCMs and AGCMs exhibit relatively high pattern correlations with the observations, where for the ENSO mode (EOF1) there are 26 (13) out of 27 (15) CGCMs (AGCMs) with correlation coefficients greater than 0.50 (0.80). For the C-mode (EOF2), there exist 20 (10) CGCMs (AGCMs) above this threshold. More importantly, it can be clearly seen that a close relationship exists between the EOF1 and EOF2 correlations, indicating the dependence of the C-mode simulation fidelity on the ENSO simulation fidelity.

Fig. 6
figure 6

a Scatterplot of pattern correlations between observed and simulated EOF1s versus observed and simulated EOF2s. b The same as (a), but for the standard deviations of the pattern normalized by the observations. Cross indicates individual model and solid circle MME average of models. Solid lines denote linear fitting of the data and R the correlations

Full size image

The relationship between skills of ENSO mode and C-mode simulations is further examined by comparing the EOF spatial standard deviations (Fig. 6b). A close relationship exists between the amplitudes of EOF1 and EOF2 in both the AGCM and CGCM simulations, confirming the dependence of the C-mode simulation on the ENSO simulation. It can be concluded that models with better performance in simulating the ENSO mode are also the models capable to reproduce a realistic C-mode with respect to its spatial pattern and amplitude, for both the CMIP5 CGCMs and AGCMs.

5 Combination tones and mechanism represented in CMIP5 models

To evaluate the simulated ENSO-AC combination tones, we analyze the near-annual timescales of the PCs corresponding to the first two EOFs simulated in the CMIP5 models by calculating the power density spectra for each time series using the Blackman-Tukey method (Blackman and Tukey 1958). The spectrum for the observed first PC (PC1) exhibits significant power at two interannual frequency bands (Fig. 7a, b). The 2–3 and 4–5 years periodicities might reflect the two observed ENSO modes coexisting during the past three decades (Ren and Jin 2013; Ren et al. 2013). The most striking features of the C-mode generated from ENSO (frequency f E = 1/2–1/8 years−1) and the AC (frequency = 1 year−1) interaction, are the genesis of the combination tone frequencies (the sum tone 1 + f E and the difference tone 1 − f E), corresponding to the periods of about 10 and 15 months, respectively. Thus, the performance of the models in simulating these combination tone frequencies is a very important indicator that the model can simulate the C-mode reasonably well.

Fig. 7
figure 7

Power spectrum curves of PC1 (red solid line) and PC2 (blue solid line) for the a ERA40, b ERA-Interim, c MME average of spectra of the CGCMs, d MME average of spectra of the AGCMs, and e spectra of MME average of the AGCMs. The dashed lines indicate the 95 % confidence interval for PC2 tested against the null hypothesis of an autoregressive model of order one. Grey rectangles indicate the near-annual combination tone frequency bands 1 − f E and 1 + f E

Full size image

The MME average of the CGCM spectra reproduces the two dominant combination tones of PC2 (Fig. 7c). Note that we only observe one ENSO frequency band for the CGCM MME average, which could reflect deficiencies of many current CGCMs in simulating both ENSO modes. However, we also see the quite similar peaks in the MME average of spectra of the AGCMs, which is presumably due to the smoothing effect of the MME mean process on the two spectrum peaks. If we obtain spectra after taking a MME average of the all the AGCM PCs, both the two ENSO frequencies and the two C-mode frequencies can be perfectly reproduced by the models (Fig. 7e).

Furthermore, we calculate the power spectra for each model (Fig. 8) and find that about half of the CGCMs can reproduce the spectral peaks of the C-mode at about 10 and/or 15 months. These models are generally the models that exhibit relatively high pattern correlations of EOF2 with the observations. This, again, reflects the smoothing effect of the MME mean because the two ENSO frequency bands do not exactly correspond among the models, and the combination tones in most of the CGCMs become less significant in the MME average. Although the MME average of the spectra of AGCMs only exhibits one ENSO frequency band, as referred to Fig. 7d, almost all the AGCMs can reproduce the two interannual frequency bands and the combination tones at about 10 and/or 15 months, likely due to the prescribed SST forcing (figure omitted). However, we found the models that have a better representation for the main periods of ENSO mode tend to have more accurate periods for the C-mode, which is due to the combination mode relationship between the two modes.

Fig. 8
figure 8

Power spectra for PC1 (red solid line) and PC2 (blue solid line) for each CGCM. The dashed line indicates the 95 % confidence interval for PC2. Grey rectangles denote the near-annual combination tone frequency bands 1 − f E and 1 + f E

Full size image

To further verify the combination mode relationship using the CMIP5 model outputs, we follow the so-called PC2SIMPLE approach used by Stuecker et al. (2013). That is, we utilize PC1 as the ENSO mode signal and multiply this time series by a sinusoidal function with 1-year period (the AC) to approximate the lowest order (quadratic) nonlinear term of the theoretical C-mode: PC2SIMPLE = PC1(t) × cos(ω a t − φ). In this equation, ω a denotes the angular frequency of the AC and φ a 1-month phase shift. This PC2SIMPLE time series exhibits by its mathematical nature pronounced combination tones. The correlation coefficients between the PC2SIMPLE and PC2 for the individual models (Fig. 9) can be used to assess the performance of the models in representing the combination tone relationship. Note that the correlations will decrease significantly if the simulated phase of the AC in the CGCM is different from the observations.

Fig. 9
figure 9

Linear correlation coefficients between PC2 and PC2SIMPLE in the a CGCMs, and b AGCMs. The models are organized in descending order according to the pattern correlations between observed and CGCM simulated EOF2

Full size image

Most of the AGCMs exhibit relatively high PC2–PC2SIMPLE correlations, and 12 out of the 15 models have a correlation coefficient larger than 0.40 (Fig. 9b). In contrast, only about half of the CGCMs exhibit a PC2–PC2SIMPLE correlation above this value, which indicates that a subset of the current coupled models are able to simulate well the combination mode mechanism. Note that the CGCMs exhibiting an EOF2 pattern similar to observations tend to also have relatively high PC2–PC2SIMPLE correlations, where the BCC-CSM1.1m model shows the highest correlation. Furthermore, it is important to emphasize that although some coupled models show low PC2–PC2SIMPLE correlations, their atmospheric component models can give a good performance in simulating the C-mode when provided with observed SST boundary conditions, such as the MRI-CGCM3 and CMCC-CM models. On the other hand, some models exhibit low correlations for both the coupled (CGCM) and uncoupled (AGCM) experiments, such as MIROC5 and MPI-ESM-MR. Additionally, we see that the CNRM-CM5 model does well in the coupled setting, but not in the uncoupled setting.

Moreover, it can be clearly seen in Fig. 9a that the correlations of the CGCMs tend to be related to the model resolution in the same family of models, such as the BCC-CSM1.1 and BCC-CSM1.1m, the IPSL-CM5A-LR and IPSL-CM5A-MR, as well as the MPI-ESM-LR and MPI-ESM-MR, based on the available information of CMIP5 models. The higher model resolution in these CGCMs is, the higher PC2–PC2SIMPLE correlation is. More interestingly, the correlations between the simulated and observed EOF1/EOF2 patterns are also direct proportional to the model resolution for these three pairs of models (Fig. 5). These results indicate that the capability of the CMIP5 models in simulating the combination tone mechanism of ENSO and AC may be related to the model resolution, at least in the same family of models.

It may be suggested that the capability of the CMIP5 coupled models in simulating the combination mode mechanism of ENSO–AC interaction may be related to the model resolution. Some studies suggested improvements in simulating ENSO with increasing horizontal resolution in atmosphere and ocean components of models (Delworth et al. 2012; Jia et al. 2015; A. Wittenberg, personal communication). Thus, the C-mode simulation, as it is dependent on the simulation of ENSO, may also become better. However, two uncoupled CMIP5 AGCMs do not support this conclusion because the AGCM correlations (Fig. 9b) do not appear to be consistent with this conclusion, e.g., for the MPI-ESM-LR and MPI-ESM-MR models. Thus, we cannot unambiguously confirm this conclusion as the CGCM sample is too small. This needs to be studied further.

The C-mode is responsible for the sudden weakening and southward shift of equatorial westerly anomalies, which has been shown to accelerate the termination process of strong El Niño events (Stuecker et al. 2013). Therefore, the phase relationship between PC1 and PC2 during the life cycle of strong El Niño events is very important (Stuecker et al. 2013). To display the evolution of PC2 during the El Niño phase transition, we do composites of the PCs for the strong wind PC1 anomaly events in observation and model simulations with respect to the AC evolution (Fig. 10). Here the strongest PC1 anomaly events include the 1982/1983, 1991/1992 and 1997/1998 El Niño events in both the observation and AGCM simulations. For the CGCM, there are 107 strongest PC1 anomaly events chosen, based on a threshold of 2 standard deviations of December–January–February mean PC1 for individual model simulation and then a composite is made using all the PC1 events. There is a rapid phase switch in the observed wind PC2 at the end of calendar year. It can be well captured in the composite El Niño for the AGCM and CGCM averages, and by the CGCM PC2SIMPLE, indicating that this subset of the current generation of models can give relatively good representations for the combination mode mechanism in terms of the spatial pattern and temporal variation.

Fig. 10
figure 10

Normalized PC1 (dashed) and PC2 (solid) composites of the strongest wind PC1 anomaly events for the observed surface wind anomalies (black) and the MME averages of the AGCMs (red) and the CGCMs (blue). Green dashed line denotes the CGCM PC2SIMPLE composite. In the composite year 0 denotes the developing phase and year 1 the decaying phase

Full size image

6 Summary and discussions

Assessing ENSO and its associated phenomena (like the C-mode) in the current generation of climate models is essential to determine model deficiencies, and improve our understanding of ENSO dynamics. Previous studies usually focused on a subsection of ENSO properties, such as spatial structures, amplitude, periodicity, propagation characteristics, and teleconnections. In this study, we analyze the extended impact of ENSO through its nonlinear interaction with the AC in the CMIP5 models. By such an assessment, we aimed to quantify the performance of the current generation of climate models in simulating the ENSO/AC interaction over the Pacific warm pool region.

We showed that most of the CMIP5 CGCMs are able to reproduce the spatial pattern and amplitude of the C-mode associated surface wind anomalies in the Pacific reasonably well. About half of the CGCMs and most of the ACGMs can reproduce the spectral peaks of the C-mode at periods of about 10 and/or 15 months, and these models are generally the models that exhibit better performance in reproducing the spatial pattern of the C-mode. Due to the prescribed SST boundary forcing, the AGCMs generally exhibit a more realistic C-mode than the CGCMs. The MME average of CGCMs captures the C-mode better than the majority of the individual CGCMs, while for the AGCMs, their MME average performs better than almost all the single models with respect to its spatial pattern. It is demonstrated that the models with better performance in simulating the ENSO mode tend to also simulate a more realistic C-mode. As expected, the spatial pattern and amplitude of the C-mode are closely related to those of ENSO itself in both the CGCMs and AGCMs.

The CMIP5 models, both CGCMs and AGCMs, are able to simulate well the rapid PC2 phase transition for the MME average. Our results also demonstrated that the CMIP5 models are able to simulate the combination mode mechanism to some degree. Generally, this results from their good performance in representing the ENSO mode. However, the other important factor is the model’s fidelity in simulating a realistic AC in the warm pool region, which is essential for the C-mode genesis and needs to be further investigated in future studies.

Although we showed the good aspects of the CMIP5 models in reproducing the C-mode associated features, there still exhibits some deficiencies which can be seen in our results. The two EOF patterns produced by individual models are fairly differential from each other even though their MME averages are similar to the observed EOF patterns. The weaker amplitude of the CMIP MME average C-mode can be to a large degree attributed to the clear divergence among the individual model patterns. Another apparent deficiency in the models is that the spectrum peaks are not able to be reproduced perfectly, not only for the C-mode frequencies, but also the basic frequencies of ENSO. Due to the big dependence of the C-mode simulation on the ENSO simulation, the diversity of main ENSO periods in the models simulations may directly yield the bias in the main C-mode periods. Thus, it will definitely help the C-mode simulation better that the model developers continually keep improving the fidelity of ENSO pattern, amplitude and periodicity in the current climate models. As the first priority, it is suggested that the main periods of ENSO needs to be further improved in the models that have poor skill, for representing a better C-mode in simulations.

Since the C-mode plays an important role in extending the direct and indirect impacts of ENSO on the climate anomalies over the western tropical and North Pacific (Widlansky et al. 2014; Stuecker et al. 2015; Zhang et al. 2015), it would be expected that with taking the C-mode into account we can have a big potential to extract more predictability for the climate anomalies over the western North Pacific, East Asian as well as adjacent areas. Furthermore, using those climate models with well reproduced ENSO and C-mode, we can also prospect a high-confidence climate prediction and projection for the relevant regions, particularly under the conditions that ENSO behaviors would vary or change evidently. Moreover, the researches on the ENSO/AC C-mode dynamics and impacts are still at the early stage, and based on this study some eligible models might be candidate for further exploration along the line.