Abstract
In the framework of the coordinated regional climate downscaling experiment (CORDEX), an ensemble of climate change projections for Africa has been created by downscaling the simulations of four global climate models (GCMs) by means of the consortium for small-scale modeling (COSMO) regional climate model (RCM) (COSMO-CLM, hereafter, CCLM). Differences between the projected temperature and precipitation simulated by CCLM and the driving GCMs are analyzed and discussed. The projected increase of seasonal temperature is found to be relatively similar between GCMs and RCM, although large differences (more than 1 °C) exist locally. Differences are also found for extreme-event related quantities, such as the spread of the upper end of the maximum temperature probability distribution function and, in turn, the duration of heat waves. Larger uncertainties are found in the future precipitation changes; this is partly a consequence of the inter-model (GCMs) variability over some areas (e.g. Sahel). However, over other regions (e.g. Central Africa) the rainfall trends simulated by CCLM and the GCMs show opposite signs, with CCLM showing a significant reduction in precipitation at the end of the century. This uncertain and sometimes contrasting behaviour is further investigated by analyzing the different models’ response to the land–atmosphere interaction and feedback. Given the large uncertainty associated with inter-model variability across GCMs and the reduced spread in the results when a single RCM is used for downscaling, we strongly emphasize the importance of exploiting fully the CORDEX-Africa multi-GCM/multi-RCM ensemble in order to assess the robustness of the climate change signal and, possibly, to identify and quantify the many sources of uncertainty that still remain.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
As one of the most vulnerable regions to weather and climate variability (IPCC 2007), Africa was selected as the first target region for the World Climate Research Programme CORDEX (coordinated regional climate downscaling experiment) (Giorgi et al. 2009), which aims to foster international collaboration to generate an ensemble of high-resolution historical and future climate projections at regional scale, by downscaling the global climate models (GCMs) participating in the Coupled Model Intercomparison Project Phase 5 (CMIP5) (Taylor et al. 2012).
In order to properly simulate the climate of such a large and heterogeneous continent, models need to replicate correctly the many physical processes and their complex feedback over multiple temporal and spatial scales. By better representing the topographical details, coastlines, and land-surface heterogeneities, regional climate models (RCMs) allow the reproduction of small-scale processes that are unresolved by the low-resolution GCMs. In the past, RCMs have been proved to be able to reproduce the general features of the African climate over specific sub-regions, in particular South Africa (e.g. Sylla et al. 2012; Diallo et al. 2014) and, especially, West Africa (e.g. Jenkins et al. 2005; Afiesimama et al. 2006; Abiodun et al. 2008), where comprehensive efforts were undertaken in both data collecting and modeling activities, including the West African monsoon modelling and evaluation (WAMME) initiative (Druyan et al. 2010; Xue et al. 2010), the African multidisciplinary monsoon analysis (AMMA) (Redelsperger et al. 2006; Ruti et al. 2011), and the ensembles-based prediction of climate changes and their impacts (ENSEMBLES) (Paeth et al. 2011). More recently, in the framework of the CORDEX initiative, several different RCMs were employed over the whole African continent driven by ‘perfect’ lateral boundary conditions (ERA-Interim) (Nikulin et al. 2012; Endris et al. 2013; Kalognomou et al. 2013; Kim et al. 2013; Krähenmann et al. 2013; Gbobaniyi et al. 2014; Panitz et al. 2014) in order to asses the ‘structural bias’ of the models (Laprise et al. 2013): although RCMs simulate the precipitation seasonal mean and annual cycle quite accurately, large differences and biases exist amongst the models in some regions and seasons.
When RCMs are driven by GCMs, biases inherited through the lateral boundary conditions are added to those of the RCM (e.g. Hong and Kanamitsu 2014); as a result, downscaling is not always able to improve the simulation skills of large-scale GCMs although added value in downscaling GCMs is found especially in the fine scales and in the ability of RCM to simulate extreme events (e.g. Kim et al. 2002; Diallo et al. 2012; Paeth and Mannig 2012; Diaconescu and Laprise 2013; Crétat et al. 2013; Haensler et al. 2013; Laprise et al. 2013; Lee and Hong 2013; Buontempo et al. 2014; Lee et al. 2014; Giorgi et al. 2014; Dosio et al. 2015)
In this work we present the results of the application of the COSMO-CLM RCM (CCLM) in the production of climate change projections for the CORDEX-Africa domain. This work builds on two previous studies: Panitz et al. (2014) investigated the structural bias of CCLM driven by ERA-Interim (evaluation run), whereas Dosio et al. (2015) analyzed the added value of downscaling low-resolution GCMs over the present climate (historical runs). Here we complete the analysis of CCLM climate runs for CORDEX-Africa not only by analyzing the climate change projections for mean variables and extreme-events related quantities, but also by comparing CCLM results to those of the driving GCMs. In fact, several discrepancies between the results of RCMs and GCMs have been found in recent studies (e.g. Mariotti et al. 2011, 2014; Laprise et al. 2013; Teichmann et al. 2013; Bouagila and Sushama 2013; Saeed et al. 2013; Coppola et al. 2014; Buontempo et al. 2014). In some of these works, RCM runs are forced by only one GCM, whether other studies are lacking a detailed analysis of the causes of the differences between RCM and GCMs’ results. Although Mariotti et al. (2014) suggested that GCMs and RCMs discrepancies may arise from the difference in the representation of the large-scale circulation (e.g. African Easterly Waves), other studies showed that the different climate sensitivity between GCMs and RCMs is related to local processes, rather than being the effect of the boundary conditions; in particular, local processes linked to land–atmosphere interaction and parameterization play a relevant role in the simulation of e.g. the precipitation trend under global warming. This aspect will be therefore analyzed in detail.
The paper is structured as follows: Sect. 2 describes the model set-up, in Sect. 3 results are shown and discussed, concluding remarks are presented in Sect. 4.
2 Model description and simulations setup
In this study, we use the three-dimensional non-hydrostatic regional climate model COSMO-CLM (CCLM) in the same configuration described in Panitz et al. (2014) and Dosio et al. (2015). Briefly, numerical integration is performed on an Arakawa-C grid with a Runge–Kutta scheme, with a time splitting method by Wicker and Skamarock (2002). The time step is 240 s. A vertical hybrid coordinate system with 35 levels is used, with the upper most layer at 30 km above sea level. The main physical parameterizations include: the radiative transfer scheme by Ritter and Geleyn (1992); the Tiedtke parameterization of convection (Tiedtke 1989) being modified by D. Mironow (German Weather Service); a turbulence scheme (Raschendorfer 2001; Mironov and Raschendorfer 2001) based on prognostic turbulent kinetic energy closure at level 2.5 according to Mellor and Yamada (1982); a one-moment cloud microphysics scheme, a reduced version of the parameterization of Seifert and Beheng (2001); a multi layer soil model (Schrodin and Heise 2001, 2002; Heise et al. 2003); subgrid scale orography processes (Schulz 2008; Lott and Miller 1997). After a series of sensitivity runs, the lower height of the damping layer was increased from its standard value, 11 km, to the approximate height of the tropical tropopause, 18 km, in order to avoid unphysical and unrealistic results. The soil albedo was replaced by a new dataset, derived from MODIS (Moderate Resolution Imaging Spectroradiometer) (Lawrence and Chase 2007), which gives more realistic results over the deserts. A thorough description of the dynamics, numerics and physical parametrizations can be found in the model documentation (e.g. Doms 2011).
The numerical domain, common to all groups participating to the CORDEX-Africa initiative, covers the entire African continent at a spatial resolution of 0.44° (Fig. 1): the model grid uses 214 points from West to East and 221 points from South to North, including the sponge zone of 10 grid points at each side, where the Davies boundary relaxation scheme is used (Davies 1976, 1983).
Model domain and topography (m) of the CORDEX Africa simulations. The domain includes a sponge zone of 10 grid points in each direction. Squares indicate the locations of the evaluation regions as defined in http://www.smhi.se/forskning/forskningsomraden/klimatforskning/1.11299
An ensemble of climate change projections has been created by downscaling the results of four GCMs from the CMIP5 climate projections, namely: the Max Plank Institute MPI-ESM-LR , the Hadley Center HadGEM2-ES , the National Centre for Meteorological Research CNRM-CM5, and EC-Earth, i.e., the Earth System Model of the EC-Earth Consortium (http://ecearth.knmi.nl/). The historical runs, forced by observed natural and anthropogenic atmospheric composition, cover the period from 1950 until 2005, whereas the projections (2006–2100) are forced by two Representative Concentration Pathways (RCP) (Moss et al. 2010; Vuuren et al. 2011), namely, RCP4.5 and RCP8.5.
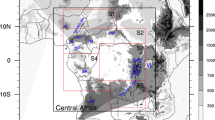
In this work we analyze the climate change projections as simulated by CCLM and we compare them to those of the driving GCMs. Some analysis is performed over sub-regions defined as in the CORDEX protocol (see Fig. 1, and http://www.smhi.se/forskning/forskningsomraden/klimatforskning/1.11299) and used in previous single- and multi-model evaluation studies over CORDEX-Africa (e.g. Nikulin et al. 2012; Laprise et al. 2013). Sub-regions are defined as follows: Atlas Mountains (AM), West Africa North (WA_N), West Africa South (WA_S), Ethiopian Highlands (EH), Central Africa North (CA_NH), Central Africa South (CA_SH), East Africa (EA), South Africa East (SA_E), South Africa West North (SA_WN) and South Africa West South (SA_WS).
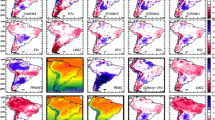
Maps of seasonal mean temperature as simulated by the ensemble mean of the GCMs and CCLM downscaled runs for austral summer (JFM). First column shows the value for the reference period (1981–2010); second and third columns show the climate change signal (i.e. 2071–2100 minus reference period) under RCP4.5 and RCP8.5 scenarios, respectively. The first row shows the GCMs’ results, the second row the CCLM ones and the third row the differences between them. White stippling indicates land points where the climate change signal or the CCLM-GCM difference is not statistically significant, at 5 %, by means of a two sample Kolmogorov–Smirnov test
Seasonal statistics are calculated for boreal winter, defined as January–February–March (JFM), and summer (July–August–September—JAS).
3 Results
3.1 Temperature climatology
In this study we define the reference period (present climate) as 1981–2010, by combining the model results of the historical simulations (1981–2005) with the first five years of the projection runs (2006–2010) under RCP4.5 (results using the first five years of the RCP8.5 runs are very similar).
Figures 2 and 3 show maps of mean seasonal temperature for the GCMs and CCLM ensemble means. Over the reference period in JFM, CCLM is generally warmer than the GCMs over Southern and Eastern Africa, and the Guinea coast, but colder over the Sahara and central Africa. These results have been already discussed in detail by Dosio et al. (2015) who showed that present climate temperature simulated by GCMs are usually too cold; downscaled simulations are not always able to improve seasonal mean statistics, however, CCLM does improve the GCMs’ results especially over South Africa and the Guinea coast. At the end of the Century (2071–2100), both GCMs’ and CCLM’s simulations show a generally similar increase in temperature for both RCPs, although local differences are noteworthy. In particular, CCLM climate signal is up to 2 °C warmer than the GCMs’ one over South Africa and the fascia around 10°N, including the Horn of Africa, for RCP8.5 (differences are limited to 1 °C for RCP4.5). On the other hand, CCLM projects a colder climate signal over the Sahara, up to −2 °C for RCP8.5. Over Central Africa differences between GCMs and CCLM are smaller and limited to 0.5 °C.
As Fig. 2 but for boreal summer (JAS)
Time evolution of seasonal mean temperature anomaly for the evaluation regions as modelled by the GCMs (black lines) and CCLM (red lines). For each region, the upper and lower panels refer to RCP8.5 and RCP4.5, respectively. Thick lines are the models’ ensemble mean values, whereas thin lines and yellow shaded areas show the inter-model variability for GCMs and CCLM, respectively, represented by the models’ maximum and minimum values. A 20 year running mean is applied to the data. Note that the selected season is dependent on the region analysed
As Fig. 4 but for seasonal maximum temperature
In JAS, in the reference period, CCLM is warmer than the GCMs over South Africa and the area above 20°N, where the downscaled results are closer to the observed temperatures than the GCMs (Dosio et al. 2015). On the other hand, CCLM is colder than the GCMs over the area between the Equator and 20°N, where the downscaling is not able to significantly add value to the low resolution simulations. At the end of the Century, both GCMs and CCLM project a strong warming, up to more than 6 °C over North Africa and the Arabian peninsula. CCLM climate signal is stronger over Central Africa and the Sahel (up to 1 and 2 °C warmer, respectively, for RCP8.5), and slightly colder over southern Africa and the Arabian peninsula.
Differences in the temperature climate signal over Africa between the driving GCM and the downscaled runs have been recently observed in several other studies (Mariotti et al. 2011; Laprise et al. 2013; Teichmann et al. 2013; Coppola et al. 2014; Buontempo et al. 2014), although the number of GCMs used was smaller (one or two, although Buontempo et al. (2014) used a large perturbed physic ensemble of the same GCM). Mariotti et al. (2011) claimed that this different climate sensitivity is related to local processes linked to land processes and parameterization. This aspect will be studied more in detail in Sect. 3.3.
In addition to the different climate sensitivity between CCLM and GCMs’ ensemble mean, a large uncertainty in the projected warming is also related to inter- and intra-model variability. Figure 4 shows the time evolution of seasonal temperature anomaly (i.e. the difference to the 1981–2010 mean value) for the evaluation regions shown in Fig. 1. Both GCMs and CCLM ensemble mean results are shown together with the minimum and maximum of the models’ values, as a measure of the uncertainty in the projection. Table 1 reports the temperature values for the reference period and the mean climate change signal (2071–2100 minus 1981–2010). From the table we first note that the CCLM intra-model variability for both the present period and the end of the century is usually smaller than the GCM inter-model variability, with the exceptions of AM (especially in JAS) and WA_N and EH in JFM. This result is somehow expected and corroborates the fact that for a RCM to simulate its own climate, small-scale processes may be more important than the forcing through the lateral boundary condition especially over a large domain (Buontempo et al. 2014). The mean climate change signal is usually similar between GCMs and CCLM (less than 0.25 °C difference) although notable exceptions in JFM are found in AM, where CCLM climate signal is 0.88 °C colder than the GCMs’ one, and SA_WN and SA_E, where the CCLM signal is considerably warmer than the GCMs’ one (0.70 and 0.81 °C difference, respectively). Inter-model variability is usually larger for the GCM ensemble, except over AM and WA_N in JFM, and, especially, SA_WN and SA_WS in JAS, where CCLM variability is more than 1 °C larger than the GCMs’ one although the climate change signals for the two ensembles are very similar.
Maps of the difference between the 99th and 50th percentile of maximum temperature, as simulated by the ensemble mean of the GCMs and CCLM downscaled runs for austral summer (JFM). First column shows the value for the reference period (1981–2010); second and third columns show the climate change signal (i.e. 2071–2100 minus reference period) under RCP4.5 and RCP8.5 scenarios, respectively. The first row shows the GCMs’ results, the second row the CCLM ones and the third row the differences between them
As Fig. 6 but for JAS
As Fig. 2 but for the Warm Spell Duration Index
The temporal evolution of seasonal maximum temperature anomaly, shown in Fig. 5, generally follows that of mean temperature especially in South Africa in JFM (where CCLM values are larger than the GCMs’ ones), WA_S in JAS (where CCLM and GCMs’ values are similar), and AM in JFM, where CCLM values are smaller than the GCMs’ ones. Differences between mean and maximum temperature trends, however, are found especially in WA_N and CA_NH in JAS (and, to less extent EH and EA) where CCLM projects a considerably larger increase in maximum temperature compared to the GCMs (nearly 1 °C difference for RCP8.5). This non uniform increase of mean and maximum temperature reflects the change in shape of the temperature probability distribution function (PDF), and, in turn, the occurrence of extreme events.
As Fig. 8 but for JAS
As Fig. 2 but for seasonal mean precipitation
As Fig. 10 but for JAS
Figures 6 and 7 show maps of the difference between the 99th and 50th percentile of seasonal maximum temperature (Tx). This quantity is a measure of the width of the PDF and, in turn, it shows how the PDF changes with time. Comparing CCLM to GCMs’ results, it is evident that at the end of the century the RCM simulates a PDF that becomes wider than the GCMs’ one especially over central Africa, both in winter and summer. The effect on heat wave duration is shown in Figs. 8 and 9, where the Warm Spell Duration Index (WSDI) is presented. WSDI is calculated here as the maximum number of at least 5 consecutive days when maximum temperature exceeds the 90th percentile of the reference value (1981–2010). Although not directly comparable, GCMs results are in line with Sillmann et al. (2013) showing a marked increase in the warm spell duration over the Guinea coast, eastern Central Africa, and the Horn of Africa. CCLM results are similar to the GCMs’ ones in the geographical distribution of the index, but large differences exist in its value. In particular, the change in WSDI is much larger (more than 15 days) over central Africa, for both seasons and scenarios, whereas in JAS CCLM shows a much smaller increase compared to the GCMs over the horn of Africa: this is consistent with a smaller warming for both mean (Fig. 3) and maximum temperature (not shown) over the region.
As Fig. 4 but for seasonal mean precipitation
Seasonal ensemble mean change of Consecutive Dry Days (CDD, left column) and total soil moisture (mrso, in %, right column) for the RCP8.5 scenario. White stippling indicates land points where the climate change signal is not statistically significant, at 5 %, by means of a two sample Kolmogorov–Smirnov test
3.2 Precipitation climatology
Figures 10 and 11 show maps of mean daily precipitation as simulated by the GCMs and CCLM runs. A thorough comparison of GCMs and CCLM results over the present climate has been already conducted by Dosio et al. (2015). Briefly, the geographical distribution of seasonal precipitation simulated by CCLM follows closely the one inherited by the GCMs (e.g the monsoon rainbelt); however, whereas GCMs tend to somehow overestimate the precipitation intensity, CCLM shows a general dry bias. Some improvement by the downscaling is evident especially over South Africa in JFM, where the GCMs wet bias is corrected. In addition, over the regions along the Gulf of Guinea it was shown that CCLM is able to better represent the bimodal distribution of the annual cycle, whereas GCMs are not able to simulate this feature and they show a unimodal distribution.
Substantial differences, however, are evident comparing the projected climate change signal. In JFM, for instance, GCMs projects a general increase in precipitation over central and east Africa not visible in the CCLM results, which show a general drying over all sub-equatorial Africa, apart from Tanzania and east Mozambique for the RCP8.5 scenario. In JAS, CCLM is consistent with the driving GCMs showing a precipitation increase over Liberia, Cote d’Ivoire and Ghana, but the sign of the climate change signal is the oppposite over Nigeria and Cameroon, Central African Republic and South Sudan, where CCLM projects a decrease in precipitation in contrast with the increase projected by the GCMs.
Seasonal ensemble mean of correlation between evapotranspiration (E) and surface temperature (T) for the reference period and the end of the century under the RCP scenarios. Following Seneviratne et al. (2006) correlations have been calculated from de-trended time series
The temporal evolution of precipitation anomaly (Fig. 12) highlights these discrepancies; in WA_N, WA_S, CA_NH and EH in JAS, and CA_SH in JFM the ensemble mean CCLM signal is opposite to the CGMs one, whereas Table 2 reports the precipitation values for the reference period and the mean climate change signal (2071–2100 minus 1981–2010) for the RCP8.5 scenario. The table highlights the large uncertainty in the climate signal associated with inter- and intra-model variability. In fact, whereas for CA_SH all CCLM runs and all GCMs agree on the sign of the precipitation trend, GCMs results in JAS vary between −0.21 and +0.61 mm/day in CA_NH, and between −0.32 and +0.28 mm/day in EH. On the other hand, over the Gulf of Guinea and the Sahel, CCLM uncertainty on the sign of the signal is very large, with values varying between −1.15 and +0.99 mm/day in WA_N and −1.33 ad +1.56 mm/day over WA_S. Over the Sahel, GCMs too do not agree on the sign of the precipitation trend, with values varying in JAS between –0.34 and 0.53 mm/day.
Significant discrepancies between GCMs and RCM precipitation signals were found also by Laprise et al. (2013), Teichmann et al. (2013), Bouagila and Sushama (2013), Saeed et al. (2013), Coppola et al. (2014), Buontempo et al. (2014), and Mariotti et al. (2014) especially over Central Africa, the Ethiopian plateau, and the coast of the Guinea gulf. Although differences in precipitation trends were related to several processes, such as large-scale circulation (African easterly Waves), local topographic detail, and response to sea surface temperature, an important role was found to be played by the different description of the land–atmosphere interaction and their feedback. This aspect will be therefore analyzed more in detail in Sect. 3.3.
The ensemble mean change in the number of consecutive dry days (CDD, where a day is defined as dry if precipitation \(<\)1 mm) for the RCP8.5 scenario is shown in Fig. 13. In the same figure the change (in %) of the total soil moisture (mrso), is also shown, which can be relevant for agriculture droughts. In fact, as claimed by Orlowsky and Seneviratne (2011), although CDD is often used to assess dryness, it does not include the impact of radiation and temperature anomalies on evapotranspiration, which can act as a driver for droughts. In particular, regions showing a consistent change of CDD and soil moisture can be considered as hot-spots for dryness.
Time evolution of seasonal mean variables for SA_E in JAS (a 20 year running mean has been applied to remove fluctuations). Each column shows the results of a single GCM (black line) and the corresponding downscaled RCM run (red line). In the temperature panel, continuous line is the mean temperature, whereas dashed-dotted lines are minimum and maximum temperature. For the surface fluxes, continuous line is the sensible heat flux (hfss) and dashed line the latent heat flux (hfls). In the precipitation panel the dashed line is the surface runoff. Note that total soil moisture is not directly comparable amongst models because it depends on e.g. the number and depth of soil layers. Runoff and soil moisture data are not available for HadGEM2-ES and EC-Earth, respectively. Finally observations are shown, for some variables, as colored boxes, where the thick line indicates the mean over the record period, and the height of the box measures the interannual variability. For the precipitation variables, daily data are taken from both TRRM and GPCP
GCMs changes in CDD are consistent with e.g. Sillmann et al. (2013) and Orlowsky and Seneviratne (2011), showing patterns similar to the change in precipitation (Fig. 10), with increasing dryness over the Atlas region, south Africa and Mauritania, and a decrease over the Horn of Africa, especially in JFM. This pattern is somehow consistent with the change in soil moisture, although large uncertainty exist in the modeling of land surface processes (Orlowsky and Seneviratne 2011).
As Fig. 15 but for CA_SH in JFM
CCLM results for the change in CDD are somehow similar to the GCMs’ one, especially in JFM, whereas in JAS longer dry spells are projected over South and Central Africa and the fascia around 15°N, consistently with the decrease in precipitation (Fig. 11). However, the change in soil moisture as modelled by CCLM is very different from that of the GCMs. It has to be noted that a direct comparison of total soil moisture between different models is not possible due to the different depth of the models’ soil layers. However, the most striking feature is a change in the sign of the soil moisture anomaly between the GCMs and CCLM over large parts of central Africa, east Africa (except for the Horn of Africa) and part of the region along the Guinea gulf, both in JFM and JAS. This difference is strongly related to the different models’ response and feedback between soil and atmosphere.
As Fig. 15 but for WA_N in JAS
3.3 Land–atmosphere interaction and inter-model variability
Soil moisture is a key variable of the climate system being both a water and energy storage, and impacting the partitioning of the incoming energy in latent and sensible heat fluxes (Seneviratne et al. 2010). For instance, a negative soil moisture anomaly can lead to an increase in surface temperature through a negative anomaly of evapotranspiration (latent heat flux). Koster et al. (2006) and Seneviratne et al. (2006) identified regions of (boreal summer) strong soil moisture/temperature coupling; our results are shown in Fig. 14. In JFM, both GCMs and CCLM results show positive correlation over sub-equatorial central Africa and negative correlation over South Africa. Regions with negative correlation are generally characterized by a soil moisture-limited evapotranspiration regime, whereas positive correlation indicates regions with energy limitation (i.e evaporative fraction is independent of the soil moisture content). At the end of the century, the geographical distribution of the correlation does not vary under either RCP scenario, although a strengthening of the negative correlation is visible in correspondence to areas of anomalous temperature increase, such as South Africa (see Fig. 2). In JAS, GCMs show negative correlation over the Sahel, the Atlas region, East and sub-equatorial Africa, whereas positive correlation is found along the coasts of Guinea, over Cameroon and the Central African Republic, and the Ethiopian Highlands. CCLM is generally in agreement with the driving GCMs, except for the western area of the gulf of Guinea, where a slightly negative correlation is found. At the end of the century, the areas of positive correlation are reduced and those of negative correlation are strengthened. Similarly to JFM, we note the correspondence between areas of strong negative correlation and anomalous temperature increase (Fig. 3).
The many processes contributing to the soil moisture/precipitation coupling are very complex, and somehow still uncertain, as models do not always agree on the sign of the feedback between evapotranspiration and precipitation (Seneviratne et al. 2010). In order to analyze the relationship between soil moisture and precipitation anomalies, and the different models’ response, we focus on three regions where: (a) CCLM and GCM show a consistent and unambiguous precipitation trend (SA_E in JAS, see Table 2); (b) CCLM and the GCMs show a markedly different sign of the precipitation climate change signal (CA_SH in JFM); (c) both CCLM and GCMs show large uncertainties in the sign of the precipitation signal (WA_N in JAS).
Time evolution of several temperature and precipitation related variables are shown for SA_E in JAS in Fig. 15, where values are reported for each single GCM and corresponding CCLM downscaled simulation. We first note that generally CCLM mean temperature is very similar to that of the driving GCM, apart for CNRM-CM5, which is colder than CCLM and the reference observational dataset (CRU) over the present climate (1989–2005). CCLM shows however a reduced temperature range (i.e the difference between maximum and minimum temperature, Tx and Tn, respectively) compared to the GCMs, especially due to overestimation of minimum temperature. Krähenmann et al. (2013) thoroughly investigated the ability of CCLM (driven by ’perfect’ boundary condition, i.e. ERA-Interim) to simulate the temperature range over Africa; over the tropics, result show a moderate warm bias in Tn but a strong warm bias in Tx, whereas the diurnal temperature range was mainly underestimated over the Sahara, due to uncertainty in the cloud cover parameterization (Kothe and Ahrens 2010) and soil thermal conductivity. Here, however, both cloud cover and shortwave radiation (rsds) are simulated similarly by CCLM and the driving GCM. Larger differences exist between CCLM and GCMs’ surface fluxes, namely latent heat flux (hfls) and sensible heat flux (hfss), with the RCM always underestimating hfls. In JAS, SA_E is a generally dry area (with present climate precipitation less than 1 mm/day see Table 2): in these conditions, evapotranspiration (and hfls) is extremely sensitive to soil moisture (soil moisture limited evapotranspiration regime) but its value and variations are too small to impact climate variability (Seneviratne et al. 2010). In addition, over South Africa the correlation between evapotranspiration and temperature is negative (Fig. 14), and hfls decreases as temperature increase under the RCP8.5 scenario, for all GCMs and CCLM runs.
Present climate precipitation is usually overestimated by the GCMs, whereas CCLM results are closer to the observed present values. As a consequence, higher-order precipitation statistics such as CDD and R95ptot (i.e., the ratio of the precipitation sum at wet days with precipitation greater than the reference, 1981–2010, 95th percentile) are also simulated better by CCLM. It is worth noting that, as pointed out by Orlowsky and Seneviratne (2011), regions that are hot-spots for dryness as defined above (i.e. with a consistent decrease in soil moisture and increase in CDD) often display decreased evapotranspiration (hfls), i.e, enhanced soil moisture limitation. This is the case for all simulations (GCMs and CCLM), which eventually show a very similar trend in the precipitation statistics and mean climate change signal (see Table 2).
On the contrary, over CA_SH in JFM CCLM and the GCMs project an opposite trend in precipitation at the end of the century (Fig. 12; Table 2), with all the RCM runs showing a decrease and all GCMs a small increase in rainfall. From Fig. 16 we note that despite differing by around 1 °C, mean temperatures simulated by CCLM and the driving GCMs are usually reasonably similar to the observation, exception being the EC-Earth simulation, noticeably too cold [see also Panitz et al. (2014)]. Larger differences between RCM and GCMs results exist for Tx and Tn, especially for CNRM-CM5 and EC-Earth. Differences in temperatures are related to a different value of the cloud cover, especially for CNRM-CM5 and HadGEM2-EA, whereas solar radiation is usually underestimated by CCLM compared to the GCMs. Also, sensible and latent heat fluxes show different behaviours: in particular hfss as simulated by CCLM tends to increase significantly at the end of the century (especially in the CNRM-CM5 and MPI-ESM-LR runs), a feature that is not shown by the GCMs. As shown in Fig. 14, CA_SH in JFM is the region where the correlation between temperature and evapotranspiration is mainly positive, i.e., not limited by soil moisture (atmosphere limited regime) and hfls increase with temperature, especially for the GCMs. For CCLM, hfls keeps more constant, but at the expenses of soil moisture, which decreases sensibly at the end of the century (Seneviratne et al. 2013).
Present climate precipitation statistics are usually in agreement with the observed values, apart for MPI-ESM-LR which overestimated sensibly the seasonal mean precipitation. However, whereas the GCMs tend to project a slight increase at the end of the century, CCLM tends to become drier with associated increase of the duration of the dry spells (CDD), which is, however, usually better simulated by CCLM in the present climate. An interesting case is MPI-ESM-LR, which overestimates precipitation over the reference period, and also projects a further increase at the end of the century. The contextual increase in the intensity of extreme rainfall (R95ptot), leads to an increase of the runoff. The differences in the hydrological cycle between MPI-ESM-LR and the downscaling RCM REMO were found to be the cause of the opposite precipitation signals over central Africa in recent works by Saeed et al. (2013) and Haensler et al. (2013).
Lastly, we analyze the case of WA_N (Sahel) in JAS, where GCMs and CCLM display a large uncertainty in the projected future precipitation trends (Fig. 12; Table 2), as a results of the different, and sometimes opposite models’ response. First, from Fig. 17 we note that present day mean temperature is simulated very differently amongst GCMs: both MPI-ESM-LR and HadGEM2-ES largely overestimate mean temperature (up to more than 2 °C) whereas CCLM is very close to the observed value. On the contrary, both EC-Earth and its downscaled simulation underestimates it. Finally, CNRM-CM5 reproduces observed temperature satisfactorily, whereas CCLM underestimates it. Large discrepancies exist between GCMs and CCLM on the value of maximum temperature, where, except for EC-Earth, Tx simulated by CCLM is very close to the mean temperature simulated by the GCMs. This may be a result of the different simulation of cloud cover and solar radiation, which are respectively over- and underestimated by CCLM compared to the driving GCM. Striking is the cloud cover value for HadGEM2-ES, which is notable lower than all the other GCMs.
When analyzing the surface fluxes and precipitation statistics, results are even more differentiated: both CNRM-CM5 and EC-Earth show an increase of hfls with temperature, and a relatively constant hfss, accompanied by a very small change in the future precipitation statistics. This may be due to the general overestimation of present climate precipitation, especially for CNRM-CM5, and consequent underestimation of CDD. As in the case of CA_SH in JFM discussed earlier, these GCMs respond as if in atmosphere limited evaoptranspiration regime. On the other hand, MPI-ESM-LR and HadGEM2-ES show a marked decrease of hfls and an increase in hfss, with resulting decrease in mean precipitation (for MPI-ESM-LR starting from the second half of the century) and marked increase in the number of CDD. These GCMs act like in a soil moisture limited evapotranspiration regime, similarly to SA_E in JAS.
CCLM responds usually as in a moisture limited evapotranspiration regime, with decreasing precipitation and hfls, and increase in hfss, with the exception of the CNRM-CM5 driven simulation, which shows an increase in the projected precipitation signal, partially due to the already overestimated rainfall in the present climate.
4 Summary and concluding remarks
In this work we presented the results of the application of the COSMO-CLM Regional Climate Model in the production of climate change projections for the CORDEX-Africa domain. We not only analyzed the climate change projections for mean variables and extreme-events related quantities, but also compared CCLM results to those of the driving GCMs, as discrepancies between the results of RCMs and GCMs have been found in several recent studies (e.g. Mariotti et al. 2011; Laprise et al. 2013; Teichmann et al. 2013; Bouagila and Sushama 2013; Saeed et al. 2013; Coppola et al. 2014; Buontempo et al. 2014).
It is found that the temperature increase projected by CCLM is overall relatively similar (with differences usually smaller than 0.25 °C) to the GCMs’ one, with CCLM usually showing a less intense warming. However, large differences (more than 1 °C) exist locally, especially over South Africa in JFM, and central Africa and the Sahel in JAS, where CCLM climate change signal is warmer than that of the driving GCMs. In addition to the different climate sensitivity between CCLM’s and GCMs’ ensemble mean, uncertainty in the projected warming is also related to the large inter- and intra-model variability, with CCLM’s uncertainty usually smaller than the GCMs’ one. As pointed out by e.g. Buontempo et al. (2014), this is somehow expected when a single RCM is used to downscale a range of different GCMs. Differences between CCLM and the driving GCMs are also found for extreme-event related quantities, such as the spread of the upper end of the maximum temperature probability distribution function and the duration of heat waves, especially over central Africa, where CCLM projects longer heat waves.
Finding a homogeneous consensus between GCMs and the RCM for future projections of precipitation is more problematic, though, as large uncertainties are found in the modelled precipitation changes; this is partly a consequence of the large inter-model (GCMs) variability over some areas (e.g. Sahel). However, over other areas (e.g. Central Africa) the GCMs and CCLM show a consistent but opposite sign in the rainfall trend, with CCLM showing a significant reduction in precipitation at the end of the century. Drought related quantities such as the change in the number of consecutive dry days are relatively similar between GCMs and CCLM. However, striking differences exist in the sign of the soil moisture anomaly, with CCLM showing a constant drying of the soil over large part of central Africa, in contrast with the GCMs. As pointed out by Seneviratne et al. (2010), regions showing a consistent and opposite change in the values of CDD and soil moisture can be regarded as hot-spots for dryness.
The importance of the different models’ response to the land–atmosphere interaction and feedback is further investigated. Over mainly dry regions, such as SA_E in JAS, evapotranspiration is extremely sensitive to soil moisture, but its value is too small to influence climate variability. The correlation between evapotranspiration and temperature is negative, with hfls decreasing as a function of temperature. Despite differences between the values of sensible and latent heat fluxes (also amongst GCMs), CCLM and GCMs show a general similar trend in the projected precipitation statistics (although the values over the present climate are better simulated by the RCM when compared to observations).
CA_SH in JFM is a region where the correlation between temperature and evapotranspiration is positive (atmosphere limited regime). In these conditions, hfls increases with temperature, especially for the GCMs. For CCLM, hfls remains more constant, but at the expenses of soil moisture, which decreases sensibly at the end of the century. As a result of the different hydrological cycle, CCLM and the CGMs show an opposite sign in the precipitation trend.
Finally, over WA_N in JAS both CCLM and GCMs show very large uncertainties in the projected precipitation trend: both CNRM-CM5 and EC-Earth show a decrease of hfls with time, and a very small change in the future precipitation statistics, which may be partly due to the overestimation of present climate precipitation and underestimation of CDD. On the other hand, MPI-ESM-LR and HadGEM2-ES show a marked decrease of hfls and an increase in hfss, with resulting decrease in mean precipitation and marked increase in the number of CDD. CCLM responds usually as in a moisture limited evapotranspiration regime, with decreasing precipitation and hfls, and increase in hfss, with the exception of the CNRM-CM5 driven simulation, which shows an increase in the projected precipitation signal.
As the African climate is strongly influenced by small scale processes, one expects that dynamically downscaling will indeed ‘add value’ to the projections of large-scale GCMs, due to the ability of RCMs to reproduce local features and heterogeneities and, in turn, better simulate higher order statistics and extreme events. However, for some areas the RCM shows behaviors in the precipitation trend that are not simply different from those of the driving GCMs, but even opposite in sign. This feature, not limited to CCLM, has been shown for other RCMs, and it is related to the different parameterization of e.g. the hydrological cycle and, in general, the different response to the soil moisture/precipitation feedbacks.
In addition, given: (a) the large uncertainty also associated with inter-model variability across GCMs, and, (b) the reduced spread in the results when a single RCM is used for downscaling, we strongly emphasize the importance of exploiting fully the CORDEX-Africa multi-GCM/multi-RCM ensemble in order to assess the robustness of the climate change signal and, possibly, to identify and quantify the many sources of uncertainty that still remain.
References
Abiodun BJ, Pal JS, Afiesimama EA, Gutowski WJ, Adedoyin A (2008) Simulation of West African monsoon using RegCM3 Part II: impacts of deforestation and desertification. Theor Appl Climatol 93(3–4):245–261. doi:10.1007/s00704-007-0333-1
Afiesimama Ea, Pal JS, Abiodun BJ, Gutowski WJ, Adedoyin A (2006) Simulation of West African monsoon using the RegCM3. Part I: model validation and interannual variability. Theor Appl Climatol 86(1–4):23–37. doi:10.1007/s00704-005-0202-8
Bouagila B, Sushama L (2013) On the Current and Future Dry Spell Characteristics over Africa. Atmosphere 4(3):272–298. doi:10.3390/atmos4030272
Buontempo C, Mathison C, Jones R, Williams K, Wang C, McSweeney C (2014) An ensemble climate projection for Africa. Clim Dyn. doi:10.1007/s00382-014-2286-2
Coppola E, Giorgi F, Raffaele F, Fuentes-Franco R, Giuliani G, LLopart-Pereira M, Mamgain A, Mariotti L, Diro GT, Torma C (2014) Present and future climatologies in the phase I CREMA experiment. Clim Change 23–38. doi:10.1007/s10584-014-1137-9
Crétat J, Vizy EK, Cook KH (2013) How well are daily intense rainfall events captured by current climate models over Africa? Clim Dyn. doi:10.1007/s00382-013-1796-7
Davies H (1983) Limitations of some common lateral boundary schemes used in regional NWP models. Mon Weather Rev 111:1002–1012. doi:10.1175/1520-0493(1983)111<1002:LOSCLB>2.0.CO;2
Davies HC (1976) A laterul boundary formulation for multi-level prediction models. Q J R Meteorol Soc 102(432):405–418. doi:10.1002/qj.49710243210
Diaconescu EP, Laprise R (2013) Can added value be expected in RCM-simulated large scales? doi:10.1007/s00382-012-1649-9
Diallo I, Sylla MB, Giorgi F, Gaye AT, Camara M (2012) Multimodel GCM-RCM ensemble-based projections of temperature and precipitation over West Africa for the early 21st century. Int J Geophys 2012:1–19. doi:10.1155/2012/972896
Diallo I, Giorgi F, Sukumaran S, Stordal F, Giuliani G (2014) Evaluation of RegCM4 driven by CAM4 over Southern Africa: mean climatology, interannual variability and daily extremes of wet season temperature and precipitation. Theor. Appl. Climatol. doi:10.1007/s00704-014-1260-6
Doms G (2011) A description of the nonhydrostatic regional COSMO model part 1: dynamics and numerics. DWD, Offenbach, Germany.http://www.cosmo-model.org/content/model/documentation/core/default.htm
Dosio A, Panitz HJ, Schubert-Frisius M, Lüthi D (2015) Dynamical downscaling of CMIP5 global circulation models over CORDEX-Africa with COSMO-CLM: evaluation over the present climate and analysis of the added value. Clim Dyn 44:2637–2661. doi:10.1007/s00382-014-2262-x
Druyan LM, Feng J, Cook KH, Xue Y, Fulakeza M, Hagos SM, Konaré A, Moufouma-Okia W, Rowell DP, Vizy EK, Ibrah SS (2010) The WAMME regional model intercomparison study. Clim Dyn 35(1):175–192. doi:10.1007/s00382-009-0676-7
Endris HS, Omondi P, Jain S, Lennard C, Hewitson B, Chang’a L, Awange JL, Dosio A, Ketiem P, Nikulin G, Panitz HJ, Büchner M, Stordal F, Tazalika L (2013) Assessment of the performance of CORDEX regional climate models in simulating East African rainfall. J Clim 26(21):8453–8475. doi:10.1175/JCLI-D-12-00708.1
Gbobaniyi E, Sarr A, Sylla MB, Diallo I, Lennard C, Dosio A, Dhiédiou A, Kamga A, Klutse NAB, Hewitson B, Nikulin G, Lamptey B (2014) Climatology, annual cycle and interannual variability of precipitation and temperature in CORDEX simulations over West Africa. Int J Climatol 34(7):2241–2257. doi:10.1002/joc.3834
Giorgi F, Jones C, Asrar G (2009) Addressing climate information needs at the regional level: the CORDEX framework. Organ (WMO) Bull 58(July):175–183
Giorgi F, Coppola E, Raffaele F, Diro GT, Fuentes-Franco R, Giuliani G, Mamgain A, Llopart MP, Mariotti L, Torma C (2014) Changes in extremes and hydroclimatic regimes in the CREMA ensemble projections. Clim Change 39–51. doi:10.1007/s10584-014-1117-0
Haensler A, Saeed F, Jacob D (2013) Assessing the robustness of projected precipitation changes over central Africa on the basis of a multitude of global and regional climate projections. Clim Change 121(2):349–363. doi:10.1007/s10584-013-0863-8
Heise E, Lange M, Ritter B, Schrodin R (2003) Improvement and validation of the multilayer soil model. COSMO Newsl 3:198–203
Hong SY, Kanamitsu M (2014) Dynamical downscaling: fundamental issues from an NWP point of view and recommendations. Asia-Pac J Atmos Sci 50(1):83–104. doi:10.1007/s13143-014-0029-2
(2007) Climate change 2007: the physical science basis: contribution of Working Group I to the fourth assessment report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge
Jenkins GS, Gaye AT, Sylla B (2005) Late 20th century attribution of drying trends in the Sahel from the Regional Climate Model (RegCM3). Geophys Res Lett 32(22):L22,705. doi:10.1029/2005GL024225
Kalognomou EA, Lennard C, Shongwe M, Pinto I, Favre A, Kent M, Hewitson B, Dosio A, Nikulin G, Panitz HJ, Büchner M (2013) A diagnostic evaluation of precipitation in CORDEX models over Southern Africa. J Clim 26(23):9477–9506. doi:10.1175/JCLI-D-12-00703.1
Kim J, Kim T, Arritt R, Miller N (2002) Impacts of increased atmospheric CO2 on the hydroclimate of the Western United States. J Clim 15:1926–1942
Kim J, Waliser DE, Mattmann CA, Goodale CE, Hart AF, Zimdars PA, Crichton DJ, Jones C, Nikulin G, Hewitson B, Jack C, Lennard C, Favre A (2013) Evaluation of the CORDEX-Africa multi-RCM hindcast: systematic model errors. Clim Dyn 42(5–6):1189–1202. doi:10.1007/s00382-013-1751-7
Koster R, Sud Y, Guo Z, Dirmeyer PA, Bonan G, Chan E, Cox P, Davies H, Gordon CT, Kanae S, Kowalczyk E, Lawrence D, Liu P, Lu CH, Malyshev S, Mcavaney B, Mitchell K, Mocko D, Oki T, Oleson KW, Pitman A, Sud YC, Taylor CM, Verseghy D, Vasic R, Xue Y, Yamada T (2006) GLACE: the global land-atmosphere coupling experiment. Part I: overview. J Hydrometeorol 7:590–610
Kothe S, Ahrens B (2010) On the radiation budget in regional climate simulations for West Africa. J Geophys Res 115(D23). doi:10.1029/2010JD014331
Krähenmann S, Kothe S, Panitz HJ, Ahrens B (2013) Evaluation of daily maximum and minimum 2-m temperatures as simulated with the Regional Climate Model COSMO-CLM over Africa. Meteorol Z 22(3):297–316. doi:10.1127/0941-2948/2013/0468
Laprise R, Hernández-Díaz L, Tete K, Sushama L, Šeparović L, Martynov A, Winger K, Valin M (2013) Climate projections over CORDEX Africa domain using the fifth-generation Canadian Regional Climate Model (CRCM5). Clim Dyn. doi:10.1007/s00382-012-1651-2
Lawrence PJ, Chase TN (2007) Representing a new MODIS consistent land surface in the Community Land Model (CLM 3.0). J Geophys Res 112(G1):G01,023. doi:10.1029/2006JG000168
Lee JW, Hong SY (2013) Potential for added value to downscaled climate extremes over Korea by increased resolution of a regional climate model. Theor Appl Climatol. doi:10.1007/s00704-013-1034-6
Lee JW, Hong SY, Chang EC, Suh MS, Kang HS (2014) Assessment of future climate change over East Asia due to the RCP scenarios downscaled by GRIMs-RMP. Clim Dyn 42(3–4):733–747. doi:10.1007/s00382-013-1841-6
Lott F, Miller MJ (1997) A new subgrid-scale orographic drag parametrization: its formulation and testing. Q J R Meteorol Soc 123(537):101–127. doi:10.1002/qj.49712353704
Mariotti L, Coppola E, Sylla MB, Giorgi F, Piani C (2011) Regional climate model simulation of projected 21st century climate change over an all-Africa domain: comparison analysis of nested and driving model results. J Geophys Res 116(D15):D15,111. doi:10.1029/2010JD015068
Mariotti L, Diallo I, Coppola E, Giorgi F (2014) Seasonal and intraseasonal changes of African monsoon climates in 21st century CORDEX projections. Clim Change 125:53–65. doi:10.1007/s10584-014-1097-0
Mellor GL, Yamada T (1982) Development of a turbulence closure model for geophysical fluid problems. Rev Geophys 20(4):851–875. doi:10.1029/RG020i004p00851
Mironov D, Raschendorfer M (2001) Evaluation of empirical parameters of the new LM surface-layer parameterization scheme: results from numerical experiments including soil moisture analysis. COSMO technical report 1, DWD, Offenbach, Germany
Moss RH, Edmonds JA, Hibbard KA, Manning MR, Rose SK, van Vuuren DP, Carter TR, Emori S, Kainuma M, Kram T, Meehl GA, Mitchell JFB, Nakicenovic N, Riahi K, Smith SJ, Stouffer RJ, Thomson AM, Weyant JP, Wilbanks TJ (2010) The next generation of scenarios for climate change research and assessment. Nature 463(7282):747–56. doi:10.1038/nature08823
Nikulin G, Jones C, Giorgi F, Asrar G, Büchner M, Cerezo-Mota R, Christensen OBs, Déqué M, Fernandez J, Hänsler A, van Meijgaard E, Samuelsson P, Sylla MB, Sushama L (2012) Precipitation climatology in an ensemble of CORDEX-Africa regional climate simulations. J Clim 25(18):6057–6078. doi:10.1175/JCLI-D-11-00375.1
Orlowsky B, Seneviratne SI (2011) Global changes in extreme events: regional and seasonal dimension. Clim Change 110(3–4):669–696. doi:10.1007/s10584-011-0122-9
Paeth H, Mannig B (2012) On the added value of regional climate modeling in climate change assessment. Clim Dyn 41(3–4):1057–1066. doi:10.1007/s00382-012-1517-7
Paeth H, Hall NM, Gaertner MA, Alonso MD, Moumouni S, Polcher J, Ruti PM, Fink AH, Gosset M, Lebel T, Gaye AT, Rowell DP, Moufouma-Okia W, Jacob D, Rockel B, Giorgi F, Rummukainen M (2011) Progress in regional downscaling of west African precipitation. Atmos Sci Lett 12(1):75–82. doi:10.1002/asl.306
Panitz HJ, Dosio A, Büchner M, Lüthi D, Keuler K (2014) COSMO-CLM (CCLM) climate simulations over CORDEX-Africa domain: analysis of the ERA-Interim driven simulations at 0.44 and 0.22 resolution. Clim Dyn 42(11–12):3015–3038. doi:10.1007/s00382-013-1834-5
Raschendorfer M (2001) The new turbulence parameterization of LM. COSMO Newsl 1:90–98
Redelsperger JL, Thorncroft CD, Diedhiou A, Lebel T, Parker DJ, Polcher J (2006) African Monsoon multidisciplinary analysis: an international research project and field campaign. Bull Am Meteorol Soc 87(12):1739–1746. doi:10.1175/BAMS-87-12-1739
Ritter B, Geleyn JF (1992) A comprehensive radiation scheme for numerical weather prediction models with potential applications in climate simulations. Mon Weather Rev 120(2):303–325
Ruti PM, Williams JE, Hourdin F, Guichard F, Boone A, Van Velthoven P, Favot F, Musat I, Rummukainen M, Domínguez M, Gaertner MA, Lafore JP, Losada T, Rodriguez de Fonseca MB, Polcher J, Giorgi F, Xue Y, Bouarar I, Law K, Josse B, Barret B, Yang X, Mari C, Traore aK (2011) The West African climate system: a review of the AMMA model inter-comparison initiatives. Atmos Sci Lett 12(1):116–122. doi:10.1002/asl.305
Saeed F, Haensler A, Weber T, Hagemann S, Jacob D (2013) Representation of extreme precipitation events leading to opposite climate change signals over the Congo Basin. Atmosphere 4(3):254–271. doi:10.3390/atmos4030254
Schrodin R, Heise E (2001) The multi-mayer version of the DWD soil model TERRA-LM. COSMO technical report 2, DWD, Offenbach, Germany
Schrodin R, Heise E (2002) A new multi-layer soil-model. COSMO Newsl 2:139–151
Schulz JP (2008) Introducing sub-grid scale orographic effects in the COSMO model. COSMO Newsl 9:29–36
Seifert A, Beheng KD (2001) A double-moment parameterization for simulating autoconversion, accretion and selfcollection. Atmos Res 59–60:265–281
Seneviratne SI, Lüthi D, Litschi M, Schär C (2006) Land-atmosphere coupling and climate change in Europe. Nature 443(7108):205–9. doi:10.1038/nature05095
Seneviratne SI, Corti T, Davin EL, Hirschi M, Jaeger EB, Lehner I, Orlowsky B, Teuling AJ (2010) Investigating soil moistureclimate interactions in a changing climate: a review. Earth-Sci Rev 99(3–4):125–161. doi:10.1016/j.earscirev.2010.02.004
Seneviratne SI, Wilhelm M, Stanelle T, Van Den Hurk B, Hagemann S, Berg A, Cheruy F, Higgins ME, Meier A, Brovkin V, Claussen M, Ducharne A, Dufresne JL, Findell KL, Ghattas J, Lawrence DM, Malyshev S, Rummukainen M, Smith B (2013) Impact of soil moisture-climate feedbacks on CMIP5 projections: first results from the GLACE-CMIP5 experiment. Geophys Res Lett 40:5212–5217. doi:10.1002/grl.50956
Sillmann J, Kharin VV, Zwiers FW, Zhang X, Bronaugh D (2013) Climate extremes indices in the CMIP5 multimodel ensemble: Part 2. Future climate projections. J Geophys Res Atmos 118(6):2473–2493. doi:10.1002/jgrd.50188
Sylla MB, Giorgi F, Stordal F (2012) Large-scale origins of rainfall and temperature bias in high-resolution simulations over southern Africa. Clim Res. doi:10.3354/cr01044
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93(4):485–498. doi:10.1175/BAMS-D-11-00094.1
Teichmann C, Eggert B, Elizalde A, Haensler A, Jacob D, Kumar P, Moseley C, Pfeifer S, Rechid D, Remedio A, Ries H, Petersen J, Preuschmann S, Raub T, Saeed F, Sieck K, Weber T (2013) How does a regional climate model modify the projected climate change signal of the driving GCM: a study over different CORDEX regions using REMO. Atmosphere 4(2):214–236. doi:10.3390/atmos4020214
Tiedtke M (1989) A comprehensive mass flux scheme for cumulus parameterization in large-scale models. Mon Wea Rev 117(8):1779–1800
Vuuren DP, Edmonds J, Kainuma M, Riahi K, Thomson A, Hibbard K, Hurtt GC, Kram T, Krey V, Lamarque JF, Masui T, Meinshausen M, Nakicenovic N, Smith SJ, Rose SK (2011) The representative concentration pathways: an overview. Clim Change 109(1–2):5–31. doi:10.1007/s10584-011-0148-z
Wicker LJ, Skamarock WC (2002) Time-splitting methods for elastic models using forward time schemes. Mon Wea Rev 130(8):2088–2097. doi:10.1175/1520-0493(2002)130<2088:TSM>2.0.CO;2
Xue Y, Sales F, Lau WKM, Boone A, Feng J, Dirmeyer P, Guo Z, Kim KM, Kitoh A, Kumar V, Poccard-Leclercq I, Mahowald N, Moufouma-Okia W, Pegion P, Rowell DP, Schemm J, Schubert SD, Sealy A, Thiaw WM, Vintzileos A, Williams SF, Wu MLC (2010) Intercomparison and analyses of the climatology of the West African Monsoon in the West African Monsoon Modeling and Evaluation project (WAMME) first model intercomparison experiment. Clim Dyn 35(1):3–27. doi:10.1007/s00382-010-0778-2
Acknowledgments
We acknowledge the World Climate Research Programme’s Working Group on Coupled Modelling, which is responsible for CMIP, and we thank the climate modeling groups for producing and making available their model output. For CMIP the US Department of Energy’s Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals. Computational resources were made available by the German Climate Computing Centre (DKRZ) through support from the German Federal Ministry of Education and Research (BMBF).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Dosio, A., Panitz, HJ. Climate change projections for CORDEX-Africa with COSMO-CLM regional climate model and differences with the driving global climate models. Clim Dyn 46, 1599–1625 (2016). https://doi.org/10.1007/s00382-015-2664-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-015-2664-4